Wykład nr 2b

Metody komputerowe w 

inżynierii materiałowej

Dr inż. Maciej Sułowski

A2, pok. 54H

Tel.:26-27

sulek@agh.edu.pl

Wykład nr 2b

Metody rozwiązywania układów 
równań nieliniowych

• Metody rozwiązywania układów równań 

linowych można podzielić na:

– kolejnych przybliżeń 
– bisekcji (połowienia przedziału)
– cięciw 
– metodę stycznych (Newtona)

Wykład nr 2b

Metody kolejnych przybliżeń

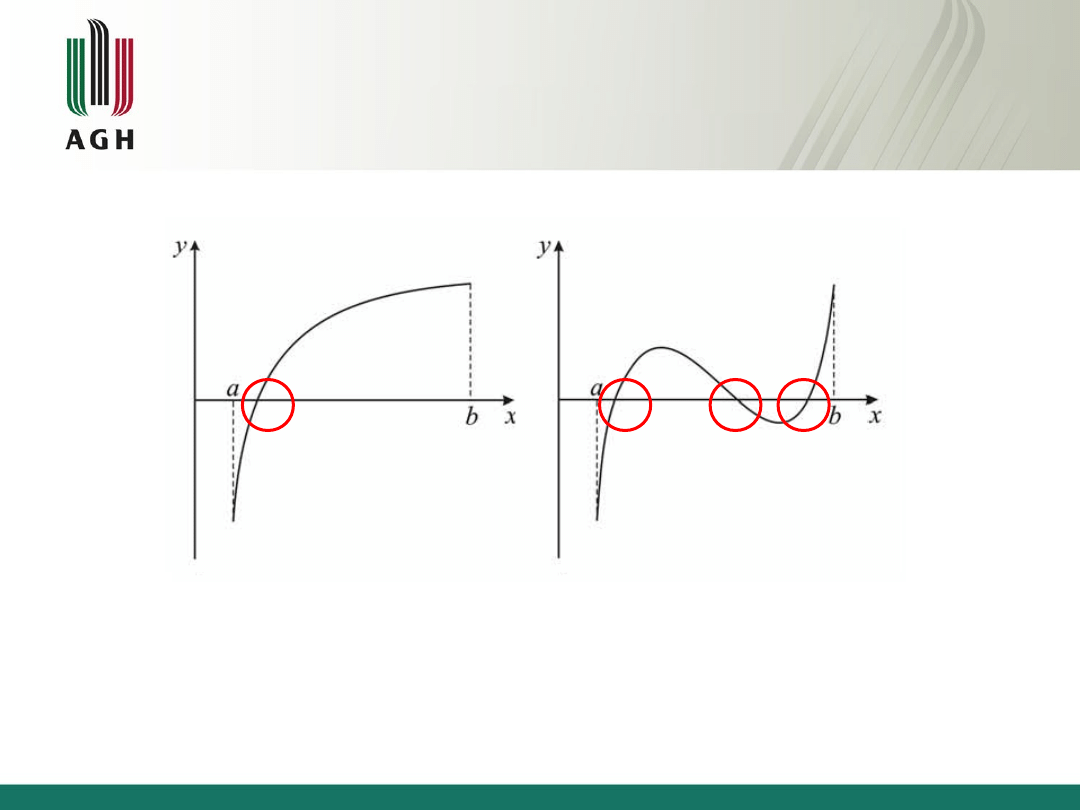
Twierdzenie 1 (Bolzano-Cauchy’ego)
• Jeżeli funkcja F(x) jest ciągła w przedziale 

domkniętym [a,b] i F(a)⋅F(b) < 0, to między 
punktami a i b znajduje się co najmniej jeden 
pierwiastek równania F(x) = 0.

Twierdzenie 2
• Jeżeli w przedziale [a, b] spełnione są założenia 

twierdzenia 1 i dodatkowo sgn F ′(x) = const dla 
x



[a,b], to przedział ten jest przedziałem izolacji 

pierwiastka równania F(x) = 0.

Wykład nr 2b

Metody kolejnych przybliżeń

Wykład nr 2b

• Przykład obliczeniowy

Metody kolejnych przybliżeń

Wykład nr 2b

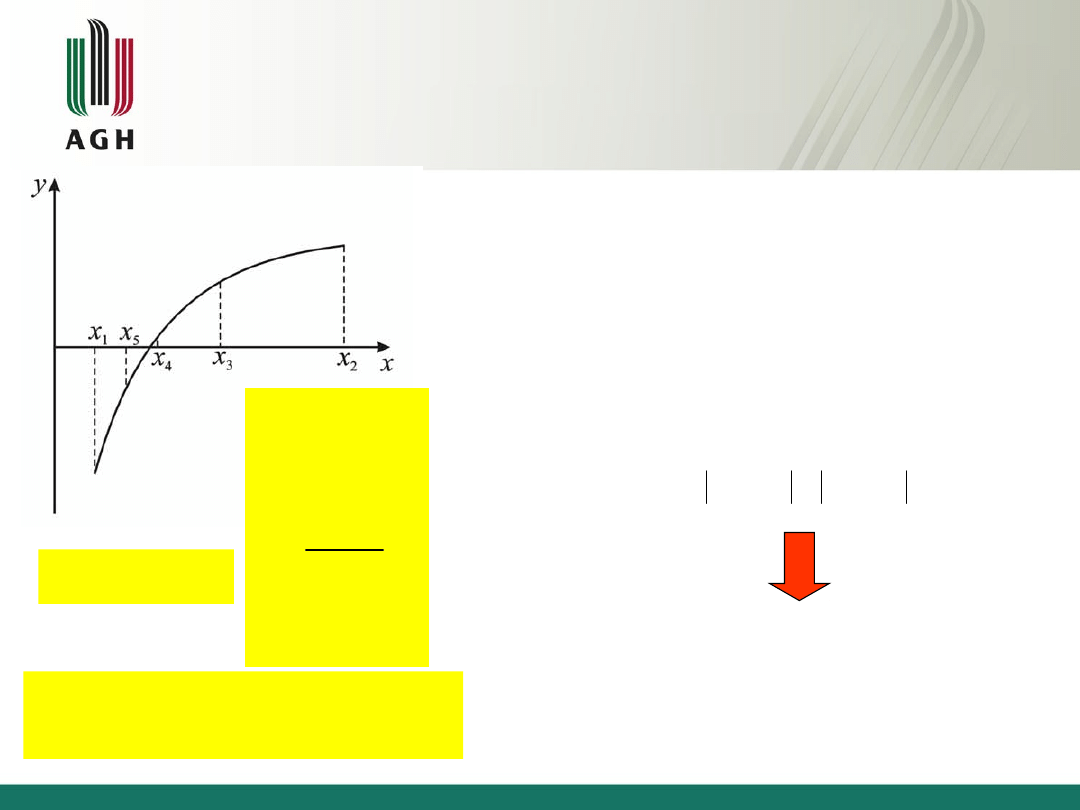
• Niech [a,b] będzie przedziałem izolacji pierwiastka 

równania F(x) = 0.

• Jako pierwsze dwa wyrazy ciągu przybliżeń 

przyjmuje się: x

1

=a x

2

 =b

• Kolejne przybliżenia wynikają ze wzoru:

• k dobierane, aby:

Metoda bisekcji









2

2

,

1

2

1













i

i

k

x

x

x

k

i

i

   

0

*

1

1













i

i

k

i

i

i

x

f

x

f

x

x

x

x

Wykład nr 2b

Metoda bisekcji

Ponieważ kolejne 
przybliżenia znajdują 
się każdorazowo w
przedziałach izolacji, 
oraz

1

1











i

i

i

i

x

x

x

x

metoda jest zbieżna

Algorytm































)

(

)

(

2

...,

,

2

,

1

1

1

2

1

2

1

x

f

y

x

f

y

x

x

x

m

i

b

x

a

x

Jeżeli y*y

1

>0 to x

1

 = x, 

W przeciwnym wypadku x

2

 = x

Wykład nr 2b

• Przykład obliczeniowy

Metoda bisekcji 

Wykład nr 2b

Metoda stycznych (Newtona)

•Jedna z najczęściej stosowanych metod 

rozwiązywania równań nieliniowych

•Pozwala obliczyć przybliżoną wartość pierwiastka 

równania nieliniowego (f(x)=0), przy założeniu, 
że w przedziale [a,b], w którym leży 
pierwiastek, funkcja f(x) ma na krańcach 
różne znaki oraz że pierwsza i druga 
pochodna funkcji mają stały znak  

Wykład nr 2b



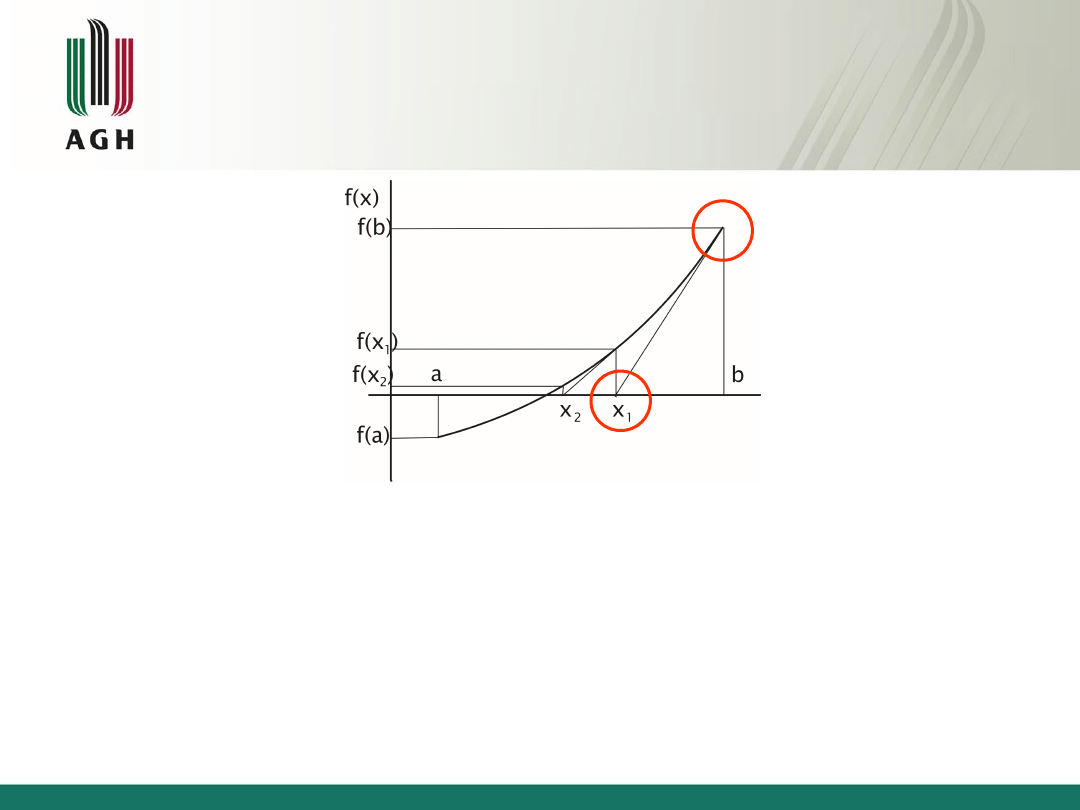
W  metodzie  Newtona  z  końca  przedziału,  w  którym 
funkcja  f(x)  ma  ten  sam  znak  co  f’’(x)  prowadzimy 
styczną  do  wykresu  funkcji  y=f(x).  Punkt  przecięcia 
osi  odciętych,  x

1

  jest  pierwszym  przybliżeniem 

szukanego pierwiastka równania. 

Metoda stycznych (Newtona)

Wykład nr 2b

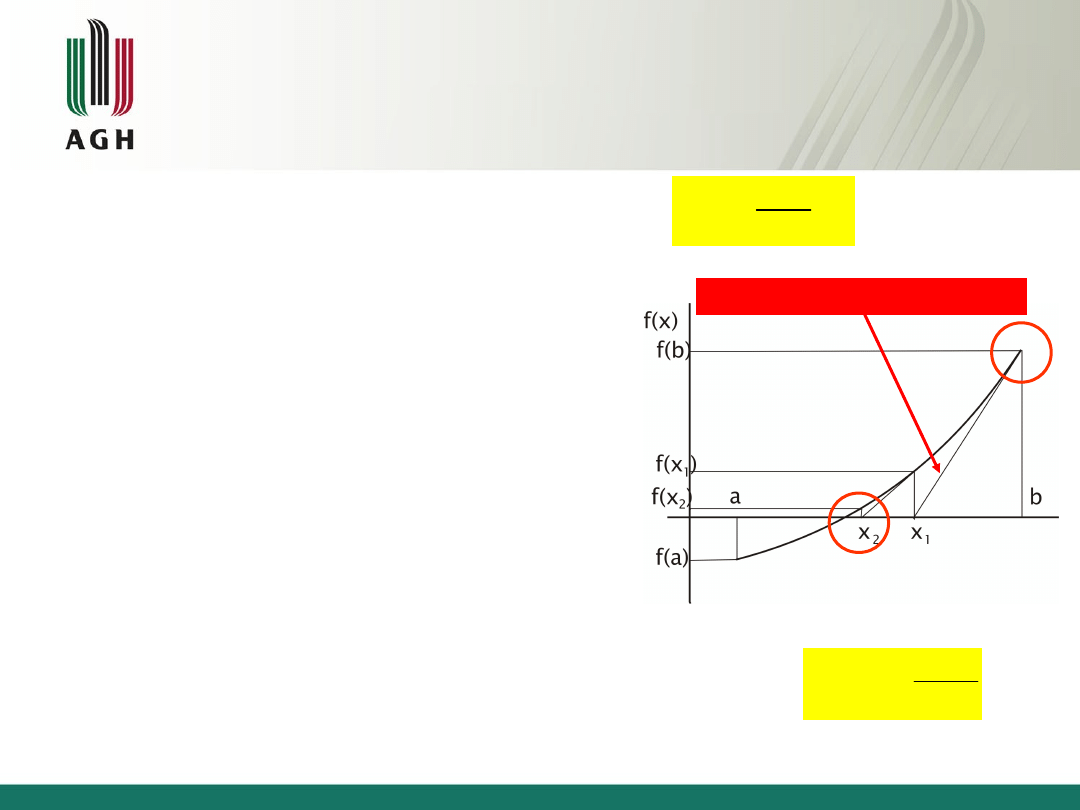
• Nietrudno zauważyć, że: 

 

0

)

(

'

1







b

f

b

f

b

x

•

Gdy otrzymane przybliżenie 
jest za mało dokładne 
(f(x

1

)>) z punktu o 

współrzędnych (x

1

, f(x

1

)) 

operację powtarzamy n razy, 
dopóki wartość funkcji w 
punkcie x

n

 nie będzie 

mniejsza od założonej 
dokładności . 

 

 

n

n

n

n

x

f

x

f

x

x

'

1







Metoda stycznych (Newtona)

• Wzór rekurencyjny opisujący kolejne 

wyrazy ciągu przybliżeń ma postać

)

(

*

)

(

'

)

(

1

1

1













n

n

n

x

x

x

f

x

f

y

Wykład nr 2b

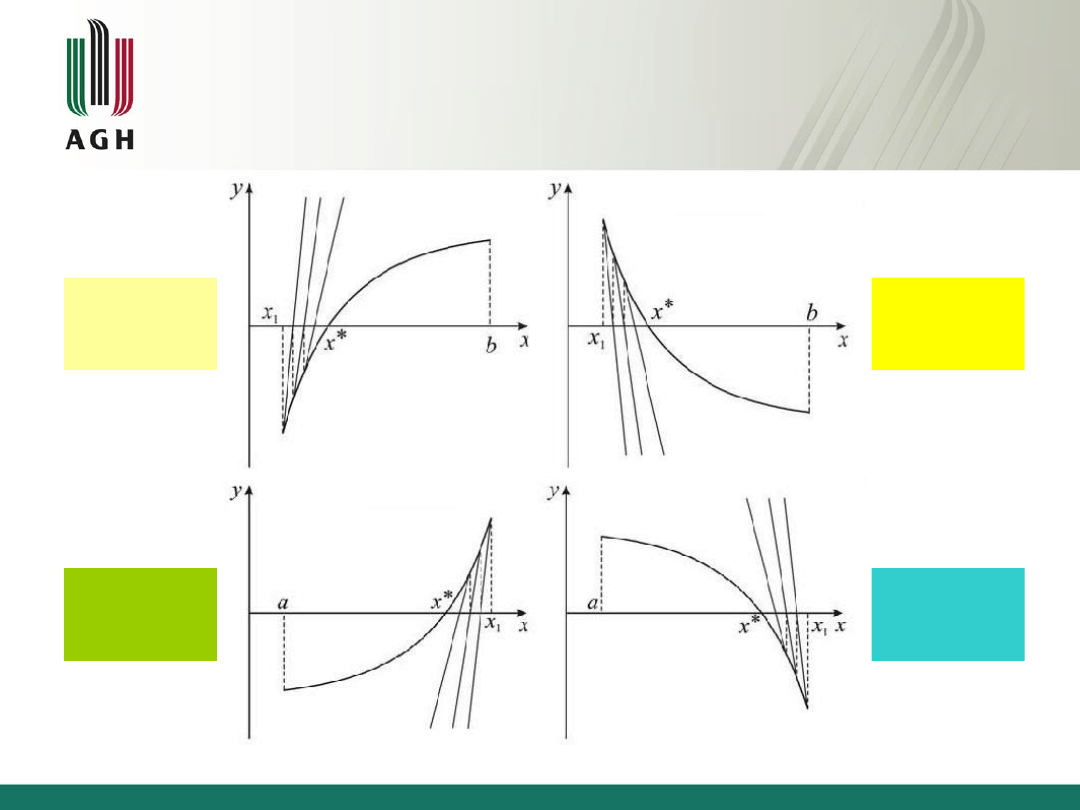
Metoda stycznych (Newtona)

f’(x)>0

f’’(x)<0

f’(x)<0

f’’(x)>0

f’(x)>0

f’’(x)>0

f’(x)<0

f’’(x)<0

Wykład nr 2b

• Ciąg przybliżeń jest ciągiem malejącym i zbieżnym.
• Operację  obliczania  rozwiązania  równania  f(x)=0 

można  stosować  dla  dowolnego  punktu  startowego 
x

o

[a,b], 

jeśli 

styczne 

do 

krzywej 

y=f(x) 

poprowadzone  z  punktów  granicznych  przecinają  oś 
odciętych wewnątrz przedziału [a,b]. 





 - założona dokładność rozwiązania

Metoda stycznych (Newtona)

Wykład nr 2b

Układ n równań nieliniowych































0

,...,

,

.

..........

..........

..........

0

,...,

,

0

,...,

,

2

1

2

1

2

2

1

1

n

n

n

n

x

x

x

f

x

x

x

f

x

x

x

f

   

*

*

1

*

*

1

n

n

n

n

x

f

x

J

x

x









Metoda stycznych (Newtona)

gdzie: x

n

* i x

n+1

* stanowią n i 

n+1 przybliżenie zmiennej x*, 
J(x

n

*) jest jakobianem funkcji 

f(x*) a wyrazy macierzy 
jakobianowej, J(x*) są 
określone równaniem:

 

 





 

k

j

jk

x

x

f

x

J







*

*

Rozwiązanie ogólne

Wykład nr 2b

• Macierz Jacobiego – macierz zbudowana z 

pochodnych cząstkowych (pierwszego rzędu) 
funkcji, której składowymi są funkcje rzeczywiste

• Jakobian – wyznacznik macierzy Jakobiego 

Metoda stycznych (Newtona)

2

2

2

1

:

)

,

(









f

f

f

1

)

,

(

)

,

(

2

3

2

1









xy

y

x

f

xy

x

y

x

f

Przykład: Niech dane 
będzie przekształcenie

Jego jakobian wynosi



 











3

2

3

3

2

2

3

3

2

3

2

2

2

1

1

2

2

3

2

3

2

1

1

det

xy

x

xy

xy

x

x

y

xy

y

x

y

xy

x

xy

y

xy

x

x

xy

x

y

f

x

f

y

f

x

f

J

f





























































Wykład nr 2b

Rozwiązanie układu równań

i

n

n

a

x

x





1

Metoda stycznych (Newtona)































0

,...,

,

.

..........

..........

..........

0

,...,

,

0

,...,

,

2

1

2

1

2

2

1

1

n

n

n

n

x

x

x

f

x

x

x

f

x

x

x

f

polega na obliczaniu kolejnych 
przybliżeń rozwiązania układu 
zgodnie ze wzorem:

Wykład nr 2b

• wartość kolejnej poprawki a

i

 dowolnej zmiennej jest 

obliczana przez rozwiązanie układu dwu równań 
liniowych, w których występują wartości funkcji f

1

, f

2

 i 

ich pochodnych w punkcie o współrzędnych x

n

, y

n

.:

Metoda stycznych (Newtona)



































































































































n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

x

x

x

f

x

x

x

x

f

a

x

x

x

x

f

a

x

x

x

x

f

a

x

x

x

f

x

x

x

x

f

a

x

x

x

x

f

a

x

x

x

x

f

a

x

x

x

f

x

x

x

x

f

a

x

x

x

x

f

a

x

x

x

x

f

a

,...,

,

,...,

,

...

,...,

,

,...,

,

..

..........

..........

..........

..........

..........

..........

..........

..........

..........

..........

..........

..........

,...,

,

,...,

,

...

,...,

,

,...,

,

,...,

,

,...,

,

...

,...,

,

,...,

,

2

1

2

1

2

2

1

2

1

2

1

1

2

1

2

2

1

2

2

2

1

2

2

1

2

1

2

1

2

1

1

2

1

1

2

2

1

1

2

1

2

1

1

1

Wykład nr 2b

•W każdej iteracji musimy więc obliczyć n

2

 elementów 

f/x i rozwiązać układ liniowy rzędu n definiujący 

wartości poprawek a. 

•Obliczanie rozwiązania układu równań nieliniowych jest 

prowadzone dopóki wartości poprawek a

i

 nie osiągną 

wartości mniejszych od założonej dokładności. 

•Metoda Newtona jest lokalnie zbieżna, to znaczy ciąg 

wyrazów jest dostatecznie bliski rozwiązaniu układu 
równań. 

•Jak widać, rozwiązanie układu równań nieliniowych 

sprowadza się do rozwiązywania układów równań 
liniowych.

Metoda stycznych (Newtona)

Wykład nr 2b

•W modelowaniu procesów występujących w inżynierii 

materiałowej rozwiązywanie układów równań liniowych 

i nieliniowych jest często stosowane

•Programowanie rozwiązań układów równań nieliniowych 

jest trudne

•Do rozwiązywania układów równań liniowych można 

wykorzystać MS Excel, narzędzie Solver 

Metoda stycznych (Newtona)

Wykład nr 2b

Praktyczne przykłady 
wykorzystania Solvera

• Rozwiązanie układu równań liniowych
• Rozwiązanie równania nieliniowego
• Rozwiązanie układu równań nieliniowych