Wykład nr 2

Metody komputerowe w

inżynierii materiałowej

Dr inż. Maciej Sułowski

A2, pok. 54H

Tel.:26-27

[e-mail]

Wykład nr 2

• Dwie macierze A=[a

ij

]

mxn

i B=[b

ij

]

pxq

nazywamy równymi, gdy mają ten sam
wymiar –p=m i q=n oraz odpowiednie
elementy równe, tj. b

ij

=a

ij

• Sumą macierzy A=[a

ij

]

mxn

i B=[b

ij

]

mxn

jest

macierz C=[a

ij

+b

ij

]

mxn

• A+B=C
• A+B=B+A
• Działanie odwrotne – odejmowanie

macierzy

• C=A-B

Działania na macierzach

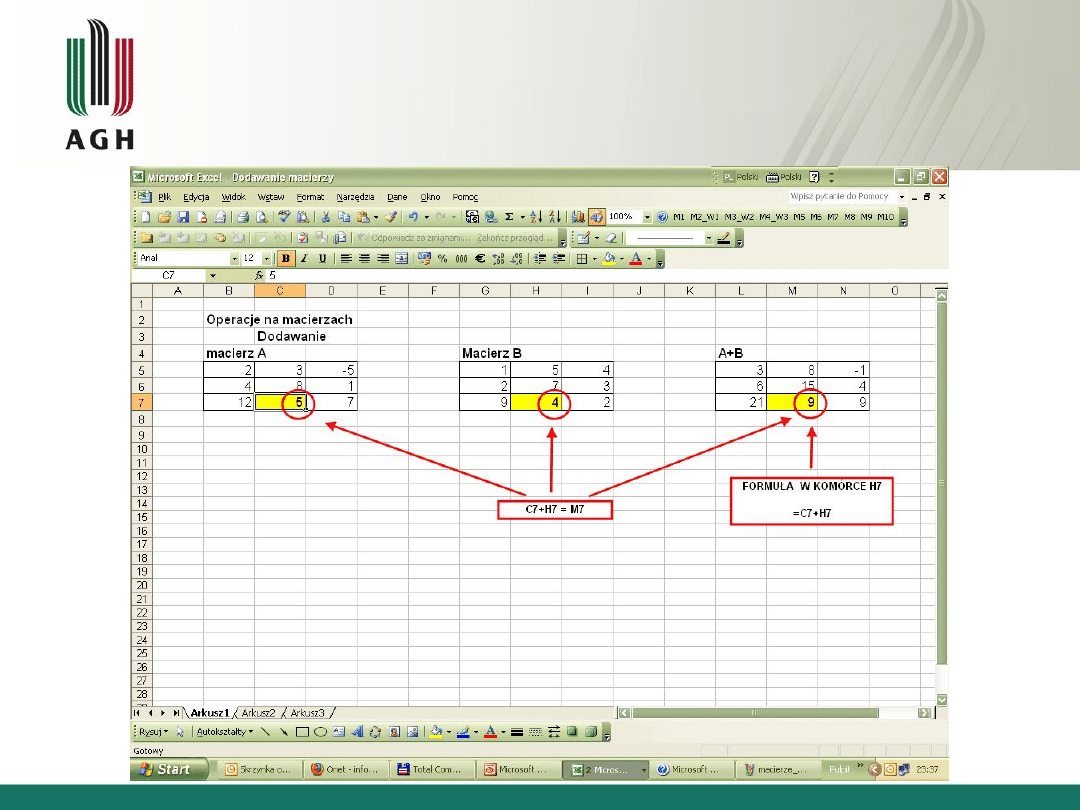
Wykład nr 2

Działania na macierzach

Wykład nr 2

Działania na macierzach

• Mnożyć można tylko takie macierze, z których

pierwsza ma tyle kolumn, ile druga wierszy.

Wymiar macierzy:mxn

• Mnożenie macierzy C=AB
• A=[a

ik

]

mxp

, B=[b

kj

]

pxn

• Macierz kwadratowa m=n
• Macierz kolumnowa n=1
• Macierz wierszowa m = 1

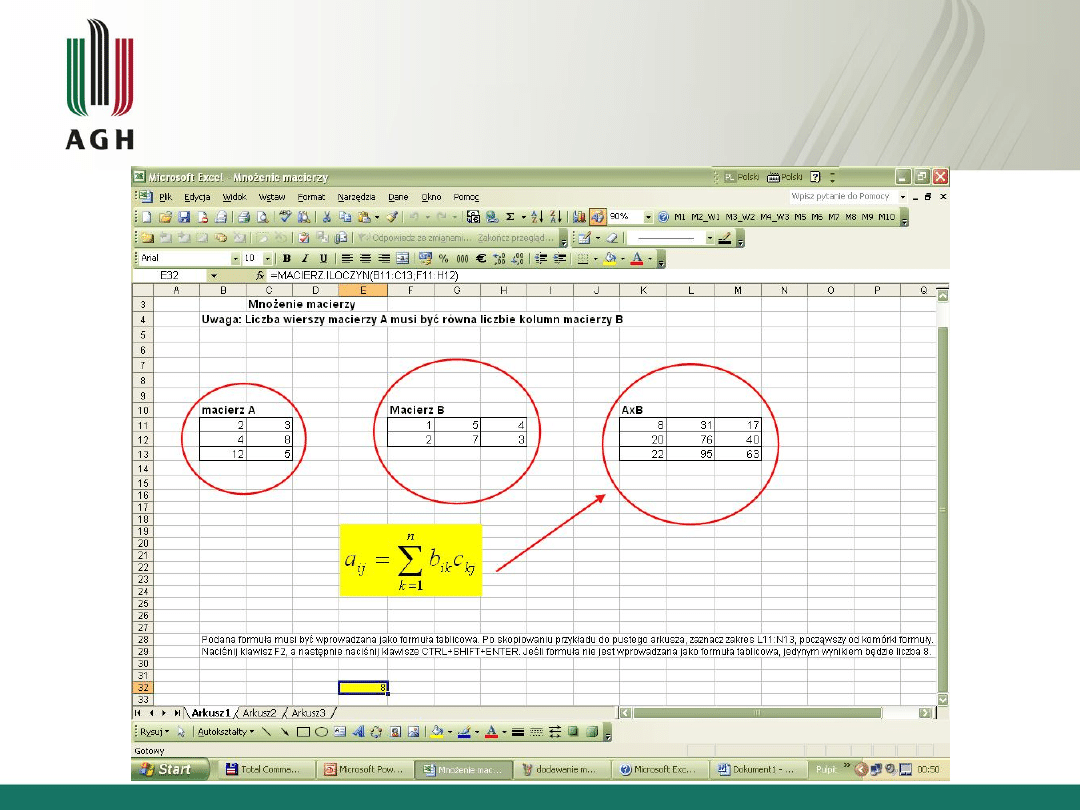
Wykład nr 2

Działania na macierzach

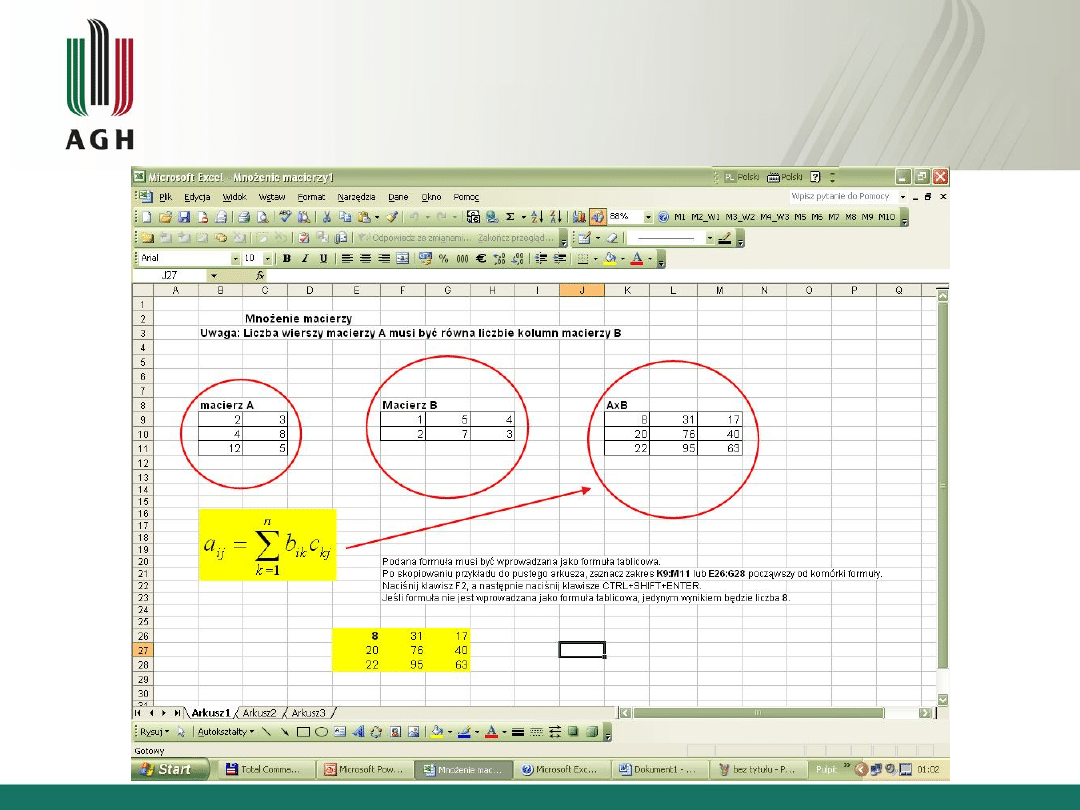
Wykład nr 2

Działania na macierzach

Wykład nr 2

Działania na macierzach

• Transpozycja macierzy

– A

T

powstaje przez

przestawienie w macierzy A jej wierszy w
miejsce kolumn

• Jeśli A ma wymiar mxn to A

T

=B=b[j,i] ma

wymiar nxm oraz b

ji

=a

ij

• Własności transpozycji:
• (A+B)

T

=A

T

+B

T

• (AB)

T

=B

T

A

T

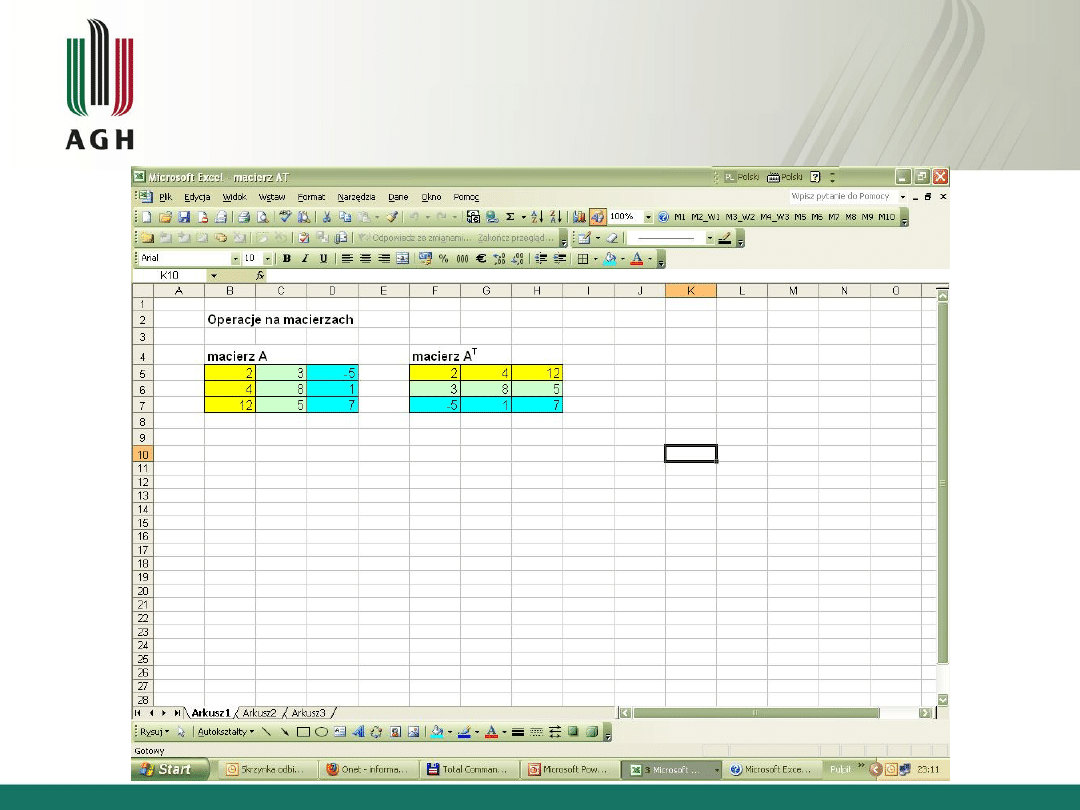
Wykład nr 2

Działania na macierzach

Wykład nr 2

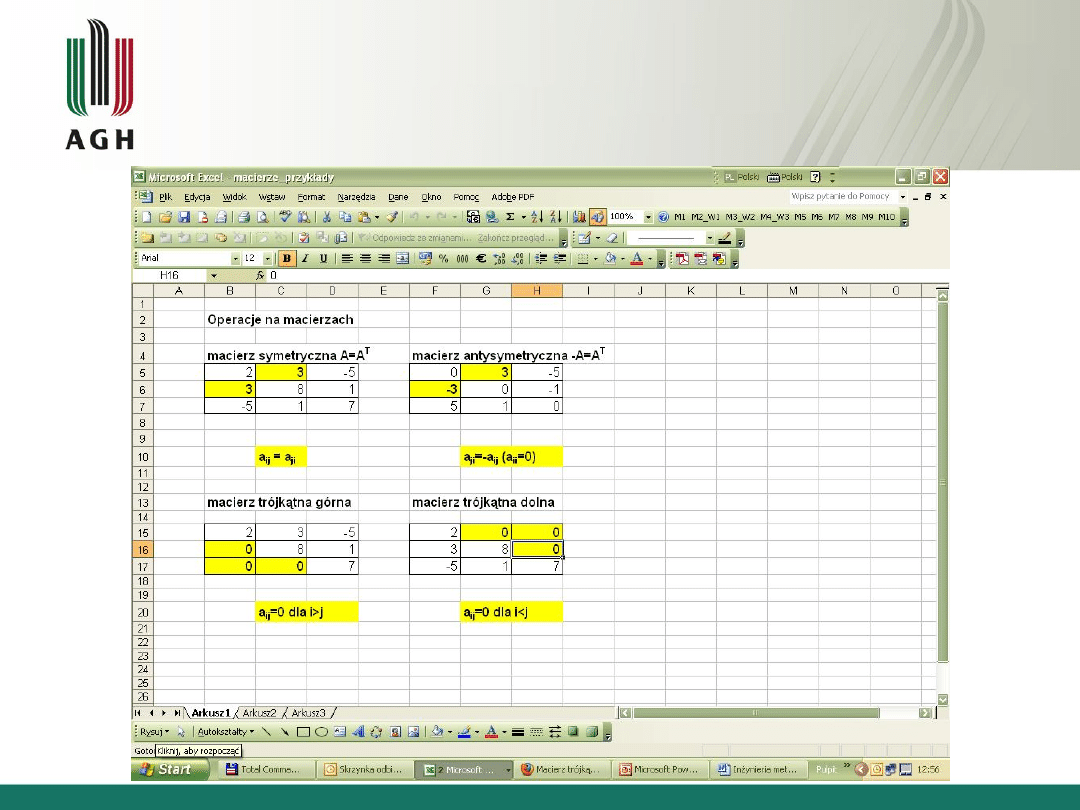
Szczególne przypadki macierzy
kwadratowych

• Macierz symetryczna a

ij

=a

ji,

A

T

=A

• Macierz antysymetryczna a

ji

=-a

ij

(a

ii

=0),

A

T

=-A

• Macierz trójkątna dolna gdy a

ij

=0 dla j>i

• Macierz trójkątna górna gdy a

ij

=0 dla i<j

Wykład nr 2

Szczególne przypadki macierzy
kwadratowych

Wykład nr 2

Szczególne przypadki macierzy
kwadratowych

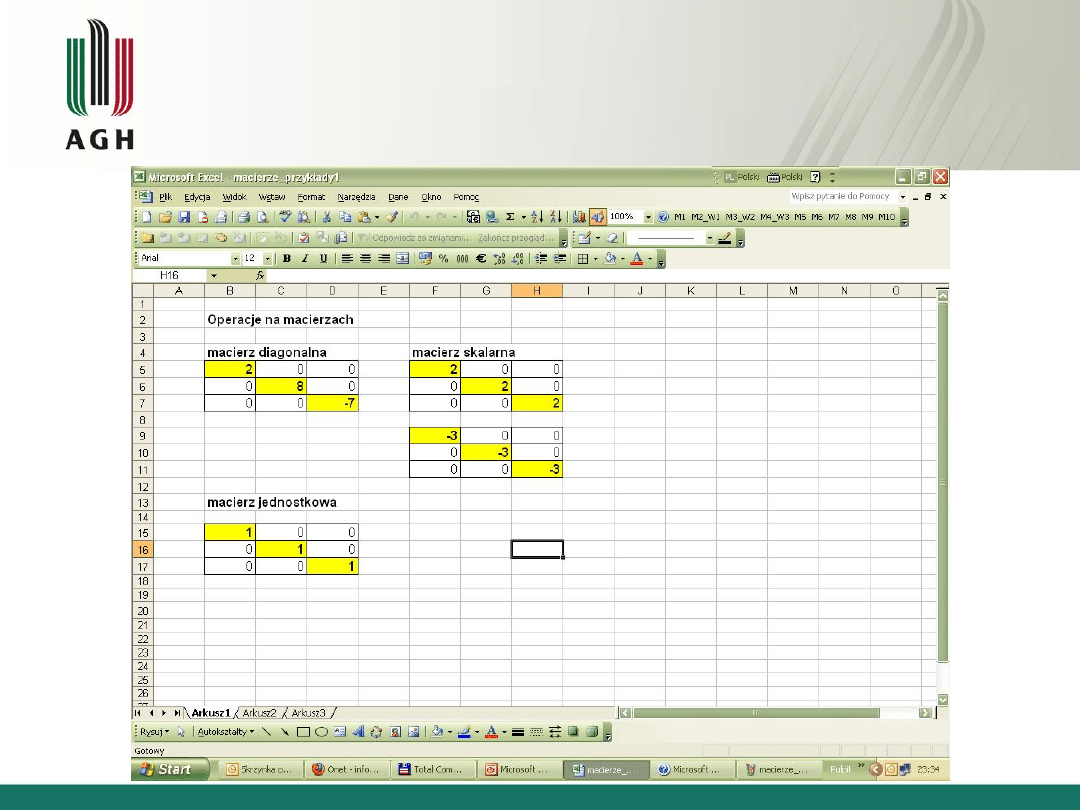
• Macierz diagonalna – wyrazy przekątnej

głównej <>0, pozostałe równe 0

• Macierz skalarna – wyrazy przekątnej

głównej jednakowe, pozostałe – równe 0

• Macierz jednostkowa E – wyrazy przekątnej

głównej równe 1, pozostałe równe 0

Wykład nr 2

Szczególne przypadki macierzy
kwadratowych

Wykład nr 2

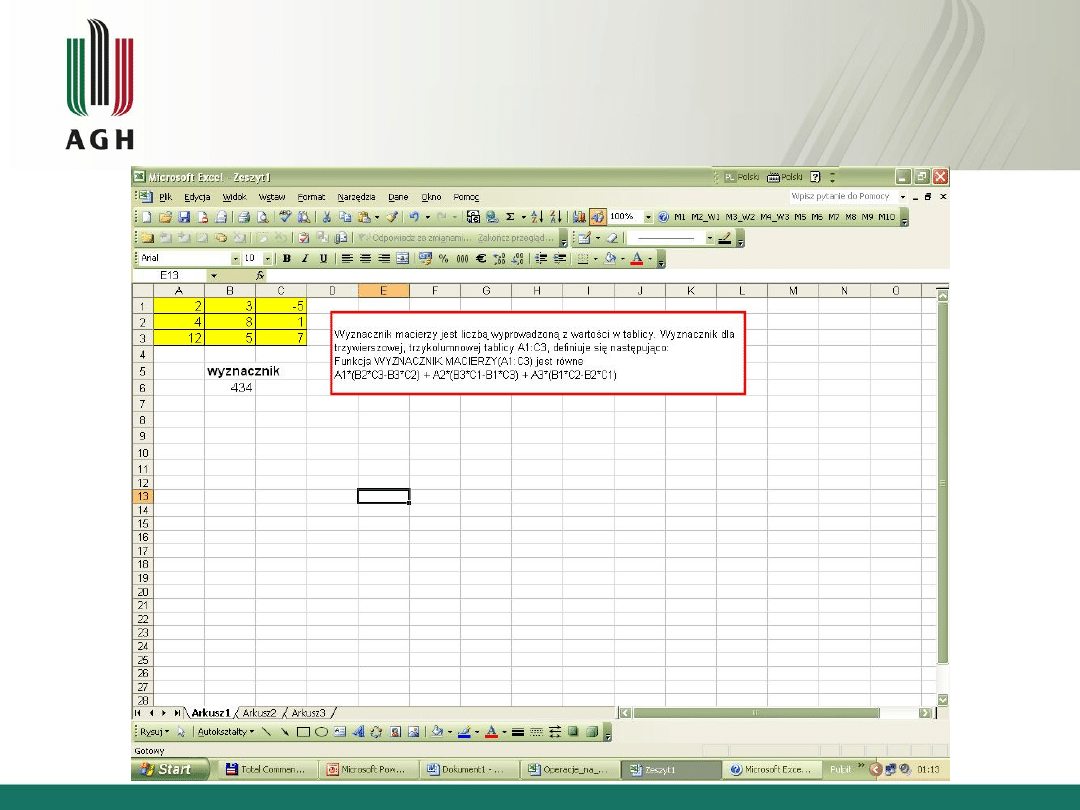
Wyznacznik macierzy

• Wyznacznik macierzy |A|
• |A|=|A

T

|

• Wyznacznik jest równy 0 gdy jeden z

wierszy lub kolumn jest liniową kombinacją
pozostałych wierszy lub kolumn

• Wyznacznik nie zmieni wartości, gdy do

wiersza lub kolumny dodamy kombinację
liniową pozostałych wierszy lub kolumn

Wykład nr 2

Wyznacznik macierzy

Wykład nr 2

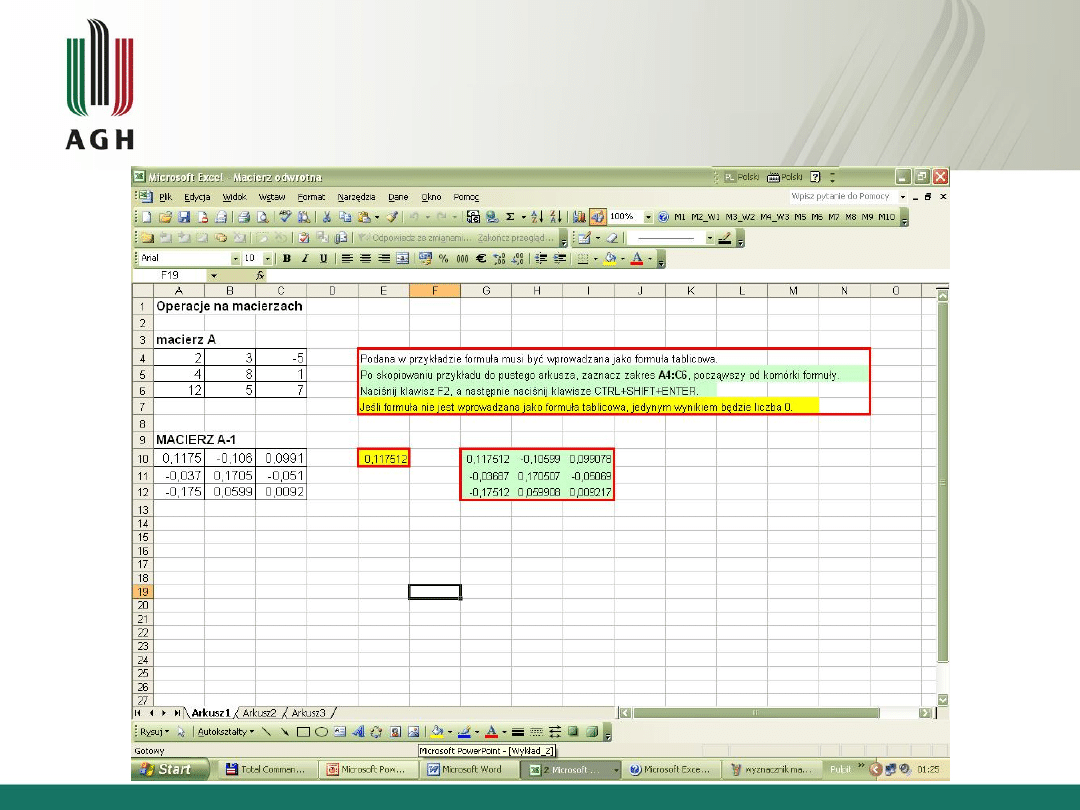
Macierze, macierz odwrotna

• |AB|=|A|*|B|
• |AB|=|BA|
• Macierz A

-1

odwrotna do macierzy A

• AA

-1

=A

-1

A=E

• Macierz A jest odwracalna tylko wtedy, gdy

jest nieosobliwa

• |A

-1

|=|A|

-1

Wykład nr 2

Macierz odwrotna