1

Estymacja punktowa

i przedziałowa

2

Wnioskowanie

statystyczne

Obejmuje zasady i metody uogólniania
wyników otrzymanych z próby losowej na
całą populację, z której ta próba pochodzi,
na

bazie

reguł

rachunku

prawdopodobieństwa.
Jest określane jako indukcyjna statystyka
matematyczna.

3

Wnioskowanie

statystyczne

Estymacja

Weryfikacja

hipotez

statystycznych

4

Teoria estymacji

Badania niepełne (obejmujące wybrane jednostki)

populacji wymagają określenia estymatorów, na

podstawie których będziemy weryfikowali hipotezy

badawcze, dotyczące ich parametrów.

Estymator – wielkość (statystyka, charakterystyka)

wyznaczona na postawie próby losowej, służąca do

oceny wartości nieznanego parametru populacji

generalnej.

Estymatorem parametru Q rozkładu zmiennej losowej X

nazywamy statystykę:

Z

n

= f(X

1

, X

2

,…, X

n

)

której rozkład prawdopodobieństwa zależy od

szacowanego parametru Q

5

Teoria estymacji c.d.

Przykładowo dla populacji generalnej o rozkładzie

normalnym N(,σ) z nieznaną wartością oczekiwaną i

wariancją, statystyki w postaci średniej arytmetycznej
oraz wariancji z próby są estymatorami, gdyż ich
rozkłady zależą od odpowiednich parametrów populacji.

Estymator jako statystyka z próby jest zmienną losową.

Posiada zatem rozkład z określonymi parametrami.
Rozkład estymatora Z

n

jest determinowany przez rozkład

zmiennej losowej X w populacji generalnej, przy czym
rozkład ten jest zależny od parametru Q. Każda z
niezależnych zmiennych X

i

(i = 1, 2, …, n) stanowiących

próbę, których funkcją jest Z

n

, ma więc taki rozkład jak

zmienna X w populacji generalnej.

6

Teoria estymacji c.d.2

Konkretną wartość liczbową z

n

= f(x

1

, x

2

, …, x

n

), jaką

przyjmuje estymator Z

n

parametru Q dla realizacji próby

(x

1

, x

2

, …, x

n

), nazywamy oceną parametru Q

. Ocena z

n

jest zatem realizacją zmiennej losowej Z

n

.

Z uwagi na to, że estymacji pewnego parametru za
pomocą określonego jego estymatora Z

n

dokonujemy na

podstawie wyników próby losowej, istnieje możliwość
popełnienia

błędu.

Błędem

szacunku

(estymacji)

parametru Q nazywamy różnicę między uzyskaną
liczbową oceną parametru i jego prawdziwą wartością, tj.
z

n

– Q.

 

7

Teoria estymacji c.d.3

W celu uzyskania dobrej precyzji szacunku tzn. małego

błędu estymacji, należy dbać zarówno o prawidłowe
losowanie próby, jak i o dobór możliwie najlepszego
estymatora Z

n

dla oszacowanego parametru Q. W tym

celu wprowadza się pewne własności, które powinien
posiadać dobry estymator. Są nimi: nieobciążalność,
zgodność,

efektywność

i

dostateczność

(wystarczalność).

8

Własności estymatora



Estymator Z

n

parametru Q nazywamy nieobciążonym,

jeżeli jego wartość oczekiwana jest równa szacowanemu

parametrowi: E(Z

n

) = Q. W przeciwnym wypadku

estymator

Z

n

nazywamy

obciążonym.

Właściwość

nieobciążoności oznacza, że przy wielokrotnym losowaniu

próby średnia z wartości przyjmowanych przez estymator

nieobciążony równa się wartości szacowanego parametru

.



Estymator jest zgodny, gdy wraz ze wzrostem liczebności

próby uzyskuje się coraz większe prawdopodobieństwo

tego, że estymator będzie przyjmować wartości coraz

bliższe wartości szacowanego parametru Q.

9

Własności estymatora
c.d.



Jeśli wyliczymy wariancję jako rozrzut ocen
szacowanego parametru Q wokół prawdziwej jego
wartości, to jako estymator najefektywniejszy
uznaje się ten, którego wartość tak wyliczonej
wariancji jest najmniejsza.



Estymator Z

n

parametru Q jest dostateczny,

jeżeli zawiera wszystkie informacje, jakie na
temat parametru Q występują w próbie i żaden
inny estymator nie może dać dodatkowych
informacji o szacowanym parametrze.

10

Własności estymatora
c.d.2

Na przykład spośród dwóch nieobciążonych estymatorów
wartości oczekiwanej E(X), którymi są średnia arytmetyczna
z próby oraz wartość:

drugi z wymienionych tu estymatorów nie jest dostatecznym,
gdyż przy jego wyznaczaniu wzięto pod uwagę jedynie dwie
wartości z próby.

2

~

max

min

x

x

X





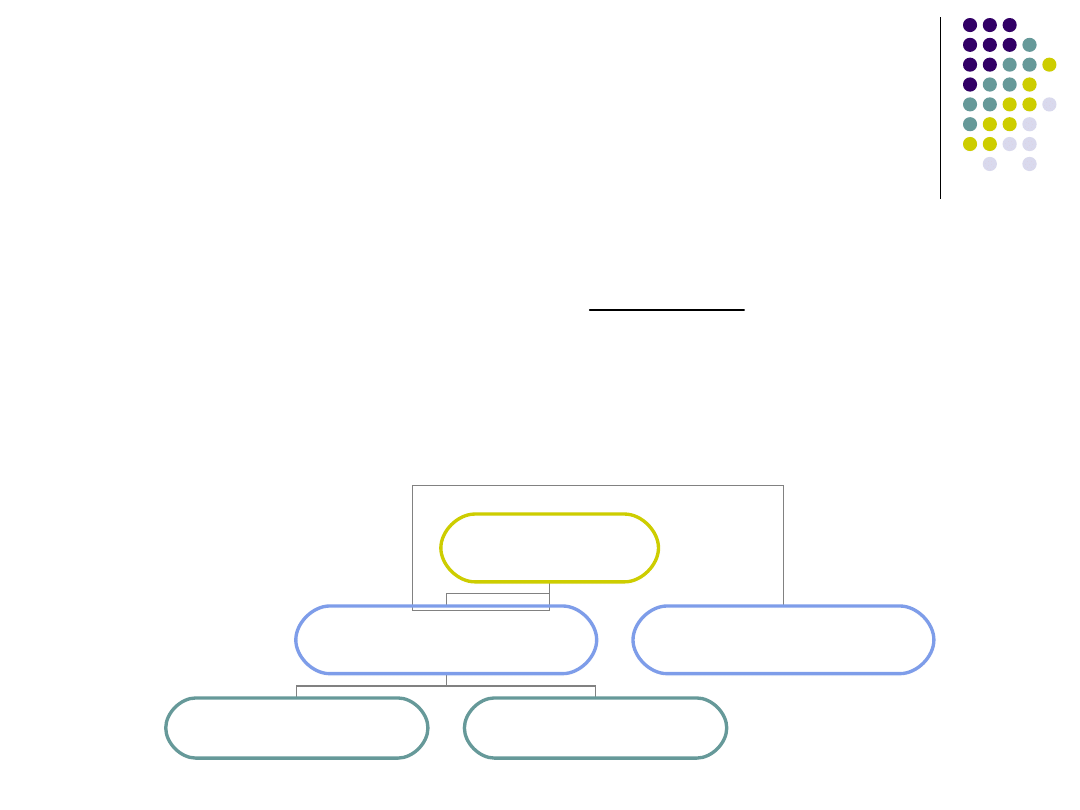
Estymatory

parametryczne

nieparametryczne

punktowe

przedziałowe

11

Przykłady estymatorów

Parametr

Estymator

Właściwości

wartość przeciętna

nieobciążony, zgodny,

w populacji μ

najefektywniejszy

wariancja

zgodny

w populacji σ

2

wariancja

nieobciążony,

w populacji σ

2

zgodny

2

1

2

1

1

)

(

1

1

)

(

1

1































X

X

n

X

X

n

X

n

n

i

i

n

i

i

n

i

i

2

^

2

S

S

X

12

Rodzaje estymacji

W estymacji punktowej za ocenę nieznanej
wartości parametru Q w populacji przyjmuje się jedną
konkretną liczbę otrzymaną – przy zachowaniu
odpowiednich reguł postępowania – z wyników próby
losowej. Zwykle przy szacowaniu danego parametru
obok jego oceny podaje się średni błąd szacunku
estymatora nieobciążonego.

Prawdopodobieństwo tego, że w populacjach ciągłych
estymator przyjmie wartość równą szacowanemu
parametrowi równa się zeru. Jest to jeden z powodów,
dla których stosuje się estymację przedziałową.

13

Rodzaje estymacji c.d.



Estymacja przedziałowa polega na konstruowaniu
przedziału liczbowego, który z określonym z góry –
bliskim jedności – prawdopodobieństwem będzie
zawierał nieznaną wartość szacowanego parametru

Q

.

Przedział ten nosi nazwę przedziału ufności, a jego
ogólna postać jest następująca:

prawd.

parametr

poziom ufności

lewy kraniec

prawy kraniec przedziału ufności

 

 















1

2

1

n

n

Z

g

Q

Z

g

P

14

Wyliczenie przedziału
ufności dla średniej
testem t-Studenta

Przedział ufności dla średniej populacji wyliczony
na podstawie n elementowej próby określamy jako:

gdzie: t

; n-1

- oznacza wartość krytyczną testu t-

Studenta dla poziomu istotności  i liczby stopni

swobody =n-1.

x

n

x

n

s

t

x

s

t

x

1

;

1

;



















15

Przedział ufności -
interpretacja parametrów

W celu prawidłowego zrozumienia od czego zależy
wielkość przedziału ufności należy przeanalizować
poszczególne zmienne które decydują o długości
przedziału ufności:

-

liczebność próby ?,

-

rozrzut wyników w obrębie próby ?,

-

średnia arytmetyczna ?

16

Przykład 1 (estymacja punktowa)

Pobrano próbę obejmującą n=10 następujących pomiarów

koncentracji

SO

2

(w µmol·mol

-1

) w powietrzu: 10,1; 10,9; 11,2; 11,6; 13,7;

14,1; 15,6;

14,1;14,2; 12,9. Na podstawie tych danych oszacować

przeciętne

stężenie dwutlenku siarki oraz błąd szacunku.

)

57

,

0

(

84

,

12

57

,

0

10

79

,

1

79

,

1

1

10

)

(

84

,

12

10

1

)

(

)

(

2

10

1

10

1

2

1























































x

i

i

i

i

n

i

i

x

x

s

x

x

s

x

x

n

x

x

s

n

s

s

s

x

17

Wniosek

Szacowane przeciętne stężenie
SO

2

w powietrzu wynosi:

)

μmol·mol

57

,

0

(

μmol·mol

84

,

12

1

1







18

Przykład 2 (estymacja
przedziałowa)

Na podstawie danych z przykładu 1 określić

-stosując 95% przedział ufności - w jakich

granicach znajduje się prawdziwa średnia wartość

stężenia dwutlenku siarki.

13

,

14

55

,

11

29

,

1

84

,

12

29

,

1

84

,

12

29

,

1

57

,

0

262

,

2

·

262

,

2

57

,

0

84

,

12

·

·

05

,

0

95

,

0

1

1

;

9

1

;

05

,

0

1

;

1

;

)

tablic

z

(





































































x

n

n

x

x

n

x

n

s

t

t

s

x

s

t

x

s

t

x

19

Z

prawdopodobieństwem

popełnienia błędu mniejszym niż
0,05 można stwierdzić, że średnia
wartość stężenia dwutlenku siarki
w powietrzu jest nie mniejsza niż
11,55 μmol·mol

-1

i nie większa niż

14,13 μmol·mol

-1

.

WNIOSEK

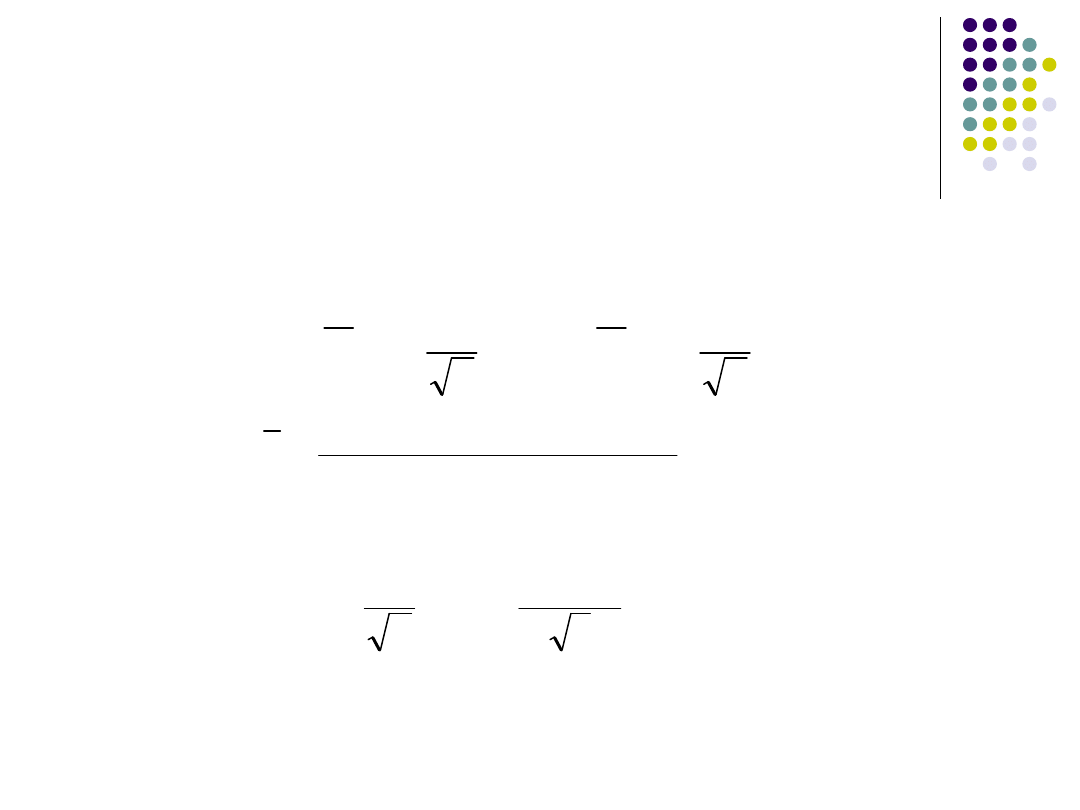
20

Przykład 3 (estymacja
przedziałowa)

W laboratorium trzykrotnie (n=3) powtarzano analizę

preparatu ze

względu na zawartość substancji czynnej i uzyskano

następujące

wyniki: 0,8403; 0,8363; 0,8447 g/l. Odchylenie standardowe
jest znane i wynosi σ=0,0068 g/l. Określić 99% przedział

ufności

średniej μ.

8505

,

0

08303

,

0

0101

,

0

8504

,

0

0101

,

0

08404

,

0

0101

,

0

3

0068

,

0

58

,

2

·

58

,

2

;

01

,

0

;

0068

,

0

8404

,

0

3

8447

,

0

8363

,

0

8403

,

0































































n

z

z

x

n

z

x

n

z

x

21

Z

prawdopodobieństwem

popełnienia błędu mniejszym niż
0,01 można stwierdzić, że średnia
wartość

koncentracji

substancji

aktywnej w preparacie jest nie
mniejsza niż 0,8303 g/l

i nie

większa niż 0,8505 g/l.

WNIOSEK