Układy o programach liniowych
1
Zaprojektować procesowo-zależny układ sterowania
dwoma siłownikami pneumatycznymi A i B
dwustronnego działania, zapewniający wykonanie
cyklu ruchów siłowników:
1 – wysunięcie siłownika A,
2 – częściowe wysunięcie siłownika B,
3 – wycofanie siłownika B,
4 – całkowite wysunięcie siłownika B,
5 – wycofanie siłownika B,
6 – wycofanie siłownika A.
Cykl pracy jest inicjowany impulsem z przycisku
START (x); uruchomienie cyklu pracy jest możliwe
tylko gdy tłoczyska obu siłowników są wycofane.
Projektowanie układów asynchronicznych o
programach
liniowych
Przykład
Układy o programach liniowych
2
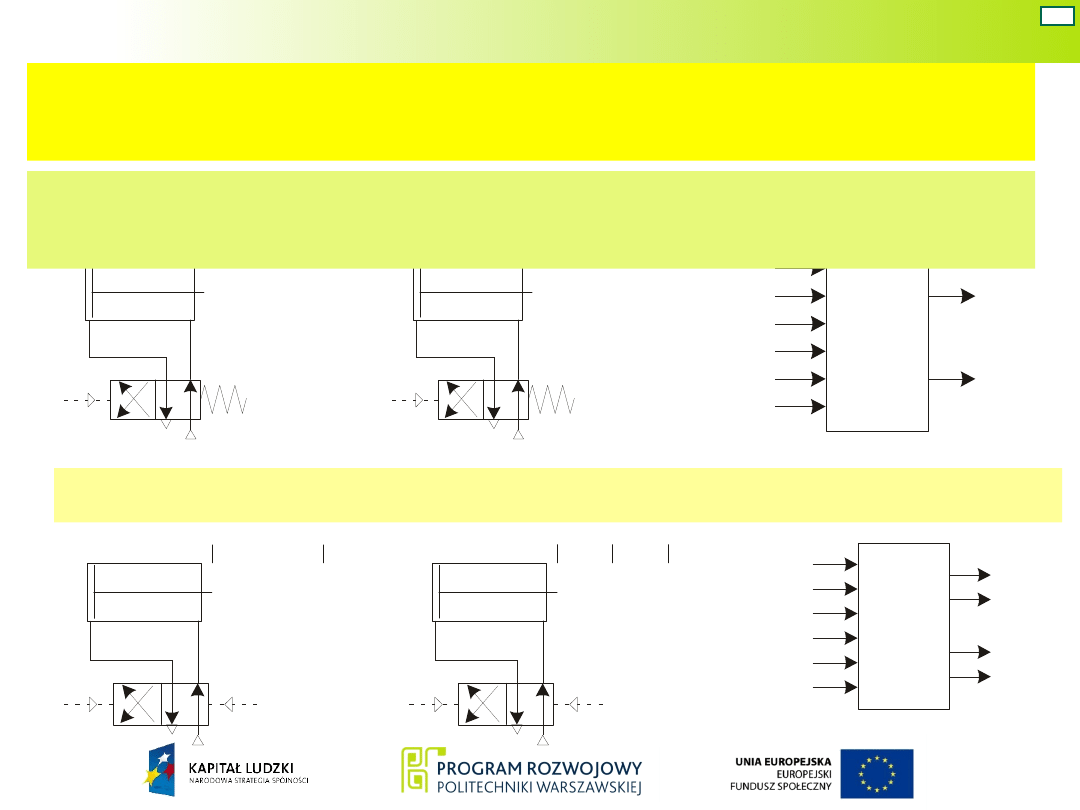
Sygnałami wejściowymi układu są sygnał x z
przycisku START oraz sygnały przekaźników a, b, c, d,
e, informujących o położeniu tłoczysk siłowników.
Usytuowanie elementów sygnałowych
Elementy sygnałowe wykrywające
położenie tłoczysk
Elementy sygnałowe wykrywające
położenie tłoków
Układy o programach liniowych
3
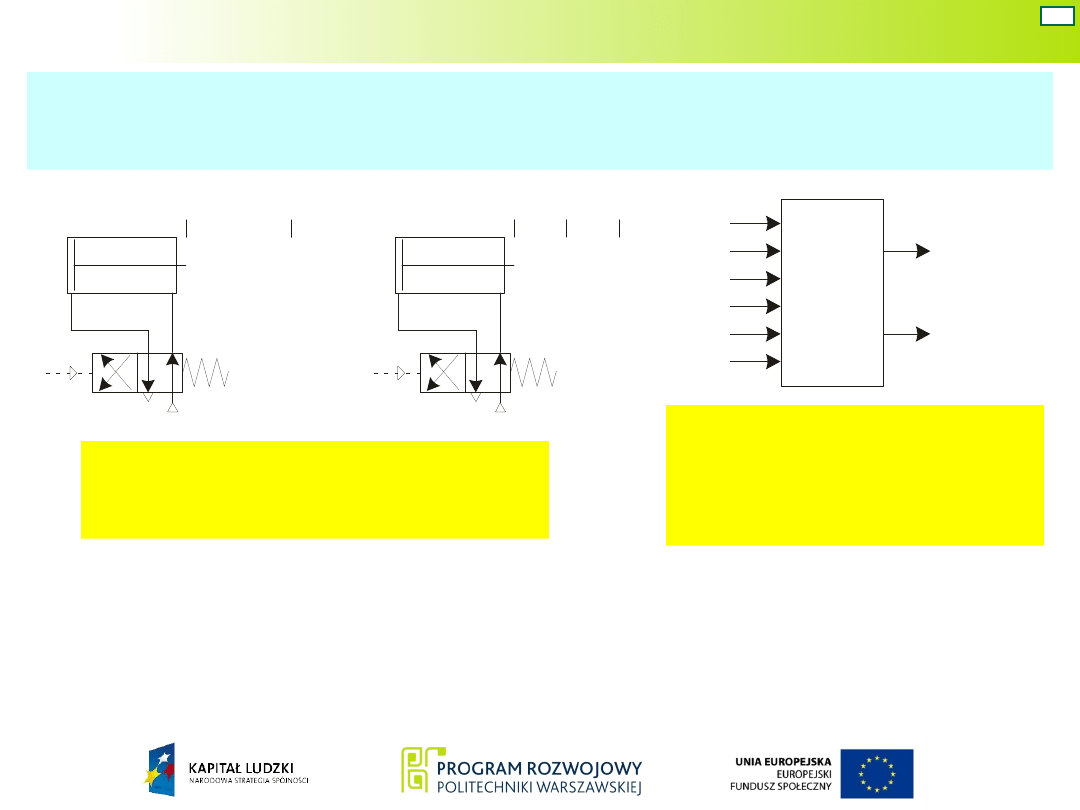
W zależności od rodzaju zastosowanych zaworów
roboczych projektowany układ może mieć:
A
B
a
b
e
c
d
y
1
y
2
a
b
c
d
e
x
y
1
y
2
dwa sygnały wyjściowe – w przypadku zaworów
monostabilnych
A
B
a
b
e
c
d
a
b
c
d
e
x
A +
B +
A -
B -
A +
A -
B +
B -
lub cztery – w przypadku zaworów bistabilnych.
Układy o programach liniowych
4
1. układ Moore’a – kod ze stałym odstępem – zawory
robocze monostabilne,
2. układ Moore’a – kod ze stałym odstępem – zawory
robocze bistabilne,
3. układ Moore’a – kod „1 z n” – zawory robocze
monostabilne,
4. układ Moore’a – kod „1 z n” – zawory robocze
bistabilne,
5. układ Mealy’ego – kod ze stałym odstępem –
zawory robocze monostabilne,
6. układ Mealy’ego – kod ze stałym odstępem –
zawory robocze bistabilne,
7. układ Mealy’ego – kod „1 z n” – zawory robocze
monostabilne,
8. układ Mealy’ego – kod „1 z n” – zawory robocze
bistabilne.
Ponadto każdy z tych wariantów może być
zrealizowany w wersji pneumatycznej lub
elektrycznej.
Możliwe są następujące warianty matematycznych
modeli układu sterującego:
Układ Moore’a – war. 1
5
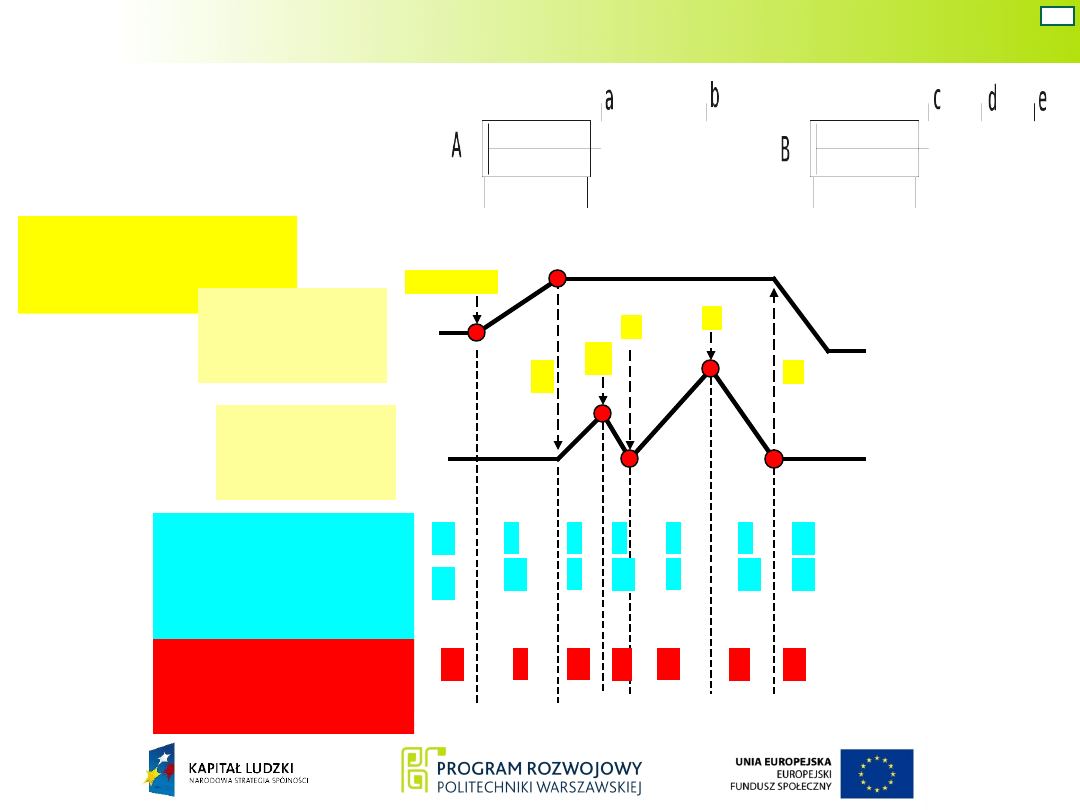
Wariant 1: układ Moore’a – kod ze stałym odstępem –
zawory robocze monostabilne
Do wykonania każdego ruchu w cyklu pracy potrzebny
jest inny zestaw sygnałów wyjściowych (inny stan
wyjść). Zatem układ Moore’a dla zrealizowania sześciu
ruchów musi mieć sześć stanów wewnętrznych.
a
b
c
d
e
x
y
1
y
2
A
B
a
b
e
c
d
y
1
y
2
Schemat układu
napędowego
Schemat blokowy
projektowanego
układu
Układy o programach liniowych
6
Diagram
stanów
Siłownik
A
Siłownik
B
Stan wyjść:
y
1
y
2
0
1 2 3 4
5 0
c
a
x
e
c
c
d
b
0
1 1
1
1
1
0
0
0
0
0
1
1
0
Stan
wewnętrzny
Układ Moore’a – war. 1
7
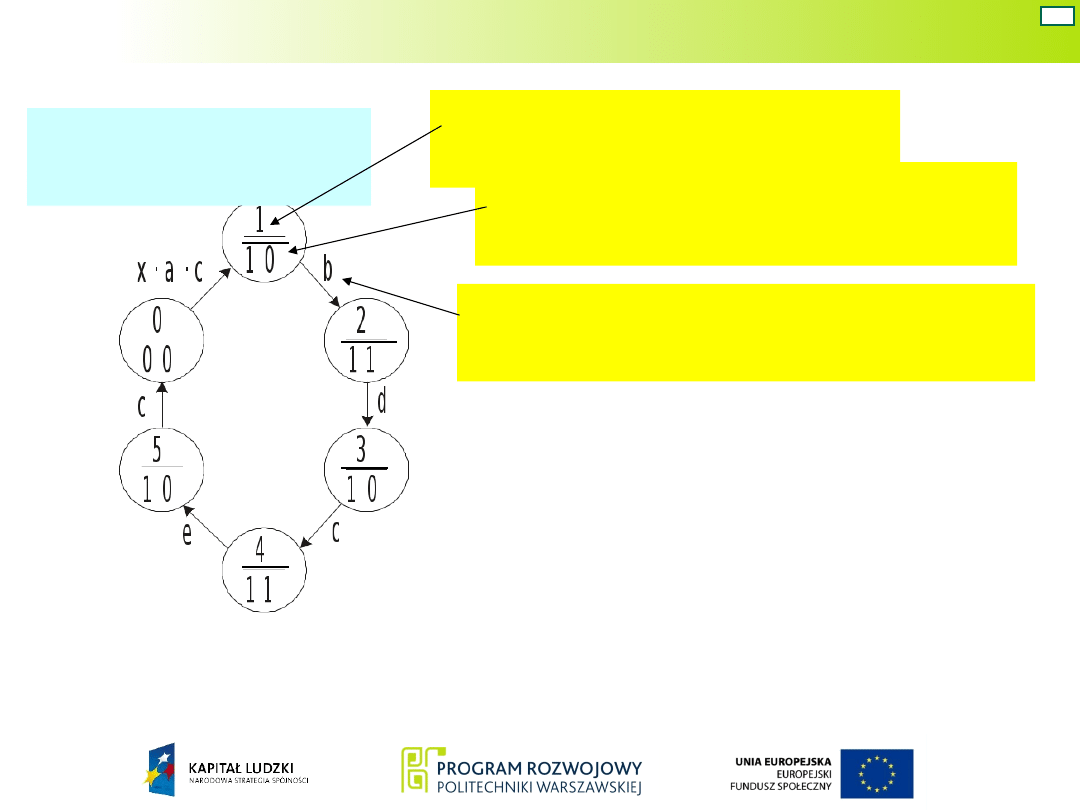
Graf układu
Moore’a
numer stanu
wewnętrznego
stan sygnałów wyjściowych
y
1
i y
2
sygnał powodujący zmianę
stanu wewnętrznego
Do zakodowania sześciu stanów wewnętrznych
niezbędne są trzy sygnały binarne.
Układ Moore’a – war. 1
8
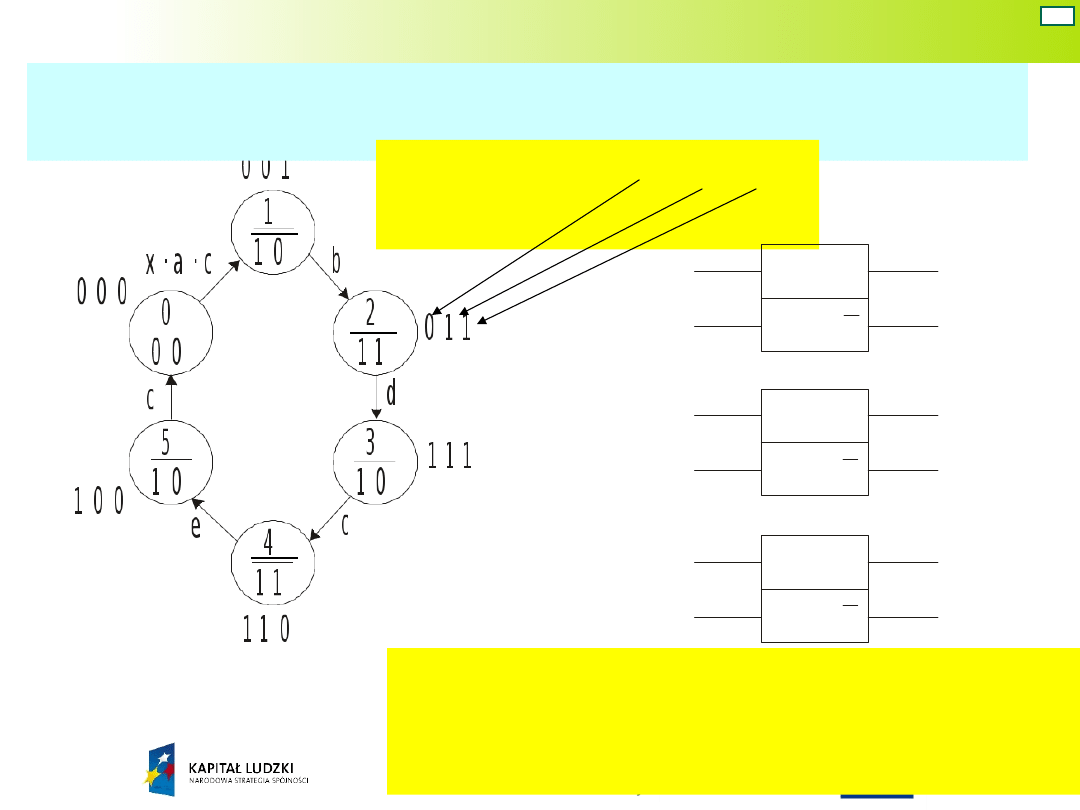
Graf z kodami stanów wewnętrznych (kod
pseudopierścieniowy)
zmienne kodowe Q
1
,
Q
2
, Q
3
W
2
Z
2
Q
2
Q
2
W
1
Q
1
Q
1
Z
1
W
3
Z
3
Q
3
Q
3
Trzon układu stanowi zestaw
przerzutników generujących sygnały
Q
1
, Q
2
, i Q
3
.
Układ Moore’a – war. 1
9
00 01 11 10
0
00 10 11
--
1
10
--
10 11
y
1
,y
2
Q
2
,Q
3
Q
1
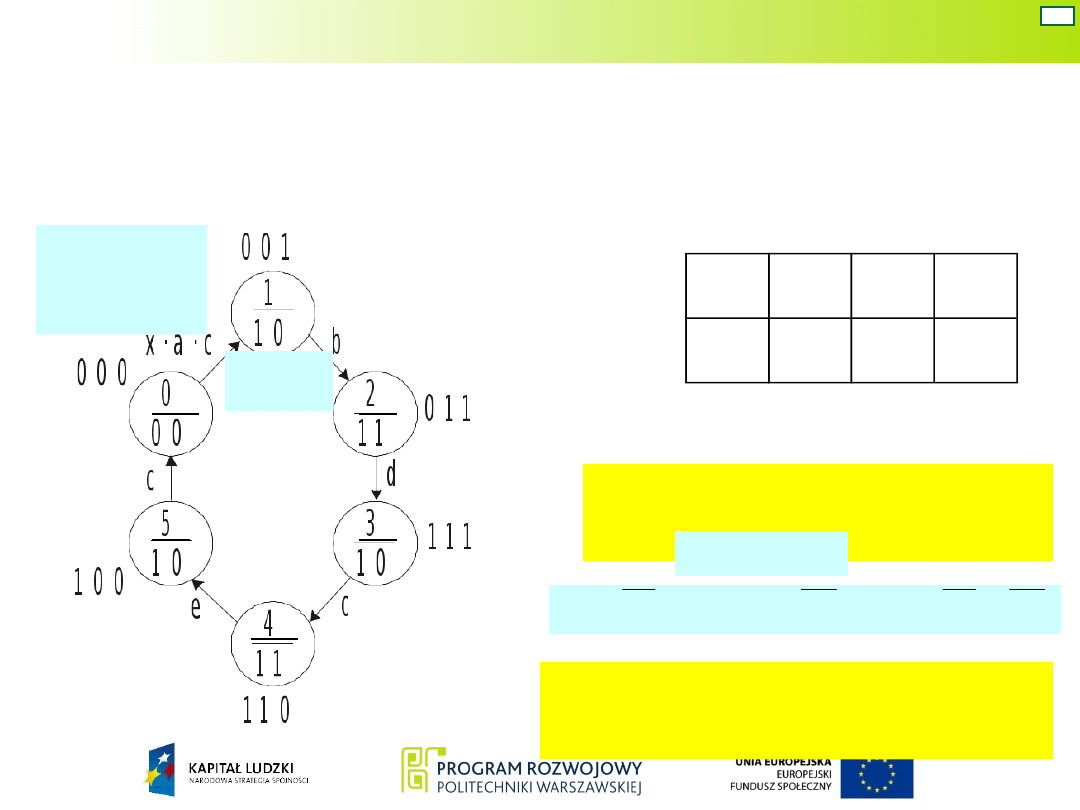
Na podstawie grafu ustala się zależność sygnałów
wyjściowych y
1
i y
2
od sygnałów Q
1
, Q
2
i Q
3
.
Q
1
,
Q
2
,Q
3
y
1
,y
2
Z tablicy wynikają
zależności:
3
1
1
Q
Q
y
)
(
3
1
2
3
2
2
1
2
Q
Q
Q
Q
Q
Q
Q
y
określające funkcje wyjść
układu.
Układ Moore’a – war. 1
10
00 01 11 10
0
00
1
01
1
11
1
--
1
00
0
--
11
0
10
0
Q
1
’,Q
2
’,Q
3
’
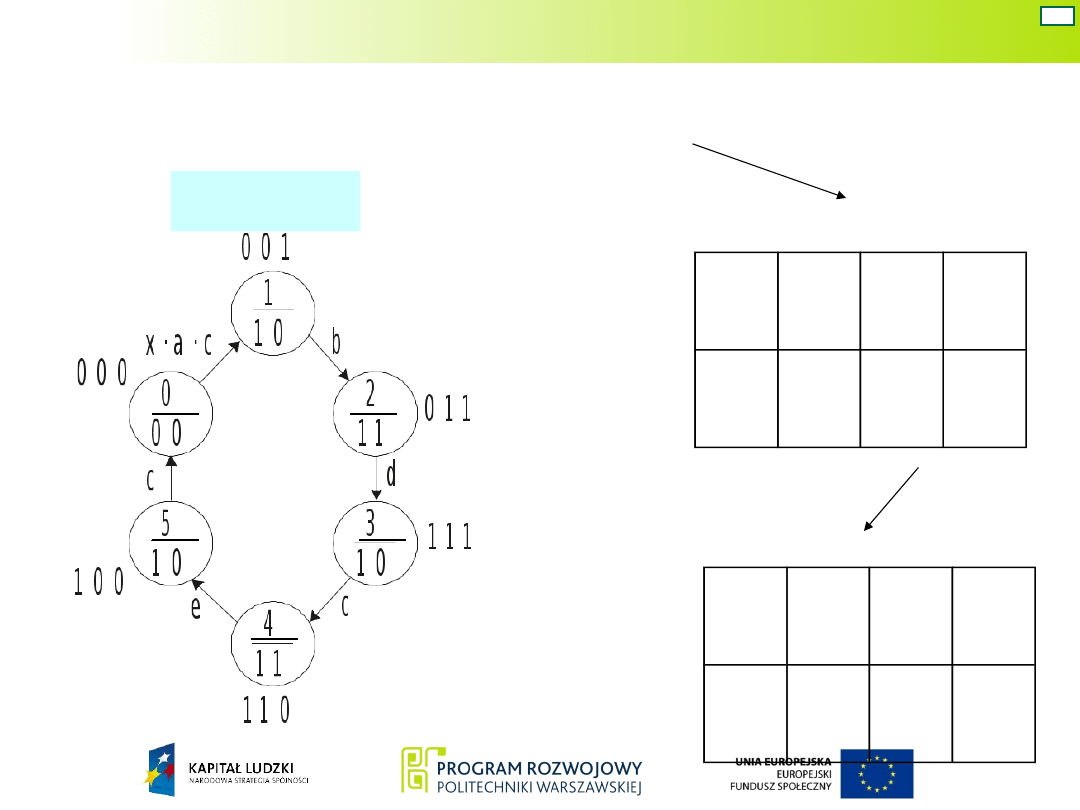
W celu wyznaczenia wzbudzeń przerzutników, na
podstawie grafu tworzy się tzw. uproszczoną
tablicę przejść
Q
1
Q
2
,Q
3
Q
1
, Q
2
,Q
3
00 01 11 10
0
00
1
0
1
1
1
1
1
--
1
0
0
0
--
11
0
1
0
0
Q
1
’,Q
2
’,Q
3
’
i następnie tablicę
uniwersalną
Q
2
,Q
3
Q
1
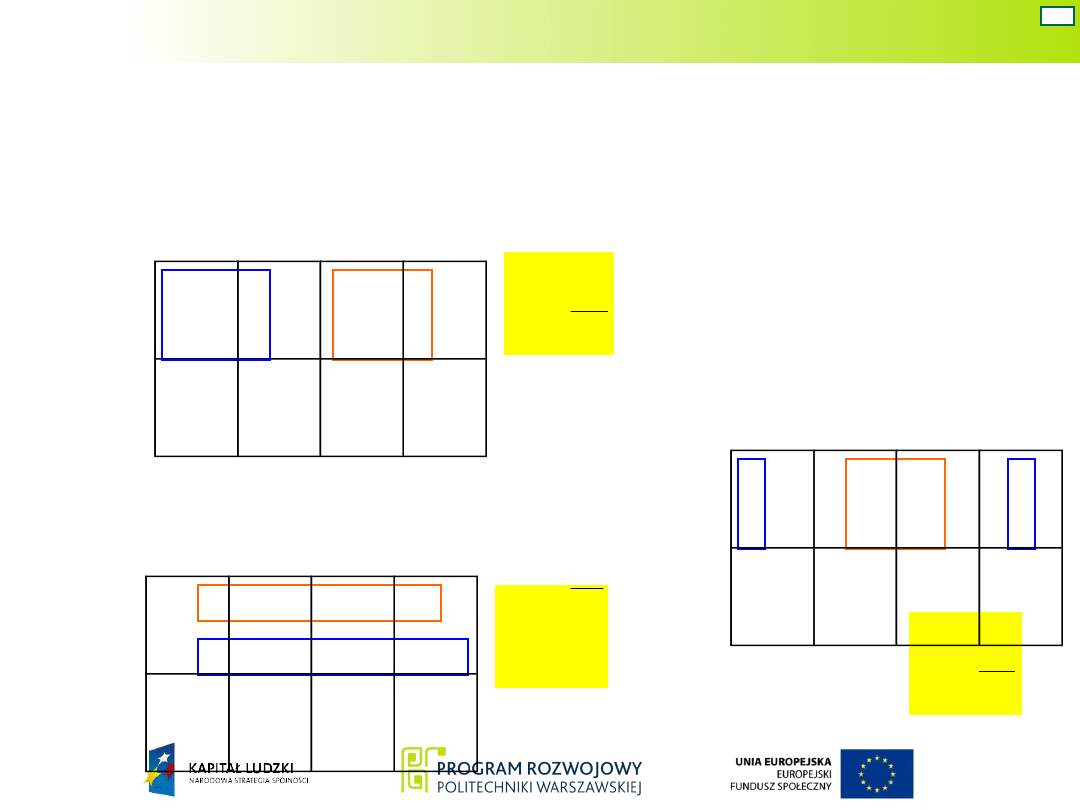
Układ Moore’a – war. 1
11
2
1
2
1
Q
z
Q
w
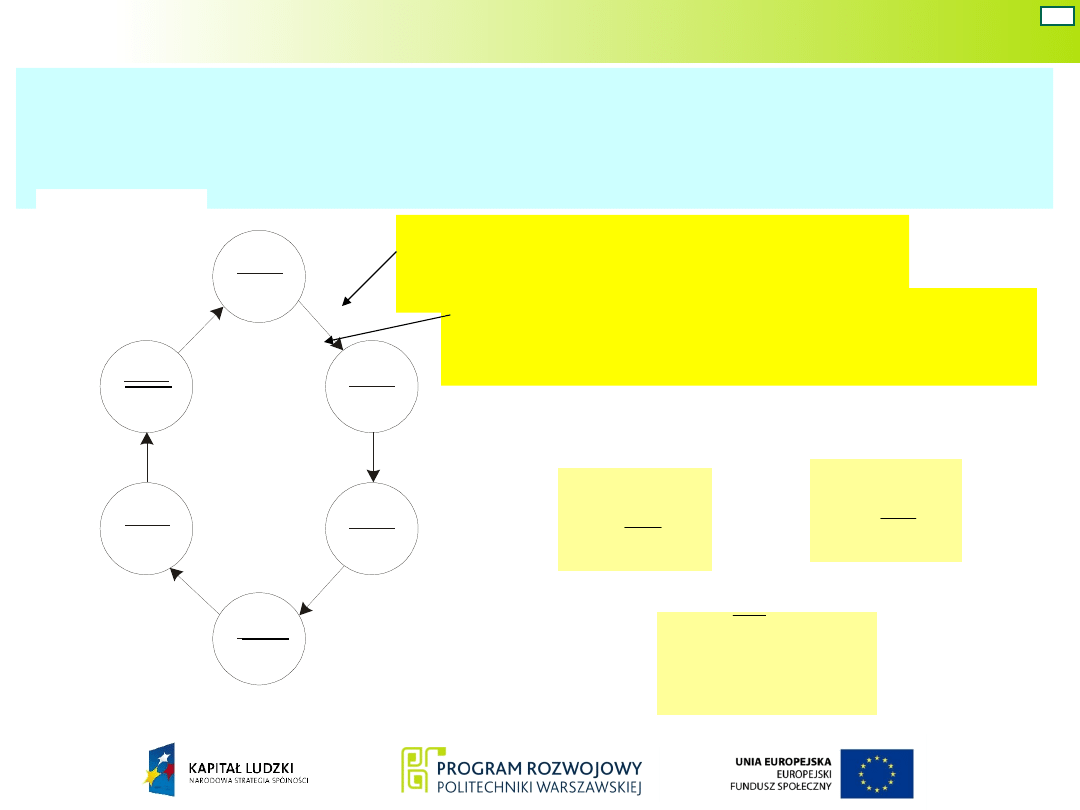
Na podstawie tablicy uniwersalnej wyznacza się
wzbudzenia zapewniające właściwa kolejność zmian
stanów wewnętrznych.
3
2
3
2
Q
z
Q
w
1
3
1
3
Q
z
Q
w
00 01 11 10
0
00
1
0
1
1
1
1
1
--
1
0
0
0
--
11
0
1
0
0
Q
1
’,Q
2
’,Q
3
’
Q
2
,Q
3
Q
1
00 01 11 10
0
00
1
0
1
1
1
1
1
--
1
0
0
0
--
11
0
1
0
0
Q
1
’,Q
2
’,Q
3
’
Q
2
,Q
3
Q
1
00 01 11 10
0
00
1
0
1
1
1
1
1
--
1
0
0
0
--
11
0
1
0
0
Q
1
’,Q
2
’,Q
3
’
Q
2
,Q
3
Q
1
Układ Moore’a – war. 1
12
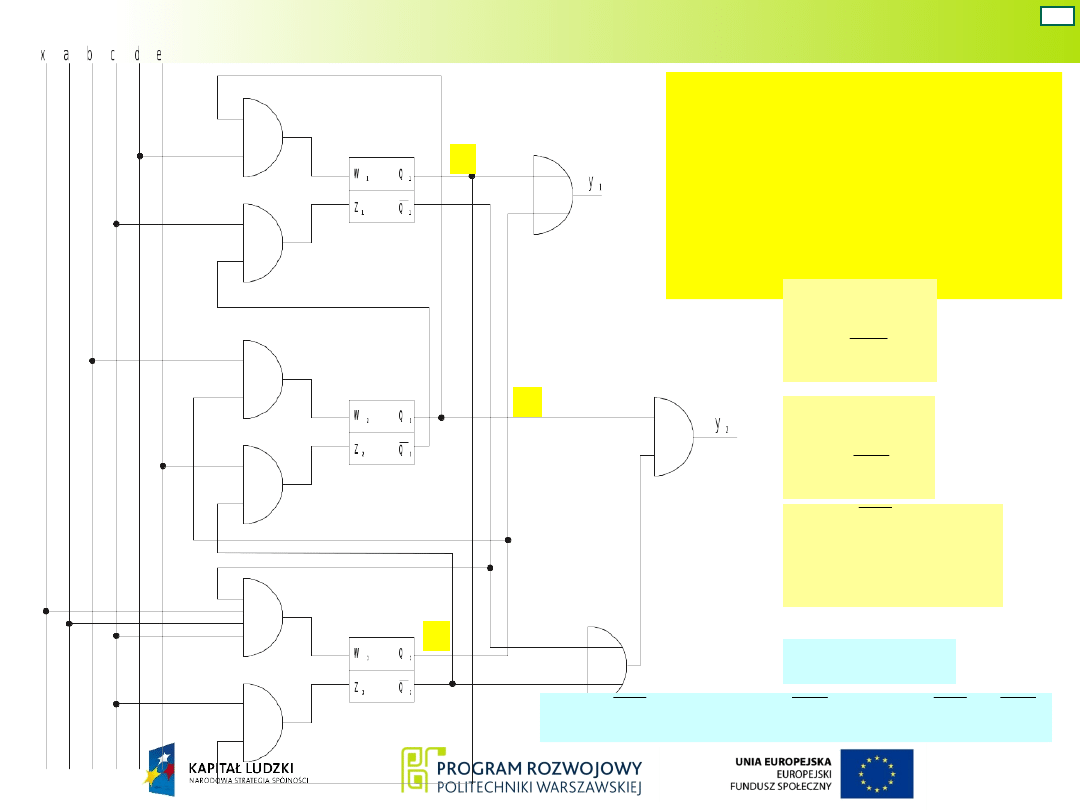
Wyznaczone wzbudzenia uzupełnia się o sygnały
zewnętrze, warunkujące przejścia do kolejnych stanów
wewnętrznych.
1
1 0
2
1 1
0
0 0
5
1 0
3
1 0
4
1 1
b
c
e
c
x · a · c
d
Q
1
2
3
Q Q
0 0 0
1 0 0
1 1 0
1 1 1
0 1 1
0 0 1
w
2
w
1
z
3
z
2
z
1
w
3
y
1
2
y
sygnał warunkujący
zmianę stanu
wzbudzenie wywołujące
zmianę stanu
Niezbędne wzbudzenia
przerzutników:
c
Q
z
d
Q
w
2
1
2
1
e
Q
z
b
Q
w
3
2
3
2
c
Q
z
c
a
x
Q
w
1
3
1
3
Q
1
,
Q
2
,Q
3
Układ Moore’a – war. 1
13
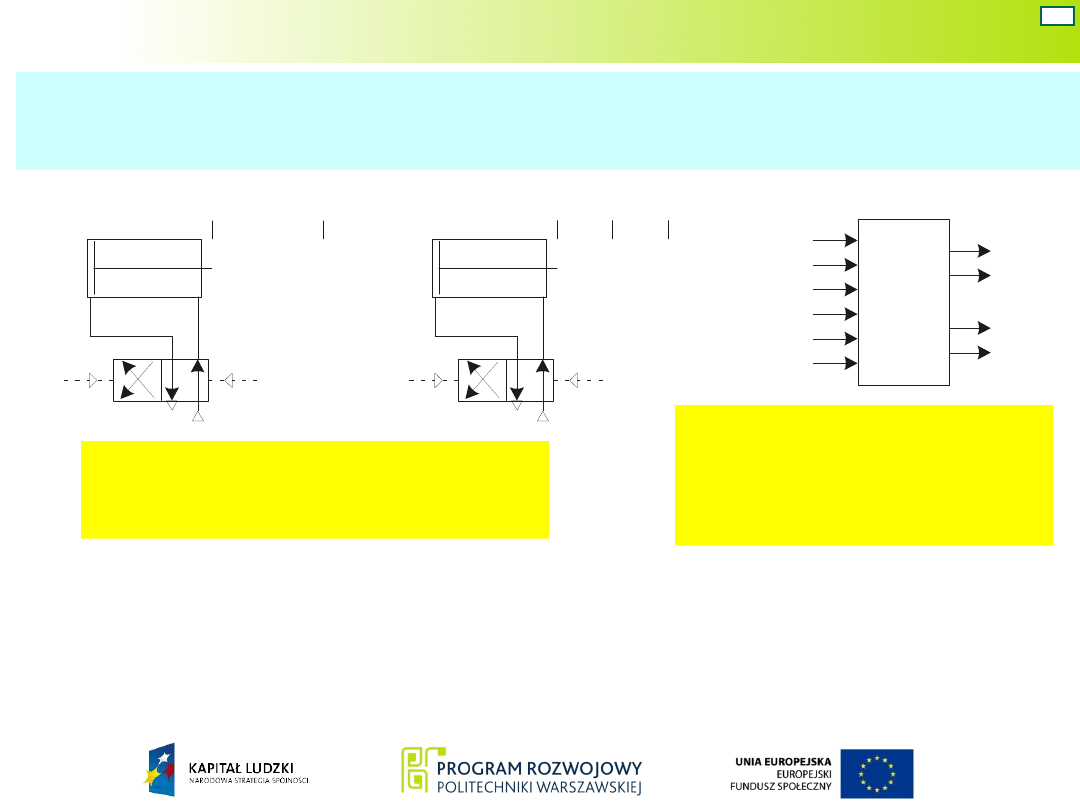
Logiczny schemat
układu sterującego
zaworami
roboczymi i jego
opis matematyczny:
c
Q
z
d
Q
w
2
1
2
1
e
Q
z
b
Q
w
3
2
3
2
c
Q
z
c
a
x
Q
w
1
3
1
3
3
1
1
Q
Q
y
)
(
3
1
2
3
2
2
1
2
Q
Q
Q
Q
Q
Q
Q
y
1
Q
2
Q
3
Q
Układ Moore’a – war. 2
14
A
B
a
b
e
c
d
a
b
c
d
e
x
A +
B +
A -
B -
A +
A -
B +
B -
Wariant 2: układ Moore’a – kod ze stałym odstępem –
zawory robocze bistabilne
Schemat układu
napędowego
Schemat blokowy
projektowanego
układu
Wariant ten różni się od poprzedniego tylko postacią
funkcji wyjść.
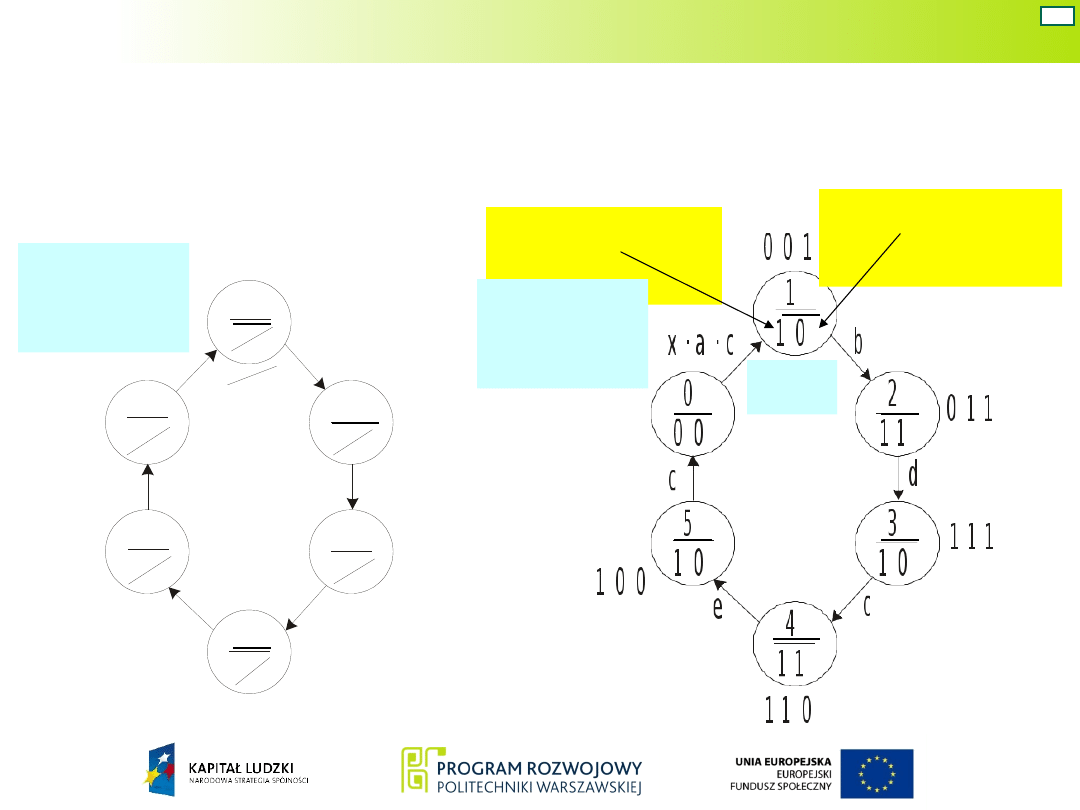
Układ Moore’a – war. 2
15
1
1 0
2
1 1
0
0 0
5
1 0
3
1 0
4
1 1
Q
1
2
3
Q Q
0 0 0
1 0 0
1 1 0
1 1 1
0 1 1
0 0 1
y y
1
2
A +
B +
B -
B +
B -
A -
Układ, zamiast sygnałów y
1
i y
2
, powinien wytworzyć
w poszczególnych stanach wewnętrznych sygnały
odpowiednio ustawiające zawory bistabilne.
A,B
stan
zaworu A
stan
zaworu B
Q
1
,
Q
2
,Q
3
Q
1
,
Q
2
,Q
3
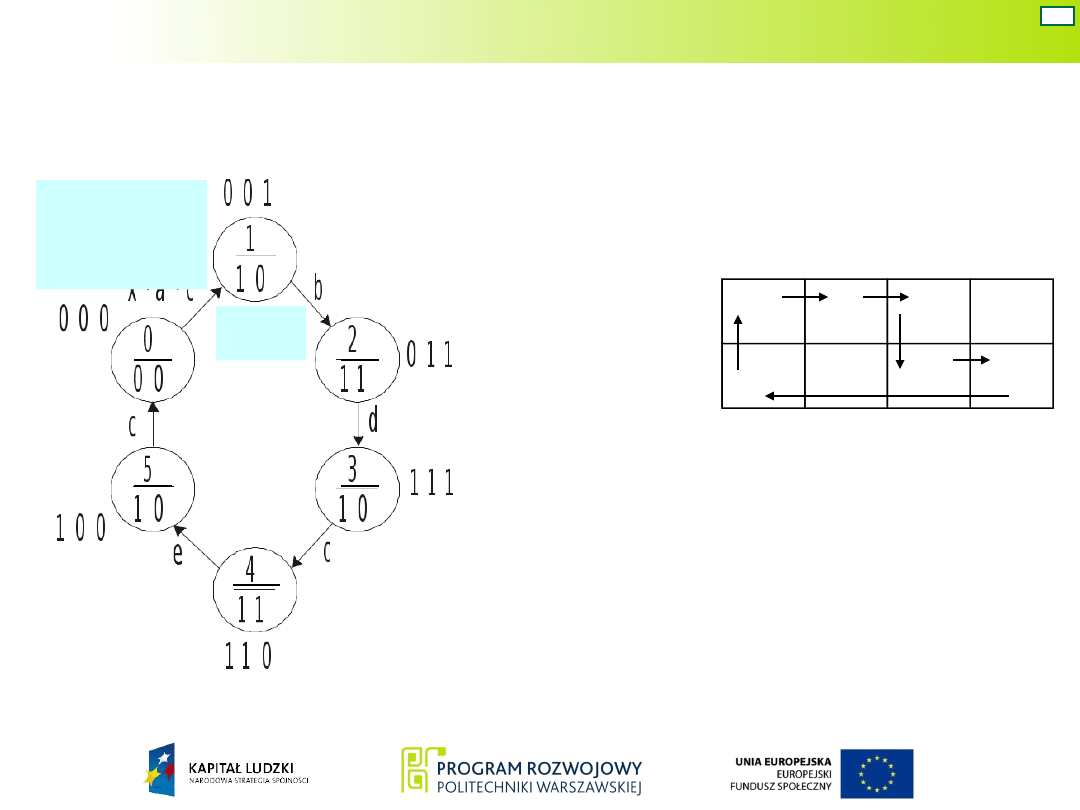
Układ Moore’a – war. 2
16
Widoczną na grafie zależność stanu zaworów od stanów
wewnętrznych można wyrazić w postaci tablicy
Karnaugha.
00 01 11 10
0
00 10 11
--
1
10
--
10 11
A,B
Q
2
,Q
3
Q
1
A,B
Strzałki w tablicy
wskazują kolejność stanów
zaworów w cyklu pracy
układu; umożliwiają
utworzenie tablicy
uniwersalnej.
Q
1
,
Q
2
,Q
3
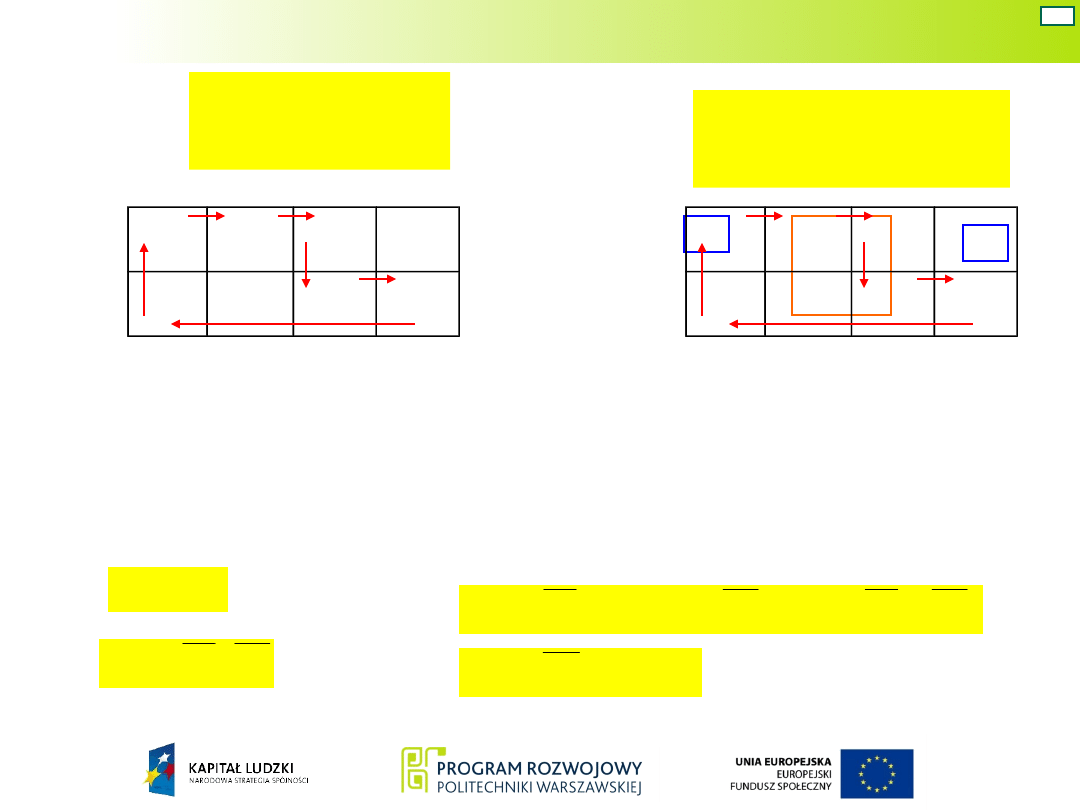
Układ Moore’a – war. 2
17
00 01 11 10
0
00 10 11
--
1
10
--
10 11
A,B
Q
2
,Q
3
Q
1
Tablica
zwykła
Tablica
uniwersalna
Na podstawie tablicy uniwersalnej wyznacza się
sygnały sterujące zaworami roboczymi jako
wzbudzenia przerzutników, którymi są zawory
bistabilne.
3
Q
A
3
1
Q
Q
A
)
(
3
1
2
3
2
2
1
Q
Q
Q
Q
Q
Q
Q
B
3
1
2
Q
Q
Q
B
00 01 11 10
0
0
0
1
0 1
1
--
1
1
0
--
1
0
1
1
A,B
Q
1
Q
2
,Q
3
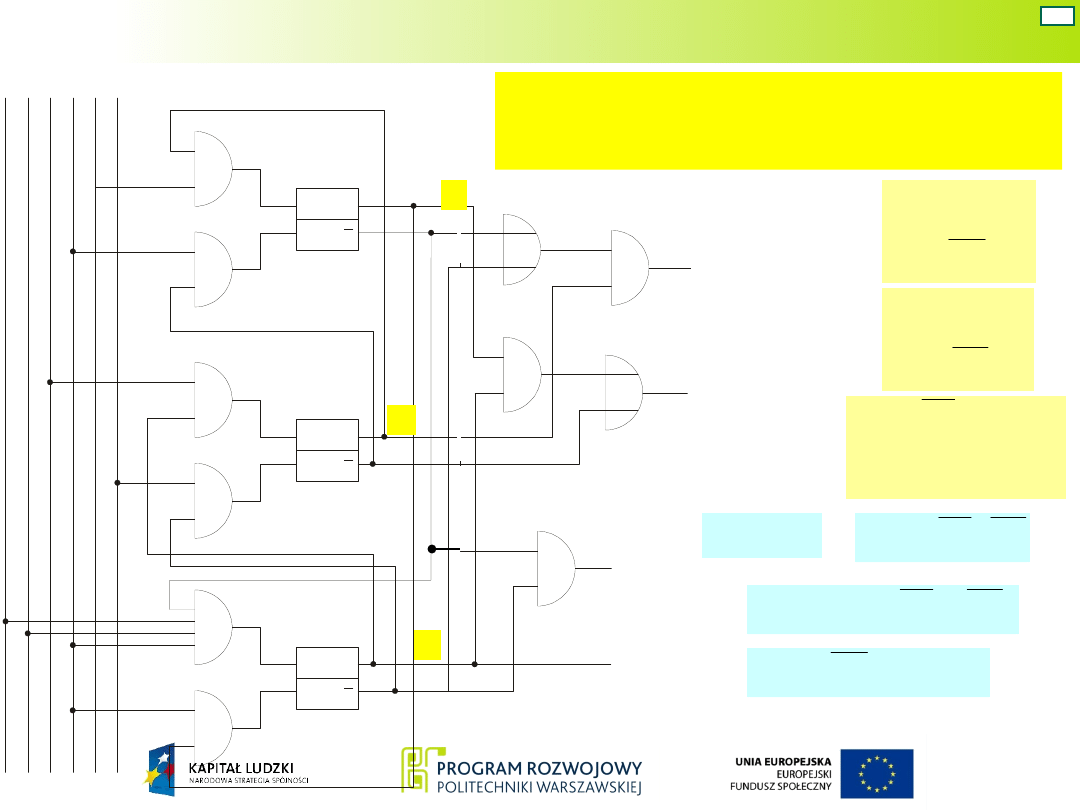
Układ Moore’a – war. 2
18
Wariant 2 - schemat logiczny
układu sterującego
c
Q
z
d
Q
w
2
1
2
1
e
Q
z
b
Q
w
3
2
3
2
c
Q
z
c
a
x
Q
w
1
3
1
3
W
1
Q
1
Q
1
Z
1
W
2
Q
2
Q
2
Z
2
W
3
Q
3
Q
3
Z
3
x
a
b
c d
e
B +
B -
A -
A +
3
Q
A
3
1
Q
Q
A
)
(
3
1
2
Q
Q
Q
B
3
1
2
Q
Q
Q
B
1
Q
2
Q
3
Q
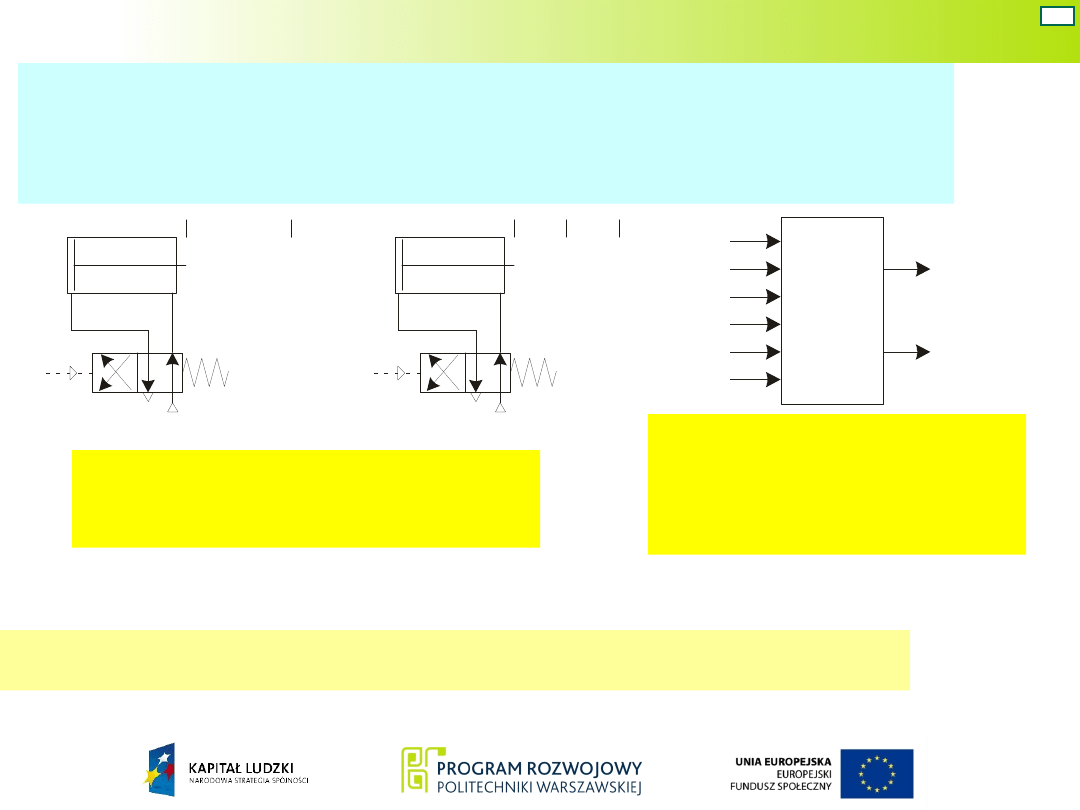
Układ Moore’a – war. 3
19
Wariant 3: układ Moore’a – kod „1 z n” – zawory
robocze
monostabilne
a
b
c
d
e
x
y
1
y
2
A
B
a
b
e
c
d
y
1
y
2
Schemat układu
napędowego
Schemat blokowy
projektowanego
układu
Do zakodowania sześciu stanów wewnętrznych
układu Moore’a w kodzie „1 z n” potrzeba sześciu
zmiennych.
Oznaczenia tych zmiennych: Q
0
, Q
1
, Q
2
, Q
3
, Q
4
i Q
5
.
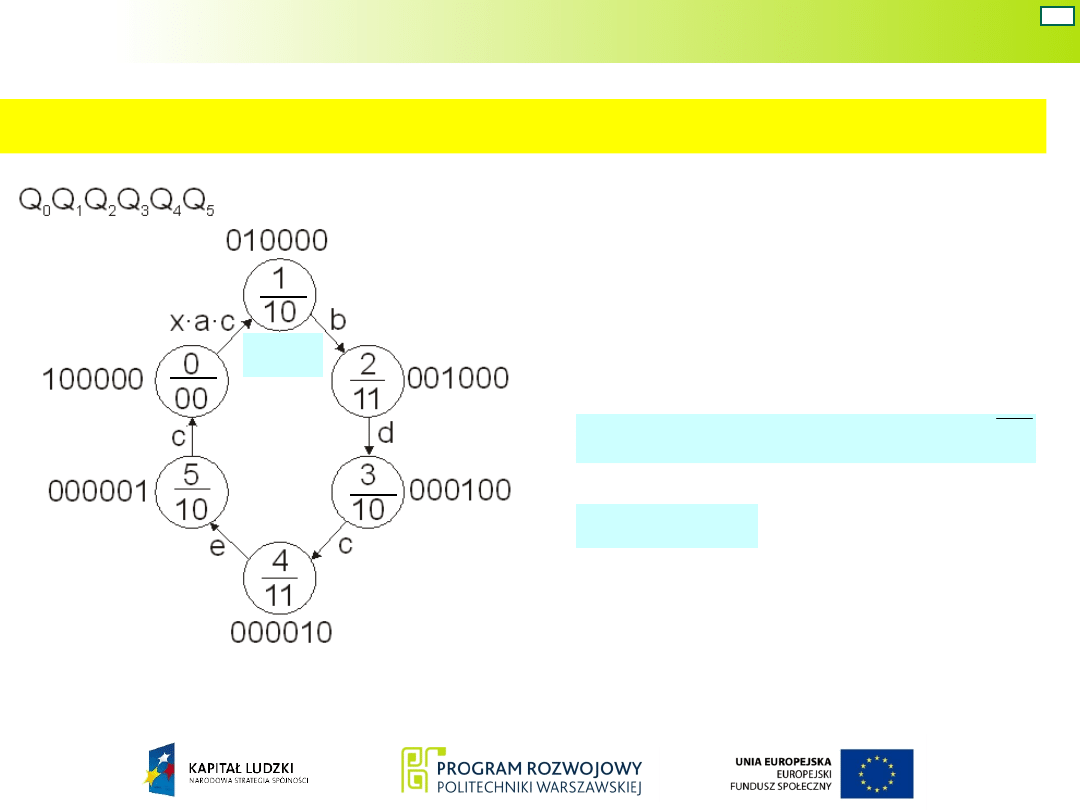
Układ Moore’a – war. 3
20
Graf układu z kodami stanów wewnętrznych w kodzie „1 z 6”
Funkcje wyjść ustala się
bezpośrednio na
podstawie
zakodowanego grafu:
0
5
4
3
2
1
1
Q
Q
Q
Q
Q
Q
y
4
2
2
Q
Q
y
2
1
, y
y
2
1
, y
y
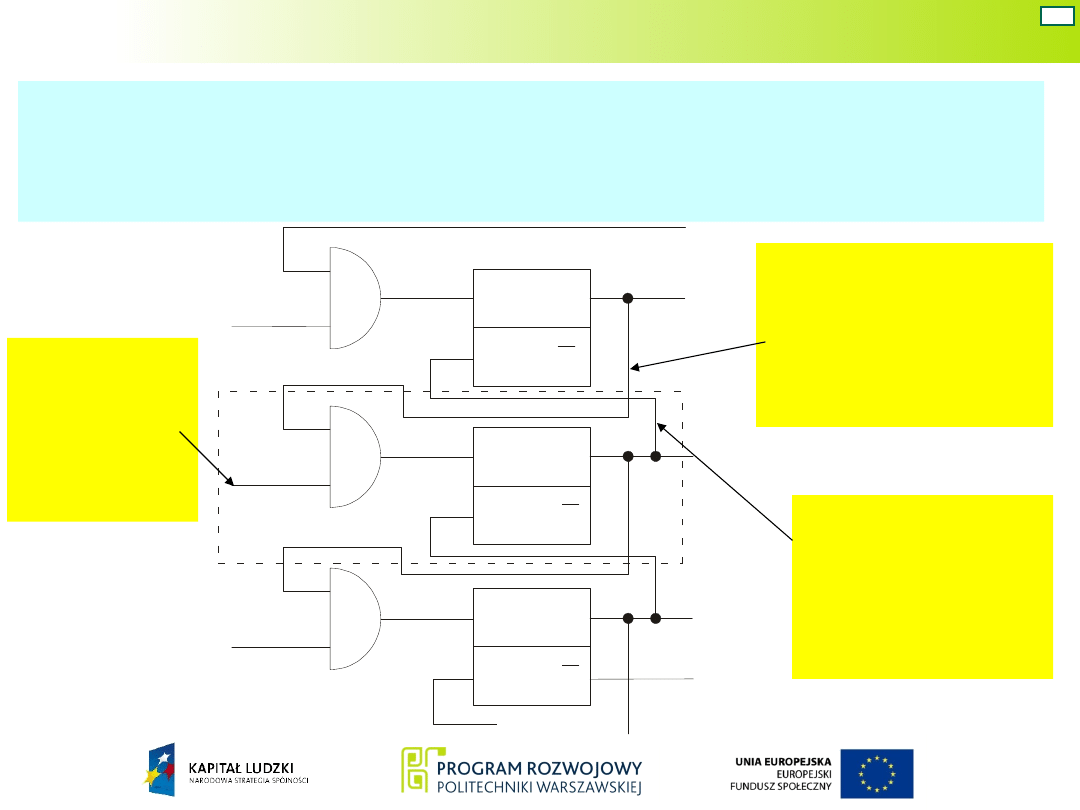
Układ Moore’a – war. 3
21
W
i
Z
i
Q
i
Q
i
W
i- 1
Q
i- 1
Q
i- 1
Z
i- 1
W
i+ 1
Z
i+ 1
Q
i+ 1
Q
i+ 1
x
i- 1
x
i
x
i+ 1
Do budowy układu realizującego zmiany stanu w
kodzie „1 z n” wykorzystuje się strukturę składającą
się z jednakowych segmentów.
sygnał
włączają
cy nowy
stan
sygnał
umożliwiający
włączenie
nowego stanu
sygnał
wyłączający
stan
poprzedni
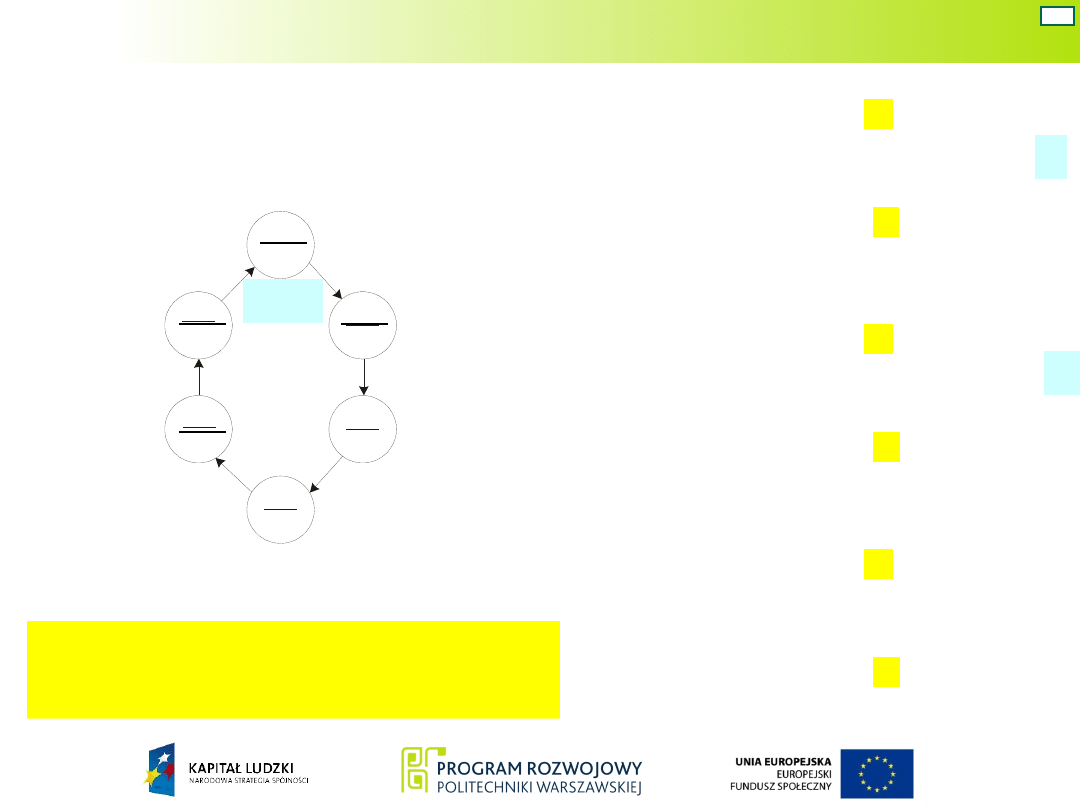
Układ Moore’a – war. 3
22
0
Q
1
Q
2
Q
3
Q
4
Q
5
Q
1
1 0
2
1 1
0
0 0
5
1 0
3
1 0
4
1 1
1 0 0 0 0 0
0 0 0 0 0 1
0 0 0 0 1 0
0 0 0 1 0 0
0 0 1 0 0 0
0 1 0 0 0 0
y y
1
2
b
c
e
c
x · a · c
d
Q
Q Q
0
4
5
Q
1
2
3
Q Q
Wariant 3 - graf i schemat
układu
2
1
, y
y
2
y
1
y
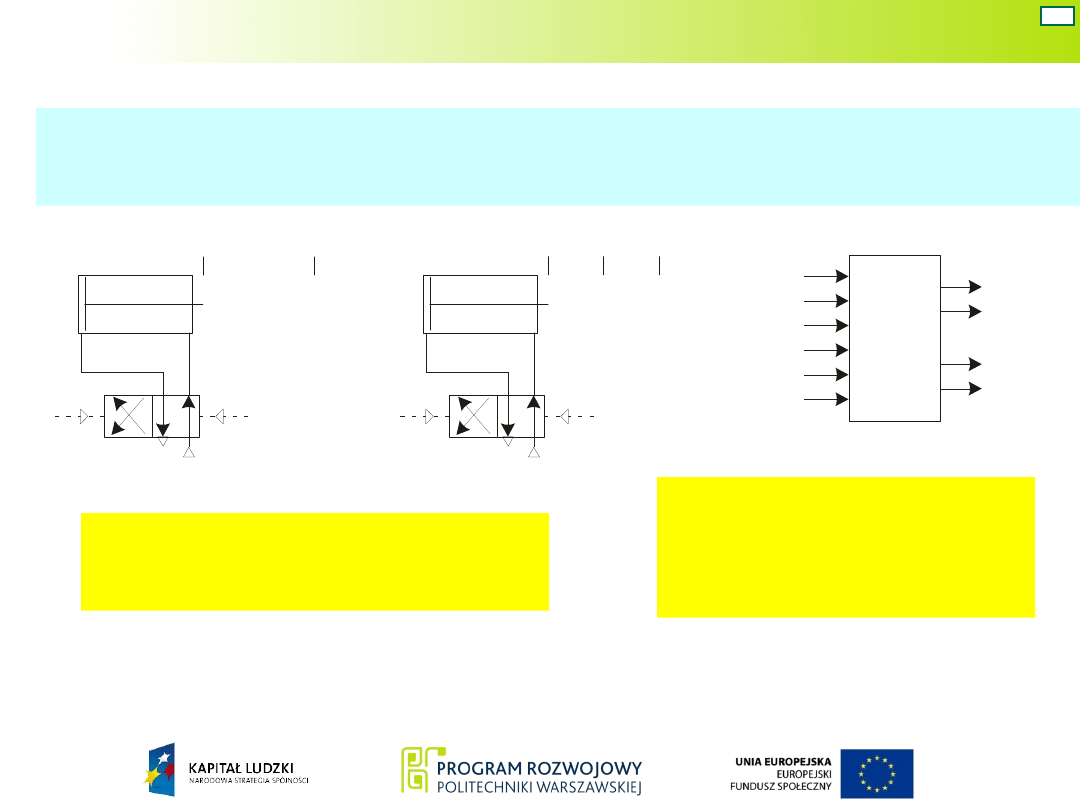
Układ Moore’a – war. 4
23
Wariant 4: układ Moore’a – kod „1 z n” – zawory
robocze bistabilne
A
B
a
b
e
c
d
a
b
c
d
e
x
A +
B +
A -
B -
A +
A -
B +
B -
Schemat układu
napędowego
Schemat blokowy
projektowanego
układu
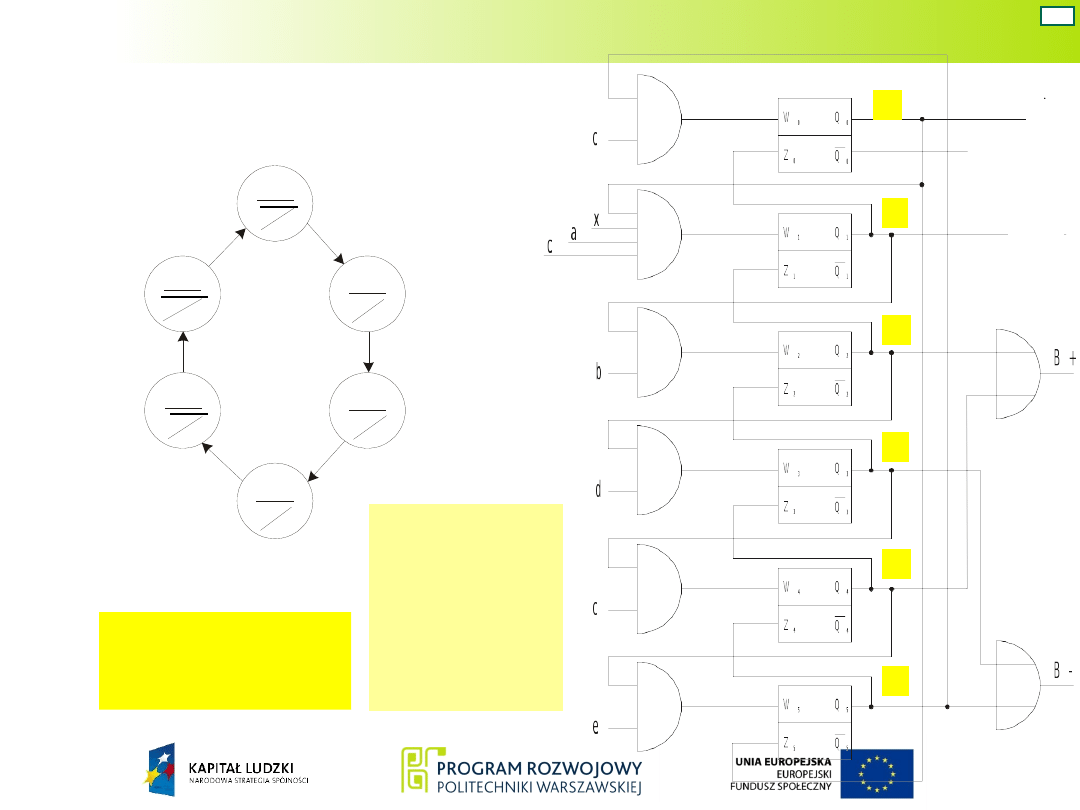
Układ Moore’a – war. 4
24
1
1 0
2
1 1
0
0 0
5
1 0
3
1 0
4
1 1
1 0 0 0 0 0
0 0 0 0 0 1
0 0 0 0 1 0
0 0 0 1 0 0
0 0 1 0 0 0
0 1 0 0 0 0
b
c
e
c
x · a · c
d
A -
B +
A +
B -
B -
B +
Q
Q Q
0
4
5
Q
1
2
3
Q Q
5
3
4
2
0
1
Q
Q
B
Q
Q
B
Q
A
Q
A
Funkcje
wyjść:
A
A
0
Q
1
Q
2
Q
3
Q
4
Q
5
Q
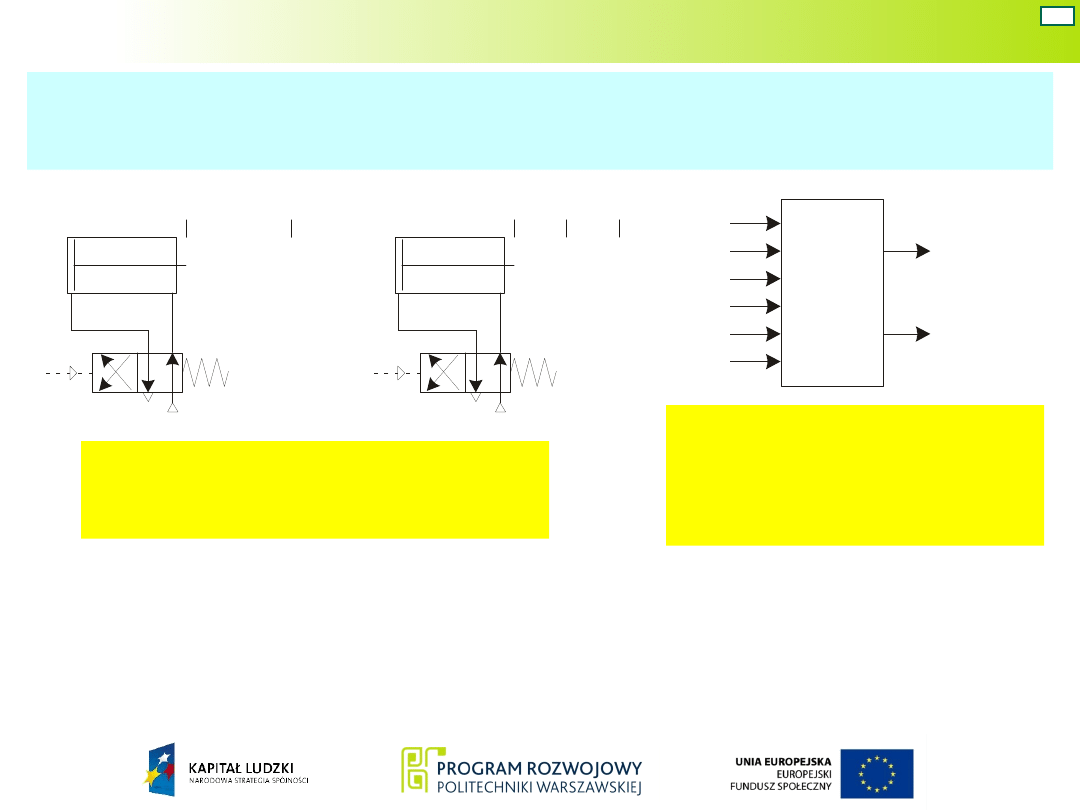
Układ Mealy’ego – war. 5
25
Wariant 5: układ Mealy’ego – kod ze stałym odstępem
– zawory robocze monostabilne
Badanie możliwości realizacji układu jako układu
Mealy’ego polega na poszukiwaniu sąsiednich stanów
wewnętrznych, w których wykonywane czynności nie
są przeciwne (nie wymagają wysuwania i wycofania
tego samego siłownika).
a
b
c
d
e
x
y
1
y
2
A
B
a
b
e
c
d
y
1
y
2
Schemat układu
napędowego
Schemat blokowy
projektowanego
układu
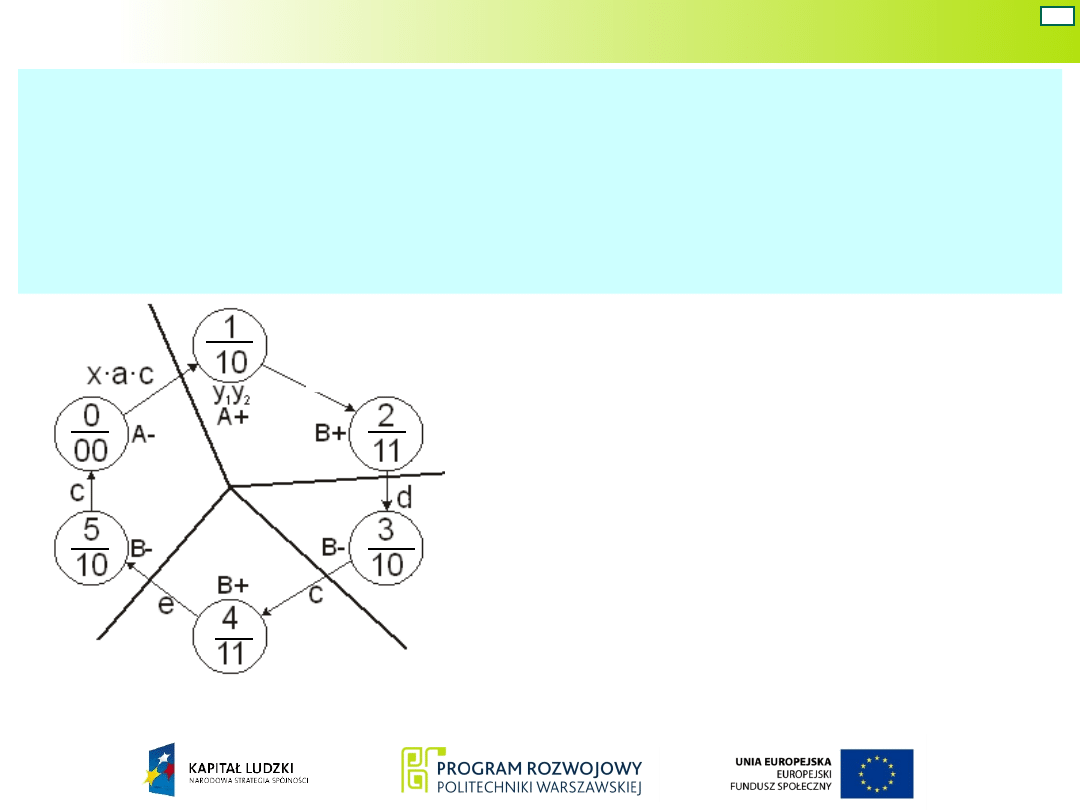
Układ Mealy’ego – war. 5
26
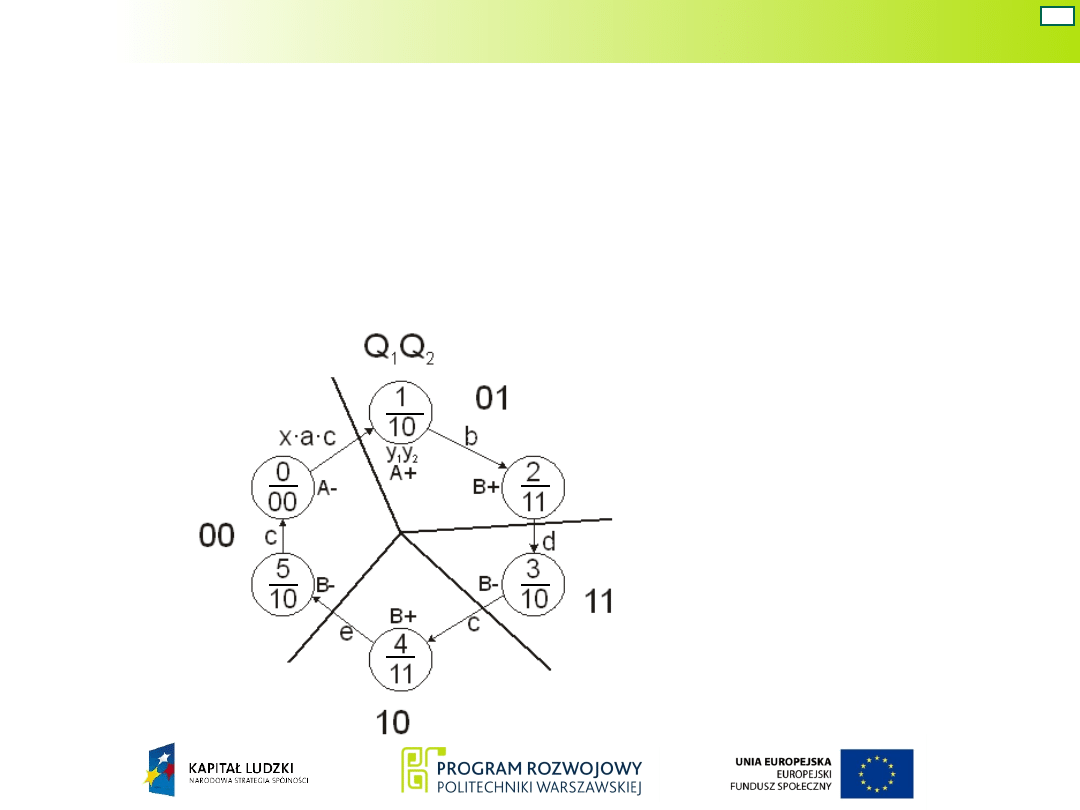
Dla ułatwienia tej czynności oznaczamy na grafie, przy
każdym stanie wewnętrznym układu Moore’a,
wykonywaną czynność, np. A+ oznacza w tym
przypadku wysuwanie siłownika A, A- oznacza
wycofanie siłownika A.
Czynności wykonywane w
stanach 1 i 2, tj. A+ i B+
nie są przeciwne, zatem te
dwa stany można w układzie
Mealy’ego traktować jako
jeden stan wewnętrzny.
Podobnie stany 5 i 0.
A
.
Układ Mealy’ego – war. 5
27
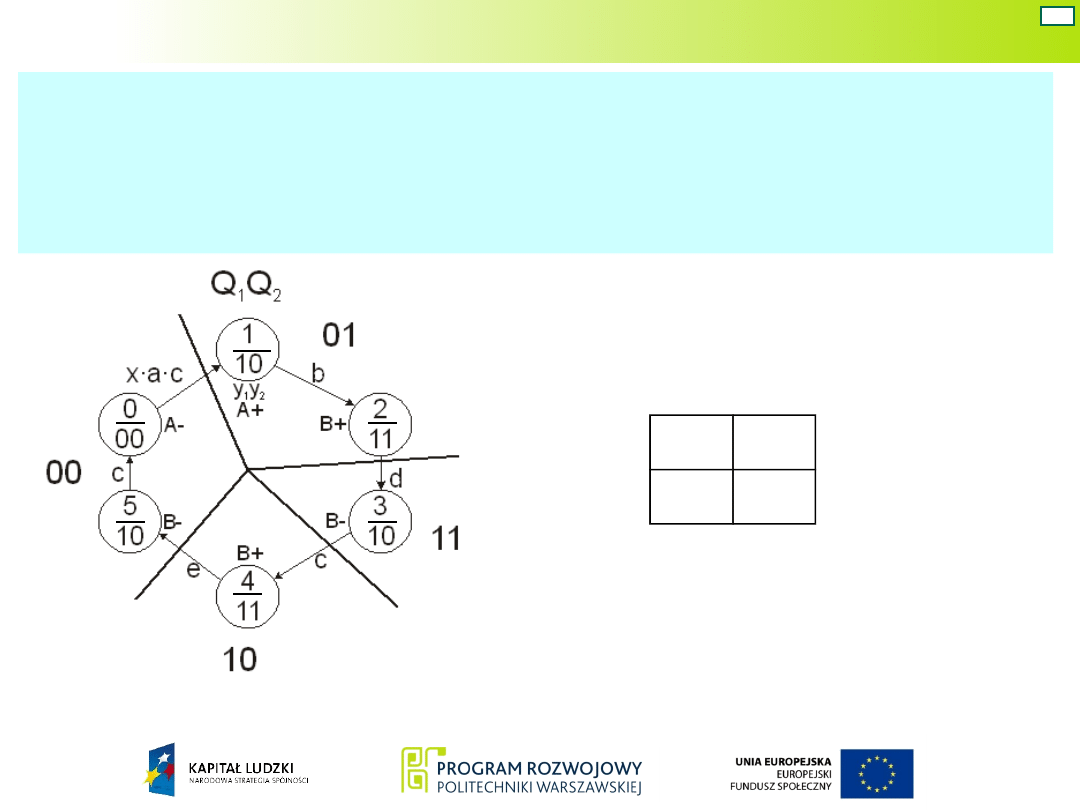
Nowe stany oddzielamy od innych liniami
wychodzącymi promieniście ze środka grafu i
wprowadzamy kody nowych stanów wewnętrznych.
W tym przypadku układ Mealy’ego ma tylko cztery
stany wewnętrzne, zatem do ich zakodowania wystarczą
dwie zmienne (dwa przerzutniki)
Q
1
i Q
2
.
Układ Mealy’ego – war. 5
28
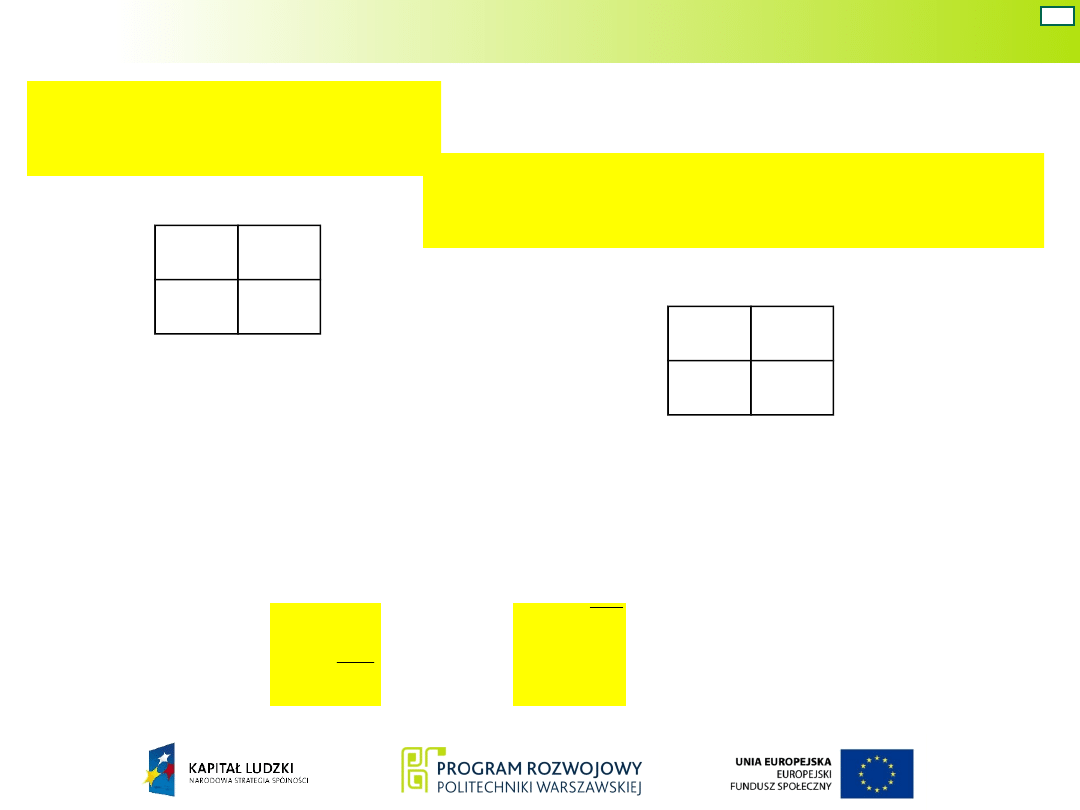
W celu ustalenia wzbudzeń przerzutników zostanie
wykorzystana metodyka jak w wariancie 1. Na
podstawie uproszczonej tablicy przejść zostaje
utworzona uniwersalna uproszczona tablica przejść.
0
1
0
01 11
1
00 10
Q
1
Q
2
'
2
'
1
,Q
Q
Uproszczona tablica
przejść
Układ Mealy’ego – war. 5
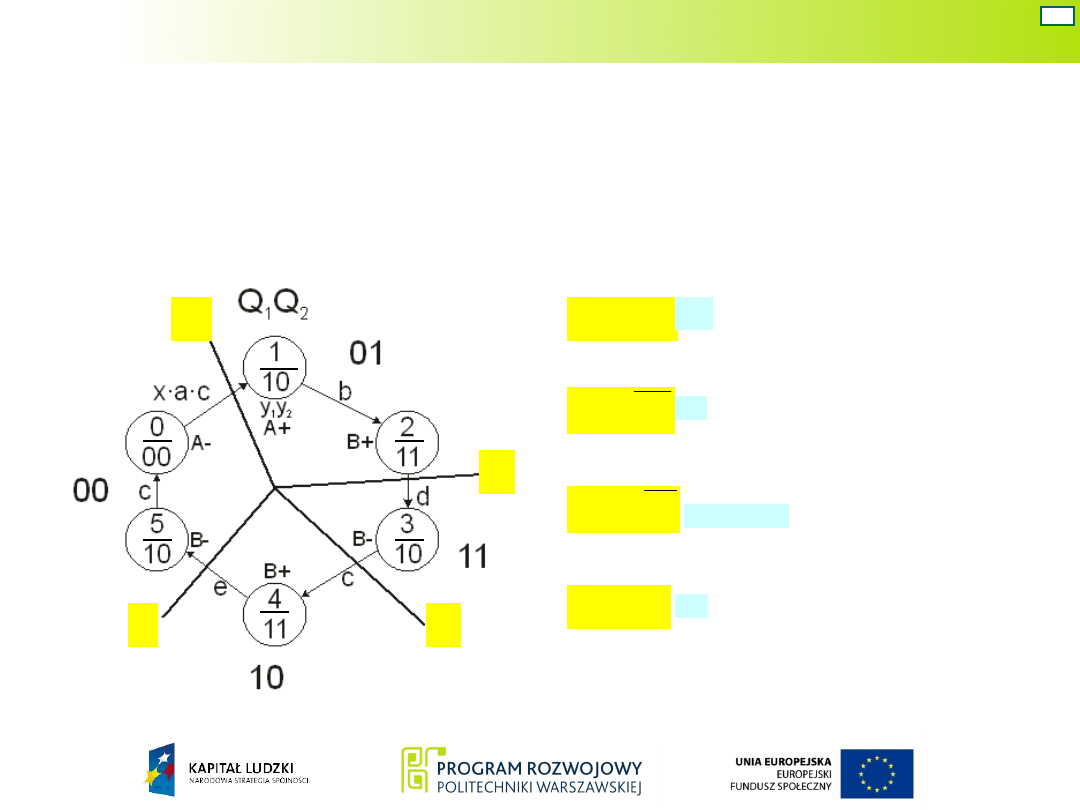
29
Uproszczona tablica
przejść
0
1
0
01 11
1
00 10
Q
1
Q
2
'
2
'
1
,Q
Q
Uproszczona uniwersalna tablica
przejść
0
1
0
0
1 1
1
1
0
0 1
0
Q
1
Q
2
'
2
'
1
,Q
Q
Na podstawie uproszczonej uniwersalnej tablicy
przejść wstępnie wyznaczamy wzbudzenia
przerzutników:
2
1
2
1
Q
z
Q
w
1
2
1
2
Q
z
Q
w
Układ Mealy’ego – war. 5
30
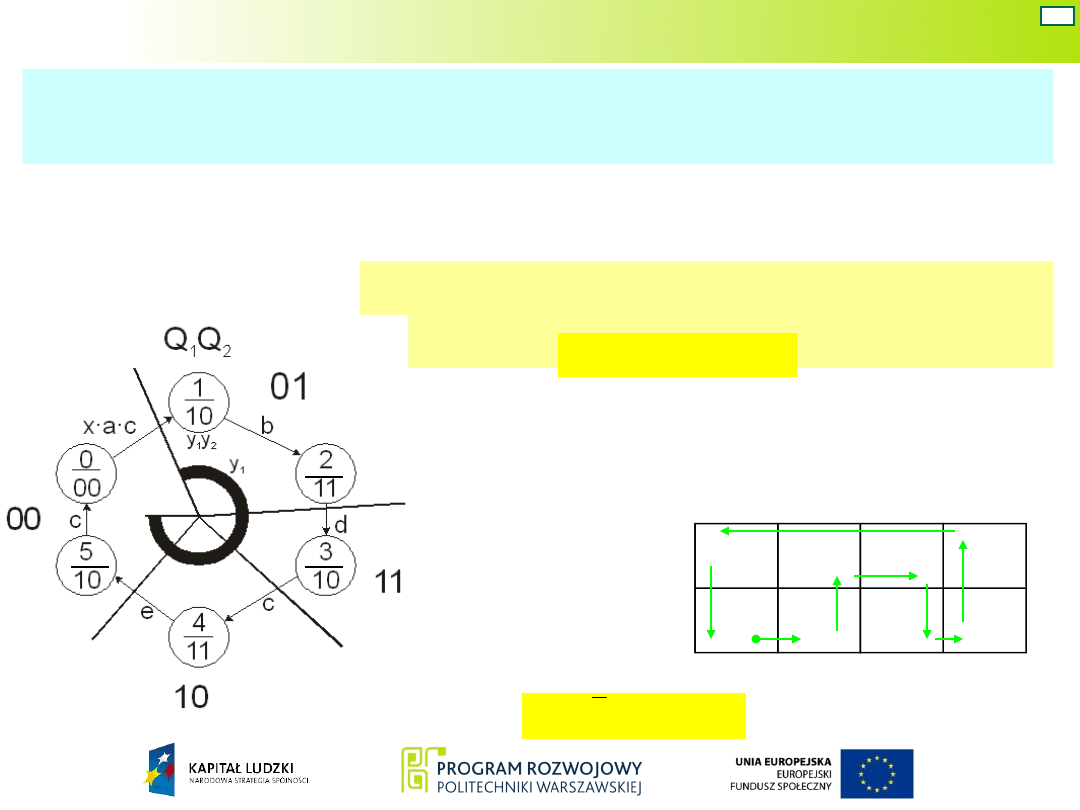
Zaznaczamy na grafie symbole wzbudzeń
powodujących zmiany stanów; uzupełniamy wstępnie
uzyskane wzbudzenia o warunki niezbędne do ich
pojawienia się:
2
1
Q
w
1
2
Q
w
2
1
Q
z
1
2
Q
z
c
a
x
d
c
e
2
w
1
w
2
z
1
z
Układ Mealy’ego – war. 5
31
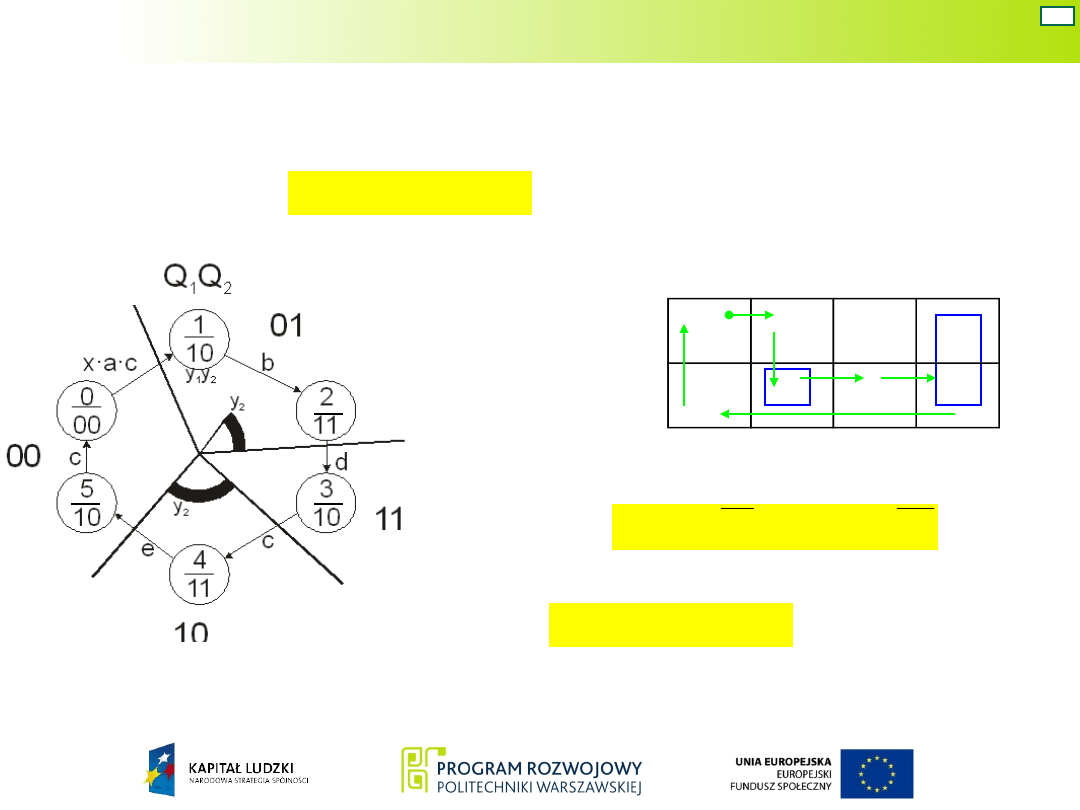
Kolejnym etapem jest wyznaczanie funkcji wyjść układu
Mealy’ego.
Z grafu układu Moore’a wynika, że układ winien
wytwarzać sygnał
y
1
= 1 w stanach 1, 2, 3, 4 i 5, a w układzie Mealy’ego w
stanach 01, 11, 10 i w stanie 00 do chwili pojawienia się
sygnału c = 1.
Zatem sygnał y
1
zależy od sygnałów
Q
1
, Q
2
i c.
)
,
,
(
2
1
1
c
Q
Q
f
y
Funkcję
przedstawia tablica Karnaugha.
2
1
1
Q
Q
c
y
00 01 11 10
0
1
1
1
1
1
0
1
1
1
y
1
c
Q
1
,Q
2
Układ Mealy’ego – war. 5
32
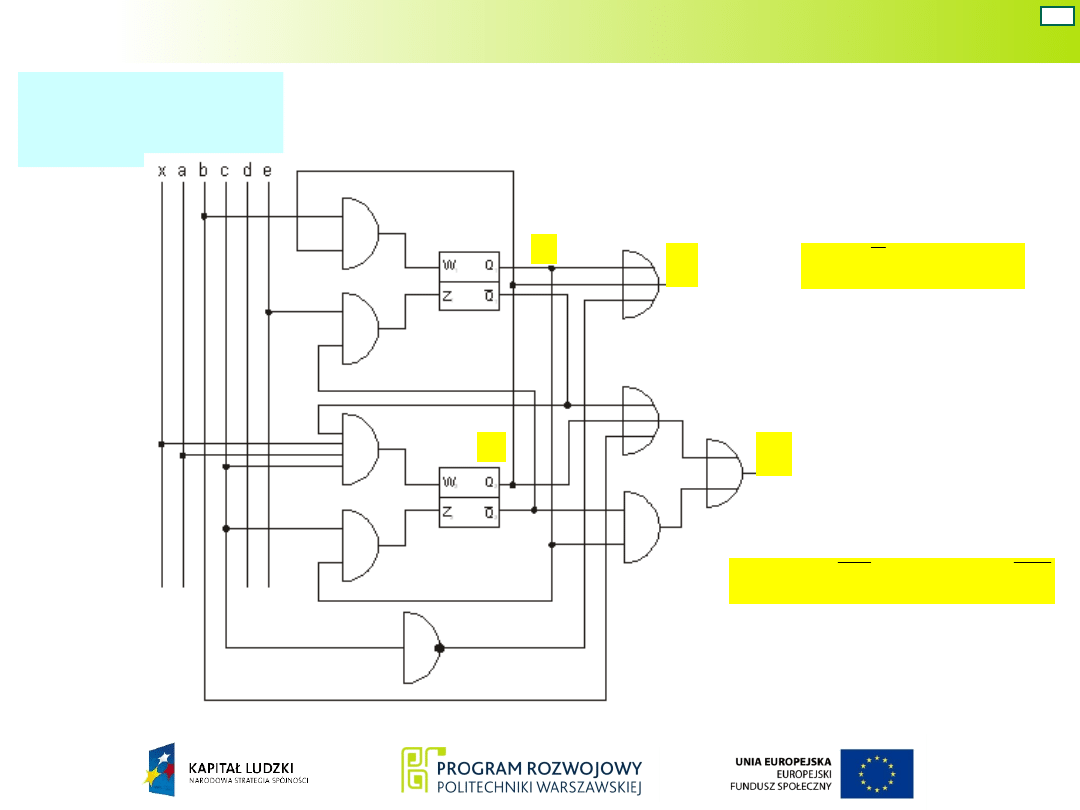
Analogicznie z grafu wynika, że sygnał y
2
= 1 powinien
być wytworzony w stanie 01 od chwili pojawienia się
sygnału b oraz w stanie 10. Zatem
)
,
,
(
2
1
2
b
Q
Q
f
y
2
1
2
1
2
Q
Q
Q
Q
b
y
)
,
,
(
2
1
2
b
Q
Q
f
y
Funkcja jest
nie w pełni określona; w stanach
11 i 10 sygnał b przyjmuje tylko
wartość 1.
00 01 11 10
0
0
0
-
-
1
0
1
0
1
y
2
b
Q
1
,Q
2
Układ Mealy’ego – war. 5
33
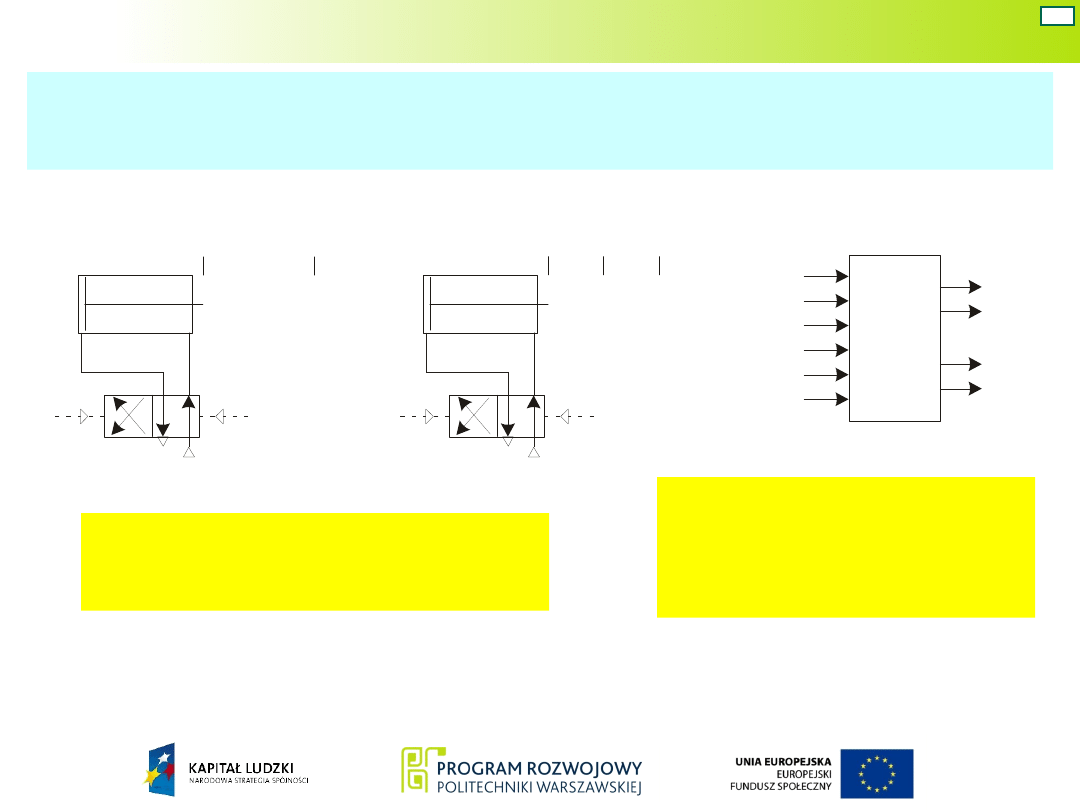
Schemat
układu
1
y
2
y
2
1
1
Q
Q
c
y
2
1
2
1
2
Q
Q
Q
Q
b
y
1
Q
2
Q
Układ Mealy’ego – war. 6
34
Wariant 6: układ Mealy’ego – kod ze stałym odstępem
– zawory robocze bistabilne
A
B
a
b
e
c
d
a
b
c
d
e
x
A +
B +
A -
B -
A +
A -
B +
B -
Schemat układu
napędowego
Schemat blokowy
projektowanego
układu
Część układu realizująca funkcję przejść pozostaje jak
w wariancie 5. Zmienia się część układu realizująca
funkcję wyjść.
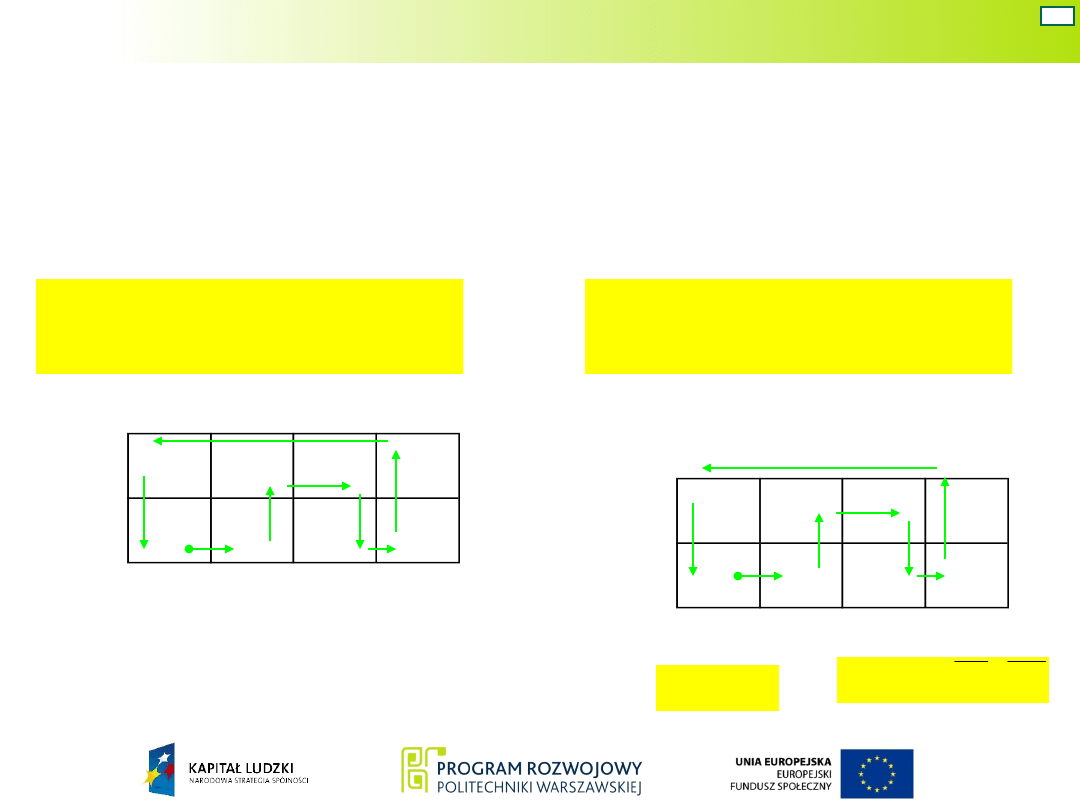
Układ Mealy’ego – war. 6
35
Analogicznie jak w wariancie 2, tablice wyjść
przekształcamy w uniwersalne tablice stanów zaworów
roboczych, na podstawie których wyznacza się sygnały
A+, A-, B+ i B-.
W tym celu niezbędne jest wskazanie kolejności zmian
stanów wyjść.
00 01 11 10
0
1
1
1
1
1
0
1
1
1
A
c
Q
1
,Q
2
Tablica stanów zaworu
A
Uniwersalna tablica
stanów zaworu A
2
Q
A
2
1
Q
Q
c
A
00 01 11 10
0
1
1
1
1
1
0
1
1
1
A
c
Q
1
,Q
2
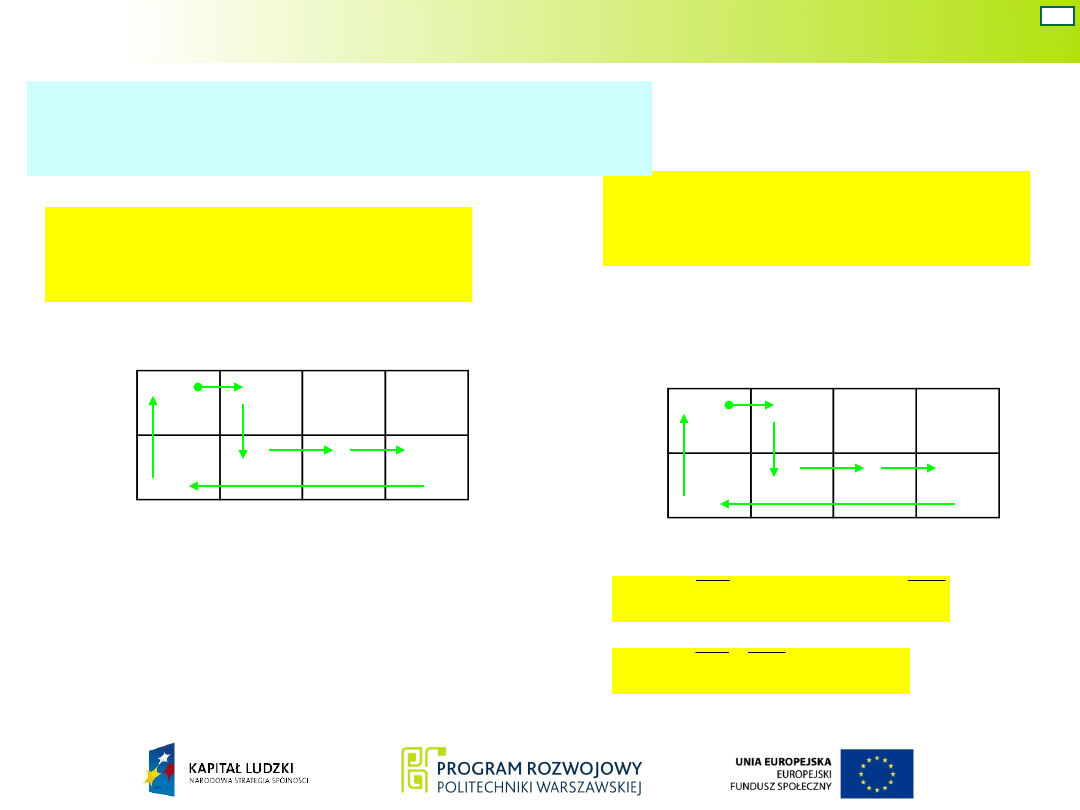
Układ Mealy’ego – war. 6
36
00 01 11 10
0
0
0
-
-
1
0
1
0
1
B
b
Q
1
,Q
2
Tablica stanów zaworu
B
Uniwersalna tablica
stanów zaworu B
2
1
2
1
Q
Q
b
Q
Q
B
2
1
2
1
Q
Q
Q
Q
B
Podobnie wyznacza się sygnały
B+ i B-.
00 01 11 10
0
0
0
-
-
1
0
1
0
1
B
b
Q
1
,Q
2
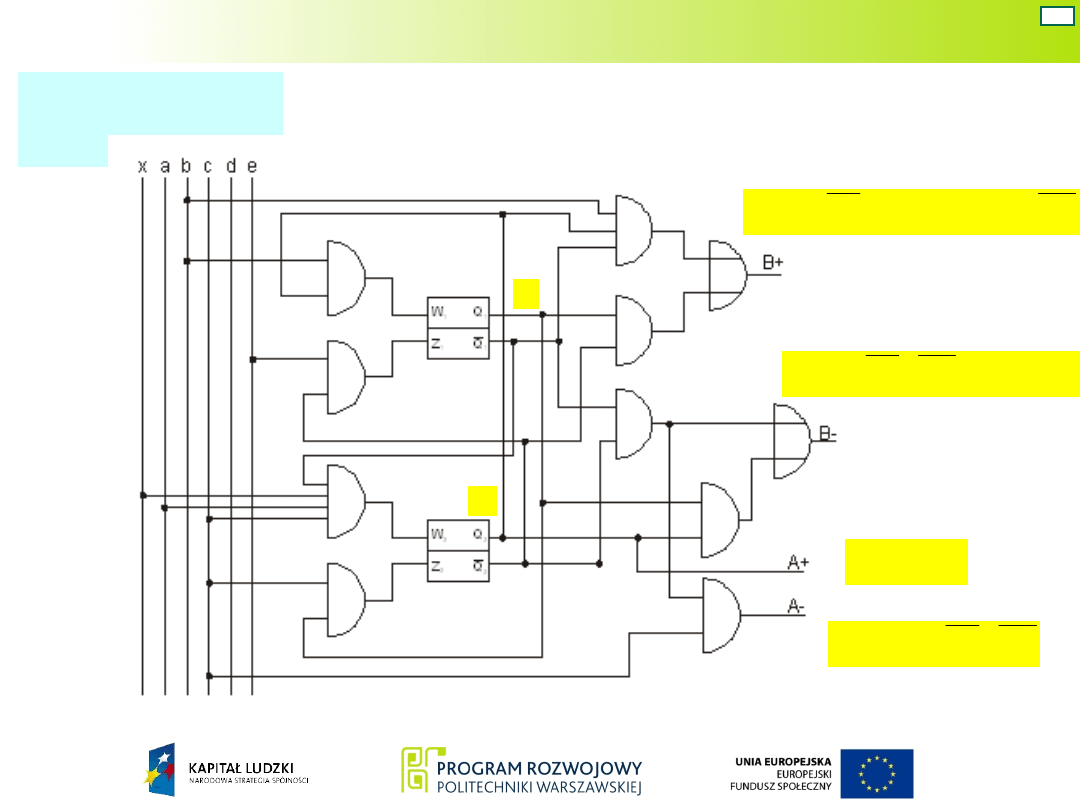
Układ Mealy’ego – war. 6
37
Schemat
układu
2
Q
1
Q
2
Q
A
2
1
Q
Q
c
A
2
1
2
1
Q
Q
b
Q
Q
B
2
1
2
1
Q
Q
Q
Q
B
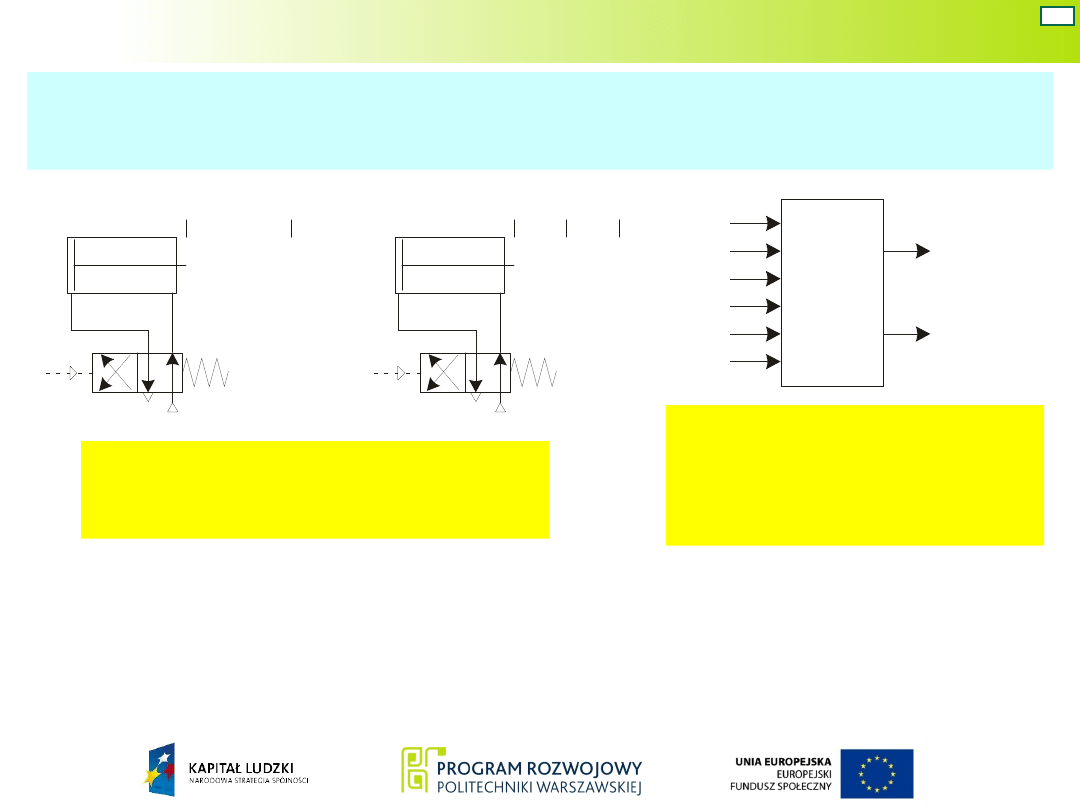
Układ Mealy’ego – war. 7
38
Wariant 7: układ Mealy’ego – kod „1 z n” – zawory
robocze monostabilne
a
b
c
d
e
x
y
1
y
2
A
B
a
b
e
c
d
y
1
y
2
Schemat układu
napędowego
Schemat blokowy
projektowanego
układu
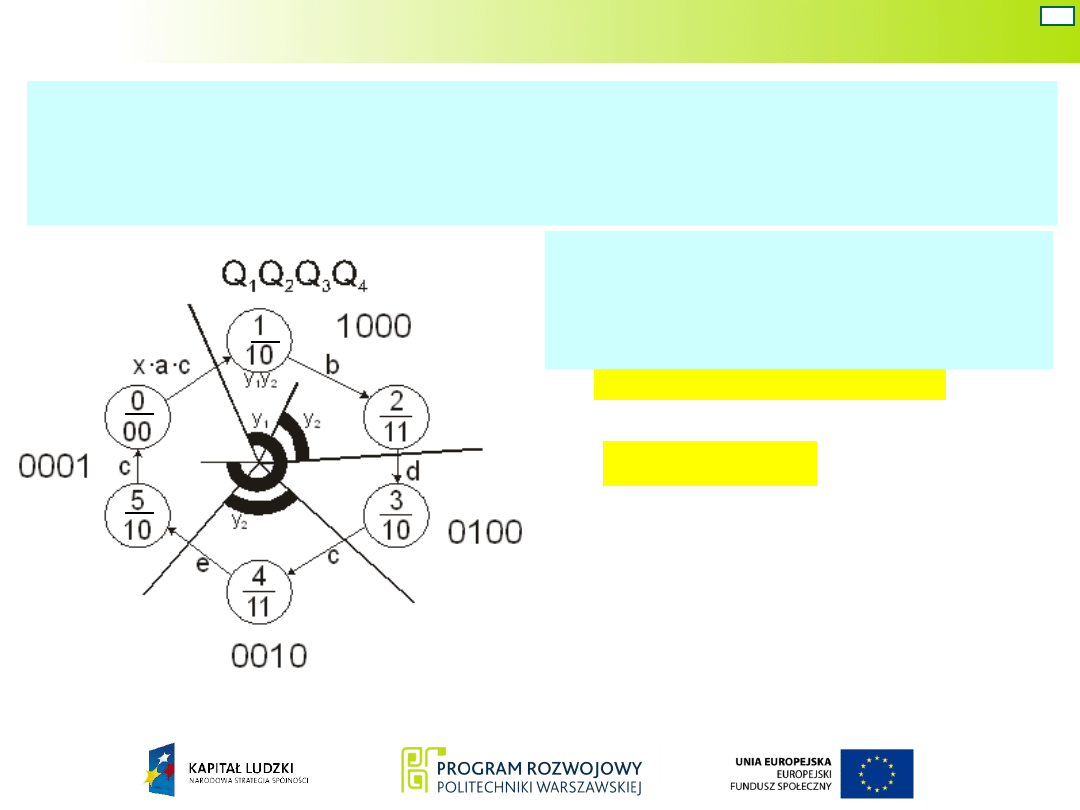
Układ Mealy’ego – war. 7
39
Do zakodowania czterech stanów wewnętrznych w
kodzie „1 z n” niezbędne są cztery zmienne, oznaczone
jako Q
1
, Q
2
, Q
3
i Q
4
.
c
Q
Q
Q
Q
y
4
3
2
1
1
3
1
2
Q
b
Q
y
Funkcje wyjść ustala się
bezpośrednio na podstawie
grafu:
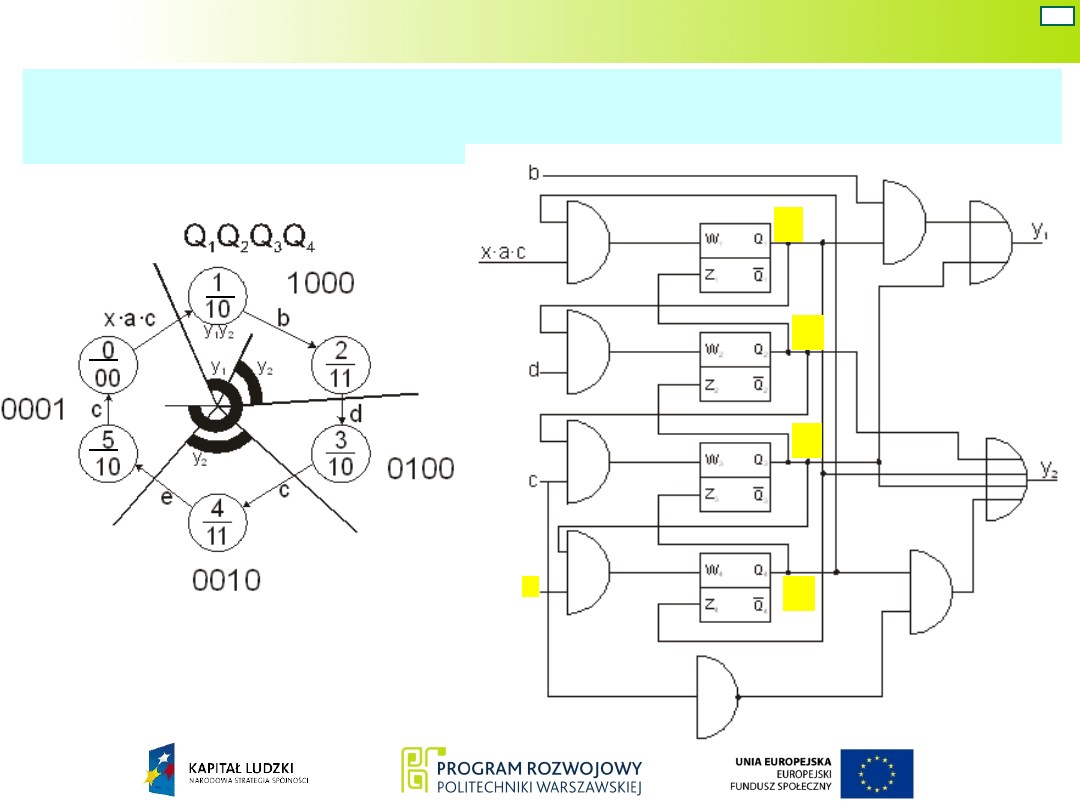
Układ Mealy’ego – war. 7
40
Także na podstawie grafu ustala się sygnały wejściowe
przerzutników.
1
Q
2
Q
3
Q
4
Q
e
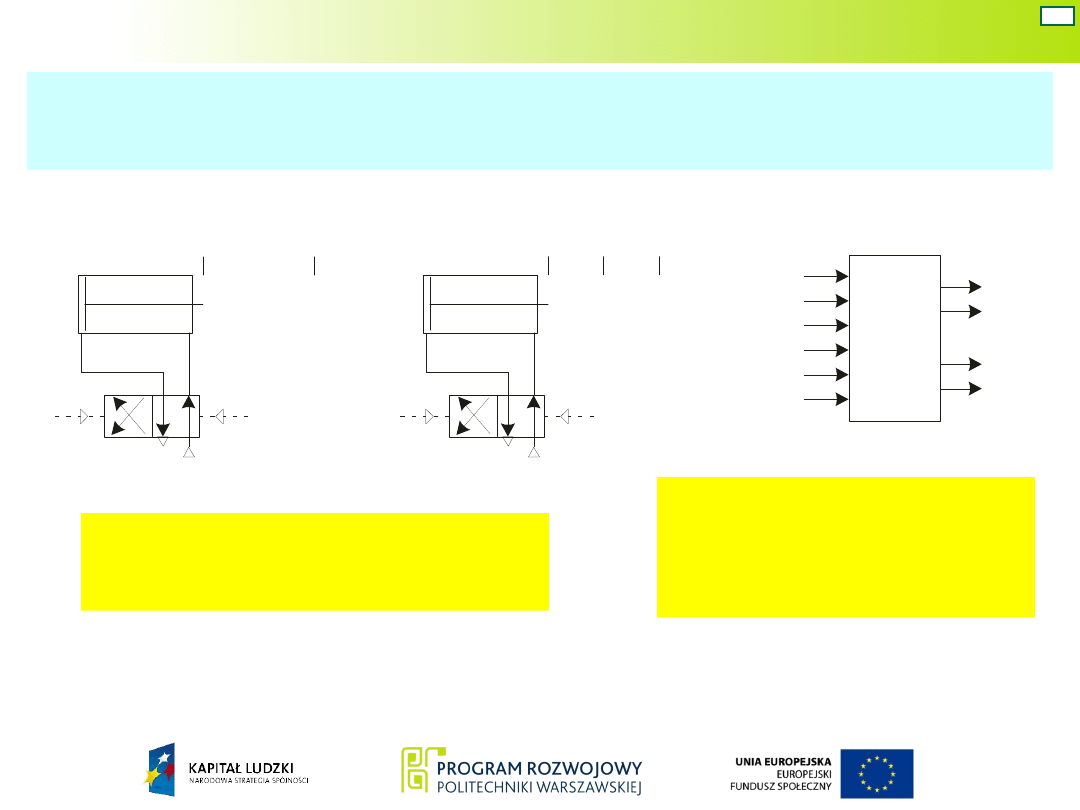
Układ Mealy’ego – war. 8
41
Wariant 8: układ Mealy’ego – kod „1 z n” – zawory
robocze bistabilne
A
B
a
b
e
c
d
a
b
c
d
e
x
A +
B +
A -
B -
A +
A -
B +
B -
Schemat układu
napędowego
Schemat blokowy
projektowanego
układu
Część układu realizująca funkcję przejść pozostaje jak
w wariancie 7. Zmienia się tylko część układu
realizująca funkcję wyjść.
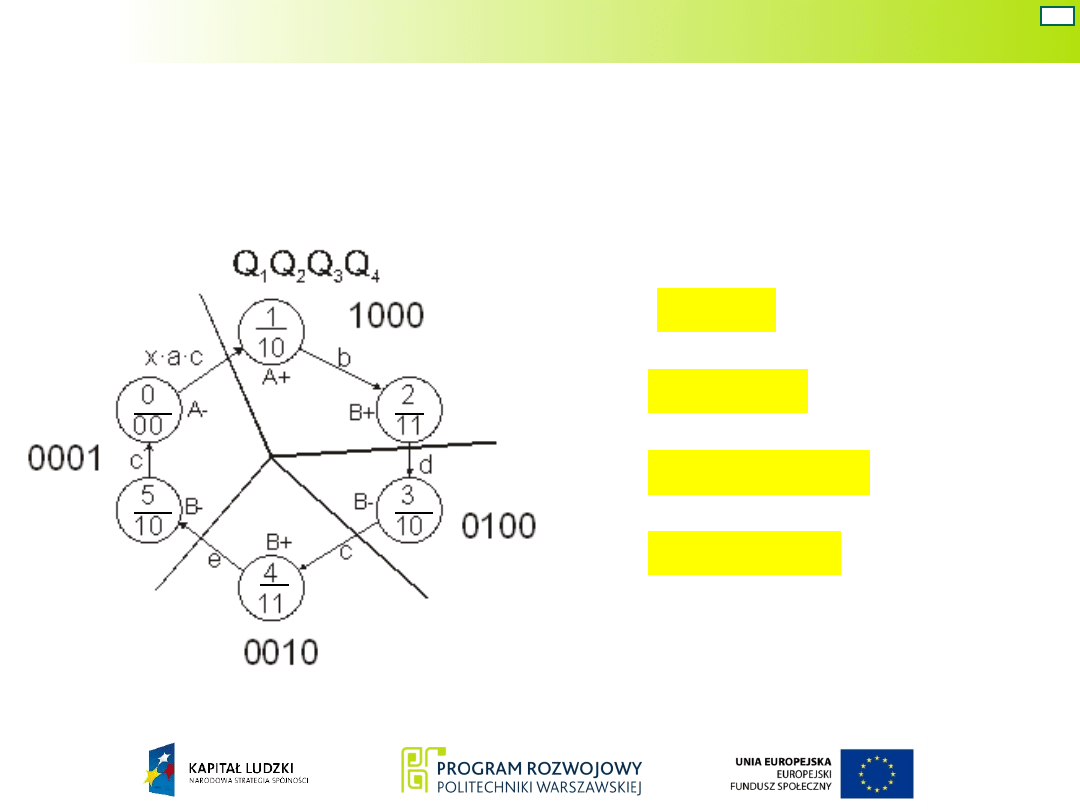
Układ Mealy’ego – war. 8
42
Oznaczając na grafie miejsca, w których należy
wytworzyć sygnały sterujące zaworami bistabilnymi,
sygnały wyjściowe układu wyznacza się bezpośrednio
na podstawie grafu.
1
Q
A
c
Q
A
4
3
1
Q
b
Q
B
4
2
Q
Q
B
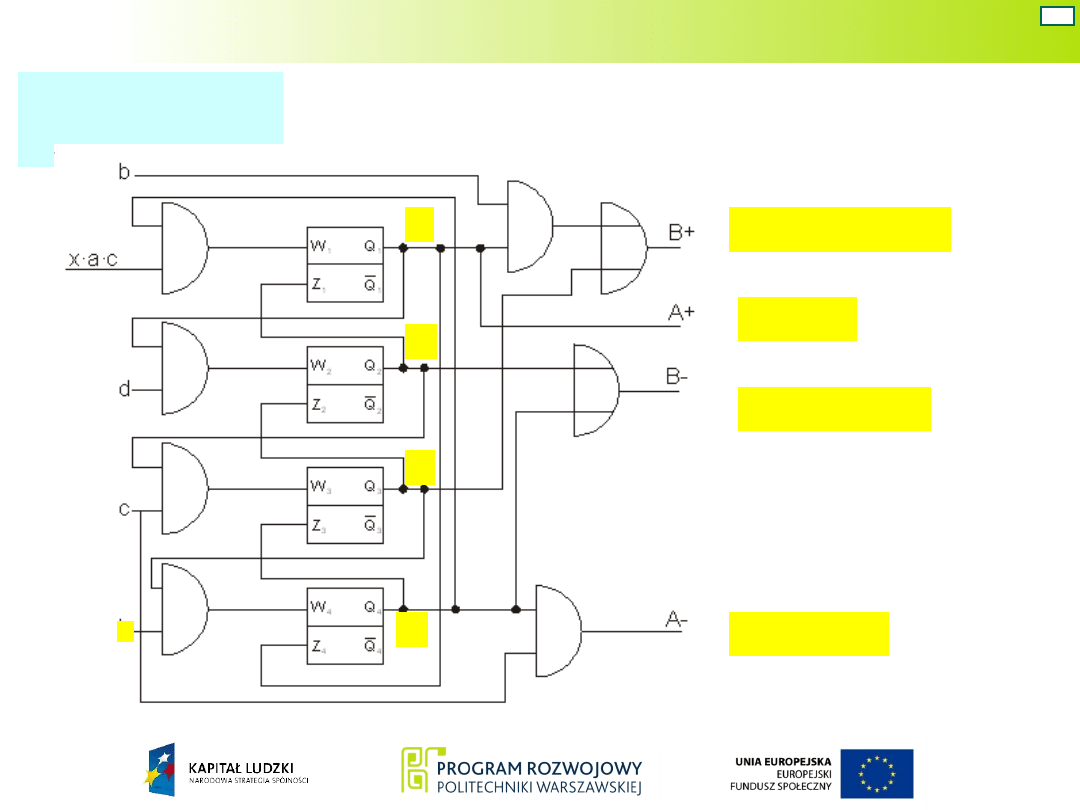
Układ Mealy’ego – war. 8
43
Schemat
układu
e
1
Q
2
Q
3
Q
4
Q
1
Q
A
c
Q
A
4
3
1
Q
b
Q
B
4
2
Q
Q
B
Zajęcia współfinansowane przez Unię Europejską w
Zajęcia współfinansowane przez Unię Europejską w
ramach
ramach
Europejskiego Funduszu Społecznego
Europejskiego Funduszu Społecznego
Dziękuję za uwagę
Dziękuję za uwagę
Document Outline