Układy sekwencyjne o programach

rozgałęzionych

1

W procesie projektowania układów sekwencyjnych
można wyróżnić etapy:

formalizacja założeń, czyli sprecyzowanie
założeń dotyczących działania układu w postaci
umożliwiającej

tworzenie

jego

opisu

matematycznego (w etapie tym wyodrębnia się
stany wewnętrzne układu, często w ilości większej
niż jest to niezbędne i przypisuje im stany wyjść -
przyjmuje się zatem model układu Moore’a;
najczęściej wyjściową formą zapisu działania
automatu jest pierwotna tablica przejść i wyjść,
graf lub sieć działań,

minimalizacja liczebności zbioru stanów
wewnętrznych
(w etapie tym podejmuje się również decyzję o
ewentualnej zmianie układu Moore'a na układ
Mealy'ego, co prowadzi do dalszego,
zmniejszenia liczby stanów wewnętrznych),

Układy sekwencyjne o programach

rozgałęzionych

2

kodowanie, czyli przypisanie poszczególnym
stanom wewnętrznym stanów sygnałów
pamięciowych,

wyznaczanie funkcji wyjść,

wyznaczanie funkcji przejść, albo - w przypadku
zastosowania wydzielonego bloku przerzutników –
wyznaczanie funkcji wzbudzeń przerzutników,

podjęcie decyzji dotyczącej techniki realizacji
układu sterującego (np.: przekaźnikowy,
bramkowy elektroniczny – pneumatyczny),

sporządzenie schematów strukturalnych i
montażowych.

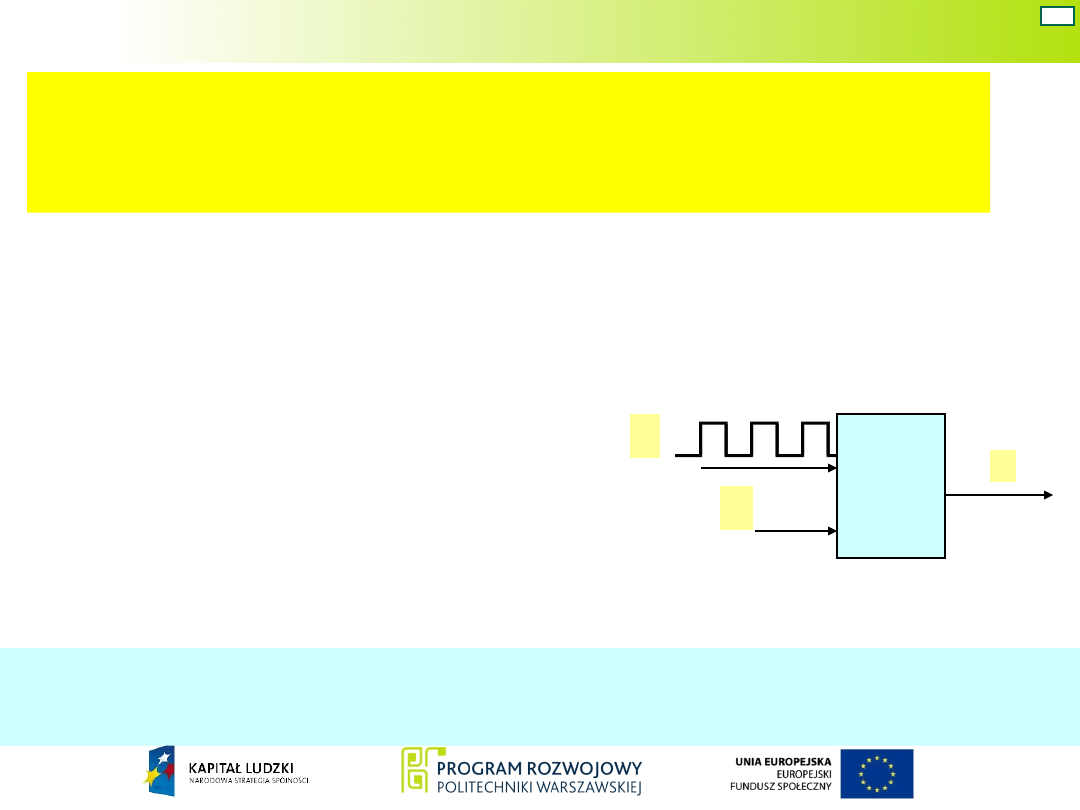
Układ Moore’a

3

Przykła
d

Sygnał wejściowy x

1

układu jest ciągiem impulsów

prostokątnych. Zadaniem układu jest odtwarzanie na
wyjściu y tych impulsów sygnału x

1

, które

rozpoczynają się w stanie gdy drugi sygnał
wejściowy x

2

ma wartość 1.

Rozwiąza
nie

y

1

x

2

x

Przebieg sygnału x

2

nie jest

określony;
rozważając zachowanie układu
należy
przewidzieć możliwe sekwencje
jego zmian w stosunku do
przebiegu sygnału x

1

.

Niezdeterminowany przebieg zmian sygnałów wejściowych jest
charakterystyczną cechą układów o programach rozgałęzionych.

Projektowanie układów Moore’a bez wydzielonego
bloku
przerzutników

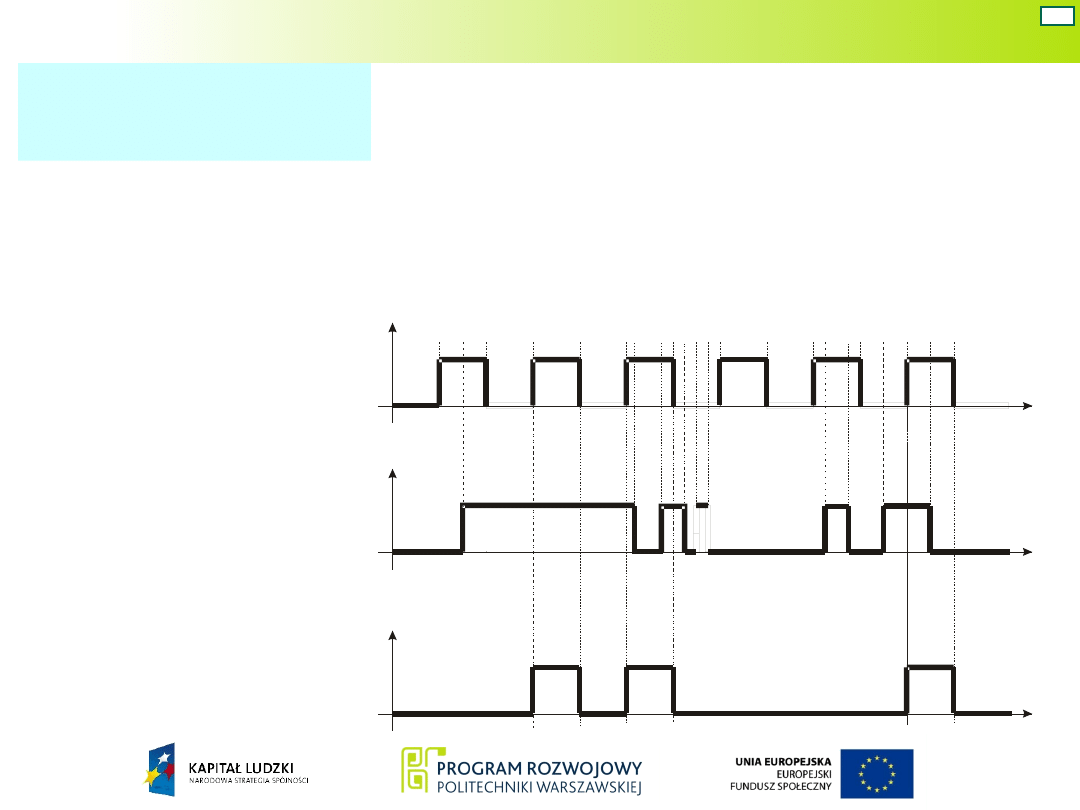
Układ Moore’a

4

Tworzymy przykładowy przebieg zmian sygnałów
wejściowych
i odpowiadający mu przebieg sygnału wyjściowego.

Formalizacja
założeń

t

t

t

x

1

x

2

y

0

2

1

3

4

4

3

5 4 0

3

3

0 1

0

1 2 1 0 3 4 5

0

Wyróżnia się tzw. pierwotne stany wewnętrzne o
różnych zestawach wartości sygnałów.

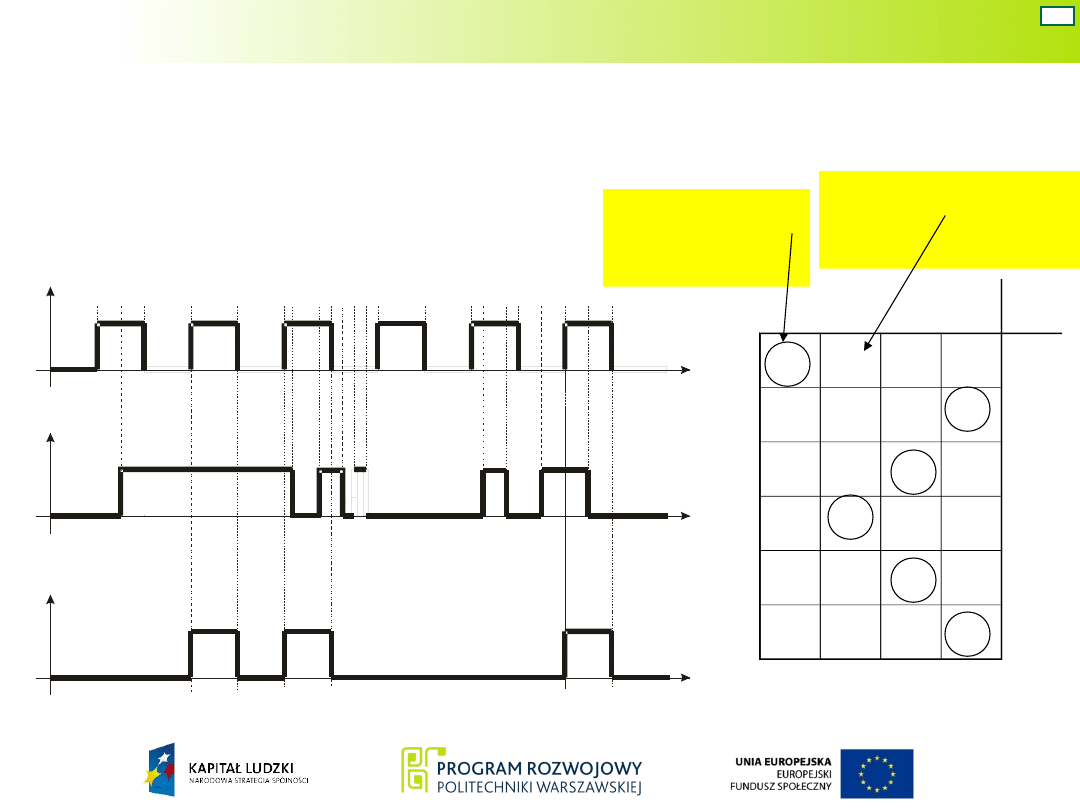
Układ Moore’a

5

t

t

t

x

1

x

2

y

0

2

1

3

4

4

3

5 4 0

3

3

0 1

0

1 2 1 0 3 4 5

0

00 01 11 10

y

0 0 3

1 0

1 0

2 1 0

2

3 2

0

3 0 3 4

0

4

3 4 5 1

5 0

4 5 1

Q

t+1

2

1

x

x

t

Q

Na podstawie przebiegu czasowego tworzy się tzw. pierwotną
tablicę przejść i wyjść, wyróżniając stany stabilne układu.

stan
stabilny

stan
niestabilny

Układ Moore’a

6

00 01 11 10

y

0 0 3

-

1 0

1 0

-

2 1 0

2 -

3 2

0

3 0 3 4

-

0

4 -

3 4 5 1

5 0

-

4 5 1

Q

t+1

00 01 11 10

y

0 0 3

-

1 0

1 0

-

2 1 0

2 -

3 2 1 0

3 0 3 4

-

0

4 -

3 4 5 1

5 0

-

4 5 1

Q

t+1

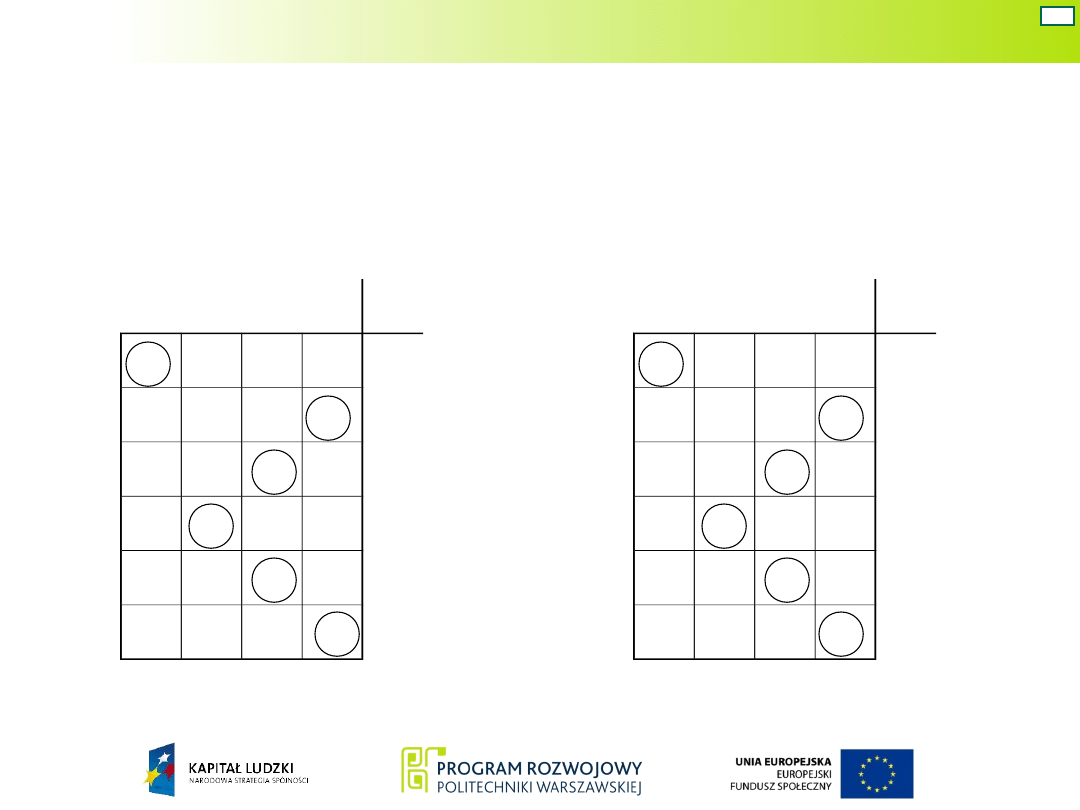
Nie wypełnione kratki mogą odpowiadać stanom nie określonym
(niemożliwym do osiągnięcia – nie jest możliwa jednoczesna zmiana
obu sygnałów wejściowych) lub nie uwzględnionym w wymyślonym
przebiegu czasowym.

t

Q

t

Q

2

1

x

x

2

1

x

x

Układ Moore’a

7

0
0

01 11 10

y

0 0 3

-

1 0

1 0

-

2 1 0

2 -

3 2 1 0

3 0 3 4

-

0

4 -

3 4 5 1

5 0

-

4 5 1

Q

t+1

00 01 11 10

y

0 0 1 0 0 0
1 0 1 2

-

0

2 0 1 2 2 1

Q

t+1

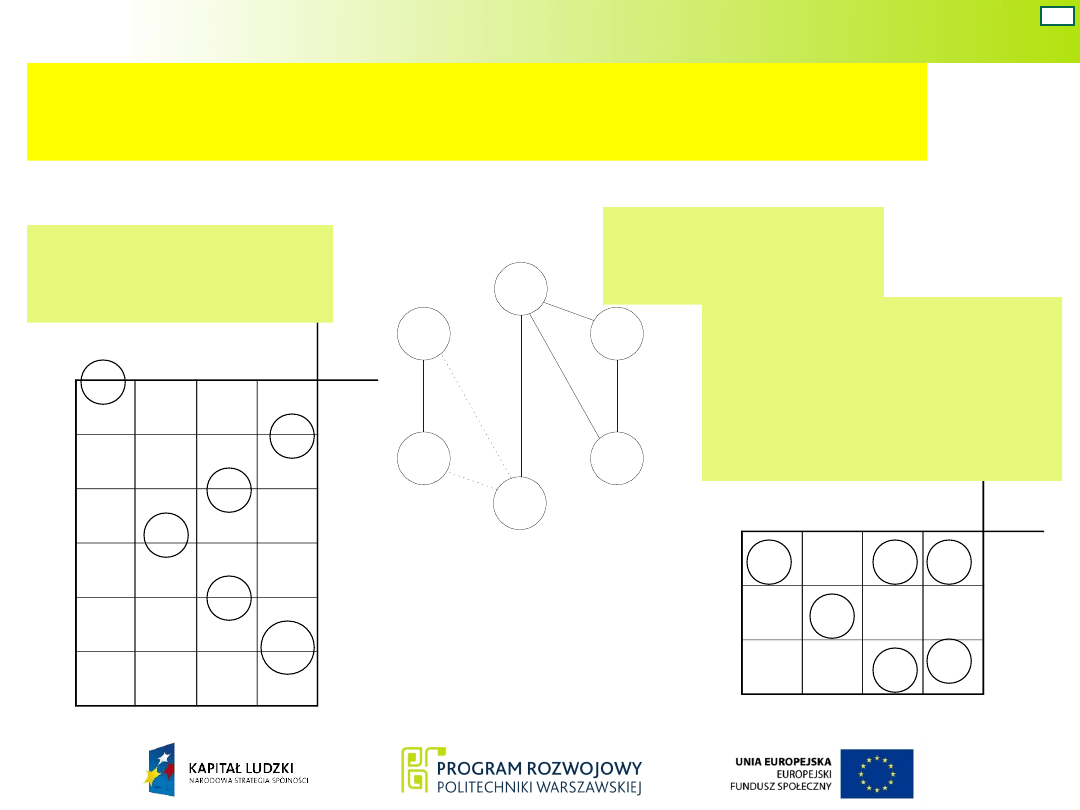
Minimalizacja liczebności zbioru stanów
wewnętrznych

0

1

2

3

4

5

t

Q

t

Q

Posługując się tzw. wykresem skracania poszukuje się możliwości
zastąpienia kilku stanów jednym.

)

2

,

1

,

0

(

)

3

(

)

5

,

4

(

Tablica
pierwotna

Wykres
skracania

Tablica minimalna
– z minimalną
liczbą stanów
wewnętrznych

2

1

x

x

2

1

x

x

Układ Moore’a

8

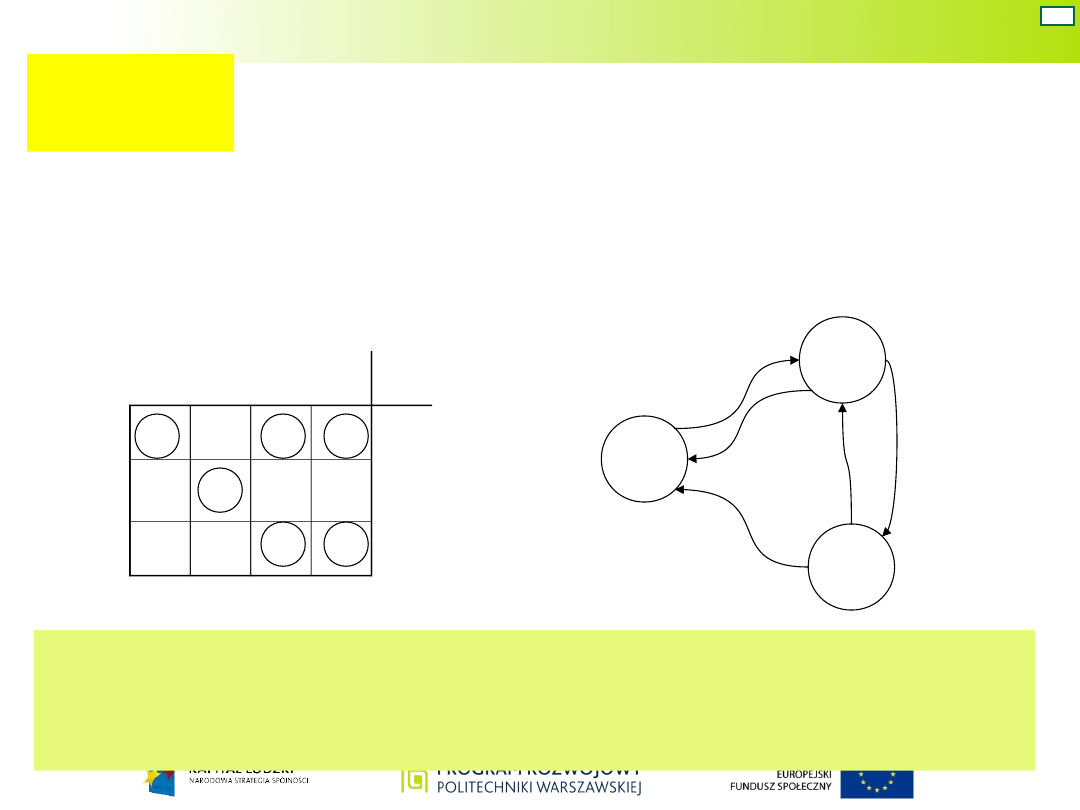
Kodowan
ie

Do zakodowania trzech stanów wewnętrznych
niezbędne są dwie zmienne, np. Q

1

i Q

2

.

.

Do analizy możliwości przypisania poszczególnym
stanom odpowiednich kodów zostanie wykorzystany
tzw. wykres przejść.

00 01 11 10

y

0 0 1 0 0 0
1 0 1 2

-

0

2 0 1 2 2 1

Q

t+1

2

1

Q

Q

0

1

2

00

01

11

Przejście ze stanu 2 do 1 wymagałoby jednoczesnej
zmiany dwóch sygnałów, co jest niemożliwe (zjawisko
wyścigu).

t

Q

2

1

x

x

Układ Moore’a

9

2

1

Q

Q

0

1

2

00

01

11

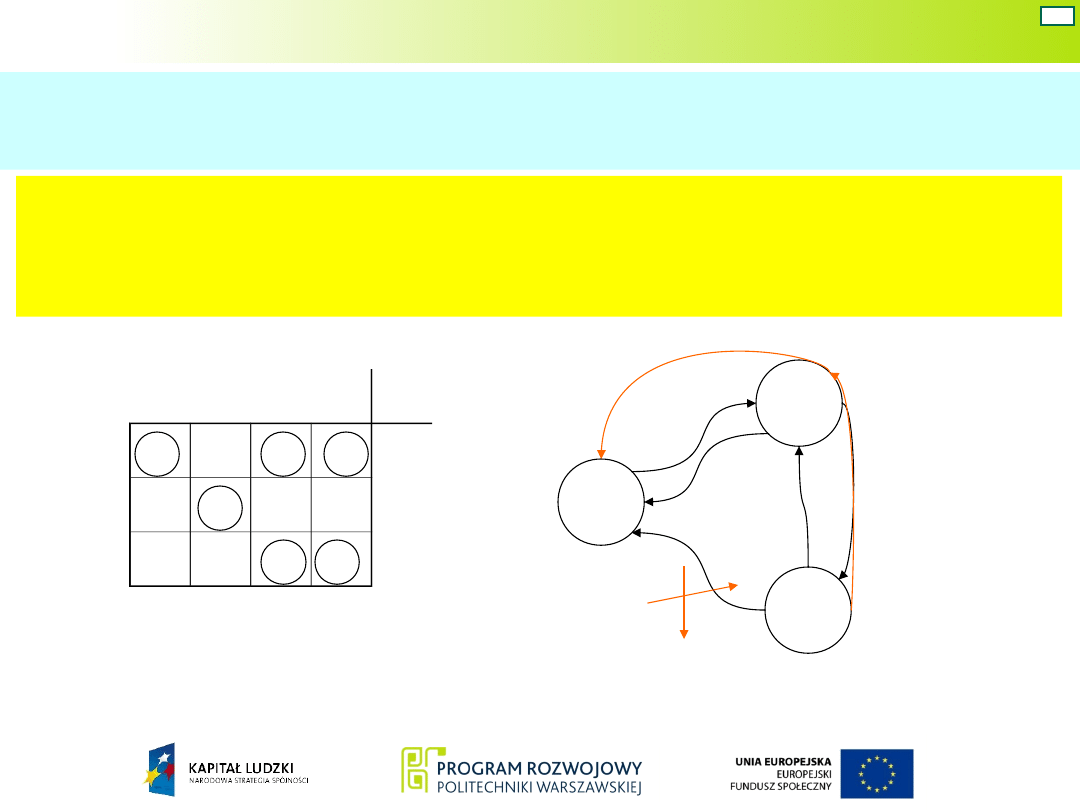
Możliwości modyfikacji tablicy przejść i wyjść w celu uniknięcia
wyścigu.

1. Zastosowanie tzw. przejścia cyklicznego poprzez

stan 1, co eliminuje konieczność przejścia ze stanu
2 do 0.

00 01 11 10

y

0 0 1 0 0 0
1 0 1 2

-

0

2

1

1 2 2 1

Q

t+1

t

Q

2

1

x

x

Układ Moore’a

10

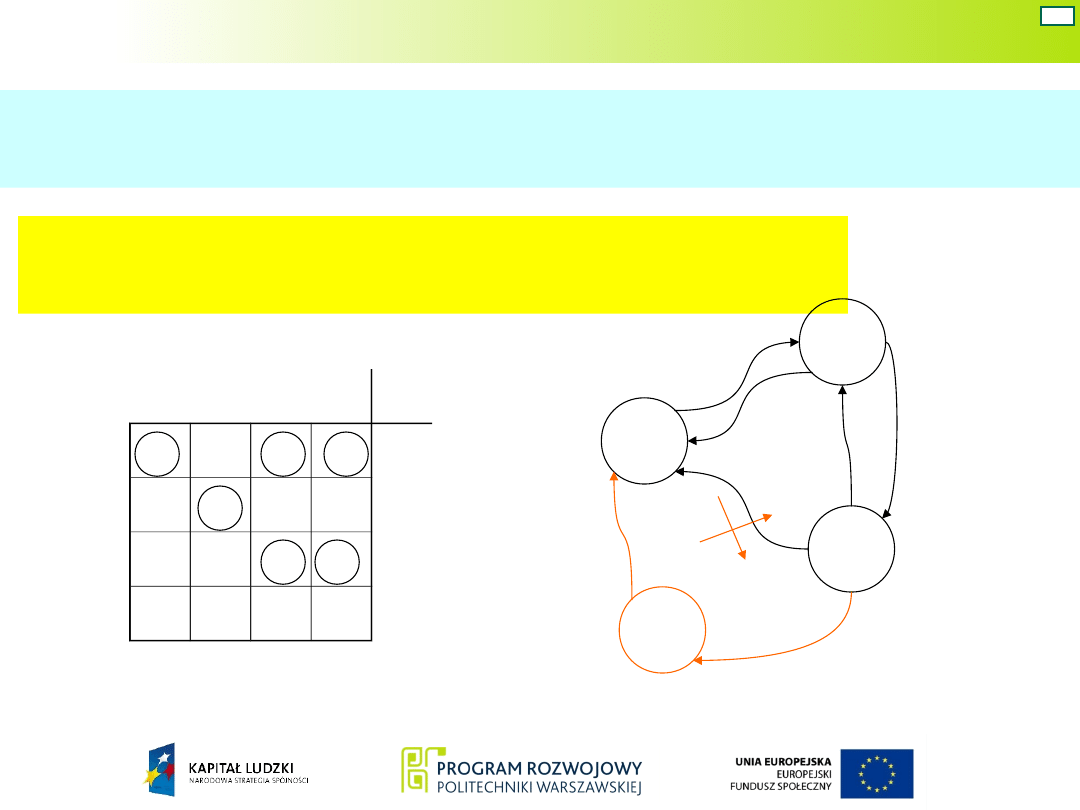
Możliwości modyfikacji tablicy przejść i wyjść w celu uniknięcia
wyścigu.

2. Wprowadzenie dodatkowego stanu

wewnętrznego

00 01 11 10

y

0 0 1 0 0 0
1 0 1 2

-

0

2

3

1 2 2 1

3

0

-

-

-

-

Q

t+1

2

1

Q

Q

0

1

2

00

01

11

3

10

t

Q

2

1

x

x

Układ Moore’a

11

Przyjmując jedno z rozwiązań uniknięcia wyścigu, np. z
dodatkowym stanem wewnętrznym, i przyjęte kody
stanów wewnętrznych, tworzy się zakodowaną tablicę
przejść.

00 01 11 10

y

0 0 1 0 0 0
1 0 1 2

-

0

2

3

1 2 2 1

3

0

-

-

-

-

Q

t+1

2

1

x

x

t

Q

00 01 11 10

y

0
0

00 01 00 00 0

0
1

00 01 11

-

0

1
1

10 01 11 11 1

1
0

00

-

-

-

-

2

1

x

x

2

1

Q

Q

'

2

'

1

Q

Q

)

0

(

)

1

(

)

2

(

)

3

(

Tablica nie zakodowana

Tablica zakodowana z uproszczoną
symboliką

'

1

Q

Q

Q

Q

t

t







Układ Moore’a

12

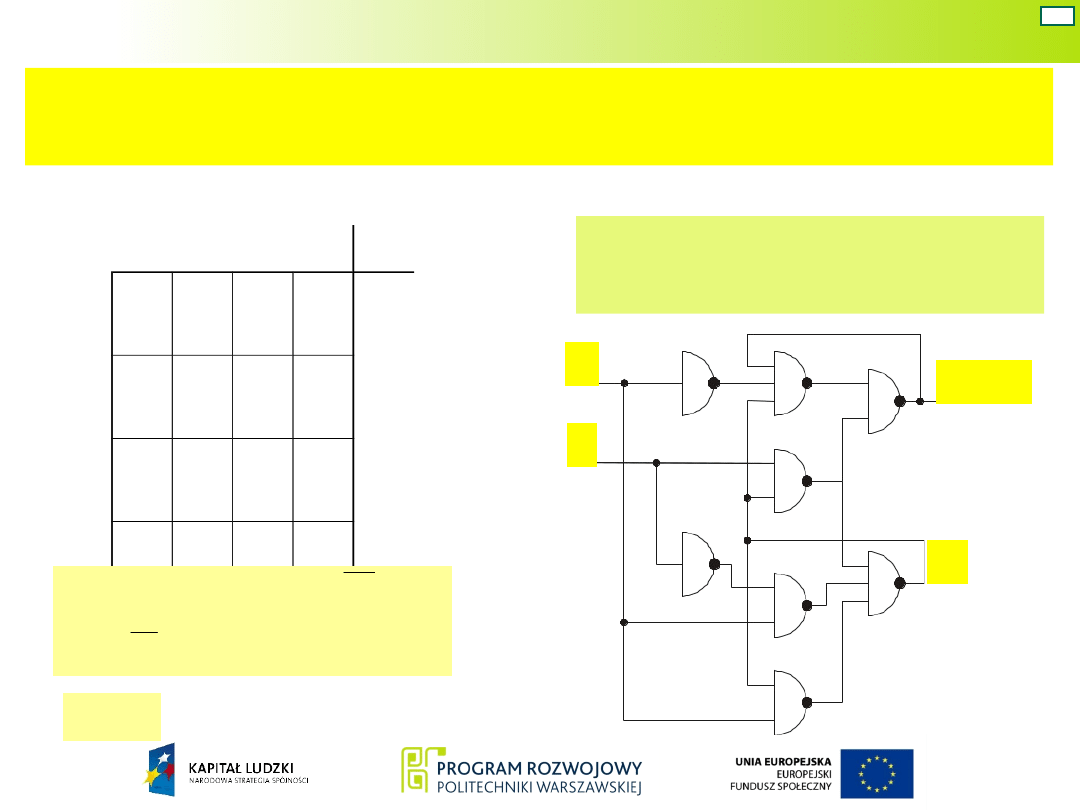
Zakodowana tablica przejść i wyjść umożliwia
wyznaczenie funkcji wyjść i funkcji przejść.

00 01 11 10 y

0
0

00 01 00 00 0

0
1

00 01 11

-

0

1
1

10 01 11 11 1

1
0

00

-

-

-

-

2

1

Q

Q

'

2

'

1

Q

Q

2

1

x

x

1

2

2

2

2

1

'

2

2

2

1

1

2

'

1

x

Q

x

Q

x

x

Q

x

Q

Q

x

Q

Q





















1

Q

y 

Schemat układu z

elementów NAND

1

x

2

x

2

Q

y

Q 

1

Układ Moore’a

13

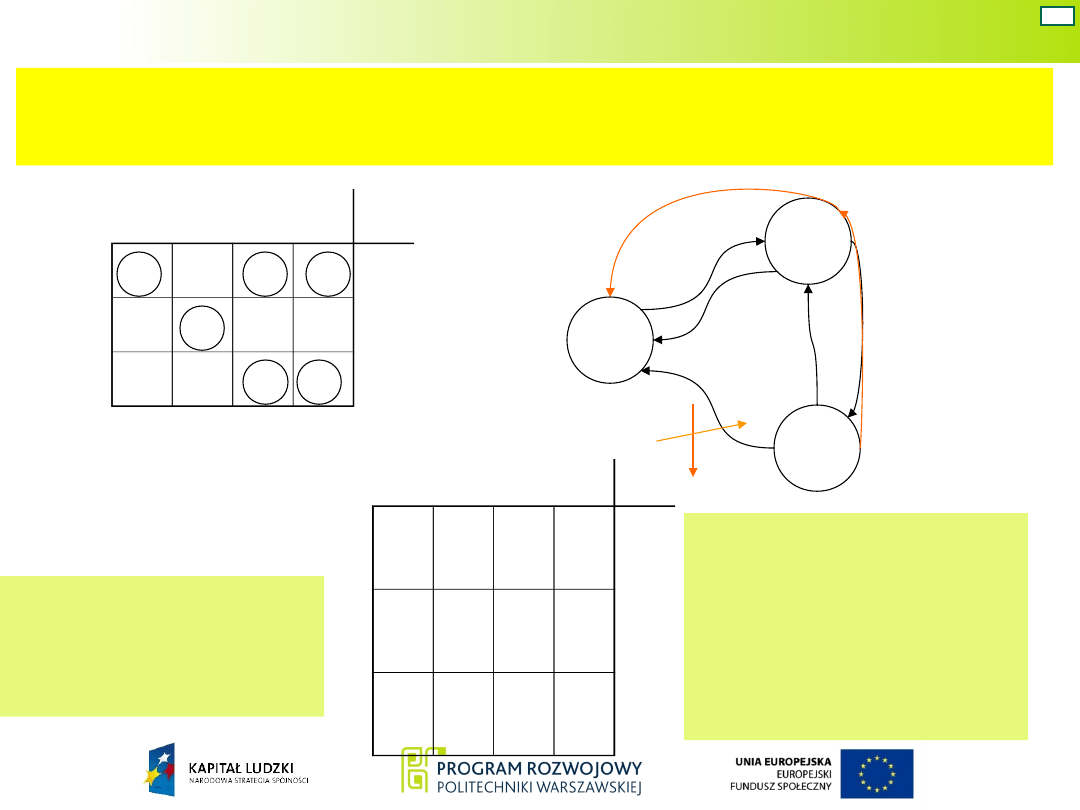
Utwórzmy także zakodowana tablicę przejść i wyjść dla
wariantu z przejściem cyklicznym.

2

1

Q

Q

0

1

2

00

01

11

00 01 11 10

y

0 0 1 0 0 0
1 0 1 2

-

0

2

1

1 2 2 1

Q

t+1

t

Q

2

1

x

x

00 01 11 10 y

0
0

00 01 00 00 0

0
1

00 01 11

-

0

1
1

01 01 11 11 1

2

1

Q

Q

'

2

'

1

Q

Q

2

1

x

x

Tablicę tę należy
rozszerzyć do
postaci pełnej
tablicy
Karnaugha.

Tablica
zakodowana
niepełna

Układ Moore’a

14

00 01 11 10 y

0
0

00 01 00 00 0

0
1

00 01 11

-

0

1
1

01 01 11 11 1

1
0

-

-

-

-

-

2

1

Q

Q

'

2

'

1

Q

Q

2

1

x

x

00 01 11 10 y

0
0

00 01 00 00 0

0
1

00 01 11

-

0

1
1

01 01 11 11 1

2

1

Q

Q

'

2

'

1

Q

Q

2

1

x

x

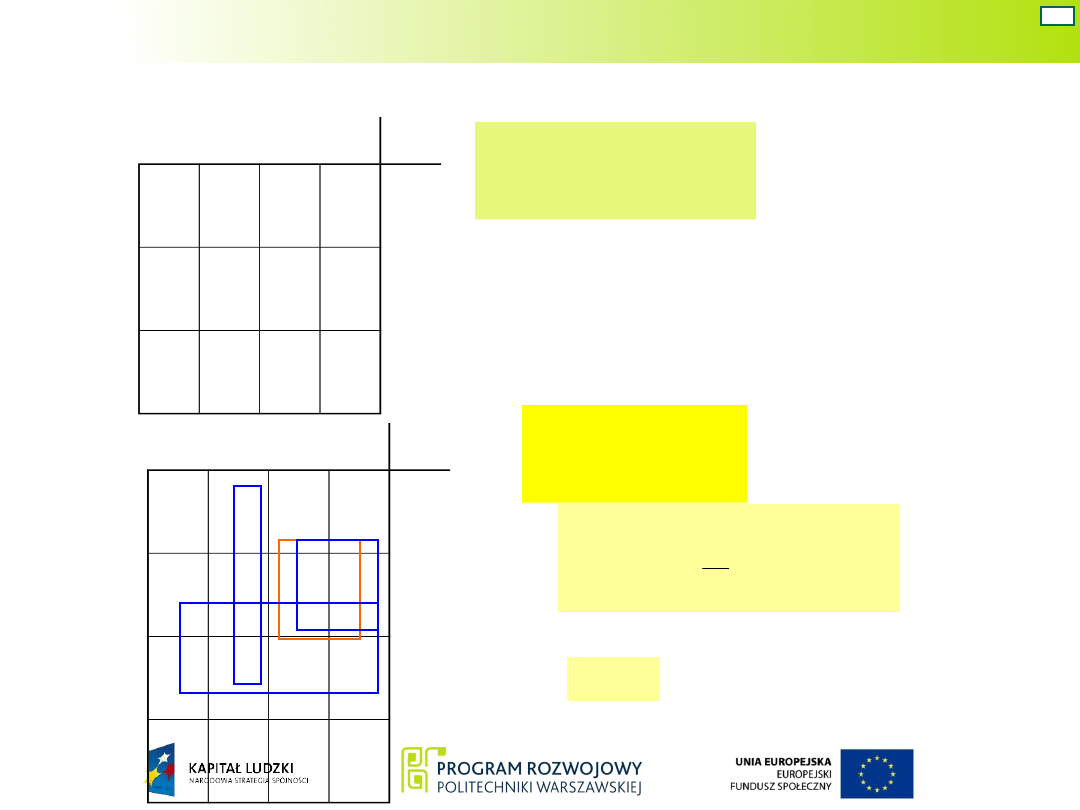
Tablica
niepełna

Tablica
pełna

2

2

2

1

1

'

2

1

2

'

1

x

Q

x

x

Q

Q

x

Q

Q















1

Q

y 

Układ Moore’a z blokiem przerzutników

15

00 01 11 10

y

0
0

00 01 00 00

0

0

1

00 01 11

-

0

1

1

10 01 11 11

1

1
0

00

-

-

-

-

2

1

Q

Q

'

2

'

1

Q

Q

2

1

x

x

1

w

1

z

1

Q

1

Q

2

w

2

z

2

Q

2

Q

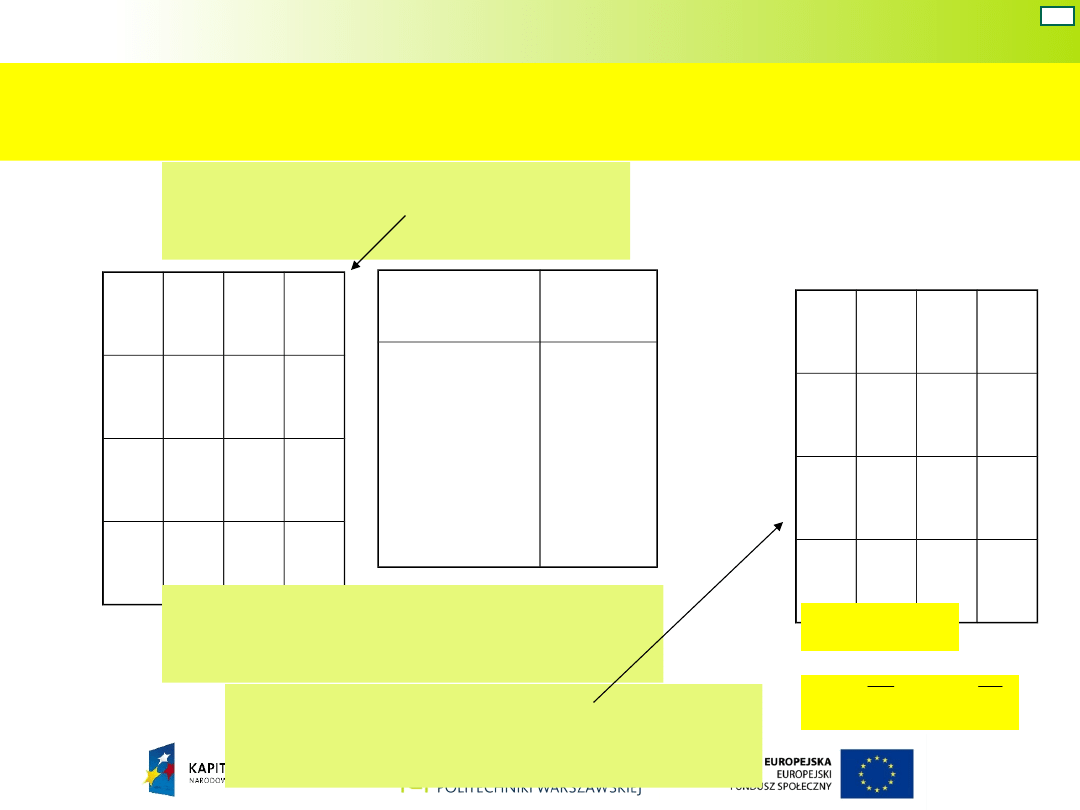
W układzie z wydzielonym blokiem przerzutników do
wytwarzania sygnałów reprezentujących stan
wewnętrzny wykorzystuje się przerzutniki wz.

y

Wykorzystajmy wariant z dodatkowym stanem
wewnętrznym.

Funkcja wyjść

1

Q

y 

Należy jeszcze wyznaczyć wzbudzenia w

1

, z

1

i w

2

, z

2

przerzutników.

Układ Moore’a z blokiem przerzutników

16

Wzbudzenia przerzutników można wyznaczyć posługując się tablicami
wzbudzeń poszczególnych przerzutników.

0

1

1

1

1

0

0

0









1





t

t

Q

Q

01

0

10

0





wz

00 01 11 10

0
0

00 01 00 00

0
1

00 01 11

-

1
1

10 01 11 11

1
0

00

-

-

-

2

1

Q

Q

'

2

'

1

Q

Q

00 01 11 10

0
0

0- 0- 0- 0-

0
1

0- 0- 10

-

1
1

-0 01 -0 -0

1
0

01

-

-

-

w

1

z

1

2

1

x

x

2

1

x

x

2

1

Q

Q

1

2

1

x

Q

w





2

2

1

1

Q

x

x

z







Zakodowana tablica
przejść

Macierz przejść
przerzutnika wz

Tablica wzbudzeń
przerzutnika Q

1

Układ Moore’a z blokiem przerzutników

17

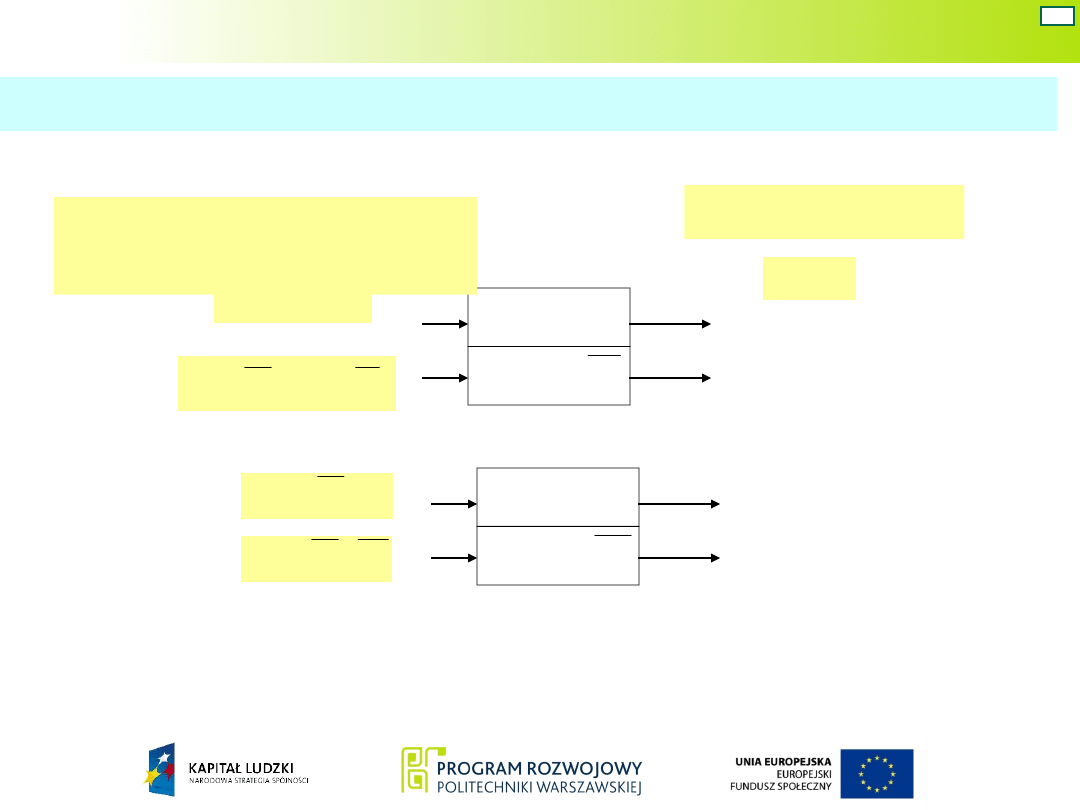
Podobnie można wyznaczyć wzbudzenia
przerzutnika Q

2

.

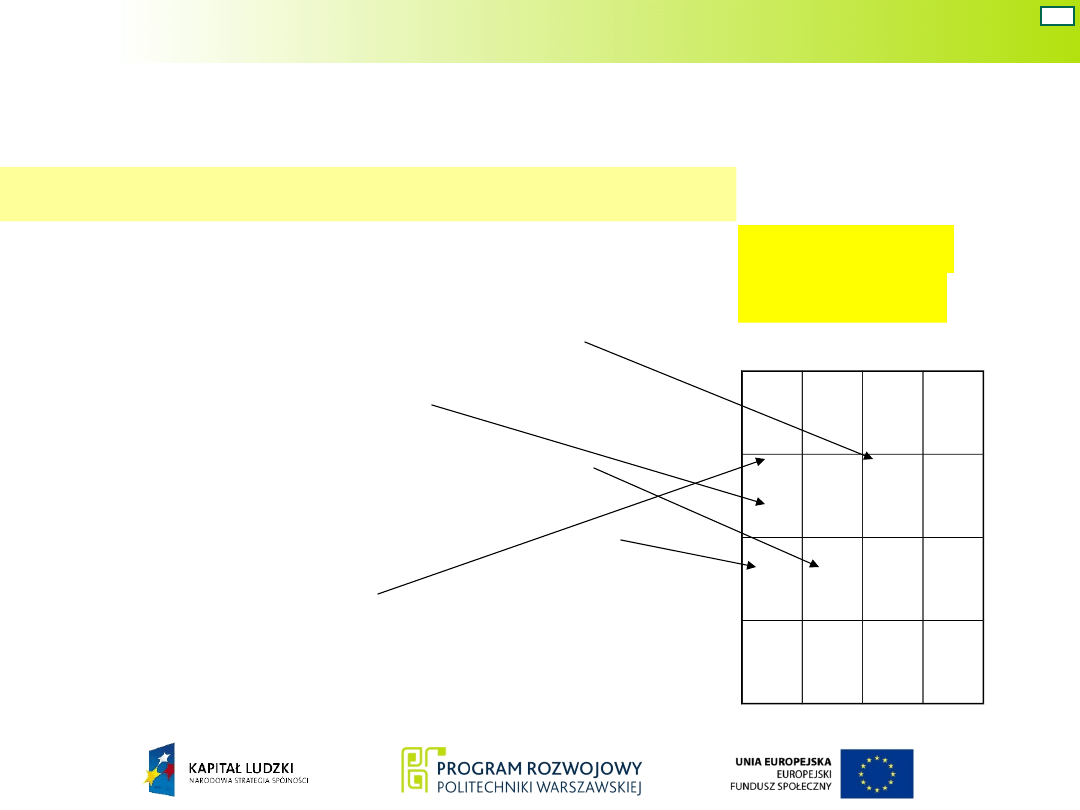
Bardziej efektywną metodą jest wykorzystanie tzw.
uniwersalnej tablicy przejść – jest to tablica przejść
z pogrubionymi stanami następnymi, różniącymi się
od stanów aktualnych.

00 01 11 10

0
0

00 01 00 00

0
1

00 01 11

-

1
1

10 01 11 11

1
0

00

-

-

-

00 01 11 10

0
0

00 0

1

00 00

0
1

0

0

01

1

1

-

1
1

1

0

0

1

11 11

1
0

0

0

-

-

-

'

2

'

1

Q

Q

'

2

'

1

Q

Q

2

1

Q

Q

2

1

Q

Q

2

1

x

x

2

1

x

x

Tablica przejść
(zwykła)

Uniwersalna tablica
przejść

Układ Moore’a z blokiem przerzutników

18

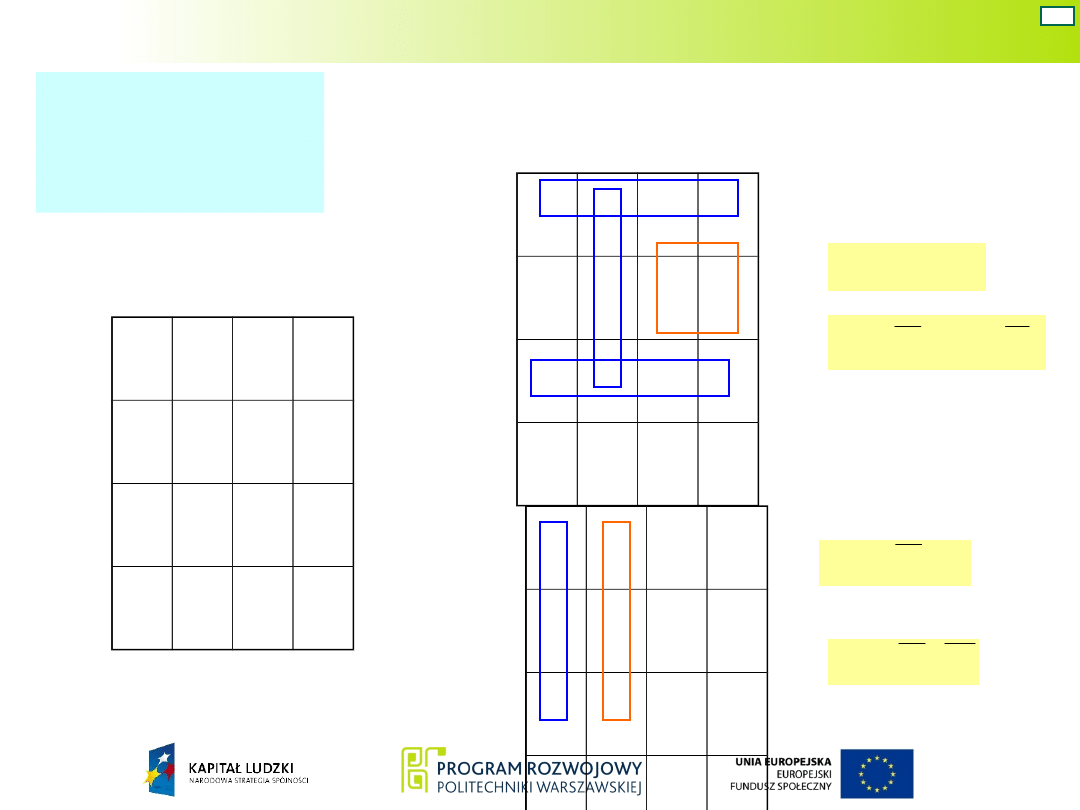
Wzbudzenia przerzutników wyznacza się na podstawie
tablicy uniwersalnej wykorzystując zależności:

w=ΣF1(F1,F-) oraz z=ΣF0(F0,F-)

F1 – pole z grubą
(czerwoną)jedynką

F1 – pole z cienką
jedynką

gdzi
e:

F- – pole z przejściem nie
określonym

F0 – pole z grubym
(czerwonym) zerem

F0 – pole z cienkim
zerem

00 01 11 10

0
0

0

0

0

0

0
1

0

0

1

-

1
1

1

0

1

1

1
0

0

-

-

-

2

1

Q

Q

2

1

x

x

'

1

Q

Tablica
dla

'

1

Q

Układ Moore’a z blokiem przerzutników

19

00 01 11 10

0
0

00 0

1

00 00

0
1

0

0

01

1

1

-

1
1

1

0

0

1

11 11

1
0

0

0

-

-

-

'

2

'

1

Q

Q

2

1

Q

Q

2

1

x

x

00 01 11 10

0
0

0

0

0

0

0
1

0

0

1

-

1
1

1

0

1

1

1
0

0

-

-

-

2

1

Q

Q

2

1

x

x

'

1

Q

w=ΣF1(F1,F-)
oraz
z=ΣF0(F0,F-)

00 01 11 10

0
0

0

1

0

0

0
1

0

1

1

-

1
1

0

1

1

1

1
0

0

-

-

-

2

1

Q

Q

2

1

x

x

'

2

Q

2

1

2

x

x

w





2

1

2

x

x

z





1

2

1

x

Q

w





2

2

1

1

Q

x

x

z







Układ Moore’a z blokiem przerzutników

20

1

w

1

z

1

Q

1

Q

2

w

2

z

2

Q

2

Q

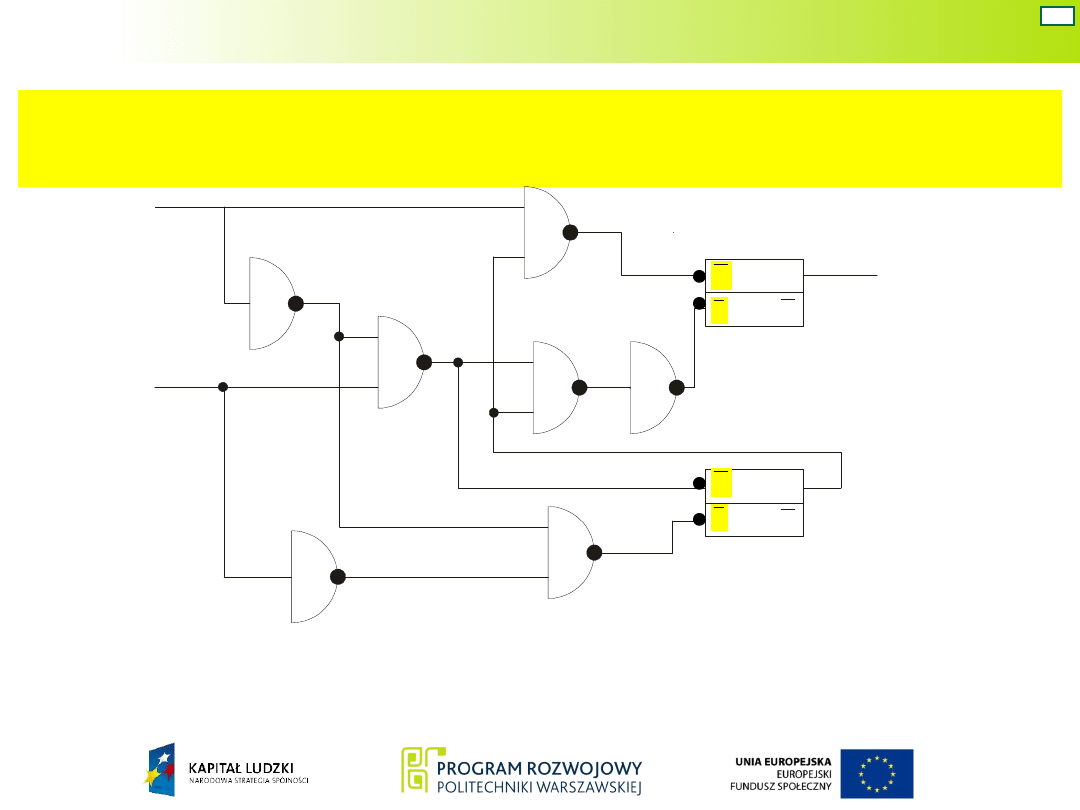
y

Funkcja wyjść

1

Q

y 

1

2

1

x

Q

w





2

2

1

1

Q

x

x

z







2

1

2

x

x

w





2

1

2

x

x

z





Końcowy opis układu z wydzielonym blokiem przerzutników

Wzbudzenia
przerzutników

Układy Moore’a z blokiem przerzutników

21

Schemat układu zrealizowanego z wykorzystaniem
elementów NAND

x

2

x

1

w

z

Q

Q

w

z

Q

Q

Q

2

Q = y

1

z

z

w

w

Układ Mealy’ego

22

0

0

01 11 10

y

0

0

3

-

1

0

1

0

-

2

1

0

2

-

3

2

1

0

3

0

3

4

-

0

4

-

3

4

5

1

5

0

-

4

5

1

Q

t+1

0

1

2

3

4

5

t

Q

Tablica
pierwotna

Wykres
skracania

2

1

x

x

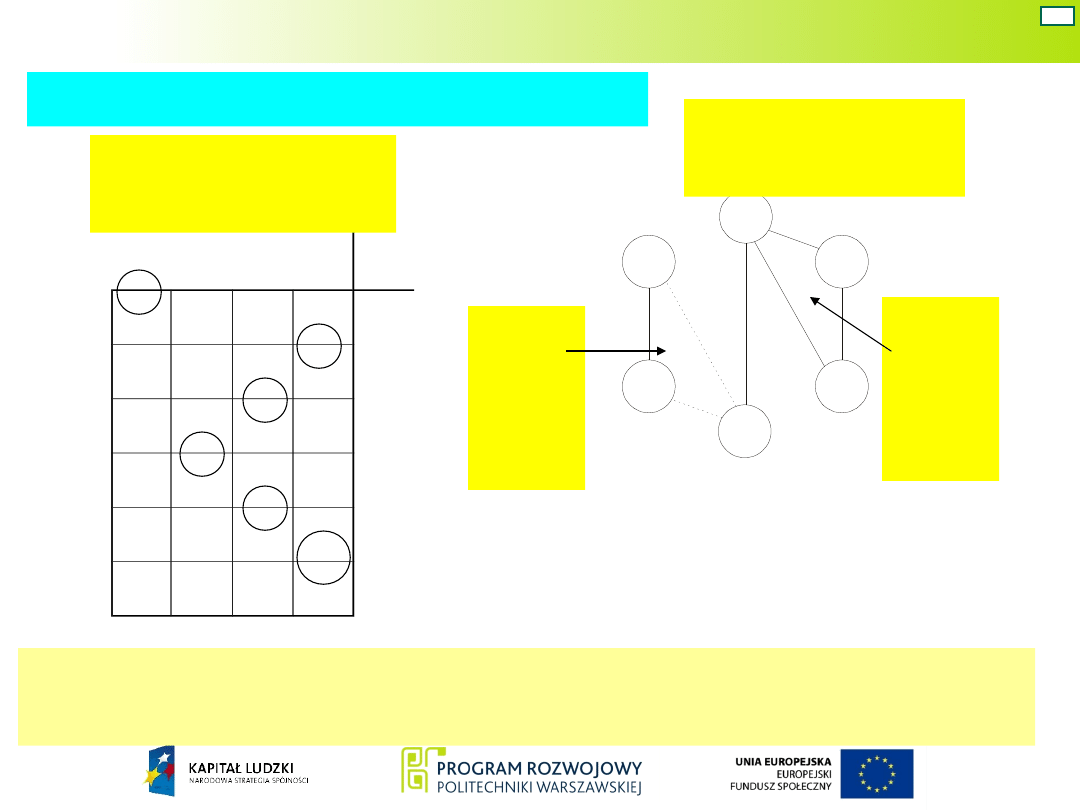
Projektowanie układu Mealy’ego

Stany połączone linią
kropkowaną są stanami
zgodnymi w sensie Mealyego;
mają jednakowe przejścia do
stanów następnych ale różne
stany wyjść.

Układ Mealy’ego może mieć w tym przypadku tylko
dwa stany wewnętrzne, które oznaczymy jako 0 i 1.

now
y
stan
0

now
y
stan
1

Układ Mealy’ego

23

00 01 11 10

0

0

1

0

0

1

0

1

1

1

Q

t+1

0
0

01 11 10 y

0

0

3

-

1

0

1

0

-

2

1

0

2

-

3

2

1

0

3

0

3

4

-

0

4

-

3

4

5

1

5

0

-

4

5

1

Q

t+1

t

Q

Tablica
pierwotna

2

1

x

x

00 01 11 10

0

0

0

0

0

1

0

0

1

1

2

1

x

x

2

1

x

x

t

Q

t

Q

)

2

,

1

,

0

(

)

5

,

4

,

3

(

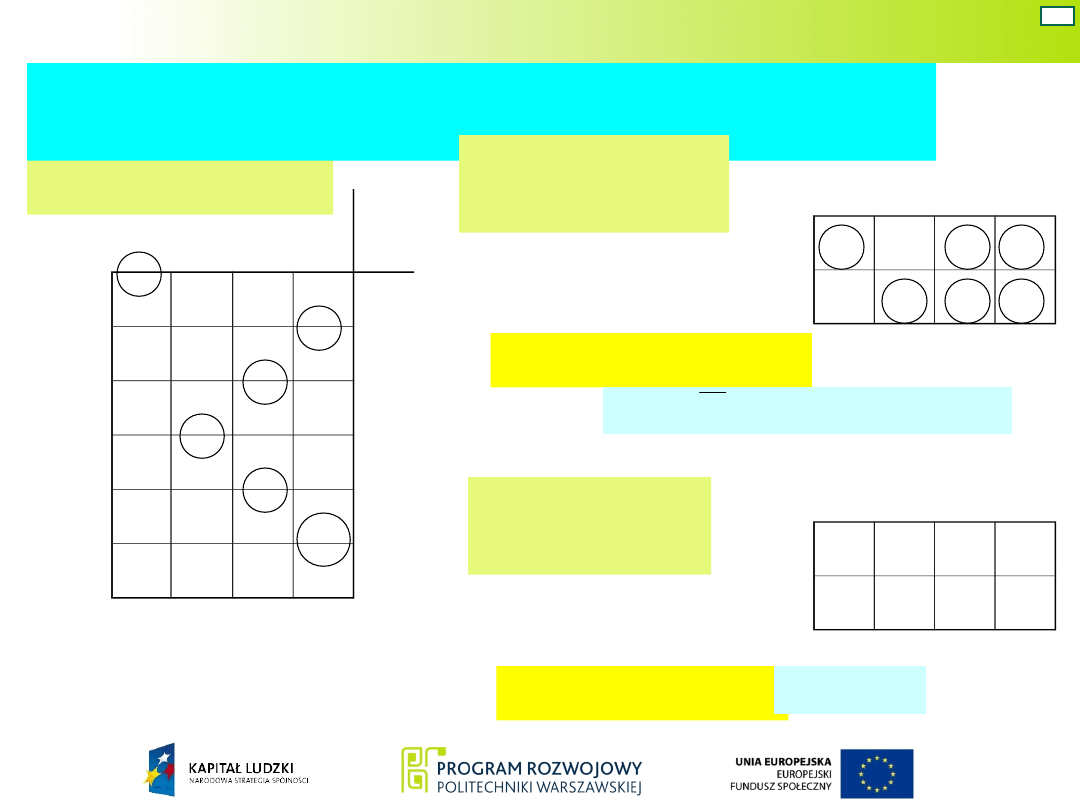
Tworzenie tablicy przejść i tablicy wyjść układu
Mealy’ego

Tablica
przejść

Tablica
wyjść

Funkcja przejść:

2

1

2

1

1

x

Q

x

Q

x

x

Q

t

t

t















Funkcja wyjść:

1

x

Q

y

t

t





y

Układ Mealy’ego

24

00 01 11 10

0

0

1

0

0

1

0

1

1

1

Q

t+1

0
0

01 11 10 y

0

0

3

-

1

0

1

0

-

2

1

0

2

-

3

2

1

0

3

0

3

4

-

0

4

-

3

4

5

1

5

0

-

4

5

1

Q

t+1

t

Q

Tablica
pierwotna

2

1

x

x

00 01 11 10

0

0

0

0

0

1

0

0

1

1

2

1

x

x

2

1

x

x

t

Q

t

Q

)

2

,

1

,

0

(

)

5

,

4

,

3

(

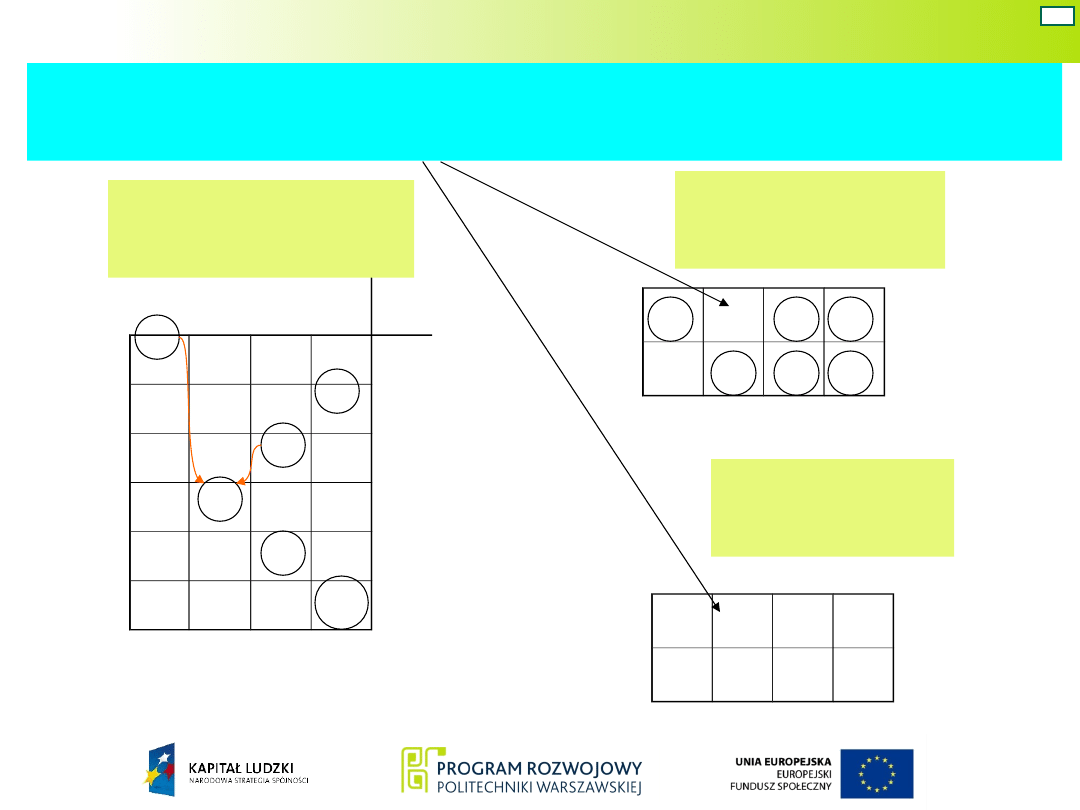
Wyjaśnienie sposobu ustalenia stanu wyjść dla stanu
przejściowego przy przejściu ze stanu 0 do1

Tablica
przejść

Tablica
wyjść

y

Układ Mealy’ego

25

00 01 11 10

0

0

1

0

0

1

0

1

1

1

Q

t+1

0
0

01 11 10 y

0

0

3

-

1

0

1

0

-

2

1

0

2

-

3

2

1

0

3

0

3

4

-

0

4

-

3

4

5

1

5

0

-

4

5

1

Q

t+1

t

Q

Tablica
pierwotna

2

1

x

x

00 01 11 10

0

0

0

0

0

1

0

0

1

1

2

1

x

x

2

1

x

x

t

Q

t

Q

)

2

,

1

,

0

(

)

5

,

4

,

3

(

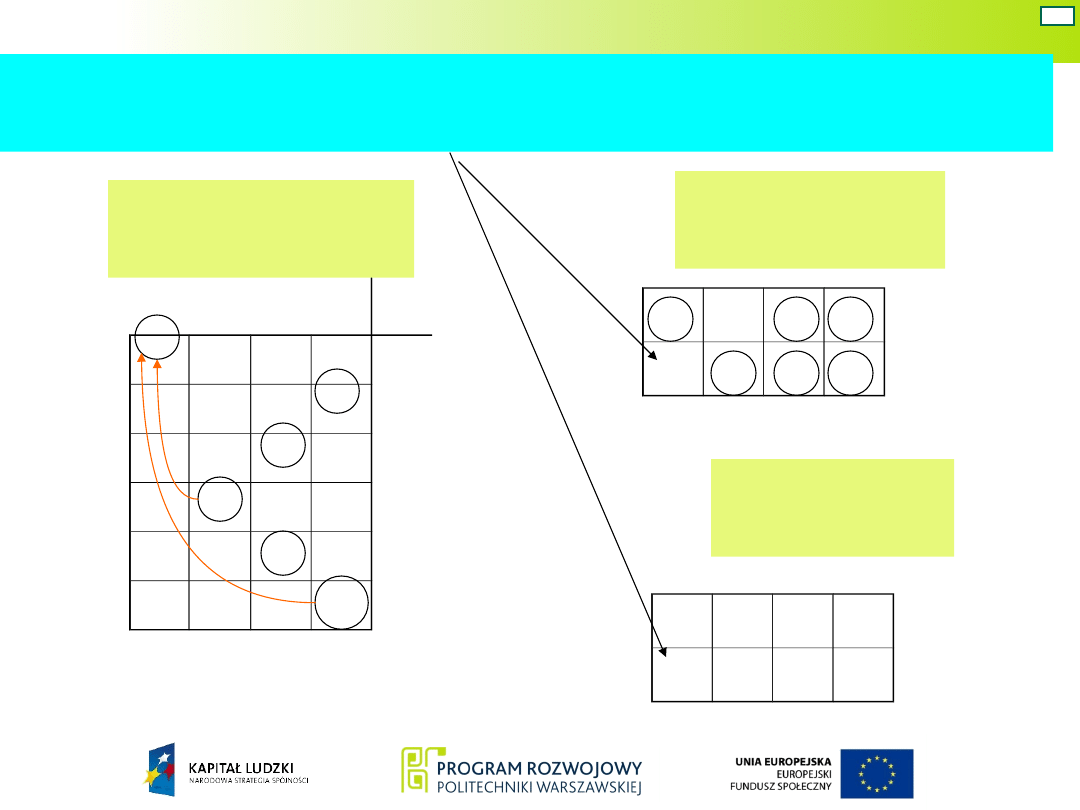
Wyjaśnienie sposobu ustalenia stanu wyjść dla stanu
przejściowego przy przejściu ze stanu 1 do 0

Tablica
przejść

Tablica
wyjść

y

Układ Mealy’ego

26

Funkcja przejść i funkcja wyjść stanowią podstawę
do realizacji układu.

Funkcja przejść:

2

1

2

1

1

x

Q

x

Q

x

x

Q

t

t

t















Funkcja wyjść:

1

x

Q

y

t

t





Zrealizujmy układ z elementów
NAND.

2

1

2

1

2

1

2

1

2

1

2

1

1

x

Q

x

Q

x

x

x

Q

x

Q

x

x

x

Q

x

Q

x

x

Q

t

t

t

t

t

t

t











































1

1

x

Q

x

Q

y

t

t

t









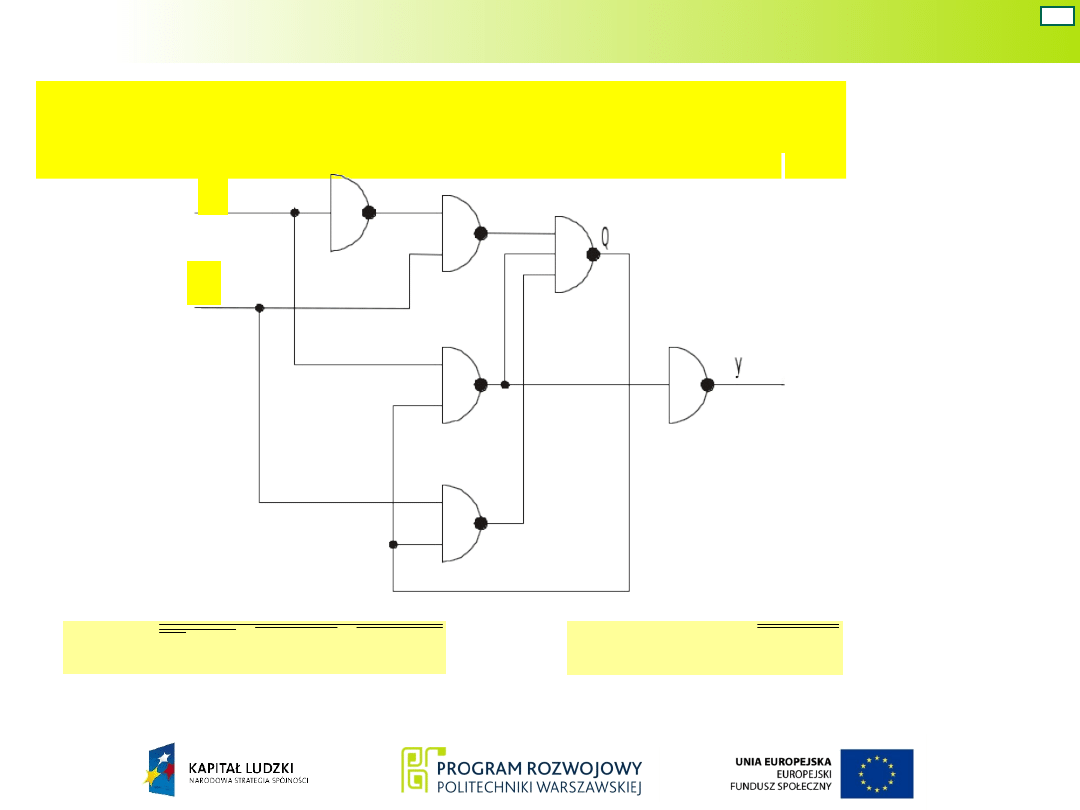
Układy Mealy’ego

27

Schemat układu Mealy’ego z elementów
NAND

2

1

2

1

1

x

Q

x

Q

x

x

Q

t

t

t















1

1

x

Q

x

Q

y

t

t

t









1

x

2

x

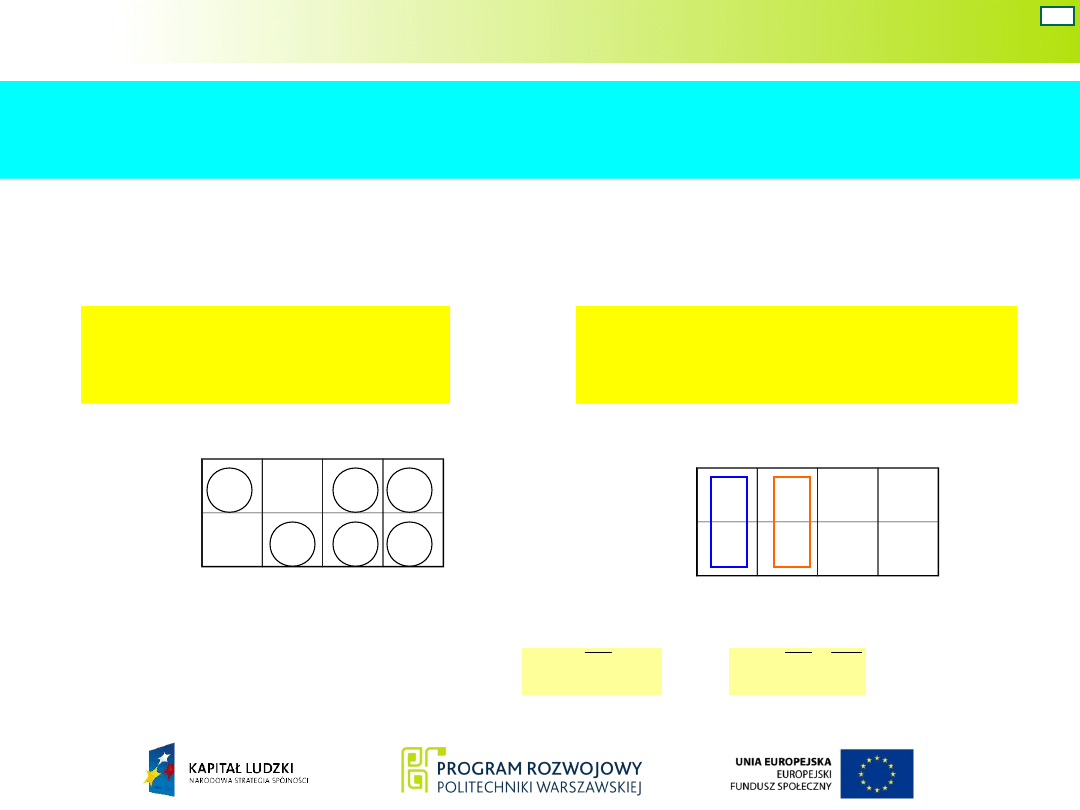
Układ Mealy’ego

28

00 01 11 10

0

0

1

0

0

1

0

1

1

1

Q

t+1

2

1

x

x

t

Q

)

2

,

1

,

0

(

)

5

,

4

,

3

(

Tablica przejść
zwykła

Układ Mealy’ego można także zrealizować z wydzielonym blokiem
przerzutników, w tym przypadku z jednym przerzutnikiem Q.

Przekształcamy tablicę przejść do postaci tablicy uniwersalnej.

00 01 11 10

0

0

1

0

0

1

0

1

1

1

Q

t+1

2

1

x

x

t

Q

)

2

,

1

,

0

(

)

5

,

4

,

3

(

Tablica przejść
uniwersalna

2

1

x

x

w





2

1

x

x

z





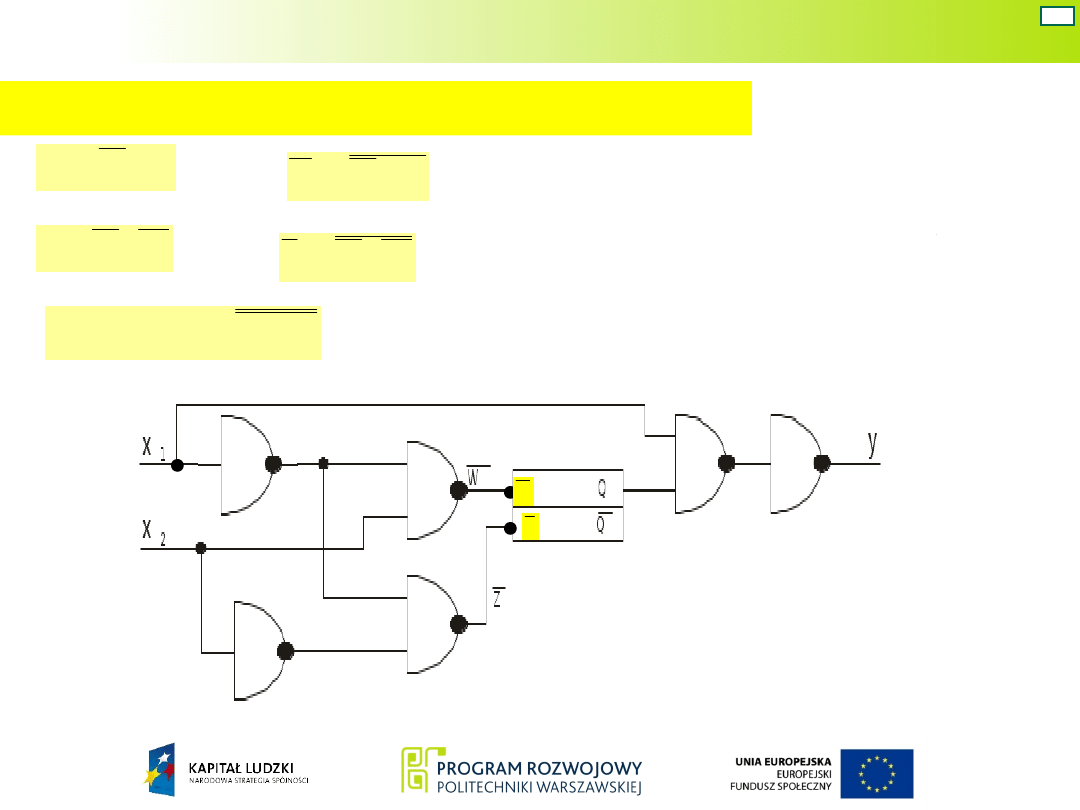
Układy Mealy’ego

29

Schemat układu Mealy’ego przerzutnikiem

2

1

x

x

w





2

1

x

x

z





1

1

x

Q

x

Q

y

t

t

t









2

1

x

x

w





2

1

x

x

z





w

z

Zajęcia współfinansowane przez Unię Europejską w

Zajęcia współfinansowane przez Unię Europejską w

ramach

ramach

Europejskiego Funduszu Społecznego

Europejskiego Funduszu Społecznego

Dziękuję za uwagę

Dziękuję za uwagę