CHEMIA OGÓLNA

CHEMIA OGÓLNA

prof. dr hab. MARIA MIKOS - BIELAK

prof. dr hab. MARIA MIKOS - BIELAK

POSTULATY TEORII 

POSTULATY TEORII 

RUTHERFORDA

RUTHERFORDA

I.

I.

W skład atomu wchodzą ładunki elektryczne: 

W skład atomu wchodzą ładunki elektryczne: 

dodatnie – protony, obojętne – neutrony i ujemne 

dodatnie – protony, obojętne – neutrony i ujemne 

– elektrony

– elektrony

II.

II.

Elektrony mają znikomo małą masę 1/1837 masy 

Elektrony mają znikomo małą masę 1/1837 masy 

protonu

protonu

III.

III.

Protony i neutrony znajdują się w jądrze, którego 

Protony i neutrony znajdują się w jądrze, którego 

średnica 10 

średnica 10 

-13

-13

 cm, tu też skupiona jest cała masa

 cm, tu też skupiona jest cała masa

IV.

IV.

Ilość ładunków dodatnich jest charakterystyczna 

Ilość ładunków dodatnich jest charakterystyczna 

dla każdego pierwiastka i decyduje o jego 

dla każdego pierwiastka i decyduje o jego 

położeniu w układzie okresowym. Liczbę 

położeniu w układzie okresowym. Liczbę 

protonów określa liczba porządkowa pierwiastka 

protonów określa liczba porządkowa pierwiastka 

w układzie okresowym

w układzie okresowym

PLANETARNY MODEL BUDOWY 

PLANETARNY MODEL BUDOWY 

ATOMU WG. BOHRA

ATOMU WG. BOHRA

1.

1.

Elektrony krążą po orbitach znajdujących się w ściśle 

Elektrony krążą po orbitach znajdujących się w ściśle 

określonej odległości od jądra

określonej odległości od jądra

2.

2.

Energia własna elektronu zależy od promienia orbity 

Energia własna elektronu zależy od promienia orbity 

– im większy promień tym wyższa energia elektronów

– im większy promień tym wyższa energia elektronów

3.

3.

Elektrony krążące po torach stacjonarnych nie 

Elektrony krążące po torach stacjonarnych nie 

emitują i nie pochłaniają energii

emitują i nie pochłaniają energii

4.

4.

Pochłonięta z zewnątrz energia przesuwa elektron na 

Pochłonięta z zewnątrz energia przesuwa elektron na 

orbitę dalszą od jądra a atom pierwiastka przechodzi 

orbitę dalszą od jądra a atom pierwiastka przechodzi 

w stan wzbudzony

w stan wzbudzony

5.

5.

Pochłonięcie przez elektron dużej ilości energii 

Pochłonięcie przez elektron dużej ilości energii 

powoduje jego wybicie poza obręb oddziaływania 

powoduje jego wybicie poza obręb oddziaływania 

jądra – powstaje kation

jądra – powstaje kation

TRWAŁOŚĆ JĄDRA

TRWAŁOŚĆ JĄDRA

I. 

I. 

DEFEKT MASY

DEFEKT MASY

.

,

rzecz

e

n

p

M

M

M









Dla Helu
Δ M 

He

 = [2 ∙ 1,0078 + 2 ∙1,0086] – 4,0015 = 0,0314 D

Dla Fluoru 

9

F                   M 

rzecz.

 = 18,9984

Δ M

F

 = [ 9 ∙ 1,0078 + 9 ∙1,0086 + 9 ∙ 1/1840 D] – 

18,9984
Δ M

F

 = 0,1596 D

                            

                            

Po przeliczeniu na energię

Po przeliczeniu na energię

ΔM

ΔM

He

He

 = 0,0314 ∙ 931,5 MeV = 29,25 MeV

 = 0,0314 ∙ 931,5 MeV = 29,25 MeV

ΔM

ΔM

F

F

 = 0,1596 ∙ 931,5 MeV = 148,7 MeV

 = 0,1596 ∙ 931,5 MeV = 148,7 MeV

II. EFEKT UPAKOWANIA JĄDRA

f = ΔM / A

określa wielkość defektu masy na jeden nukleon

REGUŁY TRWAŁOŚCI JĄDRA

REGUŁY TRWAŁOŚCI JĄDRA

HARKINSA

HARKINSA

1.

1.

Żadne zwykłe jądro z wyjątkiem wodoru nie zawiera 

Żadne zwykłe jądro z wyjątkiem wodoru nie zawiera 

mniej „n” niż „p” , stosunek n/p nie przekracza 1,6

mniej „n” niż „p” , stosunek n/p nie przekracza 1,6

2.

2.

Pierwiastki o parzystych liczbach atomowych są 

Pierwiastki o parzystych liczbach atomowych są 

trwalsze, mają więcej izotopów i występują częściej

trwalsze, mają więcej izotopów i występują częściej

3.

3.

Pierwiastki o parzystej liczbie „n” są trwalsze od 

Pierwiastki o parzystej liczbie „n” są trwalsze od 

pierwiastków z nieparzystą liczbą „n”

pierwiastków z nieparzystą liczbą „n”

4.

4.

Bardzo stabilne są jądra w których liczba protonów 

Bardzo stabilne są jądra w których liczba protonów 

lub neutronów osiąga wartość liczb magicznych : 2, 

lub neutronów osiąga wartość liczb magicznych : 2, 

8, 20, 28, 50, 82, 126

8, 20, 28, 50, 82, 126

5.

5.

Odkryto: 267 trwałych jąder i ~1200 naturalnych 

Odkryto: 267 trwałych jąder i ~1200 naturalnych 

lub sztucznych jąder nietrwałych

lub sztucznych jąder nietrwałych

                                  

                                  

Największe efekty upakowania mają pierwiastki od 30 

Największe efekty upakowania mają pierwiastki od 30 

do 63

do 63

III. Najtrwalsze jądra mają stosunek:

1,0 < n/p < 1,2     TRWAŁE

1,2 < n/p < 1,4     NIETRWAŁE

1,4 < n/p < 1,6     PROMIENIOTWÓRCZE

   

NIETRWAŁOŚĆ JĄDRA

NIETRWAŁOŚĆ JĄDRA

I.     n>p

I.     n>p

no

antyneutri

p

n















1

1

1

0









S

P

32

16

32

15

Masa nie ulega zmianie

                                

                                

II.     n<p 

II.     n<p 

a)

a)

 

 

b)

b)

 

 

n

p

1

0

1

1









   emisja 
pozytonu

 









B

C

11

5

11

6

wychwyt elektronów z 

powłoki K

n

e

p

1

0

1

1





Li

e

Be

7

3

7

4





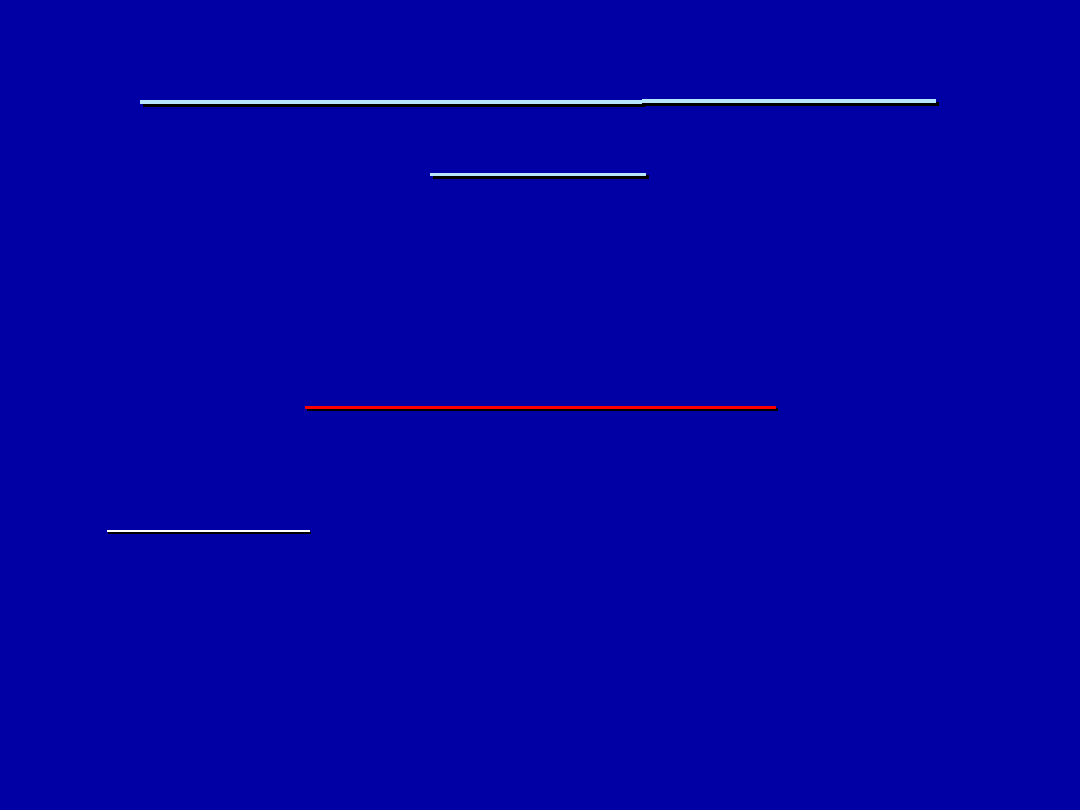
POZAJĄDROWA

POZAJĄDROWA

 BUDOWA 

 BUDOWA 

ATOMU

ATOMU

Powłoki elektronowe zajmują przestrzeń 10

Powłoki elektronowe zajmują przestrzeń 10

5

5

 razy większą 

 razy większą 

od jądra. Ich średnica wynosi 10

od jądra. Ich średnica wynosi 10

-8

-8

 cm.

 cm.

LICZBY KWANTOWE

LICZBY KWANTOWE

I.

I.

Główna „n”

Główna „n”

 – określa poziom energetyczny . 

 – określa poziom energetyczny . 

Przyjmuje wartości      liczb całkowitych:

Przyjmuje wartości      liczb całkowitych:

1 < n ≤ 7

1 < n ≤ 7

w układzie okresowym równa jest numerowi okresu.

w układzie okresowym równa jest numerowi okresu.

II.

II.

   

Poboczna liczba kwantowa „l” – określa podpoziom i 

rodzaj orbitalu. Przyjmuje wartości:  

0 ≤ l ≤ n – 1

podpoziomy

podpoziomy

s

s

l = 0

l = 0

orbitale

orbitale

s – kulisty

s – kulisty

p

p

l = 1

l = 1

p – hantla

p – hantla

d

d

l = 2

l = 2

d – podwójna

d – podwójna

      

      

hantla

hantla

f

f

l = 3

l = 3

f – potrójna hantla 

f – potrójna hantla 

dalsze nieokreślone

                                

                                

III.

III.

Magnetyczna liczba kwantowa „m” – określa zmianę 
stanu energetycznego elektronu spowodowanego 
skręceniem płaszczyzny orbitalu elektronowego pod 
wpływem pola magnetycznego.

n = 

1 

l = 0 

(s)

m = 0  (1 

orbital s) 

n = 

2

l = 0 

(s)

l = 1 

(p)

m = 0  (1 

orbital s)

m =  -1
m =   0 (3 

orbitale p) 

m = +1

n = 

3 

l = 0 

(s)

l = 1 

(p)

l = 2 

(d)

m = 0  (1 

orbital s)

m =  -1
m =   0 (3 

orbitale p) 

m = +1
m = - 2

m = - 1
m =   0 (5 

orbitali d) 

m =   1

m =   2

                           

                           

IV.

IV.

    Liczba kwantowa spinu – określa kierunek 
obrotu

 

e

 

wokół własnej osi, przyjmuje wartości:

 - ½ = s = + ½ (zgodny ze wskazówkami 
zegara)

Pojemność orbitali, podpoziomów i poziomów

Orbital: część przestrzeni poza jądrem określona 3 
liczbami kwantowymi: n, l, m – każdy orbital może 
mieć maksymalnie 2

 

e

o różnych 

spinach.

                              

                              

Podpoziom: określają dwie liczby kwantowe „n” i „l”

Poziom: określa tylko „n”

                        

                        

Pojemność orbitali podpoziomów i poziomów

Pojemność orbitali podpoziomów i poziomów

Orbital:

Orbital:

 część przestrzeni o określonym kształcie, 

 część przestrzeni o określonym kształcie, 

opisany przy pomocy trzech liczb kwantowych – n, l, m. 

opisany przy pomocy trzech liczb kwantowych – n, l, m. 

Każdy orbital

Każdy orbital

 mieści dwa elektrony o przeciwnych 

 mieści dwa elektrony o przeciwnych 

spinach. 

spinach. 

Pojemność podpoziomów:

Pojemność podpoziomów:

                              

                              

Pojemność poziomów

Pojemność poziomów

                            

                            

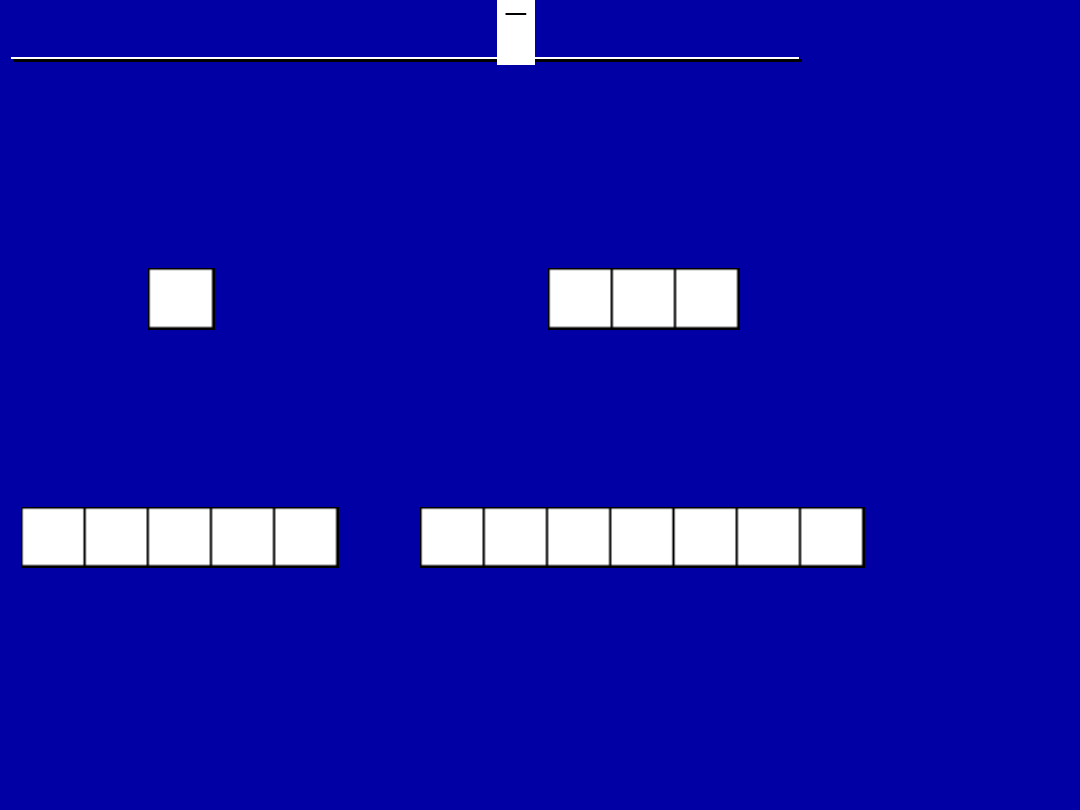
Przedstawienie zapisu    i orbitali

Przedstawienie zapisu    i orbitali

e

Orbital     s                             Orbitale     p

     

   

Orbitale d                               Orbitale     f

                           

                           

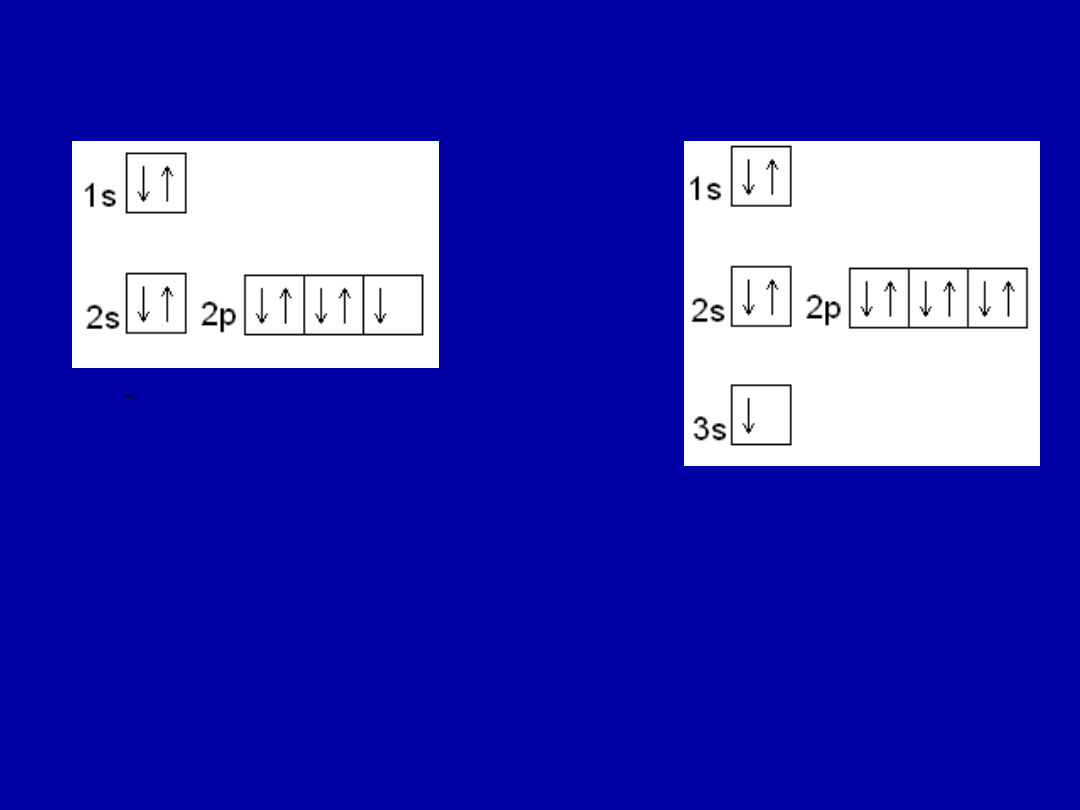
np. 

np. 

9

9

F                                                

F                                                

11

11

Na

Na

lub 1s

2

 2s

2

 2p

5

                                      lub 1s

2

 2s

2

 2p

6

 

3s

1

„F” – ma 2 powłoki wiec leży w 2 okresie, na ostatniej 
powłoce ma
         2 elektrony + 5 elektronów = 7 elektronów    - VII 
grupa

 

„Na” – 3 powłoki = 3 okres, 1 elektron na ostatniej 

powłoce – 

           I grupa

e

 

                             

                             

KOLEJNOŚĆ ZAJMOWANIA ORBITALI I POZIOMÓW 

KOLEJNOŚĆ ZAJMOWANIA ORBITALI I POZIOMÓW 

ENERGETYCZNYCH

ENERGETYCZNYCH

W stanie podstawowym atomów elektrony zajmują 

W stanie podstawowym atomów elektrony zajmują 

możliwie najniższe poziomy energetyczne. Dla różnych 

możliwie najniższe poziomy energetyczne. Dla różnych 

pierwiastków można to przedstawić schematem:

pierwiastków można to przedstawić schematem:

                           

                           

KOLEJNOŚĆ ZAPEŁNIANIA ORBITALI

KOLEJNOŚĆ ZAPEŁNIANIA ORBITALI

ZAKAZ PAULIEGO

ZAKAZ PAULIEGO

W atomie dozwolone są tylko takie stany energetyczne 

W atomie dozwolone są tylko takie stany energetyczne 

elektronów w których  różnią się miedzy sobą 

elektronów w których  różnią się miedzy sobą 

przynajmniej jedną liczbą kwantową

przynajmniej jedną liczbą kwantową

LUB INACZEJ

LUB INACZEJ

W atomie stan elektronu określony czterema liczbami 

W atomie stan elektronu określony czterema liczbami 

kwantowymi n, l, m, s o konkretnych wartościach tych 

kwantowymi n, l, m, s o konkretnych wartościach tych 

liczb może być obsadzony tylko przez jeden elektron

liczb może być obsadzony tylko przez jeden elektron

                           

                           

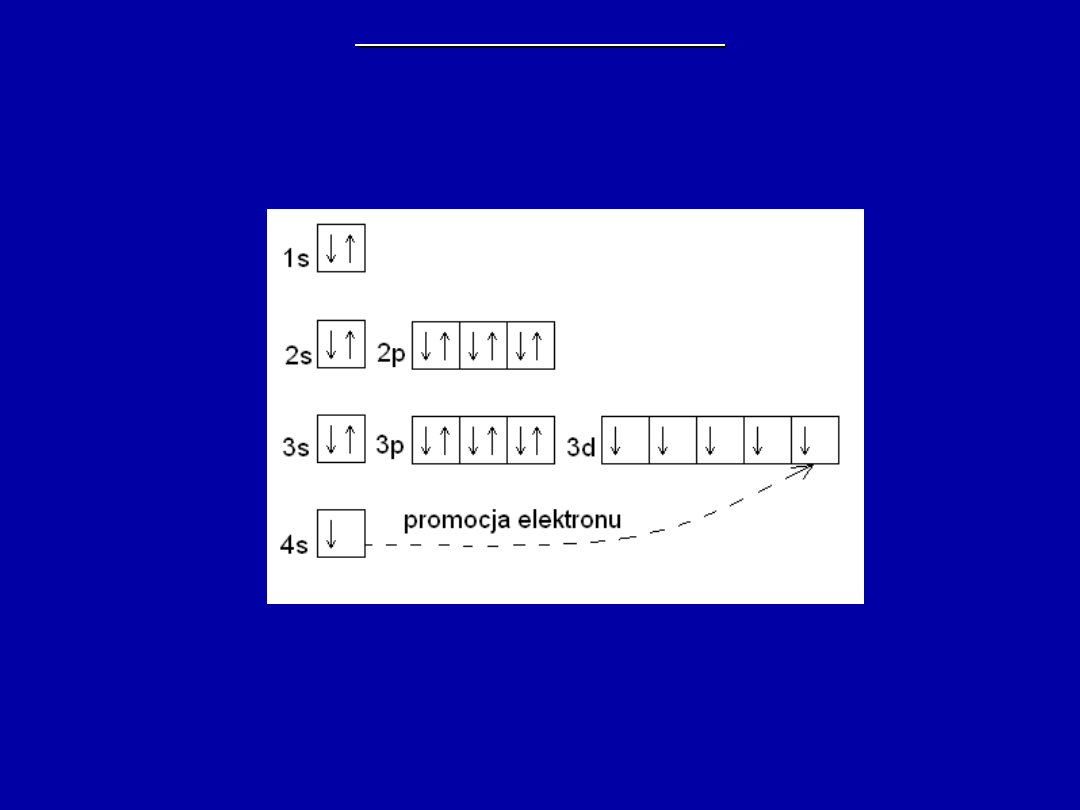
WYJĄTKI OD REGUŁY

WYJĄTKI OD REGUŁY

24Cr     1s

24Cr     1s

2

2

 2s

 2s

2

2

 2p

 2p

6

6

 3s

 3s

2

2

 3p

 3p

6

6

 4s

 4s

1

1

 3d

 3d

5

5

 – okres IV, grupa VI B, 

 – okres IV, grupa VI B, 

blok d

blok d

                           

                           

29

29

Cu – okres IV, grupa I B, blok d

Cu – okres IV, grupa I B, blok d

LANTANOWCE od 57La     …..5p

6

 6s

2

 5d

1

 4f

…..

AKTYNOWCE   od 89Ac     …..6p

6

 7s

2

 6d

1

 5f

…..

                           

                           

REGUŁY

REGUŁY

:

:

1.

1.

Elektrony zajmują najpierw ten orbital, dla którego 

Elektrony zajmują najpierw ten orbital, dla którego 

suma (n+l) jest najmniejsza.

suma (n+l) jest najmniejsza.

2.

2.

Gdy dwa lub więcej orbitali ma jednakową sumę (n+l), 

Gdy dwa lub więcej orbitali ma jednakową sumę (n+l), 

o porządku ich zajmowania decyduje mniejsza 

o porządku ich zajmowania decyduje mniejsza 

wartość n.

wartość n.

3.

3.

Orbitale o jednakowych n i l a różnych m nazywamy 

Orbitale o jednakowych n i l a różnych m nazywamy 

zdegenerowanymi np. orbitale p [p

zdegenerowanymi np. orbitale p [p

x

x

 p

 p

y

y

 p

 p

z

z

] (trójkrotnie 

] (trójkrotnie 

zdegenerowane), d – pięciokrotnie.

zdegenerowane), d – pięciokrotnie.

REGUŁA HUNDA:

W orbitalach zdegenerowanych pary elektronów 

powstają dopiero po obsadzeniu każdego orbitalu przez 

jeden elektron. Nie sparowane elektrony na 

zdegenerowanych orbitalach mają jednakowe spiny.

 

 

   

   

Uporządkowanie 

Uporządkowanie 

pierwiastków w układzie 

pierwiastków w układzie 

okresowym

okresowym

Właściwości chemiczne i fizyczne pierwiastka wynikają z liczby     i 

Właściwości chemiczne i fizyczne pierwiastka wynikają z liczby     i 

sposobu ich rozmieszczenia na orbitalach.

sposobu ich rozmieszczenia na orbitalach.

Periodyczne powtarzanie cech fizykochemicznych pierwiastków 

Periodyczne powtarzanie cech fizykochemicznych pierwiastków 

wynika z powtarzającego się podobieństwa rozkładu na     

wynika z powtarzającego się podobieństwa rozkładu na     

zewnętrznych powłokach.

zewnętrznych powłokach.

e

e

                           

                           

Układ okresowy Thompsona – Bohra

Układ okresowy Thompsona – Bohra

Grupa I A – pierwiastki posiadające 1 elektron  na orbitalu 

Grupa I A – pierwiastki posiadające 1 elektron  na orbitalu 

typu s.

typu s.

Grupa II A – pierwiastki posiadające 2 elektrony na 

Grupa II A – pierwiastki posiadające 2 elektrony na 

orbitalu typu s ostatniej powłoki.

orbitalu typu s ostatniej powłoki.

Obie te grupy należą do bloku s.

Obie te grupy należą do bloku s.

Grupy od III A do VIII A to pierwiastki bloku p.

Grupy od III A do VIII A to pierwiastki bloku p.

Grupy od I B do VIII B – pierwiastki bloku d.

Grupy od I B do VIII B – pierwiastki bloku d.

Pierwiastki rozbudowujące orbitale f należą do bloku f.

Pierwiastki rozbudowujące orbitale f należą do bloku f.

                           

                           

Pionowe kolumny

Pionowe kolumny

 – grupy odpowiadają liczbie elektronów  

 – grupy odpowiadają liczbie elektronów  

na ostatniej powłoce.

na ostatniej powłoce.

Poziome szeregi

Poziome szeregi

 – okresy odpowiadają liczbie powłok 

 – okresy odpowiadają liczbie powłok 

elektronowych.

elektronowych.

Liczba porządkowa

Liczba porządkowa

 = liczbie protonów w jądrze i 

 = liczbie protonów w jądrze i 

elektronów na powłokach.

elektronów na powłokach.

Pierwiastki grup głównych (A)

Pierwiastki grup głównych (A)

 – posiadają elektrony  

 – posiadają elektrony  

walencyjne na orbitalach s i p ostatniej powłoki.

walencyjne na orbitalach s i p ostatniej powłoki.

Pierwiastki grup pobocznych (B)

Pierwiastki grup pobocznych (B)

 – zwane także 

 – zwane także 

przejściowymi mają elektrony walencyjne na orbitalach 

przejściowymi mają elektrony walencyjne na orbitalach 

s ostatniej powłoki i na orbitalach d przedostatniej 

s ostatniej powłoki i na orbitalach d przedostatniej 

powłoki.

powłoki.

Pierwiastki wewnątrzprzejściowe

Pierwiastki wewnątrzprzejściowe

 – mają elektrony 

 – mają elektrony 

walencyjne na orbitalach s ostatniej, d

walencyjne na orbitalach s ostatniej, d

1

1

 z 

 z 

przedostatniej, oraz f powłoki 3- od końca.

przedostatniej, oraz f powłoki 3- od końca.

                            

                            

Elektroujemność i potencjał jonizacyjny w układzie 

Elektroujemność i potencjał jonizacyjny w układzie 

okresowym

okresowym

Potencjał jonizacyjny

Potencjał jonizacyjny

 – praca jaką należy wykonać, aby 

 – praca jaką należy wykonać, aby 

wynieść elektron poza obręb oddziaływania jądra.

wynieść elektron poza obręb oddziaływania jądra.

W układzie okresowym potencjał jonizacyjny najniższy 

W układzie okresowym potencjał jonizacyjny najniższy 

posiadają pierwiastki zawierające mało elektronów  na 

posiadają pierwiastki zawierające mało elektronów  na 

powłokach ( I, II grupa) i dużo powłok ( VI, VII) – rośnie 

powłokach ( I, II grupa) i dużo powłok ( VI, VII) – rośnie 

on w układzie okresowym od lewej do prawej i od dołu 

on w układzie okresowym od lewej do prawej i od dołu 

do góry. Najniższy potencjał jonizacyjny ma Cs.

do góry. Najniższy potencjał jonizacyjny ma Cs.

Powinowactwo elektronowe

Powinowactwo elektronowe

 – zdolność przyciągania 

 – zdolność przyciągania 

dodatkowych elektronów na powłokę walencyjną.

dodatkowych elektronów na powłokę walencyjną.

Charakterystyka cząstek 

Charakterystyka cząstek 

elementarnych

elementarnych

Trwałe

Trwałe

 

 

I.Elektrony = negatony

:    , β, β-

e

  Ładunek jednostkowy ujemny = 1,6 · 10

-19

 C

  Masa = 1/1837 m

p

 lub 0,000548 D

II.Protony:

 

p

p

1

1

,

   Posiadają jednostkowy ładunek dodatni = 1,6 · 10

-19

 

C

   m

p

 = 1,0078 D ( jednostki masy atomowej )

n

n

1

0

,

III.Neutrony:

   

       Pozbawione ładunku
       m

n

 = 1,0086 D

                             

                             

Nietrwałe

Nietrwałe

Lekkie: neutrino, antyneutrino: ładunek k = 0
            Pozytony: ładunek + 1,6 · 10

-19

 C        m = 

m

e

            Mezony:

 









,

mm = 0,118 D

 

Średnie: mezony Π i antymezony    m = 0,158 

D

              ładunek: ± 1,6 · 10

-19

 C

Ciężkie: bariony i antybariony
              protony, neutrony = nukleony
              hiperony
                            o spinach s = ½ - fermiony
                            s = liczbie całkowitej – 

bozony

Nobel z fizyki 1995

Kwarki – najpóźniej odkryte cząstki elementarne z których 

      

zbudowane są protony i neutrony 

                                   

                                   



Rodzina I                     górny i dolny                  

Rodzina I                     górny i dolny                  



Rodzina II                    dziwny i powabny                   

Rodzina II                    dziwny i powabny                   

KWARKI

KWARKI



Rodzina III                   denny i szczytowy

Rodzina III                   denny i szczytowy

•

Elektron i neutrino elektr.

•

Mion i neutrino mionowe                         LEPTONY

•

Taon i neutrino taonowe

                            

                            

PODSTAWOWE DEFINICJE

PODSTAWOWE DEFINICJE



DALTON = jednostka masy atomowej równa 1/12 masy 

DALTON = jednostka masy atomowej równa 1/12 masy 

izotopu węgla 

izotopu węgla 

12

12

C

C



Względna masa atomowa

Względna masa atomowa

 – liczba określająca ile razy 

 – liczba określająca ile razy 

masa atomowa danego pierwiastka jest większa od 

masa atomowa danego pierwiastka jest większa od 

1/12 masy 

1/12 masy 

12

12

C

C



Liczba masowa

Liczba masowa

 „A” – określa sumę protonów i 

 „A” – określa sumę protonów i 

neutronów w jądrze

neutronów w jądrze



Liczba atomowa

Liczba atomowa

 „Z” – określa liczbę protonów w jądrze

 „Z” – określa liczbę protonów w jądrze



Pierwiastek chemiczny

Pierwiastek chemiczny

 – rodzaj materii której wszystkie 

 – rodzaj materii której wszystkie 

atomy mają jednakową liczbę atomową

atomy mają jednakową liczbę atomową

                           

                           



Izotopy

Izotopy

: atomy których jądra posiadają jednakową 

: atomy których jądra posiadają jednakową 

liczbę protonów a różnią się liczbą neutronów

liczbę protonów a różnią się liczbą neutronów

np.

 

H

H

H

3

1

2

1

1

1

,

,

i 

C

C

14

6

12

6

,

STANDARDOWY MODEL 

STANDARDOWY MODEL 

BUDOWY MATERII U PROGU 

BUDOWY MATERII U PROGU 

XXI WIEKU

XXI WIEKU

Wszystko co istnieje składa się z kwarków które 

Wszystko co istnieje składa się z kwarków które 

zawsze występują w parach z leptonami. Naruszenie 

zawsze występują w parach z leptonami. Naruszenie 

symetrii leptonów z kwarkami burzy poprawność 

symetrii leptonów z kwarkami burzy poprawność 

matematyczną modelu standardowego.

matematyczną modelu standardowego.

- Kwark w języku niemieckim to głupstwo, drobnostka

- Kwark w języku niemieckim to głupstwo, drobnostka

                            

                            

Kwarki i leptony zgrupowane są w 3 rodzinach:

Kwarki i leptony zgrupowane są w 3 rodzinach:

I

I

 

 

Rodzina to kwarki:

Rodzina to kwarki:

 dolny (d) i górny (u)

 dolny (d) i górny (u)

           

           

oraz leptony:

oraz leptony:

 elektron (e) i neutrino elektronowe 

 elektron (e) i neutrino elektronowe 

(

(

ν

ν

e

e

)

)

Kwarki obdarzone są ładunkiem o wartości 1/3 lub 2/3 

Kwarki obdarzone są ładunkiem o wartości 1/3 lub 2/3 

ładunku elektronu.

ładunku elektronu.

Bardzo trudno było odkryć neutrino a przy jego braku 

Bardzo trudno było odkryć neutrino a przy jego braku 

trudno było uzasadnić zasadę 

trudno było uzasadnić zasadę 

zachowania energii

zachowania energii

, gdyż 

, gdyż 

podczas rozpadu promieniotwórczego część energii 

podczas rozpadu promieniotwórczego część energii 

ginęła.

ginęła.

Dopiero odkrycie neutrina, które z olbrzymią łatwością 

Dopiero odkrycie neutrina, które z olbrzymią łatwością 

przenika materię unosząc brakującą część energii 

przenika materię unosząc brakującą część energii 

pozwoliło na potwierdzenie tej zasady. Fermi odkrył 

pozwoliło na potwierdzenie tej zasady. Fermi odkrył 

neutrino w 1931 roku, a doświadczalne jego istnienie 

neutrino w 1931 roku, a doświadczalne jego istnienie 

potwierdzono 25 lat później.

potwierdzono 25 lat później.

Tryliony neutrin wypełniają kosmos a ich miliardy w każdej 
sekundzie przenikają nasze ciało – ale złapać ich było 
bardzo trudno – dlatego aż 25 lat trzeba było czekać na 
potwierdzenie ich istnienia.

                             

                             

II rodzina to kwarki

II rodzina to kwarki

: dziwny (s) i powabny (c) 

: dziwny (s) i powabny (c) 

          

          

oraz leptony

oraz leptony

: mion (

: mion (

μ

μ

) i neutrino mionowe (

) i neutrino mionowe (

ν

ν

μ

μ

) 

) 

Te cząstki zaliczane do cięższych można otrzymać w 

Te cząstki zaliczane do cięższych można otrzymać w 

akceleratorze, ale natychmiast po wyprodukowaniu 

akceleratorze, ale natychmiast po wyprodukowaniu 

rozpadają się.

rozpadają się.

Istnieje teoria, że powstały one po wielkim wybuchu, który 

Istnieje teoria, że powstały one po wielkim wybuchu, który 

zapoczątkował istnienie wszechświata. Rozpadały się 

zapoczątkował istnienie wszechświata. Rozpadały się 

one w miarę jego chłodzenia i rozszerzania – do końca 

one w miarę jego chłodzenia i rozszerzania – do końca 

jednak nie określono roli jaką spełniła ta rodzina.

jednak nie określono roli jaką spełniła ta rodzina.

W połowie lat 70-tych XX wieku Martin Perl odkrył nową 

W połowie lat 70-tych XX wieku Martin Perl odkrył nową 

cząstkę Taon – który stanowił zaczątek nowej rodziny.

cząstkę Taon – który stanowił zaczątek nowej rodziny.

III rodzina to kwarki

III rodzina to kwarki

: denny (b) i szczytowy (t) – top

: denny (b) i szczytowy (t) – top

           

           

oraz leptony

oraz leptony

:  taon (

:  taon (

τ

τ

) i neutrino (

) i neutrino (

ν

ν

τ

τ

)

)

Ostatnia odkryta cząstka z tej rodziny to kwark szczytowy 

Ostatnia odkryta cząstka z tej rodziny to kwark szczytowy 

– top z roku 1994

– top z roku 1994

                           

                           

 

 

Czy rodzin jest więcej ?

Czy rodzin jest więcej ?

Na poziomie obecnej wiedzy – nie.

Na poziomie obecnej wiedzy – nie.

Ale – być może budowa potężniejszych akceleratorów 

Ale – być może budowa potężniejszych akceleratorów 

zbliżonych parametrami do piekła bardzo wczesnego 

zbliżonych parametrami do piekła bardzo wczesnego 

wszechświata pozwoli na wykrycie hipotetycznych w progu 

wszechświata pozwoli na wykrycie hipotetycznych w progu 

XXI wieku cząstek – 

XXI wieku cząstek – 

Preonów

Preonów

 z których byłyby zbudowane 

 z których byłyby zbudowane 

kwarki.

kwarki.

-

W nauce może się jeszcze wiele zdarzyć

W nauce może się jeszcze wiele zdarzyć

Obok kwarków istnieje 8 gluonów (g)

Obok kwarków istnieje 8 gluonów (g)

- są to kleje, które wiążą kwarki w 

- są to kleje, które wiążą kwarki w 

Hadrony – stanowiące 

Hadrony – stanowiące 

obecnie granicę rozwijalności materii

obecnie granicę rozwijalności materii

.

.

Kwarki i glony to jak dotąd składniki doskonałe, które nie 

Kwarki i glony to jak dotąd składniki doskonałe, które nie 

istnieją samoistnie ale powiązane ze sobą.

istnieją samoistnie ale powiązane ze sobą.

                           

                           

Światem cząstek elementarnych rządzą

Światem cząstek elementarnych rządzą

4 typy oddziaływań:

4 typy oddziaływań:

- silne

- silne

- słabe

- słabe

- elektromagnetyczne

- elektromagnetyczne

- grawitacyjne (ultrasłabe)

- grawitacyjne (ultrasłabe)

Kwarki

Kwarki

 podlegają oddziaływaniom: silnym, słabym i 

 podlegają oddziaływaniom: silnym, słabym i 

elektromagnetycznym

elektromagnetycznym

Leptony

Leptony

 – elektromagnetycznym i słabym

 – elektromagnetycznym i słabym

Neutrina

Neutrina

 – tylko słabym

 – tylko słabym

Ultrasłabym oddziaływaniom grawitacyjnym podlegają 

Ultrasłabym oddziaływaniom grawitacyjnym podlegają 

wszystkie cząstki materii, są to zawsze przyciągające 

wszystkie cząstki materii, są to zawsze przyciągające 

oddziaływania.

oddziaływania.

                           

                           

Nośniki oddziaływań:

Nośniki oddziaływań:

Silnych – gluony (g)

Silnych – gluony (g)

Elektromagnetycznych – fotony (

Elektromagnetycznych – fotony (

γ

γ

)

)

Słabych – bozony (w i z)

Słabych – bozony (w i z)

Model standardowy opisuje całość zjawisk mikroświata.

Model standardowy opisuje całość zjawisk mikroświata.

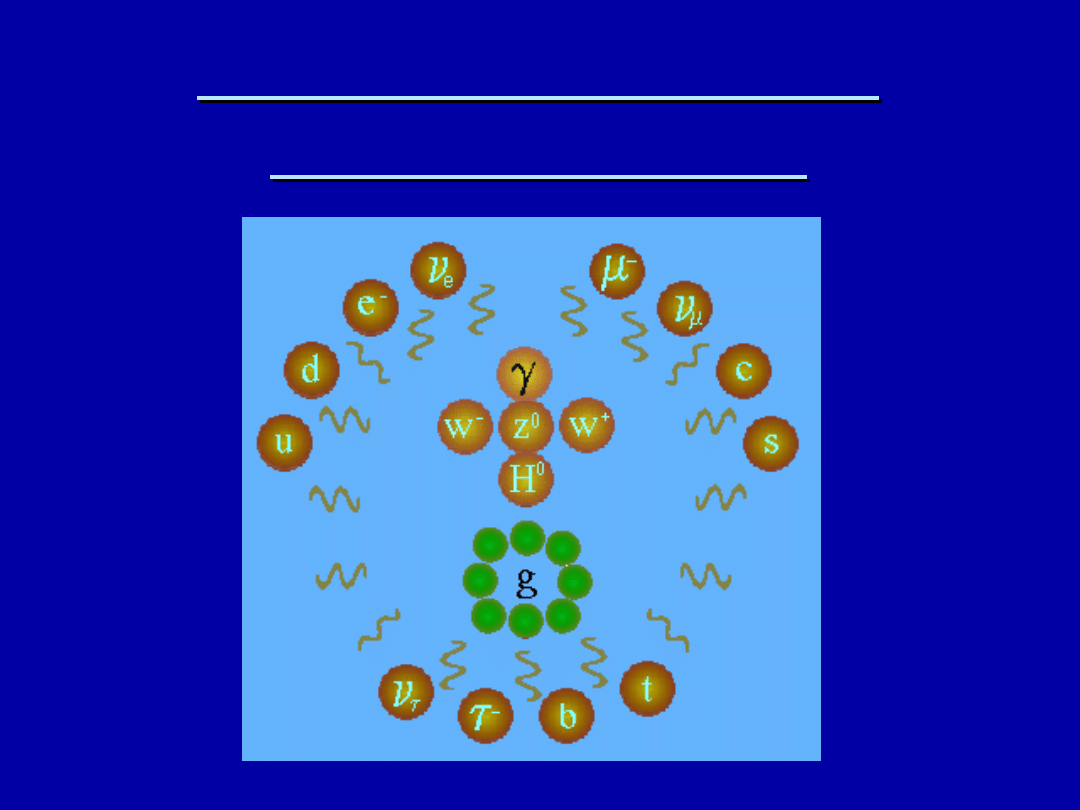
WSZYSTKIE CZĄSTKI 

WSZYSTKIE CZĄSTKI 

WSZECHŚWIATA

WSZECHŚWIATA

                           

                           



Te 25 cząstek elementarnych (oraz ich antycząstki, nie 

Te 25 cząstek elementarnych (oraz ich antycząstki, nie 

pokazane na rysunku) tworzy cały Wszechświat. 

pokazane na rysunku) tworzy cały Wszechświat. 

Pozwalają wyjaśnić wszystkie zachodzące w nim 

Pozwalają wyjaśnić wszystkie zachodzące w nim 

zdarzenia. Materia składa się z kwarków (u – górny, d – 

zdarzenia. Materia składa się z kwarków (u – górny, d – 

dolny, c – powabny, s – dziwny, b – denny, t- szczytowy) 

dolny, c – powabny, s – dziwny, b – denny, t- szczytowy) 

i leptonów (e – elektron, 

i leptonów (e – elektron, 

ν

ν

e

e

 – neutrino elektronowe, 

 – neutrino elektronowe, 

μ

μ

– 

– 

mion, 

mion, 

ν

ν

μ

μ

– neutrino mionowe, 

– neutrino mionowe, 

τ

τ

 – taon, 

 – taon, 

ν

ν

τ

τ

– neutrino 

– neutrino 

taonowe), które łączą się w trzy rodziny.

taonowe), które łączą się w trzy rodziny.



Na materię działają różne siły, które sprawiają że świat 

Na materię działają różne siły, które sprawiają że świat 

jest pełen zjawisk: elektrycznych, magnetycznych, 

jest pełen zjawisk: elektrycznych, magnetycznych, 

promieniotwórczych, jądrowych. Pola tych sił składają 

promieniotwórczych, jądrowych. Pola tych sił składają 

się z kwantów, czyli też cząstek. To te wewnątrz 

się z kwantów, czyli też cząstek. To te wewnątrz 

rysunku, czyli 

rysunku, czyli 

γ

γ

– foton, W

– foton, W

+

+

, W

, W

-

-

, Z

, Z

0

0

 – bozony 

 – bozony 

pośredniczące, H

pośredniczące, H

0

0

 – cząstka Higgsa, której jeszcze nie 

 – cząstka Higgsa, której jeszcze nie 

znaleziono, g – osiem glonów (różniące się ładunkiem 

znaleziono, g – osiem glonów (różniące się ładunkiem 

silnym, czyli jak mówią fizycy – kolorem).

silnym, czyli jak mówią fizycy – kolorem).

                           

                           

Nagrodę Nobla w dziedzinie fizyki w 1999 r. otrzymali 

Nagrodę Nobla w dziedzinie fizyki w 1999 r. otrzymali 

dwaj Holendrzy: Gerarduus’t Hooft prof. W Ultrechcie i 

dwaj Holendrzy: Gerarduus’t Hooft prof. W Ultrechcie i 

Martinus J. G. Veltman – emerytowany prof. z Bilthoven.

Martinus J. G. Veltman – emerytowany prof. z Bilthoven.

Dzięki ich badaniom (obliczeniom) przetestowano model 

Dzięki ich badaniom (obliczeniom) przetestowano model 

standardowy atomu w wielu eksperymentach i 

standardowy atomu w wielu eksperymentach i 

stwierdzono że opisuje on niezwykle dokładnie to co 

stwierdzono że opisuje on niezwykle dokładnie to co 

dzieje się rzeczywiście na poziomie mikroświata. Wielkości 

dzieje się rzeczywiście na poziomie mikroświata. Wielkości 

oddziaływań mikrocząstek między sobą – wyliczone przez 

oddziaływań mikrocząstek między sobą – wyliczone przez 

tych uczonych zgadzają się co do promili z danymi 

tych uczonych zgadzają się co do promili z danymi 

doświadczalnymi, które można było przeprowadzić w 

doświadczalnymi, które można było przeprowadzić w 

akceleratorach cząstek elementarnych, które rozróżniają 

akceleratorach cząstek elementarnych, które rozróżniają 

struktury o rozmiarach około 10

struktury o rozmiarach około 10

-16

-16

 cm czyli 100 milionów 

 cm czyli 100 milionów 

razy mniejsze od rozmiarów atomów (10

razy mniejsze od rozmiarów atomów (10

-8

-8

 cm).

 cm).

 

 

Wydzielono dwie grupy cząstek elementarnych:

Wydzielono dwie grupy cząstek elementarnych:



Fermiony = leptony i kwarki 

Fermiony = leptony i kwarki 



Bozony

Bozony

                           

                           



Leptony

Leptony

: elektron, mion i taon, oraz ich neutrina „czują” 

: elektron, mion i taon, oraz ich neutrina „czują” 

oddziaływania elektromagnetyczne i słabe oddziaływania 

oddziaływania elektromagnetyczne i słabe oddziaływania 

które odpowiedzialne są za reakcje jądrowe.

które odpowiedzialne są za reakcje jądrowe.



Kwarki

Kwarki

: za pośrednictwem oddziaływań silnych 

: za pośrednictwem oddziaływań silnych 

dominujących w jądrach atomowych zapewniają im 

dominujących w jądrach atomowych zapewniają im 

stabilność 

stabilność 



Leptonów i kwarków jest dokładnie tyle samo i istnieje 

Leptonów i kwarków jest dokładnie tyle samo i istnieje 

między nimi jednoznaczna odpowiedniość

między nimi jednoznaczna odpowiedniość



Fermiony to materia

Fermiony to materia



Bozony

Bozony

 odpowiadają za różnorodne oddziaływania, są 

 odpowiadają za różnorodne oddziaływania, są 

cząstkami „przenoszącymi oddziaływania” elementarne  

cząstkami „przenoszącymi oddziaływania” elementarne  



Bozony W i Z są nośnikami oddziaływań słabych a 8 

Bozony W i Z są nośnikami oddziaływań słabych a 8 

gluonów g – przenoszą oddziaływania silne. Foton 

gluonów g – przenoszą oddziaływania silne. Foton 

γ

γ

 

 

– 

– 

przenosi elektromagnetyczne oddziaływania a nie 

przenosi elektromagnetyczne oddziaływania a nie 

zaobserwowany do tej pory 

zaobserwowany do tej pory 

grawiton jest nośnikiem sił 

grawiton jest nośnikiem sił 

grawitacyjnych ultra słabych

grawitacyjnych ultra słabych

.

.



Źródłem każdego oddziaływania jest ładunek. 

Źródłem każdego oddziaływania jest ładunek. 

Źródłem 

Źródłem 

fotonów są ładunki elektryczne

fotonów są ładunki elektryczne

, a ładunki oddziaływań 

, a ładunki oddziaływań 

słabych i silnych noszą nazwę 

słabych i silnych noszą nazwę 

zapachu i koloru

zapachu i koloru

. 

. 

                             

                             

LEPTONY

LEPTONY

ładunek

elektrycz

ny

zapach

masa

[GeV/c

2

]

0

ν

e

< 2 ∙ 10 

- 8

neutrino e

-1

e

5,18 ∙ 10 

- 

4

elektron

0

ν

μ

<2,5 ∙ 10 

4

neutrino μ

-1

μ

0,106

mion

0

ν

τ

<3,5 ∙ 10 

2

neutrino 

taonowe

-1

τ

1,784

taon

                           

                           

KWARKI

KWARKI

ładunek

elektrycz

ny

zapach

masa

[GeV/c

2

]

+2/3

u górny

4 ∙ 10 

3

-1/3

d dolny

7 ∙ 10 

3

+2/3

c 

powab

ny

1,5

-1/3

s dziwny

0,15

+2/3

t 

szczyto

wy

78

-1/3

b denny

4,7

                            

                            

       

       

Bozon

y

γ

W 

-

W 

+

Z 

0

q

Ładun

ek

0

-1

+1

0

0

Masa

GeV/c

2

0

81

81

92

0

      

      

      

      

Oddziaływania

Grawitac

yjne

Elektrosłabe

Silne

Odpowiedzia

lne za

stabilność 

jądra

Słabe

Elektro

magnetyczne

Działa na:

Energię i 

masę

zapach

Ładunek 

elektronów

Kolor

Cząstki pośredniczące

Grawiton W

- 

Z

0

 

W

+

ultrasła

be

γ (foton)

g (gluon)

Siła w 

porównani

u z 

oddziaływa

niami

Elektrycznymi 

dwóch 

kwarków 

„u” w 

odległości

10 

-18 m

10 

41

0.8

1

25

3 ·10 

-17 m

10 

41

10

4

1

60

           

           

JEDNOSTKI

JEDNOSTKI

Zgodnie ze wzorem Einsteina E = mc

Zgodnie ze wzorem Einsteina E = mc

2

2

                                 

                                 

           c - prędkość światła

           c - prędkość światła

 

 

m = E/c

m = E/c

2

2

1eV – to energia elektronu przyśpieszonego przez różnicę 

1eV – to energia elektronu przyśpieszonego przez różnicę 

potencjału 1V

potencjału 1V

1GeV (Giga eV) = 10

1GeV (Giga eV) = 10

9

9

 V

 V

1eV – odpowiada masie 1,78268 · 10

1eV – odpowiada masie 1,78268 · 10

-33

-33

g

g

1GeV = 1,78268 · 10

1GeV = 1,78268 · 10

-33

-33

 · 10

 · 10

9

9

 = 1,78268 · 10

 = 1,78268 · 10

-25

-25

g

g

Masa protonu

Masa protonu

 w tych jednostkach

 w tych jednostkach

2

938

,

0

c

GeV

m

p



a w Daltonach       m

p

= 

1,0078D

 

                    

                    



Dzięki pracom Holendrów można było wyliczyć masę 

Dzięki pracom Holendrów można było wyliczyć masę 

ostatniego kwarka – najcięższego t czyli szczytowego, 

ostatniego kwarka – najcięższego t czyli szczytowego, 

który odkryto kilkanaście lat później. Jego odkrycie 

który odkryto kilkanaście lat później. Jego odkrycie 

udowodniło że matematyczny model elektrosłabych 

udowodniło że matematyczny model elektrosłabych 

oddziaływań poprawnie opisuje rzeczywistość.

oddziaływań poprawnie opisuje rzeczywistość.



Została do wykrycia cząstka Higginsa – która musi 

Została do wykrycia cząstka Higginsa – która musi 

istnieć. Jest ona prawdopodobnie źródłem masy dla 

istnieć. Jest ona prawdopodobnie źródłem masy dla 

wszystkich innych cząstek elementarnych.

wszystkich innych cząstek elementarnych.



W 1999 r. nagrodę nobla w dziedzinie chemii otrzymał 

W 1999 r. nagrodę nobla w dziedzinie chemii otrzymał 

Egipcjanin – Achmed Zewail za konstrukcję aparatu 

Egipcjanin – Achmed Zewail za konstrukcję aparatu 

fotograficznego w którym czas ekspozycji równy jest 

fotograficznego w którym czas ekspozycji równy jest 

jednej femtosekundzie = 10

jednej femtosekundzie = 10

-15

-15

s. Odpowiada to czasowi 

s. Odpowiada to czasowi 

łączenia się cząstek podczas reakcji chemicznych . 

łączenia się cząstek podczas reakcji chemicznych . 

Pozwala krok po kroku śledzić ruchy atomów.

Pozwala krok po kroku śledzić ruchy atomów.

TYPY WIĄZAŃ CHEMICZNYCH

TYPY WIĄZAŃ CHEMICZNYCH

1. 

1. 

Wiązanie atomowe

Wiązanie atomowe

 – polega na tworzeniu 

 – polega na tworzeniu 

wspólnych par elektronowych pochodzących od 

wspólnych par elektronowych pochodzących od 

obu związanych atomów – prowadzi to do 

obu związanych atomów – prowadzi to do 

zwiększenia gęstości elektronowej pomiędzy 

zwiększenia gęstości elektronowej pomiędzy 

dwoma jądrami atomów które uczestniczą w 

dwoma jądrami atomów które uczestniczą w 

tworzeniu wiązania. Wiążące się atomy dążą do 

tworzeniu wiązania. Wiążące się atomy dążą do 

osiągnięcia minimum energii – czemu odpowiada 

osiągnięcia minimum energii – czemu odpowiada 

maksymalne nakładanie się ich orbitali wiążących. 

maksymalne nakładanie się ich orbitali wiążących. 

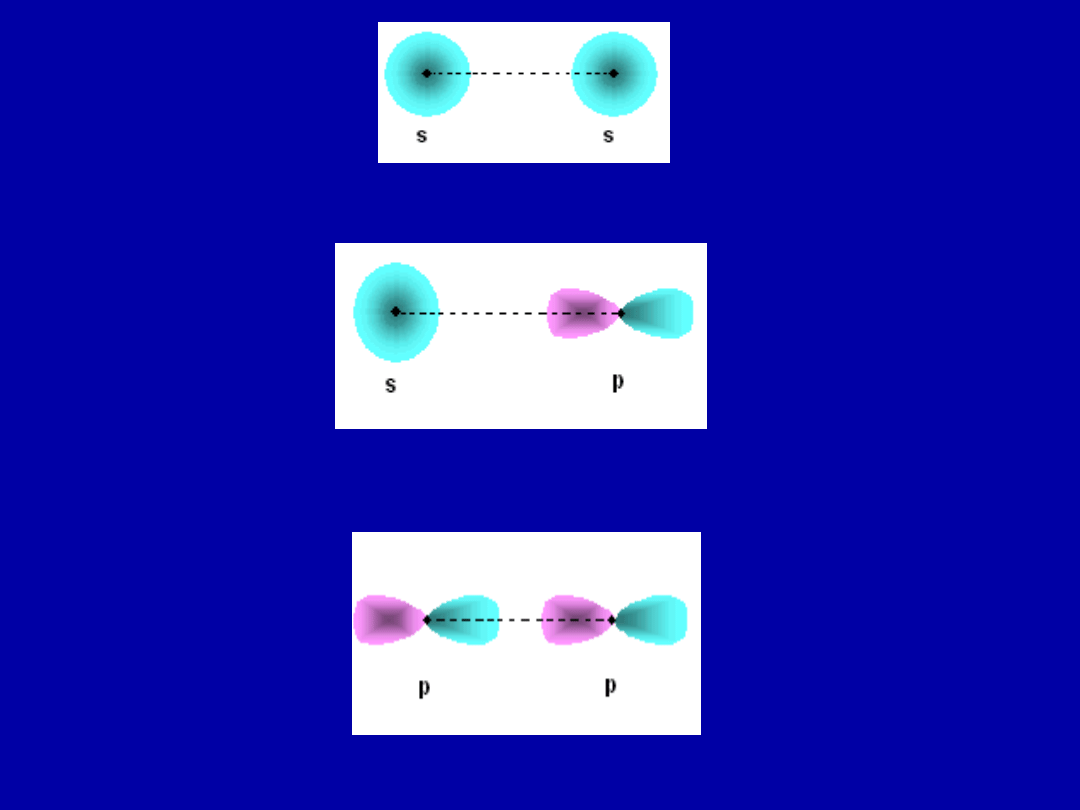
Rozkład     wykazuje obrotową symetrię wokół linii 

Rozkład     wykazuje obrotową symetrię wokół linii 

łączącej oba jądra. Wiązanie wykazujące taką 

łączącej oba jądra. Wiązanie wykazujące taką 

symetrię nazywa się σ.

symetrię nazywa się σ.

e

  

  

H                         H

 

       H                             O

       H                             Cl

O                         O

 

 

Wiązania atomowe można podzielic na :

Wiązania atomowe można podzielic na :

- atomowe niespolaryzowane – gdy wspólne pary    

- atomowe niespolaryzowane – gdy wspólne pary    

znajdują się w połowie długości wiązania

znajdują się w połowie długości wiązania

- atomowe spolaryzowane – wspólne pary    przesunięte są 

- atomowe spolaryzowane – wspólne pary    przesunięte są 

w stronę pierwiastka któremu mniej  brakuje do oktetu – 

w stronę pierwiastka któremu mniej  brakuje do oktetu – 

bardziej elektroujemnego np. H – Cl wspólna para 

bardziej elektroujemnego np. H – Cl wspólna para 

elektronowa przesunięta jest w stronę chloru

elektronowa przesunięta jest w stronę chloru

Wiązania atomowe niespolaryzowane

Wiązania atomowe niespolaryzowane

Powstają wtedy gdy różnica elektroujemności 0 ≤ ΔE ≤ 0,4

Powstają wtedy gdy różnica elektroujemności 0 ≤ ΔE ≤ 0,4

Spolaryzowane:                                              0,4 < ΔE ≤ 

Spolaryzowane:                                              0,4 < ΔE ≤ 

1,7

1,7

Jonowe:                                                          1,7 < ΔE ≤ 

Jonowe:                                                          1,7 < ΔE ≤ 

3,3

3,3

e

e

   

   

2.

2.

 Wiązania jonowe

 Wiązania jonowe

Powstają pomiędzy pierwiastkami leżącymi w układzie 

Powstają pomiędzy pierwiastkami leżącymi w układzie 

okresowym w skrajnych grupach I, II – VI, VII

okresowym w skrajnych grupach I, II – VI, VII

Polegają na oddaniu    przez pierwiastki mniej 

Polegają na oddaniu    przez pierwiastki mniej 

elektroujemne (które wtedy przejdą w jony dodatnie) 

elektroujemne (które wtedy przejdą w jony dodatnie) 

pierwiastkom bardziej elektroujemnym (które tworzą 

pierwiastkom bardziej elektroujemnym (które tworzą 

jony ujemne)

jony ujemne)

e

Na

0

 – 1    Na

+ 

              E = 0,7

                                                                ΔE = 2,1

Cl

0

 + 1    Cl

- 

                E = 2,8 

 

Wzajemne oddziaływanie utworzonych jonów nazywa się 

wiązaniem jonowym

e

e

  

  

3.

3.

 Wiązanie semipolarne lub koordynacyjne

 Wiązanie semipolarne lub koordynacyjne

Podobne jest do wiązania atomowego ale wiążąca para   

Podobne jest do wiązania atomowego ale wiążąca para   

pochodzi od jednego pierwiastka (donora) a obierana 

pochodzi od jednego pierwiastka (donora) a obierana 

jest przez akceptor który ma pusty orbital walencyjny

jest przez akceptor który ma pusty orbital walencyjny

e

 

 

  

  

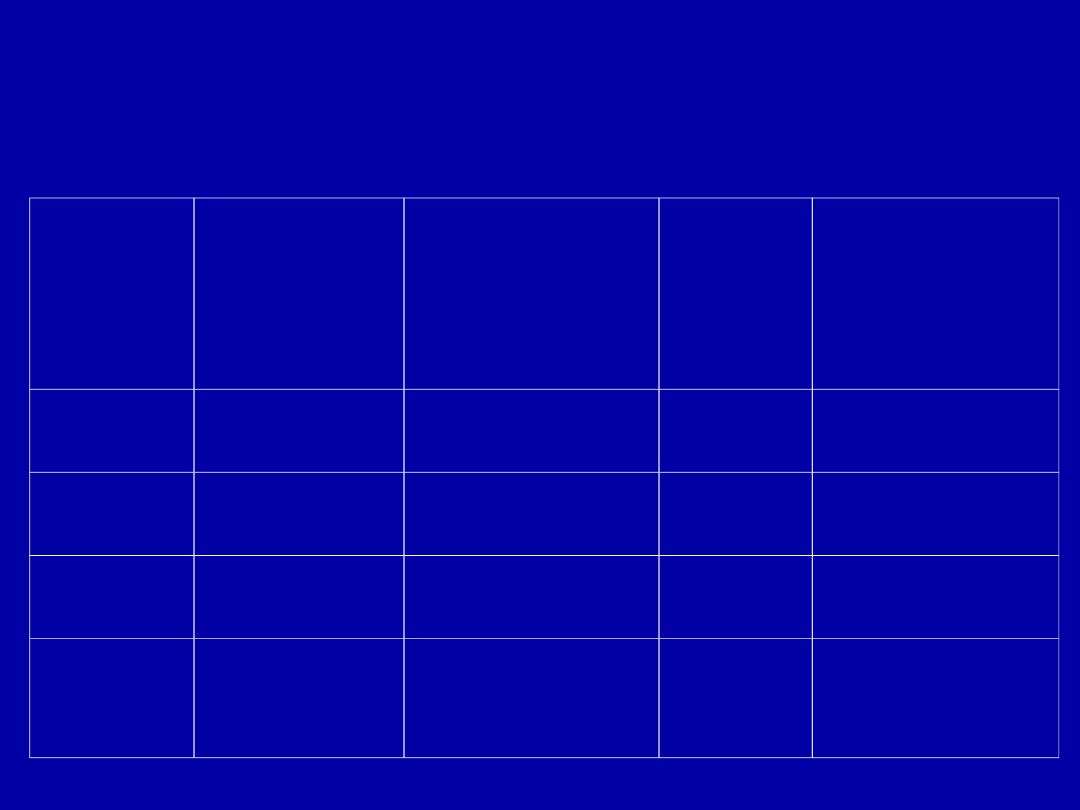
Numer

grupy

A

Liczba e

walencyjnyc

h 

B = 8 - A

Liczba wiązań 

atomowych

 e = A – 

B

Liczba
wolnych 

e

D = e /2

Liczba

wiązań 

koordynacyjny

ch

IV 

 C, Si

4

4

0

0

V 

N, P

5

3

2

1

VI

S, Cr

6

2

4

2

VII

Cl, Br, J

Mn

7

1

konieczne

6

3

możliwe

  

  

WIĄZANIE METALICZNE

WIĄZANIE METALICZNE

Występuje pomiędzy atomami metalu w stanie stałym. 

Różni się od pozostałych wiązań istnieniem swobodnych    

niezwiązanych z pojedynczymi atomami, a przynależnych 

wszystkim atomom metalu. W sieci krystalicznej każdy 

atom metalu otoczony jest większą liczbą takich samych 

atomów (najczęściej 8 – 12).

Węzły sieci przestrzennej metalu osadzone są przez 

dodatnio naładowane rdzenie, zwane też zrębami 

atomowymi. Ich  walencyjne tworzą gaz elektronowy.

Metale w stanie gazowym nie wykazują cech 

charakteryzujących je w stanie stałym i ciekłym. Gazowy 

metal jest przeźroczysty, nie przewodzi prądu 

elektrycznego w sposób metaliczny, a wymaga 

uprzedniego zjonizowania tak jak inne gazy. W metalach 

w postaci pary istnieją związki dwuatomowe z typowymi 

wiązaniami atomowymi – każdy atom przekazuje do tego 

wiązania jeden    i jeden orbital.

e

e

e

      

      

WŁASNOŚCI METALI  - WYNIKAJĄCE Z OBECNOŚCI WIĄZANIA 

WŁASNOŚCI METALI  - WYNIKAJĄCE Z OBECNOŚCI WIĄZANIA 

METALICZNEGO

METALICZNEGO

1.

1.

Dobre przewodnictwo cieplne i elektryczne.

Dobre przewodnictwo cieplne i elektryczne.

2.

2.

Połysk metaliczny. 

Połysk metaliczny. 

3.

3.

Plastyczność – klepalność, kowalność.

Plastyczność – klepalność, kowalność.

4.

4.

Malejące przewodnictwo elektryczne przy 

Malejące przewodnictwo elektryczne przy 

podgrzaniu.

podgrzaniu.

5.

5.

Metale oddające więcej elektronów  walencyjnych 

Metale oddające więcej elektronów  walencyjnych 

do tworzenia sieci krystalicznej mają strukturę 

do tworzenia sieci krystalicznej mają strukturę 

krystaliczną twardszą

krystaliczną twardszą

- 

- 

potasowce z jednym elektronem  walencyjnym tworzą 

potasowce z jednym elektronem  walencyjnym tworzą 

miękkie struktury o t.t. niskich Rb t.t. = 38,9 

miękkie struktury o t.t. niskich Rb t.t. = 38,9 

o

o

C ; Cs t.t. = 

C ; Cs t.t. = 

28,7 

28,7 

o

o

C

C

- 

- 

wapniowce – dwa  walencyjne do sieci t.t. Ca = 383 

wapniowce – dwa  walencyjne do sieci t.t. Ca = 383 

o

o

C   

C   

   

   

t.t. Ba = 714 

t.t. Ba = 714 

o

o

C

C

 

 

WŁAŚCIWOŚCI KRYSZTAŁÓW O WIĄZANIU JONOWYM

WŁAŚCIWOŚCI KRYSZTAŁÓW O WIĄZANIU JONOWYM

1. Sole tworzą krystaliczne sieci jonowe, ich kryształy nie 

1. Sole tworzą krystaliczne sieci jonowe, ich kryształy nie 

przewodzą prądu, stopione – przewodzą prąd.

przewodzą prądu, stopione – przewodzą prąd.

2. Rozpuszczają się w rozpuszczalnikach polarnych, a ich 

2. Rozpuszczają się w rozpuszczalnikach polarnych, a ich 

roztwory przewodzą prąd.

roztwory przewodzą prąd.

3. Temperatury topnienia są wysokie > 500 

3. Temperatury topnienia są wysokie > 500 

o

o

C 

C 

Temperatury wrzenia wysokie:

Temperatury wrzenia wysokie:

    

    

NaCl t.t. = 801 

NaCl t.t. = 801 

o

o

C     t.w. = 1413 

C     t.w. = 1413 

o

o

C

C

  

  

WŁAŚCIWOŚCI KRYSZTAŁÓW O WIĄZANIACH ATOMOWYCH

WŁAŚCIWOŚCI KRYSZTAŁÓW O WIĄZANIACH ATOMOWYCH

1.

1.

Nie przewodzą prądu nawet stopione

Nie przewodzą prądu nawet stopione

2.

2.

Są rozpuszczalne w rozpuszczalnikach niepolarnych 

Są rozpuszczalne w rozpuszczalnikach niepolarnych 

lub słabo polarnych

lub słabo polarnych

3.

3.

Powstają z tych samych pierwiastków lub z 

Powstają z tych samych pierwiastków lub z 

pierwiastków o podobnej elektroujemności

pierwiastków o podobnej elektroujemności

4.

4.

Wiązania sieciowe tworzą się przez uwspólnienie 

Wiązania sieciowe tworzą się przez uwspólnienie 

wszystkich elektronów walencyjnych lub ich części

wszystkich elektronów walencyjnych lub ich części

5.

5.

Wzór elementu w krysztale jest wzorem związku

Wzór elementu w krysztale jest wzorem związku

6.

6.

Mają niskie temperatury topnienia i wrzenia

Mają niskie temperatury topnienia i wrzenia

7.

7.

Reakcje w roztworach zachodzą wolniej niż reakcje w 

Reakcje w roztworach zachodzą wolniej niż reakcje w 

roztworach związków jonowych

roztworach związków jonowych

Związki kompleksowe

Związki kompleksowe

Nagroda Nobla 1893 r. – Werner

Nagroda Nobla 1893 r. – Werner

Są to związki o złożonej budowie których podstawowym 

Są to związki o złożonej budowie których podstawowym 

wiązaniem jest wiązanie koordynacyjne – wtórne.

wiązaniem jest wiązanie koordynacyjne – wtórne.

Tworzą je głównie pierwiastki bloku „ d” lub grup pobocznych 

Tworzą je głównie pierwiastki bloku „ d” lub grup pobocznych 

wg. Mendelejewa.

wg. Mendelejewa.

Dążąc do utworzenia struktury  gazu szlachetnego efekt l.a. 

Dążąc do utworzenia struktury  gazu szlachetnego efekt l.a. 

przyłączają jony lub cząstki obojętne posiadające kompletne – 

przyłączają jony lub cząstki obojętne posiadające kompletne – 

ale wolne pary elektronowe. Pierwiastki te noszą nazwę 

ale wolne pary elektronowe. Pierwiastki te noszą nazwę 

atomów centralnych 

atomów centralnych 

natomiast cząsteczki przyłączane zwane 

natomiast cząsteczki przyłączane zwane 

są 

są 

ligandami

ligandami

.

.

Mogą to być jony: F

Mogą to być jony: F

-

-

, Cl

, Cl

-

-

, I

, I

-

-

, CN

, CN

-

-

, OH

, OH

-

-

, S

, S

-2

-2

lub cząstki obojętne: H

lub cząstki obojętne: H

2

2

O     [ akwa ]

O     [ akwa ]

                                  

                                  

NH

NH

3

3

     [ amina ]

     [ amina ]

                                  

                                  

CO       [ karbonylo]

CO       [ karbonylo]

[ Co(NH

[ Co(NH

3

3

)

)

6

6

]

]

+3

+3

 3Cl

 3Cl

-

-

                                              Nobel Wernera 

                                              Nobel Wernera 

 

 

Liczba koordynacyjna

Liczba koordynacyjna

 – liczba przyłączonych przez atom 

 – liczba przyłączonych przez atom 

ligandów. Określa ona liczbę brakujących par elektronów 

ligandów. Określa ona liczbę brakujących par elektronów 

na powłokach walencyjnych pierwiastka centralnego. 

na powłokach walencyjnych pierwiastka centralnego. 

Najczęściej wynosi ona 2, 4 lub 6 

Najczęściej wynosi ona 2, 4 lub 6 

np. w reakcji:

np. w reakcji:

FeSO

FeSO

4

4

 + 6 NaCN 

 + 6 NaCN 





 Na

 Na

4

4

[Fe(CN)

[Fe(CN)

6

6

] + Na

] + Na

2

2

SO

SO

4

4

Jon żelaza ma strukturę ostatnich powłok następującą:

Jon żelaza ma strukturę ostatnich powłok następującą:

 

 

Fe

Fe

+2

+2

 ma na powłokach walencyjnych 6 pustych orbitali, może więc 

 ma na powłokach walencyjnych 6 pustych orbitali, może więc 

koordynować 6 jonów

koordynować 6 jonów

                  

                  

mających wolną parę

mających wolną parę

e

W ten sposób żelazo uzyskuje konfigurację kryptonu

29

Cu

+2

     1s

2

 2s

2

 2p

6

 3s

2

 3p

6

 4s

0

 3d

10

 4p

0

Posiada 4 puste orbitale 4s i 3 orbitale 4p, tworzy związek 
kompleksowy 2.

                                  
                     

tetraamin
a

47

Ag

+ 

     1s

2

 2s

2

 2p

6

 3s

2

 3p

6

 4s

2

 3d

10

 4p

6

 5s

0

 4d

10

 5p

0

Liczba koordynacyjna srebra najczęściej wynosi 2

2

4

3

]

[



NH

Cu

 

 

Jeżeli dodatni jon metalu koordynuje cząsteczki obojętne

Jeżeli dodatni jon metalu koordynuje cząsteczki obojętne

[H

[H

2

2

O, NH

O, NH

3

3

] to powstaje 

] to powstaje 

kation kompleksowy

kation kompleksowy

 o ładunku 

 o ładunku 

równym dodatniemu ładunkowi jonu centralnego.

równym dodatniemu ładunkowi jonu centralnego.

Jeżeli zaś ligandami są jony ujemne [Cl

Jeżeli zaś ligandami są jony ujemne [Cl

-

-

, CN

, CN

-

-

] to ładunek 

] to ładunek 

jonu kompleksowego równy jest sumie algebraicznej 

jonu kompleksowego równy jest sumie algebraicznej 

ładunków. Jon kompleksowy i towarzyszące mu jony 

ładunków. Jon kompleksowy i towarzyszące mu jony 

ostatecznie tworzą związek obojętny np. [Cu(NH

ostatecznie tworzą związek obojętny np. [Cu(NH

3

3

)

)

4

4

]SO

]SO

4

4

 , 

 , 

K

K

4

4

[Fe(CN)

[Fe(CN)

6

6

].

].

Rodzaje oddziaływań

Rodzaje oddziaływań

Jon – dipol

Jon – dipol

[Cu(NH

[Cu(NH

3

3

)

)

4

4

]

]

+2

+2

          [Mg(H

          [Mg(H

2

2

O)

O)

6

6

]

]

+2

+2

Jon – jon

Jon – jon

[FeF

[FeF

6

6

]

]

-3

-3

                   [Fe(CN)

                   [Fe(CN)

6

6

]

]

-4

-4

 

 

 

 

PRAKTYCZNE ZNACZENIE KOMPLEKSÓW

PRAKTYCZNE ZNACZENIE KOMPLEKSÓW

1. Są lepiej rozpuszczalne niż związki jonowe

1. Są lepiej rozpuszczalne niż związki jonowe

             

             

AgCl                              [Ag(NH

AgCl                              [Ag(NH

3

3

)

)

2

2

]Cl

]Cl

nierozpuszczalny w wodzie                    rozpuszczalny w wodzie

nierozpuszczalny w wodzie                    rozpuszczalny w wodzie

           

           

           

           

Cu(OH)

Cu(OH)

2                          

2                          

       [Cu(NH

       [Cu(NH

3

3

)

)

4

4

](OH)

](OH)

2

2

                  

                  

AgI                          Na

AgI                          Na

3

3

[Ag(S

[Ag(S

2

2

O

O

3

3

)

)

2

2

]

]











3

2

2

O

S

Na











OH

NH

4











OH

NH

4

  

  

2. Jony skompleksowane posiadają inne barwy

2. Jony skompleksowane posiadają inne barwy

Cu

Cu

+2

+2

 – niebieski                 [Cu(NH

 – niebieski                 [Cu(NH

3

3

)

)

4

4

]

]

+2

+2

     szafirowy  

     szafirowy  

Fe

Fe

+3

+3

 – żółty                        [Fe(CNS)

 – żółty                        [Fe(CNS)

6

6

]

]

-3

-3

     krwistoczerwony

     krwistoczerwony

3. 

3. 

Związki chelatowe

Związki chelatowe

 – są to kompleksy w których ligandy 

 – są to kompleksy w których ligandy 

są donorami dwóch    lub więcej par elektronowych 

są donorami dwóch    lub więcej par elektronowych 

występujących w różnych atomach tej samej cząsteczki. 

występujących w różnych atomach tej samej cząsteczki. 

Takie ligandy nazywamy czynnikami chelatującymi. Są to 

Takie ligandy nazywamy czynnikami chelatującymi. Są to 

najczęściej związki organiczne zawierające N, S, jako 

najczęściej związki organiczne zawierające N, S, jako 

miejsce reaktywne [chela = kleszcze, nożyce]. Związki 

miejsce reaktywne [chela = kleszcze, nożyce]. Związki 

chelatowe mają budowę pierścieniową, najtrwalsze są 

chelatowe mają budowę pierścieniową, najtrwalsze są 

kompleksy 5 lub 6 członowe, wliczając w to atom 

kompleksy 5 lub 6 członowe, wliczając w to atom 

centralny.

centralny.

 

 

W zależności od liczby par elektronowych czynniki 

W zależności od liczby par elektronowych czynniki 

chelatujące nazywamy jedno lub wielokleszczowymi. 

chelatujące nazywamy jedno lub wielokleszczowymi. 

Uchwycenie atomu centralnego w dwa kleszcze powoduje 

Uchwycenie atomu centralnego w dwa kleszcze powoduje 

zamaskowanie jego charakteru nieorganicznego, a cały 

zamaskowanie jego charakteru nieorganicznego, a cały 

kompleks zachowuje się jak związek organiczny. Chelaty 

kompleks zachowuje się jak związek organiczny. Chelaty 

są na ogół trwalsze od kompleksów niechelatowych.

są na ogół trwalsze od kompleksów niechelatowych.

Znanym związkiem chelatujacym jest kwas 

Znanym związkiem chelatujacym jest kwas 

etylenodiaminotetraoctowy lub jego sól sodowa [EDTA]

etylenodiaminotetraoctowy lub jego sól sodowa [EDTA]

 

 

Kompleksy z tymi samymi ligandami są tym trwalsze im 

Kompleksy z tymi samymi ligandami są tym trwalsze im 

mniejszy jest promień jonu centralnego.

mniejszy jest promień jonu centralnego.

Najsłabsze

Najsłabsze

 są akwokompleksy do których należą 

 są akwokompleksy do których należą 

wszystkie jony metali w wodzie. W roztworach 

wszystkie jony metali w wodzie. W roztworach 

kompleksy mniej trwałe przechodzą w trwalsze, ale 

kompleksy mniej trwałe przechodzą w trwalsze, ale 

stopniowo.

stopniowo.

 

 

Kompleksy występujące w przyrodzie

Kompleksy występujące w przyrodzie

Żelazo – porfirynowy w hemie hemoglobiny, związany z 

Żelazo – porfirynowy w hemie hemoglobiny, związany z 

białkami krwi i mięśni [ mioglobina ].

białkami krwi i mięśni [ mioglobina ].

Fe

Fe

+2

+2

 związany jest czterema wiązaniami [ dwa jonowe, 

 związany jest czterema wiązaniami [ dwa jonowe, 

dwa koordynacyjne ] z azotami pierścieni pirolowych, 5 

dwa koordynacyjne ] z azotami pierścieni pirolowych, 5 

wiązaniem – koordynacyjnym z białkiem, a 6 z tlenem 

wiązaniem – koordynacyjnym z białkiem, a 6 z tlenem 

[ łatwo odczepialnym – dlatego przenosi tlen]

[ łatwo odczepialnym – dlatego przenosi tlen]

Porfiryny

Porfiryny

 występują jeszcze w innych białkach – 

 występują jeszcze w innych białkach – 

katalazy

katalazy

 katalizujące rozkład H

 katalizujące rozkład H

2

2

O

O

2

2

 , inne enzymy

 , inne enzymy

Cytochromy

Cytochromy

 – żelazo może zmieniać stopień utlenienia 

 – żelazo może zmieniać stopień utlenienia 

nie tracąc aktywności biologicznej.

nie tracąc aktywności biologicznej.

Witamina B

Witamina B

12

12

 (kat. cent. – Co)

 (kat. cent. – Co)

chlorofil

chlorofil

, celuroplazmina, transferyna

, celuroplazmina, transferyna

 

 

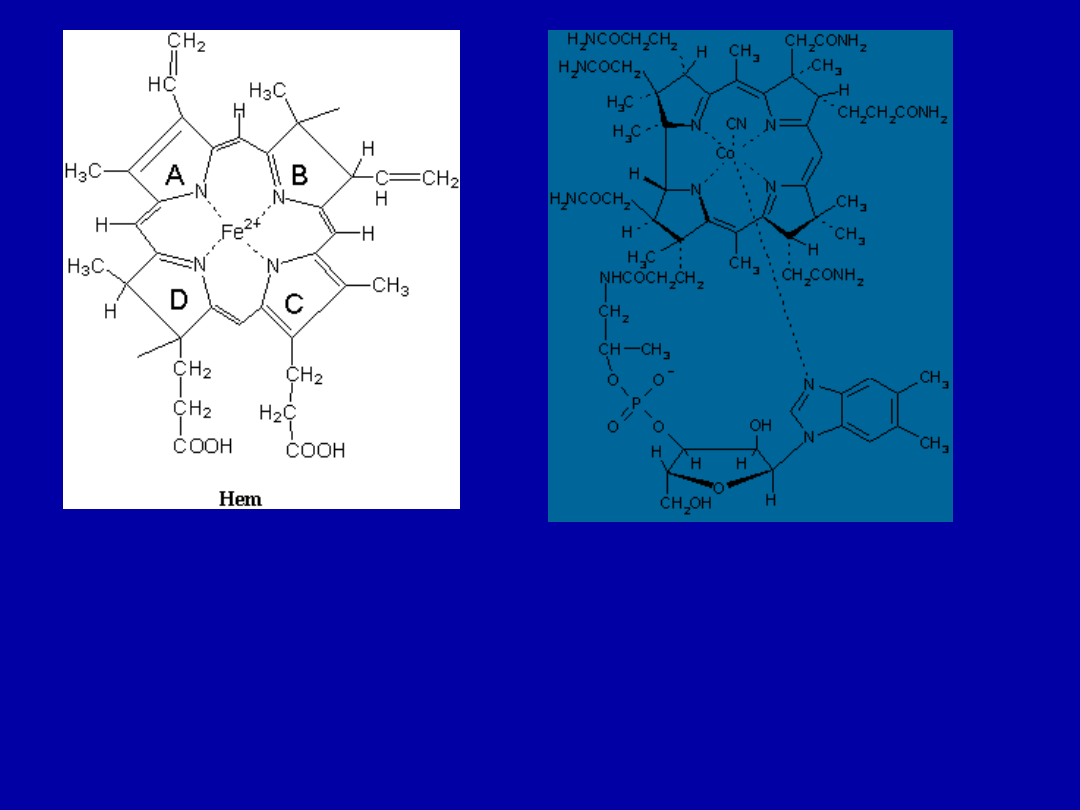
Wzór strukturalny hemu           Witamina B

12

 -  

cyjanokobaltamina

 

 

ODDZIAŁYWANIA MIĘDZYCZĄSTECZKOWE – SIŁY VAN DER 

ODDZIAŁYWANIA MIĘDZYCZĄSTECZKOWE – SIŁY VAN DER 

WAALSA

WAALSA

A. Między cząsteczkami obojętnymi

- efekty kulombowskiego elektrostatycznego przyciągania 

i odpychania zachodzące pomiędzy jądrami i 
elektronami różnych cząsteczek obojętnych

- siły magnetyczne związane z istnieniem momentów 

magnetycznych

- siły dyspersyjne związane z powstawaniem i zanikaniem 

chwilowych dipoli na skutek ruchów atomów w 
cząsteczkach są to siły przyciągania i odpychania 
chwilowego cząsteczek

   

   

B. 

B. 

Między cząsteczkami polarnymi

Między cząsteczkami polarnymi

- sprzężenie elektrostatyczne

- sprzężenie elektrostatyczne

- sprzężenie dipolowe – cząsteczka polarna indukuje 

- sprzężenie dipolowe – cząsteczka polarna indukuje 

powstanie momentu dipolowego w cząsteczce 

powstanie momentu dipolowego w cząsteczce 

niepolarnej

niepolarnej

- wiązanie wodorowe !!! najważniejsze – jest to 

- wiązanie wodorowe !!! najważniejsze – jest to 

oddziaływanie elektrostatyczne miedzy dodatnim 

oddziaływanie elektrostatyczne miedzy dodatnim 

biegunem wodoru jednej cząsteczki polarnej z 

biegunem wodoru jednej cząsteczki polarnej z 

ujemnym biegunem drugiej cząsteczki polarnej. 

ujemnym biegunem drugiej cząsteczki polarnej. 

Najczęściej powstaje ono w związkach w których 

Najczęściej powstaje ono w związkach w których 

występują wiązania H – O ; H – N ; H – S ; H – X  (F, Cl, 

występują wiązania H – O ; H – N ; H – S ; H – X  (F, Cl, 

Br, I)

Br, I)

- energia wiązania wodorowego jest znacznie mniejsza od 

- energia wiązania wodorowego jest znacznie mniejsza od 

wiązania atomowego

wiązania atomowego

- długość wiązania wodorowego jest większa od 

- długość wiązania wodorowego jest większa od 

atomowego

atomowego

 

 

 

 

Energia 

wiązania

atomowego 

[kJ/M]

Energia 

wiązania

wodorowego 

[kJ/M]

H – 

O

464

12,3 – 33,4

H – 

N

389

16,7 – 28,2

H – 

F

564

20,9 – 33,4

Np.

Długość
X – H······Y                           X – 
H
   at.   wod.                                 
 
         0,27 nm                     
0,19nm

  

  

Wiązanie to prowadzi do 

Wiązanie to prowadzi do 

asocjacji

asocjacji

np. cząsteczki HF tworzą długie zygzakowate łańcuchy t

np. cząsteczki HF tworzą długie zygzakowate łańcuchy t

w

w

 

 

29,2 

29,2 

o

o

K w tej temperaturze cząsteczce pary odpowiada 

K w tej temperaturze cząsteczce pary odpowiada 

masa molowa 68,8 tzn. jest 3,4 razy większa od M

masa molowa 68,8 tzn. jest 3,4 razy większa od M

HF

HF

 czyli 

 czyli 

że

że

cząsteczka pary ma budowę H

cząsteczka pary ma budowę H

3

3

F

F

3

3

 i H

 i H

4

4

F

F

4

4

 – zasocjowane 3 - 

 – zasocjowane 3 - 

4 cząsteczki

4 cząsteczki

Również porównując temperaturę wrzenia wody i innych 

Również porównując temperaturę wrzenia wody i innych 

związków o podobnej masie molowej wyraźnie widać, że 

związków o podobnej masie molowej wyraźnie widać, że 

woda jest zasocjowana 

woda jest zasocjowana 

tw

tw

H20

H20

 = 100 

 = 100 

o

o

C               m

C               m

H20

H20

 = 18             C

 = 18             C

2

2

H

H

6

6

     tt = 

     tt = 

-86,6 

-86,6 

o

o

C

C

tw

tw

CH4

CH4

 = -161,6 

 = -161,6 

o

o

C          m

C          m

CH4

CH4

 = 16             m

 = 16             m

C2H6

C2H6

 = 30

 = 30

   

   

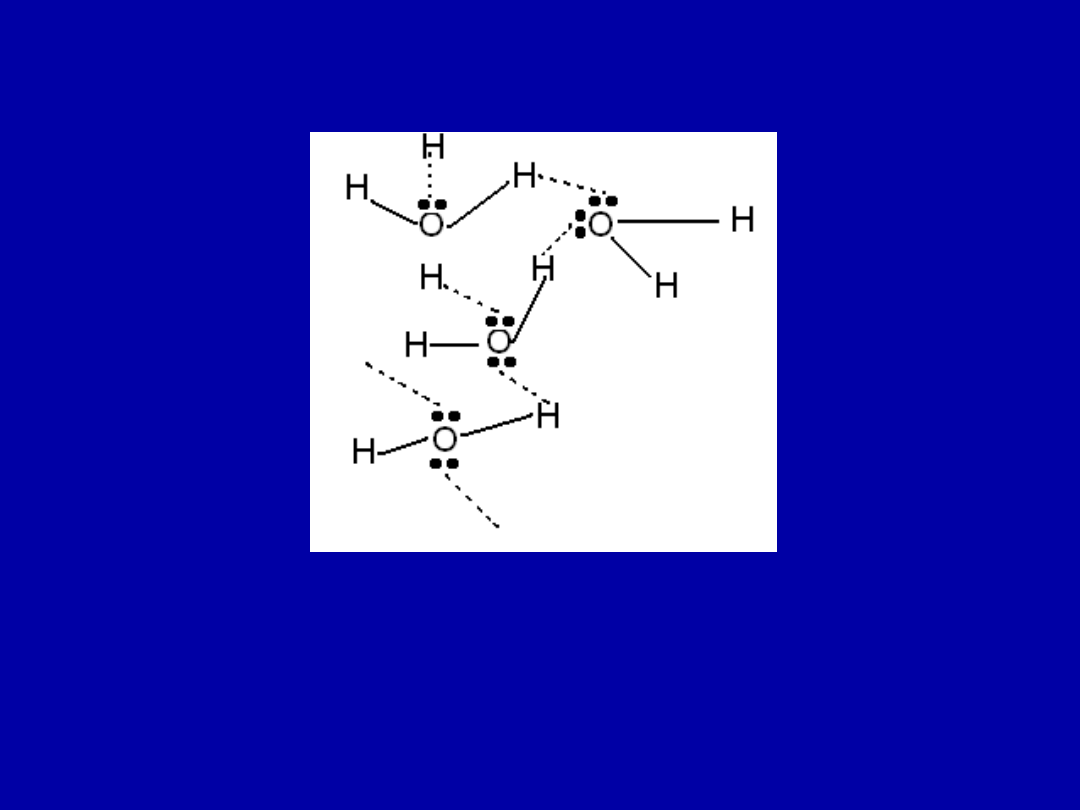
Każdy atom „O” w wodzie jest otoczony 4 H

Każdy atom „O” w wodzie jest otoczony 4 H

Wiązanie takie występuje w alkoholach, aminach, 
białkach, kwasach nukleinowych – warunkuje ono 
aktywność biologiczną wielu enzymów.

STANY SKUPIENIA MATERII

STANY SKUPIENIA MATERII

KINETYCZNA TEORIA BUDOWY MATERII

KINETYCZNA TEORIA BUDOWY MATERII



- Podstawowe elementy znajdują się w ciągłym ruchu 

- Podstawowe elementy znajdują się w ciągłym ruchu 

–   energia własna

–   energia własna



- Istnieją między nimi siły wzajemnego oddziaływania 

- Istnieją między nimi siły wzajemnego oddziaływania 

–  przyciąganie

–  przyciąganie

W zależności od stopnia uporządkowania cząsteczek 

W zależności od stopnia uporządkowania cząsteczek 

lub atomów i tego który rodzaj oddziaływań przeważa 

lub atomów i tego który rodzaj oddziaływań przeważa 

– przyciąganie czy energia własna, materia 

– przyciąganie czy energia własna, materia 

występuje w 3 stanach:

występuje w 3 stanach:



- gazowym – wysoka energia własna, małe 

- gazowym – wysoka energia własna, małe 

przyciąganie międzycząsteczkowe

przyciąganie międzycząsteczkowe



- ciekłym – maleje energia własna a rosną siły 

- ciekłym – maleje energia własna a rosną siły 

przyciągania cząsteczek

przyciągania cząsteczek



- stałym – mała energia, duże siły oddziaływań 

- stałym – mała energia, duże siły oddziaływań 

międzycząsteczkowych

międzycząsteczkowych

 

 

STAN GAZOWY

STAN GAZOWY

GAZ DOSKONAŁY – wyidealizowany stan materii 

GAZ DOSKONAŁY – wyidealizowany stan materii 

spełniający kilka warunków:

spełniający kilka warunków:

- cząsteczki gazu zachowują się jak jednorodne kule 

- cząsteczki gazu zachowują się jak jednorodne kule 

doskonale sprężyste

doskonale sprężyste

- objętość własna cząsteczek jest znikomo mała w 

- objętość własna cząsteczek jest znikomo mała w 

porównaniu z objętością zajmowaną przez mol gazu

porównaniu z objętością zajmowaną przez mol gazu

- cząsteczki znajdujące się w ciągłym chaotycznym ruchu 

- cząsteczki znajdujące się w ciągłym chaotycznym ruchu 

zderzają się sprężyście, zgodnie z prawami mechaniki 

zderzają się sprężyście, zgodnie z prawami mechaniki 

zderzeń sprężystych

zderzeń sprężystych

- do zderzenia ruch cząsteczek jest prostoliniowy, bez 

- do zderzenia ruch cząsteczek jest prostoliniowy, bez 

żadnego  uprzywilejowanego kierunku

żadnego  uprzywilejowanego kierunku

Żaden z gazów rzeczywistych nie spełnia tych warunków, 

Żaden z gazów rzeczywistych nie spełnia tych warunków, 

dopiero w wysokich temperaturach i przy dużych 

dopiero w wysokich temperaturach i przy dużych 

rozrzedzeniach zbliżają się one do tego idealnego modelu.

rozrzedzeniach zbliżają się one do tego idealnego modelu.

  

  

PRAWA GAZÓW DOSKONAŁYCH

PRAWA GAZÓW DOSKONAŁYCH

1. Boyle’a i Mariotta

1. Boyle’a i Mariotta

    

    

W stałej T objętość gazu jest odwrotnie proporcjonalna 

W stałej T objętość gazu jest odwrotnie proporcjonalna 

ciśnienia

ciśnienia

    

    

T = const. 

T = const. 

    

    

T

T

0

0

 ≠ T

 ≠ T

1

1

0

1

1

0

V

V

p

p



1

1

1

0

0

0

T

V

p

T

V

p







1

1

0

0

1

p

T

V

p

V







  

  

2. Gay – Lussaca

2. Gay – Lussaca

Przy stałym P objętość danej masy gazu podczas 

Przy stałym P objętość danej masy gazu podczas 

ogrzewania zwiększa się z każdym stopniem o 1/273 

ogrzewania zwiększa się z każdym stopniem o 1/273 

objętości jaką gaz ten zajmuje w temp. 0 

objętości jaką gaz ten zajmuje w temp. 0 

o

o

C

C

                                                         

                                                         

p = const

p = const

 

 

   

   

lub

lub

273

0

0

t

V

V

V







)

273

1

(

0

C

t

V

V

o





 

 

Wprowadzając T w stopniach Kelwina [ stały jej punkt to 

Wprowadzając T w stopniach Kelwina [ stały jej punkt to 

temperatura punktu potrójnego wody T = 273,16 K lub 

temperatura punktu potrójnego wody T = 273,16 K lub 

0,098 

0,098 

o

o

C]

C]

Prawo Gay – Lussaca ma postać:

Prawo Gay – Lussaca ma postać:

Przy p = const     V/T = const

Przy p = const     V/T = const

0

0

T

T

V

V 

 

 

3. 

3. 

Równanie gazu doskonałego – podsumowanie 1,2:

Równanie gazu doskonałego – podsumowanie 1,2:

                                 

                                 

[ R ] – stała gazowa

[ R ] – stała gazowa

lub     pV = RT       dla 1 mola gazu

lub     pV = RT       dla 1 mola gazu

przyjmując: 

przyjmując: 

                  

                  

T = 273K                        p = 1 atm

T = 273K                        p = 1 atm

                  

                  

V = 22,4 dm

V = 22,4 dm

3

3

/mol 

/mol 

Wyliczono R = 0,082 dm

Wyliczono R = 0,082 dm

3

3

 ∙ atm ∙ K ∙ mol

 ∙ atm ∙ K ∙ mol

-1

-1

lub R = 8,314 J/mol ∙ K

lub R = 8,314 J/mol ∙ K

R – nie zależy od ilości i rodzaju gazu

R – nie zależy od ilości i rodzaju gazu

const

T

pV



 

 

Dla n moli gazu jest to równanie Clapeyrona

Dla n moli gazu jest to równanie Clapeyrona

Prawo to może być uogólnione dla wszystkich gazów, bo jak z 

Prawo to może być uogólnione dla wszystkich gazów, bo jak z 

prawa Avogadra wynika – jednakowe objętości wszystkich 

prawa Avogadra wynika – jednakowe objętości wszystkich 

gazów przy takim samym p i T zawierają taką samą liczbę 

gazów przy takim samym p i T zawierają taką samą liczbę 

cząsteczek.

cząsteczek.

Dla 1 mola jest to 6,02 ∙ 10

Dla 1 mola jest to 6,02 ∙ 10

23

23

 objętość molowa zawsze 

 objętość molowa zawsze 

wynosi 22,4 dm

wynosi 22,4 dm

3

3

/mol.

/mol.

mola

gazu

M

m

n

RT

M

m

pV





nRT

pV 

 

 

Stała Boltzmana

Stała Boltzmana

Prawo Clapeyrona dla gazów rzeczywistych

Prawo Clapeyrona dla gazów rzeczywistych

1.

1.

W gazach rzeczywistych duży wpływ wywierają 

W gazach rzeczywistych duży wpływ wywierają 

oddziaływania międzycząsteczkowe.

oddziaływania międzycząsteczkowe.

2.

2.

Nie może być pominięta objętość własna ich 

Nie może być pominięta objętość własna ich 

cząsteczek.

cząsteczek.

]

/

[

10

02

,

6

314

,

8

10

02

,

6

23

23

K

J

R

k









 

 

•

oddziaływania międzycząsteczkowe są tym większe im 

oddziaływania międzycząsteczkowe są tym większe im 

wartość energii tych oddziaływań bliższa jest energii 

wartość energii tych oddziaływań bliższa jest energii 

kinetycznej wyrażonej przez iloczyn k ∙ T

kinetycznej wyrażonej przez iloczyn k ∙ T

•

odstępstwa od doskonałości są tym większe im wyższe 

odstępstwa od doskonałości są tym większe im wyższe 

jest ciśnienie, a niższa temperatura

jest ciśnienie, a niższa temperatura

•

odstępstwa od doskonałości najlepiej widać na tzw. 

odstępstwa od doskonałości najlepiej widać na tzw. 

współczynniku ściśliwości

współczynniku ściśliwości

    

    

Dla gazów doskonałych z = 1

Dla gazów doskonałych z = 1

    

    

Uwzględniając poprawki na oddziaływania 

Uwzględniając poprawki na oddziaływania 

międzycząsteczkowe i objętość własną cząsteczek van 

międzycząsteczkowe i objętość własną cząsteczek van 

der Waals zaproponował równanie dla gazu 

der Waals zaproponował równanie dla gazu 

rzeczywistego:

rzeczywistego:

RT

pV

z 

 

 

                                                       

                                                       

dla 1 mola

dla 1 mola

         

         

- poprawka na ciśnienie, tzw. ciśnienie wewnętrzne

- poprawka na ciśnienie, tzw. ciśnienie wewnętrzne

   

   

b – poprawka na objętość własną cząsteczek, np. dla CO

b – poprawka na objętość własną cząsteczek, np. dla CO

2

2

 b 

 b 

=   42,7 cm/M

=   42,7 cm/M

Równanie van der Waalsa dla dowolnej ilości gazu 

Równanie van der Waalsa dla dowolnej ilości gazu 

rzeczywistego:

rzeczywistego:

 

 

RT

b

V

V

a

p







)

)(

(

2

2

V

a

RT

M

m

b

M

m

V

V

a

M

m

p











]

[

]

)

(

[

2

2

 

 

STAN CIEKŁY

STAN CIEKŁY

- ograniczenie energii własnej cząsteczek przez oddziaływania 

- ograniczenie energii własnej cząsteczek przez oddziaływania 

międzycząsteczkowe

międzycząsteczkowe

- swobodny ruch cząsteczek powoduje że ciecze nie mają 

- swobodny ruch cząsteczek powoduje że ciecze nie mają 

określonego kształtu ale już określona ilość cieczy ma stałą 

określonego kształtu ale już określona ilość cieczy ma stałą 

objętość

objętość

- ciecze tworzą swobodną powierzchnię graniczną

- ciecze tworzą swobodną powierzchnię graniczną

- gęstość cieczy w mniejszym stopniu niż u gazów zależy od T i 

- gęstość cieczy w mniejszym stopniu niż u gazów zależy od T i 

p

p

- struktura cieczy jest quasi – statyczna tzn. w cieczy istnieją 

- struktura cieczy jest quasi – statyczna tzn. w cieczy istnieją 

obszary uporządkowania przypominające sieć krystaliczną, 

obszary uporządkowania przypominające sieć krystaliczną, 

jednak ich istnienie ma charakter dynamiczny, tworzą się na 

jednak ich istnienie ma charakter dynamiczny, tworzą się na 

krótko i zanikają, a w ich miejsce powstają nowe

krótko i zanikają, a w ich miejsce powstają nowe

- stan ciekły ograniczają dwie temperatury: topnienia i wrzenia

- stan ciekły ograniczają dwie temperatury: topnienia i wrzenia

 

 

                                                               

                                                               

(krystalizacji) 

(krystalizacji) 

(skraplania)

(skraplania)

 

 

Wielkości charakteryzujące ciecze

Wielkości charakteryzujące ciecze

1.

1.

Temperatury: topnienia i wrzenia – t.t i t.w

Temperatury: topnienia i wrzenia – t.t i t.w

2.

2.

Lepkość

Lepkość

3.

3.

Napięcie powierzchniowe

Napięcie powierzchniowe

       

       

Lepkość -  to tarcie wewnętrzne pomiędzy 

Lepkość -  to tarcie wewnętrzne pomiędzy 

poruszającymi się warstwami cieczy.

poruszającymi się warstwami cieczy.

    

    

Istnieje ścisłe powiązanie:

Istnieje ścisłe powiązanie:

PŁYNNOŚĆ = ODWROTNOŚĆ LEPKOŚCI

PŁYNNOŚĆ = ODWROTNOŚĆ LEPKOŚCI

Wyróżnia się lepkość:

Wyróżnia się lepkość:

•

bezwzględną – dynamiczna i kinematyczna

bezwzględną – dynamiczna i kinematyczna

•

względną – umowną w porównaniu z wodą

względną – umowną w porównaniu z wodą

Jednostką lepkości dynamicznej jest 1 P [ poise]

Jednostką lepkości dynamicznej jest 1 P [ poise]

 

 

Lepkość cieczy

Lepkość cieczy

 – równa jest 1 P jeśli siła potrzebna do 

 – równa jest 1 P jeśli siła potrzebna do 

przesunięcia warstwy 1 cm

przesunięcia warstwy 1 cm

2

2

 cieczy z prędkością 1 cm/s 

 cieczy z prędkością 1 cm/s 

względem drugiej takiej warstwy oddalonej od niej o 1 

względem drugiej takiej warstwy oddalonej od niej o 1 

cm równa jest 10

cm równa jest 10

5

5

 N.

 N.

Lepkość kinematyczna

Lepkość kinematyczna

Jest to stosunek lepkości dynamicznej do ciężaru 

Jest to stosunek lepkości dynamicznej do ciężaru 

właściwego cieczy

właściwego cieczy

]

/

[

2

s

cm









ρ = gęstość cieczy g / cm

3

Jednostką lepkości kinematycznej jest Stockes.
Pomiar lepkości cieczy polega na pomiarze czasu 

przepływu określonej ilości cieczy przez rurkę kapilarną w 
ściśle określonej temperaturze [ wiskozymetry ].

 

 

Lepkość względna Englera

Lepkość względna Englera

Określa ona stosunek czasu przepływu 200cm

Określa ona stosunek czasu przepływu 200cm

3

3

 danej 

 danej 

cieczy przez kalibrowany otwór lepkościomierza w ściśle 

cieczy przez kalibrowany otwór lepkościomierza w ściśle 

określonej temperaturze, do czasu przepływu takiej 

określonej temperaturze, do czasu przepływu takiej 

samej ilości wody destylowanej w temp. 20 

samej ilości wody destylowanej w temp. 20 

o

o

C.

C.

- woda została wybrana jako wzorzec, ponieważ jej 

- woda została wybrana jako wzorzec, ponieważ jej 

lepkość kinematyczna w t = 20,2 

lepkość kinematyczna w t = 20,2 

o

o

C równa jest

C równa jest

 

 

1 St.

1 St.

 

 

NAPIĘCIE POWIERZCHNIOWE

NAPIĘCIE POWIERZCHNIOWE

- każda cząsteczka w głębi cieczy jest równomiernie 

- każda cząsteczka w głębi cieczy jest równomiernie 

otoczona innymi cząsteczkami, jej siły wzajemnych 

otoczona innymi cząsteczkami, jej siły wzajemnych 

oddziaływań są wysycane, ich wypadkowa = 0

oddziaływań są wysycane, ich wypadkowa = 0

- natomiast cząsteczki powierzchniowe doznają tylko 

- natomiast cząsteczki powierzchniowe doznają tylko 

jednostronnych oddziaływań od strony cieczy, bo ich 

jednostronnych oddziaływań od strony cieczy, bo ich 

oddziaływania z cząsteczkami gazu są bardzo małe

oddziaływania z cząsteczkami gazu są bardzo małe

- wypadkowa tych sił działa prostopadle do powierzchni i 

- wypadkowa tych sił działa prostopadle do powierzchni i 

skierowana jest do wnętrza cieczy, ulega więc 

skierowana jest do wnętrza cieczy, ulega więc 

jednostronnemu wciąganiu do wnętrza cieczy, tak więc 

jednostronnemu wciąganiu do wnętrza cieczy, tak więc 

cząsteczki powierzchniowe wywierają na 

cząsteczki powierzchniowe wywierają na 

wnętrze cieczy 

wnętrze cieczy 

ciśnienie zwane powierzchniowym albo wewnętrznym

ciśnienie zwane powierzchniowym albo wewnętrznym

- na skutek działania tych sił ciecze dążą do zmniejszenia 

- na skutek działania tych sił ciecze dążą do zmniejszenia 

liczby cząsteczek na powierzchni, zmniejsza się 

liczby cząsteczek na powierzchni, zmniejsza się 

powierzchnia swobodna cieczy, dla tego krople cieczy 

powierzchnia swobodna cieczy, dla tego krople cieczy 

mają kształt kulisty jako najmniejszy przy danej 

mają kształt kulisty jako najmniejszy przy danej 

objętości

objętości

 

 

Tak więc w warstwie powierzchniowej cieczy istnieją siły 

Tak więc w warstwie powierzchniowej cieczy istnieją siły 

zmniejszające powierzchnię

zmniejszające powierzchnię

 działające wzdłuż powierzchni 

 działające wzdłuż powierzchni 

w każdym jej punkcie. Jest to właśnie

w każdym jej punkcie. Jest to właśnie

Napięcie powierzchniowe 

Napięcie powierzchniowe 

σ

σ

Jest ono niezależne od wielkości powierzchni, ale od 

Jest ono niezależne od wielkości powierzchni, ale od 

charakteru cieczy i temperatury

charakteru cieczy i temperatury

- każda ciecz wykazuje charakterystyczne dla siebie 

- każda ciecz wykazuje charakterystyczne dla siebie 

σ

σ

 

 

Jednostki napięcia powierzchniowego

Jednostki napięcia powierzchniowego

Można je podawać w jednostkach pracy na jednostkę 

Można je podawać w jednostkach pracy na jednostkę 

powierzchni

powierzchni

- jest to praca potrzebna do zwiększenia powierzchni 

- jest to praca potrzebna do zwiększenia powierzchni 

swobodnej   cieczy o 1m

swobodnej   cieczy o 1m

2

2

 [J/m

 [J/m

2

2

]

]

W jednostkach siły na jednostkę długości [N/m]

W jednostkach siły na jednostkę długości [N/m]

 

 

Napięcie powierzchniowe różnych cieczy:

Napięcie powierzchniowe różnych cieczy:

    

    

t = 18 

t = 18 

o

o

C

C



σ

σ

H2O

H2O

 = 0,073 N/m

 = 0,073 N/m



σ

σ

CH3OH

CH3OH

 = 0,022 N/m

 = 0,022 N/m



σ

σ

Hg

Hg

 = 0,491 N/m

 = 0,491 N/m

    

    

t = 20 

t = 20 

o

o

C

C



σ

σ

C6H6

C6H6

 = 0,0289 N/m

 = 0,0289 N/m

Istnienie energii powierzchniowej wskazują proste 

Istnienie energii powierzchniowej wskazują proste 

doświadczenia

doświadczenia



Utrzymywanie się leżącej żyletki na powierzchni cieczy

Utrzymywanie się leżącej żyletki na powierzchni cieczy



Możliwość rozciągnięcia cieczy w formie błonki na ramce

Możliwość rozciągnięcia cieczy w formie błonki na ramce

 

 

Zależność napięcia powierzchniowego czystych cieczy od 

Zależność napięcia powierzchniowego czystych cieczy od 

temperatury

temperatury

- napięcie 

- napięcie 

σ

σ

 maleje ze wzrostem T

 maleje ze wzrostem T

- zwiększenie powierzchni cieczy wiąże się z 

- zwiększenie powierzchni cieczy wiąże się z 

pochłanianiem ciepła

pochłanianiem ciepła

- ciepło pochłonięte przy zwiększeniu powierzchni o 1cm

- ciepło pochłonięte przy zwiększeniu powierzchni o 1cm

2

2

 

 

nazywamy 

nazywamy 

ciepłem tworzenia powierzchni

ciepłem tworzenia powierzchni

- w temperaturze krytycznej, kiedy zanika granica między 

- w temperaturze krytycznej, kiedy zanika granica między 

cieczą i parą 

cieczą i parą 

σ

σ

 uzyskuje wartość „0”

 uzyskuje wartość „0”

 

 

Napięcie powierzchniowe roztworów

Napięcie powierzchniowe roztworów

- 

- 

większość związków dodanych do cieczy zmniejsza jej 

większość związków dodanych do cieczy zmniejsza jej 

napięcie powierzchniowe

napięcie powierzchniowe

- wpływ substancji rozpuszczonej na 

- wpływ substancji rozpuszczonej na 

σ

σ

 zależy od tego czy 

 zależy od tego czy 

jej stężenie w warstwie powierzchniowej jest większe 

jej stężenie w warstwie powierzchniowej jest większe 

czy mniejsze niż w głębi roztworu

czy mniejsze niż w głębi roztworu

- wszystkie związki hydrofilowe [elektrolity] dla których 

- wszystkie związki hydrofilowe [elektrolity] dla których 

oddziaływanie z wodą jest bardzo duże zwiększają 

oddziaływanie z wodą jest bardzo duże zwiększają 

napięcie σ np. jony mocnych elektrolitów ulegając 

napięcie σ np. jony mocnych elektrolitów ulegając 

dysocjacji otaczają się cząsteczkami wody i wciągane są 

dysocjacji otaczają się cząsteczkami wody i wciągane są 

w głąb roztworu i dlatego ich stężenie w warstwie 

w głąb roztworu i dlatego ich stężenie w warstwie 

powierzchniowej jest mniejsze niż w głębi roztworu

powierzchniowej jest mniejsze niż w głębi roztworu

- związki hydrofilowe – nie zwilżalne [należą tu głównie 

- związki hydrofilowe – nie zwilżalne [należą tu głównie 

związki organiczne] albo rozpuszczają się w sposób 

związki organiczne] albo rozpuszczają się w sposób 

ograniczony, albo rozpuszczone gromadzą się w 

ograniczony, albo rozpuszczone gromadzą się w 

warstwie powierzchniowej np. mydła

warstwie powierzchniowej np. mydła

   

   

Takie gromadzenie się substancji przy powierzchni 

Takie gromadzenie się substancji przy powierzchni 

oddzielającej dwie fazy nazywa się 

oddzielającej dwie fazy nazywa się 

adsorpcją

adsorpcją

.

.

 

 

STAN SZKLISTY

STAN SZKLISTY

Szkłem nazywamy każdą substancję organiczną lub 

Szkłem nazywamy każdą substancję organiczną lub 

nieorganiczną, która przy ochłodzeniu przeszła w 

nieorganiczną, która przy ochłodzeniu przeszła w 

sposób ciągły ze stanu zwykłej cieczy (o lepkości 10p) 

sposób ciągły ze stanu zwykłej cieczy (o lepkości 10p) 

do stanu w którym jej lepkość jest większa niż 10

do stanu w którym jej lepkość jest większa niż 10

13

13

p. 

p. 

Szkła przy lepkości 10

Szkła przy lepkości 10

8

8

 – 10

 – 10

9

9

p tworzą stan plastyczny. 

p tworzą stan plastyczny. 

Wykorzystywane to jest przy formowaniu szkła poprzez 

Wykorzystywane to jest przy formowaniu szkła poprzez 

ciągnięcie, wydmuchiwanie, prasowanie.

ciągnięcie, wydmuchiwanie, prasowanie.

W stanie szklistym nie można otrzymać metali, soli, 

W stanie szklistym nie można otrzymać metali, soli, 

kwasów, tlenków ani gazów szlachetnych

kwasów, tlenków ani gazów szlachetnych

 gdyż mają 

 gdyż mają 

one zdefiniowane typy wiązań – jonowe, atomowe, 

one zdefiniowane typy wiązań – jonowe, atomowe, 

metaliczne. Natomiast substancje o wiązaniach typu 

metaliczne. Natomiast substancje o wiązaniach typu 

mostków wodorowych czy tlenków można otrzymać w 

mostków wodorowych czy tlenków można otrzymać w 

stanie szklistym.

stanie szklistym.

 

 

STAN STAŁY

STAN STAŁY



ciała krystaliczne

ciała krystaliczne



ciała bezpostaciowe – izotropowe brak ostrego przejścia 

ciała bezpostaciowe – izotropowe brak ostrego przejścia 

do

do

                                         

                                         

stanu ciekłego

stanu ciekłego

 

 

Podstawowe cechy kryształów

Podstawowe cechy kryształów

- stan pełnego uporządkowania atomów lub jonów w 

- stan pełnego uporządkowania atomów lub jonów w 

dowolnym kierunku

dowolnym kierunku

- tworzenie kształtu regularnych wielościanów wypukłych 

- tworzenie kształtu regularnych wielościanów wypukłych 

ograniczonych płaskimi ścianami

ograniczonych płaskimi ścianami

- anizotropia kryształów – zależność ich właściwości od 

- anizotropia kryształów – zależność ich właściwości od 

kierunku np. właściwości mechaniczne : twardość, 

kierunku np. właściwości mechaniczne : twardość, 

wytrzymałość, przewodnictwo elektryczne, cieplne itp.

wytrzymałość, przewodnictwo elektryczne, cieplne itp.

- zewnętrzna forma kryształu jest ściśle związana z 

- zewnętrzna forma kryształu jest ściśle związana z 

budową wewnętrzną

budową wewnętrzną

- podstawową jednostką kryształu jest komórka sieciowa – 

- podstawową jednostką kryształu jest komórka sieciowa – 

jest to najmniejszy element przestrzenny tworzący sieć 

jest to najmniejszy element przestrzenny tworzący sieć 

trójwymiarową, określany za pomocą trzech krawędzi a, 

trójwymiarową, określany za pomocą trzech krawędzi a, 

b, c oraz trzech kątów 

b, c oraz trzech kątów 

α, β, γ

α, β, γ

 pomiędzy krawędziami, są 

 pomiędzy krawędziami, są 

to tzw. 

to tzw. 

parametry sieci przestrzennej

parametry sieci przestrzennej

 

 

 

 

Komórka sieciowa powtarza się w przestrzeni po 

Komórka sieciowa powtarza się w przestrzeni po 

przesunięciu translacyjnym w kierunku jednej z krawędzi 

przesunięciu translacyjnym w kierunku jednej z krawędzi 

o dowolną całkowitą ilość odległości translacyjnych 

o dowolną całkowitą ilość odległości translacyjnych 

(odległość dwóch analogicznych węzłów leżących na 

(odległość dwóch analogicznych węzłów leżących na 

prostej sieciowej).

prostej sieciowej).

 

 

lp.

układ

parametry

kształty komórki

1

regularny

a = b = c

α = β = γ = 

90

o

sześcian

2

tetragonal

ny

a = b ≠ c

α = β = γ = 

90

o

prostopadłościan

o podstawie 

kwadratu

3

heksagonal

ny

a = b ≠ c

α = β = 90

o

γ = 120

 o

prostopadłościan

o podstawie 

romboidalnej

4

trygonalny

a = b = c

α = β = γ ≠ 

90

o

romboedr

5

rombowy

a ≠ b ≠ c

α = β = γ = 

90

o

prostopadłościan

o podstawie 

prostokąta

6

jednoskośn

y

a ≠ b ≠ c

α = γ = 90

o

β ≠ 90

o

równoległościan

7

trójskośny

a ≠ b ≠ c

α ≠ β ≠ γ

równoległościan

PODSTAWOWE UKŁADY KRYSTALOGRAFICZNE

RÓWNOWAGI FAZOWE

RÓWNOWAGI FAZOWE

UKŁAD:

UKŁAD:

 Stan skupienia materii wraz z zawartą w nim   energią

 Stan skupienia materii wraz z zawartą w nim   energią

Układ fizycznie jednorodny

Układ fizycznie jednorodny

 – każda najmniejsza jego część 

 – każda najmniejsza jego część 

wykazuje te same cechy co cały układ – jest jednorodny pod 

wykazuje te same cechy co cały układ – jest jednorodny pod 

względem fizycznym i chemicznym

względem fizycznym i chemicznym

Układ fizycznie niejednorodny

Układ fizycznie niejednorodny

 – różne jego części wykazują 

 – różne jego części wykazują 

różne właściwości i zwane są fazami. Są to części 

różne właściwości i zwane są fazami. Są to części 

jednorodne układu oddzielone od innych jego części 

jednorodne układu oddzielone od innych jego części 

powierzchnią rozdziału np. lód i woda.

powierzchnią rozdziału np. lód i woda.

Stopień swobody układu niejednorodnego

Stopień swobody układu niejednorodnego

: liczba parametrów 

: liczba parametrów 

zewnętrznych [ p, t, c ] które można zmienić nie powodując 

zewnętrznych [ p, t, c ] które można zmienić nie powodując 

zaniku żadnej z faz.

zaniku żadnej z faz.

 

 

REGUŁA FAZ GIBBSA

REGUŁA FAZ GIBBSA

Liczba stopni swobody układu równa jest różnicy

Liczba stopni swobody układu równa jest różnicy

 

 

liczby składników i faz powiększonej o 2

liczby składników i faz powiększonej o 2

s = n – f  + 2

s = n – f  + 2

s – liczba stopni swobody

s – liczba stopni swobody

n – liczba składników

n – liczba składników

f – liczba faz

f – liczba faz

 

 

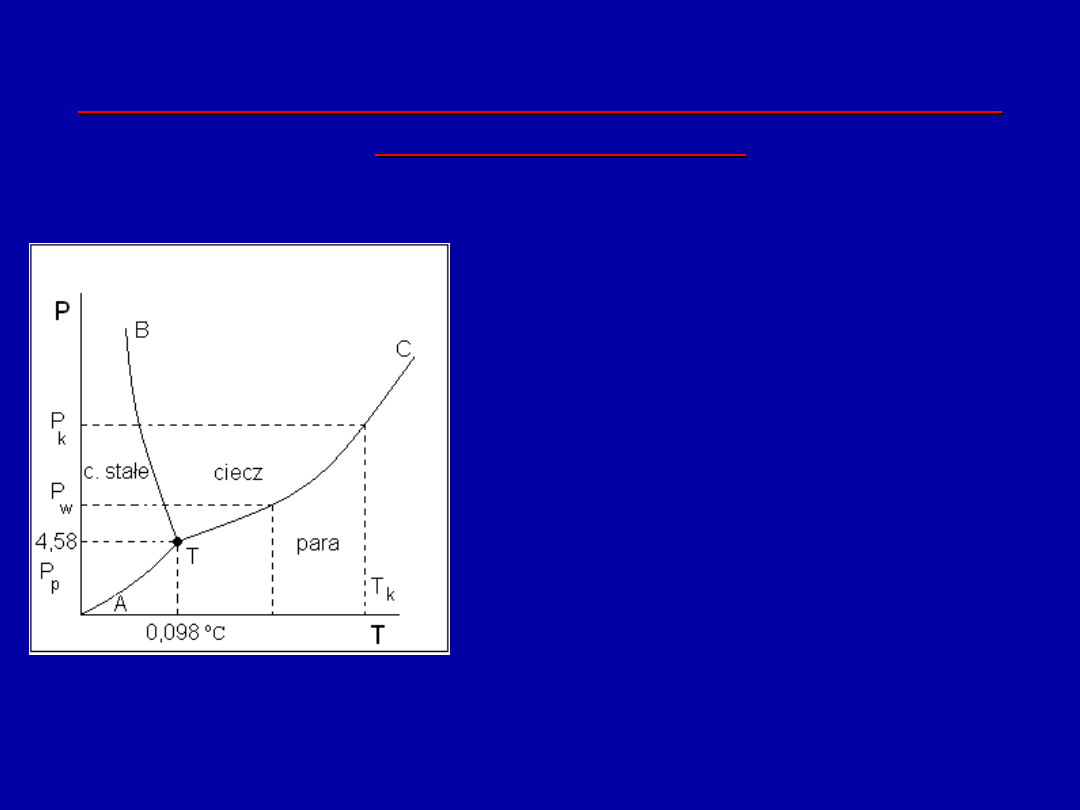
RÓWNOWAGI FAZOWE DLA UKŁADU n = 1 f = 3 NA 

RÓWNOWAGI FAZOWE DLA UKŁADU n = 1 f = 3 NA 

PRZYKŁADZIE WODY

PRZYKŁADZIE WODY

Diagram fazowy wody:

P

p

 = 4,58 mmHg = 601,44 hPa

P

w

 = 1 atm = 1013 hPa

P

k

 = 217 atm = 219821 hPa

T – temperatura punktu potrójnego H

2

O t  = 0,098

o

C T = 

273,14

o

K

T

w

 = 100

o

C     T

k

 = 374

o

C

Krzywe: TA; TB; TC – równowag 

2-fazowych

T – Punkt potrójny wody: 3-
fazowy

 

 

A. 

A. 

Równowagi fazowe w głębi cieczy, pary, ciała stałego

Równowagi fazowe w głębi cieczy, pary, ciała stałego

n = 1     f = 1

n = 1     f = 1

s = 1 – 1 + 2 = 2

s = 1 – 1 + 2 = 2

Można zmienić dwa parametry nie powodując zaniku 

Można zmienić dwa parametry nie powodując zaniku 

żadnej z faz

żadnej z faz

B. 

B. 

Równowagi fazowe wzdłuż krzywych

Równowagi fazowe wzdłuż krzywych

TA – sublimacji – resublimacji

TA – sublimacji – resublimacji

TB – topnienia – krzepnięcia

TB – topnienia – krzepnięcia

TC – parowania – skraplania

TC – parowania – skraplania

n = 1     f = 2

n = 1     f = 2

s = 1 – 2 + 2 = 1

s = 1 – 2 + 2 = 1

układ 1 – zmiennej

układ 1 – zmiennej

W PUNKCIE POTRÓJNYM T

W PUNKCIE POTRÓJNYM T

n = 1     f = 3

n = 1     f = 3

s = 1 – 3 + 2 = 0

s = 1 – 3 + 2 = 0

Brak stopni swobody – układ „0” zmiennych

Brak stopni swobody – układ „0” zmiennych

  

  

RÓWNOWAGI FAZOWE DLA UKŁADU n = 2 LOTNEGO 

RÓWNOWAGI FAZOWE DLA UKŁADU n = 2 LOTNEGO 

ROZPUSZCZLNIKA I NIELOTNEJ SUBSTANCJI 

ROZPUSZCZLNIKA I NIELOTNEJ SUBSTANCJI 

ROZPUSZCZONEJ f = 1

ROZPUSZCZONEJ f = 1

W układzie takim prężność par substancji rozpuszczonej 

W układzie takim prężność par substancji rozpuszczonej 

jest nieznaczna, a nad roztworem w postaci pary 

jest nieznaczna, a nad roztworem w postaci pary 

znajduje się tylko rozpuszczalnik

znajduje się tylko rozpuszczalnik

- Prężność pary nad roztworem P

- Prężność pary nad roztworem P

A

A

P

P

A

A

 = P

 = P

A

A

0

0

 ∙ x

 ∙ x

A

A

P

P

A

A

0

0

 – prężność pary nad czystym rozpuszczalnikiem

 – prężność pary nad czystym rozpuszczalnikiem

x

x

A

A

   - ułamek molowy rozpuszczalnika w roztworze

   - ułamek molowy rozpuszczalnika w roztworze

x

x

B

B

   - ułamek molowy substancji rozpuszczonej w 

   - ułamek molowy substancji rozpuszczonej w 

roztworze

roztworze

x

x

A

A

 + x

 + x

B

B

 = 1          x

 = 1          x

B

B

 = 1 - x

 = 1 - x

A

A

 

 

Obniżenie prężności pary nad roztworem

Obniżenie prężności pary nad roztworem

Δp = P

Δp = P

A

A

0

0

 - P

 - P

A

A

0

0

 ∙ x

 ∙ x

A

A

 = P

 = P

A

A

0

0

 (1 - x

 (1 - x

A

A

)

)

lub

lub

Δp = P

Δp = P

A

A

0

0

 ∙ x

 ∙ x

B

B

            bo x

            bo x

B

B

 = 1 - x

 = 1 - x

A

A

 

 

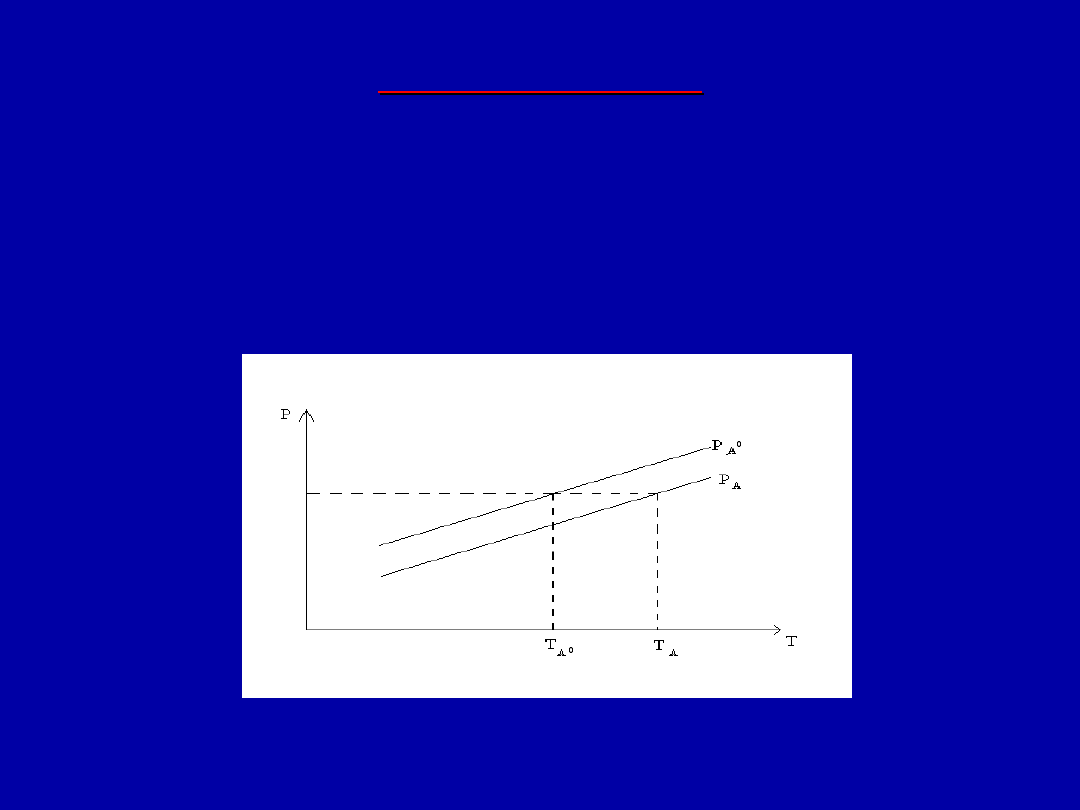
I PRAWO RAOULTA

I PRAWO RAOULTA

Obniżenie prężności pary rozpuszczalnika nad roztworem 

Obniżenie prężności pary rozpuszczalnika nad roztworem 

jest wprost proporcjonalne do ułamka molowego 

jest wprost proporcjonalne do ułamka molowego 

substancji rozpuszczonej.

substancji rozpuszczonej.

- Im większy ułamek molowy x

- Im większy ułamek molowy x

B

B

 – bardziej stężony roztwór, 

 – bardziej stężony roztwór, 

tym większe obniżenie prężności pary.

tym większe obniżenie prężności pary.

T

T

A

A

0

0

 – temperatura wrzenia rozpuszczalnika

 – temperatura wrzenia rozpuszczalnika

T

T

B

B

 – temperatura wrzenia roztworu

 – temperatura wrzenia roztworu

 

 

II PRAWO RAOULTA

II PRAWO RAOULTA

Podwyższenie temperatury wrzenia roztworu jest wprost 

Podwyższenie temperatury wrzenia roztworu jest wprost 

proporcjonalne do stężenia molalnego roztworu.

proporcjonalne do stężenia molalnego roztworu.

m

m

S

S

 – masa substancji rozpuszczonej

 – masa substancji rozpuszczonej

w – masa rozpuszczalnika 

w – masa rozpuszczalnika 

L

L

P

P

 – ciepło parowania 1g rozpuszczalnika

 – ciepło parowania 1g rozpuszczalnika

k

k

e

e

 = molarne podwyższenie T

 = molarne podwyższenie T

W

W

 rozpuszczalnika jest to 

 rozpuszczalnika jest to 

podwyższenie T

podwyższenie T

W

W

 po rozpuszczeniu 1M substancji w 

 po rozpuszczeniu 1M substancji w 

1000g rozpuszczalnika.

1000g rozpuszczalnika.

w

M

m

ke

T

s

S

W







1000

P

L

RT

ke

1000

2



 

 

III PRAWO RAOULTA

III PRAWO RAOULTA

Obniżenie T

Obniżenie T

K

K

 roztworów jest wprost proporcjonalne do 

 roztworów jest wprost proporcjonalne do 

stężenia molalnego roztworów.

stężenia molalnego roztworów.

w

M

m

K

T

S

S

K

K







1000

K

K

 – stała krioskopowa

K

K

L

RT

K

1000

2



Jest to molarne obniżenie T

K

 rozpuszczalnika – zależy od 

ciepła topnienia L

K

 

 

WYZNACZANIE CIĘŻARÓW CZĄSTECZKOWYCH W OPARCIU 

WYZNACZANIE CIĘŻARÓW CZĄSTECZKOWYCH W OPARCIU 

O PRAWO RAOULTA

O PRAWO RAOULTA

Z I prawa:

Z I prawa:

m

m

b

b

 – masa molowa substancji rozpuszczonej

 – masa molowa substancji rozpuszczonej

Z II prawa:

Z II prawa:

w – waga rozpuszczalnika

w – waga rozpuszczalnika

A

B

A

A

B

m

p

m

M

P

M











0

w

T

m

ke

M

B

B











1000

 

 

Z III prawa:

Z III prawa:

m

m

B

B

 – masa substancji rozpuszczonej

 – masa substancji rozpuszczonej

w

T

m

k

M

B

k

B









1000

 

 

PRAWA RAOULTA DLA DWÓCH CIECZY MIESZAJĄCYCH SIĘ 

PRAWA RAOULTA DLA DWÓCH CIECZY MIESZAJĄCYCH SIĘ 

NIEOGRANICZENIE

NIEOGRANICZENIE

W Daltona prężność pary nad takimi roztworami równa 

W Daltona prężność pary nad takimi roztworami równa 

jest sumie prężności par obu cieczy

jest sumie prężności par obu cieczy

                       

                       

Dla każdego ze składników prężność par równa jest jego 

Dla każdego ze składników prężność par równa jest jego 

prężności nad czystym składnikiem razy jego ułamek 

prężności nad czystym składnikiem razy jego ułamek 

molowy w roztworze.

molowy w roztworze.

B

A

P

P

P





A

A

A

x

P

P





0

B

B

B

x

P

P





0

1





B

A

x

x

B

A

x

x



1

 

 

czyli 

czyli 

B

B

A

A

x

P

x

P

P









0

0

lub 

B

B

B

A

A

x

P

x

P

P

P











0

0

0

0

0

0

)

(

A

B

A

B

P

x

P

P

P







  

  

I Prawo

I Prawo

A

B

x

A

 = 

1

x

B

 = 

1

x

B

 = 

0

x

A

 = 

0

P

B

 – prężność par benzenu

P

A

 – prężność par toluenu

P  -  prężność par nad roztworem obu 
cieczy

 

 

Prawa Raoulta spełniają:

Prawa Raoulta spełniają:

benzen + dichloroetan

heksan + heptan

woda + metanol

ciekły N

2

 + ciekły O

2

 

         są to tzw. roztwory doskonałe

 

 

 

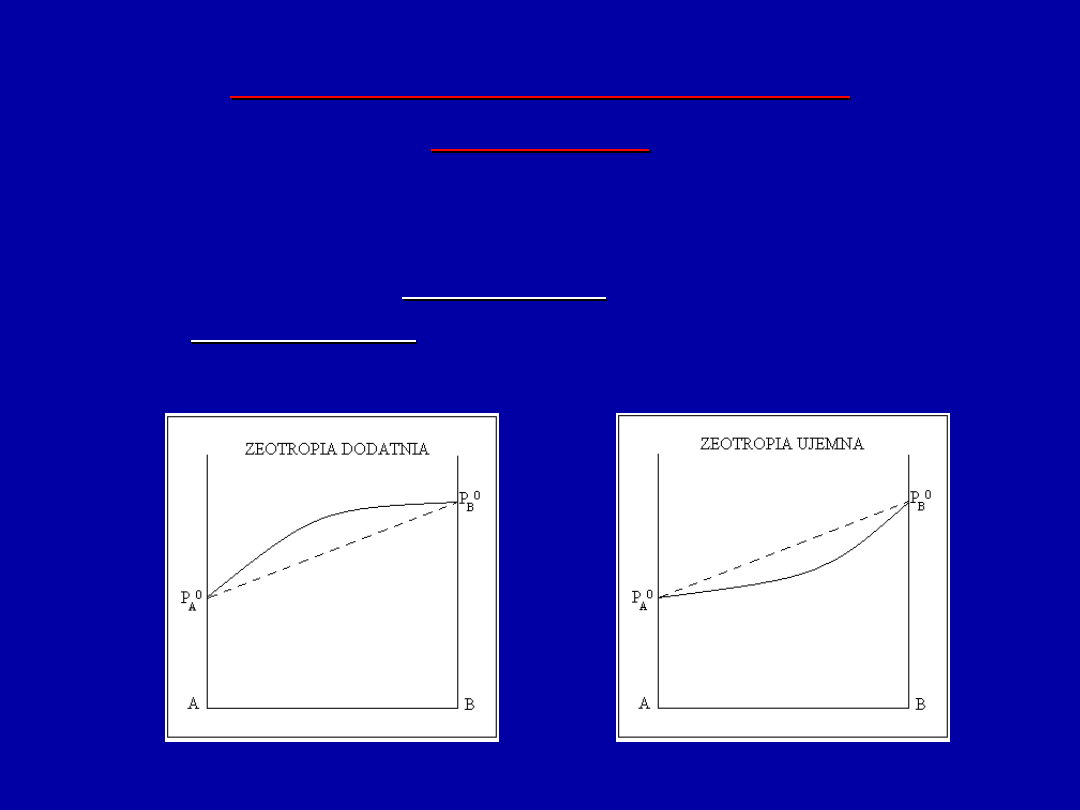
ODCHYLENIA OD PRAW RAOULTA –

ODCHYLENIA OD PRAW RAOULTA –

AZEOTROPY

AZEOTROPY

Mieszanina cieczy wykazujących odchylenia od praw 

Mieszanina cieczy wykazujących odchylenia od praw 

Raoulta nazywają się 

Raoulta nazywają się 

zeotropami

zeotropami

 gdy te odchylenia są 

 gdy te odchylenia są 

małe, lub 

małe, lub 

azeotropami

azeotropami

 gdy na krzywych pojawiają się 

 gdy na krzywych pojawiają się 

wyraźne maksima lub minima. Odchylenia mogą być 

wyraźne maksima lub minima. Odchylenia mogą być 

ujemne lub dodatnie. 

ujemne lub dodatnie. 

 

 

 

 

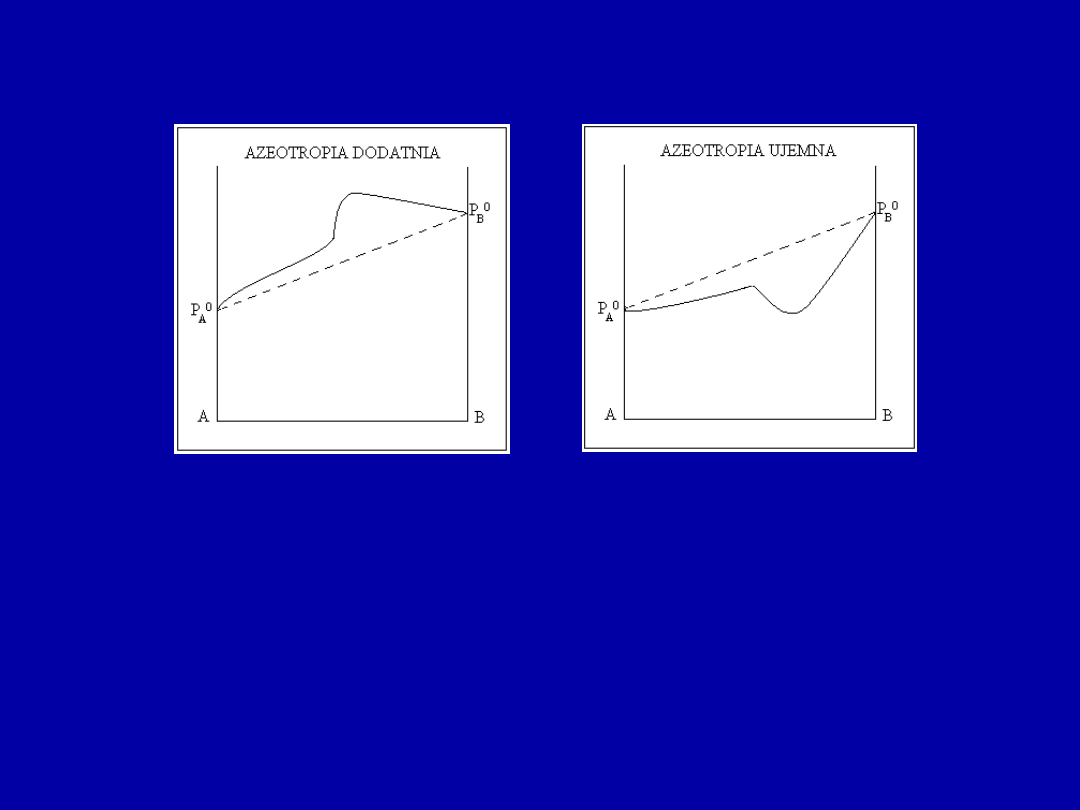
II Prawo – Temperatury wrzenia a skład cieczy i pary

II Prawo – Temperatury wrzenia a skład cieczy i pary

Proces przejścia cieczy w parę i ponowne skroplenie 

Proces przejścia cieczy w parę i ponowne skroplenie 

nazywa się 

nazywa się 

destylacją

destylacją

. Proces przejścia cieczy w parę w 

. Proces przejścia cieczy w parę w 

zależności od T można przedstawić na wykresie w 

zależności od T można przedstawić na wykresie w 

układzie współrzędnych: T i % skład cieczy.

układzie współrzędnych: T i % skład cieczy.

Destylacja

Destylacja

 – metoda rozdziału cieczy o różnych 

 – metoda rozdziału cieczy o różnych 

temperaturach wrzenia. 

temperaturach wrzenia. 

 

 

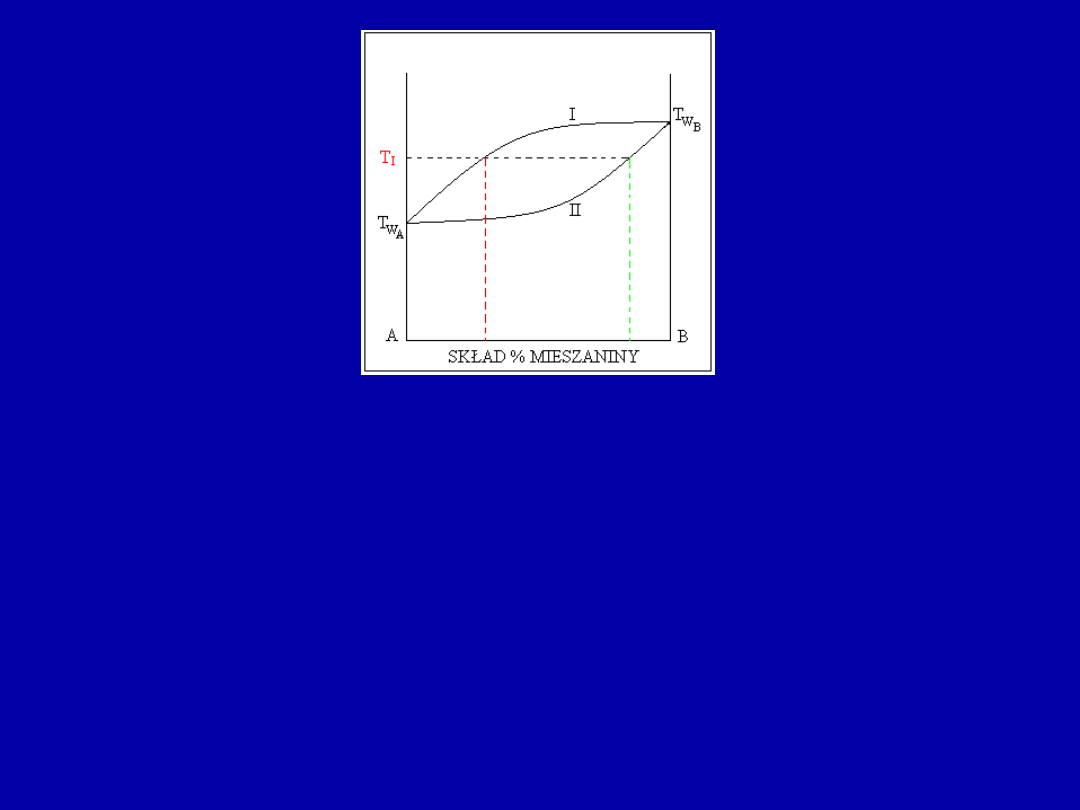
I Krzywa składu pary

II Krzywa składu cieczy

T

W

A

 , T

W

B

 – temperatury wrzenia czystych A lub B

T

W

A

 <  T

I

  < T

W

B

W tej temperaturze para bogatsza jest w składnik o 
niższej temperaturze wrzenia [A] – bardziej lotny

  

(

……….

).

Ciecz natomiast w TI bogatsza jest w składnik mniej lotny

  

(

……….

).

Całkowite rozdzielenie takich dwóch cieczy możliwe jest 
tylko na drodze tzw. rektyfikacji.

 

 

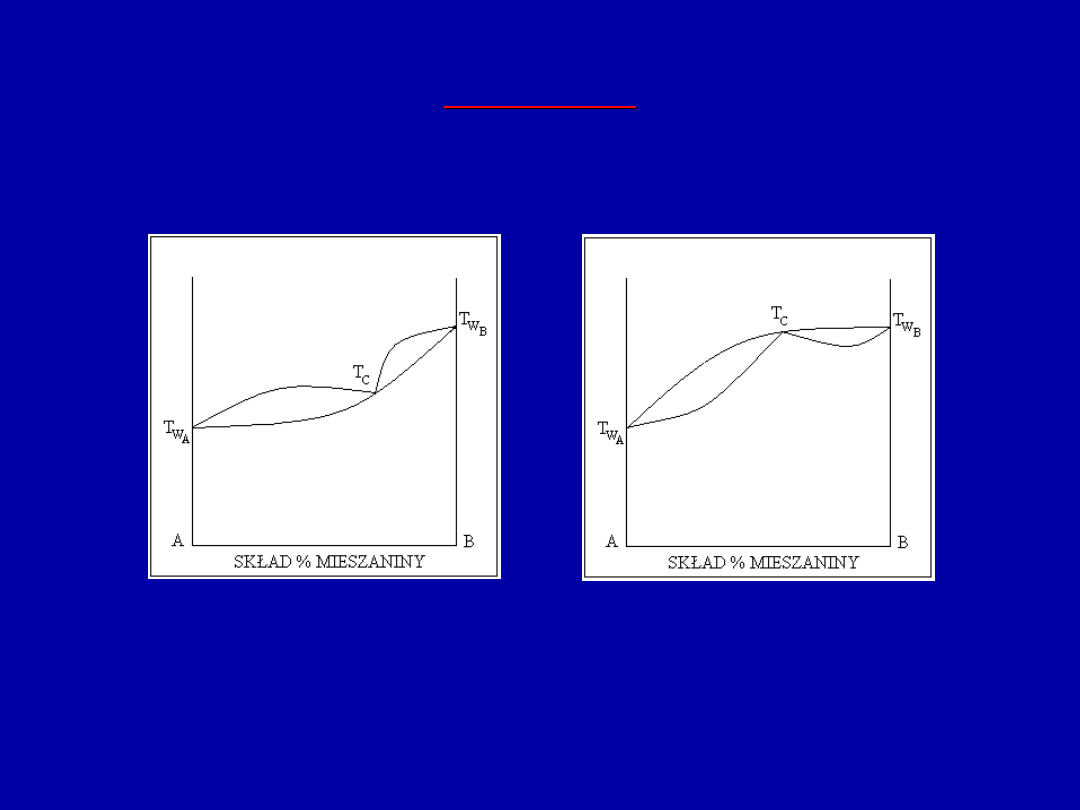
Odchylenia

Odchylenia

Na obu wykresach w temperaturze T

Na obu wykresach w temperaturze T

C

C

 skład cieczy jest 

 skład cieczy jest 

identyczny ze składem pary. Mieszanina cieczy destyluje tak 

identyczny ze składem pary. Mieszanina cieczy destyluje tak 

jak by to była jedna substancja. Punkt ten nazywa się 

jak by to była jedna substancja. Punkt ten nazywa się 

punktem azeotropowym.

punktem azeotropowym.

RÓWNOWAGA CHEMICZNA

RÓWNOWAGA CHEMICZNA

1.

1.

Prawo działania mas

Prawo działania mas

Równowaga chemiczna jest równowagą o charakterze 

Równowaga chemiczna jest równowagą o charakterze 

dynamicznym tzn. tyle ile produktów powstaje w 

dynamicznym tzn. tyle ile produktów powstaje w 

jednostce czasu, tyle samo ich przekształca się w 

jednostce czasu, tyle samo ich przekształca się w 

substraty.

substraty.

Układ znajduje się w stanie równowagi gdy jego 

Układ znajduje się w stanie równowagi gdy jego 

parametry nie zależą od czasu. Każda reakcja 

parametry nie zależą od czasu. Każda reakcja 

przebiega z określoną szybkością, której miarą jest 

przebiega z określoną szybkością, której miarą jest 

zmiana stężenia substratów lub produktów w 

zmiana stężenia substratów lub produktów w 

jednostce czasu.

jednostce czasu.

 

 

Dla reakcji 

Dla reakcji 

k

k

1

1

 i k

 i k

2

2

 – stałe szybkości reakcji

 – stałe szybkości reakcji

a, b, c, d – współczynniki stechiometryczne

a, b, c, d – współczynniki stechiometryczne

przy T = const       V

przy T = const       V

1

1

 = V

 = V

2

2

     ustala się stan równowagi

     ustala się stan równowagi

k

k

1

1

 [A]

 [A]

a

a

 ∙ [B]

 ∙ [B]

b

b

 = k

 = k

2

2

 [C]

 [C]

c

c

 ∙ [D]

 ∙ [D]

d

d

                

                

- 

- 

jest to stała stężeniowa równowagi, która nie

jest to stała stężeniowa równowagi, która nie

                  

                  

zależy  od stężenia poszczególnych 

zależy  od stężenia poszczególnych 

reagentów, zmienia się tylko przy zmianie T.

reagentów, zmienia się tylko przy zmianie T.

dD

cC

V

V

bB

aA









2

1

Szybkość reakcji

V

1

 = k

1

 [A]

a

 ∙ [B]

b

I reakcji odwrotnej 

V

2

 = k

2

 [C]

c

 ∙ [D]

d

C

K

k

k



2

1

 

 

b

a

d

c

C

B

A

D

C

k

k

K

]

[

]

[

]

[

]

[

2

1









Równanie na stałą równowagi jest matematycznym 

wyrazem Prawa działania mas 

Guldberga – Waagego:

W stanie równowagi chemicznej w stałej T stosunek 

iloczynu stężeń molowych produktów do iloczynu stężeń 

molowych substratów jest wielkością stałą 

charakterystyczną dla danej reakcji.

Jeżeli stała szybkości:

k

1

>> k

2

to w stanie równowagi znajdują się produkty w znacznie 

większych stężeniach niż substraty – reakcje takie będą 

praktycznie nieodwracalne.

 

 

2. Wpływ czynników zewnętrznych na równowagę

2. Wpływ czynników zewnętrznych na równowagę

a) REGUŁA PRZEKORY – le CHATERIERA – BRAUNA

a) REGUŁA PRZEKORY – le CHATERIERA – BRAUNA

Pod wpływem czynników zewnętrznych takich jak: zmiana 

Pod wpływem czynników zewnętrznych takich jak: zmiana 

stężenia roztworu, ciśnienia dla reakcji w stanie 

stężenia roztworu, ciśnienia dla reakcji w stanie 

gazowym czy temperatury – równowaga chemiczna 

gazowym czy temperatury – równowaga chemiczna 

ulega przesunięciu albo na korzyść produktów albo na 

ulega przesunięciu albo na korzyść produktów albo na 

korzyść substratów.

korzyść substratów.

Kierunek przesunięcia równowagi określa reguła przekory:

Kierunek przesunięcia równowagi określa reguła przekory:

Jeżeli na układ w stanie równowagi działa czynnik 

Jeżeli na układ w stanie równowagi działa czynnik 

zewnętrzny, to w układzie zajdą takie zmiany, które 

zewnętrzny, to w układzie zajdą takie zmiany, które 

będą niwelowały efekty tego działania, prowadząc do 

będą niwelowały efekty tego działania, prowadząc do 

ponownego ustalenia równowagi – układ broni się przed 

ponownego ustalenia równowagi – układ broni się przed 

zakłócaniem stanu równowagi z zewnątrz

zakłócaniem stanu równowagi z zewnątrz

.

.

 

 

Umiejętność doboru odpowiedniego bodźca zewnętrznego 

Umiejętność doboru odpowiedniego bodźca zewnętrznego 

powodującego przesunięcie równowagi w pożądanym 

powodującego przesunięcie równowagi w pożądanym 

kierunku jest bardzo ważne np. dla reakcji syntezy NH

kierunku jest bardzo ważne np. dla reakcji syntezy NH

3

3

Jeżeli zwiększymy [H

Jeżeli zwiększymy [H

2

2

], to najpierw zmaleje [N

], to najpierw zmaleje [N

2

2

], a 

], a 

wzrośnie [NH

wzrośnie [NH

3

3

], czyli że zmiany w układzie doprowadzą 

], czyli że zmiany w układzie doprowadzą 

stosunki stężeń produktów i substratów do ustalenia 

stosunki stężeń produktów i substratów do ustalenia 

nowego stanu równowagi odpowiadającemu ich nowym 

nowego stanu równowagi odpowiadającemu ich nowym 

stężeniom – czyli po zwiększeniu [H

stężeniom – czyli po zwiększeniu [H

2

2

] zwiększy się szybkość 

] zwiększy się szybkość 

syntezy NH

syntezy NH

3

3

.

.

Q

NH

H

N







3

2

2

2

3

3

2

2

2

3

]

][

[

]

[

H

N

NH

K 

 

 

Rozważając tą reakcję jako przykład reakcji gazowej :

Rozważając tą reakcję jako przykład reakcji gazowej :

1Vmol N

1Vmol N

2

2

 + 3Vmol H

 + 3Vmol H

2

2

 

 





 2Vmol NH

 2Vmol NH

3

3

Razem:                4V substratów         

Razem:                4V substratów         





  2V produktów

  2V produktów

V ~ p                              4p 

V ~ p                              4p 





 2p

 2p

Jeżeli V = const. ciśnienie po syntezie maleje. W odwrotnym 

Jeżeli V = const. ciśnienie po syntezie maleje. W odwrotnym 

kierunku działa temperatura. Reakcja syntezy NH

kierunku działa temperatura. Reakcja syntezy NH

3

3

 jest 

 jest 

egzoenergetyczna – jeżeli nie odprowadzimy ciepła 

egzoenergetyczna – jeżeli nie odprowadzimy ciepła 

powstającego podczas syntezy NH

powstającego podczas syntezy NH

3

3

, to wzrost 

, to wzrost 

temperatury zwiększy szybkość reakcji rozkładu NH

temperatury zwiększy szybkość reakcji rozkładu NH

3

3

.

.

Warunki korzystne dla syntezy NH

Warunki korzystne dla syntezy NH

3

3

 to:

 to:

1. Zwiększenie ciśnienia substratów

1. Zwiększenie ciśnienia substratów

2. Szybkie chłodzenie produktów

2. Szybkie chłodzenie produktów

 

 

Ogólnie dla reakcji gazowych

Ogólnie dla reakcji gazowych

1.

1.

Wzrost ciśnienia sprzyja reakcjom przebiegającym ze 

Wzrost ciśnienia sprzyja reakcjom przebiegającym ze 

zmniejszeniem objętości produktów

zmniejszeniem objętości produktów

2.

2.

Obniżenie ciśnienia ułatwia przebieg reakcji ze 

Obniżenie ciśnienia ułatwia przebieg reakcji ze 

zwiększeniem objętości produktów

zwiększeniem objętości produktów

3.

3.

Gdy ΔV = 0 czyli V

Gdy ΔV = 0 czyli V

sub

sub

 = V

 = V

prod

prod

 ciśnienie nie jest 

 ciśnienie nie jest 

czynnikiem regulującym stan równowagi

czynnikiem regulującym stan równowagi

 

 

                             

                             

np.            H

np.            H

2

2

 + I

 + I

2

2

 

 





 2HJ

 2HJ

1 V

1 V

mol

mol

 + 1V

 + 1V

mol

mol

 

 





 2 V

 2 V

mol

mol

Podsumowanie:

Podsumowanie:

 

 

Pod wpływem czynników zewnętrznych stan równowagi 

Pod wpływem czynników zewnętrznych stan równowagi 

może przesunąć się w kierunku wzrostu stężeń produktów lub 

może przesunąć się w kierunku wzrostu stężeń produktów lub 

substratów ale stała równowagi K zależy tylko od temperatury.

substratów ale stała równowagi K zależy tylko od temperatury.

KINETYKA CHEMICZNA

KINETYKA CHEMICZNA

Rzeczywistą szybkość reakcji w danej chwili 

Rzeczywistą szybkość reakcji w danej chwili 

określamy jako stosunek nieskończenie małej zmiany c do 

określamy jako stosunek nieskończenie małej zmiany c do 

nieskończenie małego czasu

nieskończenie małego czasu

dt

dc

dt

dc

dt

dc

T

c

V

p

s

T



















0

lim

Mierząc „V” ubytkiem c

sub

, przed ich pochodną 

umieszczamy (-) bo w miarę przebiegu reakcji c

sub

 

systematycznie maleje.

Natomiast przed pochodną produktów (+) bo ich stężenie 

w czasie reakcji rośnie.

 

 

W równaniu kinetycznym:

W równaniu kinetycznym:

Wykładniki a i b noszą nazwę rzędów reakcji w stosunku 

Wykładniki a i b noszą nazwę rzędów reakcji w stosunku 

do  odpowiednich reagentów, suma a + b = r nazywa się 

do  odpowiednich reagentów, suma a + b = r nazywa się 

ogólnym rzędem reakcji.

ogólnym rzędem reakcji.

Rząd reakcji jest liczbą całkowitą lub ułamkową 

Rząd reakcji jest liczbą całkowitą lub ułamkową 

spełniającą nierówność:

spełniającą nierówność:

r ≤ 3

r ≤ 3

Współczynniki a i b dobierane są doświadczalnie.

Współczynniki a i b dobierane są doświadczalnie.

Rząd reakcji

Rząd reakcji

: wynikający z matematycznego opisu reakcji 

: wynikający z matematycznego opisu reakcji 

jest pojęciem związanym

jest pojęciem związanym

 

 

z całym procesem stanowiącym sumę procesów 

z całym procesem stanowiącym sumę procesów 

elementarnych

elementarnych

.

.

b

a

prod

B

A

k

dt

dc

V









 

 

Reakcje I rzędu

Reakcje I rzędu

: to takie których szybkość oznaczona 

: to takie których szybkość oznaczona 

doświadczalnie zmienia się proporcjonalnie do stężenia 

doświadczalnie zmienia się proporcjonalnie do stężenia 

jednej z substancji reagujących

jednej z substancji reagujących

. Jej szybkość przedstawia 

. Jej szybkość przedstawia 

równanie kinetyczne I rzędu:

równanie kinetyczne I rzędu:

Dla znalezienia c substratu po czasie t bardziej przydatna 

Dla znalezienia c substratu po czasie t bardziej przydatna 

jest forma scałkowana w granicach c

jest forma scałkowana w granicach c

0

0

 przy t = 0 do c po 

 przy t = 0 do c po 

czasie t. 

czasie t. 

c = c

c = c

0

0

 – x          gdzie x = ubytek stężenia substancji po 

 – x          gdzie x = ubytek stężenia substancji po 

czasie t

czasie t

lub

lub

c

k

dt

dc

V

I









c

c

t

k

I

0

ln

1



c

c

t

k

I

0

log

3

,

2



 

 

Wynika stąd że log c

Wynika stąd że log c

0

0

/c jest wprost proporcjonalny do t 

/c jest wprost proporcjonalny do t 

czyli dla reakcji I rzędu wykres log c w zależności od t jest 

czyli dla reakcji I rzędu wykres log c w zależności od t jest 

linią prostą tzn. stosunek zmiany stężeń w czasie jest 

linią prostą tzn. stosunek zmiany stężeń w czasie jest 

stały.

stały.

Reakcje II rzędu

Reakcje II rzędu

: są to reakcje których szybkość 

: są to reakcje których szybkość 

oznaczona doświadczalnie jest proporcjonalna do iloczynu 

oznaczona doświadczalnie jest proporcjonalna do iloczynu 

stężeń dwóch substratów, lub do kwadratu c

stężeń dwóch substratów, lub do kwadratu c

2

2

lub

lub

 

 

Po scałkowaniu równanie przyjmuje formę:

Po scałkowaniu równanie przyjmuje formę:

2

1

c

c

k

dt

dc

V

II











2

c

k

II



2

0

1

0

0

0

1

2

2

1

log

)

(

3

,

2

c

c

c

c

c

c

t

k

II









 

 

Jeżeli c

Jeżeli c

1

1

 = c

 = c

2

2

 wzór jest prosty:

 wzór jest prosty:

Reakcje III rzędu

Reakcje III rzędu

: spotyka się je stosunkowo rzadko, gdyż 

: spotyka się je stosunkowo rzadko, gdyż 

większość reakcji można rozłożyć na szereg reakcji I lub II 

większość reakcji można rozłożyć na szereg reakcji I lub II 

rzędu. Jednak jeśli takie reakcje występują to:

rzędu. Jednak jeśli takie reakcje występują to:

lub 

lub 

c

c

t

c

c

k

II









0

0

Dla reakcji II rzędu wykres log c w zależności od t nie jest 
linią prostą ale taki przebieg ma zależność odwrotności 
stężenia 1/c 
od t.

3

2

1

c

c

c

k

V

III









3

c

k

V

III





 

 

Gdy: c

Gdy: c

1

1

 = c

 = c

2

2

 = c

 = c

3

3

 = c 

 = c 

Reakcje „0” rzędu

Reakcje „0” rzędu

: są to reakcje których szybkość nie 

: są to reakcje których szybkość nie 

zależy od stężenia

zależy od stężenia

V = k

V = k

0

0

Oznacza to że ilość substancji ulegających przemianie 

Oznacza to że ilość substancji ulegających przemianie 

w jednostce czasu jest stała, niezależna od stężenia 

w jednostce czasu jest stała, niezależna od stężenia 

substancji reagujących.

substancji reagujących.

Niektóre równania kinetyczne reakcji przyjmują 

Niektóre równania kinetyczne reakcji przyjmują 

bardzo skomplikowaną postać, wskazuje to na złożony 

bardzo skomplikowaną postać, wskazuje to na złożony 

przebieg wielu procesów jednostkowych reakcji. Do opisu 

przebieg wielu procesów jednostkowych reakcji. Do opisu 

reakcji złożonych potrzebne jest więcej niż jedno równanie 

reakcji złożonych potrzebne jest więcej niż jedno równanie 

stechiometryczne i więcej równań kinetycznych.

stechiometryczne i więcej równań kinetycznych.

2

2

0

2

2

0

2

c

c

t

c

c

k

III









 

 

REAKCJE NASTĘPCZE – ŁAŃCUCHOWE

REAKCJE NASTĘPCZE – ŁAŃCUCHOWE

To takie reakcje których produkt jednej jest substratem 

To takie reakcje których produkt jednej jest substratem 

następnej. Mogą one przebiegać z różnym szybkościami. 

następnej. Mogą one przebiegać z różnym szybkościami. 

Całkowita szybkość reakcji [ wypadkowa ] określa wtedy 

Całkowita szybkość reakcji [ wypadkowa ] określa wtedy 

szybkość reakcji przebiegającej najwolniej

szybkość reakcji przebiegającej najwolniej

.

.

Sprzężenie takie wykazują reakcje przemiany materii w 

Sprzężenie takie wykazują reakcje przemiany materii w 

organizmach żywych.

organizmach żywych.

okres półtrwania t

okres półtrwania t

1/2

1/2

 = okres połowicznej przemiany

 = okres połowicznej przemiany

Jest to następna wielkość charakteryzująca kinetykę 

Jest to następna wielkość charakteryzująca kinetykę 

reakcji. Określa czas po którym stężenie substratu 

reakcji. Określa czas po którym stężenie substratu 

zmniejszy się o połowę w stosunku do stężenia 

zmniejszy się o połowę w stosunku do stężenia 

początkowego.

początkowego.

Wartość t

Wartość t

1/2

1/2

 obliczmy podstawiając do równania na stałą 

 obliczmy podstawiając do równania na stałą 

szybkości c = c

szybkości c = c

0

0

/2 gdzie c

/2 gdzie c

0

0

 – stężenie początkowe.

 – stężenie początkowe.

 

 

Dla reakcji I rzędu:

Dla reakcji I rzędu:

czyli

czyli

Dla reakcji II rzędu:

Dla reakcji II rzędu:

0

0

2

1

0

0

2

1

ln

2

ln

1

2

ln

1

c

c

t

c

c

t

k

I











I

I

k

k

t

693

,

0

2

ln

2

1





0

2

1

1

c

k

t

II





 

 

Dla reakcji III rzędu:

Dla reakcji III rzędu:

Okres półtrwania dla tych reakcji jest odwrotnie 

Okres półtrwania dla tych reakcji jest odwrotnie 

proporcjonalny do kwadratu stężenia początkowego.

proporcjonalny do kwadratu stężenia początkowego.

Dla reakcji „0” rzędu 

Dla reakcji „0” rzędu 

2

0

2

1

2

3

c

k

t

III





0

0

2

1

2 k

c

t





 

 

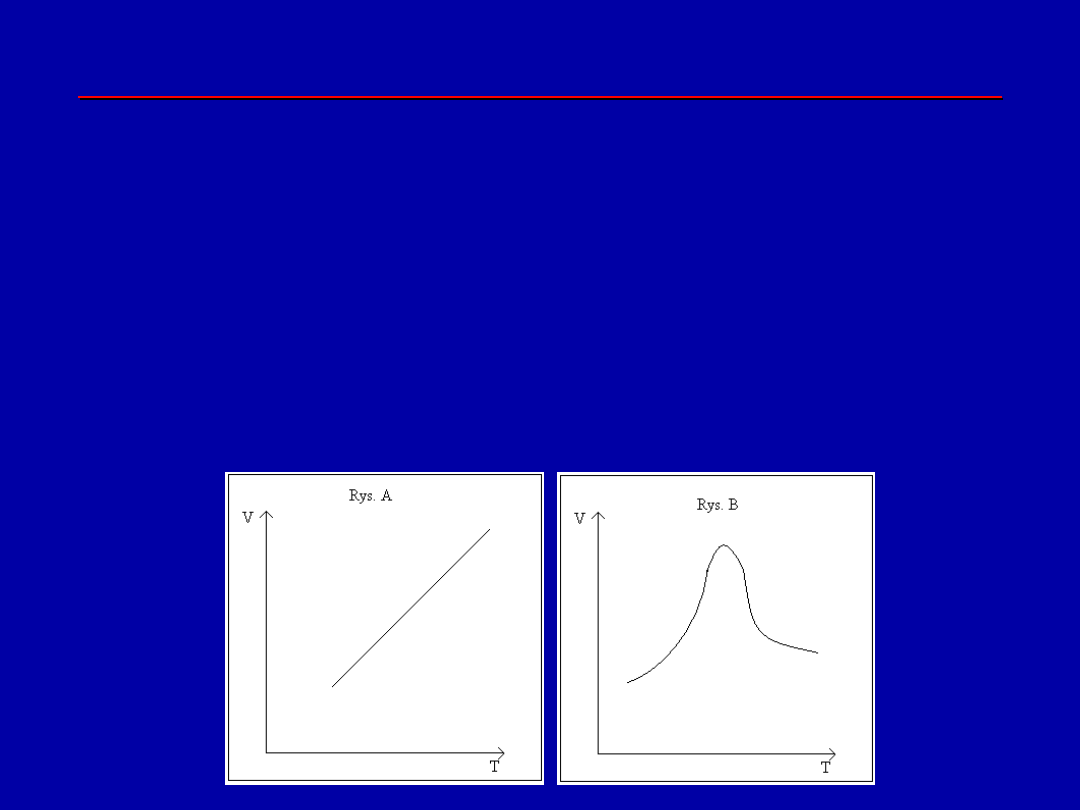
ZALEŻNOŚĆ SZYBKOŚCI REAKCJI OD TEMPERATURY

ZALEŻNOŚĆ SZYBKOŚCI REAKCJI OD TEMPERATURY

Ze wzrostem T wzrasta:

Ze wzrostem T wzrasta:

- prędkość poruszających się cząsteczek

- prędkość poruszających się cząsteczek

- energia kinetyczna cząsteczek

- energia kinetyczna cząsteczek

- liczba zderzeń efektywnych

- liczba zderzeń efektywnych

- energia zderzeń

- energia zderzeń

Dla reakcji endotermicznych szybkość rośnie z 

Dla reakcji endotermicznych szybkość rośnie z 

temperaturą w sposób wykładniczy

temperaturą w sposób wykładniczy

 

 

Znanych jest cały szereg reakcji katalizowanych przez 

Znanych jest cały szereg reakcji katalizowanych przez 

enzymy, których szybkość przyjmuje wartość max np. w 

enzymy, których szybkość przyjmuje wartość max np. w 

temperaturze 36

temperaturze 36

0

0

C (rys. B).

C (rys. B).

Dla reakcji przebiegających wg. zależności wykładniczej 

Dla reakcji przebiegających wg. zależności wykładniczej 

(rys. A) – większość reakcji ma zastosowanie 

(rys. A) – większość reakcji ma zastosowanie 

Reguła van’t 

Reguła van’t 

Hoffa

Hoffa

:

:

W reakcjach jednofazowych podwyższenie temperatury 

W reakcjach jednofazowych podwyższenie temperatury 

o 10

o 10

0

0

C zwiększa szybkość reakcji 2-4 krotnie. Wpływ T jest 

C zwiększa szybkość reakcji 2-4 krotnie. Wpływ T jest 

większy przy niskich temperaturach  - zbliżonych do T = 

większy przy niskich temperaturach  - zbliżonych do T = 

20

20

0

0

C.

C.

Współczynnik temperaturowy reakcji Q

Współczynnik temperaturowy reakcji Q

 – wskazuje ile 

 – wskazuje ile 

razy wzrośnie stała szybkości reakcji przy wzroście 

razy wzrośnie stała szybkości reakcji przy wzroście 

temperatury o 10

temperatury o 10

0

0

C.

C.

T

T

k

k

Q

10





 

 

ENERGIA AKTYWACJI

ENERGIA AKTYWACJI

Aby zderzenia były efektywne  - doprowadziły do 

Aby zderzenia były efektywne  - doprowadziły do 

utworzenia nowych wiązań, zderzające się cząsteczki 

utworzenia nowych wiązań, zderzające się cząsteczki 

muszą posiadać 

muszą posiadać 

energię większą od energii granicznej 

energię większą od energii granicznej 

charakterystycznej dla ich stanu podstawowego

charakterystycznej dla ich stanu podstawowego

.

.

Ten „nadmiar” energii – zwany 

Ten „nadmiar” energii – zwany 

energią aktywacji

energią aktywacji

 zostaje 

 zostaje 

zużyty na:

zużyty na:

- rozluźnienie wiązań w substratach

- rozluźnienie wiązań w substratach

- przegrupowanie atomów i elektronów w produktach 

- przegrupowanie atomów i elektronów w produktach 

pośrednich

pośrednich

- pokonanie sił odpychania pomiędzy cząsteczkami 

- pokonanie sił odpychania pomiędzy cząsteczkami 

substratów

substratów

 

 

Z energią aktywacji wiąże się pojęcie 

Z energią aktywacji wiąże się pojęcie 

stanu przejściowego

stanu przejściowego

 

 

lub 

lub 

kompleksu aktywnego

kompleksu aktywnego

 który jest:

 który jest:

- krótkotrwały

- krótkotrwały

- w stanie energetycznym niezbędnym do zajścia reakcji – 

- w stanie energetycznym niezbędnym do zajścia reakcji – 

osiągnął odpowiednią energię aktywacji

osiągnął odpowiednią energię aktywacji

- rozpadając się może dawać zarówno substraty jak i 

- rozpadając się może dawać zarówno substraty jak i 

produkty

produkty

Możliwość utworzenia przejściowego kompleksu 

Możliwość utworzenia przejściowego kompleksu 

aktywnego zmniejsza próg energii aktywacji ponieważ 

aktywnego zmniejsza próg energii aktywacji ponieważ 

stopniowe powstawanie kompleksu powoduje 

stopniowe powstawanie kompleksu powoduje 

„słabnięcie” wiązań pierwotnych a wzmocnienie nowych.

„słabnięcie” wiązań pierwotnych a wzmocnienie nowych.

Zapotrzebowanie na energię jest więc częściowo 

Zapotrzebowanie na energię jest więc częściowo 

kompensowane przez energię uwalnianą podczas 

kompensowane przez energię uwalnianą podczas 

tworzenia nowych wiązań.

tworzenia nowych wiązań.

 

 

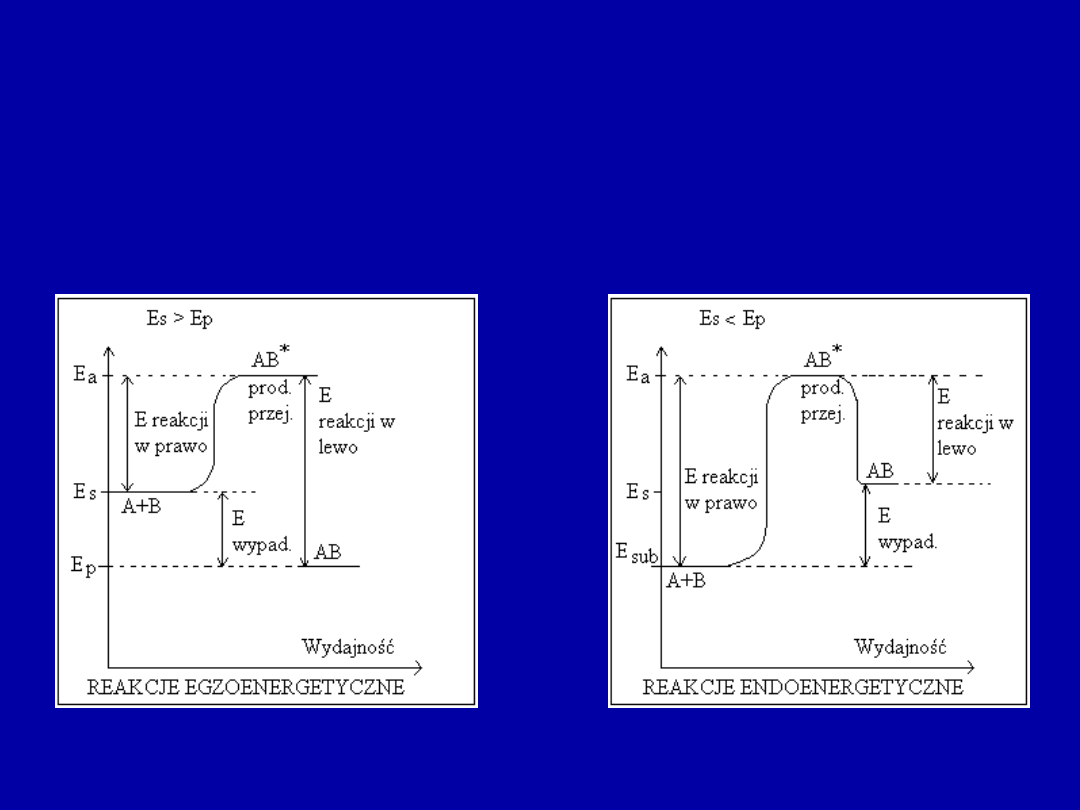
Szybkość reakcji zależeć będzie od:

Szybkość reakcji zależeć będzie od:

- stężenia kompleksu aktywnego

- stężenia kompleksu aktywnego

- szybkości jego rozpadu

- szybkości jego rozpadu

 

 

Energia 

aktywac

ji

kJ/mol

Czas 

połowiczne
j

przemiany t

1/2

reakcja I 

rzędu t = 
27

o

C

62,7

0,007 s

83,6

14,0 s

104,5

13,0 godz.

125,4

38,0 godz.

Bardzo szybko przebiegają reakcje jonowe w roztworach. 

Ich energia aktywacji jest tak mała, że prawie każde 

zderzenie może być efektywne.

Bardzo wolno zachodzą reakcje cząsteczkowe w chemii 

organicznej w temperaturze 20oC większość z nich nie 

zachodzi. Należy wtedy zastosować substancje obniżające 

energię aktywacji.

 

 

KATALIZATORY

KATALIZATORY

Katalizator przyśpiesza reakcję, obniżając energię 

Katalizator przyśpiesza reakcję, obniżając energię 

aktywacji. Jest to możliwe poprzez zmianę mechanizmu 

aktywacji. Jest to możliwe poprzez zmianę mechanizmu 

reakcji. 

reakcji. 

Katalizatory same uczestniczą w reakcji chemicznej a po jej 

Katalizatory same uczestniczą w reakcji chemicznej a po jej 

zakończeniu pozostają niezmienione.

zakończeniu pozostają niezmienione.

Kataliza może być jedno lub wieloetapowa. W I etapie może 

Kataliza może być jedno lub wieloetapowa. W I etapie może 

zachodzić wiązanie substratu  z katalizatorem i tworzenie 

zachodzić wiązanie substratu  z katalizatorem i tworzenie 

nietrwałego związku przejściowego kA.

nietrwałego związku przejściowego kA.

II etap – rozkład związku kA pod działaniem substratu B i 

II etap – rozkład związku kA pod działaniem substratu B i 

powstanie produktu AB, a równocześnie uwalnia się 

powstanie produktu AB, a równocześnie uwalnia się 

katalizator.

katalizator.

kA* + B 

kA* + B 





  kAB*  

  kAB*  





 AB + k

 AB + k

kompleks

kompleks

aktywny

aktywny

 

 

Aby katalizowana reakcja miała dużą szybkość powstające 

Aby katalizowana reakcja miała dużą szybkość powstające 

związki przejściowe nie mogą być zbyt trwałe.

związki przejściowe nie mogą być zbyt trwałe.

Różnica między procesem katalizowanym nie polega na 

Różnica między procesem katalizowanym nie polega na 

sposobie pokonywania bariery energetycznej. Przy 

sposobie pokonywania bariery energetycznej. Przy 

udziale katalizatora tych barier jest większa liczba, 

udziale katalizatora tych barier jest większa liczba, 

ale są niżej energetyczne.

ale są niżej energetyczne.

Zmniejszenie energii aktywacji zależy od aktywności 

Zmniejszenie energii aktywacji zależy od aktywności 

katalizatora.

katalizatora.

Katalizator nie zmienia

Katalizator nie zmienia

:

:

- położenia równowagi reakcji

- położenia równowagi reakcji

- termodynamicznych warunków reakcji

- termodynamicznych warunków reakcji

- ilości otrzymanych produktów z określonej ilości substratów

- ilości otrzymanych produktów z określonej ilości substratów

Zmienia

Zmienia

: jedynie szybkość dochodzenia reakcji do stanu 

: jedynie szybkość dochodzenia reakcji do stanu 

równowagi.

równowagi.

 

 

Cechy charakterystyczne katalizatora

Cechy charakterystyczne katalizatora

- aktywność: efektywnie mają działać nawet jego małe 

- aktywność: efektywnie mają działać nawet jego małe 

dawki, gdyż jest on regenerowany w czasie reakcji. 

dawki, gdyż jest on regenerowany w czasie reakcji. 

Katalizatory są tym aktywniejsze im silniej obniżają 

Katalizatory są tym aktywniejsze im silniej obniżają 

energię aktywacji

energię aktywacji

- selektywność lub specyficzność: np. reagują tylko z 

- selektywność lub specyficzność: np. reagują tylko z 

substancją „A” lub katalizują tylko jedną możliwą 

substancją „A” lub katalizują tylko jedną możliwą 

reakcję

reakcję

- odporność na starzenie: powodujące zmianę jego 

- odporność na starzenie: powodujące zmianę jego 

struktury krystalicznej, zmieniające liczbę centrów 

struktury krystalicznej, zmieniające liczbę centrów 

aktywnych, prowadzące nawet do utraty aktywności

aktywnych, prowadzące nawet do utraty aktywności

- odporność na zatrucia: zdolność zachowania aktywności 

- odporność na zatrucia: zdolność zachowania aktywności 

nawet w obecności zanieczyszczeń występujących w 

nawet w obecności zanieczyszczeń występujących w 

niewielkich ilościach

niewielkich ilościach

 

 

INHIBITOR

INHIBITOR

 – to katalizator który tworzy związek 

 – to katalizator który tworzy związek 

przejściowy o wyższej barierze energetycznej, trwały z 

przejściowy o wyższej barierze energetycznej, trwały z 

trudem przechodzący w produkt.

trudem przechodzący w produkt.

KATALIZA HOMOGENICZNA

KATALIZA HOMOGENICZNA

 – katalizator i substraty 

 – katalizator i substraty 

znajdują się w tej samej fazie.

znajdują się w tej samej fazie.

KATALIZA HETEROGENICZNA

KATALIZA HETEROGENICZNA

 – katalizator jest 

 – katalizator jest 

najczęściej w fazie stałej, a katalizuje proces w gazach lub 

najczęściej w fazie stałej, a katalizuje proces w gazach lub 

cieczach.

cieczach.

W takich procesach duże znaczenie mają procesy 

W takich procesach duże znaczenie mają procesy 

adsorpcji substratów na powierzchni katalizatora.

adsorpcji substratów na powierzchni katalizatora.

Taka kataliza obejmuje cały szereg procesów.

Taka kataliza obejmuje cały szereg procesów.

3

2

2

2

2

5

2

SO

O

SO

O

V



 





DYFUZJA I OSMOZA

DYFUZJA I OSMOZA

 

 

 

 

Dyfuzja

Dyfuzja

 – to samoistne mieszanie się cząsteczek 

 – to samoistne mieszanie się cząsteczek 

różnych substancji spowodowane kinetycznym ruchem 

różnych substancji spowodowane kinetycznym ruchem 

cząsteczek.

cząsteczek.

- Przemieszczanie się cząsteczek w przestrzeni lub w 

- Przemieszczanie się cząsteczek w przestrzeni lub w 

roztworze zachodzi zawsze z przestrzeni o 

roztworze zachodzi zawsze z przestrzeni o 

wyższym 

wyższym 

stężeniu do przestrzeni o stężeniu niższym

stężeniu do przestrzeni o stężeniu niższym

, nawet 

, nawet 

wbrew zasadzie ciężkości.

wbrew zasadzie ciężkości.

- Dyfuzja najszybciej zachodzi w gazach a najwolniej w 

- Dyfuzja najszybciej zachodzi w gazach a najwolniej w 

ciałach stałych, ale zawsze wzrasta wraz z 

ciałach stałych, ale zawsze wzrasta wraz z 

temperaturą.

temperaturą.

 

 

Ilościowo proces dyfuzji ujmuje prawo Ficka

Ilościowo proces dyfuzji ujmuje prawo Ficka

- określając liczbę moli substancji rozpuszczonej (n) 

- określając liczbę moli substancji rozpuszczonej (n) 

przechodzącą w jednostce czasu przez powierzchnię 

przechodzącą w jednostce czasu przez powierzchnię 

roztworu o przekroju A pomiędzy punktami o różnicy stężeń 

roztworu o przekroju A pomiędzy punktami o różnicy stężeń 

Δc,

Δc,

odległymi o Δx 

odległymi o Δx 

D – współczynnik dyfuzji ilościowo równy ilości substancji

D – współczynnik dyfuzji ilościowo równy ilości substancji

 

 

dyfundującej w jednostce czasu przez „A” = 1 cm

dyfundującej w jednostce czasu przez „A” = 1 cm

2

2

 

 

gdy Δc/Δx = 1

gdy Δc/Δx = 1

Δc/Δx = gradient stężenia – jest to spadek stężenia Δc 

Δc/Δx = gradient stężenia – jest to spadek stężenia Δc 

przypadający na odcinek Δx

przypadający na odcinek Δx

x

c

DA

n









 

 

Szybkość dyfuzji w gazach zależy od

Szybkość dyfuzji w gazach zależy od

:

:

- temperatury, powierzchni wymiany

- temperatury, powierzchni wymiany

- gradientu ciśnienia pomiędzy gazem w cieczy i nad cieczą

- gradientu ciśnienia pomiędzy gazem w cieczy i nad cieczą

- odwrotnie proporcjonalna do „M” gazu, długości drogi 

- odwrotnie proporcjonalna do „M” gazu, długości drogi 

dyfuzji, lepkości cieczy

dyfuzji, lepkości cieczy

Rozpuszczalność gazów w cieczach zależy od

Rozpuszczalność gazów w cieczach zależy od

:

:

- rodzaju obu substancji, ich polarności

- rodzaju obu substancji, ich polarności

- podobny rozpuszczalnik rozpuszcza podobne substancje 

- podobny rozpuszczalnik rozpuszcza podobne substancje 

[polarny – polarny]

[polarny – polarny]

- reakcji towarzyszących rozpuszczaniu

- reakcji towarzyszących rozpuszczaniu

- temperatury i ciśnienia i prawo Henry’ego

- temperatury i ciśnienia i prawo Henry’ego

T = const.

T = const.

 

 

p

k

m





 

 

p

k

m





T = const

T = const

.

.

[m] masa rozpuszczonego gazu w określonej objętości 

cieczy jest wprost proporcjonalna do ciśnienia parcjalnego 

(p) gazu nad roztworem.

k- współczynnik proporcjonalności zależny od T, rodzaju 

gazu i rozpuszczalnika

- rozpuszczalność gazu w cieczy maleje ze wzrostem T

  

  

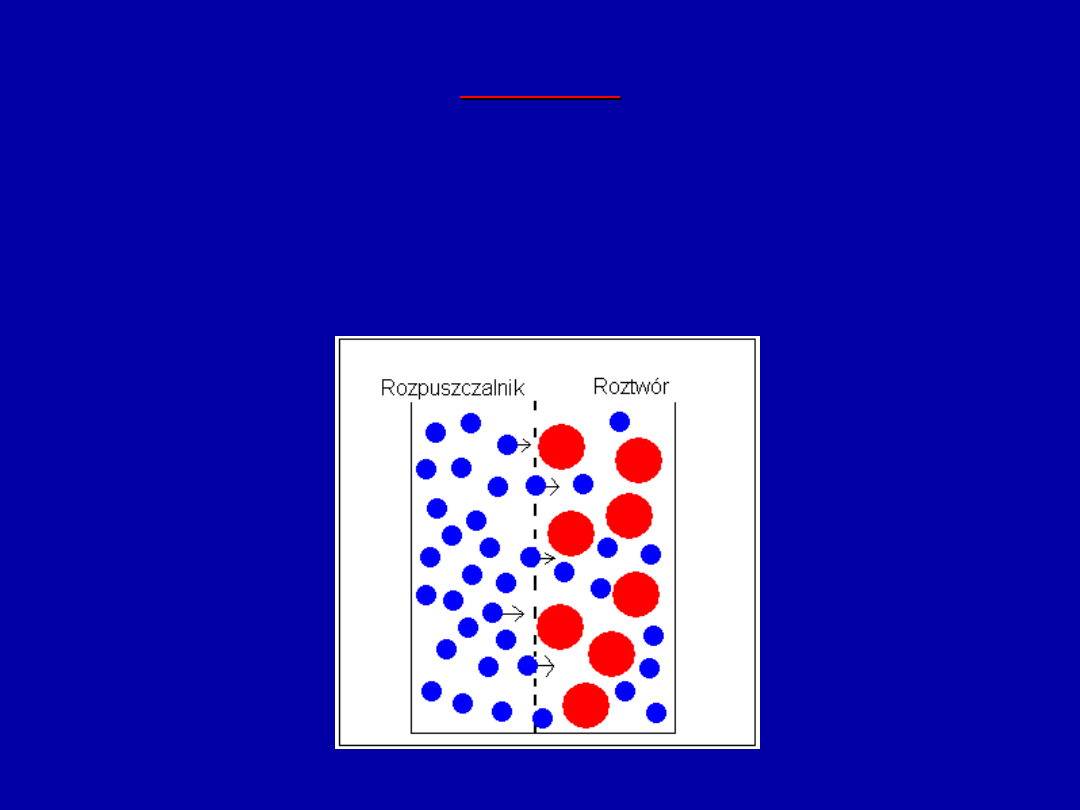
OSMOZA

OSMOZA

Jednostronna dyfuzja rozpuszczalnika przez błonę 

Jednostronna dyfuzja rozpuszczalnika przez błonę 

półprzepuszczalną oddzielającą rozpuszczalnik i 

półprzepuszczalną oddzielającą rozpuszczalnik i 

roztwór.

roztwór.

 

 

Przez małe otwory błony półprzepuszczalnej mogą 

Przez małe otwory błony półprzepuszczalnej mogą 

przenikać tylko małe cząsteczki rozpuszczalnika. Od 

przenikać tylko małe cząsteczki rozpuszczalnika. Od 

strony roztworu część przejść w błonie blokowana jest 

strony roztworu część przejść w błonie blokowana jest 

przez większe cząsteczki substancji rozpuszczonej. Na 

przez większe cząsteczki substancji rozpuszczonej. Na 

skutek przenikania rozpuszczalnika do roztworu maleje 

skutek przenikania rozpuszczalnika do roztworu maleje 

stężenie roztworu, zwiększa się jego objętość, wzrasta 

stężenie roztworu, zwiększa się jego objętość, wzrasta 

ciśnienie hydrostatyczne. Wraz ze wzrostem ciśnienia 

ciśnienie hydrostatyczne. Wraz ze wzrostem ciśnienia 

hydrostatycznego maleje szybkość osmozy (przenikanie 

hydrostatycznego maleje szybkość osmozy (przenikanie 

rozpuszczalnika).

rozpuszczalnika).

Ciśnienie hydrostatyczne przy którym ustaje osmoza 

Ciśnienie hydrostatyczne przy którym ustaje osmoza 

nazywa się ciśnieniem osmotycznym.

nazywa się ciśnieniem osmotycznym.

Przy takim ciśnieniu liczba cząstek rozpuszczalnika 

Przy takim ciśnieniu liczba cząstek rozpuszczalnika 

przenikających przez błonę w obie strony jest jednakowa.

przenikających przez błonę w obie strony jest jednakowa.

  

  

Van’t Hoff uważał że cząsteczki substancji rozpuszczonej 

Van’t Hoff uważał że cząsteczki substancji rozpuszczonej 

przypominają swym zachowaniem cząsteczki gazu 

przypominają swym zachowaniem cząsteczki gazu 

doskonałego wypełniającego dostępną przestrzeń.

doskonałego wypełniającego dostępną przestrzeń.

Wobec tego dla ciśnienia osmotycznego roztworu można 

Wobec tego dla ciśnienia osmotycznego roztworu można 

wyprowadzić zależność podobną do prawa Clapeyrona:

wyprowadzić zależność podobną do prawa Clapeyrona:

c  – stężenie molalne roztworu – dla rozcieńczonych r-rów 

c  – stężenie molalne roztworu – dla rozcieńczonych r-rów 

       

       

wodnych = C

wodnych = C

m

m

V – objętość roztworu

V – objętość roztworu

n -  liczba moli substancji rozpuszczonej

n -  liczba moli substancji rozpuszczonej

R – stała gazowa                  T – temperatura 

R – stała gazowa                  T – temperatura 

o

o

K

K

cRT





V

n

c 

nRT

V 



 

 

Ciśnienie osmotyczne

Ciśnienie osmotyczne

 roztworu równe jest ciśnieniu, jakie 

 roztworu równe jest ciśnieniu, jakie 

wywarła by substancja rozpuszczona gdyby jako gaz w 

wywarła by substancja rozpuszczona gdyby jako gaz w 

danej T zajęła objętość taką jak roztwór.

danej T zajęła objętość taką jak roztwór.

Wynika stąd że

Wynika stąd że

: 

: 

- w T = const. W roztworach nieelektrolitów 

- w T = const. W roztworach nieelektrolitów 

Π

Π

 ~ c [stężenia] 

 ~ c [stężenia] 

czyli ilości cząsteczek osmotycznie czynnych

czyli ilości cząsteczek osmotycznie czynnych

- wielkość 

- wielkość 

Π

Π

 przy V = const. i T = const. nie zależy od 

 przy V = const. i T = const. nie zależy od 

substancji rozpuszczonej ani od rodzaju rozpuszczalnika, 

substancji rozpuszczonej ani od rodzaju rozpuszczalnika, 

ale od liczby osmotycznie czynnych indywiduów, którymi 

ale od liczby osmotycznie czynnych indywiduów, którymi 

mogą być cząsteczki nieelektrolitu, jony itp.

mogą być cząsteczki nieelektrolitu, jony itp.

- ciśnienie 

- ciśnienie 

Π

Π

 jest wprost proporcjonalne do T jeśli V = const.

 jest wprost proporcjonalne do T jeśli V = const.

- równe objętości roztw. o jednakowym 

- równe objętości roztw. o jednakowym 

Π

Π

 zawierają  

 zawierają  

jednakową liczbę cząsteczek osmotycznie czynnych jeżeli 

jednakową liczbę cząsteczek osmotycznie czynnych jeżeli 

ich „V” jest taka sama

ich „V” jest taka sama

- roztwory równocząsteczkowe mają takie same 

- roztwory równocząsteczkowe mają takie same 

Π

Π

- 

- 

Π

Π

 roztworów zawierających kilka substancji osmotycznie 

 roztworów zawierających kilka substancji osmotycznie 

czynnych równe jest Σ 

czynnych równe jest Σ 

Π

Π

 poszczególnych składników

 poszczególnych składników

- w roztworach elektrolitów o dużym stopniu dysocjacji 

- w roztworach elektrolitów o dużym stopniu dysocjacji 

każdy jon jest odpowiedzialny za 

każdy jon jest odpowiedzialny za 

Π

Π

  

  

inRT





Współczynnik izotoni

e

teoretyczn

e

erymenta

i







ln

exp

= poprawka dla elektrolitów

Warunek konieczny dla osmozy

Różna liczba cząstek osmotycznie czynnych po obu 
stronach błony półprzepuszczalnej.

Roztwory izoosmotyczne – posiadają jednakowe Π przy 
takiej samej ilości osmotycznie czynnych cząsteczek.
Jednostką Π jest Osmol. Jest to Π jakie w t = 0

o

C wywiera 

roztwór nie dysocjującego o c = 1M/kg rozpuszczalnika. 
Roztwory takie względem wody wykazują ciśnienie Π = 
22690 hPa = 22,4 atm

 

 

Naturalne błony półprzepuszczalne

Naturalne błony półprzepuszczalne

- jelita, pęcherz moczowy

- jelita, pęcherz moczowy

Roztwory izotoniczne

Roztwory izotoniczne

 – takie dwa roztwory, które 

 – takie dwa roztwory, które 

oddzielone błoną półprzepuszczalną, nie wykazują 

oddzielone błoną półprzepuszczalną, nie wykazują 

żadnego ciśnienia Π np. 0,85 – 0,90 % NaCl i krew

żadnego ciśnienia Π np. 0,85 – 0,90 % NaCl i krew

Roztwory hipertoniczne

Roztwory hipertoniczne

 – roztwory o Π wyższym niż 

 – roztwory o Π wyższym niż 

inne roztwory. [plazmoliza krwinek – obkurczanie]

inne roztwory. [plazmoliza krwinek – obkurczanie]

Roztwory hipotoniczne

Roztwory hipotoniczne

 – jeżeli ich Π jest niższe od 

 – jeżeli ich Π jest niższe od 

innych roztworów

innych roztworów

Krwinka umieszczona w takim roztworze pobiera 

Krwinka umieszczona w takim roztworze pobiera 

H

H

2

2

O, najpierw pęcznieje, następnie pęka 

O, najpierw pęcznieje, następnie pęka 

wydzielając hemoglobinę – [hemoliza] krwinek w 

wydzielając hemoglobinę – [hemoliza] krwinek w 

0,45% roztworze NaCl

0,45% roztworze NaCl

 

 

UKŁADY DYSPERSYJNE

UKŁADY DYSPERSYJNE

W zależności od stopnia rozdrobnienia substancji 

W zależności od stopnia rozdrobnienia substancji 

rozpuszczonej wyróżnia się 3 typy układów 

rozpuszczonej wyróżnia się 3 typy układów 

dyspersyjnych:

dyspersyjnych:

1.

1.

Roztwory właściwe – rozdrobnienie cząstek  

Roztwory właściwe – rozdrobnienie cząstek  

mniejsze od 10

mniejsze od 10

-7

-7

 cm

 cm

2.

2.

Roztwory koloidalne – cząstki substancji 

Roztwory koloidalne – cząstki substancji 

rozpuszczonej mają wymiary 10

rozpuszczonej mają wymiary 10

-7

-7

 – 10

 – 10

-5

-5

 cm

 cm

3.

3.

Mieszaniny niejednorodne – zawiesiny o cząstkach 

Mieszaniny niejednorodne – zawiesiny o cząstkach 

>10

>10

-5

-5

 [rozdrobnienie mechaniczne]

 [rozdrobnienie mechaniczne]

 

 

CECHY CHARAKTERYSTYCZNE TYCH UKŁADÓW

CECHY CHARAKTERYSTYCZNE TYCH UKŁADÓW

I. Roztwory 

właściwe

II. Koloidy

III. Zawiesiny

1. nie 

widoczne 
w ultra-

mikroskopie
1. przechodz

ą przez

ultrasączki
3.   

dyfundują, 
dializują

1.   widoczne w 

ultramikro-

      skopie
2.   przechodzą 

przez bibułę

      ultrasączka

3.   nie dyfundują
4.   nie dializują lub 

bardzo wolno

5.   wykazują ruchy 

Browna

6.   wykazują małe 

wartości

      ΔT

w

 i ΔT

k

 i Π

1. widoczne w 

mikroskopie

2. nie przechodzą 

przez zwykłą 
bibułę

3. nie dyfundują
4. nie dializują
5. nie wykazują 

ruchów Browna

 

 

I. Rodzaje układów koloidalnych

I. Rodzaje układów koloidalnych

faza

rozproszo

na

faza

rozpraszają

ca

koloid

przykład

gaz

ciecz

ciało stałe

gaz

gaz
gaz

---

aerozol ciekły

aerozol stały

---

mgła

dym, kurz

gaz

ciecz

ciało stałe

ciecz
ciecz

ciecz

piana

emulsja

zole =

roztwory 

koloidowe

mydlana, piwna

mleko, majonez, 

krem

zole tlenków 

metali,

wodorotlenków, 

farby,

polimery, lakiery

gaz

ciecz

ciało stałe

ciało stałe

ciało stałe
ciało stałe

piana trwała

emulsja stała

zole stałe 

pumeks, styropian

opale, galaretki

szkło rubinowe,

barwne kryształy

 

 

II. Podział ze względu na wymiary cząstek

II. Podział ze względu na wymiary cząstek

- monodyspersyjne – trzy wymiary cząstek jednakowe

- monodyspersyjne – trzy wymiary cząstek jednakowe

- polidyspersyjne – cząstki mają różne wymiary

- polidyspersyjne – cząstki mają różne wymiary

III. Zachowanie po odparowaniu suchej pozostałości

III. Zachowanie po odparowaniu suchej pozostałości

- odwracalne typu żelatyny, gumy arabskiej

- odwracalne typu żelatyny, gumy arabskiej

- nieodwracalne – lakiery

- nieodwracalne – lakiery

 

 

IV. Stosunku fazy rozproszonej i ośrodka rozpraszającego

IV. Stosunku fazy rozproszonej i ośrodka rozpraszającego

- liofilowe:   siarczki i wodorotlenki metali

- liofilowe:   siarczki i wodorotlenki metali

- liofobowe: siarka koloidalna

- liofobowe: siarka koloidalna

Najważniejsze i najbardziej rozpowszechnione są układy 

Najważniejsze i najbardziej rozpowszechnione są układy 

cieczy w cieczy i ciała stałe w cieczy – zole (większość 

cieczy w cieczy i ciała stałe w cieczy – zole (większość 

płynów ustrojowych).

płynów ustrojowych).

zol                    żel

zol                    żel

























PEPTYZACJA

KOAGULACJA

 

 

zol

zol

 – pojedyncze cząstki są od siebie izolowane przez 

 – pojedyncze cząstki są od siebie izolowane przez 

rozpuszczalnik

rozpuszczalnik

żel

żel

 – konsystencja galarety w której substancja 

 – konsystencja galarety w której substancja 

rozpuszczona tworzy sieć przestrzenną a rozpuszczalnik 

rozpuszczona tworzy sieć przestrzenną a rozpuszczalnik 

wypełnia w niej puste miejsca

wypełnia w niej puste miejsca

Rozdrobnienie koloidalne wykazuje bardzo dużą 

Rozdrobnienie koloidalne wykazuje bardzo dużą 

powierzchnię fazy rozproszonej, np. 1g ciała stałego o 

powierzchnię fazy rozproszonej, np. 1g ciała stałego o 

strukturze sześcianu o wymiarze 1 cm

strukturze sześcianu o wymiarze 1 cm

2

2

 ma powierzchnię 6 

 ma powierzchnię 6 

cm

cm

2

2

, po rozdrobnieniu do 10

, po rozdrobnieniu do 10

-5

-5

 cm otrzymuje się 10

 cm otrzymuje się 10

15

15

 

 

sześcianów cząstek koloidalnych co daje   6 ∙ 10

sześcianów cząstek koloidalnych co daje   6 ∙ 10

-5

-5

 ∙ 10

 ∙ 10

15

15

 

 

cm

cm

2

2

 = 60m

 = 60m

2

2

.  Koloidy mają więc zdolność sorbowania na 

.  Koloidy mają więc zdolność sorbowania na 

swojej powierzchni dużej ilości jonów z roztworu.

swojej powierzchni dużej ilości jonów z roztworu.

 

 

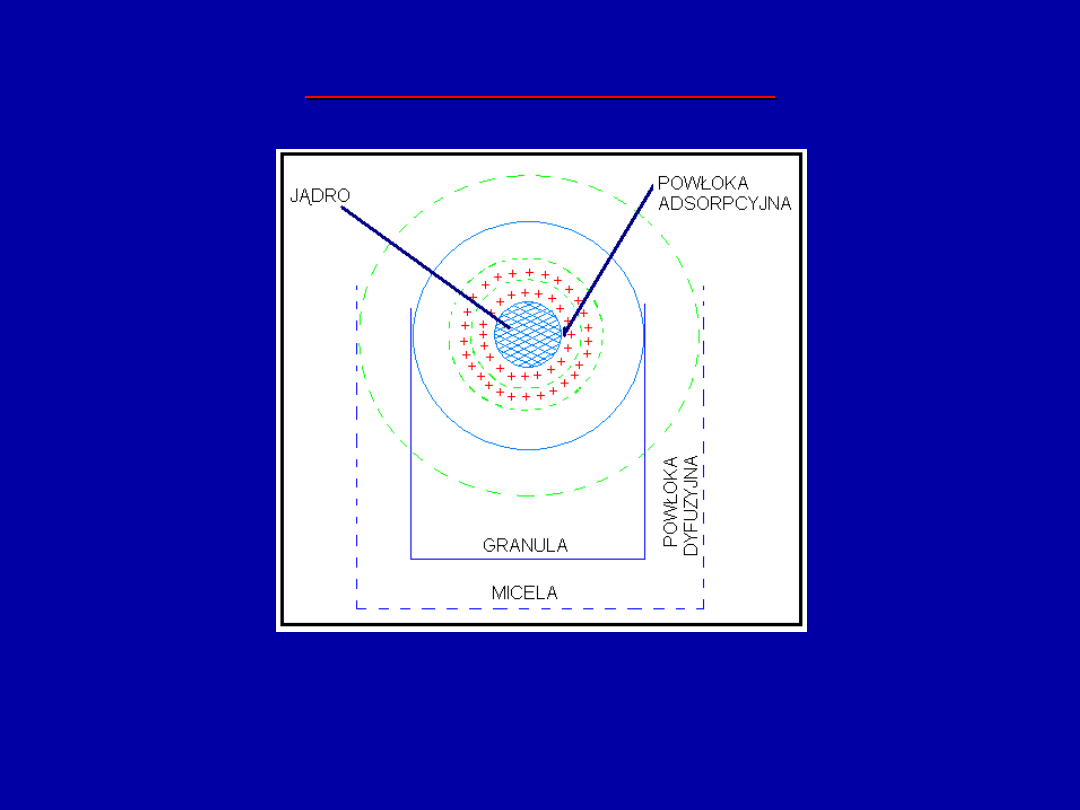
BUDOWA MICELI KOLOIDU

BUDOWA MICELI KOLOIDU

GRANULA = JĄDRO + POWŁOKA ADSORPCYJNA

GRANULA = JĄDRO + POWŁOKA ADSORPCYJNA

MICELA = GRANULA + POWŁOKA DYFUZYJNA

MICELA = GRANULA + POWŁOKA DYFUZYJNA

 

 

Roztwory micelarne

Roztwory micelarne

 – ich cząsteczki mają niewielkie 

 – ich cząsteczki mają niewielkie 

rozmiary i niewielkie ciężary cząsteczkowe: mydła, 

rozmiary i niewielkie ciężary cząsteczkowe: mydła, 

detergenty, kwasy żółciowe. Jeżeli ich stężenie jest 

detergenty, kwasy żółciowe. Jeżeli ich stężenie jest 

niewielkie, to ich właściwości zbliżone są do właściwości 

niewielkie, to ich właściwości zbliżone są do właściwości 

roztworów rzeczywistych.

roztworów rzeczywistych.

Roztwory molekularne

Roztwory molekularne

 – koloidy o dużych rozmiarach 

 – koloidy o dużych rozmiarach 

cząsteczek i dużych ciężarach cząsteczkowych: 

cząsteczek i dużych ciężarach cząsteczkowych: 

wielkocząsteczkowe biopolimery, kwasy nukleinowe, 

wielkocząsteczkowe biopolimery, kwasy nukleinowe, 

białka, polisacharydy.

białka, polisacharydy.

Emulsje

Emulsje

 – koloidy tworzone przez tłuszcze, glikolipidy, 

 – koloidy tworzone przez tłuszcze, glikolipidy, 

fosfolipidy.

fosfolipidy.