1
Osmoza
Definicja chemiczna
Osmoza jest procesem dyfuzji rozpuszczalnika przez
błonę półprzepuszczalną od roztworu o niskim stężeniu
do roztworu o wysokim stężeniu aż do momentu
wyrównania się stężeń.
•Definicja biologiczna
•Osmoza jest procesem dyfuzji (przenikania) wody przez
błony komórkowe.
2
Osmoza jest spowodowana oddziaływaniami między
cząsteczkami wody i cząsteczkami lub jonami substan-
cji rozpuszczonej (hydratacją)
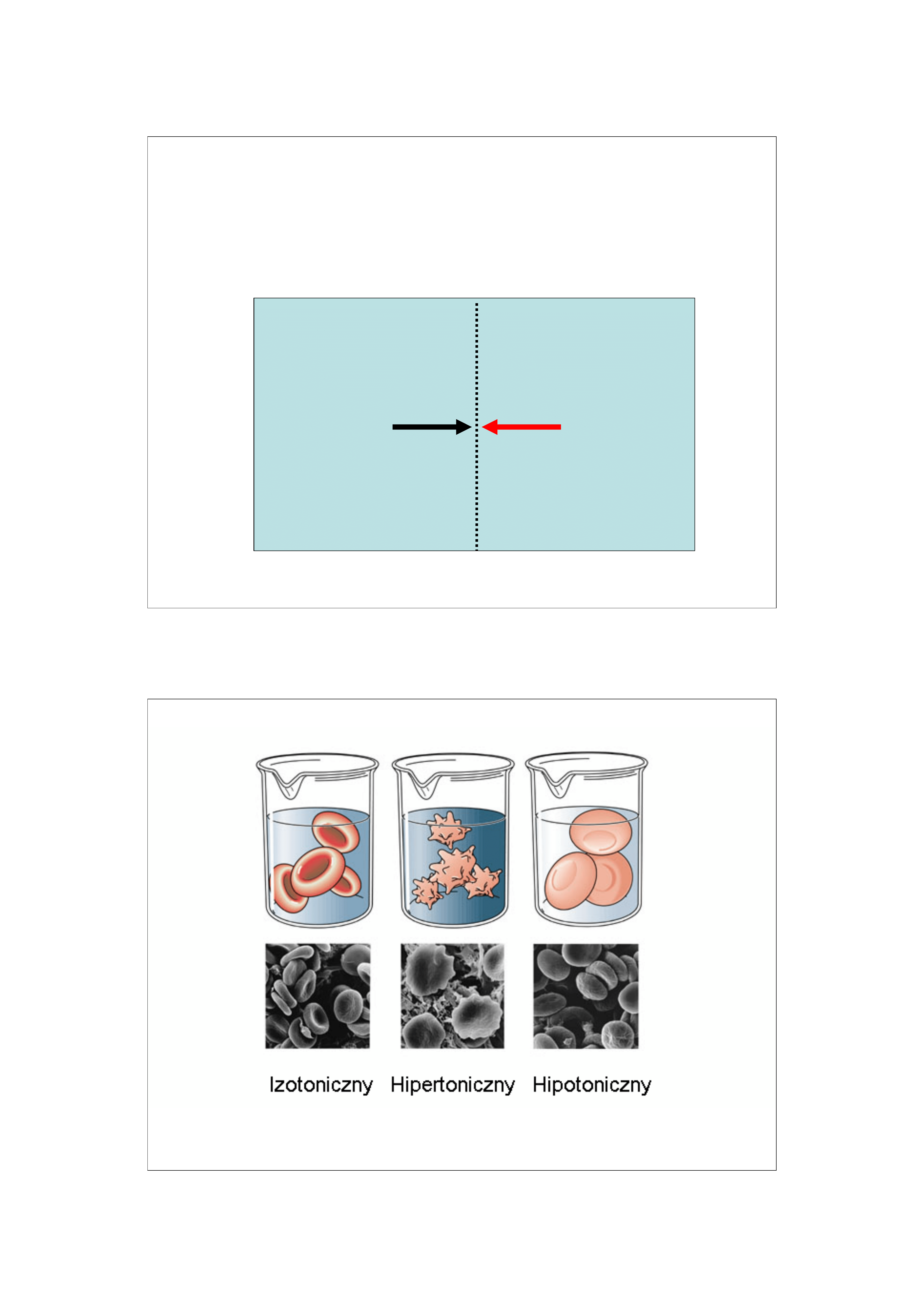
3
Osmotyczny
przepływ
Ciśnienie
osmotyczne
Niskie stężenie
Wysokie stężenie
Ciśnienie osmotyczne jest zewnętrznym ciśnieniem, które
trzeba zastosować aby zatrzymać osmotyczny przepływ
rozpuszczalnika przez błonę półprzepuszczalną.
4
5
Ciśnienie osmotyczne,
π
, zależy od stężenia
molowego jonów i cząsteczek aktywnych osmotycznie.
Stężenie to nazywane jest osmolowością roztworu.
+
_
_
_
+
_
+
6
π
= i f c RT
i - liczba jonów w cząsteczce
f - współczynnik aktywności
c - stężenie molowe substancji
R - stała gazowa
T - temperatura w skali Kelvina
osmolowość
Roztwory izotoniczne mają równą osmolowość
7
Bufory
Bufory są roztworami zawierającymi słaby kwas i jego
sprzężoną zasadę, które mają zdolność zobojętniania
wprowadzanych z zewnątrz mocnych kwasów i zasad.
Dzięki tej właściwości bufory minimalizują zmiany pH jakie
następują po wprowadzeniu do ich roztworu mocnego
kwasu lub mocnej zasady (w porównaniu ze zmianą
obserwowaną po wprowadzeniu tych związków do wody).
Bufory można przygotowywać przez zmieszanie różnych
substancji, ważnym jest aby w roztworze końcowym była
obecna para sprzężona słaby kwas-zasada.
8
Stosunek stężeń molowych składników buforu nie może być
dowolny.
Musi być zawarty w przedziale 0,1 - 10.
0,1 ≤ C
zasada
/C
kwas
≤ 10
pH każdego buforu można obliczyć za pomocą równania
Hendersona-Hasselbacha:
pH = pK
a
+ log
C
zasada
C
kwas
9
pH danego buforu zależy od wartości pK
a
słabego kwasu
wchodzącego w skład buforu i od stosunku stężeń
C
zasada
/C
kwas
.
C
zasada
/C
kwas
musi się mieścić w zakresie 0,1-10 czyli
najniższa możliwa wartość logarytmu tego stosunku wynosi
-1, a najwyższa +1.
Z tego wynika że pH każdego buforu zawarte jest w
zakresie:
pH = pK
a
± 1
Powyższe równanie nazywane jest zakresem buforowym.
10
Dlaczego bufory minimalizują zmiany pH po
wprowadzeniu do ich roztworu H
3
O
+
lub OH
-
?
Kwasowy składnik buforu zobojętnia OH
-
, natomiast
zasadowy składnik zobojętnia H
3
O
+
.
Zobojętnianie mocnych kwasów lub zasad zapobiega
znacznym zmianom pH w roztworze buforowym.
Zmienia się stosunek stężeń molowych C
zasada
/C
kwas
podczas gdy pH zmienia się nieznacznie.
11
Przykład skutków buforowania:
Po dodaniu 10 cm
3
1molowego HCl to 1000 cm
3
wody
pH spada z 7 do 2.
∆pH = 7 – 2 = 5
Po dodaniu 10 cm
3
1molowego HCl to 1000 cm
3
buforu
octanowego zawierającego 0.1molowy kwas octowy i
0.1molowy octan sodu pH spada z 4,77 to 4,68.
∆pH = 4,77 – 4,68 = 0,09
12
HCO
3
+ H
3
O H
2
CO
3
+ H
2
O
Mechanizm działania buforu węglanowego
H
2
CO
3
/HCO
3
-
po dodaniu mocnego kwasu (A) i
po dodaniu mocnej zasady (B).
(A)
(B)
H
2
CO
3
+ OH HCO
3
+ H
2
O
13
Nazwa
Składniki
pK
a
Zakres
buforowy
Octanowy
CH
3
COOH + CH
3
OO
_
4,7 3,7 – 5,7
Fosforanowy
H
3
PO
4
+ H
2
PO
4
_
2
1 – 3
Fosforanowy
H
2
PO
4
_
+ HPO
4
2
_
7
6 – 8
Fosforanowy
HPO
4
2
_
+ PO
4
3
_
12
11 – 13
Amonowy
NH
4
+
+ NH
3
9
8 – 10
Węglanowy
H
2
CO
3
+ HCO
3
_
6,5 5,5 – 7,5
Węglanowy
HCO
3
_
+ CO
3
2-
10
9 – 11
Przykłady buforów
14
Po dodaniu do buforu małej ilości mocnego kwas (np.
HCl) maleje stosunek C
zasada
/C
kwas
z powodu zużycia
pewnej ilości zasady potrzebnej na zobojętnienie HCl i
wzrostu stężenia słabego kwasu, który jest produktem
tego zobojętnienia.
pH = pK
a
+ log
C
zasada
- x
C
kwas
+ x
pH nieznacznie spada
15
Niewielki dodatek mocnej zasady (np. NaOH) daje skutek
odwrotny. Stosunek stężeń składników buforu
C
zasada
/C
kwas
rośnie ponieważ przybywa zasady kosztem
jej sprzężonego kwasu.
pH = pK
a
+ log
C
zasada
+ x
C
kwas
- x
pH nieznacznie rośnie
16
Dodawanie do buforu niewielkich ilości wody nie zmienia
stosunku stężeń składników C
zasada
/C
kwas
ponieważ ich
stężenia maleją tyle samo razy.
pH = pK
a
+ log
C
zasada
x
C
kwas
x
( x np. 0,5)
pH nie ulega zmianie
Dodanie dużej ilości wody np. rozcieńczenie buforu 10-
100 razy powoduje, że pH buforu zbliża się do 7.
17
Pojemność buforowa
Pojemność buforowa jest stosunkiem ilości moli H
+
lub
OH
-
dodanej do buforu do zmiany pH, którą ten dodatek
wywołuje.
∆n/V
(dm
3
)
∆pH
β
=
gdzie:
∆n - ilość moli dodanego mocnego kwasu lub zasady
(zwykle podaje się dla 1 dm³ bufora, (∆n/V)
∆pH - zmiana pH wywołana dodaniem tej ilości kwasu
lub zasady.
18
Pojemność buforowa jest wielkością nie mianowaną (nie
ma jednostek).
Jest liczbą, która informuje o zdolności danego buforu do
przeciwstawiania się zmianom pH.
Pojemność buforowa zależy od bezwzględnych wartości
stężenia buforu (rozumianego jako sumę stężeń
składników buforu) oraz stosunku stężen składników.
Nie zależy od objętości roztworu.
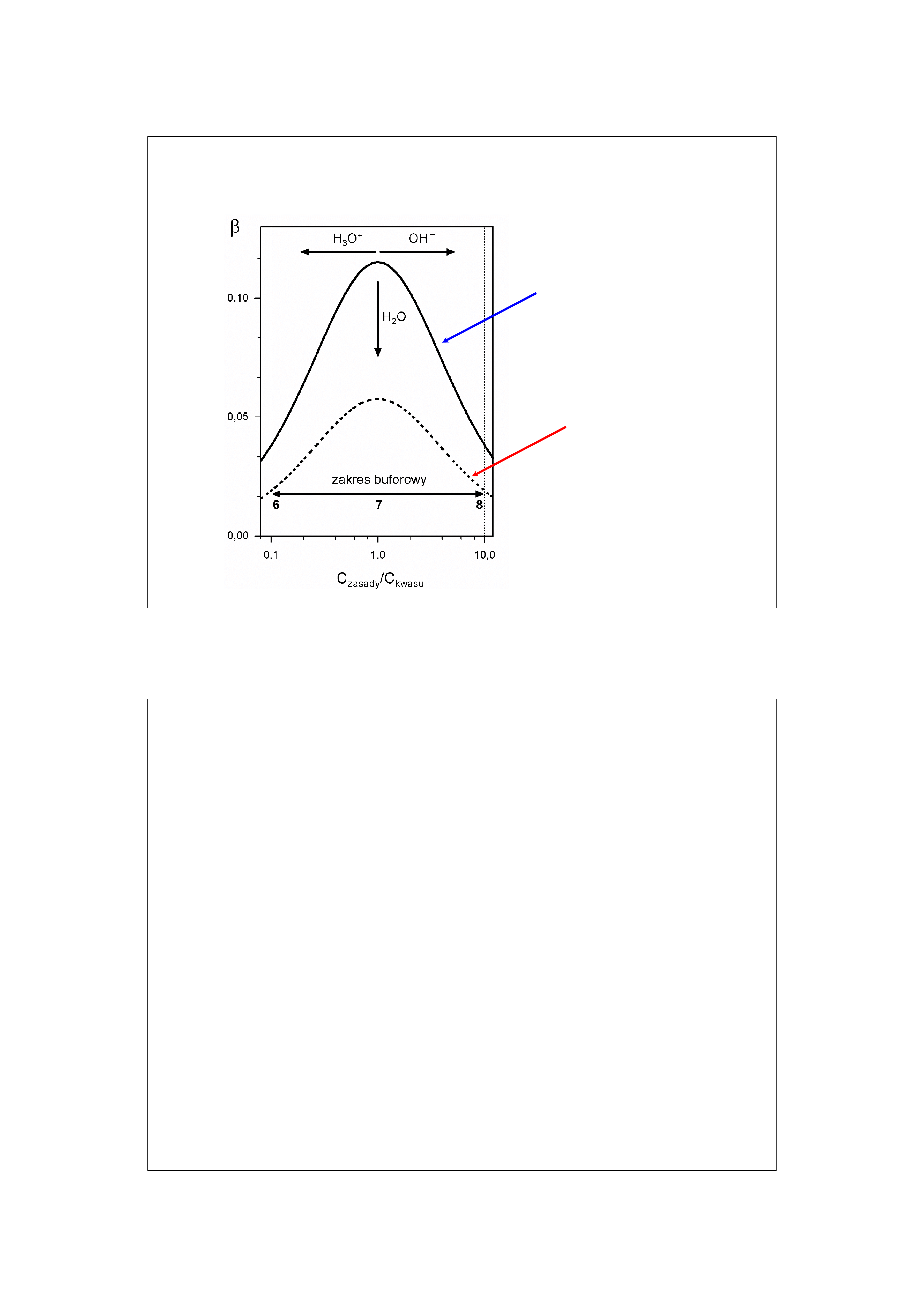
19
Zależność pojemności buforowej układu H
2
PO
4
-
/HPO
4
2
-
od stężenia i stosunku stężeń składników
Bufor 0,2 molowy
Bufor 0,1 molowy
20
Krzywe miareczkowania
Krzywe miareczkowania są graficznym przedstawieniem
zmian zachodzących w roztworze w czasie
miareczkowania.
Zależnie od rodzaju reakcji chemicznej stanowiącej
podstawę miareczkowania rozróżniamy krzywe:
alkacymetryczne
dla reakcji kwasowo-zasadowych,
(rejestrowane są zmiany pH),
potencjometryczne,
redoksymetryczne,
konduktometryczne.
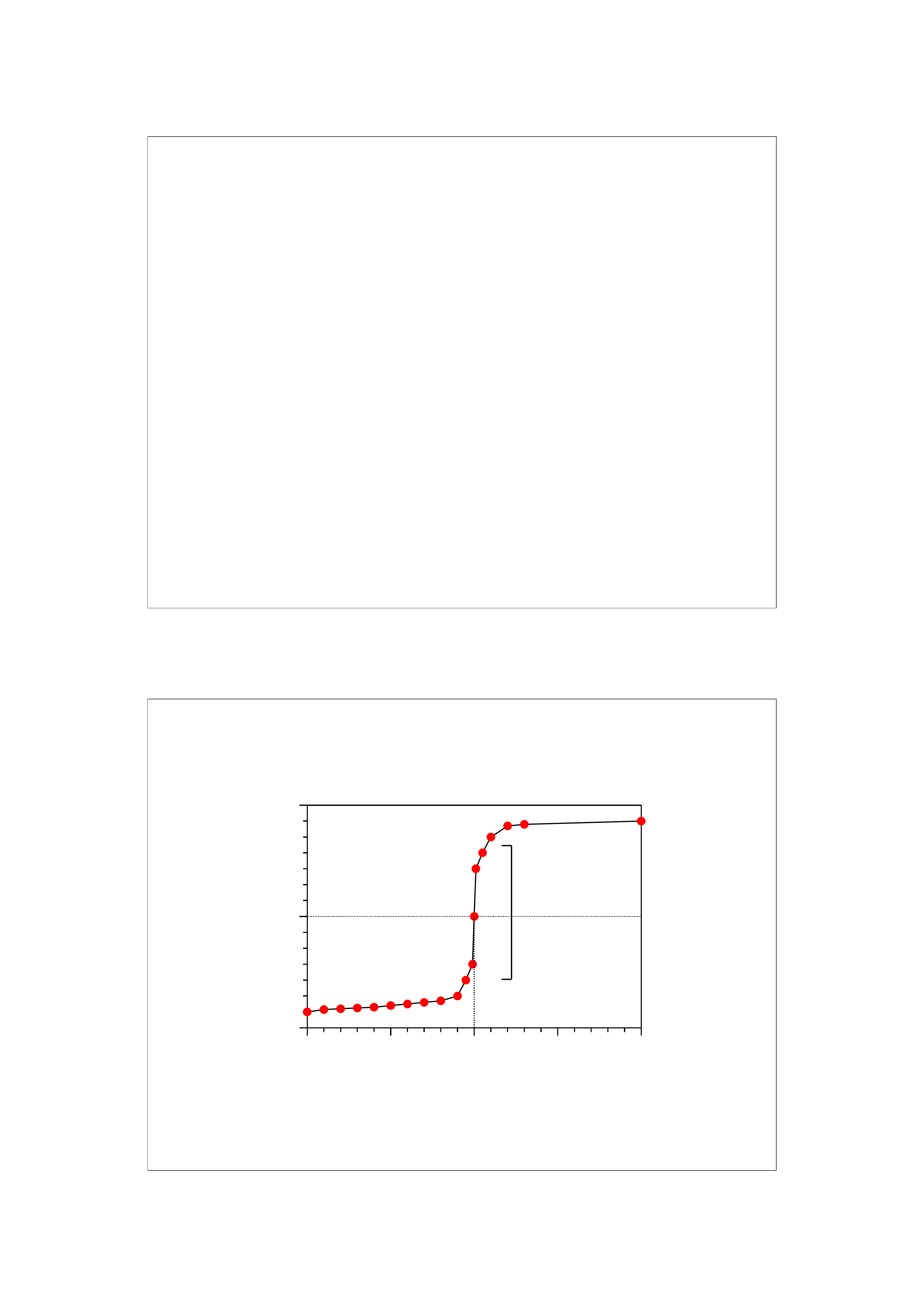
21
Charakterystyczne punkty i odcinki alkacymetrycz-
nych krzywych miareczkowania:
PR – punkt równoważnikowy, wskazuje miejsce na
krzywej odpowiadające idealnej równowadze między
ilością moli kwasu i zasady.
pK – punkt na krzywej gdzie pH roztworu jest równe
liczbowo wartości pK słabego kwasu.
Skok miareczkowania – odcinek krzywej w pobliżu
punkt równoważnikowego, gdzie obserwuje się
gwałtowne zmiany pH.
Zakres buforowy – odcinek krzywej obejmujący
zakres pK ± 1.
22
0
7
14
pH
0
5
10
15
20
V(ml)
x
Skok miareczkowania duży 7-10 jednostek, PR = 7
PR
Skok
miareczkowania
Miareczkowanie mocnego kwasu mocną zasadą
23
0
7
14
pH
0,0
0,5
1,0
1,5
Stosunek molowy HCl/ NAOH
PR
x
Miareczkowanie mocnej zasady mocnym kwasem
Skok miareczkowania duży 7-10 jednostek, PR = 7
24
0
7
14
pH
0
5
10
15
20
NaOH (cm )
3
x
pK
a
PR
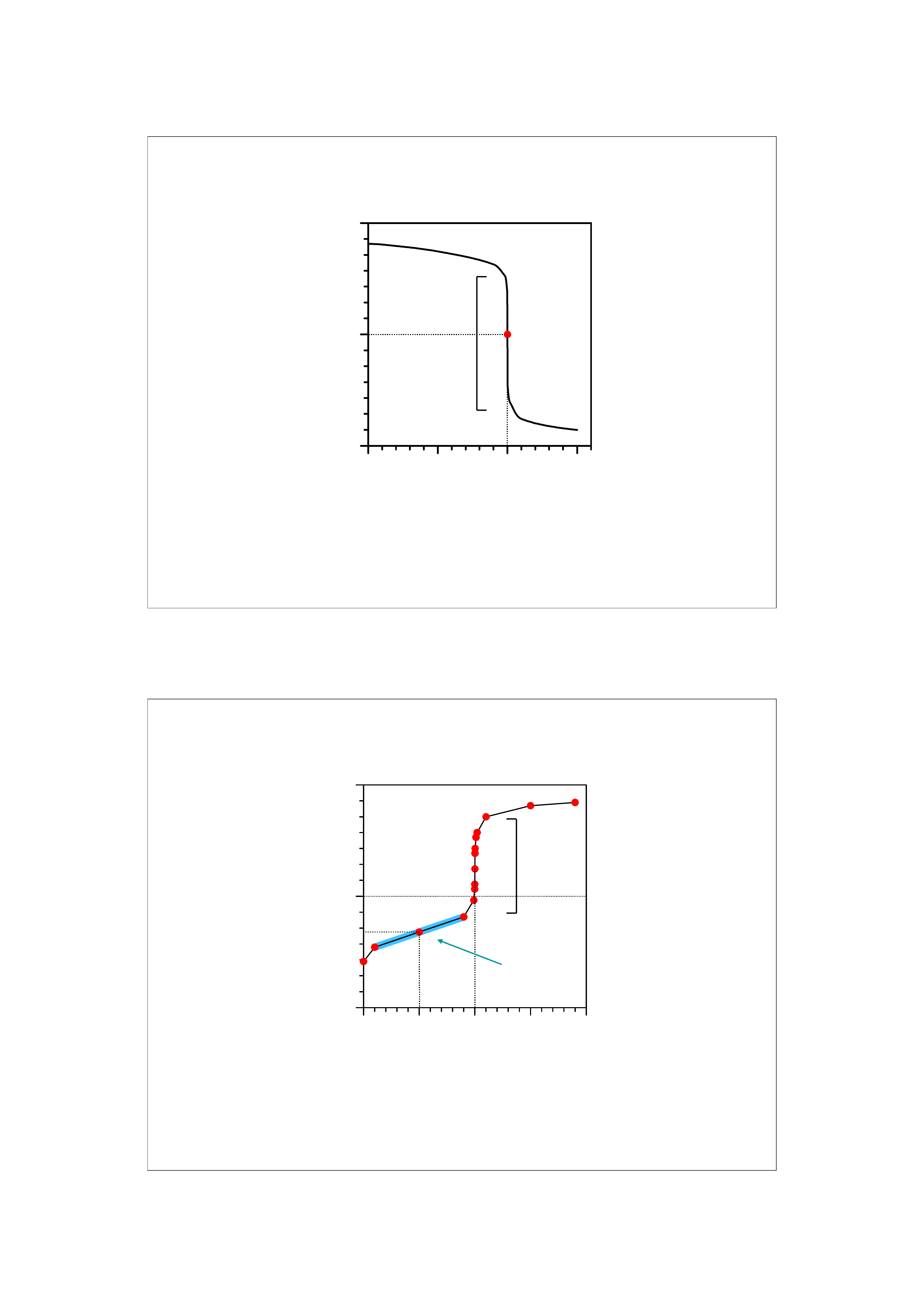
Miareczkowanie słabego kwasu mocną zasadą
Skok miareczkowania mały 2-5 jednostek, PR > 7
Zakres buforowy
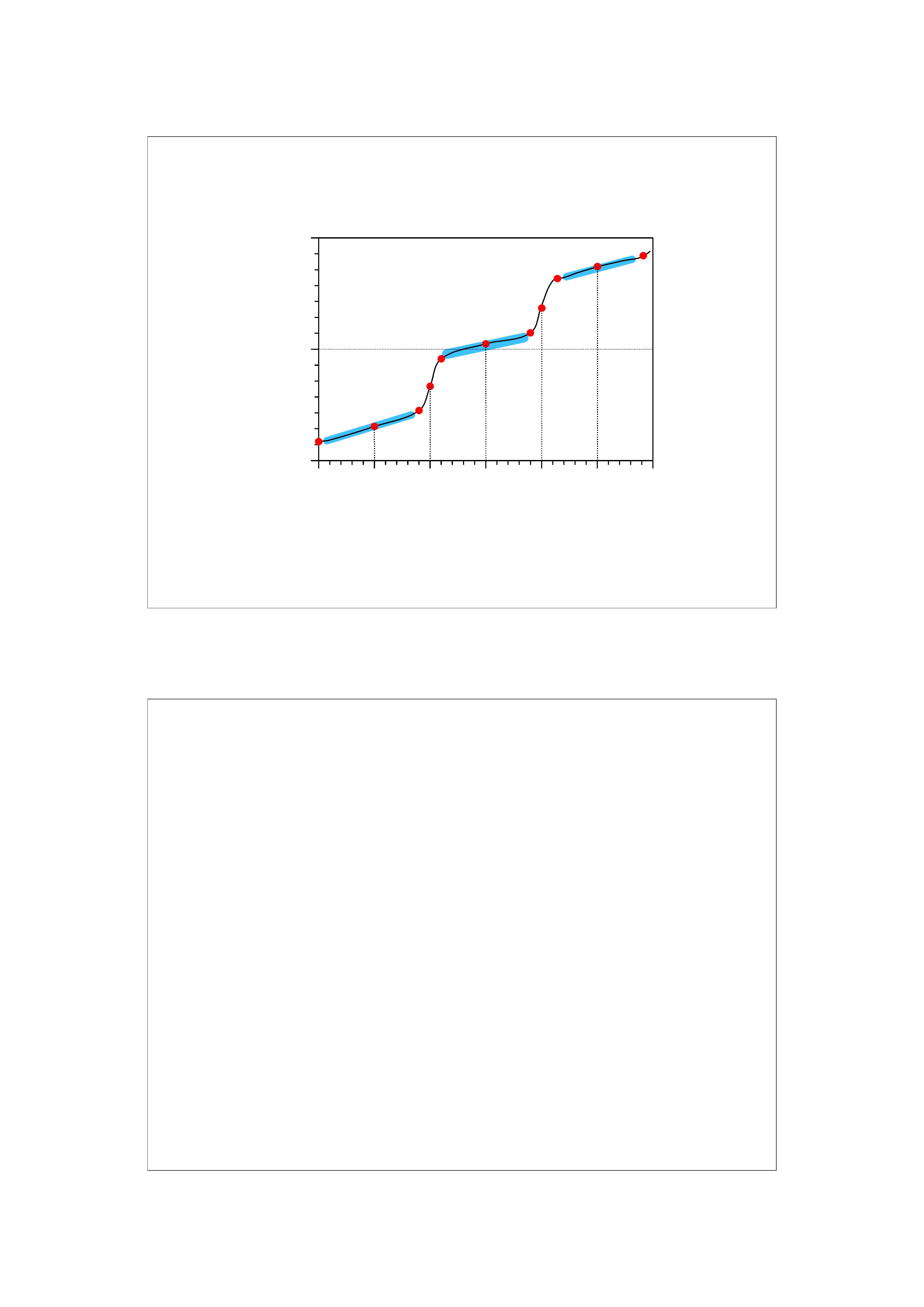
25
0
7
14
pH
0,0
0,5
1,0
1,5
2,0
2,5
3,0
Stosunek molowy NaOH/H PO
3
4
x
x
x
x
x
pK
1
pK
2
pK
3
PR1
PR2
Miareczkowanie kwasu trójprotonowego mocną zasadą
26
Krzywe miareczkowania mocnych kwasów i zasad
mają tylko punkt równoważnikowy i skok
miareczkowania.
Krzywe miareczkowania słabych jednoprotonowych
kwasów i słabych jednowodorotlenowych zasad mają
jeden PR, jedną wartość pK i jeden zakres buforowy.
Krzywe miareczkowania dwuprotonowych kwasów i
dwuwodorotlenowych zasad mają dwa PR, dwie
wartości pK i dwa zakresy buforowy.
Itd.
Temperatura krzepnięcia i temperatura wrzenia
roztworów
Roztwory różnią się od rozpuszczalników temperaturami
krzepnięcia i wrzenia.
W porównaniu z czystym rozpuszczalnikiem roztwory
mają niższą temperaturę krzepnięcia, a wyższą
temperaturę wrzenia.
Fakty te stały się podstawą do sformułowania prawa
Raoulta.
27
Prawo Raulta
Prężność pary nasyconej nad roztworem równa się
prężności pary nasyconej nad czystym
rozpuszczalnikiem, pomnożonej przez ułamek molowy
rozpuszczalnika.
p = p
0
.
x
gdzie p oznacza prężność (ciśnienie) cząstkowe
rozpuszczalnika nad roztworem, p0 – ciśnienie czystego
rozpuszczalnika, x = ułamek molowy rozpuszczalnika.
Ponieważ ułamek molowy jest zawsze mniejszy od 1, to
p < p
0
28
Różnica między temperaturą krzepnięcia roztworu, a
temperaturą krzepnięcia rozpuszczalnika (DTk) zależy od
stężenia substancji rozpuszczonej i właściwości
rozpuszczalnika.
∆Tk = Tk
o
– Tk’
Gdzie:
Tk
o
– temperatura krzepnięcia czystego rozpuszczalnika
Tk’ – temperatura krzepnięcia roztworu
∆Tk jest wprost proporcjonalna do stężenia molalnego
(
Uwaga! Nie molowego
) roztworu. Czyli
∆Tk = K
.
C
M
gdzie K – stała krioskopowa, Cm – stężenie molalne
29
Współczynnik proporcjonalności w powyższym równaniu
nazywany jest stałą krioskopową. Stała krioskopowa K
jest molalnym obniżeniem temperatury krzepnięcia
roztworu.
Zależy ona wyłącznie od właściwości rozpuszczalnika.
Rozpuszczalnik Stała krioskopowa (
o
C)
Woda
1,86
Benzen
4,90
Czterochlorek węgla
26
Rodzaj substancji rozpuszczonej nie ma znaczenia dla
wielkości
∆Tk.
30
Różnica między temperaturą wrzenia roztworu, a
temperaturą wrzenia rozpuszczalnika (
∆Tw) zależy od
stężenia substancji rozpuszczonej i właściwości
rozpuszczalnika.
∆Tw = Tw’ – Tw
0
Gdzie:
Tw
o
– temperatura wrzenia czystego rozpuszczalnika
Tw’ – temperatura wrzenia roztworu
∆Tw jest wprost proporcjonalna do stężenia molalnego
(
Uwaga! Nie molowego
) roztworu. Czyli
∆Tw = E
.
C
M
gdzie E – stała ebulioskopowa, Cm – stężenie molalne
31
Stała ebulioskopowa E jest molalnym obniżeniem
temperatury krzepnięcia roztworu.
Zależy ona wyłącznie od właściwości rozpuszczalnika.
Rozpuszczalnik Stała ebulioskopowa (
o
C)
Woda
0,52
Etanol
1,19
Eter dietylowy
2,11
Rodzaj substancji rozpuszczonej nie ma znaczenia dla
wielkości zarówno
∆Tk jak i ∆Tw . Czyli różne substancje
powodują bardzo zbliżone zmiany Tk i Tw jeżeli są
rozpuszczone w tym samym rozpuszczalniku i mają
jednakowe stężenia.
32