Regresja liniowa

Jeżeli badamy populację ze względu na dwie
cechy X i Y (lub więcej cech) to można
zastanawiać się, czy zmienną Y (zależną) da
się przedstawić jako liniową funkcję zmiennej
X (niezależnej) ?
Zależność liniową można przedstawić jako

Y = b X + a

b = b

yx

- współczynnik regresji liniowej Y na

X

współczynnik kierunkowy prostej

a – współczynnik „przesunięcia” (wyraz
wolny)

Regresja liniowa

Model (matematyczny) regresji liniowej:

y

i

= b

yx

x

i

+ a + e

i

(i =1

i

.......n)

y

i

- wartość i-tej obserwacji zmiennej zależnej Y

x

i

- wartość i-tej obserwacji zmiennej

niezależnej X
e

i

- wartość błędu losowego, związanego z i-tą

obserwacją tzn. z y

i

Zakłada się, że x

i

są znane bez błędu

Problemy do rozwiązania:
a) estymacja parametrów b

yx

i a

b) ocena istotności współczynnika regresji

liniowej (tzn. weryfikacja hipotezy H

0

: b

yx

= 0)

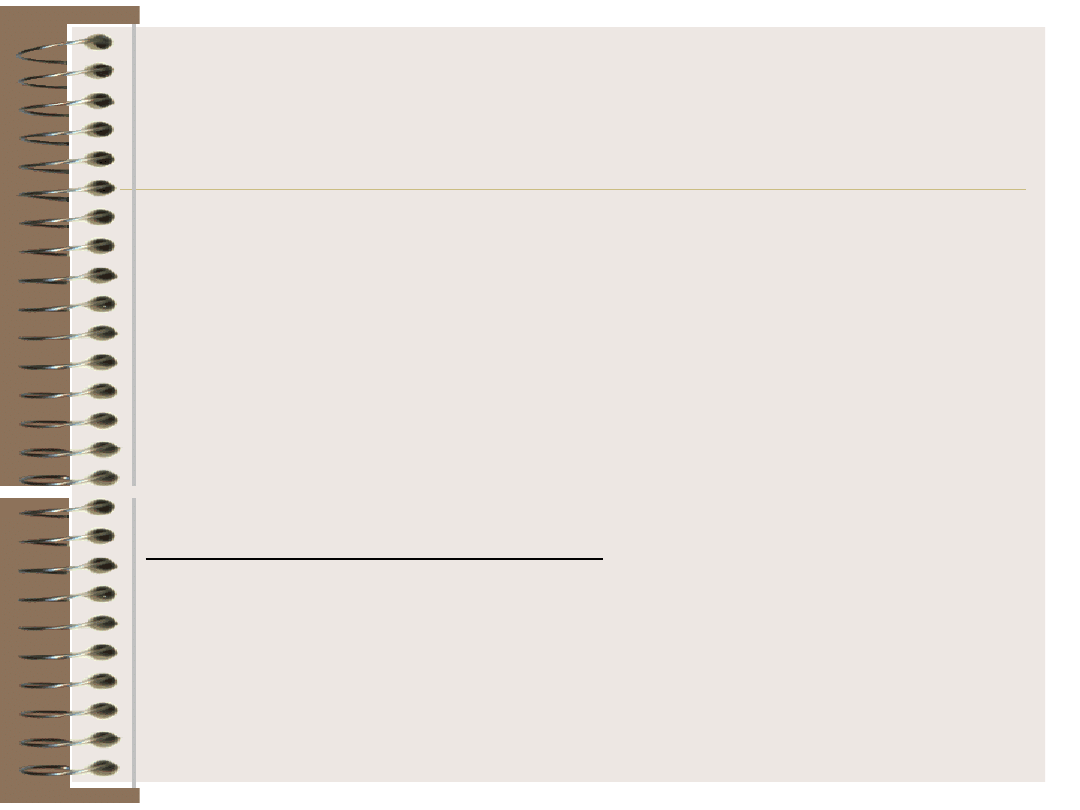
Przykład zależności liniowej

x

i

y

i

Prosta regresji

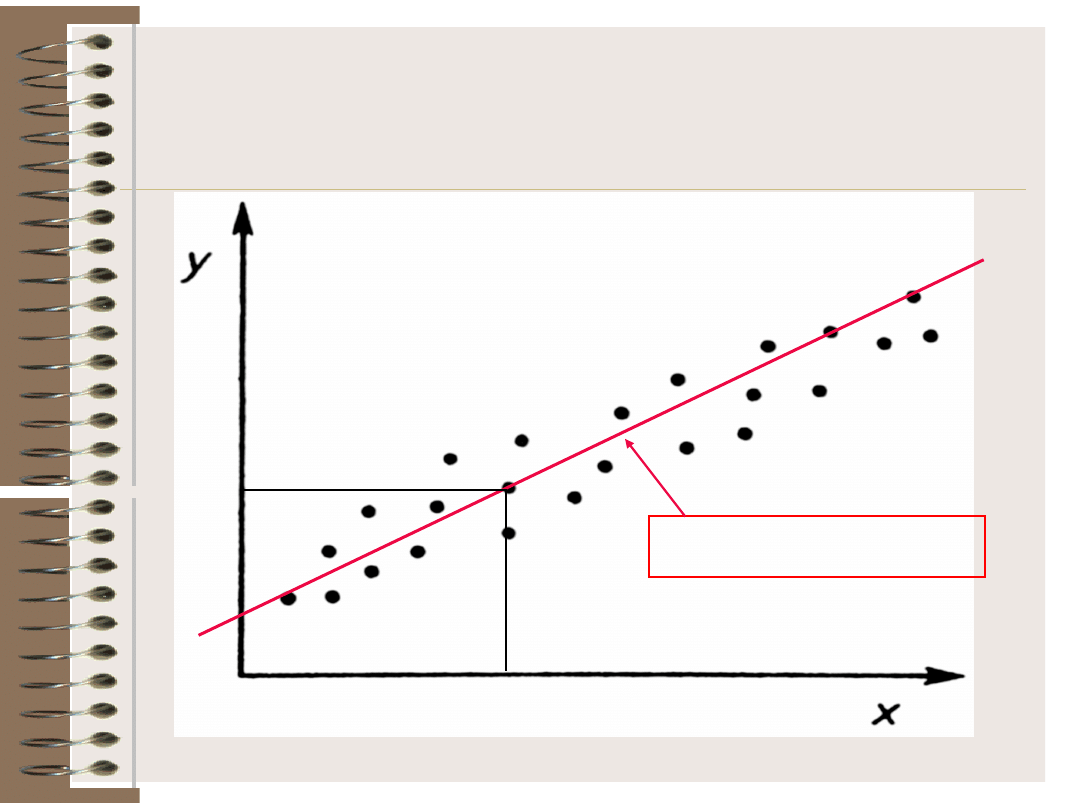
Przykład zależności

krzywoliniowej

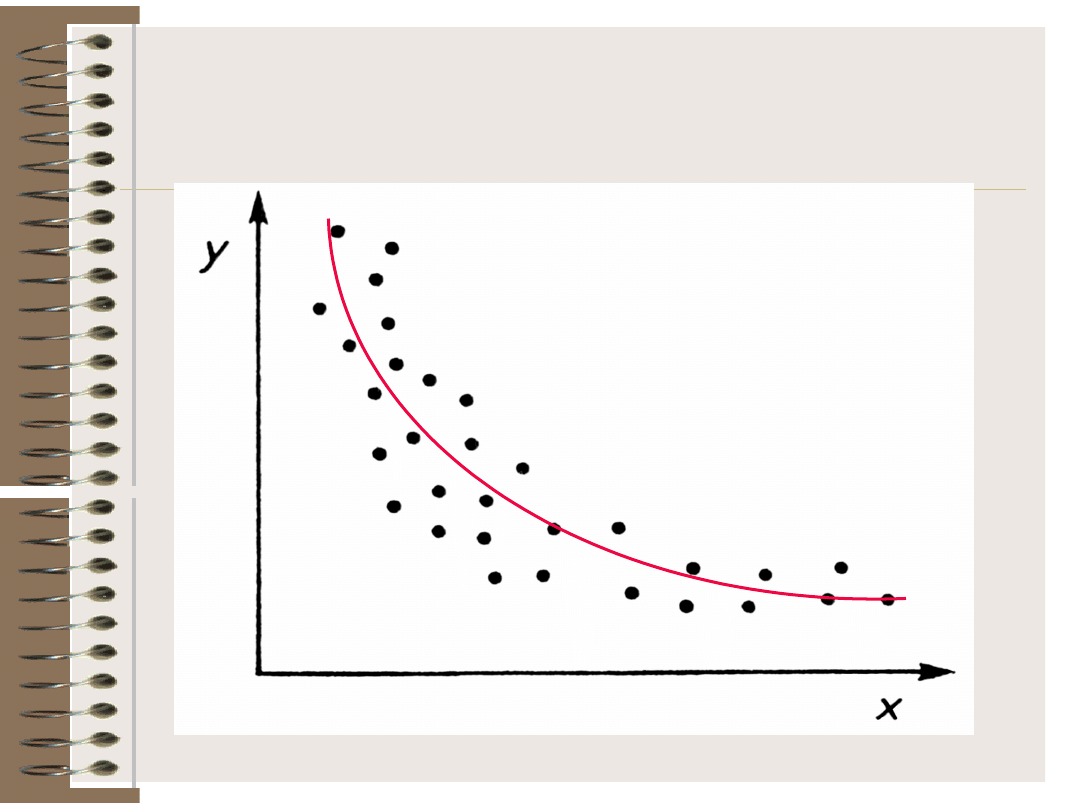
Przykład braku zależności

Regresja liniowa

Przykład: Badano związek między dzienną

wydajnością mleka (Y) krów pewnej rasy, a

ilością paszy treściwej (X) spożywanej przez

krowy w ciągu dnia. Czy istnieje zależność

liniowa między wydajnością mleka (Y) a

ilością paszy (X) ?

Próba: n – par liczb (x

i

, y

i

)

Dla i-tej krowy:

x

i

– pasza spożyta przez i-tą krowę

y

i

– dzienna wydajność mleka i-tej krowy

oczekiwana wydajność dzienna: E(y

i

) = b

yx

x

i

+

a

b

yx

–

współczynnik

regresji

dziennej

wydajności (Y) na zużytą paszę (X)

Regresja liniowa

Błąd

(e

i

),

jaki

popełniamy

przy

szacowaniu dziennej wydajności na
podstawie prostej regresji:

e

i

= y

i

– E(y

i

) = y

i

– ( b

yx

x

i

+

a )

czyli stanowi różnicę między wartością
obserwowaną (y

i

) a oczekiwaną

(E(y

i

)),

przy założeniu zależności liniowej
zmiennej Y od zmiennej X

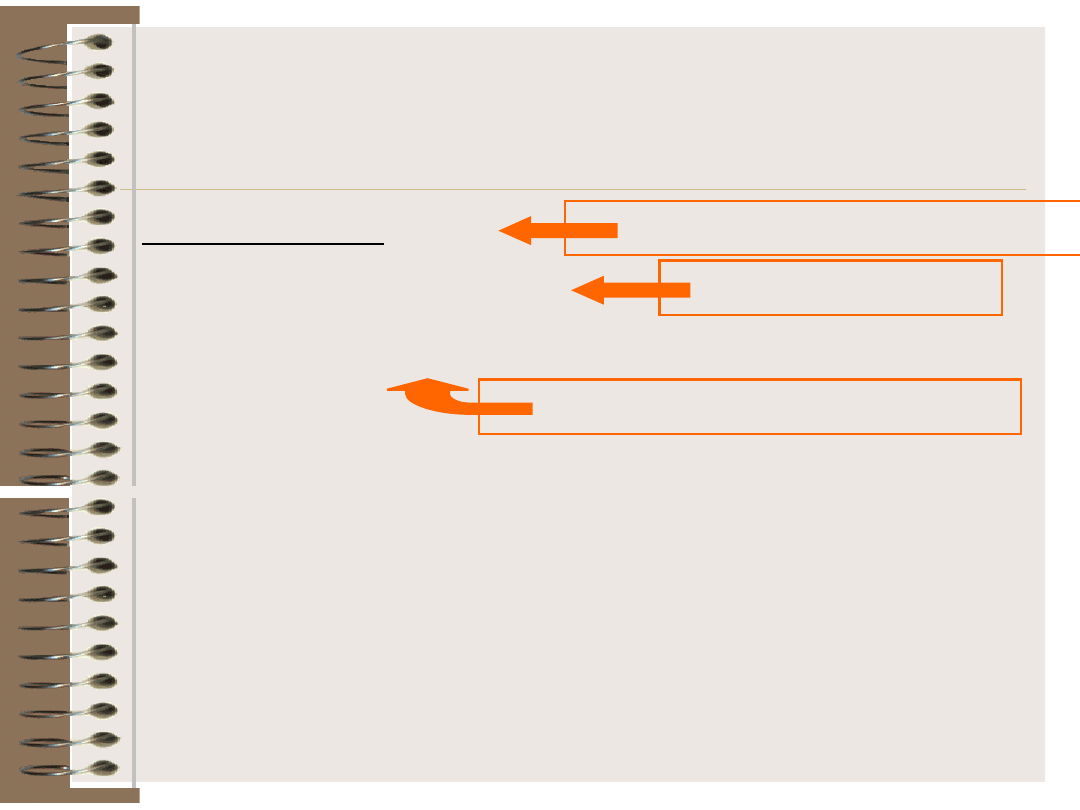
Regresja liniowa

Założenia: E(e

i

)=0

var(e

i

) =



2

cov(e

i

,e

j

) = 0 dla i



j

Oszacowania a i b (tzn. )
wyznaczamy metodą najmniejszych
kwadratów minimalizując funkcję S(a,b)
będącą sumą kwadratów błędów tzn.

bˆ

i

aˆ

2

n

1

i

i

i

2

n

1

i

i

i

n

1

i

2

i

)

a

bx

y

(

]

)

a

bx

(

y

[

e

)

b

,

a

(

S



























wartość oczekiwana błędów

kowariancja między błędami

wariancja błędów

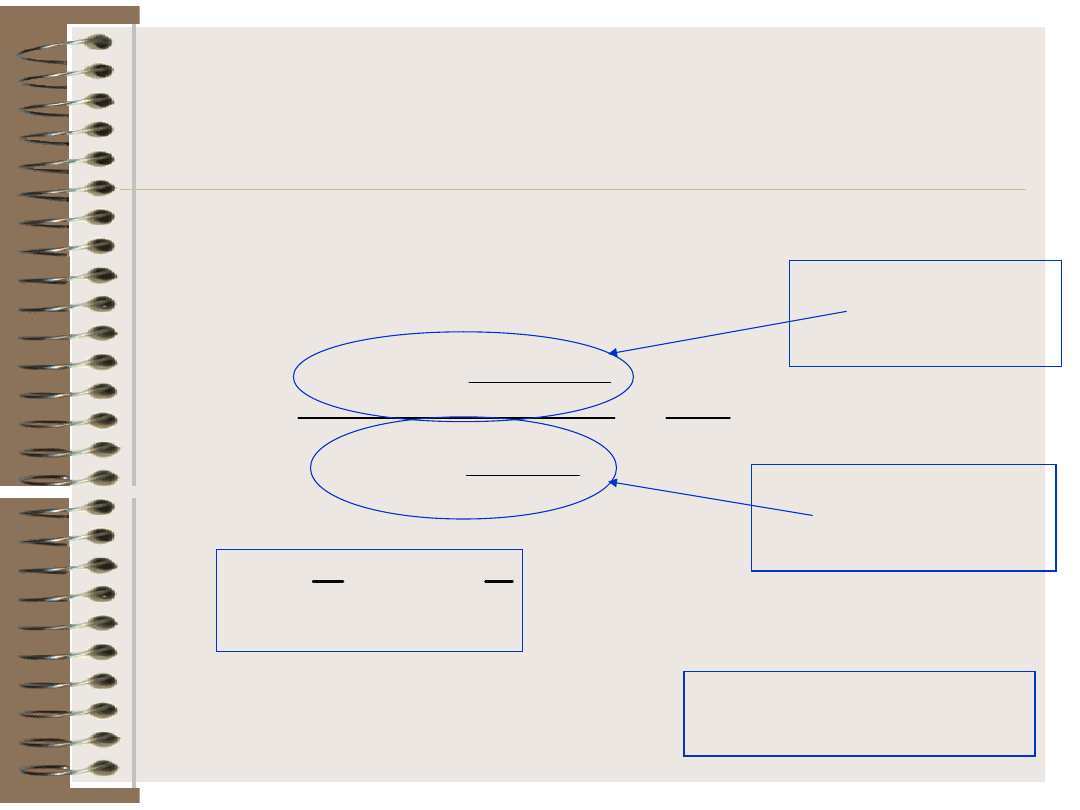
Regresja liniowa

Jako wynik minimalizacji uzyskujemy

oszacowania parametrów prostej regresji Y na X





2

x

2

xy

n

x

2

i

n

y

x

i

i

yx

s

s

x

y

x

b

ˆ

2

i

i

i











 





x

b

ˆ

y

aˆ

yx





x

b

ˆ

aˆ

)

y

(

E

yˆ

yx







iloczyn
mieszany

suma
kwadratów

Równanie regresji

Regresja liniowa

Interpretacja współczynnika regresji
:

wskazuje, o ile zmieni się (wzrośnie
lub zmaleje) wartość cechy Y gdy wartość
cechy X wzrośnie o jedną jednostkę

yx

b

ˆ

yx

b

ˆ

Regresja liniowa

krowa

pasza

(kg)

mleko

(kg)

i

x

i

y

i

x

i

y

i

x

i

2

1

12

35,0

420,0

144

2

5

17,5

87,5

25

3

9

25,0

225,0

81

4

1

12,5

12,5

1

5

7

27,5

192,5

49

6

3

17,5

52,5

9

suma

37

135,0

990,0

309

Regresja liniowa





95

,

1

83

,

80

5

,

157

17

,

228

309

5

,

832

990

309

990

x

y

x

b

ˆ

6

)

37

(

6

)

135

(

)

37

(

n

x

2

i

n

y

x

i

i

yx

2

2

i

i

i



























 







48

,

10

03

,

12

5

,

22

17

,

6

95

,

1

5

,

22

x

b

ˆ

y

aˆ

17

,

6

x

5

,

22

y

yx

6

37

6

135

























Obliczanie parametrów prostej regresji:

Σx

i

Σy

i

Σx

i

y

i

Σx

i

2

37

135 990 309

Regresja liniowa

Równanie prostej regresji:

48

,

10

x

95

,

1

aˆ

x

b

ˆ

yˆ

yx









Interpretacja współczynnika regresji
Jeśli ilość paszy (X) wzrośnie o jeden kg
(jedną jednostkę) to ilość mleka (Y)
wzrośnie o 1,95 kg.

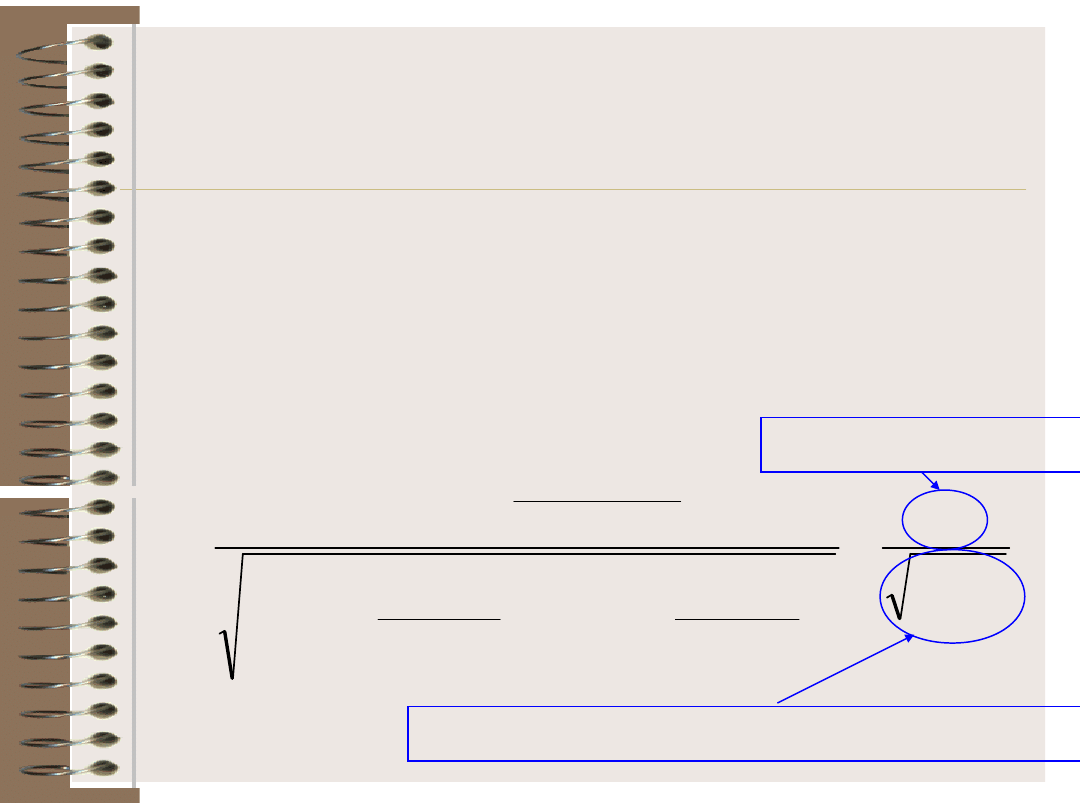
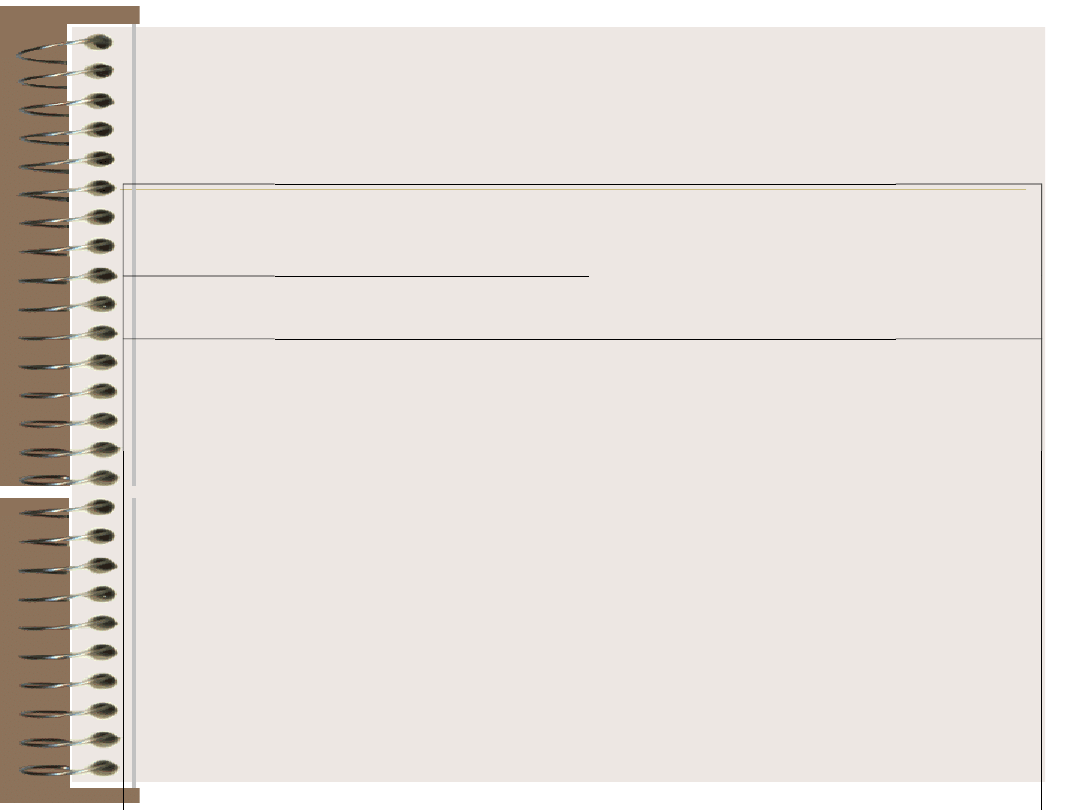
Współczynnik korelacji

Miarą związku liniowego między cechami
X i Y jest współczynnik korelacji liniowej
(ozn. r). Oblicza się go według wzoru:

2

y

2

x

xy

2

i

2

i

2

i

2

i

i

i

i

i

s

s

s

)

n

)

y

(

y

n

)

x

(

x

n

y

x

y

x

rˆ























































kowariancja

pierwiastek z iloczynu wariancji

Współczynnik korelacji -

przykład

krowa pasza

(kg)

mleko

(kg)

i

x

i

y

i

x

i

y

i

x

i

2

y

i

2

1

12

35,0

420,0

144 1225,

0

2

5

17,5

87,5

25

306,2

5

3

9

25,0

225,0

81

625,0

4

1

12,5

12,5

1

156,2

5

5

7

27,5

192,5

49

756,2

5

6

3

17,5

52,5

9

306,2

5

suma

37

135,0 990,0

309 3375,

0

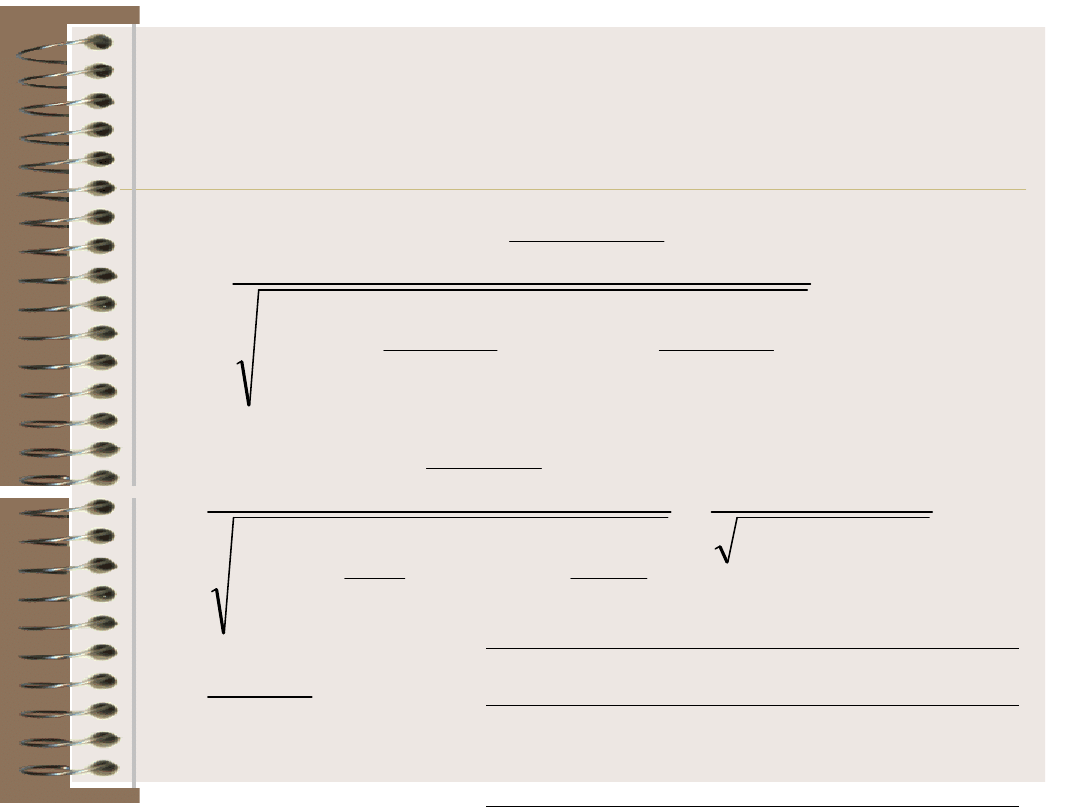
Współczynnik korelacji -

przykład

95

,

0

17

,

165

5

,

157

5

,

337

83

,

80

5

,

157

6

135

3375

6

37

309

6

135

37

990

)

n

)

y

(

y

n

)

x

(

x

n

y

x

y

x

rˆ

2

2

2

i

2

i

2

i

2

i

i

i

i

i



































































































Σx

i

Σy

i

Σx

i

y

i

Σx

i

2

Σy

i

2

37 135 990 309 337

5

Współczynnik korelacji

Własności współczynnika korelacji liniowej

:

1. r jest liczbą bez miana

3. Jeśli r = 0 to oznacza, że między cechami
nie występuje zależność liniowa

4. Jeśli r = -1 lub r = 1 to oznacza, że jedna
cecha jest funkcją liniową drugiej cechy

2. -1 ≤ r ≤ 1 tzn. |r| ≤1

Współczynnik korelacji

Własności współczynnika korelacji liniowej:

5. Jeśli r > 0 to oznacza, że wraz ze

wzrostem wartości jednej z cech
wzrastają wartości drugiej cechy
(funkcja rosnąca)

6. Jeśli r < 0 to oznacza, że wraz ze

wzrostem wartości jednej z cech
maleją wartości drugiej cechy
(funkcja malejąca)

Współczynnik korelacji

Własności współczynnika korelacji liniowej:

7. Niska korelacja jeśli | r |  0,4

8. Średnia korelacja jeśli 0,4 < | r |

< 0,8

9. Wysoka korelacja jeśli | r | 

0,8

10. Korelacja zupełna jeśli | r | =

1

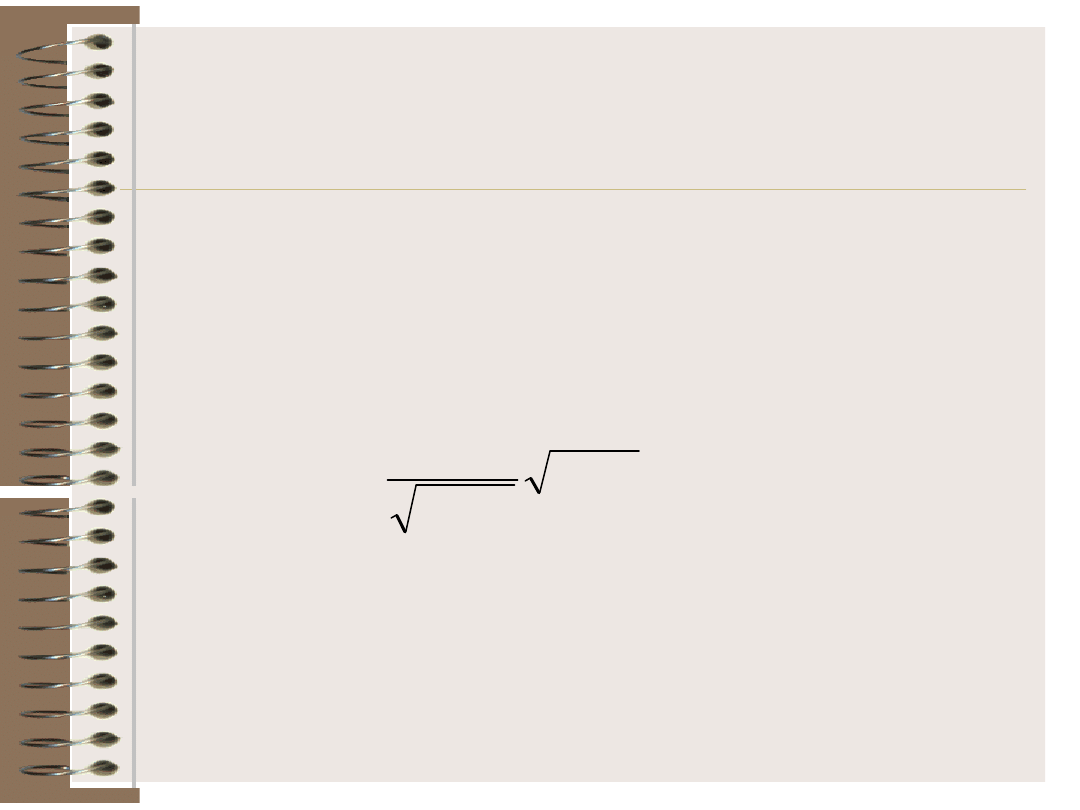
Testowanie istotności

współczynnika korelacji (

H

0

:

r=0

vs

H

A

: r0

)

1. Małe próby (n < 30)

Obliczamy wartość statystyki o

rozkładzie t-Studenta z (n-2)
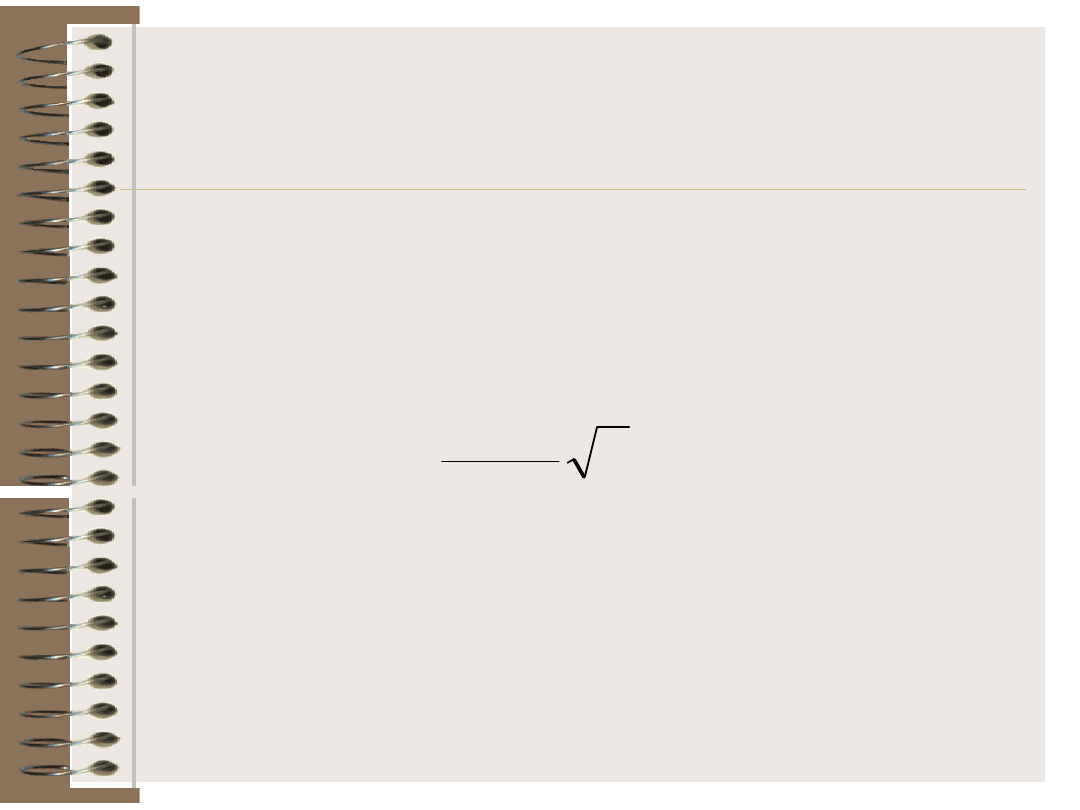
stopniami swobody jako:

2

n

r

1

r

t

2

0







Jeśli | t

0

| > t

α

to H

0

odrzucamy na poziomie

istotności α czyli między cechami X i Y
istnieje istotna współzależność liniowa

Testowanie istotności

współczynnika korelacji (

H

0

:

r=0

vs

H

A

: r0

)

2. Duże próby (n > 30)
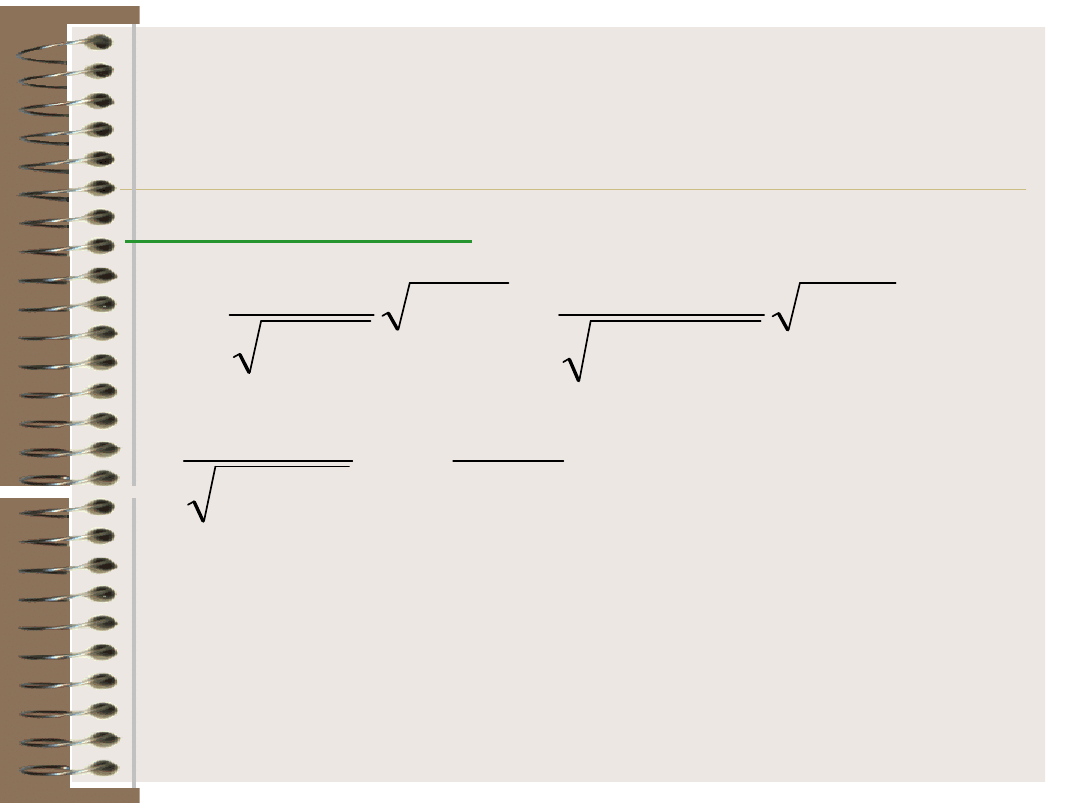
Obliczamy wartość statystyki o
rozkładzie normalnym jako:

n

r

1

r

u

2

0





Jeśli | u

0

| > u

α

to H

0

odrzucamy na poziomie

istotności α czyli między cechami X i Y
istnieje istotna współzależność liniowa

Testowanie istotności

współczynnika korelacji -

przykład

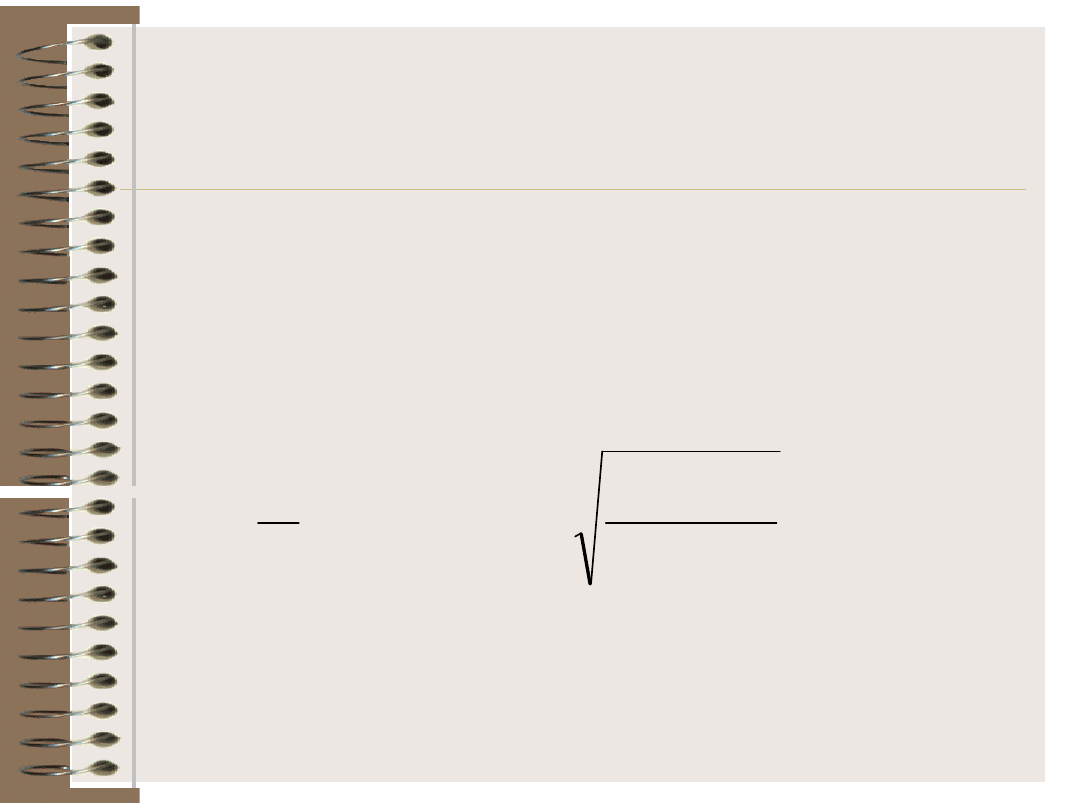
Przypadek 1. Małe próby (n = 6)

09

,

6

2

045

,

3

2

312

,

0

95

,

0

2

0975

,

0

95

,

0

2

6

95

,

0

1

95

,

0

2

n

r

1

r

t

2

2

0





























t

α

= t

0,05

= 2,776 dla (n-2) = 4 stopni

swobody

|t

0

|> t

0,05

to odrzucamy H

0

tzn. r jest istotnie różny

od zera czyli występuje zależność liniowa obu cech

Współczynnik determinacji

Współczynnik determinacji

wskazuje, jaka część zmienności
cechy Y (traktowanej jako zmienna
zależna) zależy od cechy X
(traktowanej jako zmienna
niezależna)

Współczynnik determinacji

(

r

2

)

jest kwadratem współczynnika
korelacji (r) i przyjmuje wartości z
przedziału <0,1> tzn.

0 ≤ r

2

≤ 1

Współczynnik determinacji -

przykład

r

2

= 0,95

2

= 0,9025

0,9025 · 100% = 90,25%

tzn. że ponad 90% zmienności w
wydajności mleka (Y) jest
spowodowane wpływem paszy (X),
a jedynie niecałe 10% -
zmiennością przypadkową

Testowanie istotności regresji

H

0

: b=0

α – poziom istotności

H

A

: b0

Zakładamy normalność rozkładu błędów
(e).
Aby zweryfikować

H

0

obliczamy wartość

która jest wartością statystyki t-Studenta
o (n-2) stopniach swobody

2

x

2

2
x

2

y

b

b

0

s

)

2

n

(

b

s

s

s

gdzie

s

b

t









Testowanie istotności regresji

Jeśli H

0

jest prawdziwa (tzn. b=0) to

znaczy, że nie istnieje regresja liniowa

cechy Y na cechę X

Jeśli zachodzi nierówność |t

0

| < t

α

to nie

mamy podstaw do odrzucenia hipotezy

zerowej H

0

Jeśli zachodzi nierówność |t

0

| > t

α

to

odrzucamy hipotezę zerową i

przyjmujemy hipotezę alternatywną H

A

co oznacza, że w populacji istnieje

zależność liniowa Y od X

Testowanie istotności regresji

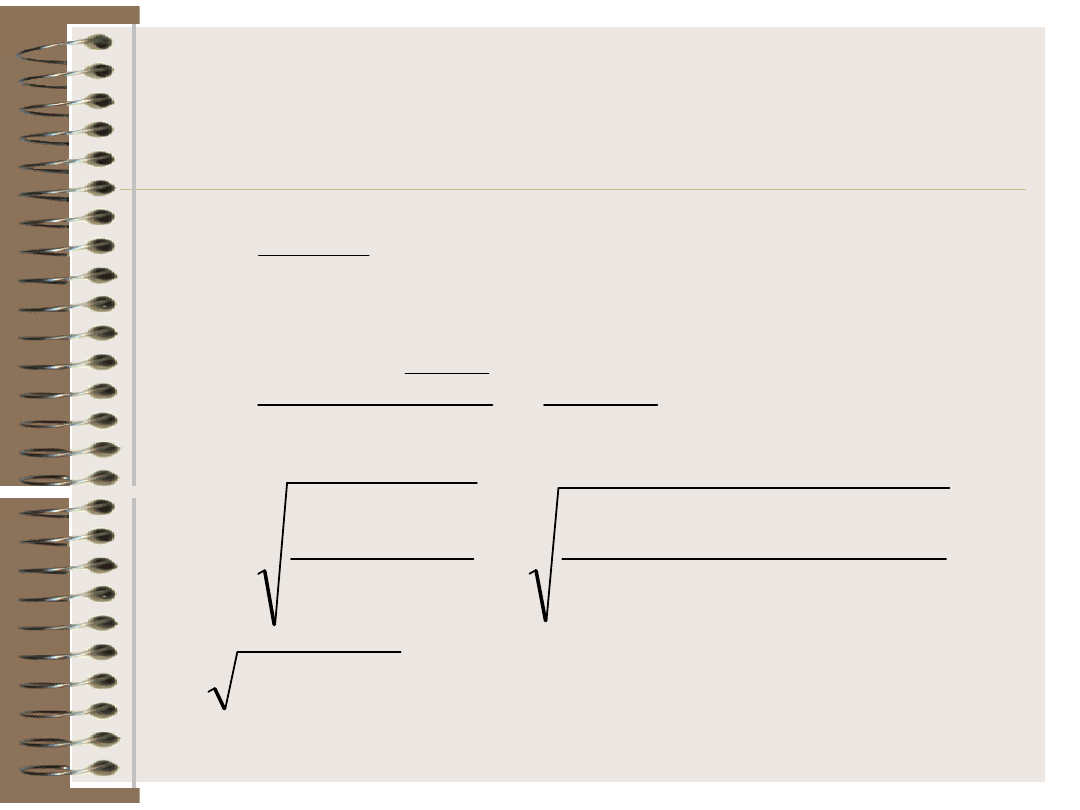
3055

,

0

09323

,

0

166

,

16

4

95

,

1

166

,

16

5

,

67

s

)

2

n

(

b

s

s

s

5

,

67

5

5

,

337

5

3375

s

166

,

16

5

83

,

80

s

2

2

x

2

2

x

2

y

b

6

)

135

(

2

y

2

x

2































Testowanie istotności regresji

383

,

6

3055

,

0

95

,

1

s

b

t

b

0







t

α

= t

0,05

= 2,776 dla (n-2)=4 stopni swobody

|t

0

| = 6,383 > t

0,05

= 2,776 a

zatem H

0

odrzucamy i przyjmujemy H

A

mówiącą,
że współczynnik regresji b jest
istotnie
różny od zera