Regresja i korelacja

(

materiał z internetu do wykorzystania jako powtórzenie

)

materiały dydaktyczne

Regresja liniowa

W populacji generalnej rozważamy dwie zmienne X i Y takie, że zmienna

losowa Y ma rozkład normalny z parametrami

μ = m(x) i σ = σ

y/x

zaś zmienna X jest zmienną rzeczywistą (lub losową).

Wartość oczekiwana zmiennej losowej Y jest funkcją liniową zmiennej X

postaci:

m(x) = b + ax.

Wariancja σ

2y/x

oznacza, że zmienność cechy Y jest niezależna od zmiennej X

(jest stała).

Estymacja parametrów modelu

Nieznane parametry modelu

y = b +ax

muszą być estymowane na podstawie odpowiedniej próby losowej.
Zagadnienie estymacji parametrów modelu sprowadza się do takiego
dobrania parametrów aby suma kwadratów odległości każdego
punktu empirycznego od prostej regresji była jak najmniejsza.

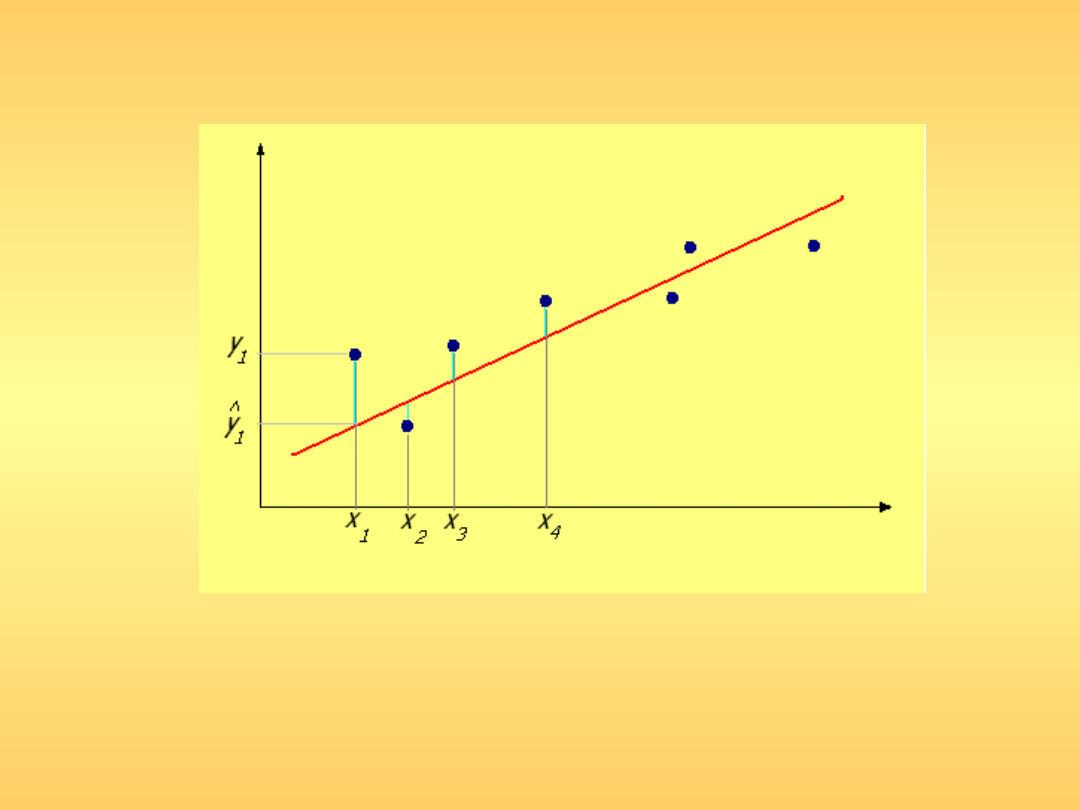
Estymacja parametrów modelu

gdzie (y

i

, x

i

) oznacza elementy próby losowej.

Estymacja parametrów modelu

Każdą obserwację empiryczną można zapisać jako:

y

i

= b + a·x

i

+

i

.

Problem estymacji sprowadza się do wyznaczenia minium funkcji s danej
wzorem.























n

i

i

i

n

i

i

x

a

b

y

b

a

s

1

2

1

2

)

(

)

,

(



Estymacja parametrów modelu

Funkcja s jest funkcją dwóch niewiadomych (a i b), aby znaleźć

minimum tej funkcji musimy wyznaczyć pochodne cząstkowe funkcji s

względem obu niewiadomych:

i przyrównać te pochodne do zera.































n

i

i

i

i

a

n

i

i

i

b

x

a

b

y

x

s

x

a

b

y

s

1

1

)

(

2

'

)

(

2

'

Otrzymujemy układ równań postaci:





































0

)

ˆ

ˆ

(

0

)

ˆ

ˆ

(

1

1

n

i

i

i

i

n

i

i

i

x

a

b

y

x

x

a

b

y

x

xy

x

x

x

x

y

y

a

n

i

i

n

i

i

i

var

cov

)

(

)

)(

(

ˆ

1

2

1



















x

a

y

b







ˆ

ˆ

Estymacja parametrów modelu

Rozwiązując mamy:

Istotność równania regresji

Istotność wyestymowanego równania regresji badamy weryfikując
hipotezę zerową

H

0

: a = 0 wobec H

1

: a ≠ 0

Przy prawdziwości H

0

statystyka:

ma rozkład t Studenta z liczbą stopni swobody równej n - 2. Wyrażenie
jest oszacowaniem wariancji odchyleń od regresji z próby:

x

s

a

s

a

t

x

y

b

var

ˆ

ˆ

2

/

ˆ





s

y x

/

2

2

cov

ˆ

var

ˆ

2

/

2

/









n

xy

a

y

s

x

y

x

y



Istotność współczynnika regresji

Jeżeli |t| > t

kryt

, to H

0

: a = 0 odrzucamy jako statystycznie mało

prawdopodobną i mówimy o istotności wyznaczonego równania

regresji.

Jeśli nie to wyniki próby nie przeczą hipotezie H

0

i funkcja regresji

jest stała.

Współczynnik regresji mówi nam o tym, o ile zmieni się zmienna

zależna y przy wzroście zmiennej x o jednostkę.

Dopasowanie prostej regresji

Odchylenie obserwowanej wartości od jej średniej można zapisać

następująco:



 



y y

y y

y y

i

i

i

i















Pierwszy składnik to część całkowitego odchylenia zmiennej y, która

jest wyjaśniona regresją liniową y względem x, drugi składnik to

część zmienności całkowitej, która nie została wyjaśniona regresją.

Współczynnik determinacji

Wyrażenie to nazywamy współczynnikiem determinacji.

r

2

<0; 1>

Informuje on o tym,

jaka część zmienności całkowitej zmiennej losowej Y została

wyjaśniona regresją liniową względem X.













y y

y y

y y

i

i

n

i

i

n

i

i

i

n























2

1

2

1

2

1













y

xy

a

y

y

y

y

r

n

i

i

n

i

i

var

cov

ˆ

ˆ

1

2

1

2

2

















Jeżeli między zmiennymi Y i X istnieje pełna zależność, to wszystkie
punkty empiryczne leżą na prostej, reszty są zerowe, a r

2

= 1.

W przypadku braku zależności (a = 0) funkcja regresji jest stała
i r

2

= 0.

-3

-2

-1

0

1

2

3

0.00

0.05

0.10

0.15

0.20

0.25

0.30

0.35

0.40

-t

n,



t

n,





/2



/2

1-



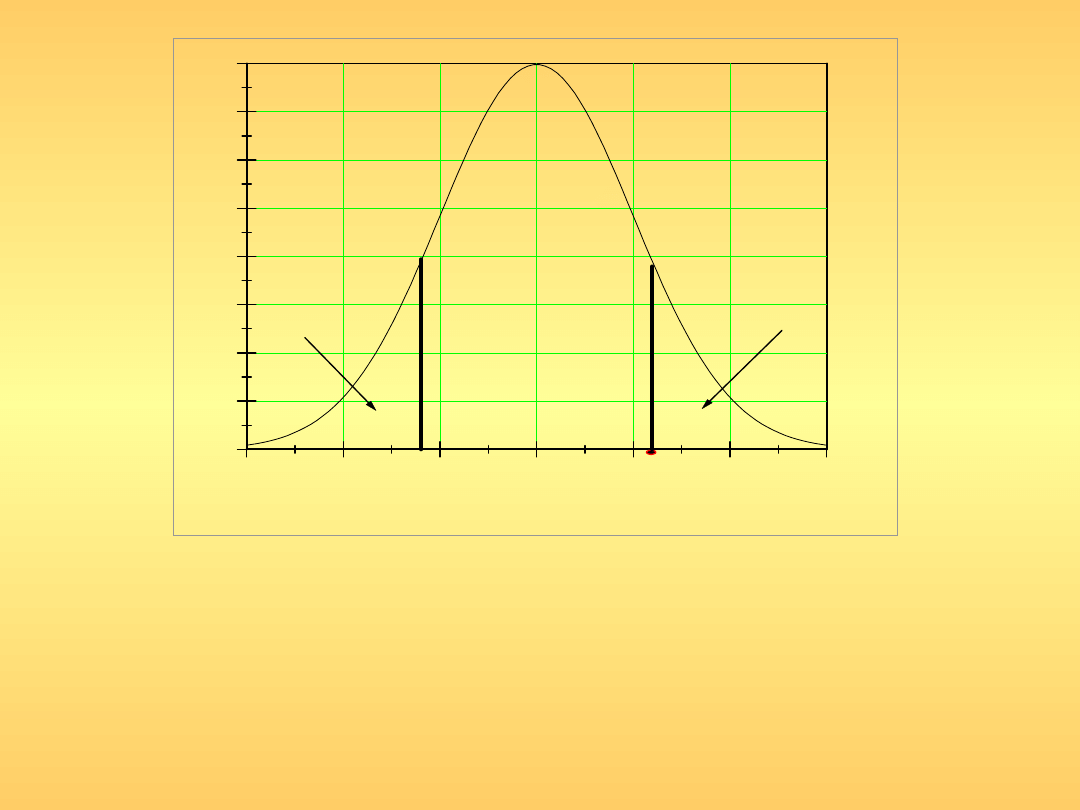
Z tablic rozkładu Studenta odczytujemy, dla wcześniej przyjętego
poziomu istotności , wartość krytyczną t

n-2,

. Jeżeli obliczona wartość

t znajduje w dwustronnym obszarze krytycznym (-, - t

n-2,

), (t

n-2,

,

+), to H

0

należy odrzucić na korzyść hipotezy H

1

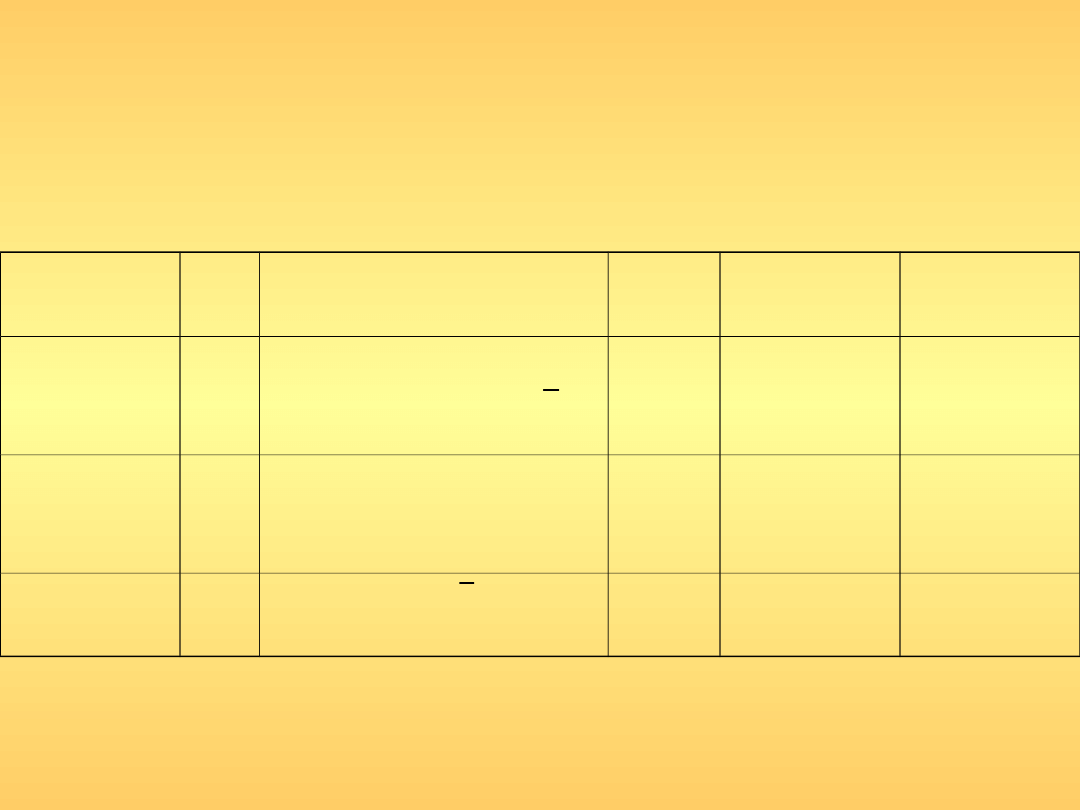
Weryfikacja hipotezy o istotności

regresji













n

i

i

R

y

y

SS

1

2

ˆ





SS

y y

y

T

i

i

n











2

1

var

Zmiennoś
ć

df

SS

M.S

F

emp

.

F



Regresji

1

MS

R

F

R

Odchyleń

n-2

SS

E

MS

E

F



,1,n-2

Całkowita n-1

Weryfikacji hipotezy o istotności regresji testem F
Fishera-Snedecora.

Analiza wariancji ma postać

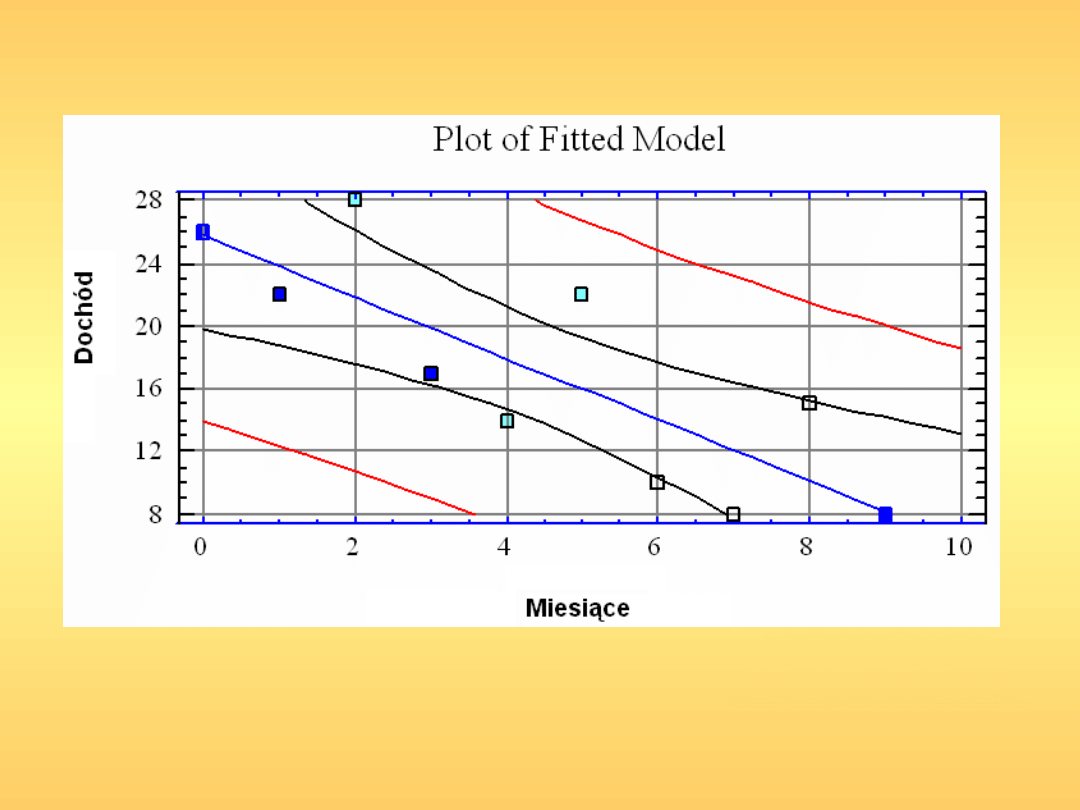
Predykcja na podstawie regresji

liniowej

Model regresji można wykorzystać do przewidywania wartości które

przyjmie zmienna Y przy ustalonych wartościach zmiennej niezależnej

X.

Jest to zagadnienie predykcji lub prognozowania.

Niestety, im wartość x, dla której dokonujemy predykcji jest bardziej

odległa od średniej z próby tym mniejsza dokładność prognozy.

Przedział ufności dla wartości z

modelu

Dla regresji liniowej statystyka:

ma rozkład t Studenta z liczbą stopni swobody n - 2.
Na tej podstawie możemy wyznaczyć przedział ufności dla wartości z modelu:

t

m x

m x

S

m x





 ( )

( )

 ( )

S

t

x

m

S

t

x

m

x

m

x

m

n

x

m

n













)

(

ˆ

2

,

)

(

ˆ

2

,

)

(

ˆ

;

)

(

ˆ

)

(





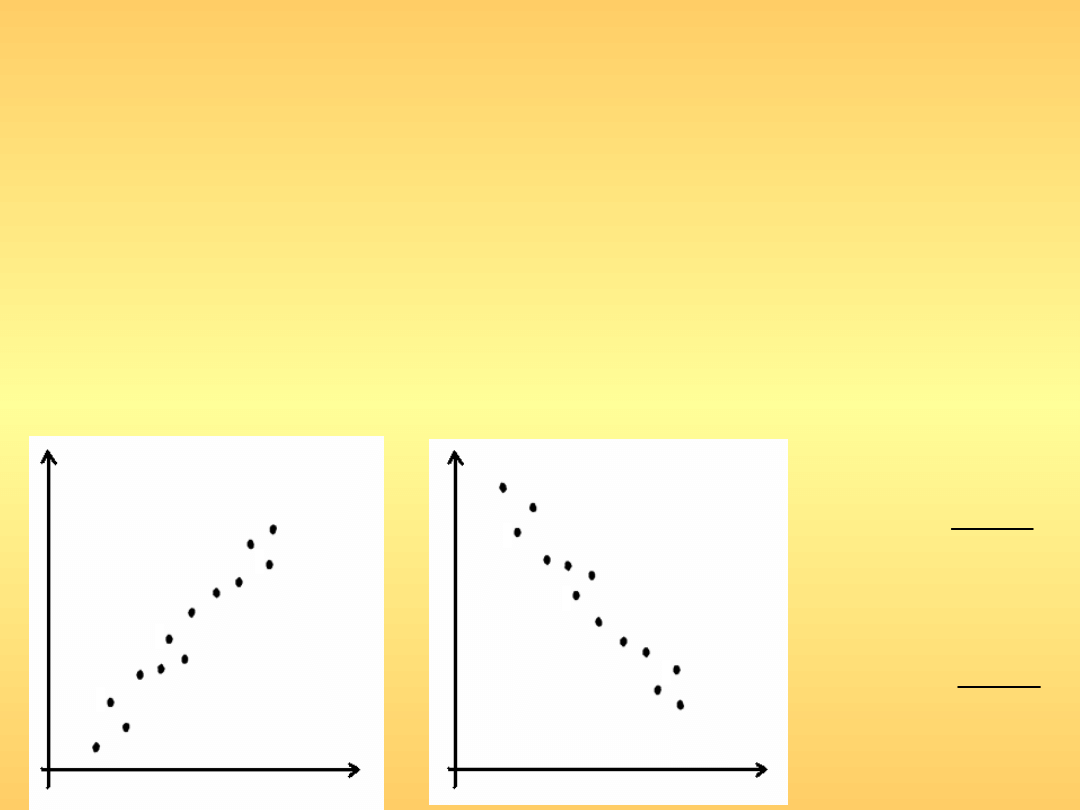
Współczynnik korelacji

Miarą siły związku między zmiennymi losowymi jest współczynnik korelacji



,

Empiryczny współczynnik korelacji r ma wszystkie własności określone dla
współczynnika korelacji



.

Współczynnik korelacji określa także kierunek zależności.

r = 1

r = -1

y

x

xy

S

S

S

r 

y

x

xy











Kwadrat

współczynnika

korelacji

z

próby

nazywany

jest

współczynnikiem determinacji i jest on, drugim poza współczynnikiem
korelacji miernikiem siły związku między zmiennymi.
Interpretacja współczynnika determinacji – podaje on w jakiej części
zmienność jednej cechy jest wyjaśniona przez drugą cechę.

Weryfikacja hipotezy o istotności

korelacji

Założymy, że rozkład zmiennych losowych Y i X w populacji generalnej jest

normalny. Na podstawie n - elementowej próby chcemy zweryfikować

hipotezę, że zmienne te są liniowo niezależne:

wobec

Jeżeli H

0

jest prawdziwa, to statystyka:

ma rozkład t Studenta z liczbą stopni swobody v = n – 2.
Hipoteza o istotności korelacji może być także zweryfikowana poprzez

porównanie wyznaczonego współczynnika z próby z wartościami
krytycznymi współczynnika korelacji wielokrotnej Pearsona.

H

0

0

:





H

1

0

:





t

r

r

n







1

2

2

1

,

,







k

n

k

R

r



Regresja wielokrotna liniowa

Dotychczas rozpatrywaliśmy tylko dwie zmienne: Y i X.

Częściej mamy do czynienia z przypadkami w których jest zmienna
losową Y oraz k zmiennych X (stałych lub losowych).

Y N m x

x

k

y x

x

k

~ ( ( ,..., ),

)

/ ,...,

1

1



k

k

k

x

b

x

b

b

x

x

m

y

















1

1

0

1

)

,...

(

Współczynniki modelu b

1

, ..., b

k

będziemy nazywać

cząstkowymi współczynnikami regresji.

y

b bx

b x

e

j

j

k kj

j

 





0

1 1

Kryterium estymacji : należy tak dobrać parametry modelu, aby suma
kwadratów odchyleń od modelu była jak najmniejsza:





s

e

y b bx

b x

j

j

j

j

k kj

j









 







2

0

1 1

2

min

Badanie istotności regresji

wielokrotnej

Hipotezę o nieistotności regresji wielokrotnej
możemy zapisać jako:

jej weryfikacja testem F Fishera-Snedecora.
Tabela analizy wariancji ma postać:
Zmienność d.f SS MS Femp.
F



Regresji

k SS

R

MS

R

F

R

Odchyleń n-k-1 SS

E

MS

E

Całkowita n-1 SS

T

H b b

b

k

0

1

2

0

:   

F

k n k



, ,   1

Sumy kwadratów odchyleń i średnie kwadraty
potrzebne do zweryfikowania hipotezy o
istotności regresji mogą być wyznaczone z niżej
podanych wzorów.

SS

y

T

var

SS

b

x y MS

SS

k

R

i

i

i

R

R







 cov

SS

y

b

x y

MS

SS

n k

E

i

i

E

E

i







 



var

 cov

1

Hipotezę

H b b

b

k

0

1

2

0

:   

F

F

R

k n k



 



, ,

1

Odrzucenie hipotezy H

0

jest równoznaczne z tym, że

co najmniej jeden współczynnik regresji jest różny od zera;

tzn. istnieje związek funkcyjny liniowy między zmienną zależną a

zmiennymi niezależnymi.

Problem statystyczny

które zmienne niezależne powinny pozostać w modelu

regresji.

odrzucamy

gdy

Badanie istotności regresji

wielokrotnej

Weryfikacja hipotez o istotności

cząstkowych współczynników regresji

Problem sprowadza się do zweryfikowania serii k
hipotez zerowych mówiących o tym, że i-ty cząstkowy
współczynnik regresji jest równy zero.

Hipotezy te mogą być weryfikowane testem t-Studenta

Weryfikacja hipotez

Wyrażenie

jest oszacowaniem średniego kwadratu odchyleń od
regresji.
Przy prawdziwości hipotez zerowych tak określone
statystyki mają rozkład t-Studenta z liczbą stopni
swobody równą n-k-1

H b

i

0

0

: 

s

y

b

x y

n k

y x

x

i

i

i

k

/ ,...

var

 cov

1

2

1





 



Hipotezę

będziemy odrzucać, jeżeli wartość statystyki t znajdzie się w obszarze
krytycznym.

Jeżeli zmienne niezależne są z sobą powiązane
to oceny istotności cząstkowych współczynników regresji nie
są niezależne.

0

:

0



i

b

H

Problem doboru zmiennych

W przypadku istnienia silnych współzależności między zmiennymi

niezależnymi analizując funkcję regresji wielokrotnej dochodzimy do

wniosku, że jest ona istotna statystycznie (testem F).

Weryfikując dalej hipotezy o istotności cząstkowych współczynników

uzyskujemy wartości testu t Studenta, które nie przeczą hipotezom

zerowym.

Czyli mamy istotną funkcję regresji ale wszystkie zmienne (analizowane

oddzielnie) są nieistotne, powinny więc być usunięte z modelu.

Zaczynamy od pełnego zestawu potencjalnych zmiennych niezależnych,

a następnie kolejno usuwamy z modelu tę zmienną niezależną, której

rola w opisywaniu zależności między zmienną Y a zmiennymi

niezależnymi jest najmniejsza. Podejście takie nosi nazwę regresji

krokowej.

Regresja krokowa

Algorytm postępowania:

1. Zaczynamy od pełnego (potencjalnie) zestawu zmiennych

niezależnych. Estymujemy model i wyznaczamy

2. Wyznaczamy wektor wartości empirycznych statystyk t dla

hipotez

.
3. Usuwamy z modelu tę zmienną, dla której uzyskaliśmy najmniejszą

wartość empiryczną statystyki t (co do wartości bezwzglednej) i

ponownie estymujemy model.

Postępowanie takie kontynuujemy tak długo, dopóki w modelu nie

pozostaną tylko zmienne istotne.

R

s

y x

x

k

2

2

1

oraz

/ ,...,

H b

i

0

0

: 

W trakcie wykonywania regresji krokowej powinniśmy obserwować

zmiany wartości współczynnika determinacji jak i średniego kwadratu

błędu.

Postępowanie ma doprowadzić do

maksymalizacji wartości współczynnika

maksymalizacji wartości współczynnika

determin

determin

a

a

cji

cji

przy

jednoczesnej minimalizacji średniego kwadratu

jednoczesnej minimalizacji średniego kwadratu

błędu

błędu

.

.

Miarą stopnia dopasowania modelu jest korelacja wielokrotna R lub jej
kwadrat (współczynnik determinacji D).

Dobierając model funkcji regresji powinniśmy dążyć do uzyskania jak
największego współczynnika determinacji (korelacji), ale przy
możliwie małym średnim kwadracie odchyleń od regresji:

R

b

x y

y

i

i

i





 cov

var

D R



2

s

y

b

x y

n k

y x

x

i

i

i

k

/ ,...

var

 cov

1

2

1





 



Ocena dopasowania modelu

Regresja wielomianowa

(krzywoliniowa)

W wielu przypadkach interesuje nas nieliniowy związek między

zmienną Y a zmienną X, np.:

Linearyzacja modelu regresji

wielomianowej

Przykład modelu nieliniowego z dwoma zmiennymi niezależnymi:

2

1

5

2

2

4

2

3

2

1

2

1

1

0

x

x

b

x

b

x

b

x

b

x

b

b

y













Wnioskowanie dla regresji

wielokrotnej

Współczynniki regresji:

• i-ty, cząstkowy współczynnik regresji opisuje o ile średnio
zmieni się wartość zmiennej Y przy wzroście i-tej wartości
zmiennej X o jednostkę przy ustalonych wartościach
pozostałych zmiennych niezależnych.

W przypadku większości modeli regresji krzywoliniowej

taka interpretracja nie jest możliwa.

Funkcje wielomianowe

Model regresji wielomianowej dwóch zmiennych niezależnych jest

postaci:

Etap pierwszy - Wyznaczanie funkcji regresji dla jednej zmiennej

niezależnej tzn. zmienna Y jest funkcją tylko jednej zmiennej

niezależnej, np.

2

1

5

2

2

4

2

1

3

2

2

1

1

0

x

x

a

x

a

x

a

x

a

x

a

a

y













2

1

2

1

1

0

20

2

1

)

(

x

b

x

b

b

x

x

x

y









2

2

2

2

1

0

10

1

2

)

(

x

a

x

a

a

x

x

x

y









Problemy z estymacją funkcji regresji

Estymacja funkcji regresji jest zagadniem trudnym ponieważ:

1. Brak jest pewności, że zbiór analizowanych zmiennych

niezależnych jest pełny.

2. Typ funkcji regresji nie jest znany dlatego pojawia się problem

doboru kształtu funkcji regresji i zestawu zmiennych

niezależnych.

3. W wielu sytuacjach można uzyskać porównywalną „dobroć

dopasowania modelu”, współczynnik korelacji lub R

2

, dla różnych

typów funkcji regresji i zestawów zmiennych niezależnych.