Lista 3

(Korelacja i regresja)

Zad.1

.

W grupie 10 przedsiębiorstw obserwowano poziom produkcji pewnych wyrobów (w

szt.) i koszty całkowite (tys. zł)

Produkcja

11

12

13

13

14

14

17

18

18

20

Koszty całkowite

18

20

20

20

22

24

26

27

26

27

a) Oszacować parametry funkcji regresji opisującej zależność kosztów całkowitych od

wielkości produkcji i nanieść ją na korelacyjny wykres rozrzutu

b) Korzystając z wyznaczonej prostej regresji przewidzieć całkowite koszty produkcji 25

sztuk wyrobów

c) Jaka jest siła i rodzaj zależności liniowej między produkcją, a kosztami?
d) Podać interpretacje parametrów wyznaczonej prostej regresji

Zad.2

.

Badając zależność między powierzchnią ( w m

2

) a wysokością opłat za energię

elektryczną ( w PLN ) dla 20 losowo wybranych mieszkań otrzymano:
średnia powierzchnia 58 m

2

, średnie opłaty 165 PLN

wariancja powierzchni 64 m

4

, wariancja opłat 900 (PLN)

2

oraz c(x,y) = 204

a) wyznaczyć regresję wysokości opłat za energię względem powierzchni mieszkań,

podać miano i interpretację odpowiedniego parametru a

b) oszacować wysokość opłat w mieszkaniu o powierzchni 65 m

2

Zad.3

.

Analiza popytu na produkt A w zależności od ceny dała następujące wyniki:

– średnia sprzedaż w badanym okresie wynosiła 5,1 ton, a średnia cena 19,9 zł;
– współczynniki zmienności popytu i ceny wynosiły odpowiednio: 8,3 % i 7,6 %;
– zależność sprzedaży od ceny w tym okresie była liniowa, a współczynnik korelacji

liniowej wyniósł r = –0,92.
a) Podać przedział zmienności ceny i wielkości sprzedaży;
b) Wyznaczyć parametry funkcji sprzedaży w zależności od ceny;
c) Podać miano wyznaczonego współczynnika regresji i jego interpretację;
d) Korzystając z punktu (a) i (b) wyznaczyć graficznie prostą regresji.

Zad.4.

Pewien prowadzący ćwiczenia ze statystyki zbadał zależność między liczbą punktów

otrzymanych na kolokwium, liczbą godzin poświęconych na naukę. Na podstawie 10
elementowej próby otrzymał następujące wyniki:

h

y

pkt

x

4

12

10

1

2

10

1

2

2

)

(

5

)

(

i

i

i

i

y

y

x

x

10

1

10

)

)(

(

i

i

i

y

y

x

x

a) ocenić siłę i rodzaj zależności pomiędzy badanymi cechami
b) oszacuj liczbę punktów studenta, który uczył się do kolokwium 6 h
c) podać interpretację parametrów wyznaczonej linii regresji
d) obliczyć współczynnik determinacji i podać jego interpretację

Zad.5

.

Ustalić siłę i rodzaj związku korelacyjnego pomiędzy ceną karnetu (X) oraz liczbą

kilometrów tras narciarskich (Y) . Ustalić teoretyczną cenę karnetu w ośrodku narciarskim w
którym jest 400 km tras, oraz podać interpretację współczynnika kierunkowego oszacowanej prostej

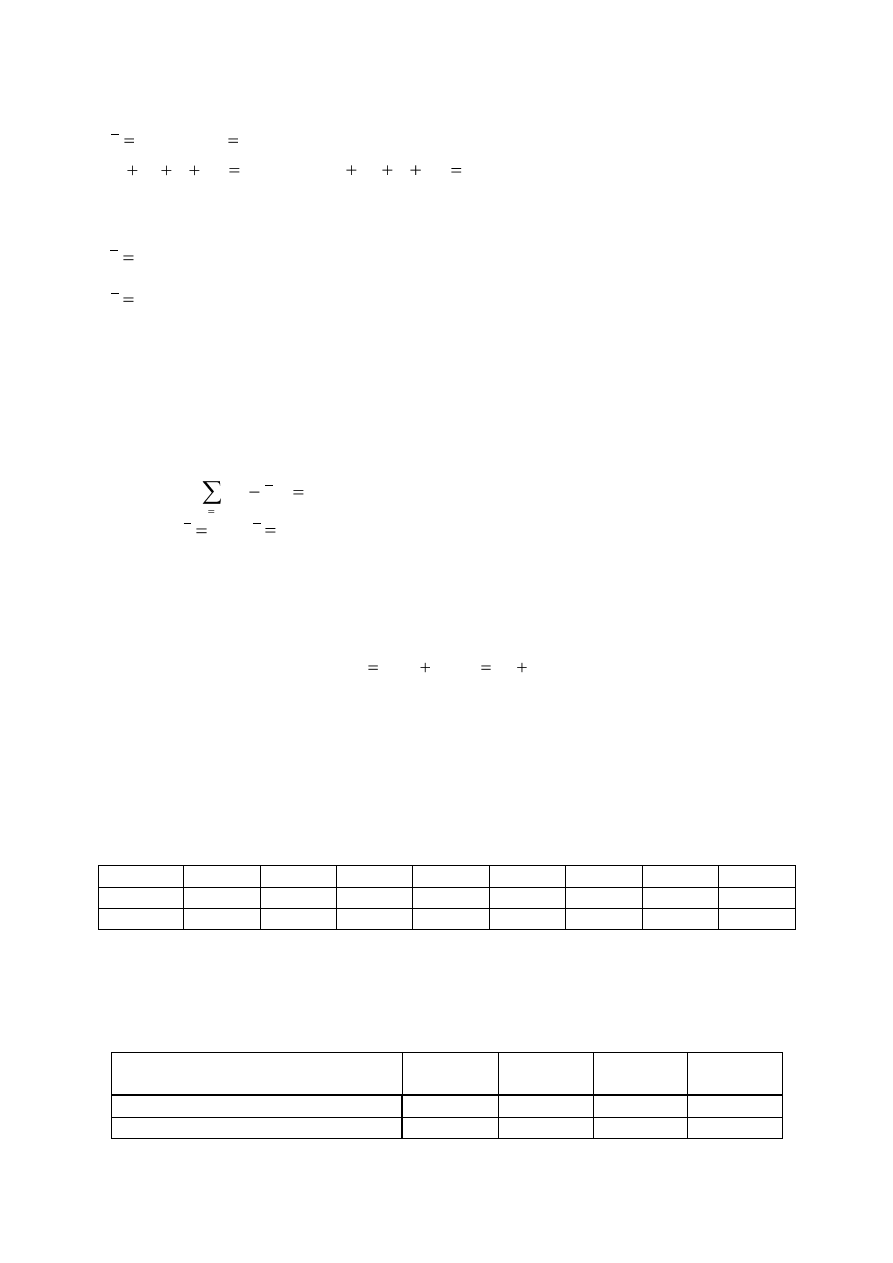
regresji. Pomiar długości tras w analizowanych ośrodkach i cen karnetów dał następujące wyniki:

km

y

200

,

km

s

y

110

i c (x;y) = 8910

2500

...

25

2

1

x

x

x

oraz

452500

...

2

25

2

2

2

1

x

x

x

.

Zad.6.

Analizując zadłużenie ( w tys. zł.) dla 10 podmiotów gospodarczych z tytułu

kredytów Y i wartość produkcji sprzedanej X (w mln PLN) otrzymano:

50

x

mln PLN S

x

= 5 mln PLN

250

y

tys. zł. V

y

= 10 % r (x;y) = - 0,96

a) wyznaczyć kowariancję
b) podać równanie regresji wartości produkcji sprzedanej względem zadłużenia
c) podać interpretację i miano parametru regresji
d) czy można przewidzieć wielkość produkcji sprzedanej przy zadłużeniu 400 tys. zł.

Zad.7

.

Obserwowano przez 12 miesięcy roku 2001 jak kształtowała się stopa bezrobocia (X)

i stopa procentowa (Y). Na podstawie tej próby otrzymano następujące wyniki:

C(x;y)=145

12

1

2

48

)

(

i

i

x

x

r

xy

= 0,7

%

15

x

%

5

,

2

y

Oszacować wielkość bezrobocia przy stopie procentowej 3,4 %.

Zad.8

.

W 50 zakładach przeprowadzono badania w celu ustalenia zależności między

wydajnością mierzoną w sztukach X, a płacą w Euro Y. Otrzymano następujące równania
regresji:

ˆ

ˆ

0, 4

10

2

5

x

y

y

x

a) Czy w obliczeniach nie został popełniony błąd i wyznaczone proste mogą być

prostymi regresji? Odpowiedź proszę uzasadnić

b) Co można powiedzieć o sile i kierunku zależności pomiędzy badanymi cechami?
c) Obliczyć średnią płacę i średnią wydajność

Zad.9. Żołnierze zostali ocenieni pod względem karności X i wyników ze strzelania Y.
Karność została określona kolejnością , a wyniki ze strzelania podano w punktach.

Obliczyć odpowiedni współczynnik i określić kierunek i siłę współzależności między X i Y.

Zad.10.Korzystając z odpowiedniego współczynnika określić czy występuje zależność
wypalania ceramiki od rodzaju zastosowanego materiału ceramicznego, jeśli wyniki
empiryczne są następujące

Rodzaj materiału

Wynik wypalania

Materiał A Materiał B Materiał C Materiał D

Wyrób zniszczony

22

27

34

31

Wyrób gatunku II

48

56

41

52

Żołnierze A

B

C

D

E

F

G

H

karność

2

3

4

8

1

6

7

5

strzelanie 198

196

193

187

195

195

190

192

Wyrób gatunku I

30

17

25

17

Zad 11. W produkcji zastosowano zmiany procesie technologicznym. Na podstawie
poniższych danych sprawdzić, stosując odpowiednie miary, czy jakość produkowanych
wyrobów zależy od wprowadzonych zmian.

Technologia produkcji

Gatunek wyrobu
I

II

III

Przed zmianą

50

10

20

Po zmianie

40

20

10

Zad 12. Przebadano 200 osobową grupę dzieci w wieku przedszkolnym pod względem
występowania wad postawy. Występowały one u 20 chłopców i 30 dziewczynek.
U 90 chłopców i 60 dziewczynek nie stwierdzono żadnych nieprawidłowości. Czy
występowanie wad postawy jest związane z płcią?


Dodatkowo proszę rozwiązać zadania z podręcznika S. Ostasiewicz, Z. Rusnak , U.
Siedlecka „Statystyka elementy teorii i zadania” wyd.6 , W-w 2006 z rozdziału 11: 11.5,
11.9, 11.10, 11.7, 11.13, 11.14, 11.15, 11.20, 11.21, 11.23, *11.29, *11.30, *11.31.

Zwrócić szczególną uwagę na zadania zaznaczone kursywą wytłuszczonym drukiem