MECHANIKA

KWANTOWA

Wszystkie cząstki mają tę własność, że czasem, w
niektórych eksperymentach zachowują się jak fale, a
czasem jak zwykłe cząstki. Wzory

obowiązują zawsze

IDEA DE BROGLIE’A





h

p

hf

E 

Potrzebny jest nowy język i nowy aparat matematyczny do opisu takich
tworów

MECHANIKA KWANTOWA

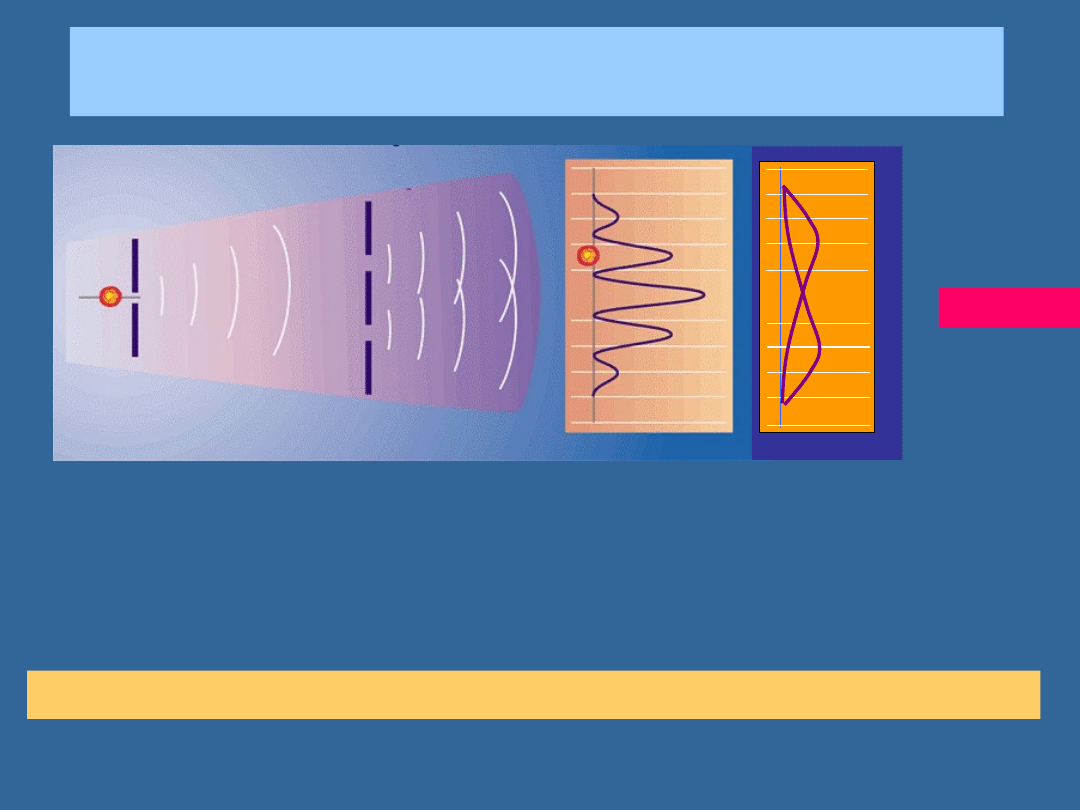
ilość
elektronów

PRZEJŚCIE CZĄSTEK PRZEZ SZCZELINY:

ELEKTRONY

Elektrony:

Davisson, Germer, 1927
Jönsson, 1961

interfer

Dyfrakcja elektronów na sieci krystalicznej jest klasyczną metodą badania
struktury

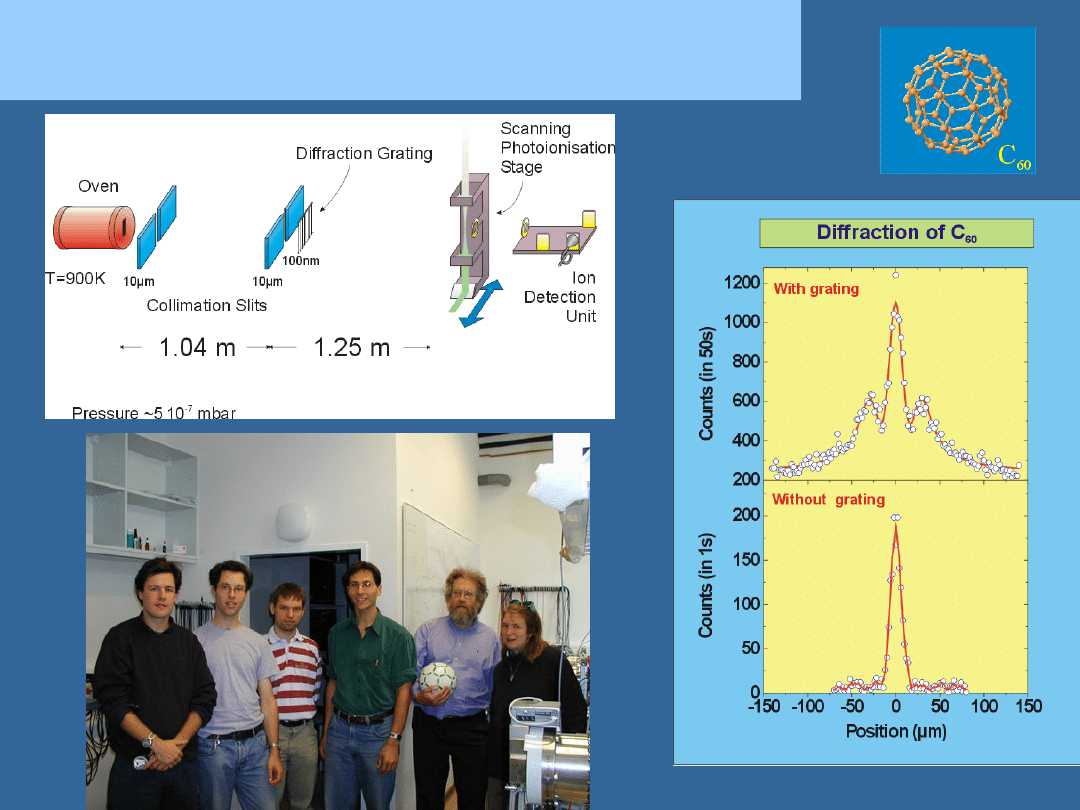
A. Zillinger, 1999

PRZEJŚCIE CZĄSTEK PRZEZ SZCZELINY:

FULERENY

0

50000

100000

150000

200000

0

100

200

300

400

500

600

Fe

3

O

4

N

at

ęż

e

n

ie

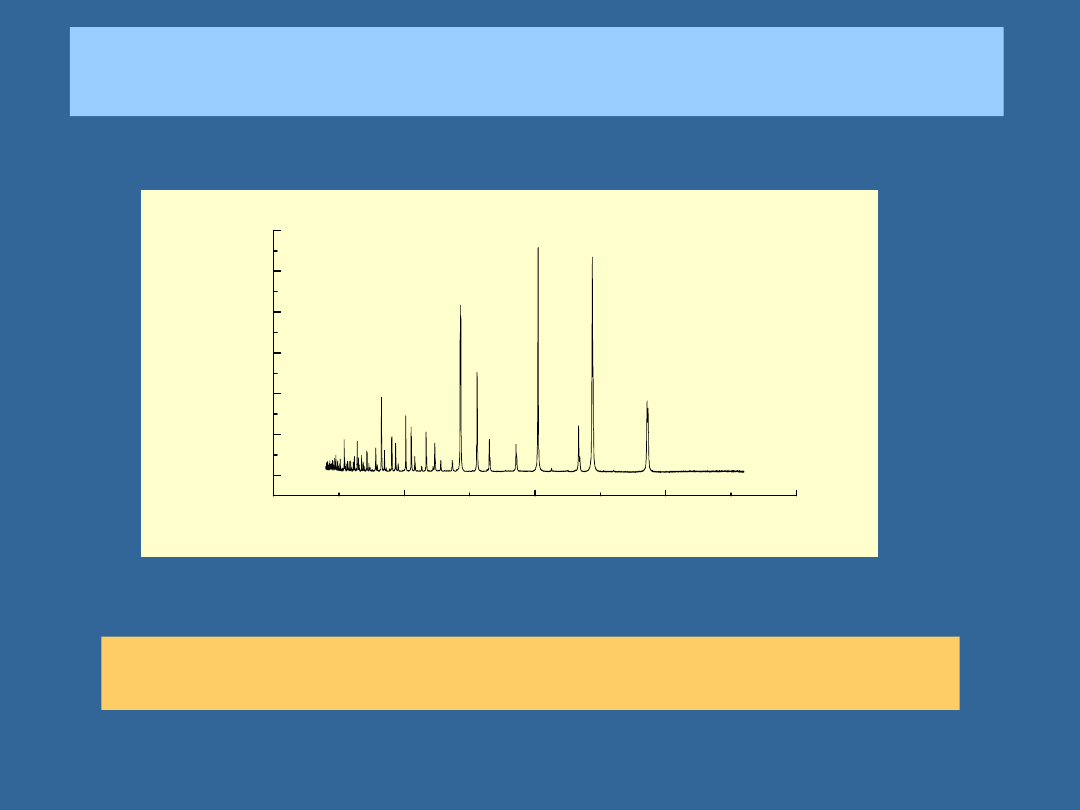
czas przelotu  długość fali

neutronu

Dyfrakcja neutronów jest klasyczną metodą badania struktury i
ułożenia momentów magnetycznych

PRZEJŚCIE CZĄSTEK PRZEZ SZCZELINY:

NEUTRONY

FUNKCJA FALOWA I RÓWNANIE SCHRÖDINGERA

Paradoks interferencji cząstek na szczelinach, lub zjawiska fotoelektrycznego
może być rozwiązany przyjmując, że opis cząstki wymaga podania amplitudy
prawdopodobieństwa

(x, y, z, t)

(funkcji falowej) , która jest funkcją

położenia i czasu.

Prawdopodobieństwo, znalezienia cząstki w chwili t w miejscu (x,y,z) jest
kwadratem modułu funkcji falowej

P(x, y, z, t)= l(x, y, z, t)l

2

Jeśli interesują nas tylko stany cząstek które nie zależą od czasu (tj.
stany o określonej energii), to wystarczy rozwiązać równanie
Schrödingera niezależne od czasu

)

x

(

E

)

x

(

))

x

(

V

dx

d

m

2

(

2

2

2













równanie na funkcje
własne (x) i wartości

własne E

Jak znaleźć funkcję
falową?

Nie jest możliwa jednoczesna znajomość pewnych własności „cząstek”

Wielkości, które nie mogą być jednocześnie określone nazywają się
wielkościami „

komplementarnymi

”

ZASADA NIEOZNACZONOŚCI HEISENBERGA

- Nie jest możliwe jednoczesne określenie pędu cząstki i jej położenia

x* p

x

 

-Czym krótszy czas pomiaru, tym mniej dokładny jest pomiar energii

E* t  

- Nie jest możliwe jednoczesne określenie szczeliny przez którą
„cząstka” przechodzi i zobaczenie efektu interferencyjnego

DWA RODZAJE CZĄSTEK: FERMIONY I BOZONY

BOZONY

FERMIONY

Fotony (i inne cząstki o spinie h/2

lub wielokrotności)

Jeśli elektron, lub inna cząstka o spinie
“połówkowym” jest w pewnym stanie
kwantowym, to żadna inna taka
cząstka w tym samym stanie znaleźć
się nie może. (Zakaz Pauliego)

prawdopodobieństwo tego, że do
grupy cząstek w tym samym stanie
dojdzie jeszcze jedna jest tym
większe, im więcej cząstek już w
tym stanie przebywa.

budowa atomów, układ okresowy,
własności materii

lasery,
nadprzewodnictwo

Elektrony ( i wszystkie innych cząstki
o wewnętrznym momencie pędu,
spinie, równym 1/2 h/2, lub

nieparzystej wielokrotności)

PRZYKŁAD:

ELEKTRON W NIESKOŃCZONEJ STUDNI

POTENCJAŁU

(x)=

0

V=

V=0

V=


(x)=

0

x

0

L

Znaleźć możliwe energie E i
odpowiadające im funkcje falowe
(x) elektronu w nieskończonej

studni potencjału

)

x

(

dx

d

m

2

)

x

(

E

2

2

2











Elektron nie może być w tym

obszarze: (x)=0 dla x<0 i x>L

)

x

(

)

x

(

V

)

x

(

dx

d

m

2

)

x

(

E

2

2

2















ROZWIĄZANIE

elektron jest swobodny

x<0 i x>L

V(x)=

0<x<L  V(x)=0

równanie Schrödingera

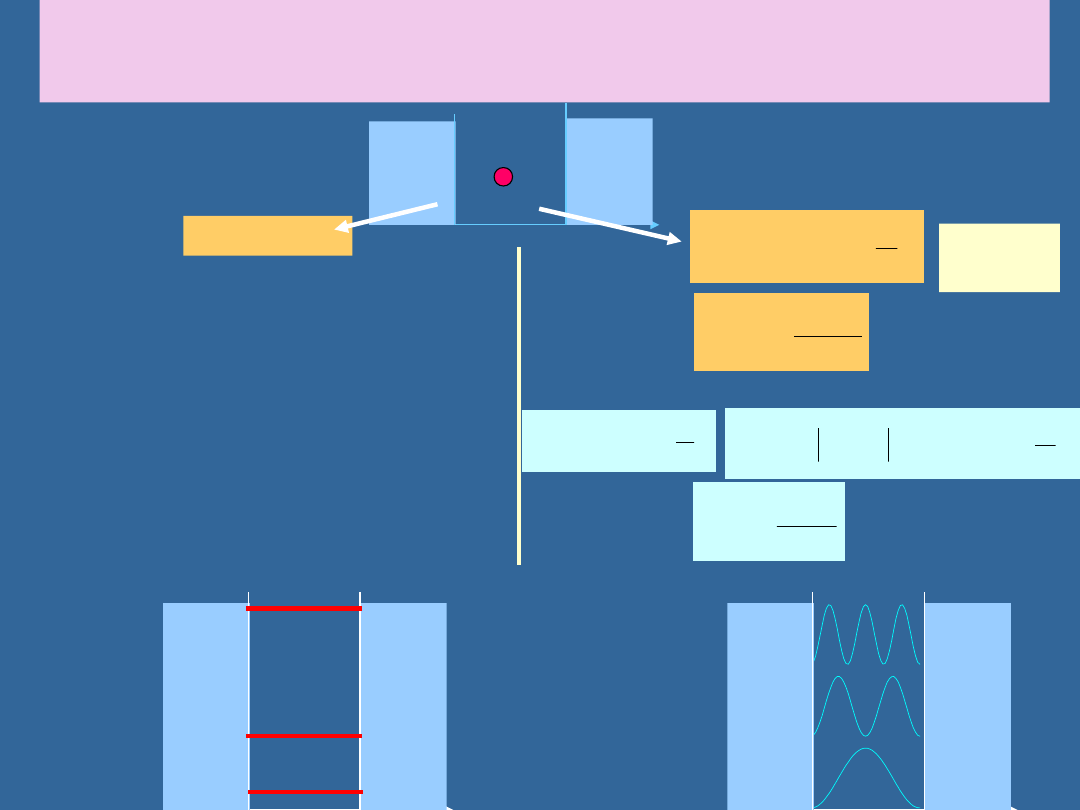
ELEKTRON W NIESKOŃCZONEJ STUDNI POTENCJAŁU:

ROZWIĄZANIE

x

L

n

sin

A

)

x

(

n







n=1,2,3
...

Odgadnięte
rozwiązanie

2

2

2

2

n

mL

2

n

E







x

L

2

sin

A

)

x

(

)

x

(

P

2

2

2

2

2









Np.. dla
n=2

x

L

2

sin

A

)

x

(

2







2

2

2

2

mL

2

E







(x)=0

(x)=

0

V=0

(x)=

0

x

0

L

x

n=1

n=2

n=3

Dozwolon
e energie

n=1

n=2

n=3

P

n

(x)

Prawdopo
dobieństw
a

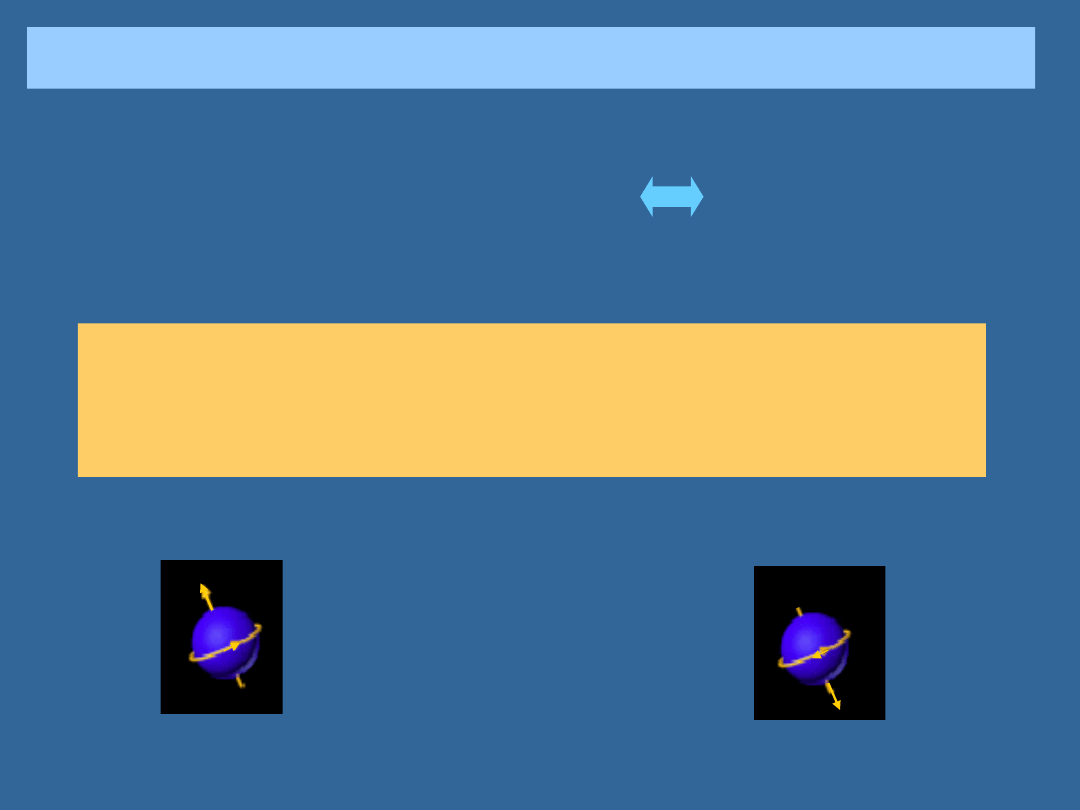
Elektrony ( i wszystkie innych cząstki o
wewnętrznym momencie pędu, spinie,
równym 1/2 h/2, 3/2 h/2, 5/2 h/2, itd,

ogólnie: o spinie “połówkowym”: protony
neutrony...): podlegają zakazowi Pauliego.

ELEKTRON JEST FERMIONEM;

Zakaz Pauliego

Jeśli elektron, lub inna cząstka o spinie “połówkowym” jest
w pewnym stanie kwantowym, to żadna inna taka cząstka
w tym samym stanie znaleźć się nie może.

FERMIONY

To są dwa różne stany kwantowe

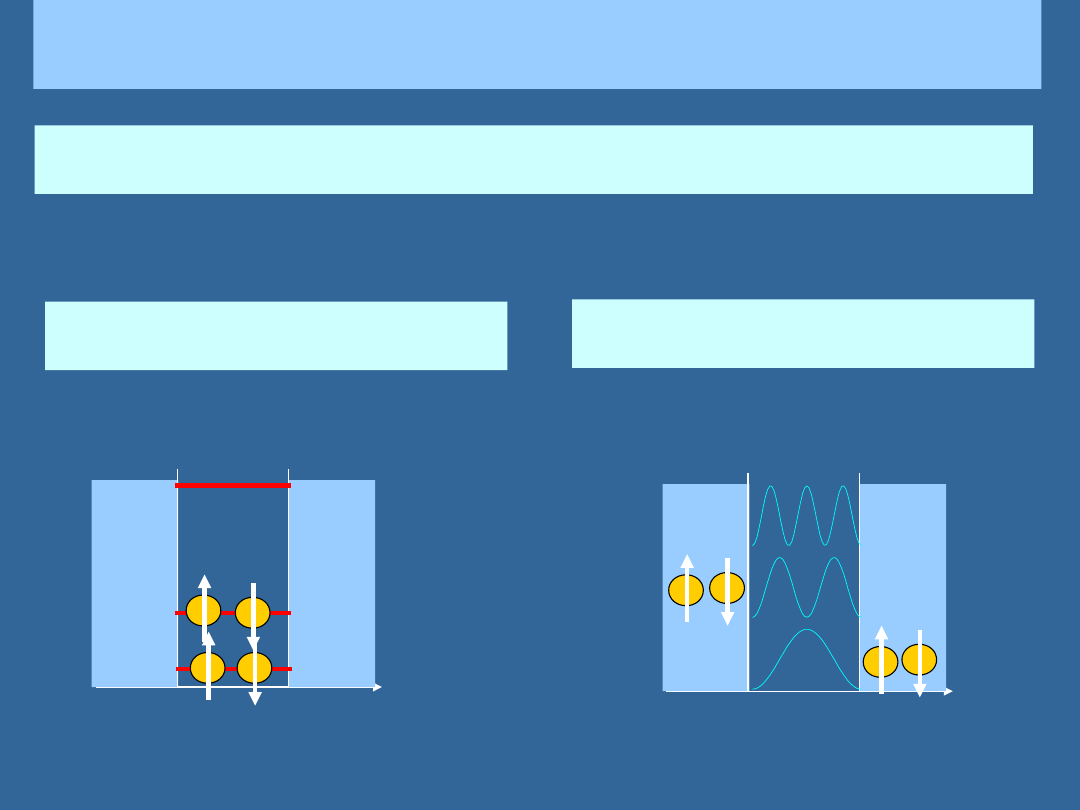
ELEKTRONY W NIESKOŃCZONEJ STUDNI POTENCJAŁU

Jeśli do studni potencjału „wrzuci” się wiele elektronów, to rozłożą się one tak,
aby zakaz Pauliego był spełniony

x

0

L

n=1

n=2

n=3

Możliwe energie elektronu (energie
własne)

Możliwe stany elektronu (funkcje
własne)

x

0

L

n=1

n=2

n=3

P

n

(x)

Np. 4 elektrony w studni potencjału

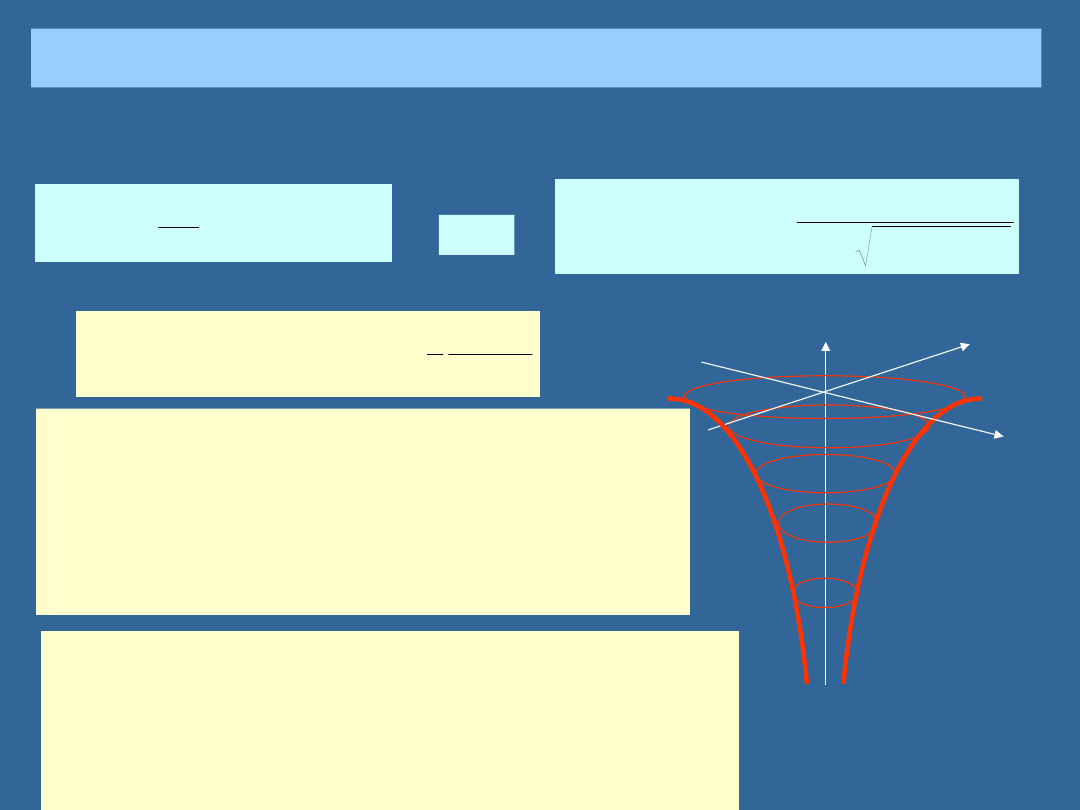
ELEKTRONY W ATOMIE WODORU

Elektron w atomie wodoru

2

2

2

0

2

z

y

x

4

e

)

z

,

y

,

x

(

V

)

r

(

V















)

r

(

)

r

(

V

)

r

(

m

2

)

r

(

E

2























oraz

Rozwiązanie

2

0

2

2

4

n

m

,

l

,

n

h

n

me

8

1

E

E

);

r

(

)

r

(

l



















V(r)

x

y

Funkcja falowa zależy od 4 parametrów::
-n (główna liczba kwantowa)
- l (azymutalna liczba kwantowa)
- m

l

( magnetyczna liczba kwantowa).

-s (spinowa liczba kwantowa)
Natomiast energia określona jest tylko przez główna
liczbę kwantową

1

,

1

s

l

m

l

lub

l

,

1

l

,

2

l

,

.....

,

2

l

,

1

l

,

l

m

1

n

l

0

lub

1

n

,

......

,

2

,

1

,

0

l

.....

,

3

,

2

,

1

n

l

l









































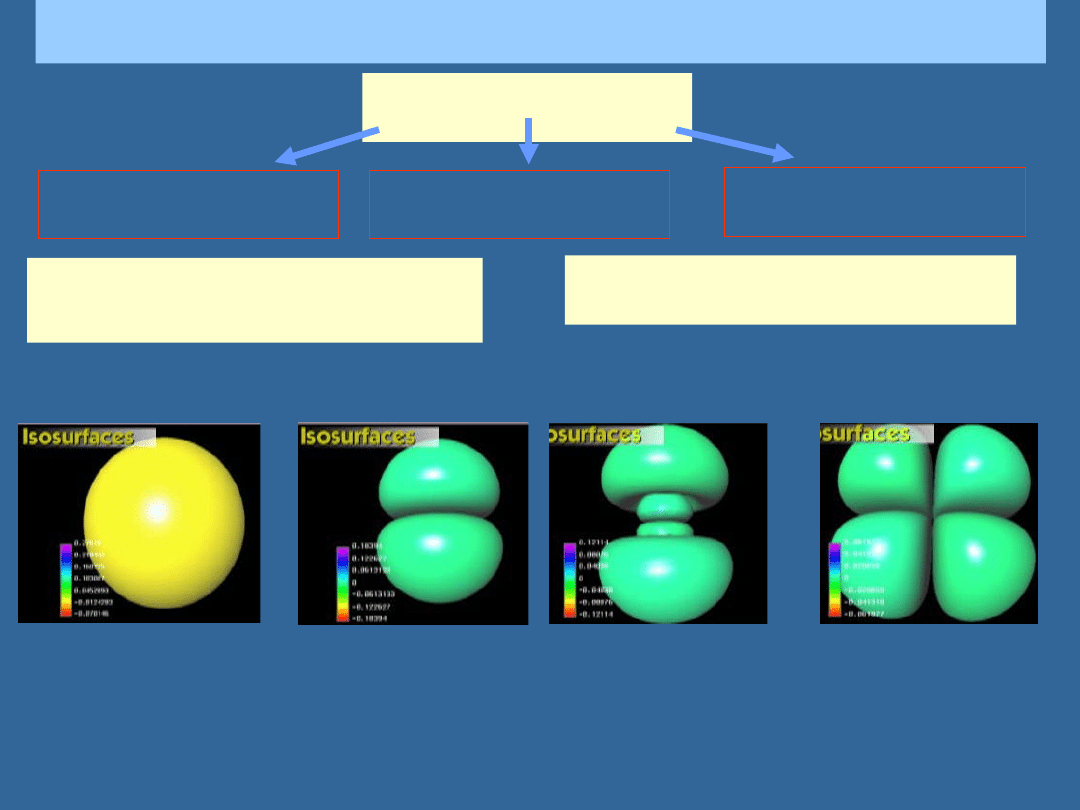
STANY ELEKTRONÓW W ATOMACH

Energia każdego
elektronu

Potencja kulombowski
jądra

Potencja kulombowski
innych elektronów

Mechanika kwantowa:
zakaz Pauliego

Funkcja falowa zależy od liczb
kwantowych n, l, m

l

Energia zależy od liczb
kwantowych n, l, m

l

, s

Stany p

2
p

3p

Stany d

3d

Stany s

2s

PRZYKŁAD: STANY ELEKTRONÓW W ATOMACH W

PRZYBLIŻENIU MAŁEJ ENERGII ODDZIAŁYWANIA

Liczy się tylko potencjał kulombowski jądra, czyli energia każdego elektronu
zależna jest tylko od liczby n

1

1,

s

l

m

l

lub

l

1,

l

2,

l

,

.....

2,

l

1,

l

l,

m

1

n

l

0

lub

1

n

,

......

2,

1,

0,

l

.....

3,

2,

1,

n

l

l









































I orbita n = 1: 1 stan: wodór

stany s (l=0)

stany

p

(l=1)

stany s (l=0)

I orbita pełna n = 1: 2 stany:
hel

I orbita pełna, n = 2: l=0, m

l

=0: lit

I orbita pełna, n = 2: l=0, m

l

=0, l=1,

m

l

=-1, 0, 1: azot

I orbita pełna, n = 2: l=0, m

l

=0, l=1,

m

l

=-1, 0, 1: neon

powłoka 1

powłoka 2

STANY ELEKTRONÓW W ATOMACH

0

20

40

60

80

en

e

rg

ia

5d

4f

6s

5p

4d

5s

4p

3d

4s

3p

3s

2p

2s

1s

Z

Ze względu na oddziaływanie między elektronami regularne zapełnianie powłok
jest zaburzone dla atomów o większych Z

UKŁAD OKRESOWY PIERWIASTKÓW

uklad
okresowy