EWR mechanika kwantowa 2

1

POSTULATY MECHANIKI KWANTOWEJ

1.

Każdemu układowi fizycznemu odpowiada funkcja
falowa (funkcja stanu)

Ψ Ψ

=

( , , , )

x y z t

która jest ciągła wraz z pierwszymi pochodnymi w
całym zakresie zmienności funkcji.

2.

Prawdopodobieństwo znalezienia układu
opisywanego funkcją falową

Ψ

w elemencie

przestrzeni d

τ

τ

d

P

2

Ψ

=

3.

Każdej dynamicznej wielkości fizycznej F

odpowiada

operator

$

F

. W wyniku pomiaru

otrzymuje się zawsze jedną z wartości własnych

operatora

$

F

.

n

n

n

f

a

f

=

F

ˆ

4.

Funkcja falowa spełnia równanie Schrödingera

t

i

∂

∂

Ψ

=

Ψ

h

H

ˆ

5.

Wartość oczekiwana przy pomiarze wielkości
fizycznej opisywanej operatorem

$

A

w układzie

opisywanym funkcją falową

Ψ

, jest dana przez

< >=

∗

∫

A

d

Ψ Ψ

Ω

$

A

τ

EWR mechanika kwantowa 2

2

FUNKCJA FALOWA

Funkcja falowa

)

,

,

,

(

t

z

y

x

Ψ

•

zawiera w sobie wszystkie informacje o stanie
cząstki

•

pozwala znaleźć prawdopodobieństwo
otrzymania określonego wyniku dowolnego
pomiaru

Sens fizyczny ma

2

)

,

,

,

(

t

z

y

x

Ψ

równy gęstości prawdopodobieństwa znalezienia
cząstki w danym punkcie.

Warunek unormowania

∫∫∫

=

τ

Ψ

1

)

,

,

,

(

2

d

t

z

y

x

Funkcja falowa i jej pochodne muszą być
określone i ciągłe.

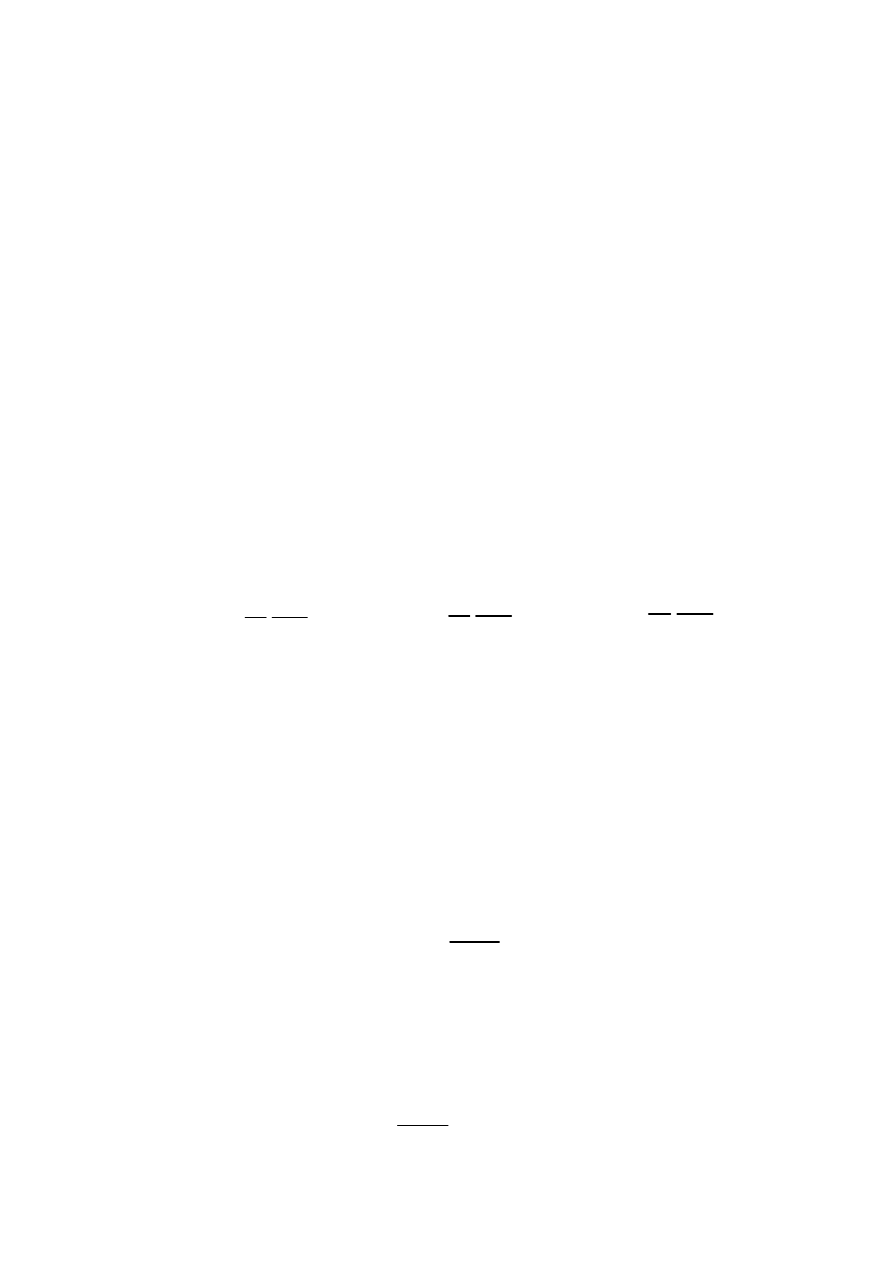
EWR mechanika kwantowa 2

3

OPERATORY

Równanie własne operatora:

ˆ

n

n n

f

a f

=

A

f

n

– funkcja własna

a

n

– wartość własna

Przykłady operatorów w reprezentacji położeniowej:

•

Operatory składowych pędu

x

i

p

x

∂

∂

=

h

ˆ

y

i

p

y

∂

∂

=

h

ˆ

z

i

p

z

∂

∂

=

h

ˆ

•

Operatory położenia

,

ˆ

,

ˆ

,

ˆ

z

z

y

y

x

x

=

=

=

•

Operator energii kinetycznej

∆

−

=

m

2

T

ˆ

2

h

•

operator Hamiltona

2

ˆ

ˆ

H

( )

2

U r

m

= −

∆ +

h

r

EWR mechanika kwantowa 2

4

WYNIKI POMIARÓW

Dla układu opisywanego funkcją falową

)

,

,

,

(

t

z

y

x

Ψ

Prawdopodobieństwo otrzymania wyniku

a

n

2

*

)

,

,

,

(

)

,

,

,

(

)

(

∫

Ψ

=

τ

d

t

z

y

x

t

z

y

x

u

a

P

n

a

n

Wartość średnia dużej ilości pomiarów

2

*

)

,

,

,

(

ˆ

)

,

,

,

(

∫

Ψ

Α

Ψ

>=

<

τ

d

t

z

y

x

t

z

y

x

a

EWR mechanika kwantowa 2

5

RÓWNANIE SCHRÖDINGERA

t

i

U

z

y

x

m

∂

Ψ

∂

−

=

Ψ

−













∂

Ψ

∂

+

∂

Ψ

∂

+

∂

Ψ

∂

h

h

2

2

2

2

2

2

2

2

U

- energia potencjalna

Jeżeli U jest niezależne od czasu

)

(

)

,

,

(

)

,

,

,

(

t

f

z

y

x

t

z

y

x

ψ

=

Ψ

to równanie to daje się rozdzielić na dwa równania

•

równanie opisujące zależność od czasu

f

E

t

f

i

⋅

−

=

∂

∂

−

h

•

stacjonarne równanie Schrödingera

(

)

0

2

2

2

2

2

2

2

2

=

ψ

−

+













∂

ψ

∂

+

∂

ψ

∂

+

∂

ψ

∂

U

E

z

y

x

m

h

W jednym wymiarze

(

)

0

2

2

2

2

=

ψ

−

+

∂

ψ

∂

U

E

m

x

h

EWR mechanika kwantowa 2

6

ELEKTRON SWOBODNY

Stacjonarne równanie Schrödingera

(

)

0

2

2

2

2

=

ψ

−

+

∂

ψ

∂

U

E

m

x

h

dla elektronu swobodnego (dla

U

=

0

)

0

2

2

2

2

=

+

ψ

ψ

h

p

dx

d

Rozwiązanie jest w postaci

)

exp(

)

exp(

)

(

2

1

x

B

x

A

x

α

α

ψ

+

=

gdzie

,

2

1

h

h

p

i

p

i

−

=

=

α

α

Po podstawieniu p = ħk i rozwiązania równania
czasowego f(t) otrzymuje się falę de Broglie’a:

)]

(

exp[

)]

(

exp[

)

(

t

kx

i

B

t

kx

i

A

x

ω

ω

ψ

−

−

+

−

=

EWR mechanika kwantowa 2

7

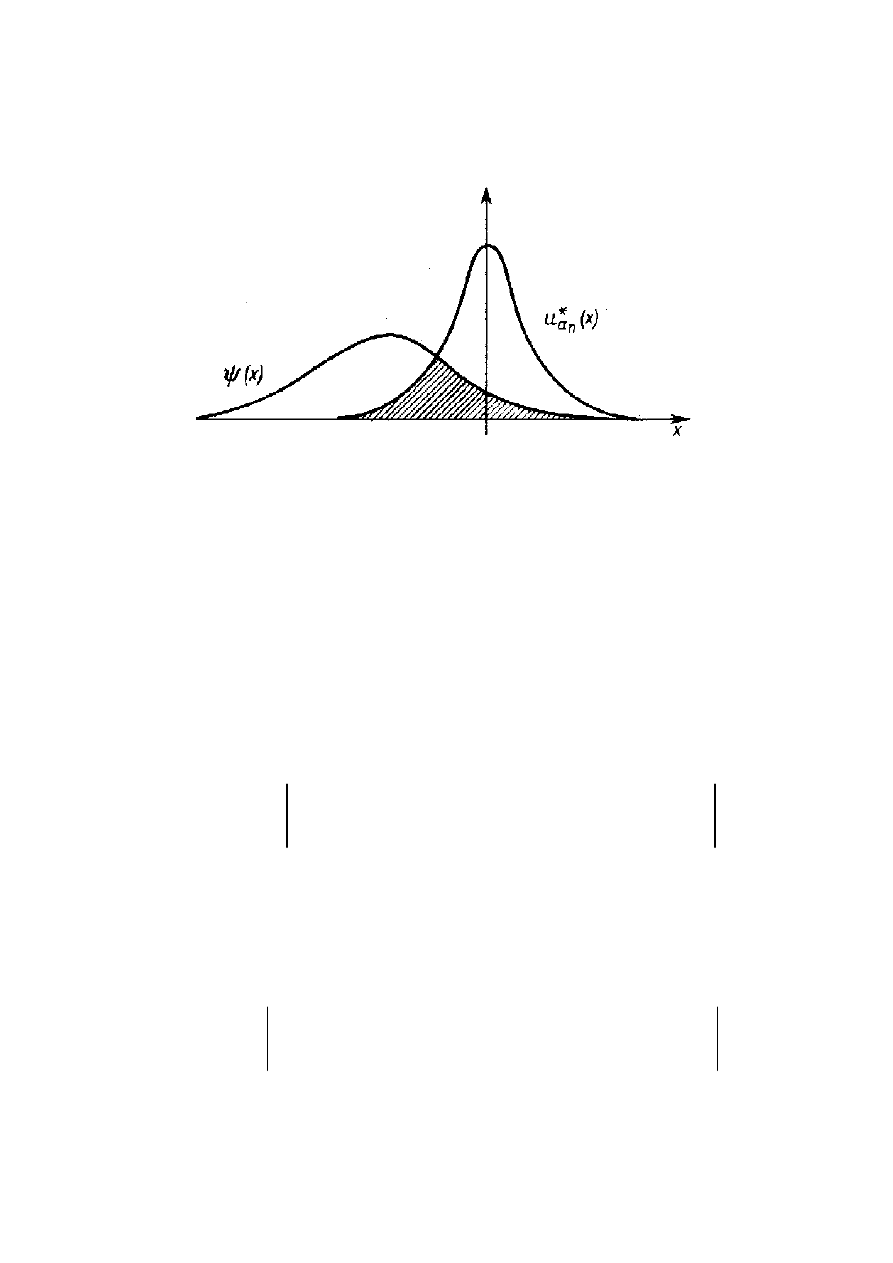
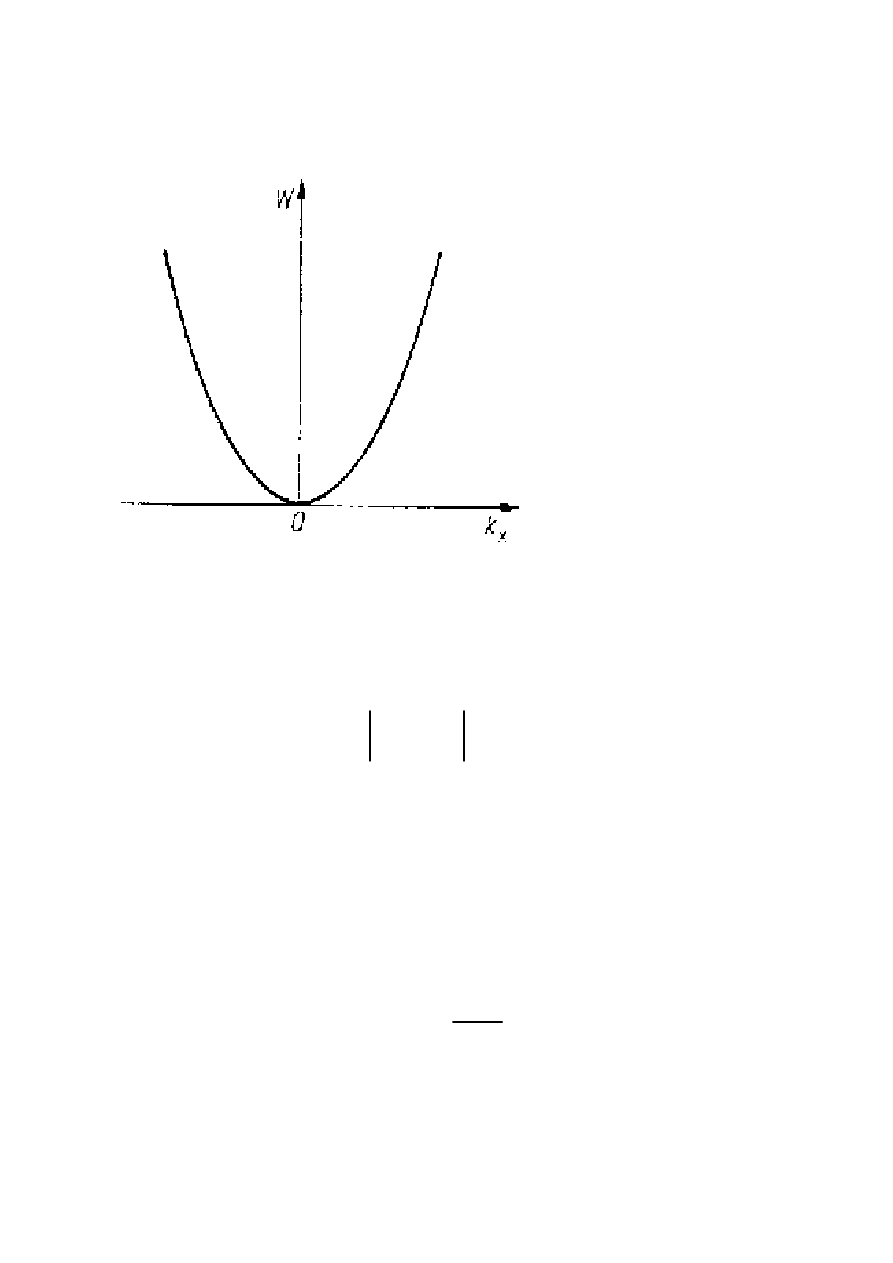
ELEKTRON SWOBODNY

wektor falowy

k = p/ħ

częstość

kołowa

ω

= E

/ ħ

Gęstość prawdopodobieństwa znalezienia elektronu

2

2

)

(

A

x

=

ψ

nie zależy od położenia.

Dozwolone są dowolne wartości energii kinetycznej

m

p

E

2

2

=

na wykresie W ≡ E oznacza energię całkowitą

EWR mechanika kwantowa 2

8

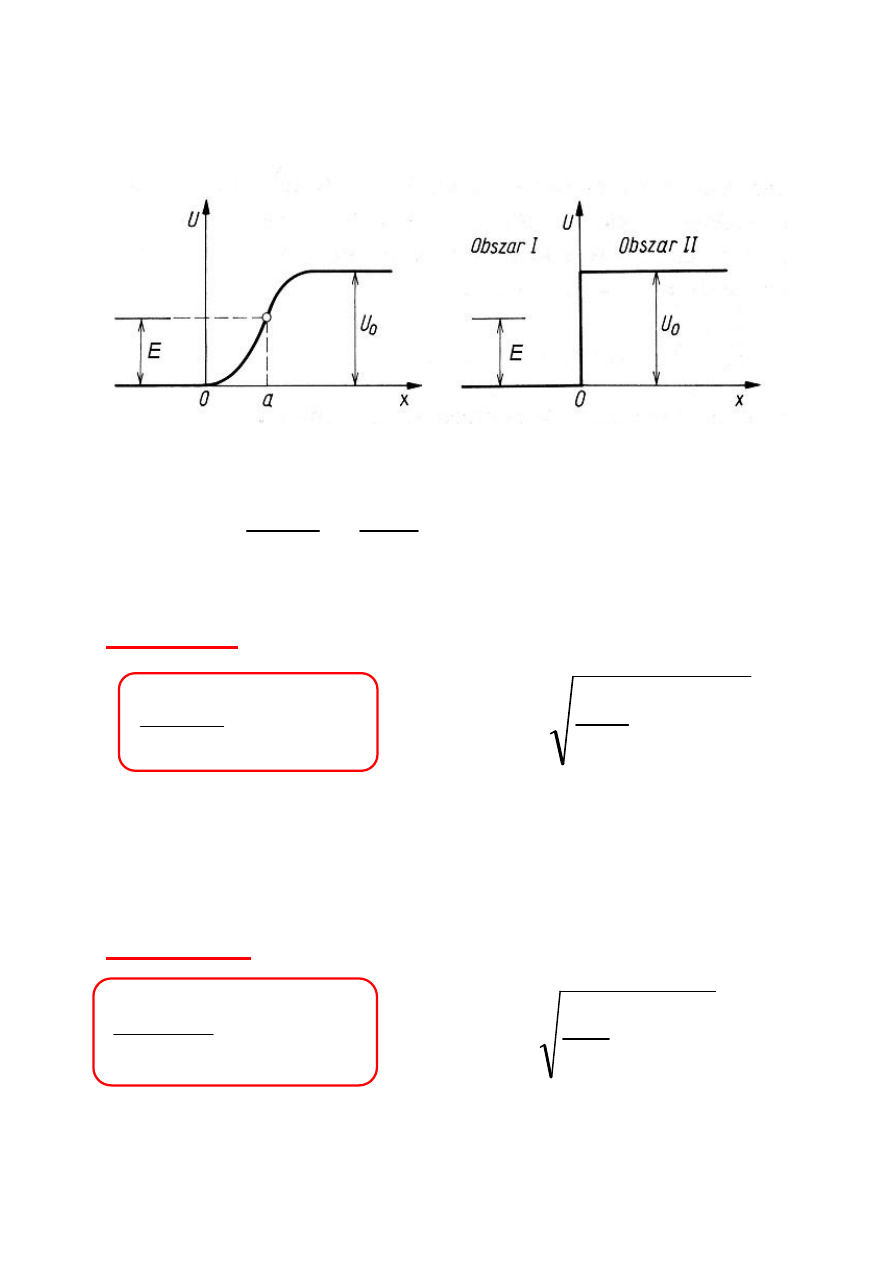
SKOK POTENCJAŁU

stacjonarne równanie Schrödingera

(

)

0

2

2

2

2

=

ψ

−

+

∂

ψ

∂

U

E

m

x

h

Obszar I E - U > 0

1

2

1

2

1

2

ψ

ψ

k

dx

d

−

=

(

)

U

E

m

k

−

=

2

1

2

h

rozwiązanie w postaci

)

exp(

)

exp(

)

(

1

1

1

x

ik

B

x

ik

A

x

−

+

=

ψ

Obszar II E - U < 0

1

2

2

2

1

2

ψ

ψ

k

dx

d

=

(

)

E

U

m

k

−

=

2

2

2

h

rozwiązanie w postaci

)

exp(

)

exp(

)

(

2

2

2

x

k

D

x

k

C

x

+

−

=

ψ

EWR mechanika kwantowa 2

9

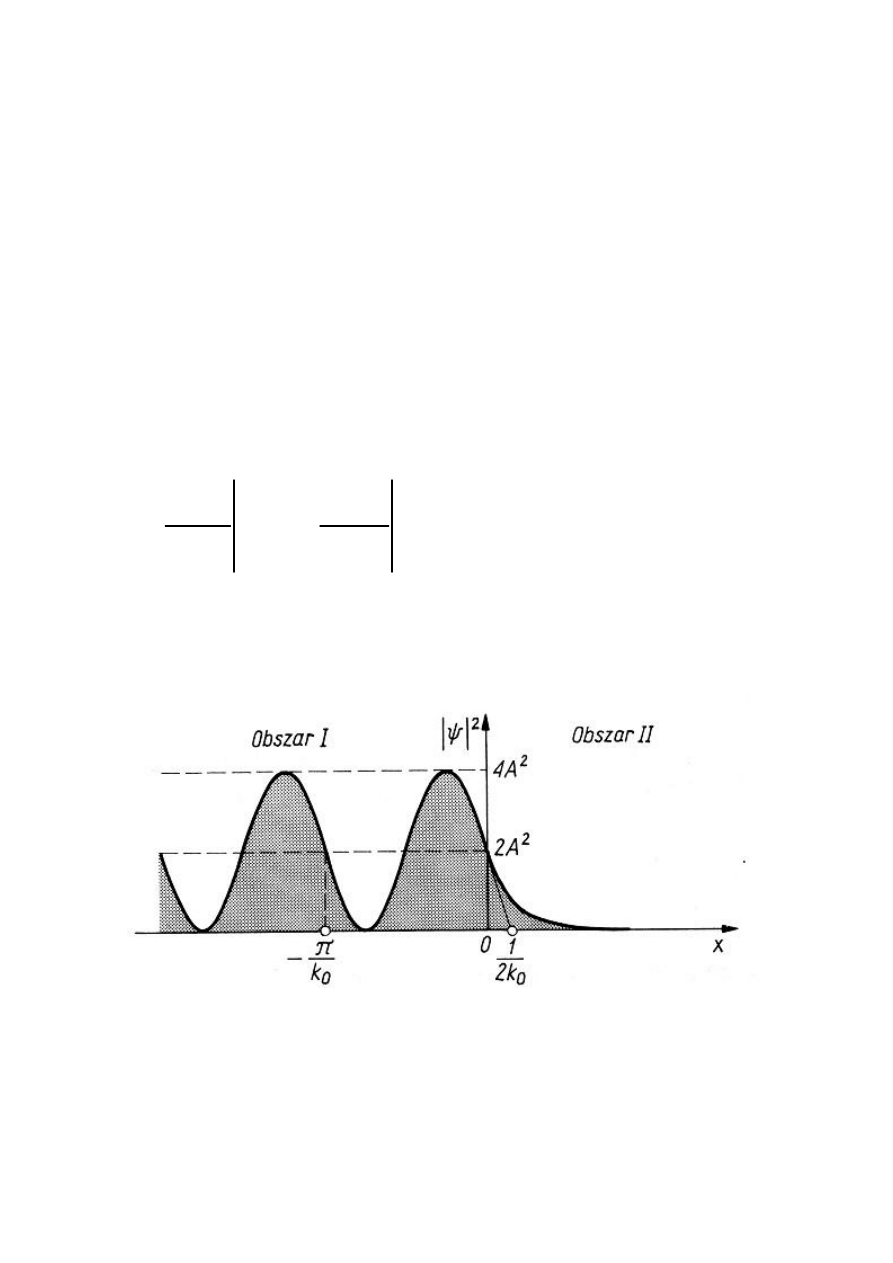
SKOK POTENCJAŁU

D = 0

)

exp(

)

exp(

)

(

1

1

1

x

ik

B

x

ik

A

x

−

+

=

ψ

)

exp(

)

(

2

2

x

k

C

x

−

=

ψ

Warunki dopasowania dla x = 0

)

0

(

)

0

(

2

1

ψ

ψ

=

0

2

0

1

=

=

=

x

x

dx

d

dx

d

ψ

ψ

dają amplitudy A, B i C

Jan Hennel, rys 2/4

EWR mechanika kwantowa 2

10

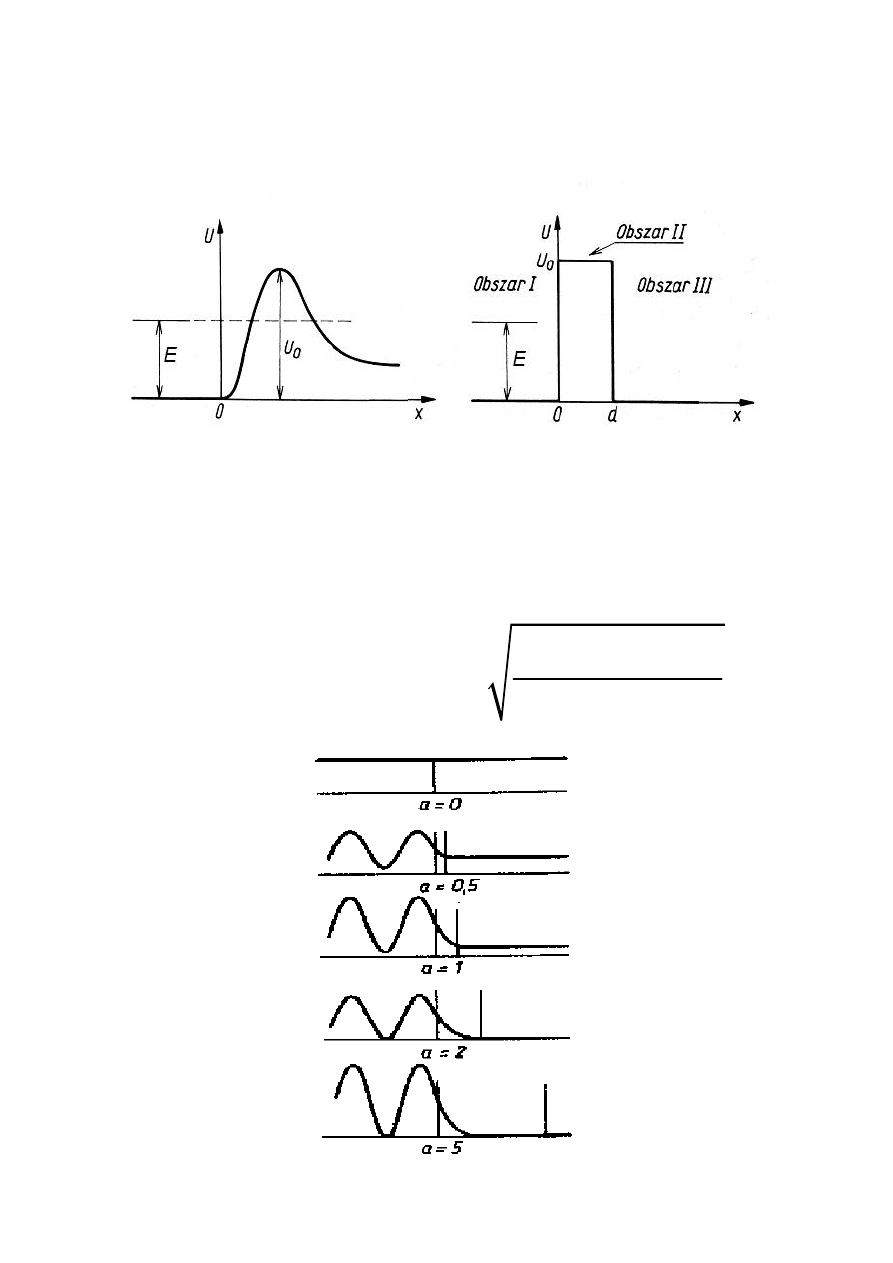
BARIERA POTENCJAŁU

Istnieje różne od zera prawdopodobieństwo

przeniknięcia cząstki przez barierę potencjału.

Współczynnik transmisji:

2 kd

T

e

−

≈

2

0

2

8

(

)

m U

E

k

h

π

−

=

EWR mechanika kwantowa 2

11

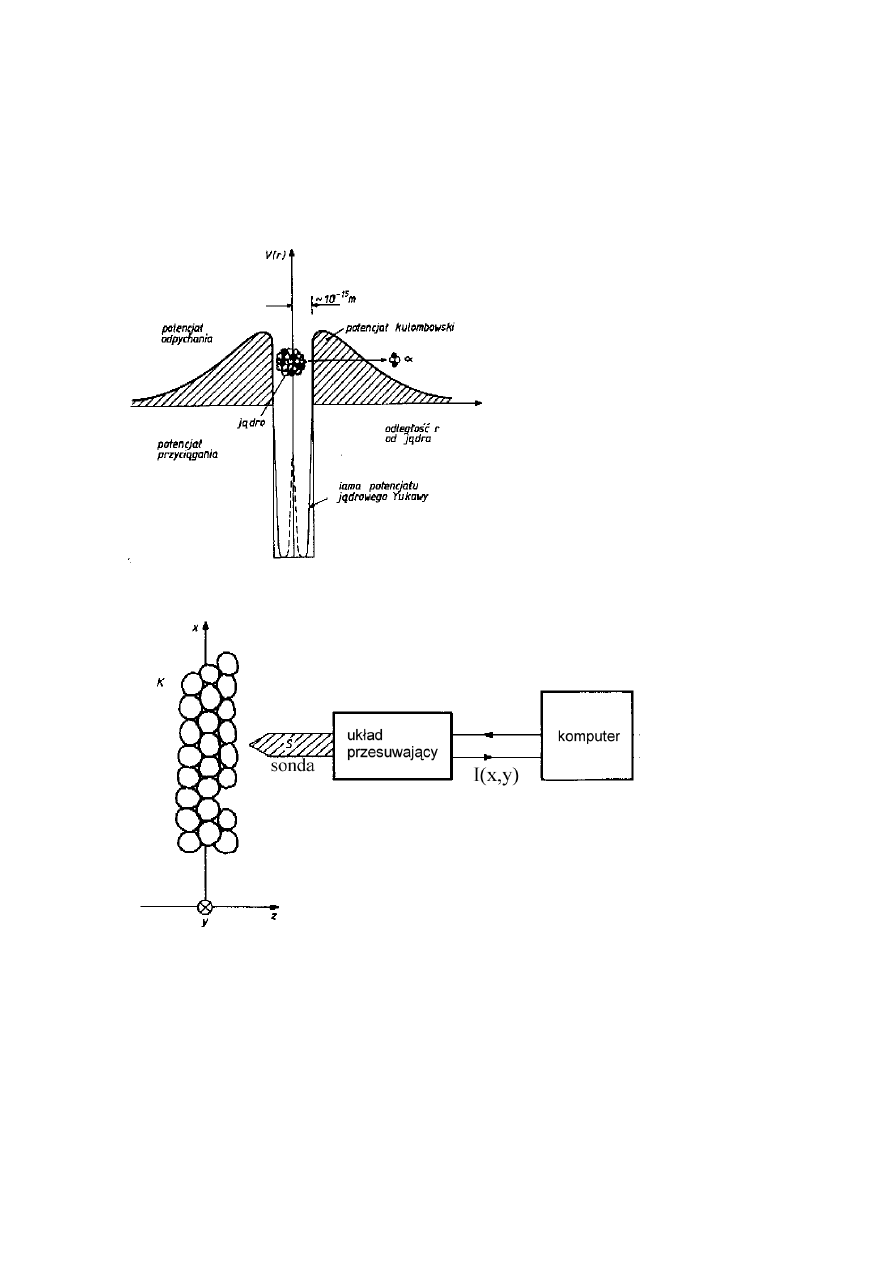
ZJAWISKO TUNELOWE

przechodzenie cząstek
alfa przez barierę
potencjału w jądrze
atomowym

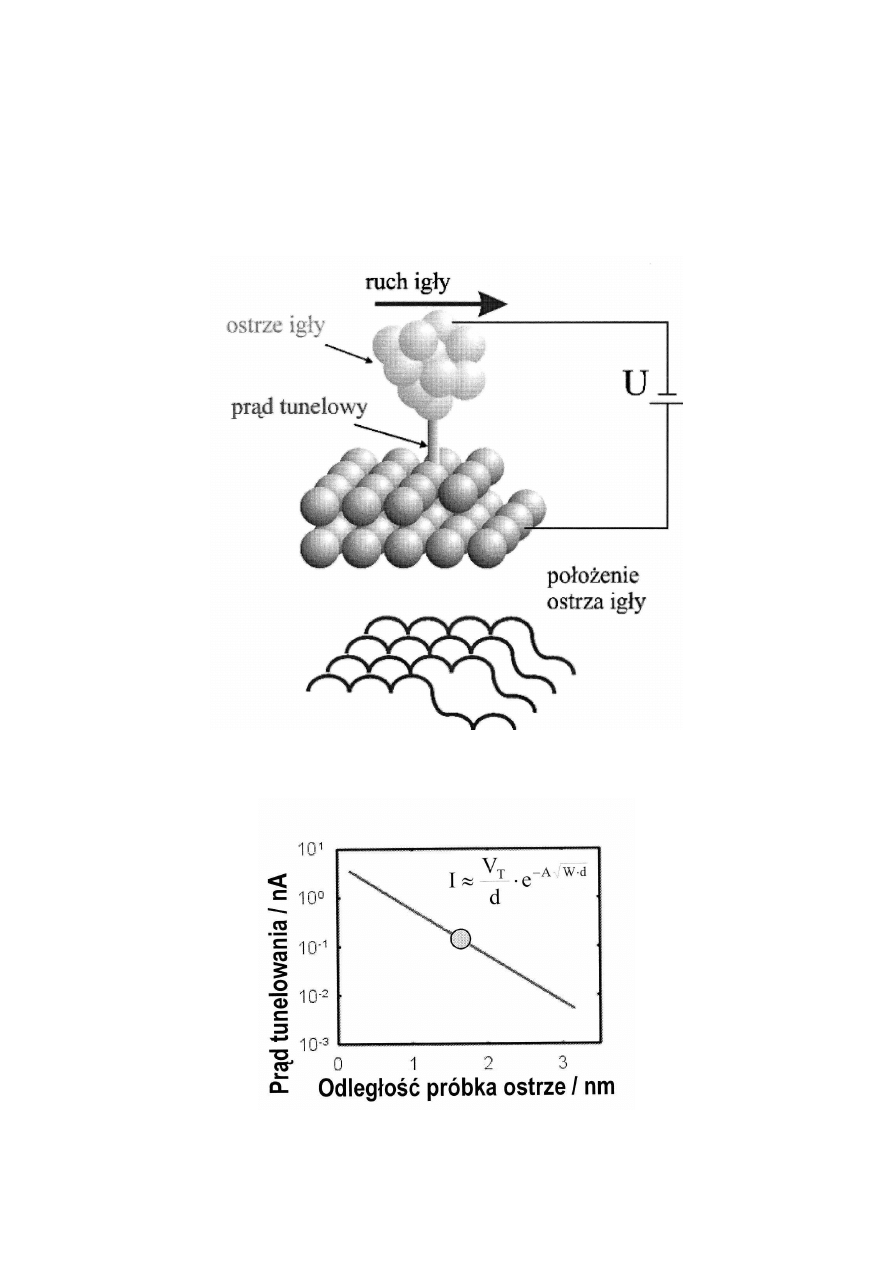
Mikroskop

tunelowy

Skaningowy mikroskop tunelowy (STM od

Scanning Tunneling Microscope) - umożliwia

uzyskanie obrazu powierzchni materiałów

przewodzących ze zdolnością rozdzielcza rzędu

pojedynczego atomu.

EWR mechanika kwantowa 2

12

TUNELOWY MIKROSKOP

SKANINGOWY

EWR mechanika kwantowa 2

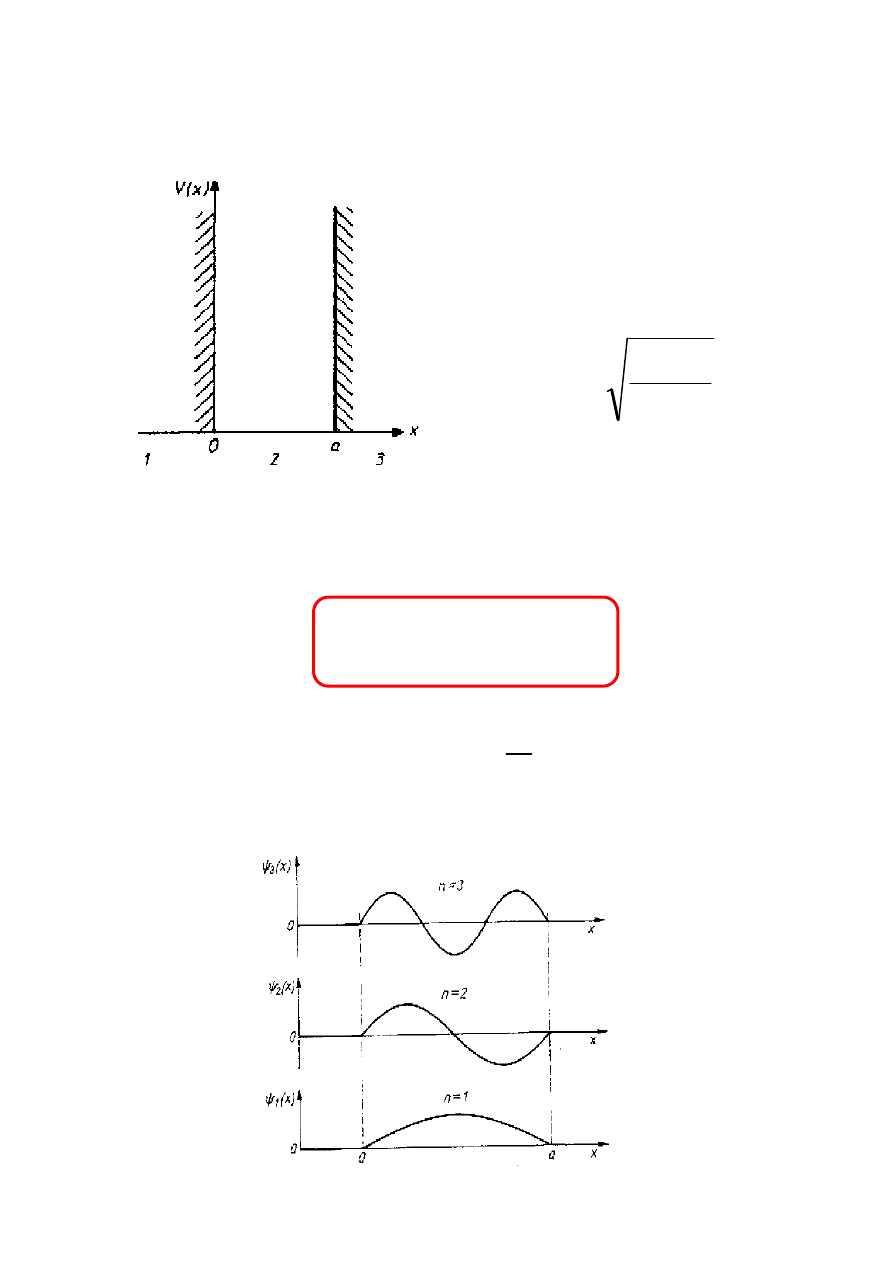
13

NIESKOŃCZONA STUDNIA POTENCJAŁU

ikx

ikx

Be

Ae

x

−

+

=

)

(

ψ

2

2

h

mW

k

=

Rozwiązaniem równania Schrödingera są funkcje
falowe o postaci:

)

sin(

'

)

(

kx

A

x

=

ψ

a

n

k

n

π

=

funkcje falowe:

EWR mechanika kwantowa 2

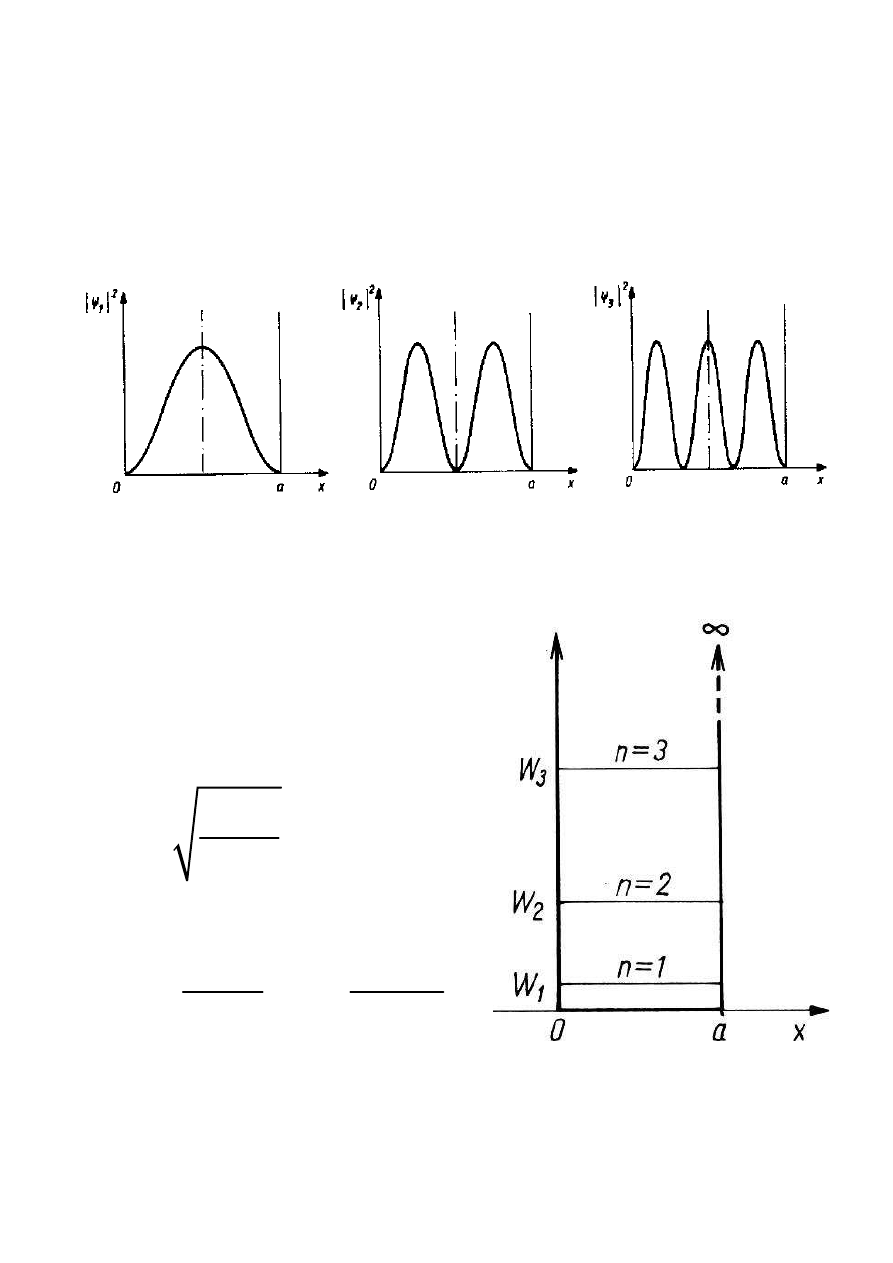
14

NIESKOŃCZONA STUDNIA POTENCJAŁU

Gęstość prawdopodobieństwa:

Poziomy energetyczne:

2

2mE

k

=

h

2 2

2

2

2

2

8

k

h

E

n

m

ma

=

=

h

W≡E

E

EWR mechanika kwantowa 2

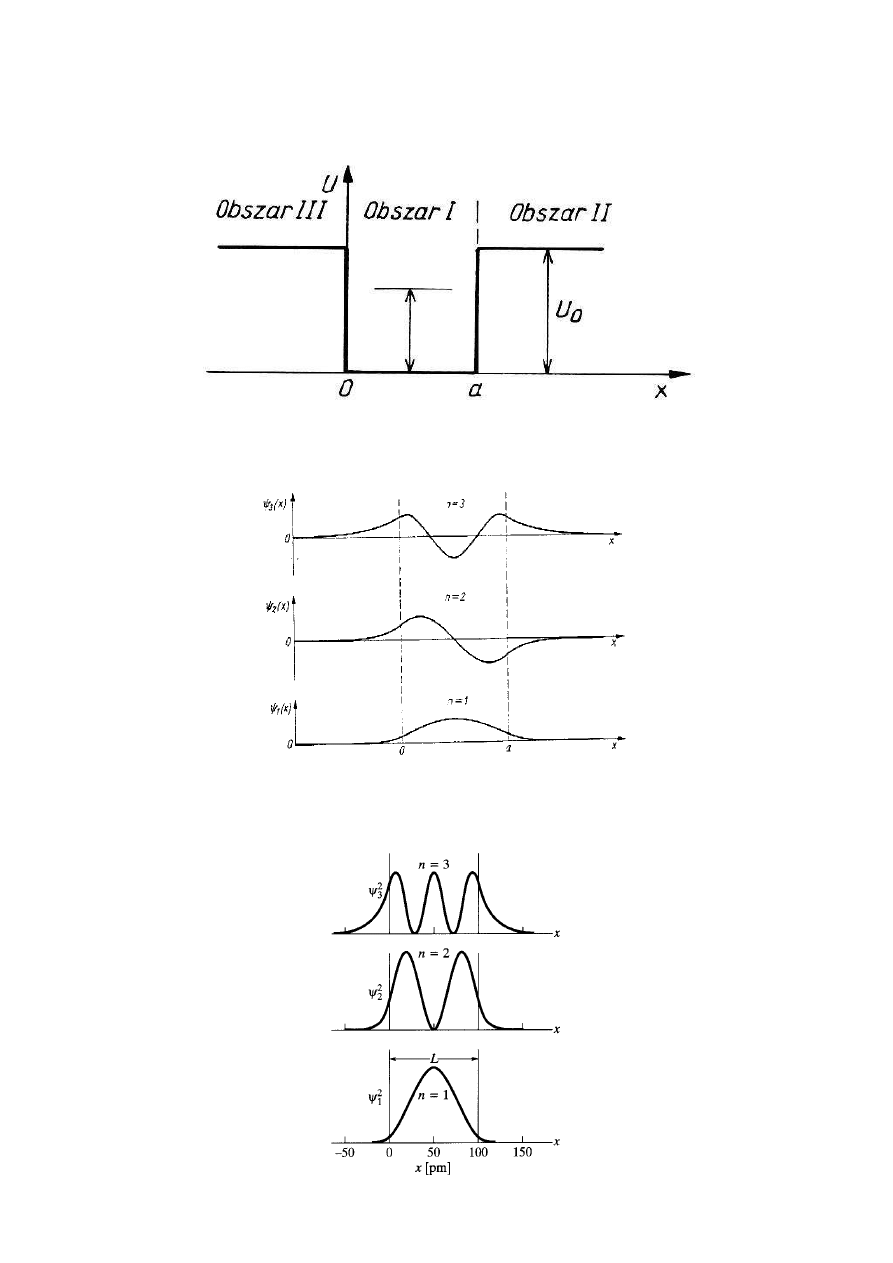
15

SKOŃCZONA STUDNIA POTENCJAŁU

Funkcje falowe

gęstość prawdopodobieństwa

E

EWR mechanika kwantowa 2

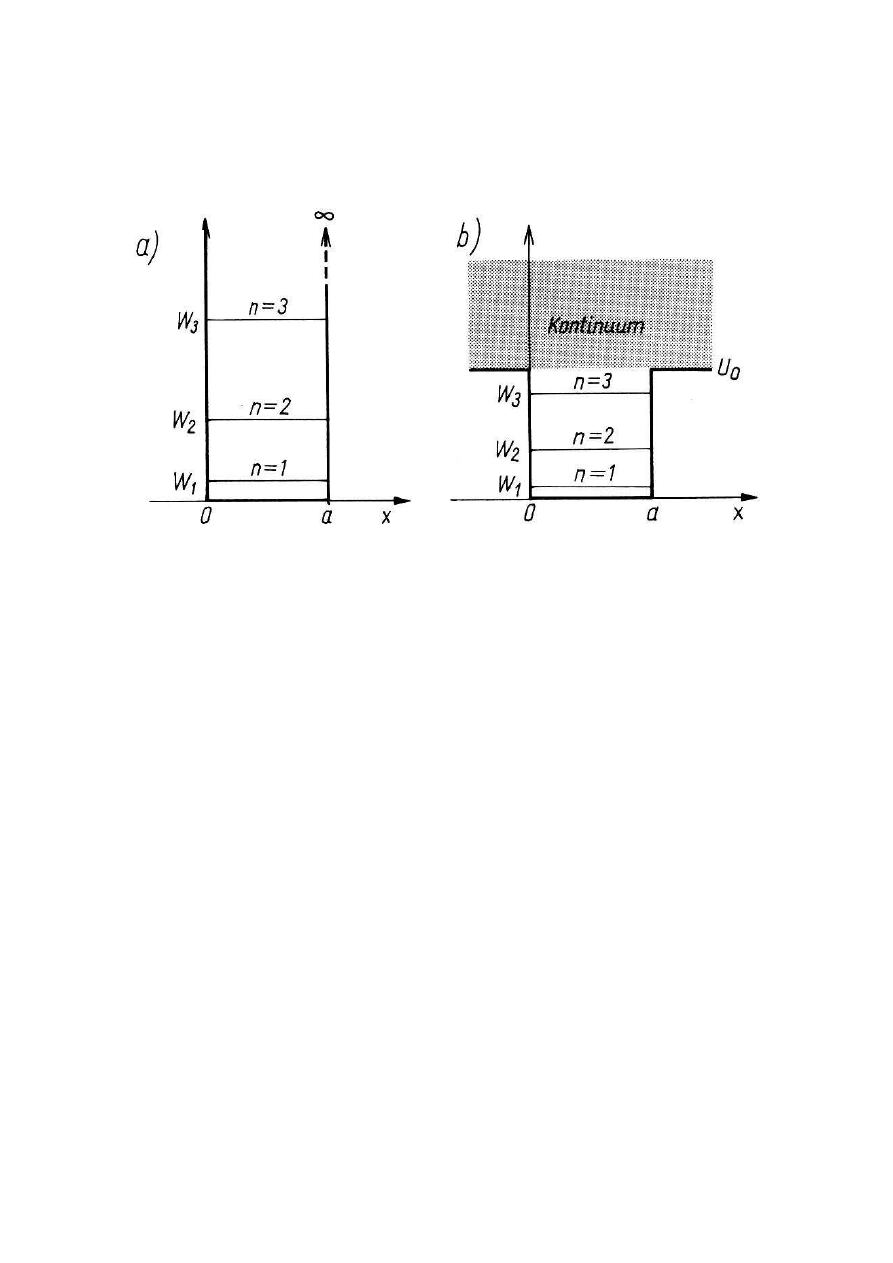
16

POZIOMY ENERGETYCZNE

W≡E

Zasada lokalizacji

Lokalizacji fali w przestrzeni prowadzi
do kwantyzacji, a więc do powstania
dyskretnych stanów o dyskretnych
energiach. Zlokalizowana cząstka może
mieć tylko takie energie.

Zasada korespondencji

Dla dostatecznie dużych liczb kwantowych
przewidywania fizyki kwantowej przechodzą
w sposób ciągły w przewidywania fizyki
klasycznej.

E

E

E

EWR mechanika kwantowa 2

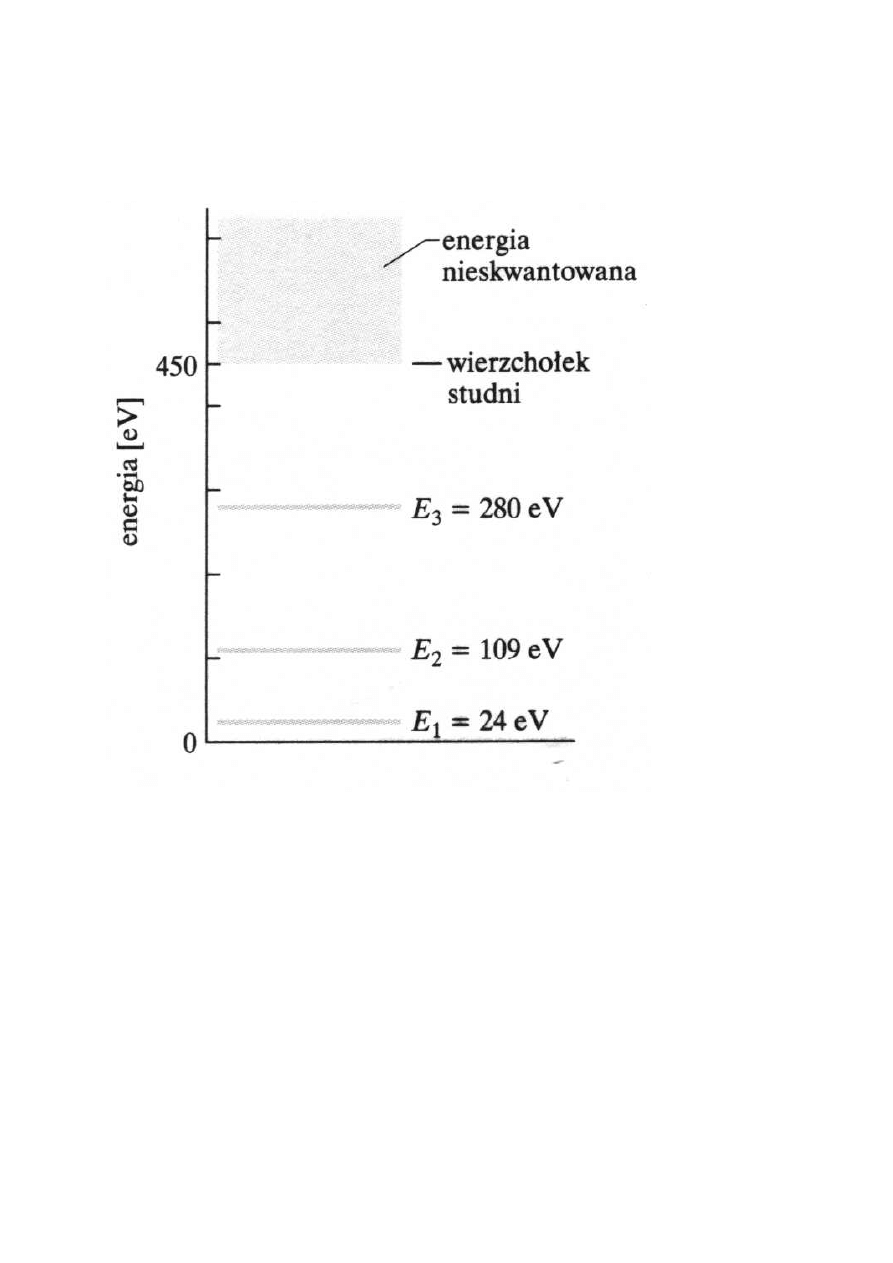
17

STANY ZWIĄZANE

U

0

= 450 eV L =100 pm