Obwody Elektryczne 2
Doc. dr inż. Hanna Morawska
Zakład Elektrotechniki Teoretycznej
Instytut Elektrotechniki Teoretycznej,
Metrologii i Materiałoznawstwa
Tel.0 42 631 25 15
mail: haniamo@p.lodz.pl
lub haniamo@o2.pl
Konsultacje:
środa, godz. 13:30- 15:00
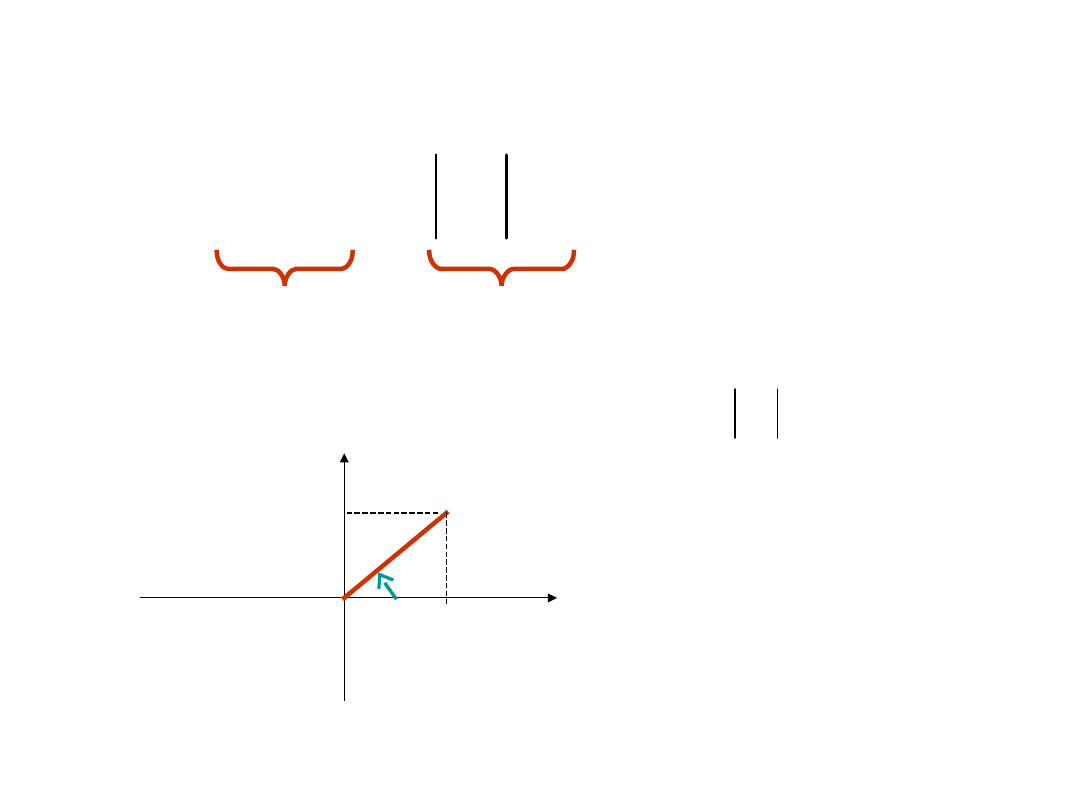
Podstawowe właściwości liczb
zespolonych
j
e
X
jb
a
x
Postać algebraiczna
Postać
wykładnicza
a
- cześć rzeczywista
liczby x
b
- część urojona
liczby x
Re x
Im x
x
a
b
X
- moduł liczby x
- argument liczby x
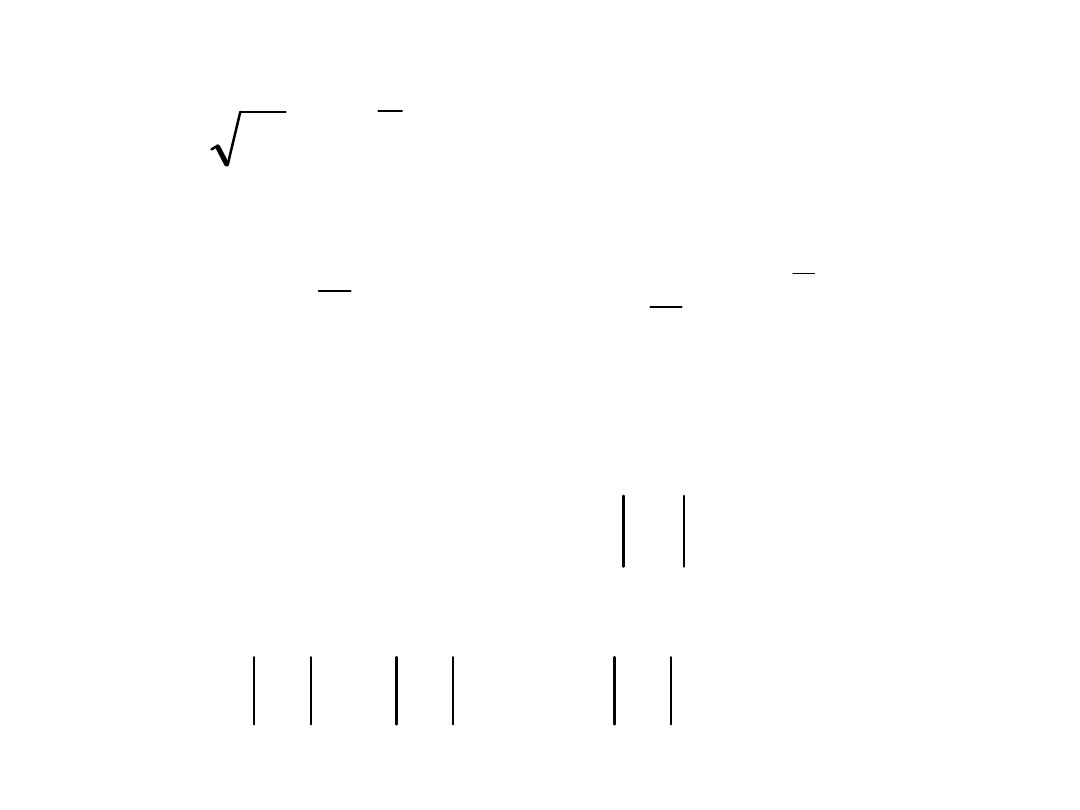
2
j
e
1
-
j
2
j
-
e
j
-
j
e
j
j
j
j
j
2
2
1
1
)
(
1
-j
e
j
X
b
a
x
liczba zespolona sprzężona z
x
2
2
2
b
a
X
e
X
e
X
x
x
j
j
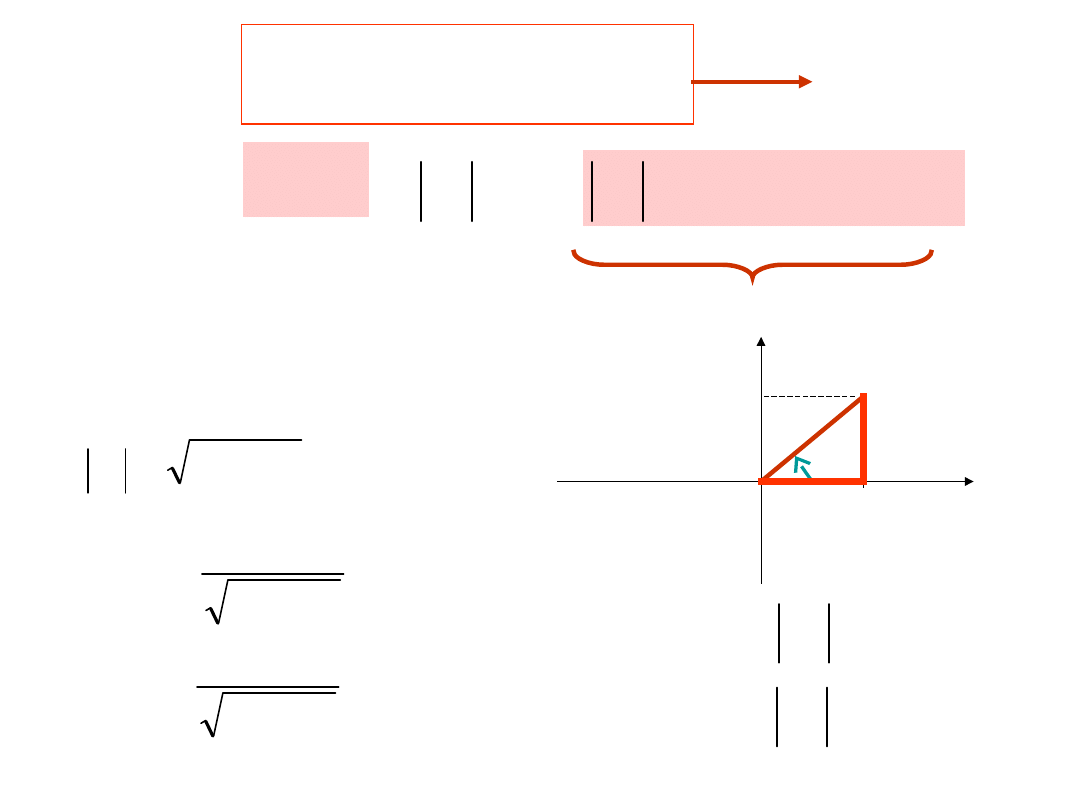
Wzór
Eulera
jsin
cos
e
j
to
Ponieważ
sin
cos
e
j
j
j
X
X
b
a
x
Jak przejść z jednej postaci do
drugiej ?
2
2
b
a
X
2
2
2
2
sin
cos
b
a
b
b
a
a
oraz
sin
cos
X
b
X
a
postać
trygonometryczna
Re x
Im x
x
a
b
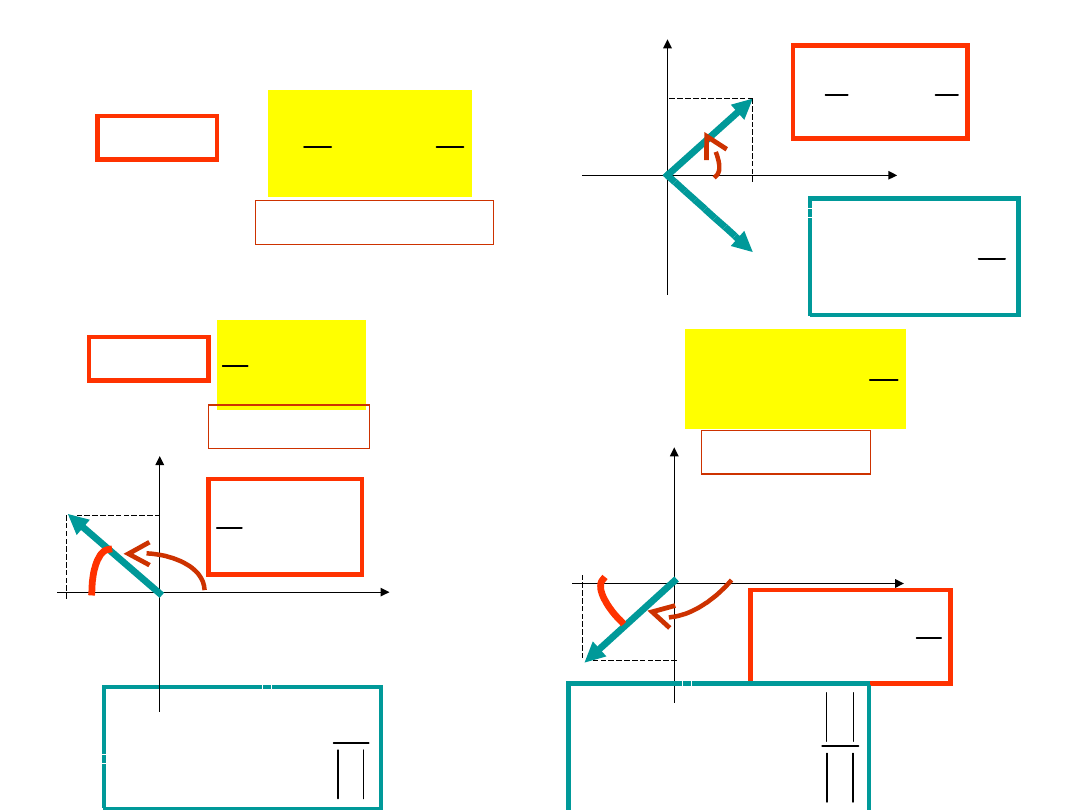
UWAGA!!! Jeżeli
a > 0
2
2
a < 0
a
b
tg
arc
2
lu
b
2
a
tg
arc
b
a
b
Im
Re
a
b
Im
Re
2
2
2
a
b
Im
Re
2
a
b
tg
arc
b
a
x
j
I lub IV ćwiartka
II ćwiartka
III ćwiartka
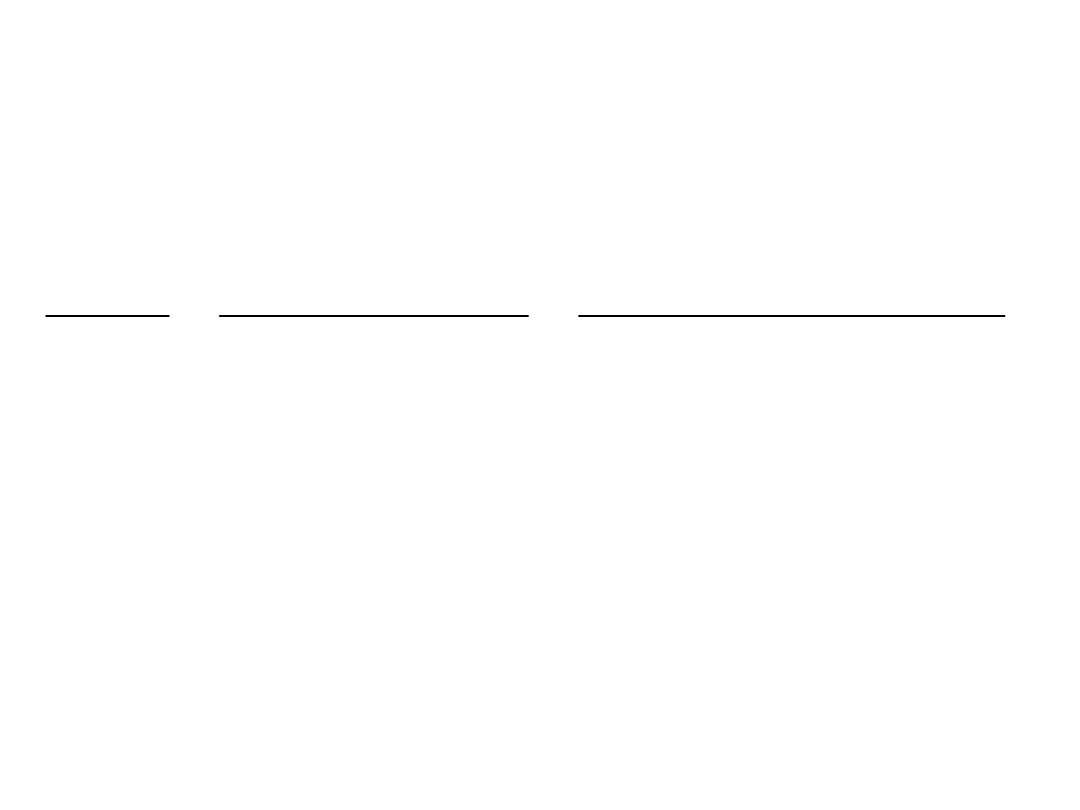
Podstawowe obliczenia dla liczb
zespolonych
)]
(
)
[(
)
)(
(
ad
bc
j
bd
ac
jd
c
jb
a
2
2
)
(
)
(
)
)(
(
)
)(
(
d
c
ad
bc
j
bd
ac
jd
c
jd
c
jd
c
jb
a
jd
c
jb
a
)
(
)
(
)
(
)
(
d
b
j
c
a
jd
c
jb
a
)
(
)
(
)
(
)
(
d
b
j
c
a
jd
c
jb
a
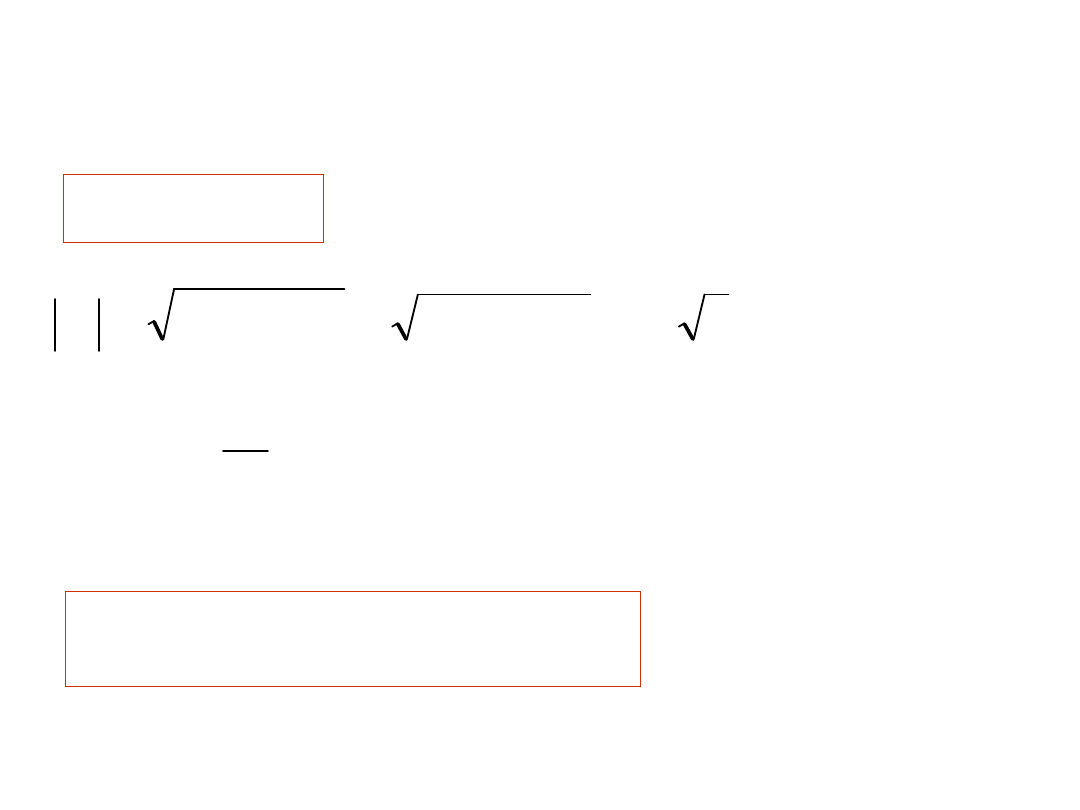
Przedstawimy liczbę daną w postaci algebraicznej w postaci
wykładniczej:
20
10 j
x
3
,
22
5
10
400
100
20
10
2
2
X
44
,
63
10
20
arctg
więc
44
,
63
3
,
22
20
10
j
e
j
x
A)
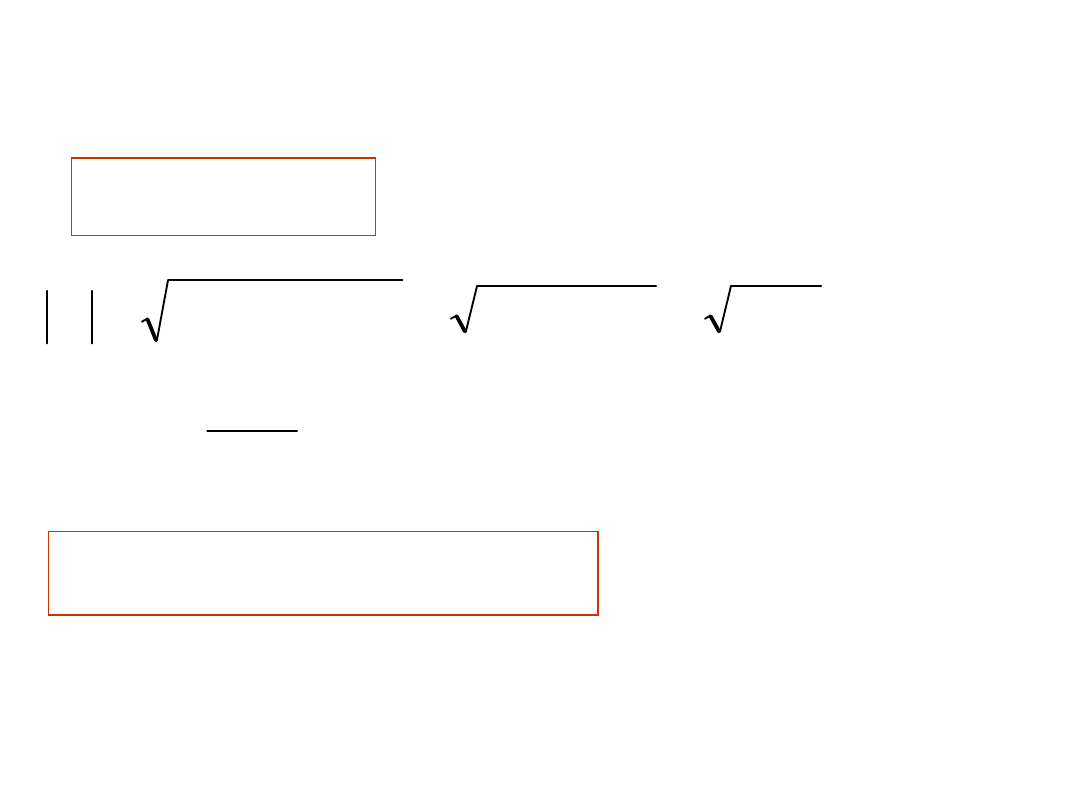
B)
20
30 j
x
05
.
36
1300
400
900
)
20
(
30
2
2
X
69
.
33
30
)
20
(
arctg
69
.
33
05
.
36
20
30
j
e
j
x
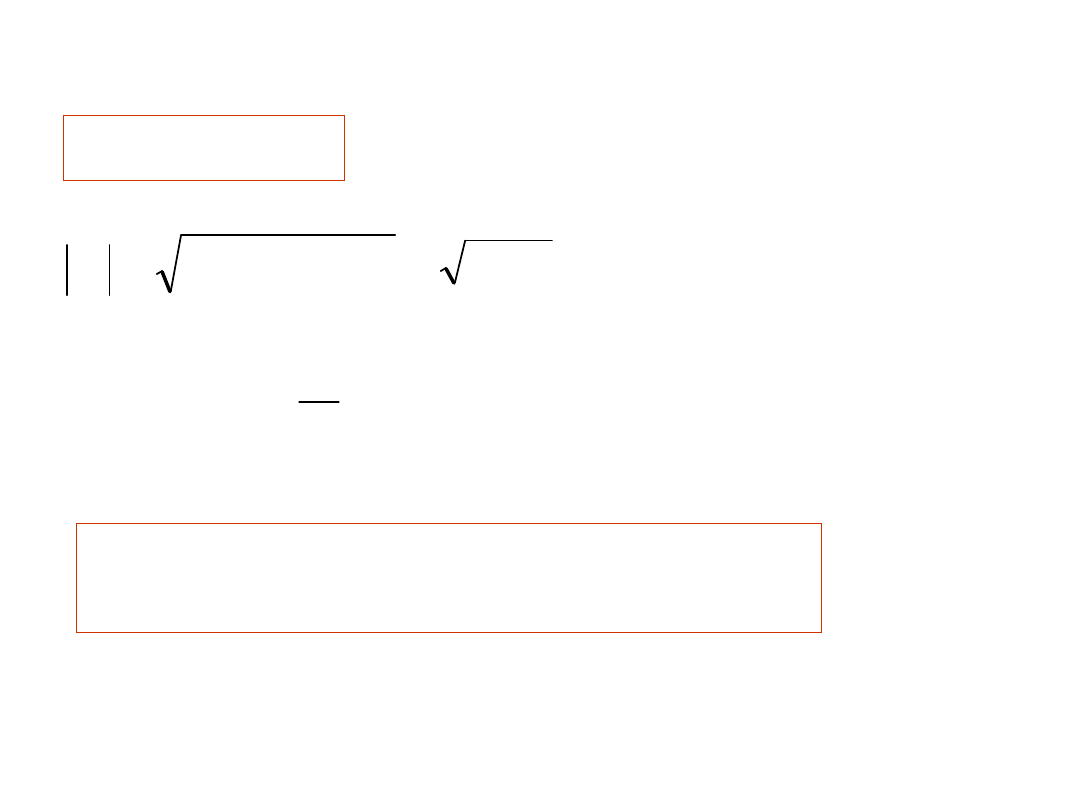
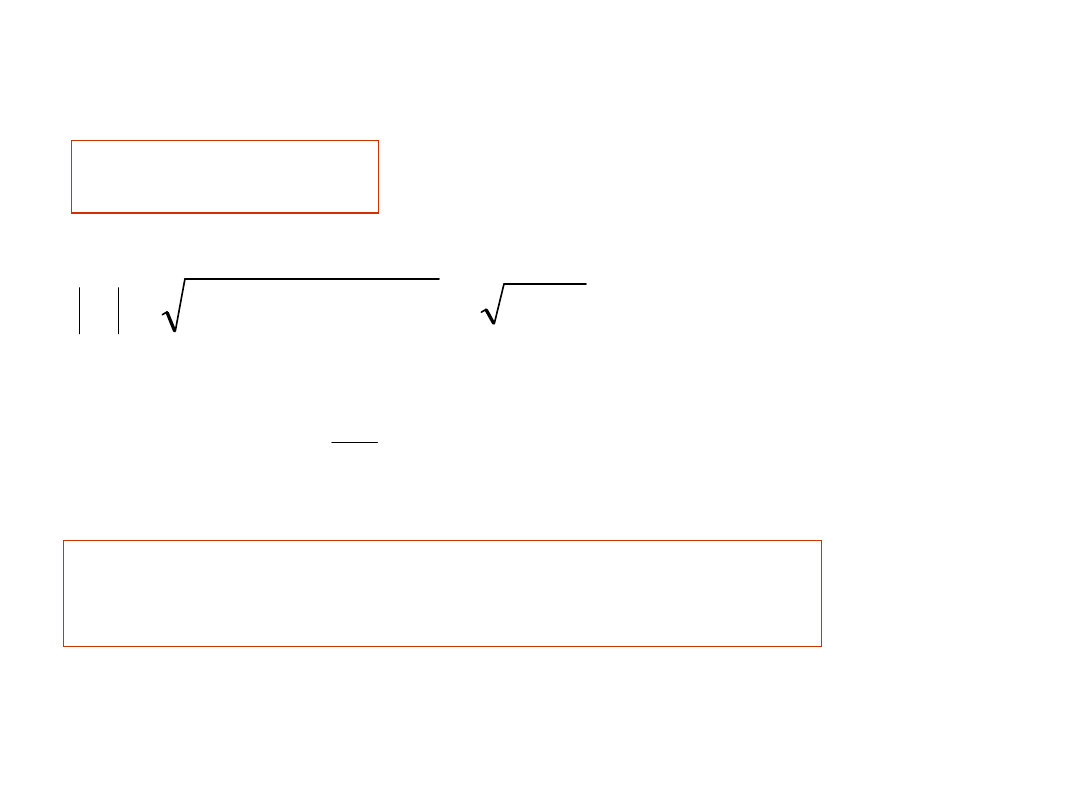
60
40 j
x
C)
11
,
72
5200
60
)
40
(
2
2
X
69
.
123
31
.
56
180
40
60
180
arctg
69
,
123
11
,
72
60
40
j
e
j
x
D)
50
20 j
x
85
.
53
2900
)
50
(
)
20
(
2
2
X
0
0
0
0
82
,
111
2
,
68
180
20
50
180
arctg
0
82
.
111
85
.
53
50
20
j
e
j
x
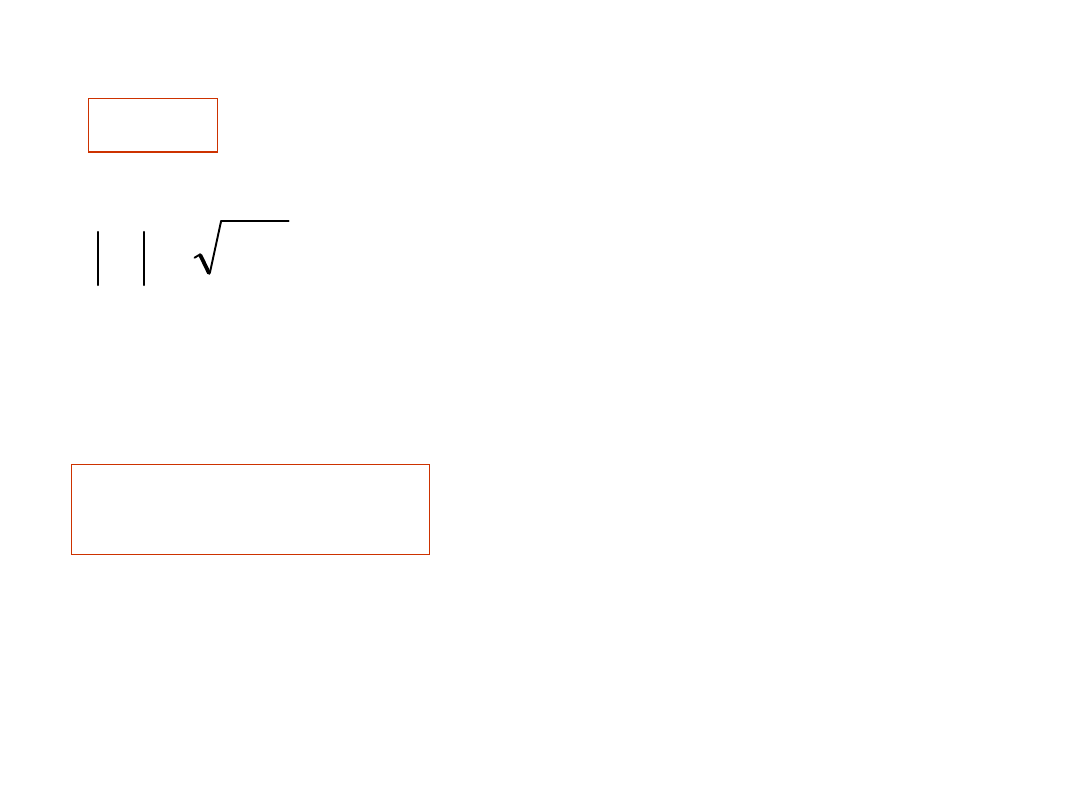
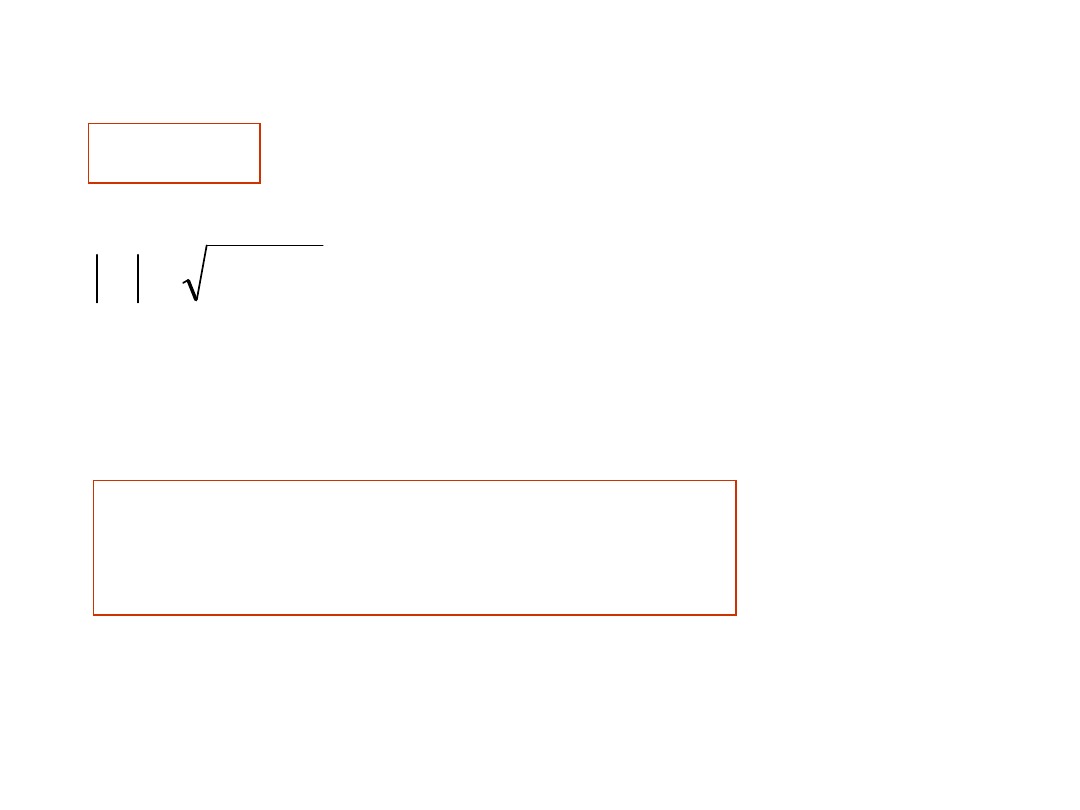
20
x
0
E)
10
10
2
X
0
10
10
j
e
x
30
x
30
)
30
(
2
X
180
180
30
30
j
e
x
E)
180
lub
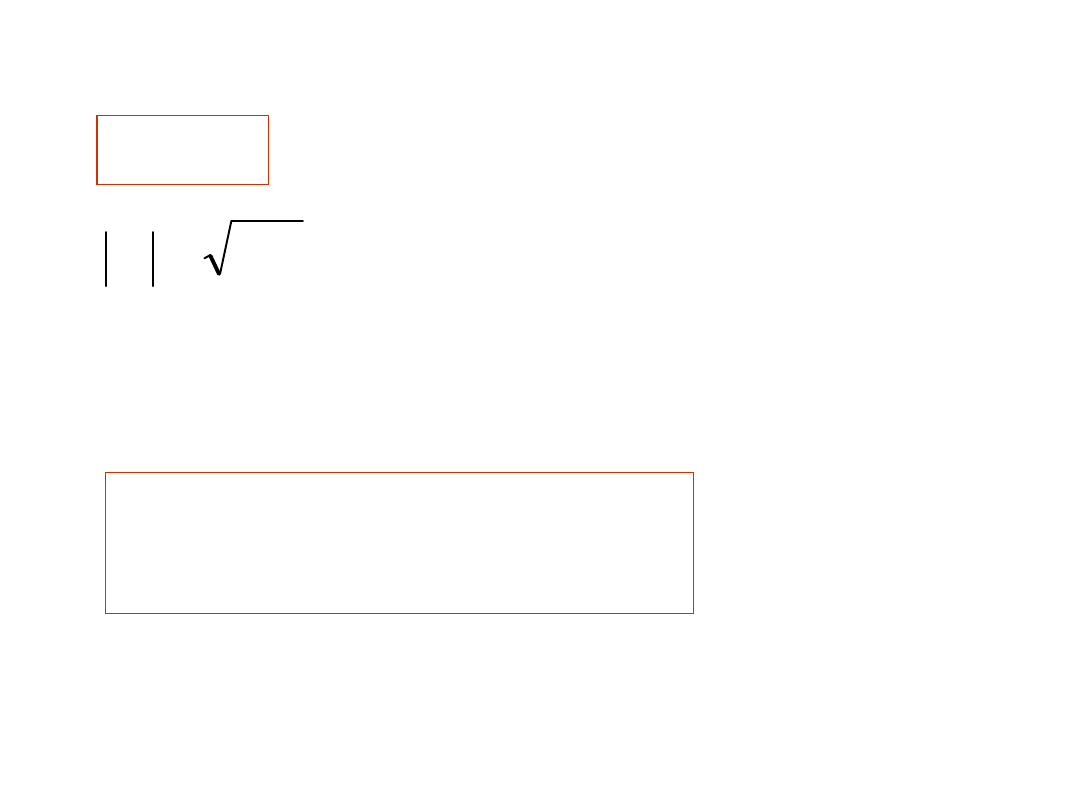
F)
50
j
x
50
50
2
X
90
90
50
50
j
e
j
x
20
j
x
20
)
20
(
2
X
o
90
o
j
e
j
x
90
20
20
o
o
o
o
o
j
j
j
j
e
e
e
e
15
)
60
45
(
60
45
2
10
20
10
20
o
o
o
o
o
j
j
j
j
e
e
e
e
30
)
30
60
(
30
60
600
600
20
30
Metoda symboliczna
Metoda ta polega na zamodelowaniu przebiegów
sinusoidalnych prądów i napięć za pomocą
liczb zespolonych.
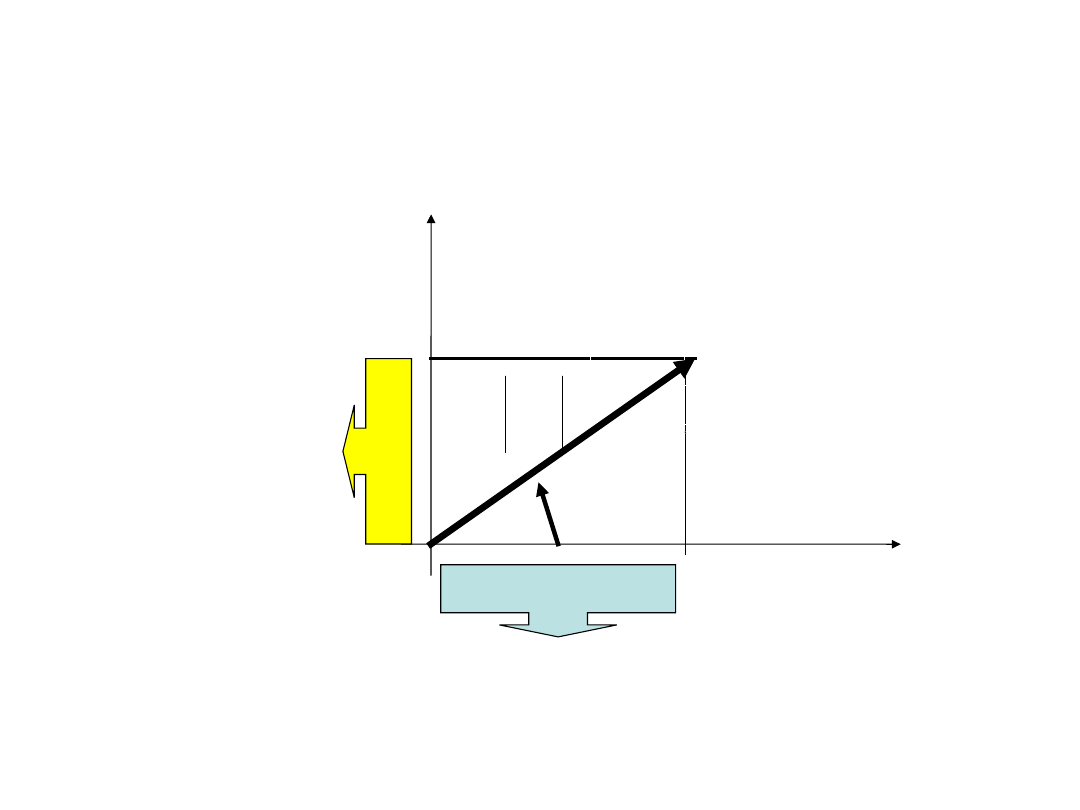
sin
j
cos
e
j
Wzór Eulera
Im(A)
Re(A)
A
A
a=Re(A
)
b=Im(A)
Podstawowe zależności metody symbolicznej:
x
x
m
t
j
m
mt
t
sin
j
t
cos
X
e
X
X
x
Wprowadzimy zespoloną funkcję czasu:
)
t
(
x
t
sin
X
X
Im
x
m
mt
)
t
(
x
t
cos
X
X
Re
x
m
mt
x
m
t
X
t
x
sin
)
(
Chcemy zamodelować funkcję sinus:
Definicja wartości symbolicznej
(zespolonej) wielkości sinusoidalnej
Wartością symboliczną (
zespoloną
) wielkości
sinusoidalnie zmiennej:
x
m
t
sin
X
)
t
(
x
nazywamy wyrażenie postaci:
x
j
e
X
X
gdzie
2
X
X
m
jest wartością skuteczną
funkcji sinusoidalnej x(t)
x
jest fazą początkową
funkcji sinusoidalnej x(t)
t
j
Xe
2
Im
)
t
(
x
)
t
(
x
)
t
sin(
X
e
X
Im
e
e
X
2
Im
Xe
2
Im
)
t
(
x
x
m
)
t
(
j
m
t
j
j
t
j
x
x
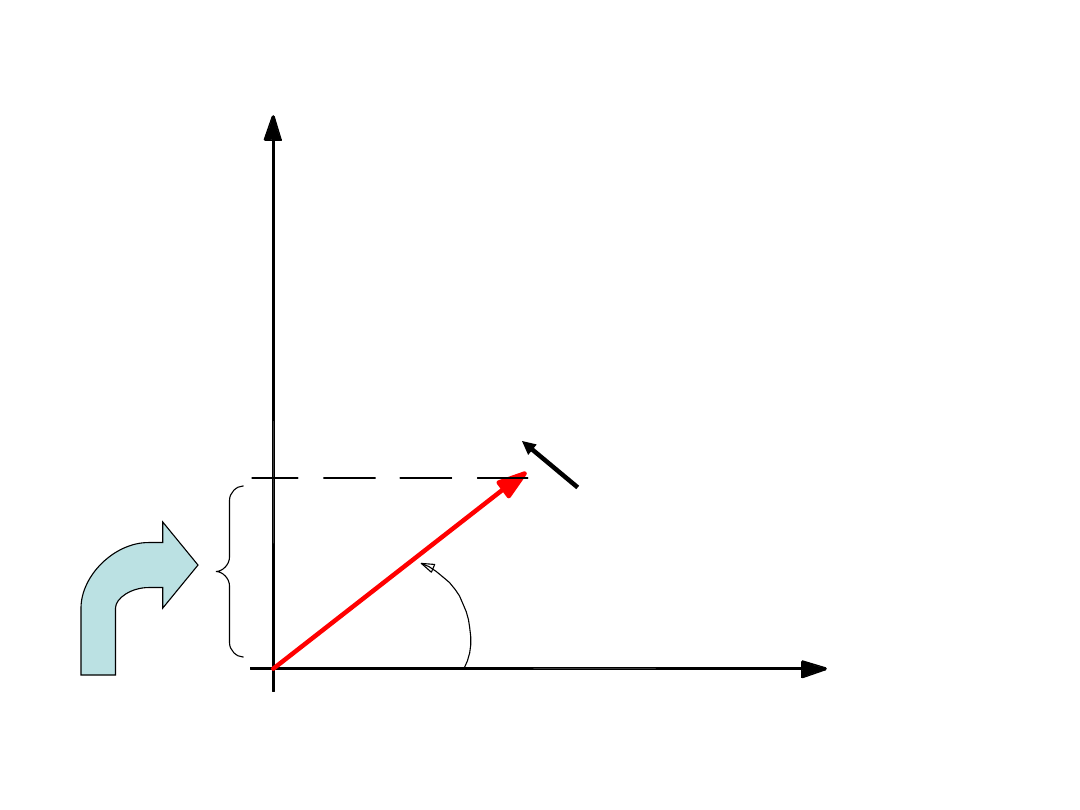
X
m
x
t
x
m
t
sin
X
)
t
(
x
Wskaz ruchomy
Im(X
mt
)
Re(X
mt
)
Jak przejść od praw obwodowych
zapisanych dla wartości chwilowych
do zależności dla wartości zespolonych?
Chcemy zbudować zależności
dla prądów i napięć dla elementów idealnych:
opornika, cewki i kondensatora
Ri
u
dt
di
L
u
dt
du
C
i
oraz prawa Kirchhoffa.
Lemat 1
J
eż
e
l
i
k
j
e
s
t
l
i
c
z
bą
r
z
e
c
z
y
w
i
s
t
ą
,
z
a
ś
)
(
t
z
k
z
e
s
p
o
l
o
ną
f
u
n
k
c
j
ą
c
z
a
s
u
(
k
=
1
,
.
.
.
m
)
,
t
o
)
(
Im
)
(
Im
1
1
t
z
t
z
k
m
k
k
m
k
k
k
Lemat 2
Jeżeli
,
2
t
j
mt
Xe
X
gdzie
j
e
x
X
X
to
mt
mt
mt
X
j
X
dt
d
X
dt
d
Im
Im
Im
Lemat 3
Jeżeli
t
j
Be
t
Im
Ae
Im
:
t
j
gdzie A i B są liczbami zespolonymi to:
B
A
m
k
k
i
1
0
t
j
k
k
e
I
i
2
Im
0
2
Im
1
t
j
k
m
k
e
I
Korzystamy z LEMATU 1:
0
2
Im
1
m
k
t
j
k
e
I
)
0
Im(
2
Im
1
t
j
m
k
t
j
k
e
e
I
Lemat 3
0
1
m
k
k
I
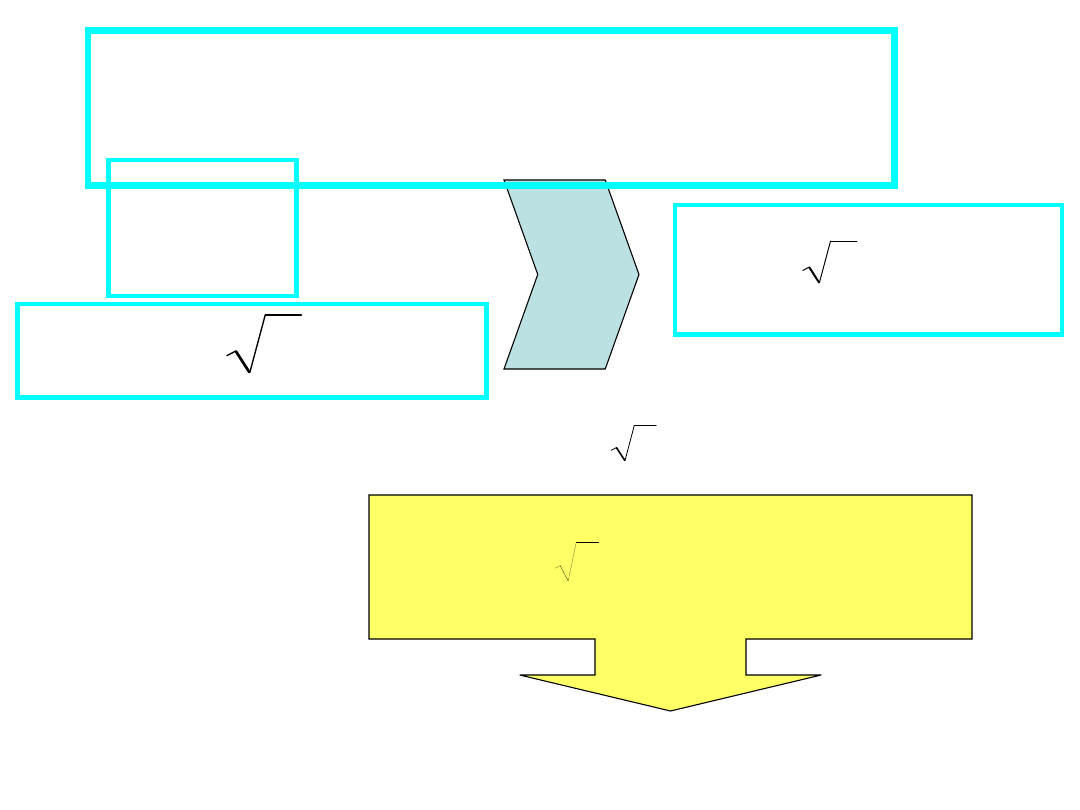
Prawa Kirchhoffa - PPK
0
1
m
k
k
I
PPK:
n
k
k
u
1
0
t
j
k
k
e
U
u
2
Im
0
2
Im
1
t
j
k
n
k
e
U
Korzystamy z LEMATU 1:
0
2
Im
1
n
k
t
j
k
e
U
)
e
Im(
e
U
Im
t
j
m
k
t
j
k
0
2
1
Lemat 3
0
1
n
k
k
U
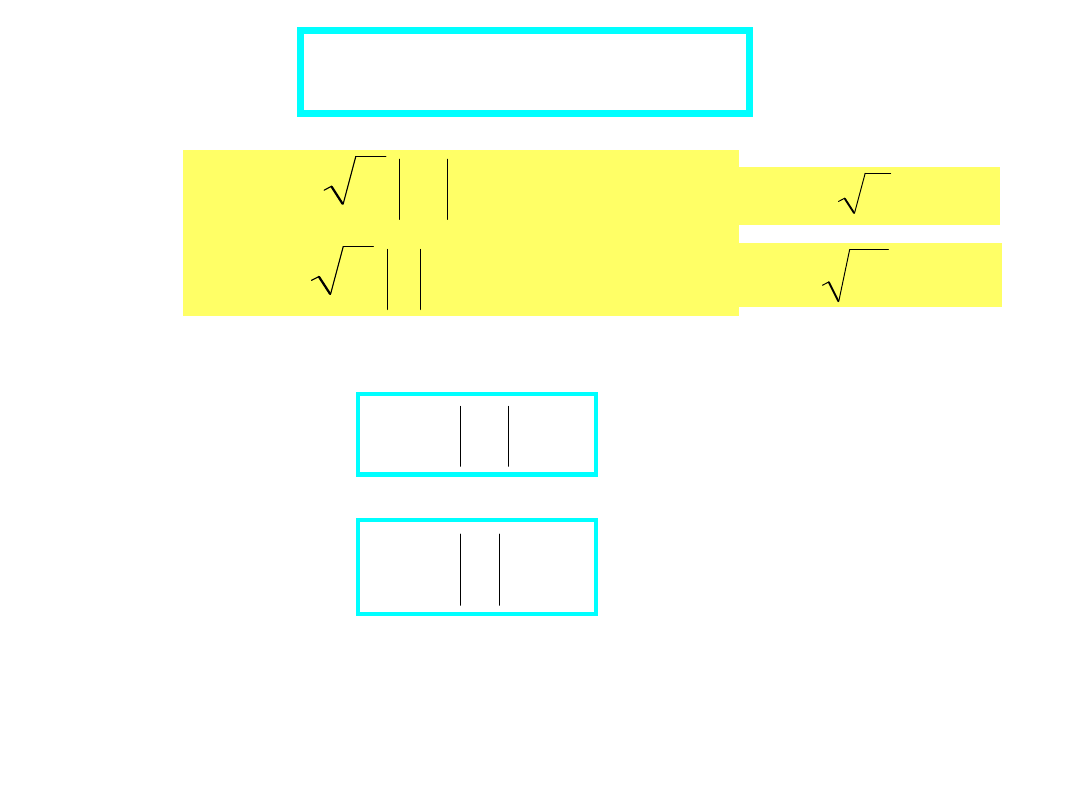
Prawa Kirchhoffa - NPK
0
1
n
k
k
U
NPK:
sin
2
)
(
sin
2
)
(
i
u
t
I
t
i
t
U
t
u
Niech:
t
j
Ue
2
Im
t
j
e
I
2
Im
gdzie
u
j
e
U
U
i
j
e
I
I
Prawo Ohma
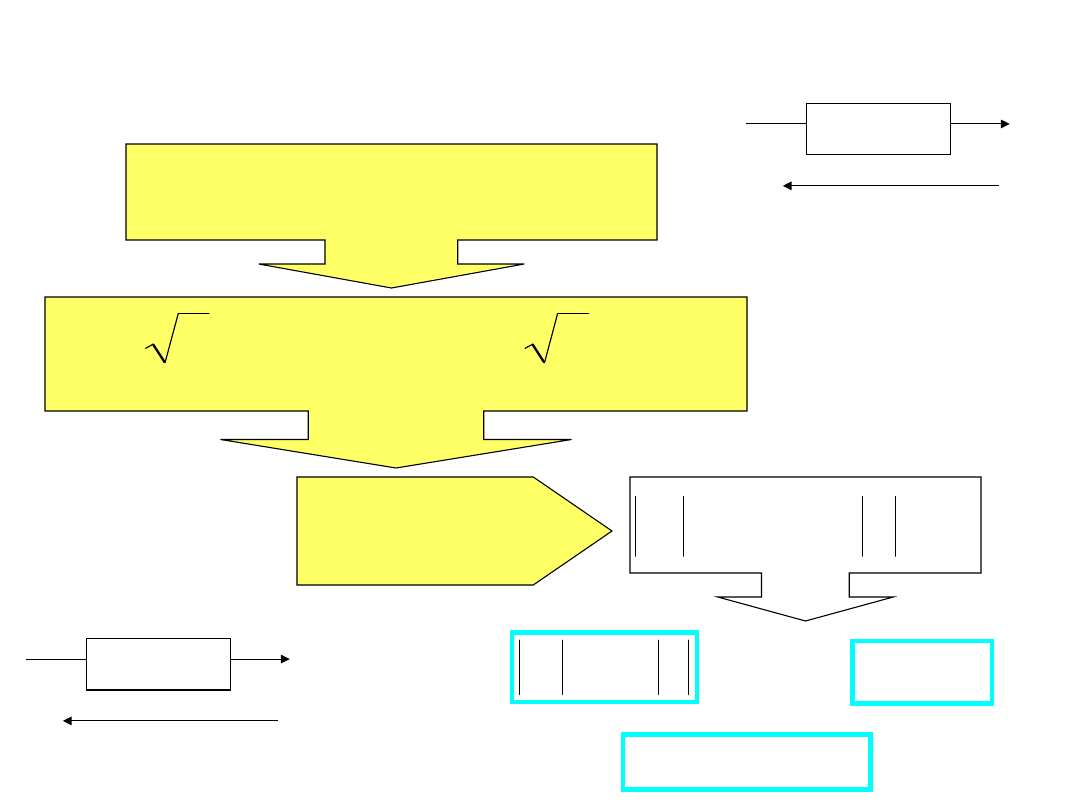
Ri
u
t
j
t
j
Ie
R
Ue
2
Im
2
Im
Lemat 3
Lemat 1
RI
U
i
u
j
j
e
I
R
e
U
I
R
U
i
u
0
i
u
I
U
R
i
u
R
Orawo Ohma dla opornika
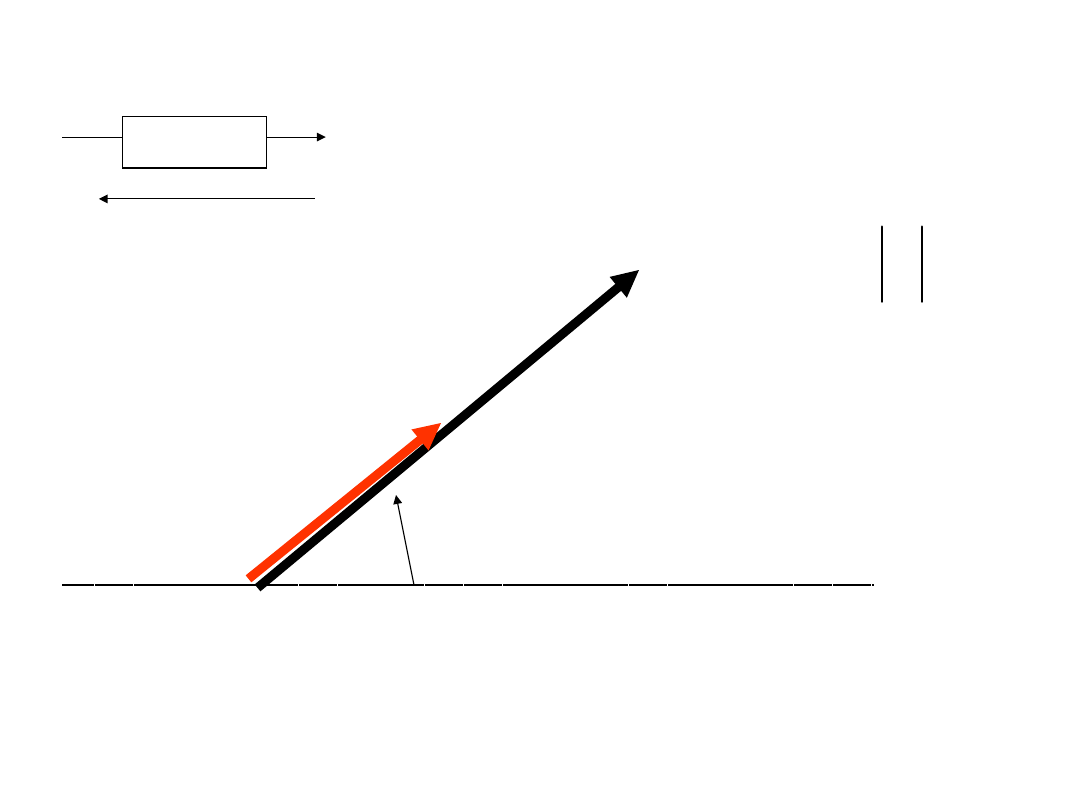
U
I
i
u
I
U
R
i
j
e
I
R
U
I
R
U
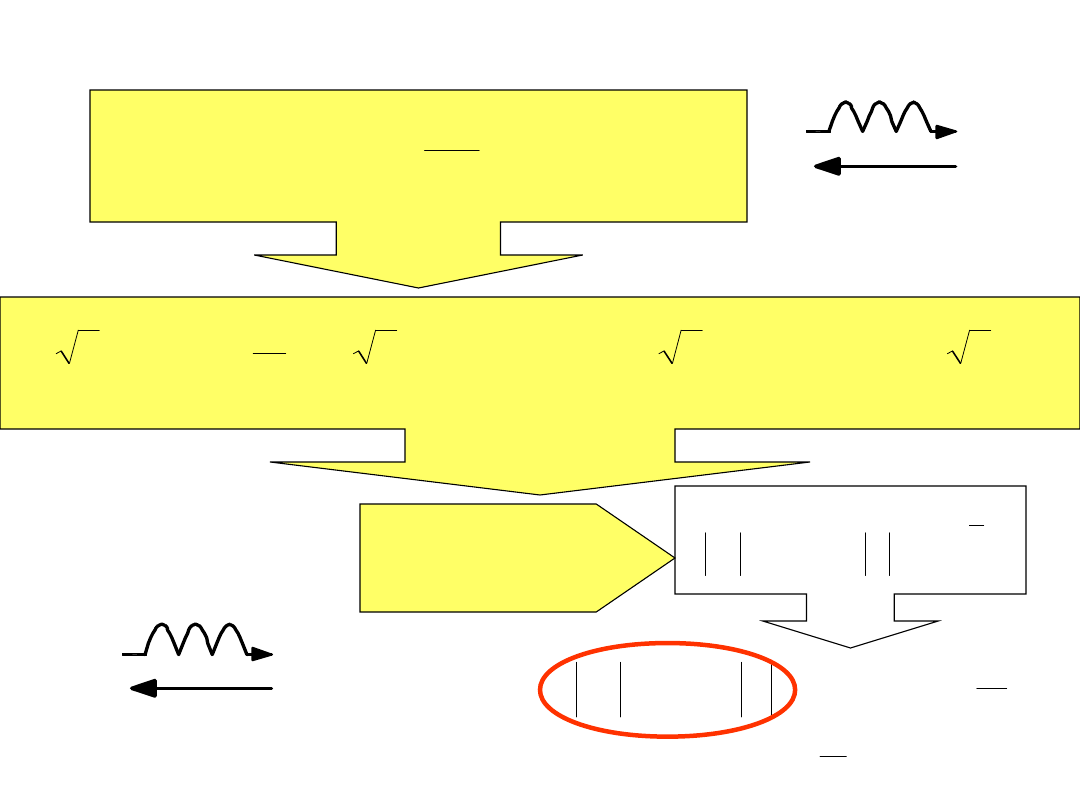
dt
di
L
u
Lemat 3
Lemat 1i2
LI
j
U
2
i
u
j
j
e
I
L
e
U
I
L
U
2
i
u
2
i
u
t
j
t
j
t
j
t
j
Ie
L
j
Ie
j
L
Ie
dt
d
L
Ue
2
Im
2
Im
2
Im
2
Im
L
i
u
L
I
U
Prawo Ohma dla cewki
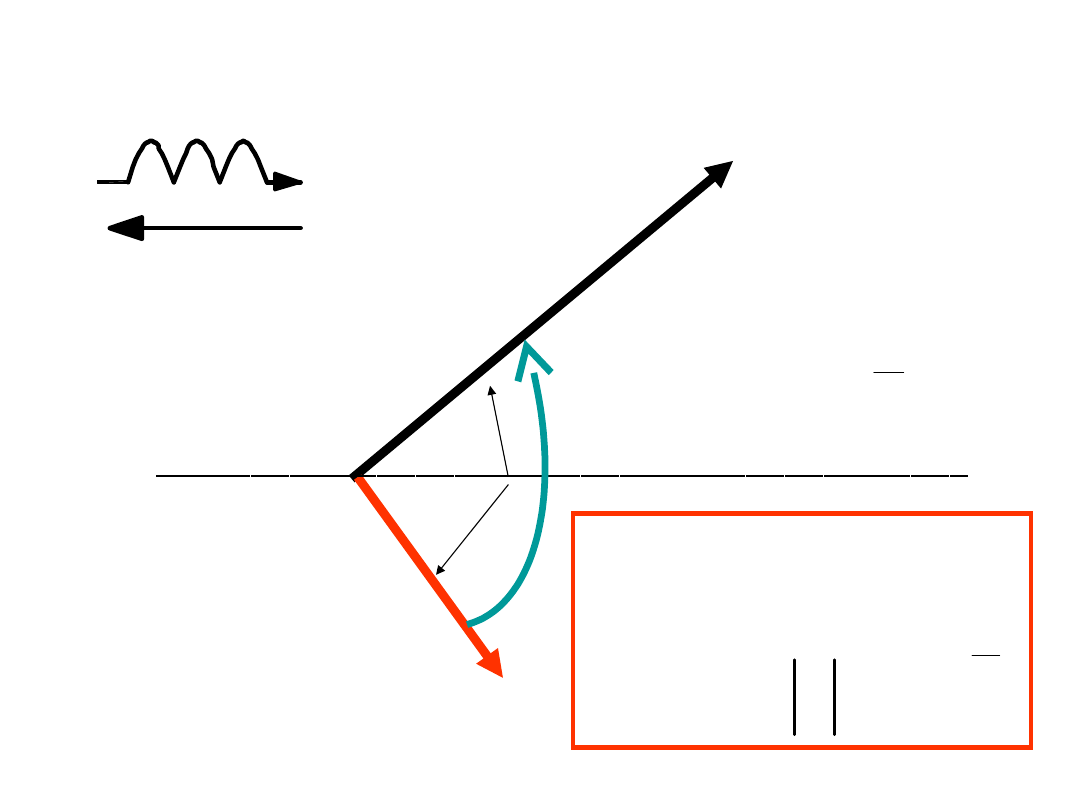
U
I
u
i
2
i
u
L
I
U
)
2
(
i
j
e
I
L
U
I
L
j
U
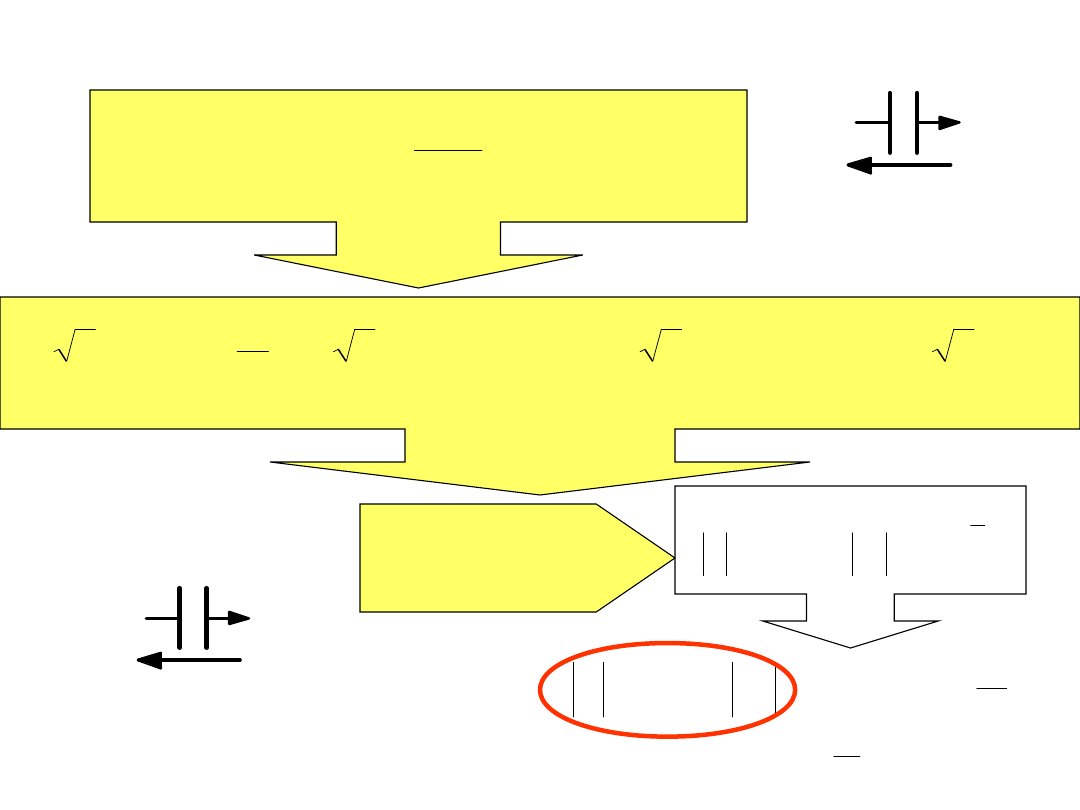
dt
du
C
i
Lemat 3
Lemat 1i2
CU
j
I
2
u
i
j
j
e
U
C
e
I
U
C
I
2
u
i
2
i
u
t
j
t
j
t
j
t
j
Ue
C
j
Ue
j
C
Ue
dt
d
C
Ie
2
Im
2
Im
2
Im
2
Im
C
i
u
C
I
U
Prawo Ohma dla kondensatora
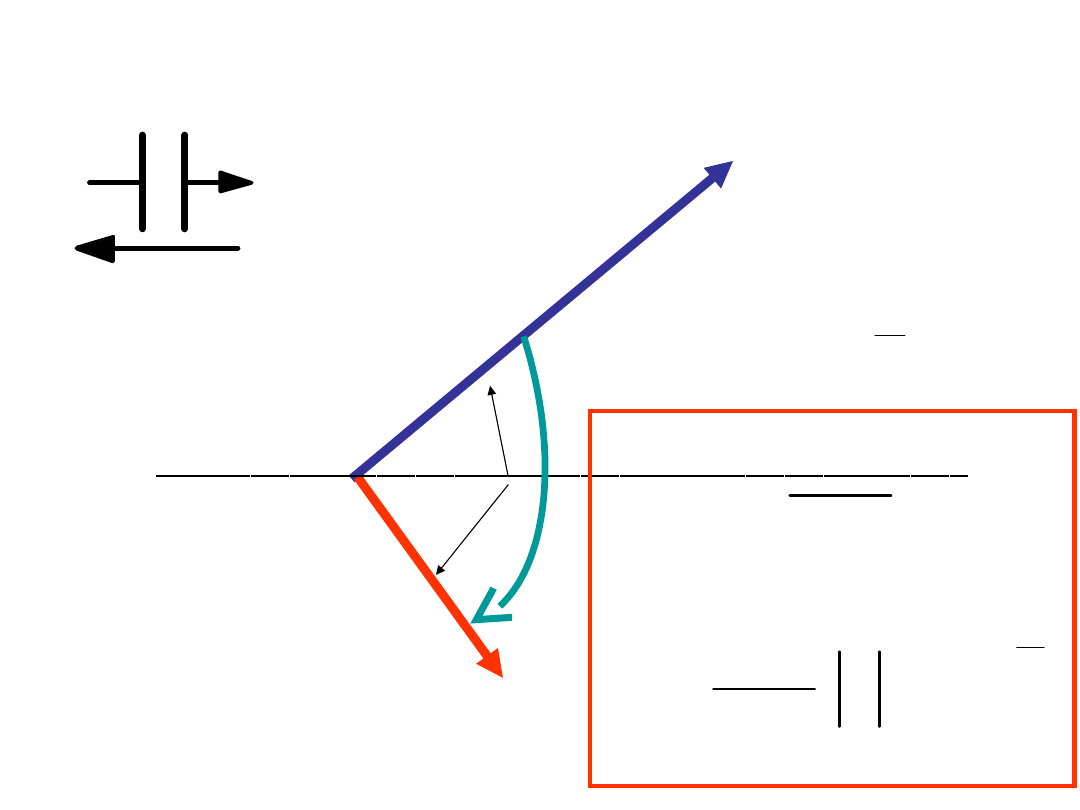
U
I
u
i
2
i
u
C
I
U
)
2
(
1
1
i
j
e
I
C
U
I
C
j
U
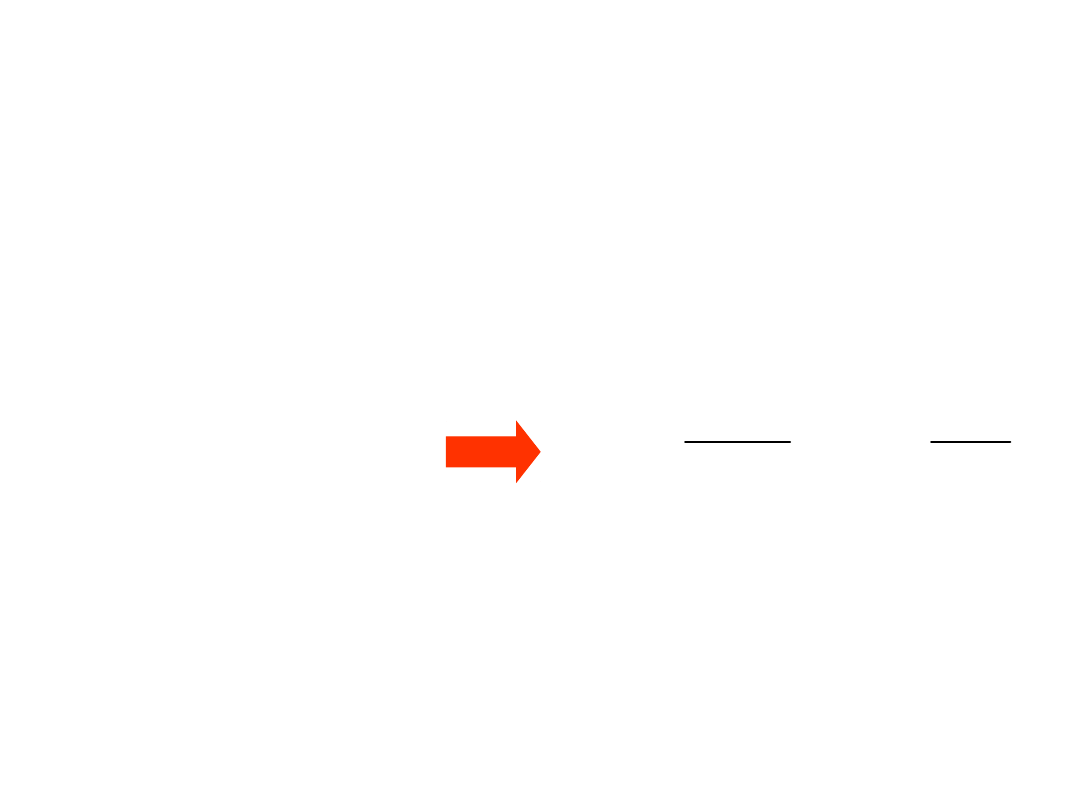
RI
U
LI
j
U
CU
j
I
I
C
j
I
C
j
U
1
1
Wykład 2
1. Impedancja
2. Admitancja
3. Obliczanie prostych obwodów
prądu sinusoidalnego
metodą symboliczną
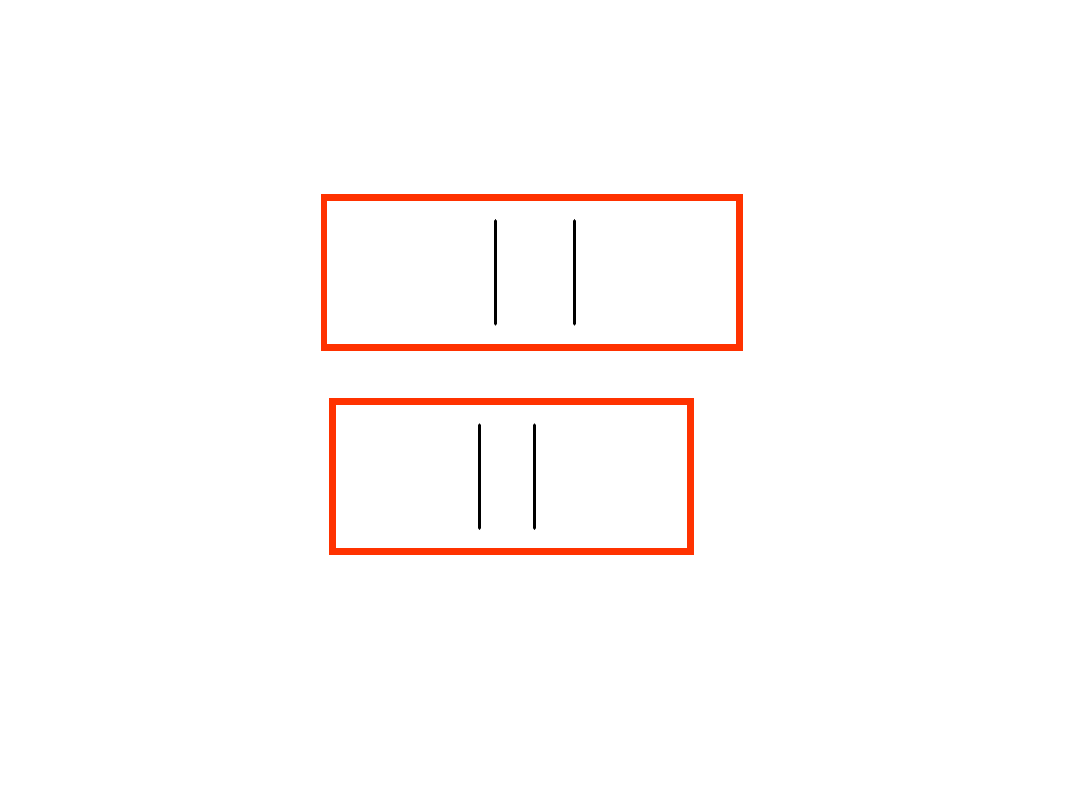
u
j
e
U
U
i
j
e
I
I
Prądy i napięcia będziemy zapisywać w postaci:
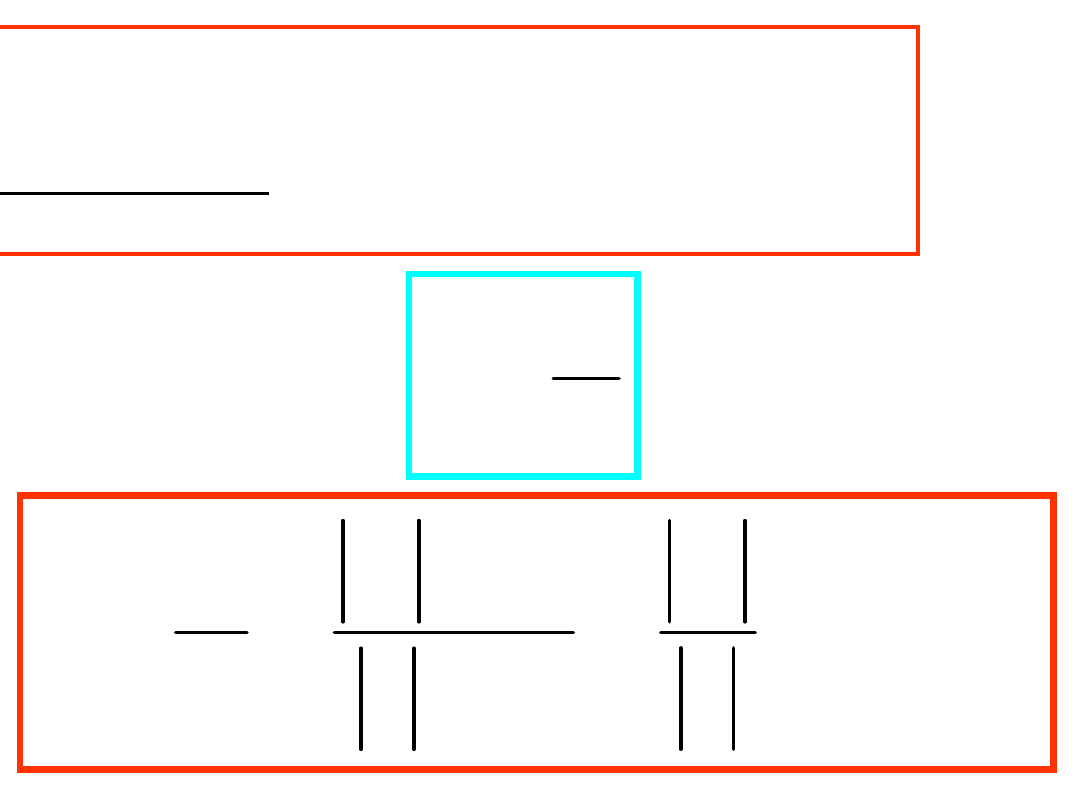
Definicja:
Impedancją nazywamy iloraz wartości
symbolicznych napięcia i prądu
I
U
Z
i
u
i
u
j
j
j
e
I
U
e
I
e
U
I
U
Z
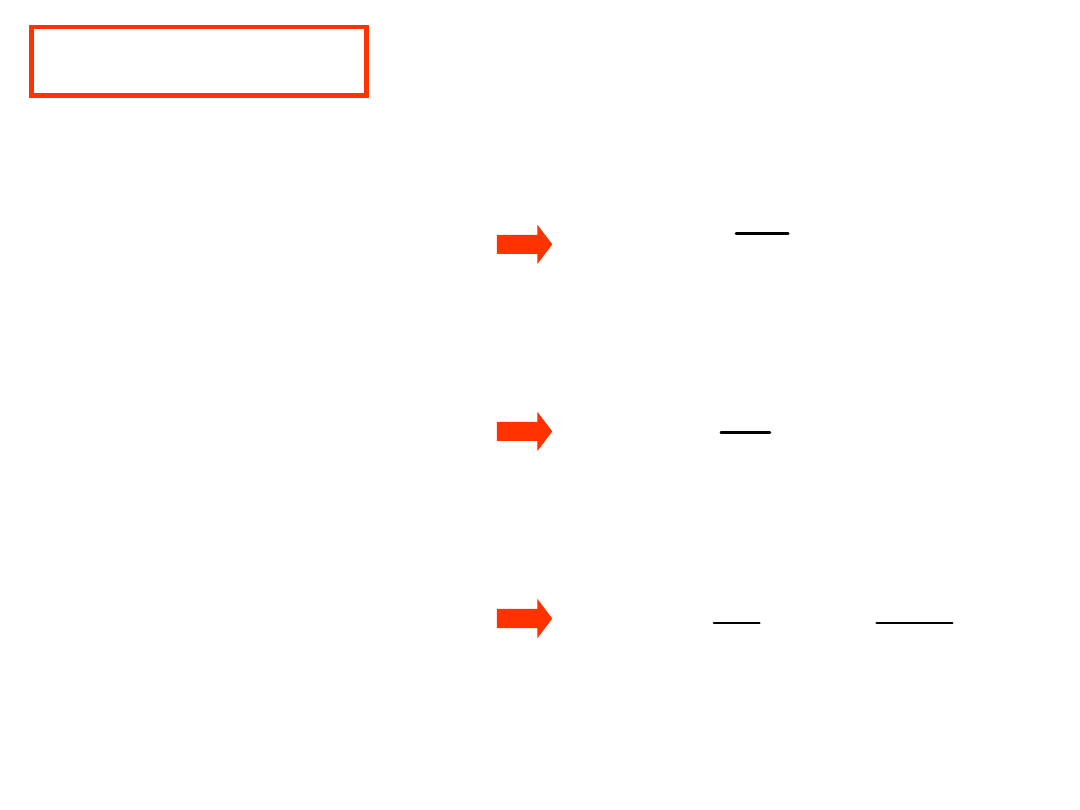
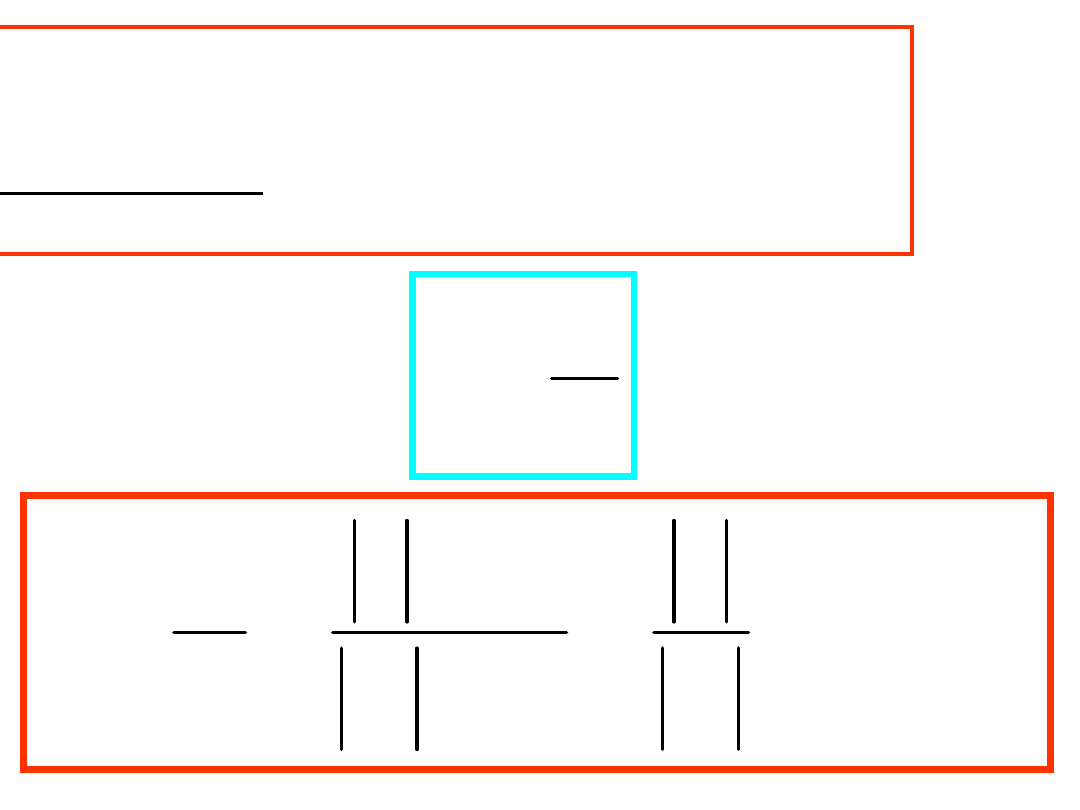
RI
U
LI
j
U
CU
j
I
R
I
U
Z
Impedancja
L
j
I
U
Z
C
j
I
U
Z
1
Definicja:
Admitancją nazywamy iloraz wartości
symbolicznych prądu i napięcia
U
I
Y
u
i
u
i
j
j
j
e
U
I
e
U
e
I
U
I
Y
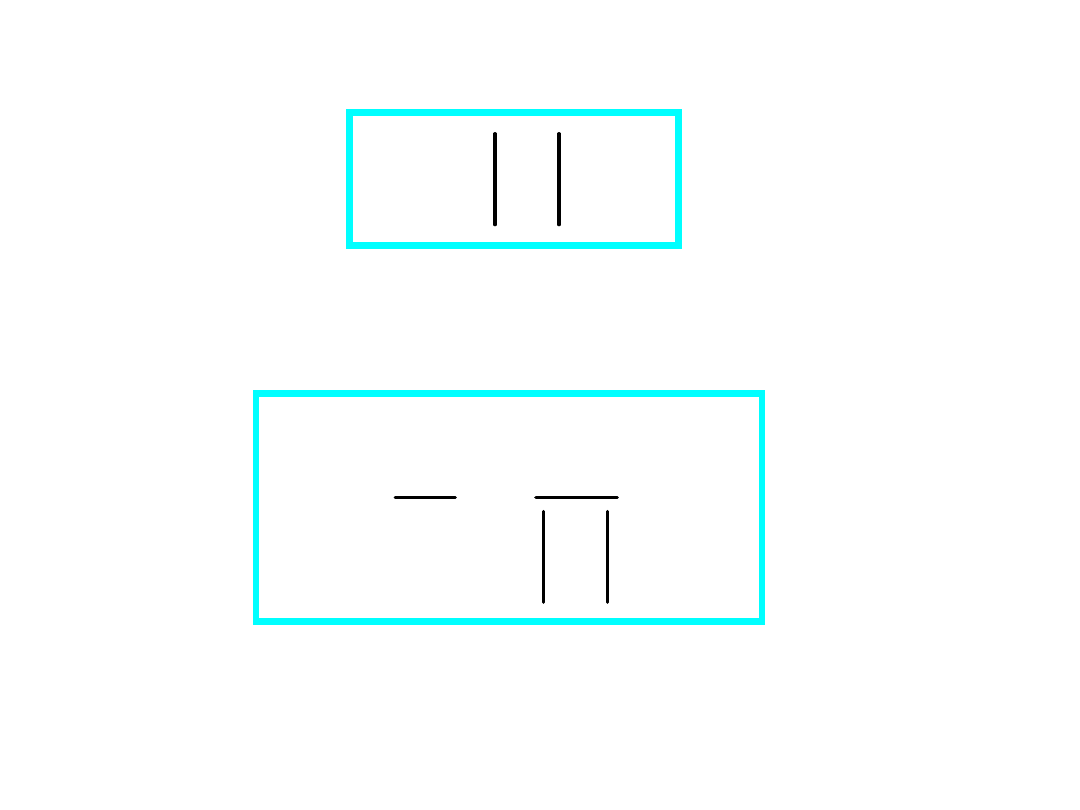
j
e
Z
Z
Y
1
1
j
e
Z
Z
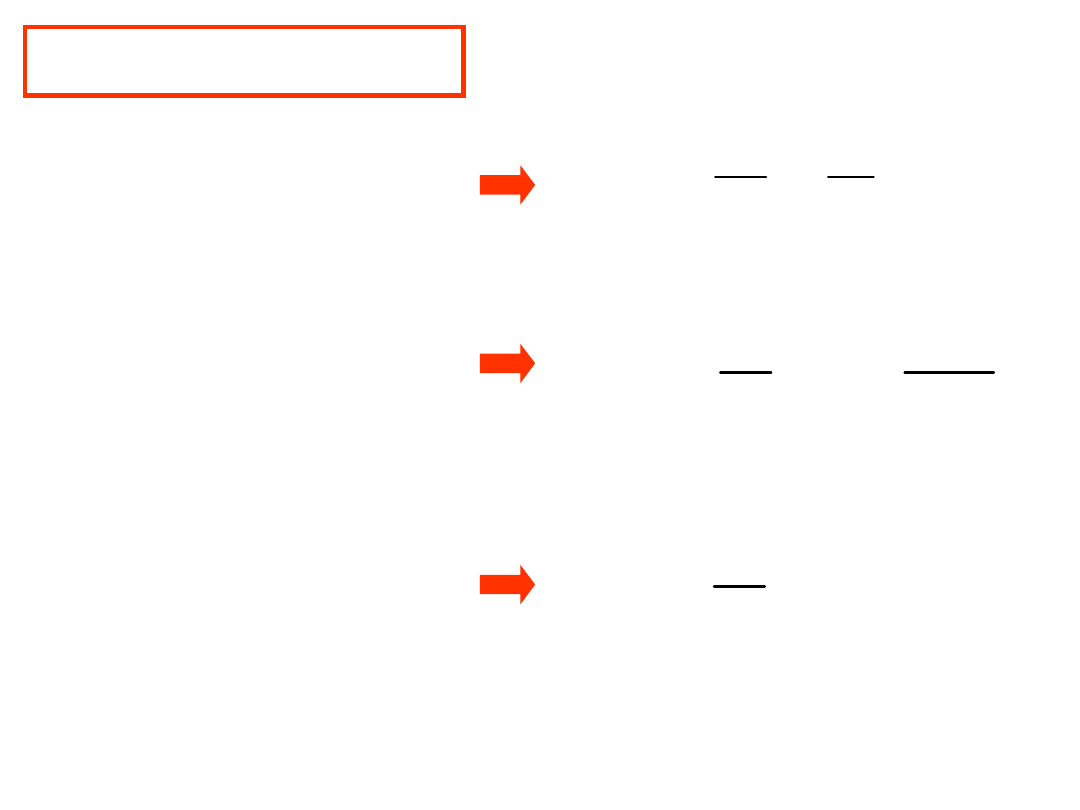
RI
U
LI
j
U
CU
j
I
G
R
U
I
Y
R
1
Admitancjancja
L
j
U
I
Y
L
1
C
j
U
I
Y
C
0
0
1
2
2
2
2
L
L
B
L
X
B
G
B
j
B
G
G
jB
G
L
j
R
Z
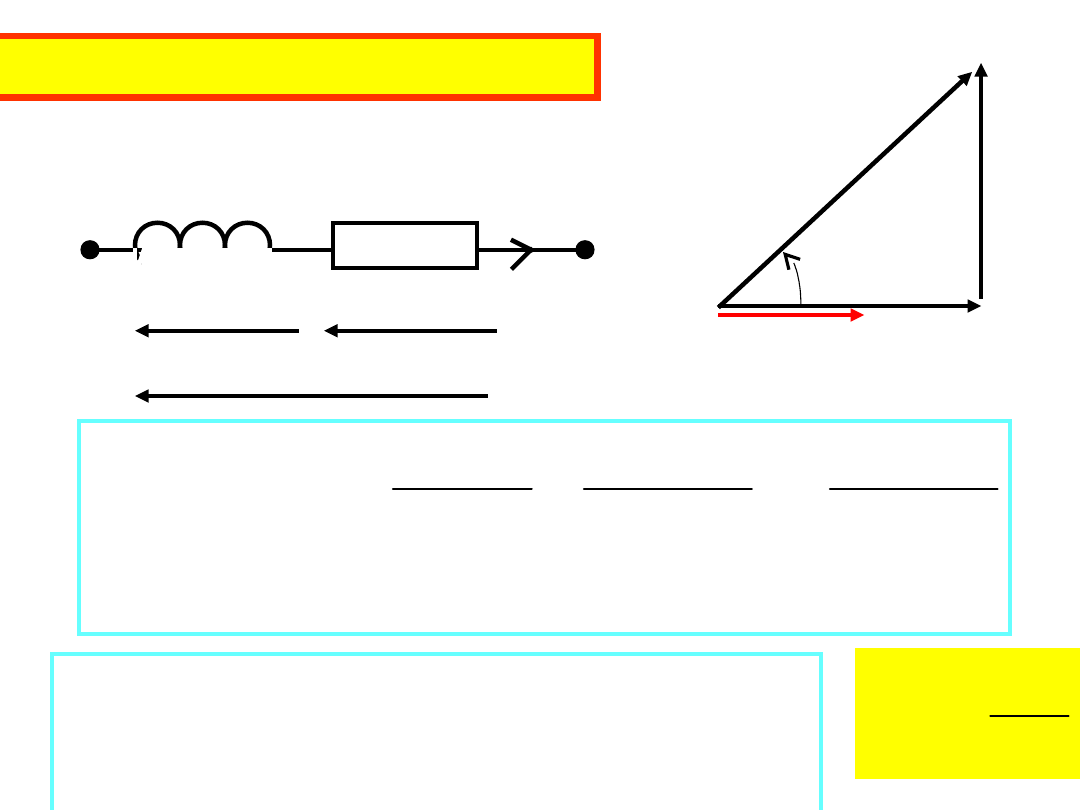
Połączenie szeregowe RL
R
L
U
L
U
R
I
U
L
R
U
U
L
jI
IR
L
j
R
I
IZ
U
I
U
R
U
L
U
R
L
tg
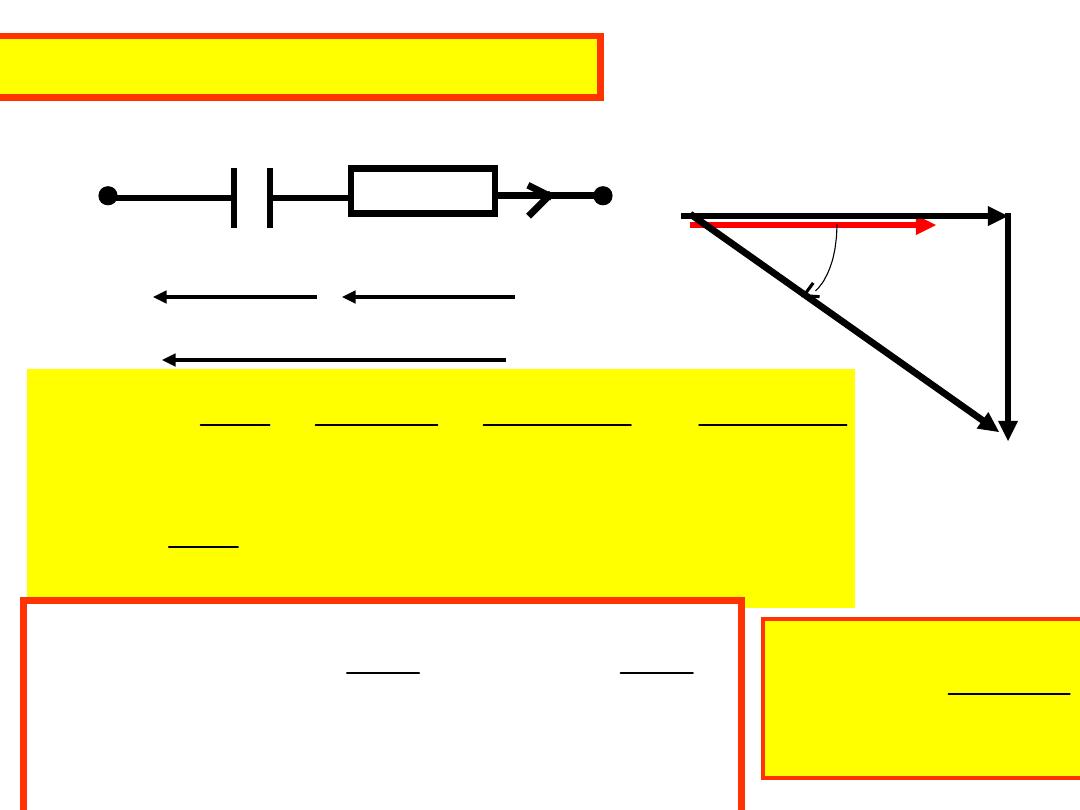
Połączenie szeregowe RC
R
C
U
L
U
R
I
U
U
R
I
U
C
U
0
0
1
1
1
2
2
2
2
C
B
C
X
B
G
B
j
B
G
G
jB
G
C
j
R
Z
C
C
C
R
U
U
C
jI
IR
C
j
R
I
IZ
U
1
1
CR
1
tg
Zależności między R i G oraz X i B
2
2
B
G
G
R
2
2
B
G
B
X
2
2
2
2
1
B
G
B
j
B
G
G
jB
G
jB
G
jB
G
jB
G
jX
R
Z