Metodologia ze

Metodologia ze

statystyką

statystyką

(

(

kurs zaawansowany)

kurs zaawansowany)

Prof. dr Jerzy Karylowski
Dr A. Fila-Jankowsa

Test Chi-kwadrat dla tablicy

Test Chi-kwadrat dla tablicy

5x3

5x3



Przykład w klasie z użyciem SPSS:

Przykład w klasie z użyciem SPSS:

stan cywilny a poziom satysfakcji z

stan cywilny a poziom satysfakcji z

życia

życia

.

.

Problem: Trudność ustalenia,

Problem: Trudność ustalenia,

które kombinacje poziomów

które kombinacje poziomów

dwóch zmiennych

dwóch zmiennych

odpowiedzialne są za istotną

odpowiedzialne są za istotną

zależność

zależność



Połączyć kategorie tak by otrzymać tabele 2x2

Połączyć kategorie tak by otrzymać tabele 2x2

(np połączyć separacje, rozwód, stan wolny i

(np połączyć separacje, rozwód, stan wolny i

wdowieństwo a także dwie kategorie satysfakcji)

wdowieństwo a także dwie kategorie satysfakcji)



Skoncentrować się w analizie na kategoriach,

Skoncentrować się w analizie na kategoriach,

które są dla badacza szczególnie interesujące (np

które są dla badacza szczególnie interesujące (np

żonaci vs kawalerowie/panny, życie nudne vs

żonaci vs kawalerowie/panny, życie nudne vs

ekscytujące)

ekscytujące)



Zrobić analizę dla wszystkich możliwych

Zrobić analizę dla wszystkich możliwych

kombinacji 2x2 (dopuszczalne tylko jeśli wynik

kombinacji 2x2 (dopuszczalne tylko jeśli wynik

analizy globalnej był istotny!)

analizy globalnej był istotny!)

Test Chi-kwadrat dla tablic

Test Chi-kwadrat dla tablic

wielowymiarowych

wielowymiarowych

(więcej niż dwie zmienne)

(więcej niż dwie zmienne)



Przykład w klasie: płeć i stan cywilny

Przykład w klasie: płeć i stan cywilny

a poziom satysfakcji z życia

a poziom satysfakcji z życia

.

.

Tabela krzy¿owa Zamê¿ny/¿onata * ¯ycie jest pasjonuj¹ce/zwyczajne/nudne * P³eæ respondenta

6

121

121

248

11,7

117,9

118,5

248,0

14

81

82

177

8,3

84,1

84,5

177,0

20

202

203

425

20,0

202,0

203,0

425,0

15

120

130

265

20,9

119,3

124,8

265,0

30

137

139

306

24,1

137,7

144,2

306,0

45

257

269

571

45,0

257,0

269,0

571,0

LiczebnoϾ
LiczebnoϾ oczekiwana
LiczebnoϾ
LiczebnoϾ oczekiwana
LiczebnoϾ
LiczebnoϾ oczekiwana
LiczebnoϾ
LiczebnoϾ oczekiwana
LiczebnoϾ
LiczebnoϾ oczekiwana
LiczebnoϾ
LiczebnoϾ oczekiwana

Tak

Nie

Zamê¿ny/¿onata

Ogó³em

Tak

Nie

Zamê¿ny/¿onata

Ogó³em

P³eæ respondenta
Mê¿czyzna

Kobieta

Nudne

Zwyczajne Pasjonuj¹ce

¯ycie jest

pasjonuj¹ce/zwyczajne/nudne

Ogó³em

Testy Chi-kwadrat

6,946

a

2

,031

6,887

2

,032

1,921

1

,166

425

3,500

b

2

,174

3,577

2

,167

2,164

1

,141

571

Chi-kwadrat Pearsona
Iloraz wiarygodnoœci
Test zwi¹zku liniowego
N Wa¿nych obserwacji
Chi-kwadrat Pearsona
Iloraz wiarygodnoœci
Test zwi¹zku liniowego
N Wa¿nych obserwacji

P³eæ respondenta
Mê¿czyzna

Kobieta

WartoϾ

df

IstotnoϾ

asymptotyczn

a

(dwustronna)

,0% komórek (0) ma liczebnoœæ oczekiwan¹ mniejsz¹ ni¿ 5. Minimalna
liczebnoϾ oczekiwana wynosi 8,33.

a.

,0% komórek (0) ma liczebnoœæ oczekiwan¹ mniejsz¹ ni¿ 5. Minimalna
liczebnoϾ oczekiwana wynosi 20,88.

b.

Miary symetryczne

,258

,000

,183

,000

425

,195

,006

,138

,006

571

Phi
V Kramera

Nominalna przez
Nominalna
N Wa¿nych obserwacji

Phi
V Kramera

Nominalna przez
Nominalna
N Wa¿nych obserwacji

P³eæ respondenta
Mê¿czyzna

Kobieta

WartoϾ

IstotnoϾ

przybli¿ona

Nie zak³adaj¹c hipotezy zerowej.

a.

U¿yto asymptotyczny b³¹d standardowy, przy za³o¿eniu hipotezy zerowej.

b.

Problem: Brak

Problem: Brak

konkluzywnych informacji co

konkluzywnych informacji co

do istotności efektu

do istotności efektu

interakcji

interakcji

Alternatywne metody analizy

Alternatywne metody analizy

dostarczające informacji o

dostarczające informacji o

istotności interakcji

istotności interakcji



Analiza logliniowa

Analiza logliniowa



Analiza wariancji (satysfakcja jako

Analiza wariancji (satysfakcja jako

zmienna zależna) –

zmienna zależna) –

przykład w klasie

przykład w klasie

Moc testu statystycznego

Moc testu statystycznego



Moc testu statystycznego związana jest z

Moc testu statystycznego związana jest z

błędem drugiego rodzaju

błędem drugiego rodzaju



Błąd drugiego rodzaju – nie odrzucenie

Błąd drugiego rodzaju – nie odrzucenie

hipotezy zerowej (hipotezy o braku

hipotezy zerowej (hipotezy o braku

związku) gdy jest ona fałszywa

związku) gdy jest ona fałszywa



β = prawdopodobieństwo błędu drugiego

β = prawdopodobieństwo błędu drugiego

rodzaju

rodzaju



Moc testu to prawdopodobieństwo

Moc testu to prawdopodobieństwo

odrzucenia hipotezy zerowej gdy jest ona

odrzucenia hipotezy zerowej gdy jest ona

fałszywa (gdy związek istnieje)

fałszywa (gdy związek istnieje)



Moc testu = 1 – β

Moc testu = 1 – β

Pomiar siły efektu

Pomiar siły efektu



Istotność statystyczna dotyczy

Istotność statystyczna dotyczy

prawdopodobieństwa, że efekt w

prawdopodobieństwa, że efekt w

rzeczywistości nie występuje ale nie

rzeczywistości nie występuje ale nie

przesądza jeszcze o sile efektu

przesądza jeszcze o sile efektu



Na istotność statystyczną ma wpływ

Na istotność statystyczną ma wpływ

wielkość próby

wielkość próby



Gdy próba jest mała, silny efekt może nie

Gdy próba jest mała, silny efekt może nie

być statystycznie istotny

być statystycznie istotny



Gdy próba jest duża, słaby efekt może być

Gdy próba jest duża, słaby efekt może być

bardzo istotny

bardzo istotny



Siła efektu nie zależy od wielkości próby

Siła efektu nie zależy od wielkości próby

Miary siły efektu

Miary siły efektu



Najpopularniesze to r, eta oraz

Najpopularniesze to r, eta oraz

d

d

Współczynnik korelacji r

Współczynnik korelacji r

Pearsona

Pearsona



Im większa próba tym mniejsza

Im większa próba tym mniejsza

wartość współczynnika korelacji

wartość współczynnika korelacji

konieczna dla stwierdzenia

konieczna dla stwierdzenia

statystycznej istotności

statystycznej istotności



r

r

2

2

(współczynnik determinacji) to

(współczynnik determinacji) to

proporcja wariancji jednej zmiennej

proporcja wariancji jednej zmiennej

kontrolowana przez drugą zmienną

kontrolowana przez drugą zmienną

Współczynnik siły związku

Współczynnik siły związku

Eta

Eta



Analogiczny do r Pearsona ale

Analogiczny do r Pearsona ale

obliczany w przypadkach gdy

obliczany w przypadkach gdy

stosuje się analizę wariancji

stosuje się analizę wariancji



Może się wahać od 0 do 1

Może się wahać od 0 do 1



Eta

Eta

2

2

interpretuje się tak samo jak r

interpretuje się tak samo jak r

2

2

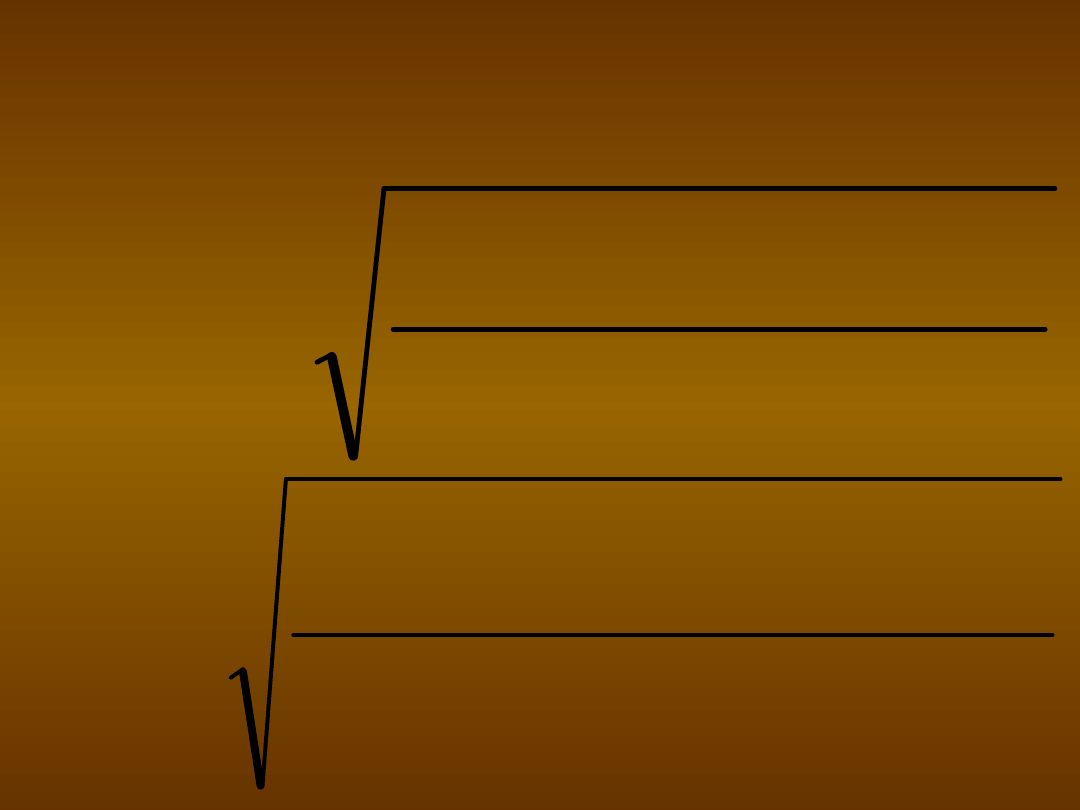
Obliczanie współczynnika eta:

Obliczanie współczynnika eta:

dwa wzory

dwa wzory

error

effect

effect

SS

SS

eta





SS

)

(

)

)(

(

)(

(

)

error

effect

effect

df

df

F

df

F

eta





Klasyfikacja wielkości efektu

Klasyfikacja wielkości efektu

eta

eta



0,1 – mały

0,1 – mały



0,3 – średni

0,3 – średni



0,5 – duży

0,5 – duży



Ta sama klasyfikacja odnosi się do

Ta sama klasyfikacja odnosi się do

współczynnika korelacji r

współczynnika korelacji r

Współczynnik siły związku

Współczynnik siły związku

d

d



Obliczany w przypadkach gdy stosuje

Obliczany w przypadkach gdy stosuje

się test t

się test t

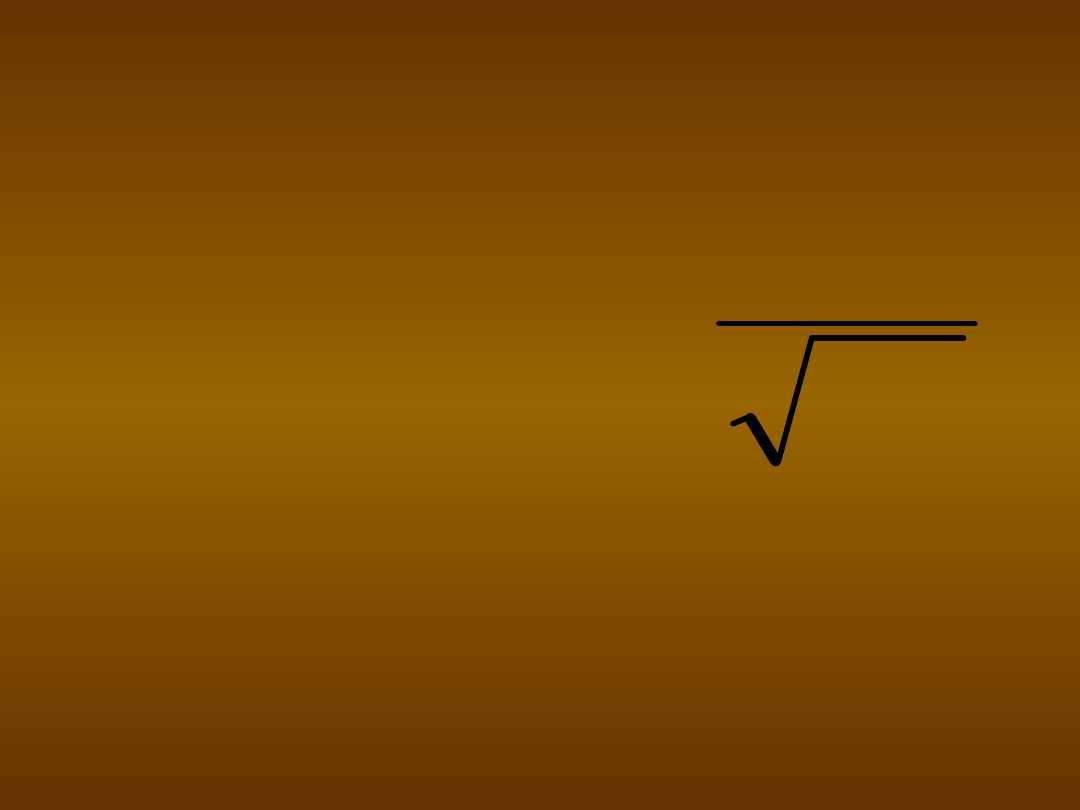
Obliczanie współczynnika siły

Obliczanie współczynnika siły

związku

związku

d:

d:

dwa wzory

dwa wzory



d=

d=

różnica między

różnica między

średnimi

średnimi

podzielona przez

podzielona przez

odchylenie

odchylenie

standardowe

standardowe

df

t

d

2



Klasyfikacja wielkości efektu d
0,2 – mały
0,5 – średni
0,8 -- duży



Uwaga: Znając t można też łatwo

Uwaga: Znając t można też łatwo

obliczyć eta (etap pośredni to

obliczyć eta (etap pośredni to

obliczenie F)

obliczenie F)



(t

(t

2

2

=F)

=F)

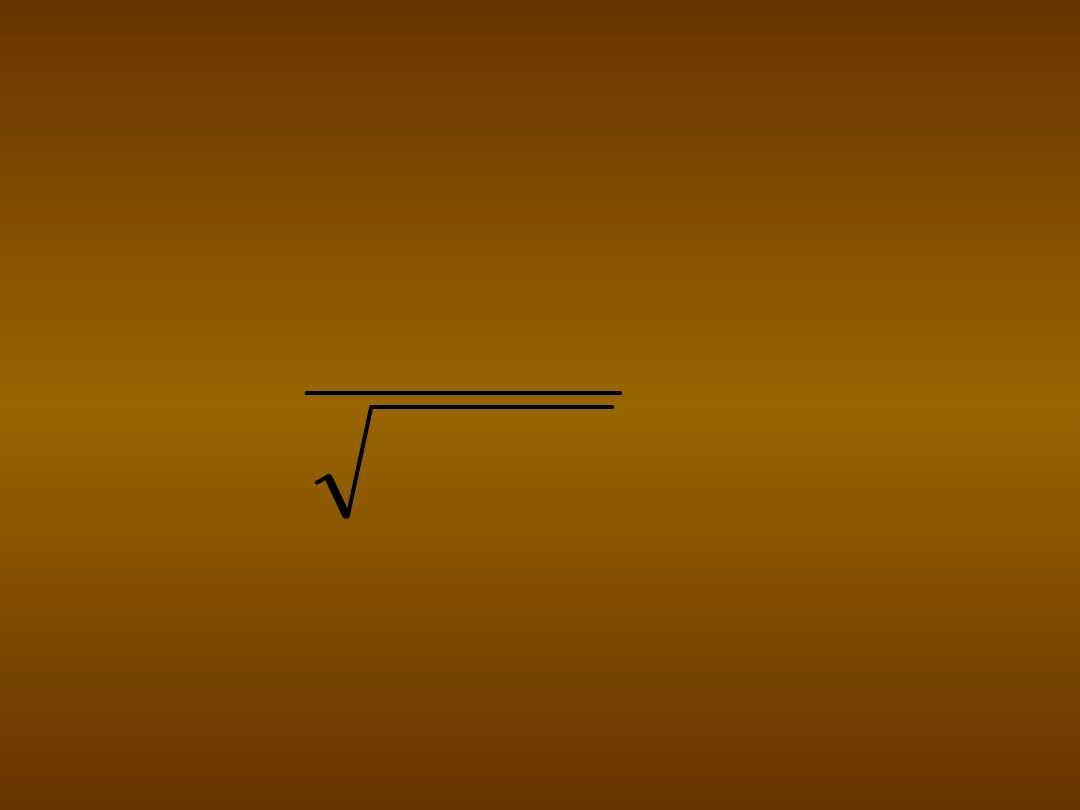
Związek między

Związek między

d

d

a

a

współczynnikiem korelacji r

współczynnikiem korelacji r

4

2





d

d

r

Przykład

Przykład



Badanie 1: N=80; t(78)=2,21; p<0,05

Badanie 1: N=80; t(78)=2,21; p<0,05



Badanie 2: N=20; t(18)=1,06; p>0,3

Badanie 2: N=20; t(18)=1,06; p>0,3

(nie istotne)

(nie istotne)



Czy wyniki tych badań są sprzeczne?

Czy wyniki tych badań są sprzeczne?



Obliczmy współczynniki siły efektu

Obliczmy współczynniki siły efektu

d

d



d

d

1=2*2,21/8.83=0,50

1=2*2,21/8.83=0,50



d

d

2=2*1,06/4,24=0,50

2=2*1,06/4,24=0,50



Efekty są identyczne!

Efekty są identyczne!

Praca semestralna pewnego studenta stanowi

Praca semestralna pewnego studenta stanowi

dokładną replikację uprzednio opublikowanego

dokładną replikację uprzednio opublikowanego

badania ale na mniejszej próbie. Można

badania ale na mniejszej próbie. Można

oczekiwać, że w porównaniu z wynikami

oczekiwać, że w porównaniu z wynikami

oryginalnego badania, wyniki pracy

oryginalnego badania, wyniki pracy

semestralnej wykażą:

semestralnej wykażą:



Podobna siłę efektu i podobny poziom istotności

Podobna siłę efektu i podobny poziom istotności



Niższą siłę efektu i mniej istotne wyniki

Niższą siłę efektu i mniej istotne wyniki



Podobną siłę efektu ale mniej istotne wyniki*

Podobną siłę efektu ale mniej istotne wyniki*



Niższą siłę efektu ale podobny poziom

Niższą siłę efektu ale podobny poziom

istotności

istotności

Meta-analiza: Analiza

Meta-analiza: Analiza

uwzględniająca wyniki więcej

uwzględniająca wyniki więcej

niż jednego badania

niż jednego badania



Czy zależność występuje? (Obliczenie

Czy zależność występuje? (Obliczenie

łącznego poziomu istotności dla wielu badań)

łącznego poziomu istotności dla wielu badań)



Jak silna jest zależność? (Obliczenie łącznego

Jak silna jest zależność? (Obliczenie łącznego

wskaźnika siły związku dla wielu badań)

wskaźnika siły związku dla wielu badań)



Od czego zależy występowanie i siła

Od czego zależy występowanie i siła

zależności (Porównywanie grup badań pod

zależności (Porównywanie grup badań pod

względem siły związku)

względem siły związku)



Metaanalizy stanowią cenne narzędzie ,

Metaanalizy stanowią cenne narzędzie ,

które ułatwia podsumowanie

które ułatwia podsumowanie

eksperymentów badających tę samą

eksperymentów badających tę samą

zmienną niezależną lub zmienną

zmienną niezależną lub zmienną

zależną.

zależną.



Sumują analizy wyników wielu

Sumują analizy wyników wielu

niezależnych eksperymentów

niezależnych eksperymentów



W eksperymentach analizuje się wyniki

W eksperymentach analizuje się wyniki

osób badanych, w metaanalizie –

osób badanych, w metaanalizie –

analizuje się wyniki eksperymentów

analizuje się wyniki eksperymentów



Metaanalizy nie zostały stworzone po

Metaanalizy nie zostały stworzone po

to, by zastąpić podsumowania

to, by zastąpić podsumowania

dotychczasowych wyników.

dotychczasowych wyników.



Mogą służyć jako narzędzie

Mogą służyć jako narzędzie

wzmacniające dowód na wysunięte

wzmacniające dowód na wysunięte

przez badaczy wnioski

przez badaczy wnioski



Formą pośrednią jest „metoda głosowania”.

Formą pośrednią jest „metoda głosowania”.

Badacze podsumowujący wyniki

Badacze podsumowujący wyniki

dotychczasowych badań zliczają liczbę

dotychczasowych badań zliczają liczbę

eksperymentów, które przyniosły lub nie

eksperymentów, które przyniosły lub nie

przyniosły istotnego statystycznie efektu

przyniosły istotnego statystycznie efektu

zmiennej niezależnej.

zmiennej niezależnej.



Metoda ta może dać zniekształcony wynik ze

Metoda ta może dać zniekształcony wynik ze

względu na tendencyjność publikacji

względu na tendencyjność publikacji



Tendencyjność pojawia się, gdy bardziej

Tendencyjność pojawia się, gdy bardziej

prawdopodobne jest opublikowanie sprawozdania

prawdopodobne jest opublikowanie sprawozdania

z badań, które wykazały istotne różnice, niż z

z badań, które wykazały istotne różnice, niż z

badań, które ich nie wykazały.

badań, które ich nie wykazały.



Metoda głosowania prowadzi wówczas do

Metoda głosowania prowadzi wówczas do

przeszacowania wielkości efektu danej zmiennej

przeszacowania wielkości efektu danej zmiennej

niezależnej

niezależnej



Rosenthal (1994) zastosował

Rosenthal (1994) zastosował

metaanalize do podsumowania

metaanalize do podsumowania

wyników 345 eksperymentów nad

wyników 345 eksperymentów nad

efektami związanymi z osobą

efektami związanymi z osobą

badacza.

badacza.



Efekt ten pojawia się, gdy ososby

Efekt ten pojawia się, gdy ososby

badane w eksperymencie reagują w

badane w eksperymencie reagują w

sposób zgodny z oczekiwaniami

sposób zgodny z oczekiwaniami

eksperymentatora

eksperymentatora

Ilustracja zastosowanie średniej miary

Ilustracja zastosowanie średniej miary

wielkości efektu w metaanalizie

wielkości efektu w metaanalizie

0,70

Ogólna średnia

Uczenie się w labiryncie i skrzynce
Skinnera

1,73

Uczenie się zwierząt

Zdolność rozróżniania ronów

1,05

Sądy psychofizyczne

Uczenie się symboli, wynik w
ćwiczeniach fizycznych

0,88

Sytuacje codzienne

Stosunek elementów zwierzęcych do
ludzkich w odpowiedziach na test
Rorschacha

0,84

Testy plam atramentowych

Percepcja sukcesów osiąganych przez
innych

0,55

Percepcja innych osób

Wyniki testu inteligencji, uczenie się
werbalne

0,54

Uczenie się

Skojarzenia słowne na podane bodźce

0,17

Czas reakcji

Wpływ deprywacji sensorycznej na
halucynacje

0,14

Wywiady w laboratorium

RODZAJ BADANIA

d

DZIEDZINA

Oczekiwania interpersonalne

Oczekiwania interpersonalne

wpływają na zachowanie ludzi

wpływają na zachowanie ludzi



Średnia wielkość efektu w 345 badaniach

Średnia wielkość efektu w 345 badaniach

analizowanych przez Rosenthala wyniosła

analizowanych przez Rosenthala wyniosła

0,70, co jest efektem umiarkowanej wielkości

0,70, co jest efektem umiarkowanej wielkości

zgodnie z klasyfikacją Cohena (1992).

zgodnie z klasyfikacją Cohena (1992).



Dla 4 z przedstawionych 8 dziedzin średnia

Dla 4 z przedstawionych 8 dziedzin średnia

wyniosła 0,80 i więcej, co wskazuje na dużą

wyniosła 0,80 i więcej, co wskazuje na dużą

wielkość efektu

wielkość efektu



Wniosek: badania nad oczekiwaniami

Wniosek: badania nad oczekiwaniami

charakteryzują się znaczną trafnością

charakteryzują się znaczną trafnością

zewnętrzna, ponieważ 6 spośród 8 dziedzin

zewnętrzna, ponieważ 6 spośród 8 dziedzin

ujawnia średnią wielkość efektu

ujawnia średnią wielkość efektu



Metaanalizy sa efektywnych i skutecznym

Metaanalizy sa efektywnych i skutecznym

sposobem podsumowania wyników dużej liczby

sposobem podsumowania wyników dużej liczby

eksperymentów

eksperymentów



Skomplikowae procedury statystyczne stanowią

Skomplikowae procedury statystyczne stanowią

istotne narzędzie wywnioskowania tylko wtedy, gdy

istotne narzędzie wywnioskowania tylko wtedy, gdy

dane z analizowanych badań zostały prawidłowo

dane z analizowanych badań zostały prawidłowo

zebrane

zebrane



Wyniki metaanaliz mogą być mylkące, gdy do

Wyniki metaanaliz mogą być mylkące, gdy do

metaanalizy włączane sa eksperymenty o słabej

metaanalizy włączane sa eksperymenty o słabej

trafności wewnętrznej

trafności wewnętrznej



Trzeba odpowiedzieć na pytanie, które badania

Trzeba odpowiedzieć na pytanie, które badania

włączać. Czy tylko opublikowane w czasopismach

włączać. Czy tylko opublikowane w czasopismach

naukowych, spełniających wysokie standardy?

naukowych, spełniających wysokie standardy?