OBLICZENIA

PRZENOŚNIKA TAŚMOWEGO

METODA PODSTAWOWA

Wydajność

Nominalna wydajność objętościowa i masowa:

 

gdzie:
A

nom

– przekrój nominalny strugi nosiwa (urobku), w m

2

;

k



- współczynnik korekcyjny

uwzględniający pochylenie trasy

przenośnika

k

z

–

współczynnik

załadowania

określający

stopień

wykorzystania

przekroju nominalnego;
v

t

– prędkość taśmy, w m/s.



- gęstość usypową nosiwa (urobku), w kg/m

3

.

z

t

nom

V

k

k

v

A

Q































z

t

nom

V

m

k

k

v

A

Q

Q

1/2 D

R

D

R

c)

l

s



b

B



u

A

1

A

2

a)

b)

l

s



2

B



u

A

1



1

l

s

A

2

A

3

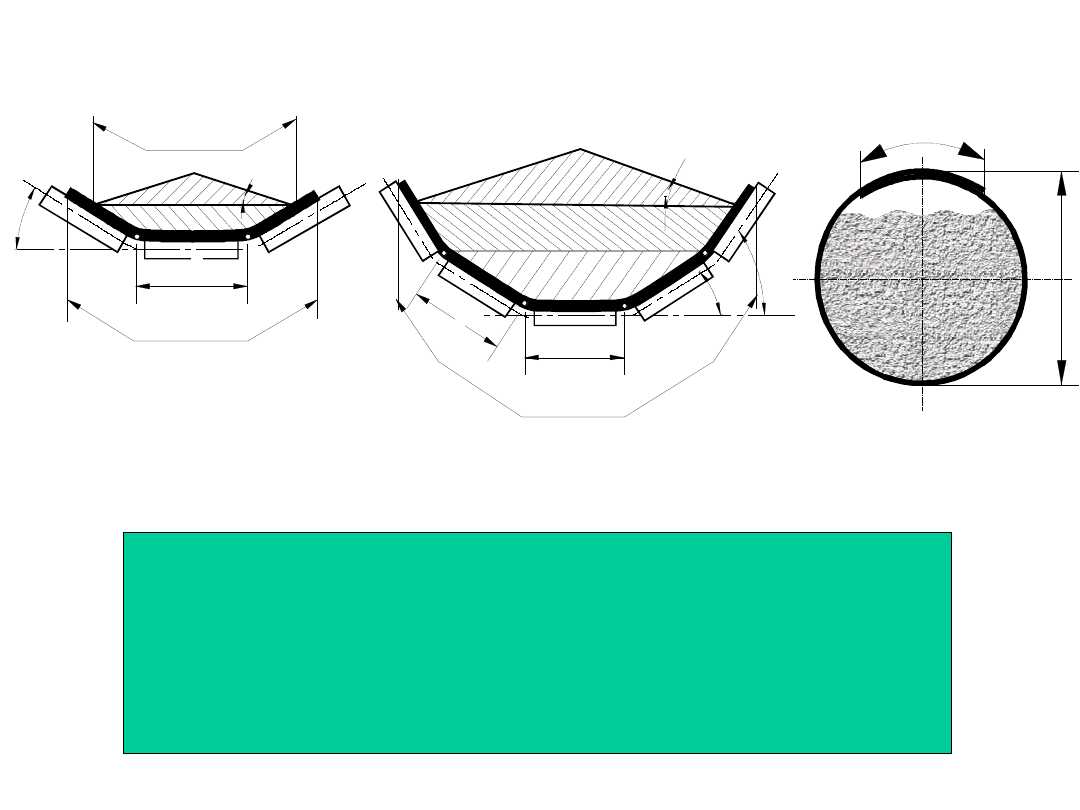
Przekrój nominalny (umowny) strugi urobku:

a)- zestaw trójkrążnikowy

b)- zestaw pięciokrążnikowy

c)- cięgno rurowe

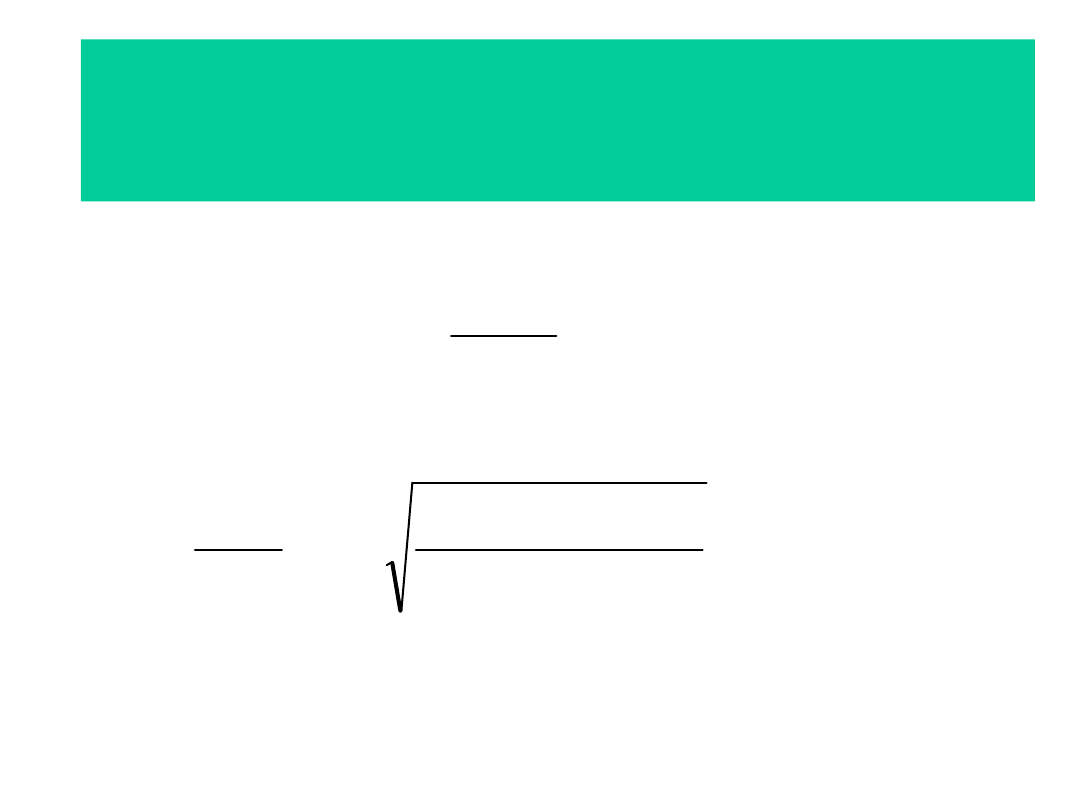
Współczynnik korekcyjny

zależny od kąta nachylenia

trasy



































u

u

nom

A

A

k

2

2

2

1

1

1

1

cos

cos

cos

u







nom

A

A

k

1

1





u







dla

dla

Dobór szerokości taśmy:

B – szerokość taśmy; d

max

- maksymalny wymiar

bryły

max

4 d

B





zawartość brył w urobku
ponad 60%:

zawartość brył w urobku w przedziale od
10% do 60:

max

d

B



3

zawartość brył poniżej 10%:

max

max

d

3

B

d

2









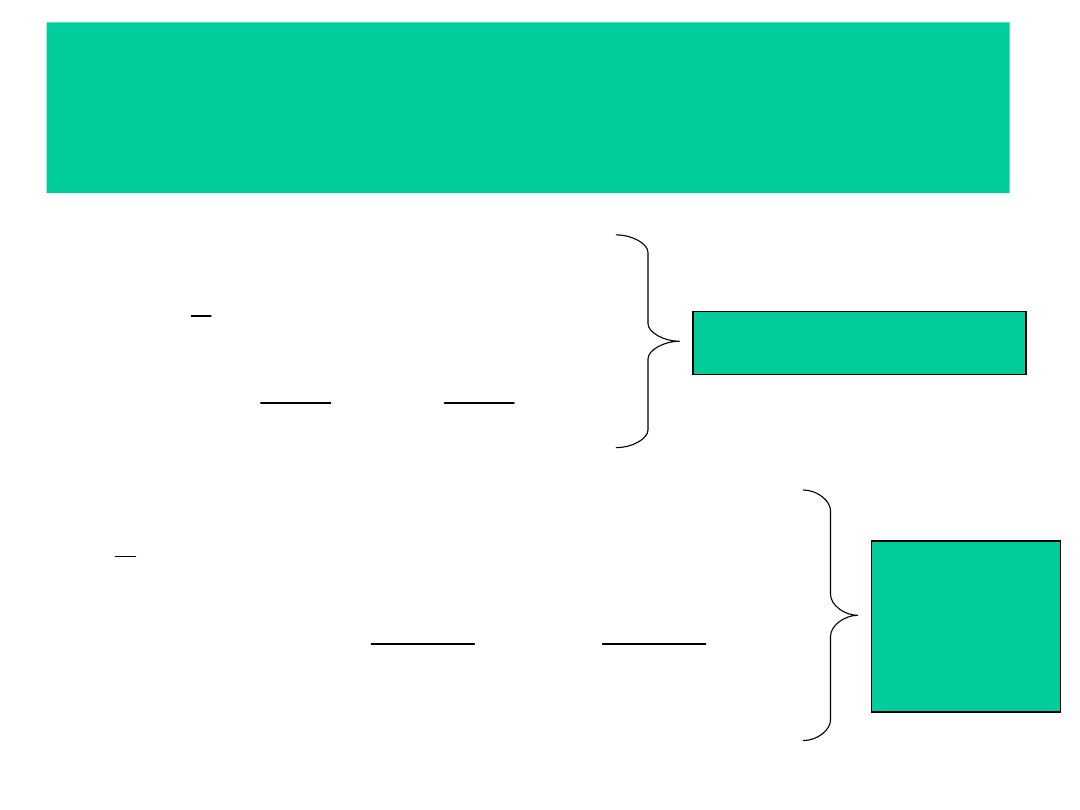
Wyznaczanie przekroju

nominalnego



























































sin

cos

tg

cos

2

2

4

1

2

2

1

2

1

s

s

s

u

s

s

nom

l

b

l

b

l

A

l

b

l

A

A

A

A



 















2

1

2

3

2

2

1

2

2

2

1

1

3

2

1

1

2

3

2

3

2

1

3

2

1

4

1



















































































sin

cos

sin

cos

cos

tg

cos

cos

k

k

k

k

u

k

k

nom

l

A

l

b

l

b

l

A

l

b

l

A

A

A

A

A

zestaw trójkrążnikowy

zestaw

pięcio-

krążnikowy

Ograniczenia prędkości

taśmy

z Ze względu na trwałość taśmy lub w celu zmniejszenia
prawdopodobieństwa spadania brył a także z uwagi na
emisję

hałasu

i

zapylenia

w

trakcie

transportu

przenośnikami

nieckowymi,

zaleca

się

następujące

maksymalne prędkości taśmy:

 

v

tmax

=7,5

m/s

przy

transporcie

nosiwa

luźnego

przenośnikami stacjonarnymi i

przesuwnymi o kącie

nachylenia trasy -5



 14;

 

v

tmax

=4,0 m/s

przy transporcie skruszonych skał zwięzłych o

ostrych

krawędziach;

 

v

tmax

=1,6 m/s

przy transporcie materiałów pylastych

(popioły, cement, miał

węglowy itp.);

   

v

tmax

=3,75 m/s

przy transporcie na odcinkach trasy

stromo nachylonych



-8 lub



14



.

Dobór prędkości taśmy

Możliwe do zrealizowania prędkości taśmy na przenośniku
wynikają

z

kombinacji:

obrotów

silników

napędu

głównego , przełożenia mechanicznego przekładni oraz
średnicy bębna napędowego. Prędkość taśmy w zależności
od tych parametrów wynosi:

gdzie:
n

zn

- obroty znamionowe silnika, w obr/min (w przypadku

silników asynchronicznych prądu przemiennego n

zn



n

synchr

=750, 1000 lub 1500 obr/min); D

bn

– średnica bębna

napędowego (z ewentualnym uwzględnieniem grubości
okładziny gumowej), w m.; h

bn

– grubość okładziny bębna

napędowego (okładzina gumowa lub ceramiczna0, w m; i

p

–

przełożenie mechaniczne przekładni napędu głównego
przenośnika

p

bn

bn

zn

t

i

h

D

n

v













60

)

2

(



Zalecane podstawowe parametry
przenośników rurowych

średnic

a

rury

D

R

, w

mm

200

250

300

350

400

450

500

szer.

taśmy

B, w

mm

730

(750

)

910

(910

)

1092

(110

0)

1274

(128

0)

1457

(146

0)

1639

(164

0)

1821

(182

0)

zalecan

a

średnic

a.

krążnik

a, w

mm

63

89

89

108

108

133

159

159

max

prędko

ść

taśmy

v

tmax

, w

m/s

3,5

5

6

6

6

8,5

8,5

5

S

1

S

4

S

3

S

2

H

L

D

K

S

1

S

4

m

u

m

T

D

K

d

S

2

S

3

opory skupione

opory skupione

W

g

W

d

L

.

g(m

T

+m

u

)

.

cos

W

ht

+W

hu

=L

.

g(m

T

+m

u

)

.

sin

L

.

g(m

T

+m

u

)

L

.

g

.

m

K

W

ht

=L

.

g

.

m

T

.

sin

L

.

g

.

m

T

L

.

g

.

m

T

.

cos

L

.

g

.

m

D

"c"

"c"

"c"

"c"

skrobak

Q

m

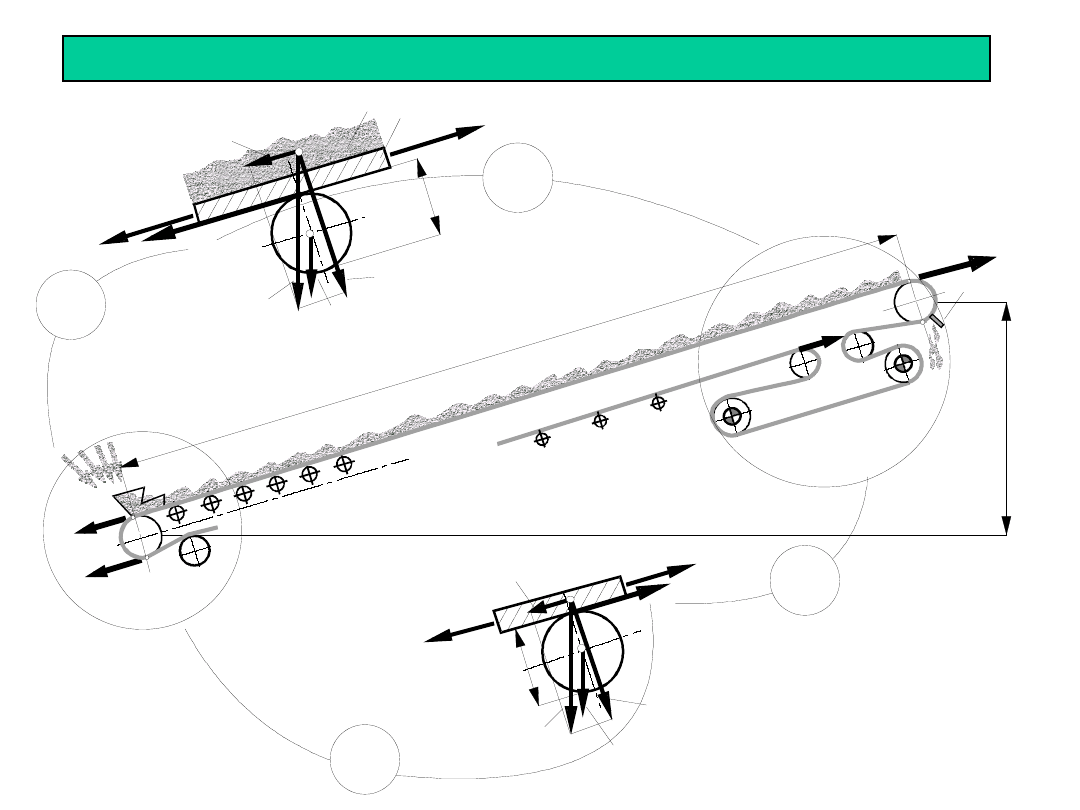
OPORY RUCHU – główne (f) i skupione (C)

Opory ruchu cięgna górnego:

 
 
Równowaga sił w cięgnie górnym:

Opory podnoszenia taśmy i urobku:







cos

















K

u

T

g

m

m

m

L

g

f

C

W





















sin

u

T

g

m

m

g

L

W

S

S

4

1

hu

ht

g

u

T

g

W

W

W

m

g

H

m

g

H

W

S

S























4

1

u

hu

T

ht

m

g

H

W

m

g

H

W













Opory ruchu w cięgnie dolnym:

 
 
Równowaga sił w cięgnie dolnym:

 
 

Całkowite opory ruchu przenośnika:

 
 





















cos

m

L

g

f

C

T

D

d

m

W

ht

d

T

d

W

W

m

g

H

W

S

S















2

3





H

m

g

m

m

m

m

g

L

f

C

W

u

D

K

u

T





























cos

2

jednostkowa (liniowa) masa taśmy:

 
jednostkowa masa urobku:

 

jednostkowa masa krążników górnych i dolnych:
 

t

T

m

B

m





t

m

u

v

Q

m 

t

V

u

v

Q

m



















z

nom

u

k

k

A

m

g

kg

g

K

l

m

z

m





d

kd

d

D

l

m

z

m





Współczynniki oporów

ruchu

W metodzie podstawowej współczynnik oporów głównych f
interpretowany jest następująco:

gdzie:
•W

G

– opory główne przenośnika (bez oporów podnoszenia taśmy i

urobku), w N;

• g - przyspieszenie ziemskie, w m/s

2

;

m – suma wszystkich ruchomych mas przenośnika, w kg;

 - kąt nachylenia przenośnika, w rad (lub stopniach).











cos

m

g

W

f

G

Współczynniki oporów

ruchu

Współczynnik C uwzględnia opory pojawiające się tylko w
określonych miejscach przenośnika takich jak bębny na
stacji czołowej i zwrotnej, urządzenia załadowcze,
czyszczące lub odwracające taśmę. Pojawiające się w tych
miejscach opory ruchu nazwane są oporami skupionymi
przenośnika. Ponieważ w metodzie uproszczonej opory
skupione wyznaczane są w sposób zryczałtowany -
proporcjonalnie do oporów głównych, to współczynnik C
jest zawsze większy od 1 i dla poziomo ustawionego
przenośnika (δ=0) wynosi:

gdzie:

•ΣW –całkowite opory ruchu przenośnika poziomego
(ΣW=W

G

+W

S

), w N;

•W

G

– opory główne (W

G

=W

g

+W

d

), w N;

•W

S

– opory skupione, w N.

G

S

G

W

W

W

W

C









1

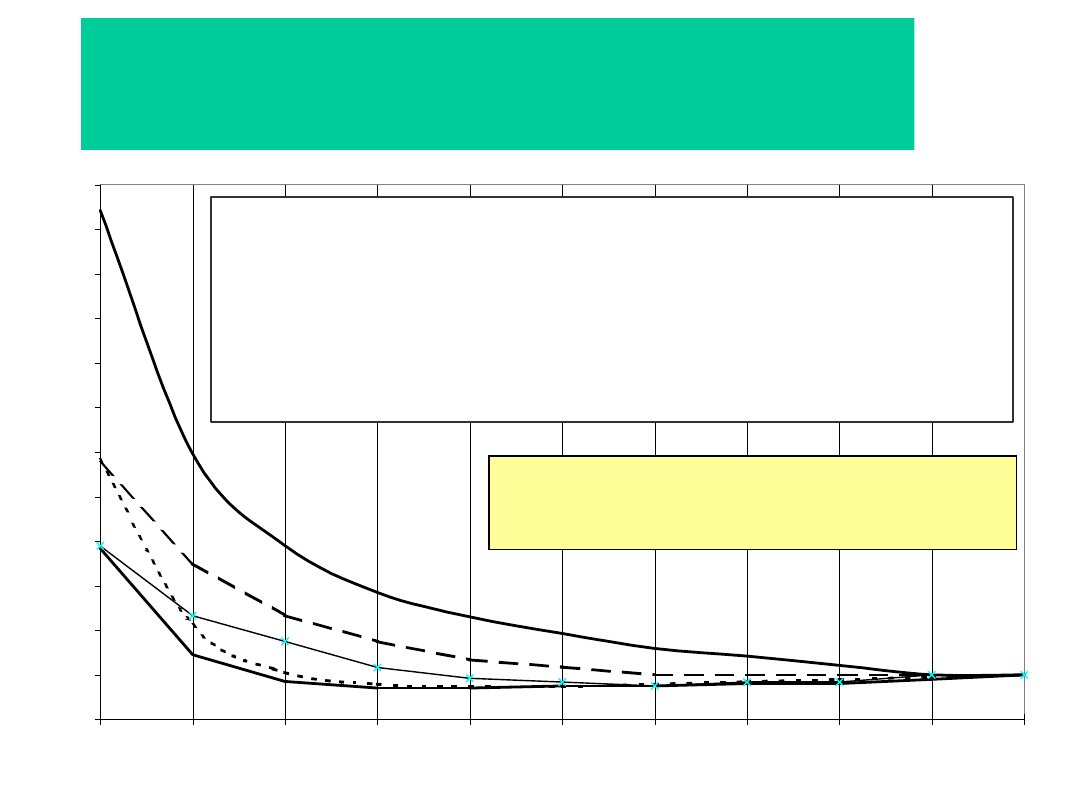
Dobór współczynnika oporów

głównych f

0,90

1,00

1,10

1,20

1,30

1,40

1,50

1,60

1,70

1,80

1,90

2,00

2,10

0

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

1

k

z

f

z

/f

n

1

2

3

4

5

1- przenośnik nadkładowy w kopalni odkrywkowej węgla brunatnego z

krążnikami w złym stanie technicznym (podwyższone opory obracania);

2- 2÷5 przenośniki z krążnikami w dobrym stanie technicznym:

2- przenośnik typu Gwarek 1200 transportujący węgiel kamienny,

3- przenośnik typu Gwarek 1400 transportujący węgiel kamienny,

4- przenośnik typu Legmet 1200 transportujący rudę miedzi,

5- przenośnik nadkładowy B-2000 Poltegor.

25 przenośniki z krążnikami w dobrym stanie technicznym:

f

n

- dla warunków znamionowych (dla

k

z

=

1

)

f

z

– dla innego załadowania

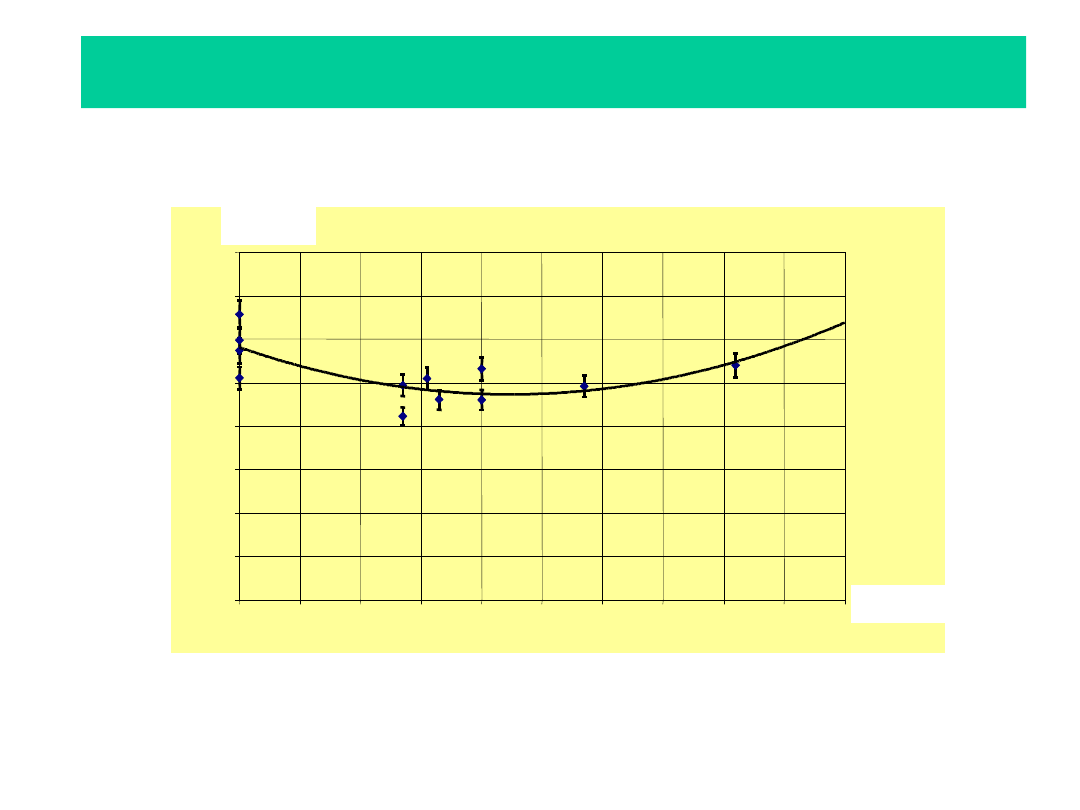
Dobór współczynnika oporów

głównych f

Wyznaczone z pomiarów (na przenośnikach pracujących w

podziemnych kopalniach węgla kamiennego zmiany współczynnika
oporów głównych w zależności od stopnia załadowania cięgna
górnego

2

027

,

0

0241

,

0

0291

,

0

)

(

f

z

z

z

z

k

k

k

f













0

0,005

0,01

0,015

0,02

0,025

0,03

0,035

0,04

0

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

1

f

k

z

f

z

k

z

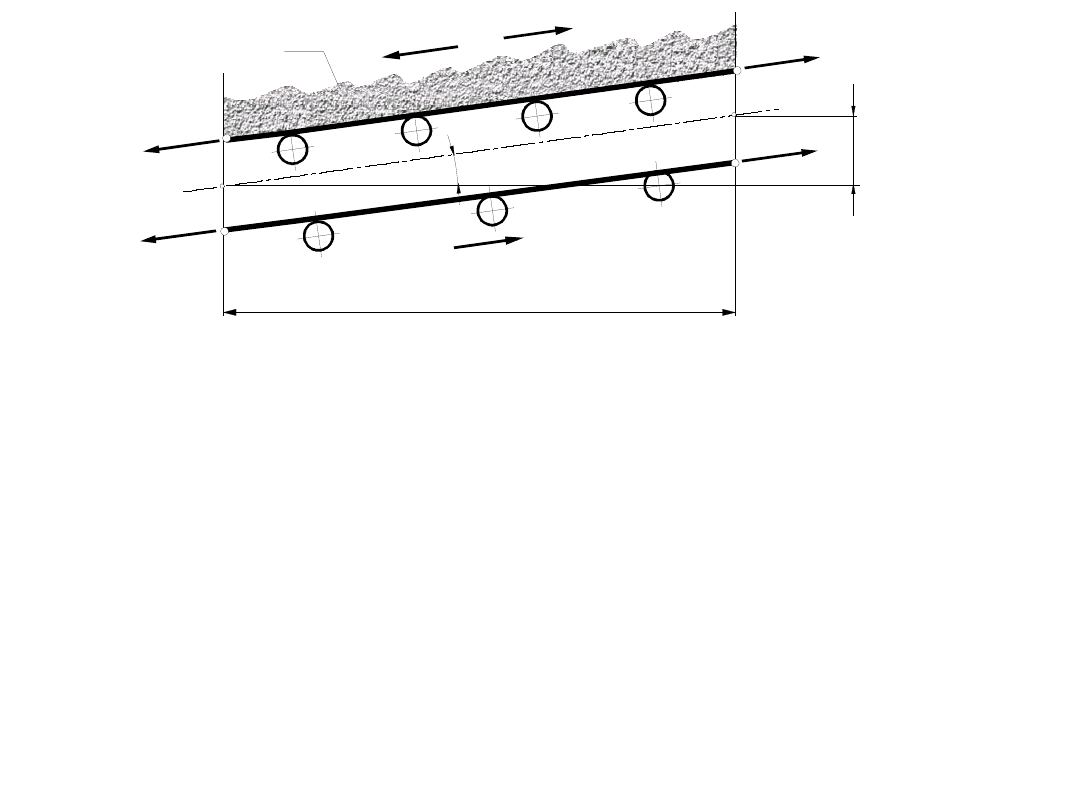
v

t

S

k

S

q

H

i

S

m

S

n

Q

M

m

u

(W

q

)

k-q

K

N

(W

d

)

m-n

L

i



i

(

W

g

)

k-q

- opory cięgna górnego na analizowanym odcinku trasy, N;

(W

d

)

m-n

- opory cięgna dolnego na analizowanym odcinku trasy, w N;

(W

hu

)

k-q

- opory podnoszenia urobku na analizowanym odcinku trasy, w

N; (W

ht

)

k-q

=(W

ht

)

m-n

- opory podnoszenia taśmy na analizowanym

odcinku trasy, w N; L

i

–długość odcinka trasy, w m; H

i

– wysokość

podnoszenia na rozpatrywanym odcinku trasy, w m;



i

– kąt

nachylenia odcinka trasy, w rad (); C(L) – współczynnik oporów

skupionych wyznaczony dla całkowitej długości przenośnika.

 





i

T

i

u

i

K

u

T

i

i

q

k

H

m

g

H

m

g

m

m

m

g

L

f

L

C

S

S

































cos

q

k

ht

q

k

hu

q

k

g

q

k

W

W

W

S

S















)

(

)

(

)

(

 





i

T

i

D

T

i

i

n

m

H

m

g

m

m

g

L

f

L

C

S

S

























cos

n

m

ht

n

m

d

n

m

W

W

S

S











)

(

)

(

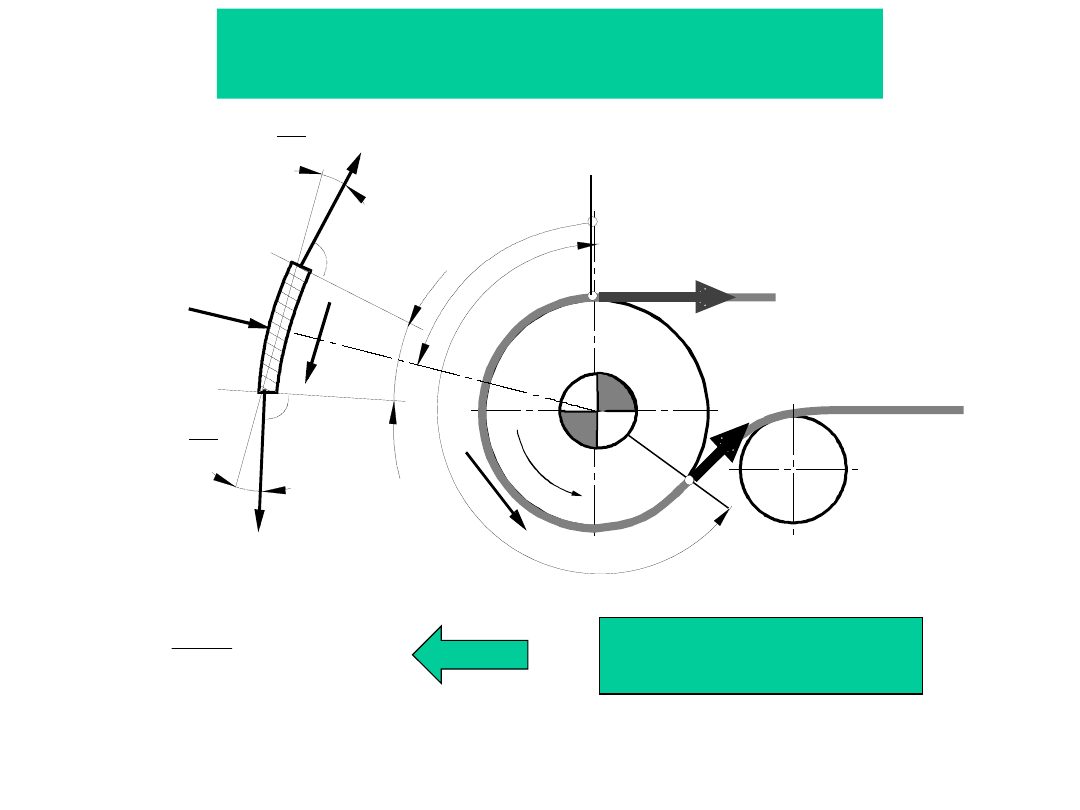
Sprzężenie cierne

T

N

S

S

1

S

2

1

2

P

0

S - dS

d 

2



d 

2



d 



.

.







e

S

S

2

1

wzór Eulera

Sprzężenie cierne

1

2

S

2

S

1



1



2

P

O2

P

O1

S

P

S

P

Zgodnie z równaniem Eulera

Mnożąc stronami obie zależności otrzymuje się:

1

1







e

S

S

p

2

2







e

S

S

p









































e

e

e

e

S

S

2

1

2

1

2

1

0

2

1

P

S

S





Sprzężenie cierne

2

1

P

O1

P

O2

P

O

= P

O1

+ P

O2

S

1

S

2

S

1

S

2

1

2

P

O

S

1

S

4

S

3

S

2

1

2

3

4

c

H

W

d

-

W

ht

W

G

+

W

ht

+

W

hn

a

b

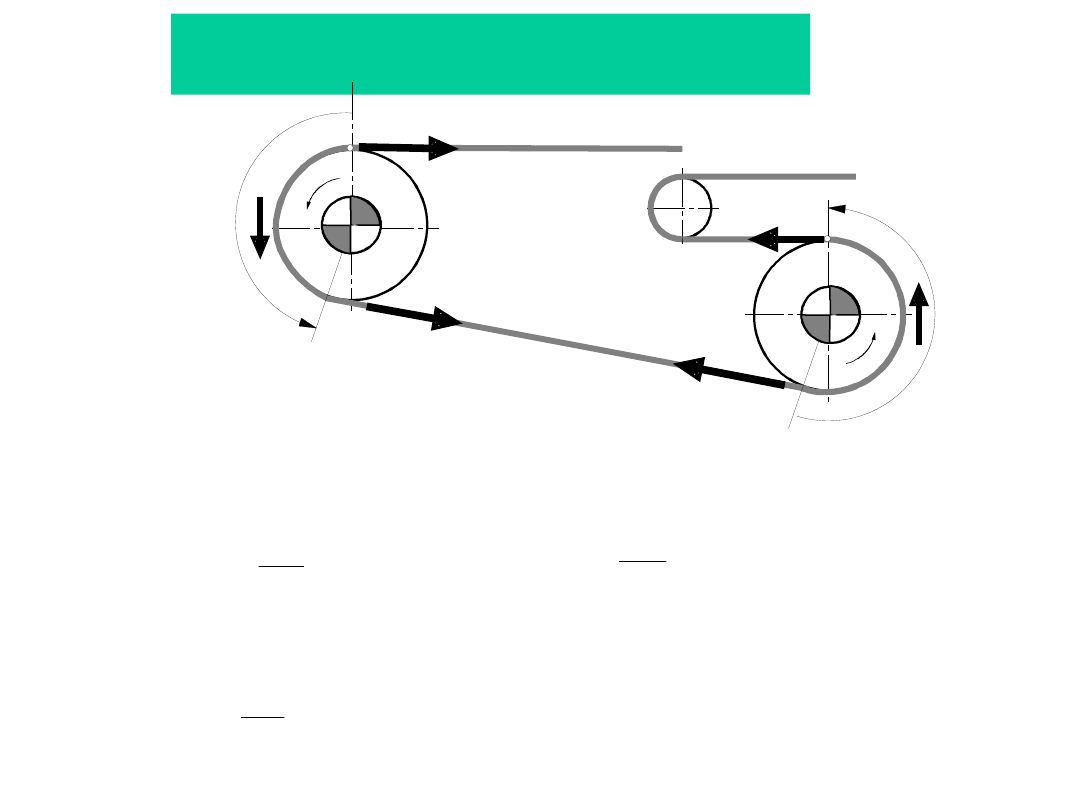
Siły w taśmie w ruchu ustalonym przenośnika z

napędem czołowym

a) - rozkład sił w cięgnie górnym i dolnym,

b) - rozkład sił na stacji napędowej jednobębnowej

c) - rozkład sił na stacji napędowej dwubębnowej

Sprzężenie cierne

Zapewnienie sprzężenia ciernego na wszystkich bębnach
napędowych przenośnika wymaga odpowiedniego doboru siły
napinającej. Siła ta realizowana jest przez okresowe lub stałe
przemieszczanie bębna napinającego. Jeżeli utrzymanie w ruchu
przenośnika wymaga przekazania do taśmy siły obwodowej P

0

, to

ze wzoru Eulera wynika, że w miejscu zbiegania z ostatniego
bębna stacji napędowej siła w taśmie musi spełniać warunek

Wzór ten w stosunku do zależności teoretycznej Eulera
skorygowany jest o współczynnik zabezpieczenia przed
poślizgiem

k

p

,

1

0

2













e

P

k

S

p

Sprzężenie cierne

W

przybliżonych obliczeniach

wstępnych

napędu dwu- lub

trójbębnowego zakłada się, że siła obwodowa rozkłada się na
poszczególne bębny proporcjonalnie do zainstalowanej mocy. Wówczas
analizowane jest sprzężenie cierne na ostatnim bębnie napędowym
(kolejność bębnów liczona jest zgodnie z kierunkiem biegu taśmy) bo
tam występują najgorsze warunki do współpracy ciernej (najniższe siły
w taśmie). Wymagane napięcie wstępne taśmy na ostatnim bębnie
czołowej stacji napędowej określa nierówność

gdzie:
z

n

- liczba zastosowanych jednostek w napędzie wielobębnowym, z

on

-

liczba jednostek na ostatnim bębnie napędowym (z

on

=1 dla trzech lub

pięciu jednostek napędowych oraz z

on

=2 dla czterech lub sześciu

jednostek napędowych na stacji czołowej); P

0n

– siła obwodowa

występująca

na

ostatnim

bębnie

napędowym

wynikająca

z

rozmieszczenia wszystkich jednostek napędowych, w N.
Dla parzystej liczby silników (4 silniki w napędzie dwubębnowym lub 6
silników w napędzie trójbębnowym) założenie to sprowadza się do
przyjęcia równomiernego rozkładu sił obwodowych

1

0

2















e

P

z

z

k

S

n

n

on

p

M

W

M

O

1

2

3

0

n

synchr

obroty silnika

(prędkość taśmy)

m

om

en

t

nadwyżka dynamiczna

ruch ustalony

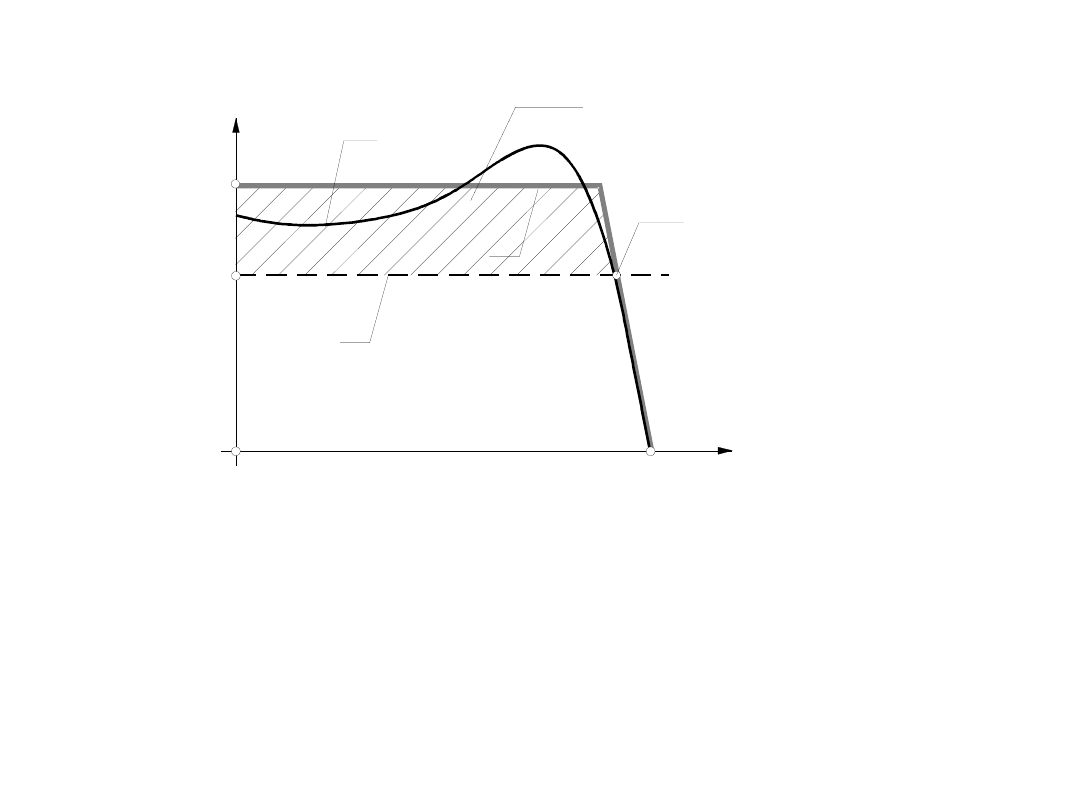
Przebieg momentu rozruchowego silnika napędu

przenośnika taśmowego

1-charakterystyka rozruchowa silnika asynchronicznego

prądu zmiennego,

2-przyjęta charakterystyka modelowa,

3-moment oporów ruchu przenośnika

S

1

S

2



1



2

a)

b)

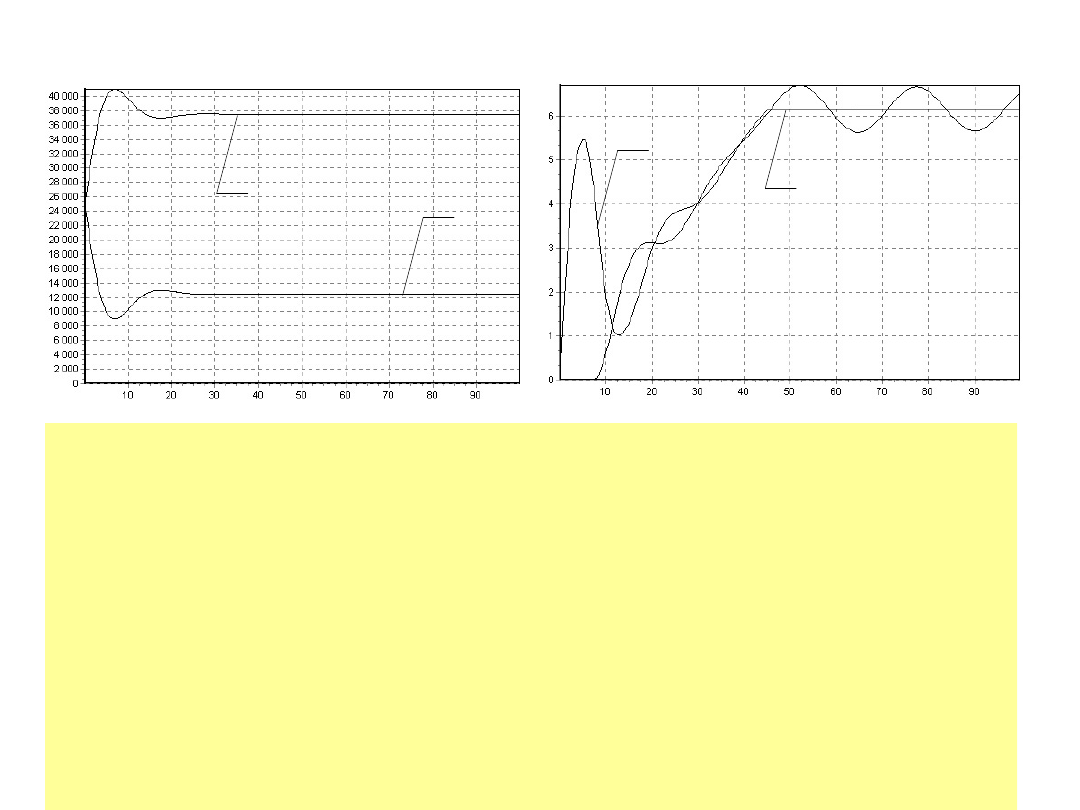
Rozruch przenośnika ze stałym położeniem bębna

napinającego

w warunkach poślizgu rozwiniętego (ciągły poślizg od

chwili t=25 s);

dla siły napięcia wstępnego S

0

=25 kN

a)- siły S

1

i S

2

na bębnie napędowym w warunkach

poślizgu

b)-przebieg prędkości kątowej czołowego bębna

napędowego



1

i bębna zwrotnego



2

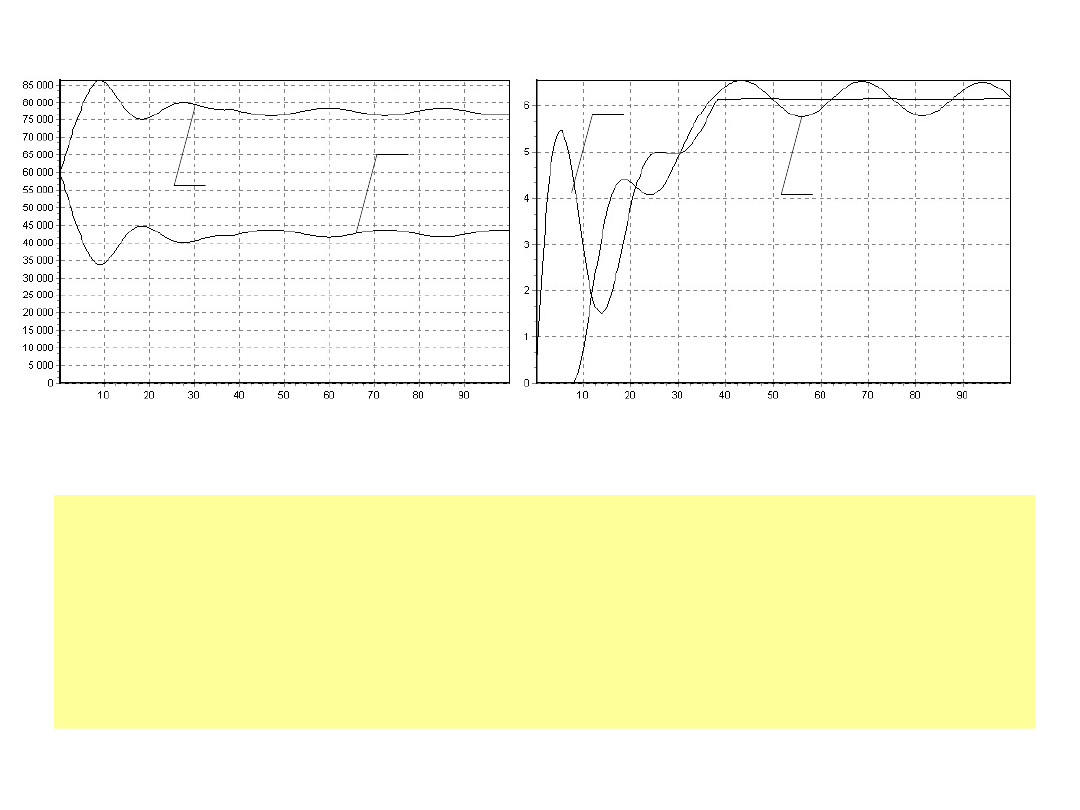
S

1

S

2



1



2

a)

b)

Rozruch przenośnika ze stałym położeniem bębna

napinającego

w warunkach braku poślizgu rozwiniętego, dla S

0

=60

kN;

a)-przebieg sił na bębnie napędowym,

b)- przebieg prędkości kątowych obu bębnów

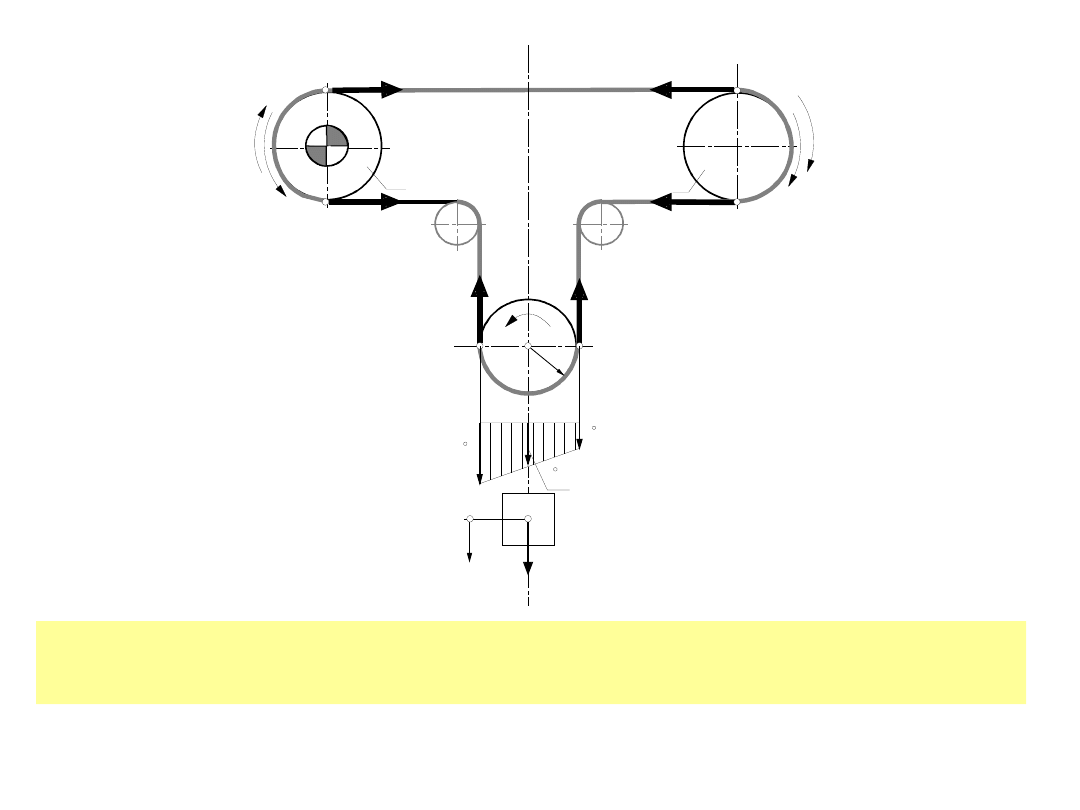
1

S

2

S

1

2

I

1

3

4

S

3

S

4

I

2

S

2

S

4

r

b

I

2

.



2

M

W

M

O

I

1

.



1

6

5



b

G

x

b

x

6

x

5

x

b

Uproszczony model przenośnika z ciężarowym

urządzeniem napinającym

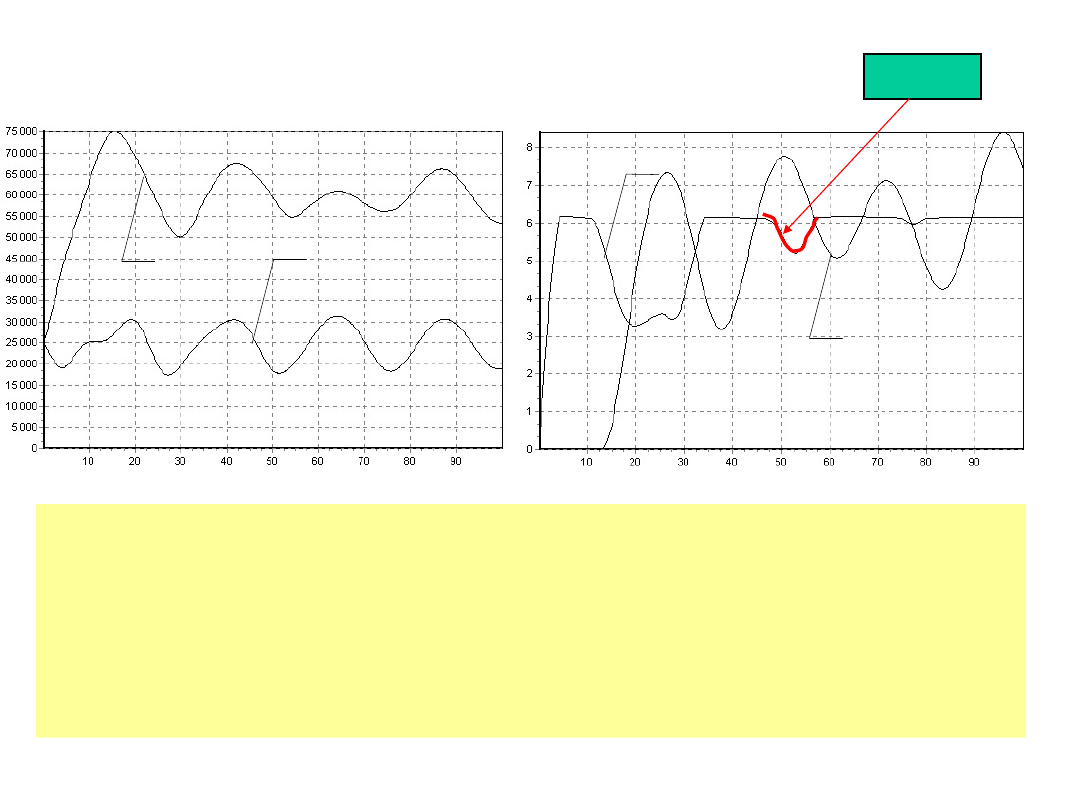
S

1

S

2



1



2

2

a)

b)

Przebieg rozruchu przenośnika z ciężarowym

napinaniem taśmy warunkach, dla napięcia wstępnego S

0

=25 kN;

a)- siły w taśmie na bębnie

b)-prędkości kątowe bębna napędowego i bębna

zwrotnego

poślizg

Moc napędu głównego

Siła obwodowa realizowana przez napęd (na obwodzie

bębna napędowego), która jest niezbędna do utrzymania
taśmy w ruchu ustalonym wynosi:

Moc napędu (w kW) wyznaczana jest z zależności

gdzie:



m

- sprawność mechaniczna napędu.

 
W napędach głównych przenośników ze sprzęgłem

podatnym przyjmuje się sprawność od



m

=0,90,95 natomiast

w mechanizmach, w których zastosowano sprzęgło
hydrokinetyczne, przyjmuje się



m

=0,820,87

hu

d

g

W

W

W

W

P











0

m

t

v

P

N









1000

0

Moc napędu głównego

W przypadku przenośników o trasie opadającej lub składającej się

tylko z niektórych odcinków opadających może zaistnieć przypadek
hamowania w ruchu ustalonym (praca generatorowa silników
napędu głównego przenośnika). Stan taki ma miejsce, gdy wartość
bezwzględna ujemnych oporów podnoszenia urobku przewyższa
opory cięgna górnego i dolnego czyliW

hu

W

g

+W

d

. Wówczas siła

obwodowa jest ujemna a wymagana moc hamowania (w kW) w
ruchu ustalonym wynosi:

Przy zmianie kierunku przepływu strumienia mocy sprawność

mechaniczna w warunkach hamowania napędem w ruchu
ustalonym wyniesie :

1000

0

mh

t

v

P

N

























m

mh





1

2

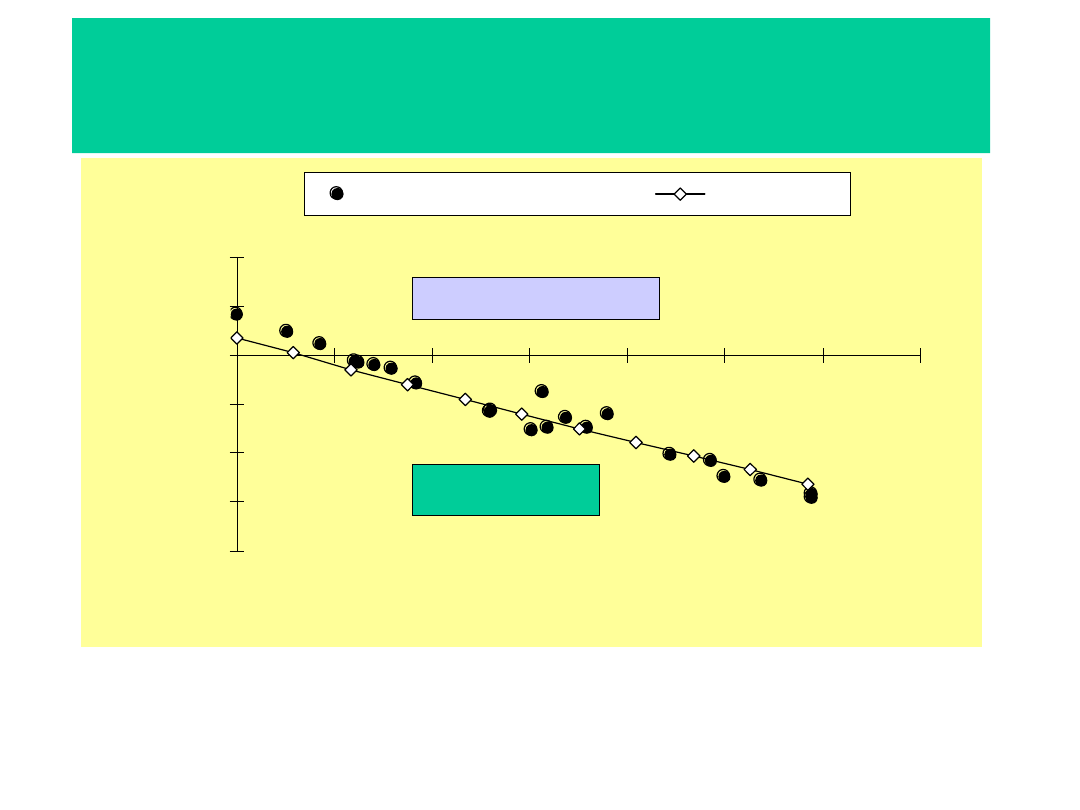
Moc napędu przenośnika

opadającego

-2000

-1500

-1000

-500

0

500

1000

0

2000

4000

6000

8000

10000 12000 14000

wydajność [m3/h]

m

o

c

[

k

W

]

pomiar na przenośniku

obliczenia

Zmierzona oraz obliczona moc napędu głównego przenośnika
opadającego (przenośnik nadkładowy o wydajności nominalnej Q

V

=12

800 m

3

/h, szerokość taśmy B=2,25 m, prędkość taśmy v

t

=5,24 m/s,

kąt nachylenia trasy

=-7,9, taśma St 3150, napęd główny na stacji

zwrotnej 41000 kW)

pędzenie

hamowanie

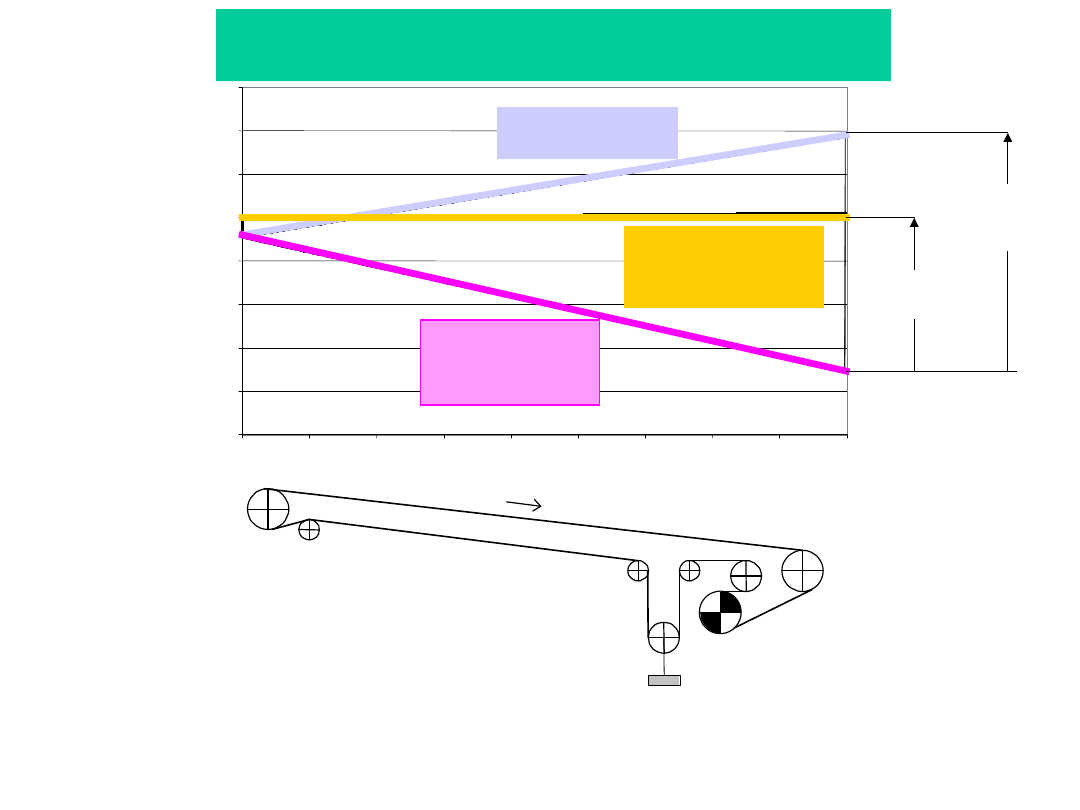
Rozkład sił w

taśmie

0

10

20

30

40

50

60

70

80

0

200

400

600

800

1000

1200

1400

1600

1800

[m]

Sił
y

w

taś
mi

e

[k
N]

Sg (pusty), N=189kW

Sg (kz=0,8, Q=3400t/h), N=128kW

Sd (dla obu przypadków)

Rozkład sił w taśmie w ruchu ustalonym przenośnika opadającego o małym
nachyleniu trasy. Dane przenośnika: δ=1,3º, H= -40 m, L=1800 m, nosiwo -

piasek/glina ρ=1600 kg/m

3

, B=1,4 m, v

t

=3,15 m/s, λ=35º, l

g

=1,0 m, taśma

EP2000/5,

cięgno górne puste

N=189 kW

cięgno górne pełne

Q= 3400 t/h

N= 128 kW

cięgno dolne

dla obu

przypadków

P

0

P

0

0

2 0

4 0

6 0

8 0

1 0 0

1 2 0

1 4 0

0

1 0 0

2 0 0

3 0 0

4 0 0

5 0 0

6 0 0

7 0 0

8 0 0

9 0 0

[m ]

S ił

y

w

taś

m i

e

[k

N ]

S g (pu s ty), N =11 1 kW

S g (k z =0,8 , Q =3 4 0 0t/h ), N = -2 2 9 kW

S d

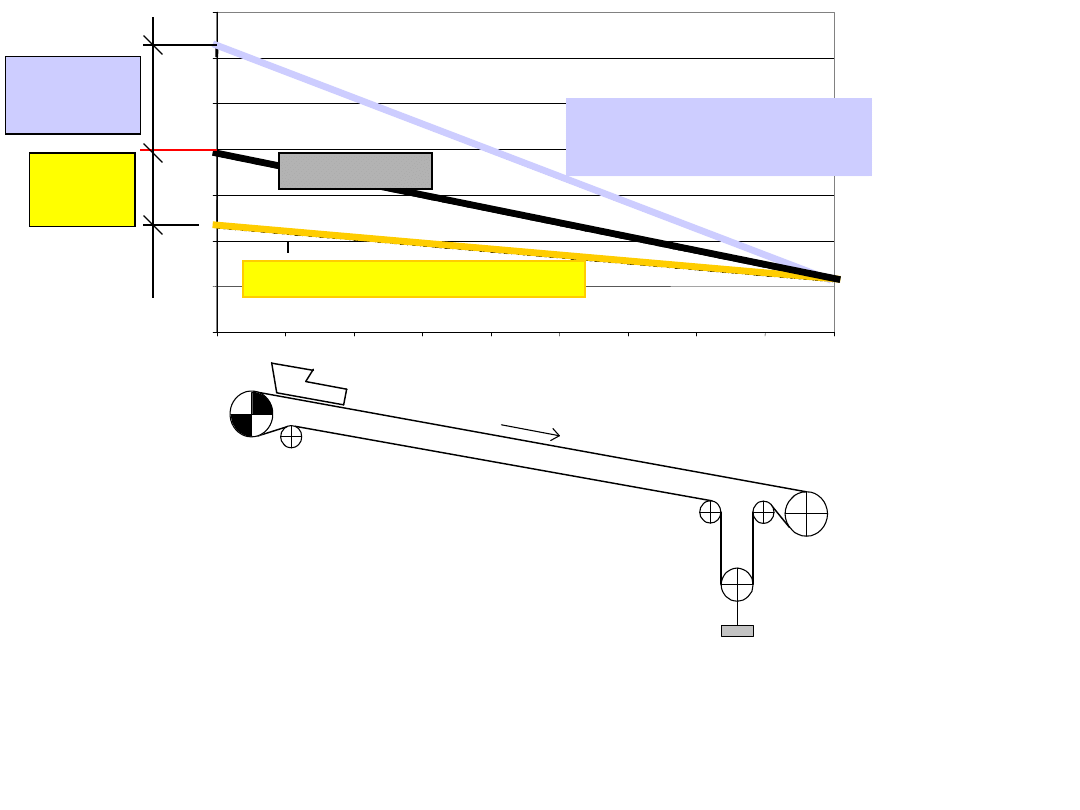
Rozkład sił w taśmie przenośnika opadającego o dużym nachyleniu trasy:

δ=3,2º, H= -50 m, L=900 m, nosiwo - piasek/glina ρ=1600 kg/m

3

, B=1,4

m, v

t

=3,15 m/s, λ=35º, l

g

=1,0 m, taśma EP2000/5 ,

cięgno górne załadowane, k

z

=0,8

Q=3400 t/h, N=

-

229 kW

cięgno górne puste, k

z

=0, N=111 kW

cięgno dolne

P

0

 0

hamowanie

P

0

 0

pędzenie

0

5 0 0 0 0

1 0 0 0 0 0

1 5 0 0 0 0

2 0 0 0 0 0

2 5 0 0 0 0

3 0 0 0 0 0

3 5 0 0 0 0

4 0 0 0 0 0

4 5 0 0 0 0

0

3 0 0

6 0 0

9 0 0

1 2 0 0

[ m ]

S

iły

w

t

a

ś

m

ie

[

k

N

]

S g ( k z = [ 1 , 0 , 1 , 0 ] )
N = 7 5 7 k W

S g ( k z = [ 1 , 1 , 1 , 1 ] )
N = 3 7 1 k W

S g ( k z = [ 0 , 1 , 0 , 1 ] )
N = - 2 4 0 k W

S g ( k z = [ 0 , 0 , 0 , 0 ] )
N = 4 5 k W

S d

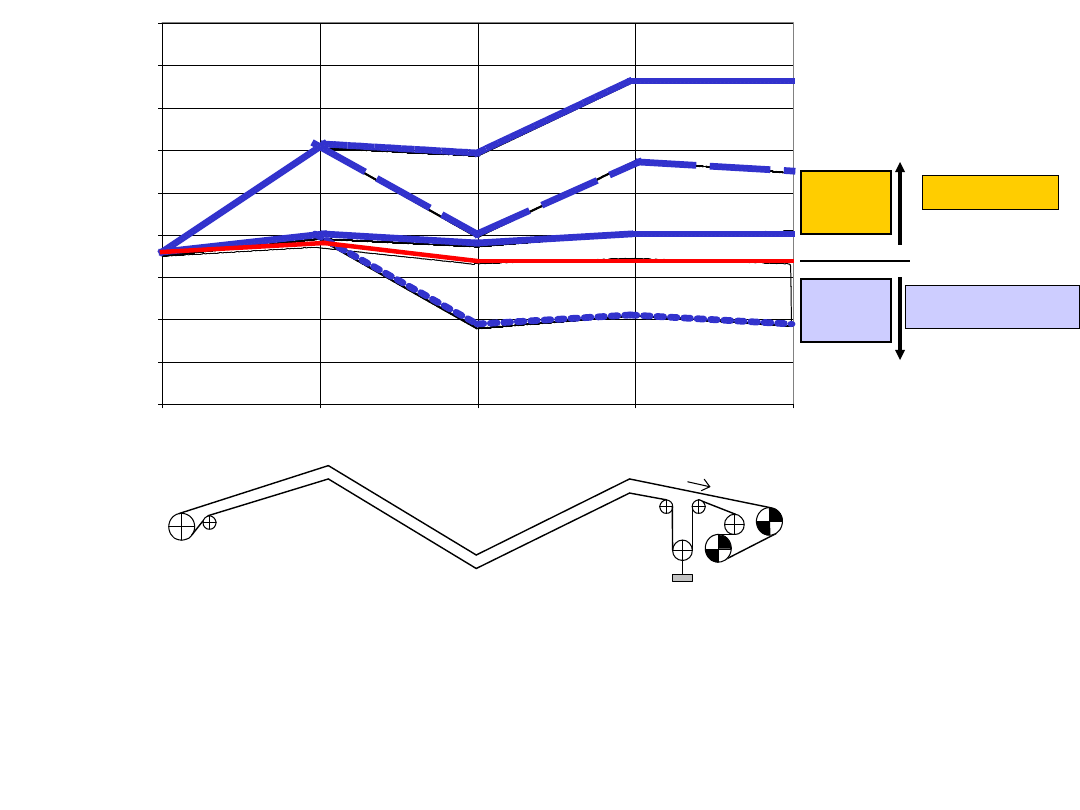
Rozkład sił w taśmie w ruchu ustalonym przenośnika o zmiennej
konfiguracji trasy:
L=1200 m, nosiwo - piasek/glina ρ=1600 kg/m

3

, B=1,4 m, v

t

=3,15 m/s,

λ=35º, l

g

=1,0 m, taśma EP2000/5 ,

S

g

- siła w cięgnie górnym,

S

d

- siła w

cięgnie dolnym;
k

z

=[1,1,1,1] - przy znamionowym załadowaniu całej trasy

k

z

=[1,0,1,0] – przy znamionowym załadowaniu tylko odcinków

wznoszących,
k

z

=[0,1,0,1] – przy znamionowym załadowaniu tylko odcinków

opadających,
k

z

=[0,0,0,0] – przy pustej taśmie

P

0

0

P

0

0

pędzenie

hamowanie

Przy analizowaniu przenośników długich o złożonym profilu trasy, gdzie

występują odcinki wznoszące i opadające, wymiarowanie napędu tylko na
podstawie mocy dla wypełnienia znamionowego na całej długości nie jest
miarodajne. Konieczne jest sprawdzenie różnych wariantów obciążeń
(różnego rozkładu strugi urobku wzdłuż trasy przenośnika). Zaleca się
rozpatrzenie następujących przypadków:



      

wszystkie odcinki wznoszące wypełnione są strugą nominalną a

odcinki opadające są próżne (moc N

1

),



      

wszystkie odcinki opadające wypełnione są strugą nominalną przy

jednoczesnym braku wypełnienia urobkiem pozostałych odcinków
wznoszących (moc N

2

),



      

cała trasa załadowana jest strugą nominalną (moc N

3

).

Po obliczeniach wariantowych moc napędu przenośnika należy

wyznaczyć z zależności:

gdzie:
N

1,2



max

- największa wartość bezwzględna ze zbioru N

1

 i N

2



 

 

2

3

3

2

1

2

2

1

6

0

N

N

N

N

N











max

,

max

,

,

Moc napędu przenośnika o

złożonym profilu trasy

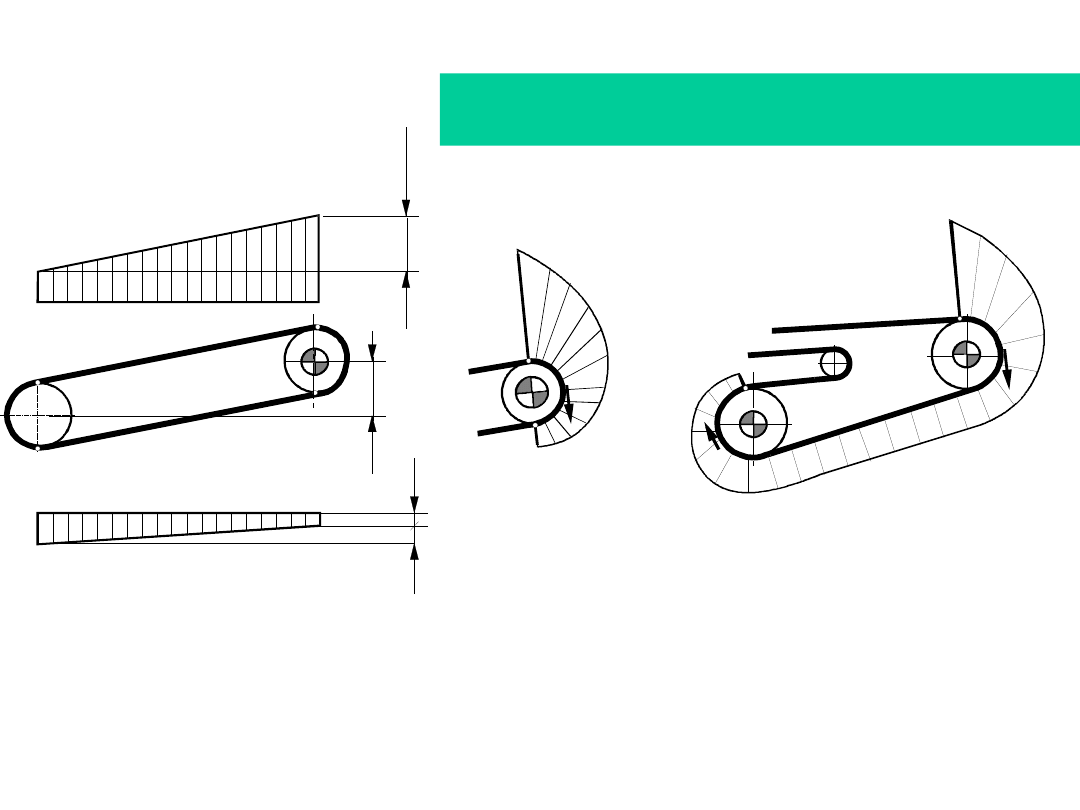
Zalecane rozwiązania

lokalizacji napędu i

urządzenia napinającego

ukształtowa

nie

trasy

przenośnika

kryterium

wymiarowania

napędu głównego

zalecane

rozmieszczenie

jednostek

napędowych

zalecane

usytuowanie

urządzenia

napinającego

taśmę

 

trasa

pozioma

wznosząca

lub opadająca

pod

niewielkim

kątem do

-1,5º

 

obliczeniowa moc

pędzenia taśmy

wypełnionej

urobkiem lub dla

trasy opadającej

taśmy pustej

stacja czołowa a po

wykorzystaniu

możliwości

sprzężenia ciernego

na stacji czołowej

dodatkowe napędy

pośrednie lub

napęd zwrotny

 
 

cięgno dolne w

pobliżu stacji

czołowej

 

trasa

opadająca

 

obliczeniowa moc

hamowania taśmy w

ruchu ustalonym

 

stacja zwrotna

cięgno dolne w

pobliżu stacji

zwrotnej

 
 

Trasa złożona

naprzemienni

e z odcinków

wznoszących

i opadających

 

obliczeniowa moc

pędzenia taśmy

większa od mocy

hamowania

napęd

wielobębnowy na

stacji czołowej

napinanie pomiędzy

bębnami czołowej

stacji napędowej

obliczeniowa moc

hamowania taśmy

większa od mocy

pędzenia

napęd

wielobębnowy na

stacji zwrotnej

napinanie pomiędzy

bębnami zwrotnej

stacji napędowej

moc pędzenia i

hamowania taśmy

(porównywalne

wielkości)

napęd rozdzielony

na stacji czołowej i

zwrotnej (z

możliwością

napędów

pośrednich

)

 

dowolne miejsce

cięgna dolnego