Podstawy statystyki vol. 3

TESTOWANIE HIPOTEZ

• Aby porównać ze sobą dwie

statystyki (średnie, mediany) z próby
stosuje się testy istotności.

• Mówią one o tym czy uzyskane

wyniki są rzeczywiste czy wynikają z
błędu pomiaru.

Na przykład

• Porównanie średniej ocen pewnego

ucznia ze średnia w całej klasie.

• Porównanie skuteczności dwóch metod

badawczych.

• Sprawdzenie różnic miedzy

rozwiązywaniem zadania w warunkach

stresu i relaksu.

• Badanie różnic miedzy kobietami a

mężczyznami w nasileniu depresyjności.

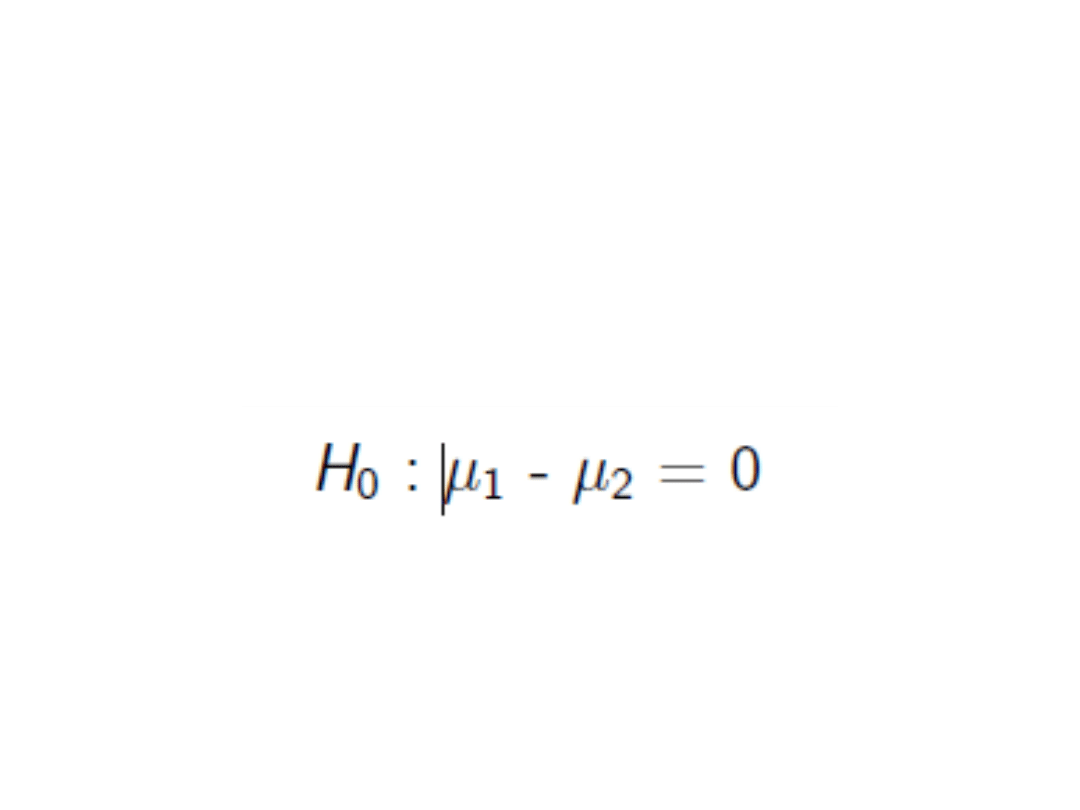
Hipoteza zerowa

• To twierdzenie o braku różnic.
• Np. uzyskujemy średnie z dwóch

grup osób badanych. Hipoteza
zerowa:

Test istotności

• Jest testem hipotezy zerowej. Pokazuje

jakie jest prawdopodobieństwo, że

otrzymane różnice sż wynikiem błędu.

• Kolejne kroki wnioskowania statystycznego:

– Zakładamy hipotezę zerowa

– Badamy dane empiryczne

– Szacujemy jakie jest prawdopodobieństwo

uzyskania różnicy równej lub większej niż

otrzymana przy losowym pobieraniu prób z

populacji przy założeniu prawdziwości H0.

– Przy małym – odrzucamy H0. Mówimy ze wynik

jest istotny.

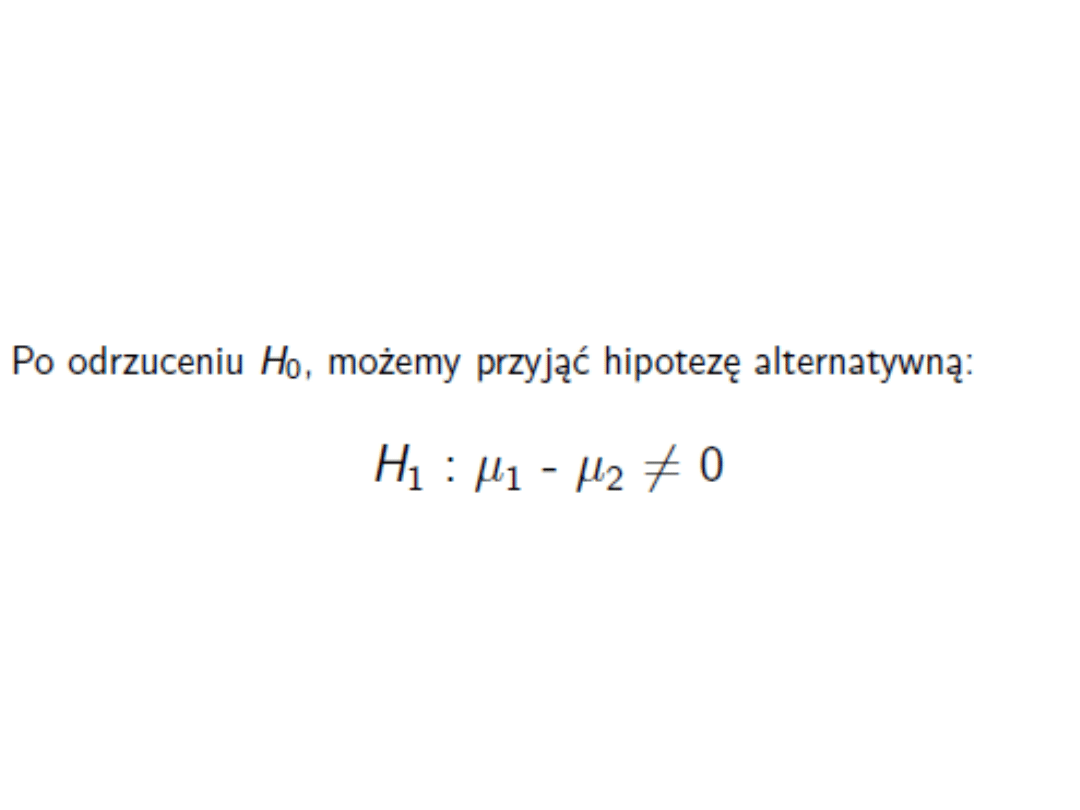
Hipoteza alternatywna

Jakie błędy można popełnic?

• Błąd I rodzaju (alfa) – przyjęcie H1,

gdy H0 jest prawdziwa

• Bład II rodzaju (beta) – odrzucenie

H1, gdy jest ona prawdziwa

• Przyjmowane poziomy istotności –

oznaczają, że istnieje x% szans na to,

że przyjęcie hipotezy alternatywnej

jest wynikiem błędu

Błąd I rodzaju

• Przy testowaniu/weryfikacji hipotez możemy

popełnić błąd pierwszego rodzaju. Błąd ten

popełniamy wtedy, gdy na podstawie

przeprowadzonej analizy statystycznej

stwierdzamy, że uzyskane wyniki są istotne

statystycznie a są one w rzeczywistości nieistotne

statystycznie.

Na popełnienie takiego błędu narażamy się wtedy,

gdy na przykład: stosujemy nieodpowiednie testy

statystyczne do weryfikacji hipotez, stosujemy dany

test statystyczny, pomimo tego, że założenia nie

zostały spełnione, aby wykonać dany test.

W praktyce oznacza to, że popełniliśmy błąd w

analizie i na tej podstawie wnioskujemy

prawdziwość postawionej hipotezy, a w

rzeczywistości nie możemy tego stwierdzić.

Błąd II rodzaju

• Przy testowaniu/weryfikacji hipotez możemy

popełnić błąd drugiego rodzaju. Błąd ten

popełniamy wtedy, gdy na podstawie

przeprowadzonej analizy statystycznej

stwierdzamy, że uzyskane wyniki są nieistotne

statystycznie, a są one w rzeczywistości istotne

statystycznie.

Na popełnienie takiego błędu narażamy się wtedy,

gdy na przykład: stosujemy nieodpowiednie testy

statystyczne do weryfikacji hipotez, stosujemy zbyt

restrykcyjnie ograniczenia dla analizy wyników.

W praktyce oznacza to, że popełniliśmy błąd w

analizie i na tej podstawie wnioskujemy fałszywość

postawionej hipotezy, a w rzeczywistości

moglibyśmy stwierdzić, że wyniki są istotne

statystycznie.

Testy bezkierunkowe

• Aby odrzucić hipotezę zerową na

poziomie istotności (przykładowo)
0,05, musimy sprawdzić, czy dany
wynik nie leży (w przypadku rozkłądu
normalnego) w przedziale +/-1,96
odchylenia standardowego

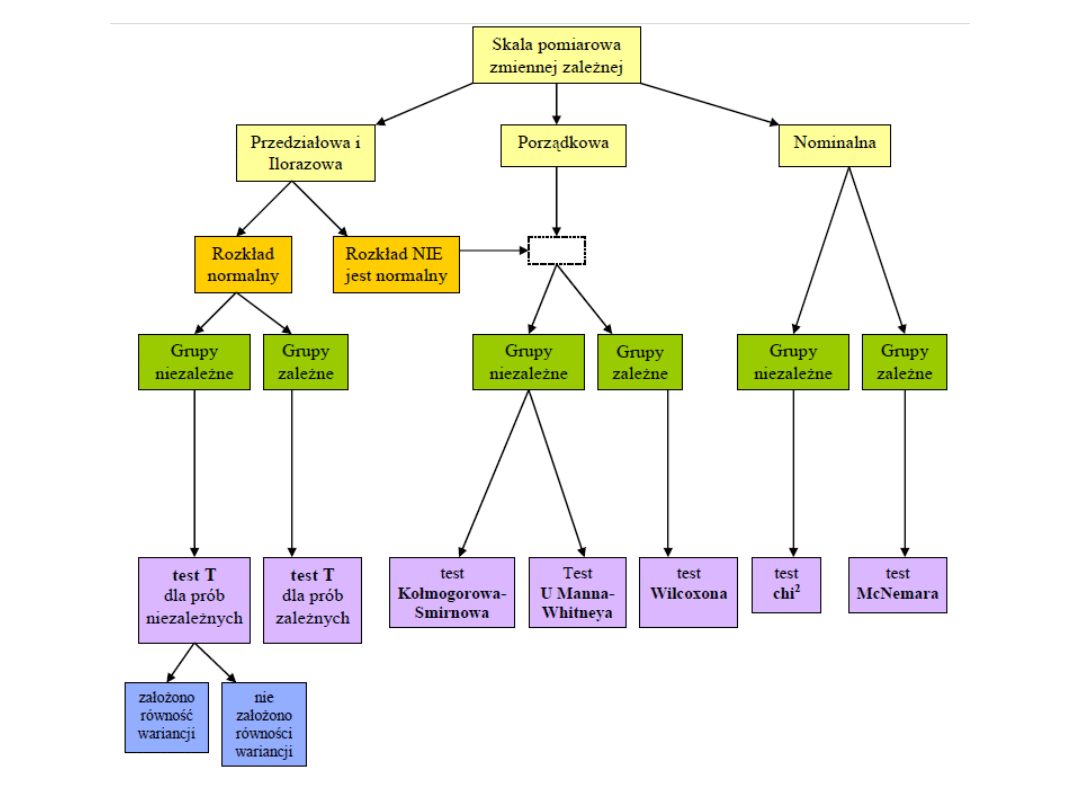
Kryteria wyboru testu

istotności różnic dla dwóch

prób

• Aby wybrać odpowiedni test istotności

różnic dla dwóch prób należy

rozpatrzeć następujące kryteria:

– · Skala pomiarowa zmiennej zależnej
– · Normalność rozkładu zmiennej zależnej
– · Charakter grup porównawczych

(niezależne vs zależne)

– · Liczebność porównywanych grup
– · Homogeniczność wariancji rozkładów

zmiennej zależnej

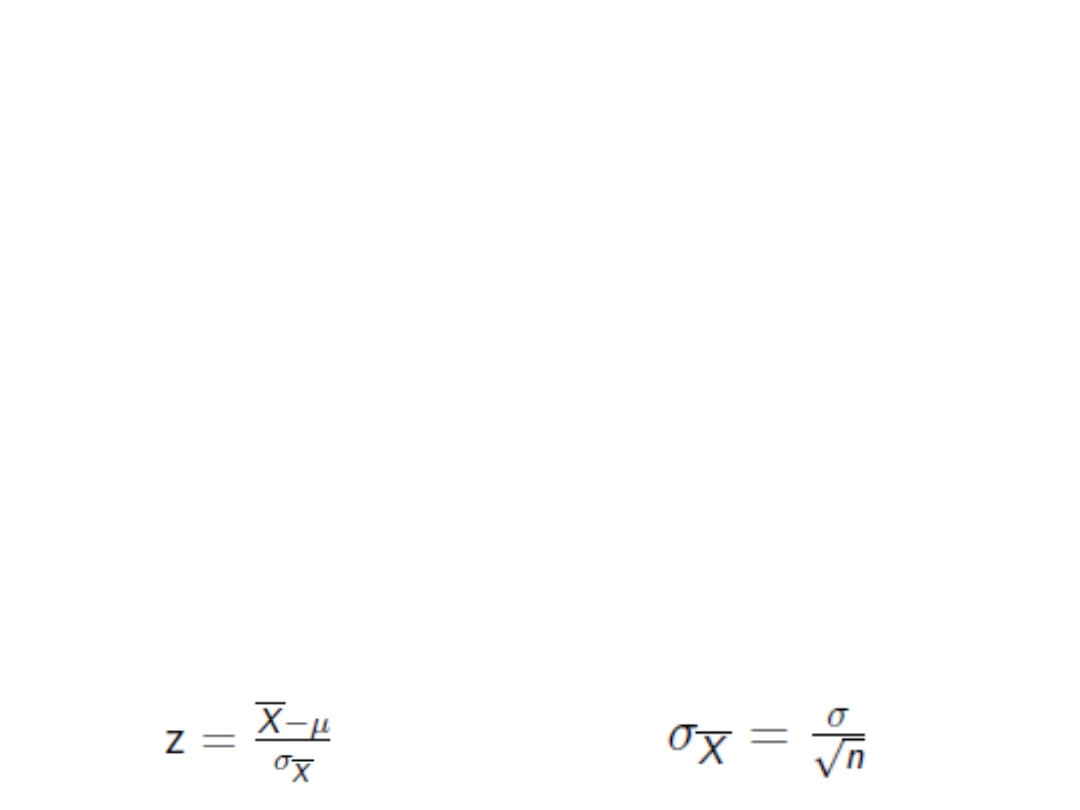
Testy istotności dla jednej

średniej

• W celu porównania danego wyniku

(średniej z próby) ze średnią z
populacji

• Na przykład czy średnia ocen ze

statystyki w naszej grupie różni się od
średniej ze wszystkich grup tego roku

• Jeśli znamy średnią i SD w populacji,

możemy odnieść się do rozkładu
normalnego i użyć wzoru:

Przykład 1

• W 25 osobowej grupie osób

badanych średnia IQ = 110. SD = 14.
Czy różni się od populacji (X = 100,
SD = 15)?

Przykład 1

• W 25 osobowej grupie osób badanych średnia

IQ = 110. SD = 14. Czy różni się od populacji
(X = 100, SD = 15)?

z = (110 – 100)/(15/pierw25) = 3,33

• Wartość z leży poza granicami 1,96 i 2,58.

Zatem różnica jest istotna statystycznie.

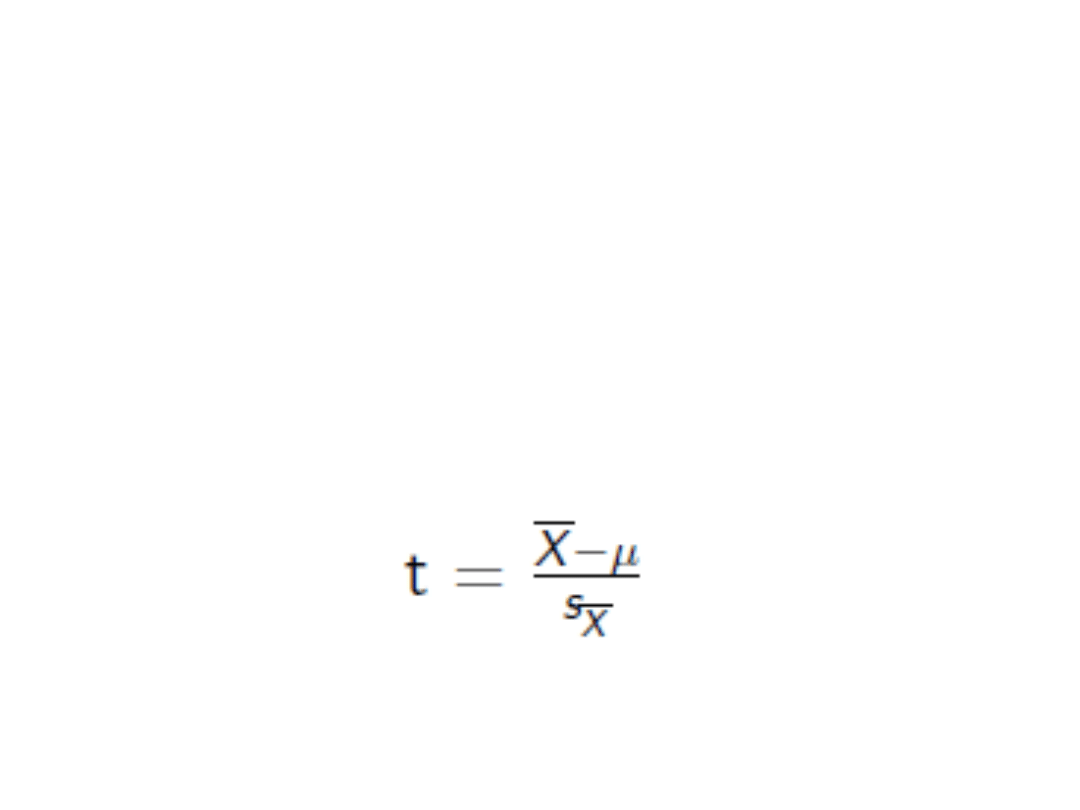
• Gdy znamy tylko średnią w populacji, ale

SD nie, to odnosimy się do rozkładu t

• Szacujemy błąd standardowy
• Stosujemy wzór:

(Mianownik – SE – błąd standardowy)

Testy istotności dla jednej

średniej

Przykład 2

• W klasie 25 osobowej średni IQ=110

a SD=14. Czy różni się od IQ w
populacji (średnia = 100)?

• Szacujemy błąd standardowy

Przykład 2

• W klasie 25 osobowej średni IQ=110

a SD=14. Czy różni się od IQ w
populacji (średnia = 100)?

• Szacujemy błąd standardowy

SE = s/√N=14/√25 = 2,8

t = (110 – 100)/2,8 = 3,57

Jakie wnioski?

Wnioski do zadania

• Wartość t przy df = 24 wynosi 2,064

(dla p=5%) i 2,797 (p=1%)

• Różnica jest istotna

Test kierunkowy

• Wykorzystujemy tylko połowę rozkładu
• W rozkładzie normalnym 5% obszaru

znajduje się powyżej z=1,64

• 1% obszaru znajduje się powyżej z=2,33
• Cel – przewidujemy kierunek zależności
• Działanie – porównujemy uzyskany

wynik z odpowiednimi wartościami dla
5% obszaru po prawej stronie rozkładu

Zadanie

• W próbie 16 studentów, średni wynik

na egzaminie wynosił 15, a s = 3.

• Czy wynik ten różni się od średniej

wśród wszystkich studentów równej
18?

• Zastosuj test kierunkowy dla 5%

poziomu istotności.

• Dane na skali ilościowej
• Podobna liczebność w grupach

• Zasada normalności rozkładu

Test t dla 2 prób

niezależnych

Testy zgodności

• Do najczęściej formułowanych hipotez tego

rodzaju należy hipoteza o  normalności
rozkładu zmiennej losowej ciągłej X:
H0: X ma rozkład normalny N(m, sigma)
przy hipotezie alternatywnej:
H1: X nie ma rozkładu normalnego N(m,
sigma)
gdzie m i sigma (wartość oczekiwana i 
odchylenie standardowe) to parametry
rozkładu normalnego.

Dlaczego?

• W hipotezie zerowej zakładamy, że n-elementowa

próba losowa pochodzi ze zbiorowości generalnej,

w której rozkład obserwowanej zmiennej losowej jest

normalny.

• Rozkład normalny jest bowiem jednym

z najważniejszych rozkładów. Rozwiązanie wielu

zagadnień statystycznych jest "prostsze", jeśli

analizowana cecha ma rozkład normalny. Wiele

analiz statystycznych i testów wymaga też założenia

o normalności rozważanej zmiennej (testy t-

Studenta, analiza wariancji, analiza regresji, analiza

kanoniczna itd.).

• Dlatego musimy przeprowadzić weryfikację

charakteru rozkładu, ilekroć chcemy zastosować

analizy statystyczne, które wymagają danych

o określonym rozkładzie.

Testy

• test Kołmogorowa i Smirnowa

Test ten opiera się na porównaniu procentów

skumulowanych zaobserwowanych z oczekiwanymi.

Jako wartość testu podawana jest maksymalna

różnica bezwzględna pomiędzy zaobserwowanymi

i oczekiwanymi procentami skumulowanymi. Test ten

wymaga jednak znajomości parametrów rozkładu

(średniej i odchylenia standardowego całej populacji).

Gdy ich nie znamy, a tak jest najczęściej, stosujemy

test Kołmogorowa i Smirnowa z poprawką Lillieforsa.

• test W Shapiro i Wilka

Test ten jest najbardziej polecany, ze względu na

dużą moc. Można go również stosować do małych

prób.

Jeśli statystyki okażą się istotne (tzn. p <0,05), to

odrzucamy hipotezę zerową o zgodności danych

z rozkładem normalnym. Oznacza to, że dana

zmienna (cecha) nie ma rozkładu normalnego.

Homogeniczność wariancji

• Jednym z założeń testów parametrycznych, np.:

testy t, analiza wariancji jest homogeniczność

wariancji. Homogeniczność możemy tutaj rozumieć

jako równość, jednolitość. Dokładniej, porównywane

ze sobą grupy, za pomocą testów parametrycznych

powinny mieć podobne wariancje. Oznacza to,

różnorodność uzyskanych wyników w

poszczególnych grupach powinna być podobna.

Aby zweryfikować, czy grupy mają podobne

wariancje, czyli czy zachowana jest homogeniczność

wariancji w grupach wykonuje się dodatkowe testy

statystyczne. Jednym z takich testów jest test

Levene'a.

Jeżeli wynik testu Levene'a jest istotny statystycznie

oznacza to, że wariancje nie są podobne.

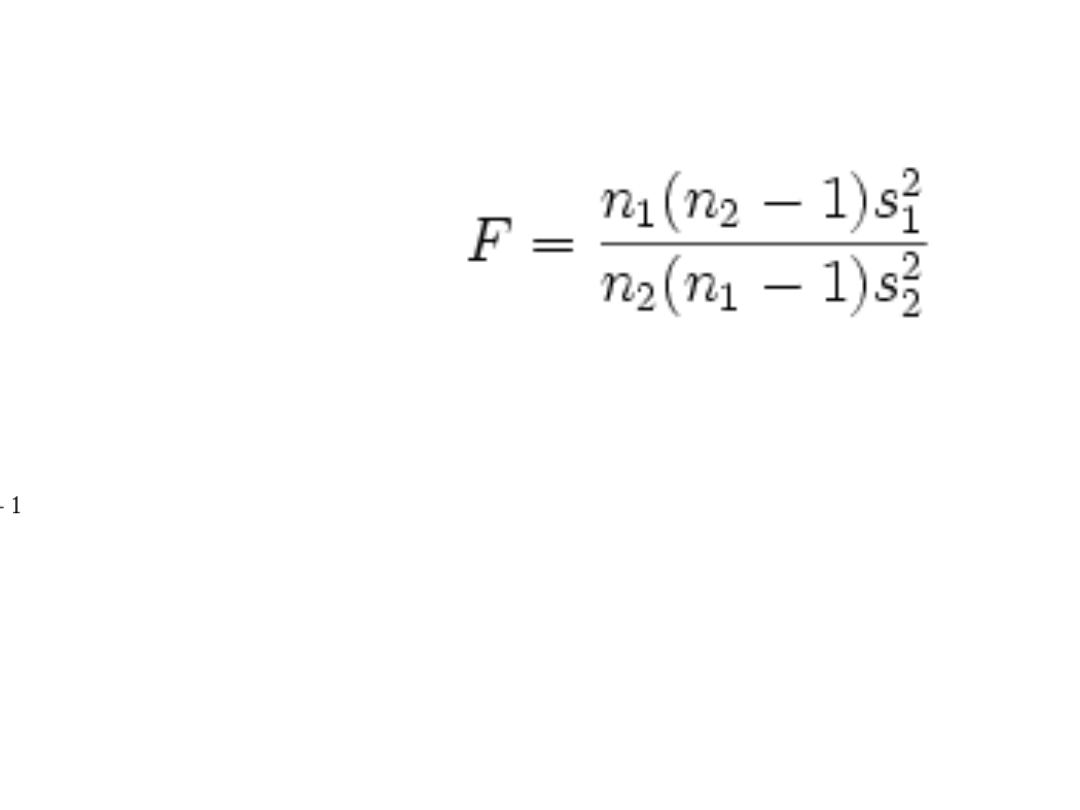
Test Fishera

• Stosujemy wzór:

• Liczba stopni swobody to:

v1 = n1 – 1
V2 = n2 - 1

• Z tablic odczytujemy wartość krytyczną
http://www.pomocstatystyczna.pl/tablice_

f.html

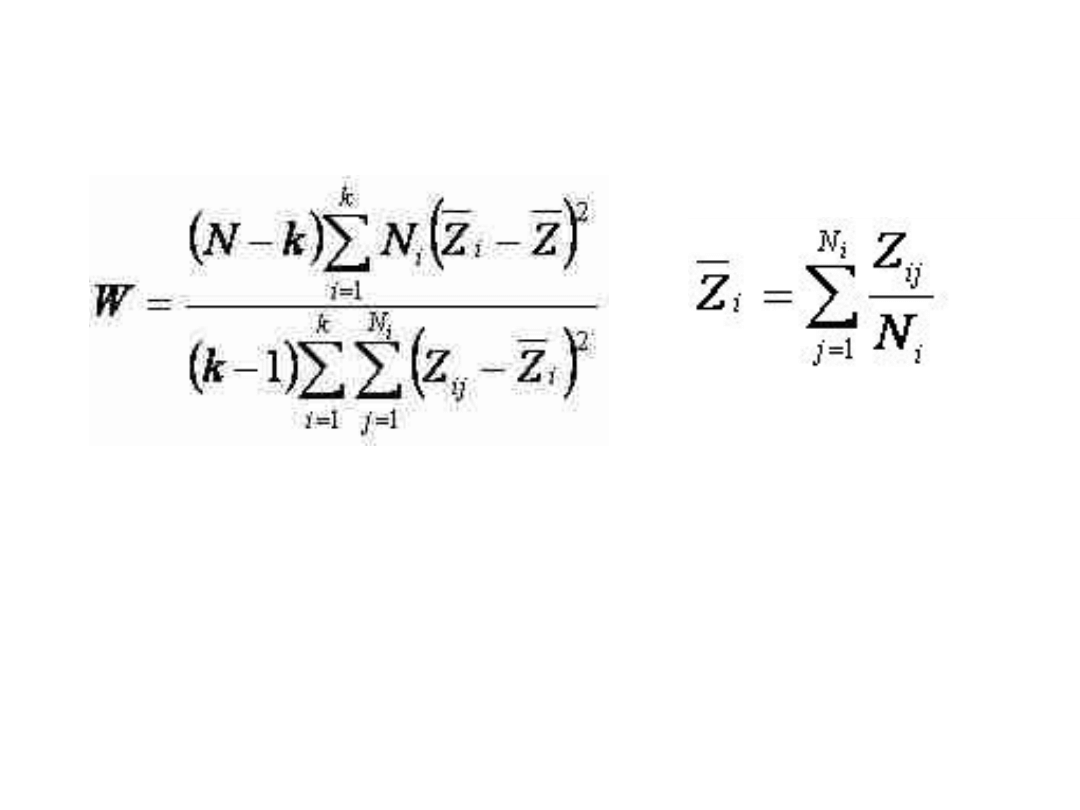
Test Levene’a

Gdzie: Ni - liczebność i-tej próbki,
xi - średnia i-tej próbki;
Zij - wartość bezwzględna odległości pomiaru j-tej
osoby z i-tej próbki od wartości średniej;
                         

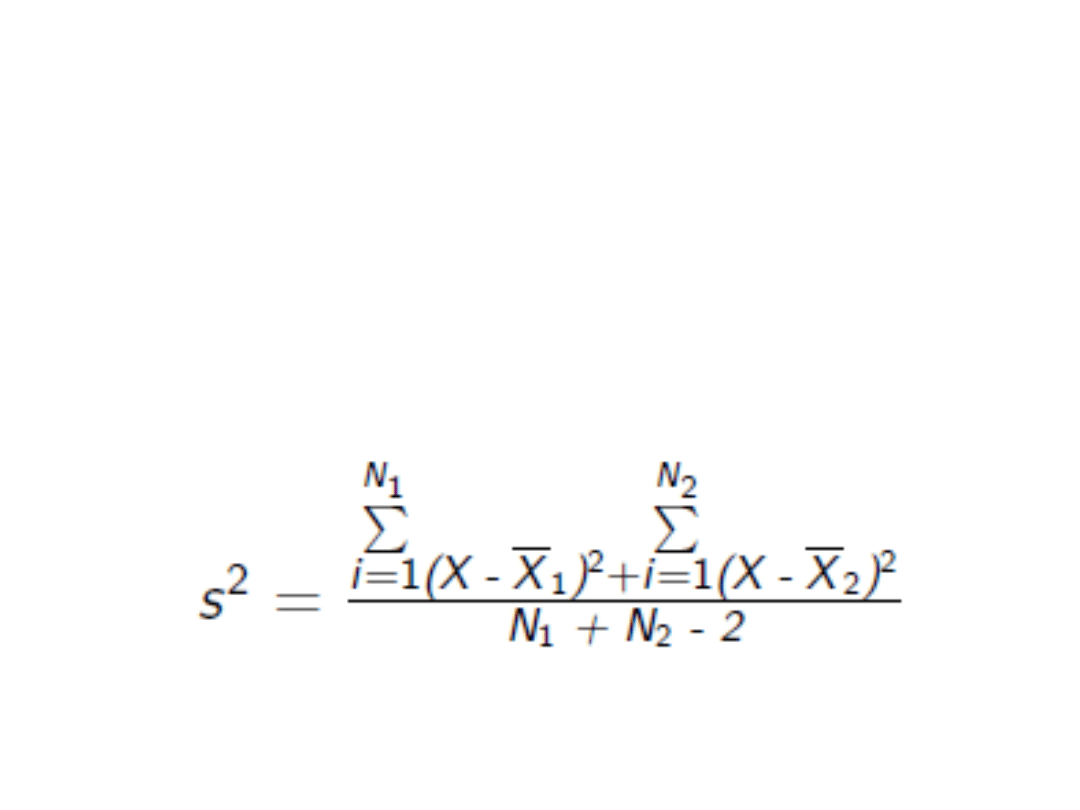
Dwie próby niezależne

• Jeżeli założenie o równości jest

uzasadnione to stosuje się wzór na
wspólna wariancje

• Jeśli nie, używamy testu Coxa-Cochrana

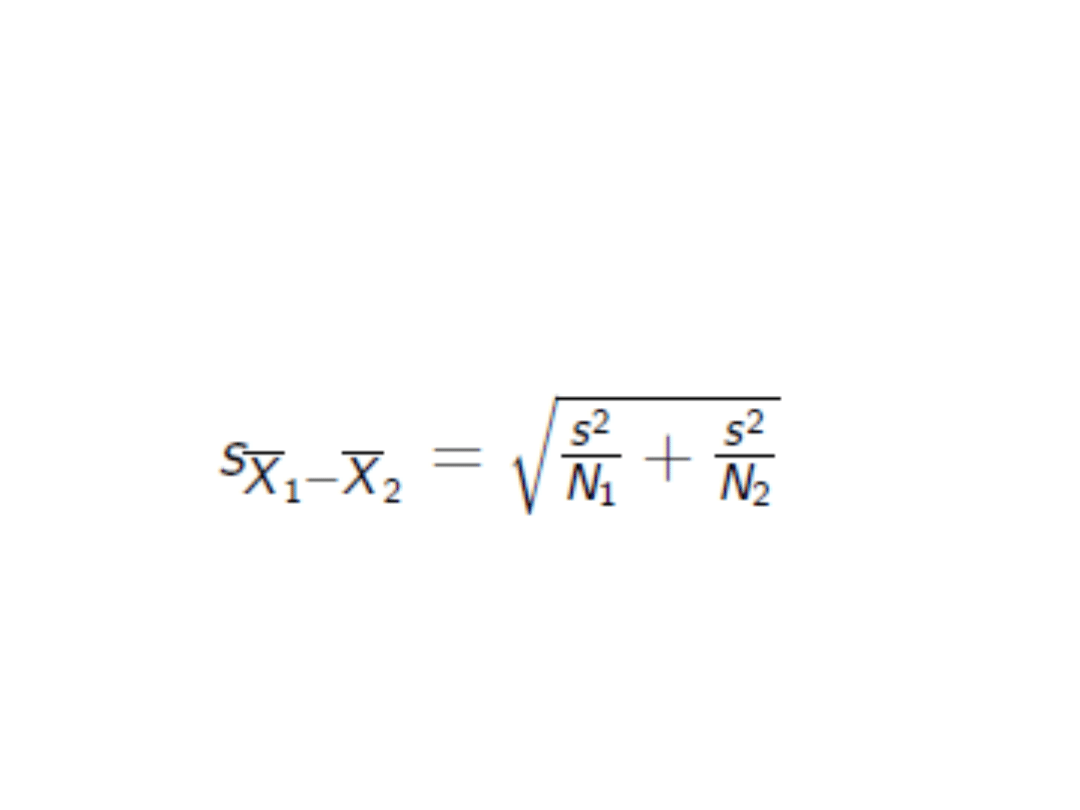
Dwie próby niezależne

• Nastepnie oblicza sie wspólny bład

standardowy:

• Liczba stopni swobody = N1 + N2 - 2

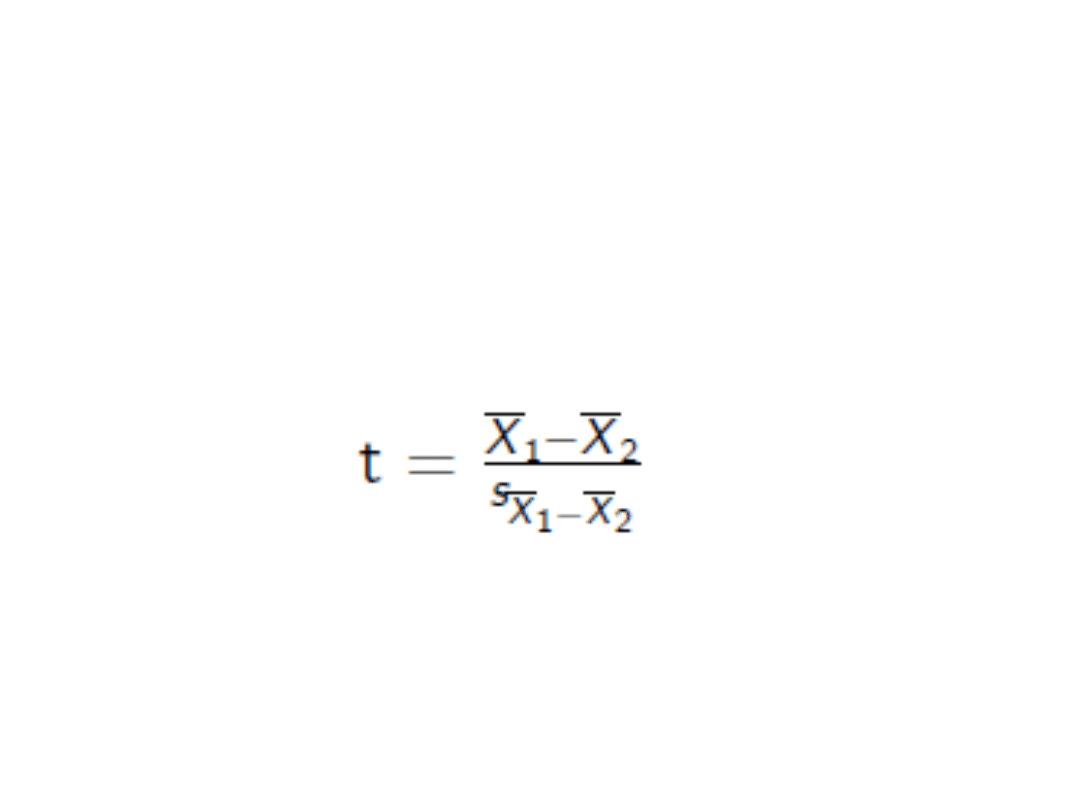
Dwie próby niezależne

• Wreszcie liczymy statystykę t

Zadanie 1

• Oceniano szczury odnośnie długości

zębów. Sprawdź testem t-studenta, czy

grupy różnią się istotnie między sobą:

• A: 16, 9, 4, 23, 19, 10, 5, 2
• B: 20, 5, 1, 16, 2, 4

• Opisz kolejne kroki postępowania. Czy

można w ogóle zastosować ten test?

Zadanie 2

• Zastosuj test kierunkowy dla

poniższych danych:

• A: 1, 6, 9, 6, 8
• B: 7, 9, 12, 15, 8, 10, 9
• (załóżmy, że grupy są równoliczne,

pomimo, że nie są ;) )

Początek pracy

• Stawiamy sobie hipotezę badawczą!

• H0 – nie ma różnic
• H1 – są różnice (jakie?)

Test t-studenta dla grup

niezależnych

1. Czy są spełnione założenia?

Test t-studenta dla grup

niezależnych

1. Czy są spełnione założenia?

a) Skala pomiarowa zmiennej zależnej

przedziałowa / ilorazowa

b) Normalność rozkładu zmiennej zależnej
c) Liczebność porównywanych grup

Test t-studenta dla grup

niezależnych

1. Czy są spełnione założenia?

a)

Skala pomiarowa zmiennej zależnej przedziałowa / ilorazowa

b)

Normalność rozkładu zmiennej zależnej

c)

Liczebność porównywanych grup

d) Homogeniczność wariancji rozkładów

zmiennej zależnej

1.d) Homogeniczność wariancji

rozkładów zmiennej zależnej

• Hipoteza zerowa:

wariancje są równe

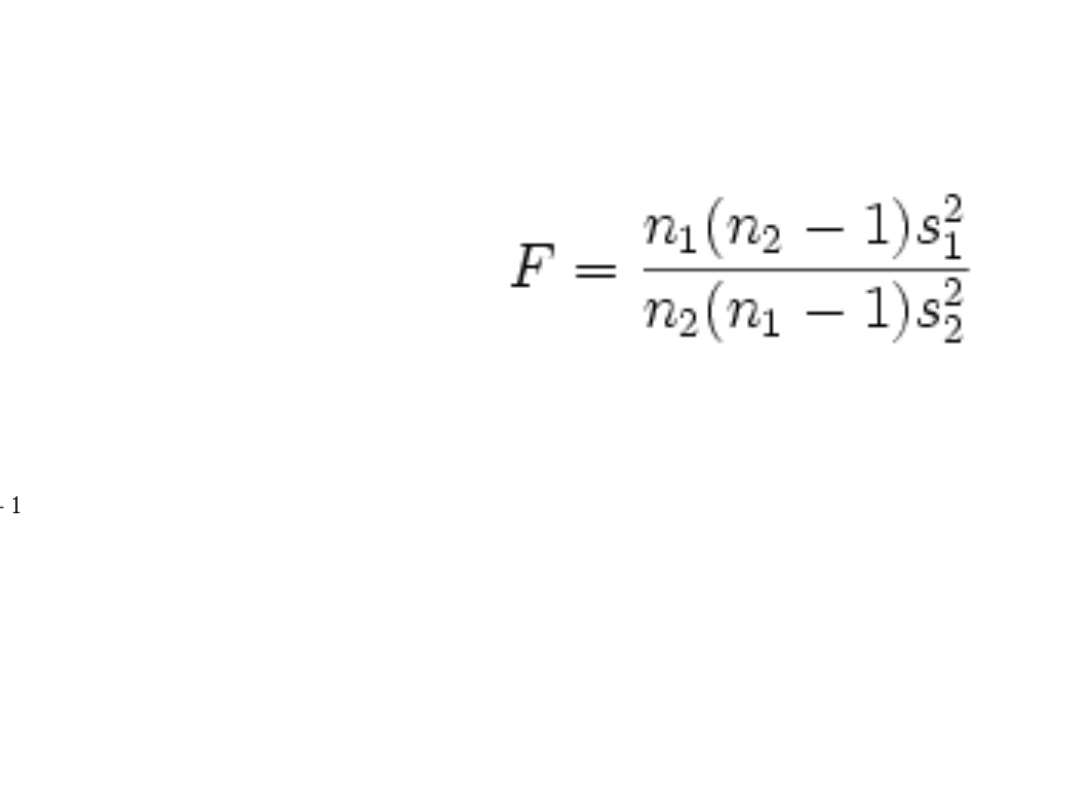
1.d) Homogeniczność wariancji

rozkładów zmiennej zależnej

• Stosujemy wzór:

• Liczba stopni swobody to:

v1 = n1 – 1
V2 = n2 - 1

• Z tablic odczytujemy wartość krytyczną
http://www.pomocstatystyczna.pl/tablice_

f.html

1.d) Homogeniczność wariancji

rozkładów zmiennej zależnej

• Jeśli uzyskany wynik łapie się w

przedziale ufności (jest mniejszy od
wartości F granicznego), możemy robić
test t studenta

• Jeśli nie, używamy poprawki na

niehomogeniczne wariancje

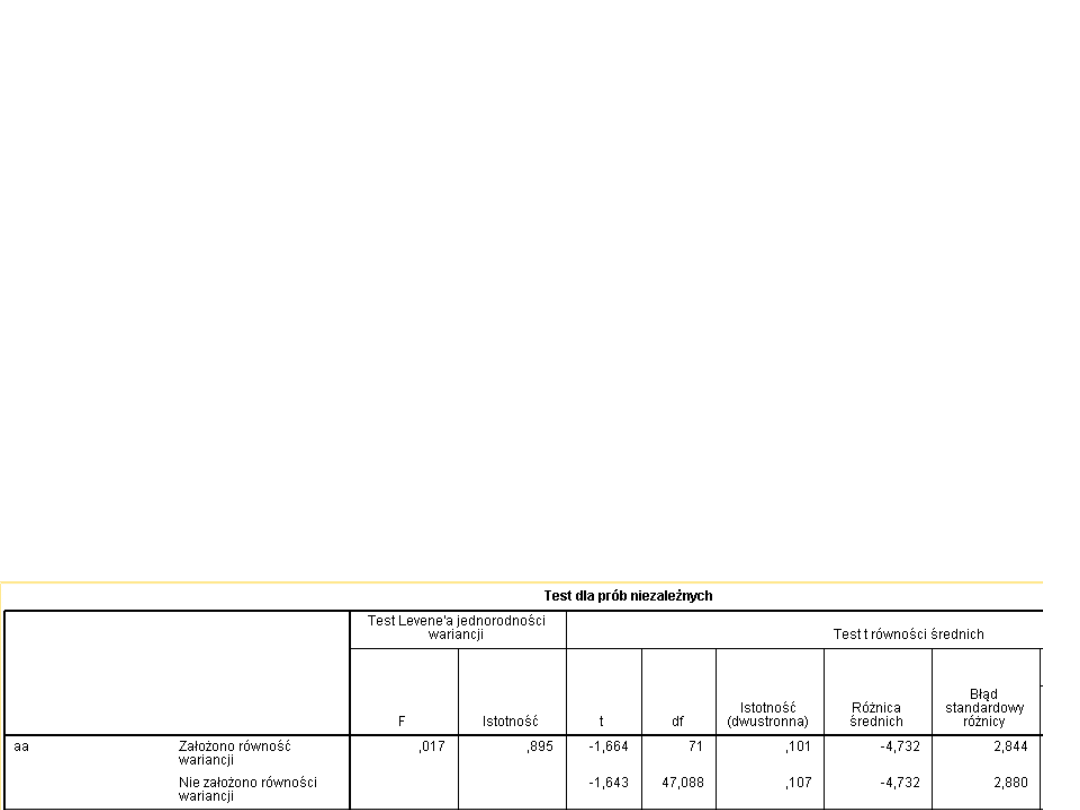
Dodatek do homogeniczności

wariancji

• Jeśli nie ma spełnionego założenia o

homogeniczności wariancji, możemy
także:

– Stosować poprawkę Welcha
– Stosować poprawkę Cox-Cochrana

• Obniża się liczba stopni swobody
• W przypadku analizy SPSS odczytuje się inne

wyniki

Test t z poprawką Welcha

Liczba stopni swobody:

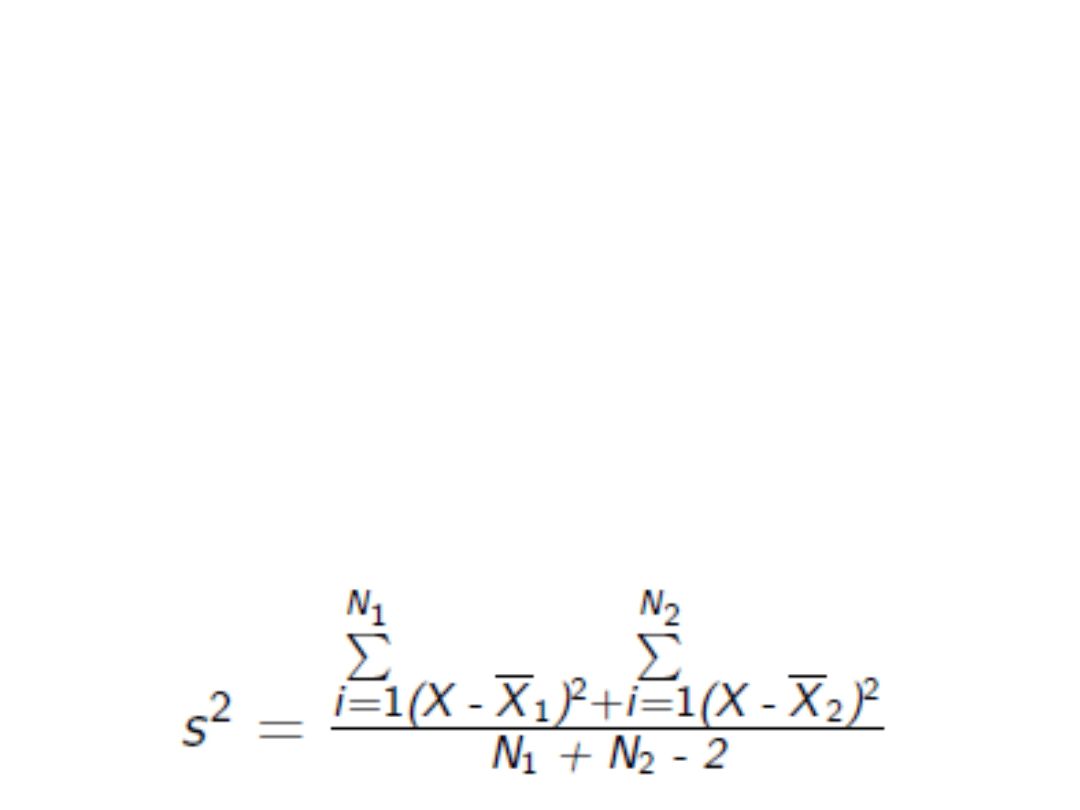
Test t-studenta dla grup

niezależnych

1. Czy są spełnione założenia?

a)

Skala pomiarowa zmiennej zależnej przedziałowa / ilorazowa

b)

Normalność rozkładu zmiennej zależnej

c)

Liczebność porównywanych grup

d)

Homogeniczność wariancji rozkładów zmiennej zależnej

TAK

2. Liczymy wspólną wariancję

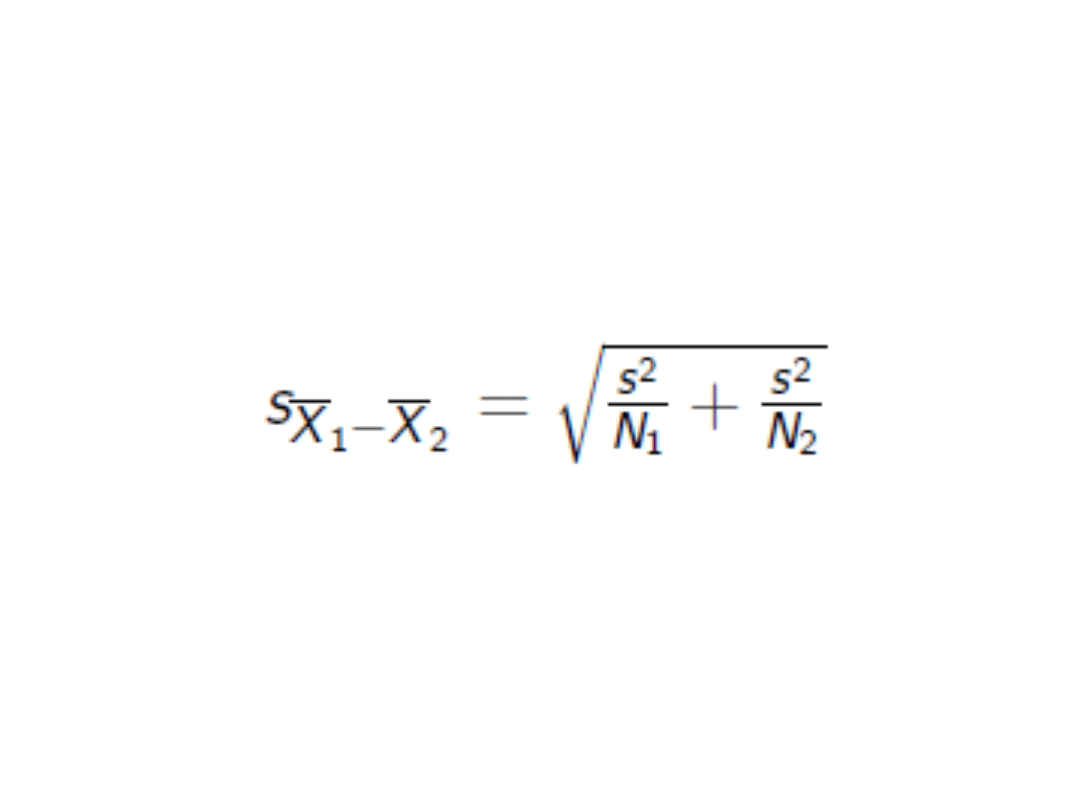
Test t-studenta dla grup

niezależnych

3. Wspólny błąd standardowy:

• Liczba stopni swobody = N1 + N2 -

2

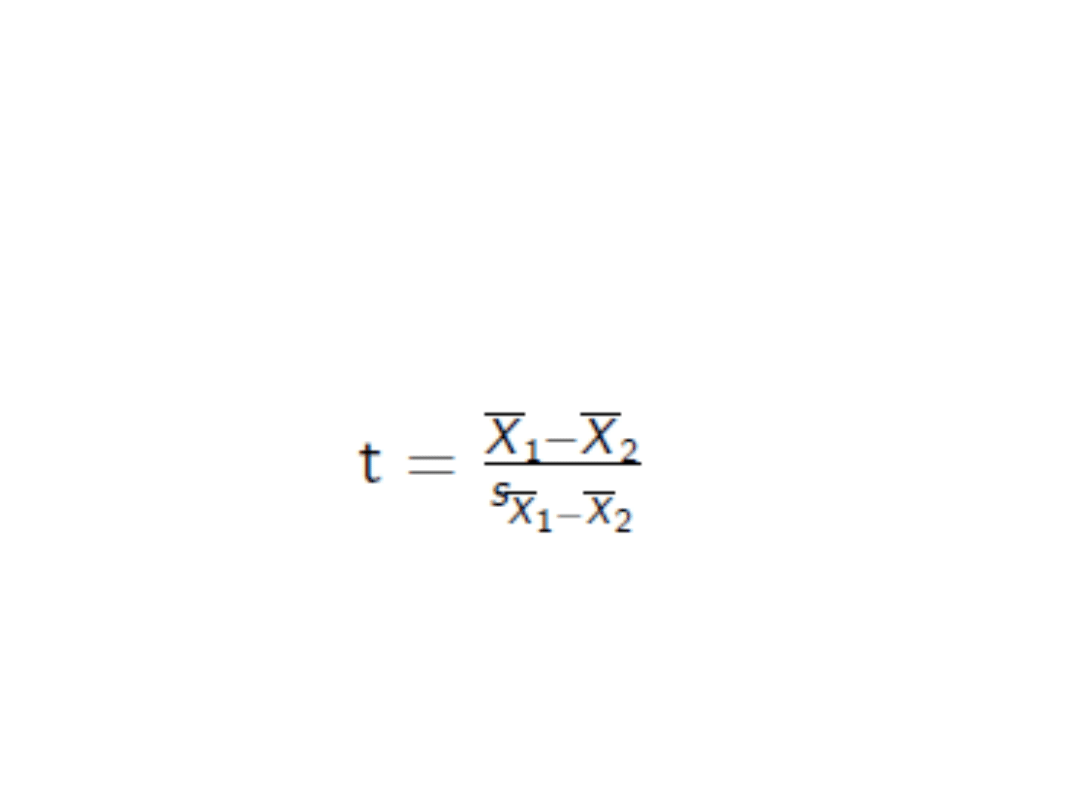
Test t-studenta dla grup

niezależnych

4. Liczymy wynik testu t

Test t-studenta dla grup

niezależnych

• Sprawdzamy z tablicami, czy wynik

testu leży poza wartością t dla
przyjętego poziomu p.

• Jeśli tak, wynik jest istotny

statystycznie

• Jeśli nie, przyjmujemy hipotezę

zerową (brak różnic)

A co, jeśli rozkład nie jest

zbliżony do rozkładu

normalnego?

• test U Manna i Whitneya
• test Kołmogorowa i Smirnowa
• test serii Walda i Wolfowitza

Kiedy U Mann-Whitney?

• Stosujemy go w celu porównania dwóch grup

danych, gdy:

– dane są mierzalne (ilościowe), ale ich rozkład

zdecydowanie odbiega od rozkładu normalnego (czyli nie

jest spełnione założenie testu t-Studenta) - w takim

przypadku możemy hipotezę zerową formułować jako brak

istotnej różnicy średnich arytmetycznych; oczywiście test

Manna i Whitneya możemy też zastosować do danych

spełniających założenia testu t-Studenta; pamiętajmy

jednak, że jego moc wynosi wówczas około 95% mocy

testu t-Studenta;

– dane są typu porządkowego - w tym przypadku hipoteza

zerowa zakłada, że badane grupy pochodzą z tych samych

populacji, tzn. rozkłady danych w analizowanych grupach

nie różnią się istotnie; dla danych porządkowych nie

można bowiem obliczać wartości średniej, a prawidłową

miarą tendencji centralnej jest mediana.

Test U Manna-Whitneya

• Co ciekawe, z tego testu możemy skorzystać

również, gdy zmienna jest mierzona na skali
dychotomicznej (czyli 0-1), dlatego, że jest
to przypadek zmiennej nominalnej, która
jest zarazem zmienną porządkową.

• Zastosowanie testu U Manna-whitneya nie

wymaga równoliczności grup, rozkładu
normalnego czy też homogenicznych
wariancji. To sprawia, że może być on
szeroko stosowany.

Test U Manna-Whitneya

• Podstawową wadą tego testu jest fakt, że test

nie bierze pod uwagę wariancji wyników w

badanych grupach. To sprawia, że grupy

mogą mieć różną wariancję wyników, co

może nie zostać "wykryte" przez test,

podczas gdy testy parametryczne biorą to

pod uwagę. Ogólnie rzecz ujmując, test U

Manna-Whitneya ma słabszą moc

interpretacyjną uzyskanych danych. W

porównaniu do testu t-Studenta należy

zachować większą ostrożność w

interpretowaniu uzyskanych wyników.

Jak to się robi?

– Punktem wyjścia w teście U Manna-Whitneya

jest nadanie wynikom obserwacji rang. Z tego

powodu test ten znany jest również (zwłaszcza

w czasopismach zagranicznych) pod nazwą

testu Wilcoxona dla sumy rang.

– Rangowanie przeprowadzamy następująco:
1. Porządkujemy rosnąco wartości obu prób.
2. Zaczynając od wartości najmniejszej,

przyporządkowujemy poszczególnym

obserwacjom kolejne liczby naturalne.

3. W przypadku wystąpienia wartości

jednakowych przyporządkowujemy im tzw. rangi

wiązane (średnia arytmetyczna z rang, jakie

powinno im się przypisać).

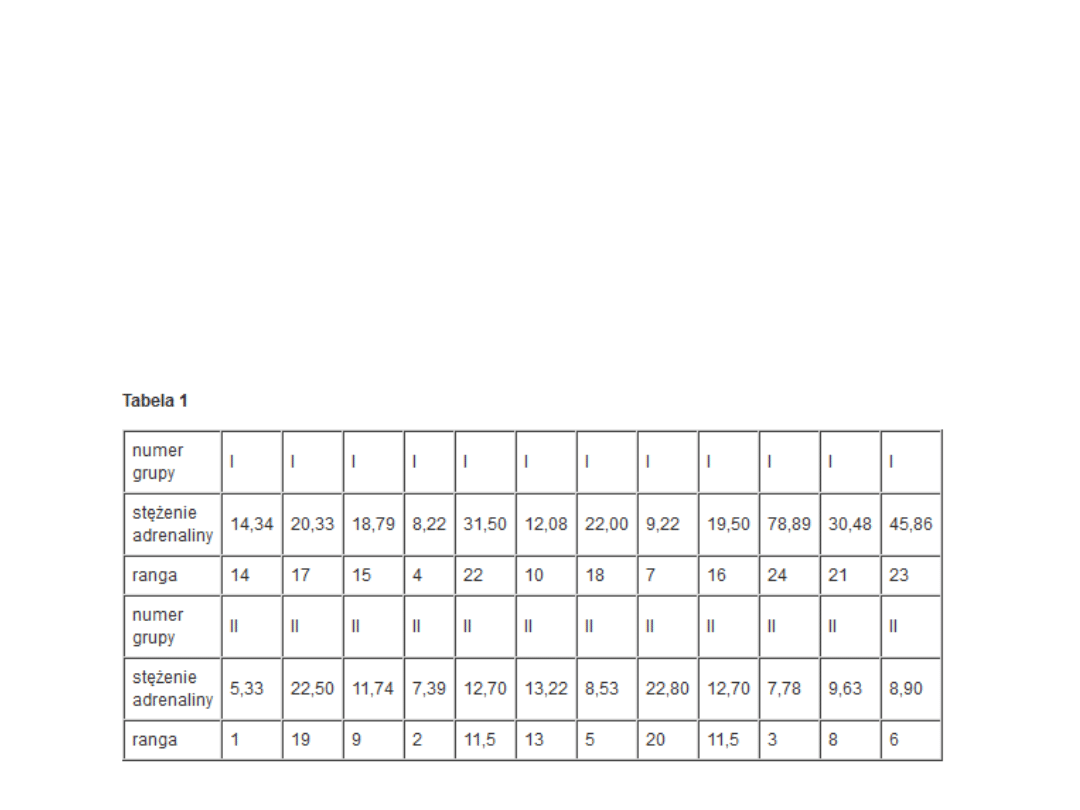
Przykład

• Przypuśćmy, że w dwóch grupach

osób cierpiących na pewną chorobę
zbadano stężenie adrenaliny w
surowicy.

Przykład

• Chcemy zweryfikować hipotezę, że

stężenie adrenaliny w obu grupach
jest jednakowe. Ponieważ zmienna
"stężenie adrenaliny" nie ma
rozkładu normalnego, nie możemy
zastosować testu t-Studenta,
posłużymy się więc jego
nieparametrycznym odpowiednikiem.

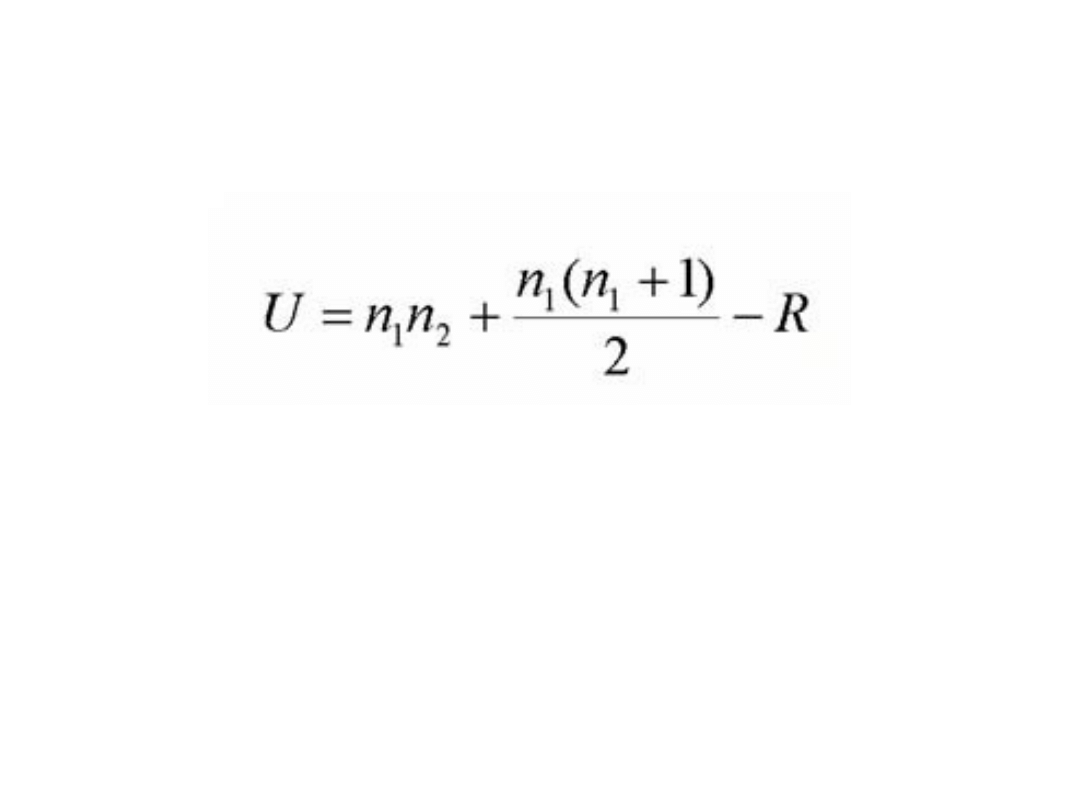
Test U Manna-Whitneya

gdzie:
R oznacza sumę rang
n1, n2 oznacza liczebność w badanych grupach

Należy podkreślić, że należy obliczyć statystykę U zarówno dla R1
(suma rang w I grupie) jak i dla R2 (suma rang w II grupie).
Mniejsza z dwóch wartości U stanowi statystykę U., a istotnośc
statystyczna odczytywana jest z tabel

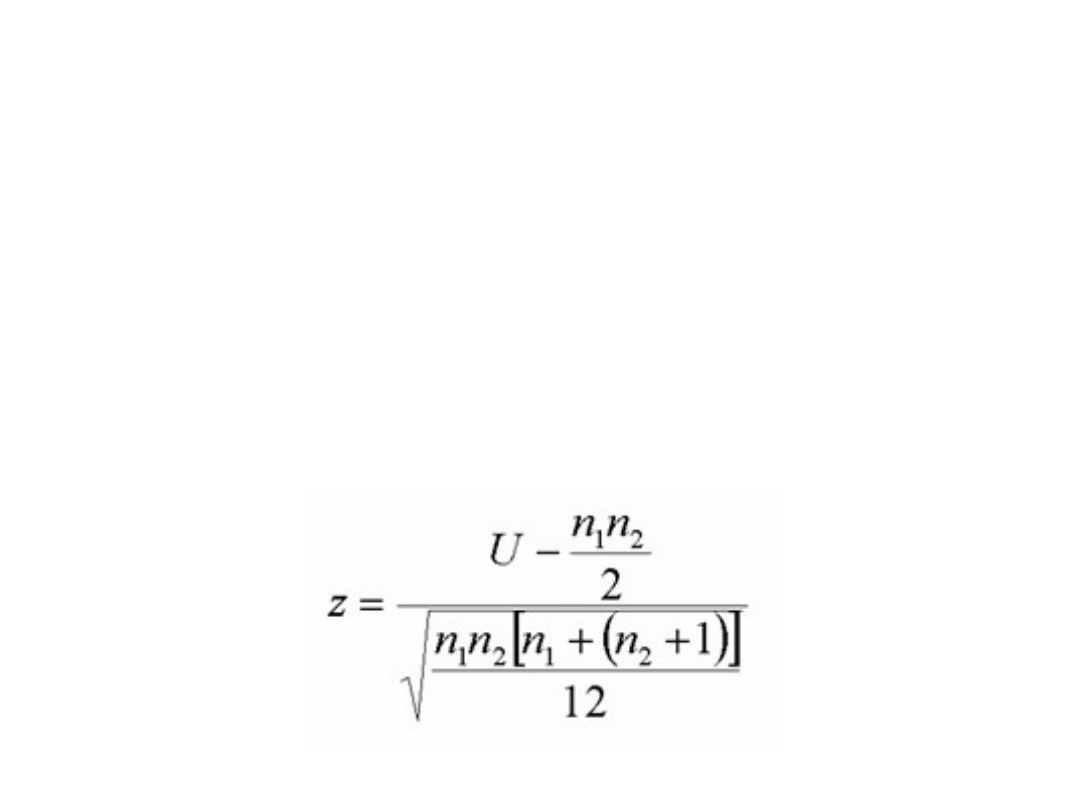
Test U Manna-Whitneya

• Dalej, dla próby większej 20, stosuje

się inny wzór, z założeniem, że dla
próby większej niż 20, rozkład U jest
w przybliżeniu normalny. Wzór ten
ma postać:

Inne testy

nieparametryczne

• Do doczytania:

http://www.mp.pl/artykuly/index.php?

lid=356

Grupy zależne

Test t-studenta dla grup

zależnych

Ideą testu t-Studenta dla prób zależnych jest

porównanie ze sobą tej samej grupy
osób, obserwacji dwukrotnie. Nasze grupy
(próby) są wobec siebie zależne, ponieważ
wynik w drugim badaniu jest zależny od
wyniku w drugim badaniu, ponieważ
dotyczy tej samej osoby, obserwacji.

Celem testu t-Studenta jest określenie

wielkości zmian w danym pomiarze wśród
badanych osob, obserwacji.

Test t-studenta dla grup

zależnych

• Przykład: Grupa koleżanek chciała

sprawdzić, czy kolejna dieta cud jest
skuteczna. Przed zastosowaniem
diety każda z nich zważyła się. Po
dwutygodniowym stosowaniu diety
ta sama grupa dziewczyn zważyła się
ponownie. Aby stwierdzić, czy dieta
cud jest skuteczna należy
zastosować test t dla prób zależnych

Test t-studenta dla grup

zależnych

• Inny przykład:

Przypuśćmy, że w pewnej grupie osób mierzymy

ciśnienie tętnicze przed podaniem i po podaniu leku.

Chcemy uzyskać odpowiedź na pytanie, czy lek ten

powoduje istotny spadek ciśnienia u pacjentów. Mamy

dwie serie pomiarów dotyczących tej samej próby

(czyli grupy pacjentów) - przed podaniem i po podaniu

leku - i chcemy zweryfikować hipotezę o średniej

wielkości różnic między tymi wynikami. Pierwsza seria

danych to wyniki pomiarów badanej cechy w jednym

momencie, druga - to wyniki pomiarów tej samej

cechy u tych samych pacjentów w innym momencie.

Test t-studenta dla grup

zależnych

• Przykładowe wyniki przed (A) i po leczeniu (B)

• Chcemy zweryfikować hipotezę, że

zastosowany lek powoduje istotny spadek
ciśnienia tętniczego u leczonych pacjentów. W
tym celu zastosujemy testy dla zmiennych
powiązanych.

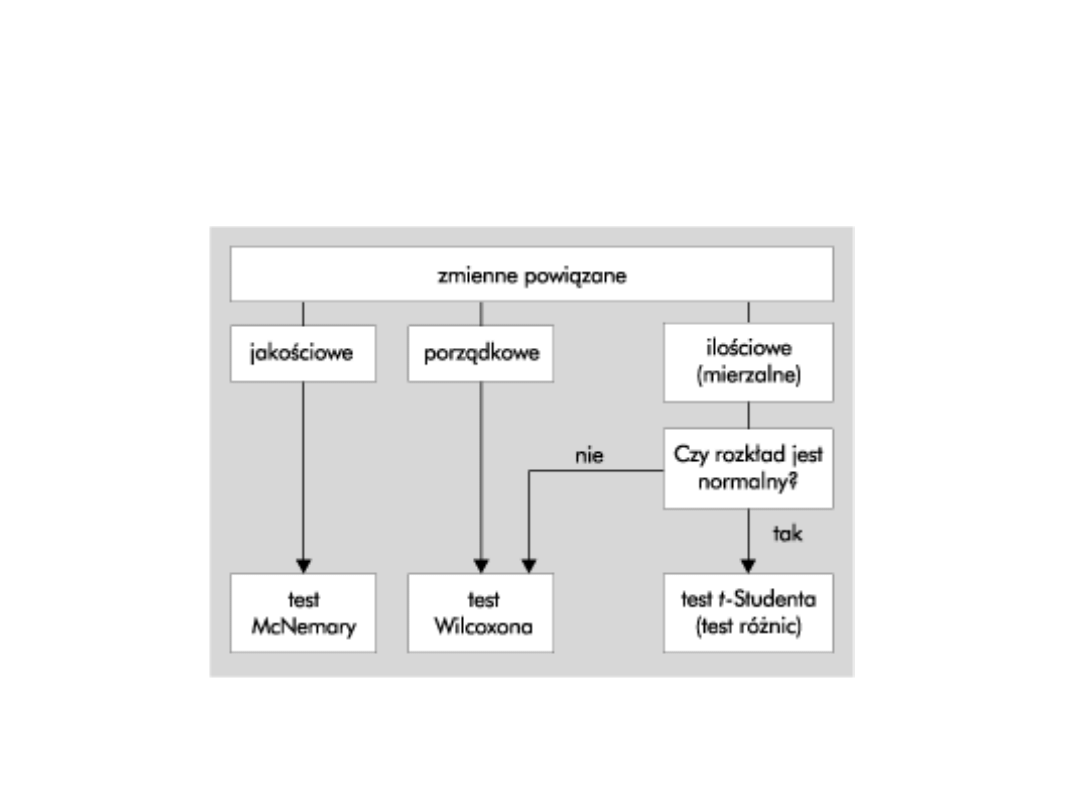
Test t-studenta dla grup

zależnych

Test t-studenta dla grup

zależnych

• Warunki stosowania testu t-Studenta

dla zmiennych zależnych są
identyczne jak dla testu t-Studenta
dla zmiennych niezależnych, z jedną
różnicą - nie musimy sprawdzać
jednorodności wariancji.

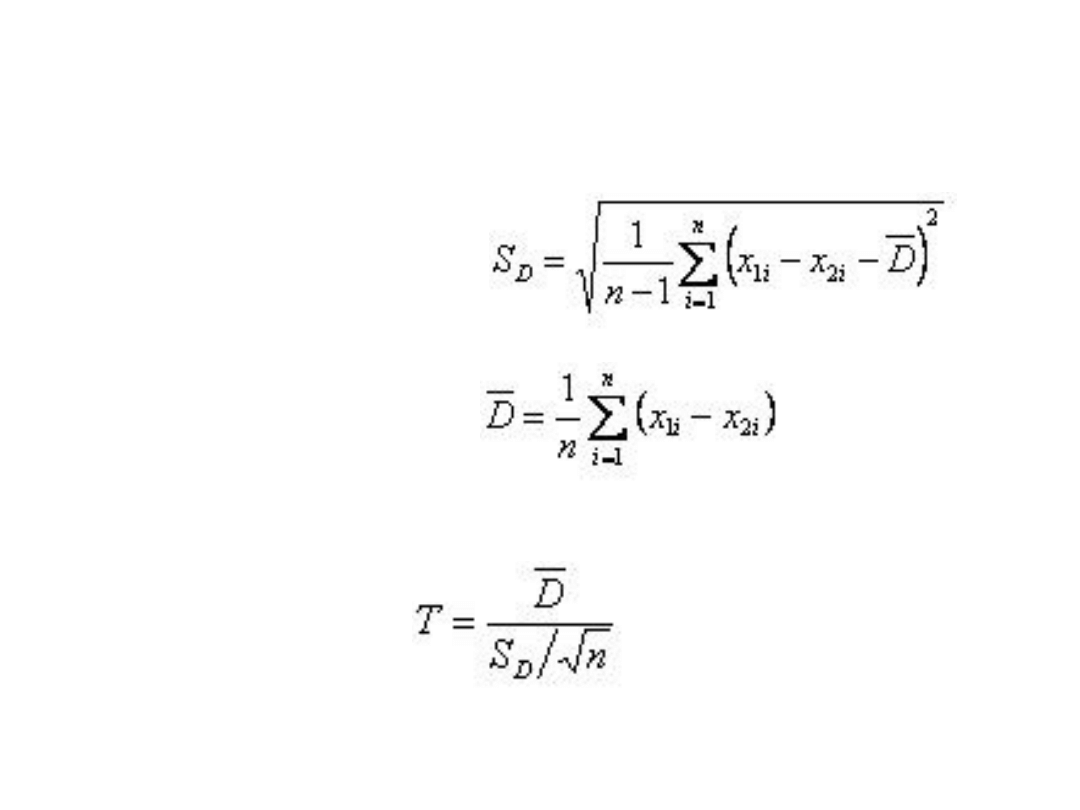
Test t-studenta dla grup

zależnych

• Wzory

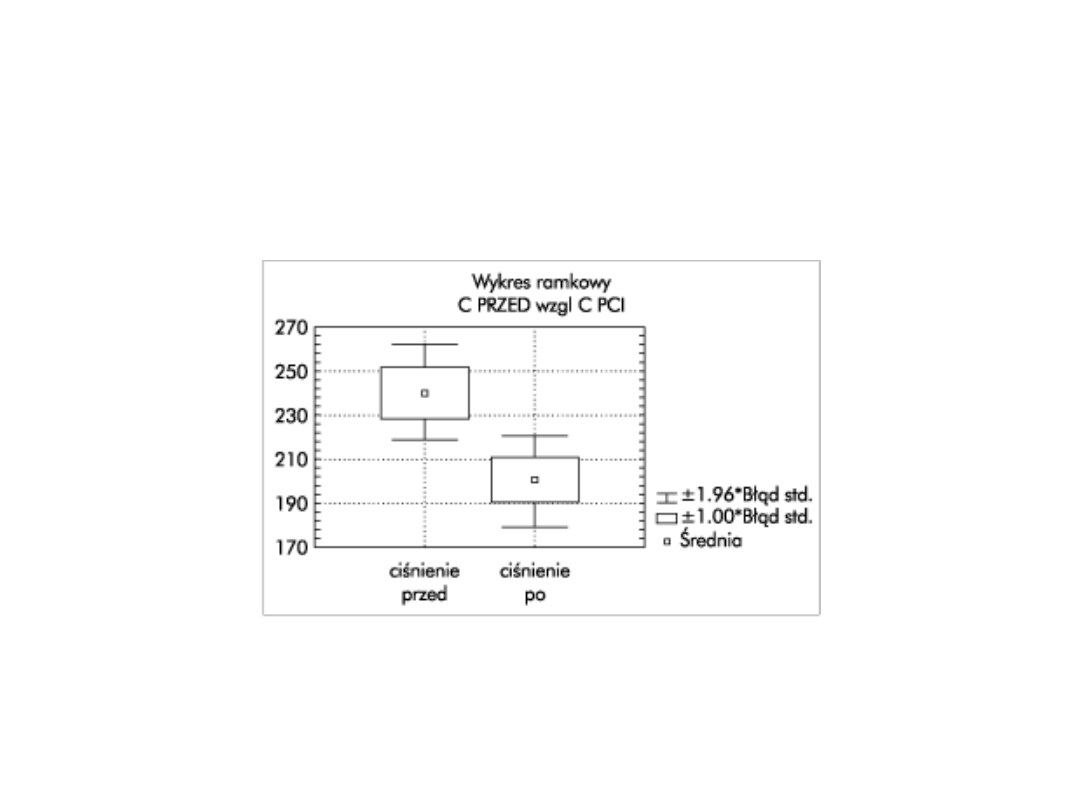
Zobrazowanie graficzne

Testy nieparametryczne dla

grup zależnych

• test znaków
• test kolejności par Wilcoxona
• test McNemary

• Stosujemy je, gdy dysponując dwoma pomiarami

(przed jakimś wydarzeniem i po), chcemy dowieść,

że pomiary te się różnią.

• Inaczej mówiąc, testy te są przeznaczone do

sprawdzania istotności różnic między dwoma

zależnymi pomiarami. Te dwa zależne pomiary to

albo dwie obserwacje u tej samej osoby (np. przed

zabiegiem i po), albo obserwacje u par osób o tych

samych właściwościach (tzw. równoważne dwójki).

• Hipoteza zerowa mówi, że wyniki obu pomiarów są

jednakowe. Testy te stosujemy również wtedy, gdy

nie są spełnione założenia testu t dla zmiennych

powiązanych. Za ich pomocą możemy stwierdzić,

czy próby różnią się między sobą pod względem

pewnych własności.

• Te łatwe w użyciu testy wymagają jedynie

założenia, że wartości badanych zmiennych

możemy uporządkować (są mierzalne na skali

porządkowej).

a) Test znaków

• Test ten oparty jest na znakach różnic między kolejnymi parami

wyników (czy są ujemne, czy dodatnie). Otrzymamy ustaloną

liczbę wyników w jednym zbiorze, które są mniejsze od swych

odpowiedników w drugim zbiorze oraz liczbę wyników, które są

większe. Tym samym dowiadujemy się, ile danych zostało

"przesuniętych" w jednym kierunku w naszym eksperymencie. Gdy

wszystkie, to w porządku. Test daje wynik istotny. Gdy tak nie jest,

to sytuacja przestaje być oczywista. Jednak możemy podać

prawdopodobieństwa związane ze wszystkimi proporcjami

(wystąpienia znaków +/-), które mogłyby wystąpić. Znając więc

prawdopodobieństwo każdej naszej kierunkowej zmiany, możemy

ocenić, czy nasze wyniki są istotne.

• Podsumowując, test znaków to ustalenie liczby plusów i minusów

oraz porównanie ich z wartością teoretyczną podaną w

odpowiednich tablicach. Test ten stosujemy więc przede wszystkim

dla cech jakościowych. Wystarczy bowiem sprawdzić, że dana

jednostka charakteryzuje się obecnością ("+") lub nieobecnością

("-") danego zjawiska. Dla danych mierzalnych nie uwzględniamy

wartości różnic, lecz jedynie ich znaki. Różnice o wartości zero są

pomijane.

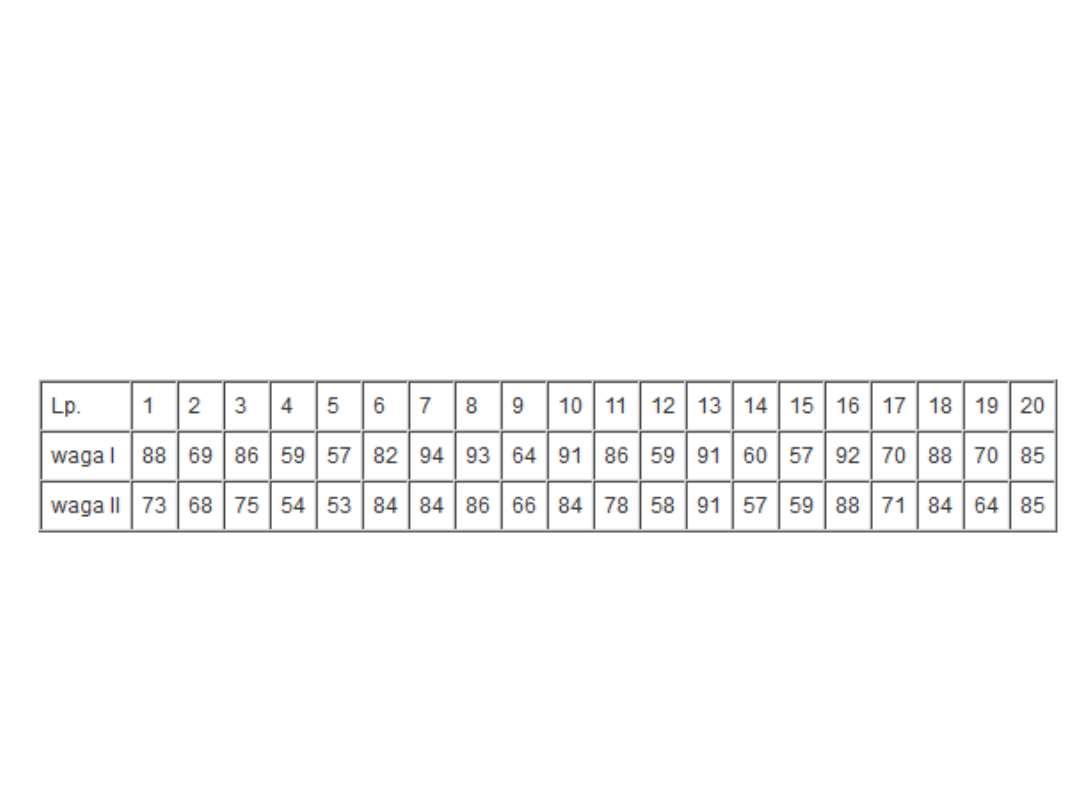
Przykład

• Załóżmy, że przeprowadziliśmy badanie

ciężaru ciała w grupie 20 kobiet przed 7-

tygodniową dietą odchudzającą i po niej.

• Chcemy sprawdzić, czy otrzymane wyniki

przeczą hipotezie, że dieta nie powoduje

zmniejszenia ciężaru ciała.

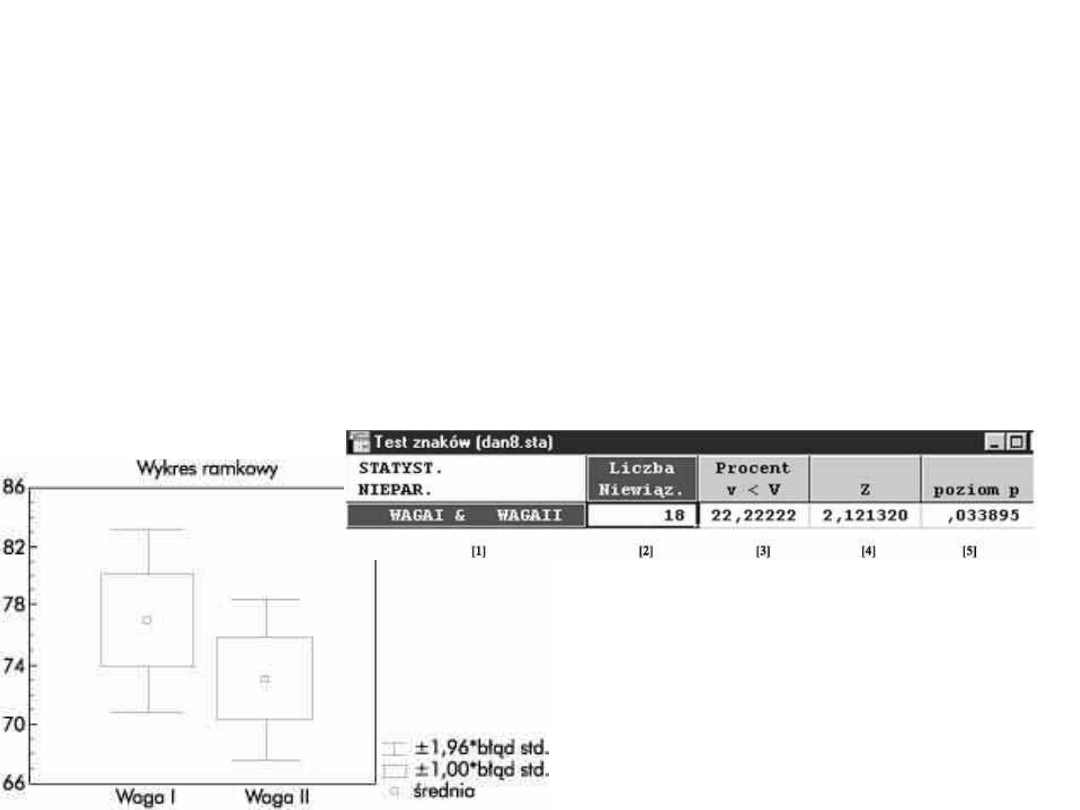
Przykład

Poszczególne wartości oznaczają:
– [1] - nazwy zmiennych
– [2] - liczebność grup
– [3] - procent liczebności zmiennych, dla których różnica ma

wartość ujemną (znak "-")

– [4] - wartość testu znaków
– [5] - poziom istotności dla testu znaków

Test Wilcoxona

• W teście znaków tracimy informację niesioną przez

liczbowe wartości różnic. Ta informacja jest w pełni

wykorzystywana przez test Wilcoxona. Staje się on

więc w tym wypadku testem mocniejszym niż test

znaków, jest więc godny uwagi.

• Test kolejności par Wilcoxona uwzględnia znak różnic,

ich wielkość, jak również ich kolejność (stąd nazwa).

Po uporządkowaniu różnic w szereg rosnący

przypisujemy im rangi. Następnie osobno sumujemy

rangi różnic dodatnich i ujemnych. Mniejsza z

otrzymanych sum to wartość testu Wilcoxona, która

po porównaniu z odpowiednią wartością teoretyczną

w tablicach decyduje o odrzuceniu hipotezy zerowej

lub nie.

Przykład

• Te same dane

– [1] - nazwy zmiennych
– [2] - liczebność grup
– [3] - wartość testu Wilcoxona dla grup n =<25
– [4] - wartość testu Wilcoxona dla grup n >25
– [5] - poziom istotności dla testu Wilcoxona

• Zwróćcie uwagę na poziom istotności!

Test znaków a Wilcoxona

• Chcemy na podstawie tych danych dokonać

oceny skuteczności szczepienia. Jak wyniki,
test znaków daje wynik nieistotny (p =
0,131), podczas gdy test kolejności par
Wilcoxona okazuje się istotny (p = 0,0346)

Jaki test wybrać?

– Zawsze kiedy możemy mówić o różnicach elementów, bardziej

pożądany będzie test Wilcoxona. Jednakże na podstawie testu

Wilcoxona widać, że czasami możliwe jest otrzymanie

nieistotnej różnicy pomiędzy zbiorami danych, gdy jest wiele

czynników rosnących (lub malejących), ale różniących się tylko

nieznacznie, a pojedynczy duży wynik "w przeciwnym

kierunku" decyduje o nieistotności. Zachęca on tym samym

badacza do wyciągnięcia wniosku, że dane pochodzą z jednej

populacji. Taki pojedynczy wynik nazywamy "samotnikiem".

Czy taki pojedynczy, ekstremalnie wielki wynik może być

odrzucony podczas analizy? Jeśli jesteśmy całkowicie pewni, że

ten w jakiś sposób nietypowy element możemy odrzucić,

zróbmy to. Jeśli nie możemy usprawiedliwić tej decyzji, nie

róbmy tego, aby nie być posądzonym o naciąganie danych.

– Czasami jednak dane mogą być faktycznie wyrażone tylko

słownie, jak na przykład ocena dotycząca jakiejś metody -

"lepsza", "taka sama", "gorsza". Zawsze kiedy możemy ustalić,

że wyniki rosną (lub maleją), ale nie jesteśmy w stanie określić

ilościowo tego przyrostu, wówczas test znaków jest jedynym do

zastosowania. Test znaków jest zatem narzędziem użytecznym

dla wielu typów badań w naukach medycznych, w których

gromadzi się dane nieliczbowe.

Sprawdzanie rozkładu

normalnego

Testy zgodności

• Testy zgodności dotyczą postaci rozkładu

teoretycznego badanej zmiennej losowej skokowej

lub ciągłej. Weryfikują one stawiane przez badaczy

hipotezy dotyczące rozkładu zmiennej losowej.

• Celem tych testów jest porównanie rozkładów

dwóch cech w jednej populacji lub jednej cechy w

dwóch populacjach. Są to oczywiście dwa różne

zagadnienia, jednakże metody obliczeniowe są w

obu przypadkach podobne. Idea tych testów jest

oczywista - jeśli jakaś cecha w dwóch populacjach

ma taki sam rozkład, to wartości liczbowe pewnych

statystyk (np. średnia, mediana) dla obu populacji

powinny się niewiele różnić. Jeśli jednak wartości te

będą istotnie różnie, to mamy prawo sądzić, że

cecha ma odmienny rozkład w różnych populacjach.

• Do najczęściej formułowanych hipotez tego

rodzaju należy hipoteza o normalności
rozkładu zmiennej losowej ciągłej X:

H0: X ma rozkład normalny N(m, sigma)

przy hipotezie alternatywnej:

H1: X nie ma rozkładu normalnego N(m,

sigma)

gdzie m i sigma (wartość oczekiwana i

odchylenie standardowe) to parametry
rozkładu normalnego.

Testy weryfikującw normalność

rozkładów:

• test Kołmogorowa i Smirnowa

Test ten opiera się na porównaniu procentów

skumulowanych zaobserwowanych z oczekiwanymi.

Jako wartość testu podawana jest maksymalna

różnica bezwzględna pomiędzy zaobserwowanymi i

oczekiwanymi procentami skumulowanymi. Test ten

wymaga jednak znajomości parametrów rozkładu

(średniej i odchylenia standardowego całej populacji).

Gdy ich nie znamy, a tak jest najczęściej, stosujemy

test Kołmogorowa i Smirnowa z poprawką Lillieforsa.

• test W Shapiro i Wilka

Test ten jest najbardziej polecany, ze względu na

dużą moc. Można go również stosować do małych

prób.

• Test chi-kwadrat Pearsona

Test

• W celu weryfikacji hipotezy o normalności

rozkładu wyniki próby dzielone są na

rozłączne klasy, a następnie porównuje się

liczebności: obserwowaną i oczekiwaną w

każdej z tych klas. Jeśli liczebności te różnią

się istotnie, to prawdopodobnie dana próba

nie pochodzi z populacji, w której rozkład

obserwowanej zmiennej losowej jest

normalny. We wszystkich tych testach, jeśli

statystyki okażą się istotne (tzn. p <0,05), to

odrzucamy hipotezę zerową o zgodności

danych z rozkładem normalnym. Oznacza to,

że dana zmienna (cecha) nie ma rozkładu

normalnego.

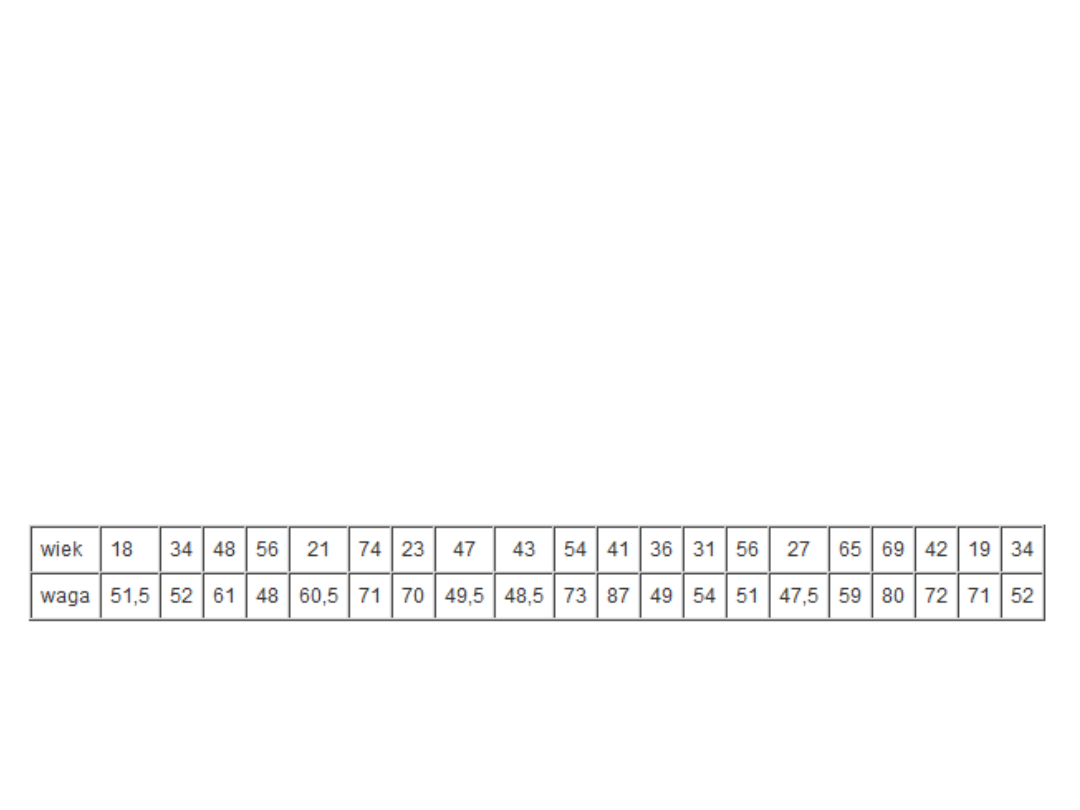
Przykład

• Na przykład sprawdzimy, czy

zmienne "wiek" i "waga" mają
rozkład normalny. Wartości tych
zmiennych dla 20-elementowej próby
podaje tabela

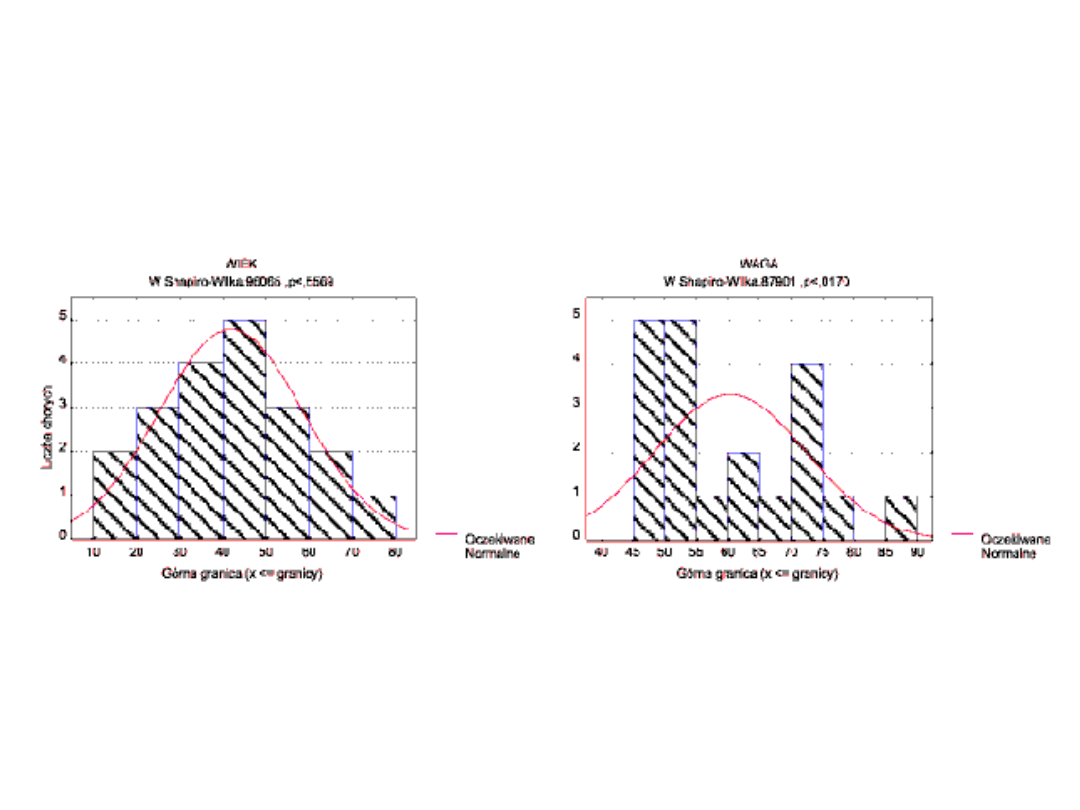
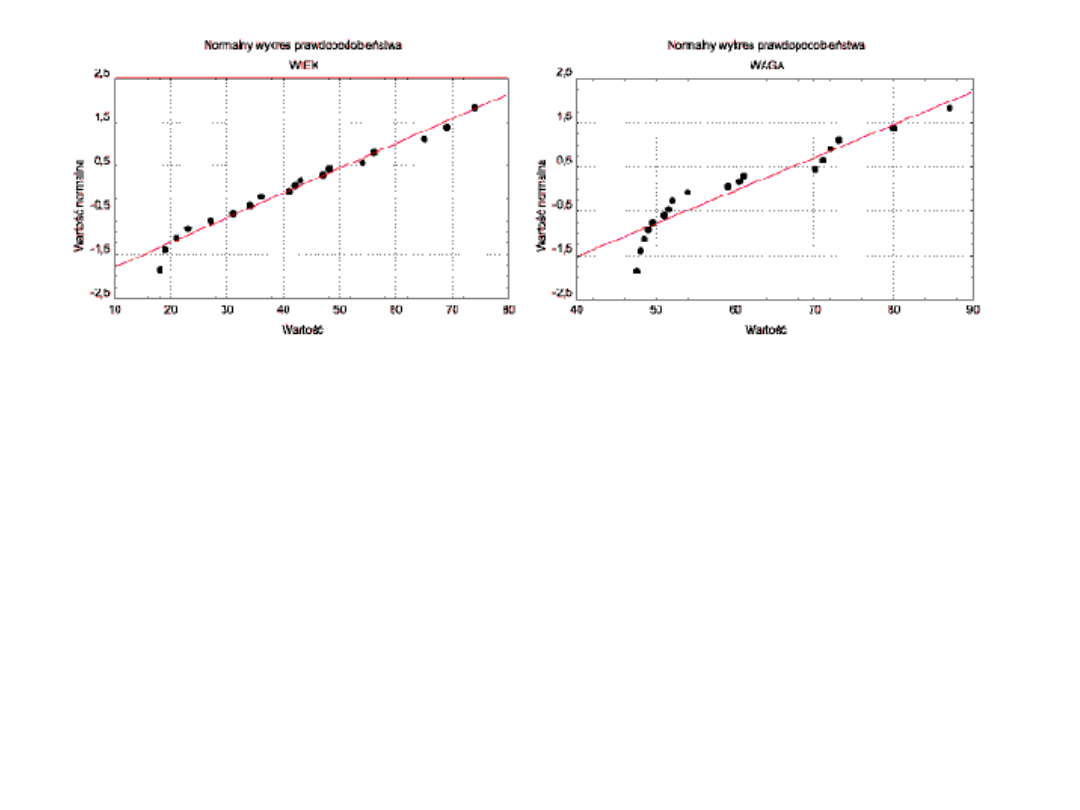
Jeżeli rozkład jest normalny, wówczas punkty powinny
leżeć na linii prostej (lewa strona); w przeciwnym razie
punkty odchylają się od prostej (prawa strona). Na
wykresie tym mogą ujawnić się również punkty odstające.
Wykres ten pozwala więc ocenić odstępstwa rozkładu
empirycznego od rozkładu normalnego, dlatego nazywany
jest testem "na rzut oka", sprawdzającym normalność
rozkładu analizowanej zmiennej. Im bardziej bowiem
wszystkie punkty układają się na prostej, tym bardziej
mamy prawo sądzić, że dany rozkład jest normalny.

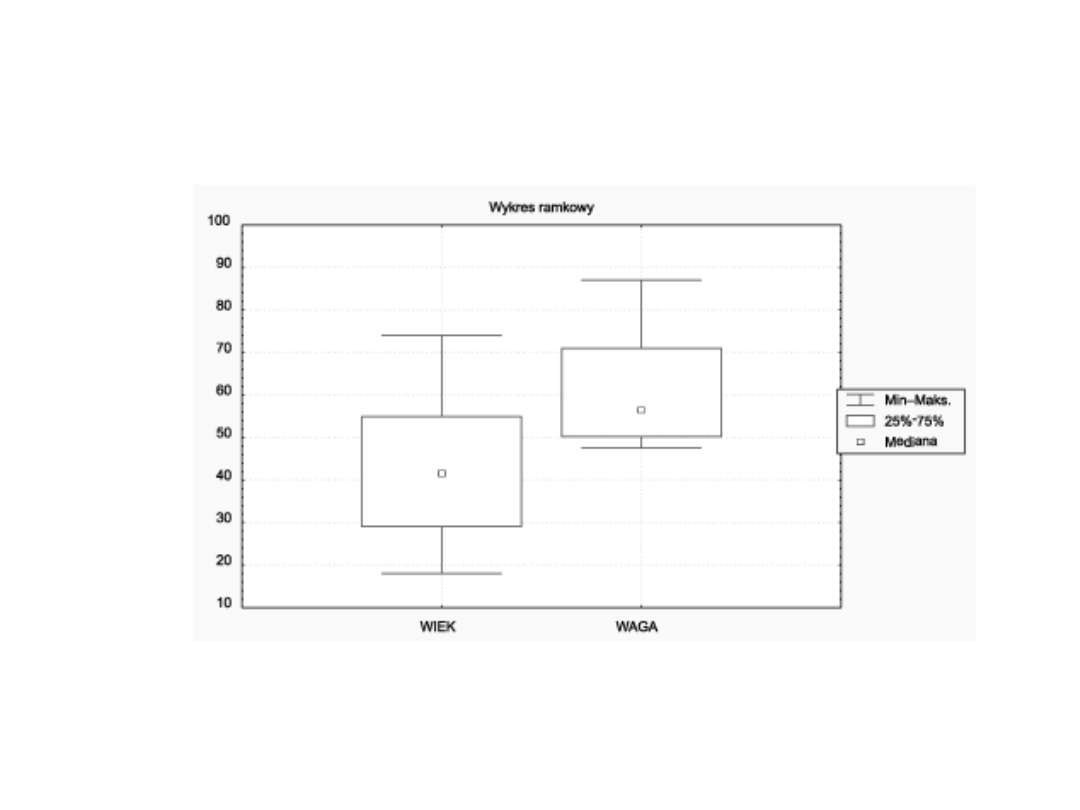
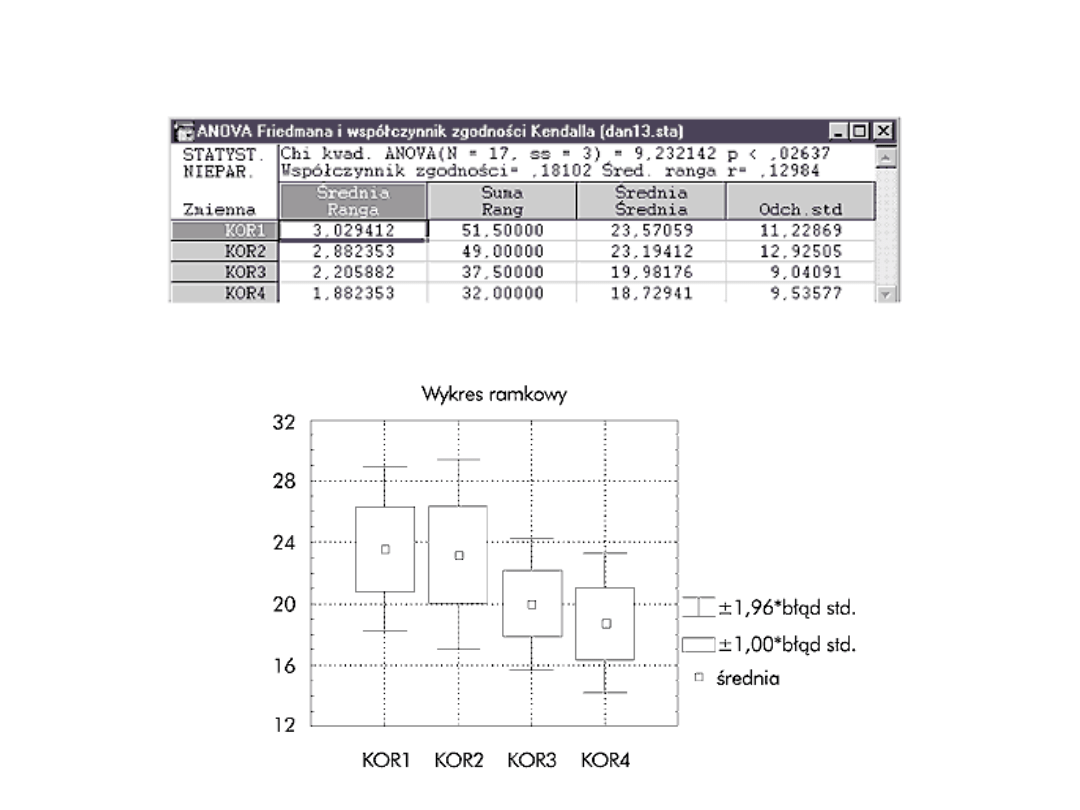
Box and whiskers

Skrzynki z wąsami (wykres skrzynkowy Tukey’a), pokazujące

zakresy wybranej zmiennej (zmiennych) oraz statystyki

opisowe (średnia, mediana, odchylenie standardowe lub

błąd standardowy). Na wykresie mogą również być

wykreślone odstające punkty danych.

Możemy utworzyć cztery grupy wykresów ramkowych w

zależności od wybranej opcji:

• punkt centralny - mediana, ramka - kwartyle, wąsy - rozstęp

• punkt centralny - średnia, ramka - błąd standardowy, wąsy -

odchylenie standardowe

• punkt centralny - średnia, ramka - odchylenie standardowe,

wąsy - 95% przedział ufności dla poszczególnych obserwacji

wokół średniej

• punkt centralny - średnia, ramka - błąd standardowy, wąsy -

95% przedział ufności dla wartości średniej

Analiza wariancji

• Czyli co zrobić, gdy porównywanych

grup jest więcej niż dwie?

Przykład

• U losowo wybranych pacjentów mierzymy temperament

czterema różnymi testami.

• Chcemy porównać wartości średnie temperamentu dla

każdego testu. Wydawałoby się, że wystarczy

przeprowadzić test t-Studenta dla każdej pary średnich.

• Nie możemy tak jednak postąpić. Przy poziomie

istotności 0,05 prawdopodobieństwo, że się nie pomylimy,

wynosi dla jednego porównania 0,95, a dla dwóch porównań

- 0,95^2, czyli 0,9025. Dla 4 średnich mamy 6 porównań,

prawdopodobieństwo to wynosi więc 0,956, czyli 0,7351.

Prawdopodobieństwo, że się pomylimy co najmniej raz,

wynosi teraz 1 - 0,7351 = 0,2649, a na tak duży błąd

pierwszego rodzaju zgodzić się nie możemy.

• Do analizy takich problemów wykorzystujemy zespół metod

statystycznych zwanych analizą wariancji.

Analiza wariancji

• Najprostsza i zarazem najbardziej popularna

jest jednoczynnikowa analiza wariancji,
czyli analiza wpływu tylko jednego czynnika
na wyniki przeprowadzanego badania.
Jednoczynnikowa analiza wariancji
weryfikuje więc hipotezę, że średnie w
grupach są jednakowe:

• H0: m1 = m2 = ... = mk

wobec hipotezy alternatywnej:

• H1: co najmniej dwie średnie różnią się

między sobą

• Dokonujemy tego poprzez podział całkowitej

zmienności (czyli sumy kwadratów odchyleń

wszystkich pomiarów od średniej) na różne źródła

związane z efektami występującymi w badaniu.

• Mamy wówczas możliwość porównania zmienności

pomiędzy grupami (określonymi przez poziomy

czynnika) ze zmiennościami wewnątrzgrupowymi.

• Zakładając brak różnic średnich między grupami

(tj. hipotezę zerową w analizie wariancji),

oczekujemy, że wariancja oszacowana w oparciu o

zmienność między grupami powinna być w

przybliżeniu równa wariancji oszacowanej w

oparciu o zmienność wewnątrzgrupową. Jeżeli tak

nie jest, możemy się spodziewać, że wartości

średniej istotnie się różnią. Stwierdzamy wówczas,

że dany czynnik wpływa na zmienną (nazywaną

zmienną objaśnianą lub zależną).

• Otaczająca nas rzeczywistość jest jednak bardziej złożona

i wielowymiarowa. Sytuacje, w których pojedyncza

zmienna pozwala wyjaśnić dane zjawisko, należą do

rzadkości. W eksperymentach psychologicznych zwykle

bierze się pod uwagę wiele czynników, zwanych

grupującymi.

• Na przykład: badając efekty trzech różnych terapii u

chorych na depresję, rozważamy dodatkowy czynnik

grupujący płeć. Dane do takiego dwuczynnikowego (rodzaj

terapii i płeć) eksperymentu możemy zapisać w postaci

tabeli o 2 wierszach (odpowiadających płci męskiej i

żeńskiej) i 3 kolumnach (odpowiadających 3 sprawdzanym

terapiom). Różnice między średnimi z wierszy są związane

z płcią pacjentów, natomiast różnice między średnimi z

kolumn wynikają z zastosowania różnych leków. W takim

eksperymencie całkowitą zmienność (sumę kwadratów

odchyleń) możemy rozdzielić na co najmniej 3 składniki:

– zmienność spowodowaną czynnikiem "płeć"

– zmienność spowodowaną zastosowaniem konkretnej

terapii

– zmienność spowodowaną błędem (zmienność

wewnątrzgrupowa)

• Zauważmy, że istnieje jeszcze jedno dodatkowe

źródło zmienności - interakcja, czyli oddziaływanie

łączne. Mówi nam ona, w jakim stopniu wpływ

jednego czynnika zależy od poziomu drugiego. Jeżeli

wpływ ten się nie zmienia, to nie ma żadnej

interakcji; w przeciwnym wypadku (tzn. gdy wpływ

jednego czynnika zależy od poziomu drugiego)

zachodzi interakcja między dwoma czynnikami.

• Przyjmijmy, że jedna terapia daje lepsze wyniki niż

pozostałe, zarówno u kobiet, jak i u mężczyzn (czyli

niezależnie od płci) - oznacza to, że interakcji nie

ma.

• Jeżeli jednak jedna terapia daje lepsze wyniki u

kobiet, a inny u mężczyzn, to mówimy o wystąpieniu

interakcji między tymi dwoma czynnikami (rodzajem

terapii i płcią).

• Możliwość wykrywania istotnych interakcji i w

związku z tym testowania bardziej złożonych hipotez

na temat otaczającej nas rzeczywistości czyni z

analizy wariancji bardzo uniwersalne narzędzie.

Posługując się testem t-Studenta, nie

otrzymalibyśmy identycznych wyników.

• Często się zdarza, że chcemy przeprowadzić

wielokrotnie ten sam test u tych samych osób po

upływie określonego czasu lub w różnych warunkach.

Interesuje nas zbadanie różnic występujących u tych

samych osób.

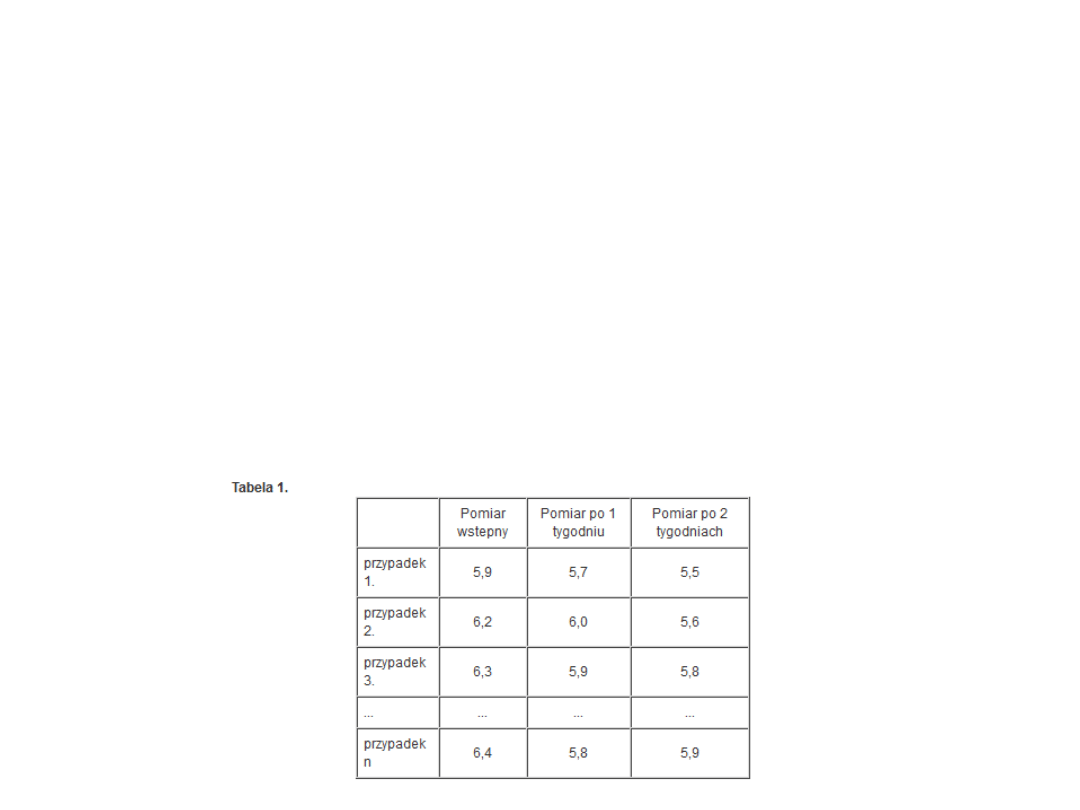
• Na przykład porównujemy stężenie kortykosteroidów

przed rozpoczęciem terapii (pierwszy pomiar - poziom

1. tzw. czynnika powtarzanych pomiarów, czyli czasu),

po tygodniu terapii (poziom 2. czynnika powtarzanych

pomiarów) i po 2 tygodniach (poziom 3. czynnika

powtarzanych pomiarów); czynnik powtarzanych

pomiarów (czas) ma więc 3 poziomy.

• Do analizy takiego zbioru danych wykorzystujemy

analizę wariancji z powtarzanymi pomiarami.

• Efekty związane z powtarzanymi pomiarami

testuje się dokładnie w taki sam sposób, jak w

przypadku międzygrupowej analizy wariancji.

Jeśli czynnik powtarzanych pomiarów ma

więcej niż 2 poziomy, wówczas mamy do

dyspozycji 2 sposoby oceny istotności

efektów związanych z tym czynnikiem.

• Tradycyjnym sposobem jest przeprowadzenie

testu jednowymiarowego. Jednakże w

ostatnich latach do analizy takich układów

coraz powszechniej stosuje się

wielowymiarową analizę wariancji, której

zaletą jest między innymi to, że wymaga

spełnienia mniej restrykcyjnych założeń.

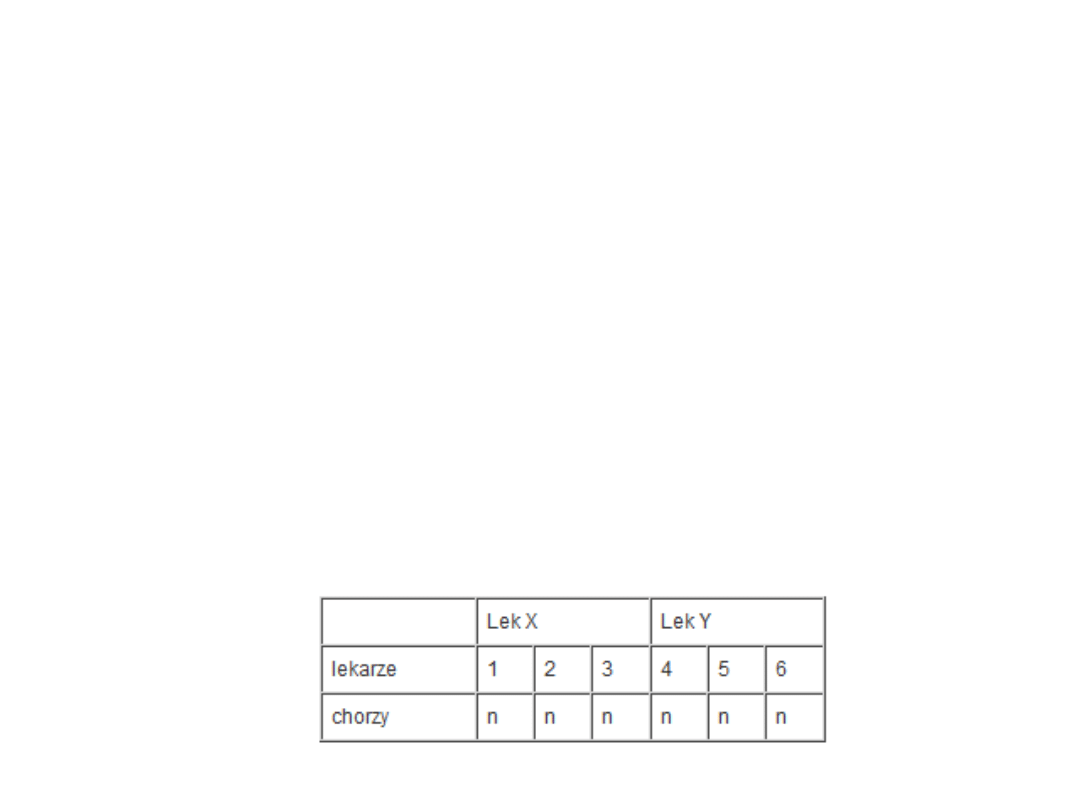
• Rozważmy teraz eksperyment, w którym ocenia się 2

leki: X i Y, stosowane w leczeniu schizofrenii.

• Leczenie prowadzi 3 lekarzy. Mamy więc 6 n-

osobowych grup chorych (2 środki x 3 lekarzy). W

takim eksperymencie każdy z lekarzy niejako

"krzyżuje się" z każdym z dwóch leków. Taki schemat

eksperymentu umożliwia badanie interakcji między

lekarzami a lekami.

• Względy praktyczne (np. koszty leczenia) powodują

czasami, że eksperyment ten zostanie

przeprowadzony nieco inaczej. Zamiast 3 lekarzy

możemy mieć 6, tzn. 3 leczących lekiem X i 3

leczących lekiem Y. W eksperymencie uczestniczy

również 6 grup n-osobowych, lecz w innych schemacie

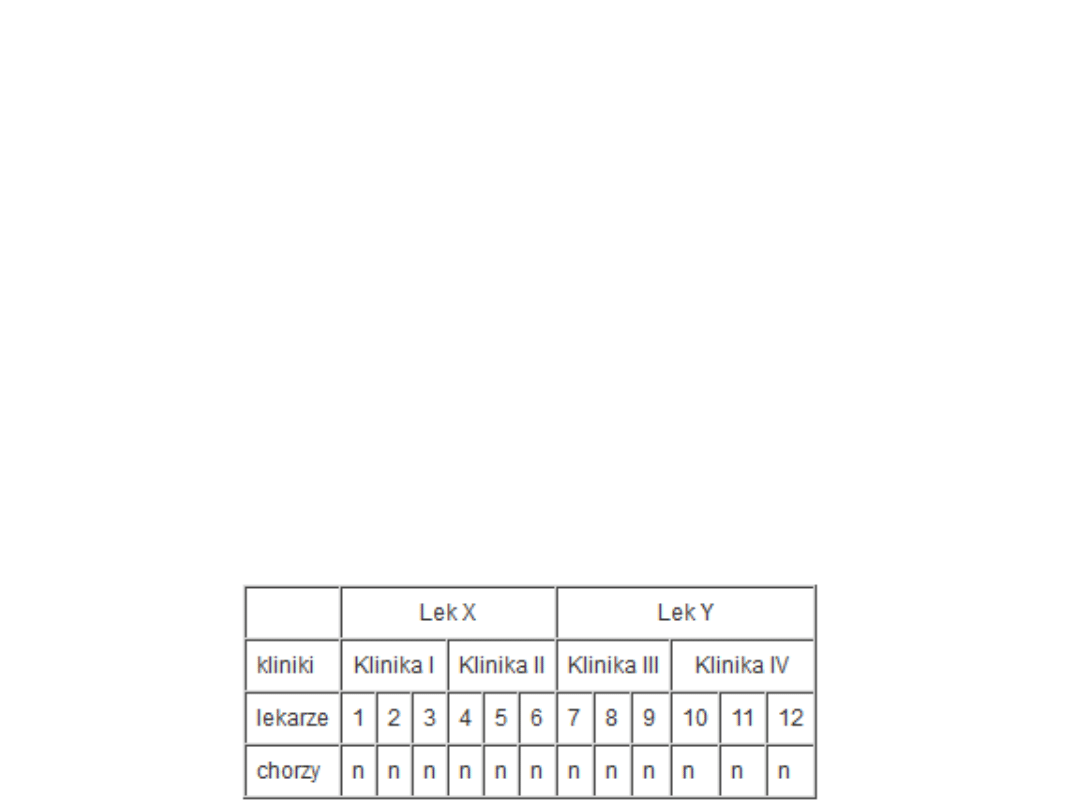
• W takiej sytuacji lekarze stanowią czynnik

"zagnieżdżony" w lekach. Analiza wariancji

zastosowana do eksperymentu tego typu nosi

nazwę analizy wariancji hierarchicznej. W

naszym przykładzie całkowitą sumę kwadratów

możemy podzielić na sumę kwadratów związaną z

lekiem, sumę kwadratów związaną z lekarzami

(czynnik zagnieżdżony) oraz sumę kwadratów

wewnątrzgrupową. Nie możemy badać interakcji

czynników, ponieważ lekarze nie są "skrzyżowani" z

lekami, lecz w nich "zagnieżdżeni". Przyjmujemy

więc założenie, że interakcja taka nie występuje lub

możemy ją zaniedbać.

• Przy większej liczbie czynników eksperymenty tego

typu mogą być bardzo skomplikowane.

• Na analizowaną zmienną (zwaną zależną)

teoretycznie może mieć wpływ bardzo duża liczba

dodatkowych zmiennych. Niektórych zmiennych nie

da się podczas eksperymentu kontrolować, a z

oddziaływania innych nie zdajemy sobie sprawy.

• Podstawowym, ale zarazem najprostszym sposobem

radzenia sobie z tą dodatkową zmiennością jest

dobór losowy. Jest to zresztą jedno z podstawowych

założeń analizy wariancji.

• Zdarzają się jednak sytuacje, w których musimy

korzystać z gotowych grup lub znane są nam

mierzalne zmienne zakłócające. Te dodatkowe

zmienne, których nie możemy przyjąć jako czynniki

grupujące, nazywane są zmiennymi towarzyszącymi.

• W takich sytuacjach powinniśmy się posłużyć

analizą kowariancji. Na przykład chcemy porównać

3 metody nauczania statystyki. Każdą metodę

stosujemy w innej grupie osób. Po pewnym czasie

nauczania we wszystkich trzech grupach

przeprowadzamy test osiągnięć w nauce i obliczamy

średnie wyniki.

• Załóżmy, że dysponujemy także wynikami testu

inteligencji wszystkich osób badanych. Trzy badane

grupy mogą się różnić pod względem poziomu

inteligencji, która koreluje z osiągnięciami w nauce.

Tym samym nie wiemy, w jakim stopniu różnice w

osiągnięciach w nauce wynikają z różnych metod

nauczania, a w jakim z różnic w poziomie inteligencji

osób w poszczególnych grupach.

• Z pomocą przychodzi nam analiza kowariancji.

Wyodrębnia ona najpierw wpływ zmiennej

towarzyszącej (wyniki testu) za pomocą metody

regresji liniowej. Następnie stosuje analizę wariancji

wobec pozostałej zmienności, czyli tej części osiągnięć

w nauce, która nie została wyjaśniona przez poziom

inteligencji. Oceniamy tym samym istotność bądź

nieistotność różnicy między średnimi reszt,

nazywanymi średnimi skorygowanymi. Średnie te

pokazują, jaka część zmienności pozostaje w średnich

osiągnięciach w nauce po oddzieleniu tej części

zmienności, za którą odpowiedzialny jest poziom

inteligencji. Analiza kowariancji łączy więc w sobie dwie

metody - analizę regresji i analizę wariancji.

• Jeżeli analiza wariancji nie pokaże istotności różnic

między rozpatrywanymi średnimi, nie przeprowadza

się już dalszych testów.

• Natomiast kiedy hipoteza zerowa zostanie

odrzucona w analizie wariancji, to powstaje pytanie,

które z porównywanych populacji są odpowiedzialne

za odrzucenie hipotezy zerowej. Chcemy wiedzieć,

które z n-średnich różnią się między sobą, a które są

jednakowe.

• Musimy wtedy przeprowadzić dokładniejsze badania

różnic między średnimi z poszczególnych grup.

Wykorzystujemy do tego celu specjalne testy post

hoc, zwane też testami wielokrotnych porównań,

oraz analizę kontrastów.

• Analiza kontrastów umożliwia testowanie

statystycznej istotności prognozowanych

szczegółowych różnic w określanych fragmentach

naszego złożonego eksperymentu.

• Tyle skomplikowanej teorii – może

Wam się przydać do wykładu, albo na
później.

• Teraz upraszczamy

Analiza wariancji

• Jednoczynnikowa: Czy płeć badanego

wpływa na wykonanie zadania

poznawczego?

• Dwuczynnikowa: Czy płeć i

osobowość badanego wpływa na

wykonanie zadania poznawczego?

• Trójczynnikowa: Czy płeć, osobowość

i pora dnia wpływa na wykonanie

zadania poznawczego?

ANOVA

• Badamy wpływ tylko jednego

czynnika klasyfikującego (mającego
kilka poziomów) na wyniki
przeprowadzanego badania.

Podstawy

• Załóżmy, że czynnik grupujący ma k poziomów.

• Możemy więc, przyjmując poziomy czynnika za

kryterium podziału, wyodrębnić w badanej grupie

k populacji.

Podstawowe założenia

• 1) analizowana zmienna zależna jest mierzalna

• 2) analizowana zmienna zależna w każdej z

rozważanych k populacji ma rozkład normalny

• 3) rozkłady te mają jednakową wariancję

W przypadku, gdy założenia analizy wariancji nie są

spełnione należy posługiwać się

testem

Kruskala-Wallisa

.

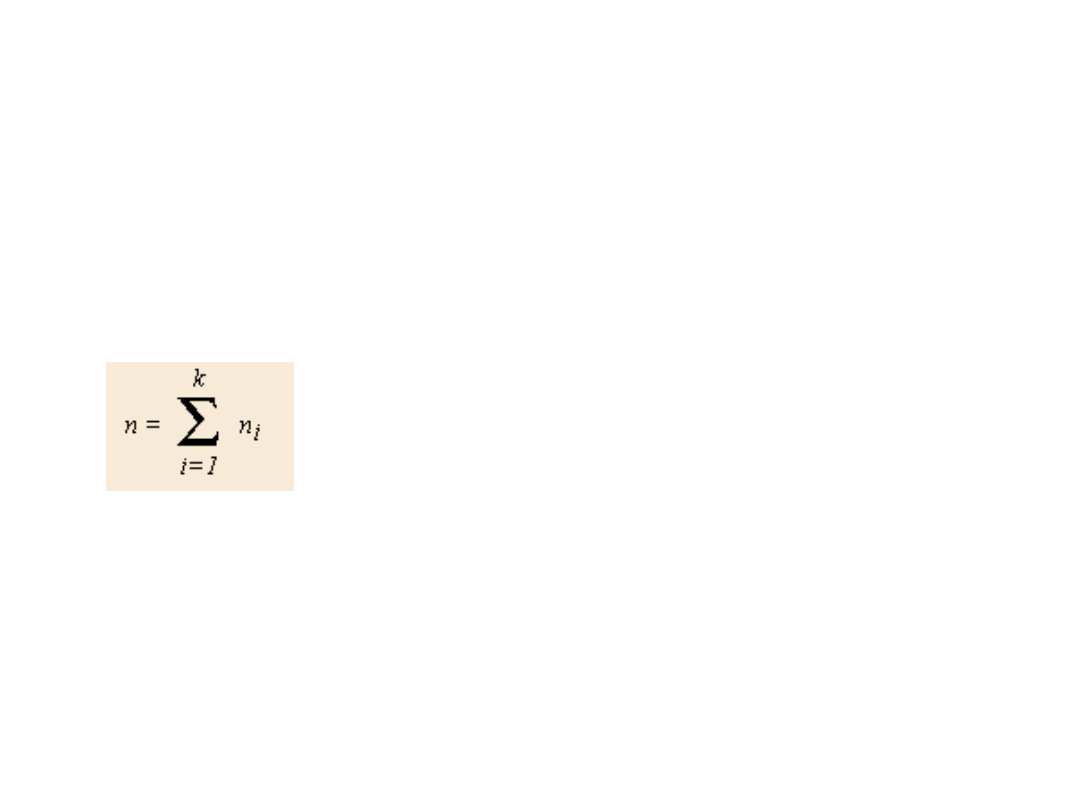
Badanie

• Z każdej z tych populacji wylosowano

próbę o liczebności n

i

elementów.

Otrzymujemy łącznie

niezależnych obserwacji x

ij

dla j = 1,

2,...n

i

. Dane te stanowią podstawę do

weryfikacji hipotezy zerowej, że średnie

w grupach są jednakowe. Hipoteza

kierunkowa brzmi?

• Dlaczego porównujemy średnie?

• Otóż jeśli średnie różnią się istotnie

między sobą, to intuicyjnie możemy

wnioskować, że analizowany czynnik

wpływa na zmienną zależną.

• Istotą analizy wariancji jest więc

równoczesne badanie istotności różnic

między wieloma średnimi

pochodzącymi z wielu grup (populacji).

Model

• W statystyce do takich analiz stosuje się

podejście modelowe. Nasze rozważania można

bowiem zapisać w postaci matematycznego

modelu:

• x

ij

= m + a

i

+ e

ij

gdzie:
- m oznacza ogólną średnią z populacji

generalnej,
- a

i

jest wpływem i-tego czynnika

eksperymentalnego (losowego)
- e

ij

jest składnikiem losowym, o rozkładzie

normalnym ze średnią równą zero i wariancją s 2.

Ogólny model

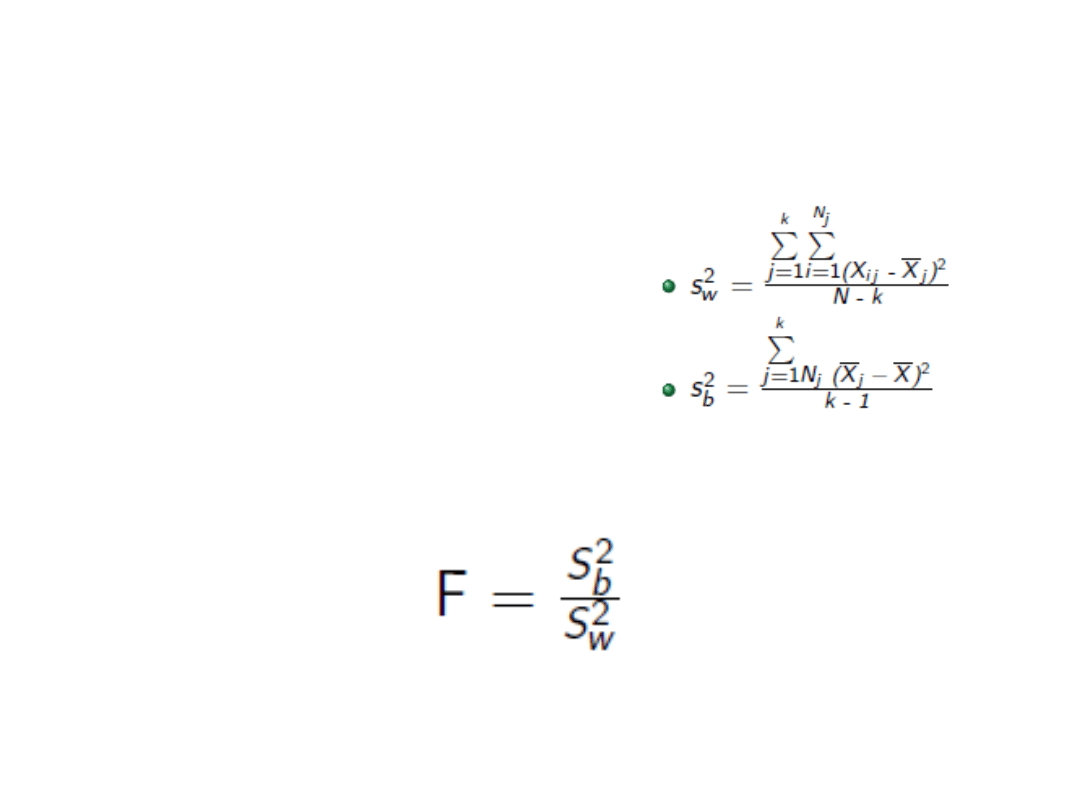
Średnie kwadraty

• Liczba stopni swobody:

– Wewnątrz (error): n-k
– Między (effect): k-1
- ogólnie: n-1
Liczymy średnie kwadraty odchyleń

Wynik testu:

Analiza wyniku

• Rozkład F-Snedecora wykorzystuje się do

sprawdzenia czy wyniki analizy wariancji są

istotne statystycznie, przy założonym poziomie

istotności. W tym celu zostały opracowane

tabelice rozkładu F-Snedecora

Aby sprawdzić, czy wyniki naszych testów są

istotne statystycznie musimy znać:

• wynik analizy wariancji
• stopnie swobody międzygrupowe i

wewnątrzgrupowe

• poziom istotności (poziom prawdopodobieństwa),

dla którego dany wynik będzie wskazywał na

istotną zależność - najbardziej popularny p = 0,05

Wnioski

• Wartości F bliskie jedności

przemawiają za sprawdzaną hipotezą
zerową, natomiast wartości dużo
większe od 1 - za jej odrzuceniem.

Przykład

• Porównano trzy grupy zwierząt pod

względem ich towarzyskości (ilości

kontaktów z innymi osobnikami w

ciągu godziny)

• Żółwie: 2, 5, 7, 9, 6, 7
• Psy: 8, 14, 29, 7, 14, 6
• Koty: 2, 4, 7, 9, 8
• Sprawdź za pomocą testu F czy

grupy różnią się miedzy sobą

A które grupy się różnią od

siebie?

• Testy post-hoc, czyli ‘po fakcie’

– analiza kontrastów i związane z nią testy

(test Scheffégo)

– testy oparte na tzw. studentyzowanym

rozstępie, umożliwiające grupowanie

średnich (test Tukeya, test Duncana, test

Newmana i Keulsa)

– wnioskowanie na podstawie przedziałów

ufności (test Scheffégo, test

Benferroniego, test Dunneta).

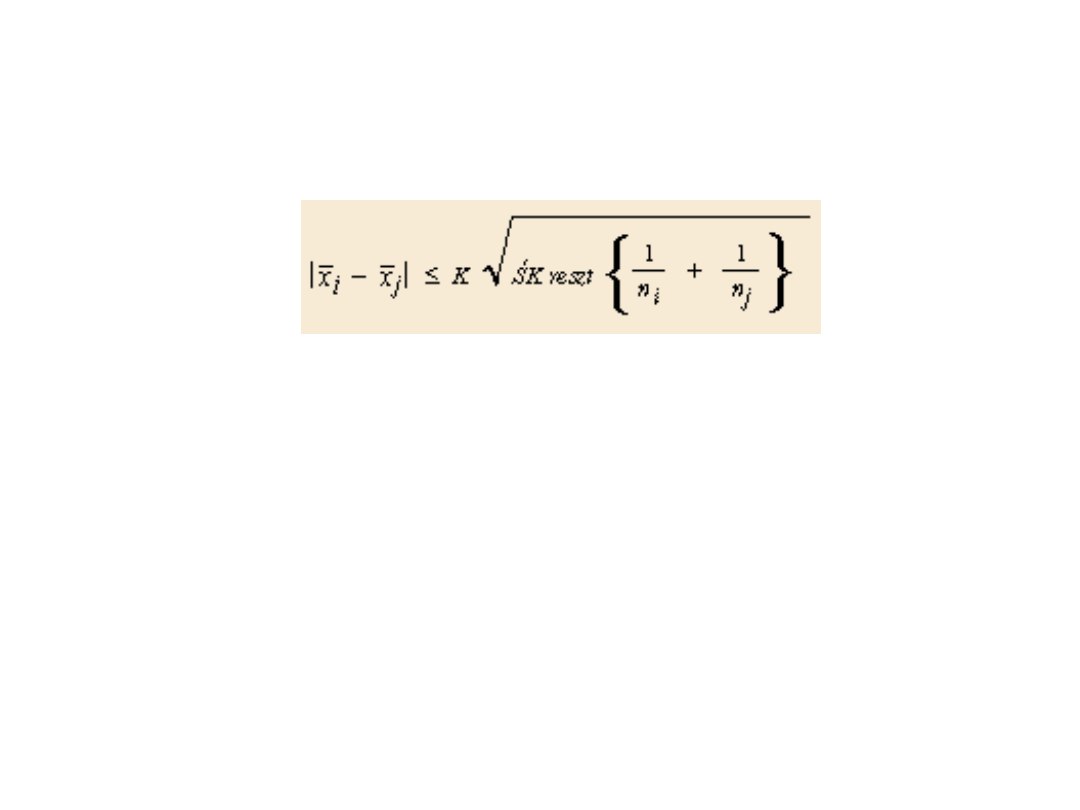
Założenie

• gdzie:
• K to odpowiednia wartość związana ze statystyką

wykorzystywaną w danej metodzie (np. rozkład F

dla testu Scheffégo)

• n

i

, n

j

to odpowiednie liczebności i-tej i j-tej grupy

• ŚK reszt jest średnim kwadratem błędu

występującego w analizie wariancji

• X

i

oraz X

j

to porównywane średnie i-tej i j-tej grupy.

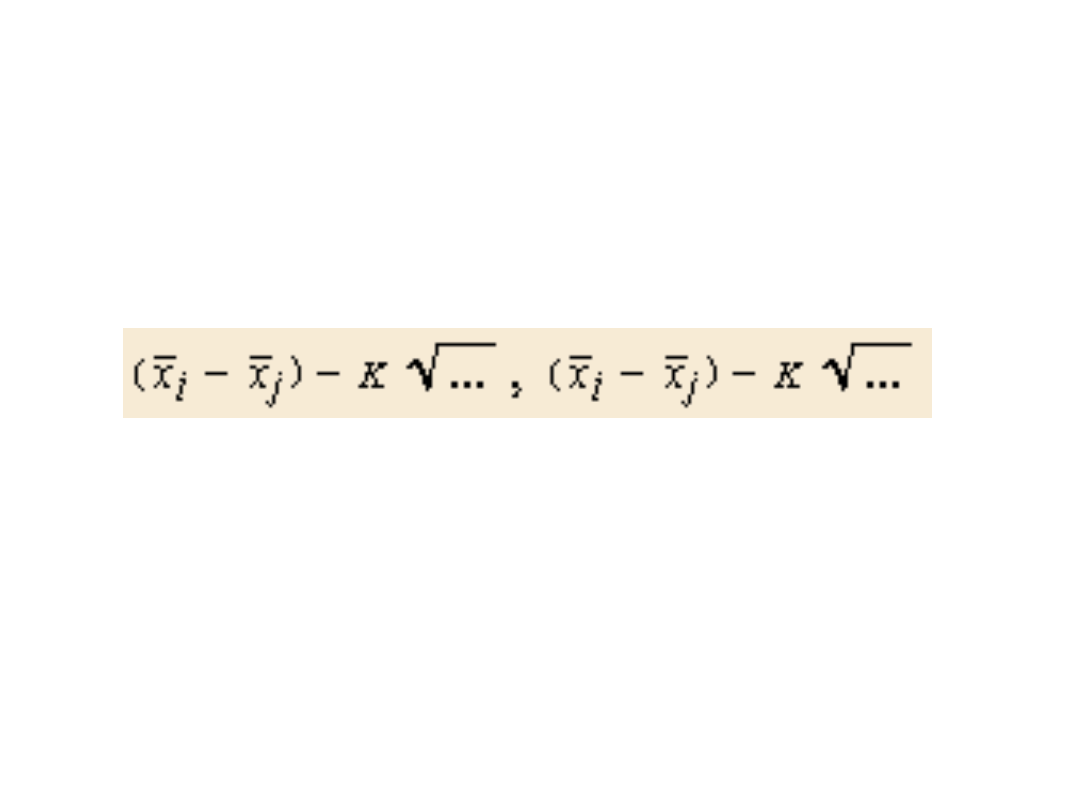
• Nierówność ta umożliwia utworzenie

przedziału ufności dla średnich x i y:

• Jeżeli tak skonstruowany przedział

obejmuje wartość 0, to średnie x i y
nie różnią się istotnie.

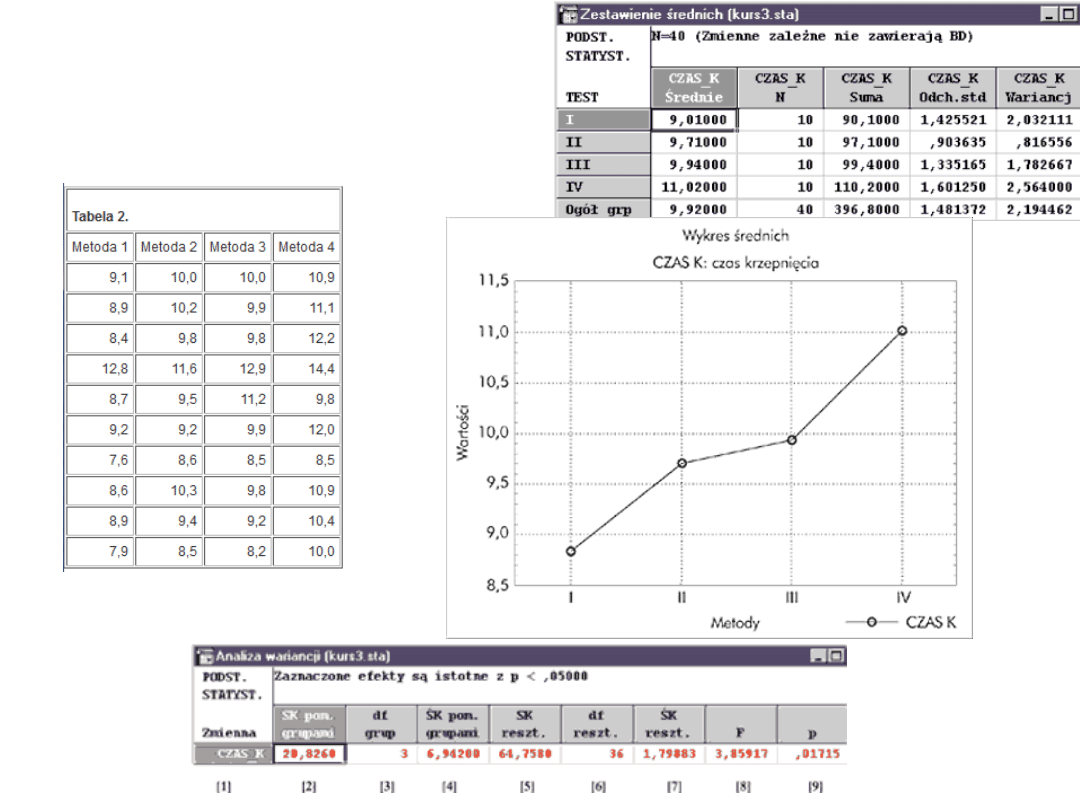
Przykład

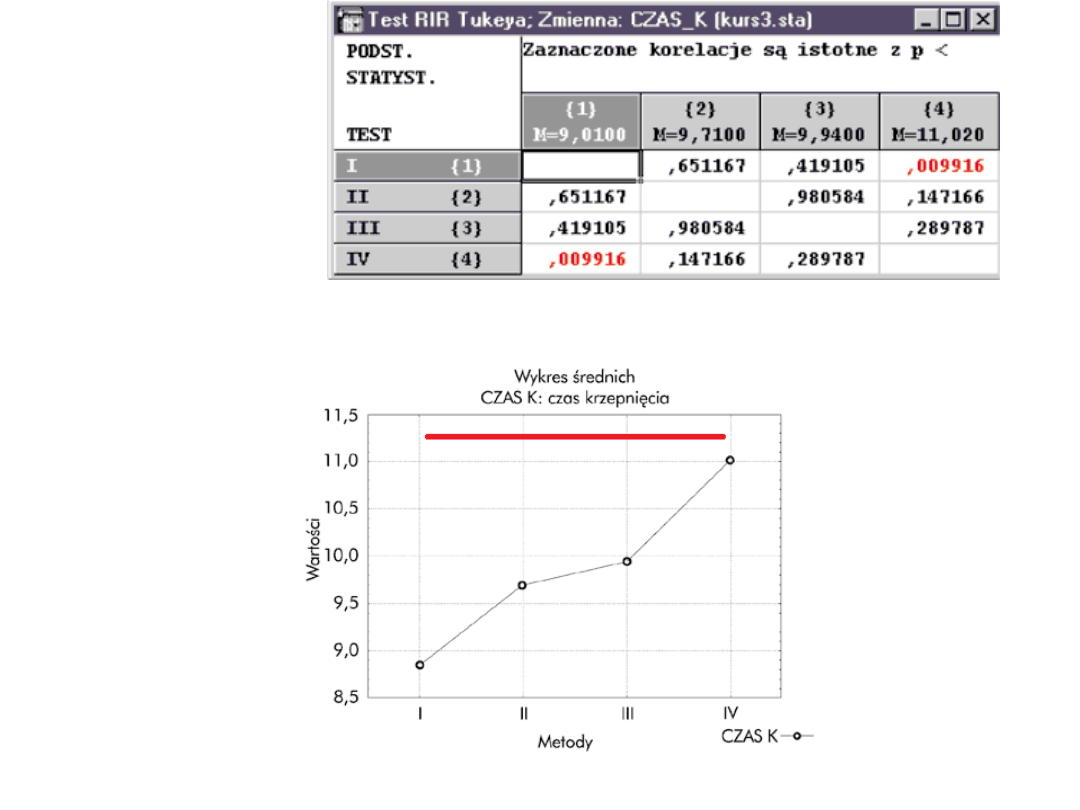
I dalej:

Test post-hoc Tukey’a

• Test Tukeya występuje w dwóch

wariantach: dla równej liczebności
próbek i dla nierównej liczebności
(test Spjotvolla i Stoline'a).

• Oparty jest na "studentyzowanym"

rozkładzie.

• Więcej o różnych testach post-hoc:
http://www.mp.pl/artykuly/?aid=10851

Zadanie

• Porównano trzy grupy osób:
• A: N = 10, suma kwadratów odchyleń

= 30, średnia 10

• B: N = 10, sko = 35, średnia 5
• C: N = 11, sko = 28, średnia 10
• Sprawdź za pomocą testu F czy

grupy różnią się miedzy sobą

Anova dla grup zależnych

• Jeśli mamy powtarzany pomiar, także

możemy zastosować ANOVĘ,
jednakże musimy zaznaczyć (w
pakiecie statystycznym), że chodzi
nam o grupy zależne (inaczej:
powtarzane pomiary)

ANOVA nieparametryczna

• Test Kruskala-Wallisa jest nieparametrycznym

odpowiednikiem jednoczynnikowej analizy

wariancji. Za pomocą tego testu sprawdzamy czy

n niezależnych próbek pochodzi z tej samej

populacji, czy z populacji z taką samą medianą.

Poszczególne próbki nie muszą mieć takiej samej

liczebności. Maksymalnie możemy porównywać 10

grup.

• Test Friedmana jest nieparametrycznym

odpowiednikiem jednoczynnikowej analizy

wariancji dla pomiarów powtarzanych. Uważany

jest za najlepszy nieparametryczny test dla

danych tego rodzaju. Najczęściej są to wyniki dla

tych samych osób otrzymane w n (n >>2) różnych

badaniach lub wyniki równoważnych grup osób.

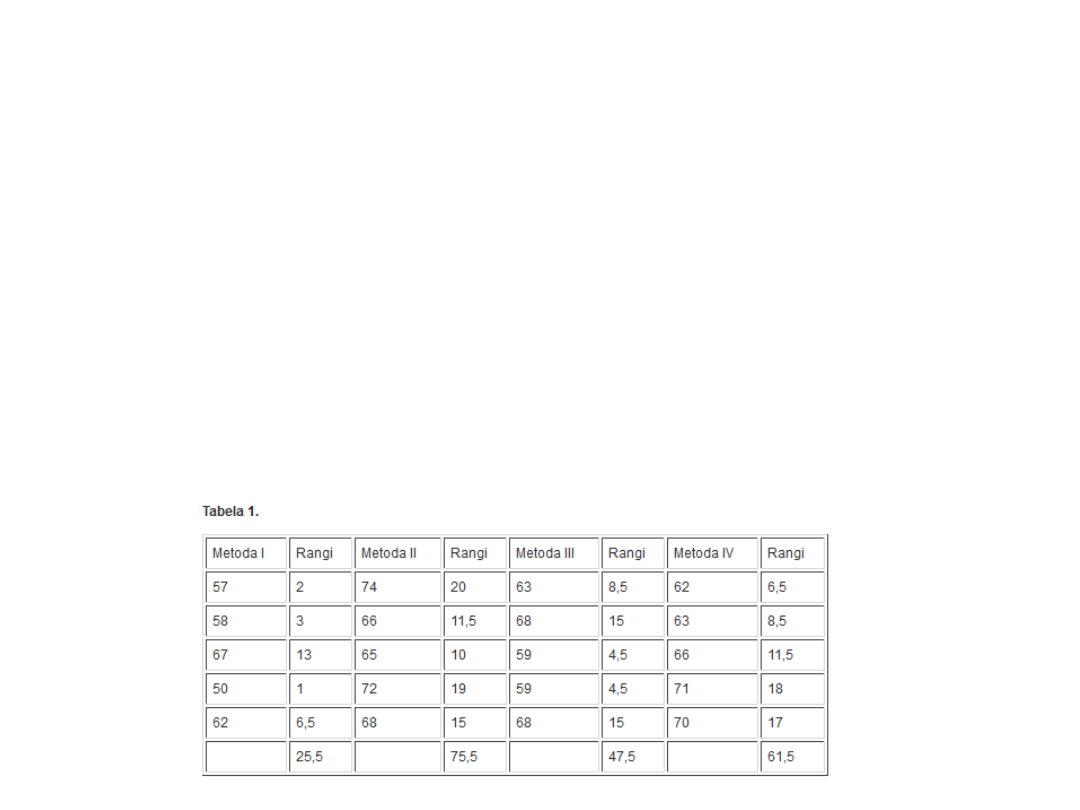
Test Kruskala-Wallisa

• Załóżmy, że przeprowadzono badania w celu

porównania 4 metod leczenia pewnej choroby.

Pobrano 5-elementowe próby losowe spośród

chorych na daną chorobę, których leczono

odpowiednio metodą I, II, III i IV. Wyniki terapii

oceniono w specjalnym teście. Wartości testu

podane w umownej punktacji przedstawia tabela

1.

• Podano w niej też rangi nadane wynikom

obserwacji. Są one bowiem punktem wyjścia do

wyliczenia wartości opisywanych testów. Proces

rangowania przebiega następująco:

• Porządkujemy rosnąco wartości obu prób.
• Zaczynając od wartości najmniejszej (lub

największej), przyporządkowujemy poszczególnym

obserwacjom kolejne liczby naturalne.

• W przypadku wystąpienia wartości jednakowych

przyporządkowujemy im tzw. rangi wiązane

(średnia arytmetyczna z rang, jakie powinno się im

przypisać).

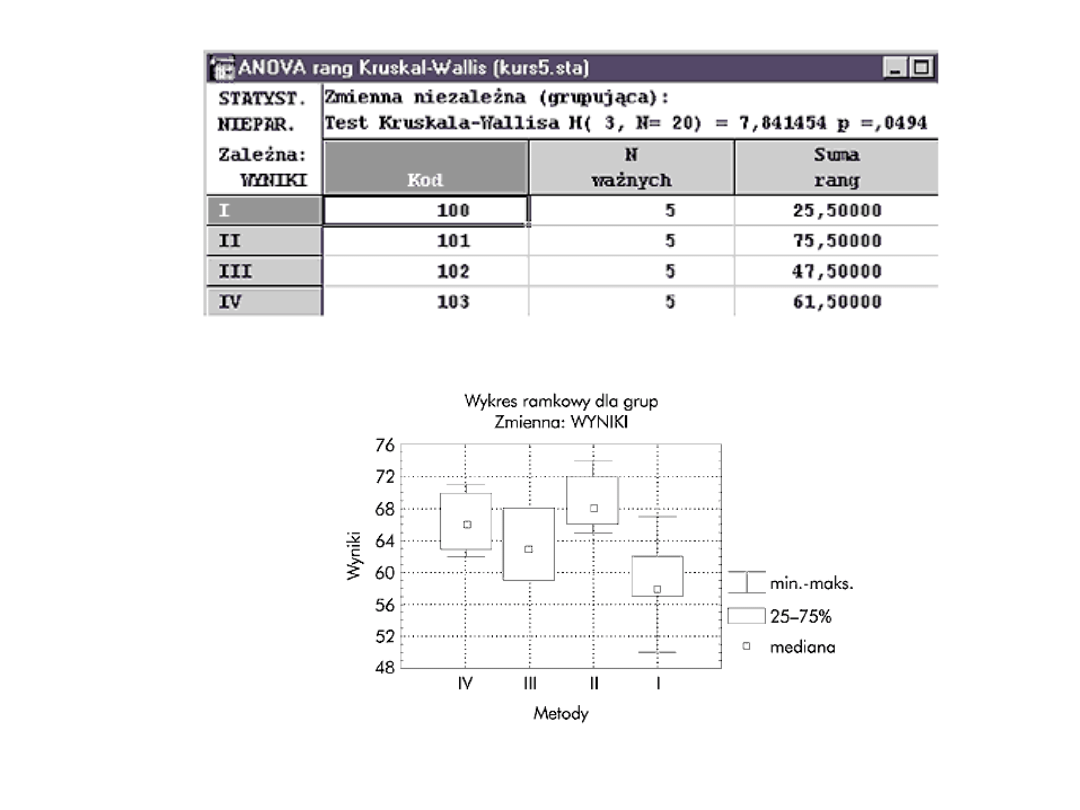
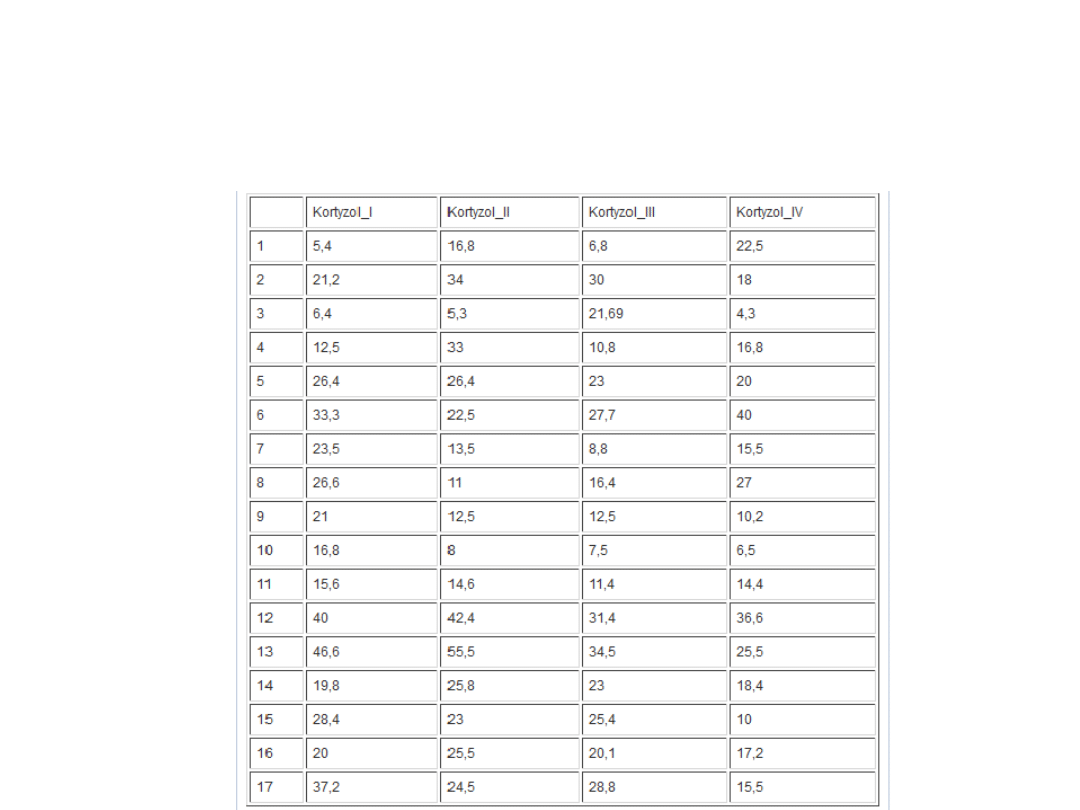
• W podanym przykładzie chcemy

zweryfikować hipotezę, że wszystkie metody

leczenia dają jednakowe wyniki. Musimy

więc zastosować test sprawdzający hipotezę,

że k niezależnych próbek pochodzi z tej

samej populacji. Użyjemy w tym celu testu

sumy rang Kruskala-Wallisa. Dane powinny

być podobnie rozmieszczone jak w analizie

wariancji. Jedna zmienna (WYNIKI) zawiera

wyniki oceny, a druga (METODA) - kod

(numer metody) do jednoznacznej

identyfikacji grup.

Test Friedmana

Testy zależności

• Korelacja
• Regresja

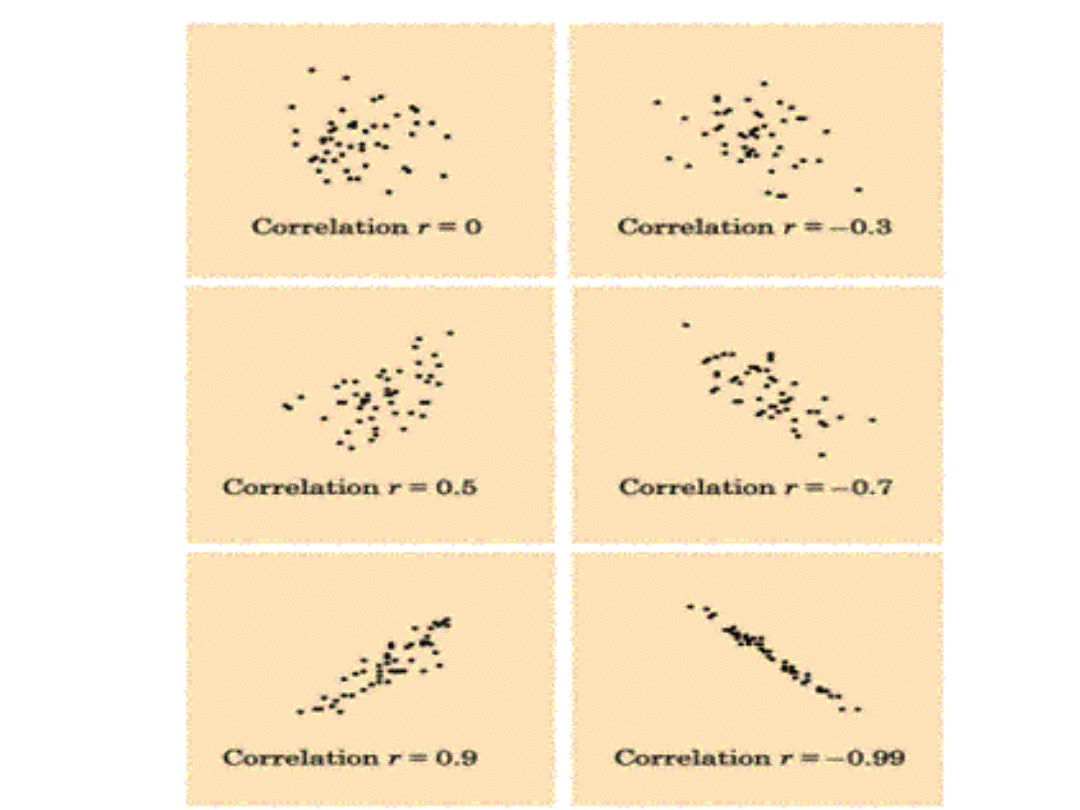
Związek między zmiennymi

• Badając związek między zmiennymi

możemy określić jego siłę (wielkość) oraz

kierunek.

• Siła. Korelacja przyjmuje wartości od -1 do

1. Im wyższa wartość bezwględna korelacji

tym silniejszy związek między zmiennymi

• Kierunek. Znak korelacji wskazuje na

kierunek związku między zmiennymi.

Testy dla danych

jakościowych

W wielu badaniach medycznych gromadzimy dane
będące liczebnościami. Na przykład możemy
klasyfikować chorych w badanej próbie do różnych
kategorii pod względem wieku, płci czy natężenia
choroby.

Pierwszy krok: przedstawienie danych w tabeli
kontyngencji.

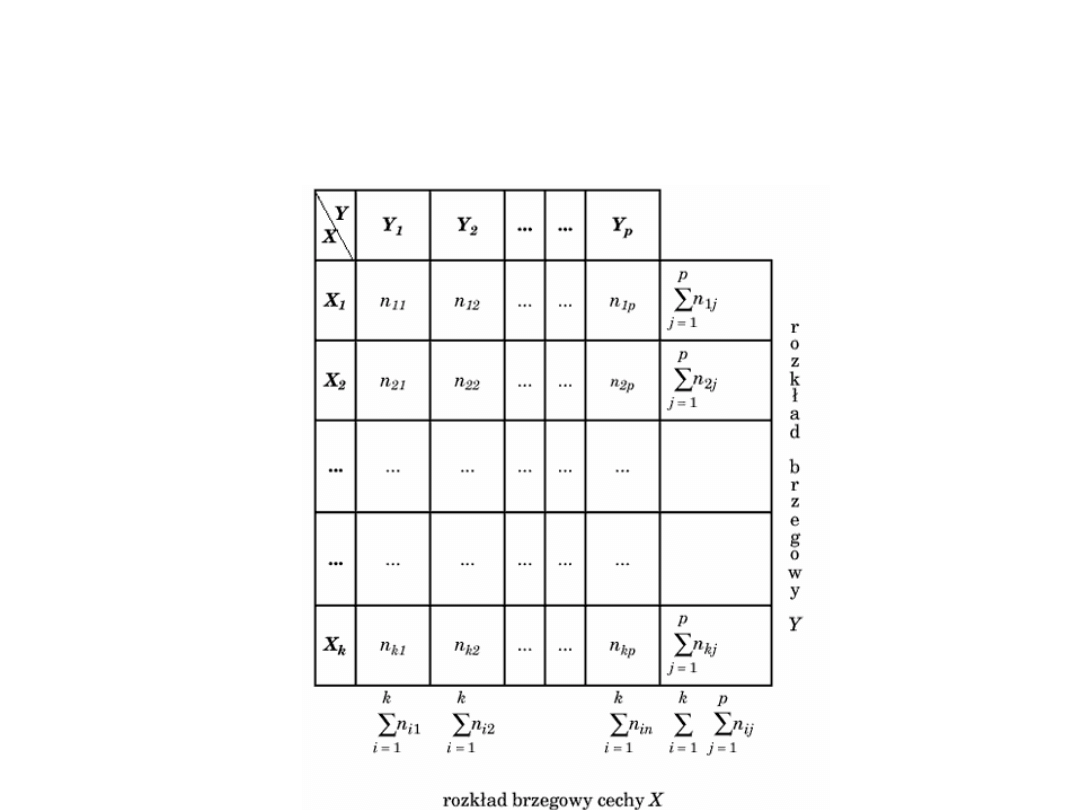
Tabela kontyngencji

Przykład

• Liczebności nij określają liczbę elementów próby, dla

których cecha X ma wariant Xi i jednocześnie cecha Y -

wariant Yj. Tablica wielodzielcza pokazuje więc określony

łączny rozkład obu cech. Liczebności w ostatnim wierszu i w

ostatniej kolumnie nazywamy empirycznymi brzegowymi

rozkładami, odpowiednio cechy Y i cechy X.

• Na przykład, chcąc ocenić wpływ używek (papieros, kawa,

alkohol) na pewną chorobę, zebraliśmy dane na temat ich

używania w grupie 90-osobowej. Zastosowano podział na 4

kategorie: nigdy (tzn. nie używano nigdy), niewiele

(używano w małych ilościach), średnio (używano w średnich

ilościach) i dużo (używano w dużych ilościach).

W badaniach brano również pod uwagę płeć respondentów.

Początkowy fragment danych dla 10 chorych (zapisanych w

4 rubrykach) przedstawia tabela 2.

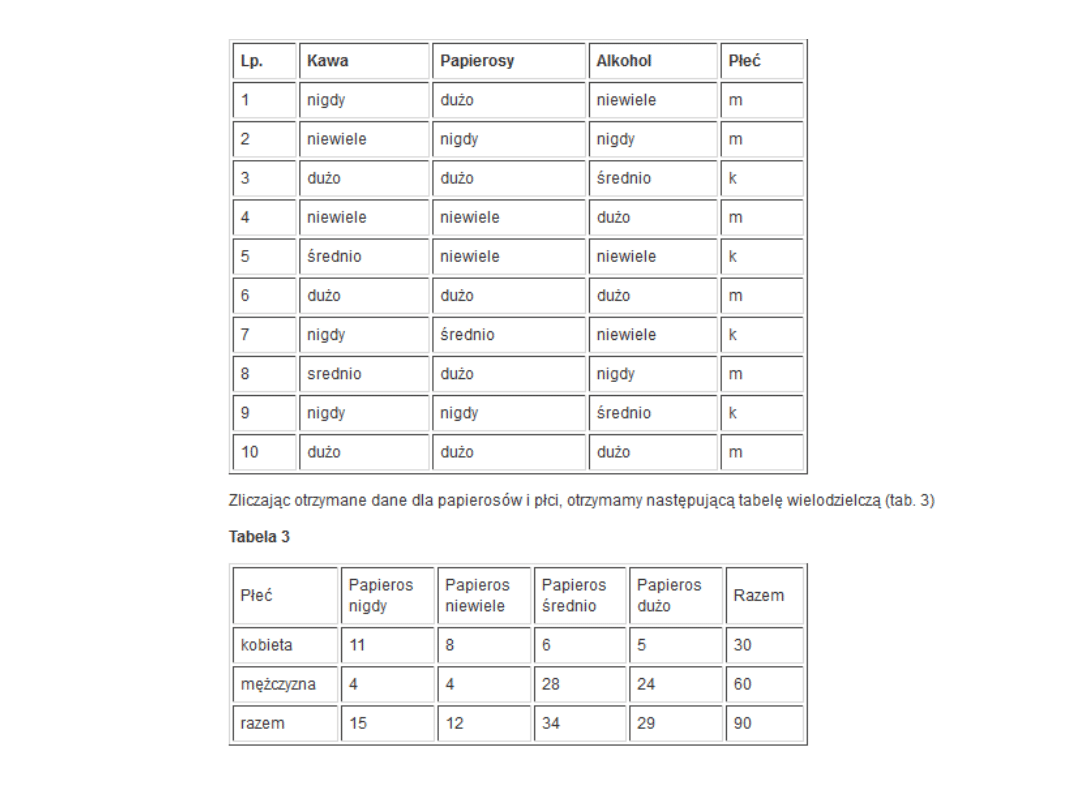
Tabela kontyngencji

• Widać wyraźną przewagę mężczyzn w

grupie palących dużą lub średnią liczbę

papierosów, natomiast około 3-krotnie

więcej kobiet niż mężczyzn nigdy nie paliło.

Informacje byłyby bogatsze po dołączeniu

danych odsetkowych. Odsetki wylicza się

względem: ostatniej rubryki (płci),

ostatniego wiersza (liczby wypalanych

papierosów) oraz całkowitej liczby

respondentów. Następny etap analizy

statystycznej tak zebranych danych to

próba weryfikacji hipotezy, że dwie

jakościowe cechy w populacji są niezależne.

Test Chi^2

Polega na porównaniu częstości zaobserwowanych z

częstościami oczekiwanymi przy założeniu hipotezy
zerowej (o braku związku między tymi dwiema
zmiennymi). Częstości oczekiwane obliczamy,
wykorzystując częstości marginalne (z tablicy
wielodzielczej) według następującego wzoru:

Test chi^2

• Wówczas hipotezę zerową orzekającą, że

cechy X i Y są niezależne, możemy

zweryfikować testem chi^2.

• Weryfikacja hipotezy zerowej:

H0: cechy X i Y są niezależne

• Wobec hipotezy alternatywnej: H1:

cechy X i Y są zależne

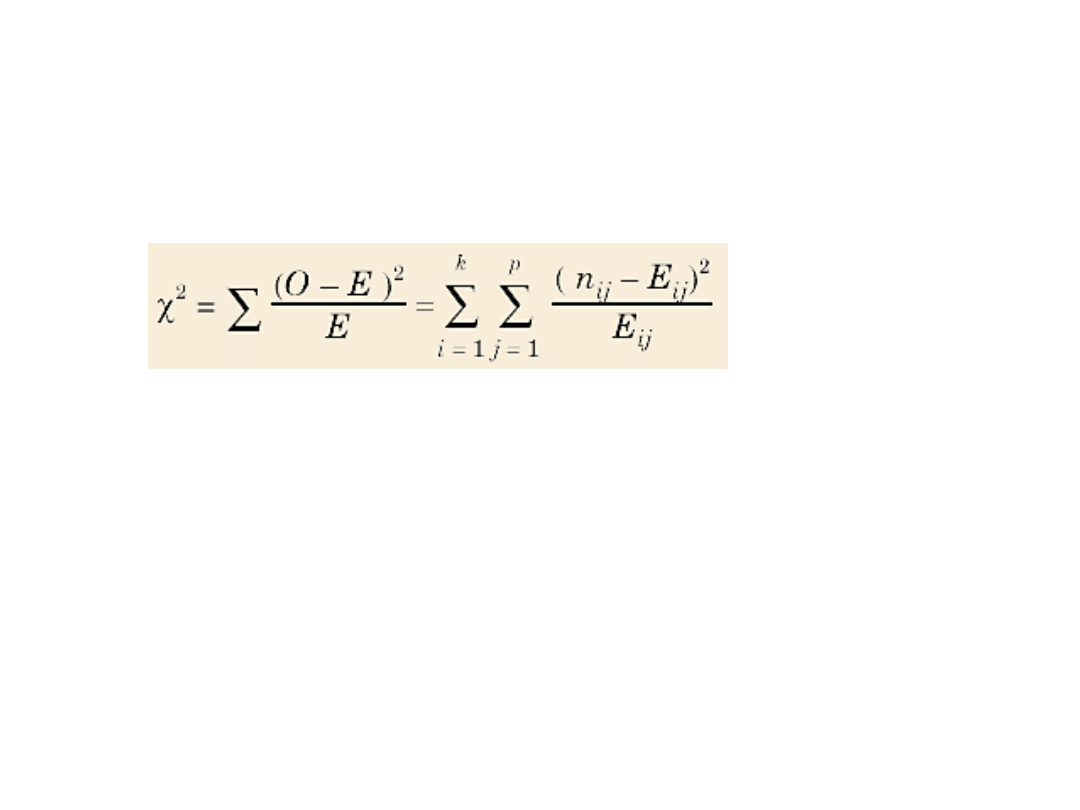
• Do weryfikacji hipotezy stosujemy statystykę:

gdzie E - oczekiwana częstość komórki
O - obserwowana częstość komórki

Przy założeniu hipotezy zerowej opisywana

statystyka ma asymptotyczny rozkład
o s = (k - 1) (p - 1) stopniach swobody

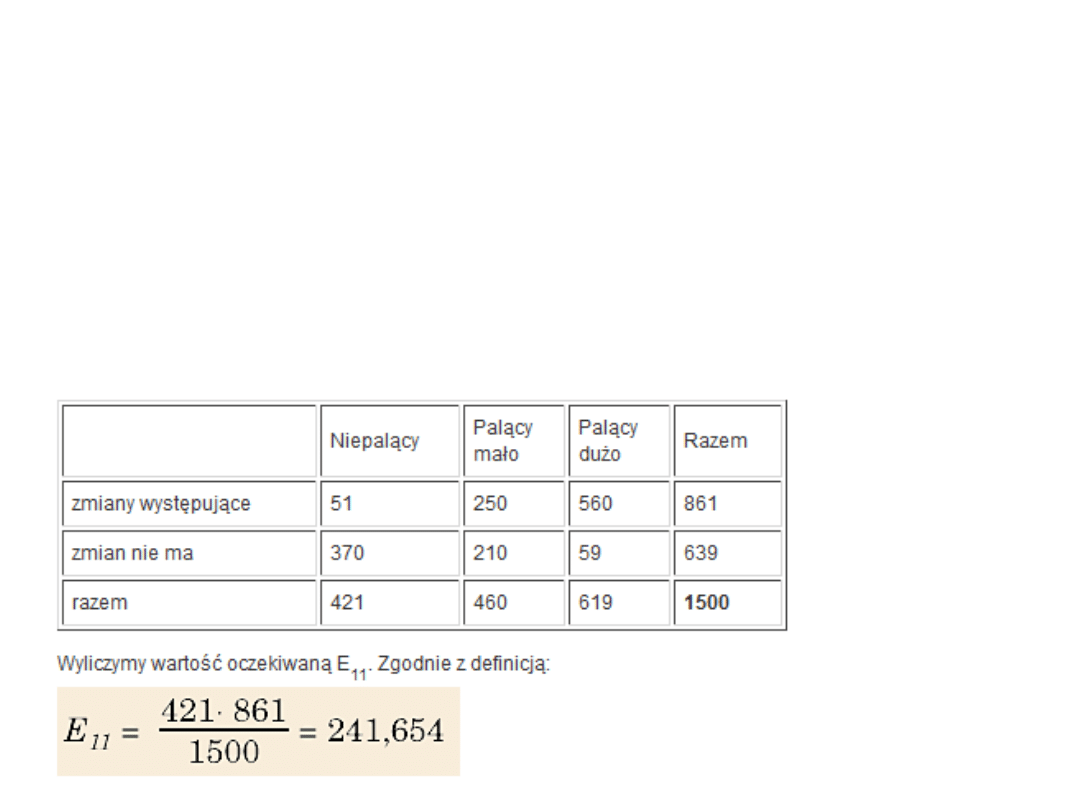
Przykład

• Na przykład badano zależność między liczbą

wypalanych papierosów a wystąpieniem
pewnych zmian patologicznych w płucach w
grupie 1500 osób.

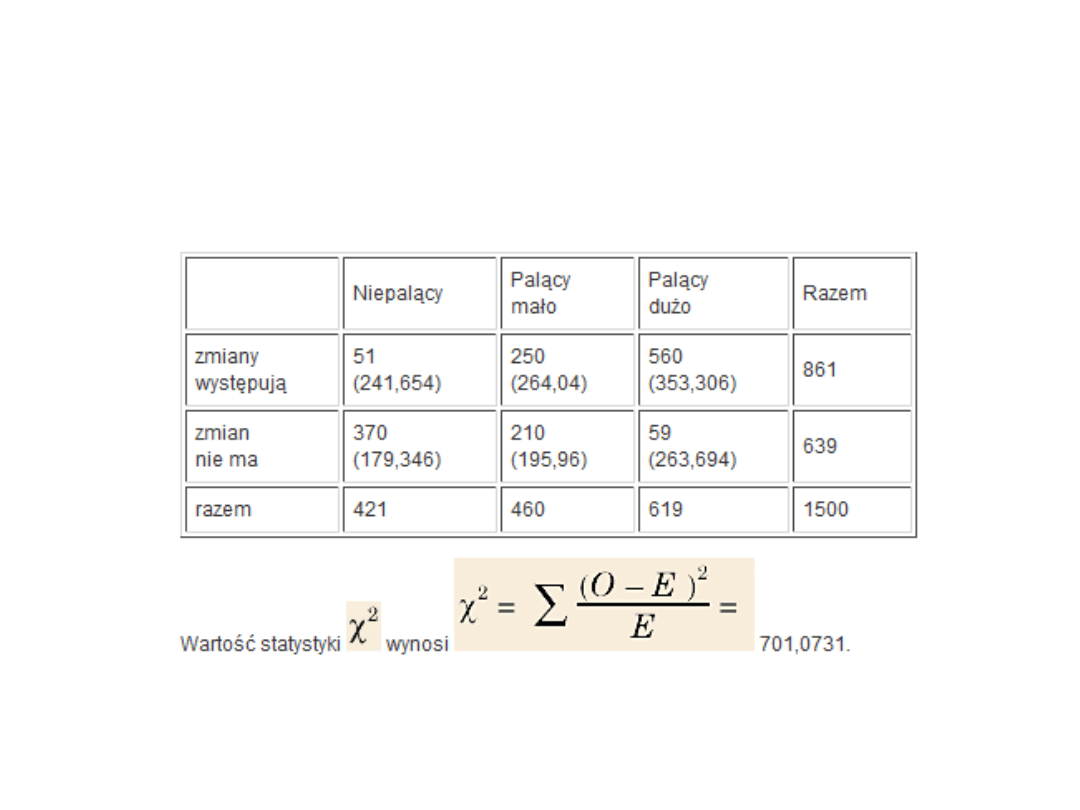
Przykład cd

Przykład cd

• Z kolei wartość krytyczna odczytana z tablic dla

poziomu istotności alfa = 0,001 wynosi 13,817.

Pozwala więc nam odrzucić hipotezę zerową i

stwierdzić, że na poziomie istotności alfa = 0,001

istnieje zależność między liczbą wypalanych

papierosów dziennie a wystąpieniem patologicznych

zmian w płucach.

• Zauważmy, że bardzo duże wartości chi^2 oznaczają

dużą różnicę pomiędzy częstościami obserwowanymi

a oczekiwanymi, i jest to dowód istnienia zależności.

Przeciwnie mała wartość (zwłaszcza bliska 0) nie daje

dowodu na istnienie korelacji

Chi^2 dla tabeli 2/2

Interpretacja

• Interpretacja wszystkich tych współczynników jest

taka sama:

• jeżeli ma wartość zero, to cechy X i Y są niezależne

• im bliższa jedności jest wartość tych

współczynników, tym silniejsze jest powiązanie

między analizowanymi cechami X i Y.

• Obliczając opisane współczynniki dla danych

dotyczących choroby wieńcowej, otrzymujemy

współczynnik Fi = V = 0,51

Korelacja

• Dwie zmienne mogą być powiązane zależnością

funkcyjną lub zależnością statystyczną (korelacyjną).

• Związek funkcyjny odznacza się tym, że każdej

wartości jednej zmiennej niezależnej (X) odpowiada

tylko jedna, jednoznacznie określona wartość

zmiennej zależnej (Y). Wiadomo na przykład, że

obwód kwadratu jest funkcją jego boku (O = 4a).

• Związek statystyczny polega na tym, że określonym

wartościom jednej zmiennej odpowiadają ściśle

określone średnie wartości drugiej zmiennej. Można

zatem obliczyć, jak się zmieni (średnio biorąc)

wartość zmiennej zależnej Y w zależności od wartości

zmiennej niezależnej X.

SENSOWNOŚĆ KORELACJI!

• Oczywiście najpierw na podstawie analizy

merytorycznej należy logicznie uzasadnić

występowanie związku, a dopiero potem przystąpić

do określenia siły i kierunku zależności.

• Znane są bowiem w literaturze badania zależności

(nawet istotnej statystycznie) między liczbą zajętych

gniazd bocianich a liczbą urodzeń na danym

obszarze czy między liczbą zarejestrowanych

odbiorników TV a liczbą chorych umysłowo.

• Zwróćmy też uwagę, że liczbowe stwierdzenie

występowania zależności nie zawsze oznacza

występowanie związku przyczynowo-skutkowego

między badanymi zmiennymi. Współwystępowanie

dwóch zjawisk może również wynikać z

bezpośredniego oddziaływania na nie jeszcze innego,

trzeciego zjawiska.

• W analizie korelacji badacz jednakowo

traktuje obie zmienne - nie
wyróżniamy zmiennej zależnej i
niezależnej. Korelacja między X i Y jest
taka sama, jak między Y i X. Mówi nam
ona, na ile obie zmienne zmieniają się
równocześnie w sposób liniowy.
Precyzyjna definicja zaś brzmi:

• Korelacja między zmiennymi X i Y

jest miarą siły liniowego związku
między tymi zmiennymi.

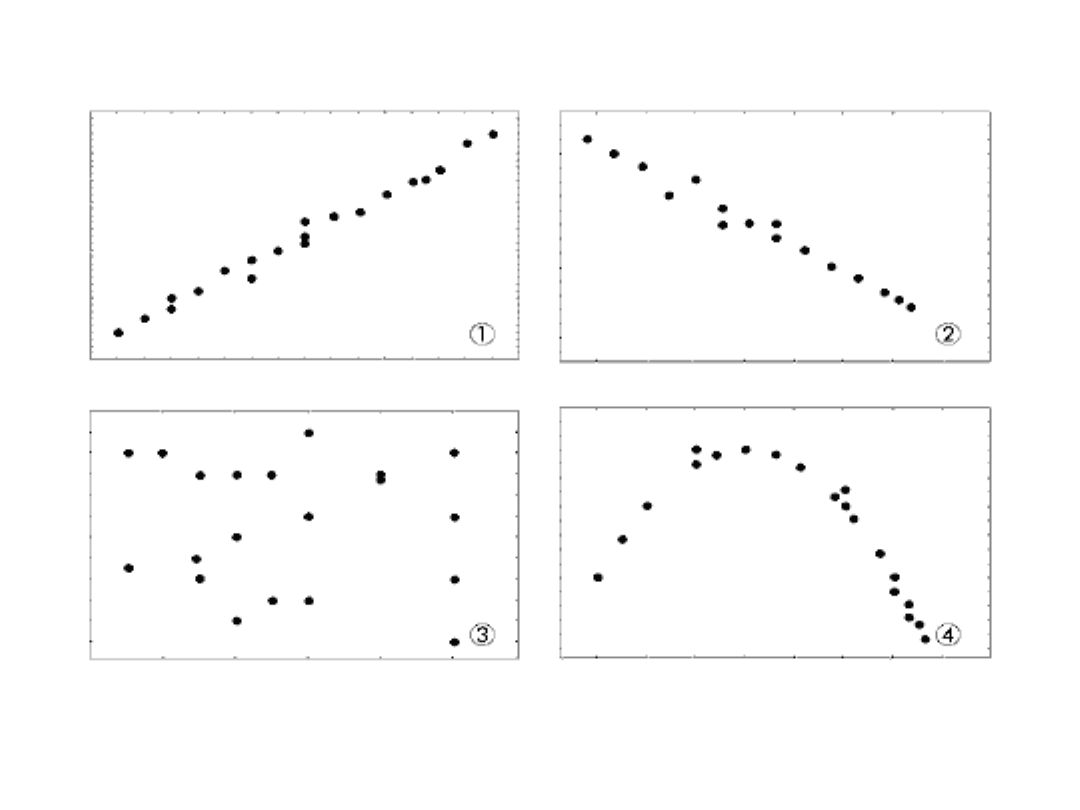
Krok 1

• Analizę związku korelacyjnego między

badanymi cechami rozpoczynamy
zawsze od sporządzenia wykresu.
Wykresy, które reprezentują
obrazowo związek pomiędzy
zmiennymi, nazywane są wykresami
rozrzutu (scatterplot).

• Wzrokowa ocena ułatwia określenie

siły i rodzaju zależności.

• Przyjmijmy, że zbiorowość jest badana ze względu na

dwie zmienne X i Y, a wartości tych zmiennych w

populacji lub próbie n-elementowej są zestawione w

postaci dwóch szeregów szczegółowych lub

rozdzielczych. W prostokątnym układzie współrzędnych

na osi odciętych zaznaczamy wartości jednej zmiennej,

a na osi rzędnych - wartości drugiej zmiennej.

• Punkty odpowiadające poszczególnym wartościom cech

tworzą korelacyjny wykres rozrzutu. Rzadko się zdarza,

że zaznaczone punkty leżą dokładnie na linii prostej

(pełna korelacja); częściej spotykana konfiguracja

składa się z wielu zaznaczonych punktów leżących

mniej więcej wzdłuż konkretnej krzywej (najczęściej linii

prostej)

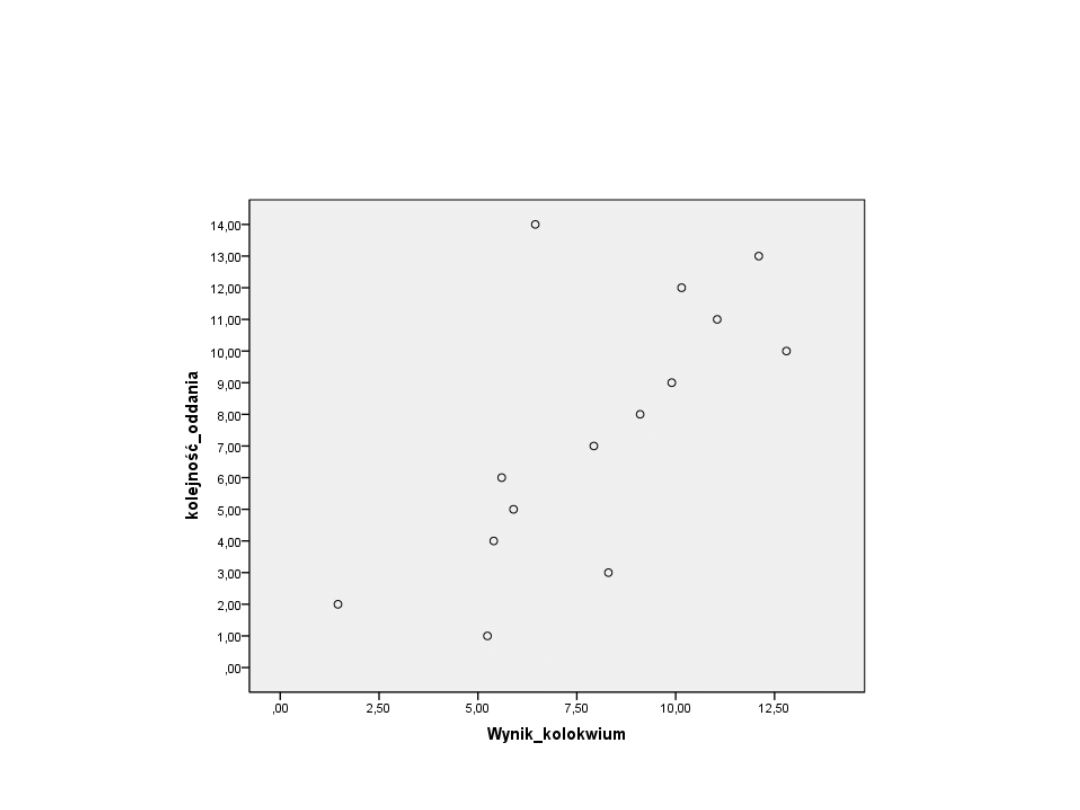
Przykład z życia

Współczynnik korelacji

• Siłę współzależności dwóch

zmiennych można wyrazić liczbowo
za pomocą wielu mierników.
Najbardziej popularny jest
współczynnik korelacji liniowej
Pearsona, oznaczony symbolem rXY
i przyjmujący wartości z przedziału [-
1, 1].

Korelacja Pearsona

• Współczynnik korelacji Pearsona wyliczamy

wówczas, gdy:
- obie zmienne są mierzalne
- mają rozkład zbliżony do normalnego
- zależność jest prostoliniowa (stąd nazwa).

Przy interpretacji współczynnika korelacji

liniowej Pearsona należy więc pamiętać, że

wartość współczynnika bliska zeru nie

zawsze oznacza brak zależności, a jedynie

brak zależności liniowej.

Wartości R-Pearsona

• Znak współczynnika korelacji informuje nas o kierunku korelacji,

natomiast jego bezwzględna wartość - o sile związku. Oczywiście

rXY jest równe rYX. Jeśli rXY = 0, oznacza to zupełny brak związku

korelacyjnego między badanymi zmiennymi X i Y (przypadek 3.

na rys. 1). Im wartość bezwzględna współczynnika korelacji jest

bliższa jedności, tym zależność korelacyjna między zmiennymi

jest silniejsza. Gdy rXY = I1I, to zależność korelacyjna przechodzi

w zależność funkcyjną (funkcja liniowa).

• W analizie statystycznej zwykle przyjmuje się następującą skalę:

• rXY = 0 zmienne nie są skorelowane

• 0 <rXY <0,1 korelacja nikła

• 0,1 =<rXY <0,3 korelacja słaba

• 0,3 =<rXY <0,5 korelacja przeciętna

• 0,5 =<rXY <0,7 korelacja wysoka

• 0,7 =<rXY <0,9 korelacja bardzo wysoka

• 0,9 =<rXY <1 korelacja prawie pełna.

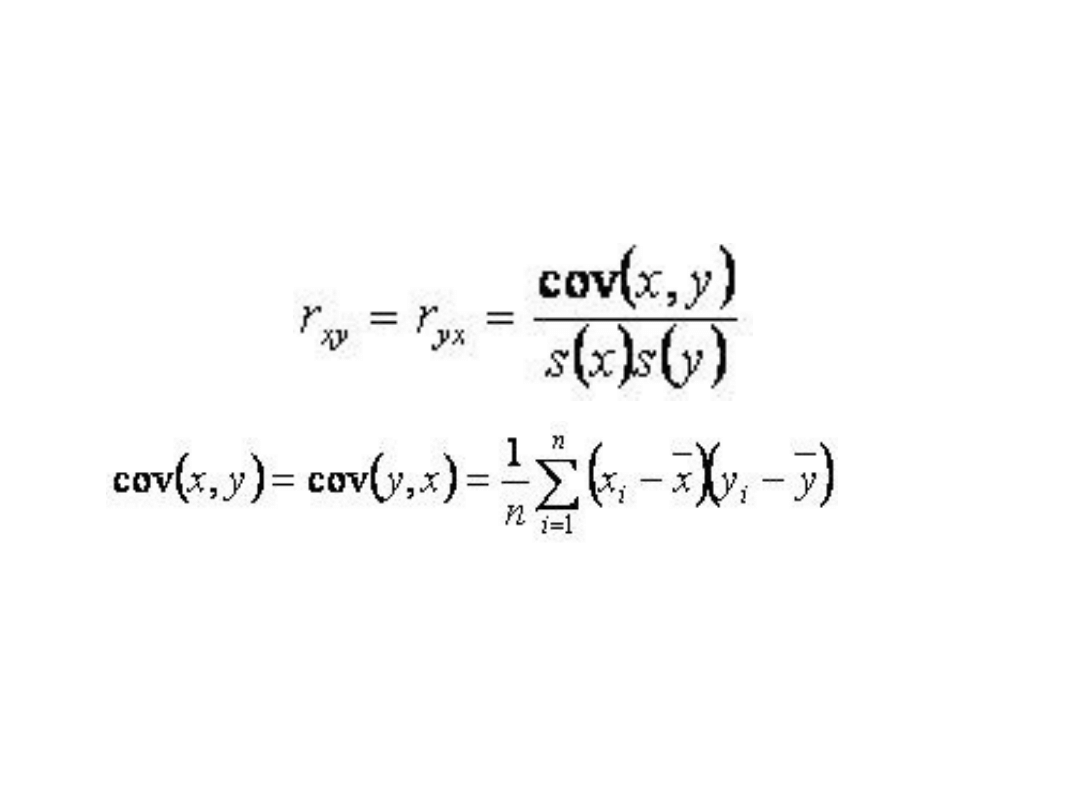
Wzór na R-Peaesona

• a s(x) i s(y) są odchyleniami

standardowymi odpowiednich

zmiennych.

Kowariancja

• Kowariancja jest nieunormowaną miarą zależności liniowej

pomiędzy dwiema zmiennymi. Stanowi ona miarę wspólnej

zmienności obu zmiennych (ko-wariancja) pomiędzy

zmiennymi. Innymi słowy czy odchylanie się obserwowanych

wyników zmiennej od wartości średniej dla tej zmiennej jest

podobne dla obu zmiennych. Jeżeli zmienne nie są ze sobą

związane to kowariancja jest bliska wartości 0. Jeżeli zmienne

są ze sobą związane to wartość kowariancji jest różna od 0.

Kowariancję możemy wyliczyć w bardzo szybki sposób.

Liczymy iloczyn pomiędzy odpowiadającymi wartościami

pierwszej i drugiej zmiennej, z tych iloczynów wyciągamy

średnią, następnie wyliczamy wartości średnie dla samych

wartości (nie iloczynów) zmiennych i korzystamy ze wzoru:

cov - symbol kowariancji (X,Y) = wartość oczekiwana

(X*Y) - (wartość oczekiwana (X) * wartość oczekiwana

(Y))

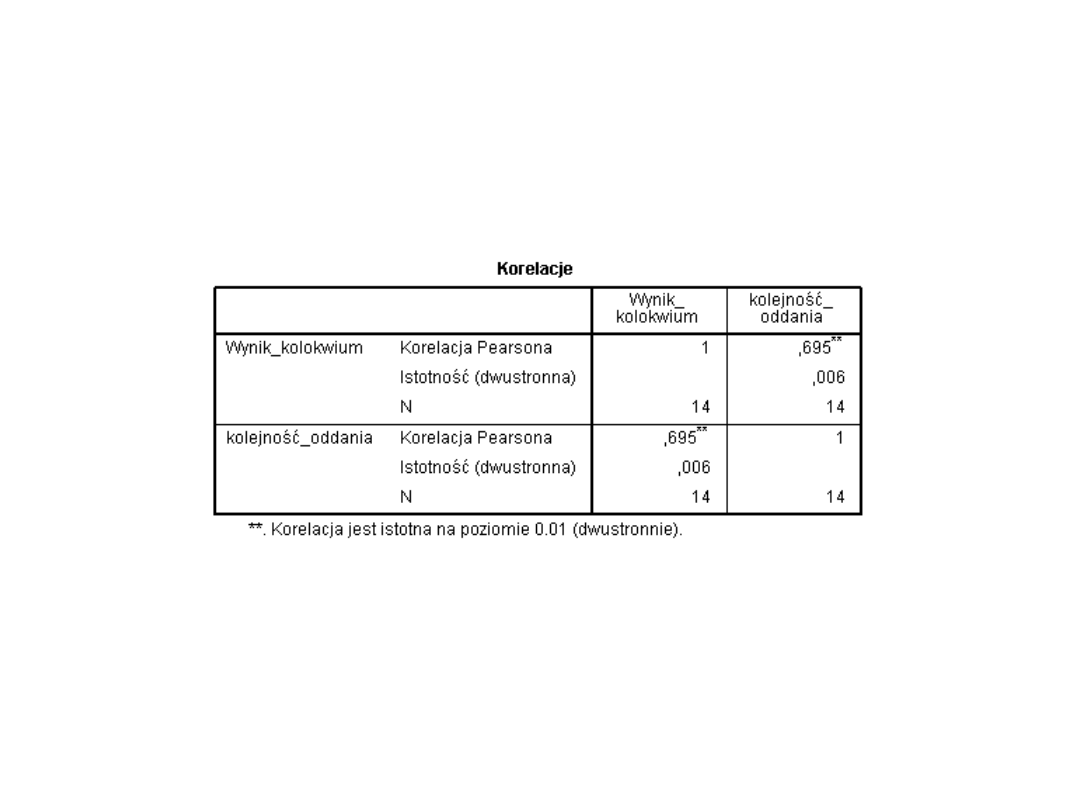
Nasz przykład

Co, jeśli dane na skali

porządkowej?

• Korelacja rho-Spearmana traktowana jest jako

korelacja nieparametryczna, co stanowi odpowiednik

parametrycznej korelacji r-Pearsona. W przypadku

korelacji rho-Spearmana wyniki są najpierw poddane

rangowaniu. Przypisywane są rangi poszczególnym

obserwacjom. Tak "przeliczone" wyniki poddawane

są analizie korelacji.

Rangowanie wyników pozwala przeanalizować

związek pomiędzy zmiennymi mierzonymi na skali

porządkowej (nie tylko ilościowej, jak miało to

miejsce w przypadku korelacji r-Pearsona). W

przypadku tej korelacji nie ma znaczenia to, czy

analizowane zmienne mają rozkłady zbliżone do

normalnego.

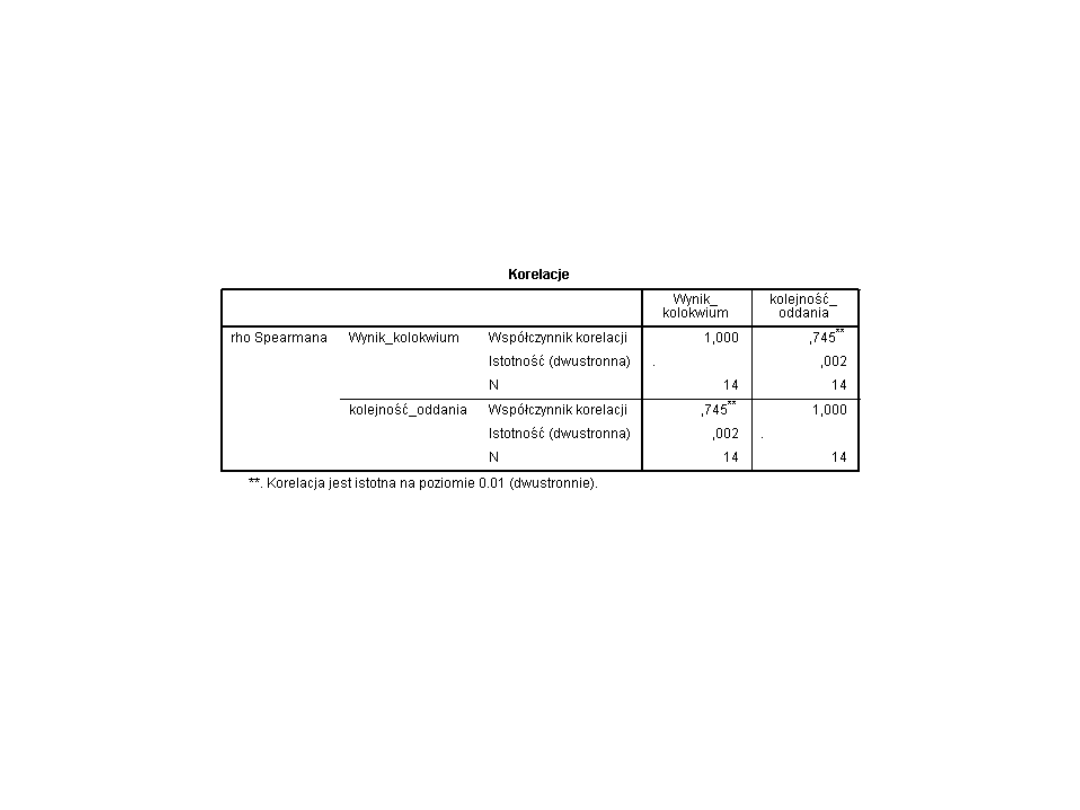
Nasz przykład 2

Co, jeśli dane na skali

jakościowej?

• Chi^2 i wyliczenie współczynnika Phi-

Yula albo V-Kramera

Regresja liniowa

• Modelowanie zależności między dwiema

zmiennymi: zmienną zależną (Y) i zmienną
niezależną (X), zakładając, że między X i Y
zachodzi związek liniowy.

• Równanie linii prostej: Y = bX + a
• b (w niektórych modelach jako B1) – kąt

nachylenia linii względem osi X

• a (w niektórych modelach b, stała) –

odległość na osi Y od punktu początkowego

do punktu przecięcia z linią prostą

Metoda najmniejszych

kwadratów

• Jak jednak znaleźć taką "dobrze

dopasowaną" linię prostą? Punktem wyjścia

są reszty, a właściwie suma kwadratów

reszt, opisująca rozbieżność pomiędzy

wartościami empirycznymi zmiennej

zależnej a jej wartościami teoretycznymi,

obliczonymi na podstawie wybranej funkcji.

Oszacowania b0 i b1 dobieramy tak, aby

suma kwadratów reszt osiągnęła minimum.

Ta najbardziej znana i najczęściej stosowana

metoda szacowania parametrów linii

regresji nosi nazwę metody

najmniejszych kwadratów.

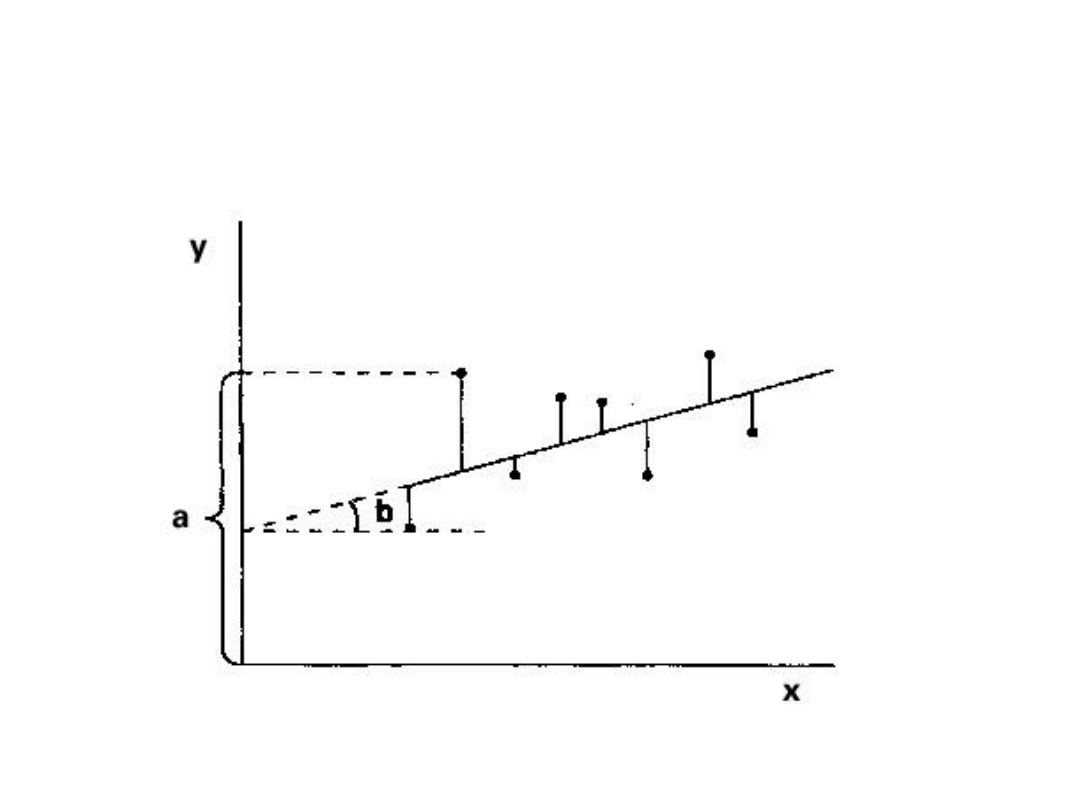
Regresja liniowa

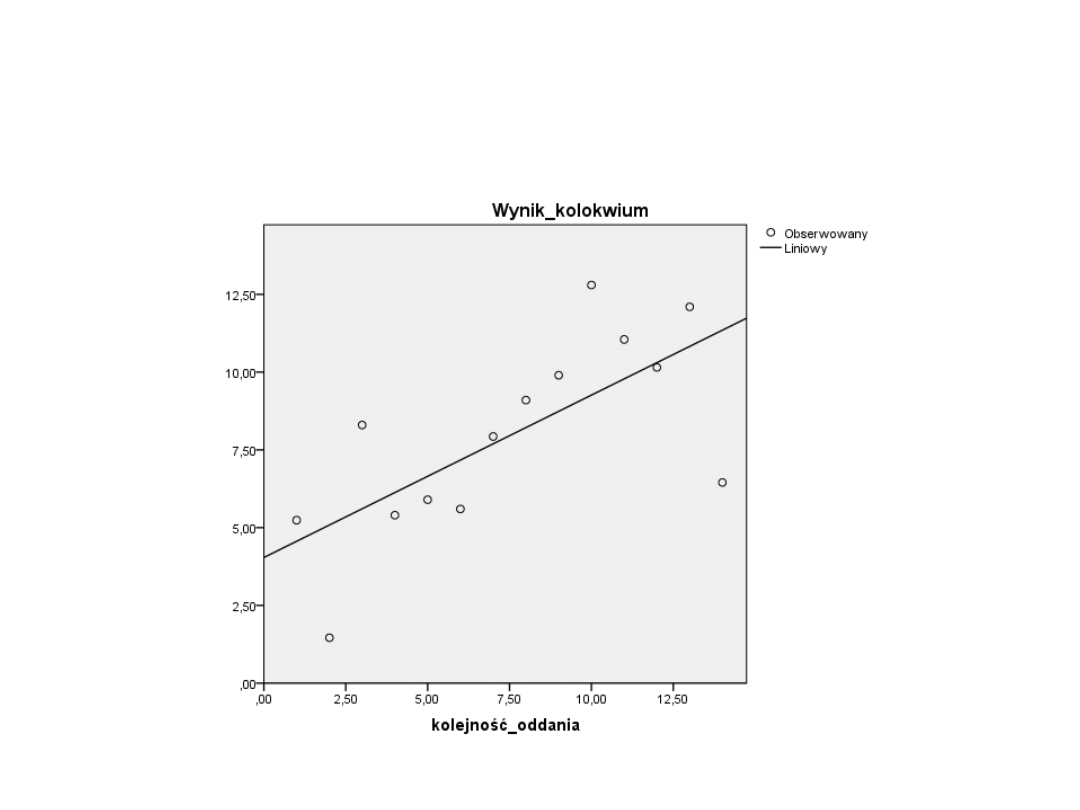
Nasz przykład

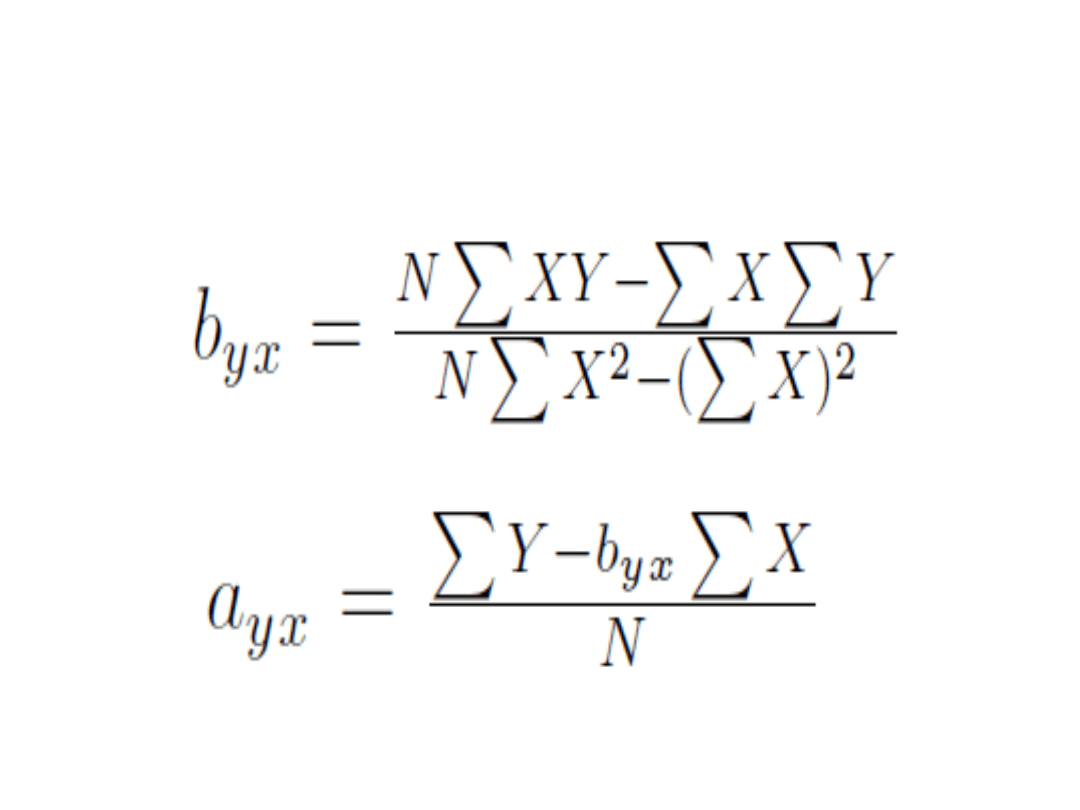
Obliczanie współczynników

a i b

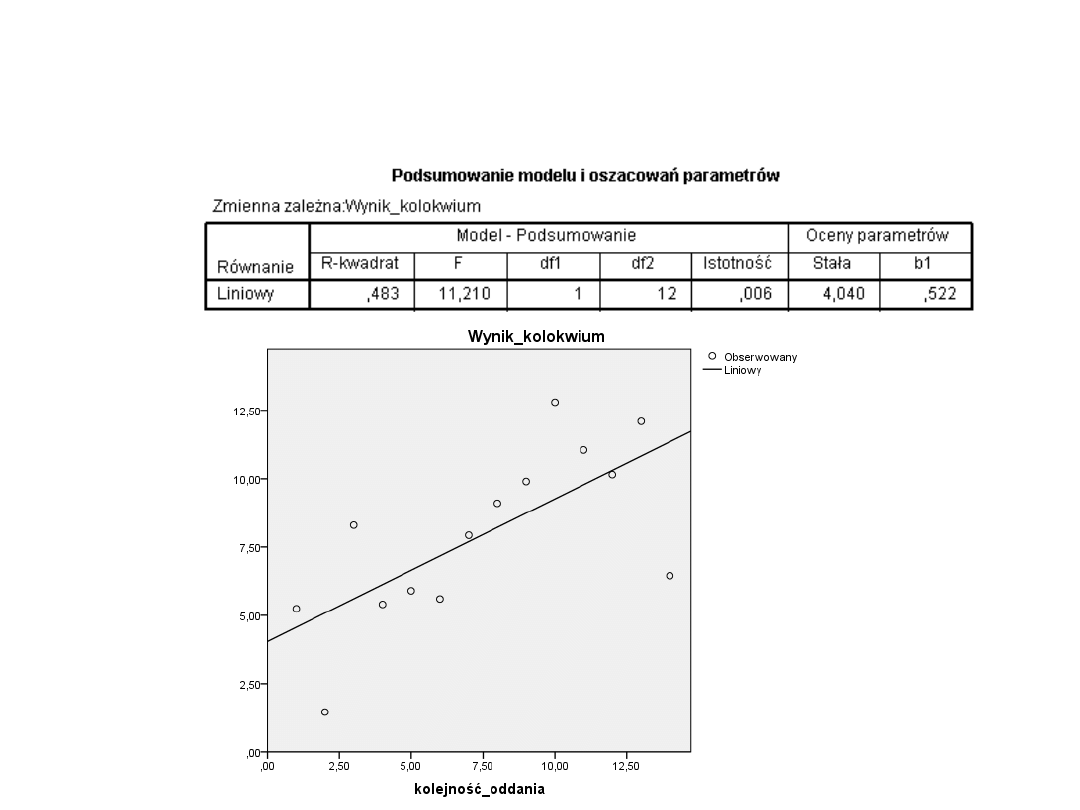
Nasz przykład

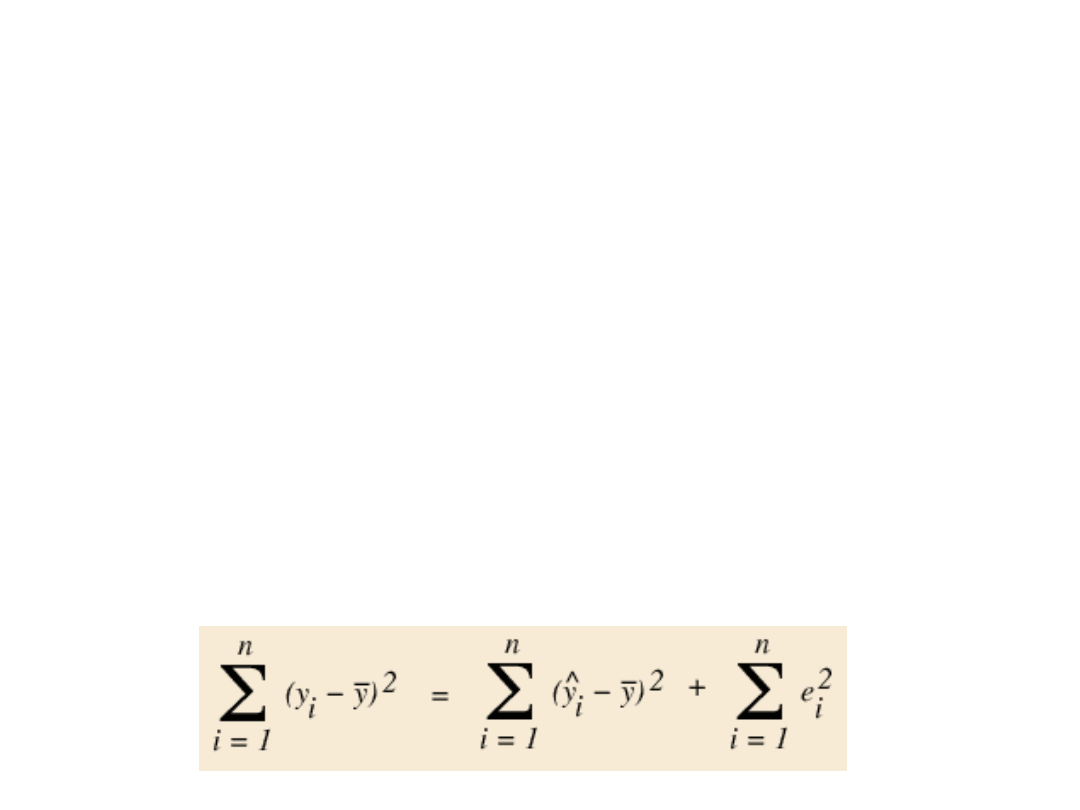
Współczynnik determinacji

R^2

• Jest to liczba z przedziału <0, 1>. R2

równe 1 oznacza doskonałe dopasowanie,

natomiast wartość R2 równa 0 - brak

powiązania między zmiennymi.

• Punktem wyjścia do utworzenia takiej

miary jest badanie sumy kwadratów

odchyleń poszczególnych obserwacji yi od

ich średniej. Można pokazać, że:

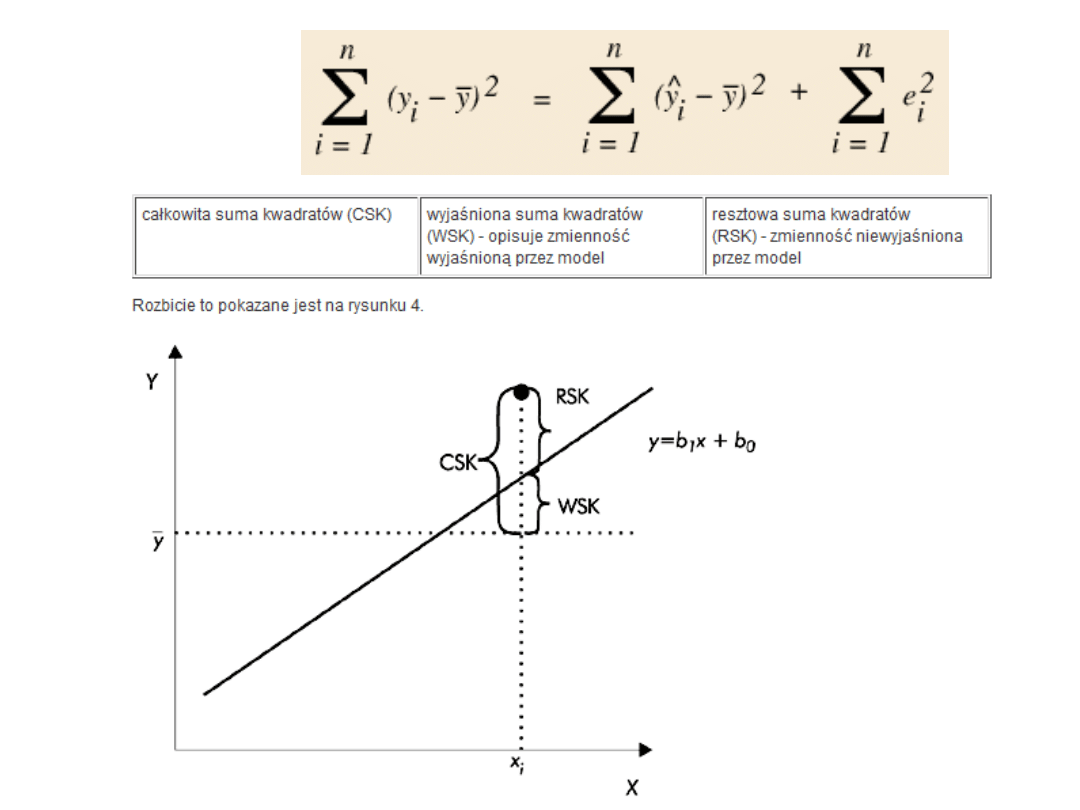
R^2

R^2

• Jako współczynnik determinacji przyjmujemy

stosunek zmienności wyjaśnionej do zmienności

całkowitej.

• Otrzymujemy więc: R2 = WSK/CSK

• Współczynnik determinacji mierzy, jaka część ogólnej

zmienności zmiennej zależnej jest wyjaśniona przez

regresję liniową. Tej miary dopasowania używamy

tylko dla regresji liniowej. Symbol R2 wziął się

stąd, że w modelu liniowym współczynnik

determinacji jest równy kwadratowi

współczynnika korelacji. Wartość R2 znajdziemy w

arkuszu wyników. W naszym przykładzie wartość ta

wynosi R2 = 0,483. Można ją wyrazić w procentach,

mówiąc że model wyjaśnia 48,3% zaobserwowanej

zmienności, a nie wyjaśnia 51,7% zmienności.

Kolejny przykład

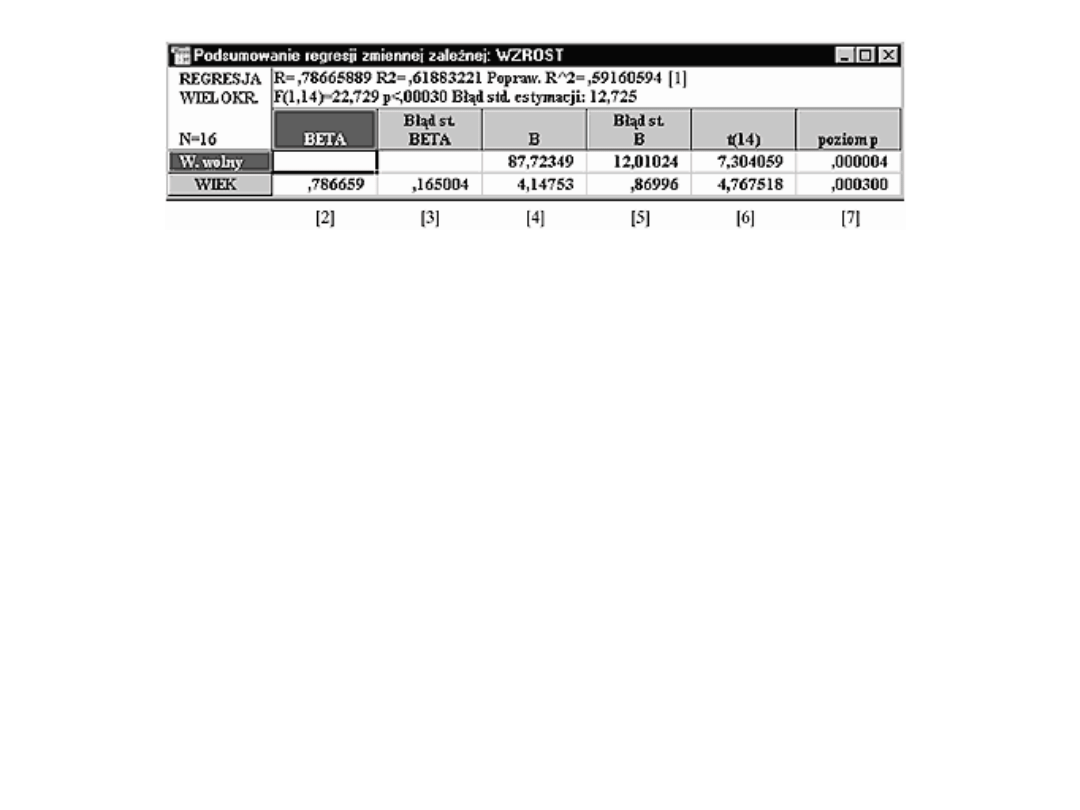
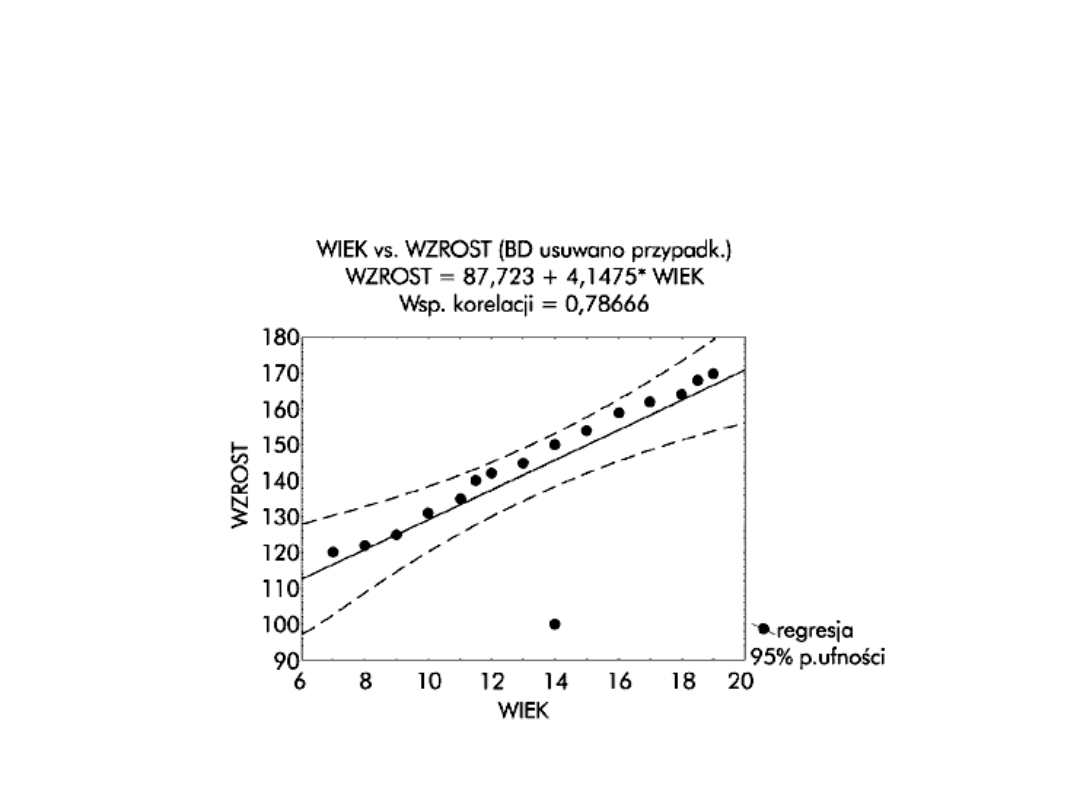
Współczynniki regresji to kolumna

oznaczona [4]. Pierwszy wiersz to

wartość stała b0, a drugi to

współczynnik b1. Tak więc poszukiwany

model ma postać:

• WZROST = 4,14753 × WIEK + 87,72349
• Parametr b0 wynosi 4,14753, co

oznacza, że jeśli wartość zmiennej WIEK

wzrośnie o jedną jednostkę (w naszym

przykładzie o rok), to oczekujemy, że

WZROST zwiększy się o 4,14753 cm.

Błąd estymacji

• W praktyce nie dysponujemy pełną informacją o populacji generalnej.

Otrzymujemy więc funkcję regresji wyliczoną metodą najmniejszych

kwadratów w oparciu o dane z losowej próby. Ta funkcja regresji, zwana

empiryczną, jest aproksymacją regresji w całej populacji. Wiąże się z tym

problem oceny rozbieżności między wartościami zmiennej niezależnej yi a

wartościami wyliczonymi z modelu. Różnice opisujące tę rozbieżność noszą

nazwę reszt. Im reszty są mniejsze, tym bliżej wartości empirycznej yi są

wartości przewidywane przez model. Najlepiej by było, gdyby reszty były

równe zero, ale w praktyce nigdy tak się nie zdarza. Nasuwa to koncepcję,

aby jako miarę omawianej rozbieżności potraktować odchylenie standardowe

reszt ei. W statystyce bowiem precyzję estymatora oddaje jego wariancja.

Tak też jest w istocie - wielkość ta, zwana błędem standardowym estymacji i

oznaczana jako Se, informuje o przeciętnej wielkości odchyleń empirycznych

wartości zmiennej zależnej od wartości wyliczonych z modelu

(teoretycznych). Jest to ważny parametr w analizie regresji, ponieważ

stanowi miarę rozproszenia elementów populacji wokół linii regresji.

Odchylenie standardowe reszt mówi więc nam o stopniu "dopasowania"

modelu do danych empirycznych. Im Se mniejsze, tym lepiej dopasowany

model. Wartość tę znajdziemy w dwóch miejscach, w oknie Wyniki regresji

wielokrotnej oraz powtórzoną w arkuszu wyników w polu oznaczonym

numerem [1]. W naszym przypadku wartość ta wynosi Se = 12,725. Oznacza

to, że przewidywane wartości zmiennej WZROST różnią się od wartości

empirycznych średnio o 12,725 cm.

Błędy współczynników

• Wyliczone współczynniki regresji b0 i b1 są, jak

wiemy, oszacowaniami współczynników regresji dla

całej populacji. Nasuwa się więc pytanie, jakim

błędem są one obciążone. Odpowiedzi na nie

udziela średni błąd szacunku parametru. Stanowi on

oszacowanie średniej rozbieżności między

parametrami modelu a jego możliwymi ocenami.

Pamiętajmy - im mniejszy średni błąd szacunku, tym

lepiej. Wartości te znajdziemy w arkuszu wyników

(rys. 3) w polu oznaczonym numerem [5]. Dla

naszego przykładu:

• oceny parametru b1(b) odchylają się od tego

parametru o Sb1 = 0,86996

• oceny parametru b0(a) odchylają się od tego

parametru o Sb0 = 12,01024.

• Szacując współczynnik kierunkowy na poziomie

4,14753, mylimy się więc średnio o 0,869.

Podobnie szacując wyraz wolny na poziomie

87,723, mylimy się średnio o 12,01. Można

zapytać, czy to dużo czy mało?

• To zależy od wartości współczynników. Dla

parametru b1 błąd szacunku stanowi około 21%

(0,86996/4,14753 0,21), natomiast dla wyrazu

wolnego - około 14% (12,01024/87,723 0,14).

Jeżeli wartość jest bliska 100% lub większa,

precyzja jest bardzo niezadowalająca. Wartości

ponad 50% powinny już zwrócić naszą uwagę na

inne oceny modelu. Przyjęło się wielkości Sb

zapisywać w nawiasach pod ocenami parametrów

modelu. Dla naszego przykładu mamy więc:

• WZROST = 4,14753 × WIEK + 87,72349 ± 12,725

                (0,86996)               (12,01024)