Transport entropii

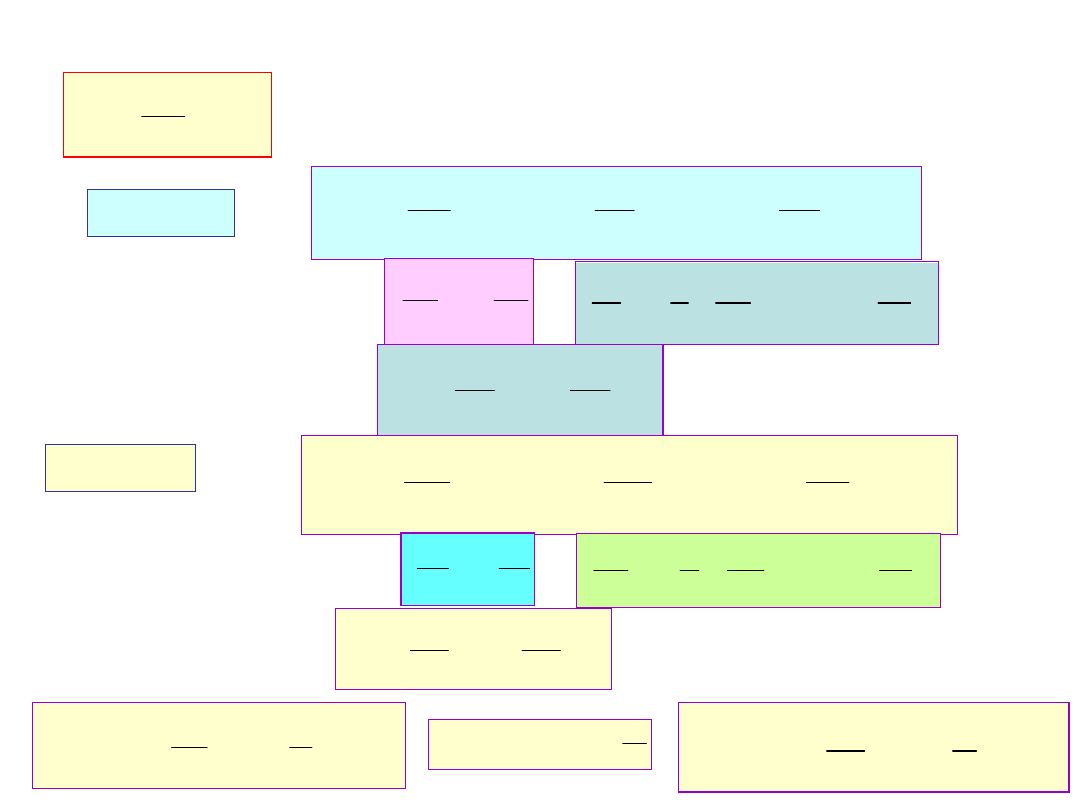
S

-entropia, odróżnia procesy odwracalne

dS = Qel /T

od nieodwracalnych

dS Qel /T

d

d

el

i

Q

S

S

T

=

+

d

i

S

-produkcja entropii wewnątrz układu

dS

- transport entropii z otoczenia

def

,

,

,

d

d

d

d

p

p T

T

S

S

S

S

T

p

T

p

x

x

x

x

� �

� �

�

�

�

� �

=

+

+

� �

� �

� �

�

�

�

� �

� �

� �

S (T,p,)

p

p

C

S

T

T

�

� �=

� �

�

� �

1

p

T

T

S

H

V

V

p

T

p

T

�

�

� �

� �

�

�

�

� �

=

-

=-

�

�

� �

� �

� �

�

�

�

� �

�

�

� �

� �

�

�

d

d

d

p

C

nR

S

T

p

T

p

=

-

(

)

( )

,

ln

p

T p

T

R

p

=

-

d

d

S

S

S (T,V,



)

,

,

,

d

d

d

d

V

T

V T

S

S

S

S

T

V

T

V

x

x

x

x

� �

�

�

�

� �

� �

=

+

+

� �

� �

� �

�

�

�

� �

� �

� �

V

V

C

S

T

T

�

� �=

� �

�

� �

1

T

T

V

S

U

p

p

V

T

V

T

�

�

�

�

�

� �

�

�

� �

=

+

=

�

�

� �

�

�

� �

�

�

�

� �

�

�

� �

�

�

d

d

d

V

C

nR

S

T

V

T

V

=

+

(

)

,

d

d

o

V

C

R

S T V

T

V b

T

V

=

+

+

�

�

(

)

,

d

d

'

o
p

C

R

S T p

T

p b

T

p

=

-

+

�

�

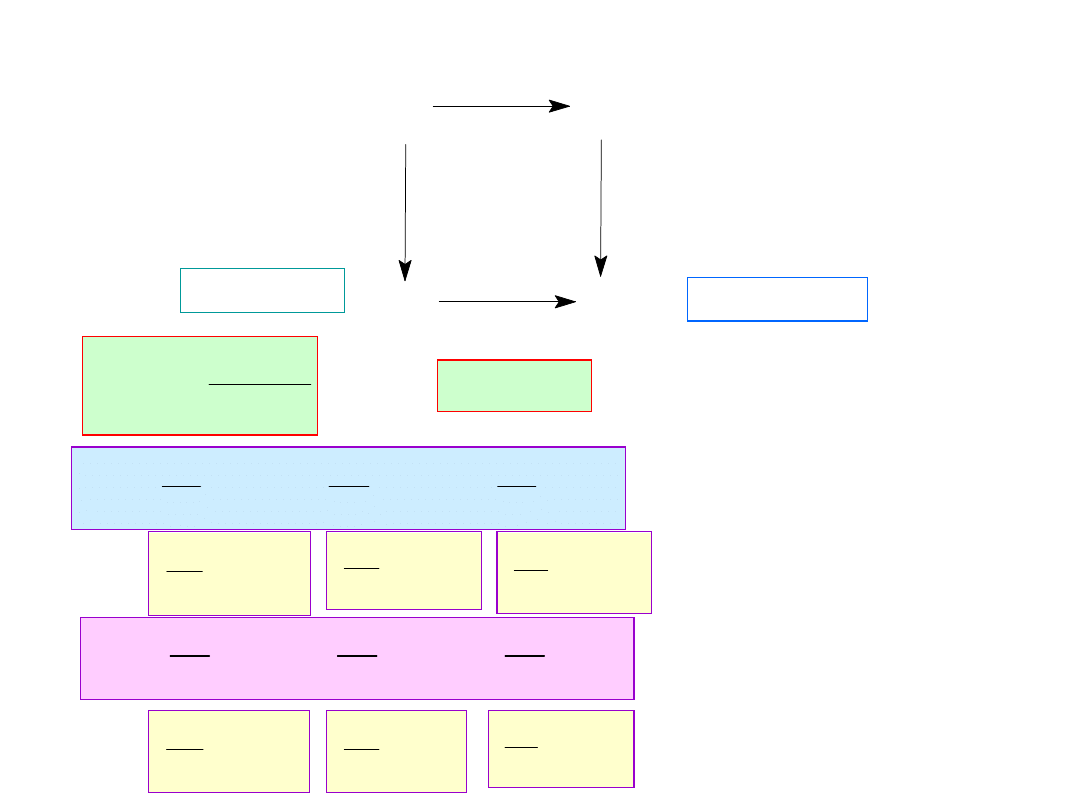
+ pV

+ pV

-TS

-TS

U

H

F

G

H,G (T,p,

)

U,F (T,V,

)

F = U TS

G = H  TS

. .,

. .,

. .,

p f k

p f k

p f k

H

S

T

D

D

=

,

,

,

d

d

d

d

V

T

V T

F

F

F

F

T

V

T

V

x

x

x

x

� �

�

�

�

� �

� �

=

+

+

� �

� �

� �

�

�

�

� �

� �

� �

,

V

F

S

T

x

�

� � =-

� �

�

� �

,

T

F

p

V

x

�

� � =-

� �

�

� �

,

V T

F

A

x

� �

�

=-

� �

�

� �

,

,

,

d

d

d

d

p

T

p T

G

G

G

G

T

V

T

p

x

x

x

x

� �

� �

�

�

�

� �

=

+

+

� �

� �

� �

�

�

�

� �

� �

� �

,

p

G

S

T

x

�

� � =-

� �

�

� �

,

T

G

V

p

x

� �

�

=

� �

�

� �

,

V T

G

A

x

� �

�

=-

� �

�

� �

. .,

0

p f k

G

D

=

1.Mol tlenu o temperaturze 300 K rozprężono izotermicznie od V

1

= 10 dm

3

do V

2

= 20 dm

3

,

przy czym gaz przesunął tłok obciążony ciśnieniem 10

5

Pa. Obliczyć zmiany entropii układu i

otoczenia. Ile entropii wyprodukowano w tym procesie? Odp.: 5,76 J/K, -3,33 J/K, 2,43 J/K.

2. Obliczyć S układu, gdy trzy mole metanu (spełniającego parametry gazu doskonałego ogrzano

i sprężono od temp. 25

o

C i ciśnienia 1 atm do temp. 125

o

C i ciśnienia 5 atm. Odp.: -11,27 J/K.

3. Obliczyć entropię molową CO w 200ºC pod ciśnieniem 50,67·105 N/m

2

wiedząc, że w 25ºC i pod ciśnieniem 1 atm jest ona równa 197,9 J·mol

–1

K

–1

, oraz,

że:

= 28,41 + 4,10·10

–3

T – 0,46·105T

–2

[J·mol

–1

K

–1

]. Odp.: 179,06 J·mol

–1

K

–1

,CO

o
p

C

o

300

S

 

R

/

V

2

5

C

o



4. Obliczyć pracę i ciepło oraz zmiany energii wewnętrznej, entalpii, entropii, energii swobodnej

i entalpii swobodnej w procesie adiabatycznego, quasi-statycznego rozprężenia 1 mola CO

od objętości 1 dm

3

do objętości 10 dm

3

. Temperatura początkowa gazu wynosiła 300 K,

a jego entropia standardowa w tej temperaturze

= 198,0 JK

–1

mol

–1

. Przyjąć

Odp.: W = U = –3754 J, Q = 0, H = –5255 J, S = 0, F = 27,2 kJ, G = 25,7

kJ.

niezależne od temperatury.

5. Jak zmieni się entropia podczas przeprowadzenia 2 moli ciekłego amoniaku o
temperaturze –40ºC w amoniak gazowy o temperaturze 200ºC pod stałym ciśnieniem
1013,25 hPa mając dane:
C

p

(NH

3

, c) = 74,82 J·mol

–1

K

–1

C

p

(NH

3

, g) = 33,61 + 29,26·10

–4

T + 21,32·10

–6

T

2

J·mol

–1

K

–1

.

Molowe ciepło parowania amoniaku w temperaturze wrzenia 239,7 K i pod ciśnieniem 1 atm
wynosi H = 23,24 kJ/mol. Odp.: wzrośnie o 248,7 J/K

6. Obliczyć zmianę entropii, entalpii swobodnej i energii swobodnej podczas izotermicznego,
odwracalnego rozprężania 1 mola azotu od objętości 1 dm

3

do 10 dm

3

w temperaturze 273 K,

traktując azot jak gaz doskonały. Odp.: 19,14 J/K, -5,23 kJ/mol

2

3

o

p

298

o

S

7. Obliczyć W, S i G, gdy 0,5 mola helu o temperaturze 298 K pod ciśnieniem

zostaje odwracalnie ogrzane pod stałym ciśnieniem o 30 K. Hel traktować jak gaz doskonały. Przyjąć

= 126 J/mol·K. Odp.: –124,9 J; 0,997 J/K; –1957J

Odp.: T

2

=253,3 K,

8 . 2 mole metanu znajdujące się w warunkach standardowych (T

1

=298 K, p=10

5

Pa) rozpręża się
adiabatycznie przesuwając tłok obciążony ciśnieniem 4,0 · 10

4

Pa do wyrównania

ciśnień po obu
stronach tłoka. Obliczyć temperaturę końcową układu, oraz S i F tego procesu.

Metan spełnia
równanie stanu sztywnych kul (b = 42,8 · 10

−6

m

3

· mol

−1

). Standardowa molowa

entropia metanu
w temperaturze 298 K wynosi

o

S

298

1

2,213

S

J K

-

D =

�

kJ

F

29

,

13





= 186,19 J · K

−1

· mol

−1

.

9. Mol pary wodnej pod ciśnieniem 5,065·10

4

Pa w temperaturze 383 K

skomprymowano do ciśnienia
1,013·10

5

Pa, następnie ochłodzono pod stałym ciśnieniem do temperatury 373 K i

skroplono.
Obliczyć zmianę entropii i entalpii swobodnej wody traktując parę wodną jako gaz
doskonały.
W 373 K i ciśnieniu 1,013·10

5

Pa ciepło parowania wynosi 40,67 kJ/mol. Ciepło

molowe (Cp

o

)

przyjmuje się za równe 30,13+11,310

-3

T [J/molK] dla pary i za równe 75,31

[J/molK] dla wody

w całym zakresie temperatur. Wartość standardowej molowej entropii ciekłej wody
wynosi 66,56 J/molK,

pary wodnej 188,65 J/molK. Odp.: S = – 115,68 J/molK, G = 4121 J

10. Obliczyć zmianę entropii, gdy zmiesza się 100 g wody o temperaturze 10

o

C z 200

g wody
o temperaturze 40

o

C, aż do uzyskania stałej temperatury w naczyniu izolowanym

adiabatycznie.
Molowa pojemność cieplna wody wynosi 75,2 Jmol

-1

K

-1

Odp.:T

x

=303 K, S=1,397

JK

-1

.

1. Mol tlenu o temperaturze 300 K rozprężono izotermicznie od V

1

= 10 dm

3

do V

2

= 20 dm

3

,

przy czym gaz przesunął tłok obciążony ciśnieniem 10

5

Pa. Obliczyć zmiany entropii układu i

otoczenia. Ile entropii wyprodukowano w tym procesie? Odp.: 5,76 J/K, -3,33 J/K, 2,43 J/K.

2

1

ln

5,76 /

ukl

V

S

R

J K

V

D

=

=

5,76 /

ukl

i

Q

S

S

J K mol

T

D

= +D =

�

2

1

(

) 10

prac

Q

W p

V V

kJ

=-

=

-

=

4

10

3,33 /

300

Q

J K mol

T

=

=

�

2,43 /

i

S

J K mol

D =

�

d

d

d

V

T

S

S

S

T

V

T

V

�

�

� �

� �

=

+

� �

� �

�

�

� �

� �

V

V

S

C

T

T

�

� �=

� �

�

� �

T

V

S

p

nR

V

T

V

�

�

� � � �

=

=

� � � �

�

�

� � � �

2. Obliczyć S układu, gdy trzy mole metanu (spełniającego parametry gazu

doskonałego ogrzano
i sprężono od temp. 25

o

C i ciśnienia 1 atm do temp. 125

o

C i ciśnienia 5 atm. Odp.:

-11,27 J/K.

C

V

= 3R,

2

1

1

2

398

1

ln

ln

3

4ln

ln

11,27 /

298

5

p

T

p

S n C

R

R

J K

T

p

�

�

�

�

D =

+

= �

+

=-

�

�

�

�

�

�

�

�

d

d

d

p

T

S

S

S

T

p

T

p

� �

�

�

� �

=

+� �

� �

�

�

� �

� �

p

p

C

S

T

T

�

� �=

� �

�

� �

;

p

T

S

V

nR

p

T

p

� �

�

�

� �

=-

=-

� �

� �

�

�

� �

� �

3. Obliczyć entropię molową CO w 200ºC pod ciśnieniem 50,67·10

5

N/m

2

wiedząc,

że w 25ºC i pod ciśnieniem 1 atm jest ona równa 197,9 J·mol

–1

K

–1

, oraz, że:

,CO

p

C

d

= 28,41 + 4,10·10

–3

T – 0,46·10

5

T

–2

[J·mol

–1

K

–1

]. Odp.: 179,06 J·mol

–1

K

–1

(

)

5

5

1

5

(

)

50,7610

1,01310

1

473

298

2

473

473

473

5

1,01310

1

298

3

2

298

298

298

5

2

2

ln

0,46 10

28,41

ln

473

0,46 10

1

1

197,9

ln

473 298

298

2

473

298

pf

T

o
p CO

Pa

Pa

K

K

T

Pa

K

C

p

S

S

dT R

T

p

p

dT

S

dT

dT R

T

T

p

�

�

�

- 3

- 3

=

+

+

=

�

+

+ 4,1�

10

-

+

=

� �

�

+28,41

+4,1�

10

-

+

-

�

�

�

�

�

� �

�

5

5

1,013 10

ln

179,06 /

50,67 10

R

J K

�

+

=

�

o
300

S

 

R

/

V

2

5

C

o



4. Obliczyć pracę i ciepło oraz zmiany energii wewnętrznej, entalpii, entropii, energii swobodnej

i entalpii swobodnej w procesie adiabatycznego, quasi-statycznego rozprężenia 1 mola CO

od objętości 1 dm

3

do objętości 10 dm

3

. Temperatura początkowa gazu wynosiła 300 K,

a jego entropia standardowa w tej temperaturze

= 198,0 JK

–1

mol

–1

. Przyjąć

Odp.: W = U = –3754 J, Q = 0, H = –5255 J, S = 0, F = 27,2 kJ, G = 25,7

kJ.

niezależne od temperatury

7
5

p

V

C
C

k =

=

1

1

2

1

2

119,4

V

T

T

K

V

k -

� �

=

=

� �

� �

6

1

1

2,494 10

pocz

RT

p

Pa

V

=

=

�

(

)

2

1

3,754 /

o

V

W

U C T T

kJ mol

=D =

-

=-

(

)

2

1

5,255 /

o
p

H C T T

kJ mol

D =

-

=-

0



S

6

300

300

2,2494 10

ln

198

ln

171,36 /

pocz

p p

pocz

o

T

K

T

K

o

o

p

S

S

R

R

J mol K

p

p

=

=

=

�

=

-

=

-

=

�

3754 171,36 (119,4 300) 27,194 /

F

U S T

kJ mol

D =D - D =-

-

�

-

=

5255 171,36 (119,4 300) 25,69 /

G

H S T

kJ mol

D =D - D =-

-

�

-

=

2

1

( )

( )

pf

pf

T

T

o

o

o

p c

pf

p g

pf

T

T

C

H

C

S n

dT n

n

dT

T

T

T

D

D =

+

+

�

�

(

)

3

4

6

2

2

239,7

23,24 10

473,15

2 74,82ln

2

2 33,61ln

2 29,26 10 (473,15 239,7)

233,15

239,7

239,7

21,32 10

2

473,15 239,7

248,7 /

2

S

J K

-

-

�

D = �

+

+ �

+ �

� �

-

+

�

�

-

=

5.

Jak zmieni się entropia podczas przeprowadzenia 2 moli ciekłego amoniaku o

temperaturze –40ºC w amoniak gazowy o temperaturze 200ºC pod stałym ciśnieniem
1013,25 hPa mając dane:
C

p

(NH

3

, c) = 74,82 J·mol

–1

K

–1

C

p

(NH

3

, g) = 33,61 + 29,26·10

–4

T + 21,32·10

–6

T

2

J·mol

–1

K

–1

.

Molowe ciepło parowania amoniaku w temperaturze wrzenia 239,7 K i pod ciśnieniem 1 atm
wynosi H = 23,24 kJ/mol. Odp.: wzrośnie o 248,7 J/K

2

1

ln

19,14 /

V

S R

J K

V

D =

=

0

U

H

D =D =

273 19,14

5,23 /

F

G

T S

kJ mol

D =D =- D =-

�

=-

d

d

d

V

T

S

S

S

T

V

T

V

�

�

� �

� �

=

+

� �

� �

�

�

� �

� �

V

V

S

C

T

T

�

� �=

� �

�

� �

T

V

S

p

R

V

T

V

�

�

� � � �

=

=

� � � �

�

�

� � � �

6. Obliczyć zmianę entropii, entalpii swobodnej i energii swobodnej podczas izotermicznego,
odwracalnego rozprężania 1 mola azotu od objętości 1 dm

3

do 10 dm

3

w temperaturze 273 K,

traktując azot jak gaz doskonały. Odp.: 19,14 J/K, -5,23 kJ/mol

;

2

3

o

p

o

S

2

3

1

1

1,834 10

nRT

V

m

p

-

=

=

�

2

3

2

2

2,019 10

nRT

V

m

p

-

=

=

�

2

1

(

)

124,9

W

p V V

J

=-

-

=-

328

( )

298

0,997 /

o
p c

C

S n

dT

J K

T

D =

=

�

338

298

331,8

623,55 /

o
p

H n C dT

J

J mol

D =

=

=

�

2

3

1(

298 )

298

2

2

3

ln

126

ln

129,4 /

3

o

o

p

p

o

T

K

T

K

o

p

S

S

R

R

J mol K

p

=

=

=

=

-

=

-

=

�

2

1

129,4 2 0,997 131,4 /

S

S

S

J mol K

= +D =

+ �

=

�

2 2

1 1

(

)

3914,45 /

G

H

T S TS

J mol

D =D -

-

=-

1

3914,45

1957

2

G

J

J

D =- �

=-

7. Obliczyć W, S i G, gdy 0,5 mola helu o temperaturze 298 K pod ciśnieniem

zostaje odwracalnie ogrzane pod stałym ciśnieniem o 30 K. Hel traktować jak gaz doskonały.

Przyjąć:

= 126 J/mol·K. Odp.: –124,9 J; 0,997 J/K; –1957J

o

S

298

1

4,426

S

J K

-

D =

�

kJ

F

29

,

13





2

1

1

2

2

1

1

3 1

253,3

4 4

V

V

p

T C

R

p

p

T

T

K

C

R

p

�

�

+

�

�

�

�

�

�

=

=

+

=

�

�

+

�

�

2

1

1

2

ln

ln

4,426 /

p

T

p

S n C

R

J K

T

p

�

�

D =

+

=

�

�

�

�

2

1

1

2

ln

ln

2,213 /

p

T

p

S C

R

J mol K

T

p

D =

+

=

�

)

(

1

1

2

2

S

T

S

T

U

F























1

1

1

2

1

2

S

nT

S

n

nS

T

T

T

nC

F

V















(

)

(

)

2 3 253,3 298

253,3 2 186,19 4,427

2 298 186,19

13294

F

R

J

D = �

-

-

�

+

- � �

=

�

�

�

�

2

1

2

1

2

1

2

1

2

2

1

d

(

)

(

)

T

V

V

prac

T

T

T

U n C T nC T T

p

V V

p nR

p

p

D

�

�

=

=

-

=-

-

=-

-

�

�

�

�

�

1

2

1

2

1

2

;

nRT

nRT

V

nb V

nb

p

p

=

+

=

+

d

d

d

p

T

S

S

S

T

p

T

p

� �

�

�

� �

=

+

� �

� �

�

�

� �

� �

p

p

C

S

T

T

�

� �=

� �

�

� �

p

T

S

V

R

p

T

p

� �

�

�

� �

=-

=-

� �

� �

�

�

� �

� �

d

d

d

V

T

S

S

S

T

V

T

V

�

�

� �

� �

=

+

� �

� �

�

�

� �

� �

V

V

S

C

T

T

�

� �=

� �

�

� �

T

V

S

p

R

V

T

V

�

�

� � � �

=

=

� � � �

�

�

� � � �

8 . 2 mole metanu znajdujące się w warunkach standardowych (T

1

=298 K, p=10

5

Pa) rozpręża się

adiabatycznie przesuwając tłok obciążony ciśnieniem 4,0 · 10

4

Pa do wyrównania ciśnień po obu

stronach tłoka. Obliczyć temperaturę końcową układu, oraz S i F tego procesu. Metan spełnia

równanie stanu sztywnych kul (b = 42,8 · 10

−6

m

3

· mol

−1

). Standardowa molowa entropia metanu

w temperaturze 298 K wynosi

= 186,19 J · K

−1

· mol

−1

.

C

V

= 3R

;

;

;

;

Odp.: T

2

=253,3 K

2

1

373

,

1

,

2

383

373

ln

ln

115,68 /

373

383

373

p

o
p pary

par

par

o
p pary

p

C

H

H

R

p

S

dp

dT

R

C

J mol K

p

T

p

D

D

D =-

+

-

=

+

-

=-

�

�

�

(

)

373

3

2

2

3

,

383

11,3 10

30,13 ( 10)

373 383

40,67 10

41,057 /

2

o
p pary

par

H

C

dT

H

kJ mol

-

�

D =

- D

=

�-

+

-

-

� =-

�

4

4

5

5

383

5.06510

,

5.06510

1,01310

1,(

, 383 )

,( 298 )

298

1,01310

3

383

188,65 30,13ln

11,3 10 (383 298)

ln0,5 202,93 /

298

o

Pa

p pary

p

Pa

p

Pa

para T

K

para t

K

Pa

C

R

S

S

dT

dp

T

p

R

J mol K

�

=

�

=

�

=

=

�

-

=

+

-

=

+

+

�

-

-

=

�

�

�

2 2

1 1

(

)

G

H

T S TS

D =D -

-

2

1

1 1

[ (

)

]

41057 [373(202,93 115,68) 383 202,93] 4121

G

H T S

S TS

J

D =D -

+D -

=-

-

-

-

�

=

9. Mol pary wodnej pod ciśnieniem 5,065·10

4

Pa w temperaturze 383 K skomprymowano do ciśnienia

1,013·10

5

Pa, następnie ochłodzono pod stałym ciśnieniem do temperatury 373 K i skroplono.

Obliczyć zmianę entropii i entalpii swobodnej wody traktując parę wodną jako gaz doskonały.
W 373 K i ciśnieniu 1,013·10

5

Pa ciepło parowania wynosi 40,67 kJ/mol. Ciepło molowe (C

p

o

)

przyjmuje się za równe 30,13+11,310

-3

T [J/molK] dla pary i za równe 75,31 [J/molK] dla wody

w całym zakresie temperatur. Wartość standardowej molowej entropii ciekłej wody wynosi 66,56 J/molK,

pary wodnej 188,65 J/molK. Odp.: S = – 115,68 J/molK, G = 4121 J

G = H  TS;

1 1

2 2

1

2

303

x

nT n T

T

K

n n

+

=

=

+

1

2

303

303

1

1

2

283

313

100 75,2

200 75,2

1,397

18

18

x

x

T

T

o

o

p

p

T

T

C

C

S n

dT n

dt

dT

dT

J K

T

T

T

T

-

D =

+

=

+

=

�

�

�

�

�

10. Obliczyć zmianę entropii, gdy zmiesza się 100 g wody o temperaturze 10

o

C z 200 g wody

o temperaturze 40

o

C, aż do uzyskania stałej temperatury w naczyniu izolowanym adiabatycznie.

Molowa pojemność cieplna wody wynosi 75,2 Jmol

-1

K

-1

Odp.:T

x

=303 K, S=1,397 JK

-1

.