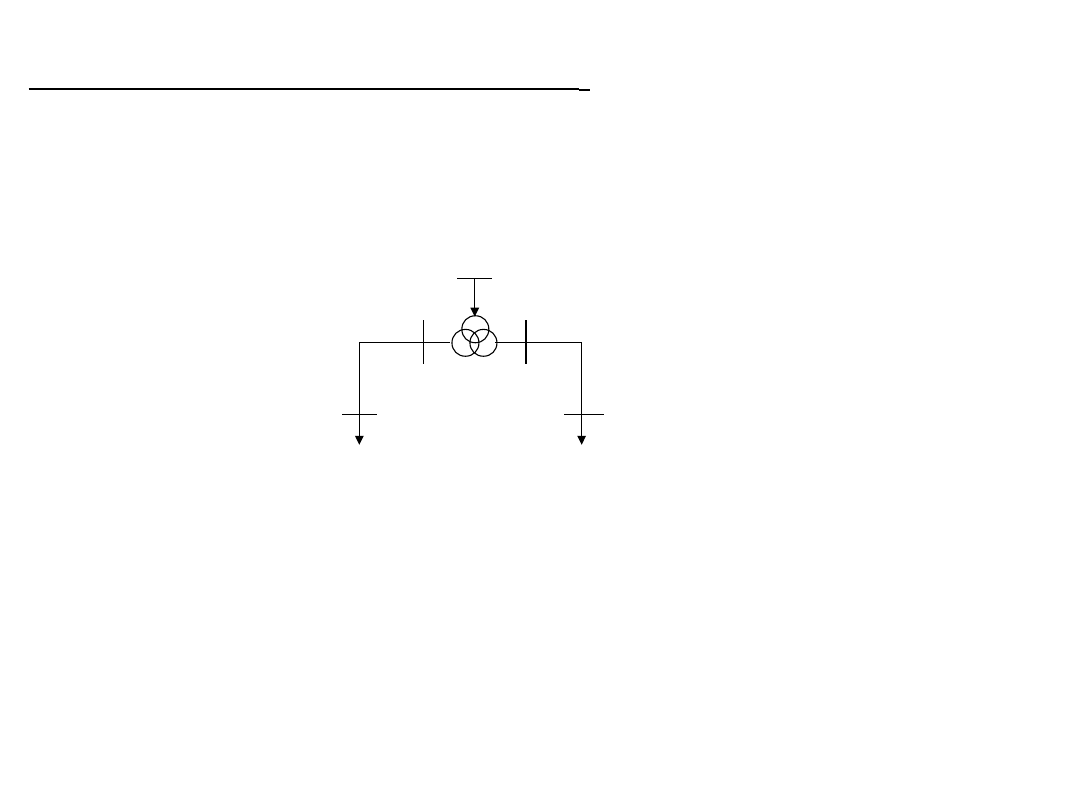
Transformatory trójuzwojeniowe

Transformator trójuzwojeniowy sprzęga ze sobą trzy sieci o różnych
poziomach napięć.

Schemat ideowy

110 kV

15 kV 6
kV

Stosunek mocy znamionowych poszczególnych uzwojeń wynosi
najczęściej 100:100:100 lub 100:67:67.

Dla transformatora trójuzwojeniowego napięcia zwarcia są podawane dla
poszczególnych par uzwojeń, jako wynik pomiaru napięcia na zaciskach
jednego z uzwojeń przy zwartym i obciążonym prądem znamionowym
uzwojeniu wtórnym oraz otwartym trzecim uzwojeniu. Podobnie (dla
poszczególnych par uzwojeń) są podawane straty napięcia na rezystancji
lub straty mocy w miedzi.

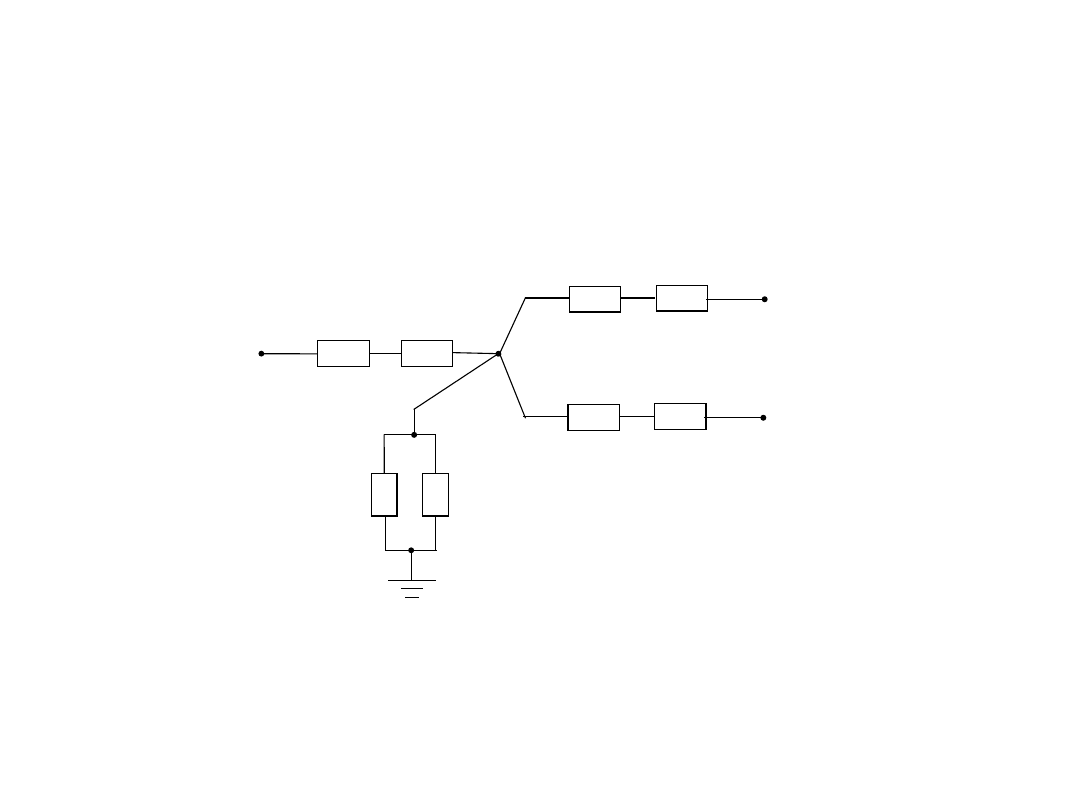
Schemat zastępczy transformatora trójuzwojeniowego

2

T

R

2

T

jX

1

T

R

1

T

jX

3

T

jX

3

T

R

T

G

T

jB

W celu obliczenia parametrów schematu zastępczego są niezbędne
następujące dane:

znamionowa przekładnia , , kV/kV/kV,

moc znamionowa

S

n

, MV

.

A,

napięcie zwarcia poszczególnych par uzwojeń , ,
, %,

straty mocy czynnej w parach uzwojeń , , (lub

dla poszczególnych par uzwojeń), % (lub kW),

prąd biegu jałowego

I

0%

, %,

straty mocy czynnej magnesowania , kW.

3

n

2

n

1

n

U

/

U

/

U





12

%

z

U



13

%

z

U



23

%

z

U



12

%

Cu

P



13

%

Cu

P



23

%

Cu

P



Fe

P



Cu

P



Rezystancja pary uzwojeń 1 i 2 jest równa sumie rezystancji
poszczególnych uzwojeń

Rezystancje uzwojeń

2

T

1

T

12

R

R

R





dla pozostałych par uzwojeń

3

T

1

T

13

R

R

R





3

T

2

T

23

R

R

R





R

12

, R

13

, R

23

– rezystancje poszczególnych par uzwojeń,

R

T1

, R

T2

, R

T3

– rezystancje poszczególnych uzwojeń.

n

2
n

12

%

Cu

12

S

100

U

P

R





n

2
n

13

%

Cu

13

S

100

U

P

R





n

2
n

23

%

Cu

23

S

100

U

P

R





%

100

S

P

P

n

12

Cu

12

%

Cu









%

100

S

P

P

n

13

Cu

13

%

Cu









%

100

S

P

P

n

23

Cu

23

%

Cu









2

T

1

T

12

R

R

R





3

T

1

T

13

R

R

R





3

T

3

T

23

R

R

R





2

R

R

R

R

23

T

13

T

12

T

1

T







2

R

R

R

R

13

T

23

T

12

T

2

T







2

R

R

R

R

12

T

23

T

13

T

3

T







Rezystancje poszczególnych uzwojeń

Reaktancja pary uzwojeń 1 i 2 jest równa sumie reaktancji
poszczególnych uzwojeń

Reaktancje uzwojeń

2

T

1

T

12

X

X

X





dla pozostałych par uzwojeń

3

T

1

T

13

X

X

X





3

T

2

T

23

X

X

X





X

12

, X

13

, X

23

– reaktancje poszczególnych par uzwojeń,

X

T1

, X

T2

, X

T3

– reaktancje poszczególnych uzwojeń.

n

2
n

12

%

X

12

S

100

U

U

X





n

2
n

13

%

X

13

S

100

U

U

X





n

2
n

23

%

X

23

S

100

U

U

X





2

12

%

Cu

2

12

%

z

12

%

X

P

U

U











2

13

%

Cu

2

13

%

z

13

%

X

P

U

U











2

23

%

Cu

2

23

%

z

23

%

X

P

U

U











2

T

1

T

12

X

X

X





3

T

1

T

13

X

X

X





3

T

3

T

23

X

X

X





Reaktancje poszczególnych uzwojeń

2

X

X

X

X

23

T

13

T

12

T

1

T







2

X

X

X

X

13

T

23

T

12

T

2

T







2

X

X

X

X

12

T

23

T

13

T

3

T







Konduktancja i susceptancja G

T

i B

T

Parametry poprzeczne schematu zastępczego transformatora
trójuzwojeniowego oblicza się tak samo, jak dla transformatora
dwuuzwojeniowego

3

2
n

Fe

T

10

U

P

G









2
n

n

%

0

T

U

100

S

I

B 

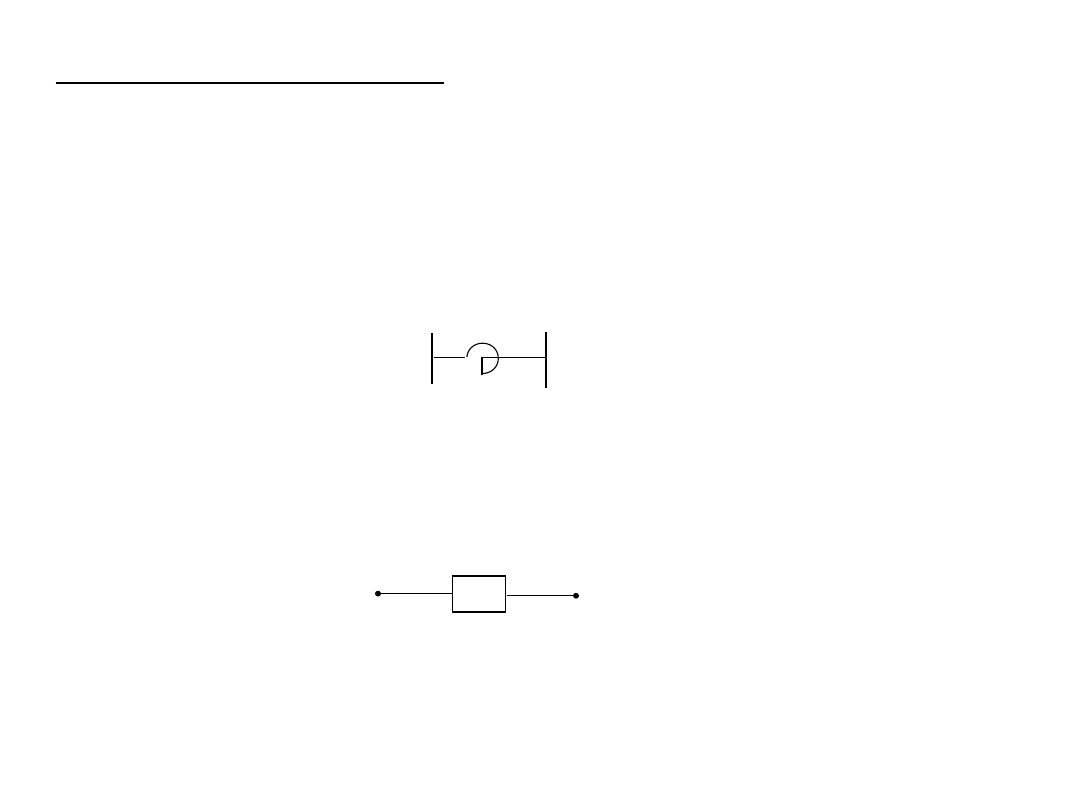
W Polsce stosuje się w sieciach średnich napięć tzw. dławiki
przeciwzwarciowe, służące do ograniczania prądów zwarciowych.

Dławiki i kondensatory

Schemat ideowy dławika

Schemat zastępczy dławika

jX

D

n

n

%

z

D

I

3

U

100

U

X





U

z%

napięcie zwarcia, %,

U

n

– napięcie znamionowe dławika, kV,

I

n

– prąd znamionowy dławika, A.

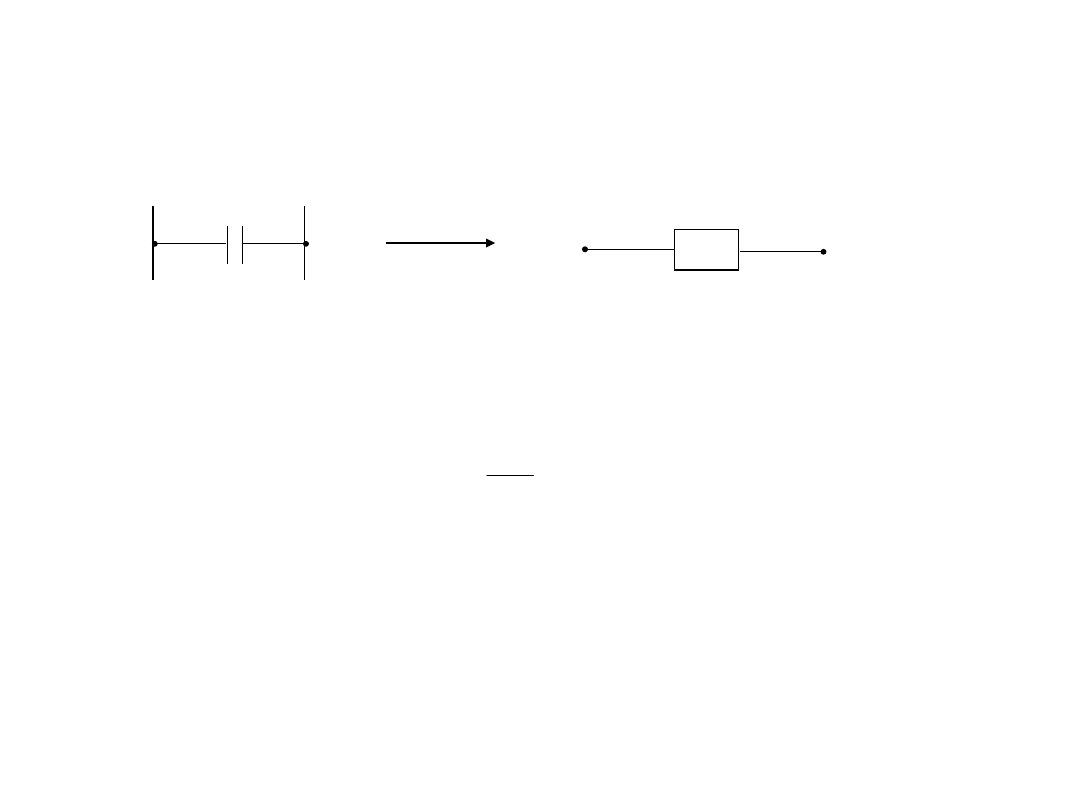
W sieciach elektroenergetycznych są stosowane kondensatory szeregowe,
służące do kompensacji reaktancji indukcyjnej linii.

jX

C

Reaktancja kondensatora szeregowego

2
n

n

C

I

3

Q

X 

Q

n

– moc znamionowa bierna kondensatora, Mvar, I

n

– prąd znamionowy,

kA.

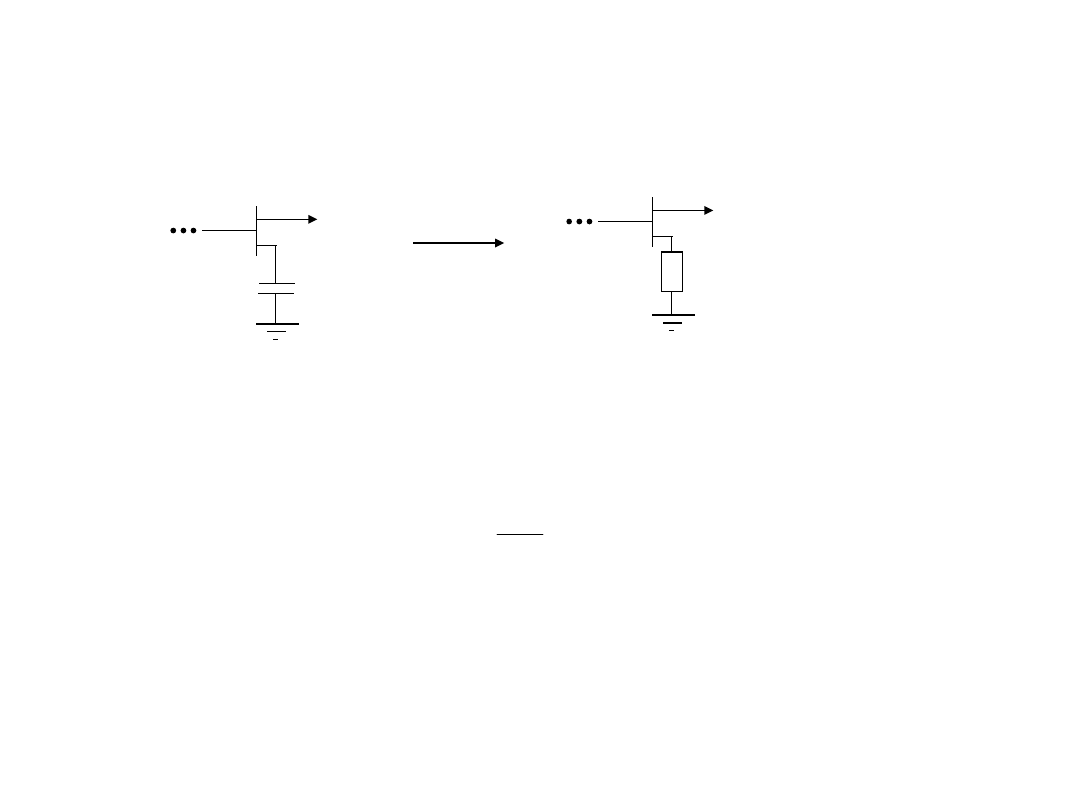
W systemie stosuje się baterie trójfazowych kondensatorów
równoległych, przyłączonych do węzłów sieci, stanowiących dodatkowe
źródło mocy biernej.

jX

C

Reaktancja pojemnościowa baterii

n

2
n

C

Q

U

X 

Generatory

Generator w obliczeniach stanów ustalonych nie jest przedstawiany
jako element fizyczny, ale jako wymuszenie węzłowe i może być
reprezentowany dwojako:

          przez moc czynną i moduł napięcia,
          przez moc czynną i bierną.
Moc czynna wynika z planowania wytwarzania, natomiast moduł
napięcia lub moc bierna wynikają z minimalizacji przesyłowych strat
mocy oraz badania stabilności systemu.

Odbiory

W obliczeniach stanów ustalonych odbiory są reprezentowane przez
moc czynną P i moc bierną Q w węzłach odbiorczych, które są znane z
prognozowania zapotrzebowania na moc przez odbiorców.