WIELOCZYNNIKOWA

WIELOCZYNNIKOWA

ANALIZA WARIANCJI

ANALIZA WARIANCJI

PRÓBY ZALEŻNE

PRÓBY ZALEŻNE

ZASTOSOWANIE PROCEDURY

ZASTOSOWANIE PROCEDURY

POWTARZANYCH POMIARÓW

POWTARZANYCH POMIARÓW

ZALETY

ZALETY



REDUKUJE WIELKOŚĆ WARIANCJI

REDUKUJE WIELKOŚĆ WARIANCJI

NIEWYJAŚNIONEJ

NIEWYJAŚNIONEJ

(SPOWODOWANEJ RÓŻNICAMI

(SPOWODOWANEJ RÓŻNICAMI

INDYWIDUALNYMI)

INDYWIDUALNYMI)



ZWIĘKSZA TO MOC WYKRYWANIA

ZWIĘKSZA TO MOC WYKRYWANIA

EFEKTU (MOC TESTU - ZMNIEJSZA

EFEKTU (MOC TESTU - ZMNIEJSZA

SIĘ RYZYKO BŁĘDU II RODZAJU)

SIĘ RYZYKO BŁĘDU II RODZAJU)



PROCEDURA BARDZO

PROCEDURA BARDZO

EKONOMICZNA – WYSTARCZA

EKONOMICZNA – WYSTARCZA

MNIEJSZA LICZBA BADANYCH

MNIEJSZA LICZBA BADANYCH

WADY

WADY



TRUDNA DO ZASTOSOWANIA GDY EFEKT

TRUDNA DO ZASTOSOWANIA GDY EFEKT

MANIPULACJI JEST DŁUGOTRWAŁY

MANIPULACJI JEST DŁUGOTRWAŁY



ZMIANA NASTAWIENIA OSÓB BADANYCH

ZMIANA NASTAWIENIA OSÓB BADANYCH

NA SKUTEK UCZENIA SIĘ SYTUACJI

NA SKUTEK UCZENIA SIĘ SYTUACJI

EKSPERYMENTALNYCH

EKSPERYMENTALNYCH



MOŻLIWOŚĆ ZMĘCZENIA BADANYCH

MOŻLIWOŚĆ ZMĘCZENIA BADANYCH



ZWIĘKSZA SIĘ PRAWDOPODOBIEŃSTWO

ZWIĘKSZA SIĘ PRAWDOPODOBIEŃSTWO

ODGADNIĘCIA HIPOTEZ

ODGADNIĘCIA HIPOTEZ



EFEKTY KOLEJNOŚCI – POTRZEBA

EFEKTY KOLEJNOŚCI – POTRZEBA

WYRÓWNANIA KOLEJNOŚCI WARUNKÓW

WYRÓWNANIA KOLEJNOŚCI WARUNKÓW

Niespełniony jest warunek

Niespełniony jest warunek

niezależności pomiarów, co

niezależności pomiarów, co

zmniejsza rzetelność statystyki

zmniejsza rzetelność statystyki

F

F

Dane zebrane w różnych warunkach

Dane zebrane w różnych warunkach

eksperymentalnych są zależne od siebie,

eksperymentalnych są zależne od siebie,

gdyż pochodzą od tych samych badanych.

gdyż pochodzą od tych samych badanych.

Dlatego też wprowadza się nowe

Dlatego też wprowadza się nowe

założenie o

założenie o

sferyczności

sferyczności

, które oznacza,

, które oznacza,

że stopień zależności pomiędzy każdą

że stopień zależności pomiędzy każdą

parą warunków eksperymentalnych jest

parą warunków eksperymentalnych jest

taki sam. To taki odpowiednik

taki sam. To taki odpowiednik

homogeniczności w modelach

homogeniczności w modelach

niezależnych. Żadna para

niezależnych. Żadna para

eksperymentalnych warunków nie może

eksperymentalnych warunków nie może

być bardziej zależna od drugiej.

być bardziej zależna od drugiej.

JAK MIERZY SIĘ SFRYCZNOŚĆ

JAK MIERZY SIĘ SFRYCZNOŚĆ

(

(

ε

ε

– epsilon) ?

– epsilon) ?

TRZEBA OBLICZYĆ RÓŻNICE MIĘDZY

TRZEBA OBLICZYĆ RÓŻNICE MIĘDZY

PARAMI GRUP, A NASTĘPNIE OBLICZYĆ

PARAMI GRUP, A NASTĘPNIE OBLICZYĆ

WARIANCJE TYCH RÓŻNIC.

WARIANCJE TYCH RÓŻNIC.

wariancja

wariancja

A-B

A-B

~ wariancja

~ wariancja

A-C

A-C

~ wariancja

~ wariancja

B-C

B-C

SPSS MA W SWYCH ZASOBACH TEST,

SPSS MA W SWYCH ZASOBACH TEST,

KTÓRY POZWALA NA TESTOWANIE

KTÓRY POZWALA NA TESTOWANIE

SFERYCZNOŚCI – TEST MAUCHLY’EGO.

SFERYCZNOŚCI – TEST MAUCHLY’EGO.

JEŚLI JEST ISTOTNY OZNACZA, ŻE SĄ

JEŚLI JEST ISTOTNY OZNACZA, ŻE SĄ

RÓŻNICE MIĘDZY WARIANCJMI RÓŻNIC I

RÓŻNICE MIĘDZY WARIANCJMI RÓŻNIC I

WTEDY ZAŁOŻENIE O SFERYCZNOŚCI NIE

WTEDY ZAŁOŻENIE O SFERYCZNOŚCI NIE

JEST SPEŁNIONE.

JEST SPEŁNIONE.

POWTARZANE POMIARY W

POWTARZANE POMIARY W

ANALIZIE JEDNOCZYNNIKOWEJ

ANALIZIE JEDNOCZYNNIKOWEJ

OTWIERAMY BAZĘ

OTWIERAMY BAZĘ

„WYKŁADOWCY”

„WYKŁADOWCY”

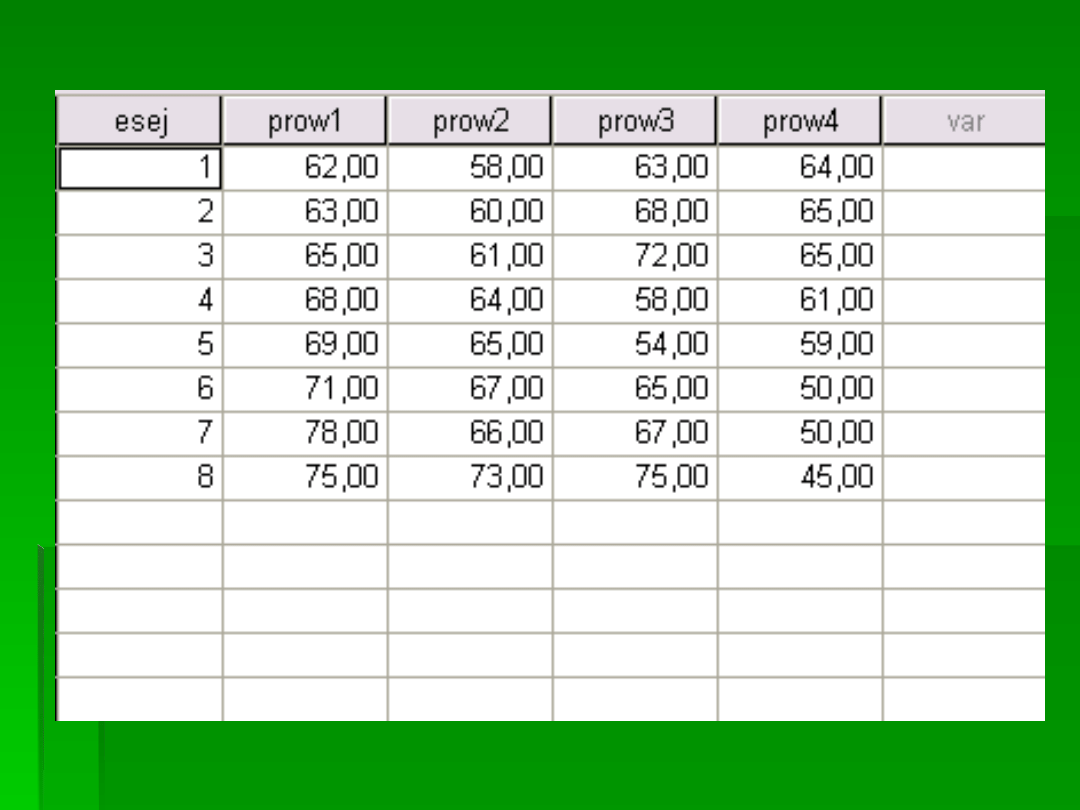
STUDENCI CHCIELI

STUDENCI CHCIELI

PORÓWNAĆ, W JAKI

PORÓWNAĆ, W JAKI

SPOSÓBRÓŻNI PROWADZĄCY

SPOSÓBRÓŻNI PROWADZĄCY

OCENIĄ TE SAME PRACE.

OCENIĄ TE SAME PRACE.

PRZEDSTAWILI 4

PRZEDSTAWILI 4

PROWADZĄCYM TE SAME 8

PROWADZĄCYM TE SAME 8

ESEJÓW, CZYLI KAŻDY

ESEJÓW, CZYLI KAŻDY

PROWADZĄCY OCENIAŁ

PROWADZĄCY OCENIAŁ

KAŻDY ESEJ.

KAŻDY ESEJ.

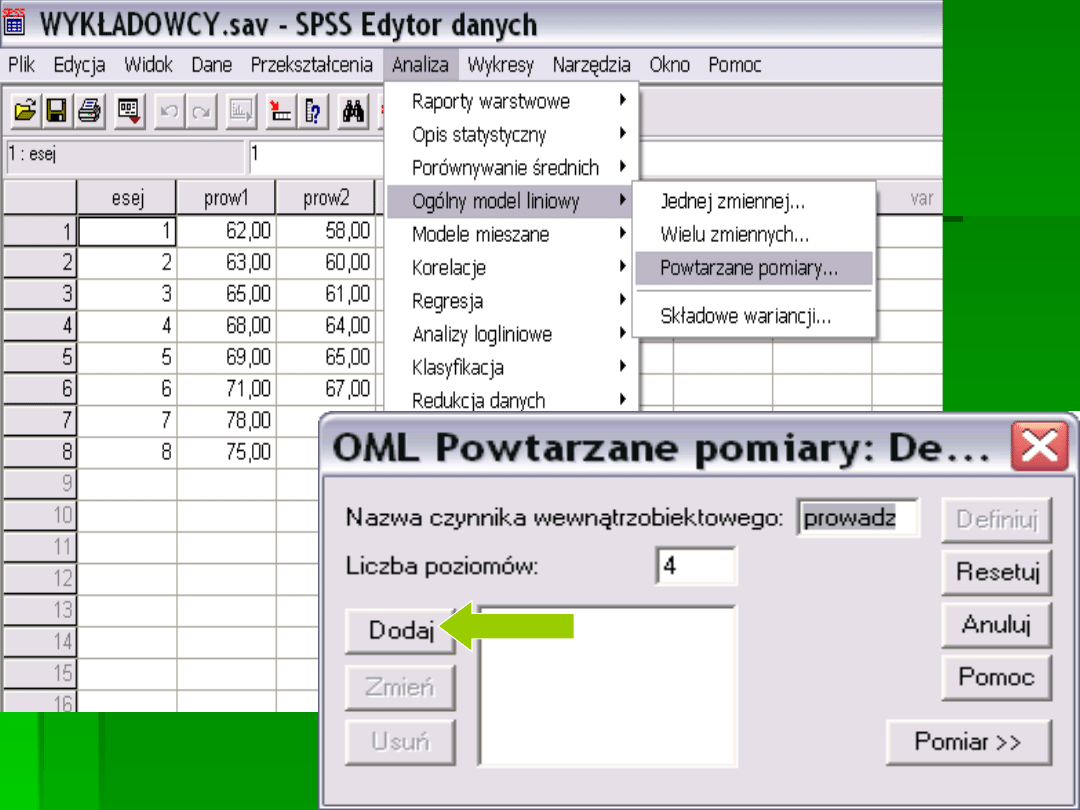
CYFRY TE

ODPOWIADAJĄ

NUMEROM

POZOMÓW ZN

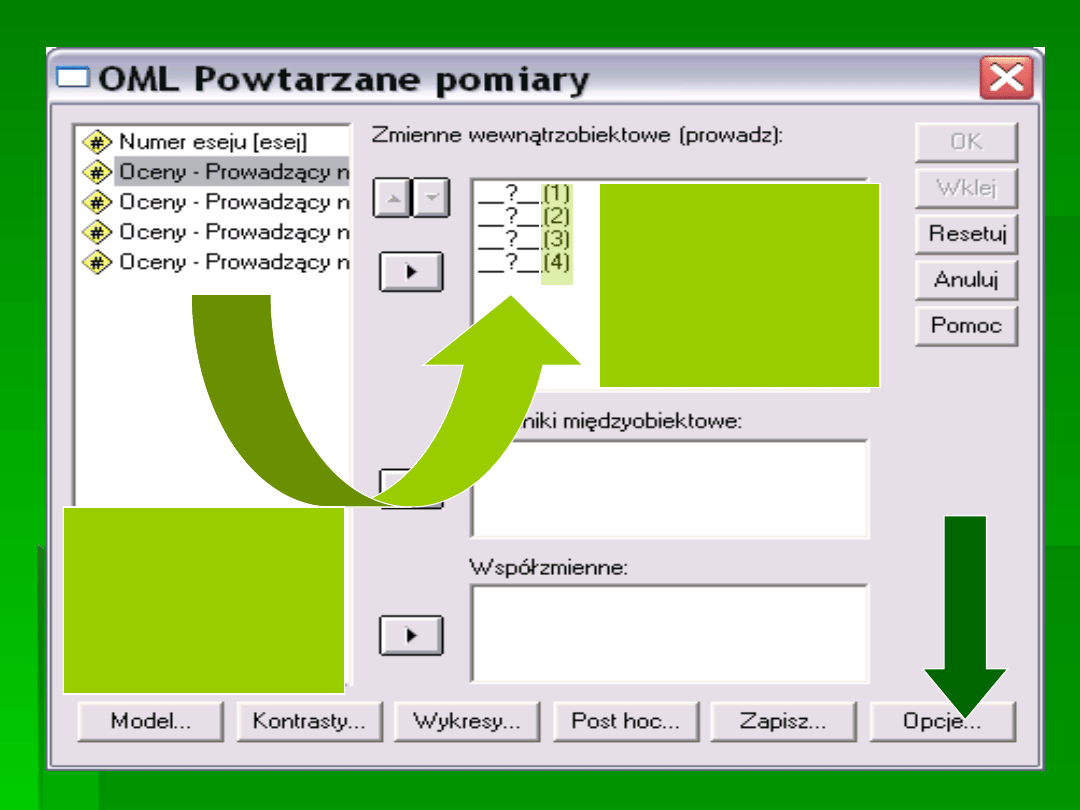
PRZENOSIMY

ZMIENNE

W ODPOWIEDNIE

MIEJSCA

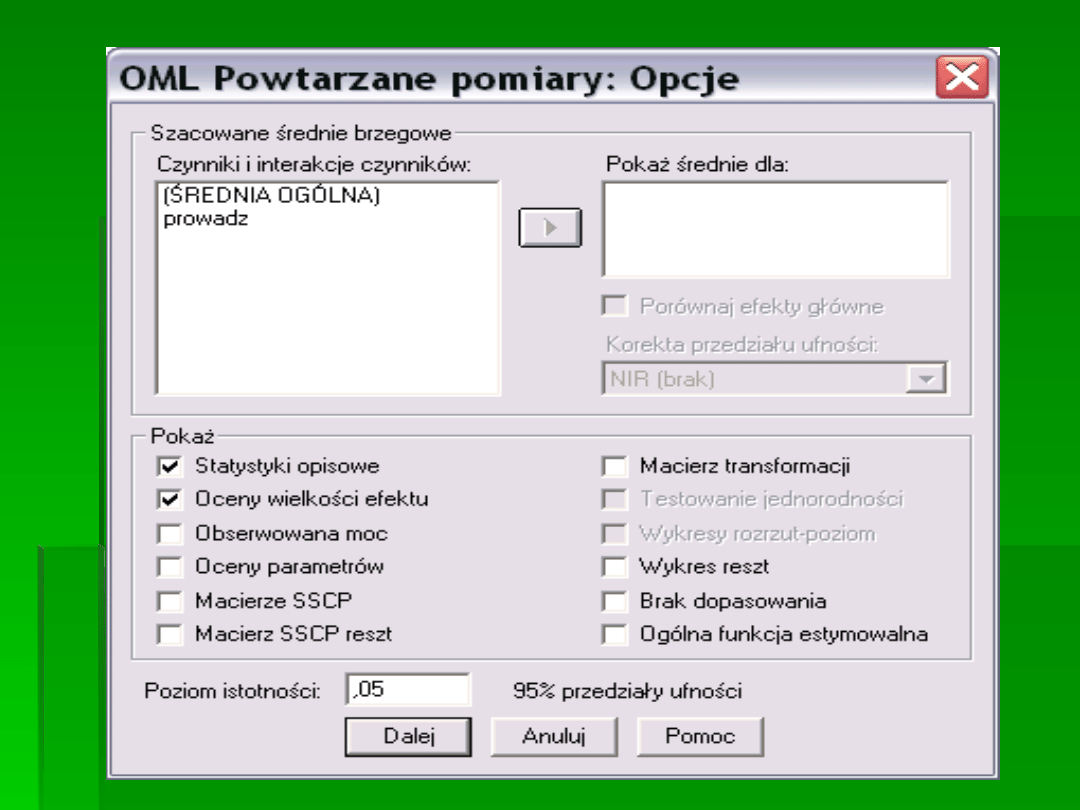
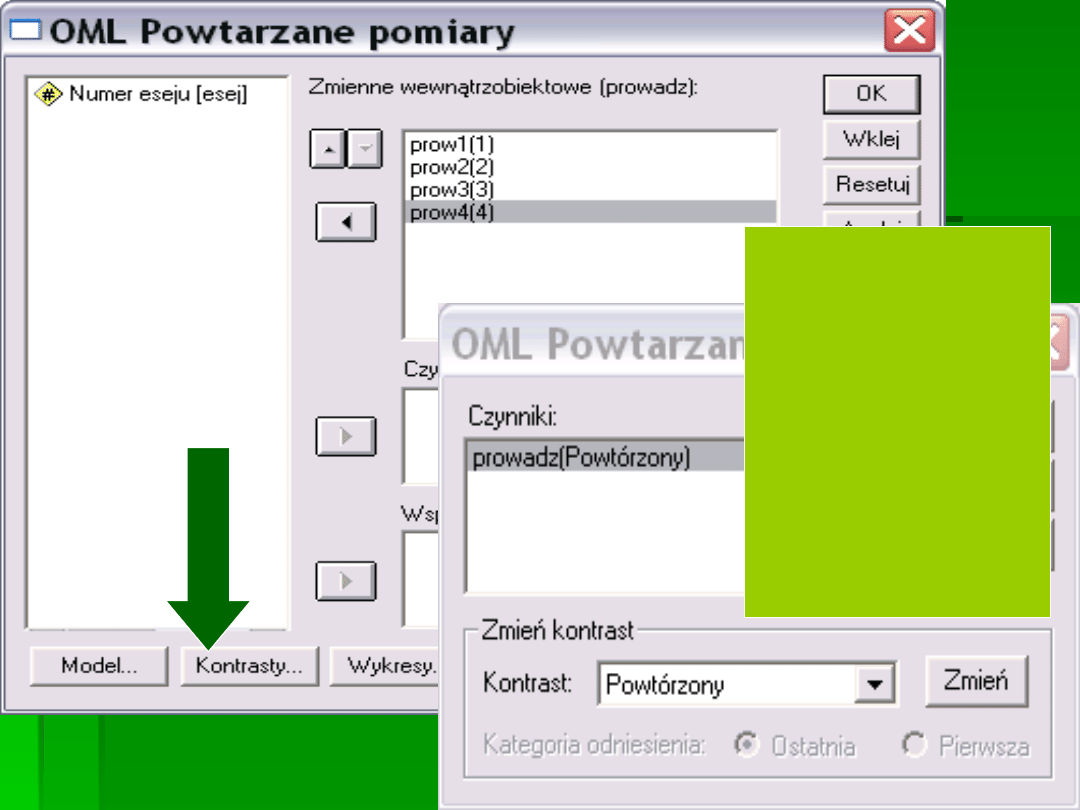
KONTRAST

POWTÓRZONY JEST

BARDZO DOBRY

PRZY

POWTARZANYCH

POMIARACH.

PORÓWNUJE KAŻDY

POZIOM

Z POPRZEDNIM

POZIOMEM.

POST HOCI

POST HOCI

PROCEDURY POST HOC NIE

PROCEDURY POST HOC NIE

SĄ DOSTĘPNE ODDZIELNIE

SĄ DOSTĘPNE ODDZIELNIE

PRZY JEDNOCZYNNIKOWEJ

PRZY JEDNOCZYNNIKOWEJ

ANOVIE, ALE SĄ ONE

ANOVIE, ALE SĄ ONE

UMIESZCZONE W OPCJACH.

UMIESZCZONE W OPCJACH.

PORÓWNANIA PARAMI.

PORÓWNANIA PARAMI.

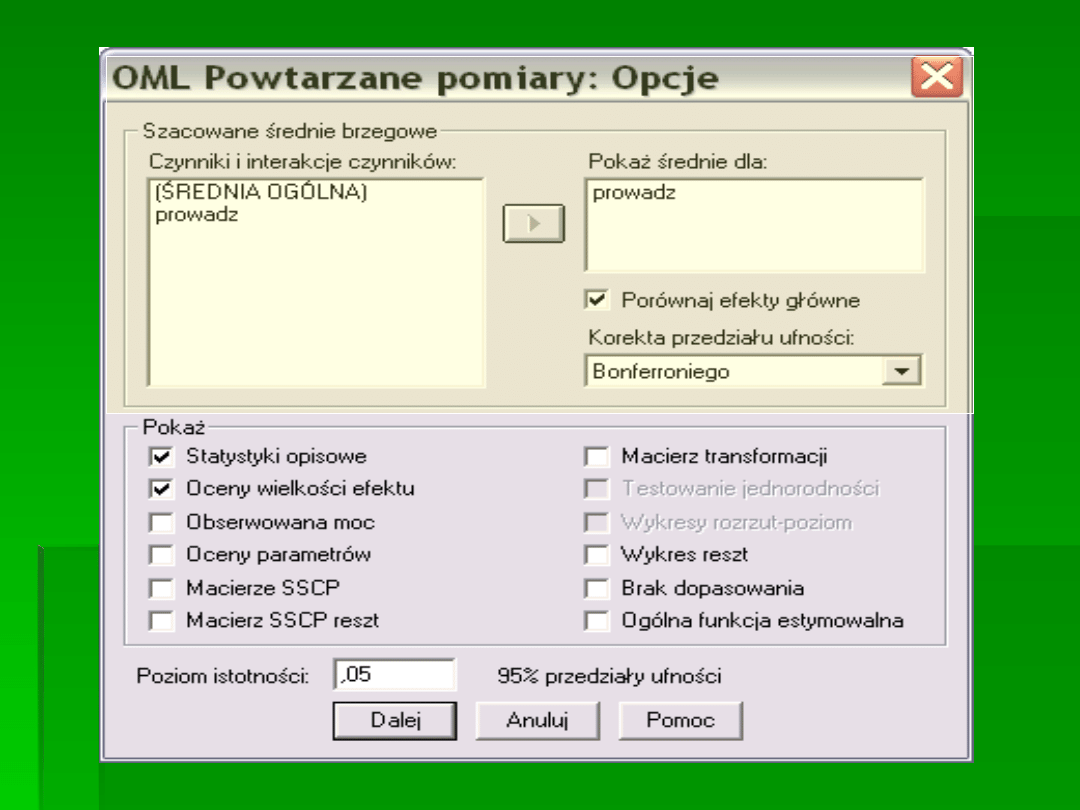
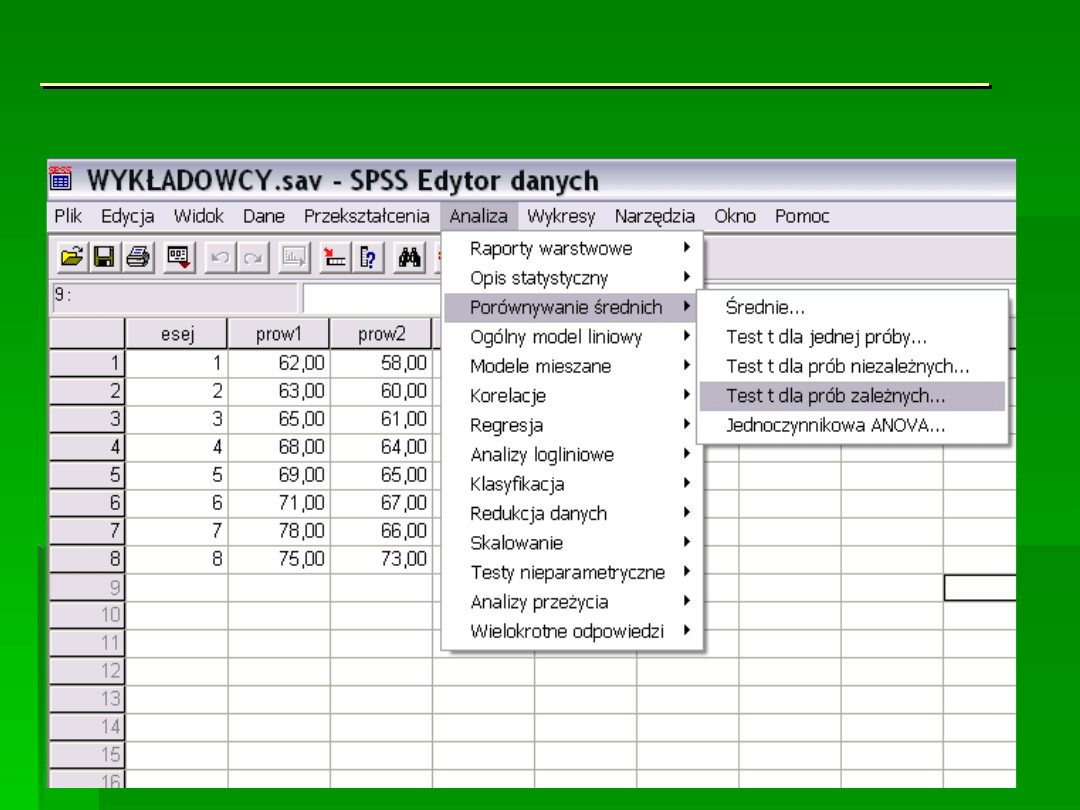
MOŻNA TEŻ OBLICZYĆ TESTY T.

MOŻNA TEŻ OBLICZYĆ TESTY T.

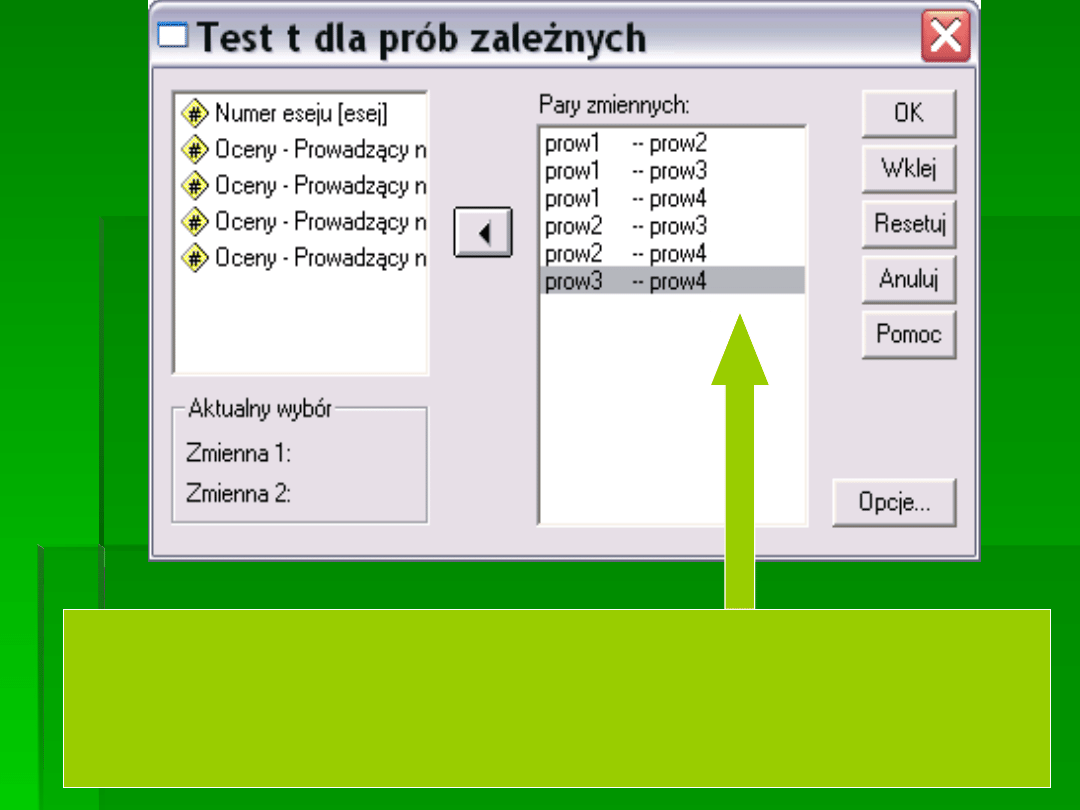
I MOŻEMY PORÓWNAĆ ZE SOBĄ WSZYSTKIE ŚREDNIE

WYNIKI

WYNIKI

Test sferyczności Mauchly'ego

b

Miara: MIARA_1

,131

11,628

5

,043

,558

,712

,333

Efekt wewnątrzobiektowy
PROWADZ

W

Mauchly'ego

Przybliżone

chi-kwadrat

df

Istotność

Greenhous

e-Geisser

Huynh-Feldt

Dolna granica

epsilon

Epsilon

a

Testuje hipotezę zerową o proporcjonalności macierzy kowariancji błędów ortonormalizowanych przekształconych zmiennych
zależnych do macierzy jednostkowej.

Może być użyte do korygowania stopni swobody dla uśrednionych testów istotności. Skorygowane testy są przedstawione w
tabeli Testy efektów wewnątrzobiektowych.

a.

Plan: Intercept
Plan wewnątrzobiektowy: PROWADZ

b.

PONIEWAŻ TEST SFERYCZNOŚCI JEST ISTOTNY

MUSIMY WZIĄĆ POD UWAGĘ POPRAWKI.



SFERYCZNOŚĆ ZAŁOŻONA

SFERYCZNOŚĆ ZAŁOŻONA

najmniej konserwatywny – można go

najmniej konserwatywny – można go

stosować tylko wtedy, gdy test jest

stosować tylko wtedy, gdy test jest

nieistotny

nieistotny



TEST HUYNH-FELDT’A

TEST HUYNH-FELDT’A

liberalny – można go stosować gdy test

liberalny – można go stosować gdy test

sferyczności jest istotny

sferyczności jest istotny



TEST GREENHOUSE-GEISSER

TEST GREENHOUSE-GEISSER

bardziej konserwatywny – test sferyczności

bardziej konserwatywny – test sferyczności

istotny

istotny

CO ZROBIĆ, GDY TEST H-F JEST

CO ZROBIĆ, GDY TEST H-F JEST

NIEISTOTNY, A TEST G-G ISTOTNY?

NIEISTOTNY, A TEST G-G ISTOTNY?

MOŻNA WYCIĄGNĄĆ ŚREDNIĄ Z OBU

MOŻNA WYCIĄGNĄĆ ŚREDNIĄ Z OBU

WARTOŚCI p.

WARTOŚCI p.

HUYNH-FELDT - p = 0,753

HUYNH-FELDT - p = 0,753

GREENHOUSE-GEISSER – p = 0,032

GREENHOUSE-GEISSER – p = 0,032

(0,753 + 0,032) / 2 = 0,393 gdy ta

(0,753 + 0,032) / 2 = 0,393 gdy ta

wartość jest większa od 0,05 to

wartość jest większa od 0,05 to

wybieramy test H. Natomiast gdyby była

wybieramy test H. Natomiast gdyby była

mniejsza od 0,05 to wybralibyśmy test G.

mniejsza od 0,05 to wybralibyśmy test G.

ZOBACZMY JAK JEST W NASZYM

ZOBACZMY JAK JEST W NASZYM

PRZYPADKU…

PRZYPADKU…

W NASZYM PRZYPADKU OBA TESTY ZAKŁĄDAJĄ SFERYCZNOŚĆ – SĄ

NIEISTOTNE. MOŻEMY WYBRAĆ TEST BARDZIEL LIBERALNY, CZYLI H-F.

Test sferyczności Mauchly'ego

b

Miara: MIARA_1

,131

11,628

5

,043

,558

,712

,333

Efekt wewnątrzobiektowy
PROWADZ

W

Mauchly'ego

Przybliżone

chi-kwadrat

df

Istotność

Greenhous

e-Geisser

Huynh-Feldt

Dolna granica

epsilon

Epsilon

a

Testuje hipotezę zerową o proporcjonalności macierzy kowariancji błędów ortonormalizowanych przekształconych zmiennych
zależnych do macierzy jednostkowej.

Może być użyte do korygowania stopni swobody dla uśrednionych testów istotności. Skorygowane testy są przedstawione w
tabeli Testy efektów wewnątrzobiektowych.

a.

Plan: Intercept
Plan wewnątrzobiektowy: PROWADZ

b.

Testy efektów wewnątrzobiektowych

Miara: MIARA_1

554,125

3

184,708

3,700

,028

,346

554,125

1,673

331,245

3,700

,063

,346

554,125

2,137

259,329

3,700

,047

,346

554,125

1,000

554,125

3,700

,096

,346

1048,375

21

49,923

1048,375

11,710

89,528

1048,375

14,957

70,091

1048,375

7,000

149,768

Sferyczność założona
Greenhouse-Geisser
Huynh-Feldt
Dolna granica epsilon
Sferyczność założona
Greenhouse-Geisser
Huynh-Feldt
Dolna granica epsilon

Źródło zmienności
prowadz

Błąd(prowadz)

Typ III sumy

kwadratów

df

Średni

kwadrat

F

Istotność

Czastkowe

Eta kwadrat

Kontrasty

Kontrasty

Testy kontrastów wewnątrzobiektowych

Miara: MIARA_1

171,125

1

171,125

18,184

,004

,722

8,000

1

8,000

,152

,708

,021

496,125

1

496,125

3,436

,106

,329

65,875

7

9,411

368,000

7

52,571

1010,875

7

144,411

PROWADZ
Poziom 1 vs Poziom 2
Poziom 2 vs Poziom 3
Poziom 3 vs Poziom 4
Poziom 1 vs Poziom 2
Poziom 2 vs Poziom 3
Poziom 3 vs Poziom 4

Źródło zmienności
PROWADZ

Błąd(PROWADZ)

Typ III sumy

kwadratów

df

Średni

kwadrat

F

Istotność

Czastkowe

Eta kwadrat

Oszacowane średnie brzegowe - MIARA_1

PROWADZ

4

3

2

1

O

sz

ac

ow

an

e

śr

ed

ni

e

br

ze

go

w

e

70

68

66

64

62

60

58

56

PORÓWNANIA PARAMI

Porównania parami

Miara: MIARA_1

4,625*

1,085

,004

2,060

7,190

3,625

2,841

,243

-3,092

10,342

11,500*

4,675

,043

,445

22,555

-4,625*

1,085

,004

-7,190

-2,060

-1,000

2,563

,708

-7,062

5,062

6,875

4,377

,160

-3,475

17,225

-3,625

2,841

,243

-10,342

3,092

1,000

2,563

,708

-5,062

7,062

7,875

4,249

,106

-2,172

17,922

-11,500*

4,675

,043

-22,555

-,445

-6,875

4,377

,160

-17,225

3,475

-7,875

4,249

,106

-17,922

2,172

(J) prowadz
2
3
4
1
3
4
1
2
4
1
2
3

(I) prowadz
1

2

3

4

Różnica

średnich (I-J)

Błąd

standardowy

Istotność

a

Dolna granica Górna granica

95% przedział ufności dla

różnicy

a

W oparciu o estymowane średnie brzegowe.

Różnica średnich jest istotna na poziomie ,05

*.

Poprawka dla porównań wielokrotnych - Najmniejsza istotna różnica (równoważnik braku poprawki).

a.

TESTY T

TESTY T

Test dla prób zależnych

4,6250

3,06769

1,08459

2,0603

7,1897

4,264

7

,004

3,6250

8,03452

2,84063

-3,0920

10,3420

1,276

7

,243

11,5000

13,22336

4,67516

,4450

22,5550

2,460

7

,043

-1,0000

7,25062

2,56348

-7,0617

5,0617

-,390

7

,708

6,8750

12,38014

4,37704

-3,4751

17,2251

1,571

7

,160

7,8750

12,01710

4,24869

-2,1715

17,9215

1,854

7

,106

Oceny - Prowadzący nr 1 -
Oceny - Prowadzący nr 2

Para
1

Oceny - Prowadzący nr 1 -
Oceny - Prowadzący nr 3

Para
2

Oceny - Prowadzący nr 1 -
Oceny - Prowadzący nr 4

Para
3

Oceny - Prowadzący nr 2 -
Oceny - Prowadzący nr 3

Para
4

Oceny - Prowadzący nr 2 -
Oceny - Prowadzący nr 4

Para
5

Oceny - Prowadzący nr 3 -
Oceny - Prowadzący nr 4

Para
6

Średnia

Odchylenie

standardowe

Błąd

standardowy

średniej

Dolna granica Górna granica

95% przedział ufności dla

różnicy średnich

Różnice w próbach zależnych

t

df

Istotność

(dwustronna)

ANOVA WIELOCZYNNIKOWA

ANOVA WIELOCZYNNIKOWA

OTWIERAMY BAZĘ

OTWIERAMY BAZĘ

„

„

POSTAWY”

POSTAWY”

KILKU BADACZY SPOŁECZNYCH

KILKU BADACZY SPOŁECZNYCH

CHCIAŁO ZBADAĆ CZY

CHCIAŁO ZBADAĆ CZY

WYOBRAŻENIA MOGĄ WPŁYNĄĆ NA

WYOBRAŻENIA MOGĄ WPŁYNĄĆ NA

POSTAWY WOBEC ALKOHOLU. CZY

POSTAWY WOBEC ALKOHOLU. CZY

NEGATYWNE WYOBRAŻENIA

NEGATYWNE WYOBRAŻENIA

ZMIENIĄ POSTAWY W STOSUNKU DO

ZMIENIĄ POSTAWY W STOSUNKU DO

RÓŻNYCH ALKOHOLI (BAD. NA

RÓŻNYCH ALKOHOLI (BAD. NA

ZLECENIE RZĄDU), A Z DRUGIEJ

ZLECENIE RZĄDU), A Z DRUGIEJ

STRONY CZY POZYTYWNE

STRONY CZY POZYTYWNE

WYOBRAŻENIA JE POPRAWIĄ (BAD.

WYOBRAŻENIA JE POPRAWIĄ (BAD.

DLA KAMPANII ALKOHOLOWEJ).

DLA KAMPANII ALKOHOLOWEJ).

KAŻDY BADANY OGLĄDAŁ 9 REKLAM

KAŻDY BADANY OGLĄDAŁ 9 REKLAM

W 3 SESJACH. PO KAŻDEJ REKALMIE

W 3 SESJACH. PO KAŻDEJ REKALMIE

OCENIALI DRINKI.

OCENIALI DRINKI.

SCHEMAT:

SCHEMAT:

3

3

(

(

ALKOHOL

ALKOHOL

: PIWO, WINO, WODA)

: PIWO, WINO, WODA)

X

X

3

3

(

(

SKOJARZENIE

SKOJARZENIE

: +, -, NEUTRALNE)

: +, -, NEUTRALNE)

Tworzycie bazę

Tworzycie bazę





PIWO

PIWO

SEXY

SEXY

1, 43, 15

1, 43, 15

TRUP

TRUP

6, 30, 15

6, 30, 15

FOTEL

FOTEL

5, 8, 12

5, 8, 12

WINO

WINO

SEXY

SEXY

28, 20, 20

28, 20, 20

TRUP

TRUP

-5, -12, -15

-5, -12, -15

FOTEL

FOTEL

4, 4, 6

4, 4, 6

WODA

WODA

SEXY

SEXY

10, 9, 6

10, 9, 6

TRUP

TRUP

-14, -10, -16

-14, -10, -16

FOTEL

FOTEL

-2, -13, 1

-2, -13, 1

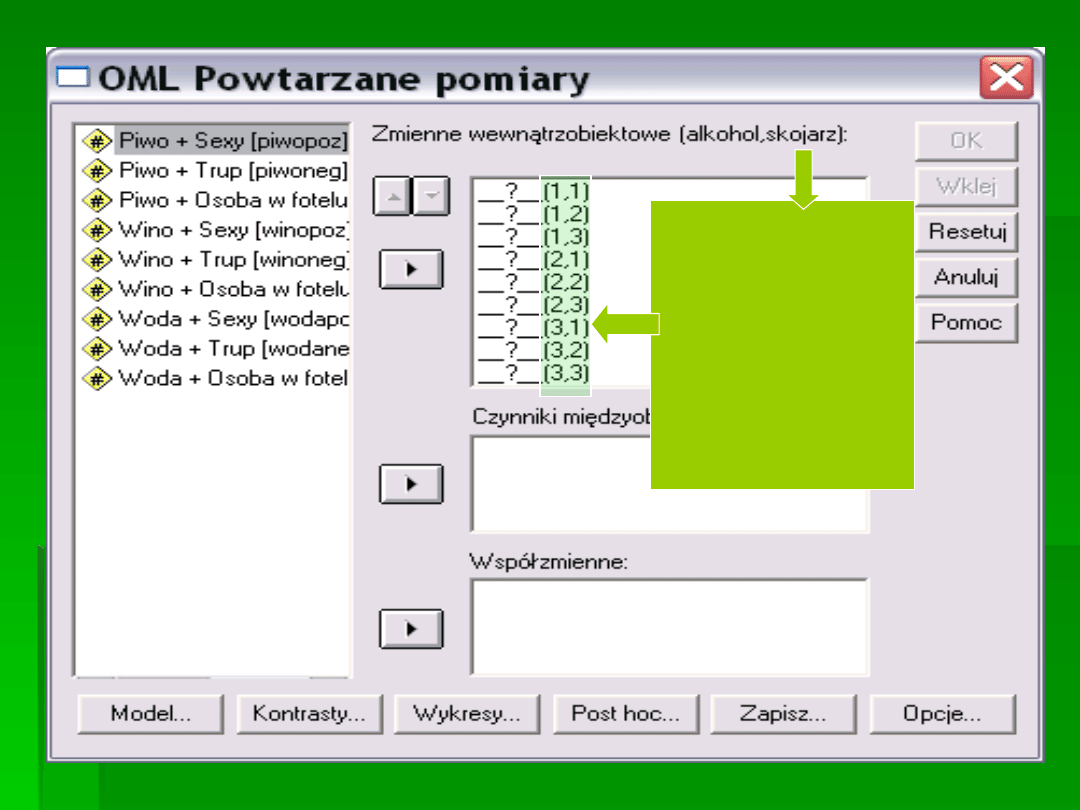
PO LEWEJ

STRONIE SĄ

POZIOMY

JEDNEJ ZMIENNEJ

A PO PRAWEJ

DRUGIEJ

HIPOTEZY:

HIPOTEZY:

CHCEMY SIĘ DOWIEDZIEĆ CZY

CHCEMY SIĘ DOWIEDZIEĆ CZY

POZYTYWNE SKOJARZENIA BĘDĄ

POZYTYWNE SKOJARZENIA BĘDĄ

NASILAĆ POSTAWY WOBEC

NASILAĆ POSTAWY WOBEC

ALKOHOLU, A NEGATYWNE JE

ALKOHOLU, A NEGATYWNE JE

OSŁABIAĆ. TAK WIĘC MUSIMY

OSŁABIAĆ. TAK WIĘC MUSIMY

PORÓWNAĆ GRUPY ALKOHOLOWE

PORÓWNAĆ GRUPY ALKOHOLOWE

DO GRUPY Z WODĄ.

DO GRUPY Z WODĄ.

WYNIKI

WYNIKI

Test sferyczności Mauchly'ego

b

Miara: MIARA_1

,267

23,753

2

,000

,577

,591

,500

,662

7,422

2

,024

,747

,797

,500

,595

9,041

9

,436

,798

,979

,250

Efekt wewnątrzobiektowy
ALKOHOL
SKOJARZ
ALKOHOL * SKOJARZ

W

Mauchly'ego

Przybliżone

chi-kwadrat

df

Istotność

Greenhous

e-Geisser

Huynh-Feldt

Dolna granica

epsilon

Epsilon

a

Testuje hipotezę zerową o proporcjonalności macierzy kowariancji błędów ortonormalizowanych przekształconych zmiennych
zależnych do macierzy jednostkowej.

Może być użyte do korygowania stopni swobody dla uśrednionych testów istotności. Skorygowane testy są przedstawione w
tabeli Testy efektów wewnątrzobiektowych.

a.

Plan: Intercept
Plan wewnątrzobiektowy: ALKOHOL+SKOJARZ+ALKOHOL*SKOJARZ

b.

PONIEWAŻ OBA TESTY SĄ NIEISTOTNE, TO WYBÓR

ZALEŻY OD NAS.

Testy efektów wewnątrzobiektowych

Miara: MIARA_1

2092,344

2 1046,172

5,106

,011

,212

2092,344

1,154 1812,764

5,106

,030

,212

2092,344

1,181 1770,939

5,106

,029

,212

2092,344

1,000 2092,344

5,106

,036

,212

7785,878

38

204,892

7785,878

21,930

355,028

7785,878

22,448

346,836

7785,878

19,000

409,783

21628,678

2 10814,339

122,565

,000

,866

21628,678

1,495 14468,490

122,565

,000

,866

21628,678

1,594 13571,496

122,565

,000

,866

21628,678

1,000 21628,678

122,565

,000

,866

3352,878

38

88,234

3352,878

28,403

118,048

3352,878

30,280

110,729

3352,878

19,000

176,467

2624,422

4

656,106

17,155

,000

,474

2624,422

3,194

821,778

17,155

,000

,474

2624,422

3,914

670,462

17,155

,000

,474

2624,422

1,000 2624,422

17,155

,001

,474

2906,689

76

38,246

2906,689

60,678

47,903

2906,689

74,373

39,083

2906,689

19,000

152,984

Sferyczność założona
Greenhouse-Geisser
Huynh-Feldt
Dolna granica epsilon
Sferyczność założona
Greenhouse-Geisser
Huynh-Feldt
Dolna granica epsilon
Sferyczność założona
Greenhouse-Geisser
Huynh-Feldt
Dolna granica epsilon
Sferyczność założona
Greenhouse-Geisser
Huynh-Feldt
Dolna granica epsilon
Sferyczność założona
Greenhouse-Geisser
Huynh-Feldt
Dolna granica epsilon
Sferyczność założona
Greenhouse-Geisser
Huynh-Feldt
Dolna granica epsilon

Źródło zmienności
ALKOHOL

Błąd(ALKOHOL)

SKOJARZ

Błąd(SKOJARZ)

ALKOHOL * SKOJARZ

Błąd(ALKOHOL*SKOJ
ARZ)

Typ III sumy

kwadratów

df

Średni

kwadrat

F

Istotność

Czastkowe

Eta kwadrat

F(1,154;21,930) = 5,11

p<0,05

F(1,495;28,403) = 122,57

p<0,0005

F(4,76) = 17,16

p<0,0005

PONIEWAŻ WYSTĄPIŁ ISTOTNY

PONIEWAŻ WYSTĄPIŁ ISTOTNY

EFEKT INTERAKCJI ALKOHOLU I

EFEKT INTERAKCJI ALKOHOLU I

SKOJARZENIA, OBA EFEKTY

SKOJARZENIA, OBA EFEKTY

GŁÓWNE SĄ OGRANICZONE.

GŁÓWNE SĄ OGRANICZONE.

ANALIZUJEMY JE I DOPISUJEMY,

ANALIZUJEMY JE I DOPISUJEMY,

ŻE ICH SENS OGRANICZA

ŻE ICH SENS OGRANICZA

ISTOTNA INTERAKCJA.

ISTOTNA INTERAKCJA.

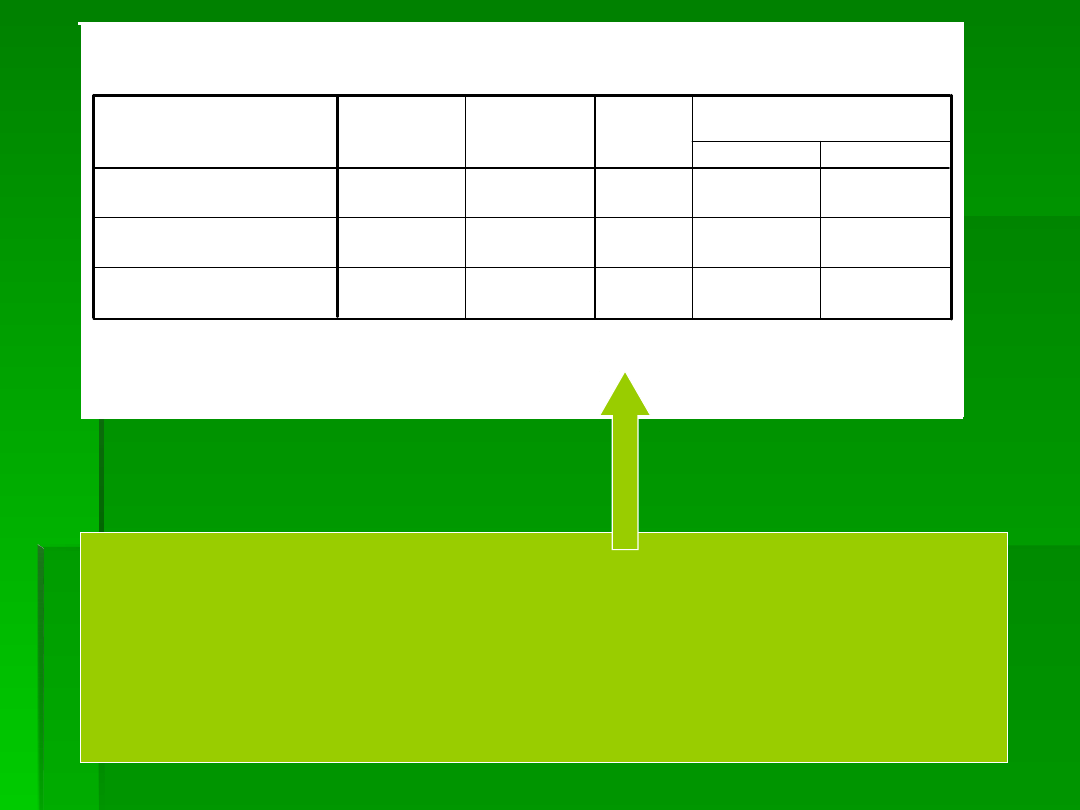
EFEKT GŁÓWNY ALKOHOLU

EFEKT GŁÓWNY ALKOHOLU

Oszacowane średnie brzegowe - MIARA_1

ALKOHOL

3

2

1

O

sz

ac

ow

an

e

śr

ed

ni

e

br

ze

go

w

e

14

12

10

8

6

4

2

BEZ UWZGLĘDNIENIA SKOJARZEŃ

RODZAJ ALKOHOLU WPŁYWAŁ

NA POSTAWY.

Porównania parami

Miara: MIARA_1

3,500

2,849

,703

-3,980

10,980

8,317

3,335

,066

-,438

17,072

-3,500

2,849

,703

-10,980

3,980

4,817*

1,116

,001

1,886

7,747

-8,317

3,335

,066

-17,072

,438

-4,817*

1,116

,001

-7,747

-1,886

(J) ALKOHOL
2
3
1
3
1
2

(I) ALKOHOL
1

2

3

Różnica

średnich (I-J)

Błąd

standardowy

Istotność

a

Dolna granica Górna granica

95% przedział ufności dla

różnicy

a

W oparciu o estymowane średnie brzegowe.

Różnica średnich jest istotna na poziomie ,05

*.

Poprawka dla porównań wielokrotnych - Bonferroniego.

a.

PORÓWNANIA PARAMI MÓWIĄ NAM, ŻE POSTAWY WOBEC

PIWA I WINA NIE RÓŻNIŁY SIĘ OD SIEBIE, NATOMIAST

BYŁY ISTOTNIE POZYTYWNIEJSZE OD POSTAW

WOBEC WODY.

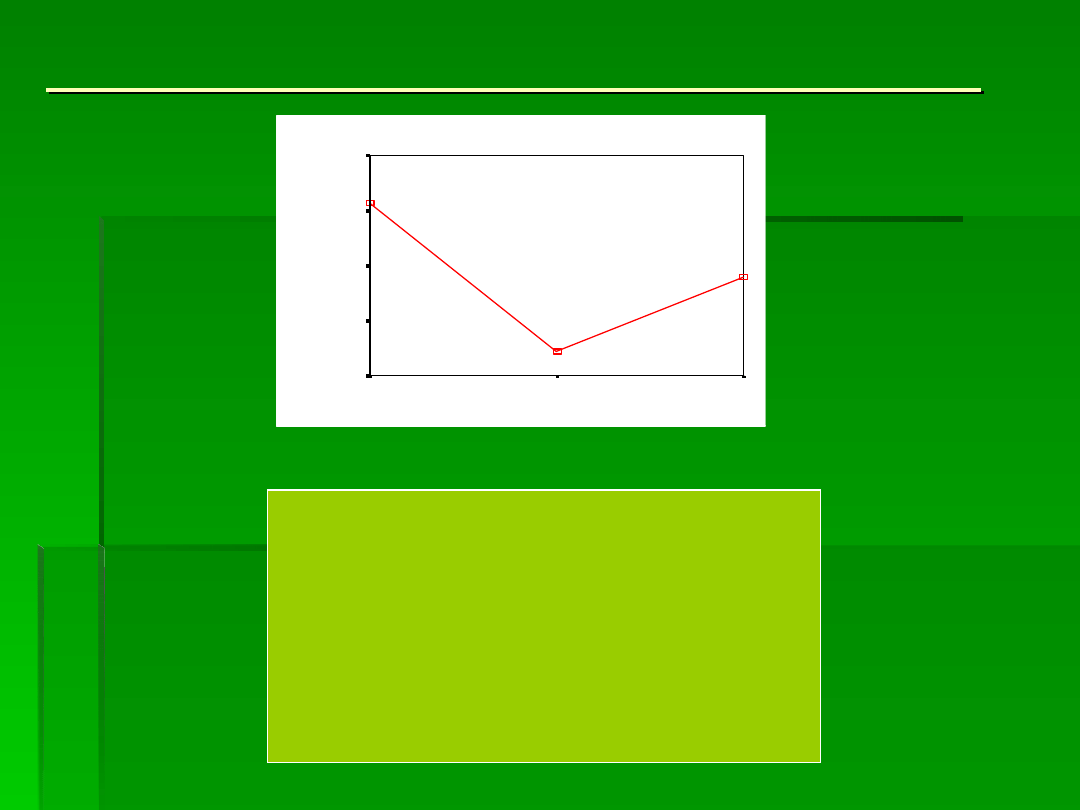
EFEKT GŁÓWNY SKOJARZEŃ

EFEKT GŁÓWNY SKOJARZEŃ

Oszacowane średnie brzegowe - MIARA_1

SKOJ ARZ

3

2

1

O

sz

ac

ow

an

e

śr

ed

ni

e

br

ze

go

w

e

30

20

10

0

-10

NIEZALEŻNIE OD ALKOHOLU

RODZAJ SKOJARZEŃ WPŁYWAŁ

ISTOTNIE NA

POSTAWY.

Porównania parami

Miara: MIARA_1

26,850*

1,915

,000

21,824

31,876

13,267*

1,113

,000

10,346

16,187

-26,850*

1,915

,000

-31,876

-21,824

-13,583*

1,980

,000

-18,781

-8,386

-13,267*

1,113

,000

-16,187

-10,346

13,583*

1,980

,000

8,386

18,781

(J) SKOJARZ
2
3
1
3
1
2

(I) SKOJARZ
1

2

3

Różnica

średnich (I-J)

Błąd

standardowy

Istotność

a

Dolna granica Górna granica

95% przedział ufności dla

różnicy

a

W oparciu o estymowane średnie brzegowe.

Różnica średnich jest istotna na poziomie ,05

*.

Poprawka dla porównań wielokrotnych - Bonferroniego.

a.

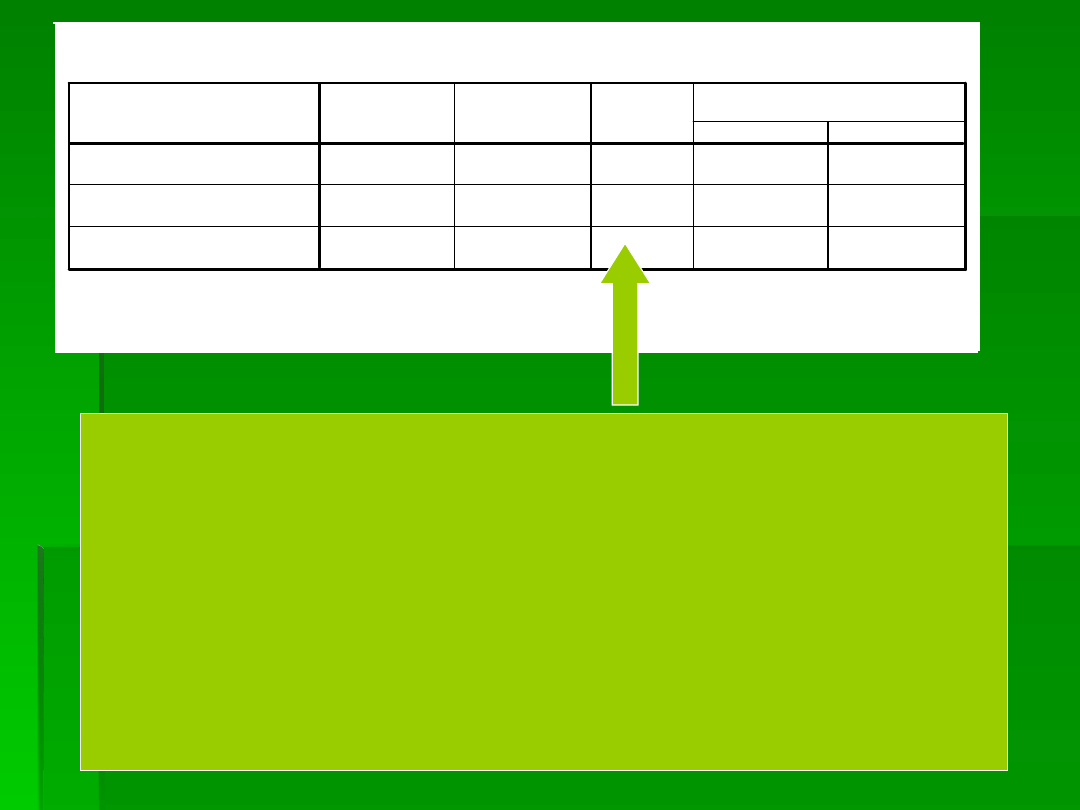
PORÓWNANIA PARAMI POKAZUJĄ NAM, ŻE WSZYSTKIE

ŚREDNIE RÓŻNIĄ SIĘ OD SIEBIE.

SKOJARZENIA POZYTYWNE

POWODOWAŁY BARDZIEJ POZYTYWNE

POSTAWY NIŻ SKOJARZENIA

NEUTRALNE I NEGATYWNE, NATOMIAST

SKOJARZENIA NEGATYWNE

POWODOWAŁY BARDZIEJ NEGATYWNE

POSTAWY OD SKOJARZEŃ

NEUTRALNYCH I POZYTYWNYCH.

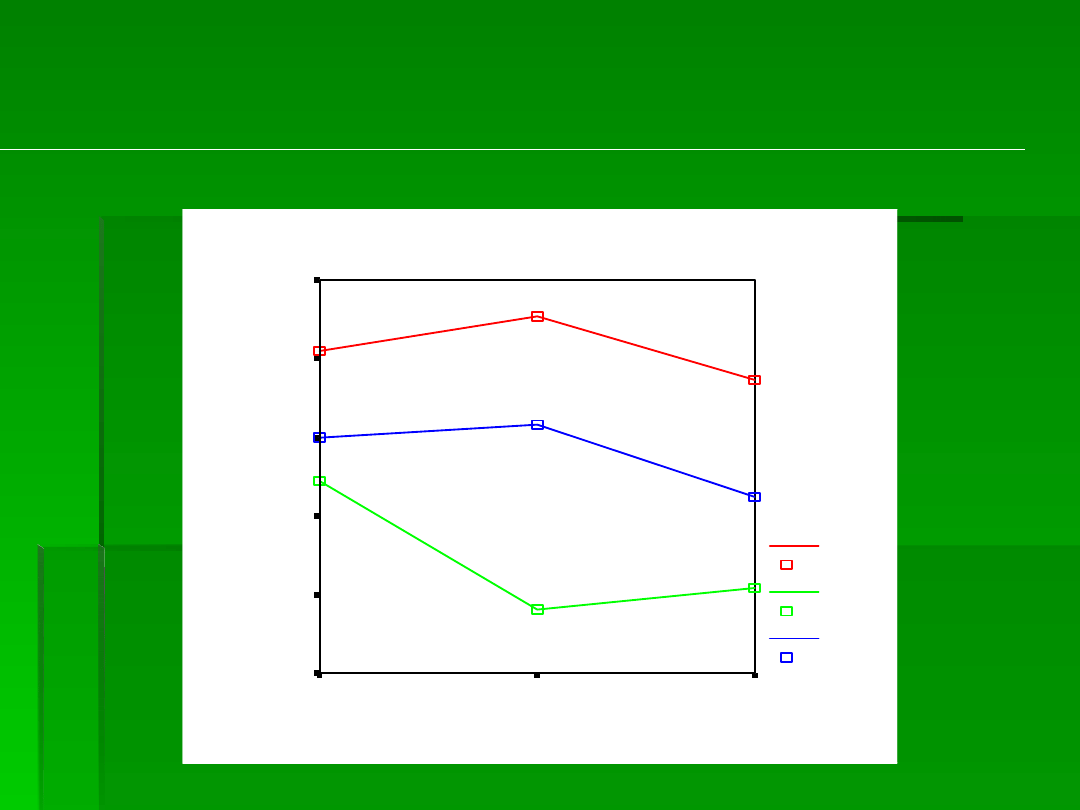
INTERAKCJA ALKOHOLU

INTERAKCJA ALKOHOLU

I SKOJARZEŃ

I SKOJARZEŃ

Oszacowane średnie brzegowe - MIARA_1

ALKOHOL

3

2

1

O

sz

ac

ow

an

e

śr

ed

ni

e

br

ze

go

w

e

30

20

10

0

-10

-20

SKOJ ARZ

1

2

3

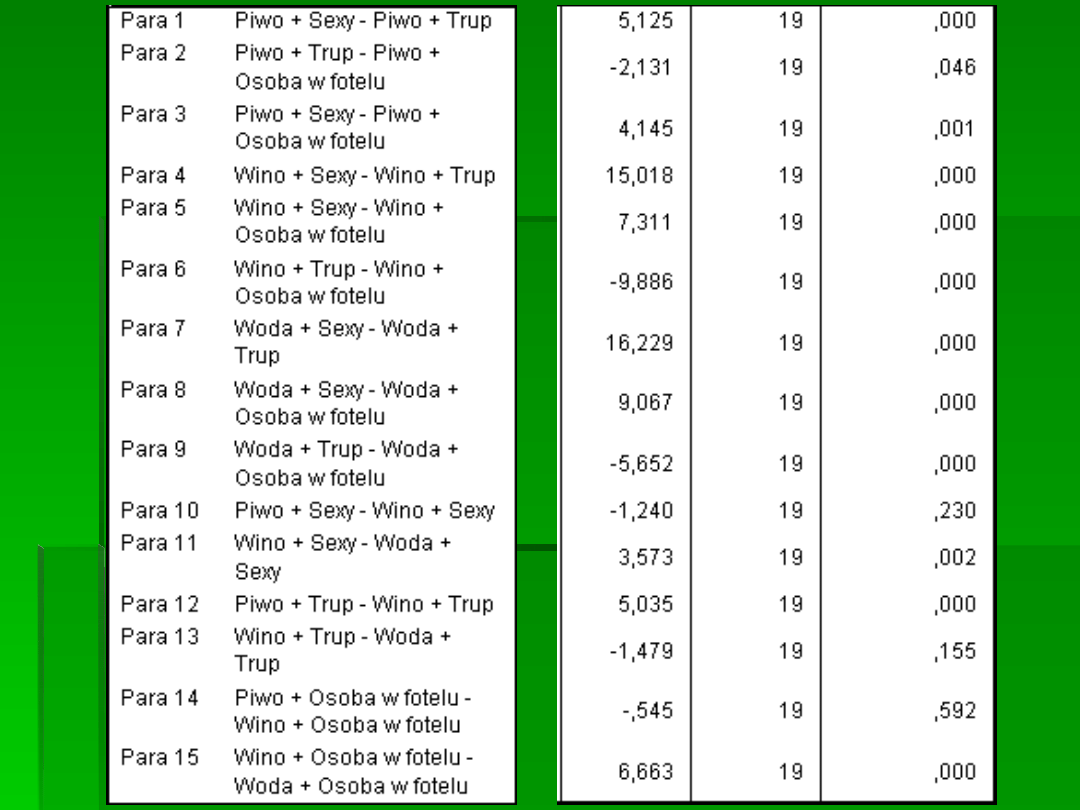
INTERPRETACJA:

INTERPRETACJA:

Analiza testów t wykazała, że efekt główny rodzaju

Analiza testów t wykazała, że efekt główny rodzaju

skojarzenia jest interpretowalny – niezależnie od

skojarzenia jest interpretowalny – niezależnie od

rodzaju alkoholu, najbardziej pozytywną postawę

rodzaju alkoholu, najbardziej pozytywną postawę

badani wykazywali wobec reklam ze skojarzeniem

badani wykazywali wobec reklam ze skojarzeniem

seksownej pani, mniej pozytywną dla osoby w

seksownej pani, mniej pozytywną dla osoby w

fotelu, a najmniej pozytywną dla bodźca

fotelu, a najmniej pozytywną dla bodźca

awersyjnego. W przypadku skojarzenia

awersyjnego. W przypadku skojarzenia

pozytywnego i neutralnego, najbardziej pozytywną

pozytywnego i neutralnego, najbardziej pozytywną

postawę badani mieli wobec piwa i wina, natomiast

postawę badani mieli wobec piwa i wina, natomiast

dla wody ta postawa była gorsza. W przypadku

dla wody ta postawa była gorsza. W przypadku

bodźca awersyjnego, najbardziej pozytywną

bodźca awersyjnego, najbardziej pozytywną

postawą badani wykazali się wobec piwa.

postawą badani wykazali się wobec piwa.

OTWIERAMY BAZĘ

OTWIERAMY BAZĘ

„

„

RĘKA W WODZIE”

RĘKA W WODZIE”

ANALIZOWANO 2 STRATGIE

ANALIZOWANO 2 STRATGIE

RADZENIA SOBIE Z BÓLEM. OŚMIU

RADZENIA SOBIE Z BÓLEM. OŚMIU

BADANYCH ZANURZAŁO DŁONIE W

BADANYCH ZANURZAŁO DŁONIE W

MROŹNEJ WODZIE I MIELI OCENIAĆ

MROŹNEJ WODZIE I MIELI OCENIAĆ

PO 30s, 60s I 90s JAK BARDZO

PO 30s, 60s I 90s JAK BARDZO

BOLESNE JEST TO DOŚWIADCZENIE

BOLESNE JEST TO DOŚWIADCZENIE

(SKALA 1-50). JEDNEGO DNIA

(SKALA 1-50). JEDNEGO DNIA

BADANI MIELI STOSOWAĆ

BADANI MIELI STOSOWAĆ

TECHNIKĘ UNIKANIA – MYŚLENIA O

TECHNIKĘ UNIKANIA – MYŚLENIA O

CZYMŚ PRZYJEMNYM, A DRUGIEGO

CZYMŚ PRZYJEMNYM, A DRUGIEGO

DNIA TECHNIKĘ SKUPIANIA SIĘ –

DNIA TECHNIKĘ SKUPIANIA SIĘ –

MYŚLENIE O WŁASNEJ RĘCE.

MYŚLENIE O WŁASNEJ RĘCE.

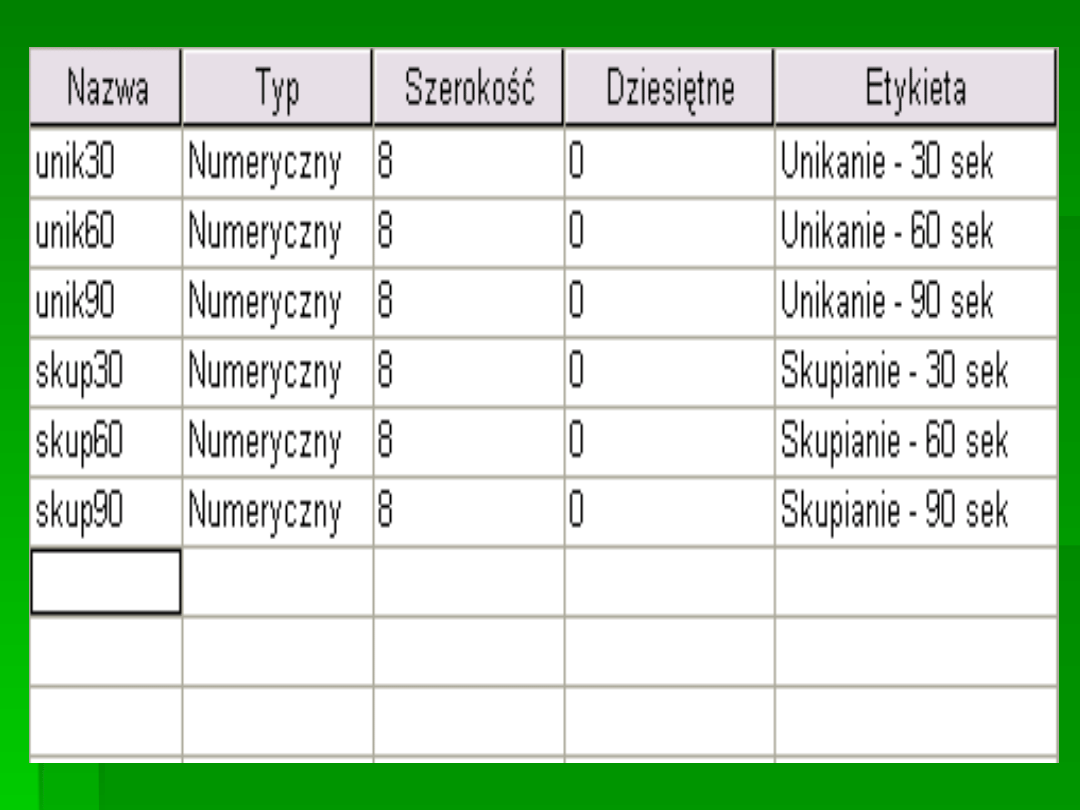
DLA ZMIENNYCH

NA 2 POZIOMACH

NIE POTRZEBUJEMY

KONTRASTÓW

1 vs 2
2 vs 3

Test sferyczności Mauchly'ego

b

Miara: MIARA_1

1,000

,000

0

.

1,000

1,000

1,000

,301

7,207

2

,027

,589

,637

,500

,801

1,328

2

,515

,834

1,000

,500

Efekt wewnątrzobiektowy
RADZENIE
CZAS
RADZENIE * CZAS

W

Mauchly'ego

Przybliżone

chi-kwadrat

df

Istotność

Greenhous

e-Geisser

Huynh-Feldt

Dolna granica

epsilon

Epsilon

a

Testuje hipotezę zerową o proporcjonalności macierzy kowariancji błędów ortonormalizowanych przekształconych zmiennych
zależnych do macierzy jednostkowej.

Może być użyte do korygowania stopni swobody dla uśrednionych testów istotności. Skorygowane testy są przedstawione w
tabeli Testy efektów wewnątrzobiektowych.

a.

Plan: Intercept
Plan wewnątrzobiektowy: RADZENIE+CZAS+RADZENIE*CZAS

b.

DLA CZASU MUSIMY WZIĄĆ

POPRAWKĘ, GDYŻ TEST

SFERYCZNOŚCI JEST ISTOTNY.

Testy wielu zmiennych

b

,216

1,924

a

1,000

7,000

,208

,216

,784

1,924

a

1,000

7,000

,208

,216

,275

1,924

a

1,000

7,000

,208

,216

,275

1,924

a

1,000

7,000

,208

,216

,891

24,589

a

2,000

6,000

,001

,891

,109

24,589

a

2,000

6,000

,001

,891

8,196

24,589

a

2,000

6,000

,001

,891

8,196

24,589

a

2,000

6,000

,001

,891

,886

23,432

a

2,000

6,000

,001

,886

,114

23,432

a

2,000

6,000

,001

,886

7,811

23,432

a

2,000

6,000

,001

,886

7,811

23,432

a

2,000

6,000

,001

,886

Ślad Pillai
Lambda Wilksa
Ślad Hotellinga
Największy
pierwiastek Roy'a
Ślad Pillai
Lambda Wilksa
Ślad Hotellinga
Największy
pierwiastek Roy'a
Ślad Pillai
Lambda Wilksa
Ślad Hotellinga
Największy
pierwiastek Roy'a

Efekt
RADZENIE

CZAS

RADZENIE * CZAS

Wartość

F

df hipotezy df błędu

Istotność

Czastkowe

Eta kwadrat

Statystyka dokładna

a.

Plan: Intercept
Plan wewnątrzobiektowy: RADZENIE+CZAS+RADZENIE*CZAS

b.

ISTOTNY EFEKT GŁÓWNY CZASU ORAZ

EFEKT INTERAKCJI



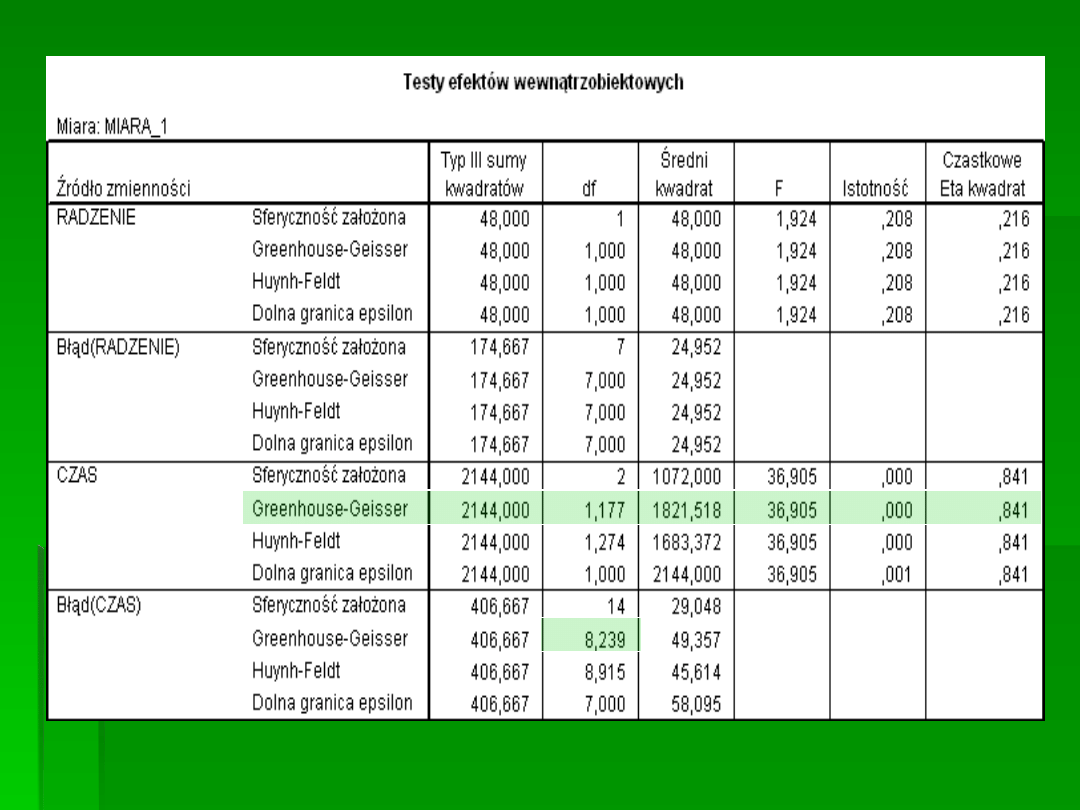
BRAK EFEKTU GŁÓWNEGO

BRAK EFEKTU GŁÓWNEGO

RADZENIA SOBIE, F(1,7) = 1,92,

RADZENIA SOBIE, F(1,7) = 1,92,

p = 0,208

p = 0,208



EFEKT GŁÓWNY CZASU,

EFEKT GŁÓWNY CZASU,

F(1,177;8,239) = 36,91,p<0,0005

F(1,177;8,239) = 36,91,p<0,0005



EFEKT INTERAKCJI RADZENIA

EFEKT INTERAKCJI RADZENIA

SOBIE I CZASU, F(2,6) =

SOBIE I CZASU, F(2,6) =

23,43, p<0,005

23,43, p<0,005

EFEKT GŁÓWNY CZASU

EFEKT GŁÓWNY CZASU

Oszacowane średnie brzegowe - MIARA_1

CZAS

3

2

1

O

sz

ac

ow

an

e

śr

ed

ni

e

br

ze

go

w

e

30

20

10

0

Porównania parami

Miara: MIARA_1

-5,000*

,813

,001

-7,542

-2,458

-16,000*

2,379

,001

-23,441

-8,559

5,000*

,813

,001

2,458

7,542

-11,000*

2,138

,004

-17,687

-4,313

16,000*

2,379

,001

8,559

23,441

11,000*

2,138

,004

4,313

17,687

(J) CZAS
2
3
1
3
1
2

(I) CZAS
1

2

3

Różnica

średnich (I-J)

Błąd

standardowy

Istotność

a

Dolna granica Górna granica

95% przedział ufności dla

różnicy

a

W oparciu o estymowane średnie brzegowe.

Różnica średnich jest istotna na poziomie ,05

*.

Poprawka dla porównań wielokrotnych - Bonferroniego.

a.

BEZ UWZGLĘDNIENIA METODY

RADZENIA SOBIE, CZAS ISTOTNIE

WPŁYWAŁ NA ODCZUWANIE BÓLU.

IM DŁUŻSZY BYŁ CZAS TRZYMANIA

RĘKI W WODZIE, TYM WIĘKSZY BÓL

DEKLAROWALI BADANI.

Testy kontrastów wewnątrzobiektowych

Miara: MIARA_1

16,000

1

16,000

1,924

,208

,216

58,222

7

8,317

400,000

1

400,000

37,838

,000

,844

1936,000

1

1936,000

26,469

,001

,791

74,000

7

10,571

512,000

7

73,143

144,000

1

144,000

17,379

,004

,713

144,000

1

144,000

7,754

,027

,526

58,000

7

8,286

130,000

7

18,571

CZAS

Poziom 1 vs Poziom 2
Poziom 2 vs Poziom 3
Poziom 1 vs Poziom 2
Poziom 2 vs Poziom 3
Poziom 1 vs Poziom 2
Poziom 2 vs Poziom 3
Poziom 1 vs Poziom 2
Poziom 2 vs Poziom 3

RADZENIE
Liniowy
Liniowy

Liniowy

Liniowy

Źródło zmienności
RADZENIE
Błąd(RADZENIE)
CZAS

Błąd(CZAS)

RADZENIE * CZAS

Błąd(RADZENIE*CZAS)

Typ III sumy

kwadratów

df

Średni

kwadrat

F

Istotność

Czastkowe

Eta kwadrat

MÓWIĄ NAM O TYM TEŻ
KONTRASTY

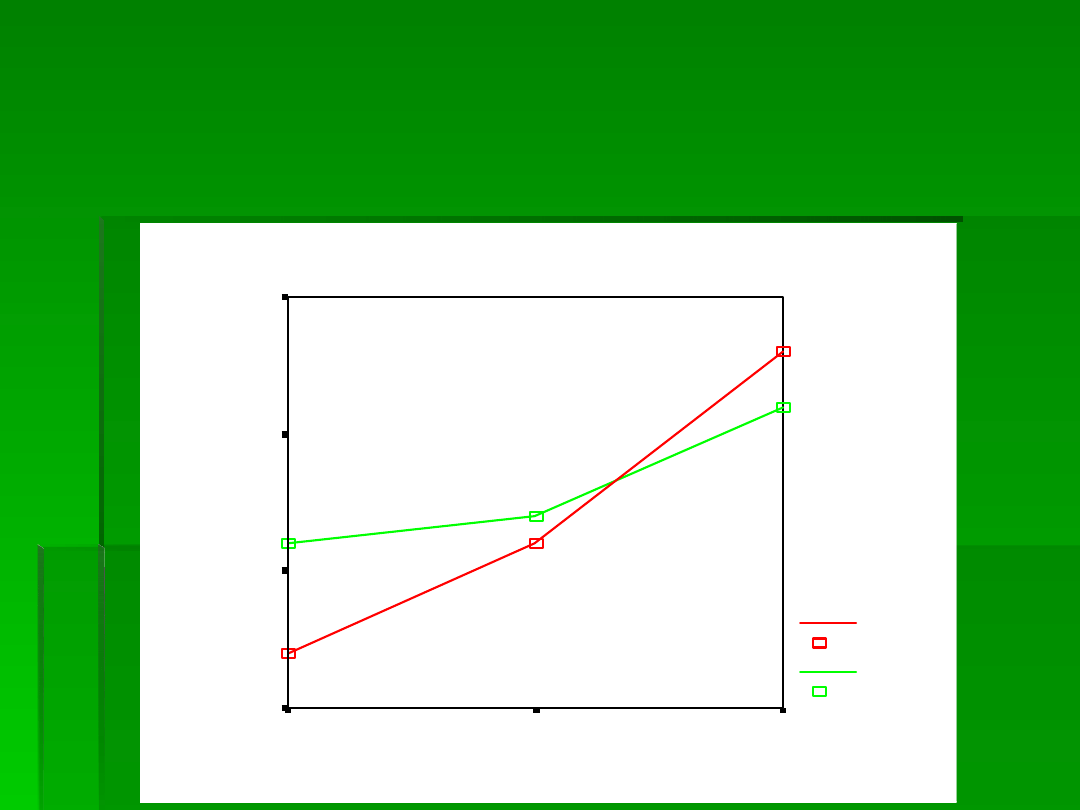
EFEKT GŁÓWNY CZASU OGRANICZA

EFEKT GŁÓWNY CZASU OGRANICZA

ISTOTNA INTERAKCJA CZASU I

ISTOTNA INTERAKCJA CZASU I

RADZENIA SOBIE.

RADZENIA SOBIE.

Oszacowane średnie brzegowe - MIARA_1

CZAS

3

2

1

O

sz

ac

ow

an

e

śr

ed

ni

e

br

ze

go

w

e

30

20

10

0

RADZENIE

1

2

JAK RÓŻNI SIĘ ODCZUWANIE

JAK RÓŻNI SIĘ ODCZUWANIE

BÓLU PRZY RÓŻNYCH

BÓLU PRZY RÓŻNYCH

CZASACH DLA

CZASACH DLA

POSZCZEGÓLNYCH STRATEGII?

POSZCZEGÓLNYCH STRATEGII?

PRZEPROWADZAMY TESTY T

PRZEPROWADZAMY TESTY T

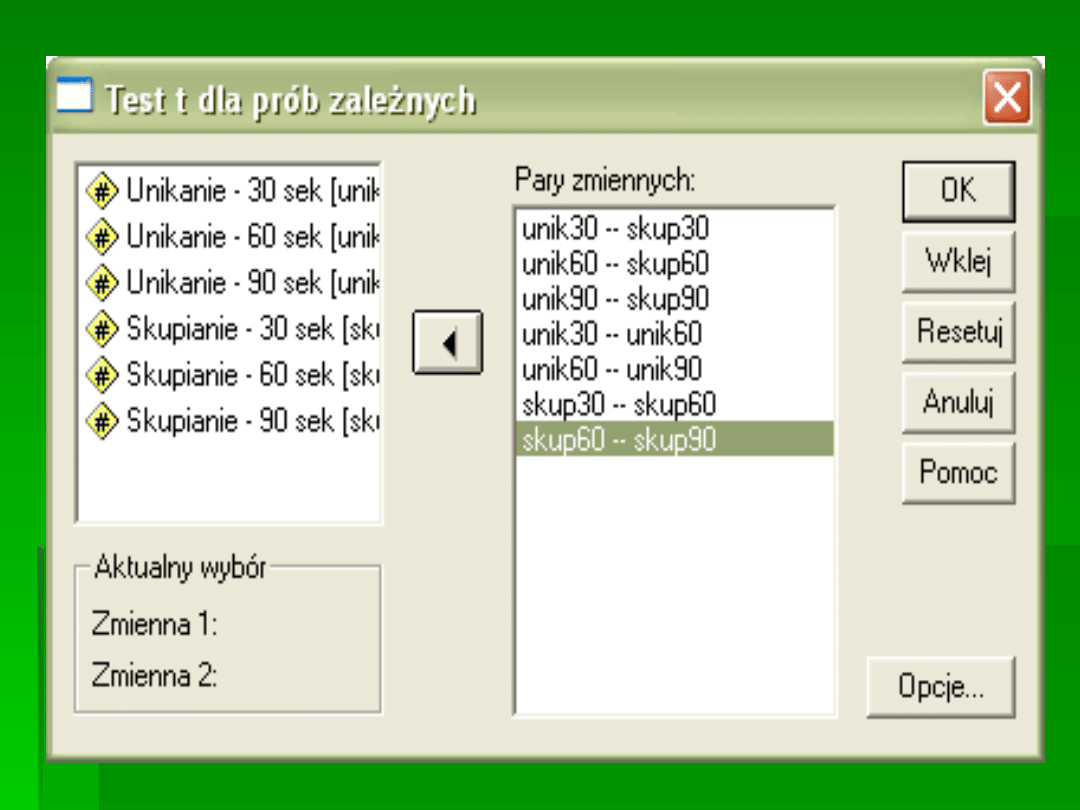
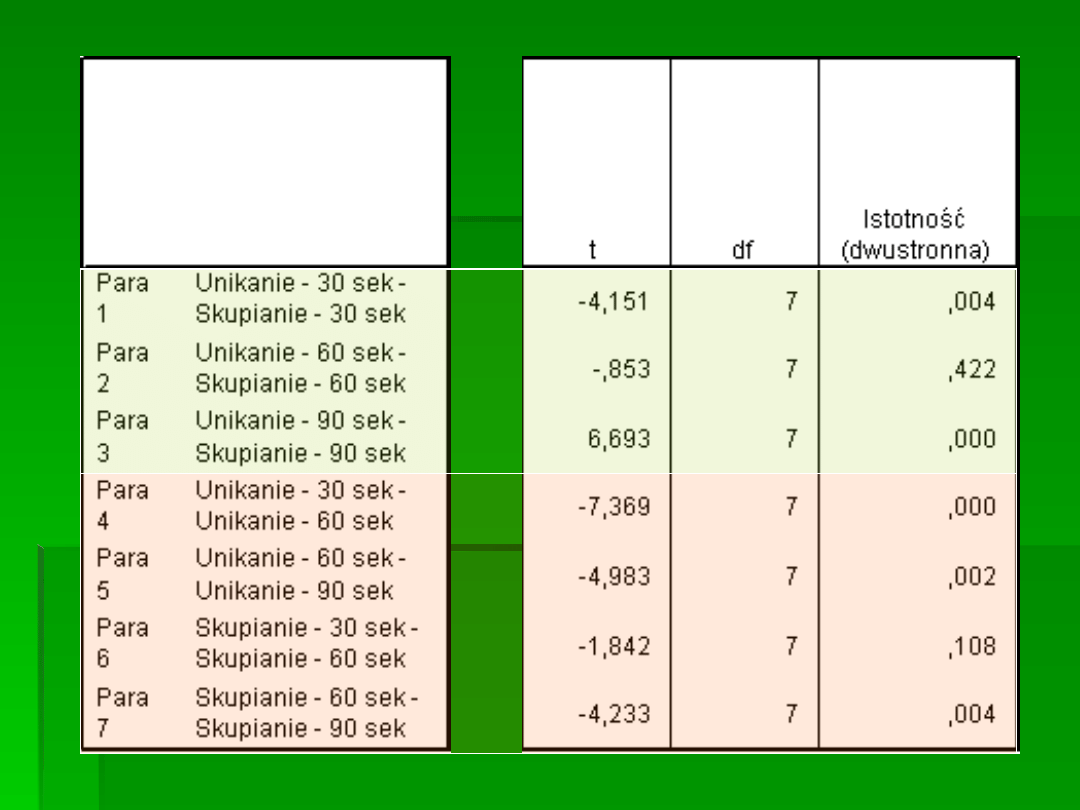
INTERPRETACJA:

INTERPRETACJA:

Podczas stosowania strategii unikania, ból rósł

Podczas stosowania strategii unikania, ból rósł

istotnie wraz ze wzrostem czasu

istotnie wraz ze wzrostem czasu

utrzymywania ręki w wodzie, natomiast przy

utrzymywania ręki w wodzie, natomiast przy

strategii skupiania, ból rósł dopiero po 90

strategii skupiania, ból rósł dopiero po 90

sekundach. Przy krótkim czasie 30 sek.

sekundach. Przy krótkim czasie 30 sek.

trzymania ręki w wodzie, mniejszy ból

trzymania ręki w wodzie, mniejszy ból

powodowała strategia unikania (M=4 vs.

powodowała strategia unikania (M=4 vs.

M=12; t(7)=4,15, p<0,005), przy 60 sek. nie

M=12; t(7)=4,15, p<0,005), przy 60 sek. nie

było różnic między strategiami (M=12 vs.

było różnic między strategiami (M=12 vs.

M=14; t<1), natomiast przy 90 sek. mniejszy

M=14; t<1), natomiast przy 90 sek. mniejszy

ból powodowała strategia skupiania się

ból powodowała strategia skupiania się

(M=22 vs. M=26; t(7)=6,69, p<0,0005).

(M=22 vs. M=26; t(7)=6,69, p<0,0005).

OTWIERAMY BAZĘ

OTWIERAMY BAZĘ

„

„

UWAGA”

UWAGA”

BADACZ BYŁ ZAINTERESOWANY, JAK SIĘ

BADACZ BYŁ ZAINTERESOWANY, JAK SIĘ

ZMIENIA ZWRACANIE UWAGI U NIEMOWLĄT

ZMIENIA ZWRACANIE UWAGI U NIEMOWLĄT

NA BODŹCE ZNANE I NOWE.

NA BODŹCE ZNANE I NOWE.

BADACZ MIERZYŁ UWAGĘ WZROKOWĄ U 60

BADACZ MIERZYŁ UWAGĘ WZROKOWĄ U 60

NIEMOWLAKÓW, NA BODŹCE NOWE I

NIEMOWLAKÓW, NA BODŹCE NOWE I

ZNANE W 4 OKRESACH CZASOWYCH – W

ZNANE W 4 OKRESACH CZASOWYCH – W

WIEKU 3,4,6 I 8 MIESIĘCY – BADANIE

WIEKU 3,4,6 I 8 MIESIĘCY – BADANIE

LONGITUDINALNE

LONGITUDINALNE

MAMY 2 ZMIENNE INTRAINDYWIDUALNE:

MAMY 2 ZMIENNE INTRAINDYWIDUALNE:

WIEK (2 vs 3 vs 6 vs 8) x BODZIEC (Znany vs.

WIEK (2 vs 3 vs 6 vs 8) x BODZIEC (Znany vs.

Nowy)

Nowy)

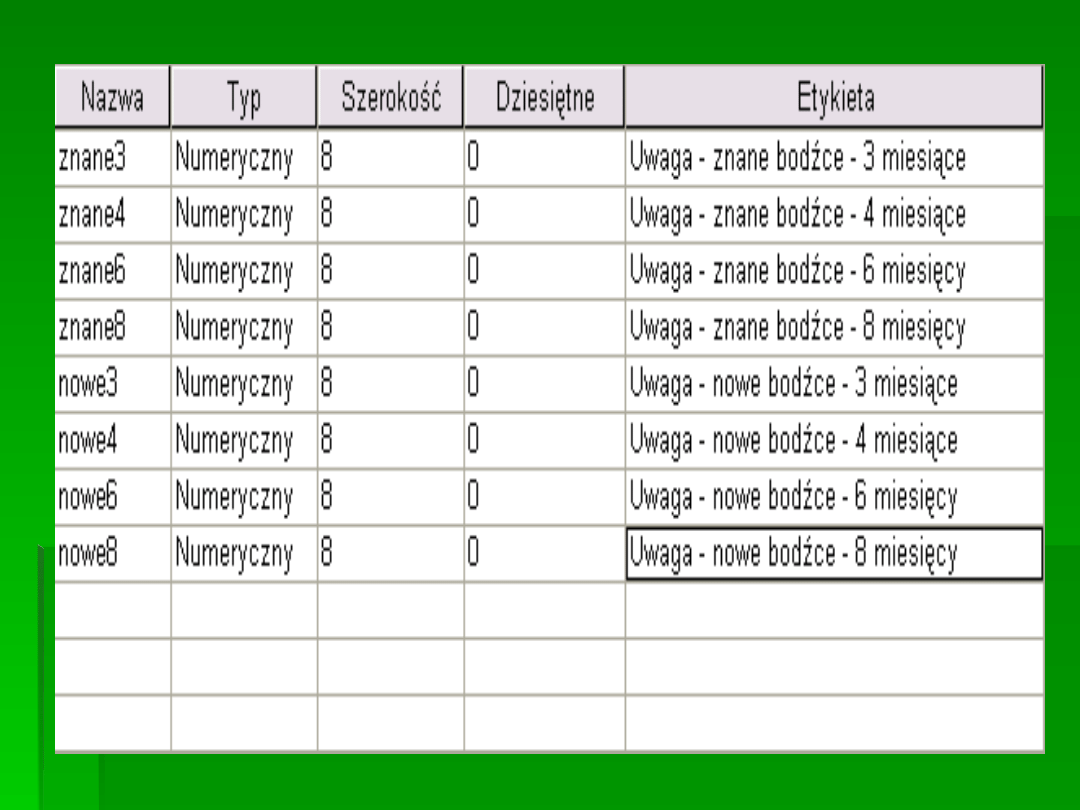
Test sferyczności Mauchly'ego

b

Miara: MIARA_1

,836

10,342

5

,066

,889

,935

,333

1,000

,000

0

.

1,000

1,000

1,000

,568

32,601

5

,000

,715

,743

,333

Efekt wewnątrzobiektowy
WIEK
BODZIEC
WIEK * BODZIEC

W

Mauchly'ego

Przybliżone

chi-kwadrat

df

Istotność

Greenhous

e-Geisser

Huynh-Feldt

Dolna granica

epsilon

Epsilon

a

Testuje hipotezę zerową o proporcjonalności macierzy kowariancji błędów ortonormalizowanych przekształconych zmiennych
zależnych do macierzy jednostkowej.

Może być użyte do korygowania stopni swobody dla uśrednionych testów istotności. Skorygowane testy są przedstawione w
tabeli Testy efektów wewnątrzobiektowych.

a.

Plan: Intercept
Plan wewnątrzobiektowy: WIEK+BODZIEC+WIEK*BODZIEC

b.

Testy efektów wewnątrzobiektowych

Miara: MIARA_1

1289,158

3

429,719

372,677

,000

,863

1289,158

2,666

483,546

372,677

,000

,863

1289,158

2,804

459,749

372,677

,000

,863

1289,158

1,000

1289,158

372,677

,000

,863

204,092

177

1,153

204,092

157,297

1,297

204,092

165,439

1,234

204,092

59,000

3,459

224,133

1

224,133

178,420

,000

,751

224,133

1,000

224,133

178,420

,000

,751

224,133

1,000

224,133

178,420

,000

,751

224,133

1,000

224,133

178,420

,000

,751

74,117

59

1,256

74,117

59,000

1,256

74,117

59,000

1,256

74,117

59,000

1,256

117,967

3

39,322

40,516

,000

,407

117,967

2,145

54,986

40,516

,000

,407

117,967

2,229

52,926

40,516

,000

,407

117,967

1,000

117,967

40,516

,000

,407

171,783

177

,971

171,783

126,577

1,357

171,783

131,504

1,306

171,783

59,000

2,912

Sferyczność założona
Greenhouse-Geisser
Huynh-Feldt
Dolna granica epsilon
Sferyczność założona
Greenhouse-Geisser
Huynh-Feldt
Dolna granica epsilon
Sferyczność założona
Greenhouse-Geisser
Huynh-Feldt
Dolna granica epsilon
Sferyczność założona
Greenhouse-Geisser
Huynh-Feldt
Dolna granica epsilon
Sferyczność założona
Greenhouse-Geisser
Huynh-Feldt
Dolna granica epsilon
Sferyczność założona
Greenhouse-Geisser
Huynh-Feldt
Dolna granica epsilon

Źródło zmienności
WIEK

Błąd(WIEK)

BODZIEC

Błąd(BODZIEC)

WIEK * BODZIEC

Błąd(WIEK*BODZIEC)

Typ III sumy

kwadratów

df

Średni

kwadrat

F

Istotność

Czastkowe

Eta kwadrat

Oszacowane średnie brzegowe - MIARA_1

BODZIEC

2

1

O

sz

ac

ow

an

e

śr

ed

ni

e

br

ze

go

w

e

4,4

4,2

4,0

3,8

3,6

3,4

3,2

3,0

2,8

Oszacowane średnie brzegowe - MIARA_1

WIEK

4

3

2

1

O

sz

ac

ow

an

e

śr

ed

ni

e

br

ze

go

w

e

7

6

5

4

3

2

1

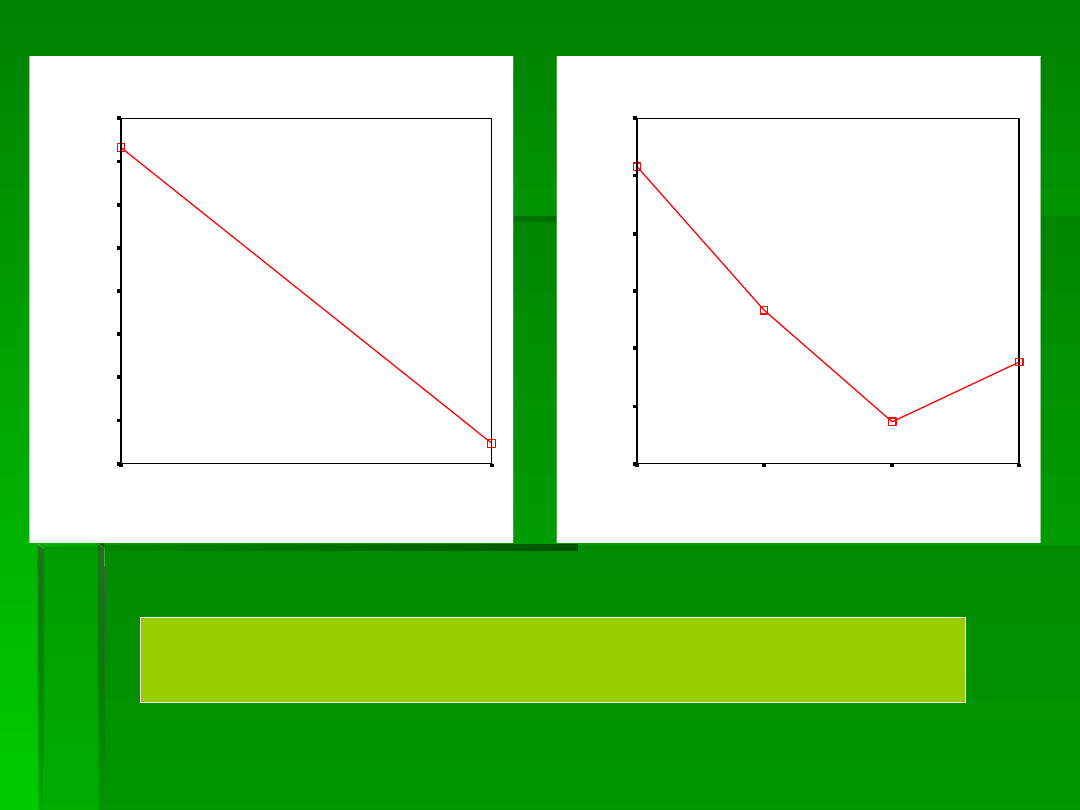
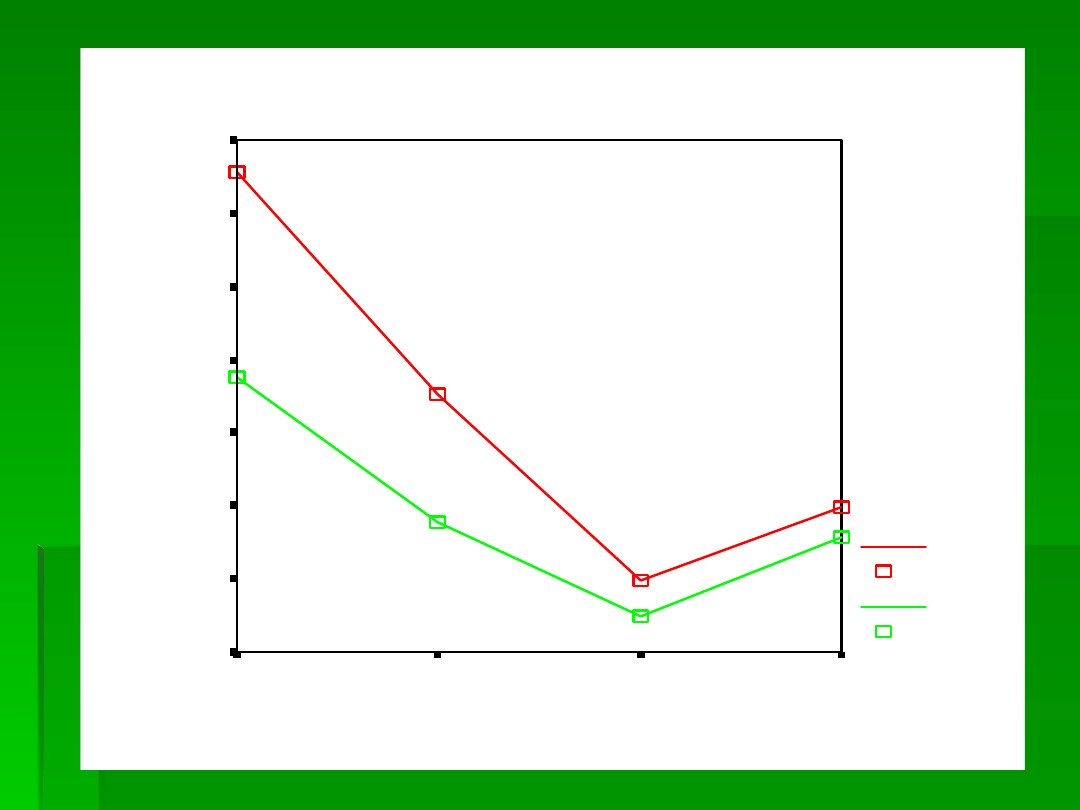
EFEKTY GŁÓWNE OGRANICZA ISTOTNA INTERAKCJA.

Oszacowane średnie brzegowe - MIARA_1

WIEK

4

3

2

1

O

sz

ac

ow

an

e

śr

ed

ni

e

br

ze

go

w

e

8

7

6

5

4

3

2

1

BODZIEC

1

2

INTERPRETACJA:

INTERPRETACJA:

Analiza testów t wykazała, że efekt główny

Analiza testów t wykazała, że efekt główny

rodzaju bodźca jest w pełni

rodzaju bodźca jest w pełni

interpretowalny – niezależnie od wieku

interpretowalny – niezależnie od wieku

dziecka, bodźce znane przyciągały

dziecka, bodźce znane przyciągały

większą uwagę, niż bodźce nowe.

większą uwagę, niż bodźce nowe.

Natomiast uwaga poświęcana bodźcom

Natomiast uwaga poświęcana bodźcom

zmniejszała się istotnie niezależnie od

zmniejszała się istotnie niezależnie od

rodzaju bodźca do 6-go miesiąca i

rodzaju bodźca do 6-go miesiąca i

ponownie wzrastała w wieku 8 miesięcy.

ponownie wzrastała w wieku 8 miesięcy.

OTWIERAMY BAZĘ

OTWIERAMY BAZĘ

„

„

LUBIENIE”

LUBIENIE”

BADACZ BYŁ ZAINTERESOWANY ZWIĄZKIEM LUBIENIA Z

BADACZ BYŁ ZAINTERESOWANY ZWIĄZKIEM LUBIENIA Z

WYGLĄDEM ZEWNĘTRZNYM. DO BADANIA WZIĄŁ DZIEWCZYNKI

WYGLĄDEM ZEWNĘTRZNYM. DO BADANIA WZIĄŁ DZIEWCZYNKI

Z KLASY 1, GDYŻ SĄ PRZESŁANKI ABY SĄDZIĆ, IŻ TO

Z KLASY 1, GDYŻ SĄ PRZESŁANKI ABY SĄDZIĆ, IŻ TO

SZCZEGÓLNIE DZIEWCZYNKI PRZYPISUJĄ ŁADNIE UBRANYM

SZCZEGÓLNIE DZIEWCZYNKI PRZYPISUJĄ ŁADNIE UBRANYM

DZIECIOM WIĘKSZĄ SYMPATIĘ, SZCZEGÓLNIE, GDY SĄ TO

DZIECIOM WIĘKSZĄ SYMPATIĘ, SZCZEGÓLNIE, GDY SĄ TO

RÓWNIEŻ DZIEWCZYNKI. 25 DZIEWCZYNEK OGLĄDAŁO 100

RÓWNIEŻ DZIEWCZYNKI. 25 DZIEWCZYNEK OGLĄDAŁO 100

ZDJĘĆ – 25 DOBRZE UBRANYCH CHŁOPCÓW I 25 DZIEWCZYNEK

ZDJĘĆ – 25 DOBRZE UBRANYCH CHŁOPCÓW I 25 DZIEWCZYNEK

ORAZ 25 ŹLE UBRANYCH CHŁOPCÓW I DZIEWCZYNEK.

ORAZ 25 ŹLE UBRANYCH CHŁOPCÓW I DZIEWCZYNEK.

BADACZ PYTAŁ DZIEWCZYNKI, CZY LUBIĄ OSOBĘ NA ZDJĘCIU.

BADACZ PYTAŁ DZIEWCZYNKI, CZY LUBIĄ OSOBĘ NA ZDJĘCIU.

ODPOWIEDZI „TAK” KODOWAŁ JAKO +1, NATOMIAST „NIE” JAKO

ODPOWIEDZI „TAK” KODOWAŁ JAKO +1, NATOMIAST „NIE” JAKO

-1. NASTĘPNIE DODAWAŁ TE WARTOŚCI DLA GRUP 25 ZDJĘĆ.

-1. NASTĘPNIE DODAWAŁ TE WARTOŚCI DLA GRUP 25 ZDJĘĆ.

Testy wielu zmiennych

b

,896

207,494

a

1,000

24,000

,000

,896

,104

207,494

a

1,000

24,000

,000

,896

8,646

207,494

a

1,000

24,000

,000

,896

8,646

207,494

a

1,000

24,000

,000

,896

,109

2,945

a

1,000

24,000

,099

,109

,891

2,945

a

1,000

24,000

,099

,109

,123

2,945

a

1,000

24,000

,099

,109

,123

2,945

a

1,000

24,000

,099

,109

,051

1,289

a

1,000

24,000

,267

,051

,949

1,289

a

1,000

24,000

,267

,051

,054

1,289

a

1,000

24,000

,267

,051

,054

1,289

a

1,000

24,000

,267

,051

Ślad Pillai
Lambda Wilksa
Ślad Hotellinga
Największy
pierwiastek Roy'a
Ślad Pillai
Lambda Wilksa
Ślad Hotellinga
Największy
pierwiastek Roy'a
Ślad Pillai
Lambda Wilksa
Ślad Hotellinga
Największy
pierwiastek Roy'a

Efekt
UBIÓR

PŁEĆ

UBIÓR * PŁEĆ

Wartość

F

df hipotezy df błędu

Istotność

Czastkowe

Eta kwadrat

Statystyka dokładna

a.

Plan: Intercept
Plan wewnątrzobiektowy: UBIÓR+PŁEĆ+UBIÓR*PŁEĆ

b.

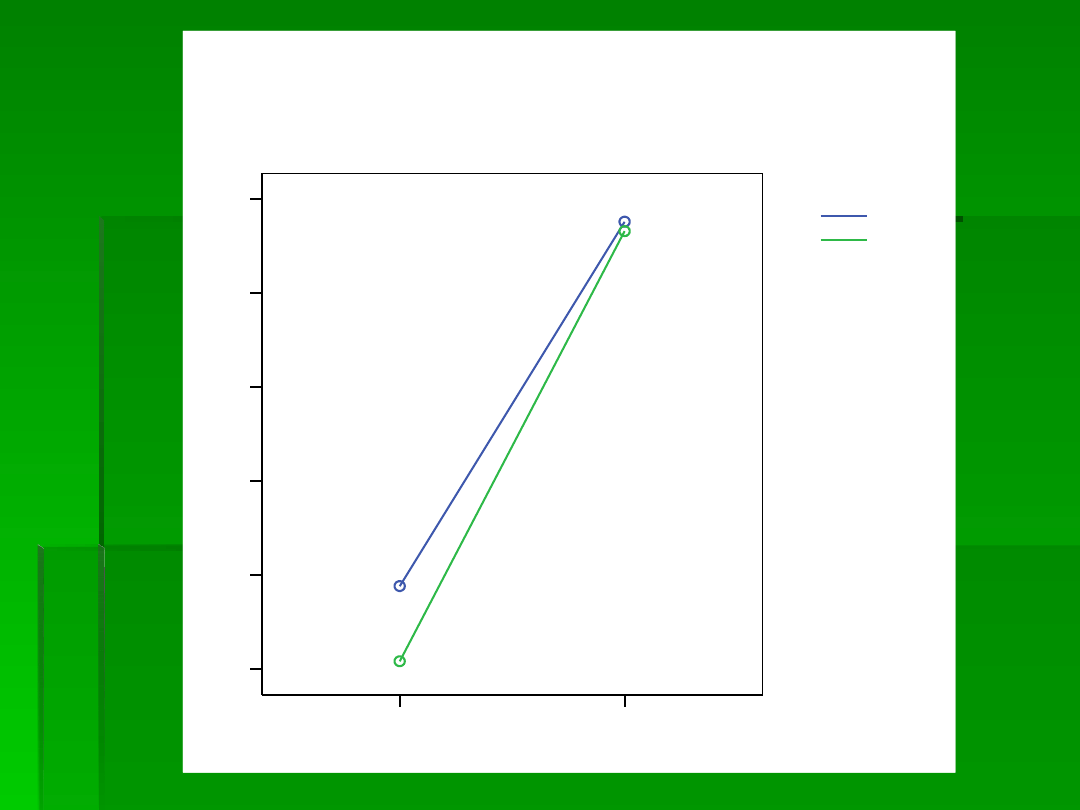
1

2

ubiór

8

10

12

14

16

18

O

sz

ac

o

w

an

e

śr

ed

n

ie

b

rz

eg

o

w

e

płeć

1

2

Oszacowane średnie brzegowe - MIARA_1