Plany z powtarzanymi

Plany z powtarzanymi

pomiarami

pomiarami

Wykład 8

(schematy ANOVA wewnątrz

osób i schematy mieszane:

między osobami i wewnątrz

osób)

Zmodyfikowane zadanie Klausa Oberauera

Zmodyfikowane zadanie Klausa Oberauera

PRÓBY POZYTYWNE

PRÓBY POZYTYWNE

(tekst był i ma ten sam kolor)

(tekst był i ma ten sam kolor)

Prezentacja

(wersja afektywna)

Ołówek Jestem mądry

Kubek Jestem

dowcipny

Test

Kubek

Jestem mądry

Odpowiedź: TAK

Zmodyfikowane zadanie Klausa Oberauera

Zmodyfikowane zadanie Klausa Oberauera

PRÓBY NOWE

PRÓBY NOWE

(tekstu nie było, kolor dowolny)

(tekstu nie było, kolor dowolny)

Prezentacja

(wersja neutralna) (wersja

afektywna)

Ołówek Jestem mądry

Kubek Jestem dowcipny

Test

Zeszyt

Jestem wesoły

Odpowiedź: NIE

Zmodyfikowane zadanie Klausa Oberauera

Zmodyfikowane zadanie Klausa Oberauera

PRÓBY INTRUZYWNE

PRÓBY INTRUZYWNE

(tekst był ale ma inny kolor)

(tekst był ale ma inny kolor)

Prezentacja

(wersja neutralna) (wersja

afektywna)

Ołówek Jestem mądry

Kubek Jestem dowcipny

Test

Kubek

Jestem mądry

Odpowiedź: NIE

Pięć powodów

Pięć powodów

wprowadzania planów z

wprowadzania planów z

powtarzanymi pomiarami

powtarzanymi pomiarami

Plan z powtarzanymi pomiarami

Plan z powtarzanymi pomiarami



repeated measures design

to taki typ planu

eksperymentalnego, w którym
każda osoba badana bierze udział
w każdym warunku eksperymentu
(tzn. pomiar jest powtarzany dla
każdej osoby)

Powód 1

Powód 1



Plan z powtarzanymi pomiarami
eliminuje zakłócający wpływ
różnic indywidualnych, ponieważ
te same osoby są przypisane do
każdego poziomu zmiennej
niezależnej

Powód 2

Powód 2



Wymaga niewielu osób badanych



Schemat 3 X 2 (między osobami)



3 (Bodziec: pozytywny vs. nowy vs. intruzywny – między)



x 2 (Kategoria: neutralny vs. negatywny – między)



Przy założeniu 20 osób w celce wymaga 3x2x20 = 120

osób



Schemat 3 X 2 (wewnątrz osób) wymaga 20 osób



Schemat 3 X 2 (mieszany)



3 (Bodziec: pozytywny vs. nowy vs. intruzywny – wewnątrz)



x 2 (Kategoria: neutralny vs. negatywny – między)



Wymaga 2 x 30 = 60 osób

Powód 3 i 4

Powód 3 i 4



Umożliwiają w efektywny sposób zbadanie

wpływu konfiguracji różnych bodźców (np.

pojedyncze vs. podwójne, łatwe vs.

trudne, obrazowe vs. werbalne...)



Niezbędny, gdy procedura badawcza

zawiera serię różnych oddziaływań (np.

ocena wielu bodźców przez jedną osobę)

Powód 5

Powód 5



Eksperyment z powtarzanymi pomiarami jest częściej

bardziej wrażliwy i ma większą moc statystyczną w

porównaniu do eksperymentu z grupami niezależnymi

(zmienne między osobami).



Wrażliwość (sensitivity) – stopień prawdopodobieństwa, z jakim

eksperyment wykryje rzeczywiście występujący wpływ zmiennej

niezależnej na zmienną zależną



Moc testu (power of test) – prawdopodobieństwo, z jakim test

statystyczny umożliwia badaczom odrzucenie fałszywej hipotezy

zerowej



Stosując ten plan łatwiej wykazać istnienie istotnych lecz

dość słabych oddziaływań

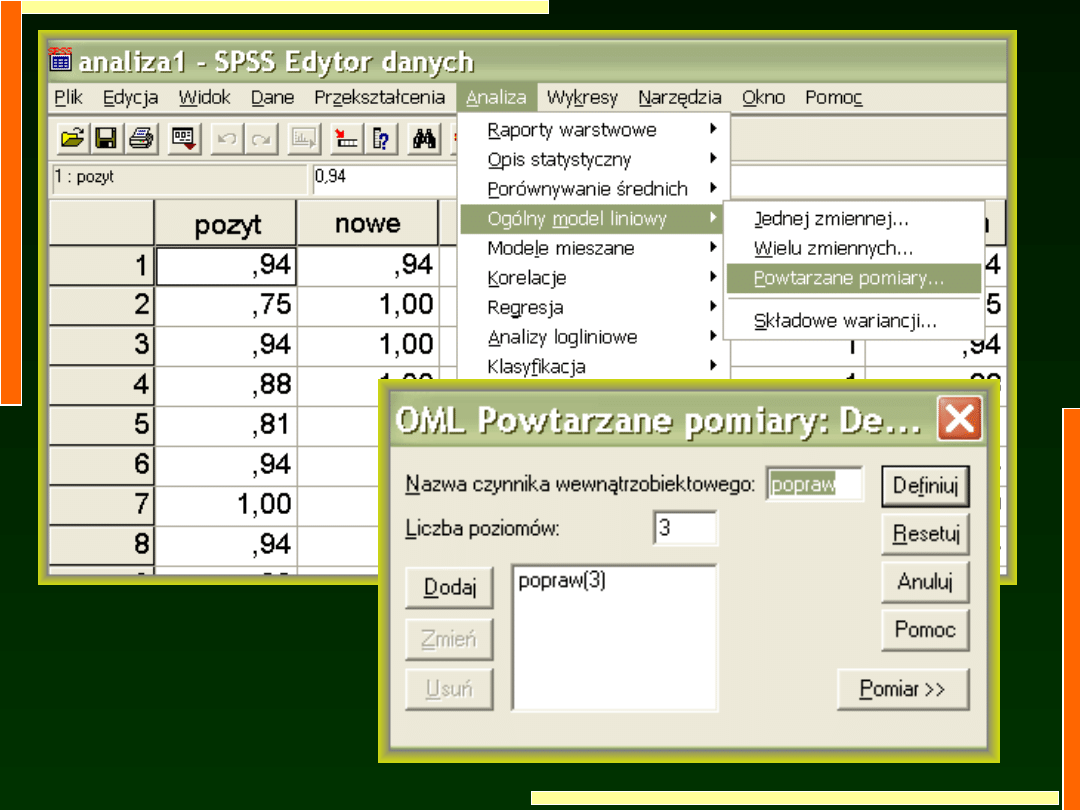
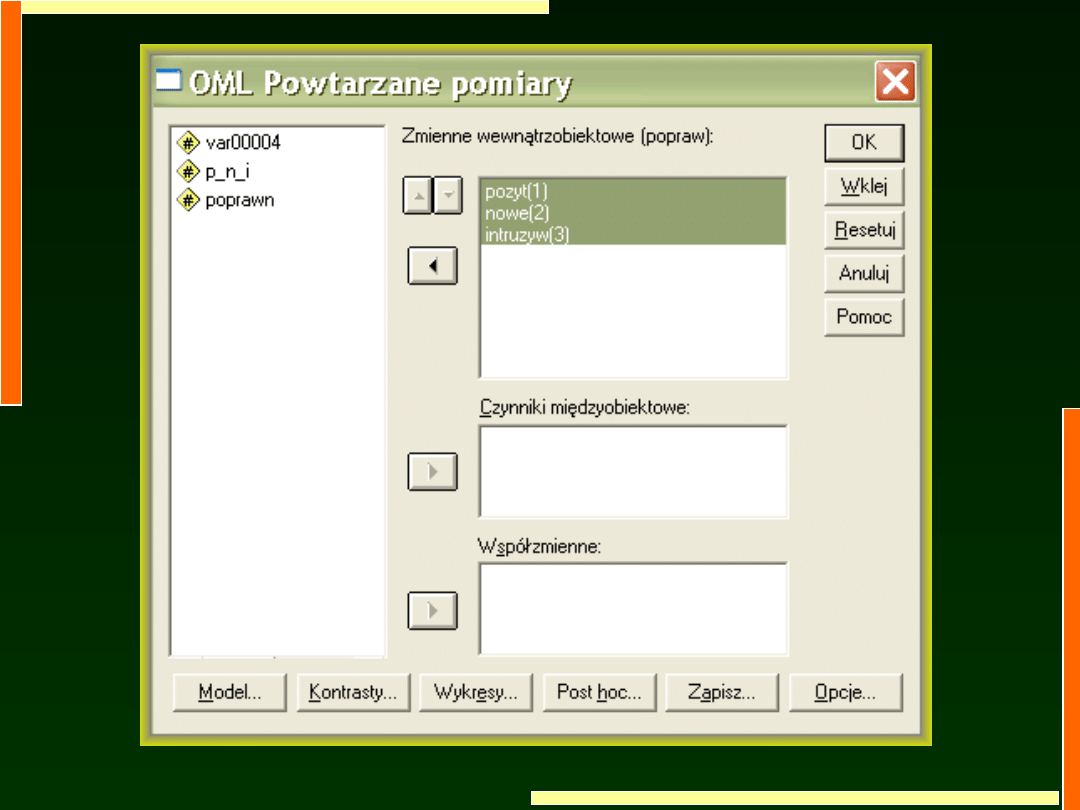
Jednoczynnikowa analiza

Jednoczynnikowa analiza

wariancji w schemacie

wariancji w schemacie

między osobami oraz

między osobami oraz

wewnątrz osób

wewnątrz osób

porównanie

Problem

Problem



Hipoteza: Najlepiej są rozpoznawane

bodźce nowe, gorzej pozytywne, zaś

najgorzej intruzywne



Schemat badania: Porównanie wyników dla

schematu między osobami i wewnątrz osób



3 (Bodziec: pozytywny vs. negatywny vs.

intruzywny – między osobami)



3 (Bodziec: pozytywny vs. negatywny vs.

intruzywny – wewnątrz osób)

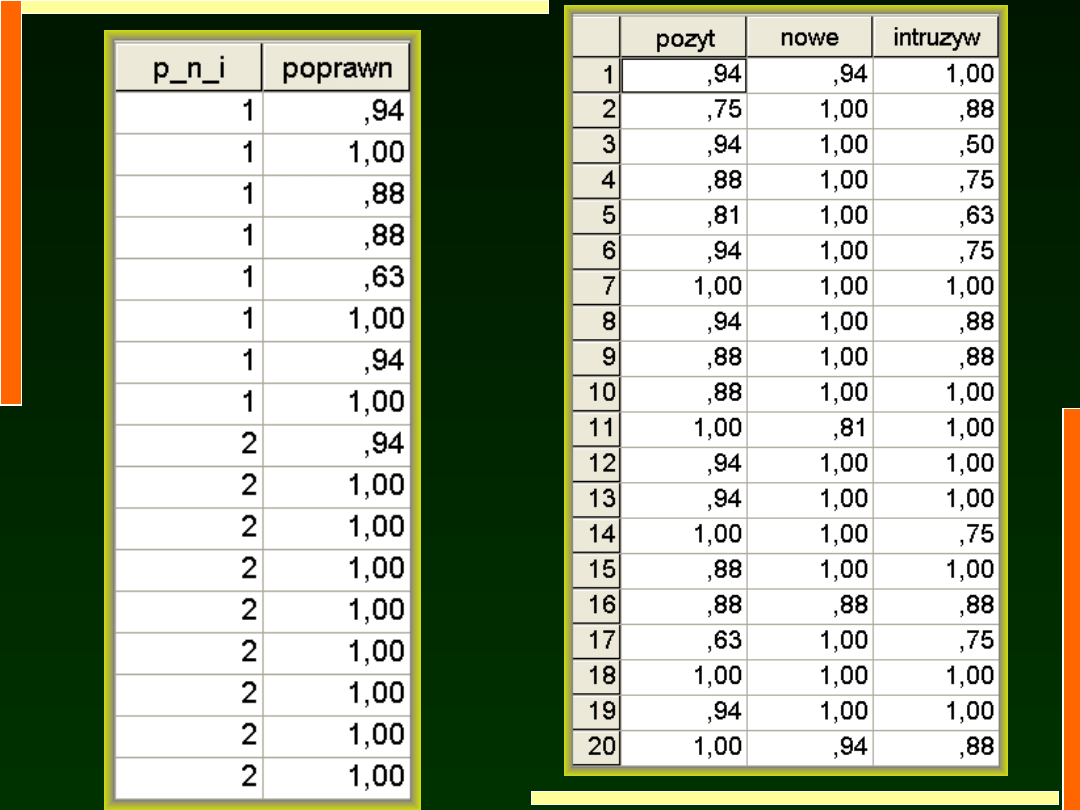
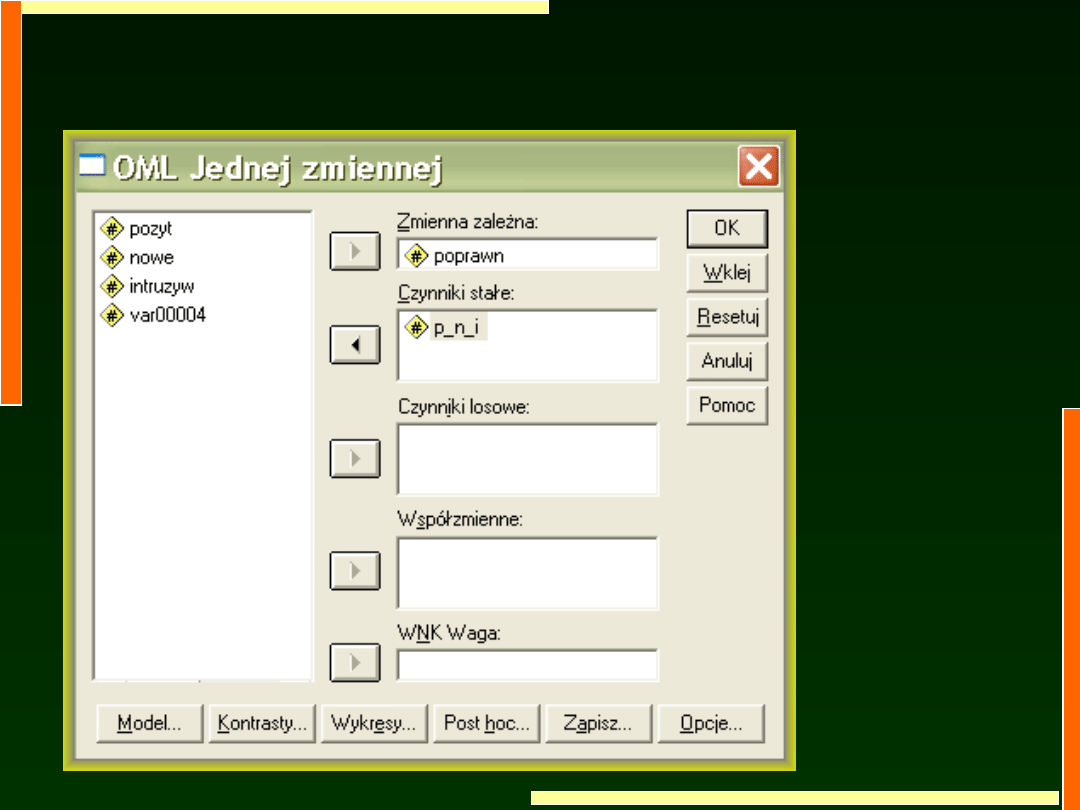
Schemat między osobami

Schemat między osobami

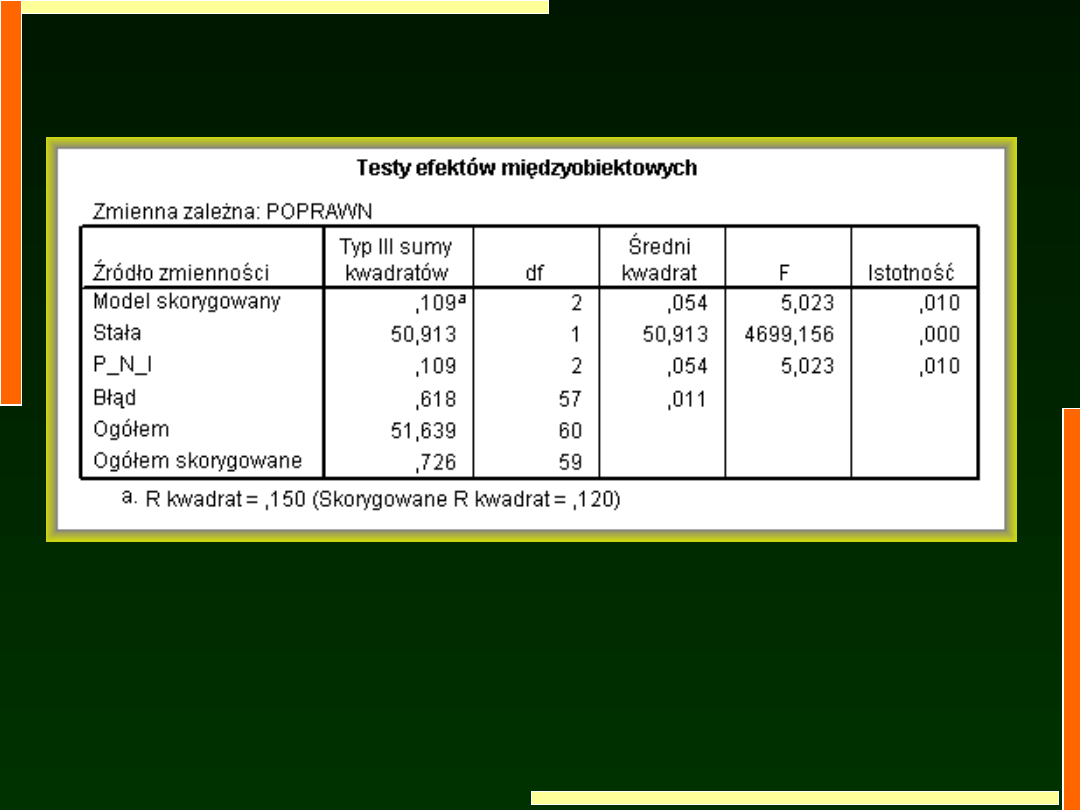
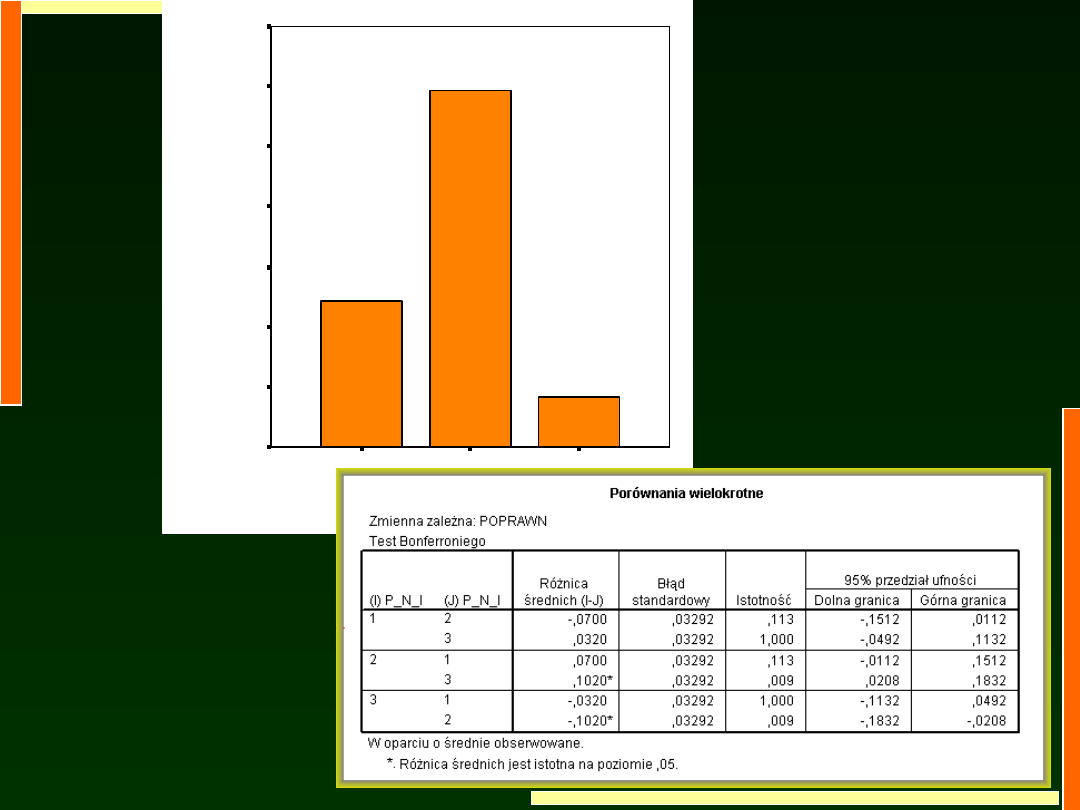
P_N_I

3

2

1

Ś

re

dn

ia

P

O

P

R

A

W

N

1,00

,98

,96

,94

,92

,90

,88

,86

INTRUZYW

NOWE

POZY T

Ś

re

dn

ia

1,00

,98

,96

,94

,92

,90

,88

,86

Zauważmy:
TE SAME średnie,
TA SAMA wariancja
wyjaśniona,
Ale:
MNIEJSZA wariancja błędu,
Wyniki bardziej istotne,
Istotne są też bardziej
subtelne porównania

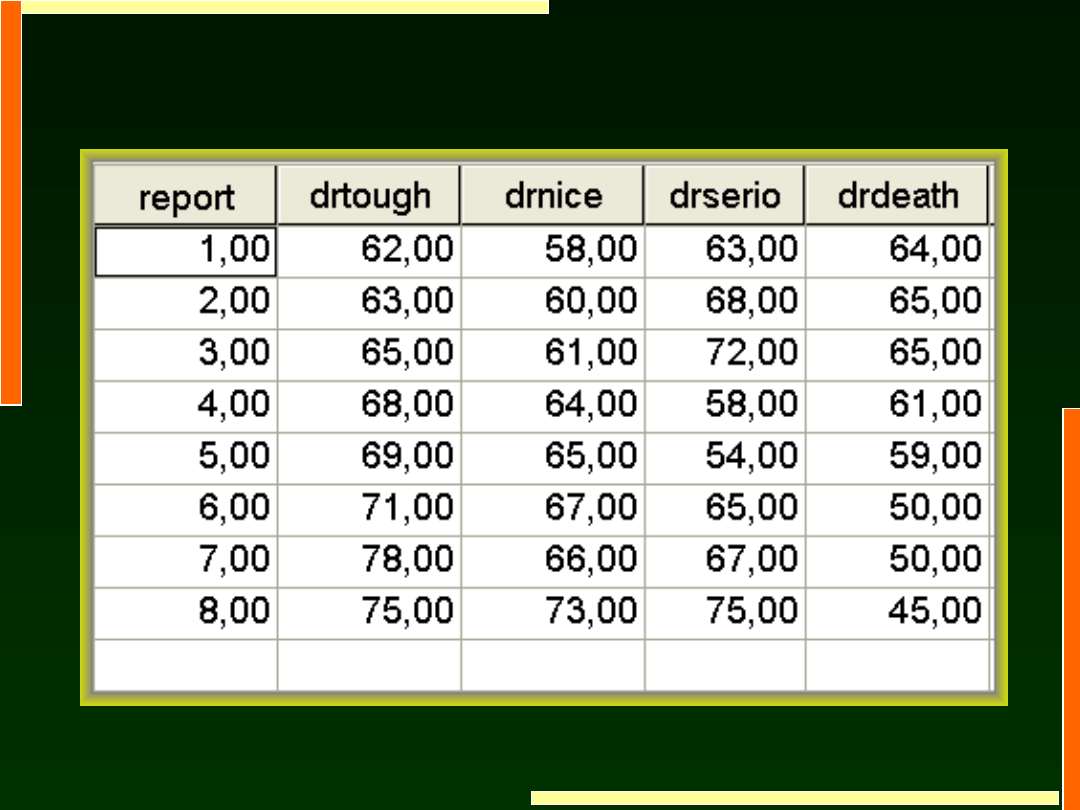
Spójność oceniania

Spójność oceniania



Powszechnie wiadomo, że
prowadzący różnią się srogością
wymagań i niektórzy mają opinię …
a inni łagodnych oceniających



Grupa 8 studentów postanowiła
sprawdzić, czy prowadzący rzeczywiście
różnią się standardami oceniania i
postanowiła dać do oceny swoje raporty
końcowe (8) czterem prowadzącym.

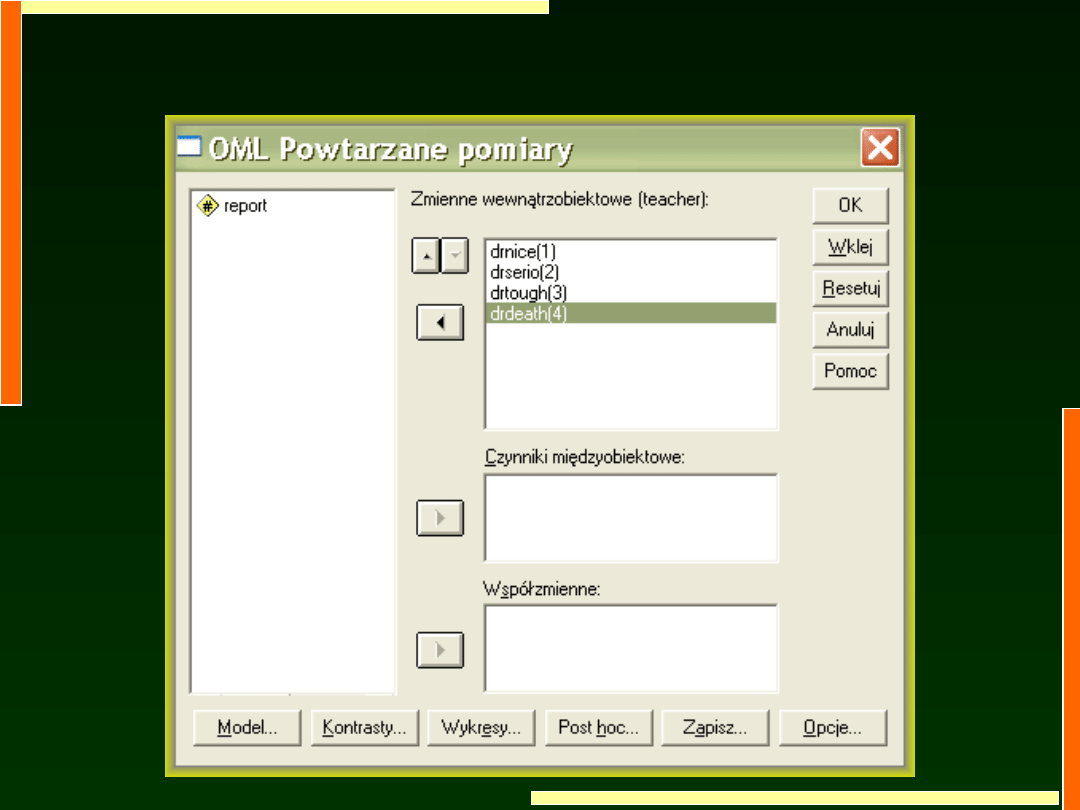
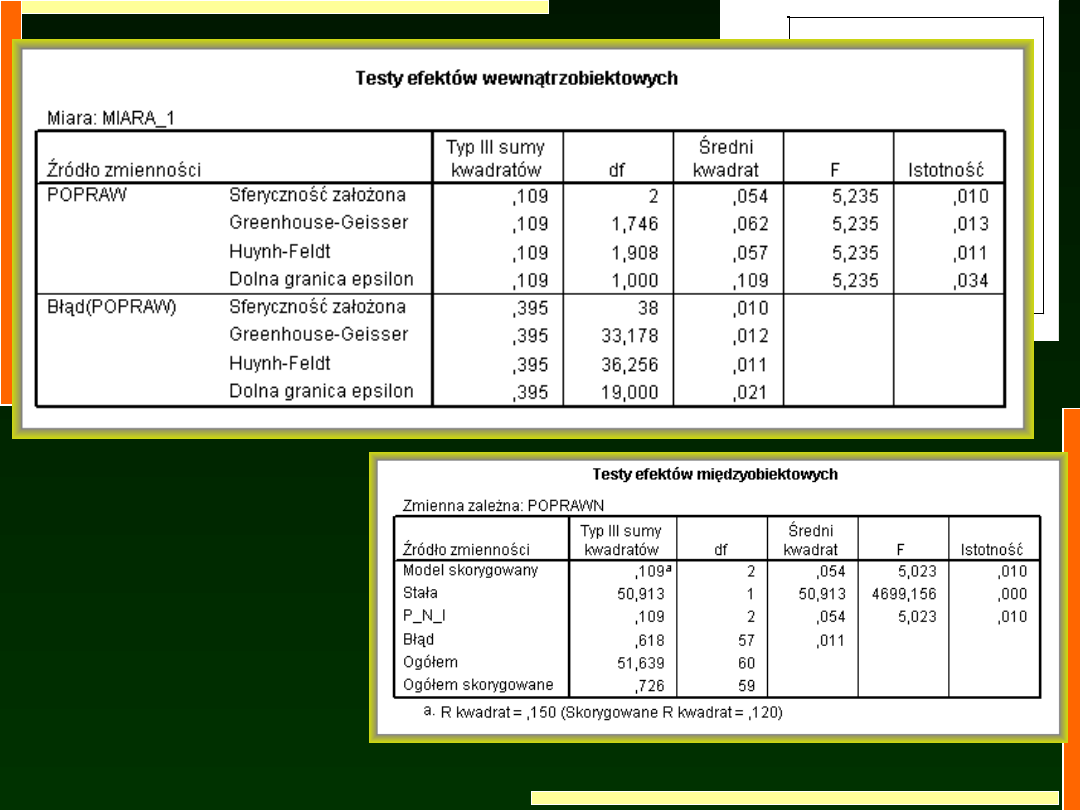
Zakładamy, że związki między parami warunków eksperymentalnych
są podobne (wariancje różnic są podobne)
Tym razem założenie to nie jest spełnione (p<0,05)

Testy efektów wewnątrzobiektowych

Miara: MIARA_1

554,125

3 184,71 3,700

,028

554,125 1,673 331,24 3,700

,063

554,125 2,137 259,33 3,700

,047

554,125 1,000 554,12 3,700

,096

1048,38

21 49,923

1048,38 11,710 89,528
1048,38 14,957 70,091
1048,38 7,000 149,77

Sferyczność założona

Greenhouse-Geisser

Huynh-Feldt

Dolna granica epsilon

Sferyczność założona

Greenhouse-Geisser

Huynh-Feldt

Dolna granica epsilon

Źródło zmienności
TEACHER

Błąd(TEACHER)

Typ III sumy

kwadratów

df

Średni

kwadrat

F

Istotność

W przypadku niespełnionego założenia o sferyczności możemy
przyjąć różne poprawki, które pokażą bardziej realistyczny wynik F

liberalny

Przy poprawkach zmianie ulegają stopnie swobody,
są one przemnażane przez statystykę epsilon
(poprawkę na zaburzenie tego założenia) – stąd też inna istotność

Z którego wiersza odczytywać wyniki?

Z którego wiersza odczytywać wyniki?



Sferyczność założona



wtedy, gdy test sferyczności jest nieistotny



The Huynh-Feldt



najmniej konserwatywny test istotności jeśli

brak założenia o sferyczności



The Greenhouse-Geisser



bardziej konserwatywny



Czasem bierze się średnią istotność z dwóch

powyższych i wybiera ten bliższy prawdzie



The lower-bound



najbardziej konserwatywny test istotności

Drugie – prostsze rozwiązanie

Drugie – prostsze rozwiązanie



W przypadku, kiedy jest niespełnione założenie o sferyczności

możemy polegać na wyniku z tabeli testu wielu zmiennych,

które nie są zależne od tego założenia,



Oparte na różnicach między poziomami czynnika (czy średnie

z różnic różnią się istotnie od zera)



Lambda Wilksa (ʎ) jest często polecana. Zapis wyniku analizy:



Lambda Wilksa = 0,259; F (3,5)=4,760; p>0,05



Warunek: N nie mniejsze niż k+10 (k – liczba poziomów

zmiennej)

Testy wielu zmiennych

b

,741 4,760

a

3,000 5,000

,063

,259 4,760

a

3,000 5,000

,063

2,856 4,760

a

3,000 5,000

,063

2,856 4,760

a

3,000 5,000

,063

Ślad Pillai

Lambda Wilksa

Ślad Hotellinga

Największy
pierwiastek Roy'a

Efekt
TEACHER

Wartość

F

df hipotezy df błędu

Istotność

Statystyka dokładna

a.

Plan: Intercept
Plan wewnątrzobiektowy: TEACHER

b.

Wady (niestety poważne...) planów

Wady (niestety poważne...) planów

badawczych w powtarzanym pomiarem

badawczych w powtarzanym pomiarem



Efekty wprawy (practice effects). Zachowanie

uczestników eksperymentu może zmieniać się po

prostu ze względu na fakt powtórnego, a nie ze

względu na manipulację zmienną niezależną

-

Pozytywne: uczenie się, nabywanie wprawy

-

Neutralne: habituacja

-

Negatywne: zmęczenie, znudzenie



Efekt wprawy może stanowić zagrożenie dla

trafności wewnętrznej eksperymentu z

powtarzaniem pomiarów, kiedy różne poziomy

zmiennej niezależnej są wprowadzane w tej

samej kolejności dla wszystkich osób badanych



Zrównoważenie (counterbalancing) nie eliminuje

efektu wprawy, ale go uśrednia

Wady (niestety poważne...) planów

Wady (niestety poważne...) planów

badawczych w powtarzanym pomiarem

badawczych w powtarzanym pomiarem



Transfer różnicowy. Pojawia się on wtedy, gdy

efekt jednego warunku utrzymuje się i wpływa

na zachowanie się osób badanych w następnych

warunkach.



Transfer różnicowy stanowi zagrożenie dla trafności

wewnętrznej ponieważ niemożliwe staje się stwierdzenie,

czy pojawiły się faktycznie różnice między warunkami.



Transfer różnicowy można wykazać analizując wpływ

kolejności warunków (np. inne efekty gdy zadanie łatwe

poprzedza zadanie trudne niż wtedy gdy zadanie trudne

poprzedza proste)



Transfer różnicowy można wykazać na podstawie

porównania wyników tej samej zmiennej zależnej

testowanej w planie powtarzanych pomiarów i planie

grup niezależnych