Różne metody

Różne metody

wprowadzania

wprowadzania

predyktorów

predyktorów

Regresje hierarchiczne i

Regresje hierarchiczne i

regresje krzywoliniowe

regresje krzywoliniowe

Regresja

wielozmiennowa

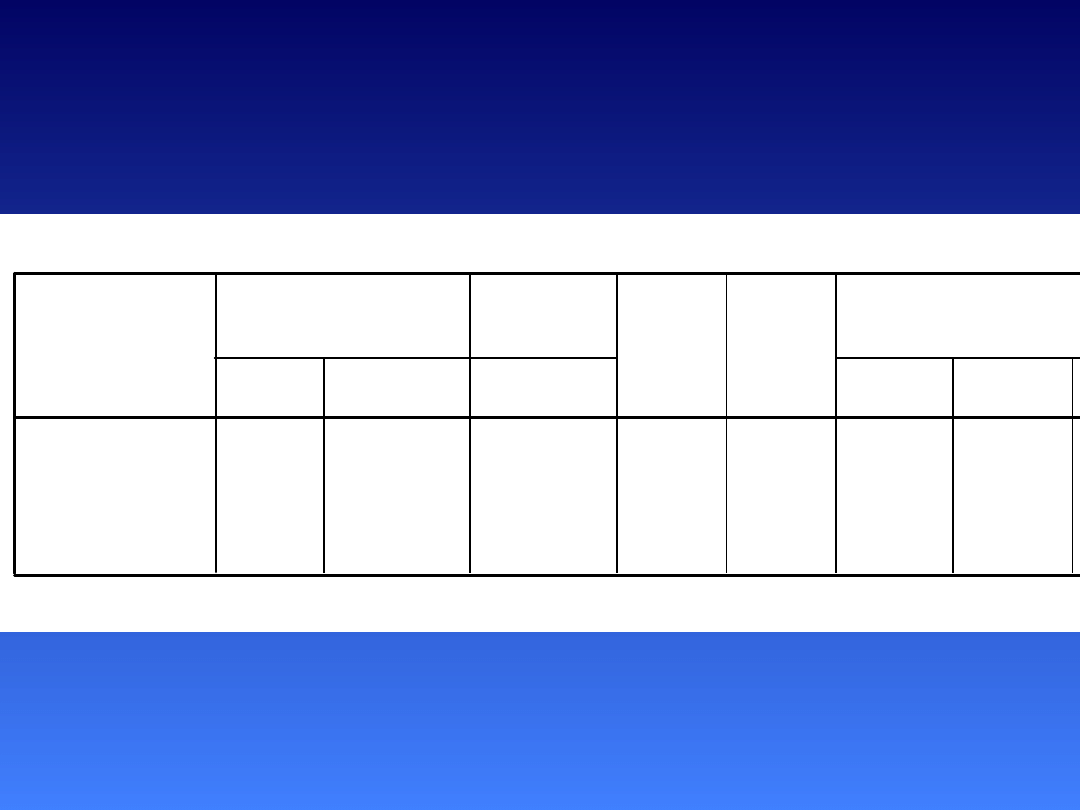
Wszystkie predyktory w

Wszystkie predyktory w

analizie:

analizie:

metoda wprowadzania

metoda wprowadzania

Współczynniki

a

,681

,874

,779

,443

,156

,130

,224

1,204

,240

,628

,234

,154

,169

,109

,252

1,546

,135

,533

,295

,198

,473

,198

,319

2,384

,025

,468

,430

,305

,441

,221

,301

1,999

,057

,549

,371

,256

(Stała)
NI_REAKT
NI_LEK
EKSTRAW
WYKSZTAŁ

Model
1

B

Błąd

standardowy

Współczynniki

niestandaryzowane

Beta

Współczynniki

standaryzowa

ne

t

Istotność

Rzędu

zerowego

Cząstkowa

Semicząs

tkowa

Korelacje

Zmienna zależna: INTEL_EM

a.

Wniosek: z czterech zmiennych, tylko ekstrawersja
jest istotnym
predyktorem inteligencji emocjonalnej

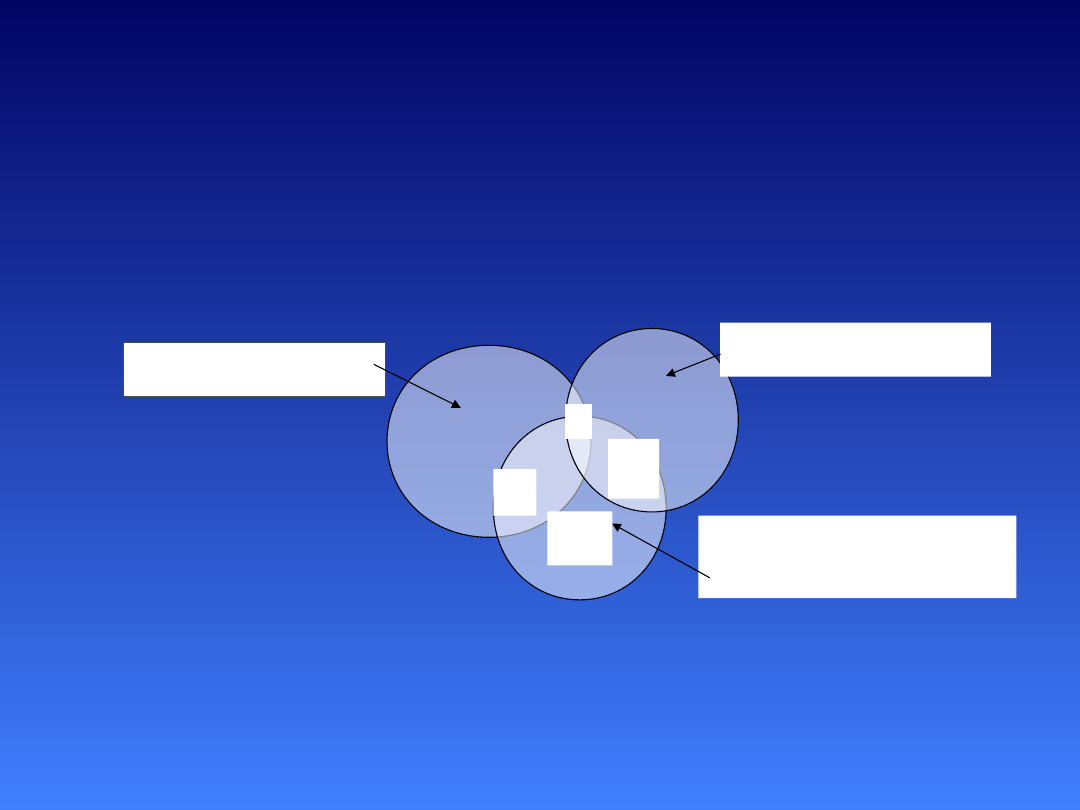
a

c

b

d

d

Predyktor X2

Predyktor
X1

Zmienna
Zależna

Ilustracja graficzna wielozmiennowej
analizy regresji
dla dwóch mało skorelowanych
predyktorów

Pole a jest to korelacja semicząstkowa zmiennej zależnej i predyktora X

1.

Pole b jest to korelacja semicząstkowa zmiennej zależnej i predyktora X

2.

Pola b + c jest to korelacja całkowita zmiennej zależnej i predyktora X

2

.

Pola a + c jest to korelacja całkowita zmiennej zależnej i predyktora X

1

.

Pola a + b + c jest to korelacja wielokrotna zmiennej zależnej i obu predyktorów.
Proporcja: a/( a + d) jest to korelacja cząstkowa zmiennej zależnej i predyktora X

1

.

Proporcja: b/( b + d) to korelacja cząstkowa zmiennej zależnej i predyktora X

2

.

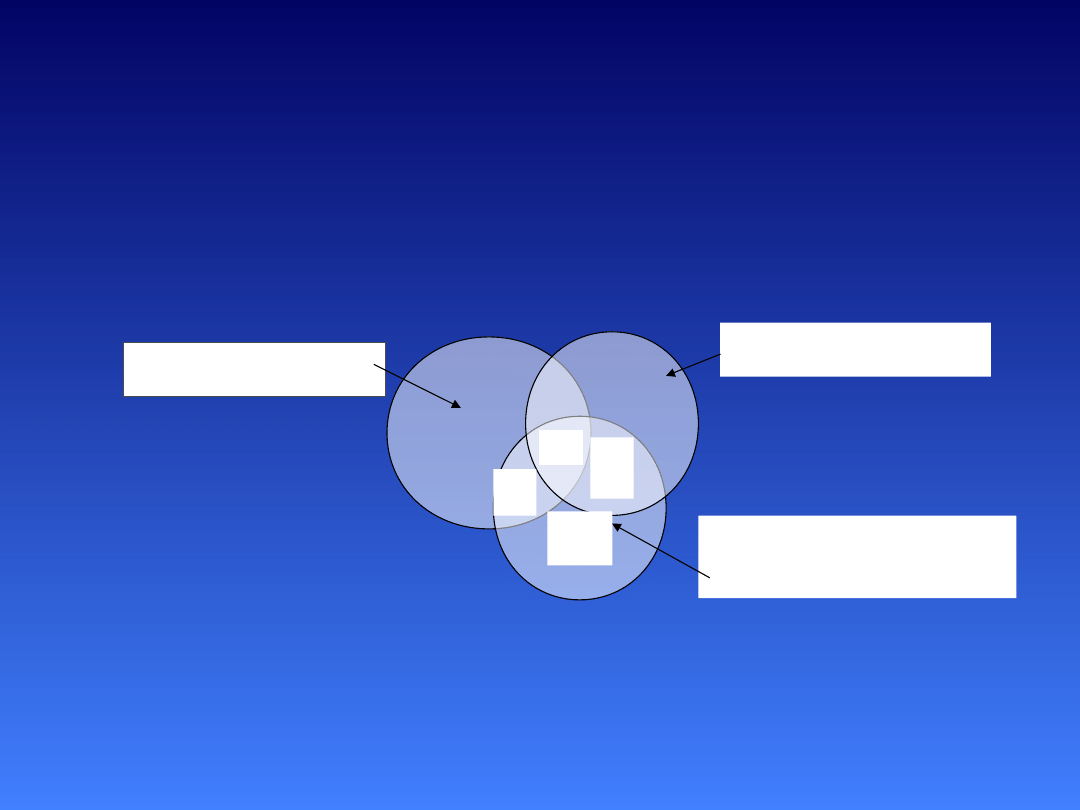
a

c b

d

d

Predyktor X2

Predyktor
X1

Zmienna
Zależna

Ilustracja graficzna wielozmiennowej
analizy regresji
dla dwóch silnie skorelowanych
predyktorów

Pole a jest to korelacja semicząstkowa zmiennej zależnej i predyktora X

1.

Pole b jest to korelacja semicząstkowa zmiennej zależnej i predyktora X

2.

Pola b + c jest to korelacja całkowita zmiennej zależnej i predyktora X

2

.

Pola a + c jest to korelacja całkowita zmiennej zależnej i predyktora X

1

.

Pola a + b + c jest to korelacja wielokrotna zmiennej zależnej i obu predyktorów.
Proporcja: a/( a + d) jest to korelacja cząstkowa zmiennej zależnej i predyktora X

1

.

Proporcja: b/( b + d) to korelacja cząstkowa zmiennej zależnej i predyktora X

2

.

Metoda wprowadzania

Metoda wprowadzania

•

Wykorzystywana do testowania

Wykorzystywana do testowania

prostych modeli mediacji

prostych modeli mediacji

Pamięć operacyjna jako

Pamięć operacyjna jako

mediator

mediator

zależności między wiekiem a

zależności między wiekiem a

rozwiązywaniem sylogizmów

rozwiązywaniem sylogizmów

Wiek

Sylogizmy

1. Zależność istotna
2. Może nie jest to wpływ bezpośredni, ale upośredniony
przez inną ważną zmienną?
3. Sprawdzamy rolę pamięci operacyjnej, jako mediatora,
pierwotnej zależności

*

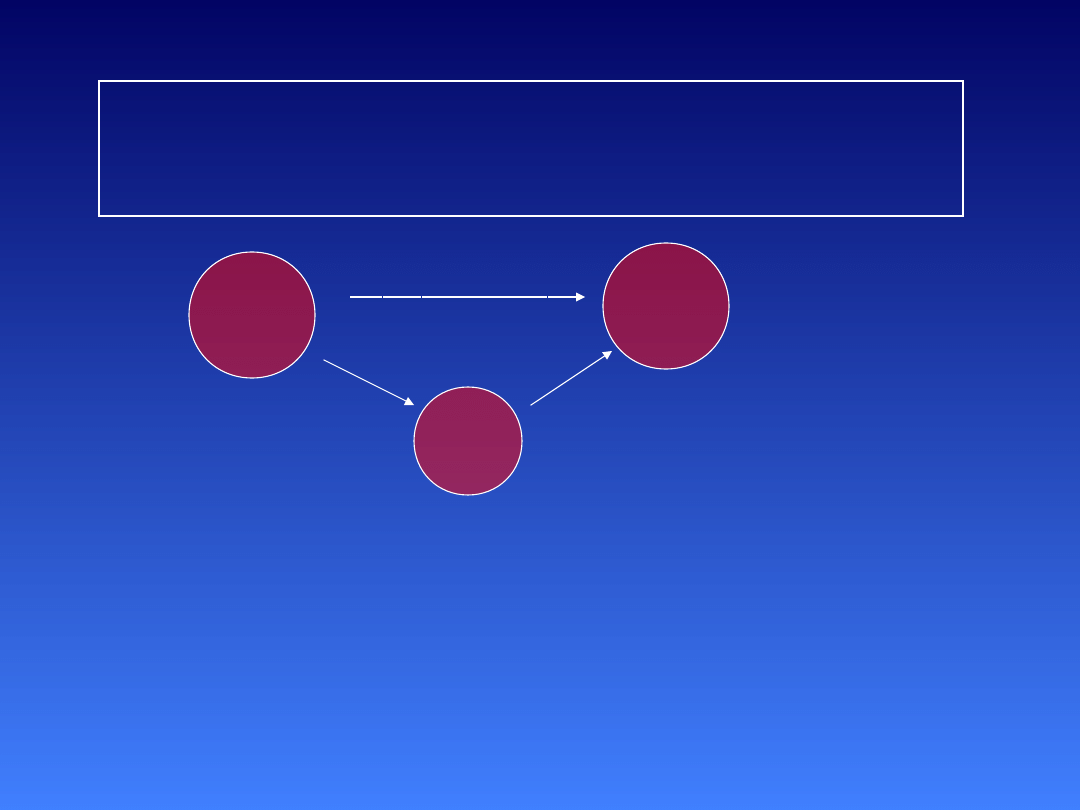
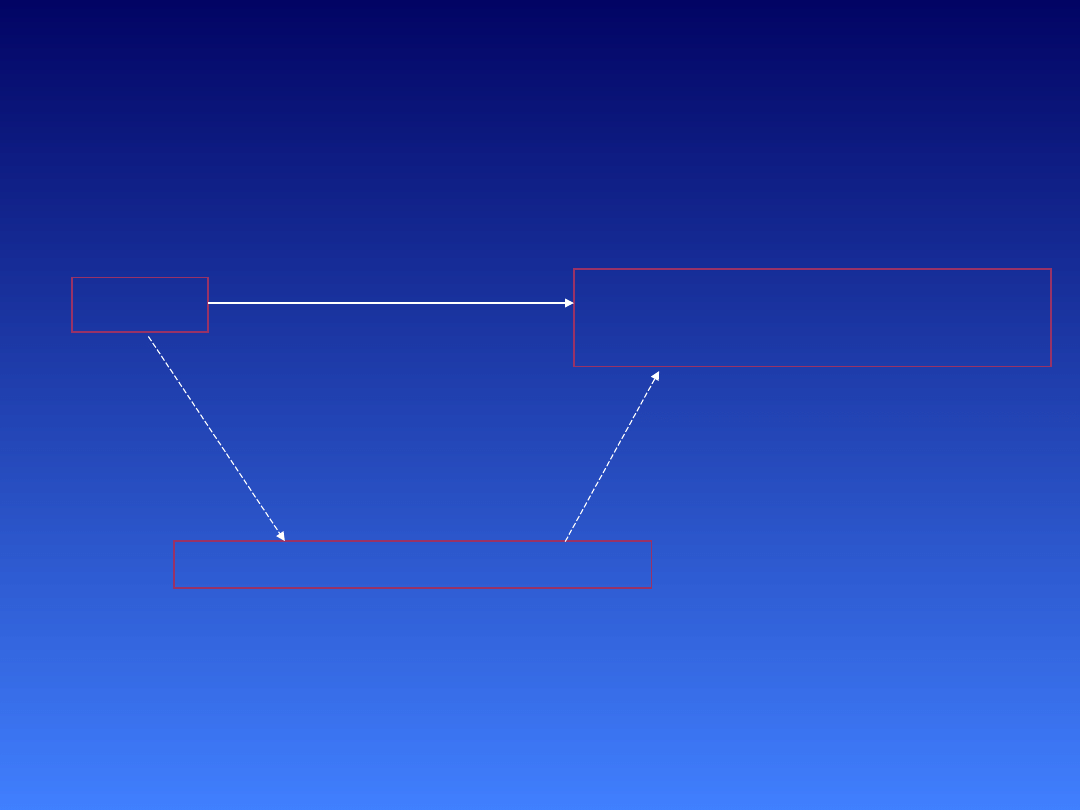
Pamięć operacyjna jako mediator zależności

Pamięć operacyjna jako mediator zależności

miedzy wiekiem a rozwiązywaniem

miedzy wiekiem a rozwiązywaniem

sylogizmów: trzy warunki

sylogizmów: trzy warunki

Wiek

Pamięć

Operac.

Sylogizmy

1. Istotny związek między predyktorem a mediatorem
2. Istotny związek między mediatorem z zmienną zależną
3. Pierwotny związek między predyktorem a zmienną zależną
staje się nieistotny lub ulega istotnemu osłabieniu

*

*

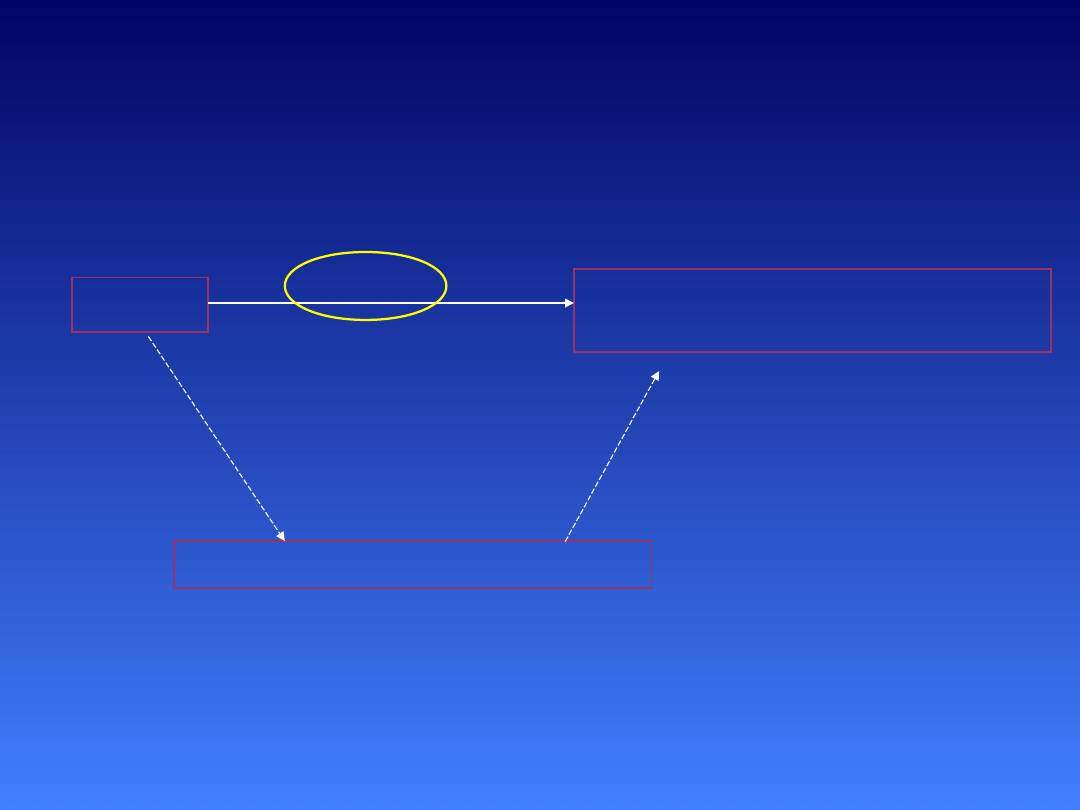
Związki korelacyjne

Związki korelacyjne

WIEK

LICZBA ROZWIAZANYCH
SYLOGIZMÓW

POJEMNOŚĆ WM (RSPAN)

-0,466***

-0,705***

0,51***

Zależności między zmiennymi (

r Pearsona)

Analiza regresji. Zmienna zależna: rozwiązywanie

Analiza regresji. Zmienna zależna: rozwiązywanie

sylogizmów. Predyktory: wiek i pamięć operacyjna

sylogizmów. Predyktory: wiek i pamięć operacyjna

Współczynniki

a

10,226

,960

10,652

,000

1,120

,836

,218

1,339

,186

,140

,065

,353

2,166

,035

(Stała)
WIEK_KAT
RSPAN

Model
1

B

Błąd

standardowy

Współczynniki

niestandaryzowane

Beta

Współczynniki

standaryzowa

ne

t

Istotność

Zmienna zależna: POPR_SYL

a.

WIEK

ILOŚĆ ROZWIAZANYCH
SYLOGIZMÓW

POJEMNOŚĆ WM (RSPAN)

-0,218 n.i.

-0,705***

0,353*

Zależności między zmiennymi, po uwzględnieniu WM jako mediatora

(współczynniki Beta w analizie regresji)

Selekcja Postępująca

Selekcja Postępująca

Współczynniki

a

3,182

,545

5,837

,000

,437

,102

,628

4,273

,000

1,884

,781

2,411

,023

,376

,100

,539

3,753

,001

,468

,213

,316

2,197

,037

(Stała)
NI_REAKT
(Stała)
NI_REAKT
EKSTRAW

Model
1

2

B

Błąd

standardowy

Współczynniki

niestandaryzowane

Beta

Współczynniki

standaryzowa

ne

t

Istotność

Zmienna zależna: INTEL_EM

a.

Metoda eliminacji

Metoda eliminacji

wstecznej

wstecznej

Współczynniki

a

,681

,874

,779

,443

,156

,130

,224

1,204

,240

,628

,234

,154

,169

,109

,252

1,546

,135

,533

,295

,198

,473

,198

,319

2,384

,025

,468

,430

,305

,441

,221

,301

1,999

,057

,549

,371

,256

,527

,872

,605

,551

,242

,092

,361

2,641

,014

,533

,460

,341

,523

,195

,353

2,680

,013

,468

,465

,346

,555

,201

,379

2,767

,010

,549

,477

,358

(Stała)
NI_REAKT
NI_LEK
EKSTRAW
WYKSZTAŁ
(Stała)
NI_LEK
EKSTRAW
WYKSZTAŁ

Model
1

2

B

Błąd

standardowy

Współczynniki

niestandaryzowane

Beta

Współczynniki

standaryzowa

ne

t

Istotność

Rzędu

zerowego

Cząstkowa

Semicząs

tkowa

Korelacje

Zmienna zależna: INTEL_EM

a.

Wniosek: okazuje się, że aż trzy z czterech wprowadzonych
predyktorów są istotnie powiązane z intel. emocjonalną

Metoda krokowa

Metoda krokowa

Współczynniki

a

3,182

,545

5,837

,000

,437

,102

,628

4,273

,000

,628

,628

,628

1,884

,781

2,411

,023

,376

,100

,539

3,753

,001

,628

,586

,518

,468

,213

,316

2,197

,037

,468

,389

,303

(Stała)
NI_REAKT
(Stała)
NI_REAKT
EKSTRAW

Model
1

2

B

Błąd

standardowy

Współczynniki

niestandaryzowane

Beta

Współczynniki

standaryzowa

ne

t

Istotność

Rzędu

zerowego

Cząstkowa

Semicząs

tkowa

Korelacje

Zmienna zależna: INTEL_EM

a.

Wniosek: z czterech wprowadzonych, dwa (niska
reaktywność
oraz ekstrawersja) są istotnymi predyktorami intel.
emocjonalnej

Metoda hierarchiczna:

Metoda hierarchiczna:

służy testowaniu precyzyjnie

służy testowaniu precyzyjnie

sformulowanych hipotez

sformulowanych hipotez

•

Hipoteza o roli wykształcenia:

Hipoteza o roli wykształcenia:

Nawet jeśli uprzednio uwzględni się wpływ

Nawet jeśli uprzednio uwzględni się wpływ

czynników emocjonalno-osobowościowych, to

czynników emocjonalno-osobowościowych, to

wykształcenie okaże się istotnym

wykształcenie okaże się istotnym

predyktorem inteligencji emocjonalnej

predyktorem inteligencji emocjonalnej

•

Analiza w dwóch blokach

Analiza w dwóch blokach

1.

1.

W pierwszym bloku: lęk, ekstrawersja

W pierwszym bloku: lęk, ekstrawersja

2.

2.

W drugim bloku: Wykształcenie

W drugim bloku: Wykształcenie

Wyniki hierarchicznej analizy

Wyniki hierarchicznej analizy

regresji

regresji

Model - Podsumowanie

,662

a

,438

,396

1,30550

,438

10,517

2

27

,000

,752

b

,566

,516

1,16929

,128

7,657

1

26

,010

Model
1
2

R

R-kwadrat

Skorygowane

R-kwadrat

Błąd

standardowy

oszacowania

Zmiana

R-kwadrat

Zmiana F

df1

df2

Istotność

zmiany F

Statystyki zmiany

Predyktory: (Stała), EKSTRAW, NI_LEK

a.

Predyktory: (Stała), EKSTRAW, NI_LEK, WYKSZTAŁ

b.

Współczynniki

a

1,694

,852

1,987

,057

,317

,098

,474

3,246

,003

,533

,530

,468

,588

,217

,396

2,716

,011

,468

,463

,392

,527

,872

,605

,551

,242

,092

,361

2,641

,014

,533

,460

,341

,523

,195

,353

2,680

,013

,468

,465

,346

,555

,201

,379

2,767

,010

,549

,477

,358

(Stała)
NI_LEK
EKSTRAW
(Stała)
NI_LEK
EKSTRAW
WYKSZTAŁ

Model
1

2

B

Błąd

standardowy

Współczynniki

niestandaryzowane

Beta

Współczynniki

standaryzowa

ne

t

Istotność

Rzędu

zerowego

Cząstkowa

Semicząs

tkowa

Korelacje

Zmienna zależna: INTEL_EM

a.

Podsumowanie

Podsumowanie

hierarchicznej analizy

hierarchicznej analizy

regresji

regresji

R

R

2

2

Wzros

Wzros

t R

t R

2

2

F -

F -

wzrost

wzrost

Beta

Beta

(wejści

(wejści

e)

e)

Ni_Lęk

Ni_Lęk

Ekstr.

Ekstr.

.

.

438

438

.438

.438

10.52

10.52

* * *

* * *

0,47

0,47

* *

* *

0,40

0,40

*

*

Wykszt.

Wykszt.

.

.

566

566

.128

.128

7,66

7,66

* *

* *

0,38

0,38

* *

* *

* p < 0,05; * * p < 0,01;

* p < 0,05; * * p < 0,01;

* * * p < 0,001;

* * * p < 0,001;