Dwuczynnikowa i

Dwuczynnikowa i

trójczynnikowa analiza

trójczynnikowa analiza

wariancji

wariancji

Wykład 7

Analizy statystyczne

(schematy ANOVA między

osobami)

Plan

Plan



Interpretacja efektów głównych i
interakcyjnych



Rola porównań planowanych w
szczegółowej interpretacji efektów
interakcyjnych



Analiza efektów prostych

Shaughnessy inni (2002) Metody badawcze w

Shaughnessy inni (2002) Metody badawcze w

psychologii, Rozdział 8 (313-345)

psychologii, Rozdział 8 (313-345)



Najprostszym planem złożonym
jest schemat 2x2 – dwie zmienne
niezależne mają po 2 poziomy

Schemat 2 x 2 ANOVA

Schemat 2 x 2 ANOVA

Interpretacja efektów głównych i

interakcyjnych

Efekt główny

Efekt główny



Efekt główny jest to ogólny wpływ
zmiennej niezależnej i wyraża
różnicę między poziomami jednej
zmiennej niezależnej uśrednionymi
poprzez poziomy drugiej zmiennej
niezależnej

Efekty interakcyjne (zmodyfikowane

Efekty interakcyjne (zmodyfikowane

definicje w por. do podręcznika)

definicje w por. do podręcznika)

Interakcja pierwszego stopnia (dwóch

zmiennych) pojawia się wtedy, gdy wpływ
jednej zmienne niezależnej zmienia się z
zależności od poziomu drugiej zmiennej
niezależnej

Interakcja drugiego stopnia (trzech

zmiennych) występuje wtedy interakcja
pierwszego stopnia zmienia się w
zależności od poziomu trzeciej zmiennej
niezależnej

Procesy uwagi

Procesy uwagi

Przykład w oparciu o

procedurę

DIVA

Analiza efektów prostych

Schemat badania i HIPOTEZY

Schemat badania i HIPOTEZY



Schemat badania 2x2



2 (Grupa: kontrolna vs. trening bezradności –

między osobami) x 2 (Zadanie: zadanie pojedyncze

vs. zadanie podwójne – między osobami)



H1. Zadanie podwójne (z obciążeniem poznawczym

będzie rozwiązywane gorzej jeśli chodzi o liczbę

trafień niż zadanie pojedyncze



H2. Obciążenie poznawcze będzie moderatorem

zależności między treningiem bezradności a liczbą

trafień (istotna interakcja Grupa x Zadanie), istotne

różnice dla treningu wystąpią tylko w przypadku

zadania podwójnego.

ZADANIE

podwójne

pojedyncze

lic

zb

a

tr

afi

eń

3,0

2,9

2,8

2,7

2,6

2,5

2,4

GR

kontrolna

treningowa

Testy F w dwuczynnikowej ANOVie

Testy F w dwuczynnikowej ANOVie



W dwuczynnikowej analizie wariancji mamy do czynienia

z trzema testami F:



1) dla efektu głównego pierwszego czynnika



2) dla efektu głównego drugiego czynnika



3) dla efektu interakcyjnego



W liczniku każdego z tych stosunków znajdzie się

wariancja międzygrupowa, która odnosi się do porównań

między średnimi dla danego efektu głównego lub

interakcyjnego



Natomiast wariancja wewnątrzgrupowa we wszystkich

trzech testach F będzie taka sama - jest to zawsze

średnia oszacowań wariancji w populacji utworzona z

wyników wewnątrz każdej z celek (wariancja błędu)

Testy efektów międzyobiektowych

Zmienna zależna: WYNIK

2,674

a

3

,891 13,458

,000

592,688

1 592,69 8950,2

,000

,023

1

,023

,342

,561

2,581

1

2,581 38,974

,000

,070

1

,070

1,059

,307

5,033

76

,066

600,395

80

7,706

79

Źródło zmienności
Model skorygowany
Stała
GR
ZADANIE
GR * ZADANIE
Błąd
Ogółem
Ogółem skorygowane

Typ III sumy

kwadratów

df

Średni

kwadrat

F

Istotność

R kwadrat = ,347 (Skorygowane R kwadrat = ,321)

a.

Dyskusja wyników (standard APA)

Dyskusja wyników (standard APA)



Hipoteza 1 została potwierdzona, w
zadaniu podwójnym było istotnie mniej
trafień (M = 2,55; SD=3,4) niż w zadaniu
pojedynczm (M = 2,90),



F (1, 76) = 38,97; p < 0,001



Hipoteza druga nie została potwierdzona,
gdyż interakcja Grupa x Zadanie okazała
się nieistotna statystycznie,



F (1, 76) = 1, 06; p < 0,31

Schemat badania i HIPOTEZY

Schemat badania i HIPOTEZY



Schemat badania 2x2



2 (Wiek: młodsi dorośli vs. starsi dorośli – między

osobami) x 2 (Zadanie: zadanie pojedyncze vs.

zadanie podwójne – między osobami)



H1. Zadanie podwójne (z obciążeniem poznawczym)

będzie rozwiązywane gorzej zarówno jeśli chodzi o

liczbę trafień jak i czas reakcji niż zadanie pojedyncze



H2. Obciążenie poznawcze będzie moderatorem

zależności między wiekiem a czasem reakcji (istotna

interakcja Grupa x Zadanie), istotne różnice dla wieku

wystąpią tylko w przypadku zadania podwójnego.



H3. Obciążenie poznawcze będzie silniejszym

moderatorem powyższej zależności dla czasu reakcji

niż dla poprawności

Procesy selektywnej uwagi a wiek

Procesy selektywnej uwagi a wiek

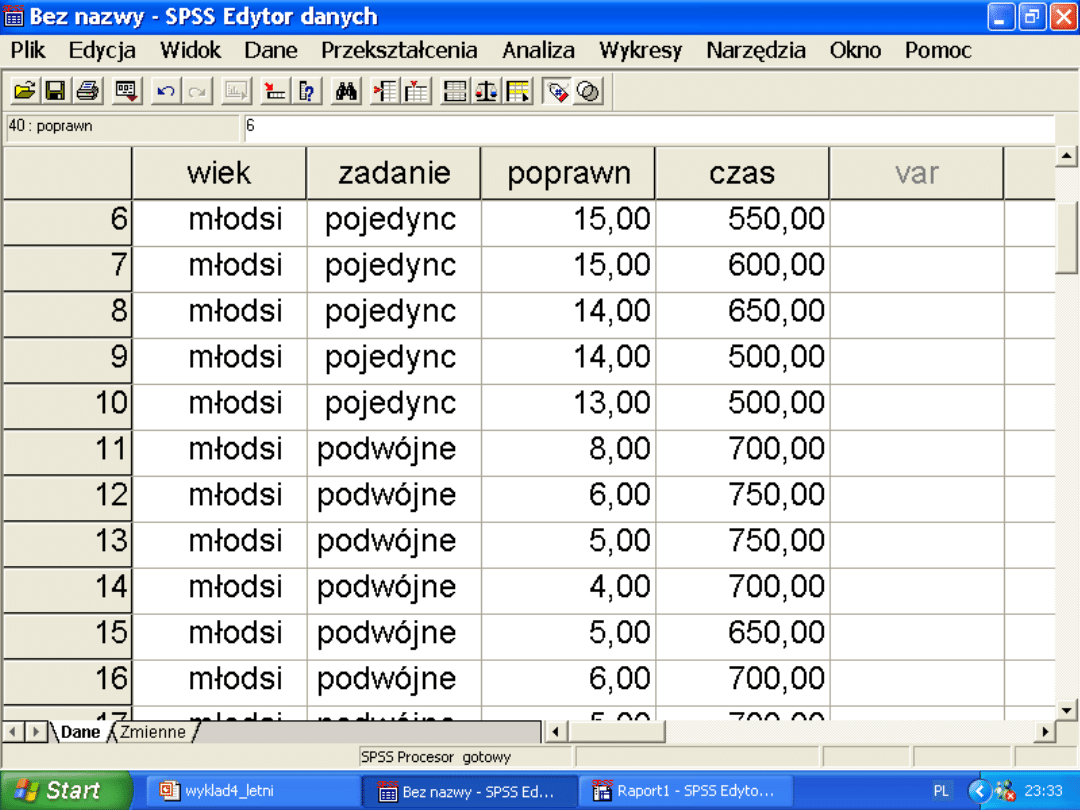
Zmienne niezależne

WIEK

MŁODSI

STARSI

ZADANI

E

Pojedyncz
e

Podwójne

Testy efektów międzyobiektowych

Zmienna zależna: POPRAWN

659,50

a

3 219,8 299,8 ,000

4040,1

1 4040 5509 ,000

,900

1 ,900 1,227 ,275

656,10

1 656,1 894,7 ,000

2,500

1 2,500 3,409 ,073

26,400

36 ,733

4726,0

40

685,90

39

Źródło zmienności
Model skorygowany

Stała

WIEK

ZADANIE

WIEK * ZADANIE

Błąd

Ogółem

Ogółem skorygowane

Typ III sumy

kwadratów

df

Średni

kwadrat

F

Istotność

R kwadrat = ,962 (Skorygowane R kwadrat = ,958)

a.

Pełna tabelka

Pełna tabelka

Istotny efekt główny zmiennej Zadanie F(1,36)=894,7; p<0,001

Wariancja nie wyjaśniona – błędu wykorzystywana w mianowniku każdej
statystyki F

Testy efektów międzyobiektowych

Zmienna zależna: CZAS

453500,0

a

3 151167 60,133

,000

1,8E+07

1 2,E+07 7142,7

,000

342250,0

1 342250 136,144

,000

81000,00

1

81000 32,221

,000

30250,00

1

30250 12,033

,001

90500,00

36 2513,9

1,9E+07

40

544000,0

39

Źródło zmienności
Model skorygowany
Stała
WIEK
ZADANIE
WIEK * ZADANIE
Błąd
Ogółem
Ogółem skorygowane

Typ III sumy

kwadratów

df

Średni

kwadrat

F

Istotność

R kwadrat = ,834 (Skorygowane R kwadrat = ,820)

a.

Czas wykonania głównego zadania

Czas wykonania głównego zadania

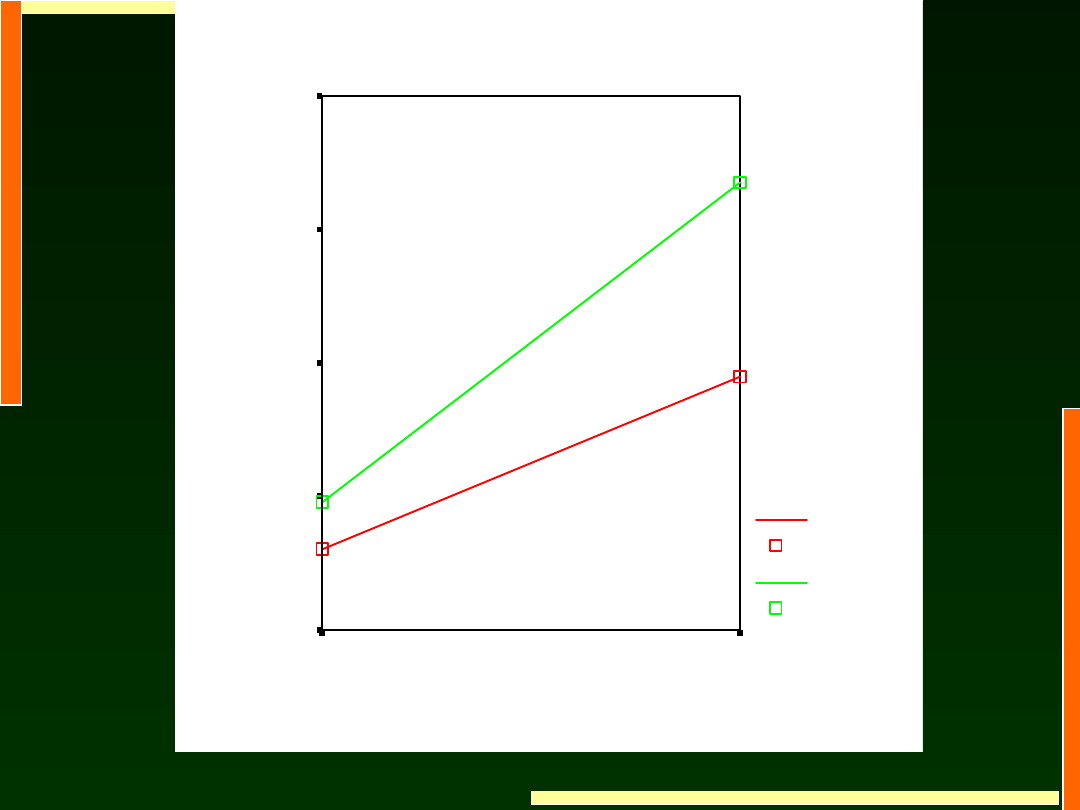
Oszacowane średnie brzegowe - CZAS

WIEK

starsi

młodsi

O

sz

ac

ow

an

e

śr

ed

ni

e

br

ze

go

w

e

900

800

700

600

500

ZADANIE

pojedyncze

podwójne

Jeśli efekt interakcji jest istotny

Jeśli efekt interakcji jest istotny



Patrzymy na efekty proste, szukamy,
które grupy różnią się między sobą
istotnie



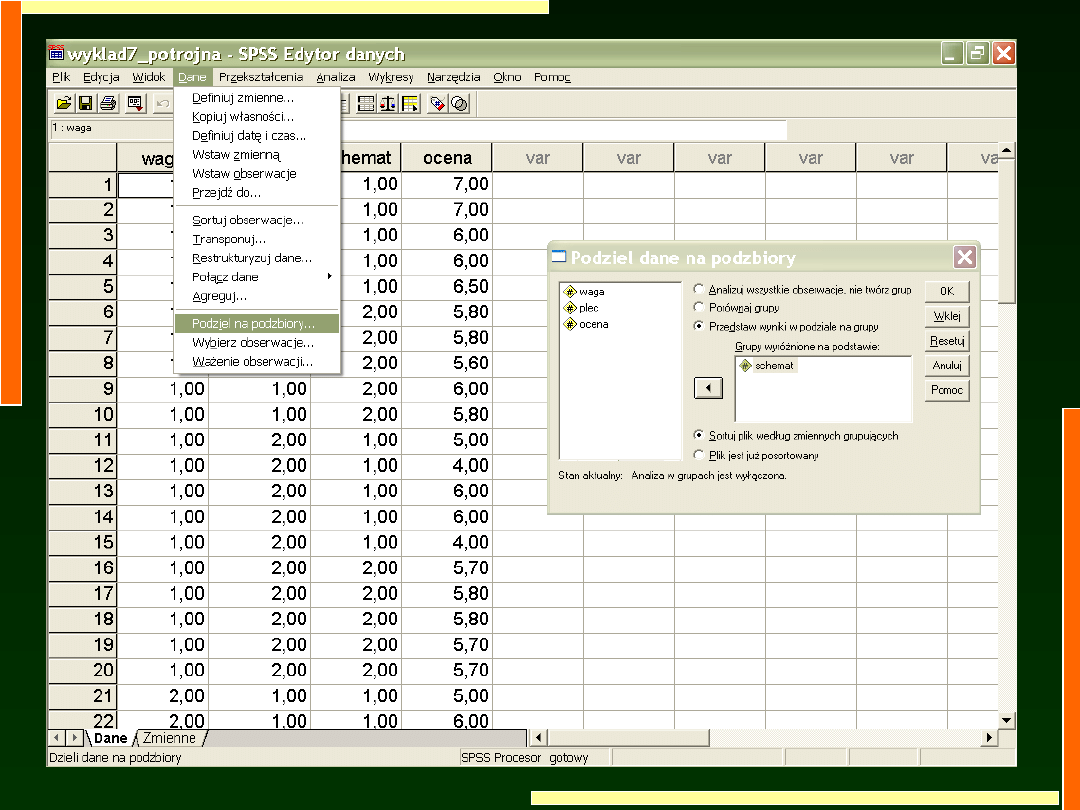
Możemy przeprowadzić analizy testami t dla
grup niezależnych wykorzystując opcję
podziel na podzbiory.



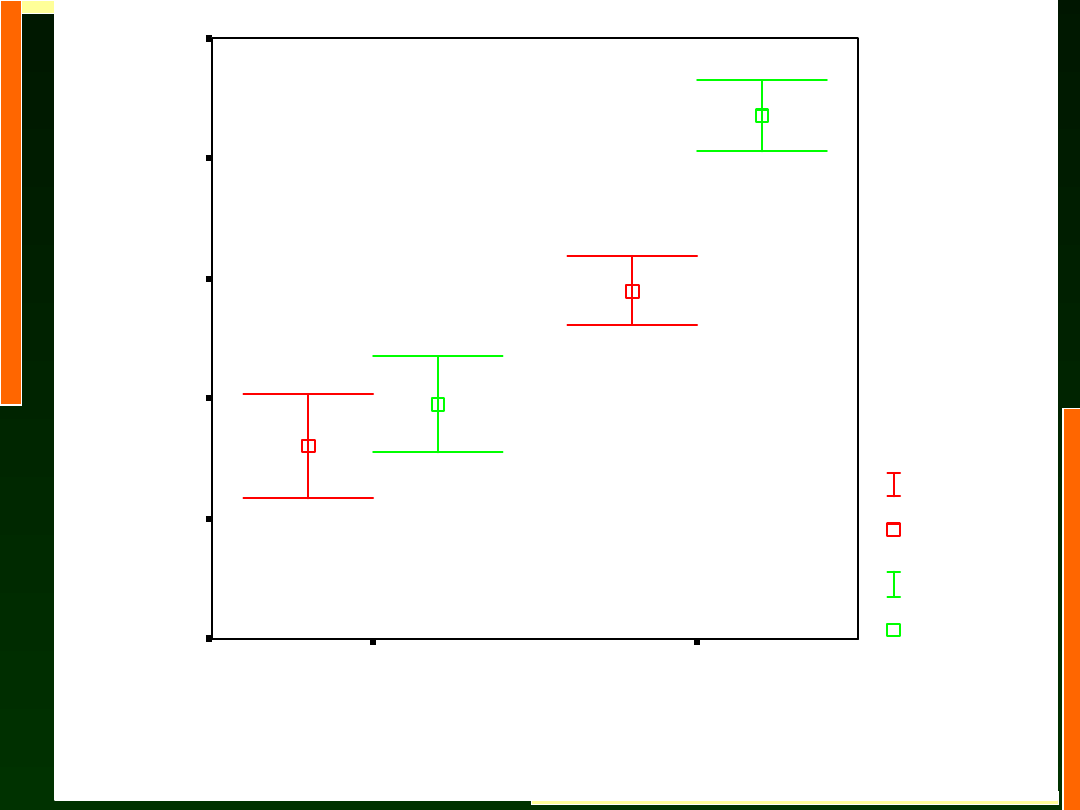
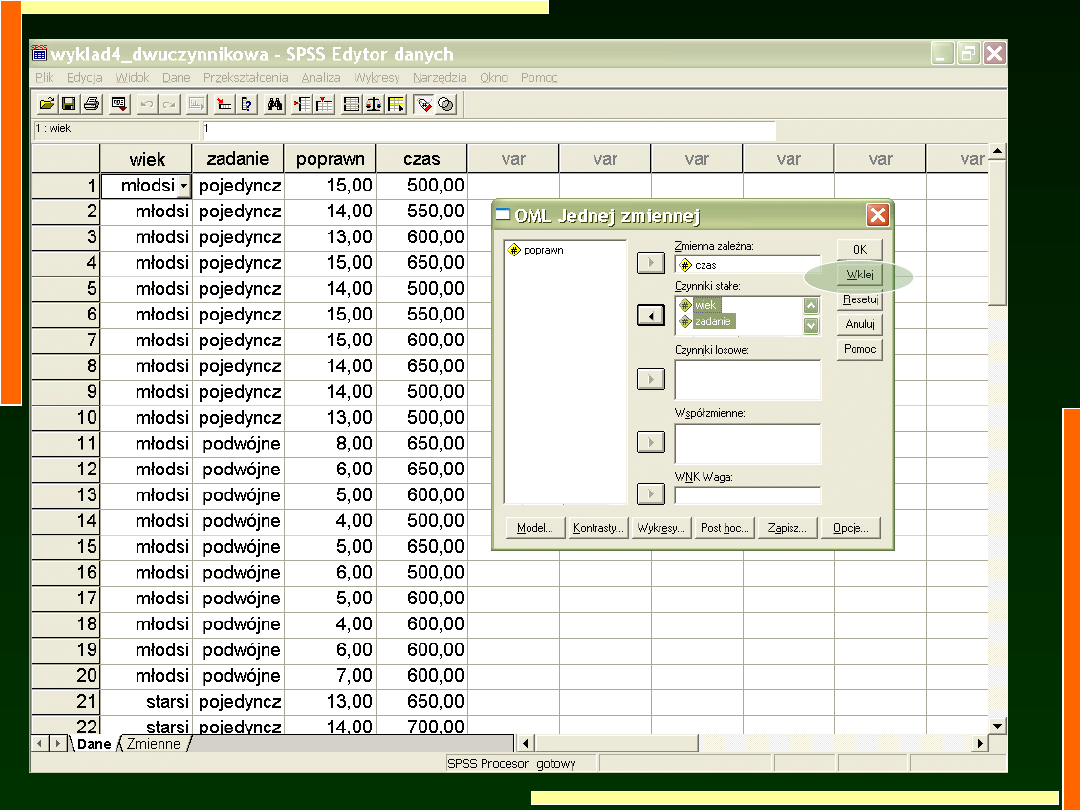
Lub spojrzeć na wykresy słupków błędu



Lub skorzystać z pakietu statystycznego
Statistica (pełna gama porównań)



Syntax w SPSS

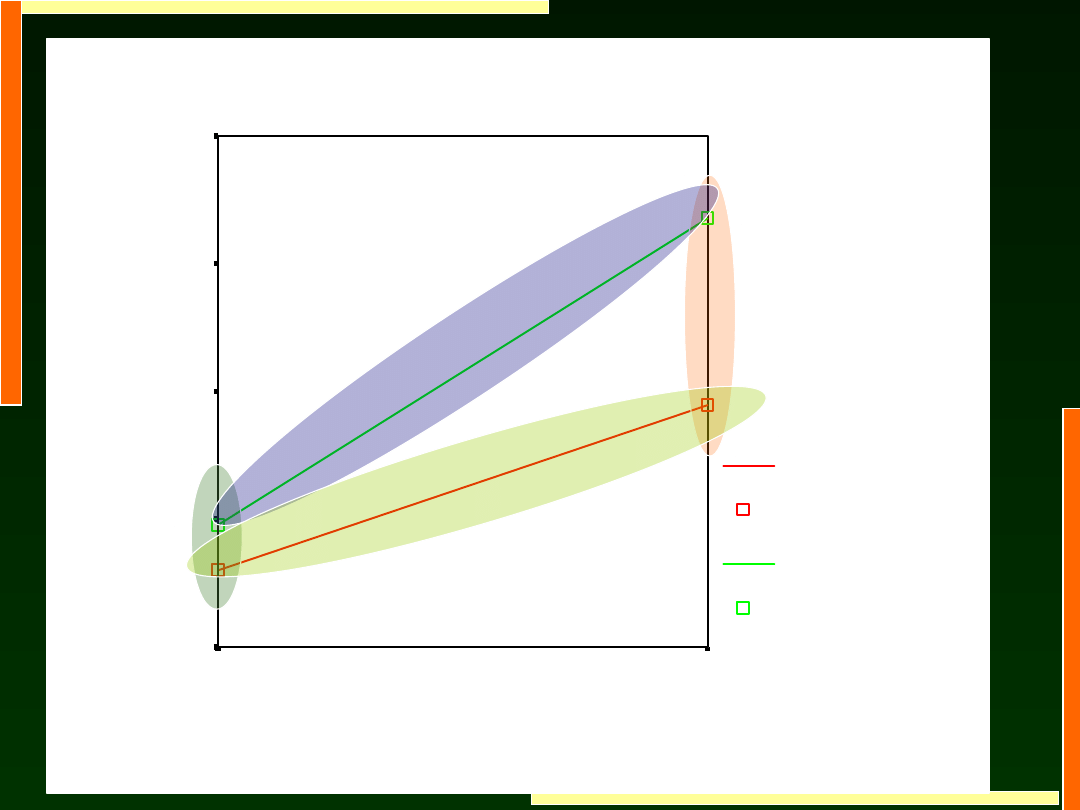
Oszacowane średnie brzegowe - CZAS

WIEK

starsi

młodsi

O

sz

ac

ow

an

e

śr

ed

ni

e

br

ze

go

w

e

900

800

700

600

500

ZADANIE

pojedyncze

podwójne

10

10

10

10

N =

WIEK

starsi

młodsi

95

%

P

U

C

Z

A

S

900

800

700

600

500

400

ZADANIE

pojedyncze

podwójne



/emmeans tables (wiek*zadanie)
compare (wiek)



/emmeans tables (wiek*zadanie)
compare (zadanie)

Porównania parami

Zmienna zależna: CZAS

-130,000*

22,423

,000

-175,475

-84,525

130,000*

22,423

,000

84,525

175,475

-240,000*

22,423

,000

-285,475

-194,525

240,000*

22,423

,000

194,525

285,475

(J) WIEK
starsi
młodsi
starsi
młodsi

(I) WIEK
młodsi
starsi
młodsi
starsi

ZADANIE
pojedyncze

podwójne

Różnica

średnich (I-J)

Błąd

standardowy

Istotność

a

Dolna granica Górna granica

95% przedział ufności dla

różnicy

a

W oparciu o estymowane średnie brzegowe.

Różnica średnich jest istotna na poziomie ,05

*.

Poprawka dla porównań wielokrotnych - Najmniejsza istotna różnica (równoważnik braku poprawki).

a.

Testy jednej zmiennej

Zmienna zależna: CZAS

84500,0

1

84500 33,613

,000

90500,0

36 2513,9

288000

1 288000 114,564

,000

90500,0

36 2513,9

Kontrast
Błąd
Kontrast
Błąd

ZADANIE
pojedyncze

podwójne

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

Każde F testuje proste efekty WIEK w ramach każdej kombinacji poziomów innych
przedstawionych efektów. Testy te są oparte na liniowo niezależnych porównaniach parami
pomiędzy oszacowanymi średnimi brzegowymi.

Porównania parami

Zmienna zależna: CZAS

-35,000

22,423

,127

-80,475

10,475

35,000

22,423

,127

-10,475

80,475

-145,000*

22,423

,000

-190,475

-99,525

145,000*

22,423

,000

99,525

190,475

(J) ZADANIE
podwójne
pojedyncze
podwójne
pojedyncze

(I) ZADANIE
pojedyncze
podwójne
pojedyncze
podwójne

WIEK
młodsi

starsi

Różnica

średnich (I-J)

Błąd

standardowy

Istotność

a

Dolna granica Górna granica

95% przedział ufności dla

różnicy

a

W oparciu o estymowane średnie brzegowe.

Różnica średnich jest istotna na poziomie ,05

*.

Poprawka dla porównań wielokrotnych - Najmniejsza istotna różnica (równoważnik braku poprawki).

a.

Testy jednej zmiennej

Zmienna zależna: CZAS

6125,000

1 6125,0

2,436

,127

90500,0

36 2513,9

105125

1 105125 41,818

,000

90500,0

36 2513,9

Kontrast
Błąd
Kontrast
Błąd

WIEK
młodsi

starsi

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

Każde F testuje proste efekty ZADANIE w ramach każdej kombinacji poziomów innych
przedstawionych efektów. Testy te są oparte na liniowo niezależnych porównaniach
parami pomiędzy oszacowanymi średnimi brzegowymi.

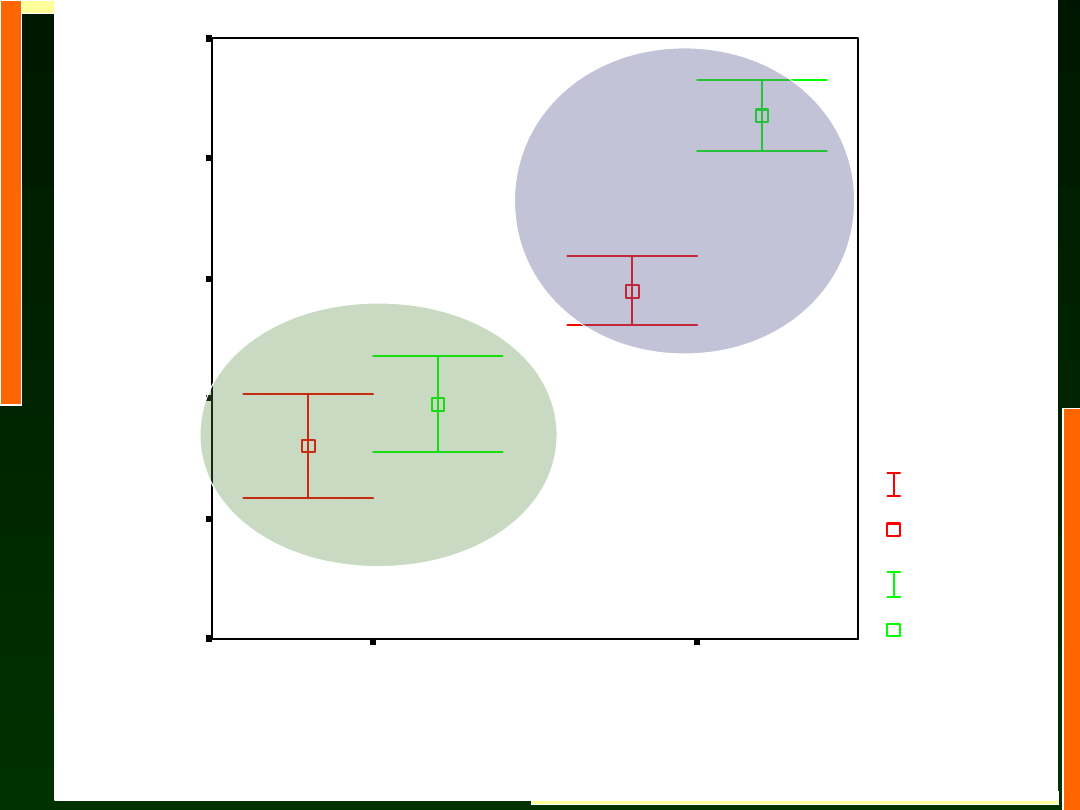
10

10

10

10

N =

WIEK

starsi

młodsi

95

%

P

U

C

Z

A

S

900

800

700

600

500

400

ZADANIE

pojedyncze

podwójne

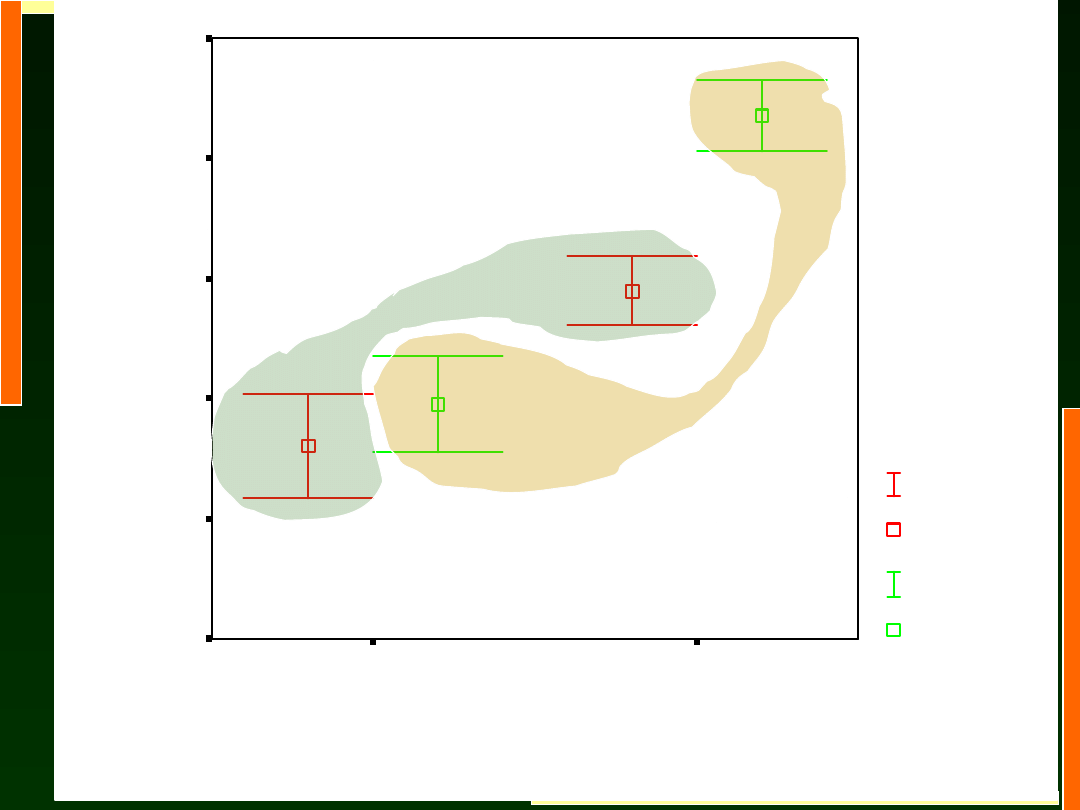
10

10

10

10

N =

WIEK

starsi

młodsi

95

%

P

U

C

Z

A

S

900

800

700

600

500

400

ZADANIE

pojedyncze

podwójne

Dyskusja wyników

Dyskusja wyników



Hipoteza 1 została potwierdzona, dla czasów reakcji

stwierdzono istotne podwyższenie czasów reakcji w

sytuacji zadania podwójnego niż pojedynczego, F (1,36)

= 32, 22; p < 0,001. Dodatkowo uzyskano istotny efekt

główny wieku, wskazujący na ogólnie wyższy czas

reakcji w grupie starszej F (1, 36) = 136, 14; p < 0,001.



Zgodnie z hipotezą drugą stwierdzono istotną interakcję

Wiek x Zadanie, F (1, 36) = 12, 03; p < 0,001. Analiza

efektów prostych (p < 0,05) wykazała, że kształt tej

interakcji różni się od przewidywań: u starszych

dorosłych wystąpiła istotna różnice w czasach reakcji w

zadaniu pojedynczym i podwójnym, natomiast dla

młodszych dorosłych ta różnica była nieistotna.



Zgodnie z hipotezą 3 interakcja Wiek x Zadanie była

silniejsza (i tylko tam istotna) dla czasu reakcji niż dla

ilości trafień

Schemat tróczynnikowy

Schemat tróczynnikowy

(Pingitore i in. 1994)
Schemat 2x2x2
2(Schemat ciała:niski vs wysoki)x

2(Waga:w normie vs ponad normę)

x2(płeć: kandydat vs kandydatka)

Testy efektów międzyobiektowych

Zmienna zależna: OCENA

60,446

a

7 8,635 31,358

,000

937,992

1 937,99 3406,2

,000

33,672

1 33,672 122,28

,000

18,632

1 18,632 67,661

,000

,702

1

,702 2,550

,120

3,422

1 3,422 12,428

,001

,812

1

,812 2,950

,096

,342

1

,342 1,243

,273

2,862

1 2,862 10,394

,003

8,812

32

,275

1007,25

40

69,258

39

Źródło zmienności
Model skorygowany

Stała

WAGA

PLEC

SCHEMAT

WAGA * PLEC

WAGA * SCHEMAT

PLEC * SCHEMAT

WAGA * PLEC *
SCHEMAT
Błąd

Ogółem

Ogółem skorygowane

Typ III sumy

kwadratów

df

Średni

kwadrat

F

Istotność

R kwadrat = ,873 (Skorygowane R kwadrat = ,845)

a.

WAGA

ponad normę

w normie

Ś

re

dn

ia

o

ce

na

p

rz

yj

ęc

ia

d

o

pr

ac

y

7

6

5

4

3

2

PLEC

kandydat

kandydatka

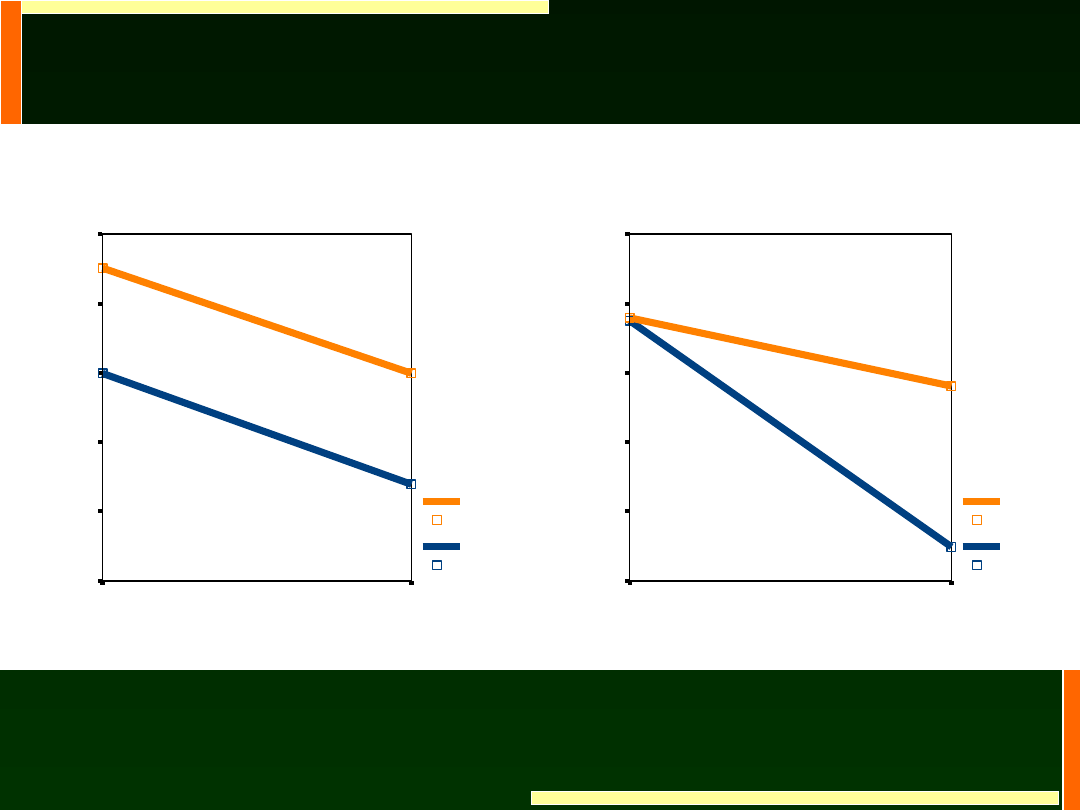
Niska ocena schematu

własnego ciała

WAGA

ponad normę

w normie

Ś

re

dn

ia

o

ce

n

pr

zy

ję

ci

a

do

p

ra

cy

7,0

6,0

5,0

4,0

3,0

2,0

PLEC

kandydat

kandydatka

Wysoka ocena schematu

własnego ciała

WAGA

ponad normę

w normie

Ś

re

dn

ia

o

ce

na

p

rz

yj

ęc

ia

d

o

pr

ac

y

7

6

5

4

3

2

PLEC

kandydat

kandydatka

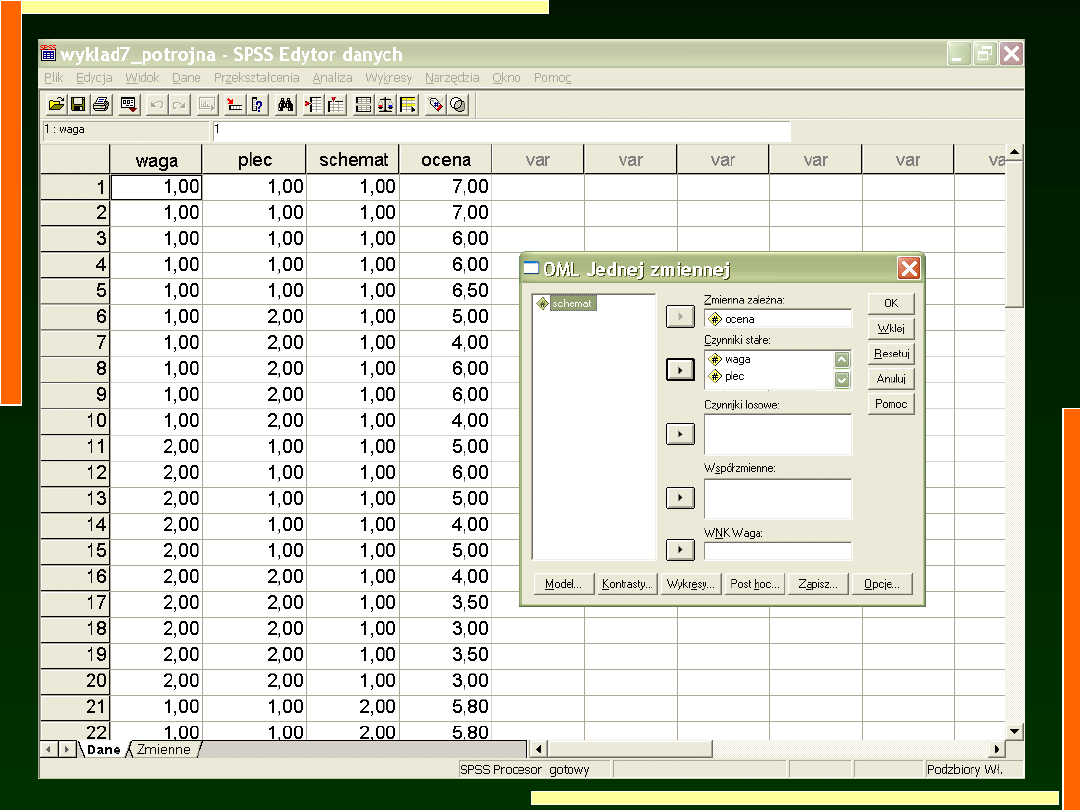
Testy efektów międzyobiektowych

b

Zmienna zależna: OCENA

24,038

a

3 8,013 16,649

,000

495,013

1 495,01 1028,6

,000

12,013

1 12,013 24,961

,000

12,013

1 12,013 24,961

,000

,013

1

,013

,026

,874

7,700

16

,481

526,750

20

31,738

19

Źródło zmienności
Model skorygowany

Stała

WAGA

PLEC

WAGA * PLEC

Błąd

Ogółem

Ogółem skorygowane

Typ III sumy

kwadratów

df

Średni

kwadrat

F

Istotność

R kwadrat = ,757 (Skorygowane R kwadrat = ,712)

a.

SCHEMAT = niska ocena schematu wł ciała

b.

Testy efektów międzyobiektowych

b

Zmienna zależna: OCENA

35,706

a

3 11,902 171,25

,000

443,682

1 443,68 6383,9

,000

22,472

1 22,472 323,34

,000

6,962

1 6,962 100,17

,000

6,272

1 6,272 90,245

,000

1,112

16

,070

480,500

20

36,818

19

Źródło zmienności
Model skorygowany

Stała

WAGA

PLEC

WAGA * PLEC

Błąd

Ogółem

Ogółem skorygowane

Typ III sumy

kwadratów

df

Średni

kwadrat

F

Istotność

R kwadrat = ,970 (Skorygowane R kwadrat = ,964)

a.

SCHEMAT = wysoka ocena schematu wł ciała

b.

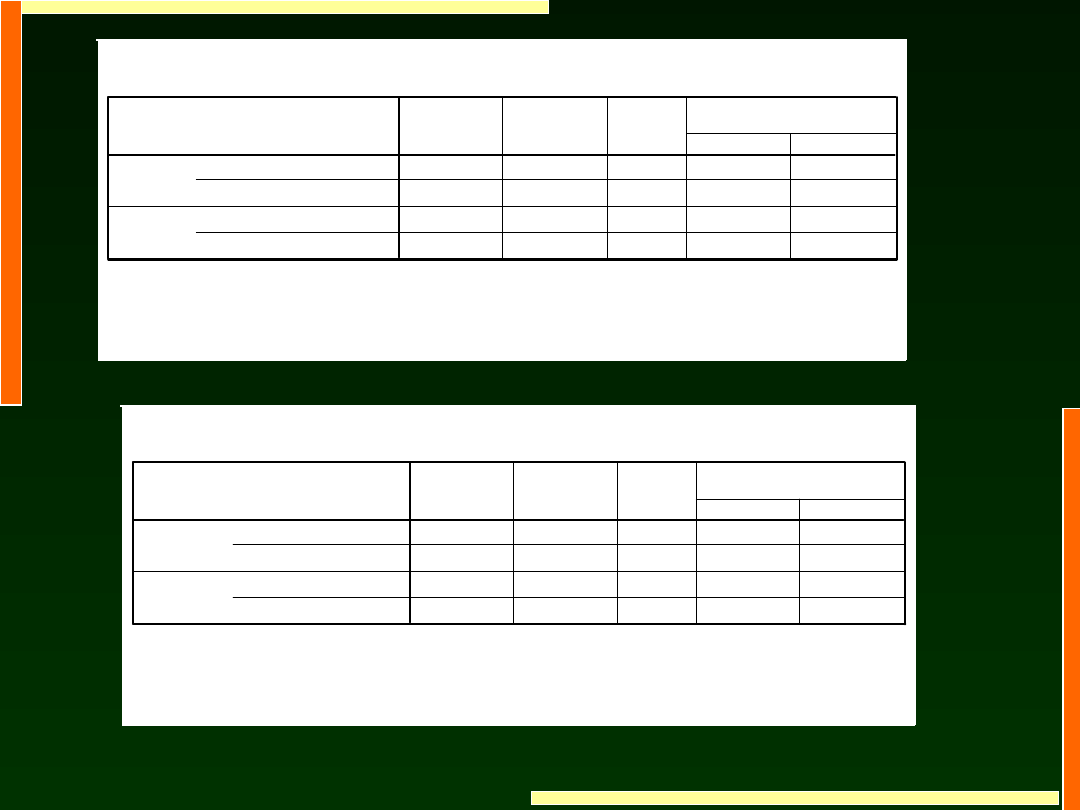
Porównania parami

b

Zmienna zależna: OCENA

1,000*

,167

,000

,647

1,353

-1,000*

,167

,000

-1,353

-,647

3,240*

,167

,000

2,887

3,593

-3,240*

,167

,000

-3,593

-2,887

(J) WAGA
ponad normę

w normie

ponad normę

w normie

(I) WAGA
w normie

ponad normę

w normie

ponad normę

PLEC
kandydat

kandydatka

Różnica

średnich (I-J)

Błąd

standardowy

Istotność

a

Dolna granica Górna granica

95% przedział ufności dla

różnicy

a

W oparciu o estymowane średnie brzegowe.

Różnica średnich jest istotna na poziomie ,05

*.

Poprawka dla porównań wielokrotnych - Najmniejsza istotna różnica (równoważnik braku poprawki).

a.

SCHEMAT = wysoka ocena schematu wł ciała

b.

Porównania parami

b

Zmienna zależna: OCENA

,060

,167

,724

-,293

,413

-,060

,167

,724

-,413

,293

2,300*

,167

,000

1,947

2,653

-2,300*

,167

,000

-2,653

-1,947

(J) PLEC
kandydatka

kandydat

kandydatka

kandydat

(I) PLEC
kandydat

kandydatka

kandydat

kandydatka

WAGA
w normie

ponad normę

Różnica

średnich (I-J)

Błąd

standardowy

Istotność

a

Dolna granica Górna granica

95% przedział ufności dla

różnicy

a

W oparciu o estymowane średnie brzegowe.

Różnica średnich jest istotna na poziomie ,05

*.

Poprawka dla porównań wielokrotnych - Najmniejsza istotna różnica (równoważnik braku poprawki).

a.

SCHEMAT = wysoka ocena schematu wł ciała

b.

Efekty w planach złożonych

Efekty w planach złożonych



Jeśli zmienne niezależne oznaczone są
przez A i B, w planie
dwuczynnnikowym może zaistnieć:
efekt główny A, efekt główny B i efekt
interakcji AxB



W planie trójczynnikowym AxBxC może
zaistnieć: efekt główny A, efekt główny
B, efekt główny C, efekty interakcyjne:
AxB, BxC, AxC oraz AxBxC