Analiza danych w modelu

Analiza danych w modelu

regresyjnym

regresyjnym

Wykład 10

Wykład 10

Howell

Howell

D

D

.

.

C.

C.

(1999).

(1999).

Fundamental Statistics for the

Fundamental Statistics for the

Behavioral Sciences, 4th edition

Behavioral Sciences, 4th edition

ZARYS PROBLEMATYKI

ZARYS PROBLEMATYKI



W jaki sposób można przewidzieć

W jaki sposób można przewidzieć

zmienność jednej zmiennej na

zmienność jednej zmiennej na

podstawie informacji o drugiej

podstawie informacji o drugiej

zmiennej

zmiennej

?

?



Jak zmieniają się wartości jednej

Jak zmieniają się wartości jednej

zmiennej wraz ze zmianą wartości

zmiennej wraz ze zmianą wartości

drugiej zmiennej?

drugiej zmiennej?



Wnioskowanie w kategoriach

Wnioskowanie w kategoriach

przyczyny i skutku

przyczyny i skutku

Według raportu Światowej

Według raportu Światowej

Organizacji Zdrowia,

Organizacji Zdrowia,



choroba wieńcowa występuje prawie 2-krotnie

choroba wieńcowa występuje prawie 2-krotnie

częściej u palaczy, niż u osób niepalących,

częściej u palaczy, niż u osób niepalących,



p

p

alenie tytoniu obok podwyższonego poziomu

alenie tytoniu obok podwyższonego poziomu

cholesterolu we krwi i nadciśnienia tętniczego

cholesterolu we krwi i nadciśnienia tętniczego

oraz otyłości jest głównym czynnikiem ryzyka

oraz otyłości jest głównym czynnikiem ryzyka

choroby wieńcowej i zawału serca.

choroby wieńcowej i zawału serca.

•

wytwarzany w czasie palenia tlenek węgla zmniejsza

wytwarzany w czasie palenia tlenek węgla zmniejsza

do

do

tleni

tleni

e

e

nie serca i mózgu oraz śródbłonka naczyń

nie serca i mózgu oraz śródbłonka naczyń

tętniczych

tętniczych

•

s

s

ama nikotyna wpływa również niekorzystnie na mięsień

ama nikotyna wpływa również niekorzystnie na mięsień

serca, zwłaszcza u osób z już istniejącą chorobą

serca, zwłaszcza u osób z już istniejącą chorobą

wieńcową

wieńcową

Nikotyna przyczyną

Nikotyna przyczyną

zwiększonego ryzyka

zwiększonego ryzyka

choroby wieńcowej

choroby wieńcowej

problem

problem



Zależność między liczbą wypalanych

Zależność między liczbą wypalanych

papierosów i chorobą wieńcową

papierosów i chorobą wieńcową



Chcielibyśmy przewidzieć

Chcielibyśmy przewidzieć

śmiertelność spowodowaną chorobą

śmiertelność spowodowaną chorobą

wieńcową dla kraju w którym dorośli

wieńcową dla kraju w którym dorośli

wypalają średnio 20 papierosów

wypalają średnio 20 papierosów

dziennie

dziennie

Palenie papierosów i

Palenie papierosów i

umieralność na chorobę

umieralność na chorobę

wieńcową w 21 krajach

wieńcową w 21 krajach

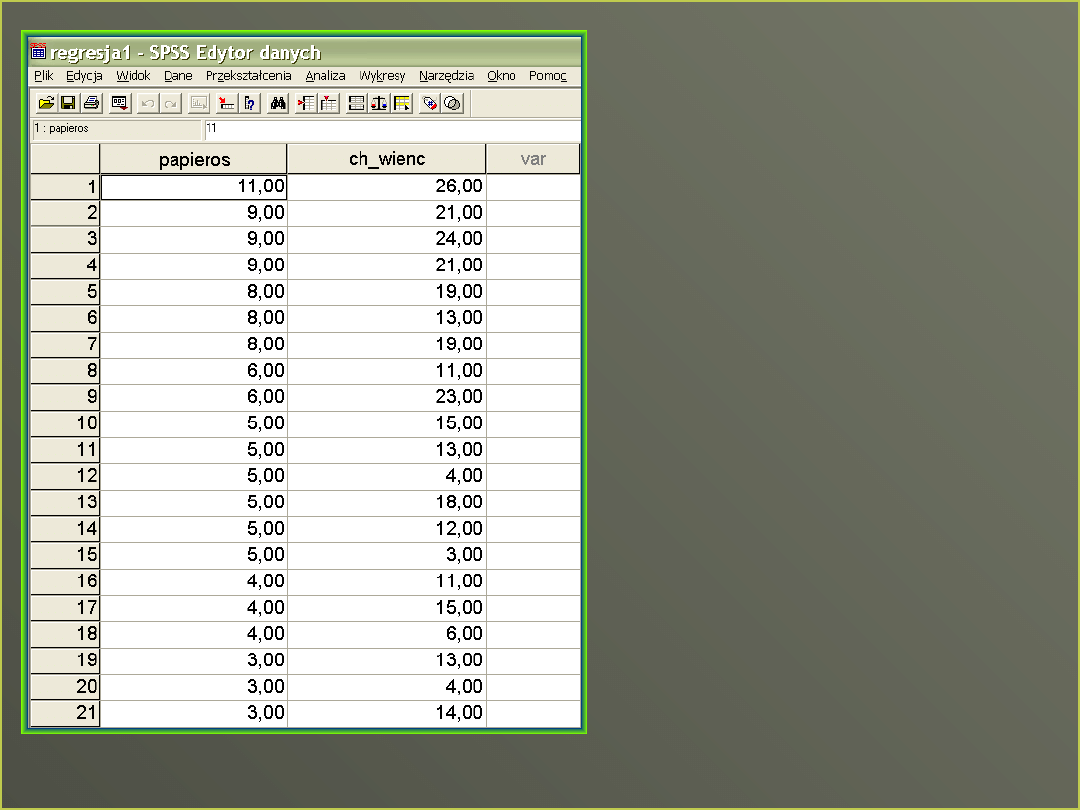
Dane w SPSS

Dane w SPSS



Dane wpisane jak w

Dane wpisane jak w

schemacie

schemacie

korelacyjnym

korelacyjnym



Zmienna na podstawie

Zmienna na podstawie

której będziemy

której będziemy

przewidywać to:

przewidywać to:



Liczba papierosów

Liczba papierosów

(zmienna

(zmienna

wyjaśniająca,

wyjaśniająca,

predyktor)

predyktor)



Umieralność to

Umieralność to

zmienna wyjaśniana,

zmienna wyjaśniana,

zmienna zależna

zmienna zależna

Niezbędna wizualizacja

Niezbędna wizualizacja

związku

związku



Zanim przeprowadzimy analizę

Zanim przeprowadzimy analizę

regresji niezbędne jest przyjrzenie się

regresji niezbędne jest przyjrzenie się

wykresowi rozrzutu dla predyktora i

wykresowi rozrzutu dla predyktora i

zamiennej kryterialnej w celu

zamiennej kryterialnej w celu

wyśledzenia:

wyśledzenia:



Zależności nieliniowej

Zależności nieliniowej

•

Interesujemy się zależnością liniową –

Interesujemy się zależnością liniową –

będziemy robić analizę regresji liniowej

będziemy robić analizę regresji liniowej



Wyników skrajnych

Wyników skrajnych

(outlierów)

(outlierów)



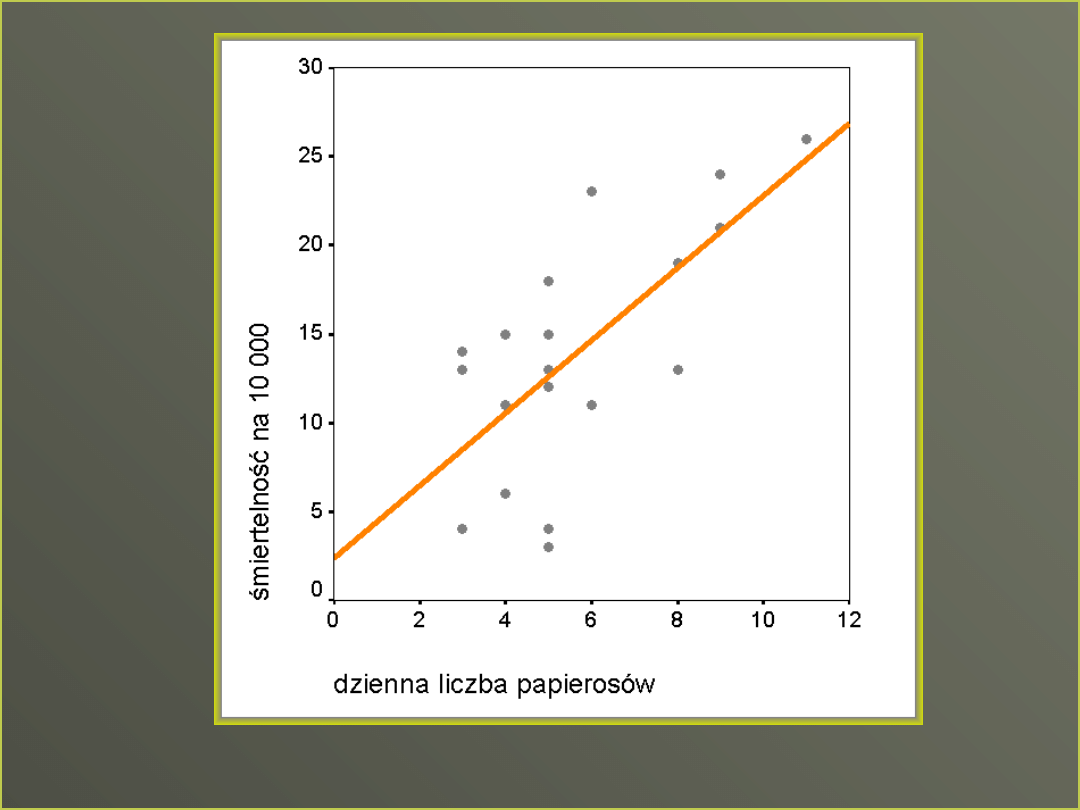
Robimy prosty

Robimy prosty

wykres rozrzutu

wykres rozrzutu



Według konwencji:

Według konwencji:

•

Predyktor na osi X

Predyktor na osi X

•

Zmienna zależna na

Zmienna zależna na

osi Y

osi Y

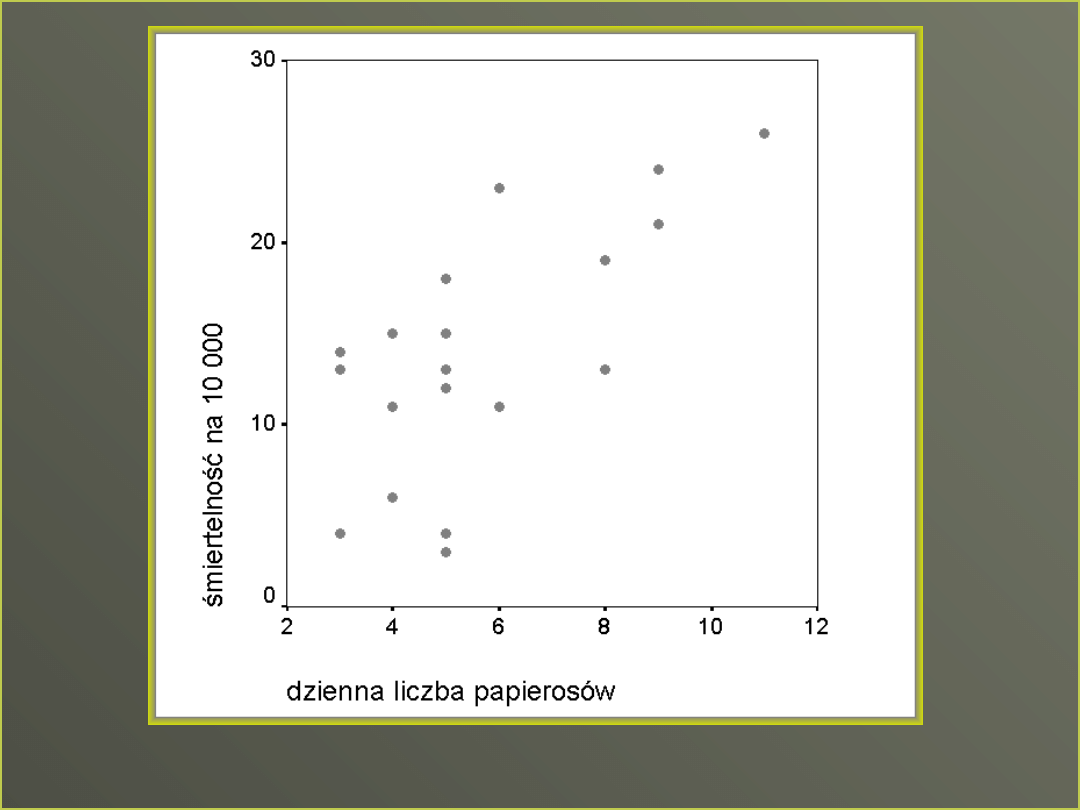
Linia regresji

Linia regresji

Co jest lepszym opisem

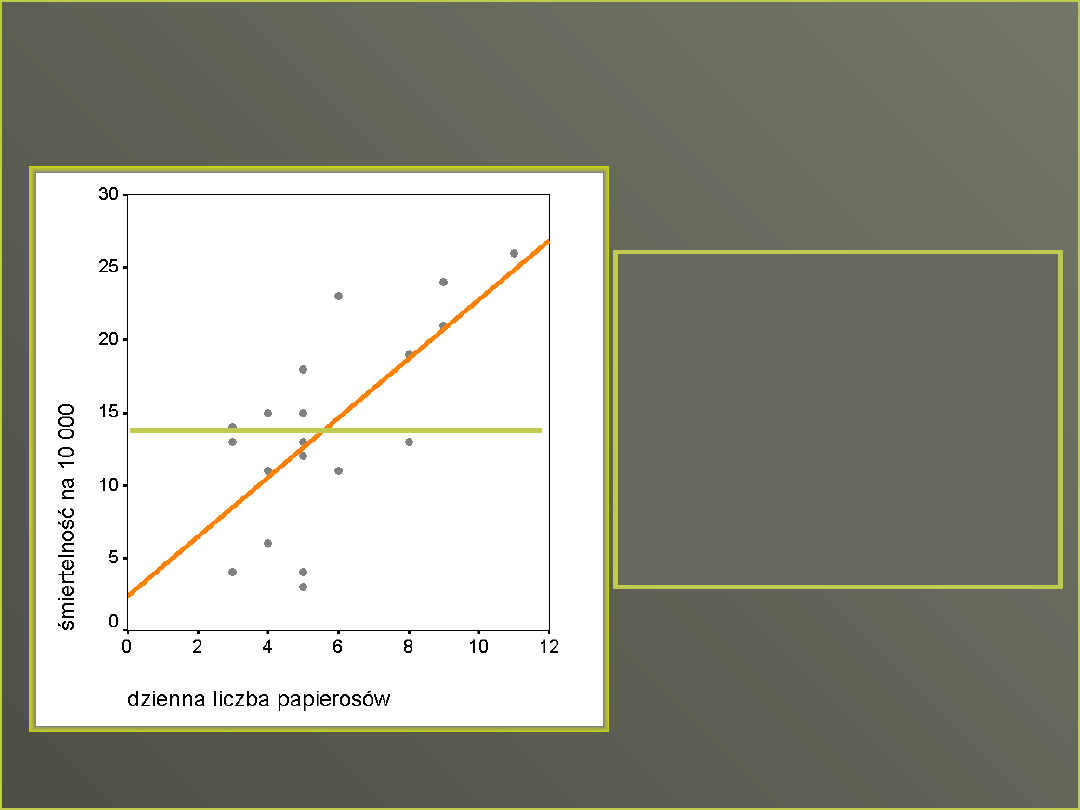
Co jest lepszym opisem

danych

danych

Średni wskaźnik
umieralności wynosi 14,52

Czy przewidywanie w oparciu
o średnią,
czy też o linię regresji
jest lepszym opisem zależności

W którym przypadku byłby
większy błąd predykcji?

Linia regresji

Linia regresji



wzór

wzór

•

Ŷ

Ŷ

=

=

przewidywana wartość

przewidywana wartość

Y

Y

(

(

wskaźnik

wskaźnik

umieralności na chorobę wieńcową na 10000)

umieralności na chorobę wieńcową na 10000)

•

X

X

=

=

liczba spalanych papierosów w danym

liczba spalanych papierosów w danym

kraju na 1 dorosłego (predyktor – zmienna

kraju na 1 dorosłego (predyktor – zmienna

niezależna)

niezależna)

•

Współczynniki regresji szacują jak dokładnie

Współczynniki regresji szacują jak dokładnie

wyniki Y są przewidywane przez to równanie

wyniki Y są przewidywane przez to równanie

liniowe

liniowe

stala

nachylenia

ˆ

B

X

B

Y





Współczynniki w równaniu

Współczynniki w równaniu

regresji

regresji



Współczynniki:

Współczynniki:



Współczynnik nachylenia

Współczynnik nachylenia

prostej

prostej

względem osi X

względem osi X

•

Zmiana w przewidywanych wartościach

Zmiana w przewidywanych wartościach

Y, gdy X wzrasta o 1 jednostkę

Y, gdy X wzrasta o 1 jednostkę



stała

stała

•

punkt przecięcia linii regresji z osią Y

punkt przecięcia linii regresji z osią Y

•

wartość

wartość

Ŷ

Ŷ

gdy

gdy

X

X

= 0

= 0

•

często w równaniu oznaczana literą „a”

często w równaniu oznaczana literą „a”

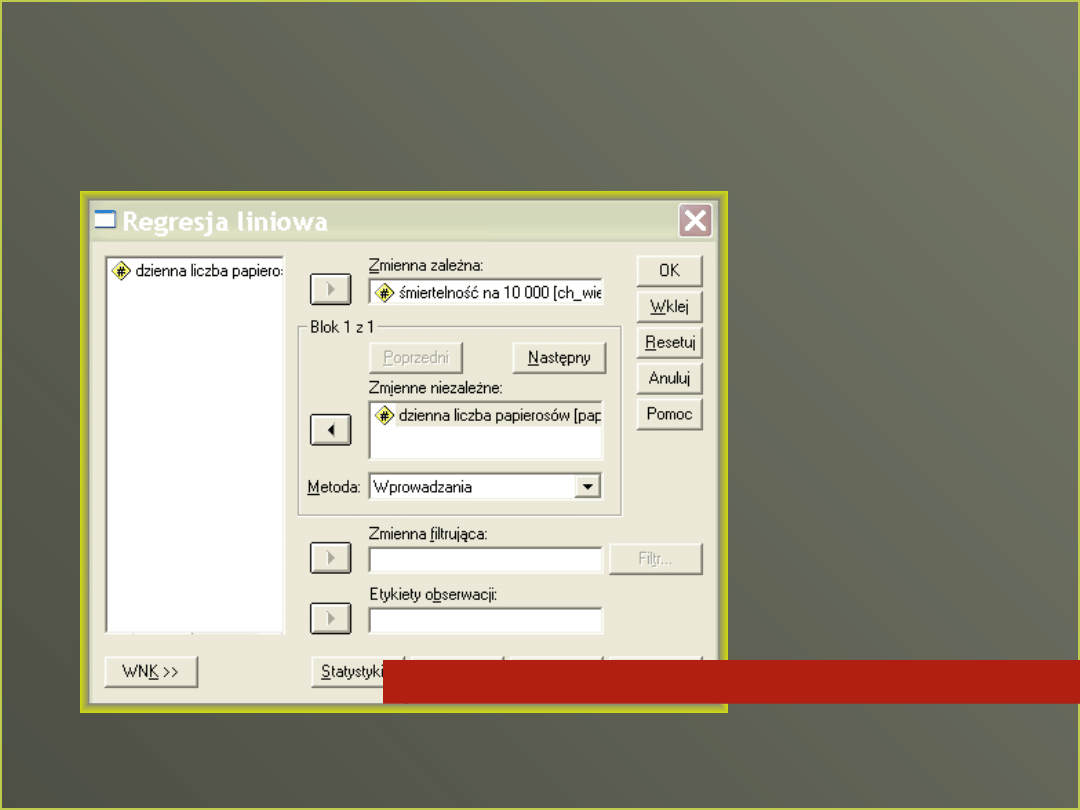
Analiza> regresja> regresja

Analiza> regresja> regresja

liniowa

liniowa

W prostej regresji liniowej mamy tylko 1 predyktor

Testowanie współczynnika

Testowanie współczynnika

nachylenia linii i stałej

nachylenia linii i stałej

•

Gdyby model był zły, wtedy zmiana jeśli zmienia się wartość

Gdyby model był zły, wtedy zmiana jeśli zmienia się wartość

predyktora, zmiana w zmiennej przewidywanej byłaby bliska zeru

predyktora, zmiana w zmiennej przewidywanej byłaby bliska zeru

•

Jeśli wybrana przez nas zmienna istotnie przewiduje zmienną zależną,

Jeśli wybrana przez nas zmienna istotnie przewiduje zmienną zależną,

wtedy współczynnik b powinien być istotnie rożny od zera

wtedy współczynnik b powinien być istotnie rożny od zera



Istotność współczynników regresji sprawdzamy za pomocą testu t,

Istotność współczynników regresji sprawdzamy za pomocą testu t,

czy są istotnie różne od zera

czy są istotnie różne od zera

•

Nawet jeśli stała jest nieistotna (tak jak w naszym przypadku), dla

Nawet jeśli stała jest nieistotna (tak jak w naszym przypadku), dla

dokładności predykcji umieszczamy ją w równaniu

dokładności predykcji umieszczamy ją w równaniu

BS

B

t 

Pr

Pr

zewidywanie

zewidywanie

•

Chcielibyśmy przewidzieć wielkość wskaźnika

Chcielibyśmy przewidzieć wielkość wskaźnika

umieralności na CW w kraju w którym średnio

umieralności na CW w kraju w którym średnio

dorosły wypala 6 papierosów dziennie.

dorosły wypala 6 papierosów dziennie.

•

Na podstawie modelu regresji

Na podstawie modelu regresji

przewidywalibyśmy, iż około 15

przewidywalibyśmy, iż około 15

/10,000

/10,000

w

w

tym kraju umrze na chorobę wieńcową.

tym kraju umrze na chorobę wieńcową.

61

,

14

37

.

2

6

*

04

.

2

ˆ

37

.

2

04

.

2

ˆ















Y

X

B

X

B

Y

stala

nachylenia

Regresja

Regresja

wielozmiennowa

wielozmiennowa

Główne punkty

Główne punkty



Problem

Problem



Przykład

Przykład



Korelacja wielokrotna

Korelacja wielokrotna



Równanie regresji

Równanie regresji



Pr

Pr

zewidywania

zewidywania

Con
t.

Problem

Problem



Zastosowanie kilku predyktorów do

Zastosowanie kilku predyktorów do

przewidywania wartości zmiennej

przewidywania wartości zmiennej

zależnej

zależnej



Określenie miary ogólnego

Określenie miary ogólnego

dopasowania

dopasowania



W

W

aga każdego predyktora

aga każdego predyktora

Przykład

Przykład



Badanie

Badanie

Kliewer

Kliewer

a i in

a i in

. (1998)

. (1998)

dotyczące

dotyczące

roli przemocy na internalizację

roli przemocy na internalizację

zachowania

zachowania

•

Defin

Defin

icja internalizacji zachowania

icja internalizacji zachowania



Pred

Pred

yktory

yktory

•

Poziom obserwowanej przemocy

Poziom obserwowanej przemocy

•

M

M

iara stresu życiowego

iara stresu życiowego

•

M

M

iara wsparcia społecznego

iara wsparcia społecznego

Przemoc a internalizacja

Przemoc a internalizacja



Badanymi były dzieci

Badanymi były dzieci

8-12

8-12

lat

lat

•

Żyjące w okolicach o dużej

Żyjące w okolicach o dużej

przestępczości

przestępczości

•

H

H

i

i

pot

pot

eza

eza

:

:

przemoc i stres prowadzą do

przemoc i stres prowadzą do

internalizacji agresywnego zachowania

internalizacji agresywnego zachowania

.

.

Macierz korelacji

Macierz korelacji

Correlations

Pearson Correlation

.050
.080

-.080

.200*

.270**

-.170

Poziom obserwowanej
przemocy
Stres zyciowy
Wparcie spoleczne
Internalizacja Przemocy

Poziom

obserwow

anej

przemocy

Stres

zyciowy

Wparcie

spoleczne

Internaliza

cja

Przemocy

Correlation is significant at the 0.05 level (2-tailed).

*.

Correlation is significant at the 0.01 level (2-tailed).

**.

Wstępne obserwacje

Wstępne obserwacje



Zauważmy, że oglądanie przemocy i

Zauważmy, że oglądanie przemocy i

stres są istotnie skorelowane z

stres są istotnie skorelowane z

internalizacją

internalizacją

.

.



Zauważmy, że predyktory są

Zauważmy, że predyktory są

niepowiązane ze sobą

niepowiązane ze sobą

.

.

Korelacja wielokrotna

Korelacja wielokrotna



Rozumiana analogicznie do

Rozumiana analogicznie do

r

r



Zawsze pisana dużymi literami

Zawsze pisana dużymi literami

(n.p.,

(n.p.,

R

R

)

)



Zawsze pozytywna

Zawsze pozytywna

•

Korelacja predyktorów ze zmienną

Korelacja predyktorów ze zmienną

zależną

zależną

•

Często podaje się wartość

Często podaje się wartość

R

R

2

2

zamiast

zamiast

R

R

(proporcjonalna redukcja błędu)

(proporcjonalna redukcja błędu)

R

R

2

2

Model - Podsumowanie

,370

a

,135

,108

2,21000

Model
1

R

R-kwadrat

Skorygowane

R-kwadrat

Błąd

standardowy

oszacowania

Predyktory: (Stała), WSPARCIE, STRES, PRZEMOC

a.

Współczynniki regresji

Współczynniki regresji



Współczynniki regresji i stała

Współczynniki regresji i stała

.

.



Każdy predyktor uwzględnia wpływ

Każdy predyktor uwzględnia wpływ

innych predyktorów

innych predyktorów

.

.



Dodatkowe współczynniki b i beta w

Dodatkowe współczynniki b i beta w

porównaniu do regresji z jednym

porównaniu do regresji z jednym

predyktorem

predyktorem

Statystyczna istotność

Statystyczna istotność

współczynników regresji

współczynników regresji

Współczynniki

a

,477

1,289

,370

,712

,038

,018

,201

2,111

,039

,273

,106

,247

2,575

,012

-,074

,043

-,166

-1,721

,087

(Stała)
PRZEMOC
STRES
WSPARCIE

Model
1

B

Błąd

standardowy

Współczynniki

niestandaryzowane

Beta

Współczynniki

standaryzowa

ne

t

Istotność

Zmienna zależna: INTERNAL

a.

Równanie regresji

Równanie regresji



Osobne współczynniki dla każdego

Osobne współczynniki dla każdego

predyktora

predyktora



Stała (tutaj b

Stała (tutaj b

o,

o,

, często oznaczane

, często oznaczane

jako a)

jako a)

477

.

0

*

074

.

0

*

273

.

0

Pr

*

038

.

0

ˆ

0

3

3

2

2

1

1

















Wsparcie

Stres

zem

b

X

b

X

b

X

b

Y

Pred

Pred

ykcja

ykcja



Załóżmy oglądanie przemocy

Załóżmy oglądanie przemocy

= 20,

= 20,

Stres = 5, and S

Stres = 5, and S

poł_Wsp

poł_Wsp

= 35.

= 35.

012

.

477

.

0

)

35

(

074

.

)

5

(

273

.

)

20

(

038

.

477

.

0

*

074

.

*

273

.

Pr

*

038

.

ˆ



















Wsparcie

Stres

zem

Y

Problem

Problem

skorelowanych

skorelowanych

predyktorów

predyktorów

Sprawdzamy założenia do

Sprawdzamy założenia do

analizy regresji

analizy regresji



Zmienna zależna – mierzona na skali

Zmienna zależna – mierzona na skali

ilościowej

ilościowej



Predyktory – ilościowe lub kategorialne

Predyktory – ilościowe lub kategorialne

(0,1)

(0,1)



Liniowy związek między predyktorem a

Liniowy związek między predyktorem a

zmienną zależną (wykresy rozrzutu)

zmienną zależną (wykresy rozrzutu)



Brak silnych korelacji między predyktorami

Brak silnych korelacji między predyktorami

•

Silna korelacja między predyktorami – podobną

Silna korelacja między predyktorami – podobną

część wariancji będą wyjaśniać w zmiennej

część wariancji będą wyjaśniać w zmiennej

zależnej - będą się znosić w modelu

zależnej - będą się znosić w modelu

Korelacja semicząstkowa i

Korelacja semicząstkowa i

cząstkowa

cząstkowa



Przy korelacji cząstkowej kontrolujemy wpływ

Przy korelacji cząstkowej kontrolujemy wpływ

trzeciej zmiennej na obie zmienne

trzeciej zmiennej na obie zmienne

•

Korelacje cząstkowe są bardziej użyteczne, gdy chcemy

Korelacje cząstkowe są bardziej użyteczne, gdy chcemy

przyjrzeć się unikalnemu związkowi dwóch zmiennych

przyjrzeć się unikalnemu związkowi dwóch zmiennych



W semicząstkowej korelacji kontrolujemy wpływ

W semicząstkowej korelacji kontrolujemy wpływ

trzeciej zmiennej, który ma ona tylko na jedną ze

trzeciej zmiennej, który ma ona tylko na jedną ze

zmiennych branych do korelacji

zmiennych branych do korelacji

•

Semicząstkowe, kiedy interesuje nas wyjaśnienie

Semicząstkowe, kiedy interesuje nas wyjaśnienie

zmienności zmiennej zależnej na podstawie kilku

zmienności zmiennej zależnej na podstawie kilku

predyktorów.

predyktorów.

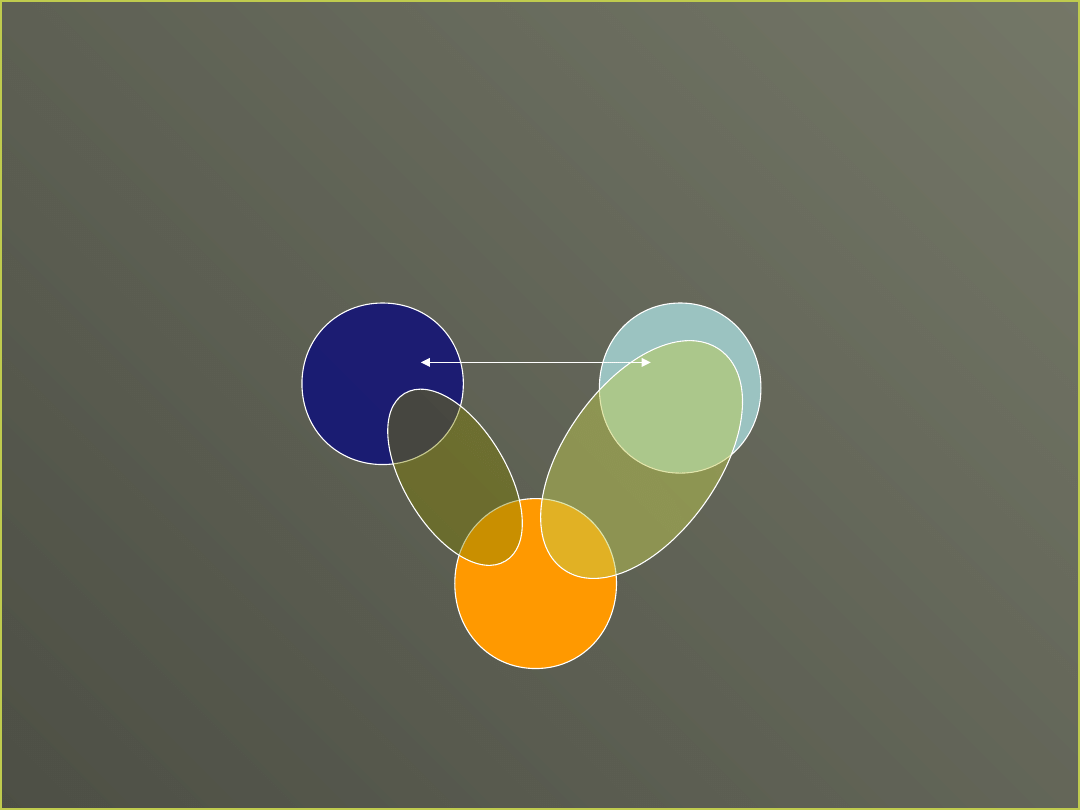
Korelacja cząstkowa

Korelacja cząstkowa

A

B

C



Kontrolujemy wpływ trzeciej zmiennej

Kontrolujemy wpływ trzeciej zmiennej



Odrzucamy jej wspólną wariancję z pierwszą i drugą zmienną

Odrzucamy jej wspólną wariancję z pierwszą i drugą zmienną



Korelujemy ze sobą oczyszczone reszty zmienności pierwszej i

Korelujemy ze sobą oczyszczone reszty zmienności pierwszej i

drugiej zmiennej ( po usunięciu wpływu trzeciej zmiennej)

drugiej zmiennej ( po usunięciu wpływu trzeciej zmiennej)

Korelacja semicząstkowa

Korelacja semicząstkowa

(częściowa)

(częściowa)



Korelacja semicząstkowa między A i B przy

Korelacja semicząstkowa między A i B przy

wyłączeniu wspólnej zmienności zmiennej C z

wyłączeniu wspólnej zmienności zmiennej C z

ze zmienną B

ze zmienną B



Korelujemy resztę ze zmiennej B ze zmienną A

Korelujemy resztę ze zmiennej B ze zmienną A

A

B

C

zależna

Wyniki analizy regresji dla

Wyniki analizy regresji dla

nisko i dla wysoko

nisko i dla wysoko

skorelowanych predyktorów

skorelowanych predyktorów



I Analiza:

I Analiza:

- Zmienna zależna: Inteligencja emocjonalna

- Zmienna zależna: Inteligencja emocjonalna

- Predyktory: Wykształcenie i ekstrawersja

- Predyktory: Wykształcenie i ekstrawersja



II analiza:

II analiza:

-

Zmienna zależna: Inteligencja

Zmienna zależna: Inteligencja

emocjonalna

emocjonalna

-

Predyktory: niska reaktywnośc i niski lęk

Predyktory: niska reaktywnośc i niski lęk

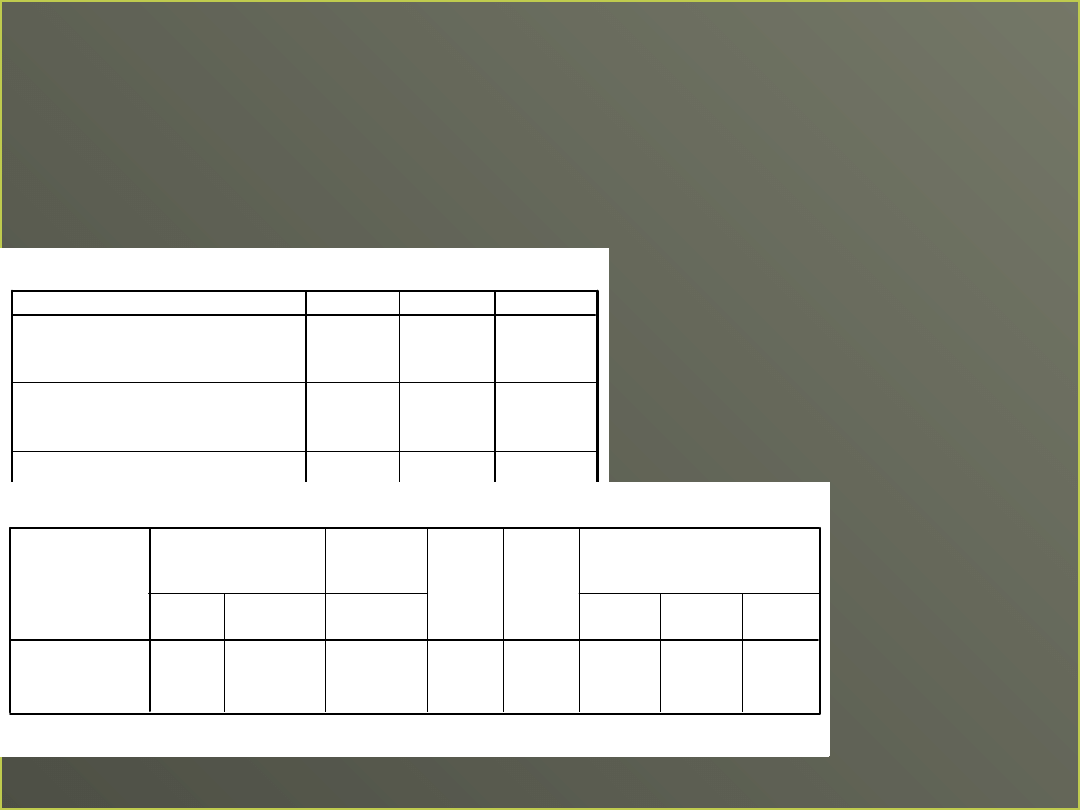
Nisko skorelowane

Nisko skorelowane

predyktory

predyktory

Korelacje

1,000

,468

,549

,468

1,000

,159

,549

,159

1,000

.

,005

,001

,005

.

,200

,001

,200

.

30

30

30

30

30

30

30

30

30

INTEL_EM
EKSTRAW
WYKSZTAŁ
INTEL_EM
EKSTRAW
WYKSZTAŁ
INTEL_EM
EKSTRAW
WYKSZTAŁ

Korelacja Pearsona

Istotność (jednostronna)

N

INTEL_EM

EKSTRAW

WYKSZTAŁ

Współczynniki

a

1,043

,939

1,110

,277

,579

,215

,390

2,696

,012

,468

,461

,385

,713

,212

,487

3,363

,002

,549

,543

,480

(Stała)
EKSTRAW
WYKSZTAŁ

Model
1

B

Błąd

standardowy

Współczynniki

niestandaryzowane

Beta

Współczynniki

standaryzowa

ne

t

Istotność

Rzędu

zerowego Cząstkowa

Semicząs

tkowa

Korelacje

Zmienna zależna: INTEL_EM

a.

Wniosek:
Zarówno
ekstrawersja
jak i wykształcenie
są
istotnymi
predyktorami
inteligencji
emocjonalnej

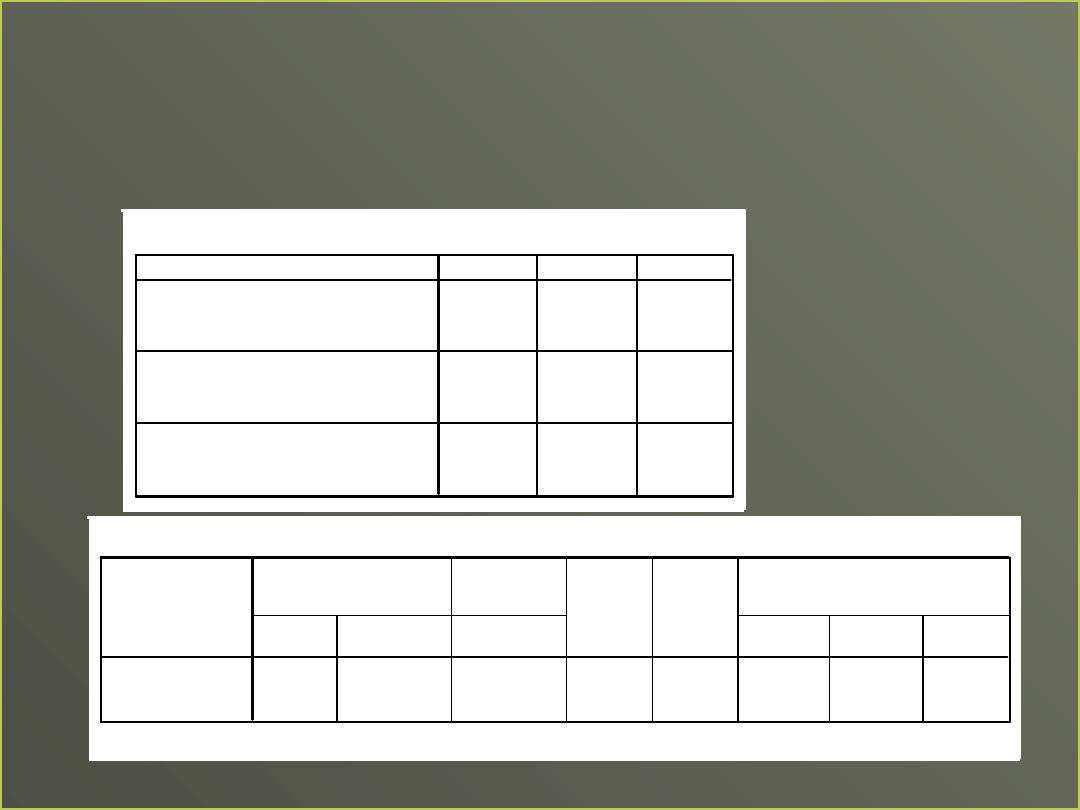
Wysoko skorelowane

Wysoko skorelowane

predyktory

predyktory

Korelacje

1,000

,628

,533

,628

1,000

,619

,533

,619

1,000

.

,000

,001

,000

.

,000

,001

,000

.

30

30

30

30

30

30

30

30

30

INTEL_EM
NI_REAKT
NI_LEK
INTEL_EM
NI_REAKT
NI_LEK
INTEL_EM
NI_REAKT
NI_LEK

Korelacja Pearsona

Istotność (jednostronna)

N

INTEL_EM

NI_REAKT

NI_LEK

Współczynniki

a

2,884

,588

4,903

,000

,337

,129

,483

2,610

,015

,628

,449

,380

,157

,124

,234

1,265

,217

,533

,236

,184

(Stała)
NI_REAKT
NI_LEK

Model
1

B

Błąd

standardowy

Współczynniki

niestandaryzowane

Beta

Współczynniki

standaryzowa

ne

t

Istotność

Rzędu

zerowego

Cząstkowa

Semicząs

tkowa

Korelacje

Zmienna zależna: INTEL_EM

a.

Wniosek:
Tylko niska
Reaktywność
jest istotnym predy-
ktorem inteligencji
emocjonalnej