PRAKTYCZNE

PRAKTYCZNE

WYKORZYSTANIE

WYKORZYSTANIE

DANYCH Z

DANYCH Z

ZAKRESU

ZAKRESU

MORFOLOGII

MORFOLOGII

mgr Aleksandra
Naczk

Plan zajęć - cz. I

Plan zajęć - cz. I

• Statystyka opisowa
• Testowanie hipotez statystycznych
• Rodzaje testów statystycznych

(dla 2 prób

niezależnych)

• Analiza wariancji ANOVA
• Analizy wielowymiarowe

STATYSTYKA

STATYSTYKA

OPISOWA

OPISOWA

Badaną próbę możemy

Badaną próbę możemy

scharakteryzować za pomocą

scharakteryzować za pomocą

następujących statystyk:

następujących statystyk:

1.

Miary położenia

Miary położenia

(miary tendencji centralnej) wskazują położenie

wartości, która najlepiej charakteryzuje wszystkie elementy naszej
próby:

a.

Miary centralne

Miary centralne

- charakteryzują średni lub typowy poziom

wartości, wokół której skupiają się wszystkie pozostałe wartości
analizowanej cechy.
- modalna (inaczej moda lub dominanta)
- wartości średnie:

średnia arytmetyczna

średnia arytmetyczna

, geometryczna,

harmoniczna
(suma wszystkich wartości zbioru danych podzielona przez
liczebność próby; wartości skrajne; liczebność próby)

b.

Kwantyle (kwartyle i mediana)

Kwantyle (kwartyle i mediana)

- wartości, które dzielą

uporządkowany zbiór danych na części o jednakowej liczbie
elementów.

CENTRALNE MIARY POŁOŻENIA

CENTRALNE MIARY POŁOŻENIA

Średnia arytmetyczna

Średnia arytmetyczna

- suma wszystkich

wartości zmiennej podzielona przez ich liczebność

•służy do oszacowania średniej populacji; wraz ze

wzrostem liczebności próby jej wartość jest coraz
bliższa średniej populacji

•duży wpływ na jej wartość mają wartości skrajne

zmiennej, zwłaszcza przy małej liczebności próby

•obliczanie jej dla rozkładów znacznie odbiegających

od normalnego nie ma sensu →

mediana

mediana

x

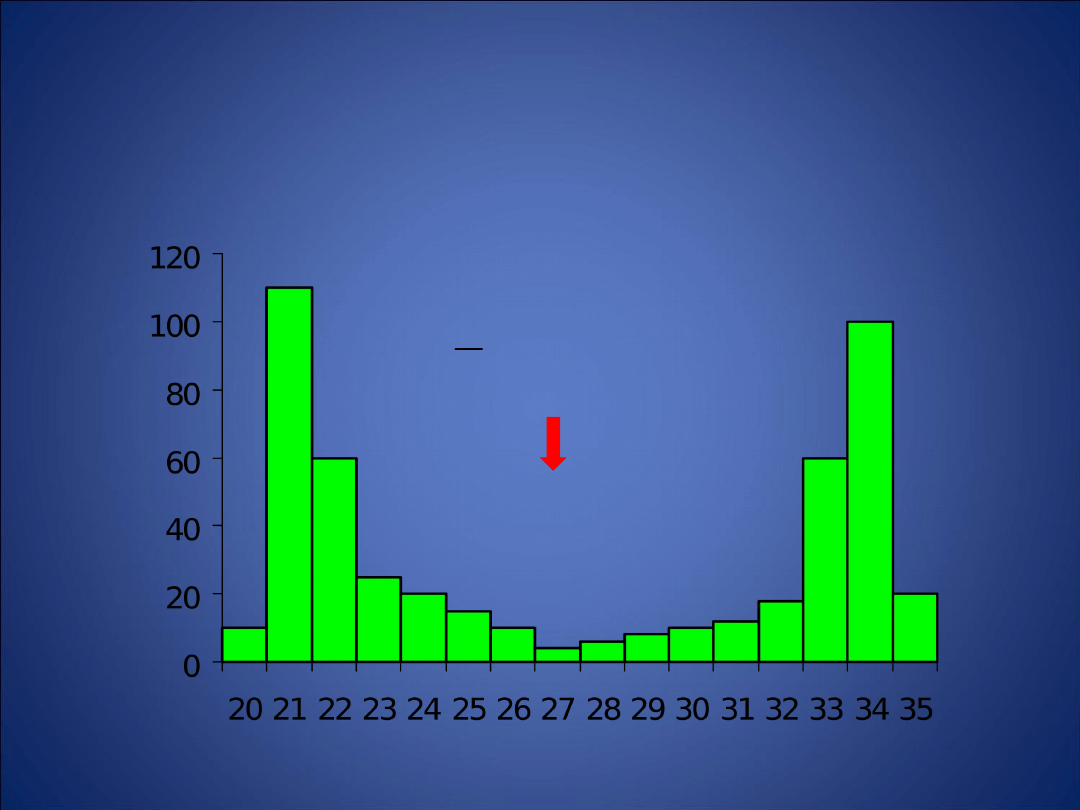
N

[mm]

=27,4

x

Rozkład długości liścia pewnego gatunku

Rozkład długości liścia pewnego gatunku

storczyka

storczyka

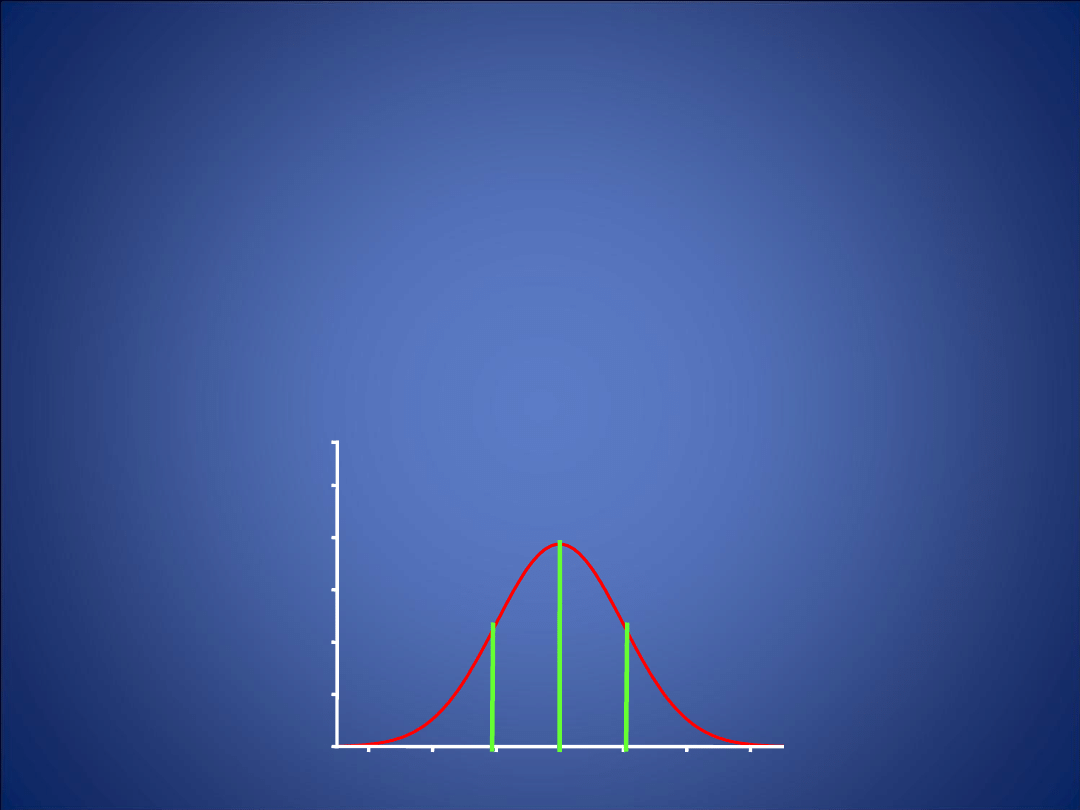
KWANTYLE

KWANTYLE

KWANTYLE

-

wartości, które dzielą zbiór danych na

części o jednakowej liczbie elementów.

Do najczęściej stosowanych należą:

•Kwartyle

(wartości ćwiartkowe) - podział na 4 części

→

mediana

mediana

= drugi kwartyl (dzieli zbiór na 2 części)

•Decyle

- podział na 10 części

•Percentyle

(centyle) - podział na 100 części

-3

-2

-1

0

1

2

3

0,0

0,1

0,2

0,3

0,4

0,5

0,6

25%

25%

25%

25%

2.

Miary rozproszenia

Miary rozproszenia

oceniające rozrzut wartości zmiennej:

a.

Rozstęp

Rozstęp

- (wartość minimalna i maksymalna) jest to różnica

między największą i najmniejszą wartością zmiennej w zbiorze
danych; całkowity obszar zmienności badanej cechy.

b.

Odchylenie ćwiartkowe (kwartylne)

c.

Odchylenie standardowe i wariancja

Odchylenie standardowe i wariancja

- są najważniejszymi

miarami rozproszenia danych wokół średniej arytmetycznej.
(SD informuje nas, o
ile przeciętnie poszczególne pomiary różnią się od średniej, czyli
wskazuje na wielkość błędu pojedynczego pomiaru; im mniejsza
wartość odchylenia, tym obserwacje są bardziej skupione wokół
średniej)

Odchylenie standardowe i wariancja

Odchylenie standardowe i wariancja





2

1

1

2

n

x

x

s

n

i

i











Odchylenie standardowe wyrażone jest w tych
samych jednostkach, co średnia arytmetyczna.

Informuje o ile średnio poszczególne pomiary
różnią się od średniej, czyli jaki jest błąd
bezwzględny pojedynczego wyniku.

Jest najważniejszą miarą rozrzutu danych wokół
średniej.

3.

Miary zmienności:

Miary zmienności:

a.

Współczynnik zmienności

- umożliwia porównanie

zmienności zbiorów danych różniących się znacznie wartością
średniej lub zawierających pomiary wykonane w różnych
jednostkach (np. kg i mm)

b.

Wskaźnik różnorodności

(wskaźnik Shannona-Wienera) -

wskaźnik różnorodności biologicznej; jego wartość określa
prawdopodobieństwo, że dwa wylosowane z próbki osobniki
będą należały do różnych gatunków

4.

Miary symetrii i spłaszczenia rozkładu:

Miary symetrii i spłaszczenia rozkładu:

a.

Kurtoza

– wskaźnik spłaszczenia/wskaźnik smukłości;

wskazuje na koncentrację danych wokół średniej

b.

Wskaźnik symetrii rozkładu

– wskaźnik skośności; jego znak

mówi o kierunku asymetrii

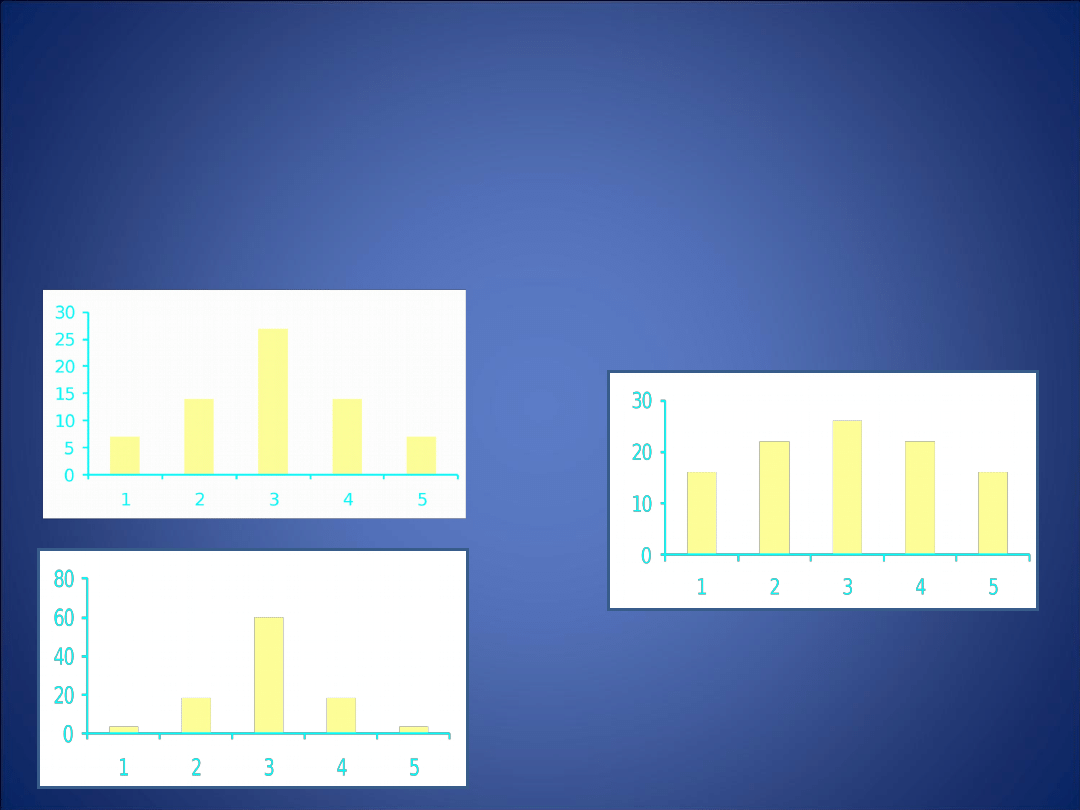
MIARA SPŁASZCZENIA ROZKŁADU

MIARA SPŁASZCZENIA ROZKŁADU

Kurtoza

Kurtoza

•gdy jest równa 0 – rozkład normalny
(mezokurtyczny)

(A)

•gdy jest dodatnia – rozkład wysmukły
(leptokurtyczny)

(B)

•gdy jest ujemna – rozkład spłaszczony
(platykurtyczny)

(C)

(A
)

(

B)

(

C)

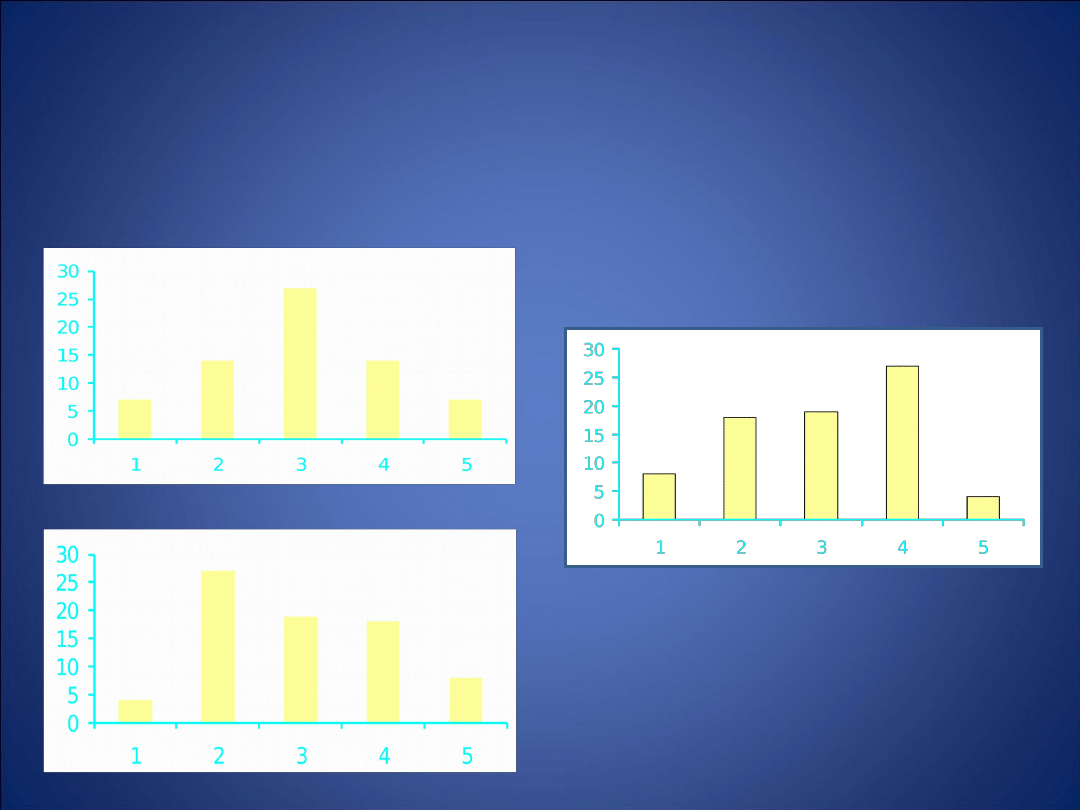
MIARA SKOŚNOŚCI ROZKŁADU

MIARA SKOŚNOŚCI ROZKŁADU

•gdy jest równy 0 – rozkład idealnie
symetryczny

(A)

•gdy jest dodatni – rozkład prawoskośny

(B)

•gdy jest ujemny – rozkład lewoskośny

(C)

(

A)

(B)

(C)

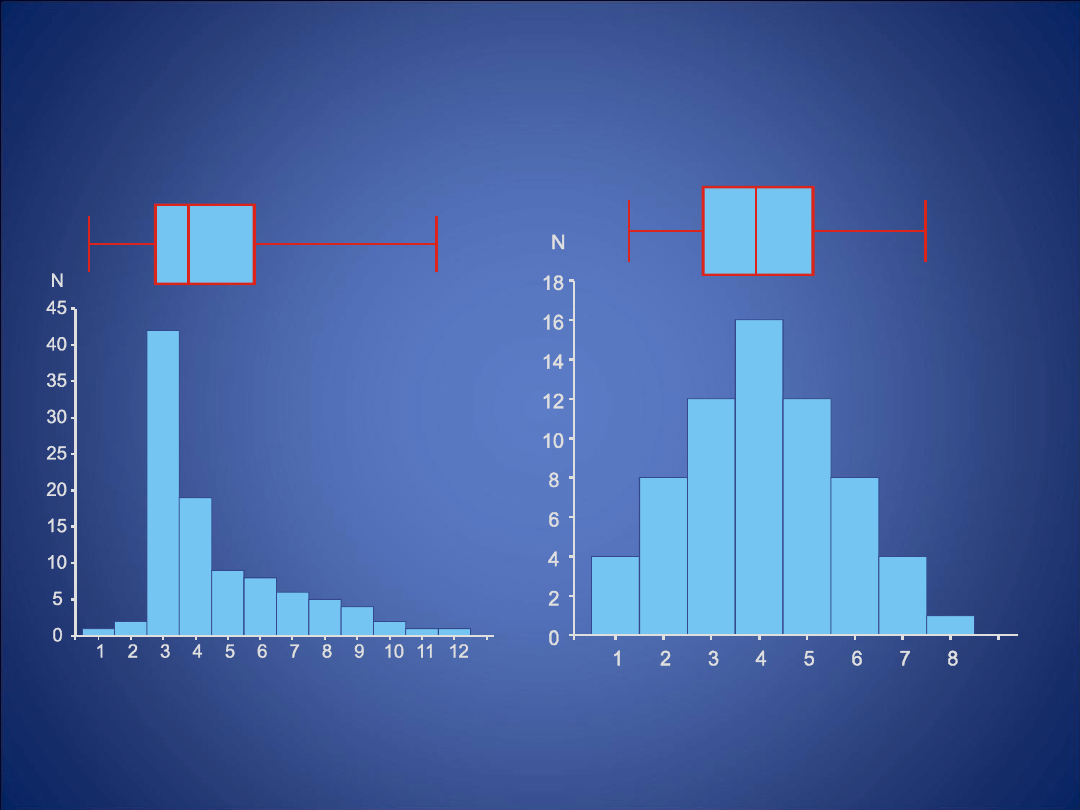
Skośność = 1,30

Rozkład prawoskośny

Rozkład symetryczny

Skośność = 0,11

Wykres ramkowy

Wykres ramkowy

Testowanie

hipotez

statystycznych

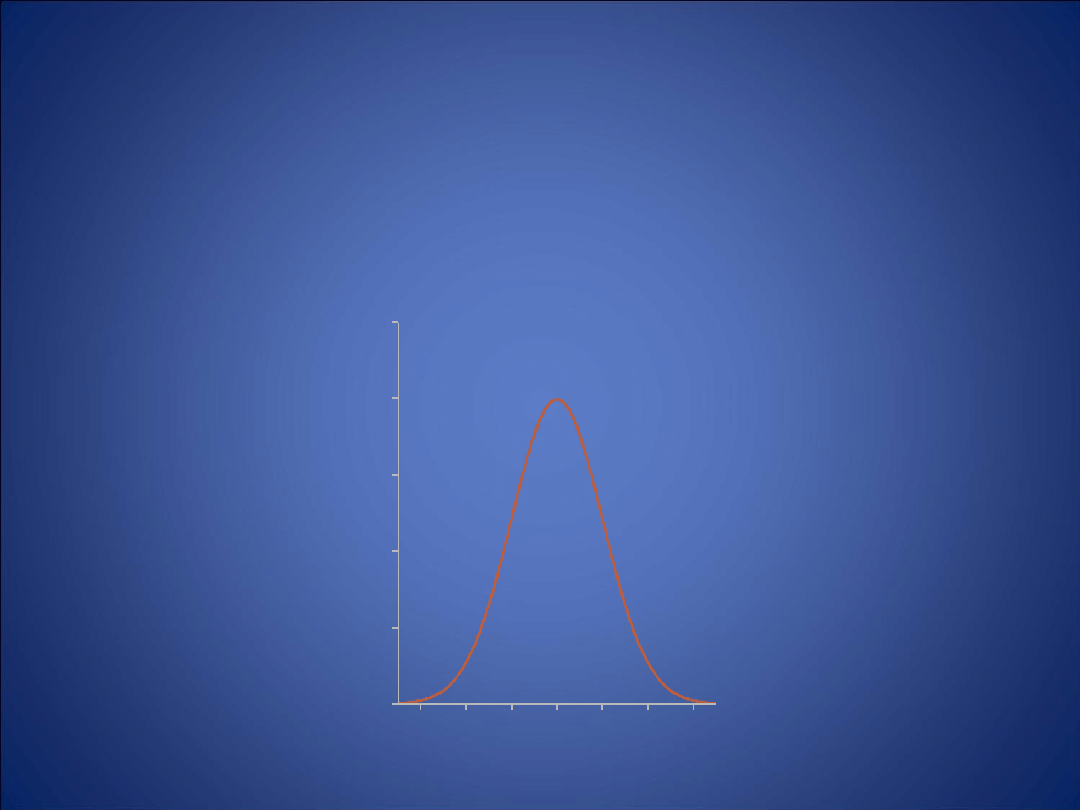
ROZKŁAD NORMALNY

ROZKŁAD NORMALNY

Rozkład normalny o średniej arytmetycznej 0 i odchyleniu

standardowym 1 nazywa się

rozkładem normalnym

rozkładem normalnym

standaryzowanym

standaryzowanym

Rozkład Gaussa

Większość pomiarów w biologii ma rozkład zbliżony do rozkładu

normalnego

-3 -2 -1 0

1

2

3

0,0

0,1

0,2

0,3

0,4

0,5

Rozkład ten jest symetryczny względem wartości średniej

p

δ

HIPOTEZY STATYSTYCZNE

HIPOTEZY STATYSTYCZNE

H

H

0

0

– Hipoteza zerowa – zakłada brak różnicy

– Hipoteza zerowa – zakłada brak różnicy

(nieistotność różnicy)

(nieistotność różnicy)

H

A

: długość skrzydła schwytanego brodźca piskliwego

różni się istotnie od średniej z populacji

H

0

: długość skrzydła schwytanego brodźca piskliwego nie

różni się istotnie od średniej z populacji

H

H

A

A

– Hipoteza alternatywna jest przeciwieństwem

– Hipoteza alternatywna jest przeciwieństwem

hipotezy zerowej

hipotezy zerowej

Każdy test statystyczny rozpoczyna się od sformułowania

hipotez

Następnie przyjmujemy poziom istotności

(prawdopodobieństwo graniczne)

0,05

FORMUŁOWANIE HIPOTEZY ZEROWEJ

FORMUŁOWANIE HIPOTEZY ZEROWEJ

Hipoteza zerowa zawsze zakłada brak

istotnych różnic między badanymi

próbami

H

0

: średni ciężar zięb i wróbli nie różni się istotnie

H

A

: średni ciężar zięb i wróbli różni się istotnie

Test dwukierunkowy (dwustronny)

Test dwukierunkowy (dwustronny)

H

A

: średni ciężar zięb jest większy niż średni ciężar wróbli

H

0

:

średni

ciężar zięb nie jest większy niż ciężar wróbli

Test jednokierunkowy (jednostronny)

Test jednokierunkowy (jednostronny)

TESTY

PARAMERTYCZNE

,

TESTY

NIEPARAMERTYCZNE

TESTY DLA
DWÓCH
PRÓB

TESTY DLA
WIĘCEJ NIŻ
DWÓCH
PRÓB

t-Studenta dla par niezależnych
t-Studenta dla par zależnych
Cochrana-Coxa
test dla 2 wsp. zmienności
test dla 2 wsk. różnorodności
test dla 2 wsp. korelacji
test F (Fishera), Levena
Lilleforsa, Shapiro-Wilka

U Manna-Whitneya
Wilcoxona
test znaków
Walda-Wolfowitza (test serii)
Kołgomorowa-Smirnowa
test mediany dla dwóch prób

ANOVA i testy post hoc:

• Tukeya

• Newman-Keulsa

• Duncana

• Scheffego

• Dunetta

Kruskala-Wallisa i testy post
hoc:

• Duna

• test mediany dla wielu
prób

• test Friedmana

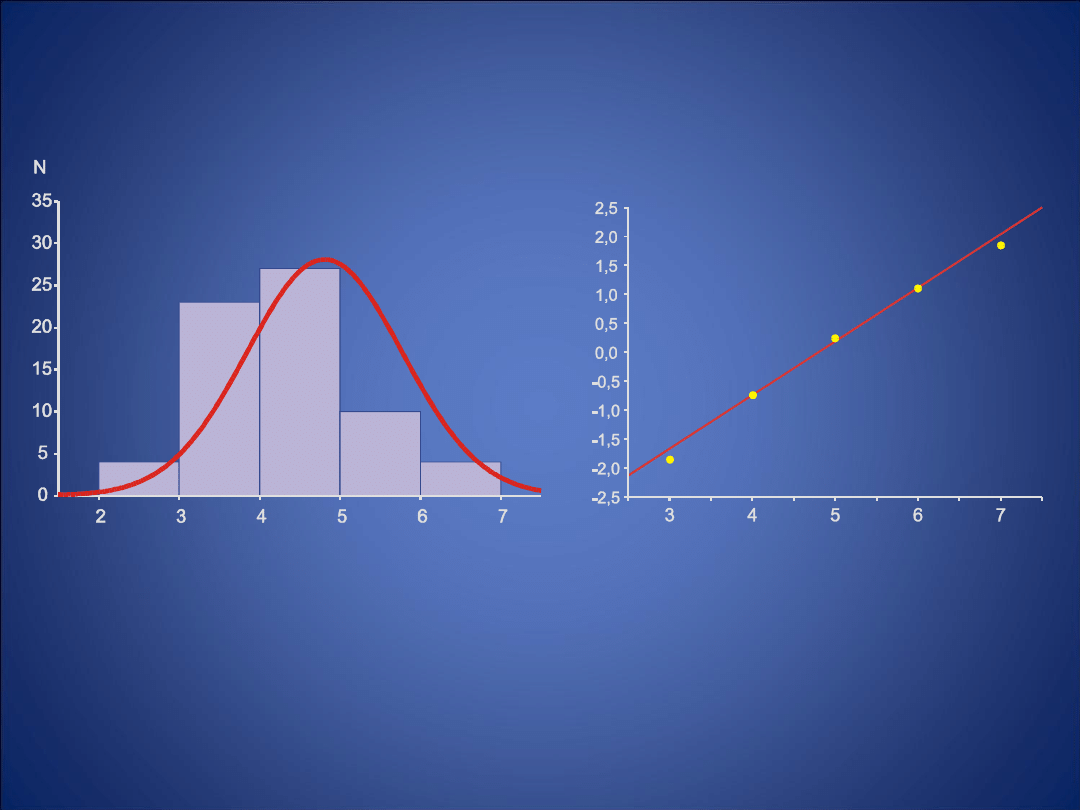
Ocena zgodności rozkładu z rozkładem normalnym

Test Shapiro-Wilka

W=0,89; p<0,0001

Skośność=0,40

Kurtoza=-0,04

Histogram z dopasowanym

rozkładem normalnym

Rozkład normalności

W a r to ś c i o b s e r w o w a n e

O

cz

ek

iw

an

y

ro

zk

ła

d

no

rm

al

ny

116

120

124

128

132

136

[mm]

młode

dorosłe

Maks

Min

X ± SD

X

384

379

Test t-studenta

Test t-studenta

H

0

: Średnia liczba jaj w gniazdach wróbla i mazurka nie różni się

istotnie

H

0

: Średnia liczba jaj w gniazdach wróbla i mazurka różni się

istotnie

N

wr

=68

N

maz

=83

wr

=4,8

maz

=4,2

s

2

=0,93 s

2

=0,54

x

x

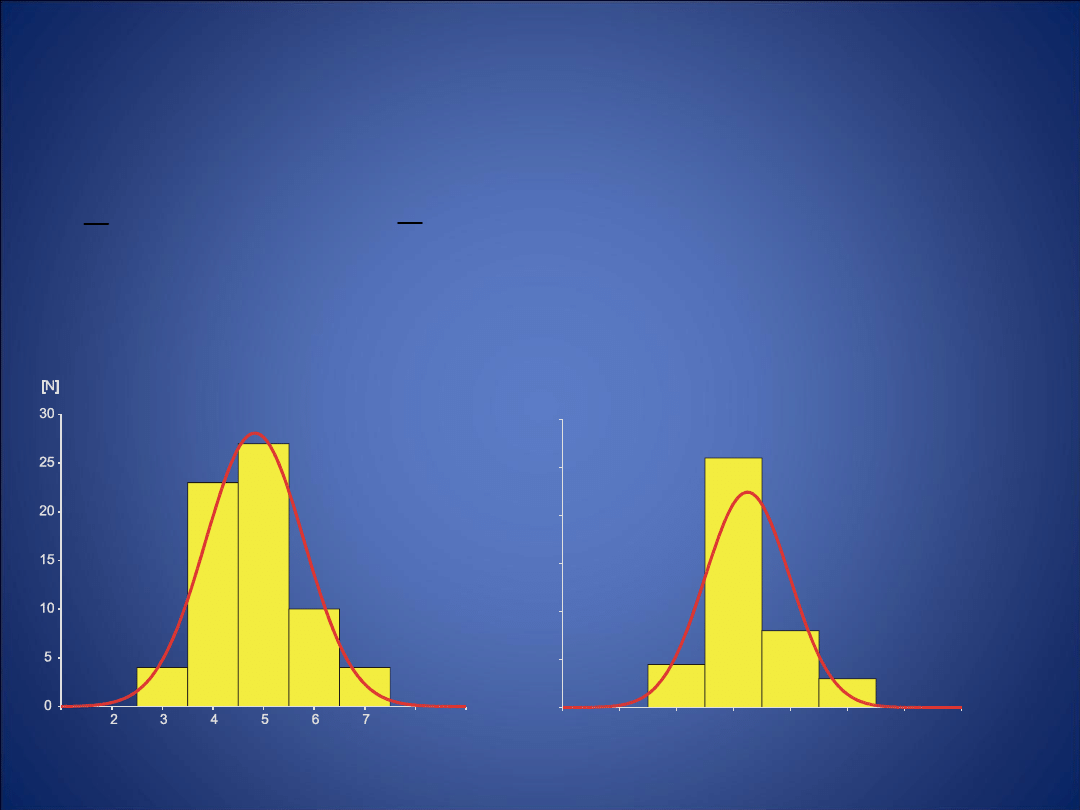
Ocena zgodności rozkładów z rozkładem

normalnym

test Shapiro-Wilka; W=0,89; p<0,001

test Shapiro-Wilka; W=0,79; p<0,001

3

4

5

6

0

1 0

2 0

3 0

4 0

5 0

6 0

2

[N ]

7

ANOVA

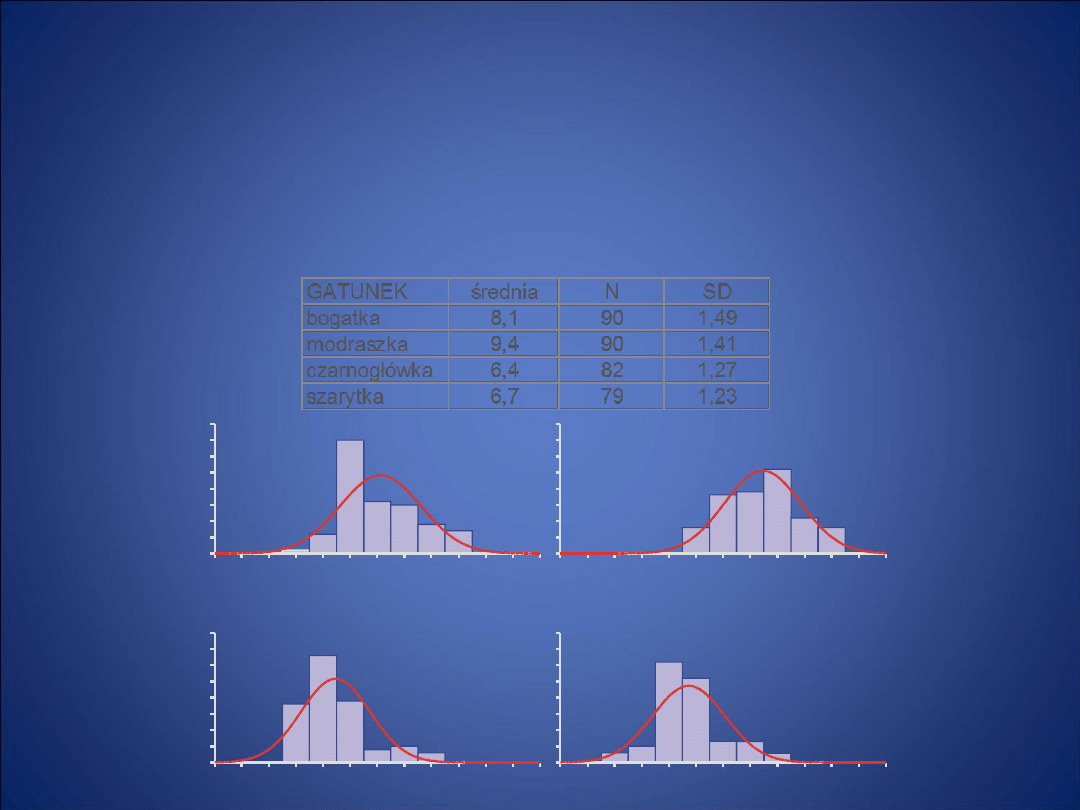
ANALIZA WARIANCJI

ANALIZA WARIANCJI

Badano wielkość zniesienia u 4 gatunków sikor. Należy

sprawdzić, czy gatunki te różnią się średnią liczbą składanych

jaj.

H

0

: Średnia liczba jaj składanych przez 4 gatunki sikor jest taka

sama.

H

A

: Średnia liczba jaj składanych przez 4 gatunki sikor

nie

jest

taka sama.

4

5

6

7

8

9

1 0 1 1 1 2

0

1 0

2 0

3 0

4 0

4

5

6

7

8

9

1 0 1 1 1 2

4

5

6

7

8

9

1 0 1 1 1 2

4

5

6

7

8

9

1 0 1 1 1 2

0

1 0

2 0

3 0

4 0

N

N

c z a r n o g łó w k a

m o d r a s z k a

s z a r y tk a

b o g a tk a

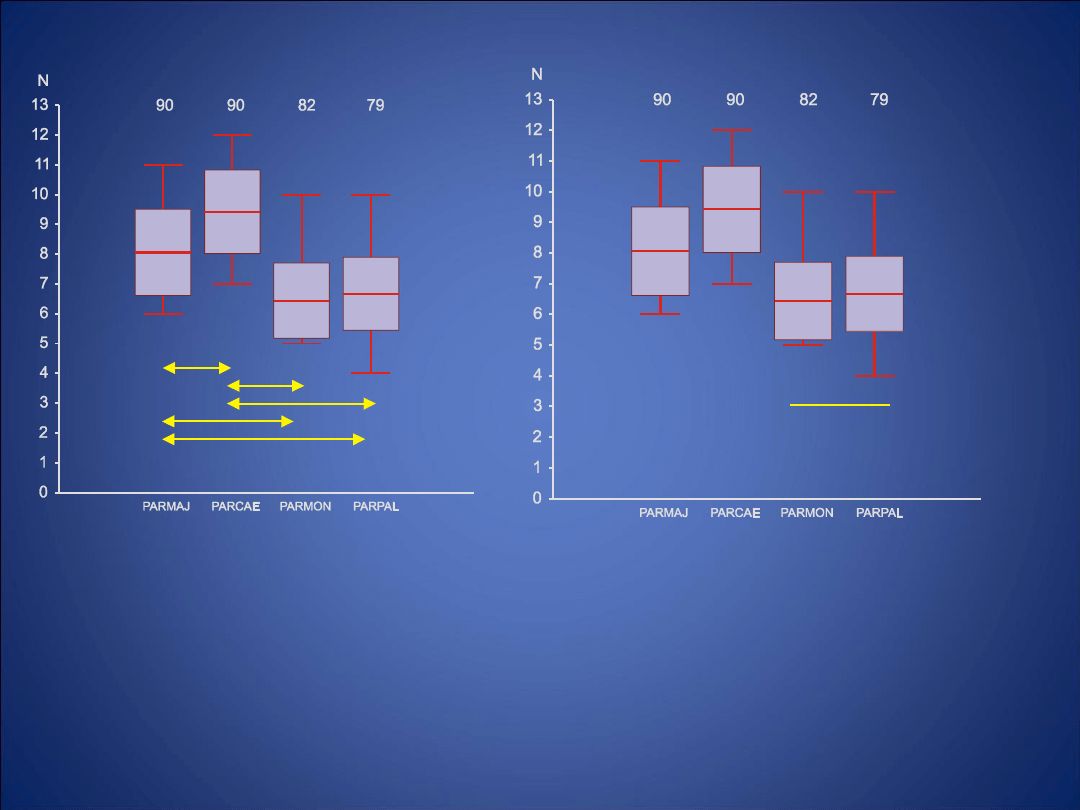
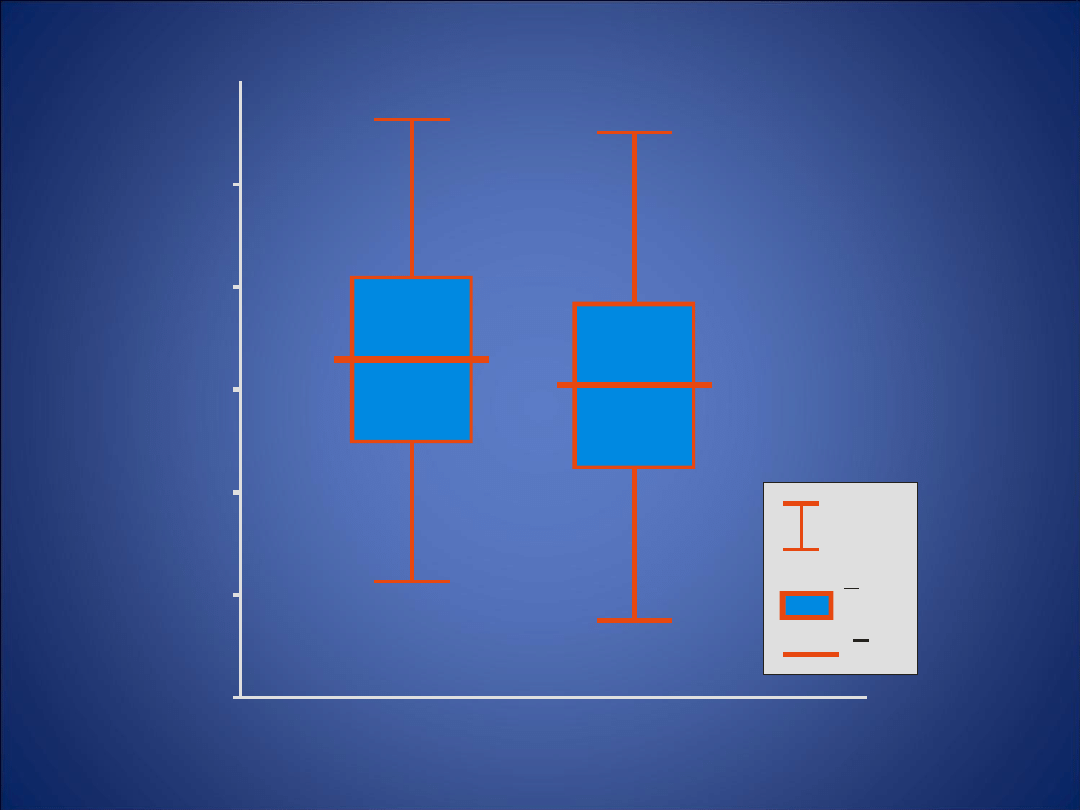
ANALIZA WARIANCJI

ANALIZA WARIANCJI

Porównanie wielkości zniesienia u 4 gatunków sikor. Linia

pozioma – średnia, prostokąt – odchylenie standardowe,

linia pionowa zakres. Nad słupkami podano liczebności

prób.

Dziękuję za uwagę

Dziękuję za uwagę