Geometria mechaniczna figur

płaskich i mas.

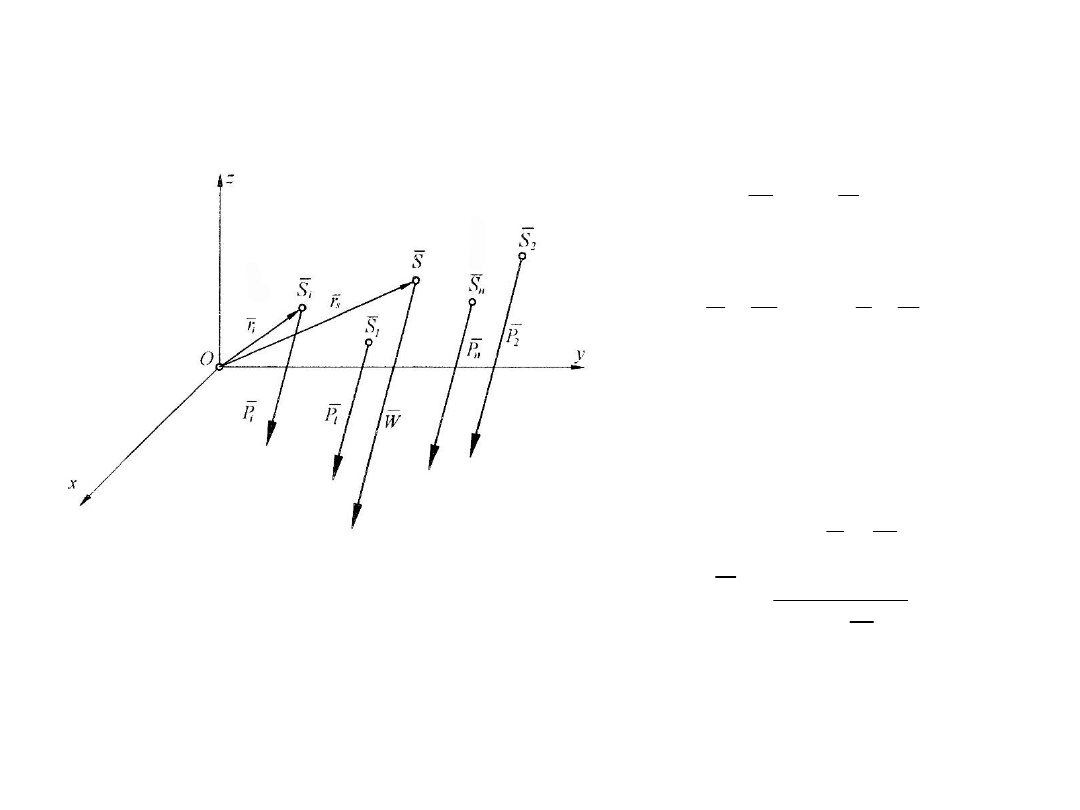
Środek sił równoległych

uczepionych







n

i

i

P

W

1

 











n

i

i

i

s

P

r

W

r

1

 













n

i

i

n

i

i

i

s

P

P

r

r

1

1

Współrzędne środka sił.











n

i

i

i

n

i

i

s

P

x

P

x

1

1











n

i

i

i

n

i

i

s

P

y

P

y

1

1











n

i

i

i

n

i

i

s

P

z

P

z

1

1

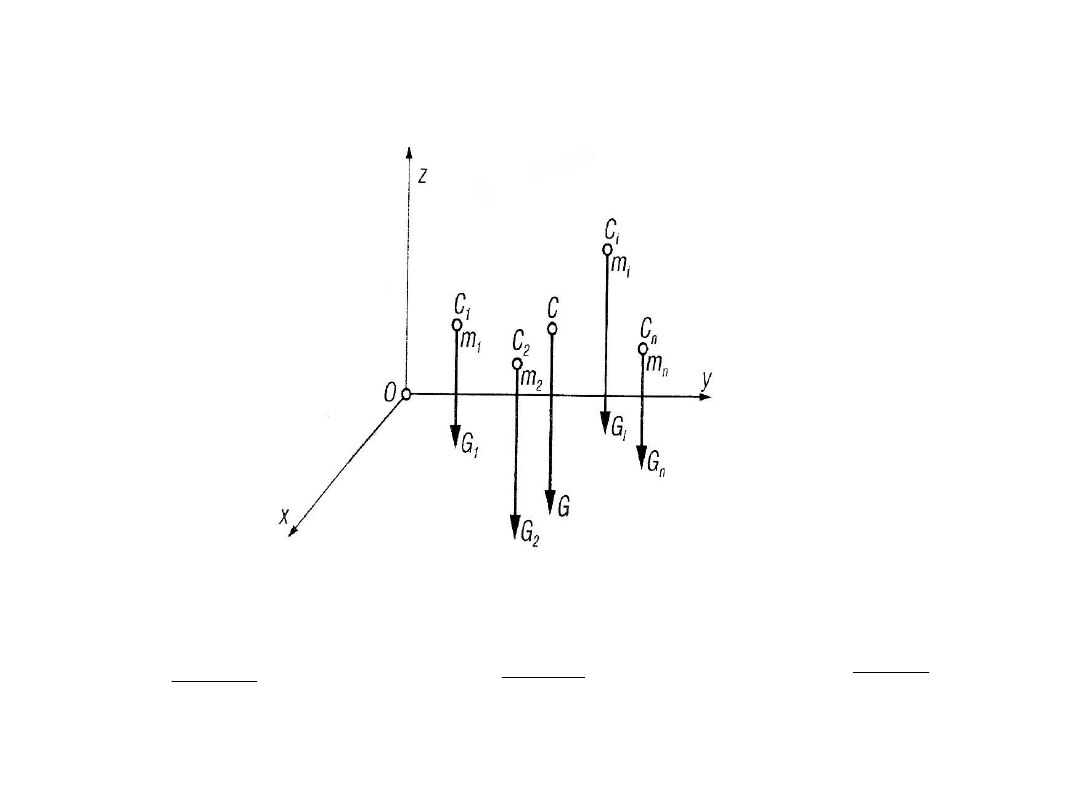
Środek ciężkości i środek

masy.











n

i

i

i

n

i

i

C

G

x

G

x

1

1











n

i

i

i

n

i

i

C

G

y

G

y

1

1











n

i

i

i

n

i

i

C

G

z

G

z

1

1

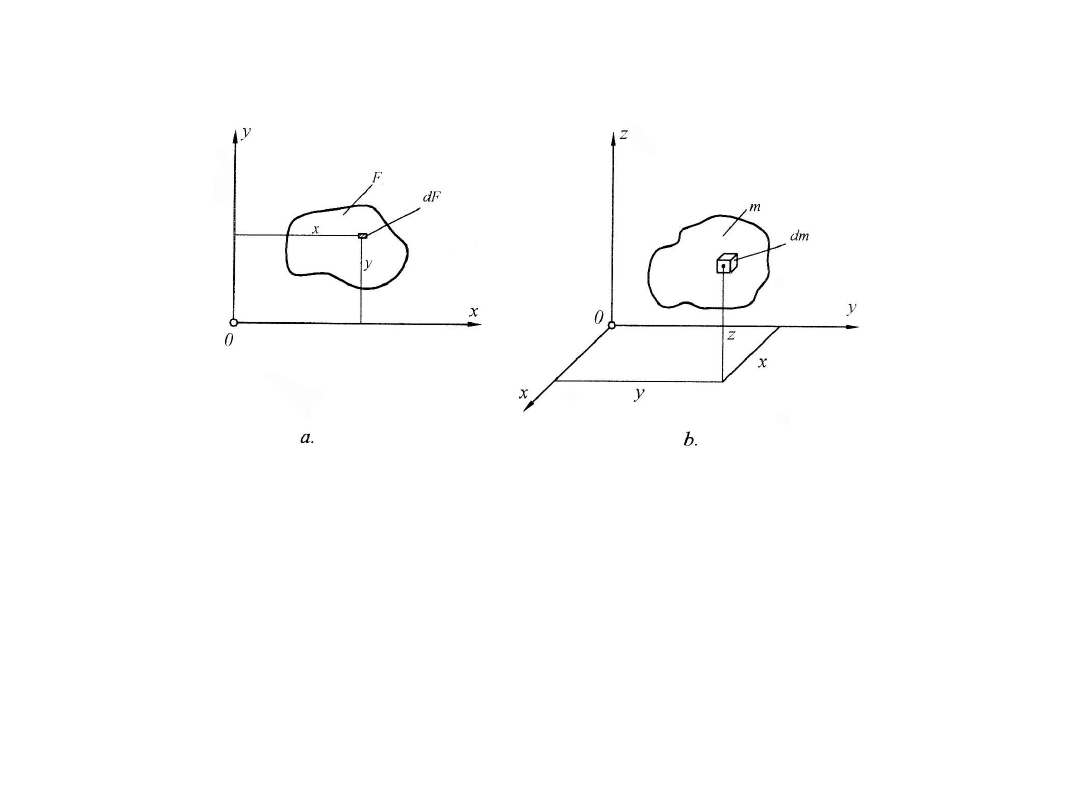
W przypadku rozpatrywania bryły materialnej należy ją rozpatrywać jako zbór ciągły,
nieskończony punktów materialnych o ciężarach dG.
W takim przypadku sumy w poprzednich wzorach są nieskończonymi, a te zgodnie
z definicją, przechodzą w całki.

G

xdG

x

G

C





G

ydG

y

G

C





G

zdG

z

G

C





Współrzędne środka ciężkości:

Jeżeli obszar sił dG jest niewielki w stosunku do kuli ziemskiej, to można przyjąć,
że siły dG tworzą pole jednorodne a dla takiego pola zachodzi zależność:

dm

g

dG





m

g

G





stąd

m

xdm

x

m

C





m

ydm

y

m

C





m

zdm

z

m

C





lub

dV

dG







V

G







I wtedy:

V

xdV

x

V

C





V

ydV

y

V

C





V

zdV

z

V

C





Analogicznie dla ciał o jednakowej grubości:

hdF

dG





hF

G





F

xdF

x

F

C





F

ydF

y

F

C





F

zdF

z

F

C





Fdl

dG





Fl

G





l

xdl

x

l

C





l

ydl

y

l

C





l

zdl

z

l

C





Istnieją ciała jednorodne w postaci linii materialnych:

Twierdzenie:

Jeżeli bryła jednorodna posiada płaszczyznę lub oś symetrii, to

środek ciężkości leży na tej płaszczyźnie lub osi symetrii, a jeżeli posiada
punkt symetrii to jest on środkiem ciężkości.

poj. Moment statyczny

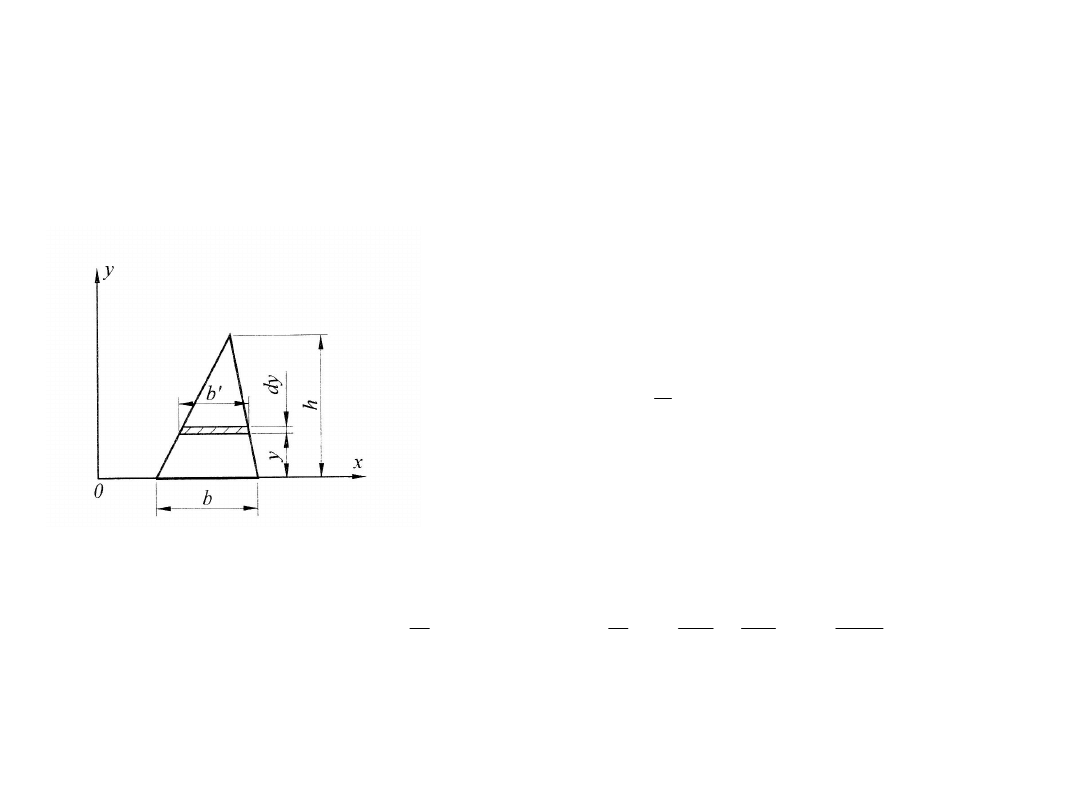
Przykład:





dy

y

h

h

b

dy

b

dF





 '





6

3

2

2

0

3

2

0

bh

y

y

h

h

b

ydy

y

h

h

b

ydF

S

h

h

F

x































Określić moment statyczny trójkąta i środek ciężkości względem podstawy!





dy

y

h

h

b

dy

b

dF





 '

Momenty bezwładności figur i

mas.





F

x

dF

y

I

2





F

y

dF

x

I

2







F

dF

x

y

I

)

(

2

2

0







m

xx

yz

dm

x

J

J

2









m

yy

xz

dm

y

J

J

2









m

zz

xy

dm

z

J

J

2













m

x

dm

z

y

J

2

2











m

y

dm

z

x

J

2

2











m

z

dm

y

x

J

2

2













m

dm

z

y

x

J

2

2

2

0

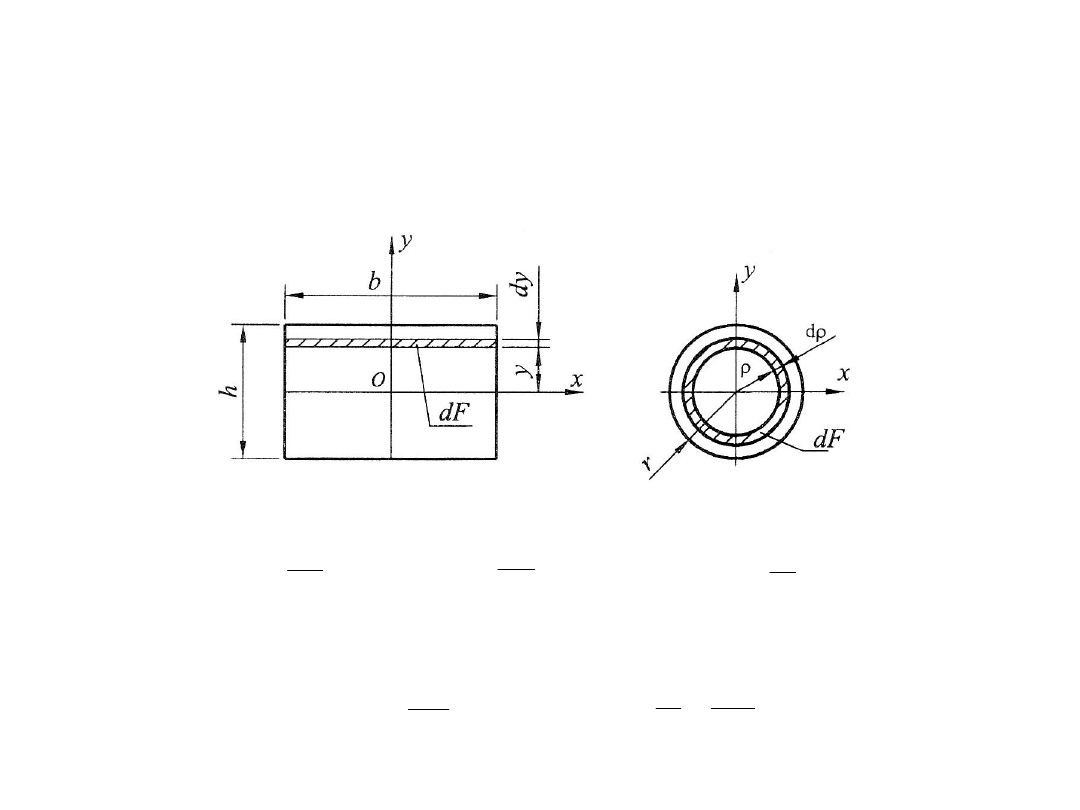
Przykład:

Obliczyć momenty bezwładności pola prostokąta o podstawie b i wysokości h
oraz pola koła o promieniu r względem osi centralnych!

12

3

2

/

2

/

2

2

bh

dy

y

b

dF

y

I

h

h

F

x













12

3

hb

I

y







2

2

0

12

b

h

bh

I

I

I

y

x

























2

/

0

4

3

2

2

0

32

2

d

F

d

d

dF

y

x

I









64

2

4

0

d

I

I

I

y

x









Transformacja równoległa momentów

bezwładności

.

Twierdzenie I: Moment bezwładności pola figury płaskiej lub masy bryły
względem jakiejś prostej lub płaszczyzny jest równy momentowi bezwładności
względem prostej lub płaszczyzny centralnej, powiększonemu
o iloczyn powierzchni pola lub masy bryły przez kwadrat odległości między tymi
osiami lub płaszczyznami.

Twierdzenie II: Moment bezwładności pola figury płaskiej lub masy bryły
względem jakiegoś punktu jest równy momentowi bezwładności
względem środka ciężkości, powiększonemu
o iloczyn powierzchni pola lub masy bryły przez kwadrat odległości między tymi
punktami.