Charakterystyki geometryczne
figur płaskich

dr hab. inż. Tadeusz Chyży

Katedra Mechaniki Konstrukcji

2

Charakterystyki geometryczne figur płaskich

Wielkości geometryczne charakteryzujące
przekrój pod względem wytrzymałościowym to:



pole przekroju (A)

, (ang. cross section),



momenty statyczne przekroju (S)

, (ang. first

moments of area),



momenty bezwładności przekroju (I )

, (ang.

second moments of area)

3

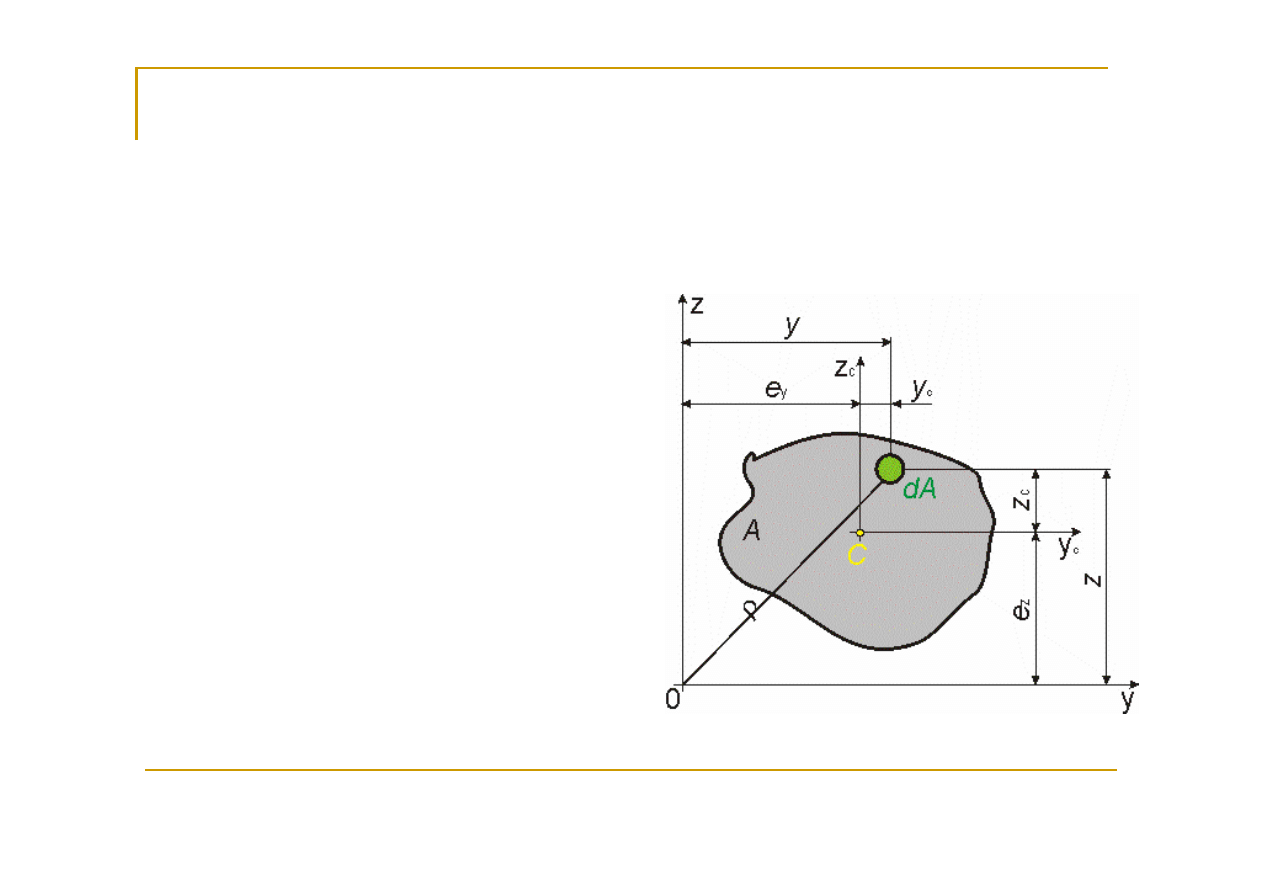
Charakterystyki geometryczne figur płaskich

Pole przekroju

(figury

płaskiej) określa się
wzorami:

Jest to wielkość zawsze

dodatnia









S

dydz

dA

A

4

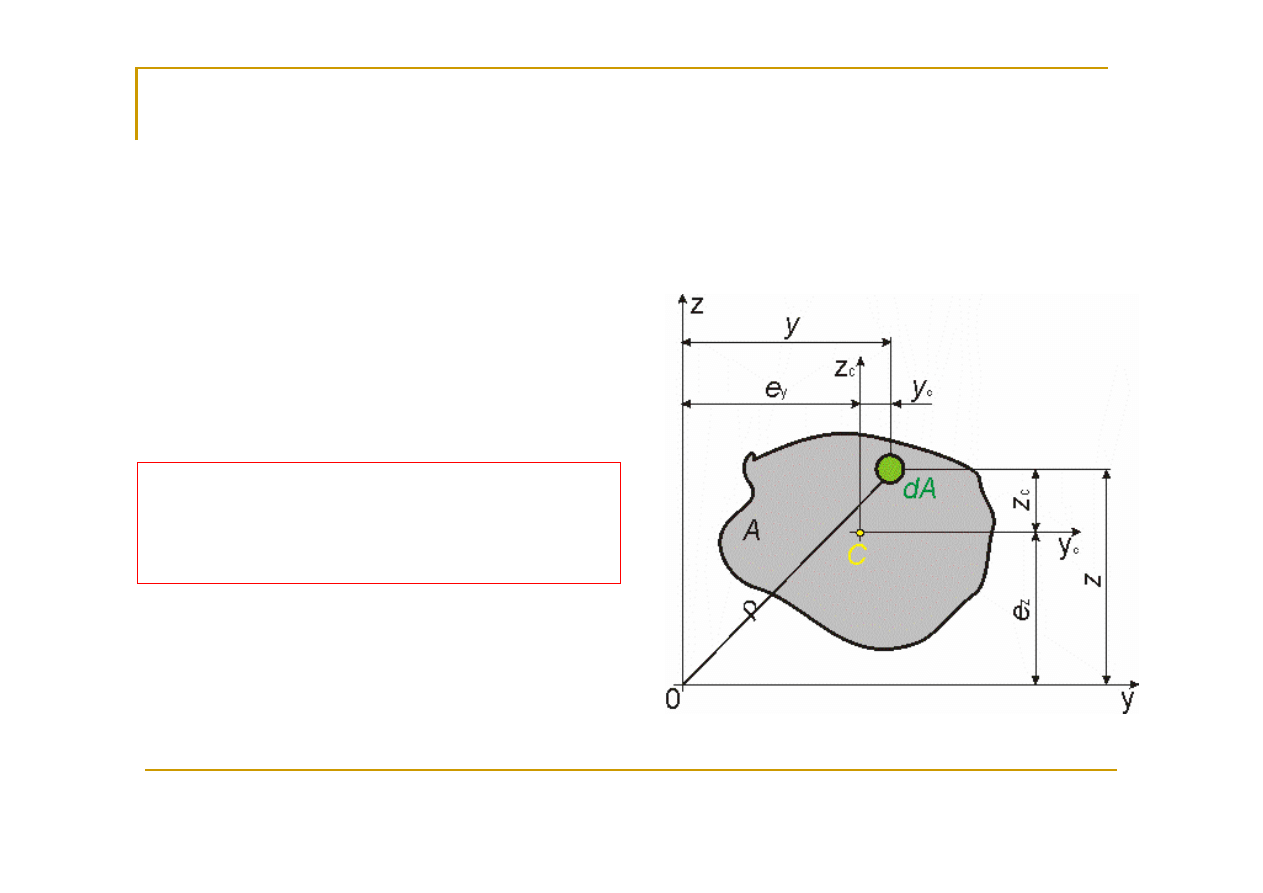
Charakterystyki geometryczne figur płaskich

Momenty statyczne
przekroju

(figury

płaskiej) względem
dowolnej osi leżącej w
płaszczyźnie tego
przekroju określa się
wzorami:

Są to wielkości

addytywne

, o

wartościach

dodatnich

lub

ujemnych

y

z

,

A

A

S

zdA

S

ydA









5

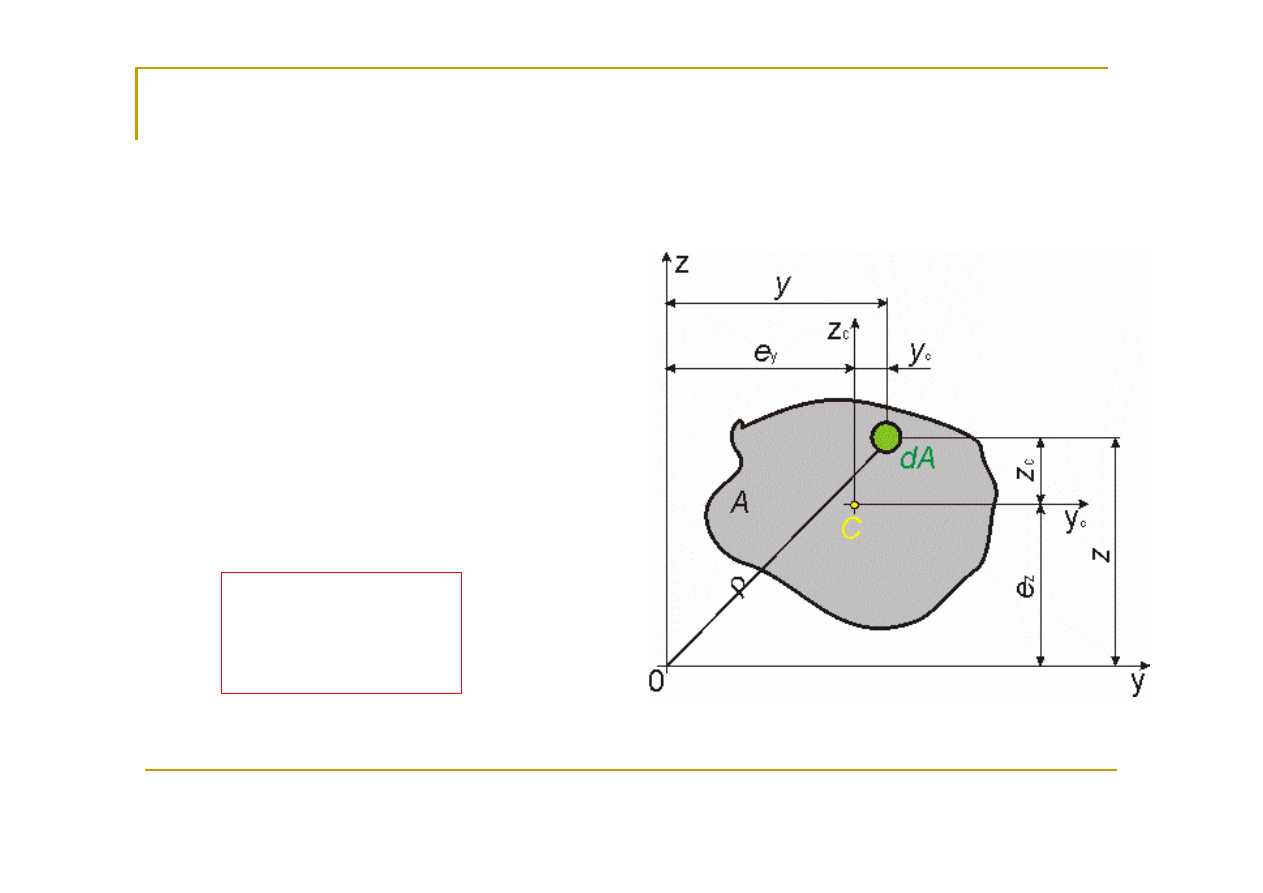
Charakterystyki geometryczne figur płaskich

Momenty statyczne

są potrzebne do obliczania

współrzędnych środków geometrycznych

(środków

ciężkości) przekrojów:

Wniosek:

moment statyczny względem dowolnej osi

centralnej (przechodzącej przez środek geometryczny
przekroju, np. y

c

, z

c

lub każda oś symetrii przekroju)

jest równy

zeru

.

y

z

y

z

,

A

A

ydA

zdA

S

S

e

e

A

A

A

A













6

Charakterystyki geometryczne figur płaskich

6

W przypadku

przekrojów złożonych

z prostych figur

geometrycznych, ze względu na addytywność momentów
statycznych, można zastosować

wzory uproszczone

(sumowanie zamiast całkowania):

Ponadto:

y

z

1

1

,

i n

i n

i

i

i

i

i

i

S

z A

S

y A

















1

1

y

z

1

1

,

i n

i n

i

i

i

i

i

i

i n

i n

i

i

i

i

y A

z A

e

e

A

A





























7

Charakterystyki geometryczne figur płaskich

8

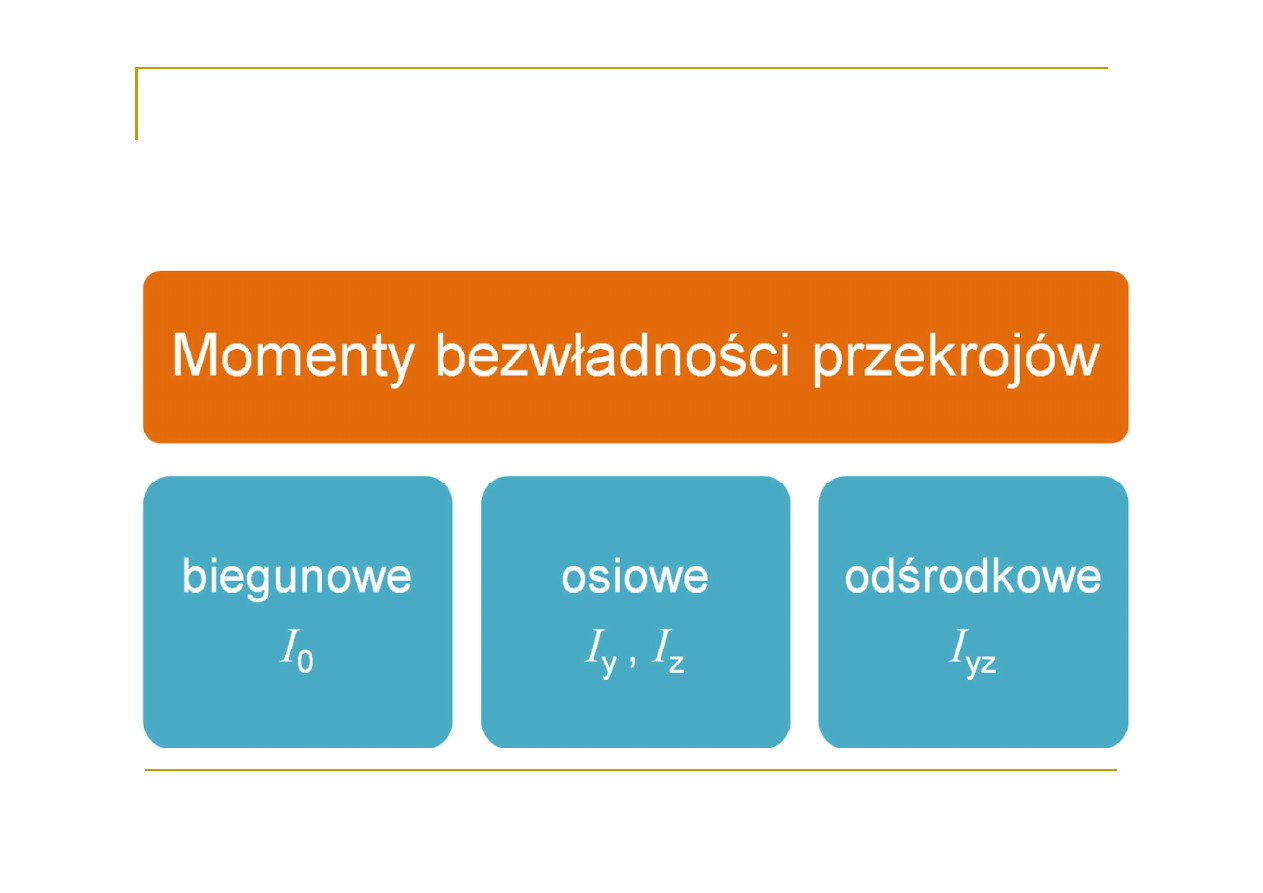
Charakterystyki geometryczne figur płaskich

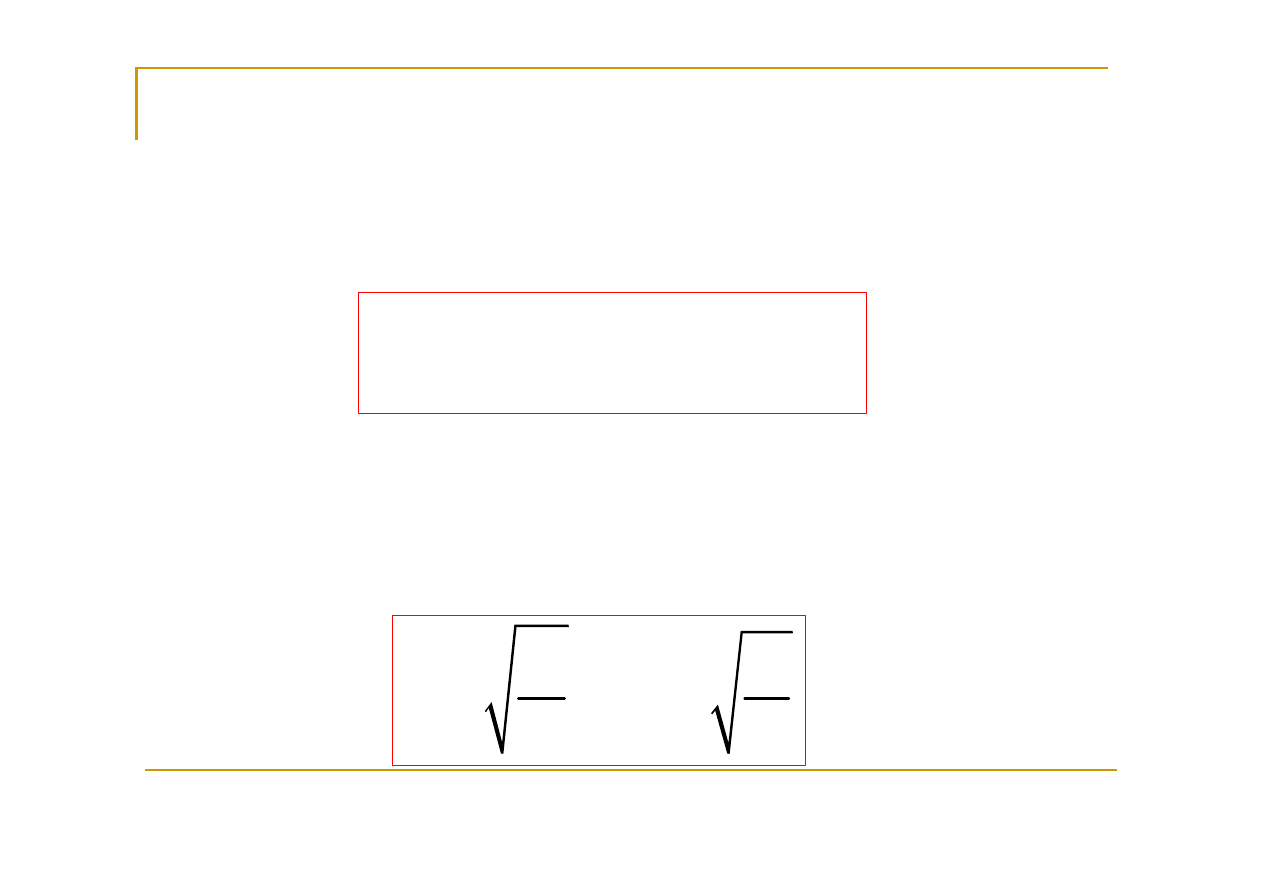
Biegunowy moment
bezwładności przekroju
(I

0

)

(moment

bezwładności przekroju
względem punktu)
oblicza się ze wzoru:

2

0

A

I

dA







9

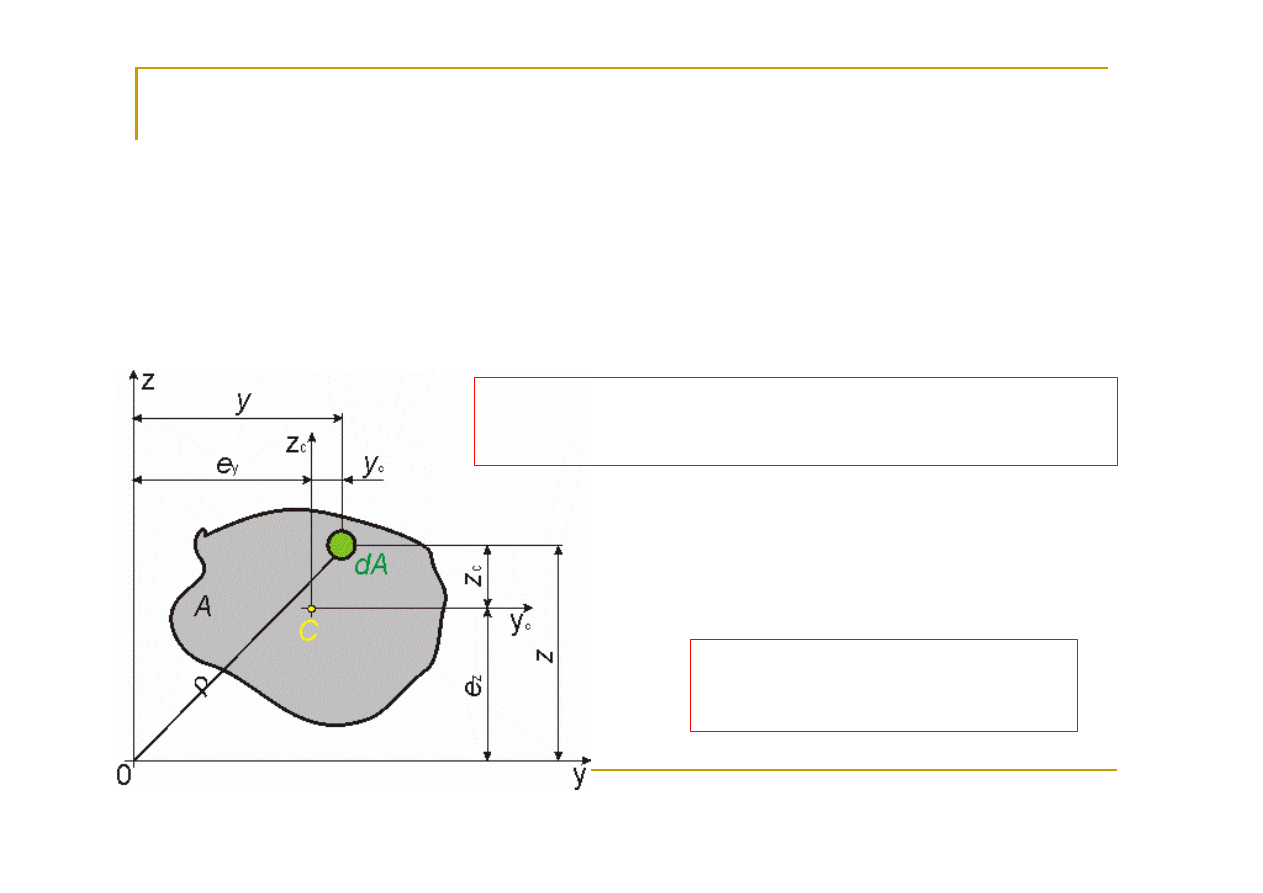
Charakterystyki geometryczne figur płaskich

9

Momenty bezwładności przekroju względem osi (I

y

, I

z

)

(momenty osiowe) są zdefiniowane przez poniższe
wzory:

Momenty bezwładności są wielkościami

addytywnymi

,

mającymi zawsze wartości

dodatnie

;

„addytywnymi”

, tzn. np. I

y

=I

y

1

+I

y

2

+...

Promieniem bezwładności

nazywa się wielkość

zdefiniowaną następująco:

2

2

y

z

,

A

A

I

z dA

I

y dA









y

z

y

z

,

I

I

i

i

A

A





10

Charakterystyki geometryczne figur płaskich

10

Odśrodkowy moment bezwładności przekroju (I

yz

)

względem układu osi yz (moment zboczenia, moment
dewiacji) wyraża się wzorem:



Momenty odśrodkowe są wielkościami

addytywnymi

,

przyjmującymi wartości

dodatnie

lub

ujemne

.



Układ osi yz, w którym

moment odśrodkowy równa się

zeru

nazywa się

układem osi głównych

; aby I

yz

=0

wystarczy, że jedna z osi jest osią symetrii przekroju,



Układ osi głównych o początku w środku

geometrycznym przekroju to

układ głównych centralnych

osi bezwładności

yz

A

I

yzdA





11

Charakterystyki geometryczne figur płaskich

W przypadku

równoległego przesunięcia

układu osi do

obliczania momentów bezwładności stosuje się

twierdzenie

Steinera

. Wyraża się ono wzorami:

c c

yz

y z

z y

I

I

Ae e





a dla momentów
odśrodkowych:

c

c

2

2

y

y

z

z

z

y

,

,

I

I

Ae

I

I

Ae









12

Charakterystyki geometryczne figur płaskich

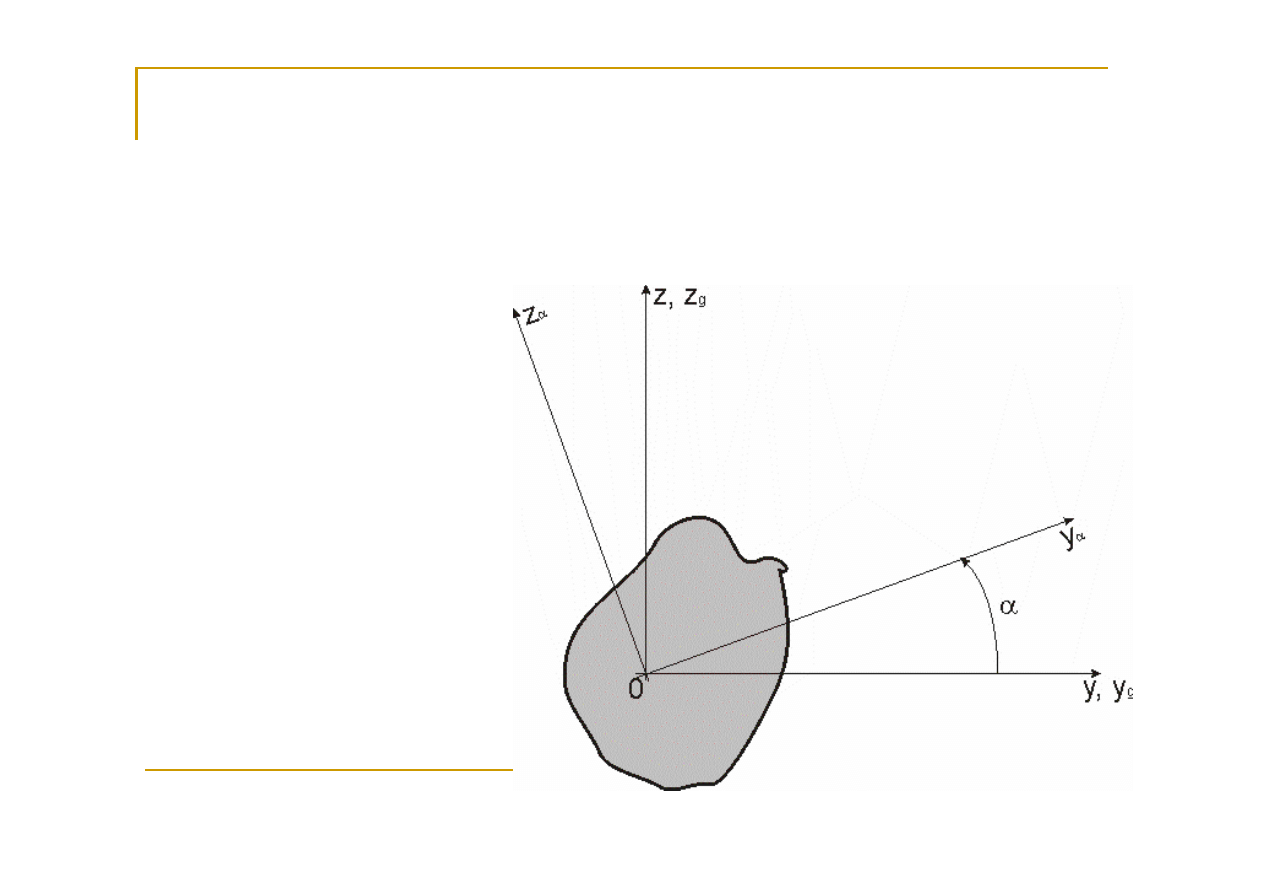
12

Gdy występuje

obrót układu odniesienia

wokół

jego początku o kąt





13

Charakterystyki geometryczne figur płaskich

13

... wówczas słuszne są następujące zależności:

α

α

α α

2

2

y

y

z

yz

2

2

z

y

z

yz

y

z

y z

yz

cos

sin

sin 2

sin

cos

sin 2

cos 2

sin 2

2

I

I

I

I

I

I

I

I

I

I

I

I



































14

Charakterystyki geometryczne figur płaskich

Dla układu osi obróconych o kąt



względem osi

głównych y

g

, z

g

powyższe równania można też zapisać w

następującej formie:

g

g

g

g

α

g

g

g

g

α

g

g

α α

y

z

y

z

y

y

z

y

z

z

y

z

y z

cos 2

2

2

cos 2

2

2

sin 2

2

I

I

I

I

I

I

I

I

I

I

I

I

I





























15

Charakterystyki geometryczne figur płaskich

15

Wniosek: przy obrocie układu odniesienia

zawsze

słuszne

są zależności:

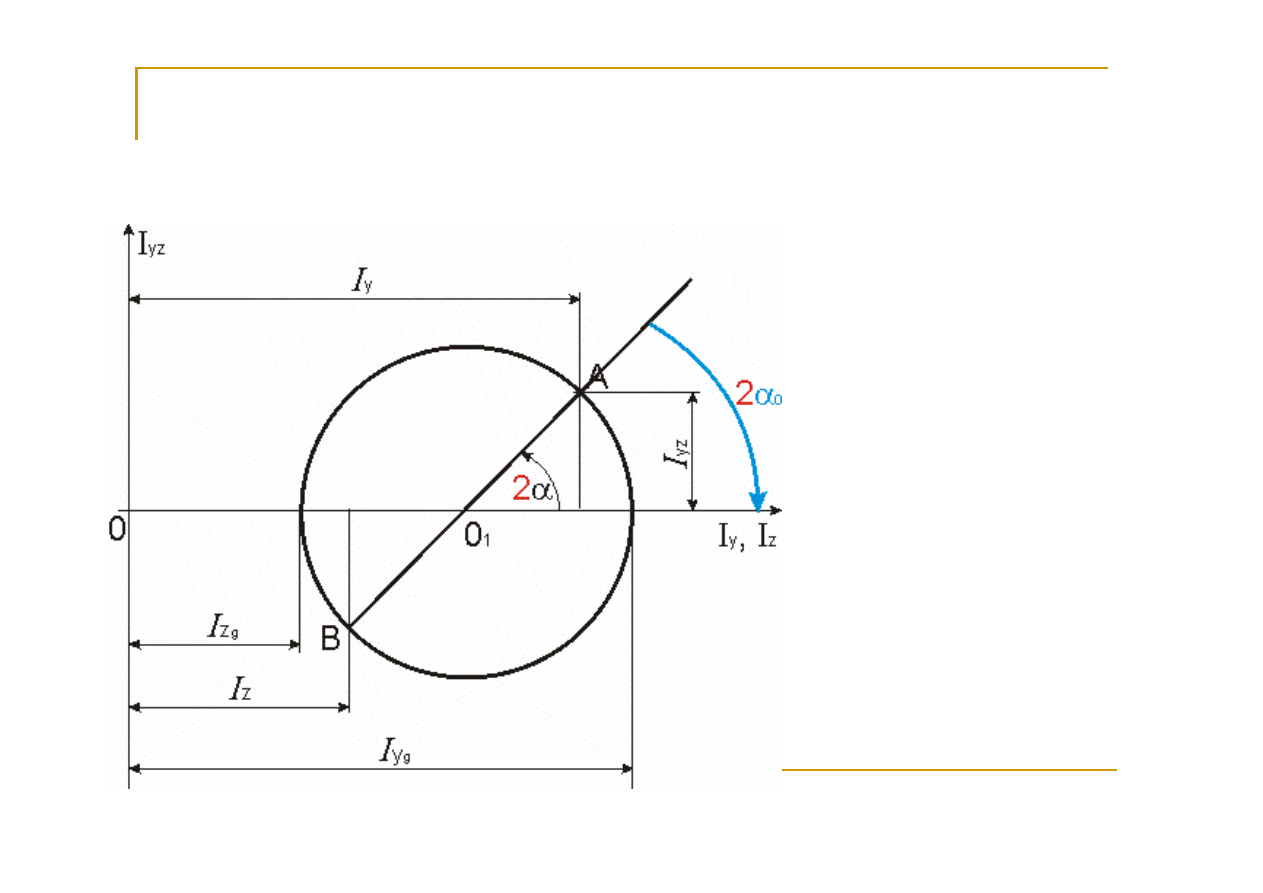
Wzory 

można przedstawić

graficznie za

pomocą tzw.

koła Mohra

.

α

α

g

g

y

z

y

z

0

I

I

I

I

I









16

Charakterystyki geometryczne figur płaskich

Koło

Mohra

pozwala odczytać
wartości
momentów I

y

, I

z

i

I

yz

dla

układu

obróconego

o

dowolny

kąt



względem układu
głównego,

albo

wartości

ekstre-

malne momentów

17

Charakterystyki geometryczne figur płaskich

17

Wniosek

: momenty bezwładności względem osi głównych

mają wartości

ekstremalne

g

g

2

y

z

y

z

2

y

yz

2

y

z

y

z

2

z

y

m

z

yz

0

y

m

a

in

ks

z

2

2

2

2

2

oraz: tg2

I

I

I

I

I

I

I

I

I

I

I

I

I

I

I

I

I























































Momenty
główne można
teraz wyrazić
wzorami, które
jednocześnie
określają
położenie osi
głównych

18

Charakterystyki geometryczne figur płaskich

18

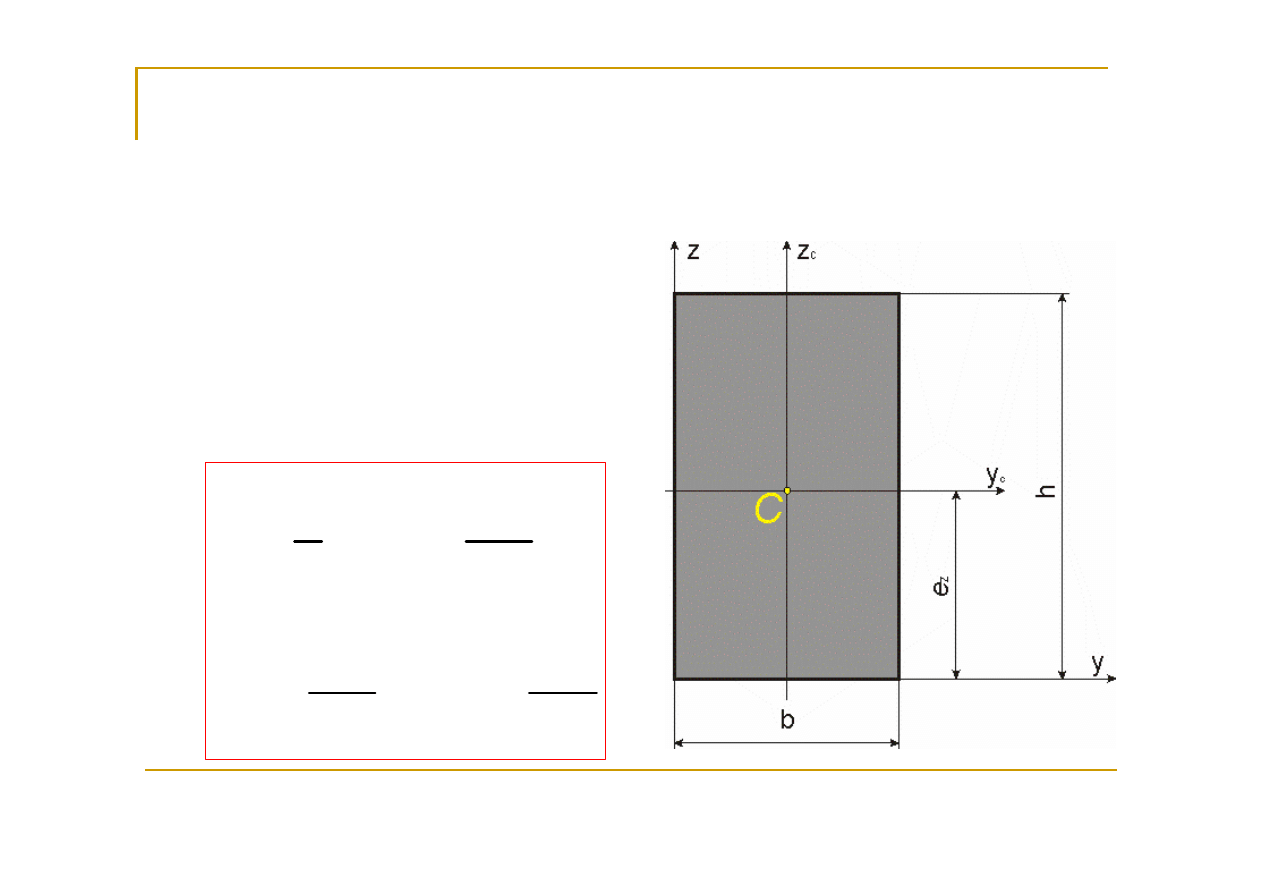
Wartości charakterystyk
geometrycznych dla
najprostszych
przekrojów:

prostokąt

c

c

3

z

y

3

3

y

z

,

2

3

,

12

12

h

bh

e

I

bh

hb

I

I









19

Charakterystyki geometryczne figur płaskich

Wartości charakterystyk
geometrycznych dla
najprostszych
przekrojów:

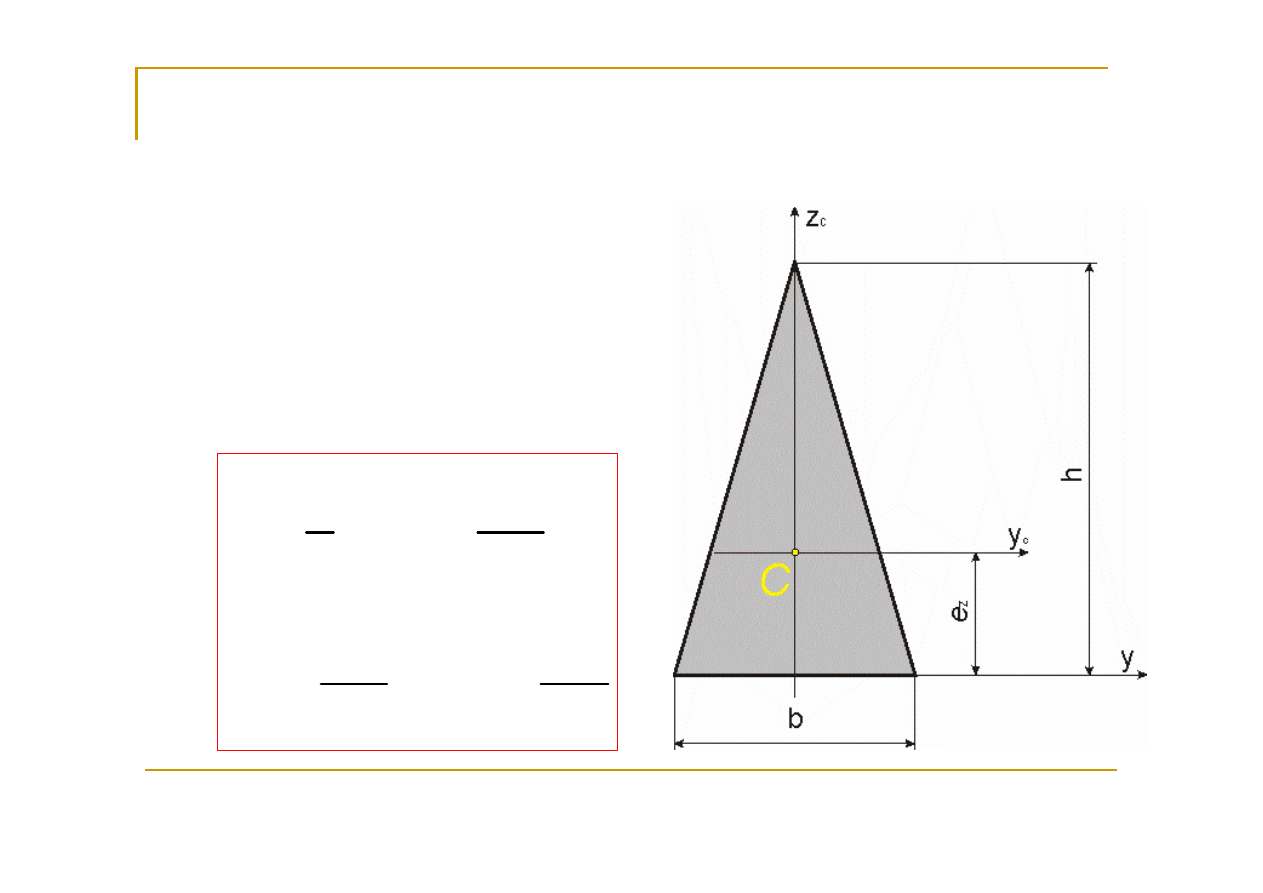
trójkąt

c

c

3

z

y

3

3

y

z

,

3

12

,

36

48

h

bh

e

I

bh

hb

I

I









20

Charakterystyki geometryczne figur płaskich

Wartości charakterystyk
geometrycznych dla
najprostszych
przekrojów:

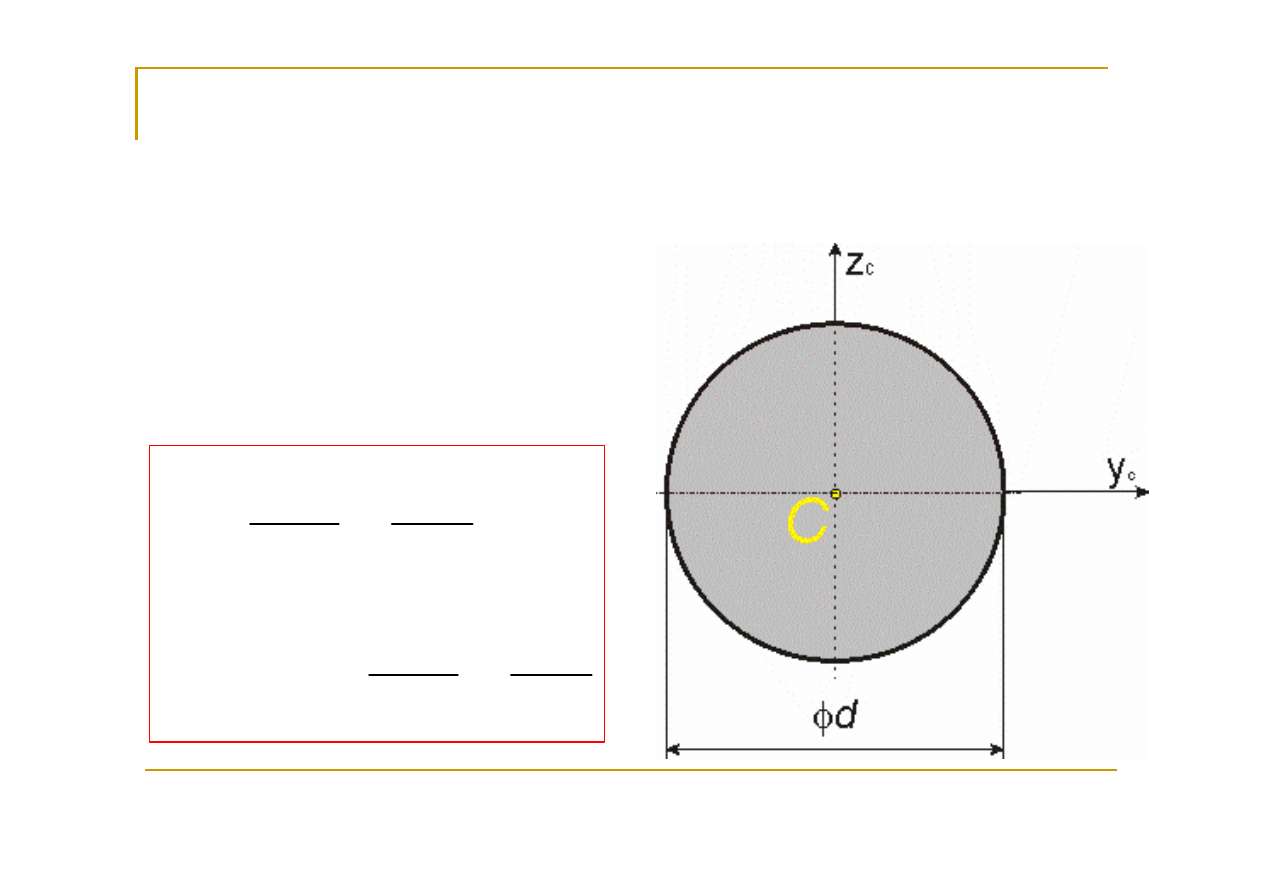
koło

c

c

4

4

0

4

4

y

z

32

2

64

4

d

r

I

d

r

I

I



















21

Charakterystyki geometryczne figur płaskich

Wartości charakterystyk
geometrycznych dla
najprostszych
przekrojów:

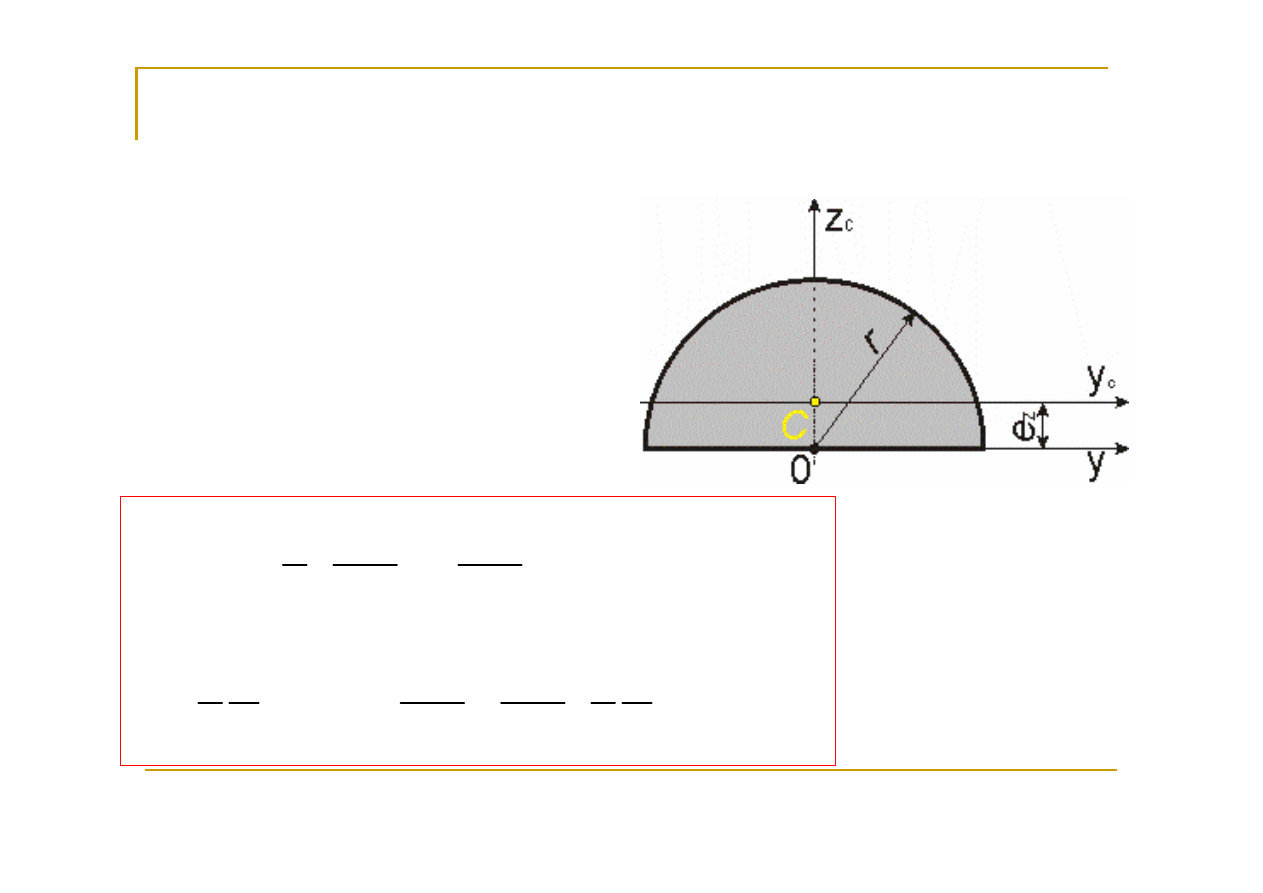
półkole

c

c

4

4

y

z

2

4

2

4

z

y

1

2

4

8

4

4

0,11

3

8

2

3

r

r

I

I

r

r

r

r

e

I

r





















































22

Charakterystyki geometryczne figur płaskich

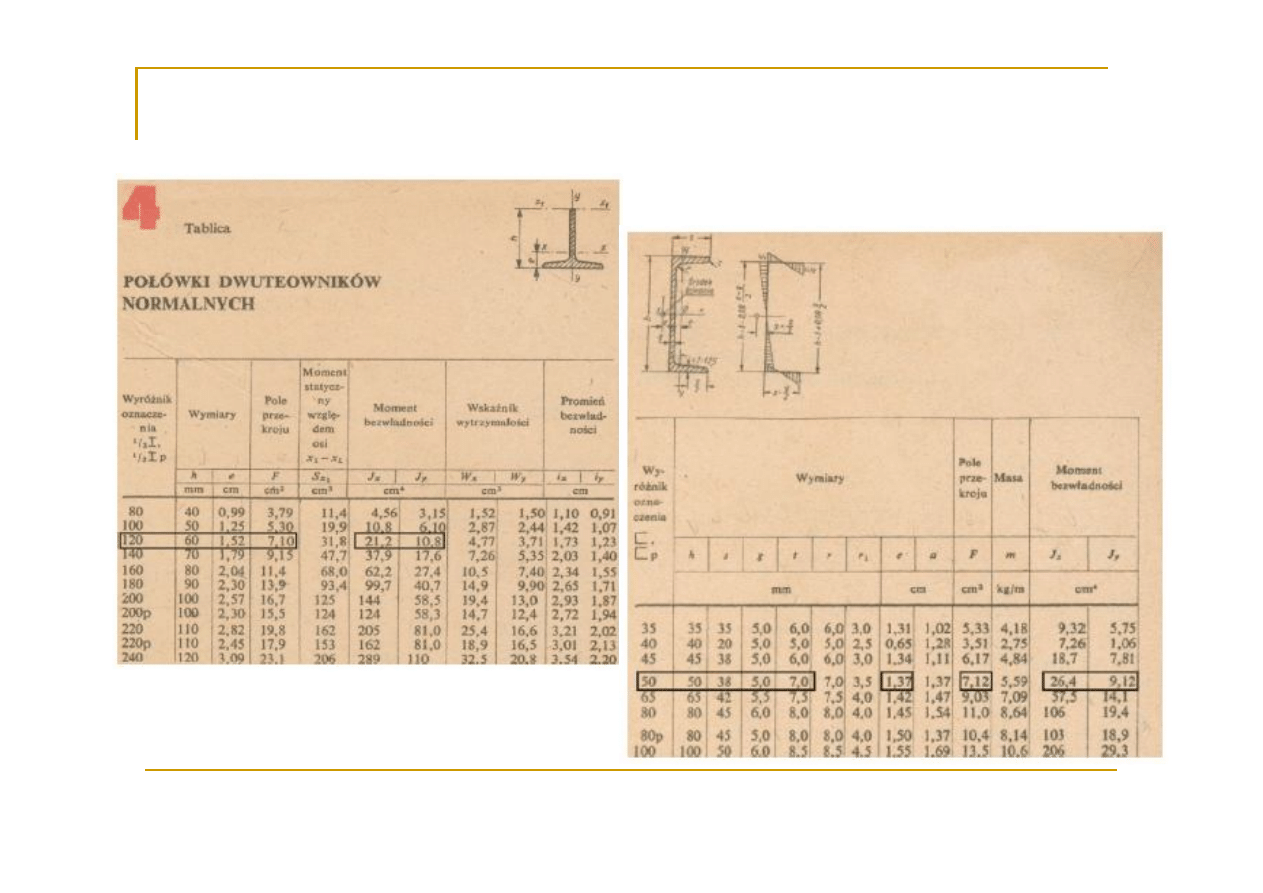
23

Charakterystyki geometryczne figur płaskich

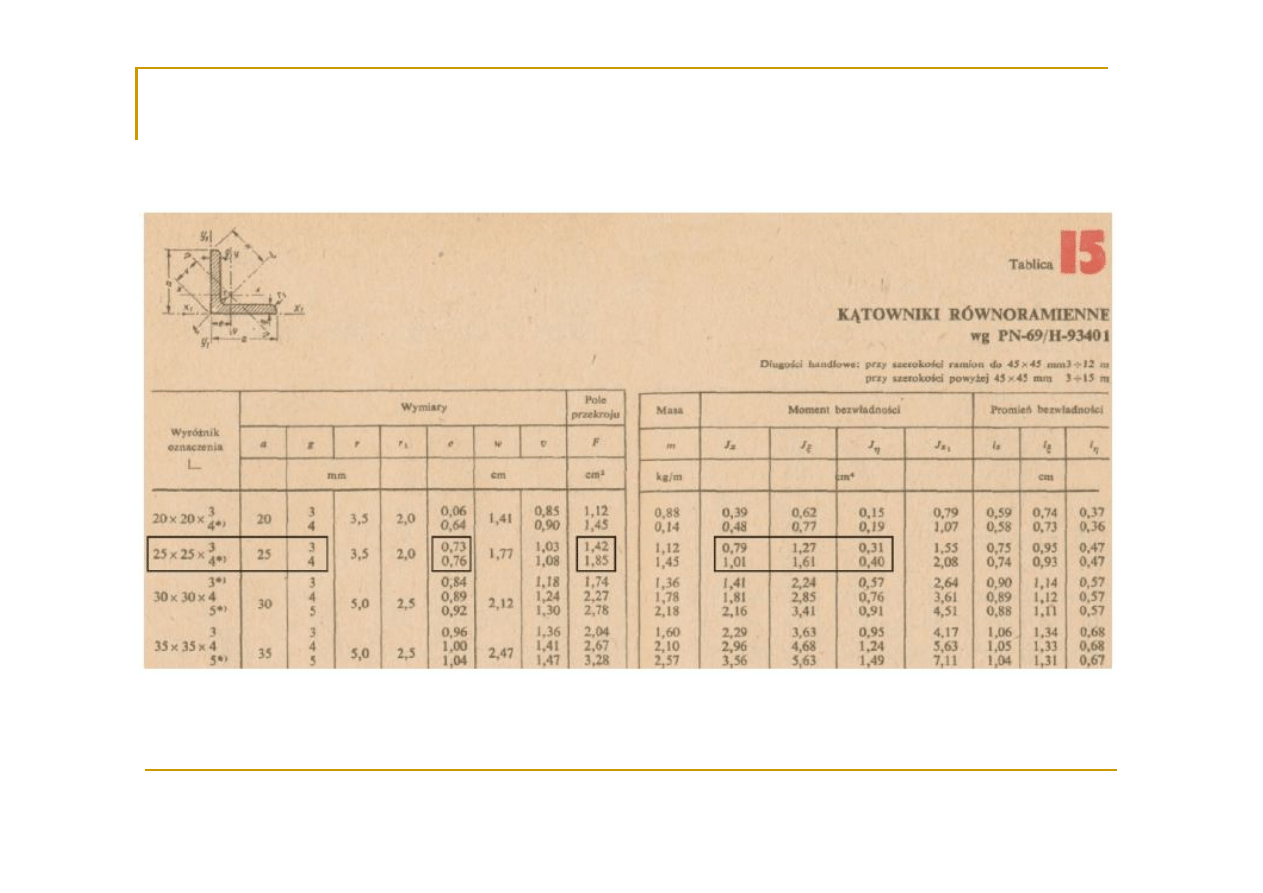
24

Charakterystyki geometryczne figur płaskich

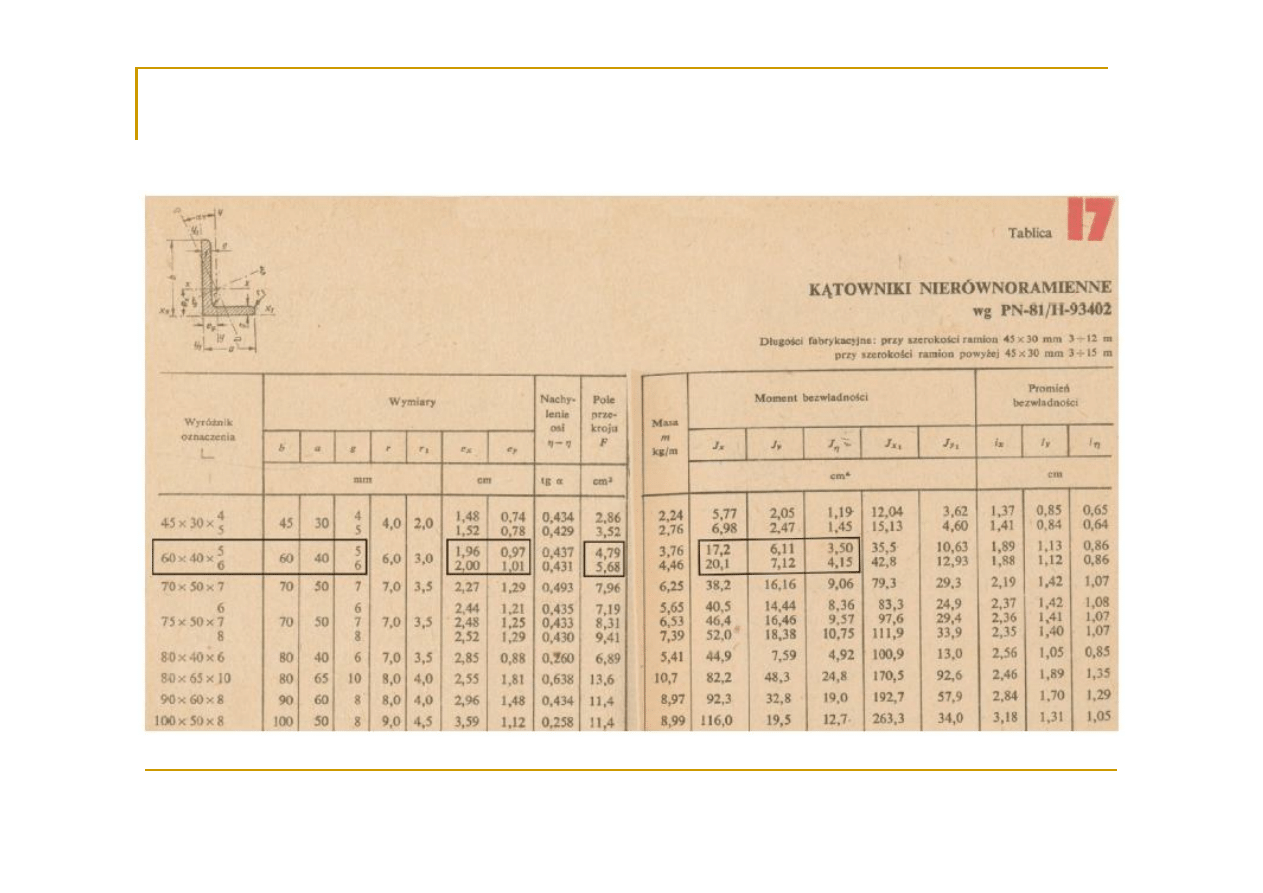
25

Charakterystyki geometryczne figur płaskich