1

I

T
P

W

ZPT

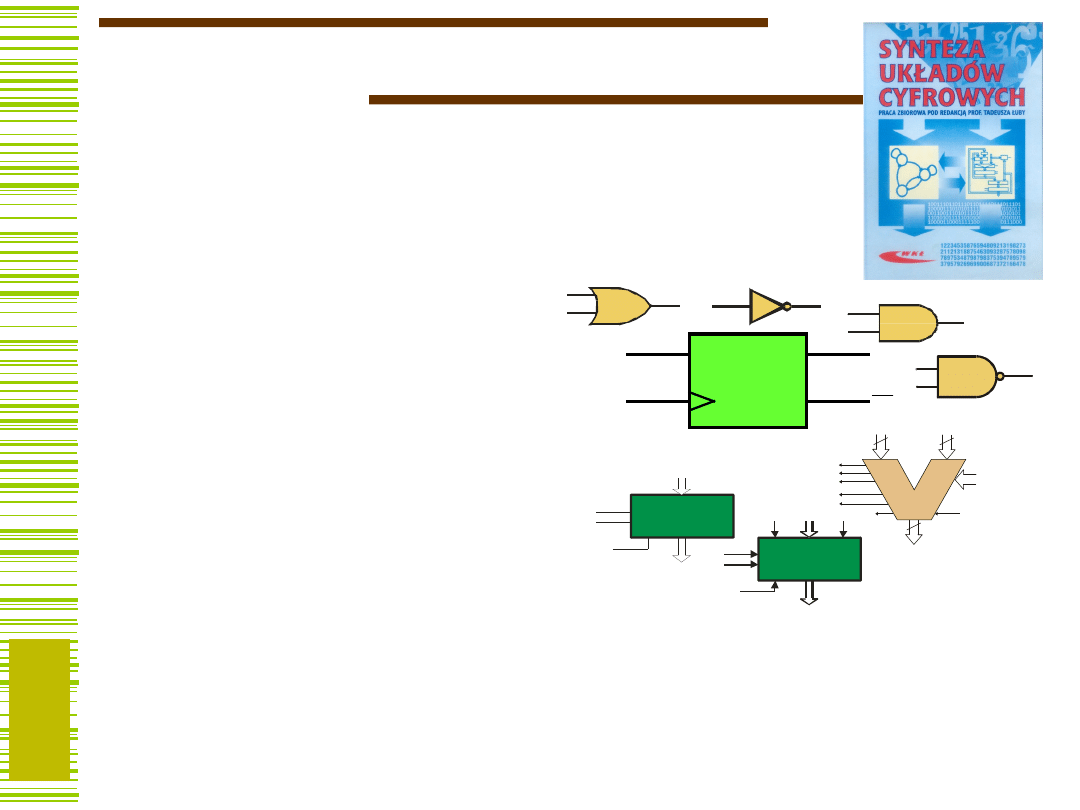
Układy cyfrowe

...konstruowane są w różnych
technologiach i na różnych poziomach
opisu.

Poziomy opisu:

1) Bramki i elementarne

układy pamięciowe
(przerzutniki)

2) Bloki funkcjonalne: układy

arytmetyczne (sumatory),
liczniki, rejestry.

Tworzą one nowe elementy konstrukcyjne, z których buduje
się złożone układy cyfrowe o różnorodnych zastosowaniach:
układy przetwarzania sygnałów, układy sterowania,
specjalizowane procesory, układy kryptograficzne

Przerzutn

ik

typu D

D

D

Clk

Clk

Q

Q

Y

B

A

n

n

n

Y

n - 1

Z

O V R

P

G

c

n

c

0

S

A L U

R

(Q)

s

1

s

2

clock

X

Y

x

l

x

p

L

(Q)

s

1

s

2

clock

X

Y

2

I

T
P

W

ZPT

Synteza strukturalna układów

cyfrowych

Każdy układ cyfrowy
składamy
z bloków funkcjonalnych

Licznik

Rejestr

B

l

o
k

i

F

u

n

k

c

j

o

n

a

l

n

e

Mux

Bloki funkcjonalne stanowią wyposażenie
bibliotek komputerowych systemów
projektowania

3

I

T
P

W

ZPT

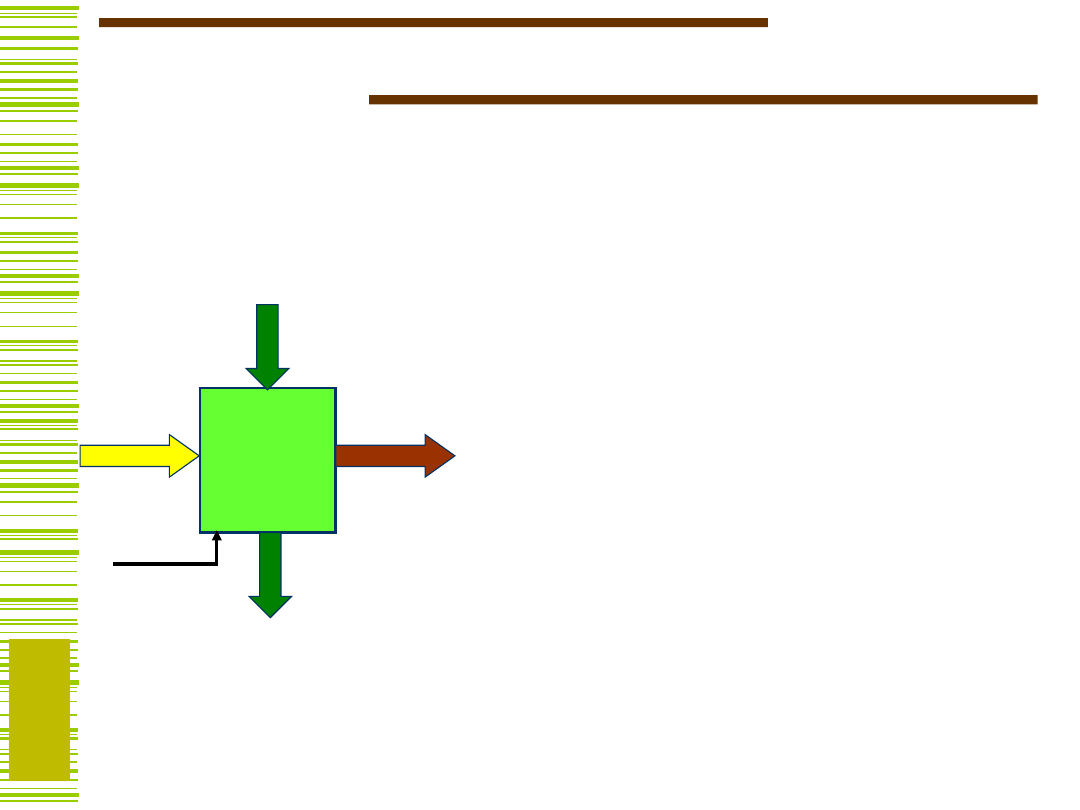
Blok funkcjonalny

P

S

X

Y

BF

clk

X, (Y) – wejścia (wyjścia)
sygnałów

reprezentujących

dane

wejściowe i wyjściowe

S – wejścia sterujące,

P – wyjścia predykatowe,

clk – wejście zegarowe

Bloki funkcjonalne stanowią wyposażenie
bibliotek komputerowych systemów
projektowania

…specjalizowany układ cyfrowy:

4

I

T
P

W

ZPT

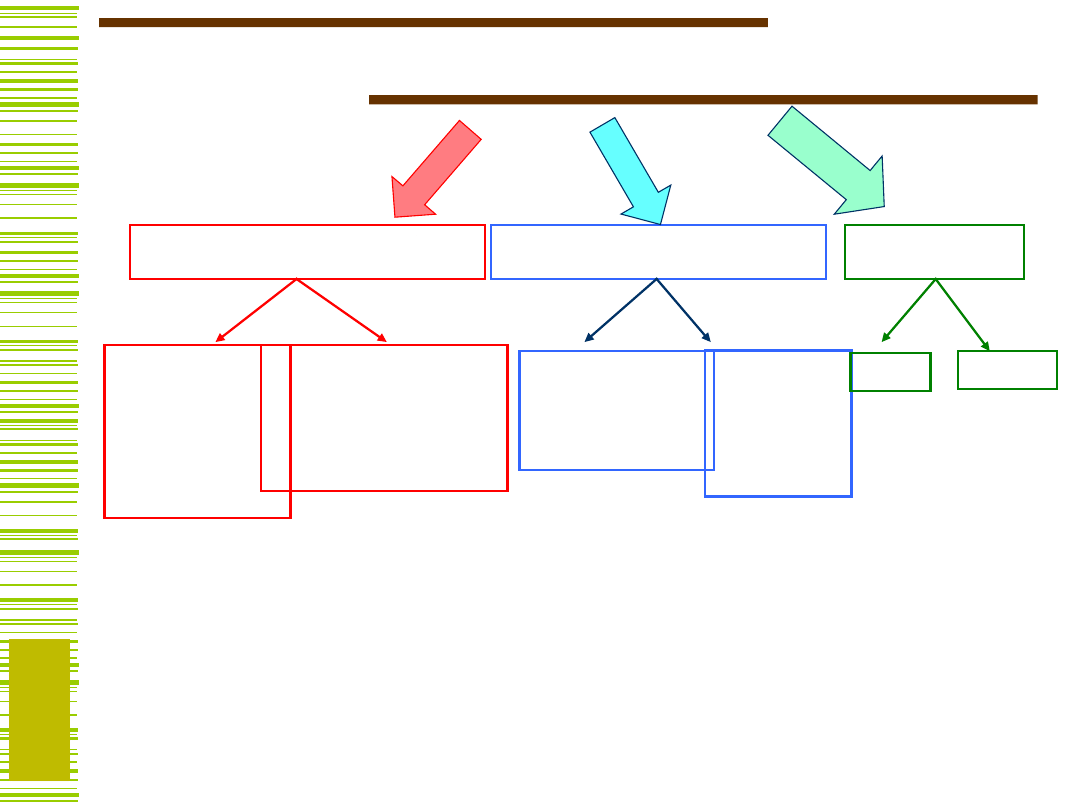
Bloki

funkcjonalne

B. kombinacyjne B. sekwencyjne Pamięci

Układy

arytmetyczne

Sumator

Układ odejmujący

Komparator

Układy

Komutacyjne

MUX

DMUX

DEC

Rejestry

Równoległe
Przesuwające

Liczniki

Zliczające
W górę
W dół

ROM

(RAM)

5

I

T
P

W

ZPT

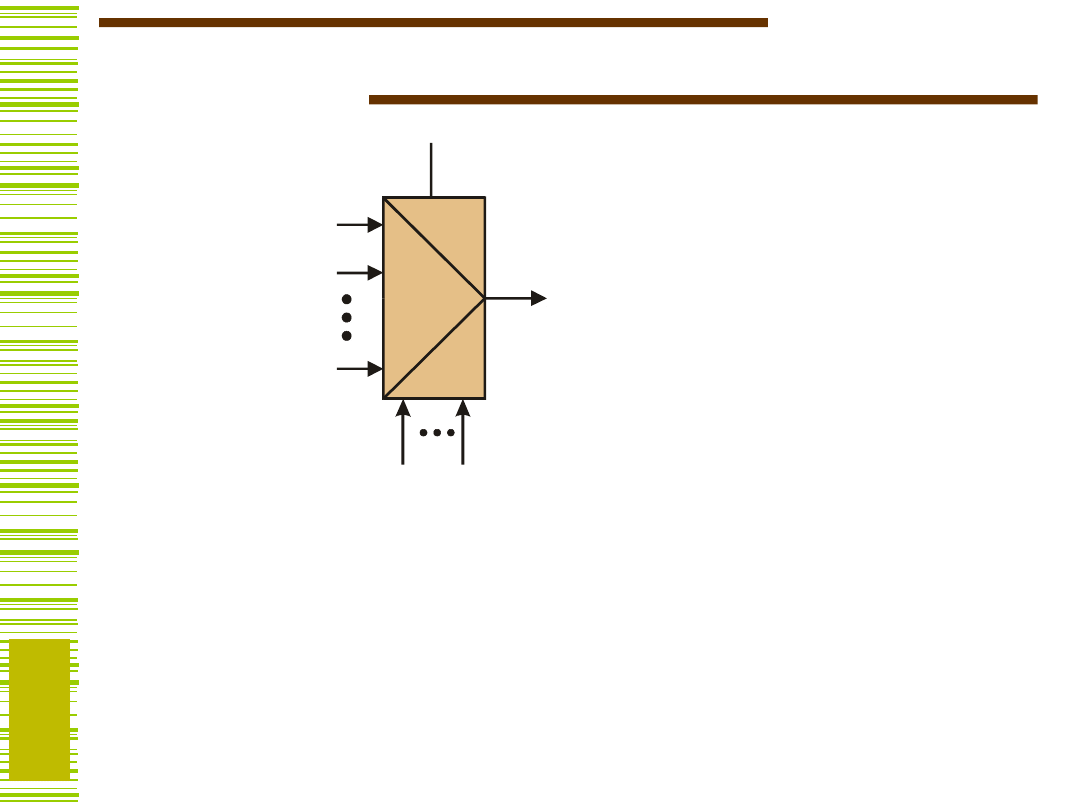
Multiplekser (MUX)

N =
2

n

gdzie P

k

(A) oznacza pełny iloczyn

zmiennych
a

n–1

,...,a

0

, prostych lub zanegowanych,

zgodnie z reprezentacją binarną liczby k
= L(A).

a

n-1

a

0

e

d

d

d

0

1

N-1









1

N

0

k

k

k

(A)d

P

e

y

6

I

T
P

W

ZPT

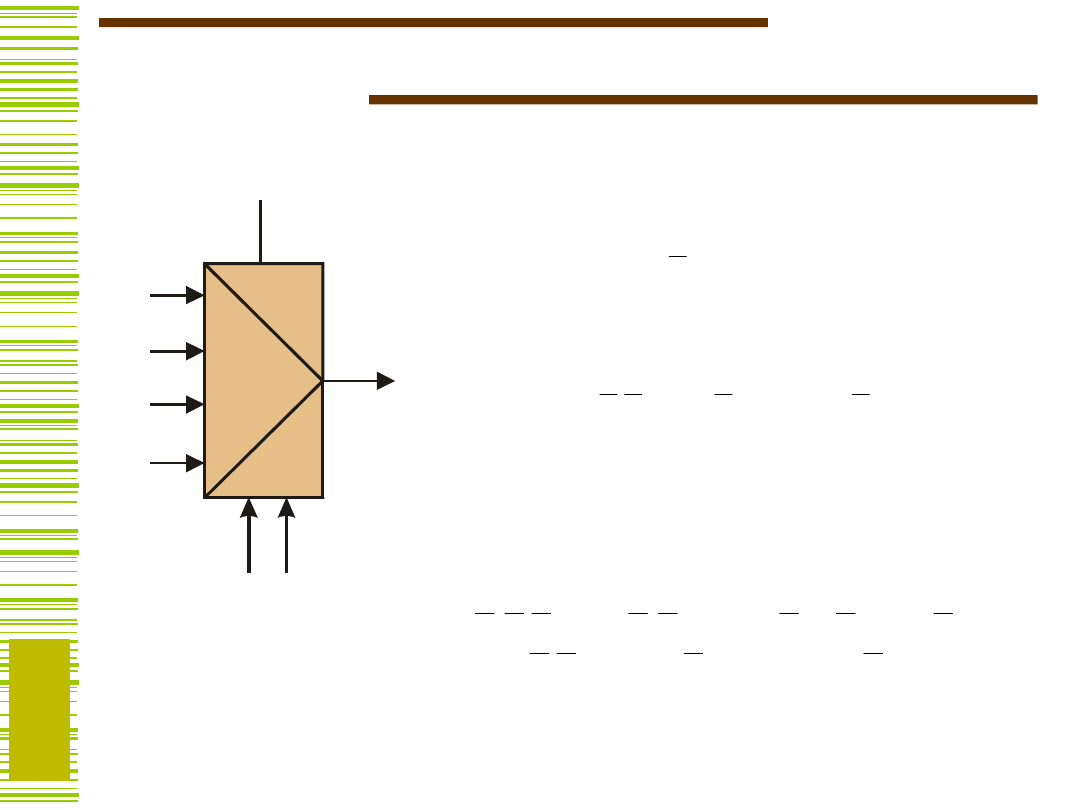
Multipleksery

1

0

ad

d

a

y





3

0

1

2

0

1

1

0

1

0

0

1

d

a

a

d

a

a

d

a

a

d

a

a

y









7

0

1

2

6

0

1

2

5

0

1

2

4

0

1

2

3

0

1

2

2

0

1

2

1

0

1

2

0

0

1

2

d

a

a

a

d

a

a

a

d

a

a

a

d

a

a

a

d

a

a

a

d

a

a

a

d

a

a

a

d

a

a

a

y



















Dla n = 1 (MUX 2 : 1):

  dla n = 2 (MUX 4 : 1):

dla n = 3 (MUX 8 : 1):

e = 1

0

1

2

3

a

1

a

0

d

d

d

0

1

3

d

d

2

d

7

I

T
P

W

ZPT

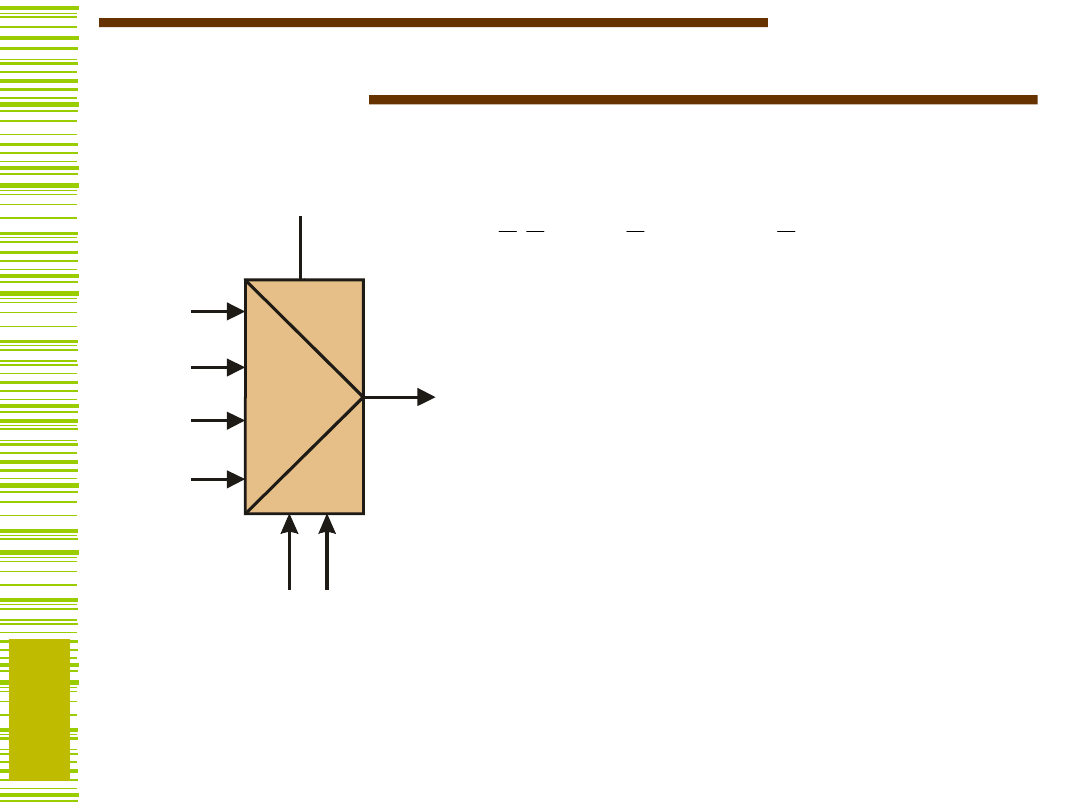
Multiplekser jako przełącznik

e = 1

0

1

2

3

0 0

0

3

0

1

2

0

1

1

0

1

0

0

1

d

a

a

d

a

a

d

a

a

d

a

a

y









0 1

1 1

0

1

1

0

1

1

8

I

T
P

W

ZPT

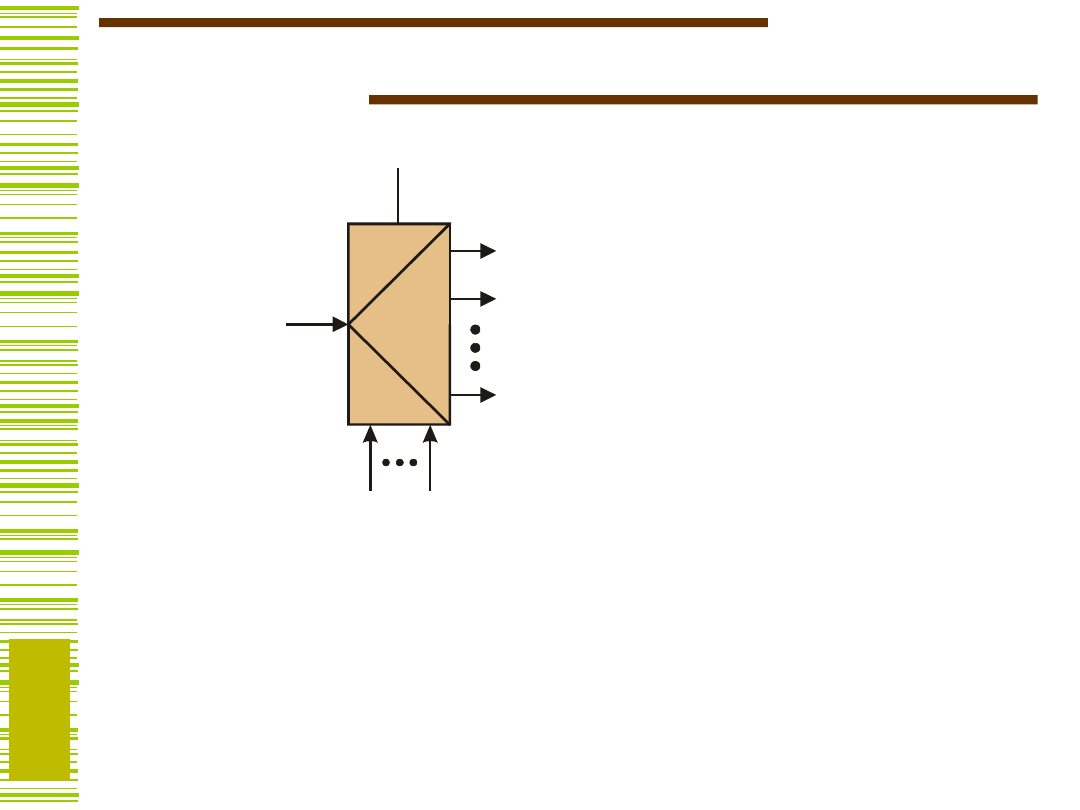
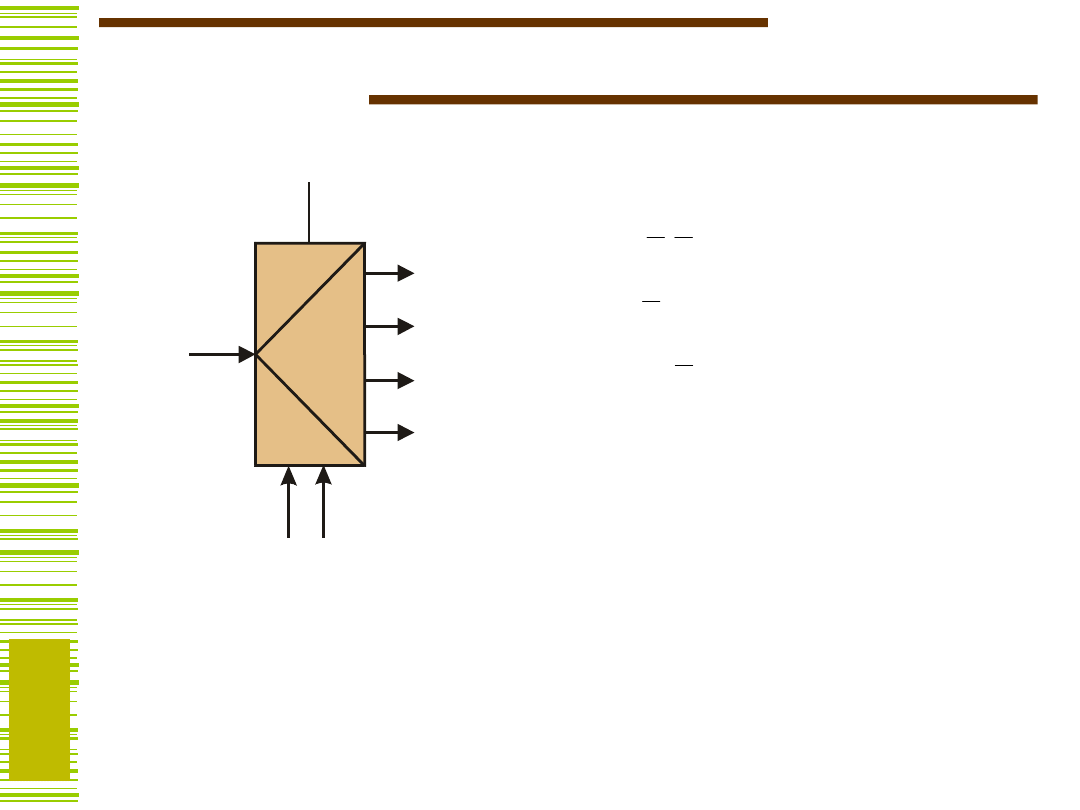
Demultiplekser

a

n - 1

a

0

e

d

y

y

y

0

1

N - 1

N = 2

n

(A)d

eP

y

k

k



gdzie P

k

(A) oznacza pełny iloczyn

zmiennych
a

n–1

,...,a

0

, prostych lub zanegowanych,

zgodnie z reprezentacją binarną liczby k
= L(A).

9

I

T
P

W

ZPT

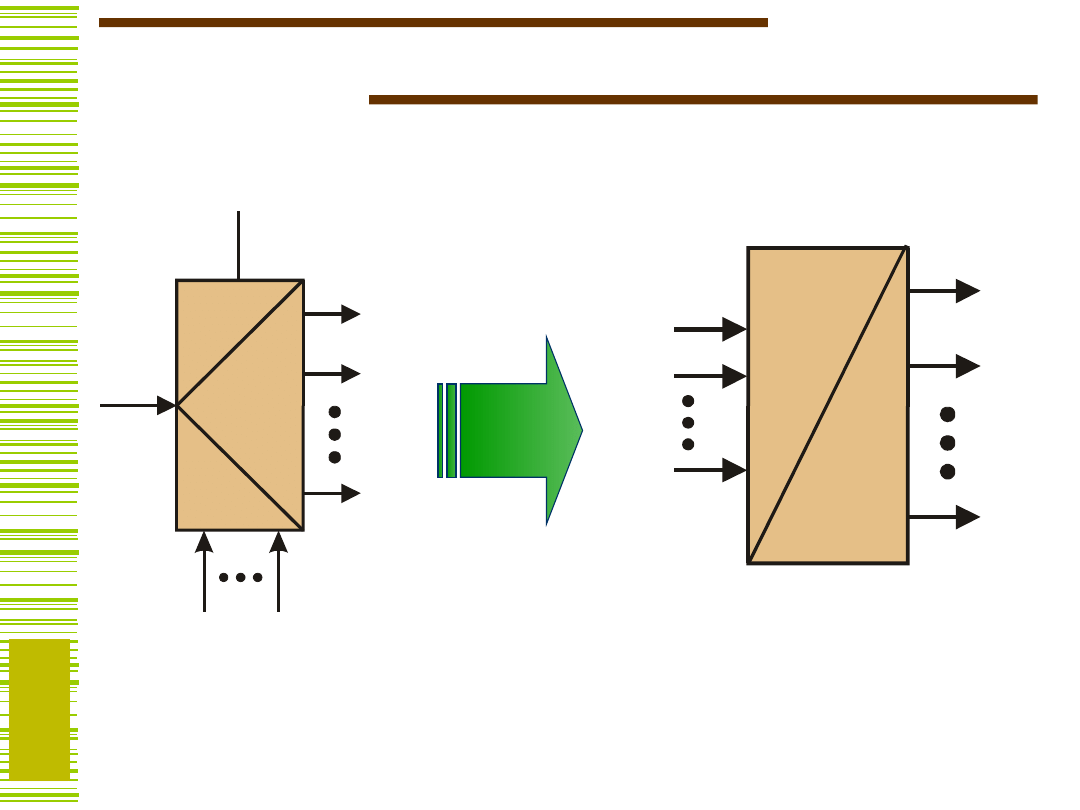
Demultiplekser jako przełącznik

e = 1

0
1
2
3

0

0

0

d

a

a

y

d

a

a

y

d

a

a

y

d

a

a

y

0

1

3

0

1

2

0

1

1

0

1

0









0

0

0

0

0

0

0 0

0 1

1 1

1

1

1

1

10

I

T
P

W

ZPT

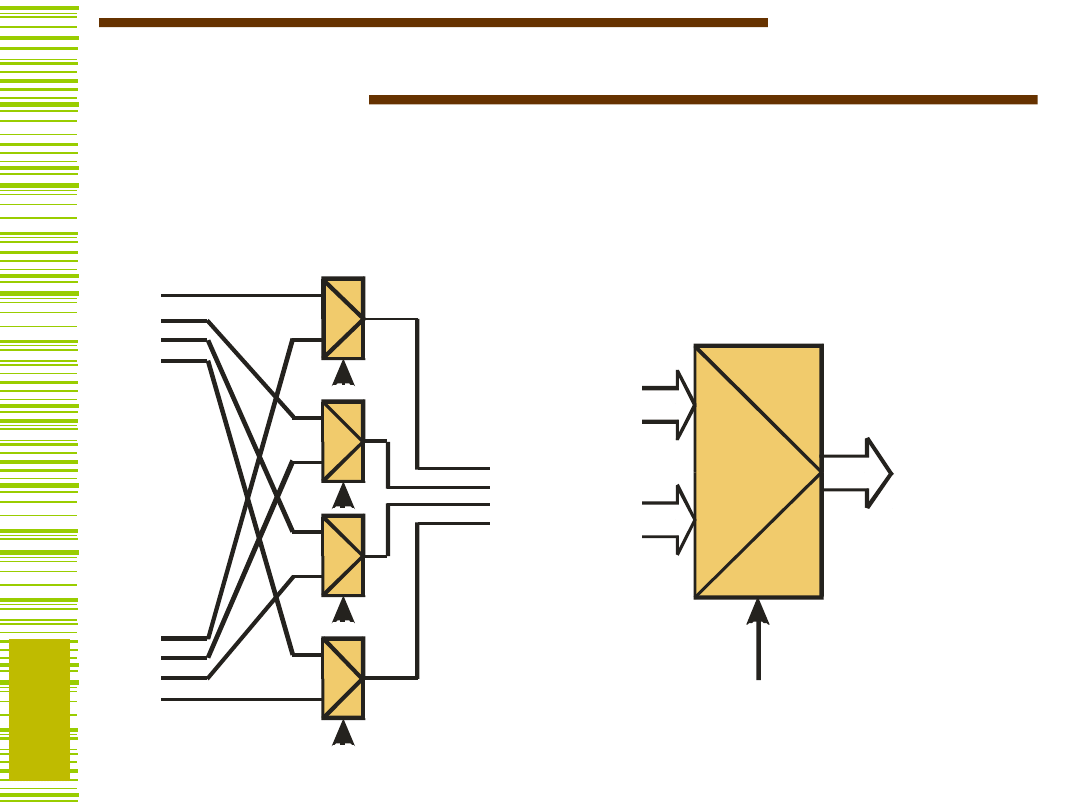
Dekoder

a

n - 1

a

0

e

d

y

y

y

0

1

N - 1

y

y

y

0

1

N - 1

a
a

a

0

1

n - 1

N =
2

n

DMU
X

DEKODER

11

I

T
P

W

ZPT

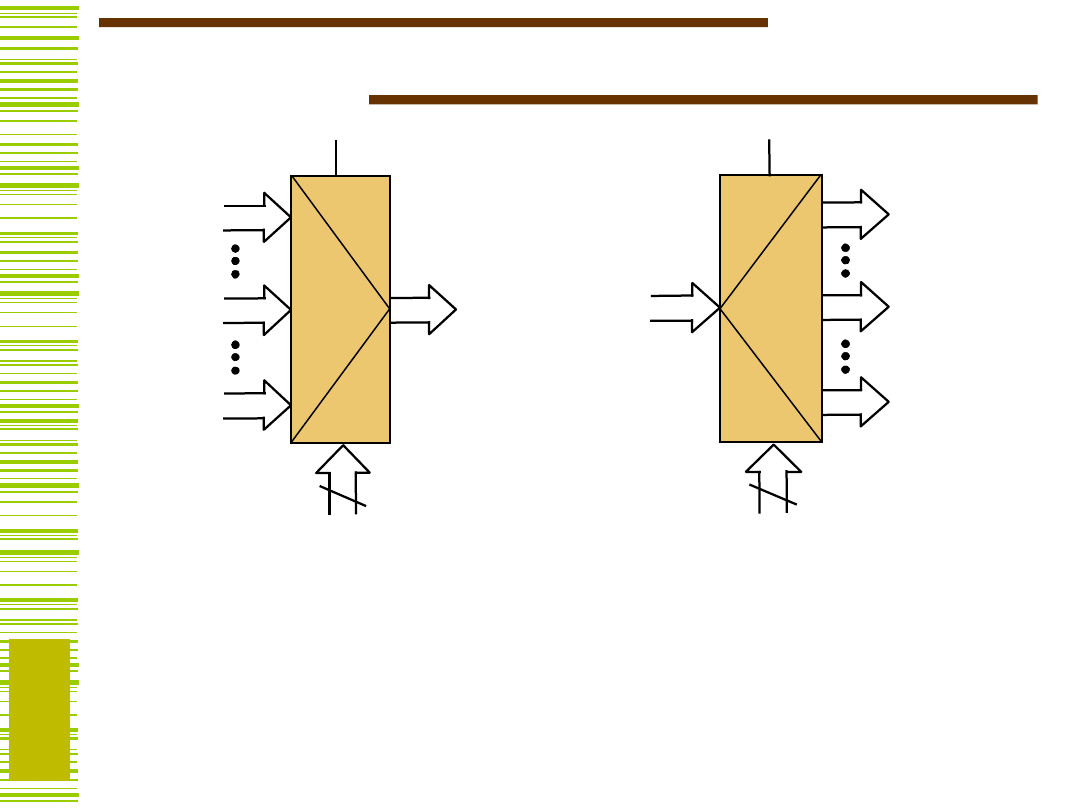
Multipleksery grupowe

A

B

A

B

Y=A

0 1

Y=B

MUX-y i DMUX-y można przystosować do przełączania

(komutacji) sygnałów wielobitowych (grupowych)

12

I

T
P

W

ZPT

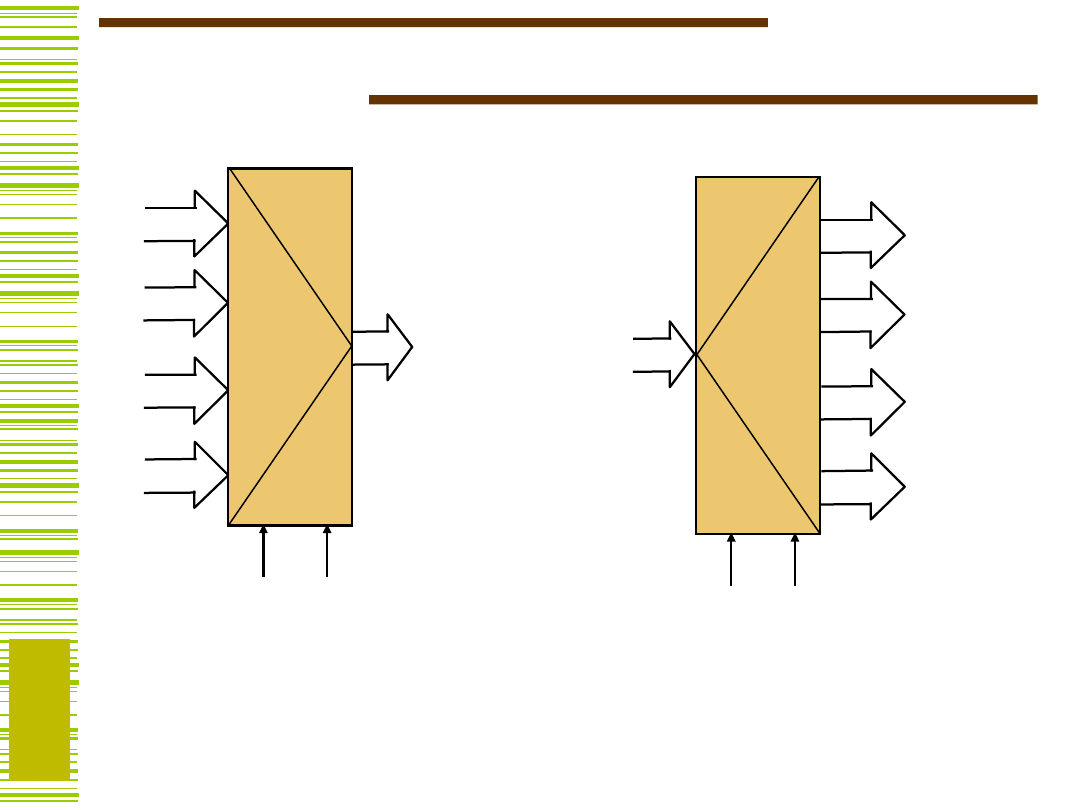
Bloki komutacyjne

Multiplekser służy do
wybierania jednego z wielu słów
wejściowych i przesyłania go na
wyjście. Na wyjściu Y pojawia
się słowo wejściowe wskazane
adresem A (wg naturalnego
kodu binarnego).

Demultiplekser służy do
przesyłania słowa X
wejściowego na jedno z
wielu wyjść; numer tego
wyjścia jest równy
aktualnej wartości adresu.

X

0

X

j

X

N-1

Y

n

A

e

Y

0

Y

j

Y

N-1

n

A

e

X

13

I

T
P

W

ZPT

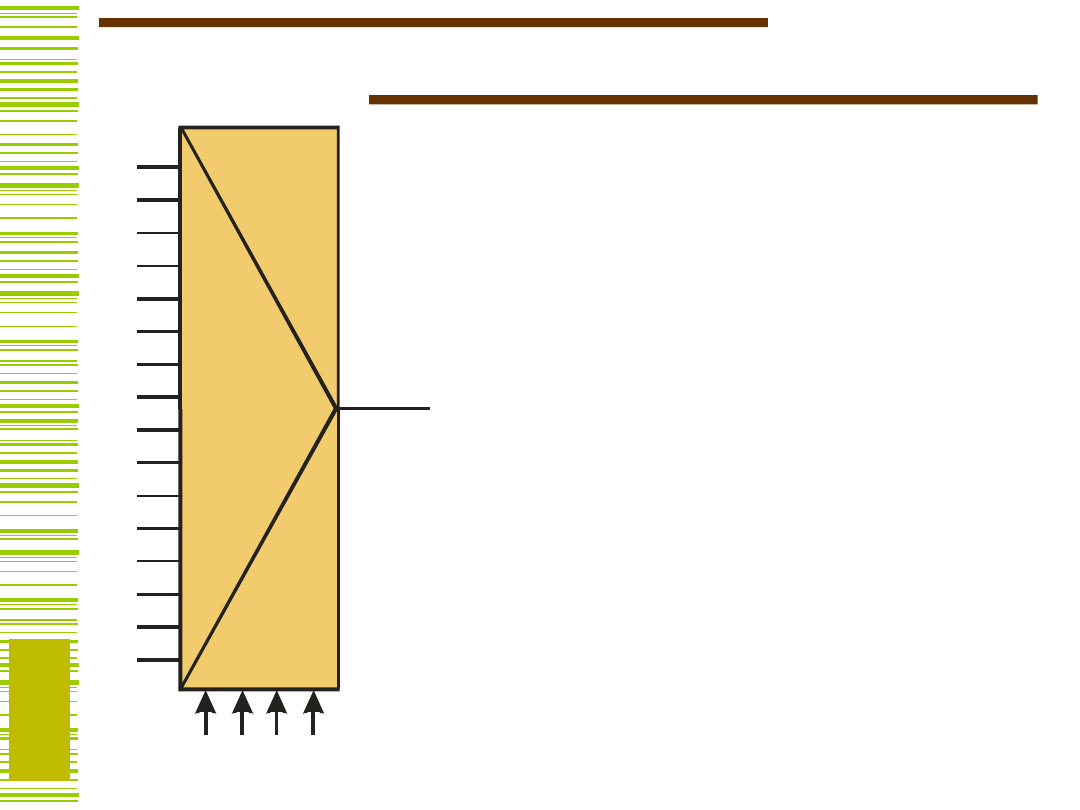
Bloki komutacyjne

1 0

0 0

1 1

a

1

a

0

0

1

2

3

0

1

0

a

1

a

0

0

1

2

3

1 0

0 0

1 1

0

1

0

0

1

1

0

0

0

1

1

1

0

1

0

0

0

0

1

1

1

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

1

0

0

1

0

0

1

0

0

1

0

Najważniejsze zastosowanie

14

I

T
P

W

ZPT

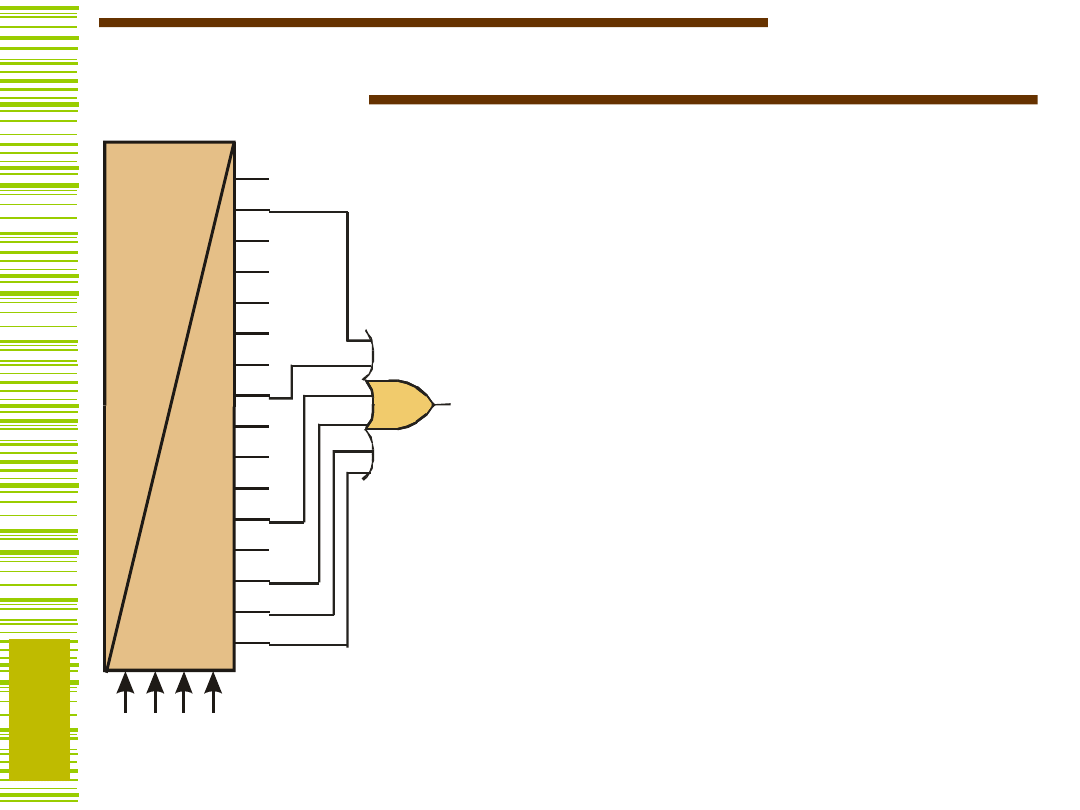
Inne zastosowania…

y =
(1,7,11,13,14,15)

0

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

y

0
1
0
0
0
0
0
1
0
0
0
1
0
1
1
1

x

3

x

2

x

1

x

0

Zastosowanie MUX do realizacji

funkcji boolowskich

15

I

T
P

W

ZPT

y =
(1,7,11,13,14,15)

0

1

2

3

4

5

6

7

8

9

1 0

1 1

1 2

1 3

1 4

1 5

x

3

x

2

x

1

x

0

y

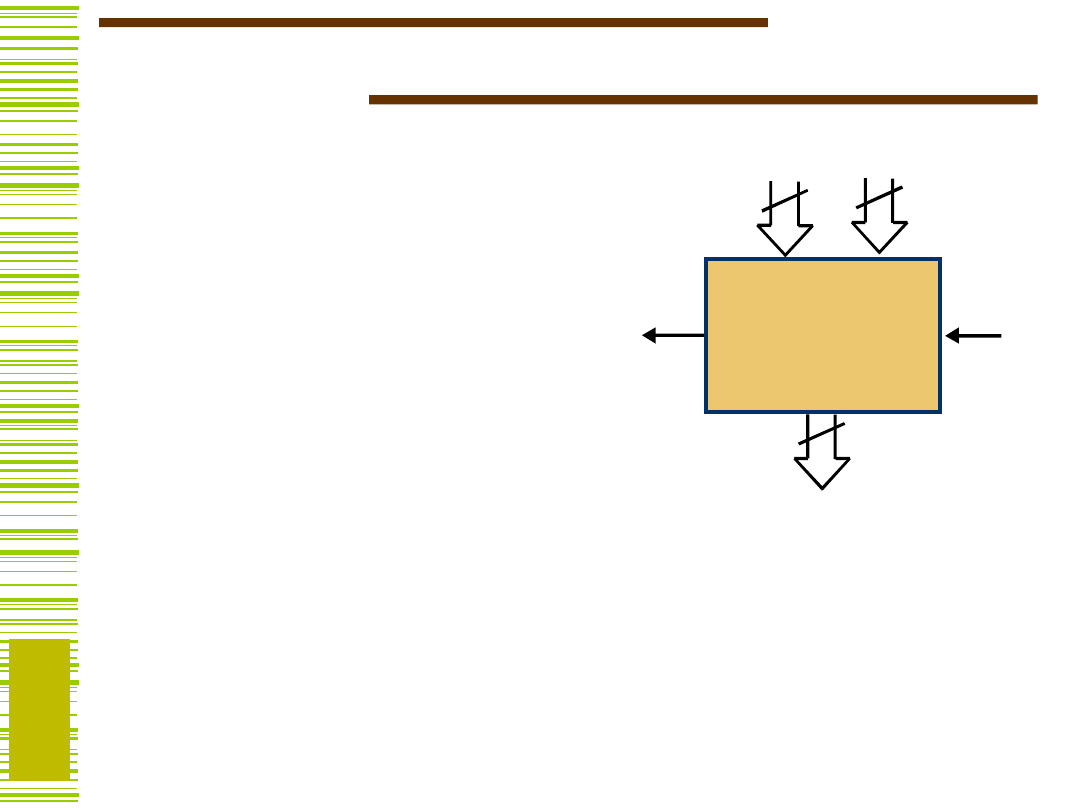
Zastosowanie dekodera do

realizacji

funkcji boolowskich

Inne zastosowania…

… należy odłożyć do kosza!

16

I

T
P

W

ZPT

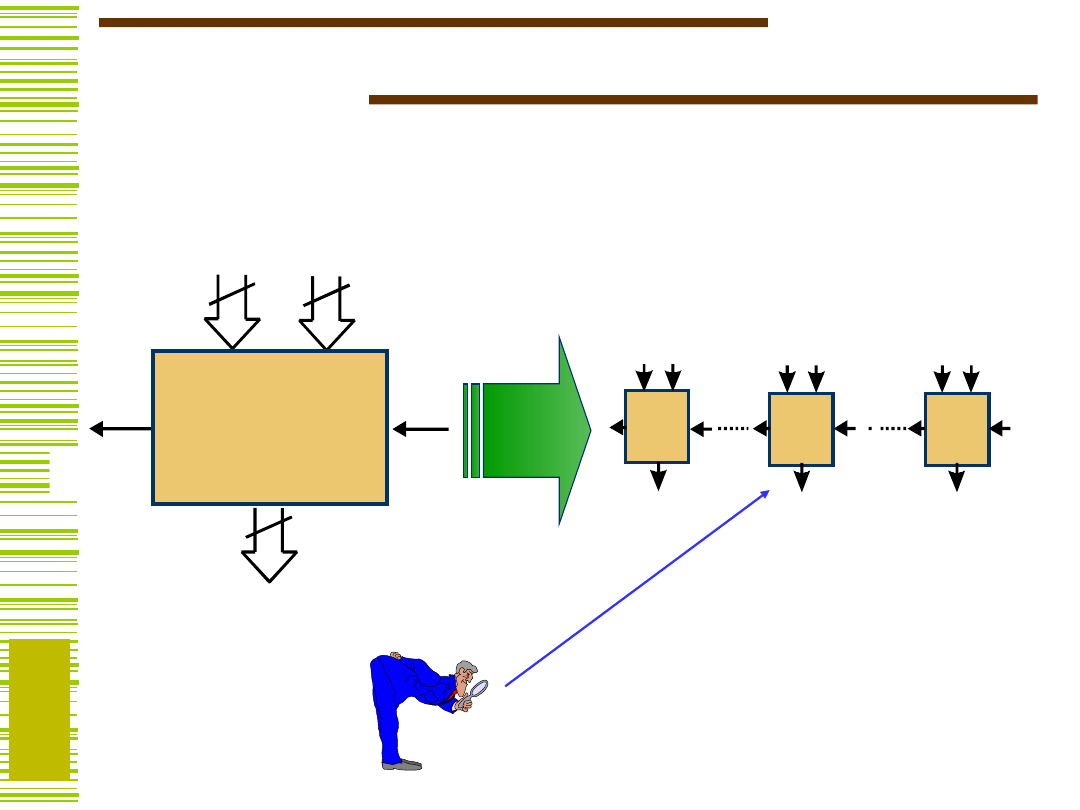
Sumatory

Sumator –
podstawowy BF
powszechnie
stosowany w
technice DSP

Inne układy
arytmetyczne:
układy odejmowania
układy mnożące
układy dzielenia

...są budowane z sumatorów

c

n

c

0

A

n

B

n

Y

n



A

17

I

T
P

W

ZPT

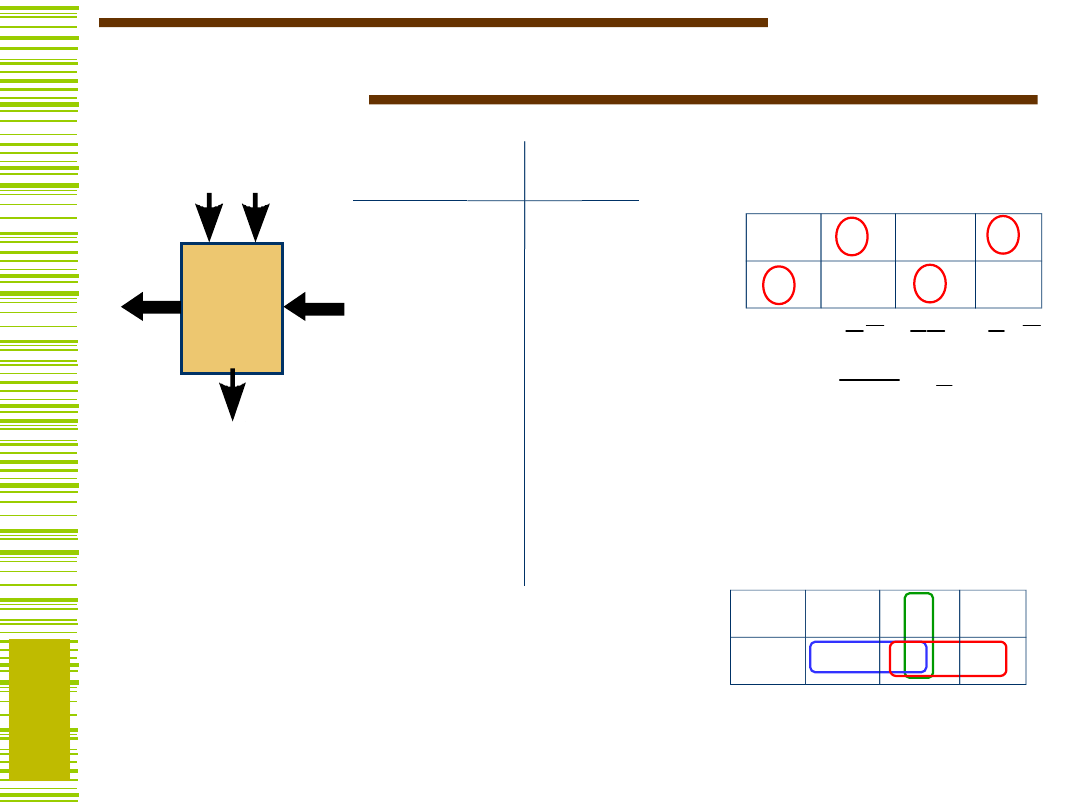
Najprostszy sumator

Kaskadowy – ripple carry adder

a b

i

i

y

i

c

i+1

c

i



a b

0

0

y

0

c

1

c

0



a b

c

n-1

n-1

y

n-1

c

n



n-1

c

n

c

0

A

n

B

n

Y

n



1001 0110

1111

C

4

=0

0111

0000

C

4

=1

Jak jest zbudowane pojedyncze ogniwo?

18

I

T
P

W

ZPT

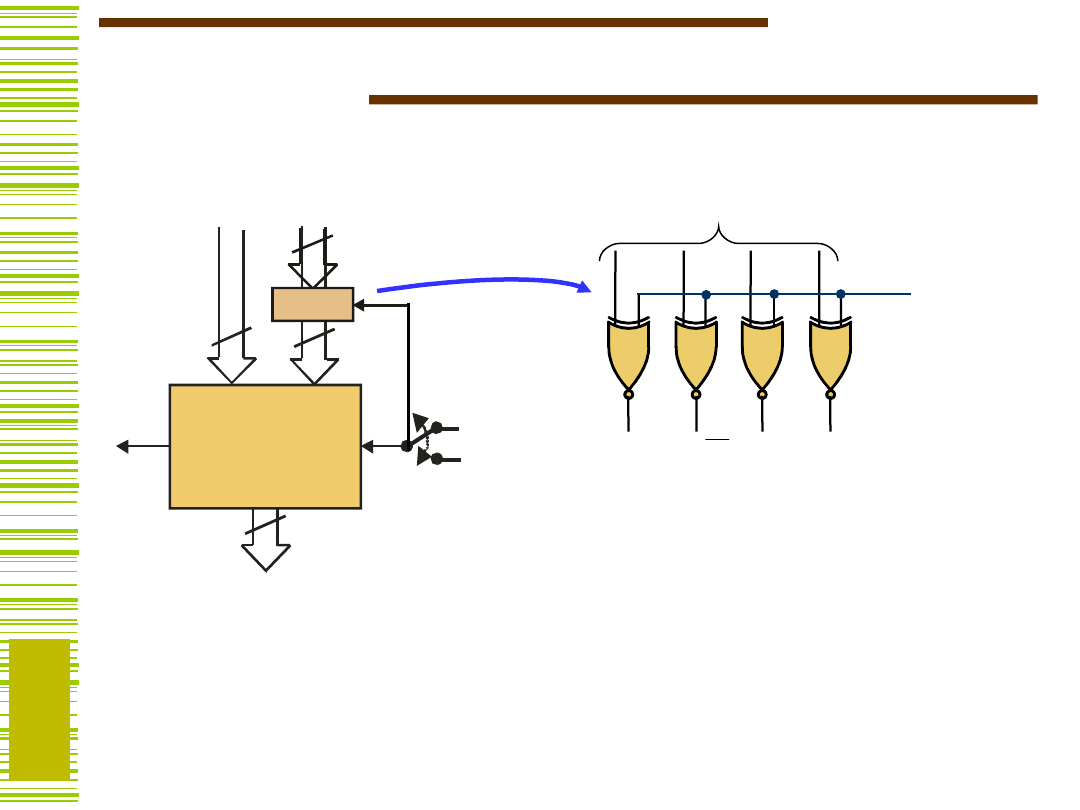
Funkcje logiczne sumatora

0
0
0
1
0
1
1
1

b)

c(a

ab

b)

c(a

ab

o

c













i

c

i

b

i

a

i

y







)

b

(a

c

b

a

c

i

i

i

i

i

1

i









a

b

c

c

o

y

0

0

0

0

0

1

0

1

0

0

1

1

1

0

0

1

0

1

1

1

0

1

1

1

y

c

o

c



a b

ab

c

00

01

11

10

0

0

1

0

1

1

1

0

1

0

ab

c

00

01

11

10

0

0

0

1

0

1

0

1

1

1

b

a

c

y











b

a

c

b

a

c





















b

a

c

b

a

c

b

a

c

cab

y









0
1
1
0
1
0
0
1

19

I

T
P

W

ZPT

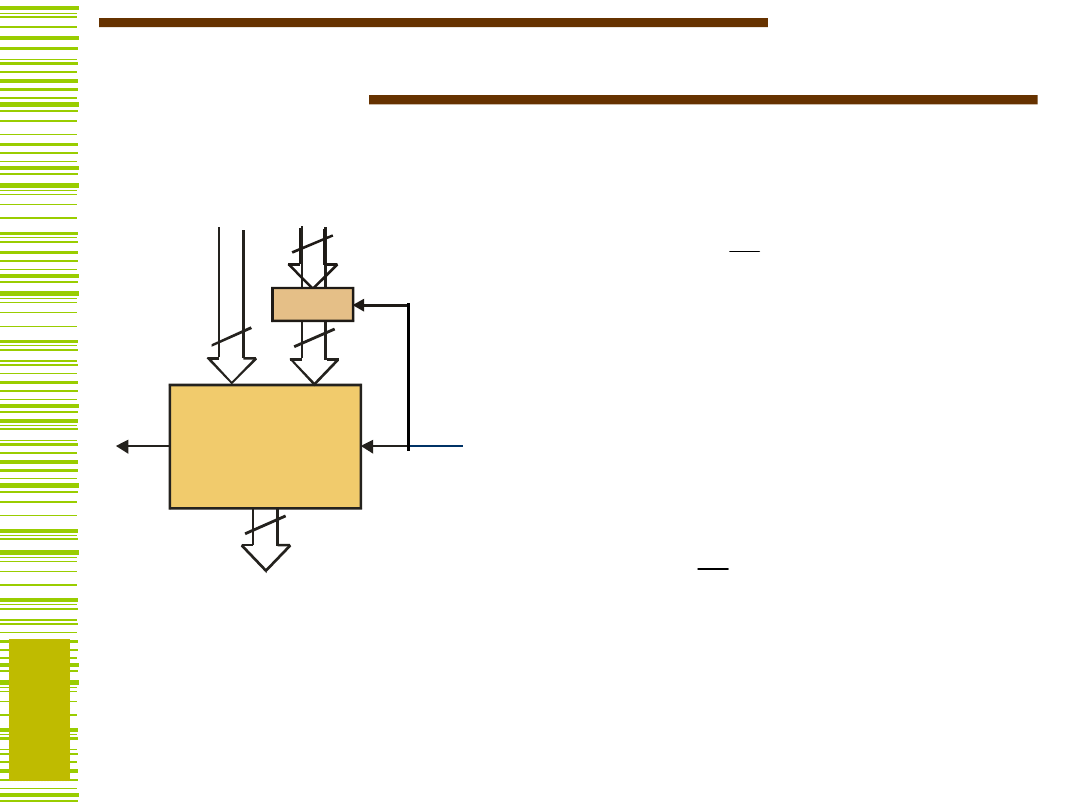
Sumator/układ odejmujący

Jak z sumatora zbudować układ odejmujący?

Y



A

c

n

c

0

n

n

B

n

X O R

n

0

–
+

1

B

C

o

=1

B

C

o

=0

B

20

I

T
P

W

ZPT

Reprezentacje liczb – NKB/U2

A = <

 

a

n–1

,..., a

j

,..., a

0 

> gdzie a

j

 {0,1}















1

n

0

j

j

j

NKB

D

2

a

A

L

A

























2

n

0

j

j

j

1

n

1

n

U2

D

2

a

2

a

A

L

A

NKB:

U2:

21

I

T
P

W

ZPT

Kod U2

A

U2

= <a

n–1

,..., a

j

,..., a

0

>, gdzie a

j

 {0,1}

Zakres: –2

n–1

≤ A

D

≤ 2

n–1

– 1

 





















2

n

0

j

j

j

1

n

1

n

U2

D

2

a

2

a

A

L

A

Bit a

n–1

można interpretować jako bit znaku.

Jeśli a

n–1

= 0, to liczba jest dodatnia;

jeśli a

n–1

= 1 to liczba jest ujemna; pozostałe bity

stanowią uzupełnienie (różnicę) wartości liczby do
najwyższej potęgi liczby 2

<0101>│

U2

= +5│

D

; <1011>│

U2

 = –

5│

D

22

I

T
P

W

ZPT

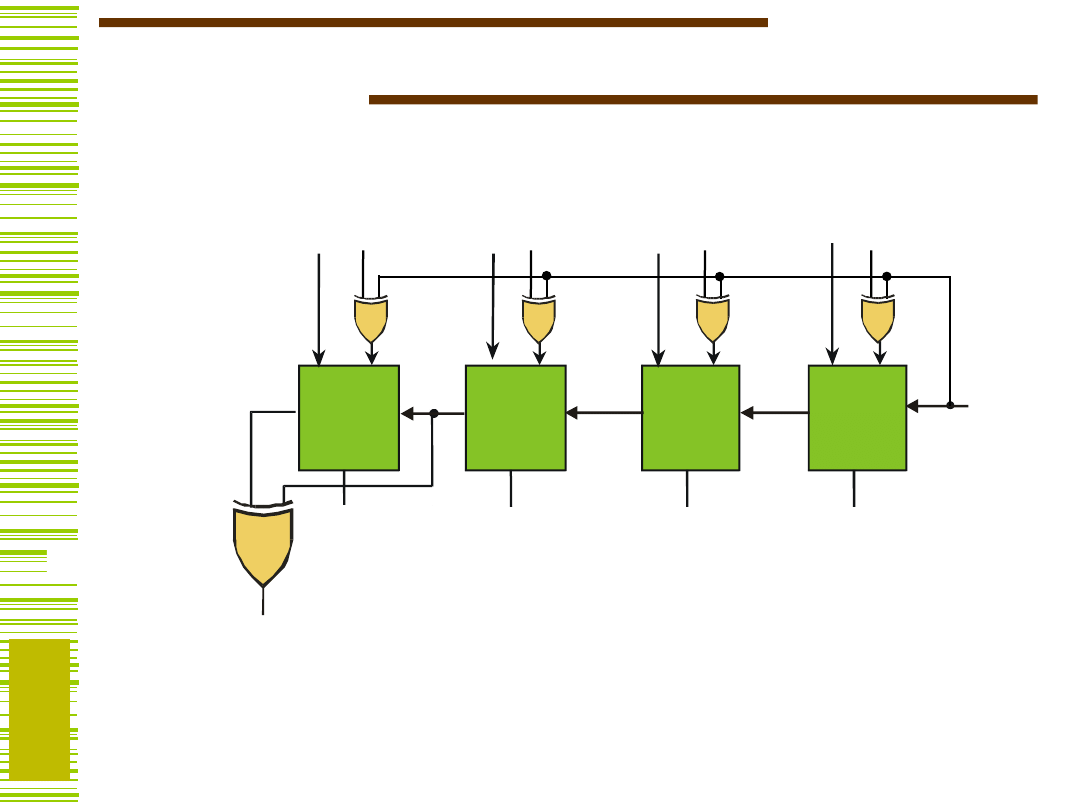
Sumator/układ odejmujący

Y = A – B = A + (–B|

U2

)

Y



A

c

n

c

0

n

n

B

n

X O R

n

B

–B|

U2

= +1 = B1 + 1

–B|

U2

= +1 = B1 + 1

–B|

U2

= +1 = B1 + 1

Dla c

0

= 1

Y = A + + 1 = A –
B

B

B

B

B

1

Dla c

0

= 0

Y = A + B 0 + 0 = A + B

0

23

I

T
P

W

ZPT

Sumator/układ odejmujący

OVR = c

n–1

c

n

A

B

CO

S

+ CI

A

B

CO

S

+ CI

A

CO

S

+ CI

A

B

CO

S

+ CI

Dodawanie/

odejmowanie

S

3

S

2

S

1

S

0

B

a

3

b

3

a

2

b

2

a

1

b

1

a

0

b

0

Overflow

OVR = c

3

c

4

c

4

c

3

24

I

T
P

W

ZPT

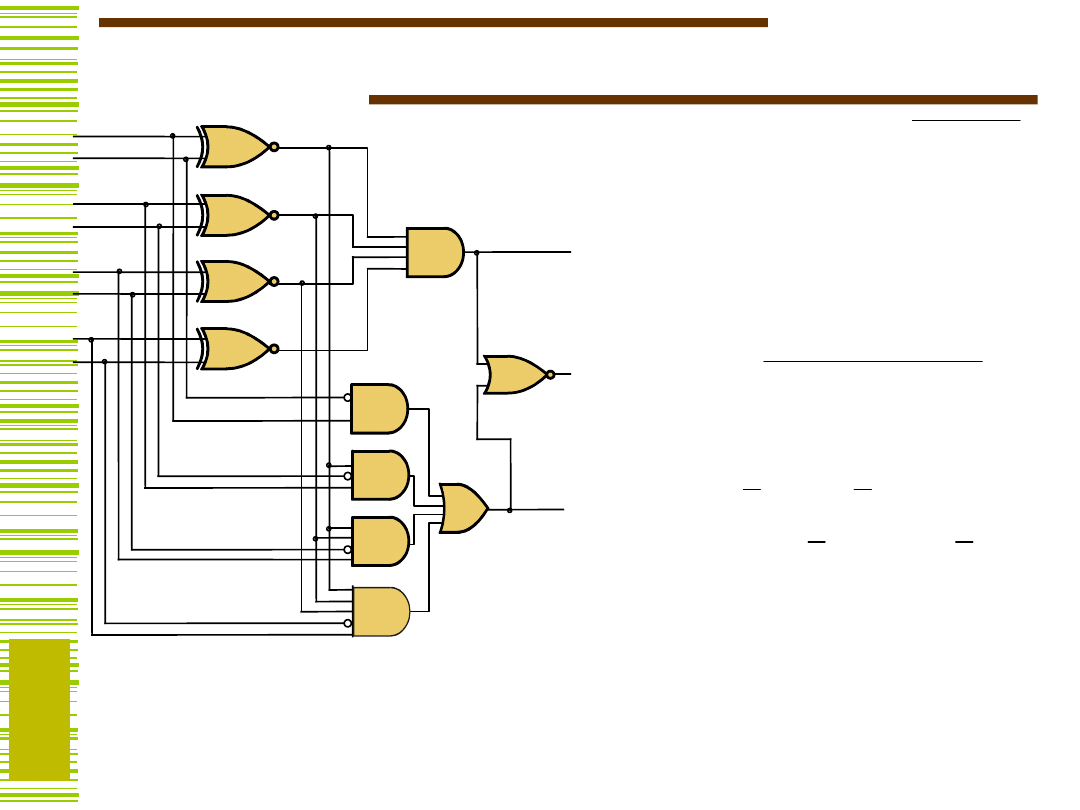
Komparator

A

n

B

n

K

„1 z 3”

A < B
A = B
A > B

25

I

T
P

W

ZPT

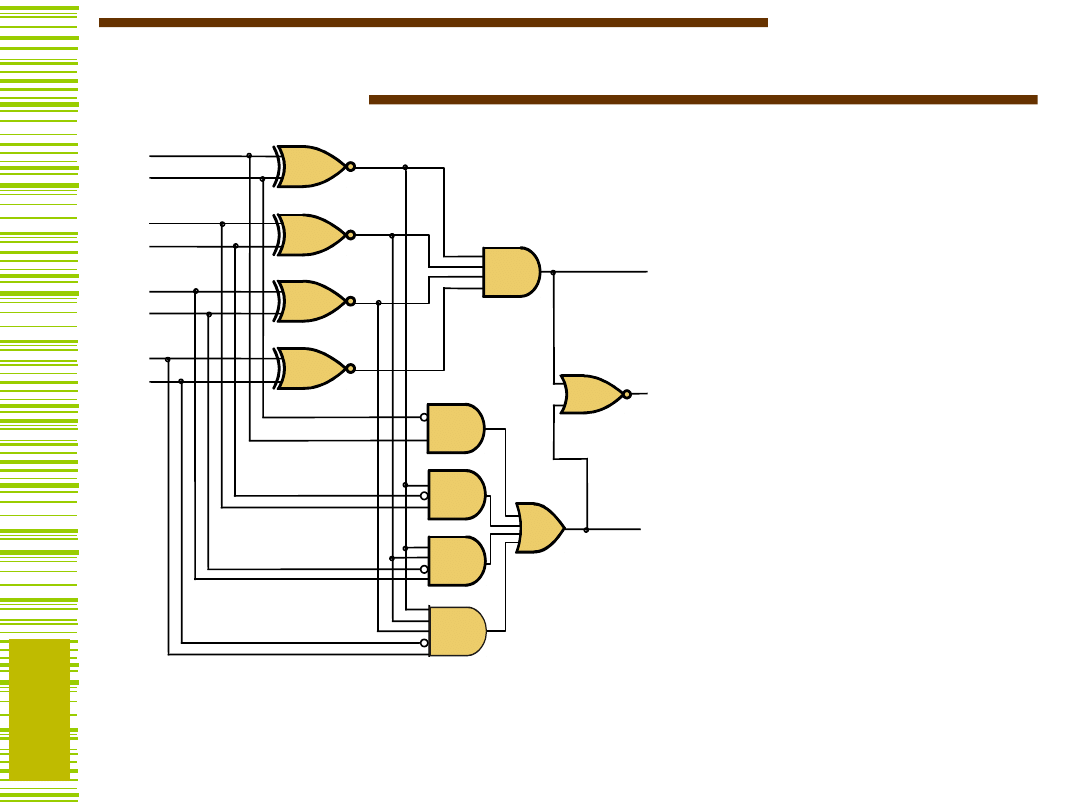
Komparator

a

k

 b

k

 A < B, gdy a

k

= 0,

b

k

=1

A > B, gdy a

k

= 1,

b

k

=0

k

k

k

b

a

i





0

0

1

2

3

1

1

2

3

2

2

3

3

3

b

a

i

i

i

b

a

i

i

b

a

i

b

a









B

A

B

A

gt

eq 

A = a

3

a

2

a

1

a

0

B =

b

3

b

2

b

1

b

0

A > B =

A < B =

A eq B =
i

3

i

2

i

1

i

0

i

0

i

1

i

2

i

3

a

3

b

3

a

2

b

2

a

1

b

1

a

0

b

0

26

I

T
P

W

ZPT

Komparator

A = a

3

a

2

a

1

a

0

B =

b

3

b

2

b

1

b

0

A > B

A < B

A = B

i

0

i

1

i

2

i

3

a

3

b

3

a

2

b

2

a

1

b

1

a

0

b

0

27

I

T
P

W

ZPT

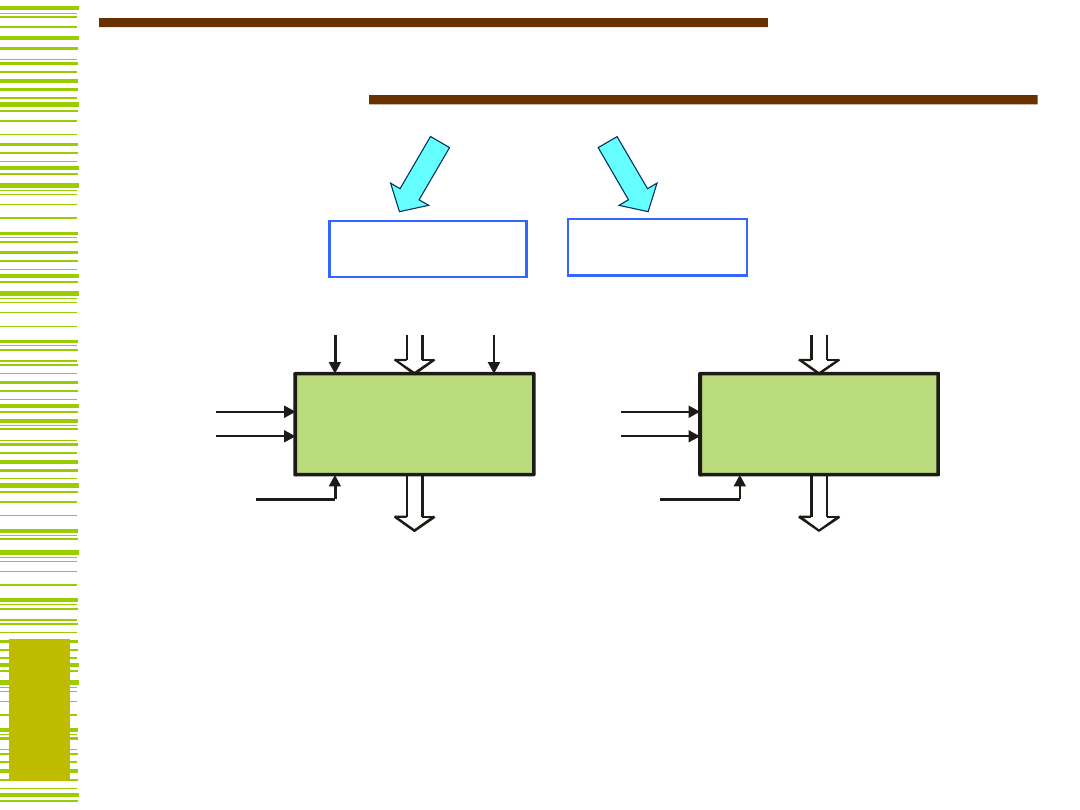
Sekwencyjne bloki funkcjonalne

Rejestry

Liczniki

L

( Q )

s

1

s

2

c lo c k

X

Y

R

( Q )

s

1

s

2

c lo c k

X

Y

x

l

x

p

Y := X LOAD
Y := Y HOLD

Y := <0...0> RESET

(CLEAR)

Y := SHR(x

p

,

Y)
Y := SHL(Y, x

l

)

Y := Y + 1 = INC(Y)
Y := Y – 1 = DEC(Y)

28

I

T
P

W

ZPT

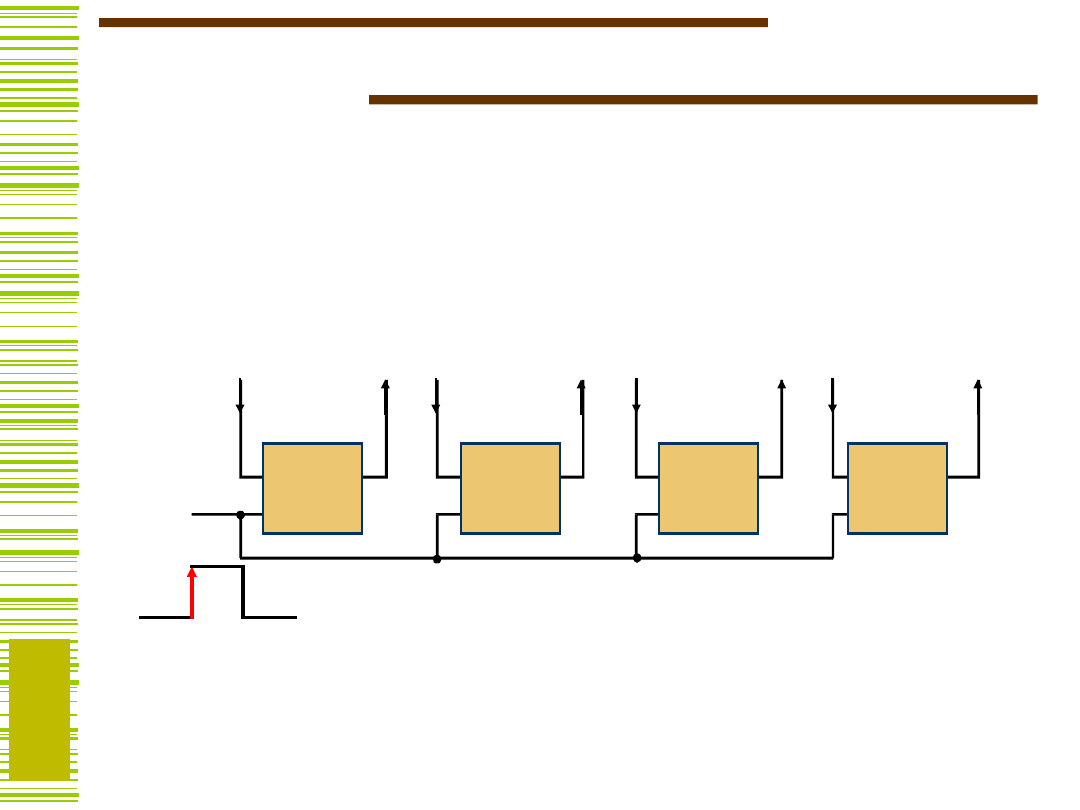
Prosty

rejestr

Rejestr zbudowany z przerzutników
– ładowanie (load) i pamiętanie

CLK

P

1

P

2

P

3

P

4

D

1

D

3

D

2

D

4

Q

1

Q

3

Q

2

Q

4

0

1

0

0

LOAD

0

1

0

0

29

I

T
P

W

ZPT

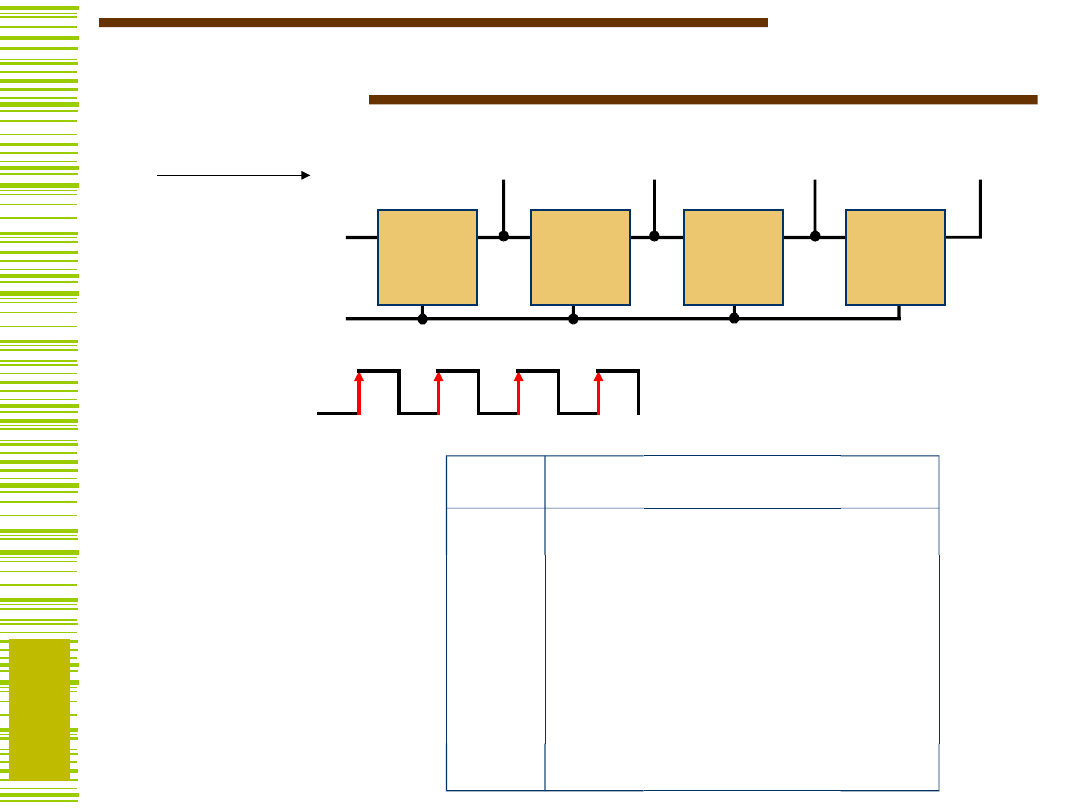
Rejestr przesuwający

WE

Q

1

Q

2

Q

3

Q

4

0

0

0

0

0

1

1

0

0

0

0

0

1

0

0

0

0

0

1

0

0

0

0

0

1

0

0

0

0

0

Q

1

Q

3

Q

2

Q

4

wejście

szeregowe

D

1

D

2

D

3

D

4

0

SHR

clk

0000 10

30

I

T
P

W

ZPT

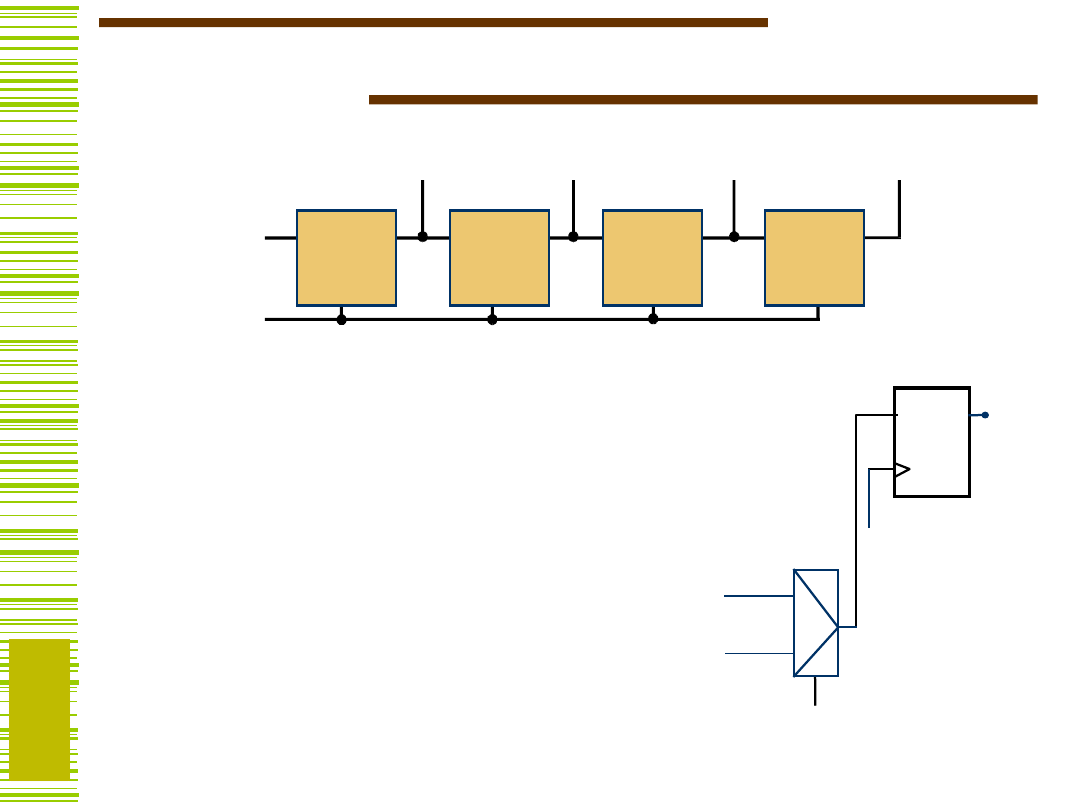
Rejestr przesuwający

Q

1

Q

3

Q

2

Q

4

CLK

wejście

szeregowe

D

1

D

2

D

3

D

4

Clock

D1

D0

D

Q

Q

Sel

Łatwo można zbudować rejestr, w
którym obie funkcje (ładowanie,
przesuwanie) wykonywane byłyby w
jednym układzie

31

I

T
P

W

ZPT

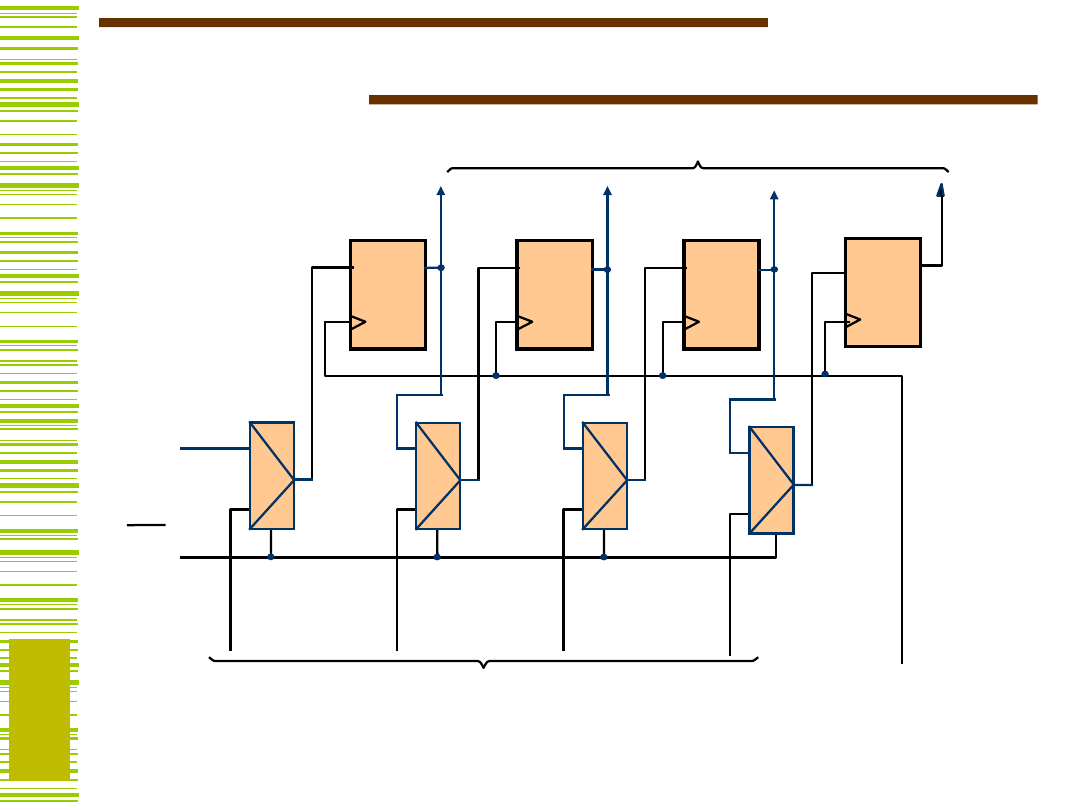
Rejestr przesuwający z wpisem
równoległym

Q

3

Q

2

Q

1

Q

0

Clock

Wejścia równoległe

Wyjścia równoległe

Wejście
szeregowe

D

Q

Q

D

Q

Q

D

Q

Q

D

Q

Shift/Load

Q

32

I

T
P

W

ZPT

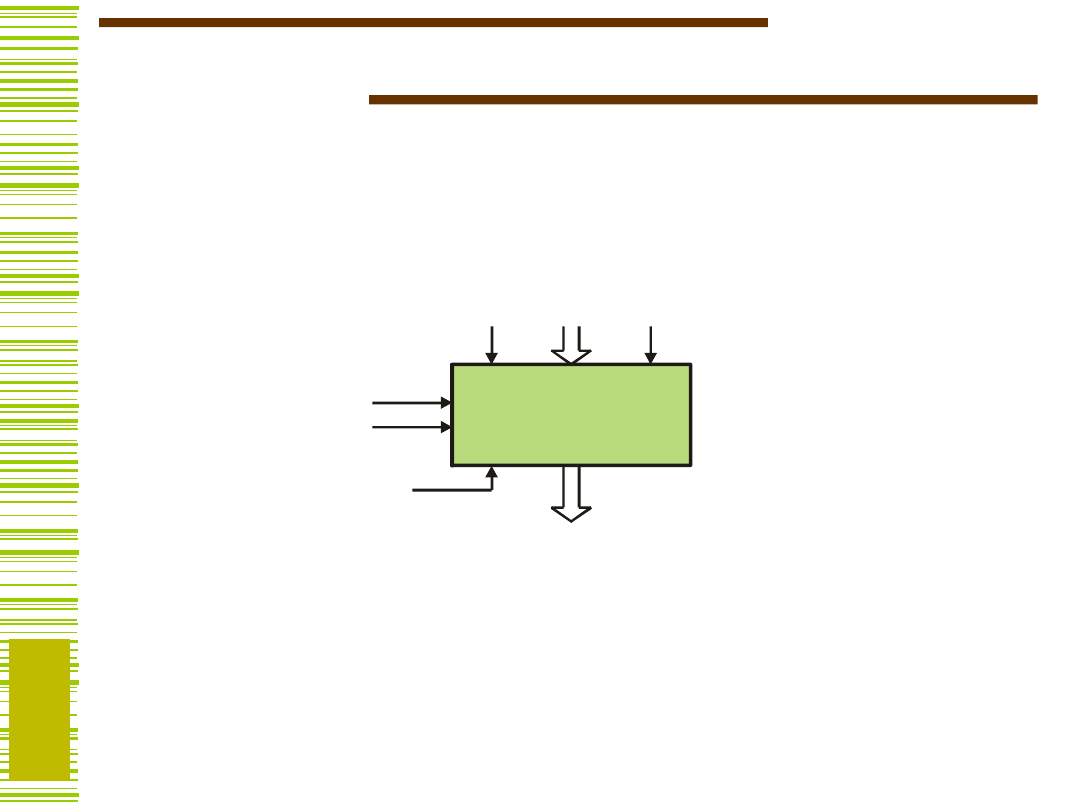
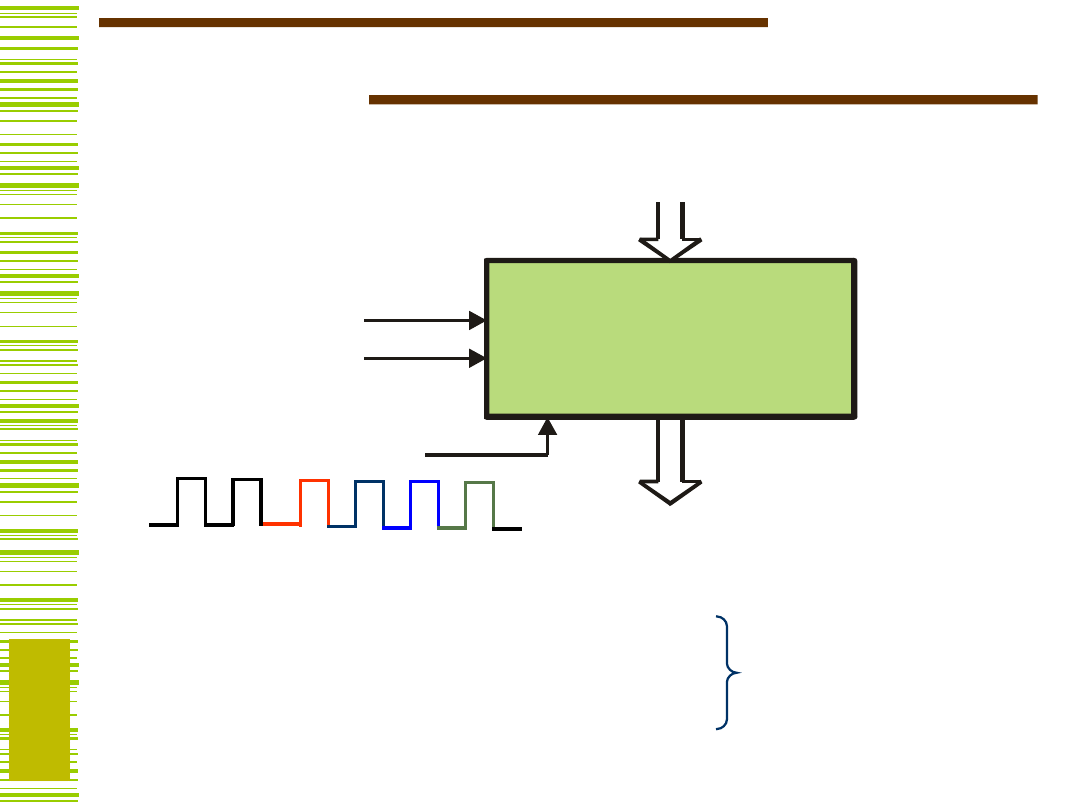
Rejestr uniwersalny

Y := X LOAD
Y := Y HOLD

Y := <0...0> RESET

(CLEAR)

Y := SHR(x

p

,

Y)
Y := SHL(Y, x

l

)

R

(Q)

s

1

s

2

clock

X

Y

x

l

x

p

33

I

T
P

W

ZPT

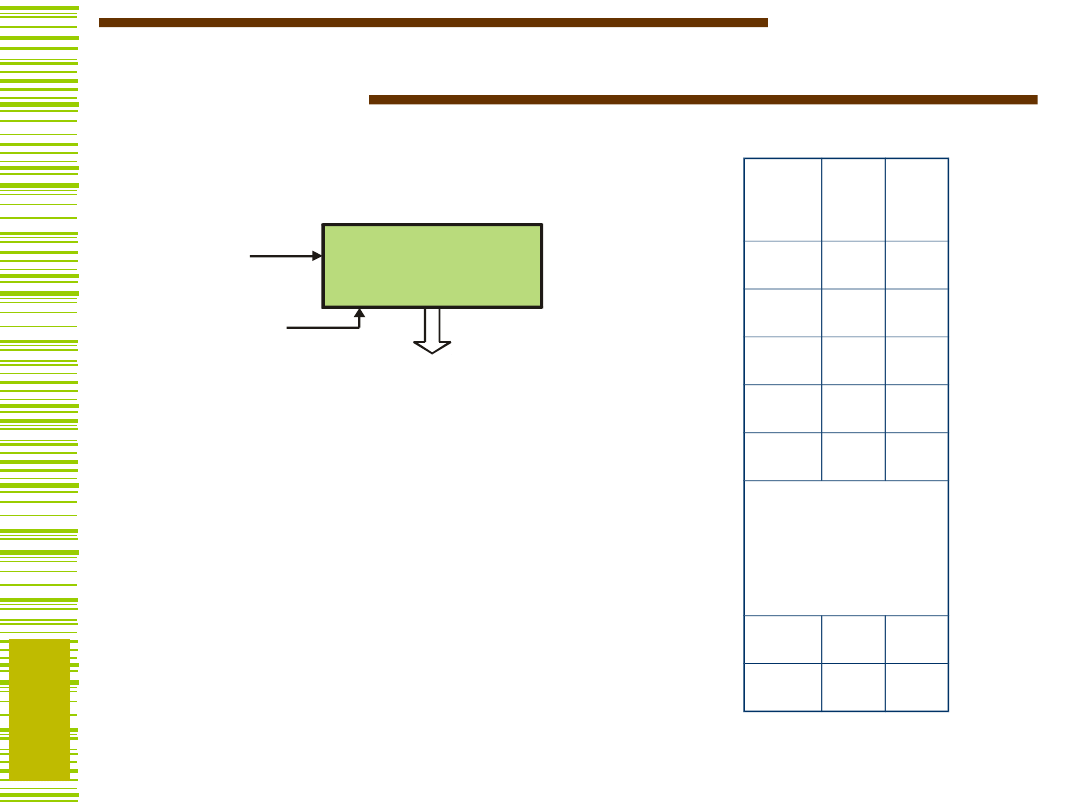
Mikrooperacje licznika

L ic z n ik

c lo c k

1100

Zliczanie

LOAD

COUNT

LOAD

HOLD

COUNT

LOAD

HOLD

0010

1101

1110

111
1

1100

34

I

T
P

W

ZPT

E

A

0

1

A

0

A

0

A

1

A

1

A

1

A

2

A

2

A

2

A

3

A

3

A

3

A

4

A

4

A

A

5







A

14

A

14

A

15

A

15

A

15

A

0

2

2

2

1

0

3

1

1

1

0

2

0

1

0

Q

T

Q

Q

EQ

T

Q

T

Q

EQ

T

EQ

T

E

T













Przykład licznika z wejściem Enable

Licznik

E

clock

Q

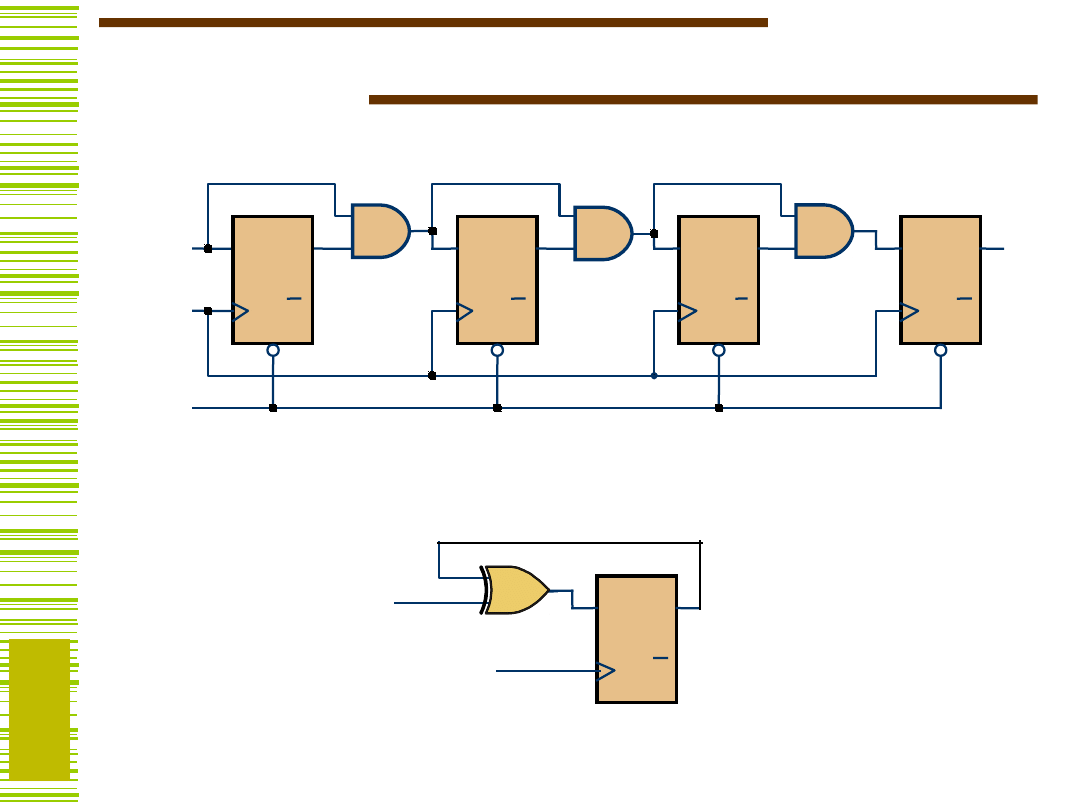
35

I

T
P

W

ZPT

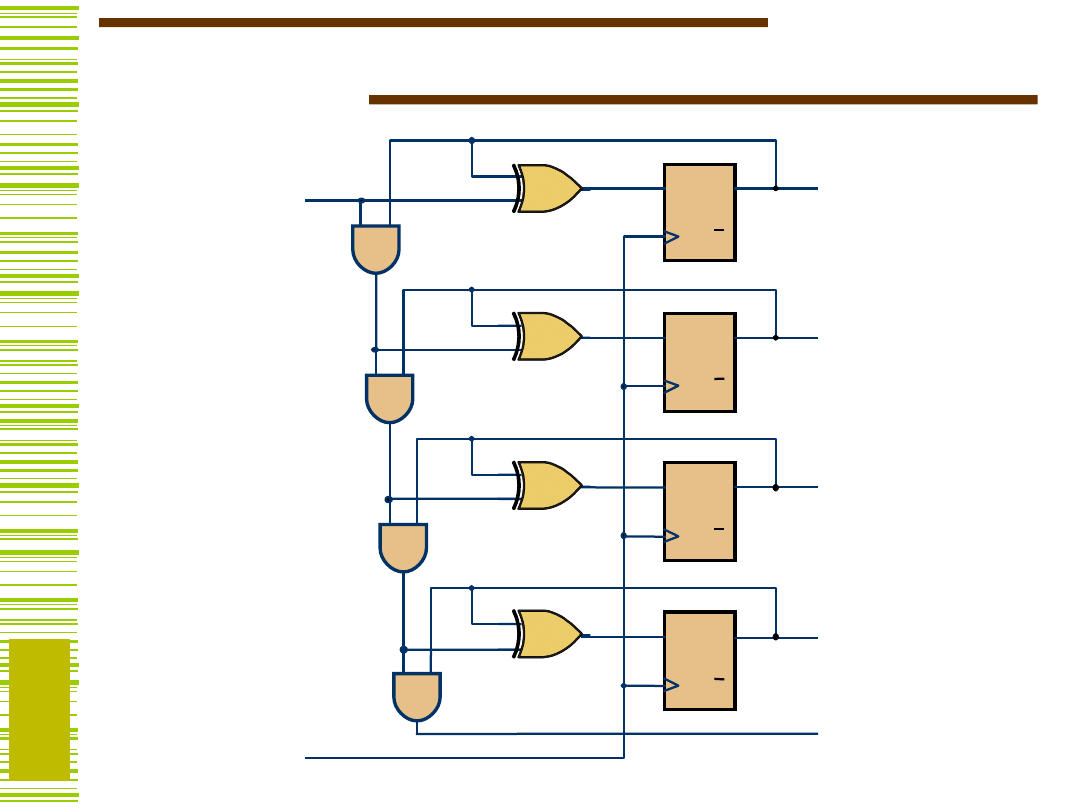
Licznik w górę

T Q

Q

Clock

T Q

Q

Enable

Rst

T Q

Q

T Q

Q

D Q

Q

T

clk

36

I

T
P

W

ZPT

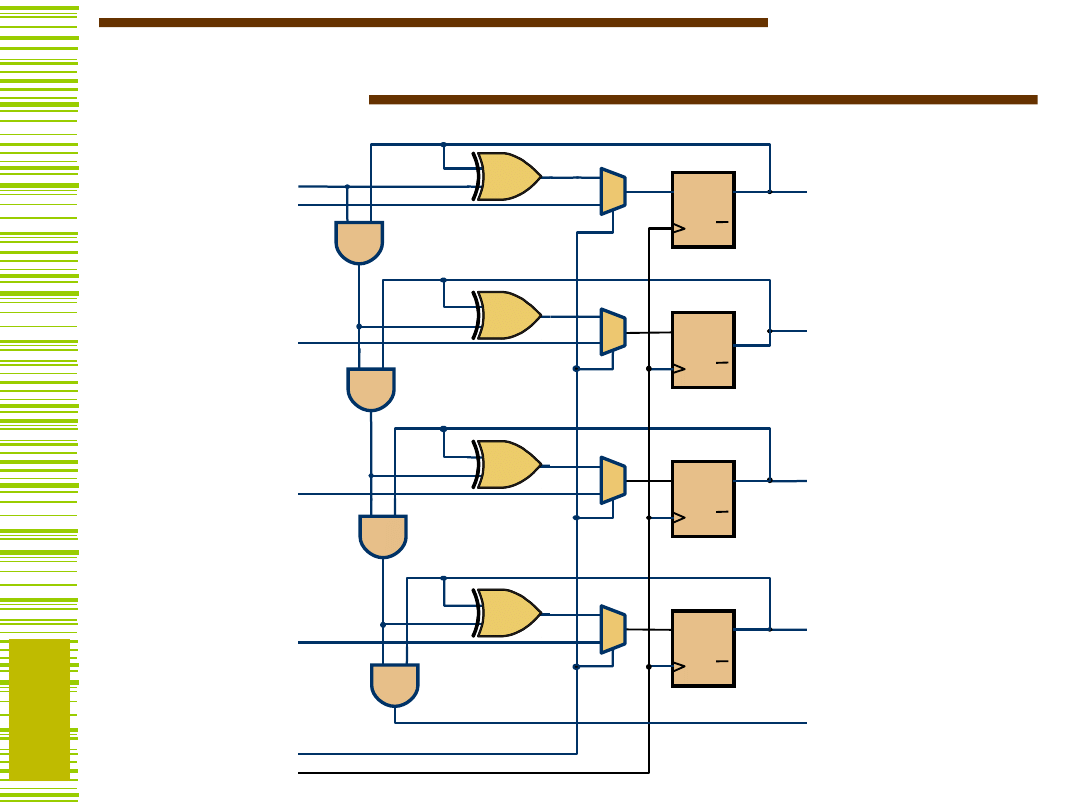
Licznik z przerzutnikami D

Clock

Enable

D Q

Q

D Q

Q

D Q

Q

D Q

Q

Q

0

Q

1

Q

2

Q

3

Output

carry

37

I

T
P

W

ZPT

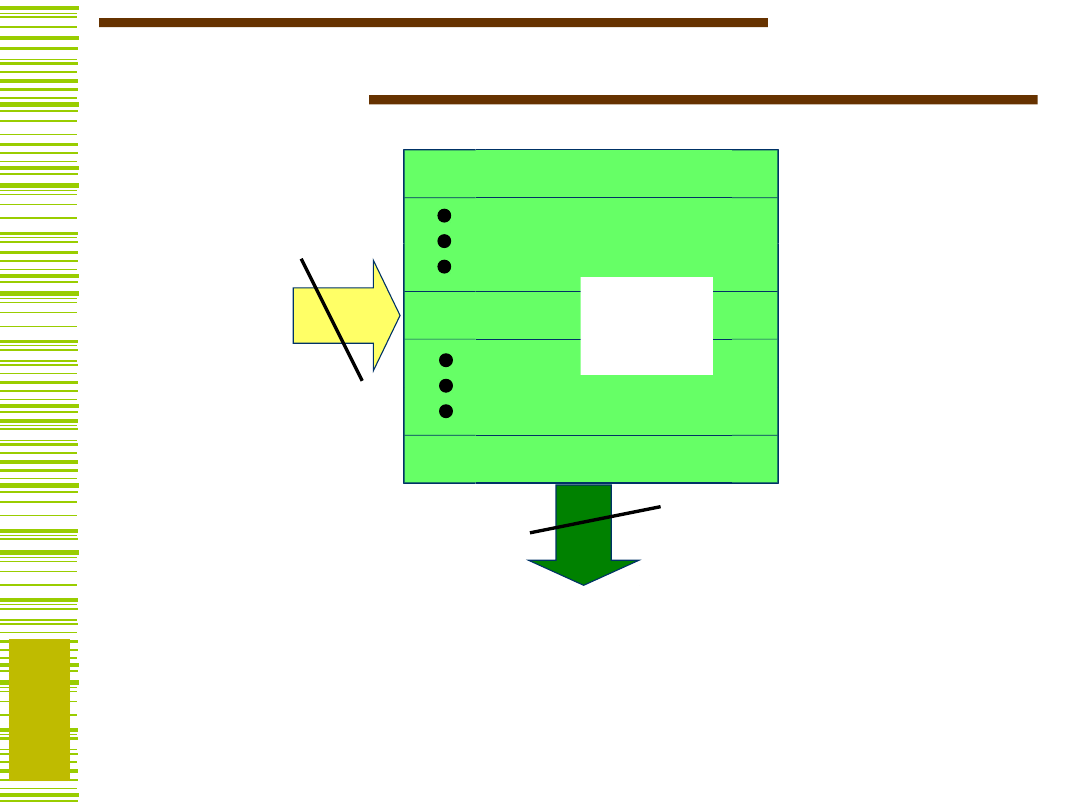
Licznik z wpisywaniem równoległym

Enable

D Q

Q

Q

0

D Q

Q

Q

1

D Q

Q

Q

2

D Q

Q

Q

3

D

0

D

1

D

2

D

3

Load

Clock

Output

carry

0
1

0

1

0
1

0
1

38

I

T
P

W

ZPT

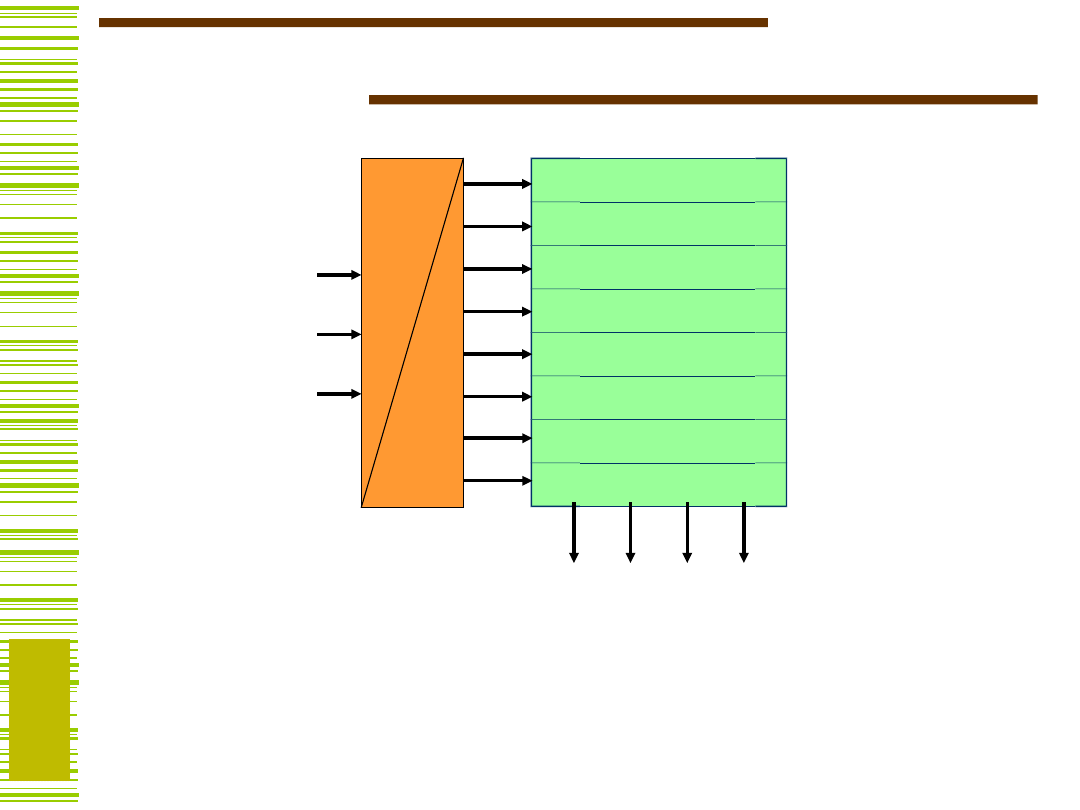
Pamięci typu ROM

ROM – uniwersalny układ kombinacyjny

A

ROM
m  n

X

0

X

i

X

m-1

p

Y

n

39

I

T
P

W

ZPT

Pamięci typu ROM

Adres

ROM
8  4

0
1
2
3
4
5
6
7

0
0
0

0
0
1

1
0
1

1 1 1 1

0 1 1 0
1 1 1 0

0 1 1 0

0 1 1 0
0 1 0 1

0 0 0 0

0 1 1 0

1 1 1 0

0 1 0 1

1 1 1 1