GEODEZJA

WYKŁAD

Układy odniesień

przestrzennych w

Polsce

Katedra Geodezji im. K. Weigla

ul. Poznańska 2/34

Układy odniesień przestrzennych

1. Lokalne (topocentryczne),

2. Globalne (geocentryczne).

Europejski układ odniesienia systemu

ETRS

(European Terrestrial Referance

Frame 1989)

Rozwój metod i techniki pozyskiwania danych

astronomicznych, geodezyjnych i geofizycznych
oraz współczesne osiągnięcia w dziedzinie
sposobów numerycznego opracowania tych
danych stworzyły podstawę do poprawienia

teorii figury Ziemi

oraz rewizji fundamentalnych

systemów odniesienia.

Ogółem ocenia się, że w Polsce funkcjonuje

około

150 układów lokalnych

utworzonych w celu

opracowania dokładnych wielkoskalowych map
dla terenów miast.

Obecnie używa się kilku różnych układów
odniesienia powiązanych z elipsoidą Krasowskiego
i układami współrzędnych: 1965, 1942, "Borowa
Góra" , Rauenberg (dla nawigacji i map morskich),
a także z miejscowymi punktami przyłożenia:
układy dla dużych miast, układ 1982, UTM i inne.

Wymienione układy, a także układy na innych
kontynentach są układami lokalnymi,
niepowiązanymi globalnie. Utworzenie jednolitego
globalnego układu współrzędnych dla celów
kartograficznych i geodezyjnych stało się możliwe
dzięki rozwojowi geodezyjnych technik
satelitarnych (GPS). Jednym z pierwszych

globalnych, geocentrycznych systemów odniesienia
stał się system WGS

(World Geodetic System),

opracowany w

1960 r

. przez Agencję Kartograficzną

DMA (Defence Mapping Agency) Armii USA na
zlecenie Departamentu Obrony Stanów
Zjednoczonych, oznaczony jako WGS-60. Obecnie
stosowany jest

system WGS-84

.

Globalny układ odniesień przestrzennych

Międzynarodowy system odniesień przestrzennych

ITRS

(International Terrestrial Referance System).

Europejski system odniesień przestrzennych

ETRS

jest podsystemem ITRS

Powierzchnia odniesienia -

geocentryczna elipsoida GRS 80

(ang. Geodetic Reference System 1980) o parametrach:

- a = 6 378 137 m, b = 6 356 752.314 m m,

- stała grawitacyjna (z atmosferą):GM=3986005*108m3s

-2

,

- współczynnik dynamiczny kształtu: J2 = 108263 x 10-8,

- spłaszczenie geometryczne: f = 1/298.257222101,

- prędkość obrotu Ziemi: = 7292115 x 10

-1

rad s

-1

.

-

współrzędne geodezyjne B, L

i wysokość H (wysokość

elipsoidalna) i

geocentryczne współrzędne prostokątne X, Y, Z

.

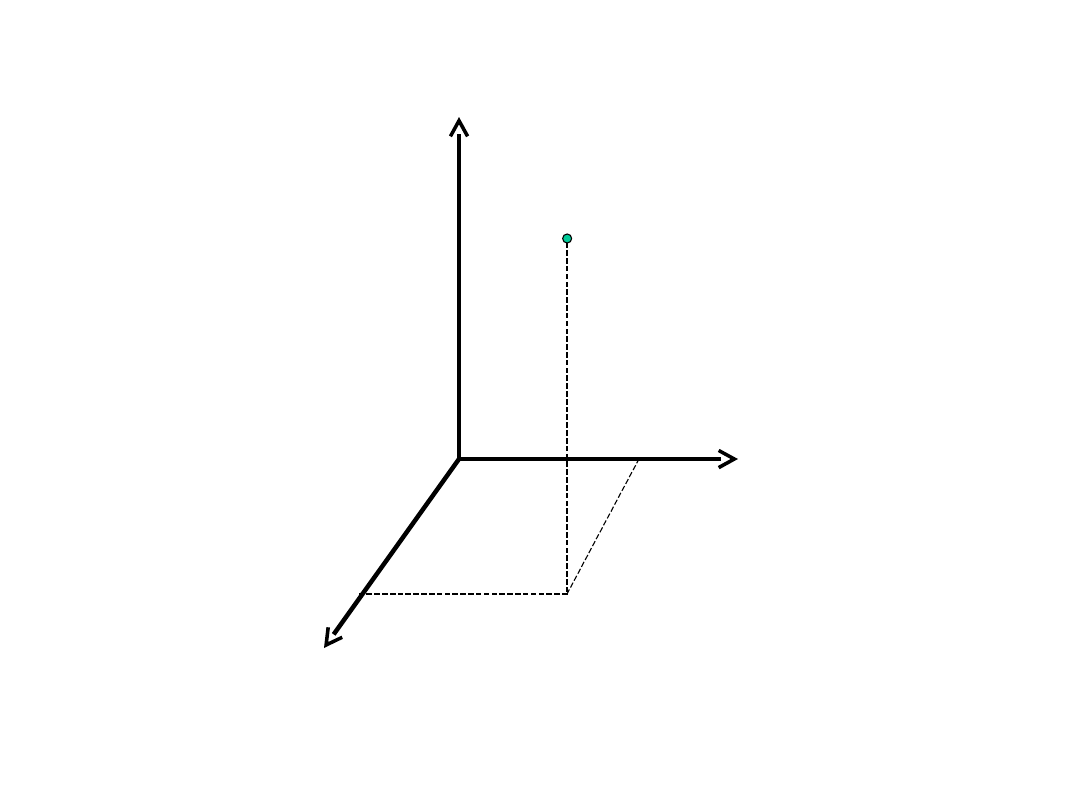
Współrzędne prostokątne X, Y, Z

X

Y

P

P’

x

P

z

P

y

P

Z

POLSKI SYSTEM ODNIESIEŃ PRZESTRZENNYCH

1. Geodezyjny układ odniesienia na obszarze Polski

"EUREF-

89",

jest rozszerzeniem europejskiego układu

ETRF

w wyniku

kampanii pomiarowej

EUREF-POL 92

, której rezultaty zostały

zatwierdzone przez Międzynarodową Asocjację Geodezyjną w
1994 r.

2. W EUREF-89 stosuje się

Geodezyjny System Odniesienia

1980 (GRS 80),

przyjęty na XVII Zgromadzeniu Generalnym

Międzynarodowej Unii Geodezji i Geofizyki (MUGG) w
Canberze, w grudniu 1979 r.

Zgodnie z rozporządzeniem Rady Ministrów z dnia 8 sierpnia
2000 r.

w sprawie państwowego systemu odniesień

przestrzennych:

Poziomem odniesienia jest poziom zerowy określony przez
mareograf w Kronsztadzie koło Sankt-Petersburga.

Układ "1965" zostaje zastąpiony

Układem współrzędnych

prostokątnych płaskich "2000„ , który

ma być stosowany w

pracach geodezyjnych związanych z wykonywaniem mapy
zasadniczej. Dla map w skali 1:10000 i w skalach mniejszych
wprowadza się

układ "1992„

Układ współrzędnych "1965"

oraz

lokalne

układy

współrzędnych

stosowane do 31 grudnia 2009r przestają

pełnić funkcję układów państwowych

.

Państwowy system odniesień przestrzennych

stosuje się

w pracach geodezyjnych i kartograficznych oraz w
systemach informacji o terenie, wykonywanych do
celów gospodarczych.

Państwowy system odniesień przestrzennych tworzą:

1) geodezyjny układ odniesienia,

2) układ wysokości, w którym wyznacza się wysokości punktów

względem przyjętego poziomu powierzchni odniesienia,
stosowany w pracach geodezyjnych i kartograficznych.

3) układ współrzędnych płaskich prostokątnych, oznaczony symbolem

"2000", stosowany w pracach geodezyjnych i kartograficznych,
związanych z wykonywaniem mapy zasadniczej.

4) układ współrzędnych płaskich prostokątnych, oznaczony symbolem

"1992", stosowany w mapach urzędowych o skali mapy 1:10.000 i
skalach mniejszych.

UKŁAD WYSOKOŚCI

Układ wysokości tworzą wartości geopotencjalne podzielone przez
przeciętne wartości przyspieszenia normalnego siły ciężkości, zwane
"wysokościami normalnymi", odniesione do średniego poziomu Morza
Bałtyckiego w Zatoce Fińskiej, wyznaczonego dla mareografu w
Kronsztadzie koło Petersburga (Federacja Rosyjska).

Wysokości normalne określa się z pomiarów geodezyjnych
nawiązanych do punktów podstawowej osnowy geodezyjnej kraju.

UKŁAD WSPÓŁRZĘDNYCH PROSTOKĄTNYCH "2000"

Układ współrzędnych płaskich prostokątnych "2000" utworzony na
podstawie matematycznie jednoznacznego przyporządkowania
punktów powierzchni Ziemi odpowiednim punktom na płaszczyźnie
według teorii odwzorowania kartograficznego Gaussa-Krügera.

UKŁAD WSPÓŁRZĘDNYCH PROSTOKĄTNYCH "1992"

Układ współrzędnych płaskich prostokątnych "1992" jest utworzony
na podstawie matematycznie jednoznacznego przyporządkowania
punktów powierzchni Ziemi według teorii odwzorowania Gaussa-
Krügera.

Zależności pomiędzy układami

Odwzorowanie kartograficzne

to zbiór równań

matematycznych wiążących współrzędne płaskie
X, Y i współrzędne przestrzenne (elipsoidalne)
B,L

Algorytm transformacji w formie kolejnych

przekształceń:

XY65 (el Krasowskiego)  BL  B’L’ (GRS80 ) 

XY2000

• Przeliczenie współrzędnych XY wg wzorów

odwzorowania do

BL

na elipsoidzie

Krasowskiego.

• Przeliczenie współrzędnych

BL

– przejście do

elipsoidy GRS80 i współrzędnych

B’L’

.a

• Przeliczenie współrzędnych XY wg wzorów

odwzorowania

Gaussa-Krügera

do XY w układzie

„2000”.

Układ odniesienia wysokości

1.

Układ wysokości

tworzą wysokości normalne,

odniesione do średniego poziomu Morza
Bałtyckiego w Zatoce Fińskiej, (zero mareografu w
Kronsztadzie), Sankt Petersburg (Rosja).

2.

Wysokością normalną

punktu jest różnica

potencjałów siły ciężkości w tym punkcie i na

powierzchni geoidy

, podzielona przez przeciętną

wartość przyspieszenia wzdłuż linii pionu
normalnego pola siły ciężkości.

śr

p,o

n

U

H







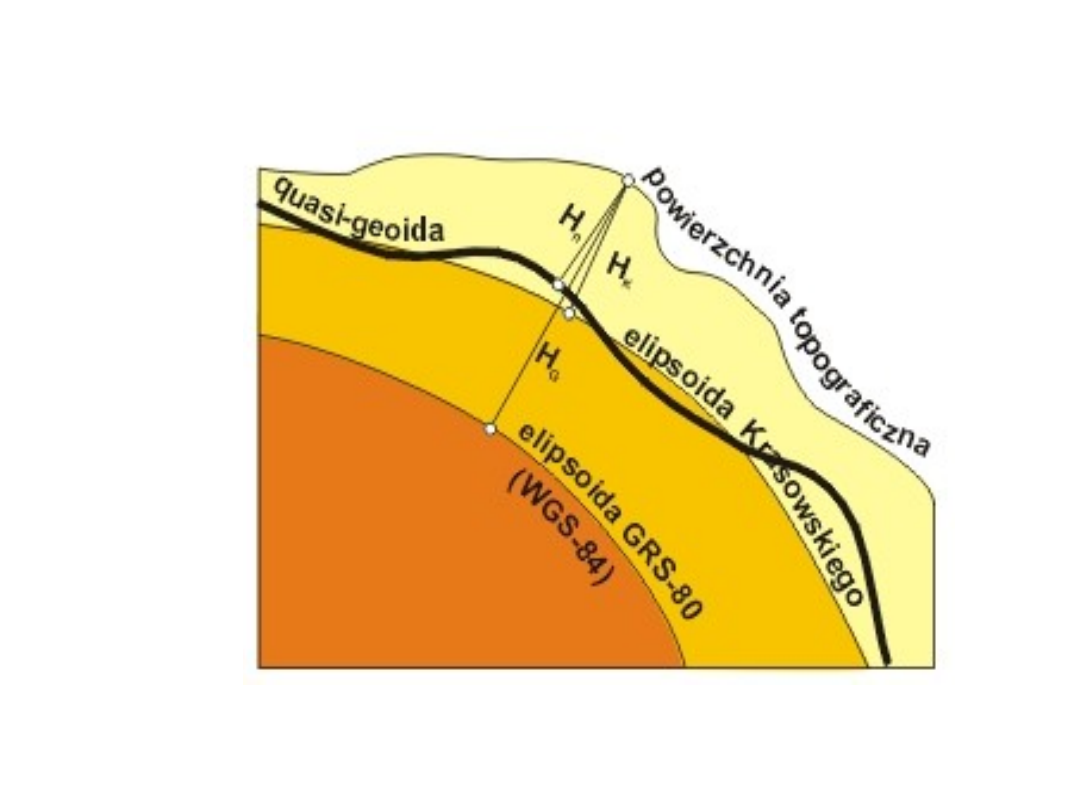
Wysokości normalne

Układ współrzędnych „2000"

1. Współrzędne płaskie prostokątne X, Y obliczane

są w odwzorowaniu elipsoidy w

trzystopniowych

pasach

dla południków osiowych:

15°, 18°, 21 °,

24°

dł. geograficznej wschodniej. Podział obszaru

kraju na

4 pasy

odwzorowania Gaussa-Krügera

oznaczone numerami: 5, 6, 7 i 8.

2. Współczynnik skali

w południku osiowym m =

0,999923.

3. Obraz równika jest linią x = 0, a obraz południka

osiowego linią:

y = 5 500 000 m na południku L

0

=15°,

y = 6 500 000 m na południku L

0

=18°,

y = 7 500 000 m na południku L

0

=21°,

y = 8 500 000 m na południku L

0

=24°.

4. Pierwsza cyfra współrzędnej Y jest numerem

pasa.

Układ współrzędnych „1992"

1.

Układ współrzędnych płaskich prostokątnych

„1992"

oparty jest na współrzędnych geograficznych

geodezyjnych w układzie europejskim

EUREF-89

(ang. European Reference Frame 1989.0) -

ETRF-89

(ang. European Terrestrial Reference Frame
1989.0).

2. Współrzędne płaskie prostokątne X, Y

dla

obszaru Polski

są obliczane w

odwzorowaniu

kartograficznym Gaussa-Krügera

, w pasie

dziesięciostopniowym

z południkiem osiowym L

0

=

19° i przy współczynniku skali w południku osiowym
0.9993

3. Początkiem układu „1992" jest punkt przecięcia
się obrazu

południka osiowego L

0

=19°

z obrazem

równika, przy czym przy określaniu współrzędnych
od X odejmuje się 5 300 000 m, a do współrzędnej Y
dodaje 500 000 m.

Strefa układu „1992” w odwz. Gaussa-
Krügera

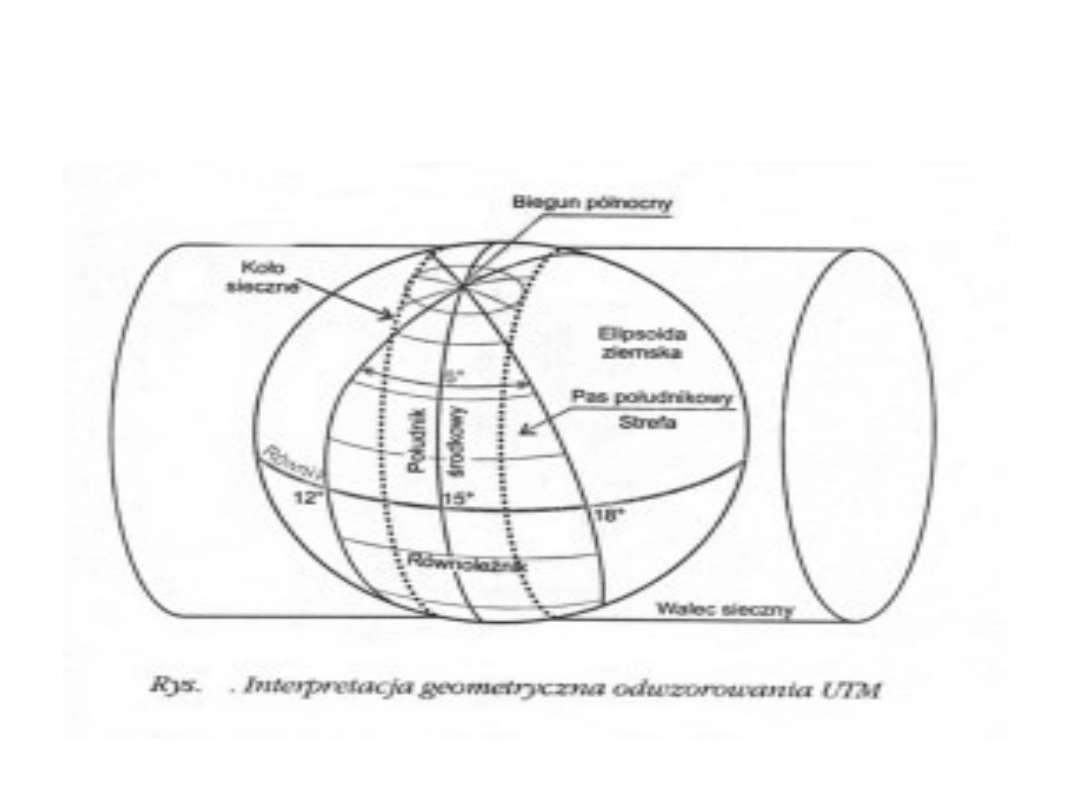
Odwzorowanie walcowe poprzeczne

(strefowe)

Gaussa-Krügera

Odwzorowanie Gaussa-Krügera

Odwzorowanie

Gaussa-Krügera

jest to wiernokątne

walcowe poprzeczne odwzorowanie powierzchni
elipsoidy obrotowej na płaszczyznę, przy czym
środkowy południk strefy odtwarza się wiernie.
Długości odcinków w odwzorowaniu Gaussa-
Krügera są obarczone zniekształceniami.

Zniekształcenia

zależą od

skali odwzorowania

, nie zależą od

orientacji odcinka.

Maksymalne na styku dwóch stref 3º dla skali m =

0,999923

,

wynoszą:

-7,7 cm/1000m na południku osiowym).

Wzór

empiryczny

z aproksymacji wielomianem 2 stopnia:

 = 

0

+m

0

* v

2

*( a

1

+ a

2

*u+ a

3

*u

2

+a

4

*v

2

)



0

- zniekształceni na południku centralnym. Dla „2000” 

0

= -7.7

cm/km

m

0

= 0,999923

a

1

= 306.752873, a

2

= -0.312616, a

3

= 0.006382, a

4

= 0.158591,

u = (X/ m

0

- 5800000)*2*10

-6

v = (Y/ m

0

)*2*10

-6

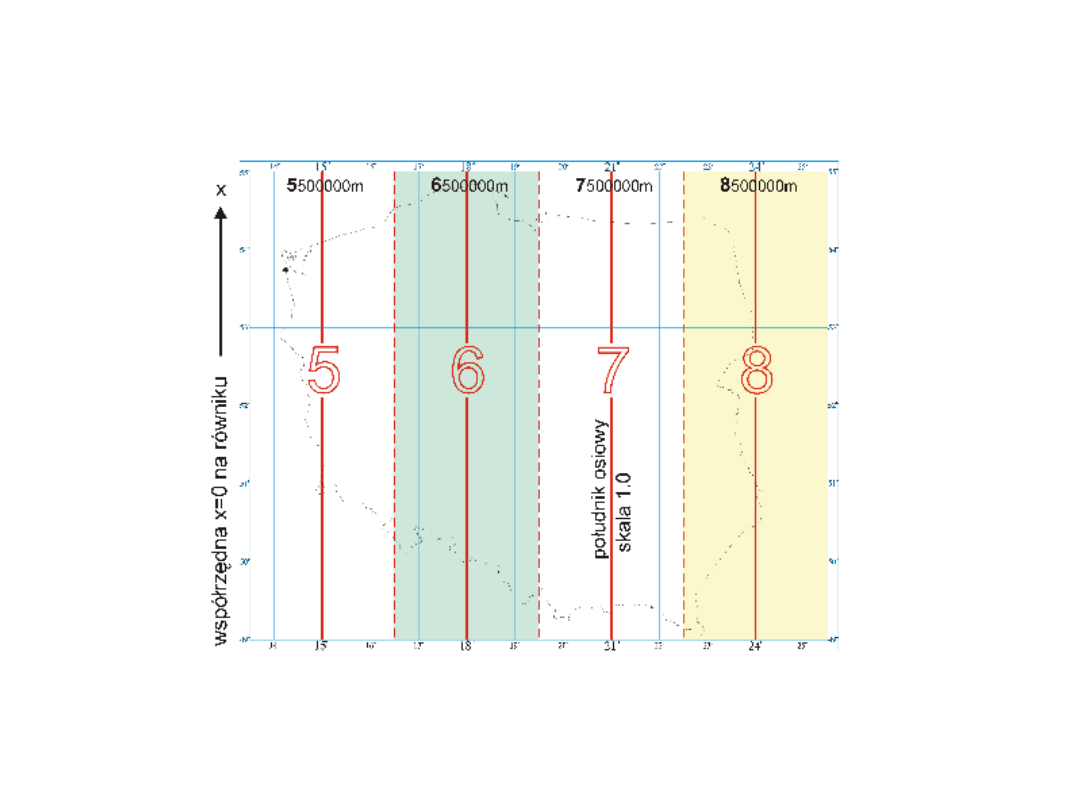
Strefy odwzorowawcze ukł. „2000”

(zniekształcenia -7,7 cm\km na południku
osiowym - do +7cm\km na brzegu strefy);

Układ współrzędnych „1965„

W 1976 roku wprowadzony został dla potrzeb cywilnej służby
geodezyjnej państwowy układ współrzędnych płaskich "1965".

„1965"

składa się z

czterech układów

współrzędnych prostokątnych

płaskich (stref) o numerach od 1 do 4) w

quasi-stereograficznym

wiernokątnym odwzorowaniu Roussilhe'a, elipsoidy Krasowskiego na
płaszczyznę oraz

jednego układu

(

strefa 5

) w od wzorowaniu

Gaüssa-

Krugera

. Skala odwzorowania w punkcie głównym (skala

podobieństwa) m

0

=0.9998, natomiast w strefie V - skala na

południku środkowym m

0

= 0. 999983.

Maksymalne poprawki odwzorowawcze do długości odcinków
wynoszą 20 cm.
W odwzorowaniu wiernokątnym

skala podobieństwa

(m) jak też

elemenarne zniekształcenie liniowe długości

odcinka nie zależą od

kierunku lecz od położenia w strefie odwzorowawczej.

Zniekształcenia długości

 oblicza się ze wzorów

empirycznych

uzyskanych z aproksymacji wielomianem 2 stopnia:

 = a

0

+a

20

* u

2

+ a

02

* v

2

+a

12

* uv

2

– dla stref I - IV

 = a

0

+a

02

* v

2

+ a

12

* uv

2

– dla strefy nr V.

u = (x-x

0

)c, v = (y-y

0

)c, c = 3*10

-6

dla strefy V : c = 4*10

-6

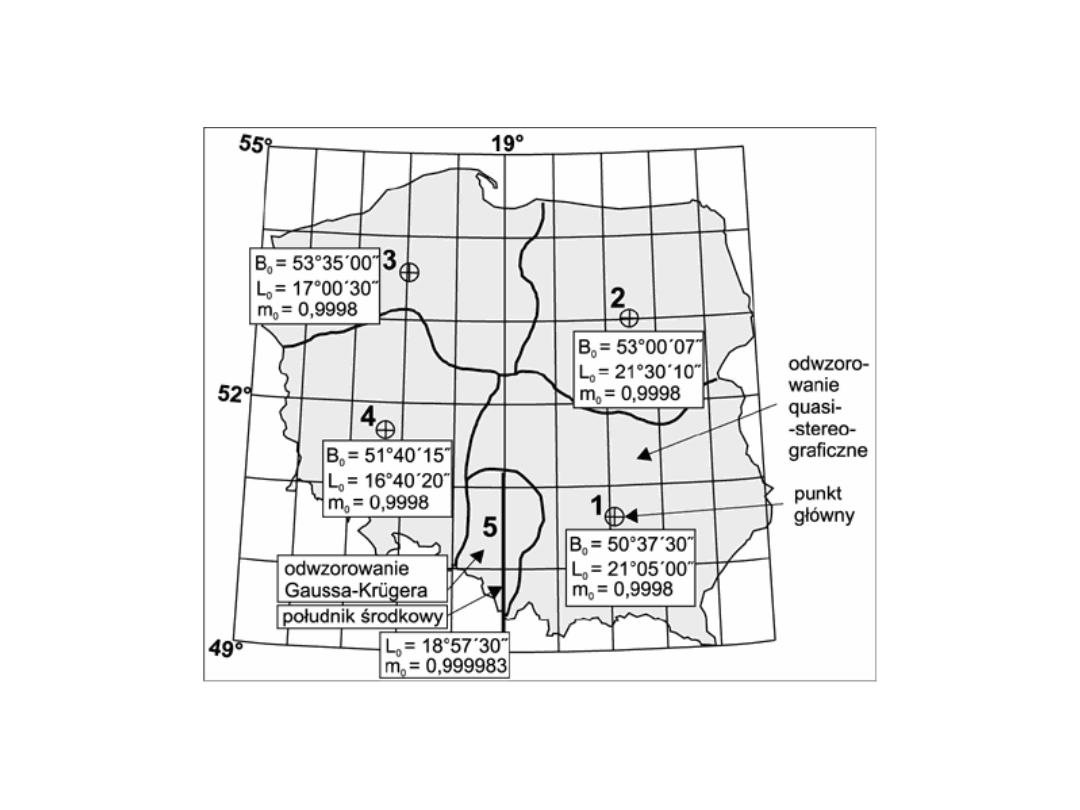
Strefy w układzie „1965”

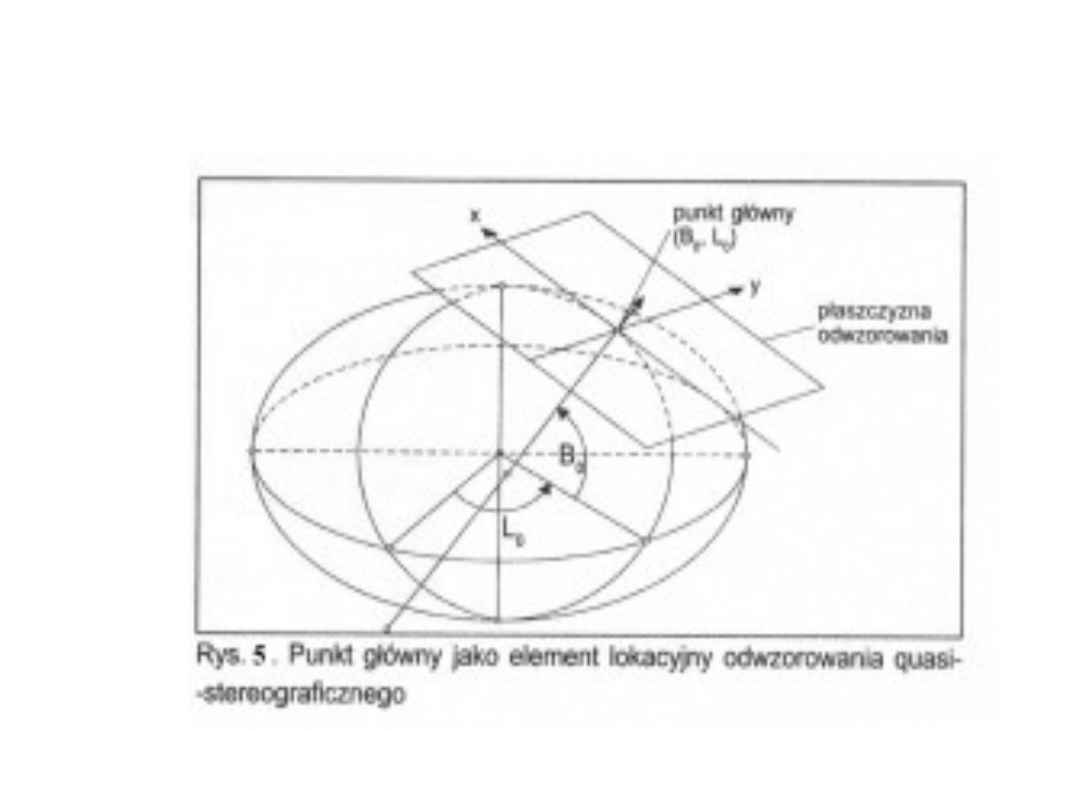
1

Odwzorowanie płaszczyznowe ukośne

(azymutalne)

Jednym z podstawowych celów

globalnego układu

geodezyjnego

jest

możliwość

ujednolicenia

lokalnych

układów.

W

praktyce

znajduje

zastosowanie

kilkaset

. lokalnych układów, łącznie z

układami na wyspach i układami lokalnymi
opartymi na obserwacjach astronomicznych,.

W pomiarach inżynierskich w dalszym ciągu
stosowane są układy lokalne. Znacznie
wygodniejsze układy lokalne związane z osią
obiektu, stosowane powszechnie w zadaniach
projektowych. Przykładem mogą być lokalne układy
wysokościowe.