Standardowa biblioteka szablonów –

podstawowe cechy i elementy

WYKŁAD 2

WAT 2006

Andrzej Walczak

PRZYKŁADY ZBIORÓW I

WIELOZBIORÓW

• #include <iostrem>
• #include <set>
•  
• int main()
• {
• typedef std::set<int> IntSet; //definicja typu

IntSet

• IntSet coll; //kontener na wartosci integer
• //*wstawi elementy od 1 do 6 w tym 1

dwukrotnie

PRZYKŁADY ZBIORÓW I

WIELOZBIORÓW

• coll.insert(3); //funkcja skladowa kontenerów

asocjacyjnych.Nowy element otrzymuje pozycje zgodnie
z wbudowanym kryterium sortowania.

Typ IntSet ma

kryterinm sortowania operatorem <.

Nie musimy

stosować funkcji push_back lub push_front.

• coll.insert(1);
• coll.insert(5);
• coll.insert(4);
• coll.insert(2);
• coll.insert(1);
• coll.insert(6);

PRZYKŁADY ZBIORÓW I

WIELOZBIORÓW

• //wypisz elementy
•  
• IntSet::const_iterator pos;
• for(pos=coll.begin();pos!=coll.end();++pos)

{std::cout<<*pos<<’’;}

• std::cout<<std::endl;
•  
• }
•  
• Elementy będą posortowane tak, że utworzą strukturę

drzewa. Zastosowany iterator pos automatycznie posortuje

drzewo. Ponieważ zastosowaliśmy zbiór (set) to

powtarzającego się elementu po posortowaniu nie będzie.

Jeśli zastosujemy multiset to będzie.

PRZYKŁADY ZBIORÓW I

WIELOZBIORÓW – tablica

asocjacyjna

• #include <iostream>
• #include <string>
• #include <

map

>

• using namespace std;

• int main()
• {
• typedef map<string, float> StringFloatMap; //definicja typu

IntStringMMap

• StringFloatMap coll; //kontener na wartosci integer-string

• coll["VAT"]=0.22;
• coll["PI"]=3.1415;
• coll["liczba"]=0.224466;
• coll["zero"]=0.0;

PRZYKŁADY ZBIORÓW I

WIELOZBIORÓW

• //wypisz elementy

• StringFloatMap::iterator pos;

• for(pos=coll.begin();pos!=coll.end();++pos) {
•

cout<<"klucz:\" "<<pos->first<<"\" "

• <<"wartosc:"<<pos->second<<endl;}

• return 0;
• }
• Deklaracja typu kontenerowego zawiera klucz i jego

wartosc

• Taka tablica ma indeks dowolnego typu niekoniecznie

integer

Definicja struktury danych

Definicja 2.1:

Strukturą danych nazywamy trójkę uporządkowaną

S=(D, R, e)

,

gdzie:

 D

– oznacza zbiór danych elementarnych

d

i, i = 1,..,|D|

(i – jest

indeksem poszczególnych danych),

 R={r

we

, N}

– jest zbiorem dwóch relacji określonych na

strukturze danych:

 – relacja wejścia do struktury danych S,
 – relacja następstwa (porządkująca)

strukturę S,

 e

– jest elementem wejściowym do struktury danych S (nie jest

to dana wchodząca w skład struktury danych S).

D

e

r

we





D

D

N





Zbiór danych elementarnych D

• Jak widać z definicji struktury danych, zbiór danych

elementarnych jest skończony i dla wygody operowania

oznaczeniem jego elementów poszczególne dane są indeksowane

od wartości 1 w kierunku wartości większych.

• Weźmy zatem dla przykładu pięcioelementową strukturę danych

S

. Zapis zbioru jej danych elementarnych może wyglądać

następująco:

• Liczność zbioru danych elementarnych wynosi 5, co zapisujemy:

• |D|=5





5

4

3

2

1

,

,

,

,

d

d

d

d

d

D 

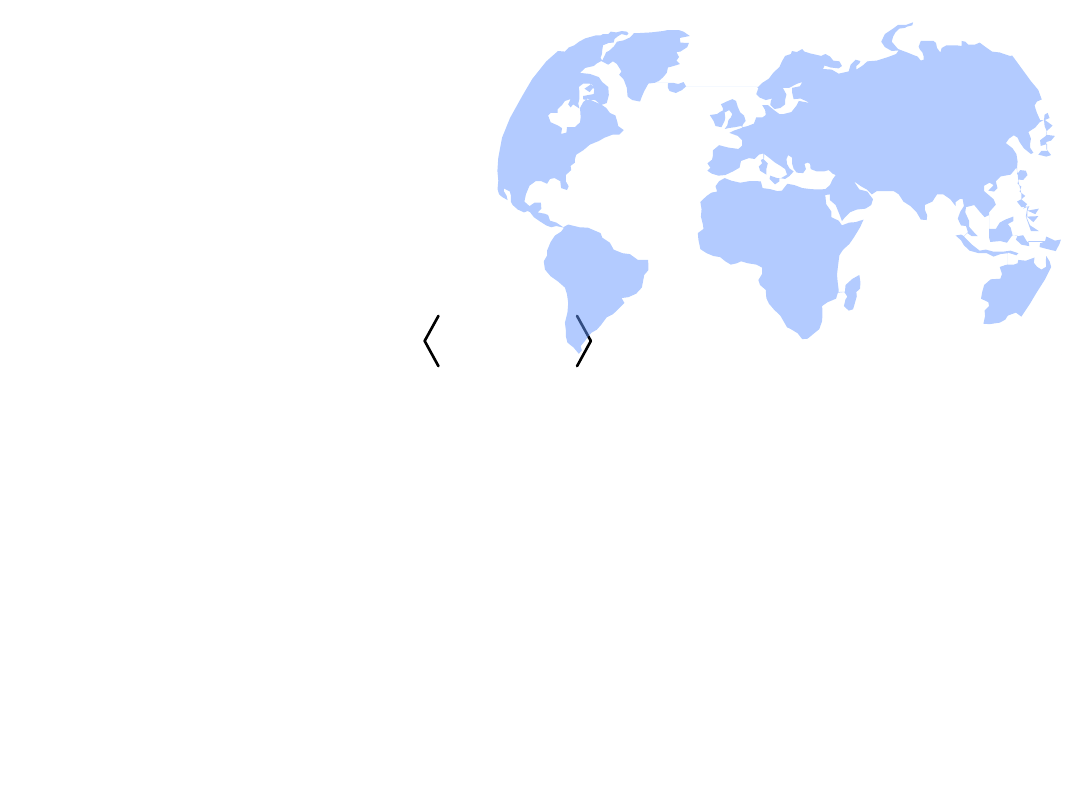
Dana elementarna, zmienna

programowa

• Dana elementarna

d

i

jest pojęciem abstrakcyjnym, rozumianym

jako tzw. „nazwana wartość”. Jest ona określana jako

uporządkowana dwójka elementów:

• , gdzie:

– n

i

– nazwa danej,

– w

i

– aktualna wartość danej z określonej dziedziny wartości.

• Zmienna programowa jest pojęciem związanym z realizacją danej

w konkretnym środowisku programistycznym. Posiada ona

zdefiniowaną etykietę (nazwę zmiennej), wraz z określeniem

dziedziny wartości, którą może przyjmować dana

reprezentowana przez zmienną, a także zdefiniowaną dla tej

dziedziny wartości dziedziną algorytmiczną.

i

i

i

w

n

d

,



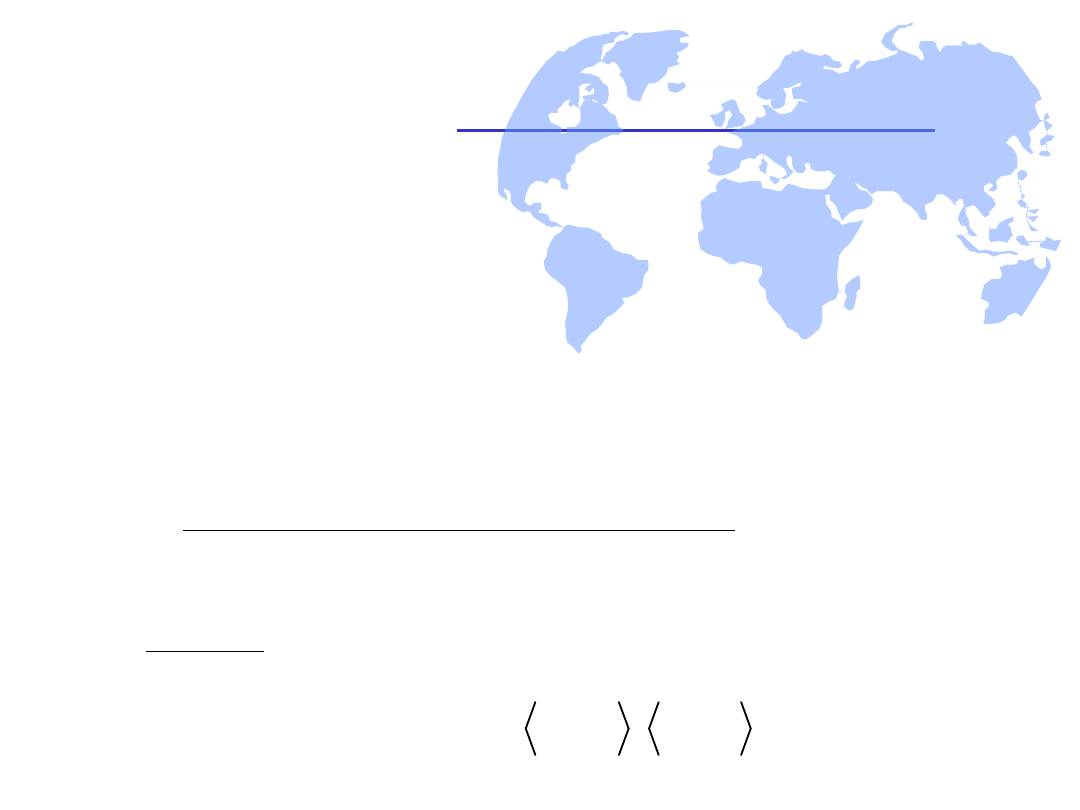
Relacja r

we

– wskazanie korzenia

struktury S

• Relacja

r

we

, jest opisywana poprzez jedno- lub wieloelementowy

zbiór dwójek uporządkowanych elementów, z których pierwszym
jest zawsze element wejściowy

e

, natomiast drugim elementem

jest jedna z danych elementarnych ze zbioru

D

.

• W sytuacji opisanej powyżej mówimy, że

– „element

e

należy do dziedziny relacji

r

we

” -

Dz(r

we

),

– „dana

d

i

należy do przeciwdziedziny

r

we

” –

PDz(r

we

)

• Element (elementy) należące do

PDz(r

we

)

są nazywane

korzeniem (korzeniami) struktury danych S. Struktura musi mieć
zdefiniowany co najmniej jeden korzeń.

Przykład: Załóżmy, że struktura S posiada dwa korzenie, według

opisu:





5

2

,

,

,

d

e

d

e

r

we



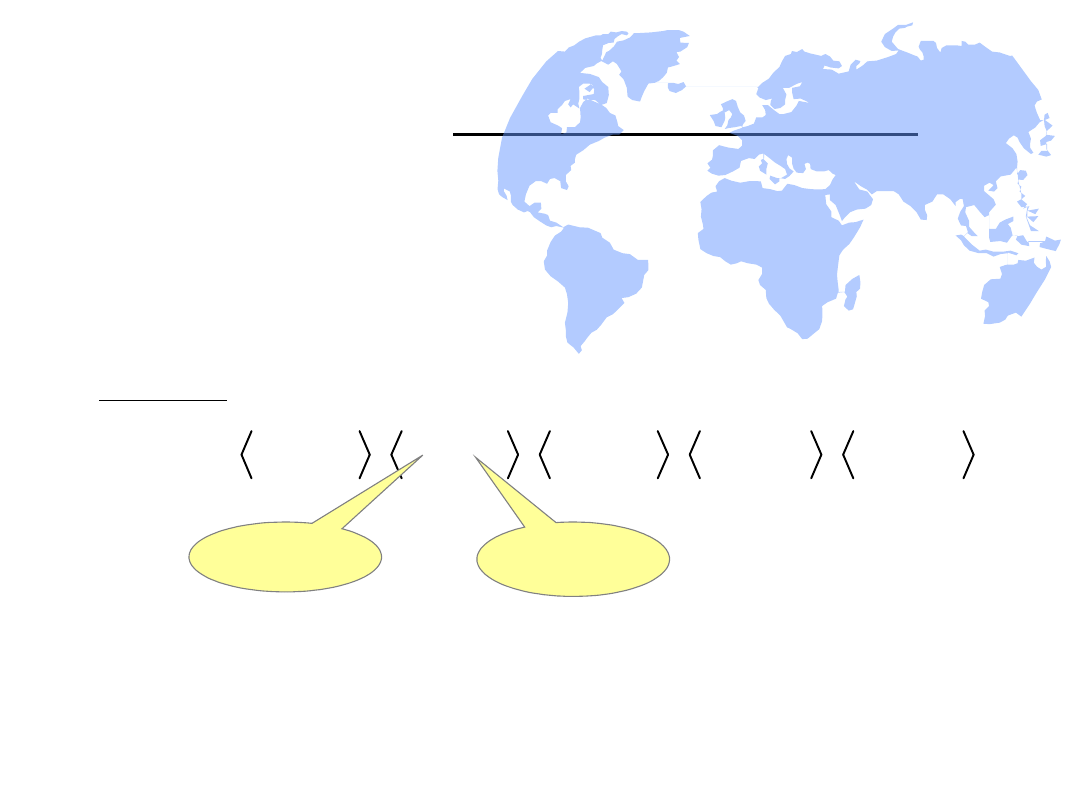
Relacja

N

– ustalenie porządku

struktury S

• Relacja następstwa N opisuje wzajemne uporządkowanie

elementów w strukturze danych S. Porządek struktury
opisujemy w postaci zestawów dwójek uporządkowanych
elementów.

Przykład: Opiszmy porządek naszej pięcioelementowej struktury

danych S:





3

5

4

3

4

1

3

1

1

2

,

,

,

,

,

,

,

,

,

d

d

d

d

d

d

d

d

d

d

N 

poprzedn

ik

następni

k

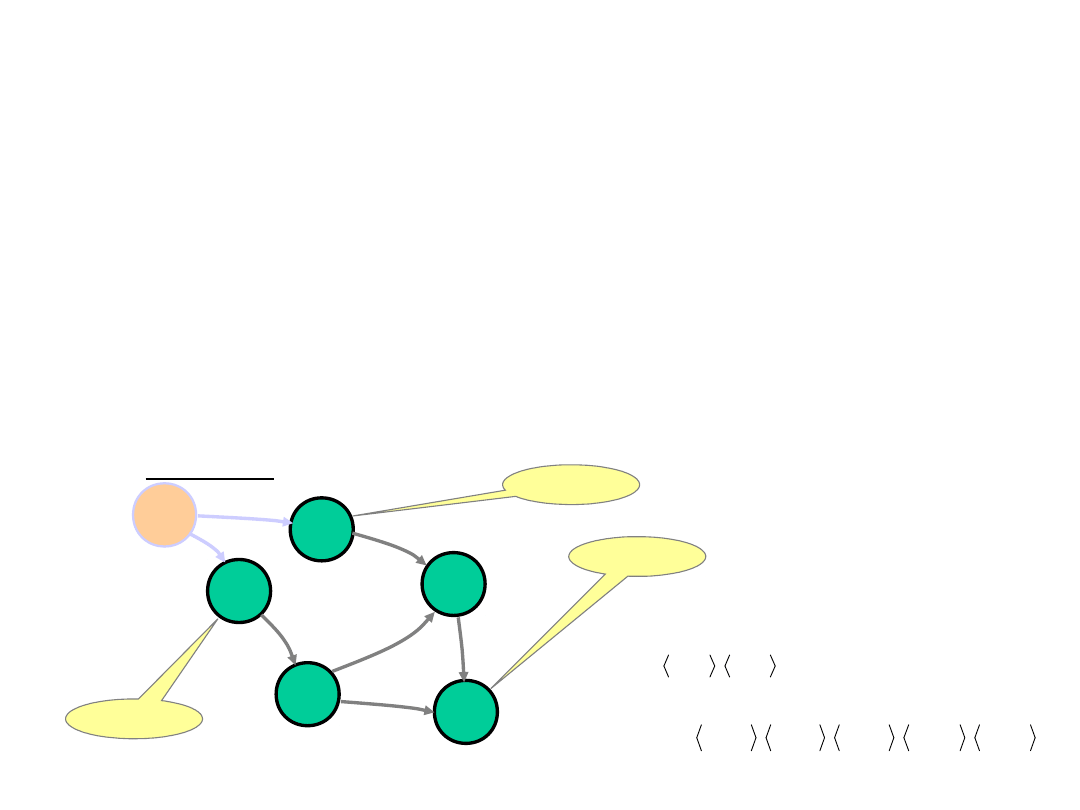
Model grafowy struktury danych

• Aby łatwiej zobrazować strukturę danych i w ten sposób

lepiej ją zrozumieć, można zbudować dla niej model grafowy.
W modelu tym:

– węzły (kółka) oznaczają poszczególne dane elementarne,
– łuki (strzałki) służą do odwzorowania następstw

poszczególnych danych elementarnych w strukturze S.

Przykład: Model grafowy dla opisywanej do tej pory struktury S:





5

4

3

2

1

,

,

,

,

d

d

d

d

d

D 





5

2

,

,

,

d

e

d

e

r

we







3

5

4

3

4

1

3

1

1

2

,

,

,

,

,

,

,

,

,

d

d

d

d

d

d

d

d

d

d

N 

e

d

2

d

5

d

1

d

3

d

4

liść

korzeń

korzeń

Drzewiaste struktury danych

Definicja 2.4:

Drzewiastą strukturą danych nazywamy strukturę danych

S=(D, R,

e)

, w której relacja porządkująca

N

opisuje kolejne, rekurencyjne

powiązania pomiędzy danymi elementarnymi drzewa, tworzącymi
kolejne „poddrzewa”.

Wniosek: Drzewo ze swojej natury jest strukturą hierarchiczną
(rekurencyjną). Niezwykle istotne jest tutaj odpowiednie
przypisanie danych elementarnych ze zbioru

D

do

kolejnych
poziomów drzewa i opisanie porządku w relacji

N

.

Drzewiaste struktury danych – kilka

pojęć podstawowych

• Korzeń drzewa – jest tylko i wyłącznie jeden korzeń dla drzewa.

Jest to dana wskazywana przez element wejściowy

e

,

• Liść drzewa – jest to dana elementarna, która nie posiada swojego

następnika w w sensie relacji

N

,

• Stopień drzewa – maksymalna liczba możliwych następników dla

dowolnego elementu drzewa. Najczęściej przyjmuje się,

że stopień drzewa jest potęgą liczby 2 (drzewa dwójkowe,

czwórkowe, ósemkowe, szesnastkowe),

• Droga w drzewie – kolejne łuki pomiędzy wskazanymi dwoma

elementami drzewa, które trzeba pokonać, aby dojść od

jednego elementu drzewa do innego

• Poziom drzewa – elementy ułożone w tej samej odległości

(długości drogi) od korzenia drzewa,

• Drzewo zupełne – takie drzewo, którego wszystkie elementy

(oprócz liści) mają taką liczbę następników, ile wynosi stopień

drzewa

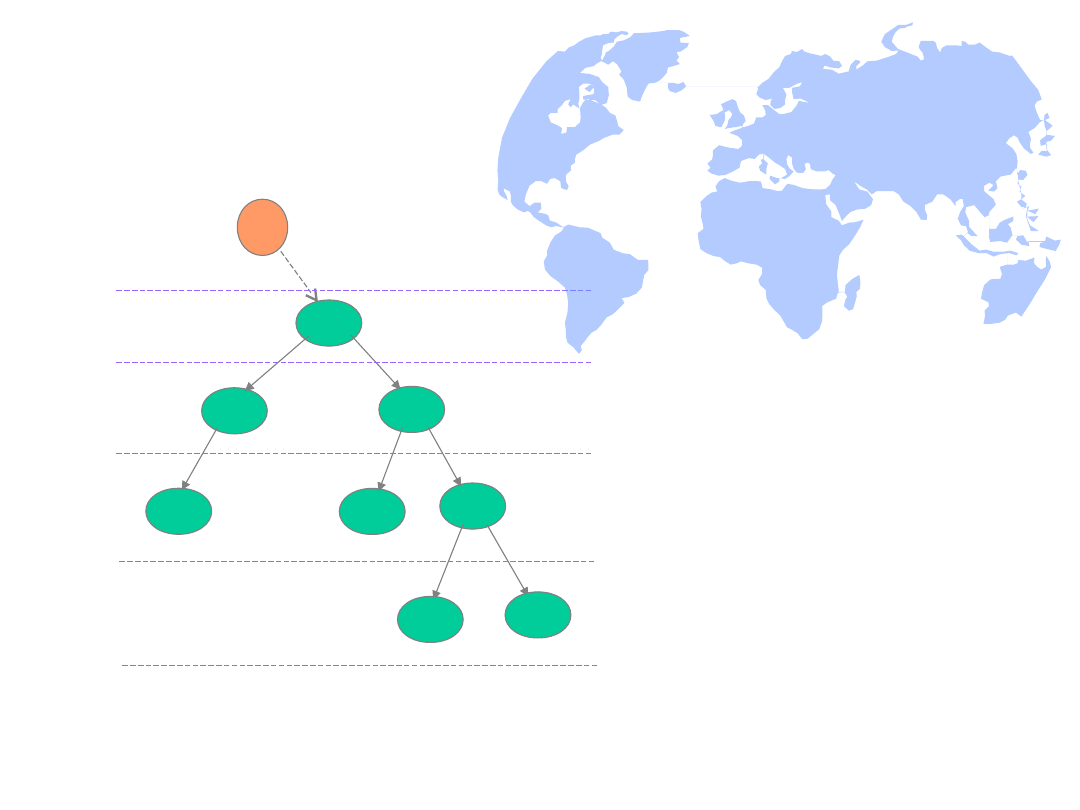
Przykład modelu grafowego drzewa

dwójkowego

(binarnego)

e

d1

d2

d3

d4

d5

d6

d7

d8

poziom 1

poziom 2

poziom 3

poziom 4

Dla powyższego drzewa: wskaż korzeń, liście, opisz zbiór D, relacje r

we

i N

Realizacje struktur danych

• Realizacje sekwencyjne (statyczne) - wtedy, gdy z góry

znamy maksymalny rozmiar przetwarzanej struktury liniowej i z

góry chcemy zarezerwować dla niej określony zasób (pamięć

operacyjne, pamięć zewnętrzna). W czasie wytwarzania

programów komputerowych bazujemy wtedy na zmiennych

statycznych,

• Realizacje łącznikowe (dynamiczne) - wtedy, gdy rozmiar

struktury nie jest z góry znany i w czasie jej przetwarzania

może istnieć konieczność dodawania do niej nowych elementów

lub ich usuwania. W czasie wytwarzania programów

komputerowych bazujemy wtedy na zmiennych dynamicznych

(wskaźnikowych),

• Realizacje łącznikowo-sekwencyjne (hybrydowe) -

połączenie obu powyższych metod - wtedy gdy konieczny jest

odpowiedni balans pomiędzy zmiennymi statycznymi i

dynamicznymi

Statyczna a dynamiczna struktura

danych

Statyczna struktura danych:

– Posiada z góry ustalony rozmiar (bez

możliwości jego zmiany);

– Jej deklaracja poprzedza uruchomienie

głównej procedury programu;

– Liczba zmiennych o typie statycznych musi

być z góry znana;

– Pamięć jest przydzielana na wstępie a

oddawana po zakończeniu programu;

Dynamiczne realizacje struktur

drzewiastych

• Zupełne drzewo binarne (dwójkowe):

– Każdy węzeł, z wyjątkiem liści, ma dokładnie dwóch potomków;

• Drzewo poszukiwań binarnych (BST):

– Dla każdego węzła (nie liścia) wszystkie wartości

przechowywane w lewym poddrzewie są mniejsze od jego

wartości oraz przeciwnie dla drzewa prawego;

• Drzewo AVL (1962 – Adelson-Velskii, Landis)

– Drzewo BST jest drzewem AVL wtedy, kiedy dla każdego

wierzchołka wysokości dwóch jego poddrzew różnią się o co

najwyżej 1 poziom;

• Kopiec

– Wartości przechowywane w potomkach każdego węzła są

mniejsze od wartości węźle;

– Drzewo jest szczelnie wypełniane od lewego poddrzewa;
– Liście leżą na co najwyżej dwóch sąsiednich poziomach;