1
1
2
Analiza matematyczna
sem. II
rok akademicki 1999/2000
dr Mariusz J.Wasilewski
Wykład 1
3
Geometria
analityczna cd.
4
1. Wybrane
powierzchnie stopnia
drugiego
Badaniem i analizą powierzchni
stopnia drugiego, których nazwa
pochodzi od stopnia równania
opisującego taką powierzchnię zajmuje
się
Geometria analityczna
.
1.1. Wstęp
5
Do najważniejszych powierzchni
stopnia drugiego należą
sfera
(
inaczej
powierzchnia kulista
)
,
oraz
tzw.
kwadryki.
Z kolei do ważnych kwadryk należą
stożek obrotowy,
paraboloida
obrotowa
i
walec kołowy,.
6
Sferą nazywamy zbiór punktów
przestrzeni
R
3
mających tę własność,
że odległość każdego z nich od
pewnego punktu
S(a,b,c)
, zwanego
środkiem sfery jest wielkością stałą. Tę
stałą wielkość nazywamy promieniem
sfery i oznaczamy literą
r
. Sferę
oznaczamy symbolicznie
K[S(a,b,c);r>0]
.
1.2. Sfera.
7
(x-a)
2
+ (y-b)
2
+ (z-c)
2
= r
2
. (1)
Niech
P(x,y,z)
będzie dowolnym
punktem sfery
K[S(a,b,c);r>0]
. Z
definicji i wzoru na odległość między
punktami
P
i
S
po podniesieniu
stronami do kwadratu otrzymujemy
równanie normalne sfery
8
Jeżeli w równaniu normalnym sfery
wykonamy wskazane działania
otrzymamy tzw.
rozwinięte równanie
sfery.
Oznaczając
A = -2a, B = -2b, C
= -2c
i D = a
2
+ b
2
+ c
2
- r
2
,
dostajemy
x
2
+ y
2
+ z
2
+ Ax + By + Cz + D = 0, (2)
przy warunku a
2
+ b
2
+ c
2
- D > 0.
9
Jeżeli warunek ten jest spełniony
wówczas równanie (2) przedstawia
sferę
10
Kulą
nazywamy sferę i jej wnętrze.
Kulę zapisujemy nierównościami
11
1.3. Wybrane
kwadryki
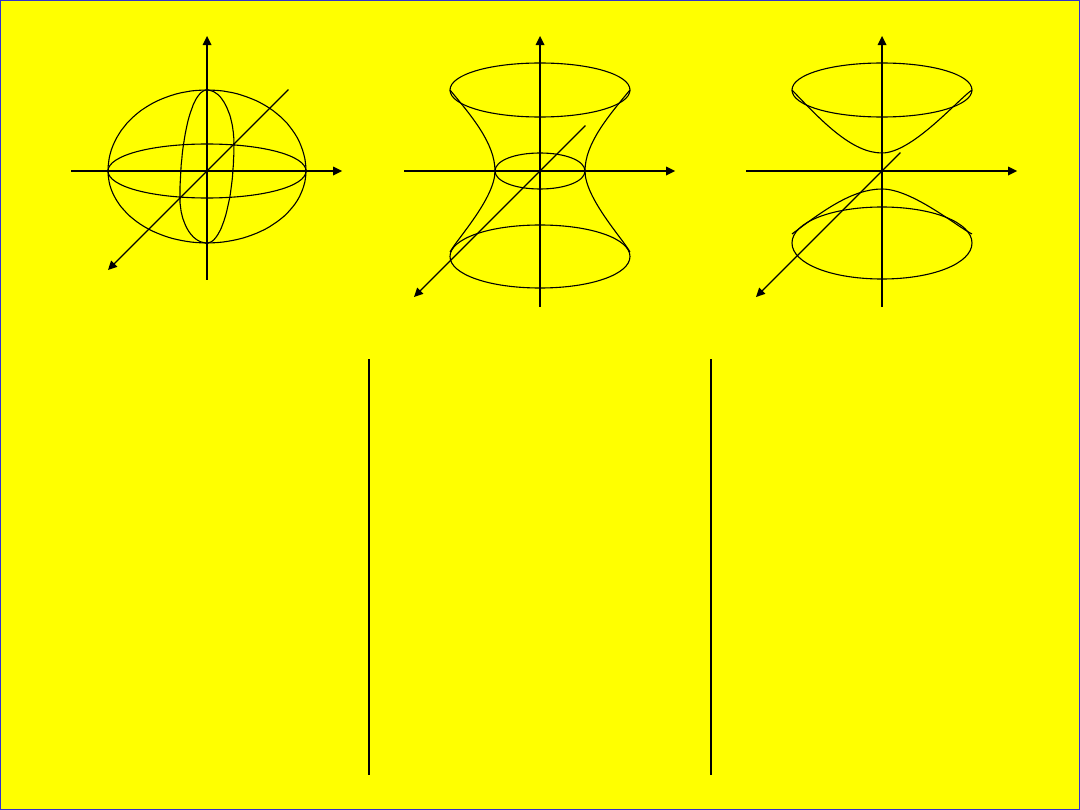
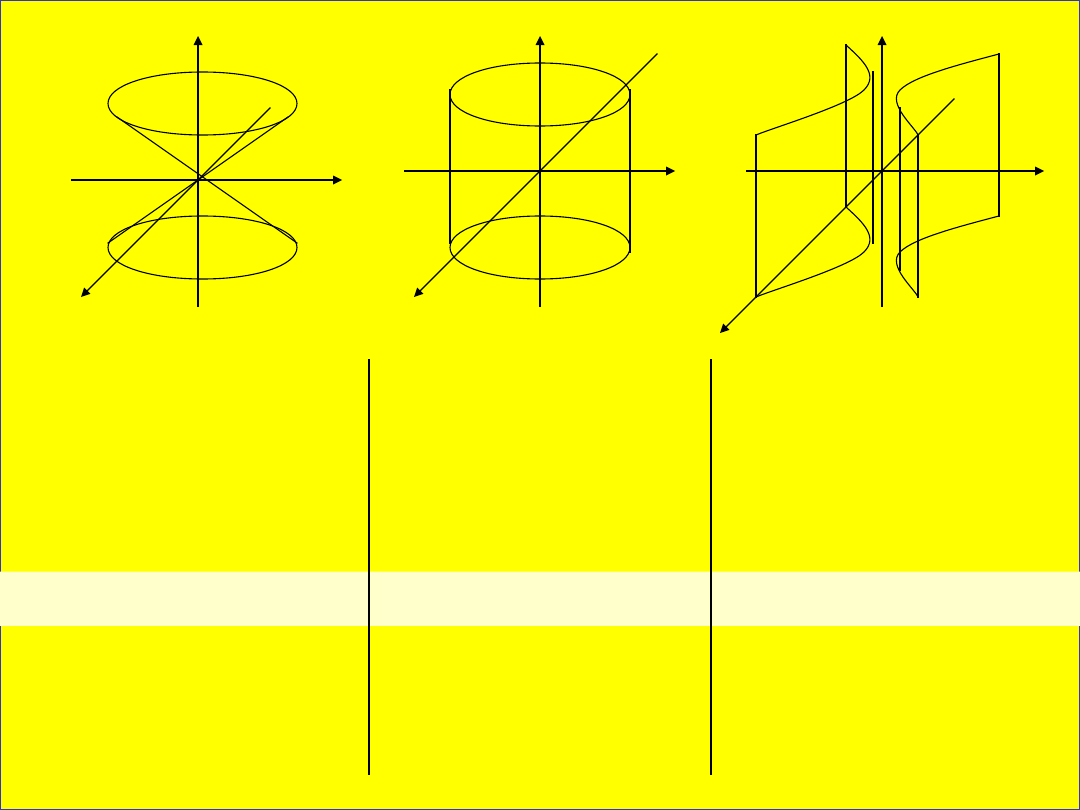
Kwadryki są to powierzchnie stopnia
drugiego charakteryzujące się tym, że
przekroje tych powierzchni są
krzywymi stożkowymi (elipsa,
hiperbola, parabola).
12
Badanie i rysowanie kwadryk, opisane
jest szczegółowo książce
„Elementy Algebry i Geometii
Analitycznej” - M.J.Wasilewski i
K.Lisiecki
.
13
z
x
y
x
y
z
x
y
14
z
x
y
z
x
y
z
x
y
15
z
x
y
z
x
y
z
x
y
16
z
x
y
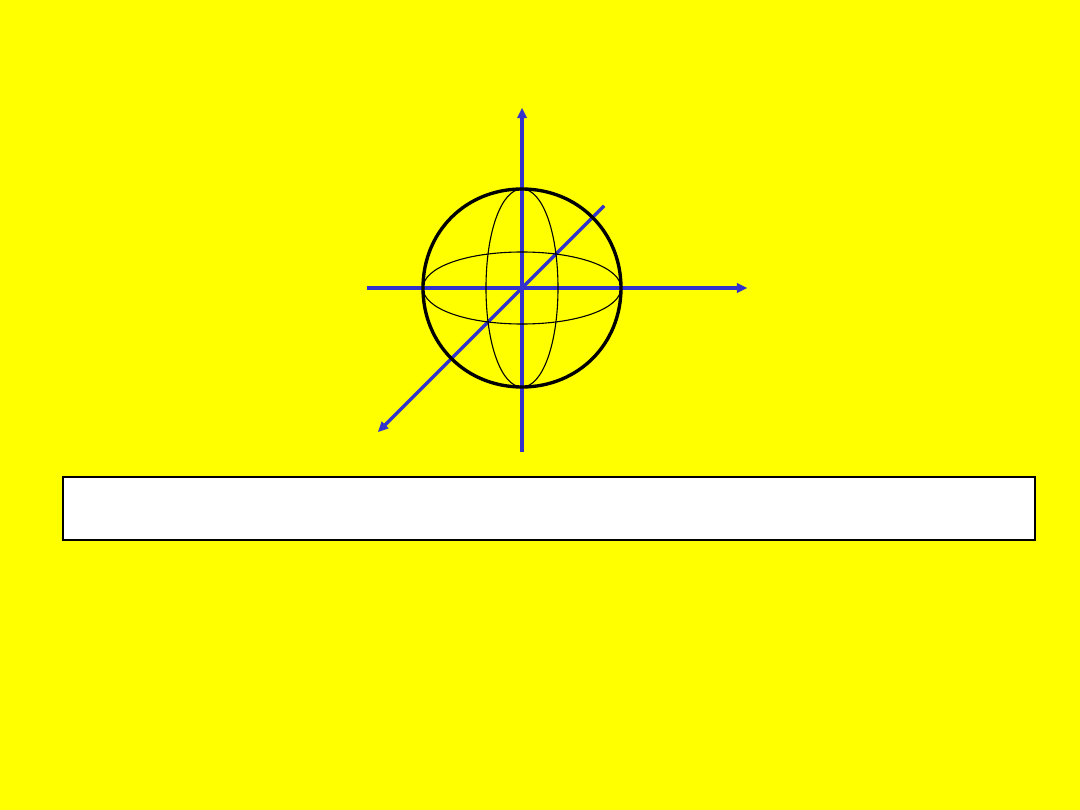
1.4.1. Sfera
(x-a)
2
+ (y-b)
2
+ (z-c)
2
= r
2
. (1)
Kula
17
z
x
y
1.4.2. Stożek obrotowy
x
2
+ y
2
- z
2
= 0.
18
z
x
y
1.4.3. Paraboloida obrotowa
z = x
2
+ y
2
19
z
x
y
1.4.4. Walec kołowy
x
2
+ y
2
= r
2
.
20
Analiza
matematyczna cd.
21
Funkcje wielu zmiennych.
Rachunek różniczkowy funkcji
wielu zmiennych.
22
2. Zbiory punktów na
płaszczyźnie
Nauczyć się z podręcznika :
2.1.
Definicje
:
•
Zbiór płaski.
• Zbiór płaski ograniczony
• Otoczenie kołowe punktu P
0
(,x
0
,y
0
)
o promieniu r
23
• Sąsiedztwo (otoczenie
pierścieniowe) punktu
P
0
(,x
0
,y
0
) o promieniu r
• Punkt wewnętrzny zbioru A
• Punkt zewnętrzny zbioru A
• Punkt brzegowy zbioru A
• Zbiór otwarty
• Zbiór spójny
24
•Obszar
•Punkt skupienia zbioru
•Brzeg zbioru
•Wnętrze zbioru
•Zewnętrze zbioru
•Obszar domknięty A* = A Č B
25
Punktem przestrzeni
n
-wymiarowej,
nazywamy ciąg
n
liczb
(x
1
,x
2
,...x
n
)
.
Liczby te nazywamy współrzędnymi
punktu przestrzeni
n
-wymiarowej.
3. Funkcje dwóch i wielu zmiennych.
3.1.
Definicje
26
•Jeżeli każdemu punktowi
P(x
1
,x
2
,...x
n
)
przestrzeni
n
-wymiarowej należącemu
do pewnego zbioru
A
przyporządkujemy dokładnie jedną
liczbę
z
, to mówimy, że na zbiorze
A
została określona funkcja
n
-
zmiennych niezależnych
x
1
,x
2
,...x
n
, co
zapisujemy
z = f (x
1
,x
2
,...x
n
) dla (x
1
,x
2
,...x
n
)
A,
lub z = f (P) dla P A.
Zmienną
z
nazywamy
zmienną zależną
.
27
•
Przy
n = 2
otrzymujemy definicję
funkcji dwu
zmiennych niezależnych
z= f (x,y) dla (x,y) A, lub z = f (P) dla P A
.
• Dziedziną funkcji
czyli
obszarem jej
określoności nazywamy zbiór
wszystkich
punktów
P
, dla których
f (P)
ma
sens.
28
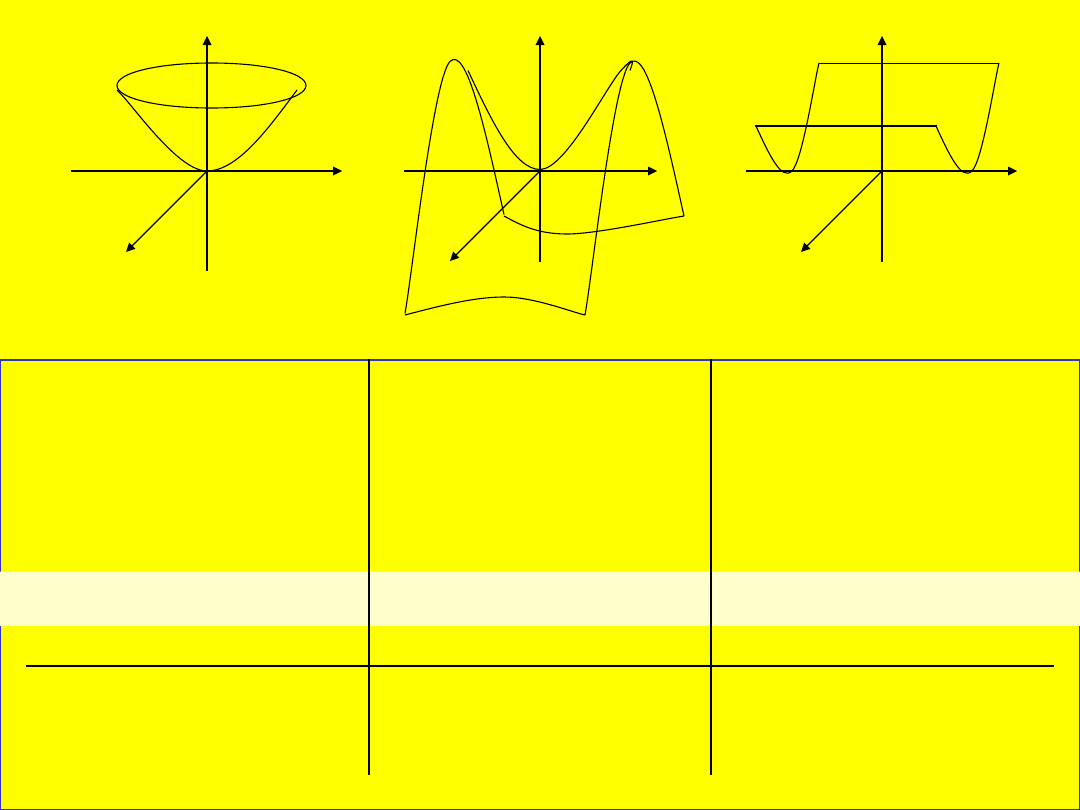
• Wykresem funkcji dwóch
zmiennych
niezależnych
z = f(x,y)
jest na
ogół pewna
powierzchnia, znajdująca się nad
lub/i pod
obszarem
D
będącym dziedziną
funkcji.
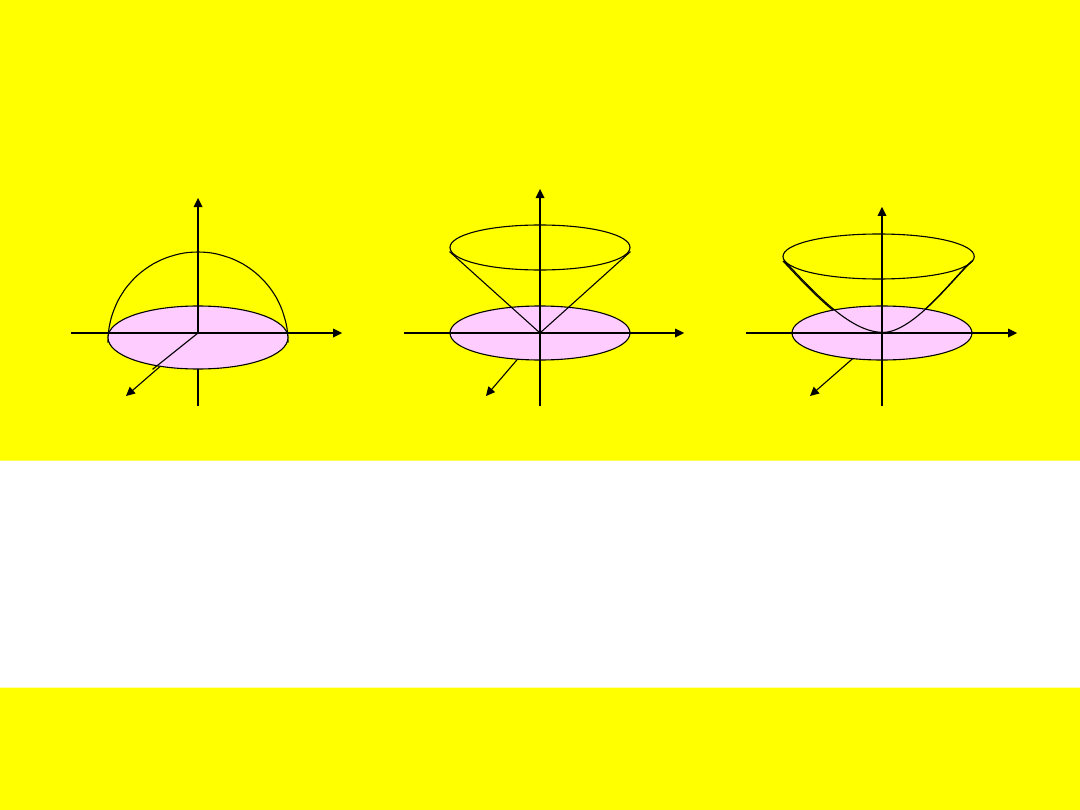
29
Górna półsfera Górny stożek
Paraboloida
obrotowa
z
x
y
z
x
y
z
x
y
A oto przykłady wykresów kilku funkcji.
30
Rozwiązanie
.
Dziedziną jest zbiór
tych punktów
P(x,y),
dla których wzór
określający funkcję ma sens, czyli
Przykład
. Wyznaczyć dziedzinę funkcji
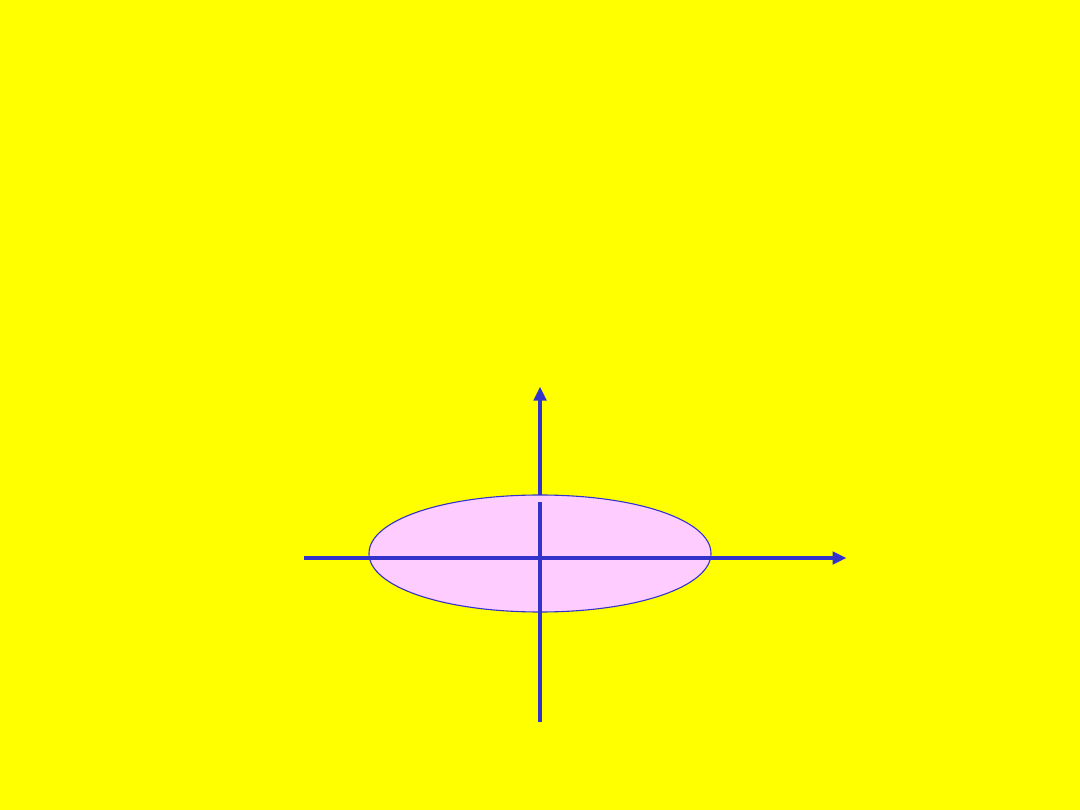
31
Jest to elipsa o półosiach
a=4
i
b=2
i jej wnętrze.
y
x
4
2
32
4. Granica i ciągłość funkcji
dwóch zmiennych
Nauczyć się z podręcznika następujących pojęć:
4.1. Definicja zbieżności ciągu
punktów na
płaszczyźnie .
4.2. Definicja granicy funkcji
Heinego.
4.3. Ciągłość funkcji wielu
zmiennych.
4.4. Własności funkcji ciągłych.
Zapoznać się z przykładami.
33
5. Pochodne cząstkowe
Pochodną cząstkową funkcji wielu
zmiennych
względem
jednej
zmiennej
nazywamy
zwykłą
pochodną tej funkcji przy założeniu,
że wszystkie pozostałe zmienne są
stałe.
5.1.
Definicja pochodnej cząstkowej
34
Wynika stąd, że wszystkie poznane
wcześniej twierdzenia i wzory
rachunku różniczkowego dla funkcji
jednej zmiennej obowiązują również
przy obliczaniu pochodnych
cząstkowych.
35
Aby obliczyć pochodną cząstkową
funkcji dwóch zmiennych
z=f(x,y)
względem zmiennej
x
, należy ustalić
wartość drugiej zmiennej np.
y= y
0
, a
następnie obliczyć pochodną funkcji
z=f(x,y
0
),
jednej zmiennej
x
(jeżeli
istnieje). Z definicji pochodnej funkcji
jednej zmiennej x w punkcie
x=x
0
mamy
36
Podobnie
definiujemy
pochodną
funkcji
z=f(x,y)
względem zmiennej
y
.
Należy
ustalić
wartość
drugiej
zmiennej np.
x=x
0
, a następnie obliczyć
pochodną funkcji
z=f(x
0
,y),
jednej
zmiennej
y
(jeżeli istnieje). Z definicji
pochodnej funkcji jednej zmiennej y w
punkcie
y=y
0
mamy
37
Pochodną cząstkową funkcji
z=f(x,y)
względem zmiennej
x
możemy
oznaczać różnymi symbolami np.
Podobnie oznaczamy pochodne
cząstkowe tej funkcji względem
zmiennej
y
.
38
Rozwiązanie.
f
x
’=2xe
yz
+z
3
+3cos(3x+2y),
f
y
’= x
2
e
yz
z+2cos(3x+2y), f
z
’= x
2
e
yz
y+3xz
2
Wedle tej samej zasady oznaczamy
pochodne cząstkowe funkcji o większej
liczbie zmiennych.
Przykład.
Obliczyć pochodne
cząstkowe rzędu pierwszego funkcji
39
5.2 Interpretacja geometryczna
pochodnej cząstkowej.
Przy obliczaniu pochodnej
cząstkowej względem
x
funkcji
z=f(x,y)
zmienną
y
ustalamy
przyjmując
y=y
0
. Oznacza to, że
obliczamy zwykłą pochodną funkcji
z=f(x,y
0
),
której wykresem jest linia
o równaniach
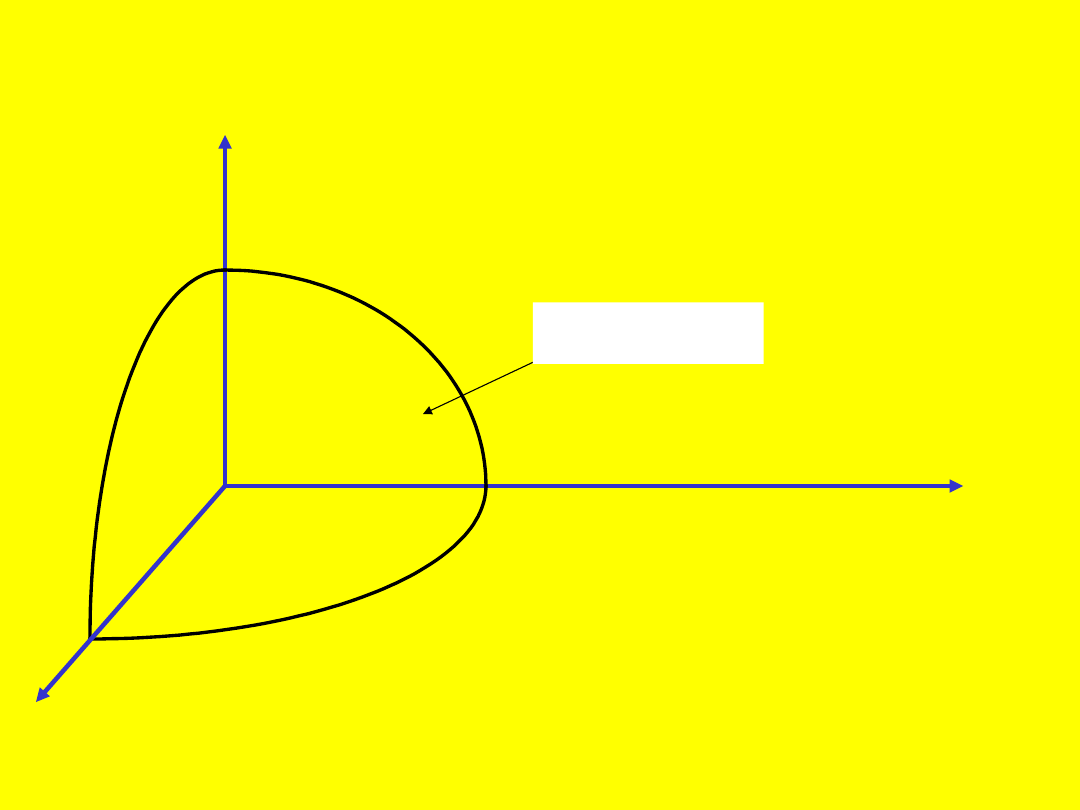
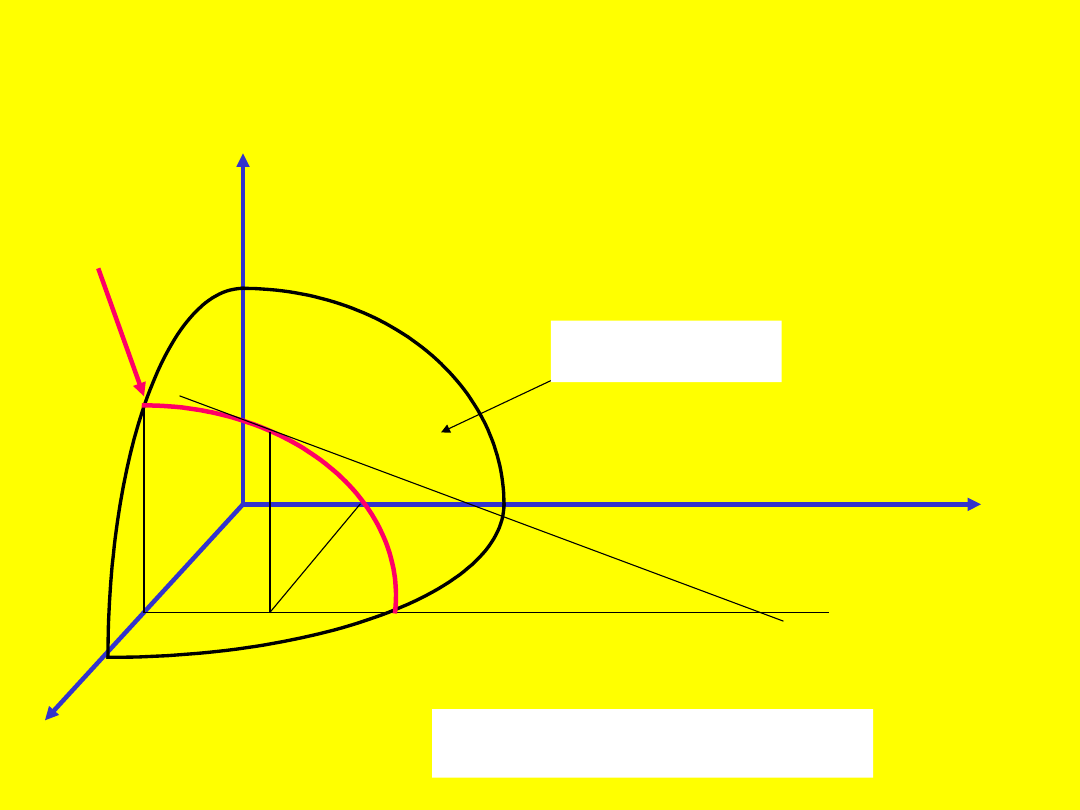
40
z
x
z = f(x,y)
y
41
z
x
y
x
0
y
0
z = f(x,y)
f
x
’(x
0
,y
0
) = tg
Linia ta jest częścią wspólną wykresu
funkcji
z=f(x,y)
i płaszczyzny
y=y
0
.
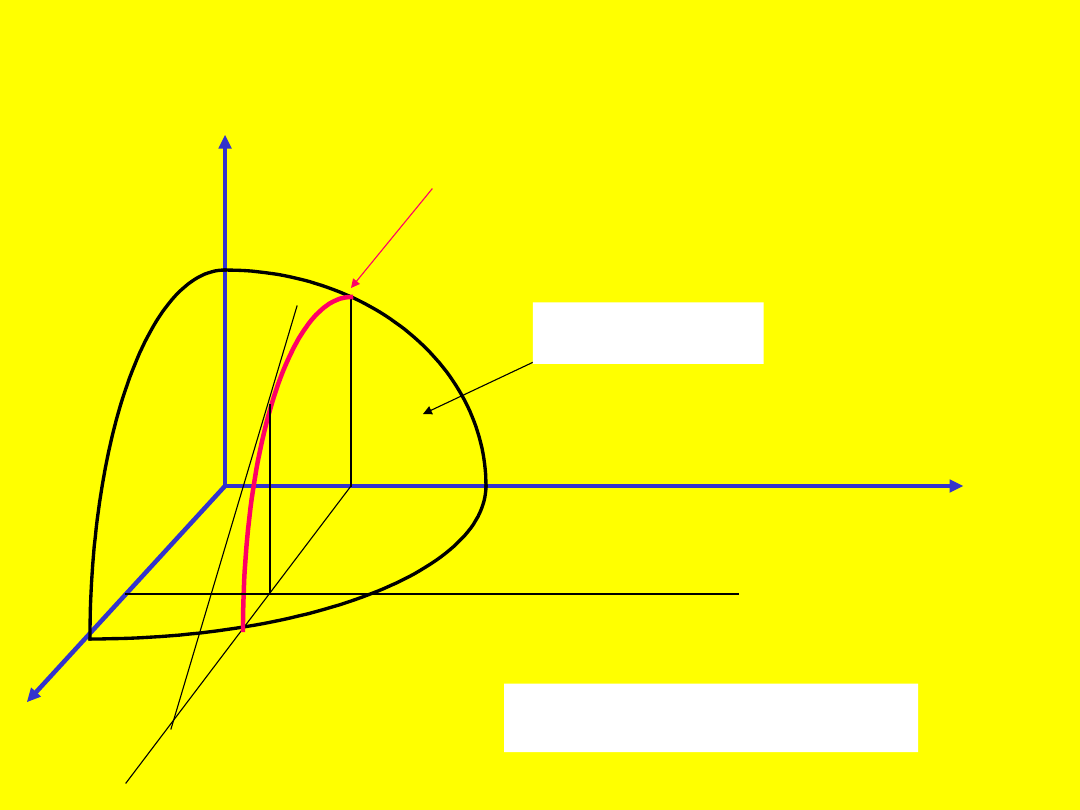
42
z
x
y
x
0
z = f(x,y)
f
y
’(x
0
,y
0
) = tg
y
0
43
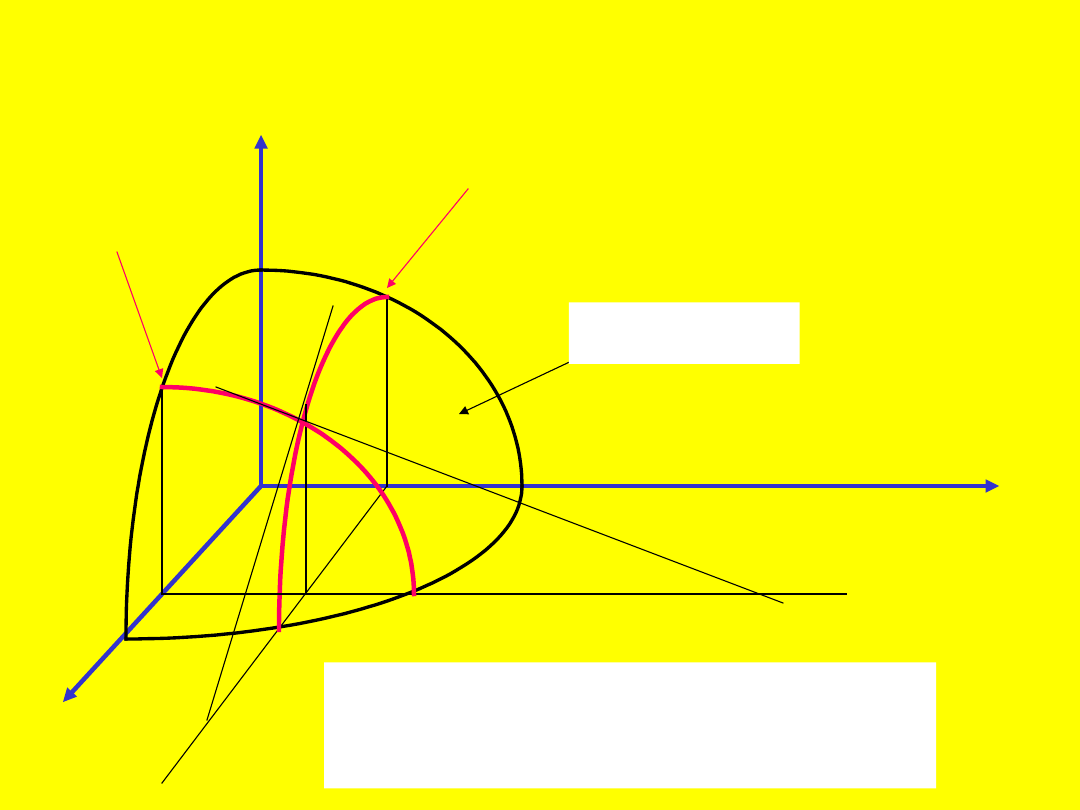
z
x
y
x
0
y
0
z = f(x,y)
f
x
’(x
0
,y
0
) = tg
f
y
’(x
0
,y
0
) = tg
44
6. Różniczka zupełna
funkcji dwóch zmiennych.
Niech
P
0
(x
0
,y
0
)
będzie punktem
należącym do dziedziny
D
funkcji
z
= f(x,y)
, w którym ma ona pochodne
cząstkowe w
f
x
’
i
f
y
’
.
45
Definicja
.
Różniczką funkcji
z =
f(x,y)
punkcie
P
0
(x
0
,y
0
)
dla
przyrostów
dx
i
dy
nazywamy
wyrażenie
46
7. Pochodne i różniczki rzędów
wyższych
Pochodne cząstkowe
są też
funkcjami zmiennych
x
i
y
. Ich
pochodne nazywamy pochodnymi
cząstkowymi rzędu drugiego funkcji
f(x,y)
i oznaczamy je symbolami
47
yx
xx
2
2
2
"
f
"
f
lub
,
x
y
f
y
f
x
,
x
f
x
f
x
48
Pochodne
f”
xy
i
f”
yx
nazywamy
pochodnymi mieszanymi rzędu
drugiego.
Twierdzenie Schwarza
Jeżeli pochodne mieszane
f”
xy
i
f”
yx
istnieją i są w pewnym punkcie
ciągłe,
to są w tym punkcie równe.
49
Ogólnie
• pochodnymi cząstkowymi rzędu
n
nazywamy pierwsze pochodne
cząstkowe pochodnych rzędu
n-1
.
•różniczką rzędu
n
funkcji
nazywamy różniczkę różniczki
rzędu
n-1
.
50
8. Pochodna w kierunku
Niech
s
oznacza półoś o równaniach
Półoś
s
wychodzi z punktu
P
0
(x
0
,y
0
)
i
tworzy z osiami
Ox
i
Oy
odpowiednio
kąty
i
.
51
Definicja
. Pochodną cząstkową funkcji
z = f(x,y)
w punkcie
P
0
(x
0
,y
0
)
w
kierunku osi
s
nazywamy granicę
prawostronną ilorazu różnicowego o
ile istnieje
52
Twierdzenie
. Jeżeli funkcja
z =
f(x,y)
ma w otoczeniu punktu
P
0
(x
0
,y
0
)
ciągłe pochodne cząstkowe
f/x
i
f/y
to pochodna
f/s
wyraża się wzorem
53
Koniec wykładu