BADANIA OPERACYJNE

opracowanie na podstawie „Metody wspomagające podejmowanie decyzji

w zarządzaniu” D. Witkowska, Menadżer Łódź 2000.

dr inż. Iwona Staniec

p. 334 Lodex

http://www.oizet.p.lodz.pl/istan

[e-mail]

zasady zaliczenia

przedmiotu



wykład pisemne kolokwium



Laboratorium praktyczne rozwiązanie postawionego

problemu (możliwa tylko jedna nieobecność)



III terminy



na każdym kolejnym terminie ocena to średnia

arytmetyczna z uzyskanych ocen



zaliczenie to średnia ważona z laboratorium z wagą

0,5 i wykładu 0,5



niezaliczenie w III terminie skutkuje powtarzaniem

całości przedmiotu



przepisywanie ocen- brak takiej możliwości

Literatura



Jędrzejczyk Z., Skrzypek J., Kukuła K., Walkosz

A. [2002]: Badania operacyjne w przykładach

i zadaniach, PWN, Warszawa.



Karwacki Z., Konarzewska I. [1997]: Elementy

teorii podejmowania decyzji, Absolwent,

Łódź.



Sikora W. (red.) [2008] Badania operacyjne

PWE Warszawa.



Łapińska-Sobczak N. (red.) [1998]: Modele

optymalizacyjne, Uniwersytet Łódzki, Łódź.



Ignasiak E. (red.) [2001] Badania operacyjne

PWE ,Warszawa.

Literatua cd.



Radzikowski W. [1997]: Badania operacyjne

w zarządzaniu

przedsiębiorstwem,

Toruńska Szkoła Zarządzania, Toruń.



Witkowska

D.

[2000]:

Metody

wspomagające podejmowanie decyzji w

zarządzaniu, Menadżer, Łódź.



Witkowska D. [2001]: Zbiór zadań z badań

operacyjnych, Menadżer, Łódź.



Krawczyk

S.

[1997]

Badania

operacyjne dla menedżerów, Wyd. AE

we Wrocławiu, Wrocław

Badania operacyjne
(ang. Operation
Research)



wyznaczanie optymalnych rozwiązań

różnorodnych problemów, głównie
technicznych, organizacyjnych,
ekonomicznych, wojskowych, za
pomocą zespołu metod
matematyczno-statystycznych



Badania operacyjne (BO) — nauka o
podejmowaniu decyzji

Cel badań operacyjnych



doskonalenie przyszłości przez
poprawę podejmowanych decyzji
(ang. Decision Making) na
podstawie znajomości
rzeczywistości

Obszar wiedzy
wykorzystywanej w BO

EKONOMIA

MATEMATYKA

STATYSTYKA

EM

SM

SE

BO

Zakres tematyczny



Budowa modeli decyzyjnych



Metoda graficzna



Metoda simpleks



Algorytm transportowy



Programowanie sieciowe

– Analiza ścieżki krytycznej CPM
– Analiza PERT



Teoria gier



Teoria kolejek



Programowanie dynamiczne

Historia rozwoju badań
operacyjnych



dostępność profesjonalnych
programów optymalizacyjnych



dostępność profesjonalnych BAZ
DANYCH



tworzenie systemów wspomagania
decyzji



rozwój metod analizy wrażliwości

Rodzaje decyzji podejmowanych przez
menedżerów

• niewykonalne (niedopuszczalne)
• wykonalne (dopuszczalne):

— optymalne

— nieoptymalne

zbiór
wszystkich
decyzji

decyzje

niedopuszczalne

decyzje

dopuszczaln
e

decyzja
optymalna

Kryterium optymalności:

•

maksymalizacja efektu

maksymalizacja efektu

(finansowego, zwykle zysku), np. jak
najdalej zajechać na kuli ziemskiej za
posiadaną kwotę

•

minimalizacja nakładów

minimalizacja nakładów (zwykle

kosztów), np. zajechać jak najtaniej
do Indii

Problem decyzyjny
charakteryzują
następujące czynniki



decydent (osoba lub grupa osób), który
ma rozwiązać jakiś problem,



cel,

który

zamierza

decydent

zrealizować,



co najmniej dwa różne sposoby działania
prowadzące do zamierzonego celu,



środowisko,

określające

warunki

działania.

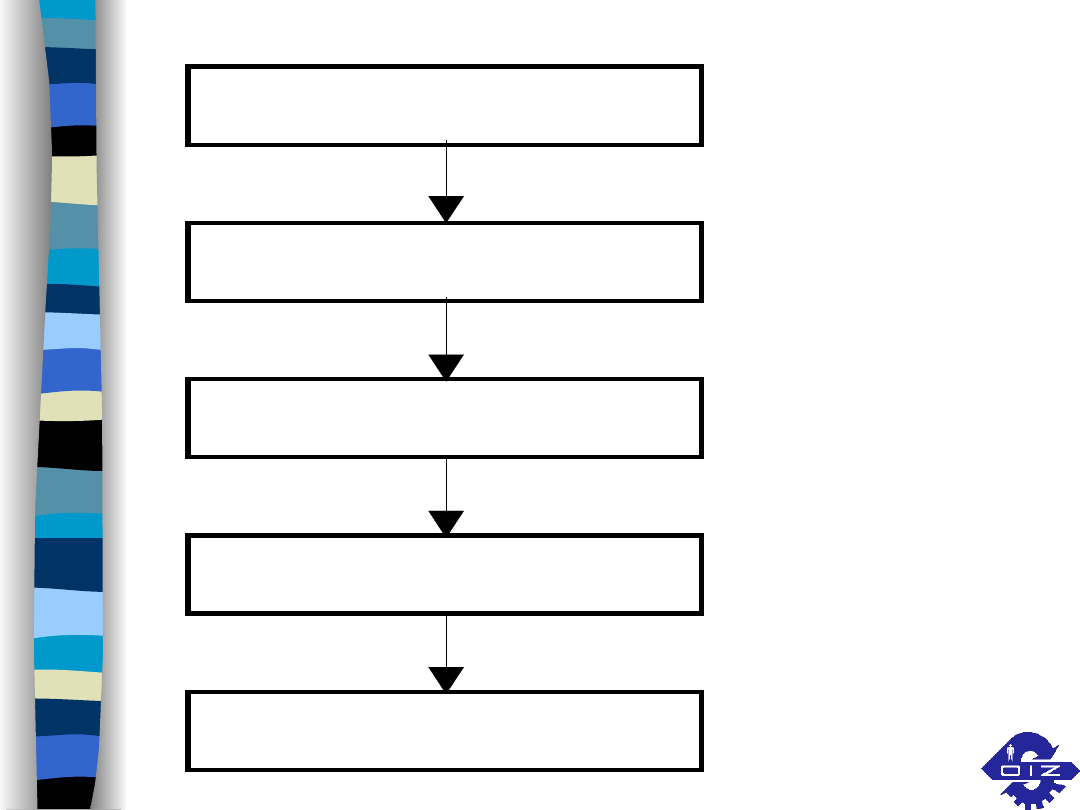
Sformułowanie

problemu decyzyjnego

Budowa modelu

matematycznego

Rozwiązanie

zadania

Weryfikacja modelu

i uzyskanie rozwiązania

Zastosowanie rozwiązania

po jego weryfikacji

Budując model
decyzyjny należy:



zdefiniować

zmienne

decyzyjne

charakteryzujące poszczególne decyzje,



określić kryterium oceny (wyboru) decyzji  w

postaci funkcji matematycznej, która będzie

maksymalizowana lub minimalizowana,



określić warunki w jakich będą podejmowane

decyzje w postaci ograniczeń równościowych

lub nierównościowych,



wyznaczyć

parametry

warunków

ograniczających oraz funkcji kryterium,

Model decyzyjny c.d.



sformułować model decyzyjny, czyli zapisać
w sformalizowany sposób ograniczenia i
kryterium wyboru decyzji,



przeprowadzić

weryfikację

modelu

polegającą

na

sprawdzeniu

czy

wprowadzone zmienne decyzyjne zostały
odpowiednio zdefiniowane i są istotne, a ich
lista kompletna, a także czy warunki
ograniczające

oraz

funkcja

kryterium

zostały poprawnie sformułowane.

W literaturze przedmiotu wyróżnia się

trzy podstawowe sytuacje, w których
podejmowane są decyzje, którymi są
warunki:



pewności, jeśli każde działanie prowadzi do
jednego z góry wiadomego wyniku,



ryzyka, kiedy każde działanie prowadzi do
pewnego znanego zbioru wyników o znanym
prawdopodobieństwie realizacji każdego z
nich,



niepewności, jeżeli wynikiem działań jest
zbiór określonych możliwych wyników o
nieznanym

prawdopodobieństwie

pojawienia się.

Rodzaje modeli
decyzyjnych (w
zależności od sytuacji
decydenta)



deterministyczne

•

probabilistyczne

•

statystyczne

stochastyczne

•

strategiczne

Zapis

matematyczny

modelu liniowego

c x

T

 max

Ax b



x 0



c x

T

 min

Ax b



x 0





gdzie:





n

T

x

x

x

...

2

1



x

- wektor zmiennych decyzyjnych, (np. wielkości
produkcji j-tego wyrobu),





n

T

c

c

c

...

2

1



c

wektor parametrów funkcji celu, (np. c

j

-

jednostkowy zysk na j-tym wyrobie w modelach
maksymalizujących funkcję kryterium lub c

j

-

jednostkowy koszt produkcji j-tego wyrobu
w modelach minimalizujących funkcję
kryterium),























mn

m

n

a

a

a

a

....

...

...

...

...

1

1

11

A





m

T

b

b

b

...

2

1



b

macierz parametrów (np. normatywy zużycia
i-tego surowaca i=1,...,m na jednostkę j-tego
wyrobu j=1,2,...,n),

wektor ograniczeń (np. b

i

- zasób i-tego

surowca).

Warunki brzegowe

x 0



C

x

j



W wielu jednak przypadkach warunki
ograniczające należy uzupełnić warunkami
całoliczbowości

lub warunkiem gwarantującym przyjmowanie
przez

zmienne

decyzyjne

tylko

wartości

binarnych.

 

1

,

0



j

x

Uwaga!

W przypadku modeli programowania liniowego

z uzupełnionymi warunkami brzegowymi
rozwiązanie wyznacza się dwu etapowo.

W pierwszym etapie rozwiązuje się zadanie za

pomocą znanych metod i sprawdza się, czy
spełnione są warunki całoliczbowości.

Jeżeli nie, to w drugim etapie stosuje się

odpowiednie metody pozwalające na
otrzymanie rozwiązania spełniającego
dodatkowe warunki brzegowe.

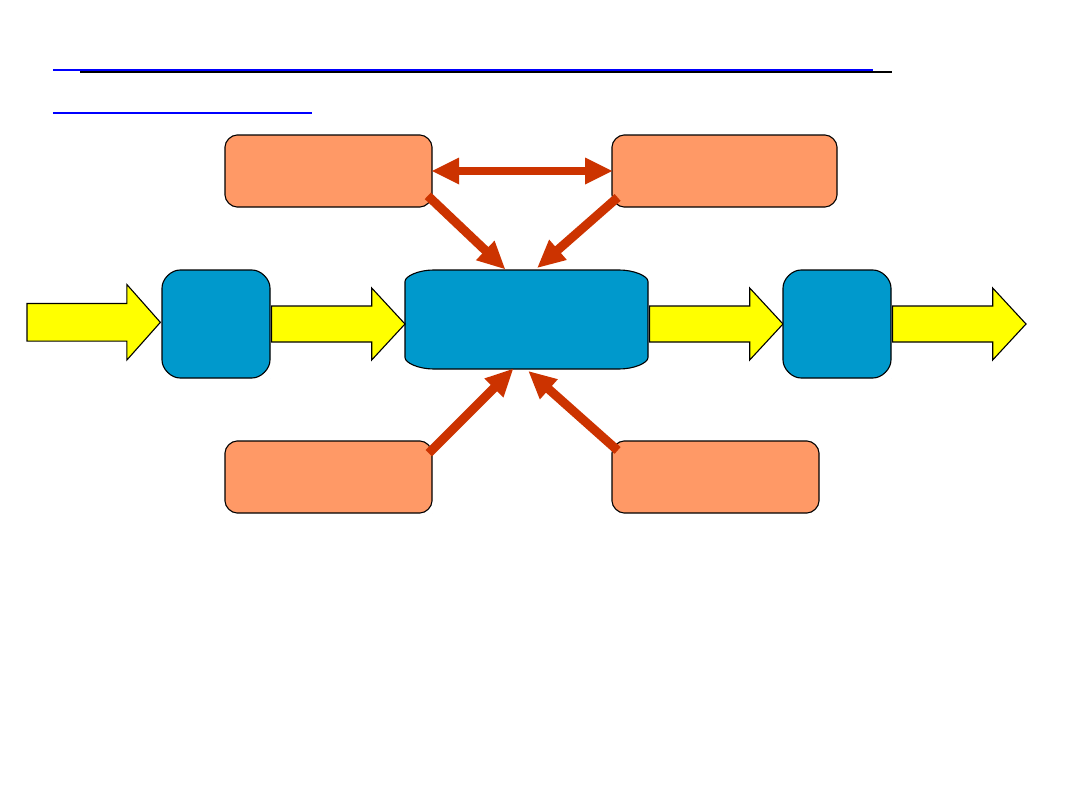
Dziesięć zastosowań BO w przedsiębiorstwie
produkcyjnym

PRODUKCJA

TRANSPORT

TRANSPORT

TRANSPORT

TRANSPORT

MAGAZYN
SUROW-
CÓW

MAGAZYN
WYRO-
BÓW

ZAOPATRZENIE — JIT

ZBYT

NAPRAWY BIEŻĄCE

REMONTY

PRACE ROZWOJOWE

INWESTYCJE



 ALOKACJA KAPITAŁU

 ALOKACJA ŚRODKÓW PRODUKCJI

 PROBLEM MIESZANKI (DIETY)

 ZAGADNIENIA TRANSPORTOWE

 ZARZĄDZANIE ZAPASAMI

 













 ZAGADNIENIE WYMIANY

 PLANOWANIE PRZEDS. NIEPR.

 TEORIA KOLEJEK (M. OBSŁUGI)

 TEORIA DECYZJI, TEORIA GIER

 SYMULACJA KOMPUTEROWA





















Wybór asortymentu
produkcji

Przedsiębiorstwo posiada m różnych środków produkcji

bvhbnnn

odpowiednio w ilościach: W ramach posiadanych

zasobów firma jest w stanie produkować n różnych wyrobów. Na
wytworzenie jednostki wyrobu j-tego rodzaju (j = 1, 2, ..., n)
potrzeba zużyć a

ij

jednostek i-tego czynnika produkcji (i = 1, 2, ...,

m), np. wyrażonych za pomocą przepracowanych roboczogodzin,
czasu maszyn potrzebnego do wytworzenia jednostki produktu
lub ilości zużytych surowców, stanowiących normatywy zużycia
środków produkcji. Wiadomo też, że zyski jednostkowe osiągane
przez firmę na każdym produkcie wynoszą odpowiednio
Należy zbudować taki plan produkcji, który pozwoli na
maksymalizację zysków.

m

S

S

S

,...,

,

2

1

m

b

b

b

,...,

,

2

1

n

c

c

c

,...,

,

2

1

Budowa modelu



Zmienne decyzyjne -

ilości (liczba)

produkowanych wyrobów z każdego
rodzaju asortymentu (j = 1, 2, ..., n)



Warunki brzegowe



Warunki ograniczające

(i = 1, 2, ..., m)



Funkcja celu

j

x

0



j

x

i

j

n

j

ij

b

x

a





1

max

1







j

n

j

j

x

c

Zagadnienie optymalnego
wykroju

Załóżmy, że do produkcji potrzebnych jest m różnych
detali wykrawanych z jednolitego surowca. Zgodnie z
otrzymanymi przez firmę zamówieniami ustalono, że
należy wyciąć b

i

detali i-tego typu (i = 1, 2, ..., m).

Przy cięciu arkusza blachy j-tym sposobem otrzymuje
się a

ij

detali i-tego rodzaju i powstaje przy tym odpad,

którego wielkość oszacowano na c

j

jednostek.

Wyznaczyć optymalny program cięcia minimalizujący
łączny odpad i pozwalający wykonać przyjęte
zamówienia.

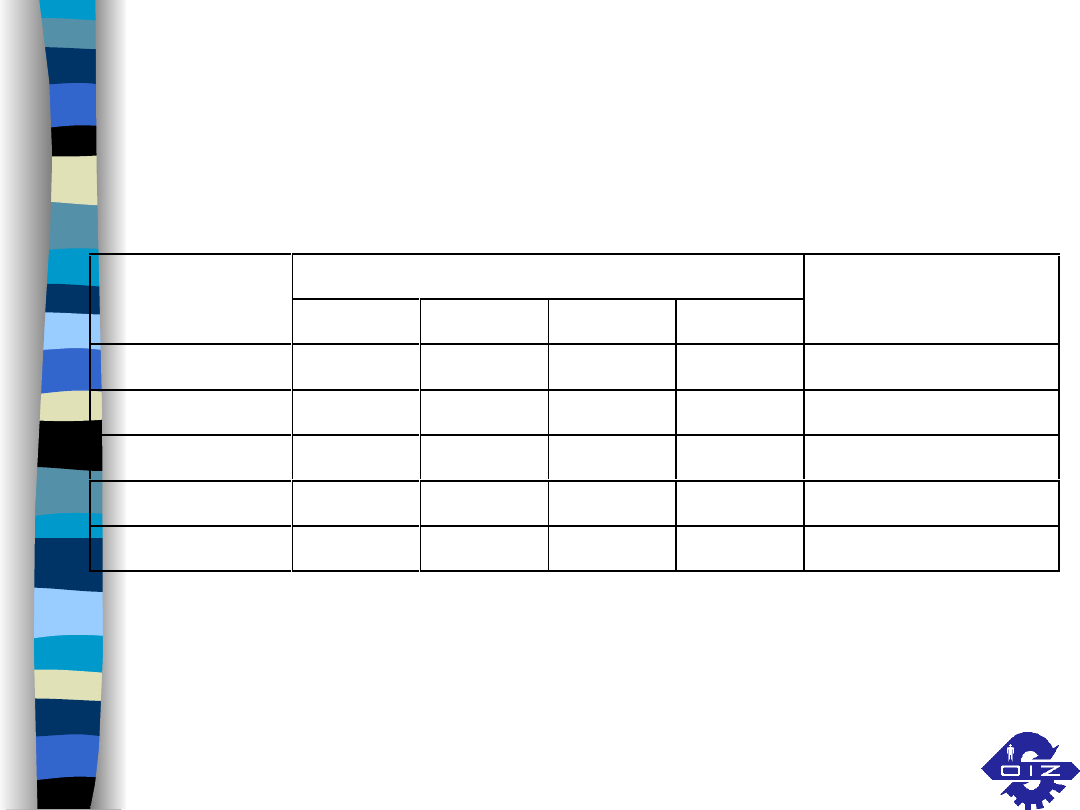
Detale

Sposoby cięcia

Minimalna

i-tego typu

j = 1

j = 2

...

j = s

liczba detali

1

a11

a12

...

a1s

b1

2

a21

a22

...

a2s

b2

...

...

...

...

...

...

m

am1

am2

...

ams

bm

Odpady

c1

c2

...

cs

Sposoby cięcia

Budowa modelu



Zmienne decyzyjne -

liczbę arkuszy, z

których wycinać się będzie detale j-tym
sposobem (j = 1, 2, ..., s)



Warunki brzegowe



Warunki ograniczające

(i = 1, 2, ..., m)



Funkcja celu

j

x

0



j

x

C

x

j



i

j

s

j

ij

b

x

a





1

min

1







j

s

j

j

x

c

Problem załadunku (plecaka)



Wybierając się na wycieczkę chcemy zabrać m rzeczy, o
objętości a

j

każda (j = 1, 2, ..., m), czyli łączna objętość

pakowanych przedmiotów wynosi



Wszystko to należy spakować do plecaka, którego pojemność
wynosi b, przy czym b<



Pojawia się więc konieczność rezygnacji z  jednego lub kilku
przedmiotów. Wiedząc, że należy spakować przynamniej d
przedmiotów, dokonaj wyboru rzeczy, które należy spakować
przyjmując jako kryterium wyboru:



1. jak najlepsze wykorzystanie miejsca w plecaku,



2.spakowanie przedmiotów najbardziej niezbędnych,



3. spakowanie jak największej liczby przedmiotów.





m

j

j

a

1





m

j

j

a

1

Budowa modelu



Zmienne decyzyjne -

decyzja o

zapakowaniu j-tego przedmiotu (j = 1,
2, ..., m)



Warunki brzegowe



Warunki ograniczające

j

x

b

x

a

j

m

j

j





1

d

x

m

j

j





1

 

1

,

0



j

x













plecaka

do

pakujemy

nie

przedmiotu

tego

plecaka

do

pakujemy

przedmiot

ty

0

1

j

j

x

j

Funkcja celu



jak najlepsze wykorzystanie miejsca w plecaku, co
oznacza, że minimalizowana jest pojemność plecaka,
która nie zostanie wykorzystana



spakowanie przedmiotów najbardziej niezbędnych,



gdzie c

j

jest wyrażonym w punktach poziomem użyteczności

poszczególnych przedmiotów przyjmuje się, że czym wyższy
poziom użyteczności tym c

j

większe



spakowanie jak największej liczby przedmiotów

min

1









j

m

j

j

x

a

b

max

1







j

m

j

j

x

c

max

1







m

j

j

x

Zadanie transportowe

Danych jest m dostawców, u których znajduje się

odpowiednio: jednostek towaru. Ładunek
ten powinien zostać dostarczony do n odbiorców,
którzy zgłosili zapotrzebowanie w ilościach
odpowiednio: jednostek. Wiadomo jest,
że koszty jednostkowe transportu od i-tego
dostawcy do j-tego odbiorcy wynoszą c

ij

(i = 1, 2, ...,

m,
j = 1, 2, ..., n). Należy wyznaczyć taki plan
przewozów, aby łączne koszty transportu były
minimalne.

m

a

a

a

,...,

,

2

1

n

b

b

b

,...,

,

2

1

Budowa modelu



Zmienne decyzyjne

























mn

m

m

n

n

x

x

x

x

x

x

x

x

x

...

...

...

...

...

...

...

2

1

2

22

21

1

12

11

•Warunki ograniczające











n

j

j

m

i

i

b

a

1

1

j

m

i

ij

b

x 



1

(j = 1, 2, ..., n)

i

n

j

ij

a

x 



1

(i = 1, 2, ..., m)



Funkcja celu



Warunki
brzegowe

min

1

1









ij

m

i

n

j

ij

x

c

x

ij

>=0











n

j

j

m

i

i

b

a

1

1

i

n

j

ij

a

x 



1

(i = 1, 2, ...,
m)

j

m

i

ij

b

x 



1

(j = 1, 2, ...,
n)











n

j

j

m

i

i

b

a

1

1

i

n

j

ij

a

x 



1

(i = 1, 2, ..., m)

j

m

i

ij

b

x 



1

(j = 1, 2, ..., n)