
Wykład 5
Protekcja błędów
1. Przestrzeń Hamminga
2. Detekcja i korekcja błędów
3. Kod z kontrolą parzystości
4. Kody cykliczne
5. Korekcja pojedynczych błędów
6. Kod z podwójną kontrolą
parzystości
7. Kod Hamminga
8. Korekcja błędów
wielokrotnych
TD5-1 / 29

Przestrzeń
Hamminga
TD5-2 / 29
Kodowanie detekcyjne i korekcyjne
w przestrzeni Hamminga
Idea detekcji i korekcji
TD5-3 / 29
Kod detekcyjny – wykrywający do k
przekłamań.
Kod korekcyjny – korygujący do k
przekłamań.
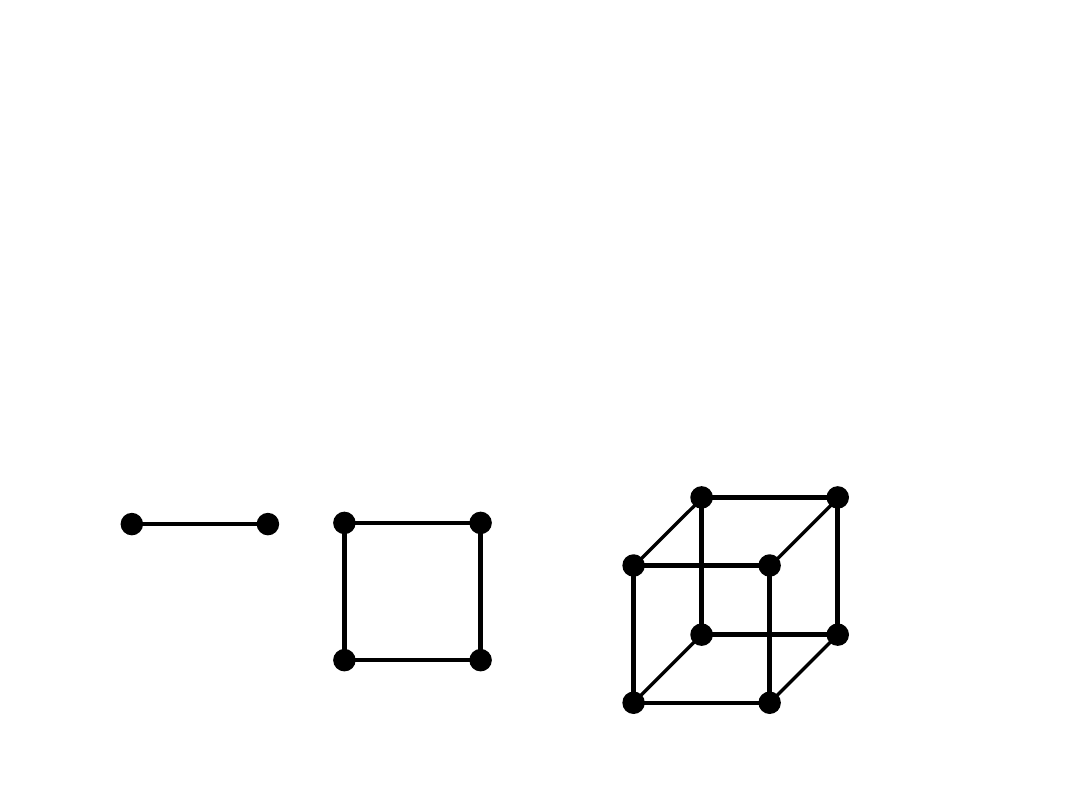
Przestrzeń Hamminga – zbiór wierzchołków n-
wymiarowej kostki o krawędzi jednostkowej.
Odległość w przestrzeni Hamminga –
minimalna liczba krawędzi między dwoma
punktami.
0
1
n=
1
0
0
0
1
n=
2
1
0
1
1
0
0
0
0
0
1
n=
3
0
1
0
0
1
1
1
0
0
1
0
1
1
1
0
1
1
1
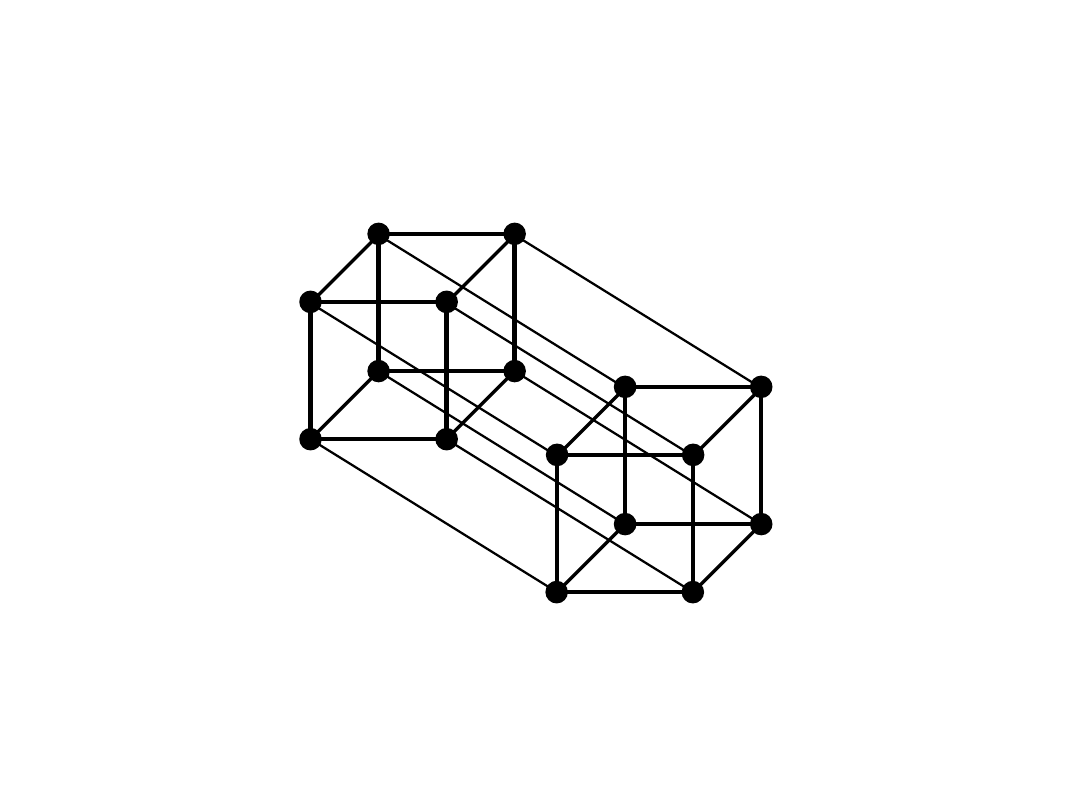
Przestrzeń 4-wymiarowa
TD5-4 / 29
0
00
0
0
00
1
n=
4
0
0
10
0
0
11
0
10
0
0
10
1
0
11
0
0
1
11
1
00
0
1
00
1
1
0
10
1
0
11
1
10
0
1
10
1
1
11
0
1
1
11
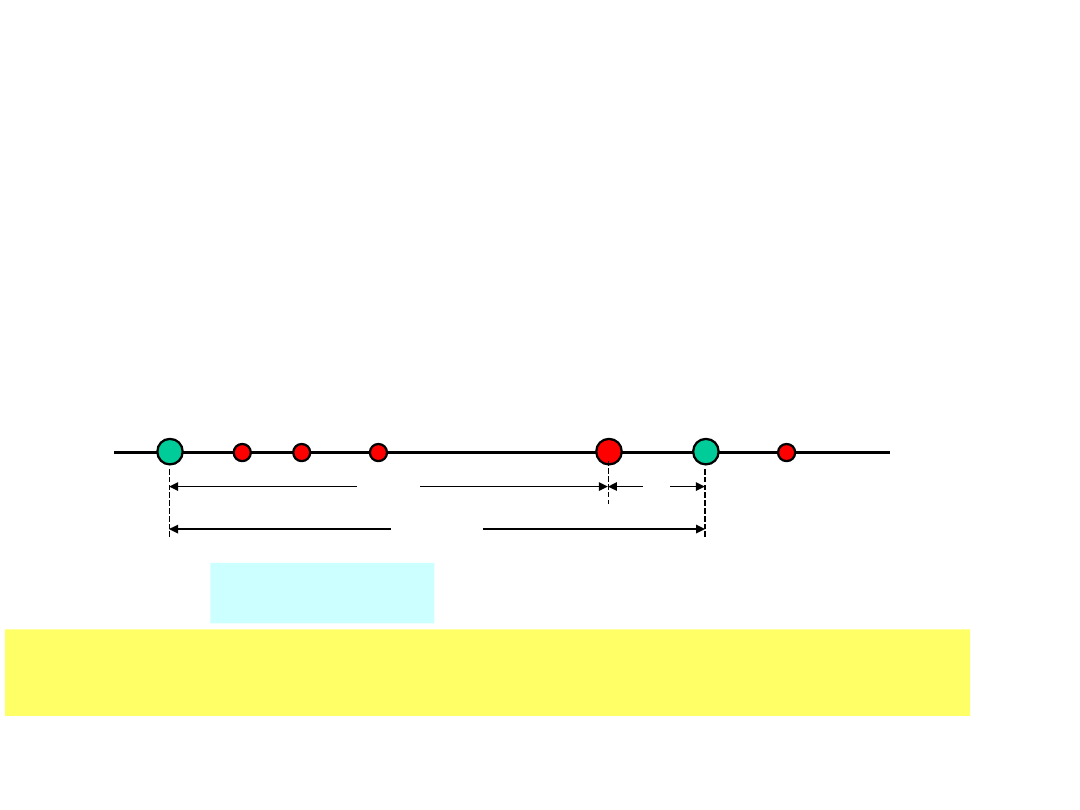
Odległość kodowa
TD5-5 / 29
Kody detekcyjne i korekcyjne używają tylko
wybranych punktów z przestrzeni Hamminga.
Odległość kodowa – to minimalna odległość
między dowolną parą punktów kodowych
(używanych przez kod).
Detekcja – wykrycie, że odebrany punkt nie jest
punktem kodowym.
k
1
k +1
d
min
= k +1
. . .
Aby kod wykrywał do k przekłamań, jego minimalna
odległość kodowa musi wynosić k + 1.
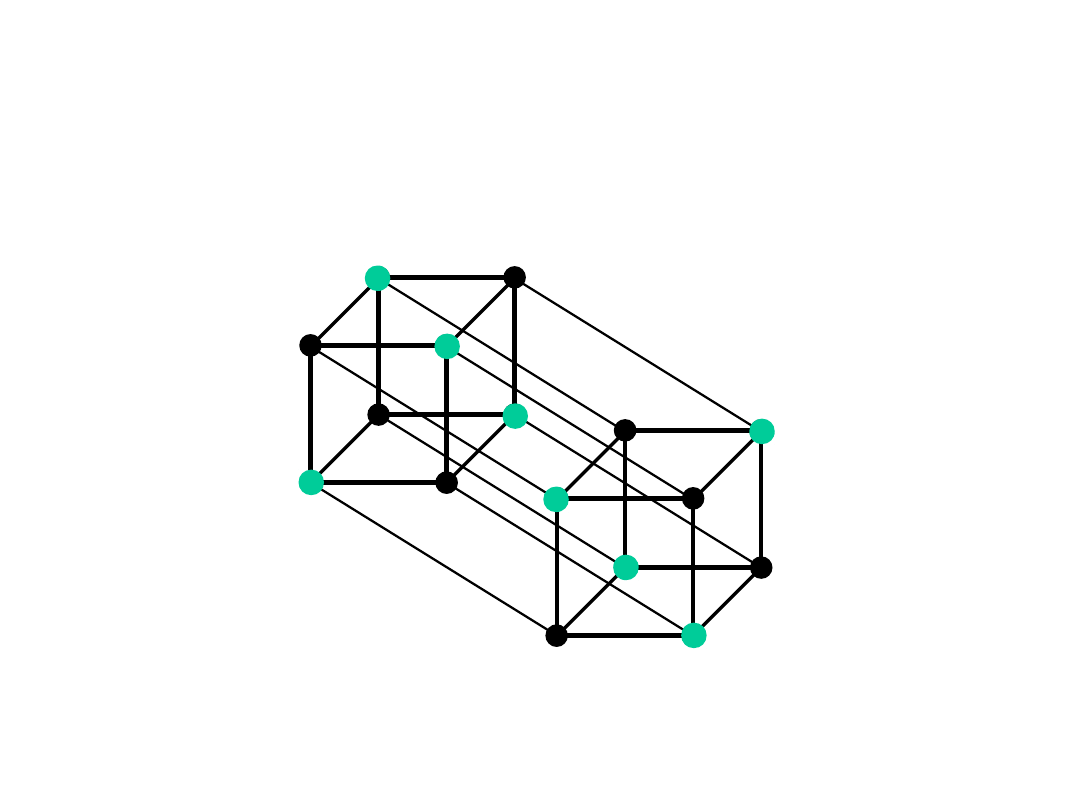
Przykład 4-wymiarowy
TD5-6 / 29
0
00
0
0
00
1
n=
4
0
0
10
0
0
11
0
10
0
0
10
1
0
11
0
0
1
11
1
00
0
1
00
1
1
0
10
1
0
11
1
10
0
1
10
1
1
11
0
1
1
11
Kod wykrywający pojedyncze przekłamania (k = 1, d
min
=2)
Odległość kodowa -
korekcja
TD5-7 / 29
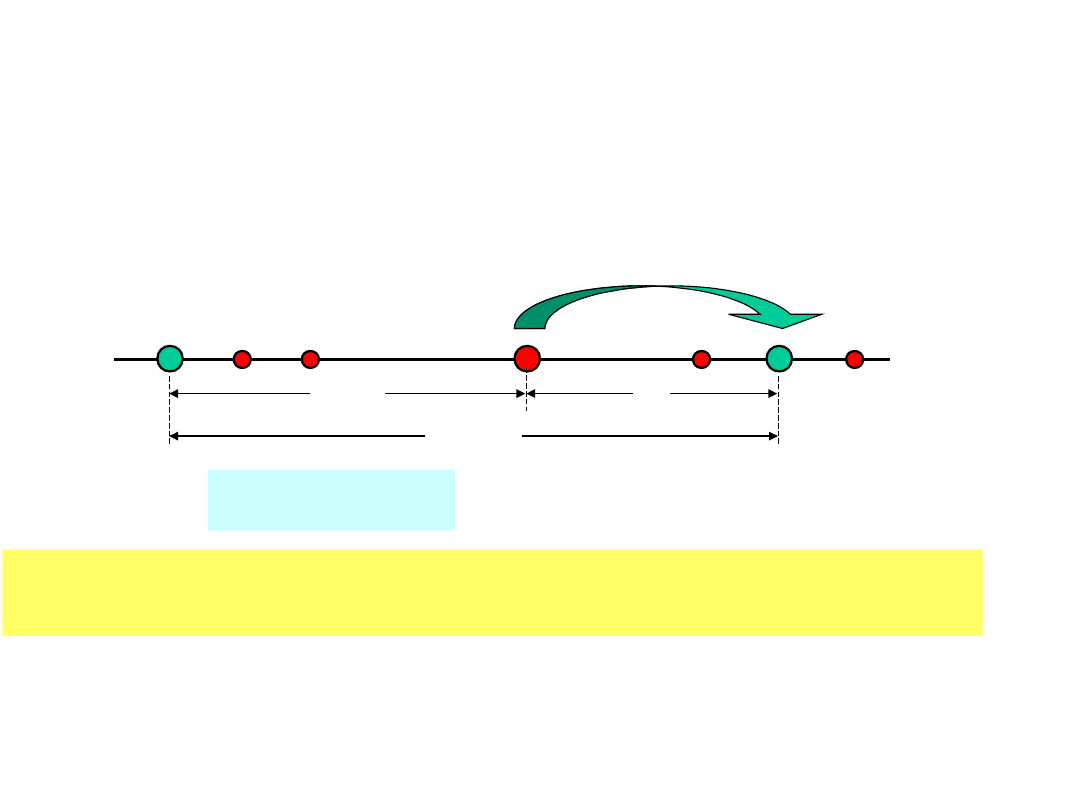
Korekcja – przejście do najbliższego punktu
kodowego
k +1
k
2k +1
d
min
= 2k +1
. . .
. . .
korekcja
Aby kod korygował do k przekłamań, jego minimalna
odległość kodowa musi wynosić 2k + 1.
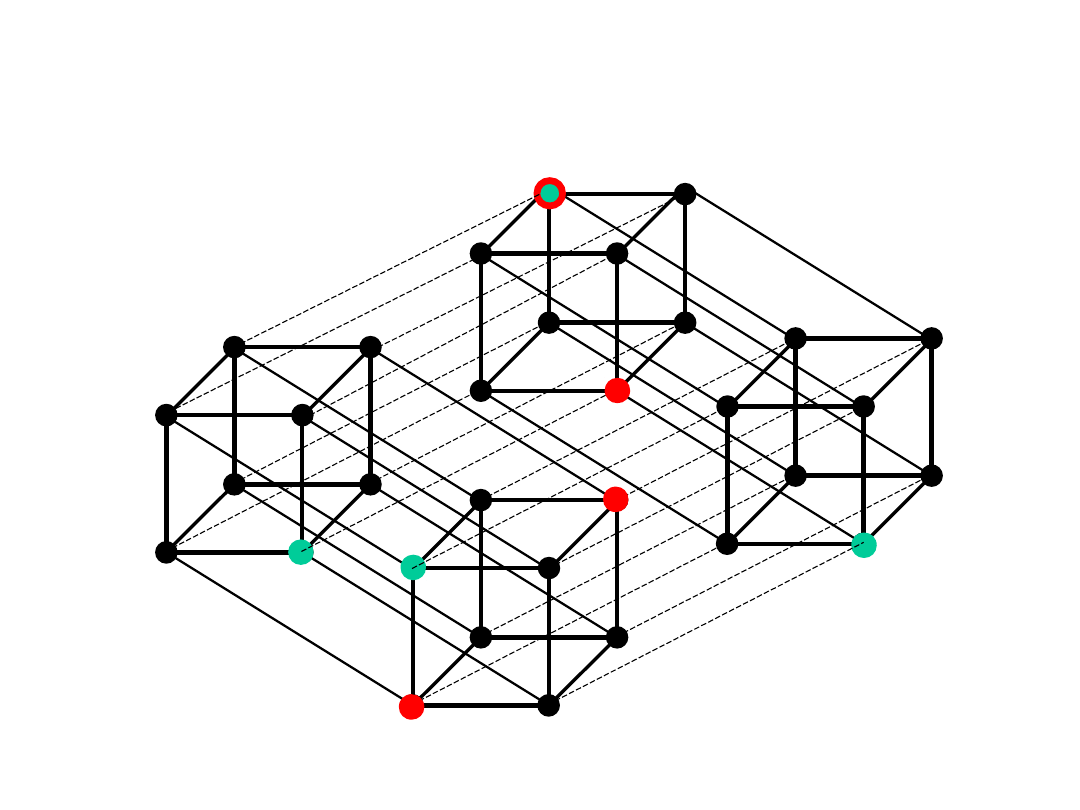
Przykład 5-wymiarowy
TD5-8 / 29
00
00
0
00
00
1
n=
5
00
0
10
00
0
11
00
10
0
00
10
1
00
11
0
00
1
11
01
00
0
001
00
1
01
0
10
01
0
11
01
10
0
01
10
1
01
11
0
01
1
11
Kody korygujące pojedyncze przekłamania (k = 1, d
min
=3)
10
00
0
10
00
1
10
0
10
10
0
11
10
10
0
10
10
1
10
11
0
10
1
11
11
00
0
101
00
1
11
0
10
11
0
11
11
10
0
11
10
1
11
11
0
11
1
11

Kody detekcyjne
TD5-9 / 29
•Kody z kontrolą parzystości
•Kody cykliczne
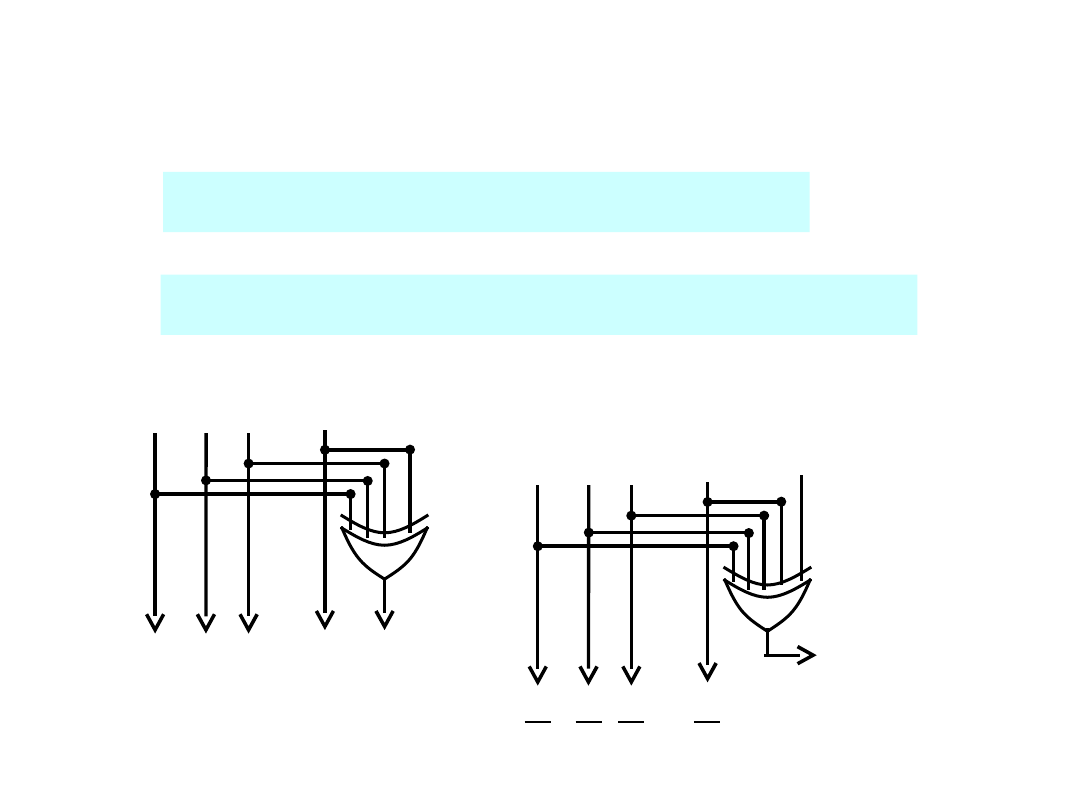
Kody parzystości
TD5-10 / 29
Odbiorcza suma kontrolna
d =
1
2
3
…
m–1
m
m+1
Nadawcza suma kontrolna
a
m+1
= a
1
a
2
a
3
… a
m–1
a
m
A
m
A
3
A
2
A
1
a
m+1
a
m
a
1
a
3
a
2
…
Koder
A
m
A
3
A
2
A
1
m+1
m
1
3
2
…
Dekoder
…
Błąd

Kody cykliczne - teoria
TD5-11 / 29
Zapiszmy ciąg bitów jako wielomian fikcyjnej zmiennej x, np.
ciąg 100011011 zapiszmy jako W(x) = x
8
+x
4
+x
3
+x+1.
Koncepcja kodów
Wielomian M(x) reprezentujący dane nadawane dzielimy przez
tzw. wielomian generujący G(x) stopnia k.
Resztę z dzielenia R(x) wysyłamy po danych (k bitów).
Tak więc nadawany jest wielomian W(x) = x
k
M(x) + R(x).
W odbiorniku dzieli się odebrane M(x) przez G(x) wyznaczając
resztę R(x).
Jeżeli obliczone R(x) jest równe odebranemu R(x), to uznaje się,
że transmisja była bezbłędna.
Wykrywane są wszystkie paczki błędów o długości niewiększej
niż k oraz większość dłuższych błędów.

Kody cykliczne - praktyka
TD5-12 / 29
Wielomiany generacyjne
W protokole HDLC
Wielomian R
*
(x) to zanegowana reszta z dzielenia M(x) / G(x).
Nadawany jest wielomian W(x) = x
k
M(x) + R
*
(x).
Odbiornik oblicza r(x) jako resztę z dzielenia W(x) / G(x)
i porównuje r(x) z ustalonym wielomianem.
CRC-16 (ITU-T) G(x) = x
16
+x
12
+x
5
+1
CRC-16 (ANSI)
G(x) = x
16
+x
15
+x
2
+1
CRC-12
G(x) = x
12
+x
11
+x
3
+1
CRC-32
G(x) = x
32
+x
26
+x
23
+x
22
+x
16
+x
12
+x
11
+x
10
+
+x
8
+x
7
+x
5
+x
4
+x
2
+x+1
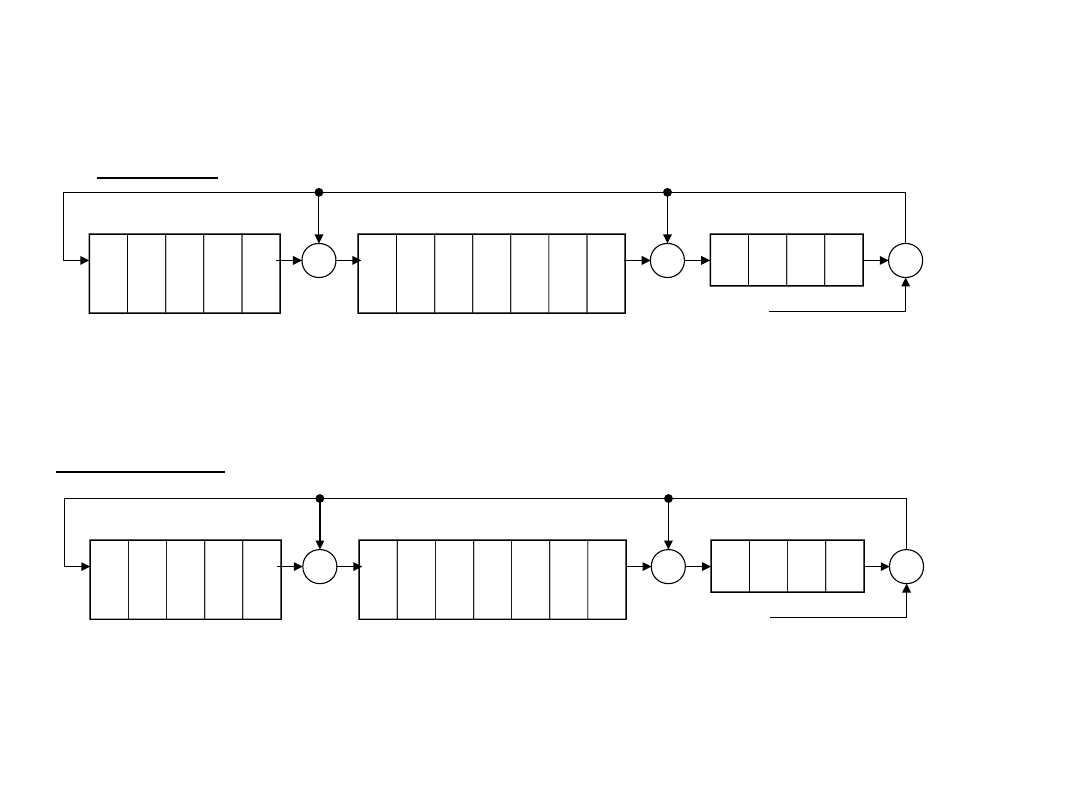
Kodowanie w HDLC
TD5-13 / 29
Koder
1
5
1
4
1
3
1
2
1
1
Dekoder
1
0
9 8 7 6 5 4
3 2 1 0
+
+
+
dane M(x)
*)
Na początku rejestr ładuje się jedynkami
1
5
1
4
1
3
1
2
1
1
1
0
9 8 7 6 5 4
3 2 1 0
+
+
+
dane odbierane W(x)
*)
Na początku rejestr ładuje się zerami

Kody korekcyjne
TD5-14 / 29
•Kody z podwójną kontrolą parzystości
•Kody Hamminga
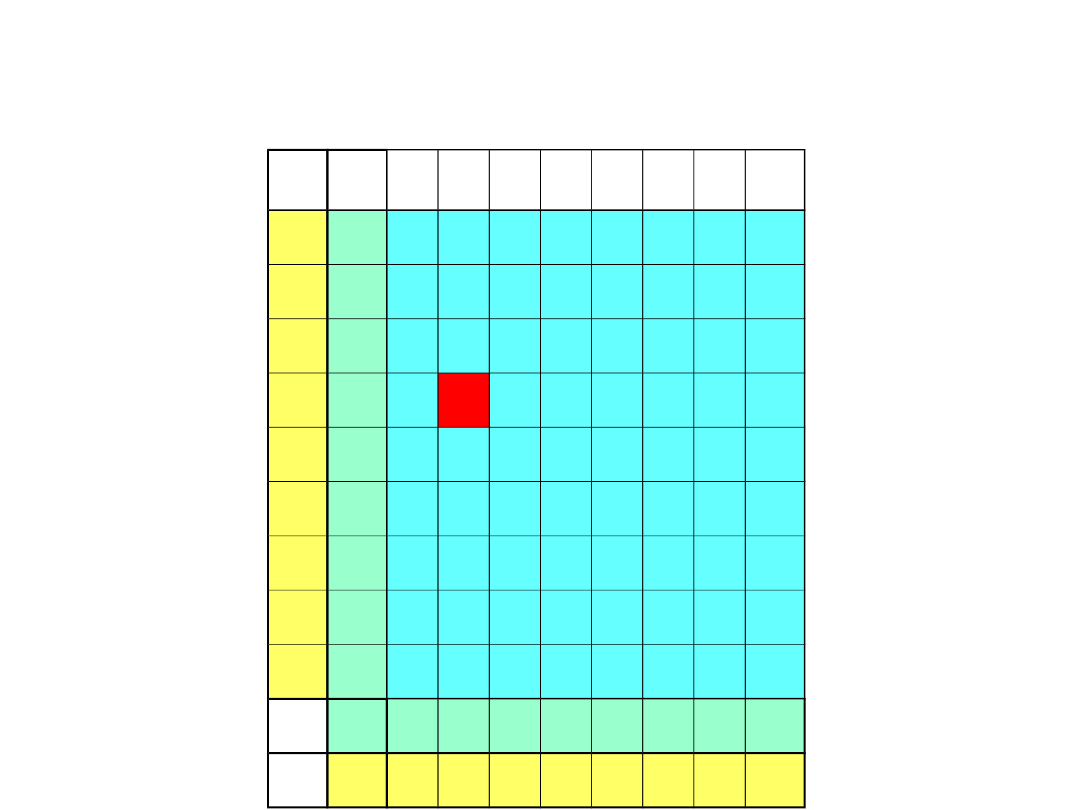
Podwójna parzystość
TD5-15 / 29
Σ
p d
8
d
7
d
6
d
5
d
4
d
3
d
2
d
1
0
0
0
1
0
0
0
0
0
Σ 0 0 1 0 0 0 0 0 0
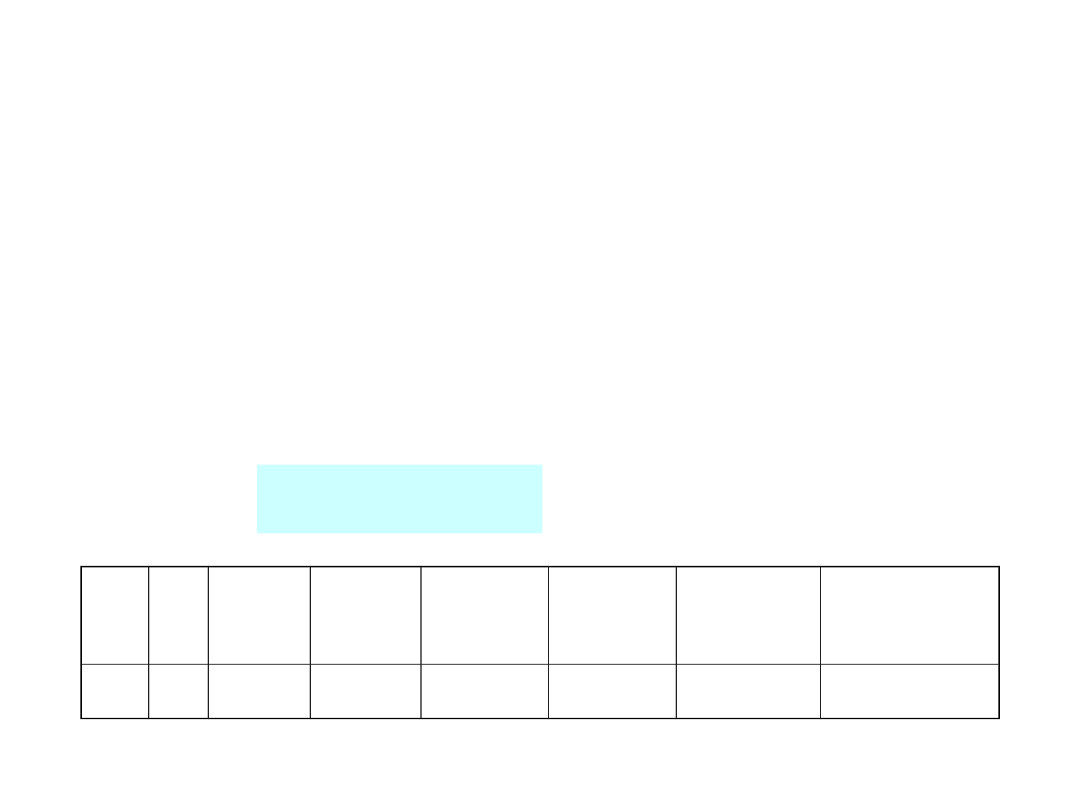
Korekcyjny kod
Hamminga
TD5-16 / 29
Kod korygujący pojedyncze przekłamanie.
m – liczba bitów informacyjnych
(użytecznych),
k – liczba bitów kontrolnych,
n = m + k
d
i
– wynik i-tej sumy kontrolnej (binarnej)
d
k
d
k–1
… d
2
d
1
– zero lub binarny numer przekłamanej pozycji
Liczba bitów kontrolnych k musi zatem spełniać warunek
2
k
> m + k
m 1 2 – 4 5 –
11
12 –
26
27 –
57
58 –
120
121 –
247
k 2
3
4
5
6
7
8
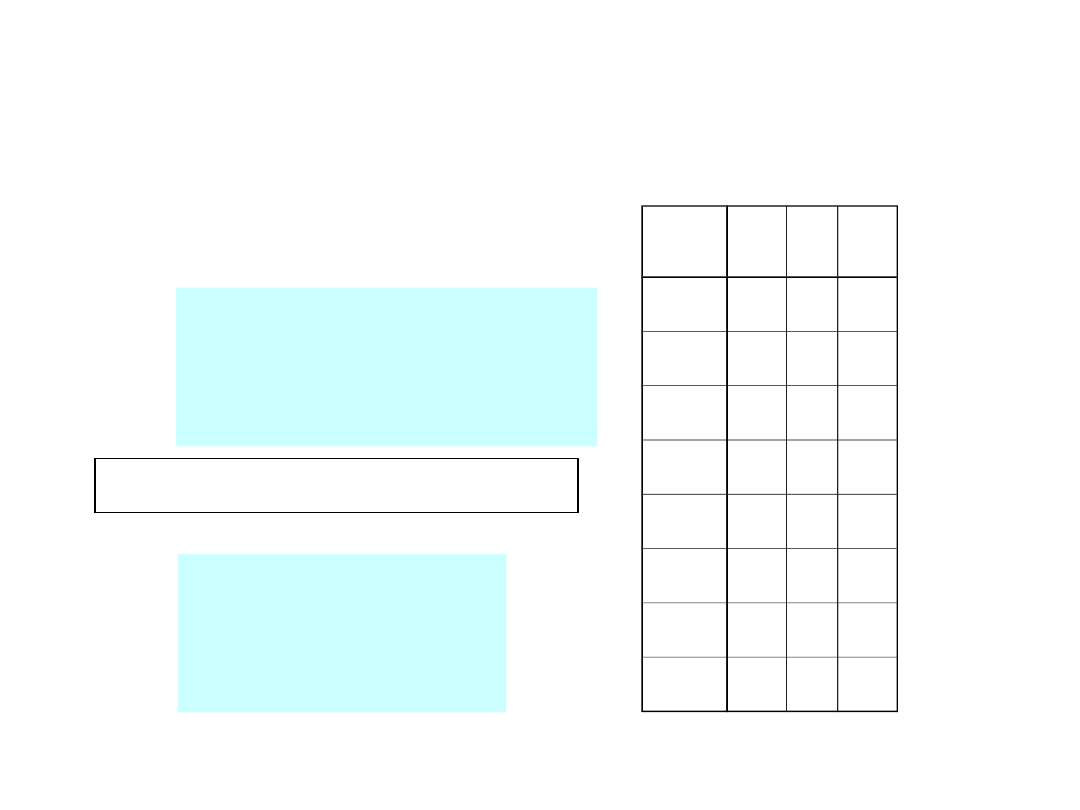
Przykład kodu Hamminga
TD5-17 / 29
m =
4,
k = 3,
n = 7,
Nr
poz.
d
3
d
2
d
1
-
0 0 0
1
0 0 1
2
0 1 0
3
0 1 1
4
1 0 0
5
1 0 1
6
1 1 0
7
1 1 1
Odbiorcze sumy kontrolne
d
1
=
1
3
5
7
d
2
=
2
3
6
7
d
3
=
4
5
6
7
Pozycje kontrolne: 1, 2, 4
Nadawcze sumy kontrolne
a
1
= a
3
a
5
a
7
a
2
= a
3
a
6
a
7
a
4
= a
5
a
6
a
7
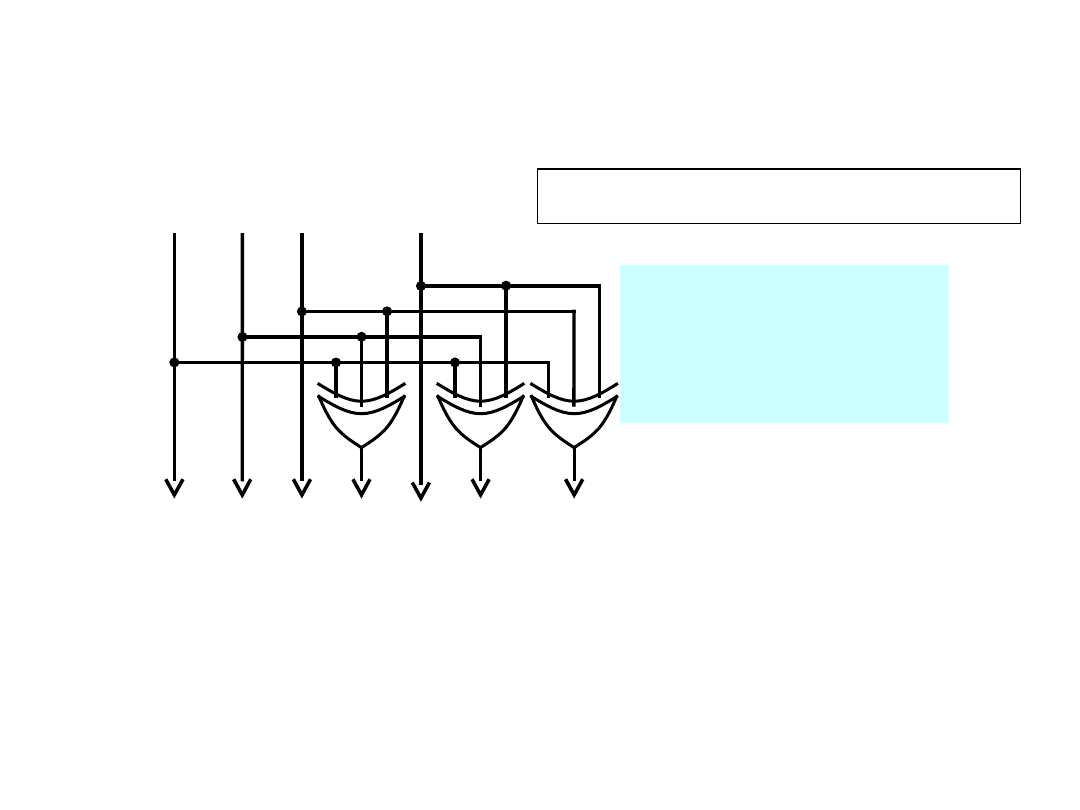
Nadajnik kodu Hamminga
TD5-18 / 29
Pozycje kontrolne: 1, 2, 4
Nadawcze sumy kontrolne
a
1
= a
3
a
5
a
7
a
2
= a
3
a
6
a
7
a
4
= a
5
a
6
a
7
A
1
A
2
A
3
A
4
a
4
a
1
a
2
a
3
a
7
a
5
a
6
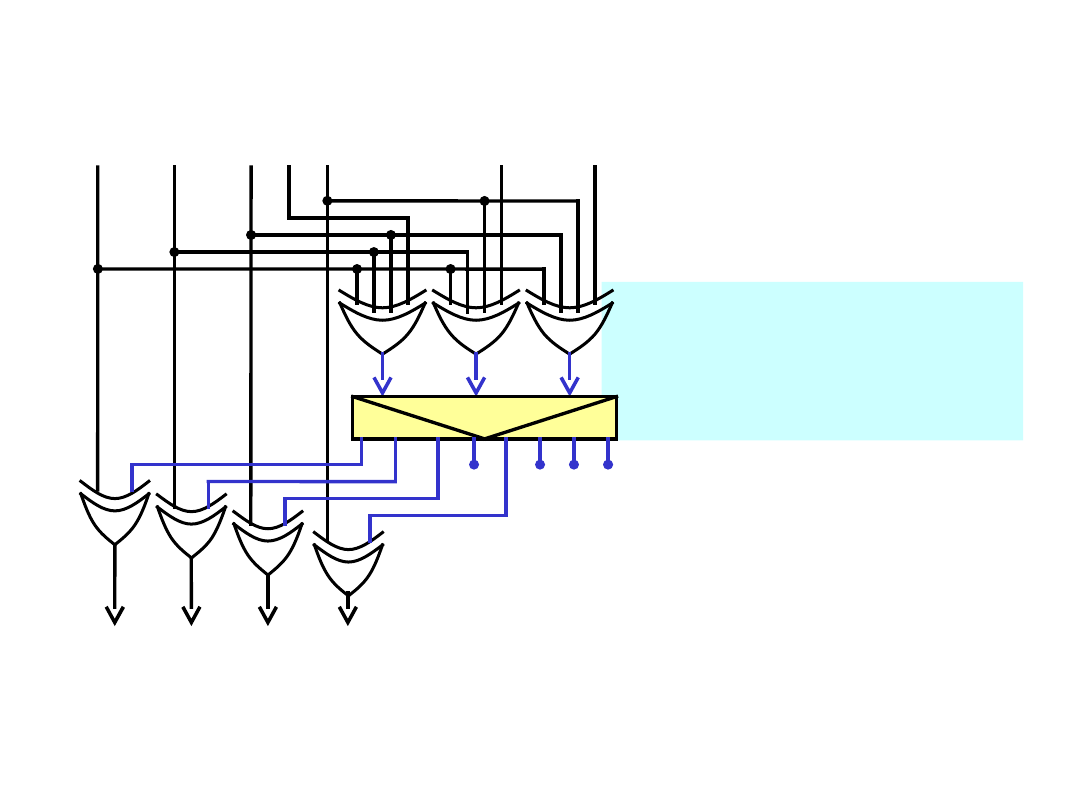
Odbiornik kodu
Hamminga
TD5-19 / 29
Odbiorcze sumy kontrolne
d
1
=
1
3
5
7
d
2
=
2
3
6
7
d
3
=
4
5
6
7
1
2
3
4
A
4
A
1
A
2
A
3
d
3
d
2
d
1
5
6
7
7
0
4 3 2 1
6 5
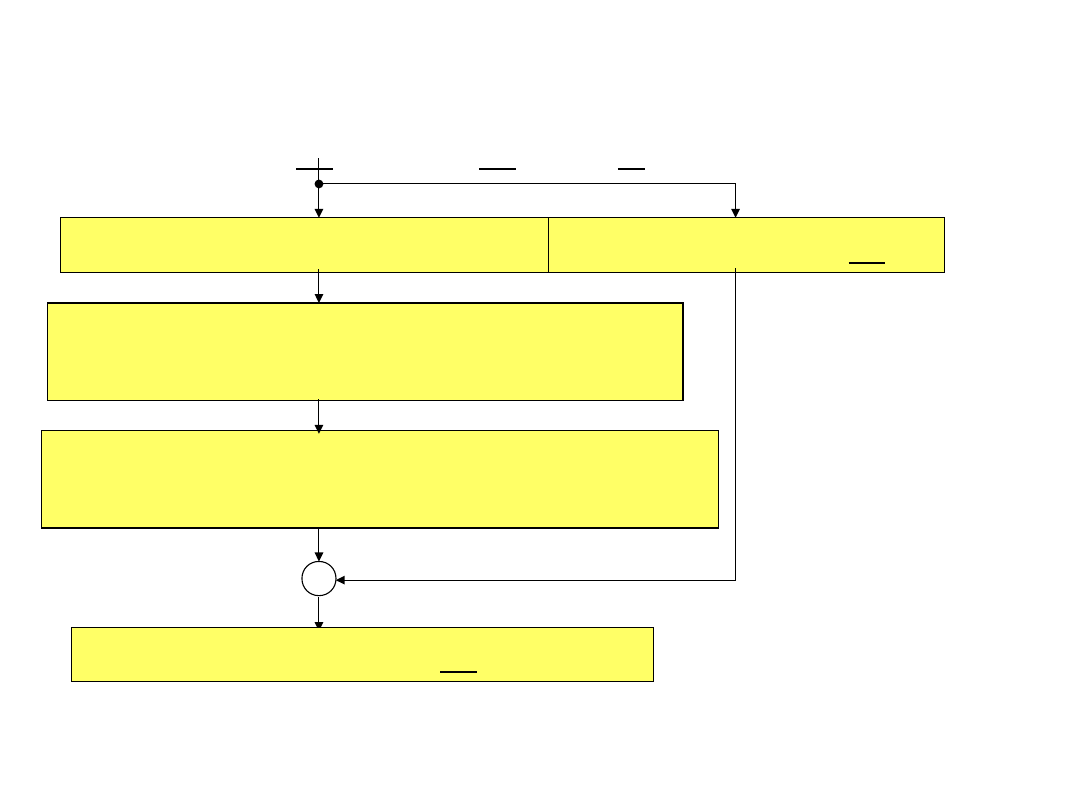
Kody cykliczne a korekcja
TD5-20 / 29
Dekoder kodu cyklicznego
Reszta r(x) z dzielenia W(x) / G(x)
(adres słowa w pamięci)
Pamięć z ciągami e(x) błędów, które
odpowiadają resztom r(x)
W(x) = x
k
M(x) + R
*
(x).
+
Dane odebrane M(x)
Dane skorygowane M(x) r(x)

Wykład 5a
Modulacje - podstawy
1. Łącze i jego elementy
2. Nośniki i ich modulacje
3. Modulacje sinusoidalne
TD5-21 / 29

Wstęp
Łącze i jego elementy
Nośnik, wiadomość, sygnał
TD5-22 / 29
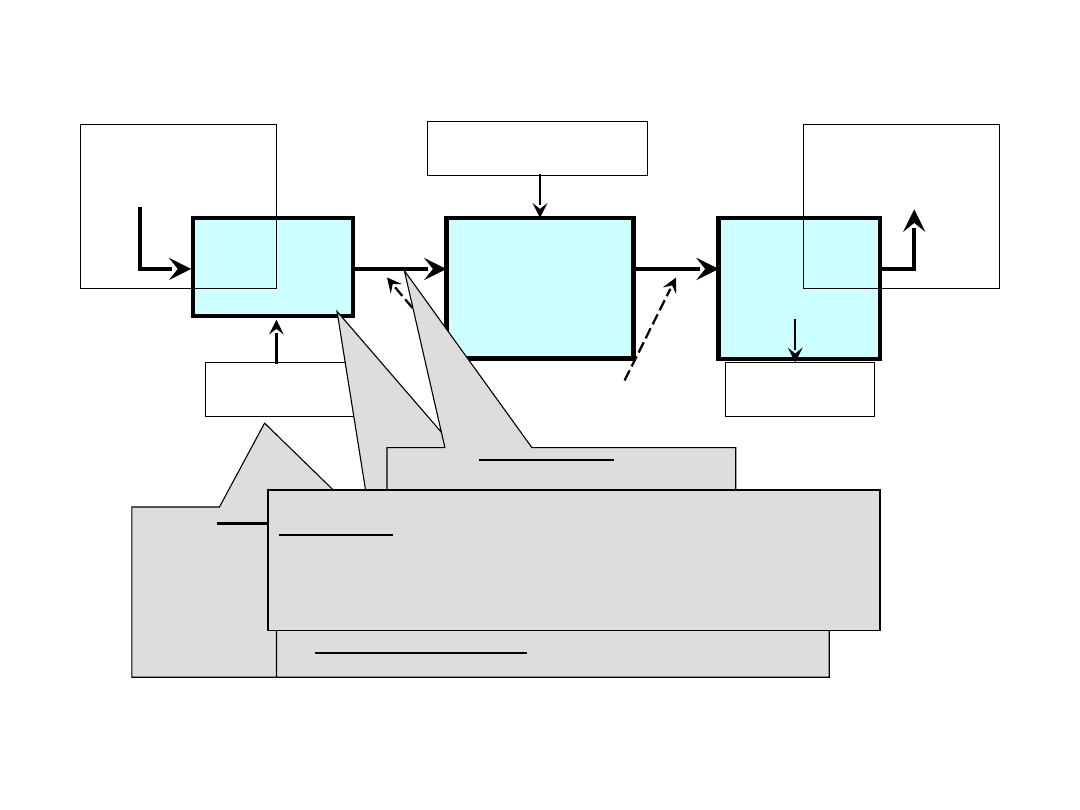
Kanał
telekomunikacyjny
TD5-23 / 29
Nośnik – wielkość
fizyczna sztucznie
wytworzona, zjawisko
posiadające możliwość
rozprzestrzeniania się
Modu-
lator
Kanał
analogo
wy
Demod
u-
lator
Zakłócenia
Wiadomo
ść
nadawan
a
Sygnał analogowy Nośnik
Nośnik
Wiadomo
ść
odbieran
a
Modulacja – proces
nakładania wiadomości
na nośnik
Modulator – urządzenie
wykonujące modulację
Sygnał –
wiadomość
nałożona na
nośnik
Łącze – zespół środków
technicznych służących do
przesyłania sygnału
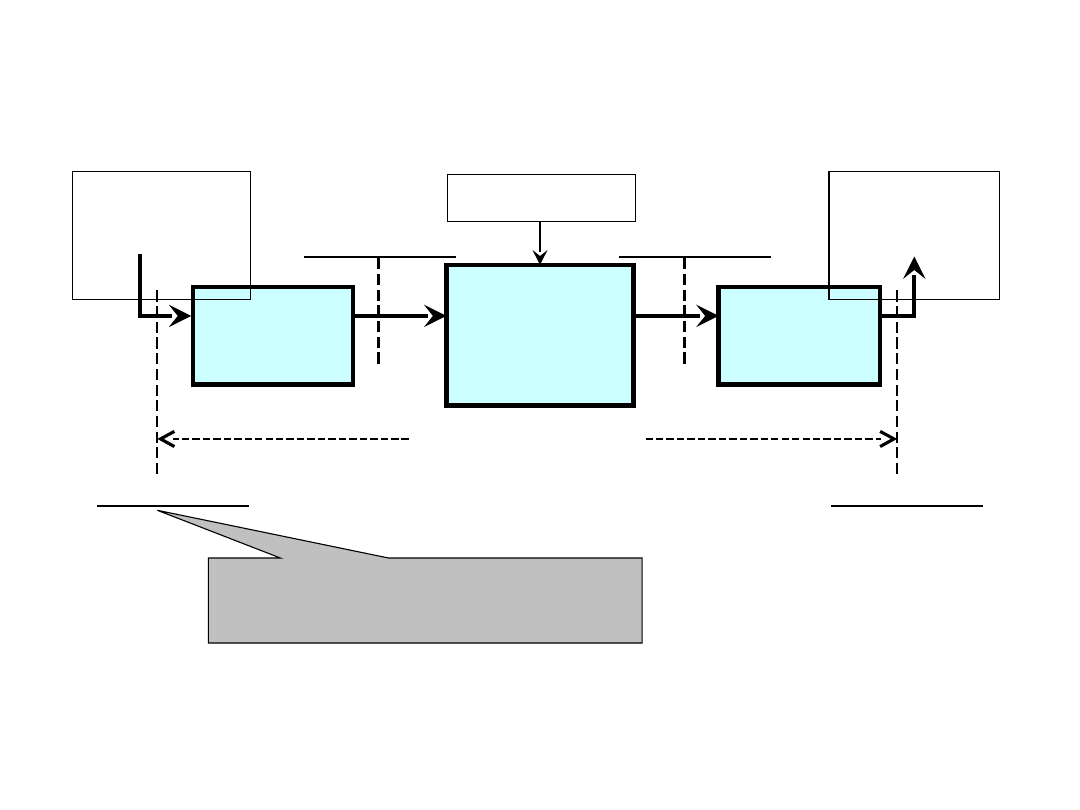
Kanał transmisji
danych
TD5-24 /
29
Szeregowy styk
binarny
Mode
m
Kanał
analogo
wy
Mode
m
Zakłócenia
Dane
nadawa
ne
Dane
odbiera
ne
Styk S1
Styk S1
Styk S2
Styk S2
Kanał binarny
Nośnik
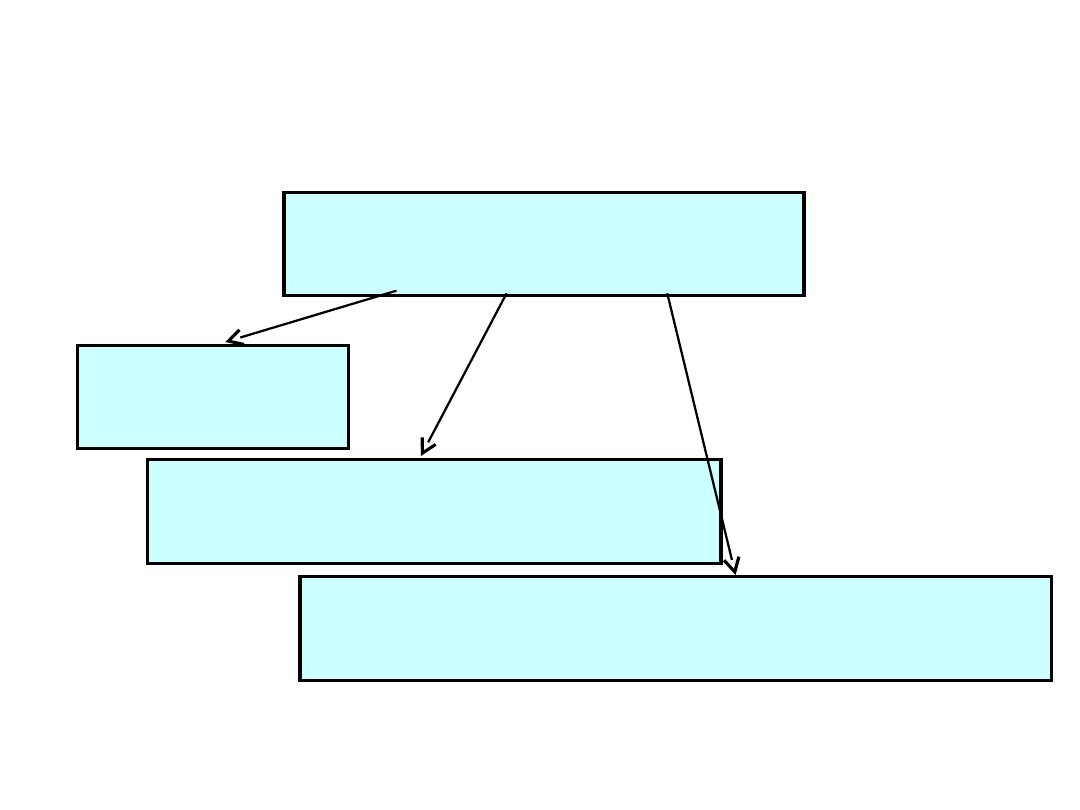
TD5-25 / 29
Nośnik
u
n
(t
) = f
(a
1
, a
2
, …, a
m
, t )
Nośnik stały
f
(A, t ) = A
Nośnik sinusoidalny
f
(A,
,
, t ) = A sin(
t
+
)
Nośnik impulsowy
f
(A,
,
, d, liczba, kod, kształt, … , t )

Modulacje
TD5-26 / 29
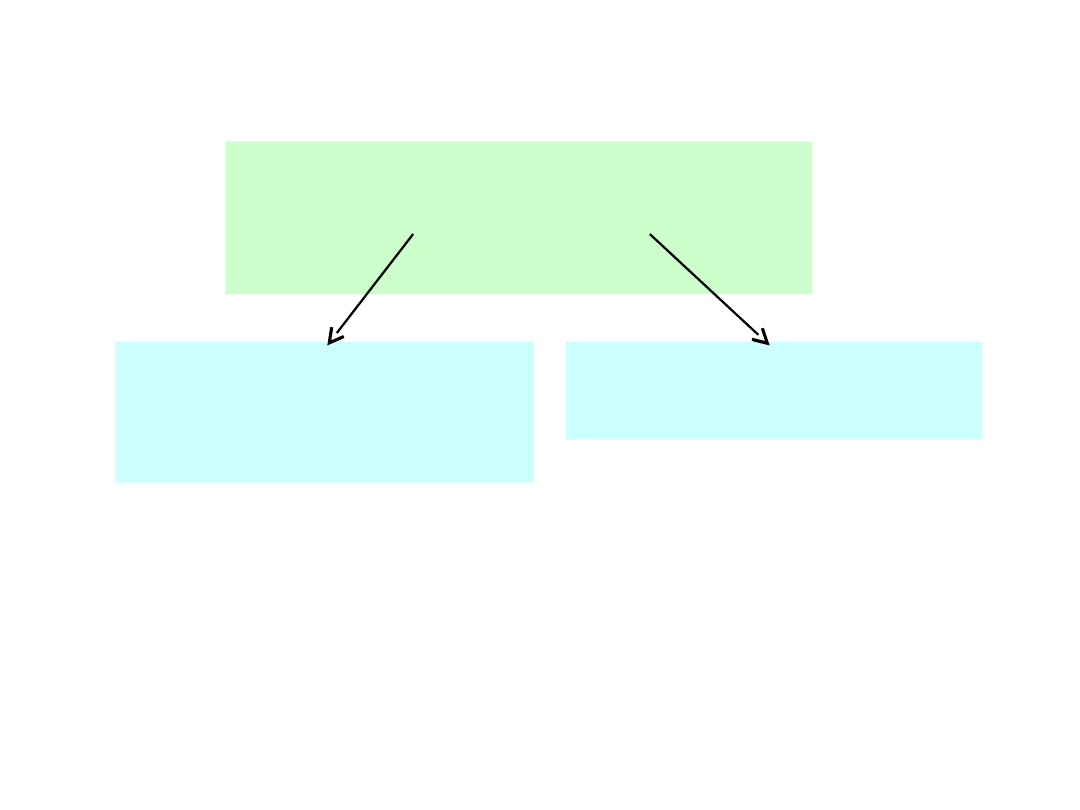
Modulacja prosta
u
x
(A, t ) = A(x
(t
))
gdzie x(t
) – przesyłana
wiadomość
TD5-27 / 29
Modulacja
napięciowa
1 – 10 V
Modulacja prądowa
4 – 20 mA
Modulacje sinusoidalne
AM – modulacja amplitudy
u
x
(A, t ) = A(x
(t
)) sin(
t +
)
TD5-28 / 29
FM – modulacja
częstotliwości
u
x
(
, t ) = A
sin(
(x (t ))
t +
)
PM – modulacja fazy
u
x
(
, t ) = A
sin(
t +
(x
(t )))
Modulacje mieszane: AM-PM,
QAM
u
x
(A,
, t ) = A(x (t ))
sin(
t +
(x
(t )))
Modulac
ja
kąta
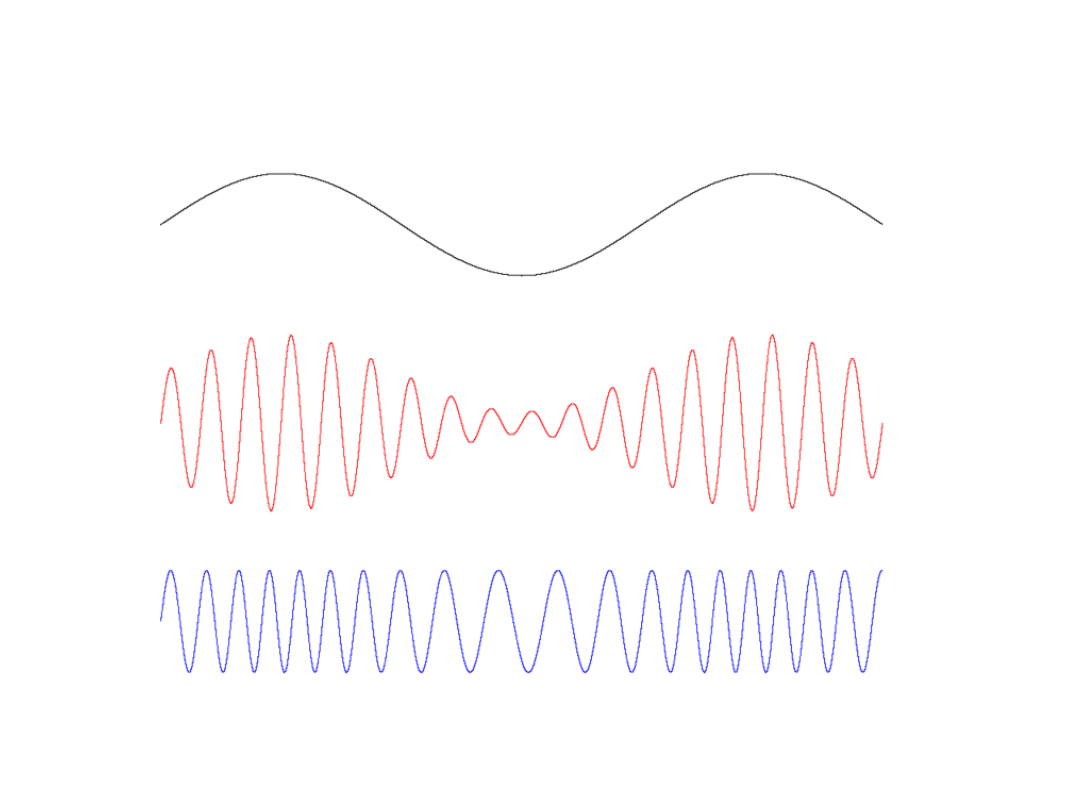
Modulacje AM i FM
TD5-29 / 29
x( t
)
AM
FM
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
Wyszukiwarka
Podobne podstrony:
TD 01
podrecznik 2 18 03 05
regul praw stan wyjątk 05
05 Badanie diagnostyczneid 5649 ppt
Podstawy zarządzania wykład rozdział 05
05 Odwzorowanie podstawowych obiektów rysunkowych
05 Instrukcje warunkoweid 5533 ppt
05 K5Z7
05 GEOLOGIA jezior iatr morza
05 IG 4id 5703 ppt
05 xml domid 5979 ppt
Świecie 14 05 2005
Wykł 05 Ruch drgający
TD 09
więcej podobnych podstron