Kombinatoryka-

matematyka

http://wazniak.mimuw.edu.pl/

„Matematyka Dyskretna” Andrzej Szepietowski

Kombinatoryka.

Jeżeli zbiór symboli zawiera dwa elementy:

a; b;

to można utworzyć dwa ciągi długości jeden:

(a); (b);

cztery ciągi długości dwa:

(a; a); (a; b); (b; a); (b; b).

Ile ciągów długości k można utworzyć z elementów
zbioru zawierającego n symboli?

4.1. Ciągi

Aby uzyskać ciągi długości trzy, postępujemy w następujący
sposób: bierzemy cztery ciągi długości dwa i najpierw do
każdego z nich dopisujemy na początku a. Otrzymujemy
w ten sposób komplet: (a; a; a); (a; a; b); (a; b; a); (a; b; b).

Potem do tych samych czterech ciągów długości dwa
dopisujemy na początku symbol b i otrzymujemy
komplet: (b; a; a); (b; a; b); (b; b; a); (b; b; b).

Komplety te są rozłączne i oba zawierają różne ciągi.
Razem tworzą zbiór wszystkich ciągów długości trzy.

Twierdzenie 4.1.

Jeżeli zbiór symboli zawiera n elementów, to powtarzając
powyższe rozumowanie, możemy się przekonać, że istnieje
n ciągów długości jeden, ciągów długości dwa i
ogólnie ciągów długości k + 1 jest n razy więcej niż ciągów
długości k. Zachodzi zatem twierdzenie.

4.2. Funkcje.

Policzmy teraz, ile jest funkcji ze zbioru A w zbiór B.
Przypuśćmy, że zbiór A zawiera k elementów: 1,..., k.

Każdą funkcję f z A w B można przedstawić jako ciąg
(f(1), f(2),..., f(k)).

Ciąg ten jest długości k, a jego elementy są wzięte ze zbioru B.
Zauważmy, że każdej funkcji odpowiada jeden ciąg, i na
odwrót, każdy ciąg (b1, b2,..., bk) opisuje jedną funkcję.
Mianowicie funkcję, która dla każdego i przypisuje wartość
f(i) = bi.

Z powyższego wynika, że funkcji ze zbioru A w zbiór B jest
tyle samo co ciągów długości k = |A| z elementami ze
zbioru B. Udowodniliśmy więc poniższe twierdzenie.

4.3. Ciągi bez powtórzeń
Policzmy teraz, ile jest ciągów bez powtórzeń, czyli ciągów
różnowartościowych. Jeżeli elementy bierzemy ze zbioru
trzyelementowego {1, 2, 3}, to możemy utworzyć trzy ciągi
jednoelementowe: (1), (2), (3),

sześć różnowartościowych ciągów dwuelementowych:
(1,2), (1, 3), (2, 1), (2, 3), (3, 1), (3, 2)
oraz sześć ciągów trójelementowych:
(1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), (3, 2, 1).

Twierdzenie Jeżeli elementy wybieramy ze zbioru n-elementowego A, to
liczba ciągów k-elementowych bez powtórzeń, które można wybrać
z tego zbioru, wynosi: n(n - 1) (n - k + 1).
W tym wyrażeniu mamy iloczyn k kolejnych liczb, poczynając od
(n - k + 1), a kończąc na n.

4.4. Permutacje

Permutacje to ciągi bez powtórzeń długości n, wybierane ze zbioru
n-elementowego. Na przykład, mamy dwie permutacje dwuelementowe:
(1,2), (2, 1), oraz sześć permutacji trzyelementowych:
(1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), (3, 2, 1).

Zgodnie z poprzednim twierdzeniem, liczba permutacji w
zbiorze n-elementowym wynosi: n(n - 1)(n - 2) ... 1, czyli jest
równa n!.

Czasami używa się innej definicji permutacji. Mianowicie
permutacja n-elementowa to dowolna funkcja różnowartościowa
ze zbioru {1, 2, ... , n} na ten sam zbiór. Na oznaczenie
permutacji używa się zapisu:

Dwie permutacje n-elementowe można składać tak, jak składa się
funkcje. Złożenie permutacji określone jest wzorem:

Zbiór wszystkich permutacji na zbiorze {1,...,n} z działaniem
złożenia ma następujące własności:

1. Złożenie permutacji jest łączne. To znaczy, dla każdych trzech
permutacji

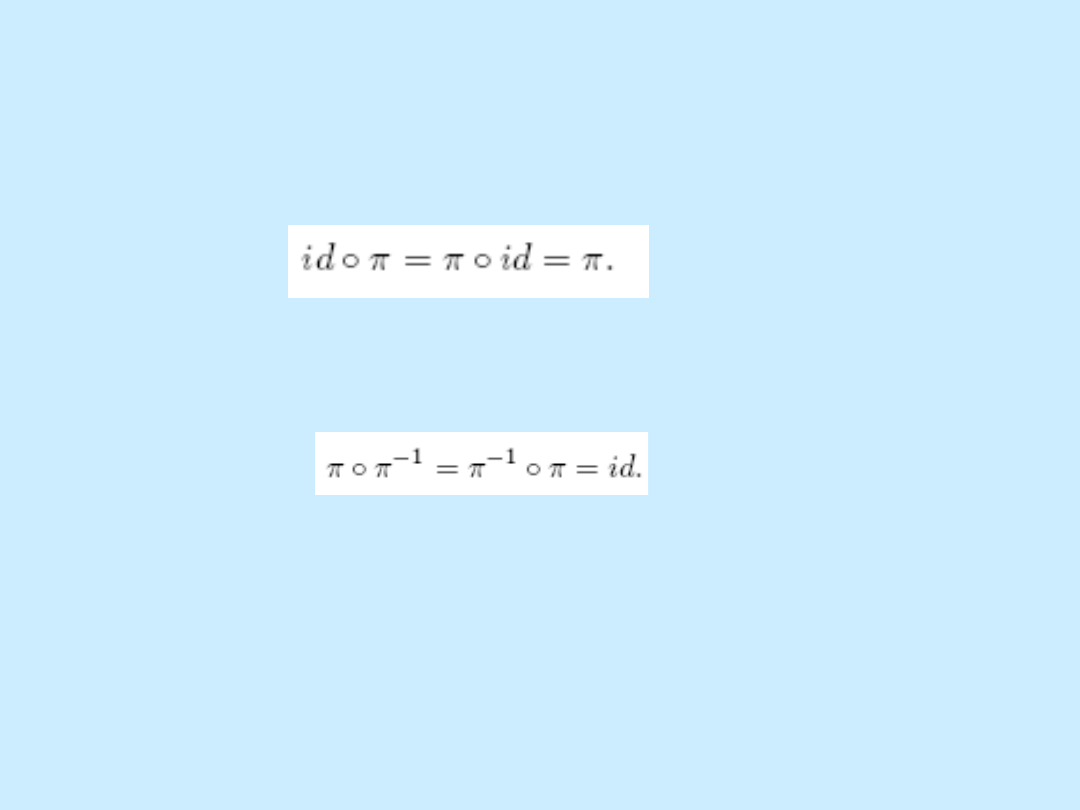
2. Wśród permutacji istnieje identyczność id, czyli permutacja, która
każdemu x z dziedziny przypisuje wartość id(x) = x. Identyczność
jest elementem neutralnym składania permutacji, ponieważ dla
każdej permutacji



:

3. Dla każdej permutacji istnieje permutacja odwrotna (funkcja
odwrotna) spełniająca warunek:

4.5. Podzbiory.

Policzmy teraz, ile podzbiorów ma skończony zbiór n-elementowy.

Jeżeli zbiór składa się z trzech elementów: {a,b,c}
to możemy łatwo wypisać wszystkie jego podzbiory:



, {a} ,{b}, {c},{a, b}, {a, c}, {b, c} ,{a,b,c}.

Rozważmy teraz ogólnie podzbiory zbioru {1,2,3,...,n}.

Z każdym podzbiorem

związana jest jego funkcja charakterystyczna, określona wzorem:

Dziedziną funkcji jest zbiór {1,2,...,n}, a przeciwdziedziną zbiór{0,1}.
Zauważmy, że każdemu podzbiorowi odpowiada jedna funkcja
charakterystyczna, i na odwrót, jeżeli weźmiemy dowolną funkcję:

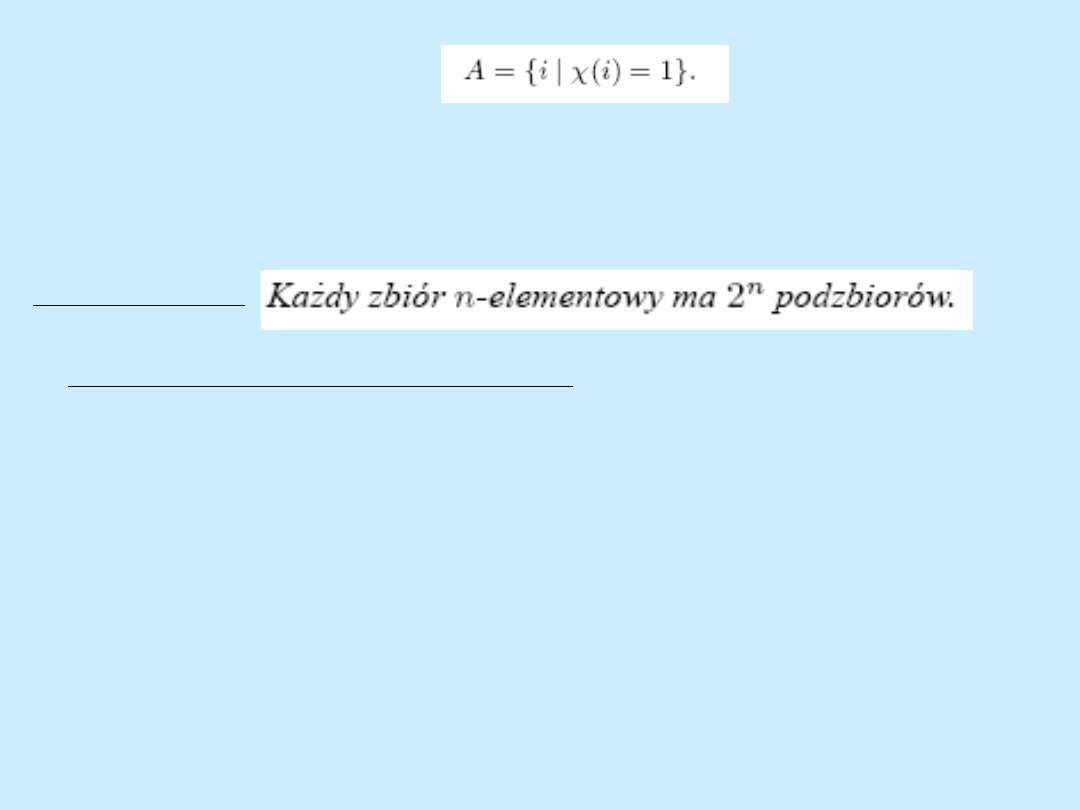
to wyznacza ona zbiór:

Z powyższych rozważań wynika, że liczba podzbiorów zbioru
n-elementowego jest równa liczbie funkcji ze zbioru {1,2,...,n}w zbiór
{0,1}. Czyli na podstawie twierdzenia 1.7 mamy twierdzenie poniższe.

Twierdzenie

4.6. Podzbiory k-elementowe.

Zastanówmy się teraz nad podzbiorami określonej mocy.
Mówimy, że zbiór jest mocy n, jeżeli zawiera n elementów.

Dla zbioru czteroelementowego {1,2,3,4} mamy jeden podzbiór pusty
(zeroelementowy), cztery podzbiory jednoelementowe: {1}, {2}, {3}, {4};
sześć podzbiorów dwuelementowych: {1,2}, {1,3}, {1,4}, {2,3}, {2,4},
{3,4}; cztery podzbiory trzyelementowe: {1,2,3}, {1,2,4},{1,3,4}, {2,3,4}
i jeden podzbiór czteroelementowy: {1,2,3,4}.

Liczbę podzbiorów k-elementowych zbioru n-elementowego oznacza
się przez

Jest to tak zwany symbol Newtona. Inaczej, jest to liczba sposobów na
jakie można wybrać k elementów ze zbioru n elementowego.
Właśnie pokazaliśmy, że:

Jeżeli 0  k  n, to symbol Newtona można obliczyć ze wzoru:

lub

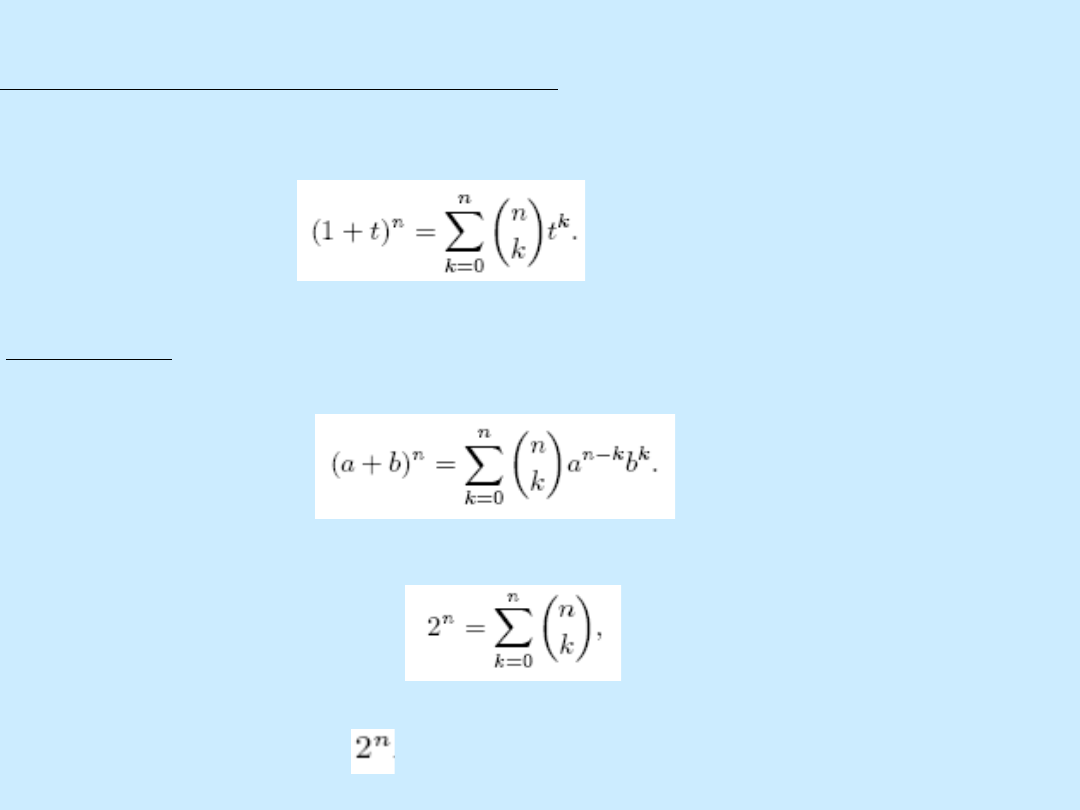
Twierdzenie (dwumian Newtona) Dla każdej liczby rzeczywistej t
oraz liczby całkowitej n



0 zachodzi:

Wniosek: Dla dowolnych liczb rzeczywistych a i b i dowolnej liczby
całkowitej n



0:

Jeżeli podstawimy t = 1 do wzoru z twierdzenia, to otrzymamy:

co potwierdza jeszcze raz, że wszystkich podzbiorów zbioru
n-elementowego jest

Zliczanie zbiorów

Gdy chcemy policzyć liczbę samochodów na parkingu, zazwyczaj
wskazujemy na kolejne samochody odliczając: jeden, dwa, trzy, itd.,
aż do momentu gdy każdy samochód zostanie wskazany. Wtedy
ostatnia liczba, którą wypowiedzieliśmy jest uważana za liczbę
samochodów na parkingu.

Aby wprowadzić matematyczny model procedury zliczania,
definiujemy początkowe odcinki liczb naturalnych:

Załóżmy, że na

parkingu stoi n samochodów. Zliczając je

wybieramy elementy Zn (zazwyczaj kolejne liczby) i przypisujemy
je do samochodów na parkingu. Uwaga: wybierając liczby z
zaczynamy od 0 i kończymy na n-1
Określamy zatem w trakcie tego zliczania bijekcję f: Zn



S , gdzie S

jest zbiorem samochodów na parkingu. W istocie jest to bijekcja, bo
dwa różne samochody mają różne numery (injektywność) i każdy
samochod jest policzony (surjektywność).

Obserwacja Gdy m<n, to nie istnieje bijekcja f: Zn



Zm.

Zasada szufladkowa Dirichleta

Jeżeli n obiektów jest rozmieszczonych w m szufladach i n > m, to
istnieje co najmniej jedna szuflada z przynajmniej dwoma
obiektami.

Dowód:

Zasady zliczania

Skrajnie niewygodne i nieefektywne byłoby, gdybyśmy za każdym
razem konstruowali bijekcję z Zn w nasz zbiór dla pewnego
naturalnego n . Na szczęście istnieje wiele reguł pozwalających
szybciej zliczać obiekty kombinatoryczne.

Poniżej przedstawiamy te podstawowe. Pierwsza z nich jest bardzo
prosta i w sposób intuicyjny stosowana od początków cywilizacji.

Trudniejsza sprawa jest, gdy zbiory nie są rozłączne.

Zasada włączania i wyłączania

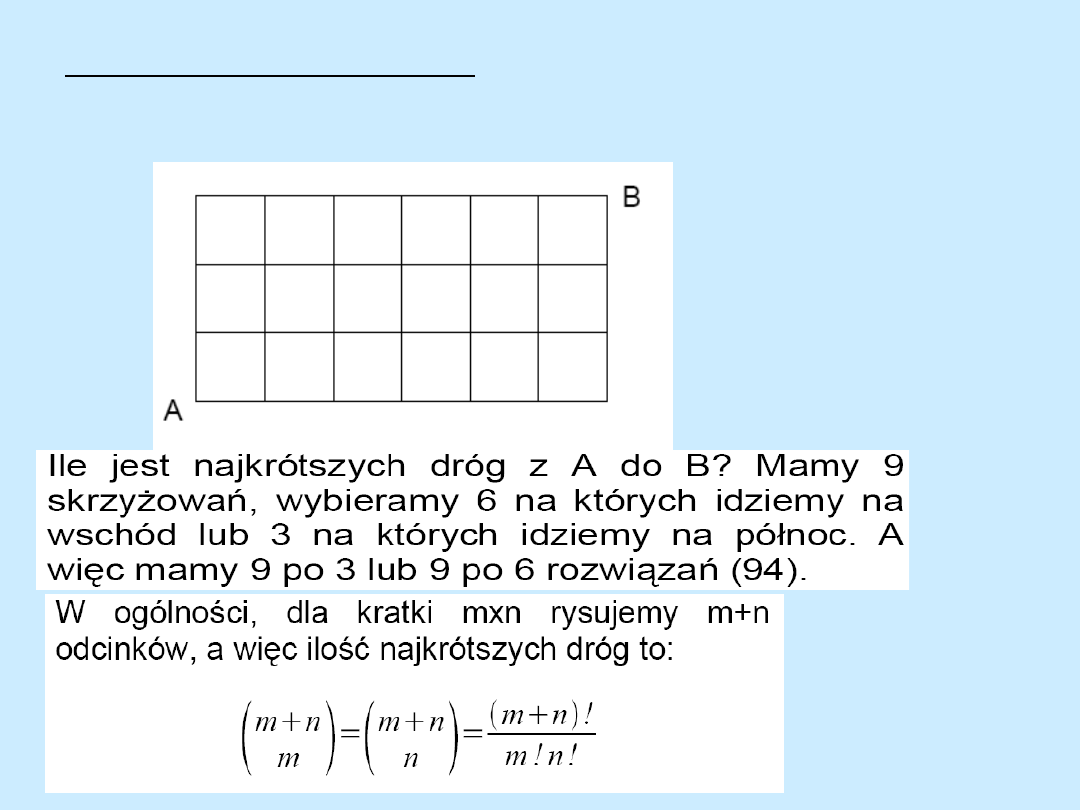
Różne sposoby zliczania

Ile jest najkrótszych dróg z punktu A do punktu B?