Symulacja komputerowa
Lab 4

Zygmunt Jacek Zawistowski

Lab 3.1: Oscylator –> układ równań 1-
go rzędu

2

sin( )

dx

v

dt

dv

v

x A

t

dt

g

w

=

=-

-

+

W

W postaci wektorowej

:

x

u

v

��

=��

��

2

sin( )

v

f

v

x A

t

g

w

�

�

=�

�

-

-

+

W

�

�

2

0 1

0

sin(Ω )

- -

x

v

A

t

ω γ

�

��� �

�

=

+

�

��� �

�

�� �

�

�

�

( , )

du

f u t

dt

=

Oscylator – rezonans -
RK4

Rozwiązanie zadania Lab3.1 – metoda

RK4

w

środowisku MATLAB

% OSCYLATOR tłumiony z pobudzeniem sin - metoda RK4
% warunek początkowy
% x(0)=0, dx/dt(0)=1, w zakresie czasów [0,8*pi]:
tinit=0; xinit=0; vinit=1; tfinal=8*pi;
% częstość kołowa własna w=2:
w=2;
% tłumienie:
g=0; %brak tłumienia
% g=0.2; % małe tłumienie
% g=0.7; % tłumienie bliskie krytycznego
% g=1.0; % duże tłumienie

M-plik w Matlabie

– wybór przypadku przez usuwanie/wprowadzanie

komentarzy (znak %):

Oscylator_Tlumiony_Sin_RK4.m

Oscylator_Tlumiony_Sin_RK
4.m

% częstość wymuszenia sin:
W=2.0; % rezonans
% W= 1.9; % małe odstrojenie
% W=1.75; % średnie odstrojenie
% W=1.5; % duże odstrojenie
% krok czasowy:
n=128; %n=64;
h=(tfinal-tinit)/n;
% warunek początkowy - przygotowanie wektorów
t, x oraz v
t=[tinit zeros(1,n)];
% u=[x;v]
u=[xinit zeros(1,n);vinit zeros(1,n)];
% funkcja f (wektor) opisująca prawą stronę
układu równań
f = @(t,u)[0 1; -w^2 -g]*u + [0; sin(W*t)];

c.d. pliku

Oscylator_Tlumiony_Sin_RK4.m

:

Oscylator_Tłumiony_Sin_RK
4.m

c.d. pliku

Oscylator_Tlumiony_Sin

_RK4.m

:

% obliczenie u(t)
for i=1:n
t(i+1)=t(i)+h;
k1=h*f(t(i),u(:,i));
k2=h*f(t(i)+h/2,u(:,i)+k1/2);
k3=h*f(t(i)+h/2,u(:,i)+k2/2);
k4=h*f(t(i)+h,u(:,i)+k3);
u(:,i+1)=u(:,i)
+(1/6)*(k1+2*k2+2*k3+k4);
end
% Wykres:
% x=u(1,:);
plot(t,u(1,:),'-')
xlabel('t')
ylabel('x')
legend('Oscylator RK4')
axis([0 8*pi -8.0 8.0])

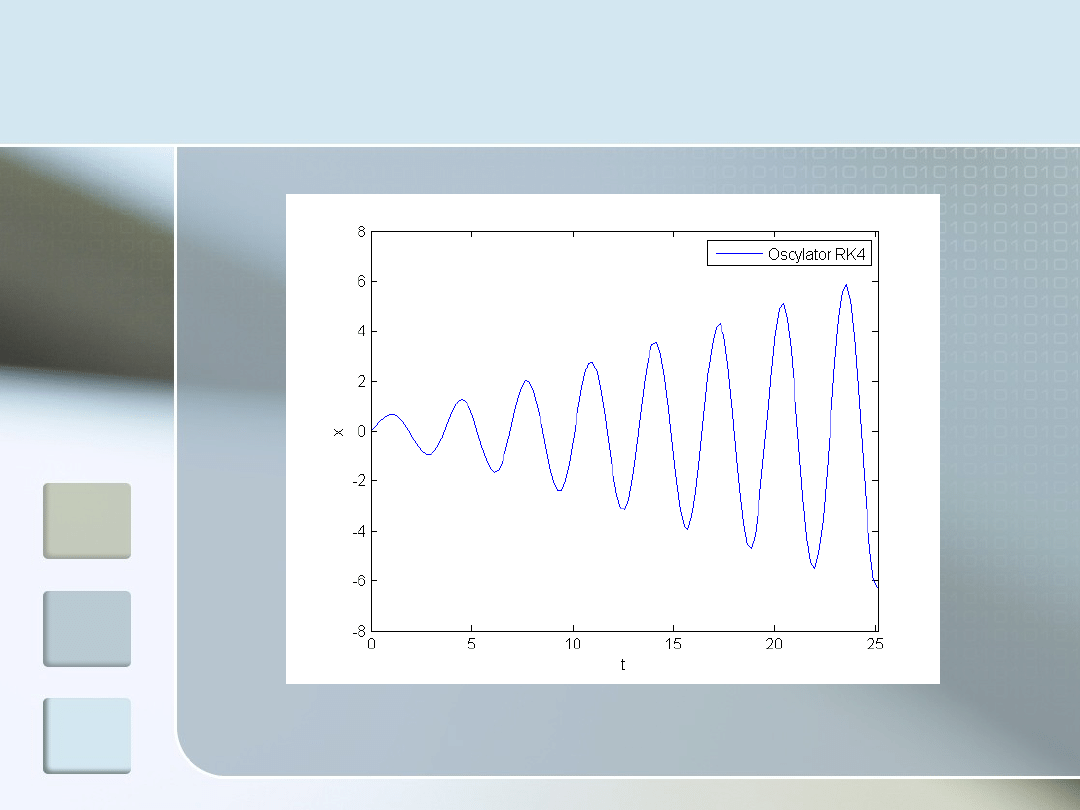
Oscylator – RK4:
rezonans

Rezonans w = W, brak tłumienia g = 0

Wynik praktycznie identyczny z otrzymanym za pomocą

ode45

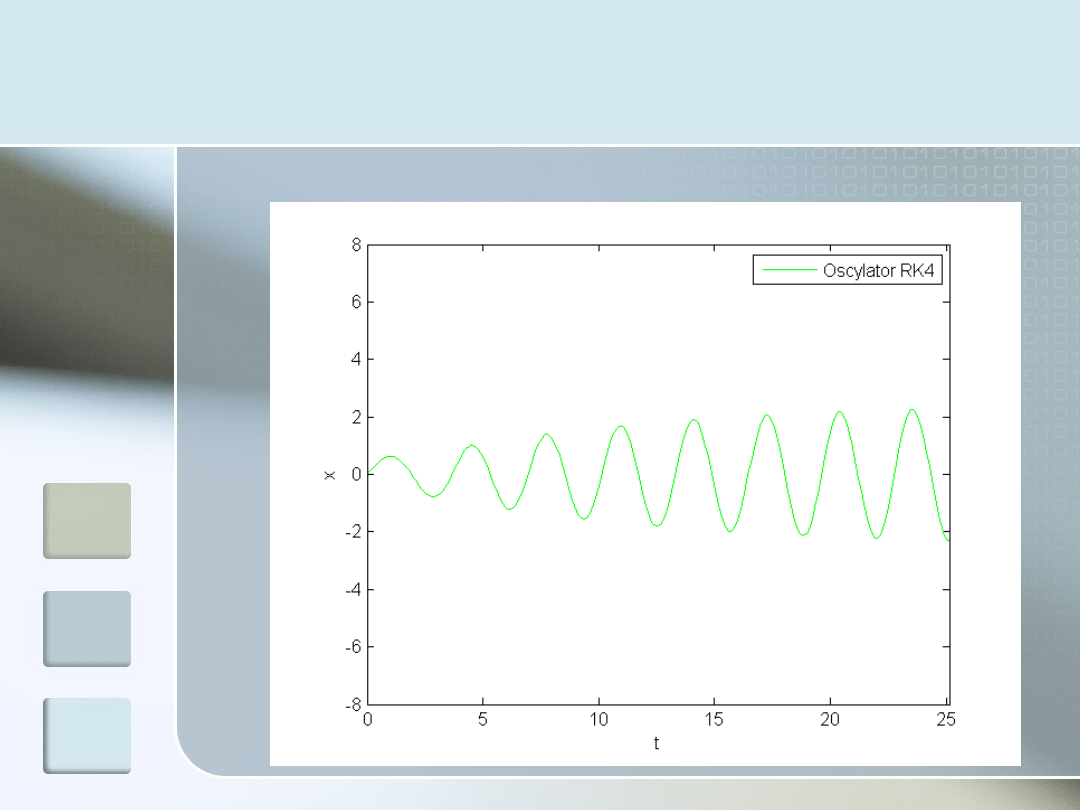
Rezonans – małe
tłumienie

W = w – rezonans, g = 0.2 – małe tłumienie

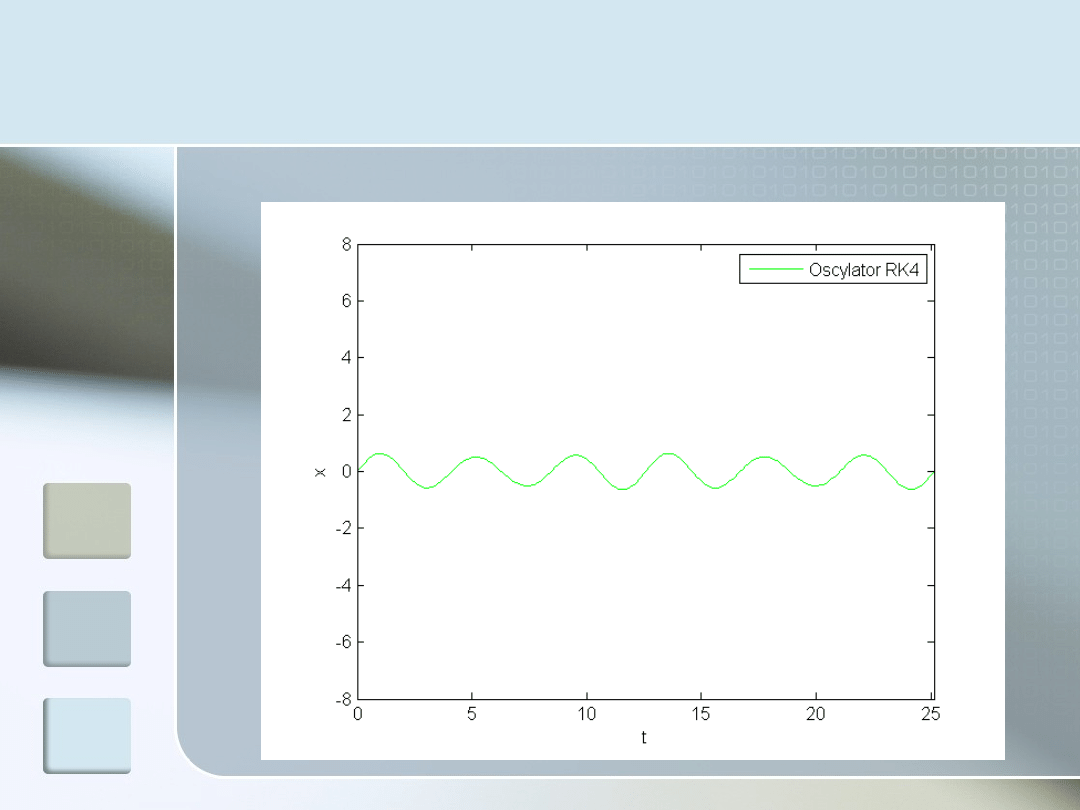
Odstrojenie - brak
tłumienia

W = 1.5, g = 0 – brak tłumienia

Oscylator – krzywa
rezonansowa

Poniższy

M-plik

w Matlabie wyznacza

krzywą rezonansową

-

zależność amplitudy od odstrojenia (wybór przypadku przez usuwanie/
wprowadzanie komentarzy - znak %):

Rezonans_Oscylator_Tlumiony_Sin_RK4_a.m

% REZONANS OSCYLATOR tłumiony z pobudzeniem sin - RK4
% warunek początkowy
% x(0)=0, dx/dt(0)=1, w zakresie czasów [0,8*pi]:
tinit=0; xinit=0; vinit=1; tfinal=8*pi;
% częstość kołowa własna w=2:
w=2;
% tłumienie:
g=0; %brak tłumienia
% g=0.05; % bardzo małe tłumienie
% g=0.2; % małe tłumienie
% g=0.7; % tłumienie bliskie krytycznego
% g=1.0; % duże tłumienie
% częstość wymuszenia sin(W*t), 21 punktów z [1.5,2.5]:
W=1.5:0.05:2.5; %

przestrajanie

– wektor wartości częstości

M-plik: Rezonans_oscylator_...
c.d.

n=128;
h=(tfinal-tinit)/n; % krok czasowy
% warunek początkowy - przygotowanie wektorów t, x
oraz v, u=[x;v]
t=[tinit zeros(1,n)];
u=[xinit zeros(1,n);vinit zeros(1,n)]; % u=[x;v]
% obliczenie max(u(1,:)) dla W=1.5,1.6,...,2.5
for j=1:21
f = @(t,u)[0 1;-w^2 -g]*u + [0;sin(W(j)*t)];
for i=1:n
t(i+1)=t(i)+h;
k1=h*f(t(i),u(:,i));
k2=h*f(t(i)+h/2,u(:,i)+k1/2);
k3=h*f(t(i)+h/2,u(:,i)+k2/2);
k4=h*f(t(i)+h,u(:,i)+k3);
u(:,i+1)=u(:,i)+(1/6)*(k1+2*k2+2*k3+k4);
end
a(j)=max(u(1,:));
end

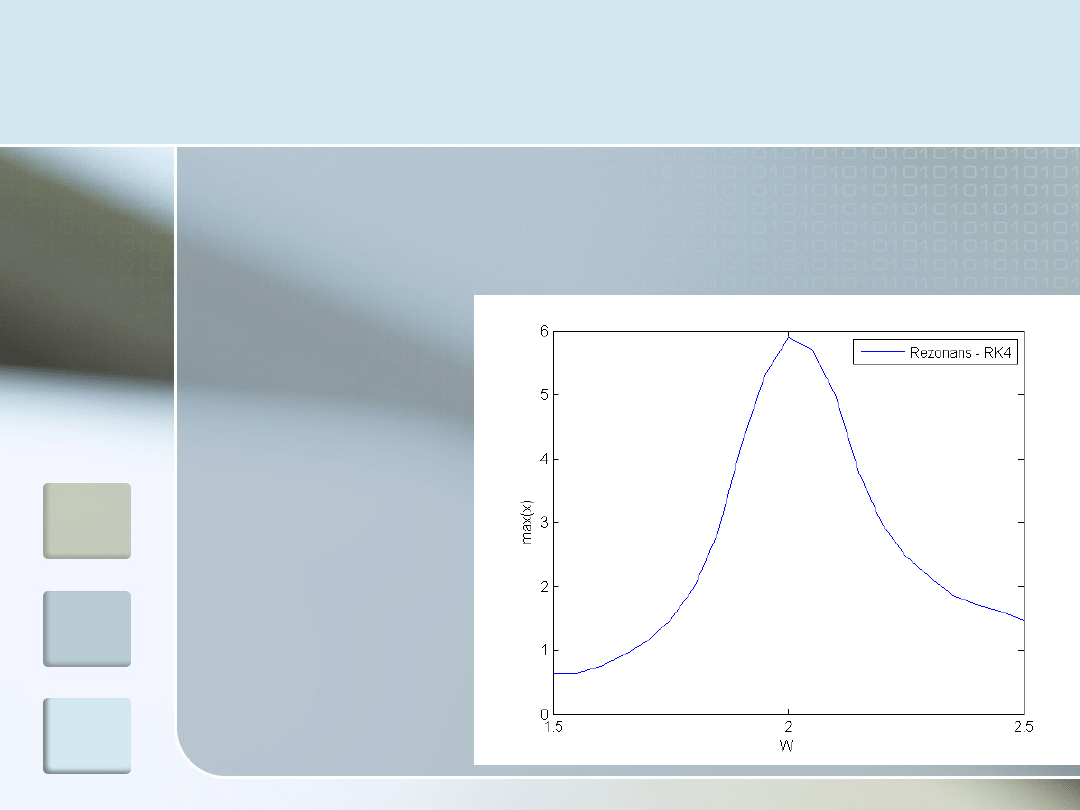
M-plik c.d. i krzywa
rezonansowa

% Wykres
max(u(1,:))
plot(W,a,'-')
xlabel('W')
ylabel('max(x)')
legend('Rezonans -
RK4')
axis([1.5 2.5 0.0
6.0])

c.d. M-pliku

:

Krzywa rezonansowa

Optymalna strefa
zgniotu

Lab4.
1

max

2

min

max

0

0

2

(

)

| ( ) |

x

v

x

v

F x dx

m

=

-

�

dla siły

F

k x

=- �

,

dobierając optymalnie k zgodnie z warunkiem :

2

2

max

|

/ | 5

50m/s oraz 10 100m/s

F

m

g

g

� �

�

,

dla

0

max

50km/ h,

0.5m

v

x

=

=

To zadanie daje się rozwiązać

analitycznie

-

patrz wykład.

Otrzymaliśmy:

min

km

46.65[

]

h

v =

Wyznaczyć numerycznie:

Przyjęcie warunku:

2

max

|

/ | 10

100m/s

F

m

g

�

�

min

km

43.03[

]

h

v =

daje

Wydłużenie strefy zgniotu do 0.7m daje

min

km

34.7[

]

h

v =

Fatalnie!

, ale

niefizycznie

:

pomijaliśmy tłumienie

(Polecenia:

sqrt

oraz

quad

)

2

max

|

/ | 5

50m/s

F

m

g

� �

dla