Testowanie hipotez

statystycznych

Testing simple hypotheses

Etapy procesu weryfikacji hipotez statystycznych

1. Formułowanie hipotezy zerowej H

0

oraz

odpowiadającej jej
hipotezy alternatywnej H

1

:

H

0

: nie ma różnicy

H

1

: istnieje różnica

2. Wybór odpowiedniego do postawionej hipotezy
zerowej testu i
obliczenie jego wartości w oparciu o dane
pochodzące z próby

3. Przyjęcie odpowiedniego poziomu istotności:

p  0.05

4. Odnalezienie przy danym poziomie istotności
obszarów
krytycznych i w oparciu o nie podjęcie decyzji o
odrzuceniu lub
nie hipotezy zerowej

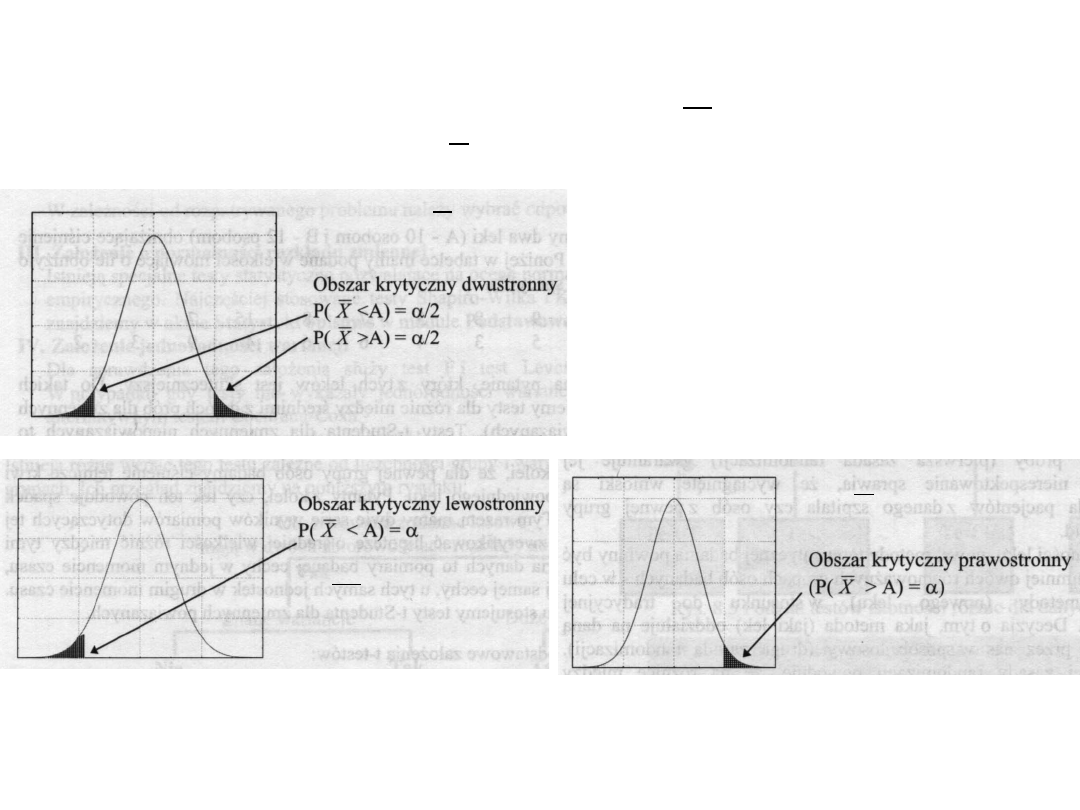
Obszary krytyczne:

Lokalizacja obszaru krytycznego zależy od postaci hipotez
alternatywnych.
Przykład: Hipoteza H

0

- średni czas działania nowego leku X jest równy

czasowi działania stosowanych do tej pory leków A t.j. X = A Hipoteza
H

1

może może zakładać:

X  A

X > A

X < A

a

b

c

- akceptujemy H

1

, jeśli p(H

0

)  0.05

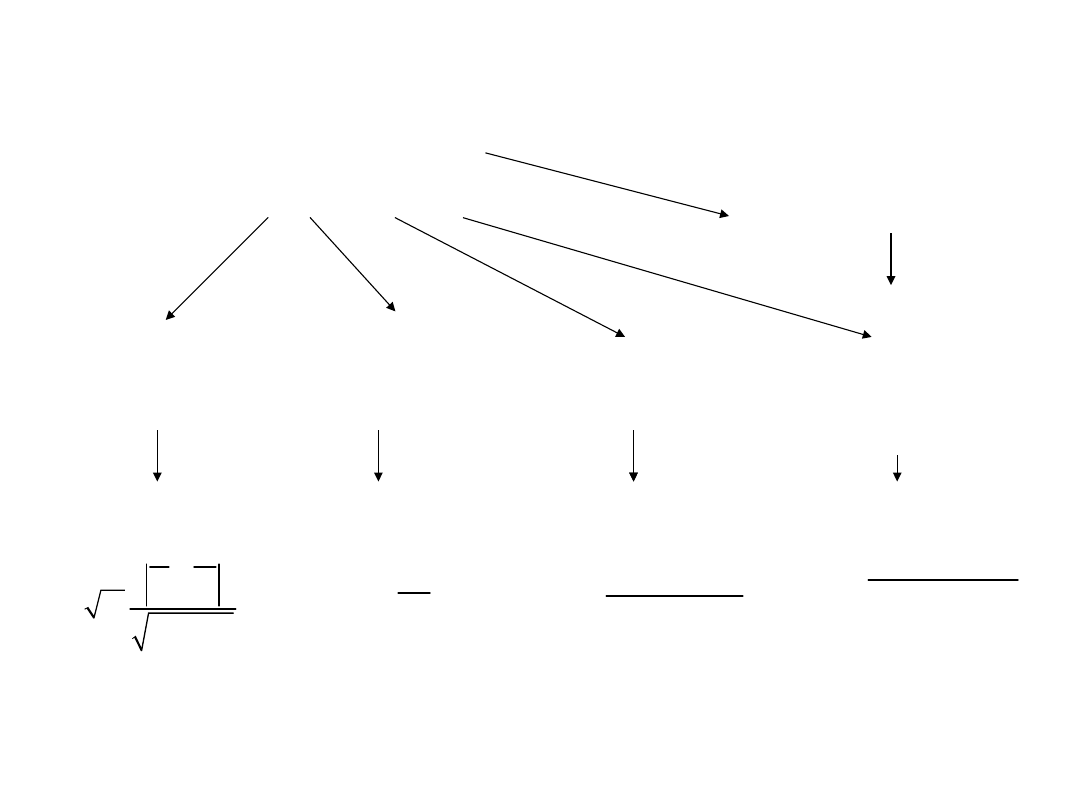
Jaki rodzaj testu zastosować?

Testy parametryczne

-rozkład normalny pomiarów

-rozkład normalny różnic m. parami
pomiarów

Testy nieparametryczne

Do porównania

dwóch średnich

t-
test

Do porównania

dwóch wariancji

F-
test

1

2

2

2

1

2

x x

t

N

s

s

-

=

+

2

1

2

2

F

s
s

=

Do porównania

dwóch rozkładów

Do porównania

obserwacji i

oczekiwań

Chi

2

-

test

2

2

1

(

)

k

i

i

i

i

Obs Exp

Exp

c

=

-

=

�

2

2

1

(

)

k

i

i

i

i

Obs Exp

Exp

c

=

-

=

�

Chi

2

-

test

Kolmogorov -

Smirnov-test

max(

)

cum

cum

KS

Obs

Exp

=

-

Chi

2

-

test

Do porównania

wielu średnich

ANOVA

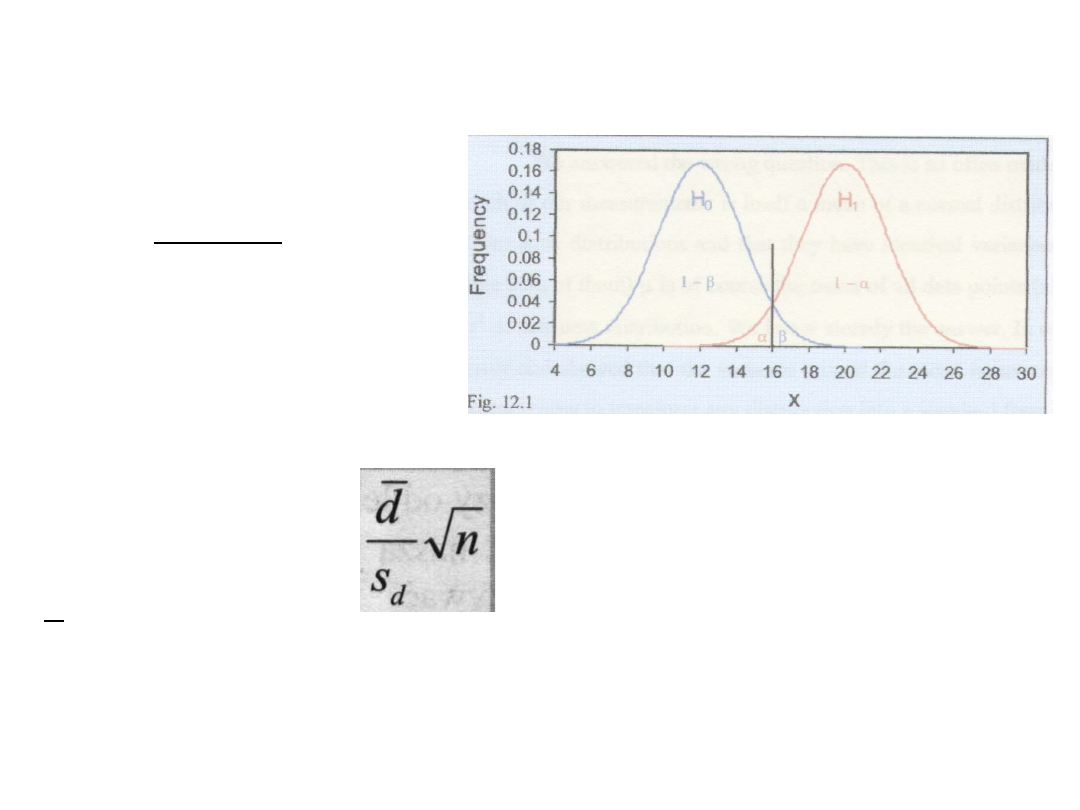
Porównywanie różnic między średnimi

1. Dla zmiennych
powiązanych:

t =

d - średnia różnica,

s

d

- odchylenie standardowe różnic

zmienna ma rozkład t-Studenta o liczbie stopni swobody n-1

Testy t - Studenta

t = n

1

- 

2





1

2

+ 

2

2



1

, 

2

- średnie populacji



1

2

+ 

2

2

- wariancje

Zadanie 1.

Pewnej grupie 10 pacjentów leczonych na nadciśnienie
podawano odpowiedni lek. Wyniki pomiarów ciśnienia
tętniczego krwi przed leczeniem (A) i po leczeniu (B) zebrano
w tabeli:
A 220 185 270 285 200 295 255 190 225 230
B 190 175 215 260 215 195 260 150 155 175
Jak zweryfikować hipotezę, że lek ten powoduje istotny
spadek ciśnienia krwi pacjentów ?

Zadanie 2.

Wybrano 11 par poletek wiązanych na łące i przeprowadzono
doświadczenie polegające na dodaniu środka owadobójczego
na jednym z poletek w każdej parze, pozostałe drugie poletko
w parze traktowano jako kontrolę. Uzyskane wyniki podano
jako suchą nadziemną biomasę roślin w [g] na poletku po
stosowaniu środka owadobójczego A i kontrolnym B:
A 821 655 915 540 431 1050 408 408 724 795 928
B 810 642 890 540 439 1020 388 403 730 780 920
Czy stosowanie preparatu owadobójczego powoduje istotny
wzrost biomasy nadziemnej roślin ?

2. Dla zmiennych
niepowiązanych:

Porównywanie różnic między średnimi

Testy t - Studenta

a. Przy równych wariancjach

t =

b. Przy różnych wariancjach

t =

m - średnia
s - odchylenie standardowe
n - liczebność

Statystyka ma rozkład t-Studenta o n

1

+ n

2

- 2 stopniach swobody

Testowanie hipotezy o braku

różnic między wariancjami

F =



1

2



2

2

Test Fishera - Snedecora



2

- wariancja

liczba stopni swobody n

1

+ n

2

- 2

Zadanie 3.

Dwa leki obniżające ciśnienie krwi podawano pewnej grupie
osób: lek A - 10 oraz lek B - 12 obniżających ciśnienie dwóm
różnym grupom. W poniższej tabelce podano wielkości o ile
obniżyło się ciśnienie po podaniu specyfiku:
Lek A 5 6 12 9 8 5 7 8 15 7
Lek B 6 5 11 5 3 4 6 6 4 9 3 2
Który z tych leków skuteczniej obniża ciśnienie ?

Zadanie 4.

W dwóch typach lasu wybrano 19 poletek (9 w dąbrowie A
oraz 10 w borze sosnowym B) i policzono na nich wszystkie
pająki krzyżaki znalezione na sieciach. Otrzymano
następujące wartości:
A 48 57 31 53 51 64 44 61 40
B 37 30 45 52 22 35 27 40 47 32
Czy istnieje istotna różnica w liczbie pająków w dąbrowie i
borze ?

Porównywanie rozkładów cech

Test 

2

(wartość oczekiwana - wartość obserwowana)

2



2

= 

wartość oczekiwana

1

k

(frekwencja oczekiwana - frekwencja obserwowana)

2



2

= N 

frekwencja oczekiwana

1

k

k - liczba obserwacji, k-1 liczna stopni swobody, N - wielkość próby

Zadanie 5.

W wyniku kojarzenia heterozygot dziwaczka o różowej barwie
kwiatów otrzymaliśmy w potomstwie następujące liczby
osobników: o kwiatach czerwonych (C) - 22, różowych (R) -
43, białych (B) - 17. Sprawdź czy otrzymane wyniki zgodne są
z prawem Mendla (1:2:1).

Analiza wariancji

(ANOVA)

1. Klasyfikacja pojedyncza

F =



2

między grupami



2

wewnątrz grup



2

między grupami

=

SS

między grupami

k - 1



2

- wariancja

k

-

liczba grup



2

wewnątrz grup

=

SS

wewnątrz grup

N - k

SS

- suma kwadratów odchyleń od średniej

N

- liczba przypadków

Zadanie 6.

Badano wpływ intensywności światła na wielkość biomasy
roślin. Hodowano je na poletkach przy 5 różnych natężeniach
światła (A-E) w 4 powtórzeniach. Po zakończeniu
eksperymentu oznaczono biomasę roślin na poletkach [g/m

2

].

Wyniki zestawiono poniżej:
A 10 12 8 10
B 15 12 15 10
C 11 15 20 14
D 5 10 15 6
E 8 10 8 6
Czy światło istotnie wpływa na wielkość biomasy roślin ?