Teoria Sterowania

Teoria Sterowania

Teoria Sterowania

Teoria Sterowania

Teoria Sterowania

Teoria Sterowania

Zadaniem układu regulacji automatycznej (URA) jest
utrzymywanie równości między wielkością regulowaną y a
wielkością zadaną w. Zadanie to może być wykonane jedynie z
pewną dokładnością, określoną przez uchyb (błąd) regulacji:

e(t) = w(t) – y(t)

lub w postaci operatorowej

E(s) = W(s) -

Y(s)

Uchyb regulacji może być wywołany np. zakłóceniami, realizacją
techniczną układu, własnościami transmitancji układu otwartego
(strukturą układu).

Przed układem stawia się określone wymagania dotyczące
zarówno przebiegu procesu przejściowego, czyli przejściowego
sygnału uchybu e

p

(t) (właściwości dynamicznych), jak i jego

wartości w stanie ustalonym e

u

(właściwości statycznych).

Wymienione czynniki stanowią o jakości regulacji. Oceny jakości
regulacji dokonuje się na podstawie szeregu kryteriów
(wskaźników) jakości.

Teoria Sterowania

Teoria Sterowania

Kryteria jakości regulacji można podzielić na kilka grup:

• kryteria związane z parametrami charakterystyki skokowej
(układu zamkniętego),

• kryteria związane z parametrami charakterystyki
częstotliwościowej (zwykle układu otwartego),

• kryteria związane z rozkładem biegunów (i ewentualnie zer)
układu zamkniętego,

• kryteria całkowe (sterowania optymalnego).

Teoria Sterowania

Teoria Sterowania

Dokładność statyczna liniowego układu regulacji

Miarą dokładności statycznej jest uchyb ustalony, tzn. taki, który
utrzymuje się po zaniku procesów przejściowych wywołanych
wymuszeniem lub zakłóceniem:

0

lim ( ) lim ( )

u

t

s

e

e t

sE s

��

�

=

=

Uchyb ustalony jest w ogólności sumą składowych związanych z
wymuszeniem i zakłóceniem:

e

u

= e

uw

+ e

uz

Regulacja powinna spełniać warunek e

u

=0 lub |

e

u

| e

umax

.

Problemy:

• jak uchyb ustalony zależy od transmitancji układu otwartego
G

o

(s) i rodzaju sygnału wymuszenia (zakłócenia),

• jakie są ogólne zasady postępowania w celu zmniejszenia e

u

.

( )

( )

u

p

e t

e e t

= +

Uchyb regulacji jest sumą składowej ustalonej i składowej
przejściowej:

Teoria Sterowania

Teoria Sterowania

Układy statyczne i astatyczne

Wśród liniowych URA można wyróżnić zasadniczo dwa typy
układów:

• układy regulacji statycznej, w których występują uchyby
ustalone proporcjonalne do wartości stałego (skokowego)
wymuszenia;

• układy regulacji astatycznej, w których uchyby ustalone przy
stałym (skokowym) wymuszeniu są równe zeru (układy astatyczne
mogą wykazywać uchyby ustalone przy innych wymuszeniach, np.
rosnących liniowo, parabolicznie itp.).

URA jest układem astatycznym, jeżeli w transmitancji układu
otwartego znajdują się szeregowo włączone człony całkujące.

Teoria Sterowania

Teoria Sterowania

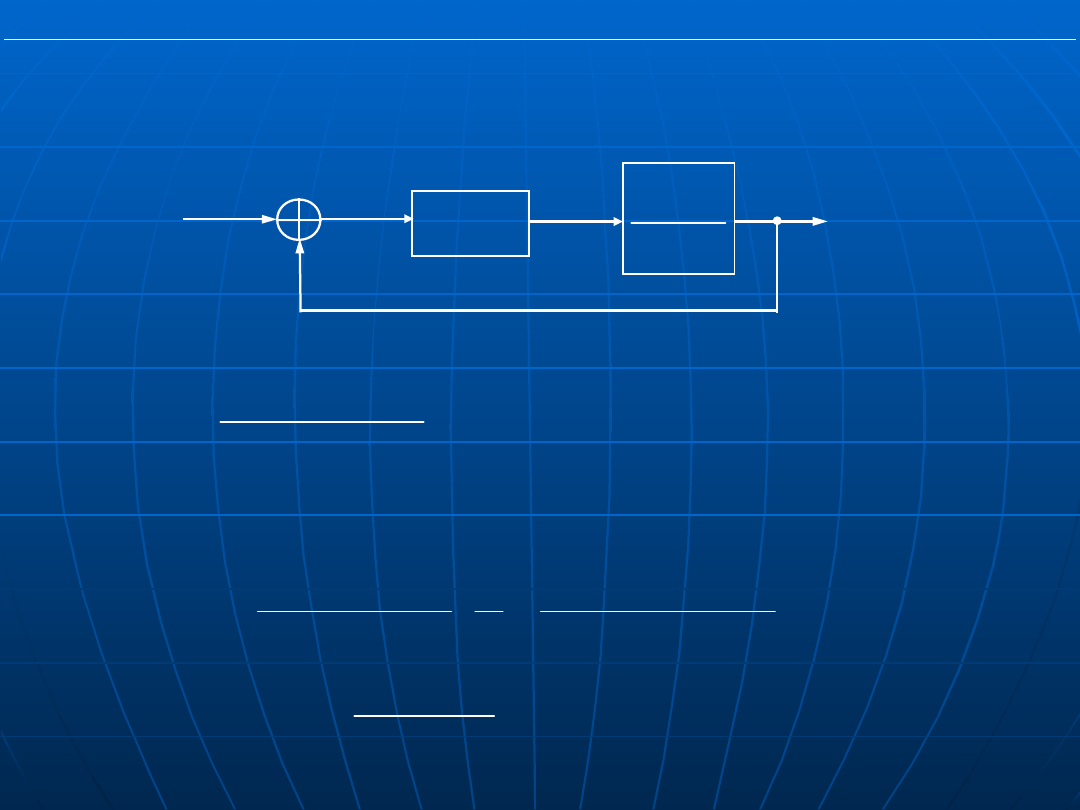
Przykład: Wyznaczyć uchyb ustalony odpowiedzi skokowej
(w(t)=A



1(t)) układu zamkniętego dla: 1) G

r

(s)=K

r

, 2) G

r

(s)=K

r

/s

G

r

(s)

1

p

K

Ts+

_

e(t

)

u(t

)

y(t

)

w(

t)

( )

1

r

p

z

r

p

K K

G s

Ts

K K

=

+ +

( )

( )

( ) [1

( )] ( )

z

E s W s Y s

G s W s

=

-

= -

(

1)

( )

1

1

(

1

)

r

p

r

p

r

p

K K

A

A Ts

E s

Ts

K K

s

s Ts

K K

�

�

+

= -

=

�

�

�

�

+ +

+ +

�

�

1)

lim ( )

1

u

s

r

p

A

e

sE s

K K

��

=

=

+

układ zamknięty jest
układem inercyjnym o
stałej czasowej T/(1+K

r

K

p

)

i współczynniku
wzmocnienia K

r

K

p

/(1+K

r

K

p

)

Teoria Sterowania

Teoria Sterowania

( )

(

1)

r

p

z

r

p

K K

G s

s Ts

K K

=

+ +

(

1)

( )

1

(

1)

(

1)

r

p

r

p

r

p

K K

A

A Ts

E s

s Ts

K K

s

s Ts

K K

�

�

+

= -

=

�

�

�

�

+ +

+ +

�

�

2)

lim ( ) 0

u

s

e

sE s

��

=

=

Układ zamknięty jest układem II rzędu (inercyjnym lub
oscylacyjnym) o współczynniku wzmocnienia równym 1.

Rozważmy w układzie regulacji ze sprzężeniem zwrotnym
transmitancję układu otwartego postaci:

1

1

1

0

1

1

( )

( )

( )

m

m

m

m

o

n

n

l

n

n

l

b s

b s

bs b

L s

G s

M s

a s

a s

a s

-

-

-

-

+

+ + +

=

=

+

+ +

K

K

1

1

0

0

l

a

a

a

-

= = = =

K

Teoria Sterowania

Teoria Sterowania

1

1

1

1

( )

(

)

( )

n

n

l

n

n

l

l

n l

n

l

l

n

n

l

M s

a s

a s

a s

s a s

a s

a

s N s

-

-

-

- -

-

=

+

+ +

=

=

+

+ +

=

K

K

Układ otwarty zawiera l połączonych szeregowo członów
całkujących, bo wielomian mianownika można zapisać jako:

gdzie N(s) jest wielomianem pełnym.
Taki układ nazywa się układem astatycznym l-tego rzędu.

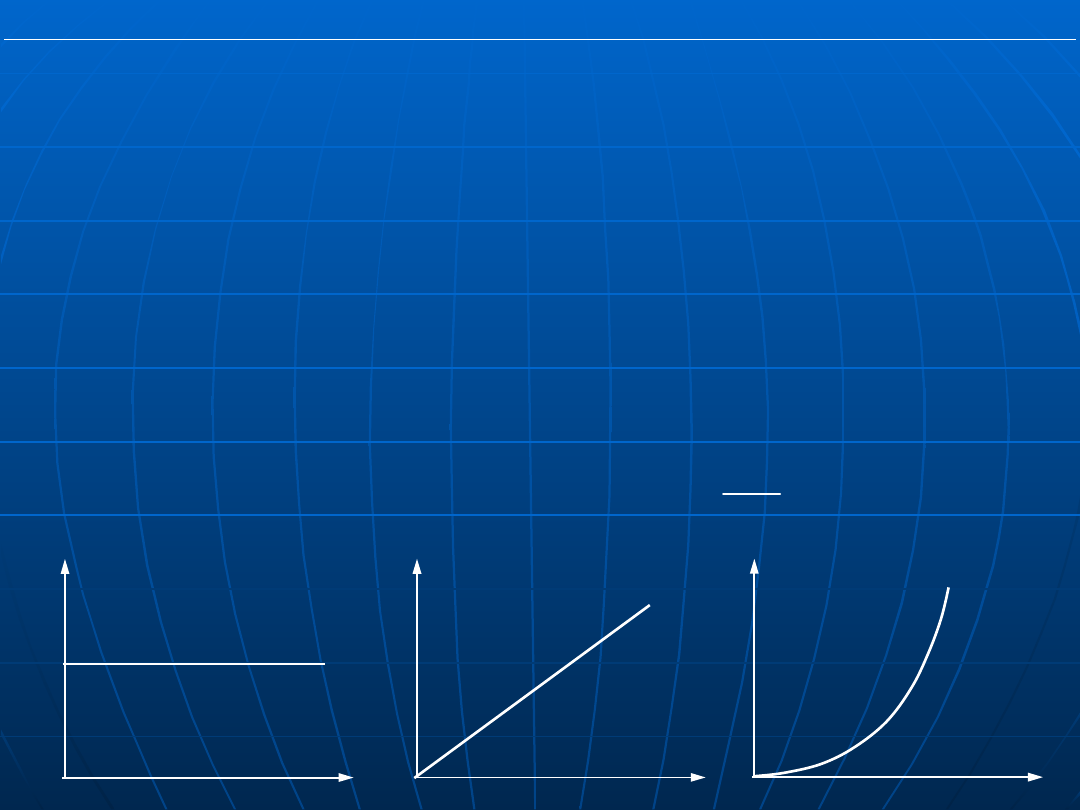
Rozważmy zależność uchybu ustalonego w układzie astatycznym
od wymuszenia (zakładamy brak zakłócenia) w postaci potęgowej
funkcji czasu:

( )

( )

k

k

w t

A t t

=

1

t

w(t),
k=0

t

w(t),
k=1

t

w(t),
k=2

1

!

( )

k

k

k

W s

A

s

+

=

Teoria Sterowania

Teoria Sterowania

Transmitancję uchybową wymuszeniową można zapisać jako:

1

( )

( )

1

( )

( )

( )

l

ew

l

o

s N s

G s

G s

s N s

L s

=

=

+

+

( )

( )

( ) ( )

( )

( )

( )

l

ew

l

s N s

E s

G s W s

W s

s N s

L s

=

=

+

Transformata uchybu i uchyb wymuszeniowy ustalony:

1

0

0

( )

lim ( ) lim

( )

( )

( )

l

uw

l

s

s

s N s

e

sE s

W s

s N s

L s

+

�

�

=

=

+

Teoria Sterowania

Teoria Sterowania

Układ regulacji statycznej to układ, w którym nie ma
szeregowo włączonych członów całkujących (l=0)

1

1

1

0

1

1

1

0

( )

( )

( )

m

m

m

m

o

n

n

n

n

b s

b s

bs b

L s

G s

N s

a s

a s

a s a

-

-

-

-

+

+ + +

=

=

+

+ +

+

K

K

Przy wymuszeniu skokowym w(t)=A

0

1(t), W(s)=A

0

/s, uchyb

ustalony:

0

0

0

0

0

lim ( ) lim

( )

1

1

( )

uw

s

s

A

A

s

e

sE s

L s s

K

N s

�

�

=

=

=

+

+

- współczynnik wzmocnienia układu
otwartego

0

0

0

b

K

a

=

Uchyb ustalony układu statycznego dla wymuszenia liniowo
narastajacego:

1

2

0

( )

lim

( )

( )

uw

s

A

sN s

e

N s

L s s

�

�׮=

+

0

1

1

uw

o

e

A

K

=

+

- współczynnik
statyzmu

Teoria Sterowania

Teoria Sterowania

Istnieje możliwość podwyższania dokładności statycznej układu
(zmniejszania

e

u

)

poprzez

zwiększanie

współczynnika

wzmocnienia układu otwartego K

o

. Nie można jednak dowolnie

zwiększać K

o

, ponieważ powoduje to zwykle pogorszenie

stabilności układu zamkniętego i zwiększa amplitudę sygnału
sterującego (a to wymaga większej mocy sterowania – większych i
droższych elementów wykonawczych).
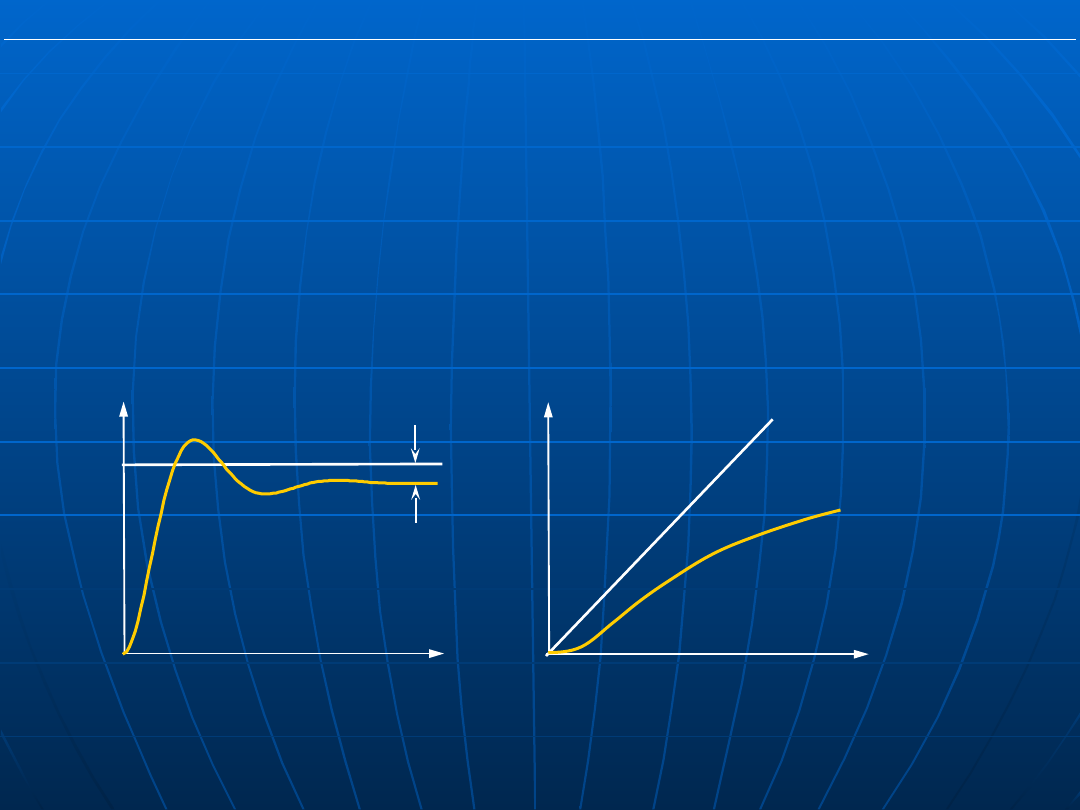
Układ statyczny nie jest w stanie nadążyć za wymuszeniem
zmieniającym się liniowo (a tym bardziej wymuszeniem wyższego
stopnia).

t

w(t
)

y(t)

e

u

t

w(t
)

y(t)

e(t)

Rys. Odpowiedź układu regulacji statycznej na wymuszenie skokowe i
liniowe

Teoria Sterowania

Teoria Sterowania

Układ regulacji astatycznej

Jeżeli na wejście układu astatycznego l-tego rzędu poda się
wymuszenie w formie funkcji potęgowej k-tego stopnia:

( )

( )

k

k

w t

A t t

=

1

1

!

( )

k

k

k

W s

A

s

+

=

1

0

!

( )

lim

( )

( )

l

k

uw

l

k

s

A k

s N s

e

s

s N s

L s s

+

�

=

�

+

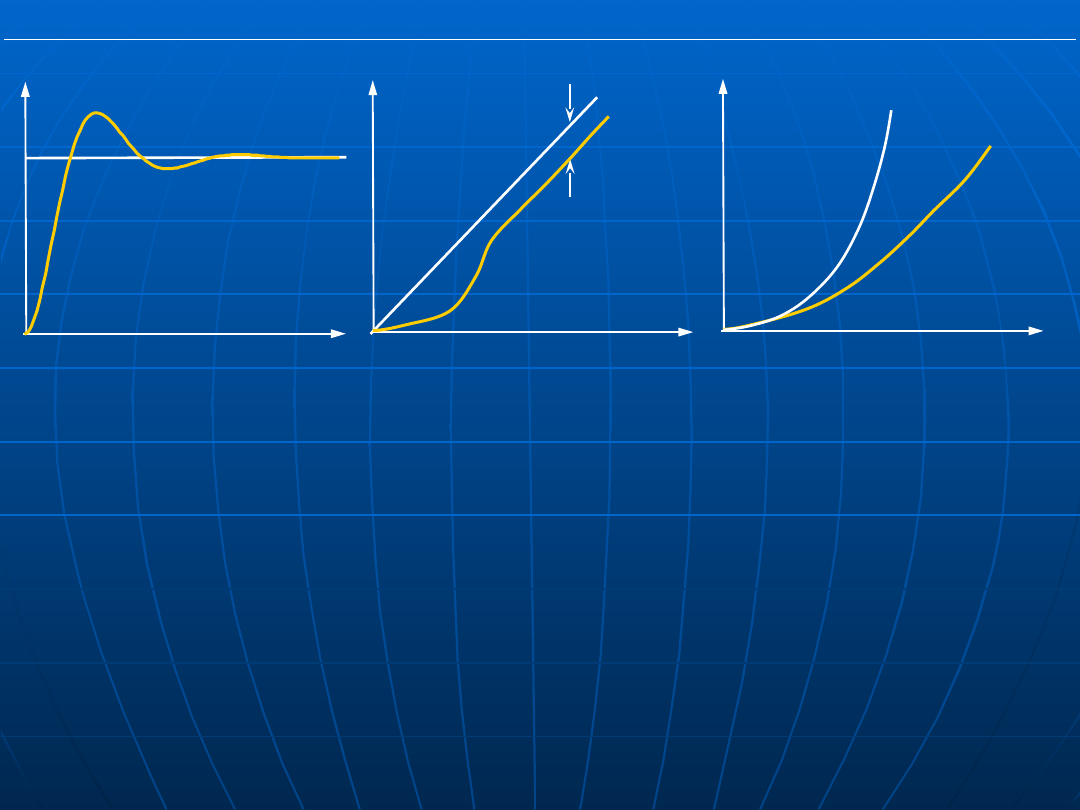
Możliwe jest wystąpienie jednego z trzech przypadków:

1. dla l > k e

uw

=0

2. dla l = k e

uw

=const

3. dla l < k e

uw

=

 

Wniosek: Układ regulacji astatycznej jest w stanie sprowadzić

do zera uchyb ustalony przy wymuszeniu potęgowym, jeżeli ma
wystarczająco wysoki rząd astatyzmu.

Podwyższanie rzędu astatyzmu (włączanie członów całkujących)

wpływa jednak niekorzystnie na stabilność układu zamkniętego
(układy astatyczne rzędu >2 są zwykle niestabilne bez
dodatkowej korekcji).

to uchyb ustalony:

Teoria Sterowania

Teoria Sterowania

t

y(t)

e

u

=0

t

y(t)

e

u

Rys. Typowe odpowiedzi układu regulacji astatycznej I rzędu na

wymuszenie skokowe, liniowe i paraboliczne.

t

y(t)

e(t)

Teoria Sterowania

Teoria Sterowania

Transmitanc

ja układu

otwartego

Typ

układu

Współczynniki

wzmocnienia

układu

otwartego

Wymuszenie

skokowe

w(t)=A

0

1

(t)

liniowe

w(t)=A

1

t1

(t)

paraboliczne

w(t)=A

2

t

2

1(t)

uchyb

statyczny

e

u

uchyb

prędkościo

wy

e

uv

uchyb

przyspieszenio

wy

e

ua

statyczn

y

l=0

statyczny





astatycz

ny

I rzędu

l=1

prędkościowy

0



astatycz

ny

II rzędu

l=2

przyspieszeni

owy

0

0

( )

( )

( )

o

L s

G s

N s

=

( )

( )

( )

o

L s

G s

sN s

=

2

( )

( )

( )

o

L s

G s

s N s

=

0

0

o

b

k

a

=

0

1

v

b

k

a

=

0

2

a

b

k

a

=

0

0

1

u

A

e

k

=

+

1

uv

v

A

e

k

=

2

2

ua

a

A

e

k

=

Teoria Sterowania

Teoria Sterowania

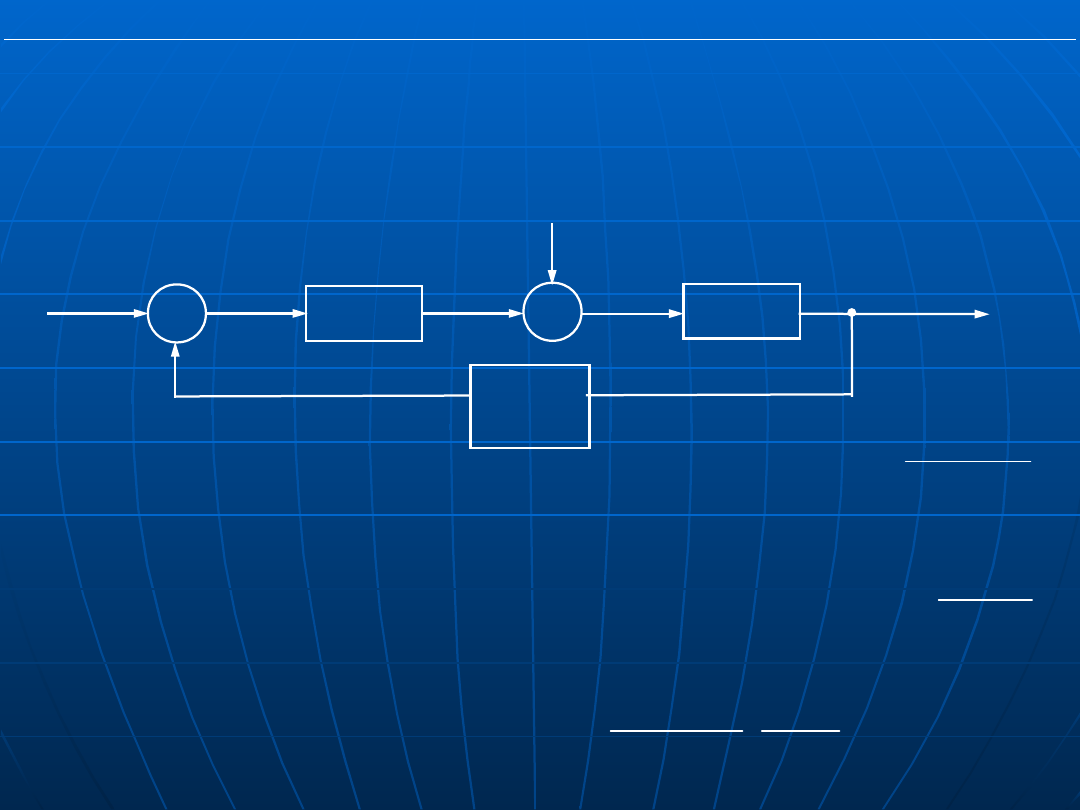
Zależność uchybu zakłóceniowego od transmitancji
regulatora

W przypadku, gdy na wejście obiektu działa zakłócenie (przy braku
wymuszenia), uchyb ustalony zależy od liczby członów całkujących
w transmitancji regulatora G

r

(s).

G

r

(s)

G

p

(s)

w(t)=0 e(t)
u(t)

∑

-

y(t)

+

∑

z(t
)

+

H(s)=

1

( )

( )

( )

r

r

r

r

L s

G s

s M s

=

)

(

1

)

(

t

t

B

t

z

m

m





1

!

)

(







m

m

s

m

B

s

Z

to uchyb ustalony od zakłócenia:

Jeżeli transmitancję regulatora przedstawimy w
postaci:

gdzie L

r

(s), M

r

(s) są wielomianami pełnymi.

a
zakłócenie:

lub w formie
operatorowej:

( )

( )

0

0

!

lim[

( ) ( )] lim

1

p

m

uz

ez

m

s

s

o

G s

B m

e

sG s Z s

G s

s

�

�

�

�

-

=

=

�

�

�

�

�

+

�

�

Teoria Sterowania

Teoria Sterowania

Zadanie: Wyznaczyć uchyb ustalony przy zakłóceniu skokowym

w układzie z obiektem o transmitancji G

p

(s), którego

współczynnik wzmocnienia K

p

=b

p0

/a

p0

dla:

1) G

r

(s)=K

r

(regulator P), 2) G

r

(s)=K

r

/s (regulator I).

Dla r=m>0 wartość uchybu ustalonego:

gdzie K

r

=b

r0

/a

r0

– współczynnik wzmocnienia regulatora.

!

m

uz

r

B m

e

K

=-

Możliwe są trzy przypadki:

1. dla r > m e

uz

= 0

2. dla r = m e

uz

=const

3. dla r < m e

uz

= -

( )

( )

0

0

0

0

lim[

( ) ( )] lim

1

1

p

p

uz

ez

s

s

r

p

r

p

G s

K B

B

e

sG s Z s

s

K G s

s

K K

�

�

�

�

-

-

=

=

�

=

�

�

�

�

+

+

�

�

1)

Jeżeli obiekt zawiera działanie całkujące, to K

p

 i e

uz

=-B

0

/K

r

.

Teoria Sterowania

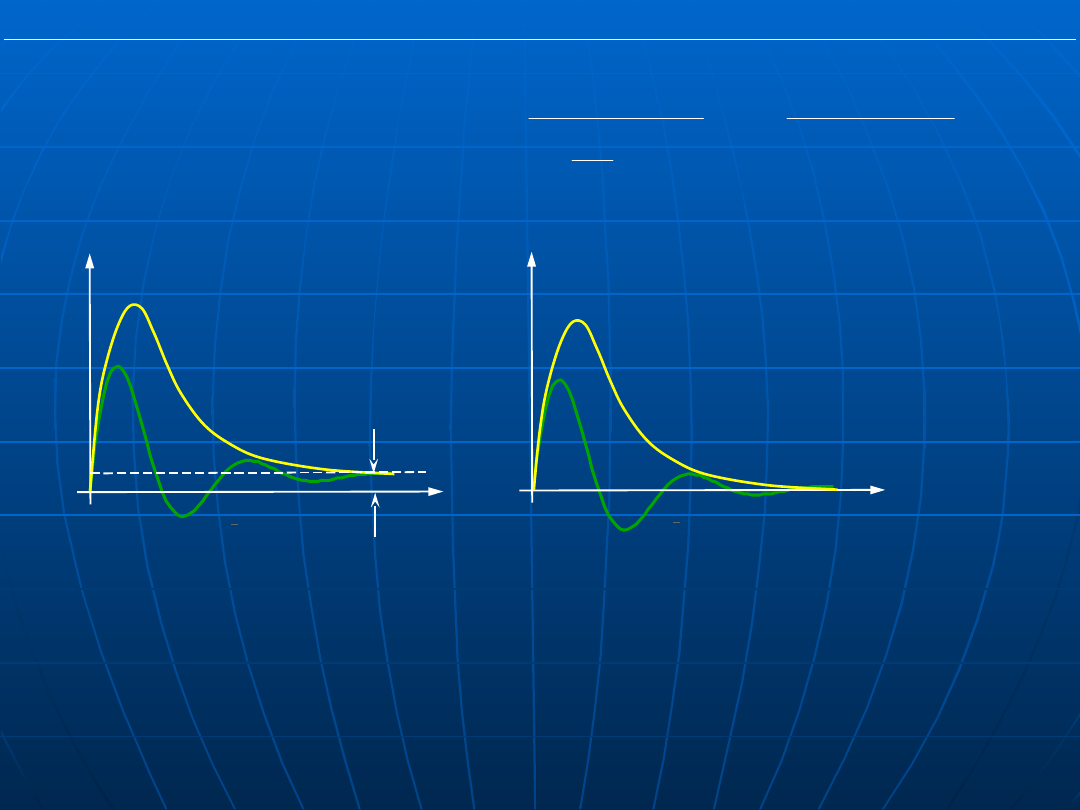
Teoria Sterowania

e

z

(t)

t

e

zu

=

0

e

z

(t)

t

e

zu

Rys. Typowe odpowiedzi (aperiodyczna i oscylacyjna) układu

regulacji na skokowe zakłócenie

( )

( )

( )

( )

0

0

0

0

0

lim[

( ) ( )] lim

lim

0

1

p

p

uz

ez

s

s

s

r

r

p

p

G s B

sG s B

e

sG s Z s

K

s K G s

G s

s

�

�

�

-

-

=

=

=

=

+

+

2)

Teoria Sterowania

Teoria Sterowania

Dokładność dynamiczna liniowego układu
regulacji

Wymagania dynamiczne stawiane układom regulacji często
sprowadzają się do żądania określonego przebiegu przejściowego
sygnału uchybu regulacji e(t) przy skokowym wymuszeniu i/lub
zakłóceniu.

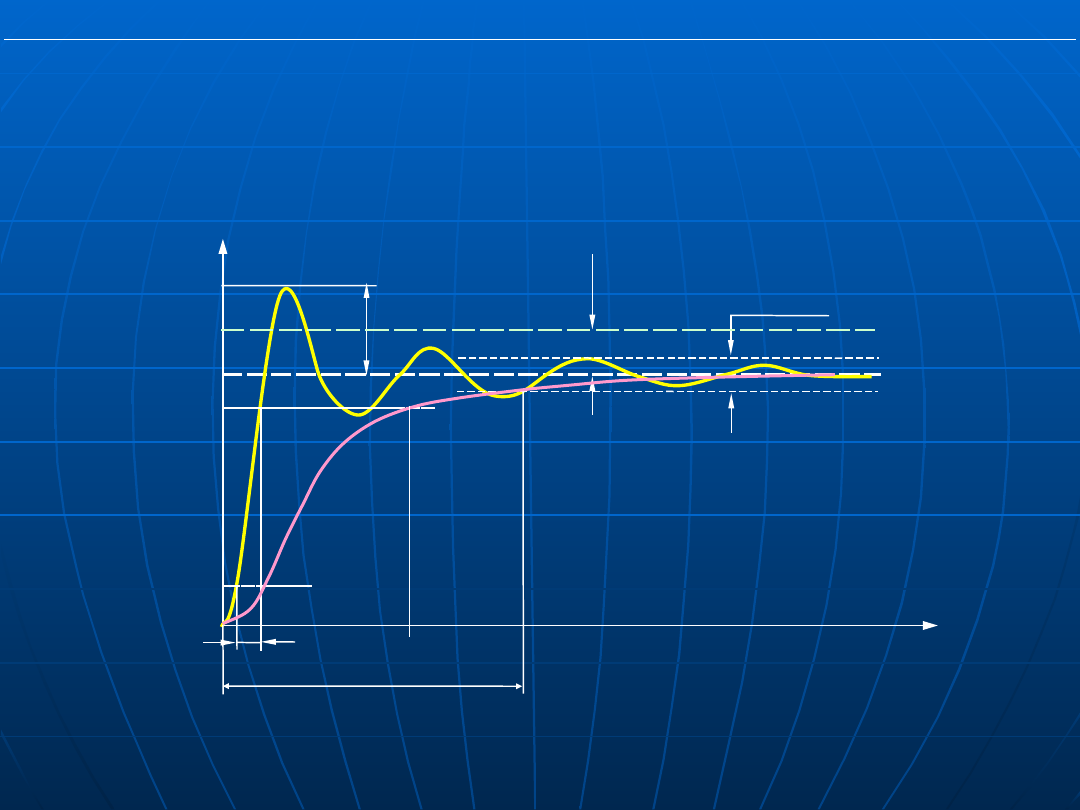
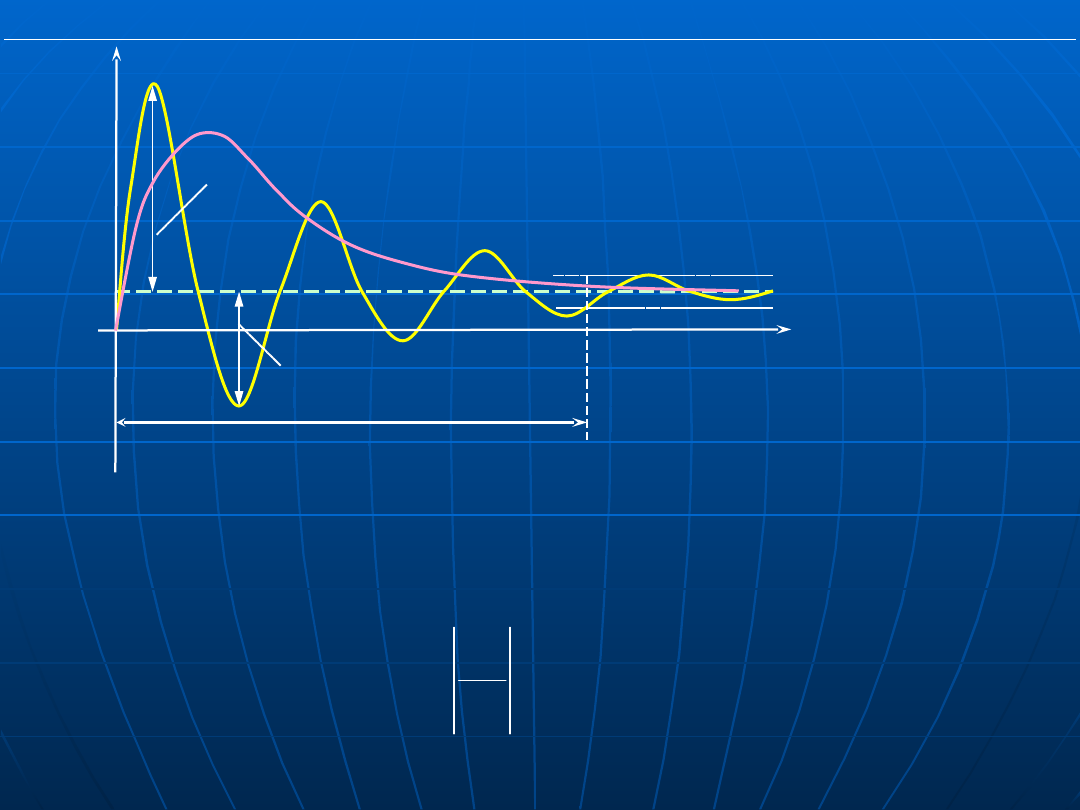
Rys. Przebieg oscylacyjnej i aperiodycznej odpowiedzi układu

regulacji przy skokowej zmianie wartości zadanej

(wymuszenia)

t

y(t
)

y

u

M

p

0,1y

u

0,9y

u

t

n

t

r

=±3% lub

±1%

e

u

w

y

ma

x

Teoria Sterowania

Teoria Sterowania

Wskaźnikami jakości związanymi z przebiegami czasowymi sygnału
sterowanego lub uchybu regulacji są:

• czas ustalania (regulacji) t

r

– jest to czas jaki upływa od chwili

doprowadzenia do układu wymuszenia (lub zakłócenia) do
momentu, gdy wahania sygnału uchybu e(t) wokół e

u

zmniejszą się

trwale poniżej założonej wartości e (zazwyczaj przyjmuje się e

równe 1 lub 3%). Czas regulacji określa czas trwania przebiegów

przejściowych w układzie i jest miarą zarówno szybkości jak i
stabilności układu.

 czas narastania t

n

– jest to czas potrzebny do tego, aby

charakterystyka skokowa układu zmieniła się od 10% do 90%
wartości ustalonej (inna definicja określa czas narastania jako czas
pierwszego osiągnięcia przez sygnał sterowany wartości zadanej).
Czas narastania określa szybkość działania układu regulacji.

 przeregulowanie M

p

- jest to stosunek maksymalnego

przeregulowania odpowiedzi skokowej do wartości stanu
ustalonego y

u

. Przeregulowanie odpowiedzi skokowej jest miarą

stabilności układu zamkniętego.

max

100%

u

p

u

y

y

M

y

-

=

�

Teoria Sterowania

Teoria Sterowania

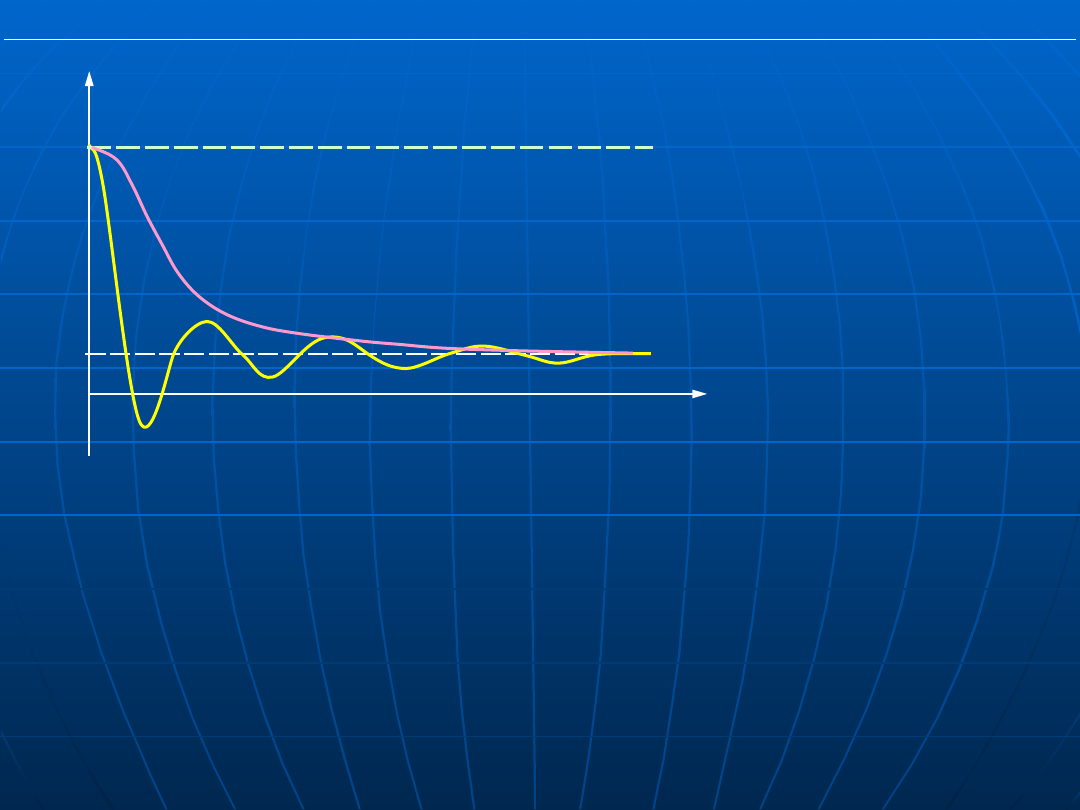
Rys. Przebieg
oscylacyjnego i
aperiodycznego
przebiegu uchybu
regulacji przy
skokowym
wymuszeniu

t

e(t)= w(t)- y(t)

e

u

w

0

Podane wymagania są wzajemnie przeciwstawne, np.
zwiększenie szybkości regulacji pogarsza stabilność układu.
Przy projektowaniu regulacji podaje się zwykle ich
maksymalne dopuszczalne wartości lub przedziały wartości.

Teoria Sterowania

Teoria Sterowania

Rys. Przebieg uchybu

regulacji przy skokowej

zmianie zakłócenia

(wymuszenie w(t)=0)

e

p1

e

p2

0

e(t
)

t

t

r

e

Jeżeli rozpatrywany jest przebieg uchybu regulacji (np. w
odpowiedzi na skokowe zakłócenie) lub odpowiedź swobodna
układu), to jako wskaźnik analogiczny do M

p

stosuje się

współczynnik zanikania



tj. iloraz wartości bezwzględnych

amplitud dwóch sąsiednich przeregulowań:

2

1

100%

p

p

e

e

k =

�

Dla przebiegów aperiodycznych
M

p

==0.

Teoria Sterowania

Teoria Sterowania

Jeżeli układ zamknięty (nawet jeśli jest to układ wyższego rzędu)
ma 2 bieguny dominujące, to można go aproksymować
transmitancją członu II rzędu:

1.4dla

0.3

4.6 dla

1%

ln

, gdzie

,

, gdzie

1.8dla

0.5,

3.5dla

3%

2.1dla

0.7

r

n

n

e

t

t

e

z

b

a

b

a

z

s

s

w

z

=

�

D =

�

-

D

�

=

=

=

�

=

=

�

�

D =

�

�

=

�

exp

100%

p

d

M

ps

w

�

�

-

=

�

�

�

�

�

























3

.

0

dla

%

35

5

.

0

dla

%

15

7

.

0

dla

%

5

p

M

2

2

2

2

)

(

n

n

n

s

s

s

G













Analizując wzór na charakterystykę skokową tego członu można
podać zależności między parametrami transmitancji a wskaźnikami
jakości:

Często spotykane wartości
przybliżone:

gdzie:

=

n

,

2

1

d

n

w

w

z

=

-

Peak time:

t

max

=/

d

Teoria Sterowania

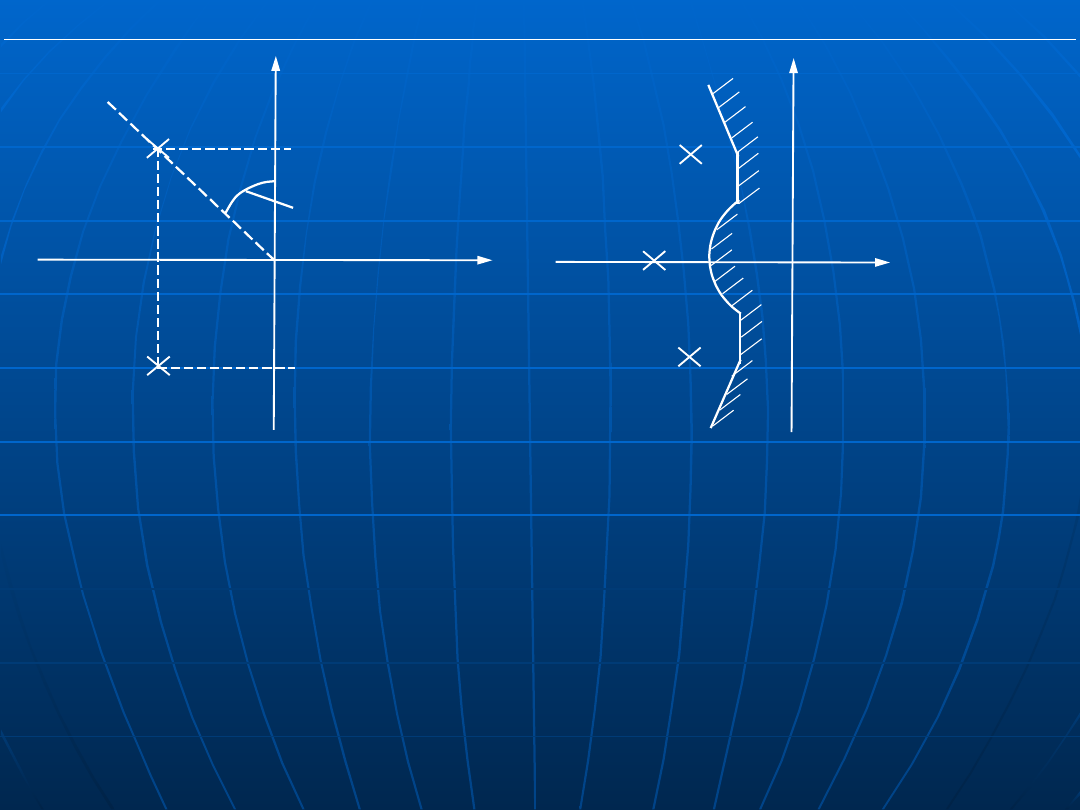
Teoria Sterowania

Re s

Im s



j



d

-j



d



n

arcsinz

Re s

Im s

obszar

zakaza

ny

Rys. Obszar zakazany dla biegunów układu zamkniętego przy

minimalnych dopuszczalnych wartościach wskaźników

(

,



n

,



)

i związanych z nimi

(

t

r

, t

n

, M

p

).

Teoria Sterowania

Teoria Sterowania

Całkowe kryteria jakości regulacji

Optymalizacja układu regulacji ma za zadanie uzyskanie możliwie
krótkiego czasu regulacji i jak najmniejszego przeregulowania.
Wymagania te są sprzeczne ze sobą i dlatego konieczny jest
kompromis. Kompromis taki zapewniają kryteria całkowe, mające
charakter kryteriów globalnych, oceniających cały przebieg
sygnału błędu e

p

(t). Polegają one na żądaniu minimalizacji

jednego z całkowych wskaźników jakości:

 kryterium ISE (Integral Squared Error):

dt

t

e

I

p

ISE







0

2

)

(

Zastosowanie kryterium ISE do układu II rzędu daje tłumienie
=0.5 i przeregulowanie M

p

=16%.

 kryterium IAE (Integral of Absolute Error):

0

| ( )|

IAE

p

I

e t dt

�

=

�

Zastosowanie kryterium IAE do układu II rzędu daje tłumienie
=1 (M

p

=0%).

Teoria Sterowania

Teoria Sterowania

 kryterium ITAE (Integral of Time by Absolute Error):

0

| ( )|

ITAE

p

I

t e t dt

�

=

�

Zastosowanie kryterium ITAE do układu II rzędu daje tłumienie
=1/2=0.707 i przeregulowanie M

p

=4%. Mnożenie przez czas t

odpowiada nadawaniu wagi wartości bezwzględnej błędu.
Kryterium ITAE znajduje szerokie zastosowanie w technice,
ponieważ prowadzi do kompromisu: niewielkie przeregulowanie
przy stosunkowo krótkim czasie regulacji.
Jeżeli układ zamknięty jest opisany transmitancją n-tego rzędu
postaci:

to optymalne w sensie ITAE wielomiany mianownika są
następujące:

)

(

)

(

)

(

)

(

0

s

M

b

s

X

s

Y

s

G

n

z





1

0

( )

M s

s w

= +

2

2

2

0

0

( )

1.41

M s

s

s

w

w

= +

+

3

2

2

3

3

0

0

0

( )

1.75

2.1

M s

s

s

s

w

w

w

= +

+

+

4

3

2 2

3

4

4

0

0

0

0

( )

2.1

3.4

2.7

M s

s

s

s

s

w

w

w

w

= +

+

+

+

gdzie 

0

oznacza częstotliwość drgań własnych układu i określa

jego zadane pasmo przenoszenia.

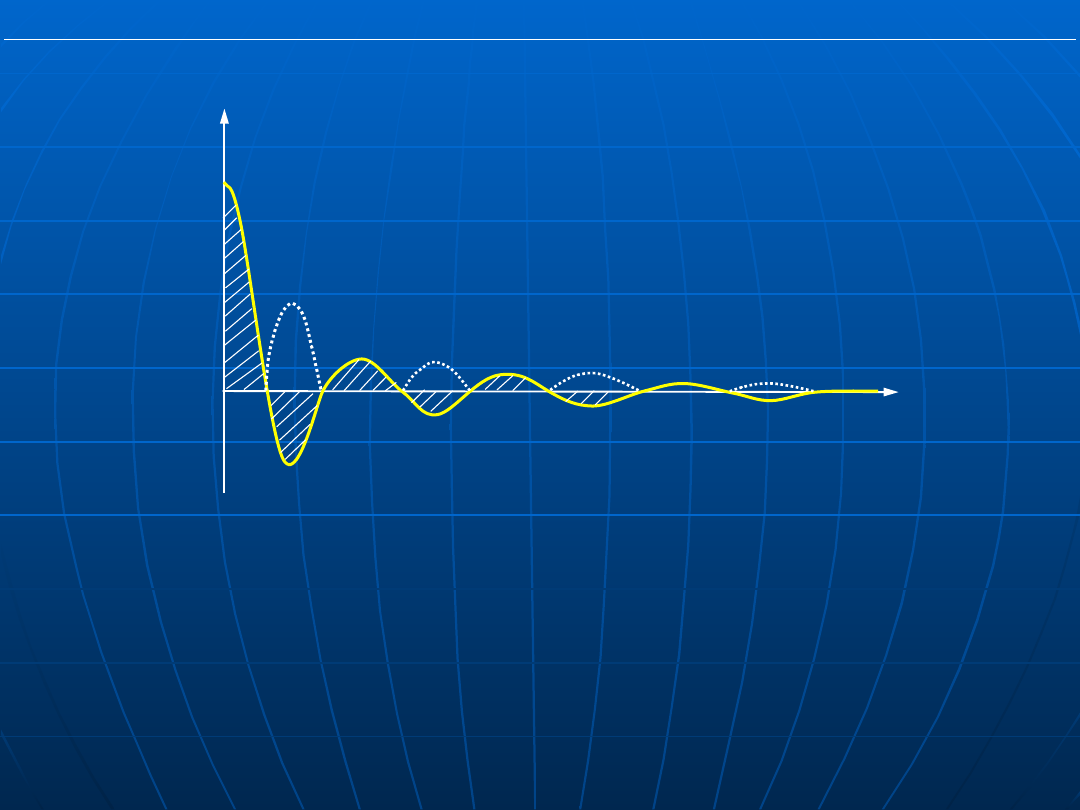
Teoria Sterowania

Teoria Sterowania

t

e

p

(t), |

e

p

(t)|

e

p

(0)

0

Minimalizacja wskaźników całkowych (tzw. funkcji kosztu) stanowi
podstawę sterowania optymalnego.
Często stosowany jest wskaźnik zawierający kombinację energii
uchybu i wielkości sterującej (



– waga):

2

2

0

[ ( )

( )]

J

e t

u t dt

r

�

=

+

�

Teoria Sterowania

Teoria Sterowania