WYKŁAD 7

• Potencjał chemiczny
• Równowaga fazowa – współczynnik podziału Nernsta
• Kataliza, reakcje enzymatyczne

Zakład Farmakokinetyki i Farmacji Fizycznej, 2004

POTENCJA

POTENCJA

Ł

Ł

CHEMICZNY

CHEMICZNY

 

]

mol

J

[

1

























i

j

n

p,

T,

i

i

n

G

μ

CZĄSTKOWA MOLOWA ENTALPIA SWOBODNA

Potencjał chemiczny substancji (

i

) przedstawia udział

wnoszony

przez tę substancję w całkowitą entalpię swobodną
układu.

G = f (T, p, n)

Dla układu jednofazowego dwuskładnikowego (np. roztwór składający
się z rozpuszczalnika A i substancji rozpuszczonej B):

G = f (T, p, n

1

, n

2

)

A

B

n

p,

T,

A

A

μ

n

G

G





















B

A

n

p,

T,

B

B

μ

n

G

G





















Całkowita entalpia swobodna roztworu:

G = n

A

G

A

+ n

B

G

B

G = n

A



A

+ n

B



B



A ,



B

-

potencjały chemiczne przy danym składzie mieszaniny

Dla układu dwuskładnikowego równanie:

dG = V dp - S dT

przybiera postać:

dG = V dp - S dT + 

A

dn

A

+



B

dn

B

maks.

e,

W

dG 

Jeżeli T, p = const

dG = 

A

dn

A +



B

dn

B

maks.

e,

W

Zatem:

= 

A

dn

A

+



B

dn

B

Praca nieobjętościowa może być spowodowana zmianą składu
chemicznego układu.

Dla mieszaniny dwuskładnikowej:

G = n

A



A

+ n

B



B

ponieważ potencjały chemiczne zależą od składu, więc gdy skład
ulega zmianie:

dG = 

A

dn

A

+



B

dn

B

+ n

A

d

A

+

n

B

d

B

Jeżeli T, p = const to:

dG = 

A

dn

A +



B

dn

B



A

dn

A

+



B

dn

B

+ n

A

d

A

+

n

B

d

B

= 

A

dn

A +



B

dn

B

n

A

d

A

+

n

B

d

B

= 0

RÓWNANIE GIBBSA – DUHEMA

RÓWNANIE GIBBSA – DUHEMA

 

0

μ

d

n

i

i

i





Potencjał chemiczny jednego ze składników mieszaniny
nie może się zmieniać w sposób niezależny od
potencjałów chemicznych pozostałych składników.

A

B

A

B

μ

d

n

n

-

μ

d



Potencjał chemiczny gazu doskonałego

Potencjał chemiczny gazu doskonałego

pod ci

pod ci

ś

ś

nieniem

nieniem

p:

p:

 

















Θ

Θ

p

p

ln

T

R

μ

μ

μ

Θ

- standardowy potencjał chemiczny, czyli

molowa entalpia swobodna czystego gazu
pod ciśnieniem 1 atm ( 10

5

Pa )

= f (T, p)

μ

Θ

Dla mieszaniny gazów A i B:

A

Θ

A

A

p

ln

T

R

μ

μ





B

Θ

B

B

p

ln

T

R

μ

μ







A ,



B

-

potencjały chemiczne składników A i B w mieszaninie lub roztworze

Potencjał chemiczny składnika mieszaniny ciekłej:

Potencjał chemiczny składnika mieszaniny ciekłej:

 

= f (T, p) - standardowy potencjał chemiczny
(a = 1)

 

i

Θ

i

a

ln

T

R

μ

μ

i





μ

Θ





i

i

Θ

i

f

X

ln

T

R

μ

μ

i





i

i

Θ

i

f

ln

T

R

X

ln

T

R

μ

μ

i







Ponieważ a

i

= X

i

f

i

X

ln

T

R

μ

μ

i

Θ

i

i





roztwór idealny (f

i

= 1):

c

ln

T

R

μ

μ

i

Θ

i

i





roztwór rozcieńczony:

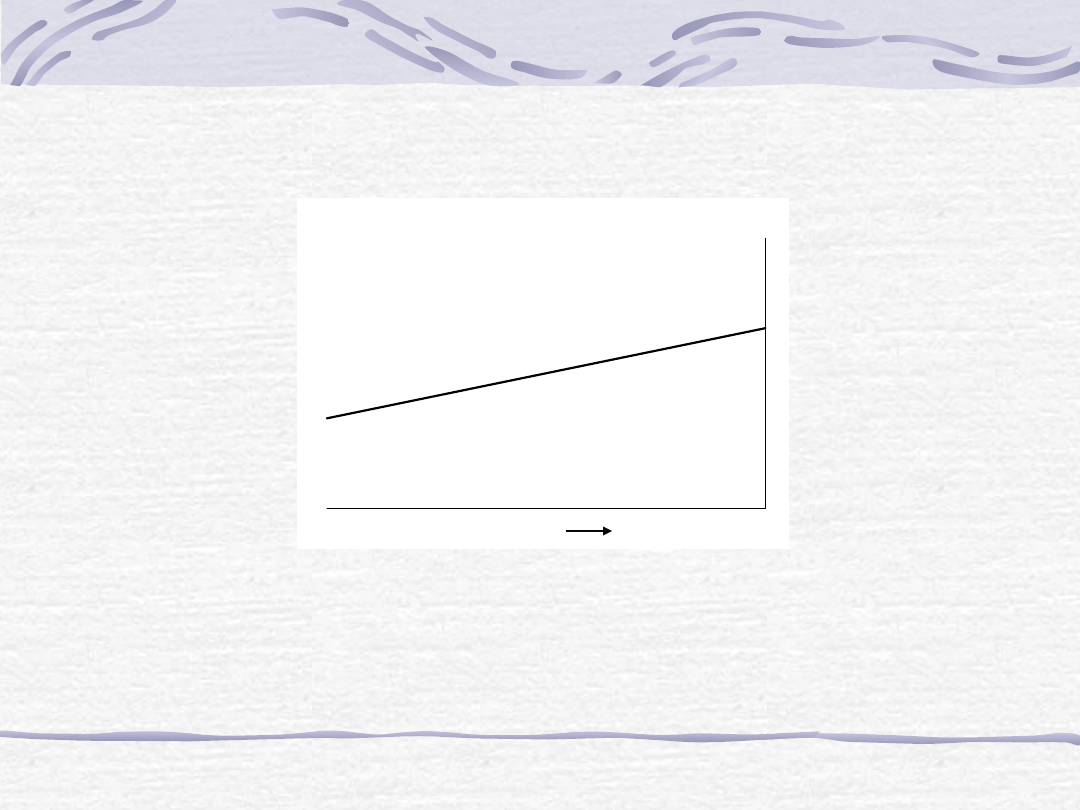
Potencjał

chemiczny

składnika

roztworu

doskonałego (

i

) jako funkcja jego ułamka

molowego X

i

lnX

i

μ

Θ

i

i

μ

0

X

ln

T

R

μ

μ

i

Θ

i

i





Potencjał chemiczny charakteryzuje zdolność danego składnika układu
do opuszczania jednej z faz układu.

W samorzutnie zachodzących przemianach fazowych
(parowanie, krzep-
nięcie, krystalizacja), przy powstawaniu roztworów i w
przebiegu reakcji
chemicznych określony składnik układu może przejść
jedynie z fazy układu o wyższym potencjale chemicznym do
fazy o niższym potencjale.

W stanie równowagi potencjały chemiczne każdego składnika
układu
są we wszystkich fazach jednakowe.

W procesie samorzutnym:

 

i

· dn

i

< 0

natomiast w stanie równowagi:

 

i

· dn

i

= 0

gdzie: dn

i

– przyrost liczby moli składnika układu

RÓWNOWAGA FAZOWA W UKŁADACH

RÓWNOWAGA FAZOWA W UKŁADACH

WIELOSKŁADNIKOWYCH, WIELOFAZOWYCH

WIELOSKŁADNIKOWYCH, WIELOFAZOWYCH

 

TERMODYNAMICZNE KRYTERIUM RÓWNOWAGI

 

W stanie równowagi potencjał chemiczny substancji w całym
układzie jest taki

sam, bez względu na liczbę faz.

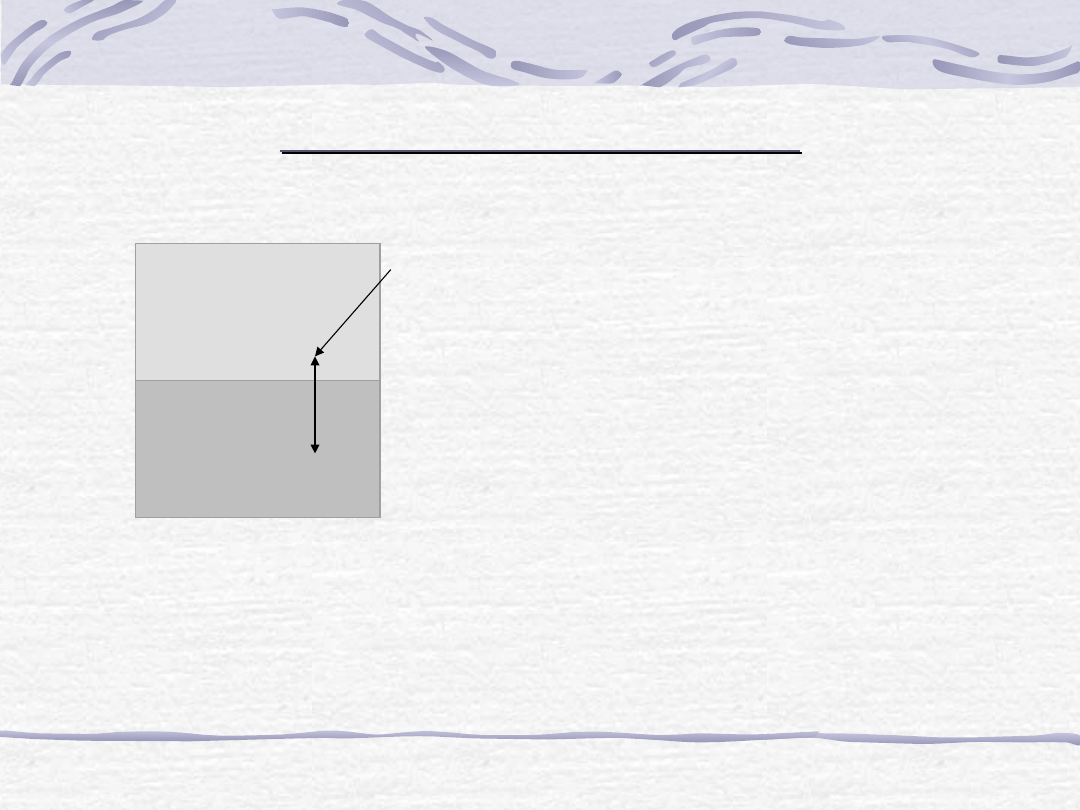
faza ciekła



 

faza ciekła



 

PRAWO PODZIAŁU NERNSTA

PRAWO PODZIAŁU NERNSTA

opisuje rozdział substancji między dwie nie mieszające się ze sobą fazy ciekłe.

 

substancja

( i )

W stanie równowagi fazowej, dla T, p =
const:

 

- standardowy potencjał chemiczny
składnika i
odpowiednio w fazie  i 

- aktywność składnika i odpowiednio
w fazie  i 

 

β

i

α

i

μ

μ 

α

i

α

Θ

i

α

i

a

ln

T

R

μ

μ





β

i

β

Θ

i

β

i

a

ln

T

R

μ

μ





μ

,

μ

β

i

α

i

a

,

a

β

i

α

i

=

β

i

α

i

μ

μ 

α

i

α

Θ

i

a

ln

T

R

μ



β

i

β

Θ

i

a

ln

T

R

μ



μ

-

μ

a

ln

T

R

-

a

ln

T

R

α

Θ

i

β

Θ

i

β

i

α

i



T

R

μ

-

μ

a

ln

-

a

ln

α

Θ

i

β

Θ

i

β

i

α

i



T

R

μ

-

μ

a

a

ln

α

Θ

i

β

Θ

i

β

i

α

i



T

R

μ

-

μ

β

i

α

i

α

Θ

i

β

Θ

i

e

a

a



W warunkach T, p = const:

czyli:

 

const

T

R

μ

-

μ

α

Θ

i

β

Θ

i



K

const

e

T

R

μ

-

μ

α

Θ

i

β

Θ

i





K

a

a

β

i

α

i



a

a

K

β

i

α

i

β

/

α



Roztwór idealny (f

i

= 1):

X

X

K

i

i

/











WSPÓŁCZYNNIK PODZIAŁU NERNSTA JEST RÓWNY
ILORAZOWI STĘŻEŃ SUBSTANCJI ROZPUSZCZONEJ W DWÓCH
NIEMIESZAJĄCYCH SIĘ FAZACH CIEKŁYCH, W STANIE
RÓWNOWAGI FAZOWEJ, W STAŁEJ TEMPERATURZE.

c

c

K

β

i

α

i

β

/

α



Roztwór rozcieńczony:

Równania słuszne gdy:

ciecze nie mieszają się ( lub mieszają się ograniczenie )

stężenie substancji rozpuszczonej w obu fazach nie jest duże
( roztwory rozcieńczone )

nie zachodzi dysocjacja ani asocjacja cząsteczek substancji
rozpuszczonej w żadnej z faz

stała temperatura
 

Wartość współczynnika podziału ( K ):

zależy od rodzaju składników układu (cieczy i substancji) oraz od
temperatury

nie zależy od ilości substancji rozpuszczonej i objętości cieczy

WSPÓŁCZYNNIK PODZIAŁU OLEJ / WODA

WSPÓŁCZYNNIK PODZIAŁU OLEJ / WODA

(

(

K

K

O/W

O/W

)

)

c

c

K

w

o

w

/

o



  C

o

- stężenie substancji w fazie olejowej (niepolarnej)

C

w

- stężenie substancji w fazie wodnej (polarnej)

 

 

dysocjacja cząsteczek substancji w fazie wodnej:

- stopień dysocjacji





α

-

1

c

c

K

w

o

w

/

o



asocjacja cząsteczek substancji w fazie olejowej:

n - stopień asocjacji

 

c

c

K

w

n

o

w

/

o







α

-

1

c

c

K

w

n

o

w

/

o



dysocjacja cząsteczek substancji w fazie wodnej i asocjacja w
fazie olejowej:

ZASTOSOWANIE WSPÓŁCZYNNIKA PODZIAŁU NERNSTA

ZASTOSOWANIE WSPÓŁCZYNNIKA PODZIAŁU NERNSTA

 

 

• określanie właściwości substancji
 
> 1

substancja ma charakter lipofilny (c

o

>

c

w

)

(większe powinowactwo do fazy olejowej)
 

< 1

substancja ma charakter hydrofilny (c

o

< c

w

)

(większe powinowactwo do fazy wodnej)

 

 

w

/

o

K

w

/

o

K

• QSAR (Quantitative Structure-Activity Relationships)

• proces ekstrakcji

(przewidywanie najkorzystniejszych warunków ekstrakcji - dobór
odpowiedniego rozpuszczalnika, przewidywanie stopnia rozdziału
składników)

Ekstrakcja substancji z fazy ciekłej

Ekstrakcja substancji z fazy ciekłej





do fazy ciekłej

do fazy ciekłej





 

m

o

– początkowa masa substancji w fazie



Zgodnie z prawem podziału Nernsta:

m



,

m



–

masa substancji zawarta odpowiednio w fazie

 i  (w stanie

równowagi fazowej)
v



,

v



– objętość fazy  i 

β

β

α

α

β

/

α

v

m

v

m

K



 

 

stan równowagi

faza ciekła



m



v



faza ciekła



m



v



Po jednorazowej ekstrakcji:

m

1

– masa substancji w fazie 

(m

0

- m

1

) - masa substancji w fazie 

po przekształceniach:

Po kolejnych ekstrakcjach w fazie



pozostaje m

2,

m

3

... m

n

gramów substancji.

 

K

v

m

-

m

v

m

β

/

α

β

1

ο

α

1



β

α

β

/

α

α

β

/

α

ο

1

v

v

K

v

K

m

m





v

v

K

v

K

m

m

n

β

α

β

/

α

α

β

/

α

ο

n



















 

Ilość przeprowadzonej substancji z fazy  do  zależy od liczby

powtarzanych

operacji

(ekstrakcji) oraz od objętości użytych cieczy. Większą wydajność ekstrakcji
osiąga się przy wielokrotnie powtarzanym wytrząsaniu małymi porcjami
fazy .

Masa substancji pozostała w fazie



po n – krotnej

ekstrakcji:

EKSTRAKCJA

EKSTRAKCJA

to

to

proces wyodrębniania substancji z

proces wyodrębniania substancji z

jednej fazy do

jednej fazy do

drugiej

drugiej

 

 

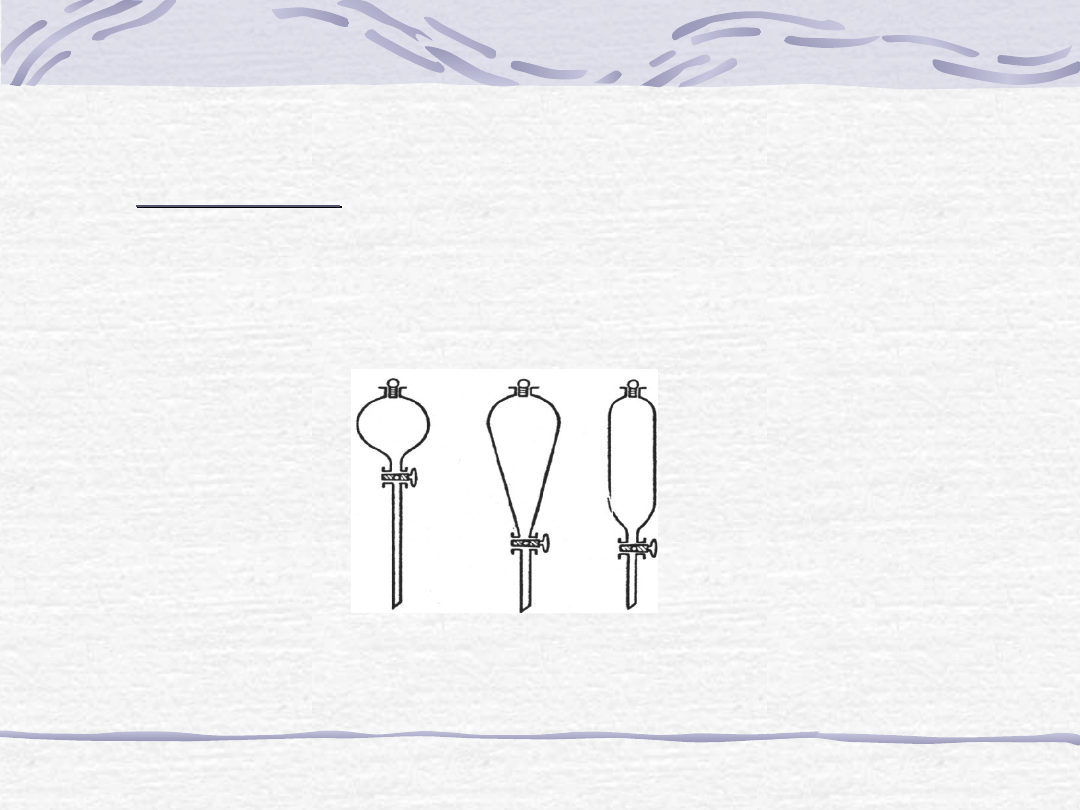
Ekstrakcja prosta (w rozdzielaczach):

Różne typy rozdzielaczy

 

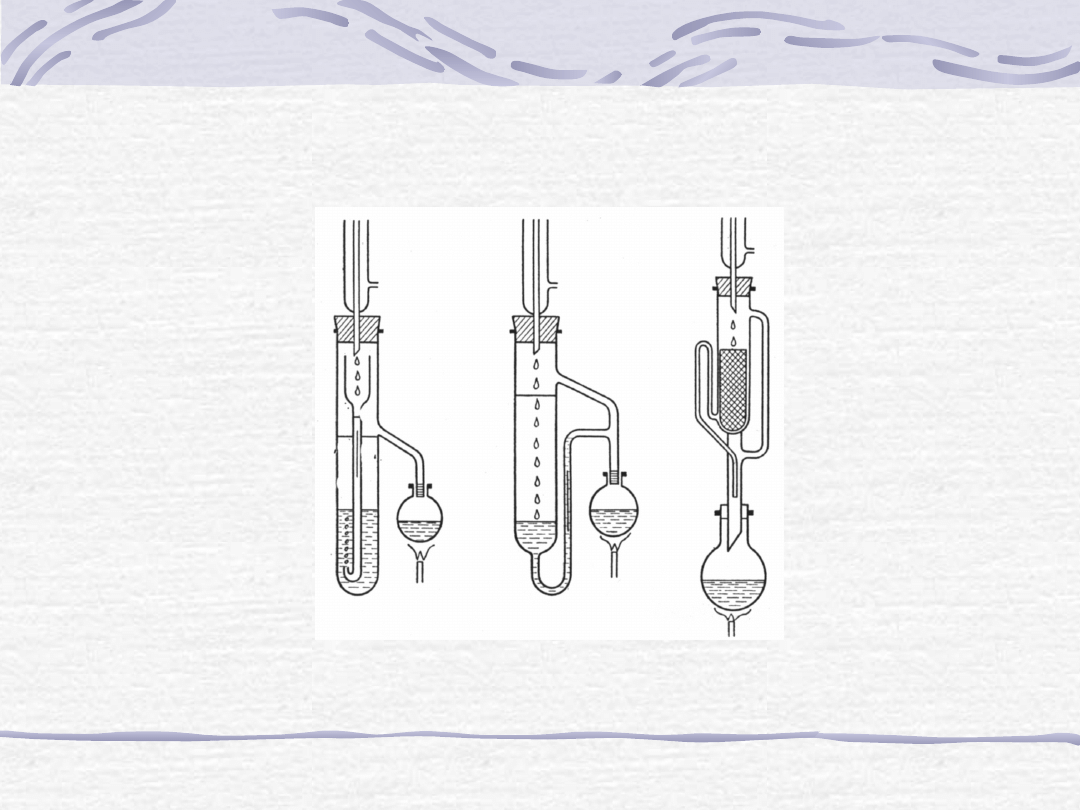
Ekstrakcja ciągła (w ekstraktorach):

Aparat do ekstrakcji ciągłej za pomocą cieczy lżejszej od wody (a), cieczy cięższej od wody (b)
oraz aparat Soxhleta do ekstrakcji substancji z ciał stałych (c).

a

b

c

KATALIZA

KATALIZA

W uk

W uk

ł

ł

adzie homogenicznym

adzie homogenicznym

(gdy katalizator oraz substraty i produkty reakcji stanowi

(gdy katalizator oraz substraty i produkty reakcji stanowi

ą

ą

jedną fazę

jedną fazę

np. utlenianie SO

np. utlenianie SO

2

2

wobec tlenków azotu, powstawanie eteru

wobec tlenków azotu, powstawanie eteru

etylowego

etylowego

wobec H

wobec H

2

2

SO

SO

4

4

)

)

W uk

W uk

ładzie heterogenicznym

ładzie heterogenicznym

(gdy katalizator stanowi odrębną fazę, przy czym

(gdy katalizator stanowi odrębną fazę, przy czym

najczęściej jest on ciałem stałym i nosi nazwę kontaktu np.

najczęściej jest on ciałem stałym i nosi nazwę kontaktu np.

czerń platynowa podczas ulteniania SO

czerń platynowa podczas ulteniania SO

2

2

, żelazo w procesie

, żelazo w procesie

konwersji gazu wodnego)

konwersji gazu wodnego)

W układzie mikroheterogenicznym

W układzie mikroheterogenicznym

(gdy heterogeniczny katalizator znajduje się w stanie

(gdy heterogeniczny katalizator znajduje się w stanie

rozdrobnienia koloidalnego np. enzym)

rozdrobnienia koloidalnego np. enzym)

Apoenzym + koenzym = holoenzym (E)

E + S

ES P + E

k

1

k

3

k

2

v

1

=k

1

[E-ES][S]

v

2

=k

2

[ES]

v

3

=k

3

[ES]

Ponieważ [ES] tworzy się z szybkością v

1

, a rozpada z z szybkością v

2

+v

3

to w stanie równowagi:

v

1

= v

2

+v

3

k

1

[E-ES][S] = (k

2

+k

3

) [ES]

m

2

K

k

k

k

[ES]

ES][S]

-

[E







1

3

gdzie K

m

to stała Michaelisa

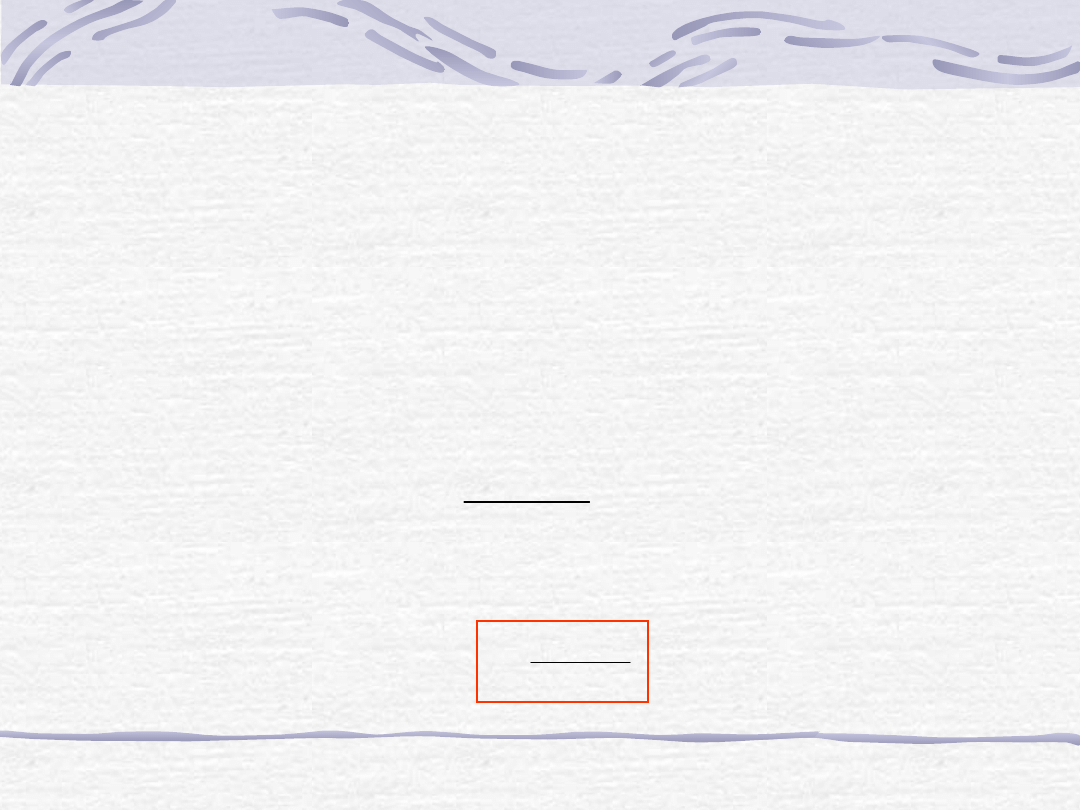
v = v

3

= k

3

[ES]

O szybkości całej reakcji enzymatycznej decyduje v

3

, czyli:

Gdy [S] jest tak duże, że wszystkie cząsteczki E wezmą udział w tworzeniu ES,
czyli gdy [ES] = [E], wówczas:

V

maks

= k

3

[E]

m

K

[ES]

ES][S]

-

[E



Jeśli wyliczymy [ES] i [E] i wstawimy je do równania:

otrzymamy:

[S]

K

[S]

V

v

m

maks





S

K

S

V

v

m

maks







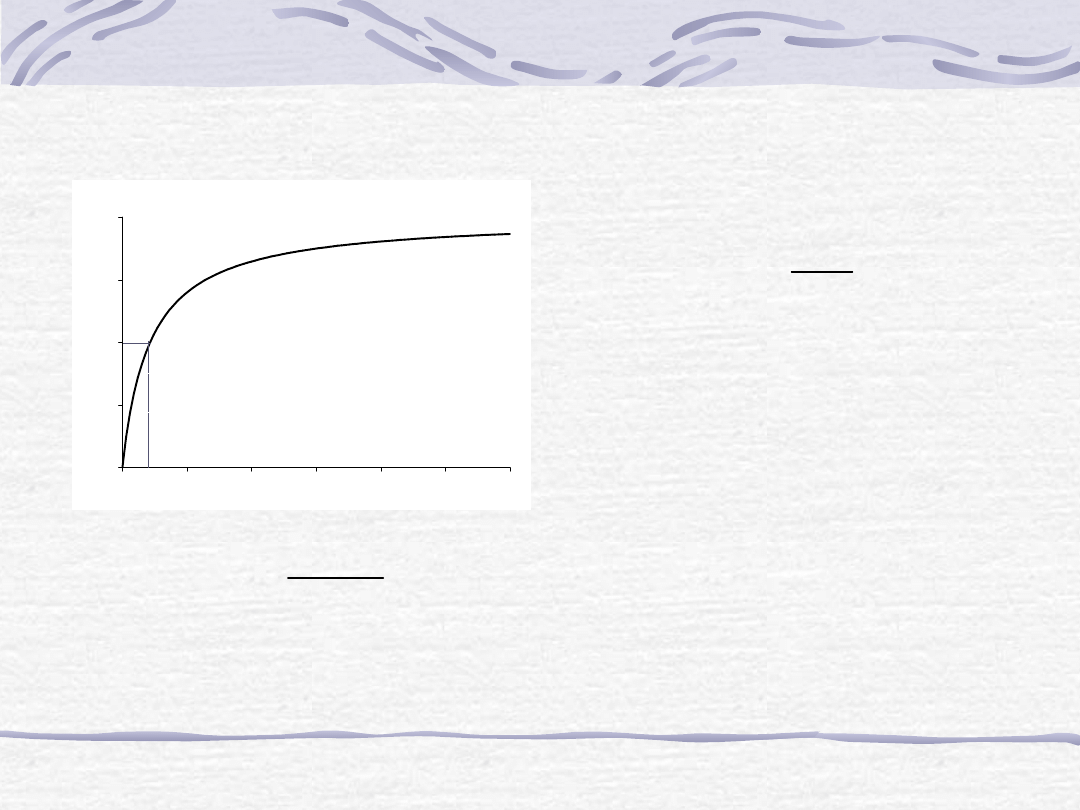
Równanie Michaelisa-Menten

S (mol/l)

0.0

0.1

0.2

0.3

0.4

0.5

0.6

v

(m

m

o

l/l

m

in

)

0.0

0.5

1.0

1.5

2.0

v – szybkość reakcji katalizowanej przez enzym
V

maks

- maksymalna szybkość reakcji

S – stężenie substratu
K

m

– stała Michaelisa, czyli takie [S], przy którym v=1/2V

maks

V

max

=2 mmol/l·min

K

m

=0.043 mol/l

Je

żeli S<<K

m

:

czyli reakcja enzymatyczna przebiega
zgodnie z kinetyką I-go rzędu

Je

żeli S>>K

m

:

jest to reakcja 0-go rzędu, w której szybkość
nie zależy od stężenia

S

K

V

v

m

maks





V

v

maks



K

m

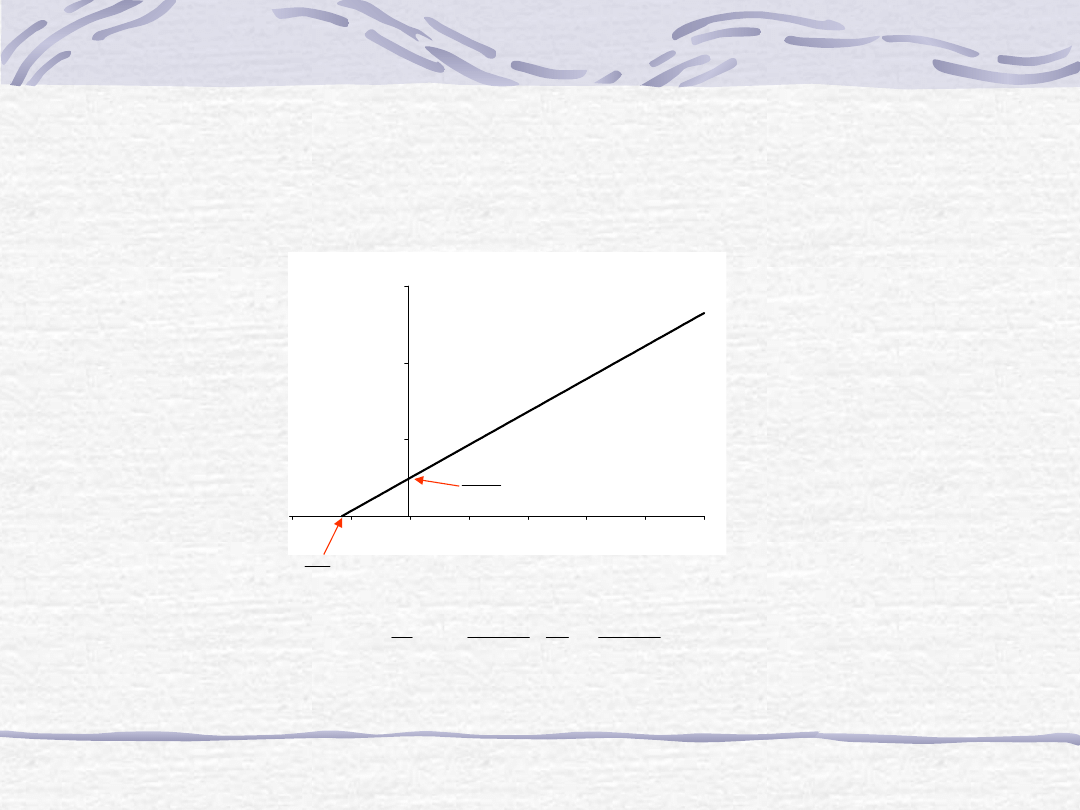
Równanie Lineweavera-Burka

-40

-20

0

20

40

60

80

100

0

1

2

3

maks

maks

m

V

1

S

1

V

K

v

1







maks

V

1

m

K

1



1

/v

(

l·

m

in

/m

m

o

l)

1/S (l/mol)

Czynniki wp

Czynniki wp

ł

ł

ywaj

ywaj

ą

ą

ce na szybko

ce na szybko

ść

ść

reakcji enzymatycznej

reakcji enzymatycznej

• ilość substratu

• temperatura

• pH środowiska

• obecność aktywatorów i inhibitorów enzymów

gdzie: I – stężenie inhibitora
K

i

– stała dysocjacji kompleksu enzym-inhibitor

S

K

S

V

v

m

maks







K

I

1

i















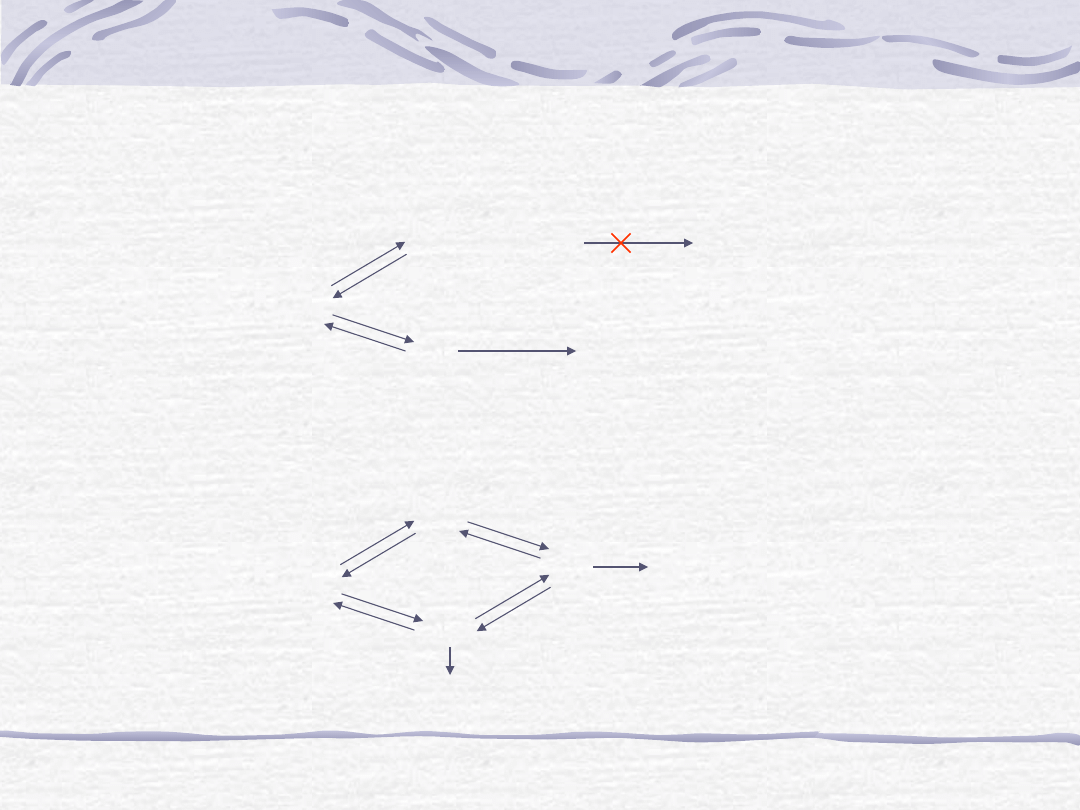
Hamowanie kompetycyjne

E

EI (nieaktywny)

ES

E + P

E + P

S



I

Hamowanie niekompetycyjne

E

EI

ES

E+P

EIS

EI + S

I

S

S

I

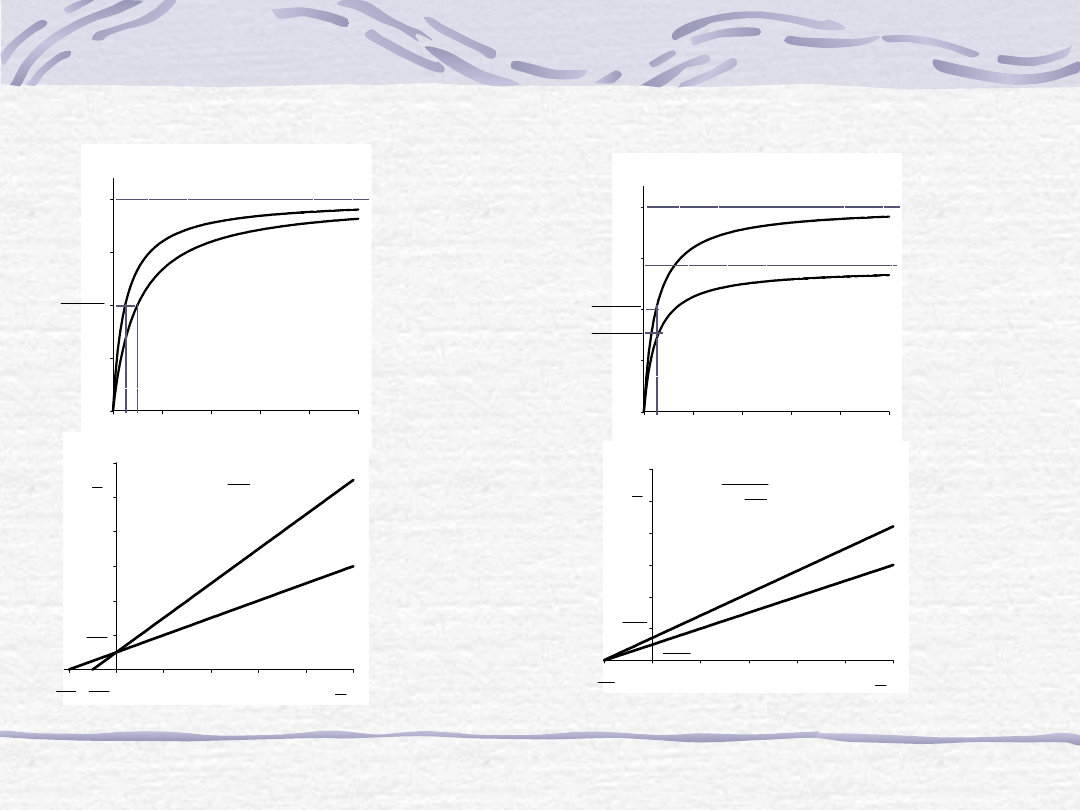
Inhibitory enzym

Inhibitory enzym

ów

ów

Inhibitory kompetycyjne

Inhibitory kompetycyjne

Inhibitory niekompetycyjne

Inhibitory niekompetycyjne

Przykłady: allopurynol, azaseryna, neostygmina,
sulfonamidy, metotreksat, 5-fluorouracyl

Przykłady: związki fosforoorganiczne, metale
ciężkie, cyjanki, azydki, związki arsenu

K

m1

K

m2

E

E+I

k

maks

V

E

E

E

E+I

nk

E+I

nk

E+I

k

maks1

V

maks2

V

K

m

)

K

]

I

[

(1

K

K

i

m1

m2





i

maks1

maks2

K

]

I

[

1

V

V





2

maks1

V

2

maks2

V

2

maks

V

m1

K

1



m2

K

1



maks

V

1

m

K

1



maks1

V

1

maks2

V

1

v

v

v

1

v

1

S

S

S

1

S

1