Całki i ich zastosowania

Całka nieoznaczona

• Niech dana będzie funkcja f(x) określona w (a,b).
• Funkcja F jest funkcją pierwotną funkcji f ,

jeżeli dla x (a,b).

• Całką nieoznaczoną funkcji f nazywamy zbiór

funkcji { F(x) + C : C  R }.

• Całkę nieoznaczoną funkcji f oznaczamy
przez  f(x)dx.

)

(

)

(

x

f

x

F











C

x

F

dx

x

f

)

(

)

(

Podstawowe wzory















































C

x

xdx

C

x

xdx

C

e

dx

e

C

a

a

dx

a

C

x

dx

x

p

C

p

x

dx

x

x

x

x

x

p

p

sin

cos

;

cos

sin

;

ln

|

|

ln

1

;

1

,

1

1

•











































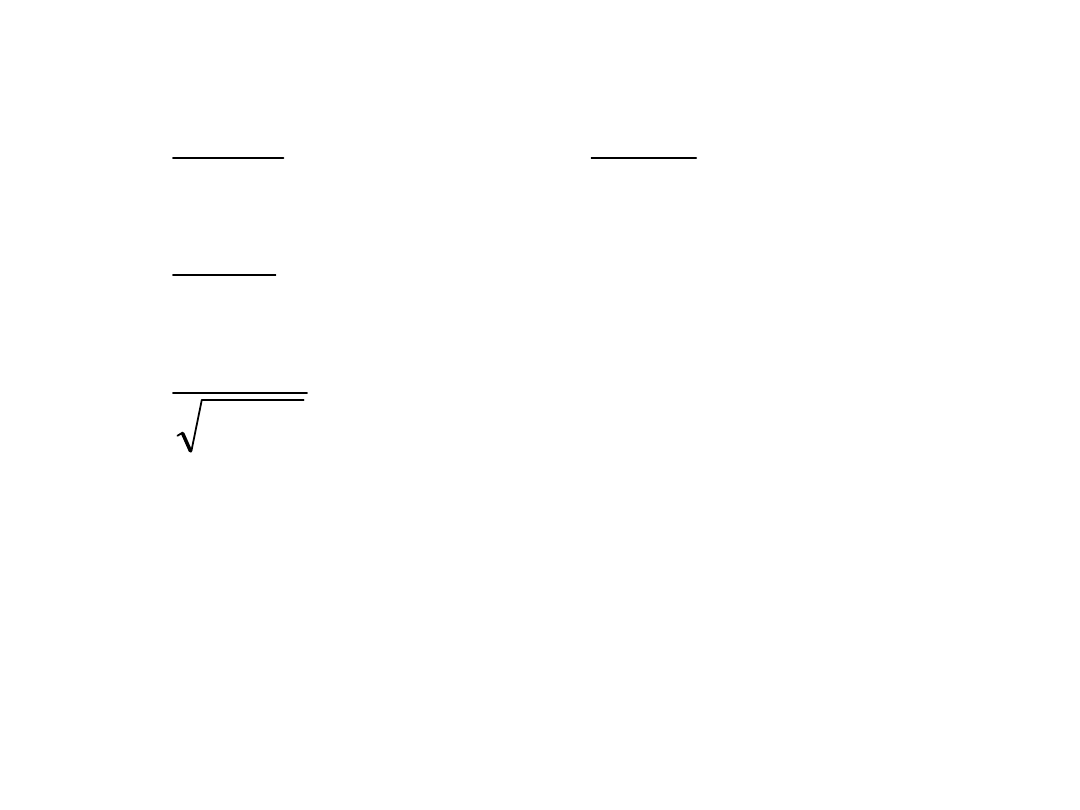
C

x

C

x

dx

x

C

arcctgx

C

arctgx

dx

x

C

ctgx

dx

x

C

tgx

dx

x

arccos

arcsin

1

1

;

1

1

;

sin

1

;

cos

1

2

2

2

2

Twierdzenia o całkach

















































)

(

)

(

)

(

))

(

(

|

)

(

|

ln

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

))

(

)

(

(

x

u

t

dla

dt

t

f

dx

x

u

x

u

f

C

x

f

dx

x

f

x

f

dx

x

v

x

u

x

v

x

u

dx

x

v

x

u

dx

x

f

A

dx

x

Af

dx

x

g

dx

x

f

dx

x

g

x

f

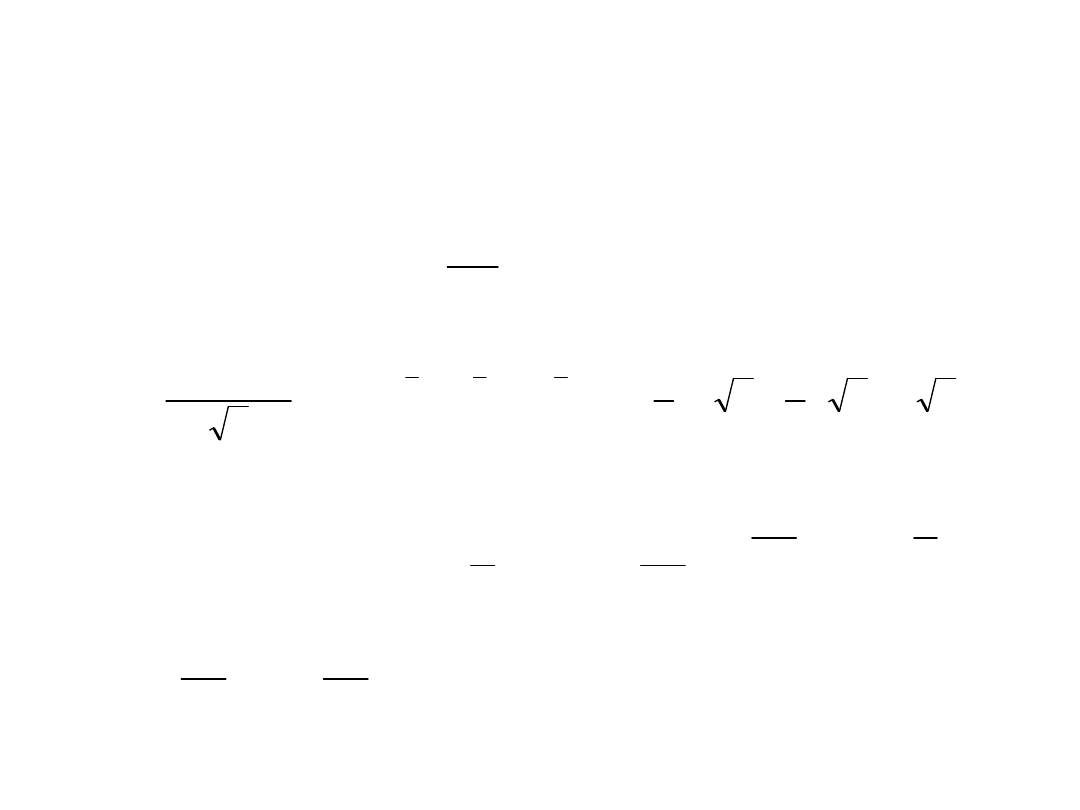
Obliczyć całki

1.

2.

3.











C

e

x

dx

e

x

x

x

2

2

)

2

(

2

C

x

x

x

x

x

dx

x

x

x

dx

x

x

x







































2

3

2

5

2

1

2

2

1

2

1

2

3

2

C

x

x

x

xdx

x

x

x

x

v

x

x

u

x

x

v

x

x

u

xdx

x















































4

ln

2

2

1

ln

2

2

)

(

,

1

)

(

)

(

,

ln

)

(

ln

2

2

2

2















































C

b

ax

a

dx

b

ax

C

e

a

dx

e

C

n

b

ax

a

dx

b

ax

C

b

ax

a

dx

b

ax

b

ax

b

ax

n

n

|

|

ln

1

1

1

1

)

(

1

)

(

)

cos(

1

)

sin(

1

Całkowanie funkcji

wymiernych

• Weźmy całkę . Jeżeli n 

m, dzielimy licznik przez
mianownik i otrzymujemy

gdzie p < m.



dx

x

W

x

W

m

n

)

(

)

(













dx

x

W

x

R

dx

x

W

dx

x

W

x

W

m

p

m

n

m

n

)

(

)

(

)

(

)

(

)

(

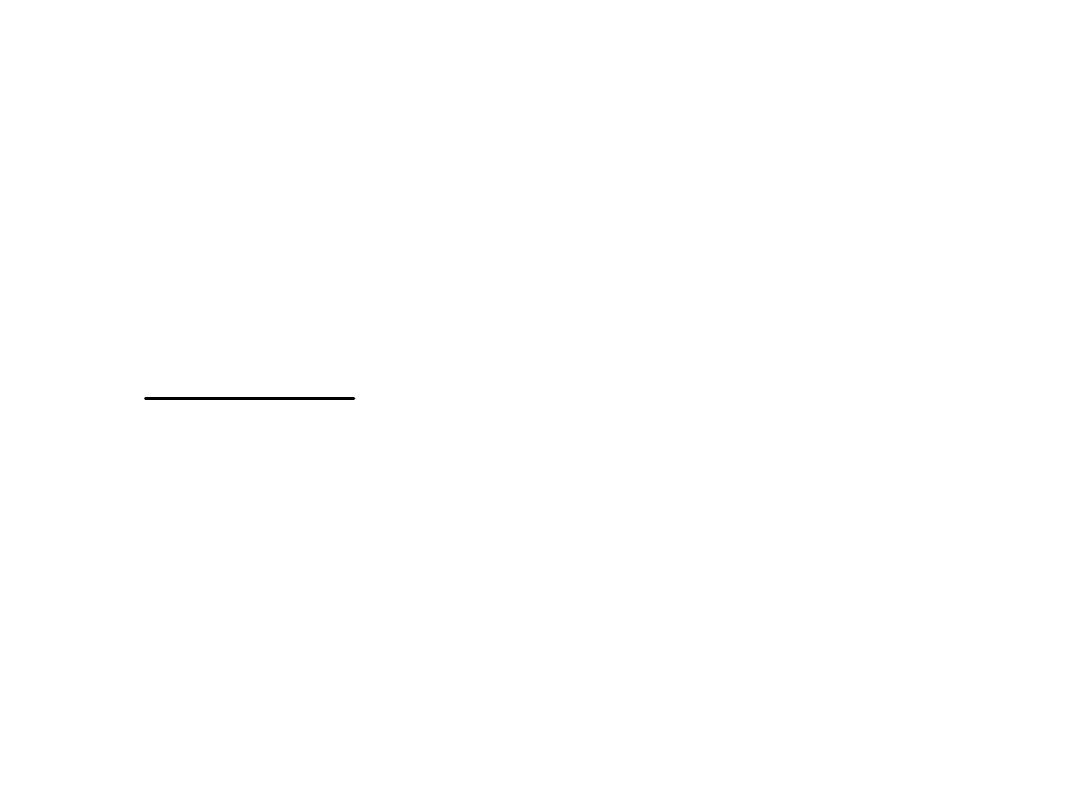
Rozkład na ułamki proste

• Funkcję wymierną właściwą postaci

, gdzie n  N oraz a,

A  R,

nazywamy ułamkiem prostym

pierwszego rodzaju.

n

a

x

A

)

( 

• Funkcję wymierną właściwą

postaci

, gdzie n  N oraz
p,q,B,C R, przy czym
nazywamy ułamkiem prostym

drugiego rodzaju.

n

q

px

x

C

Bx

)

(

2







0

4

2









q

p

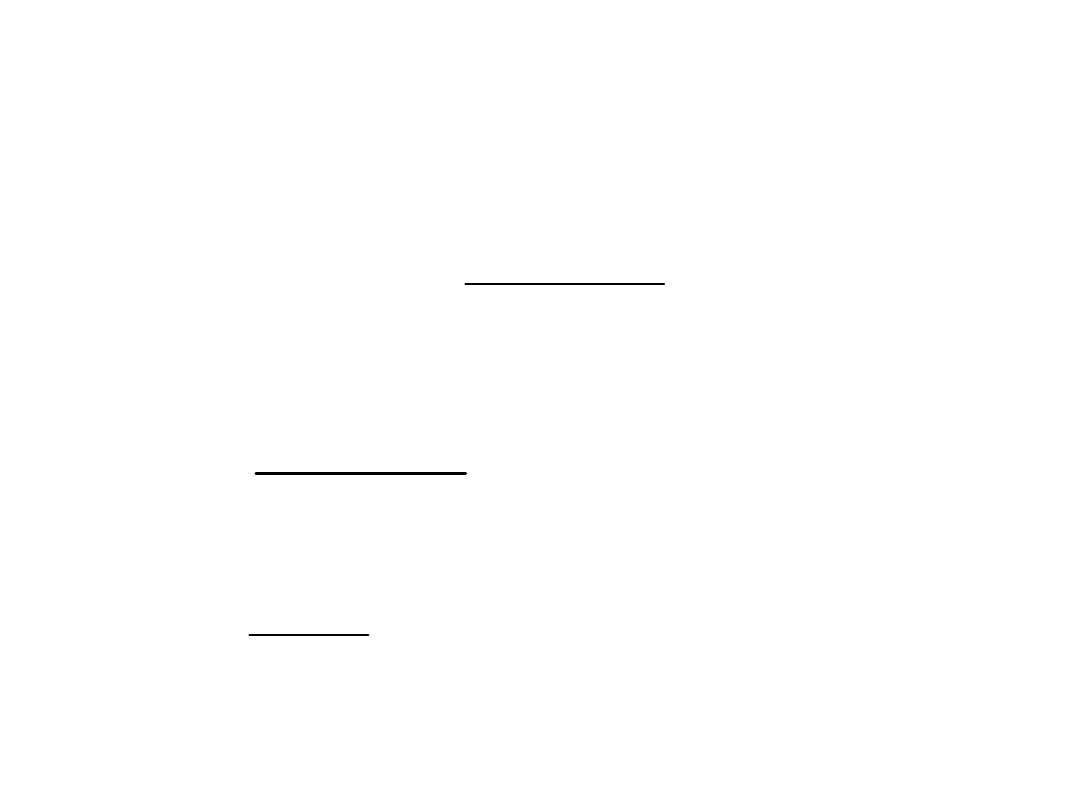
Przykład

• Obliczyć: 1)

• 2)

• 3)







dx

x

x

x

2

2

3





2

4

8x

x

dx







dx

x

x

1

1

4

4

Całkowanie funkcji

trygonometrycznych

• W całce typu
najogólniejszym podstawieniem jest:



dx

x

x

F

)

cos

,

(sin

.

1

1

cos

,

1

2

sin

,

1

2

,

2

,

2

2

2

2

2

t

t

x

t

t

x

dt

t

dx

arctgt

x

t

x

tg



















Przykład

• Obliczyć całkę







x

x

dx

cos

sin

1

• Znajdź tę funkcję pierwotną

funkcji

f(x) = x sinx, której wykres

przechodzi przez punkt (



/2 , 1 ).

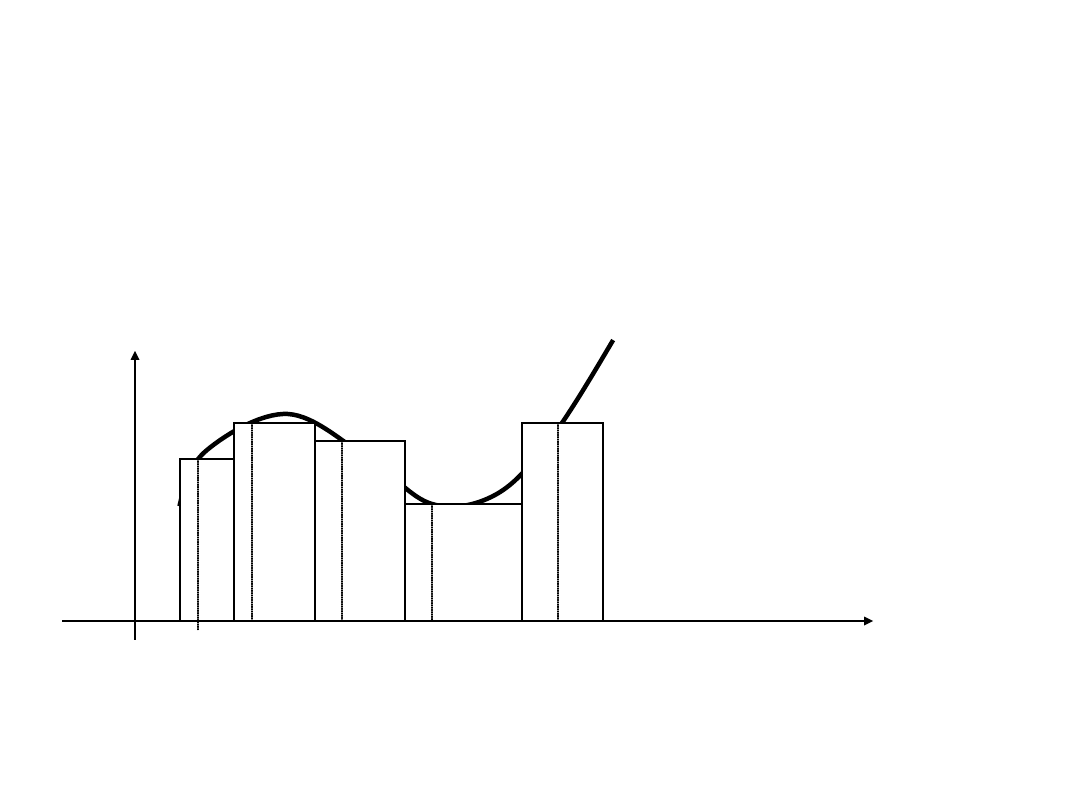
Suma całkowa funkcji























n

j

j

j

n

j

j

j

j

n

x

c

f

x

x

c

f

S

1

1

1

)

(

)

(

)

(

a x

1

x

2

x

3

x

4

b

c

1

c

5

x

y

c

2

c

3

c

4

Całka oznaczona

• Niech funkcja f będzie

ograniczona na przedziale <a, b>.
Całkę oznaczoną Riemanna z
funkcji f na przedziale <a, b>
definiujemy wzorem















n

j

j

j

n

b

a

x

c

f

dx

x

f

1

)

(

lim

)

(

Twierdzenie Newtona -

Leibniza

• Jeżeli funkcja f jest ciągła na

przedziale

<a, b>, to

gdzie F jest funkcją pierwotną

funkcji f.

)

(

)

(

)

(

a

F

b

F

dx

x

f

b

a







Własności całki

oznaczonej

)

,

(

,

)

(

)

(

)

(

)

(

)

(

0

)

(

b

a

c

dx

x

f

dx

x

f

dx

x

f

dx

x

f

dx

x

f

dx

x

f

b

c

c

a

b

a

b

a

a

b

a

a

























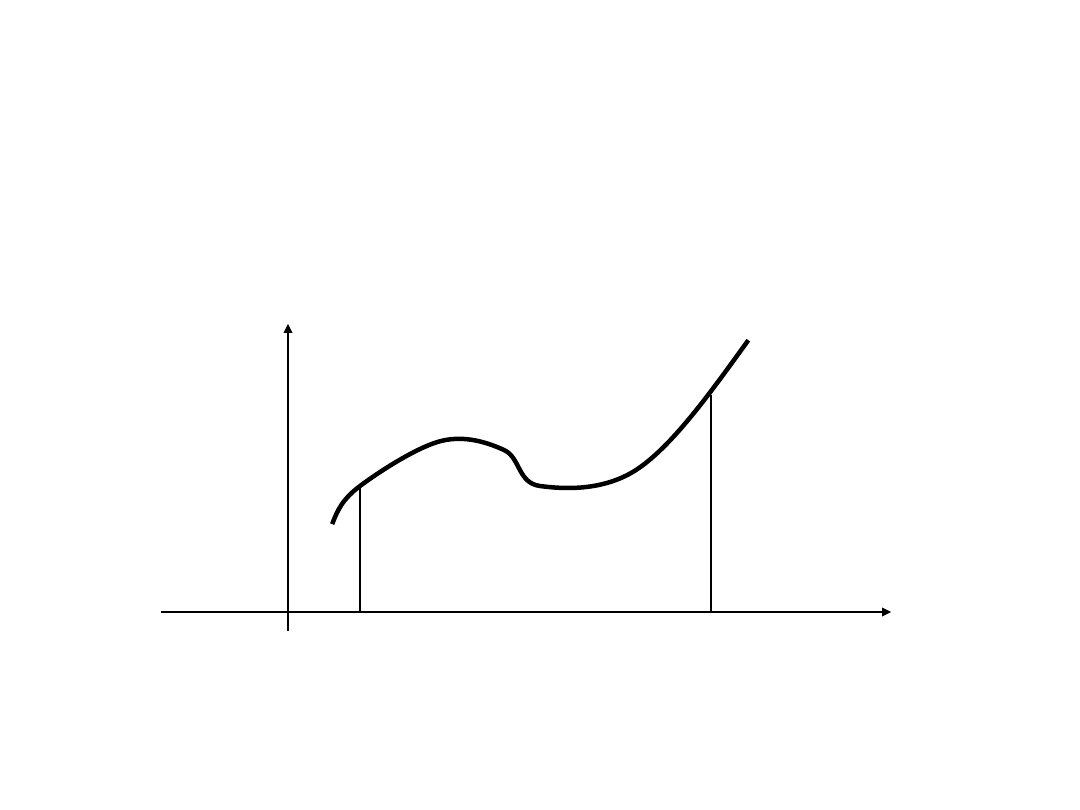
Całka oznaczona z funkcji f na

przedziale

<a, b> jest równa polu obszaru

ograniczonego wykresem funkcji
f, prostymi x = a, x = b oraz osią
Ox ( prostą y = 0 ).

a

b

y=f(x)

x

y





b

a

dx

x

f

S

)

(

O

Pole obszaru płaskiego

• D ={ (x,y): a  x  b; g(x)  y 

f(x) }







b

a

dx

x

g

x

f

D

)]

(

)

(

[

|

|

• Oblicz pole obszaru ograniczonego

krzywymi

6

5

2

2







x

y

i

x

y

• Oblicz pole ograniczone elipsą

1

2

2

2

2





b

y

a

x

Objętość bryły obrotowej

• Niech V oznacza bryłę

ograniczoną powierzchnią
powstałą z obrotu wykresu funkcji
nieujemnej y = f(x), gdzie a x

b, wokół osi Ox oraz

płaszczyznami x = a,

x = b. Objętość |V| bryły jest

granicą sumy objętości walców
aproksymujących tę bryłę:





























b

a

n

j

j

j

n

n

j

j

n

dx

x

f

x

c

f

V

V

)

(

)

(

lim

|

|

lim

|

|

2

1

2

1





• Oblicz objętość bryły powstałej w

wyniku obrotu wokół osi Ox
krzywej

w przedziale <

0,



>.

2

sin

x

y 

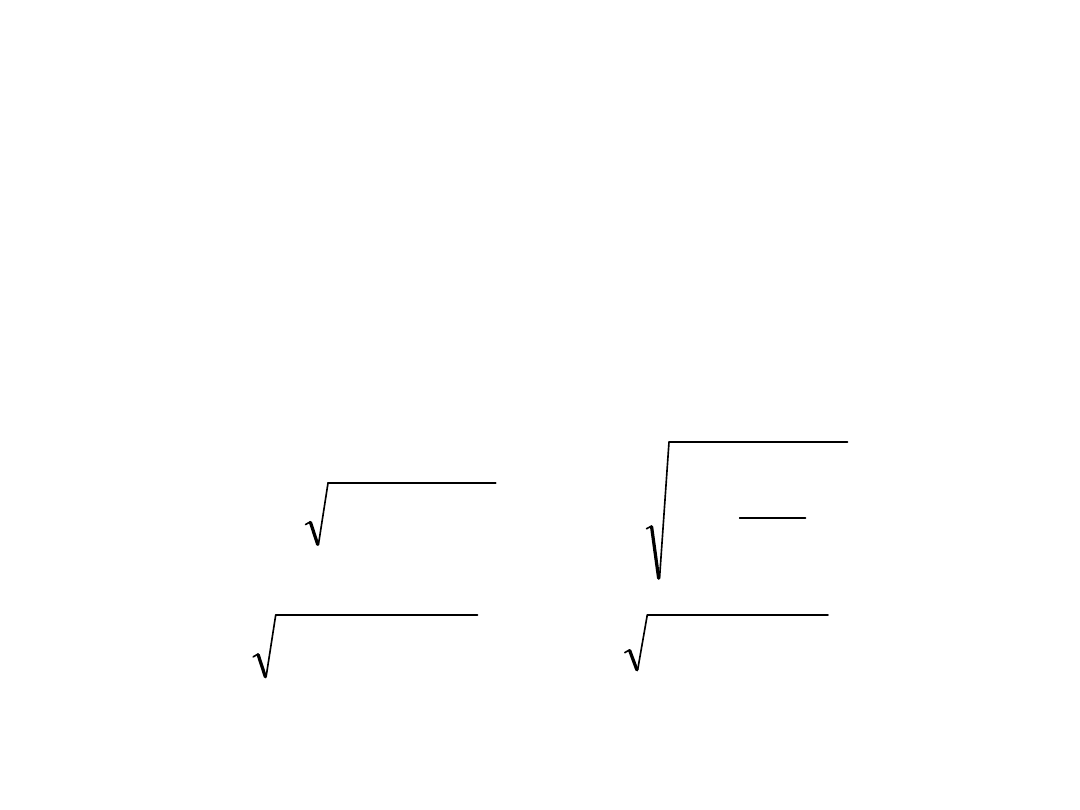
Długość łuku krzywej

• Niech L będzie wykresem funkcji

y = f(x), gdzie a x b. Długość |

L| łuku L jest granicą sum
odcinków aproksymujących ten
łuk.

dx

x

f

x

c

f

x

x

y

y

x

L

b

a

n

j

j

j

n

n

j

j

j

j

n

n

j

j

j

n













































































2

1

2

1

2

1

2

2

)]

(

[

1

))

(

(

1

lim

1

lim

lim

|

|

• Oblicz długość krzywej

od x = 0 do x

= 2.

2

x

y 

Obliczyć całki

1.

2.

3.

86

,

0

)

(

0

2

2

0

2

0





















e

e

e

dx

e

x

x

2

2

4

1

4

1

2

1

4

1













x

dx

x

x

dx

7854

,

0

4

0

1

1

1

1

0

1

0

2

















arctg

arctg

arctgx

dx

x

Wartość średnia funkcji

• Wartością średnią funkcji f na

przedziale <a, b> nazywamy
liczbę







b

a

śr

dx

x

f

a

b

f

)

(

1

Obliczyć wartość średnią

funkcji

1.

2.

.

64

,

0

2

)

cos

(

1

sin

1

,

0

,

sin

)

(

0

0































x

xdx

f

x

x

f

śr

.

33

,

0

3

1

6

1

2

1

1

,

1

,

)

(

1

1

3

1

1

2

2























x

dx

x

f

x

x

f

śr

Całki niewłaściwe

• Całki niewłaściwe I rodzaju:

.

)

(

)

(

)

(

,

)

(

lim

)

(

,

)

(

lim

)

(

















































b

b

b

c

c

b

c

a

c

a

dx

x

f

dx

x

f

dx

x

f

dx

x

f

dx

x

f

dx

x

f

dx

x

f

• Całki niewłaściwe II rodzaju

.

)

(

lim

)

(

lim

)

(

,

)

(

lim

)

(

,

)

(

lim

)

(

0

0

0

0







































b

c

c

a

b

a

b

a

b

a

b

a

b

a

dx

x

f

dx

x

f

dx

x

f

dx

x

f

dx

x

f

dx

x

f

dx

x

f















