1

GRAFICZNE
PRZEDSTAWIENIE
DANYCH
LICZBOWYCH

TABELE I RYSUNKI

2

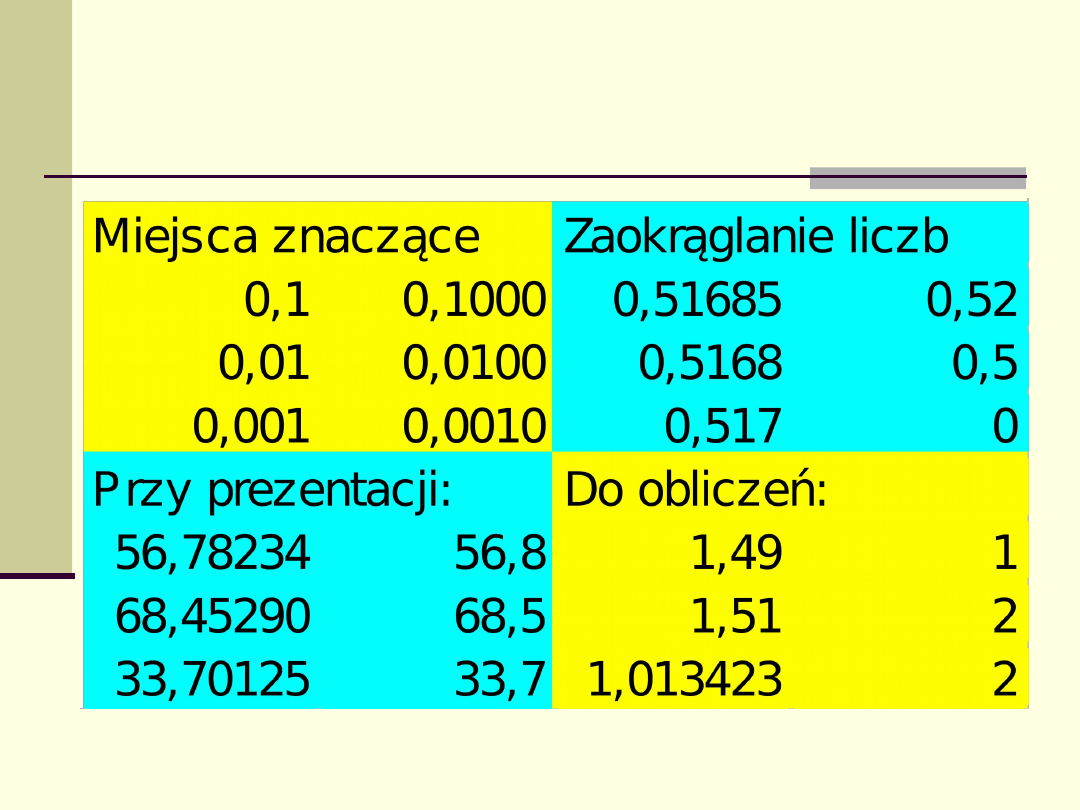
Miejsca znaczące i
zaokrąglanie liczb

3

TABELA CZY RYSUNEK ?

Wyniki przedstawiamy w formie tabeli lub wykresu,

ewentualnie stosujemy opis słowny. Tabele w

konfrontacji z wykresami mają następujące zalety:



dokładność podawania danych,



większa ilość danych zawarta na danej przestrzeni.

Forma przedstawiania danych zależy od autora i

powinna być dopasowana do przekazywanych

treści. Jeżeli jest taka możliwość, to

wyniki należy

przedstawiać w formie rysunków

gdyż są one:



bardziej

czytelne,

szczególnie

w

przypadku

wygłaszania referatu lub prezentacji publicznej

danych.

Generalną zasadą przy tworzeniu tabel i wykresów

jest ich czytelność bez odwoływania się do treści

pracy.

4

Ogólne zasady sporządzania
tabel

Tabela określa zestawienie liczbowe lub

określenia słowne np. różnych cech tych

samych obiektów doświadczalnych.



Tabele tytułujemy od góry.



Tabela po numerze powinna być opatrzona

tytułem wskazującym precyzyjnie i w sposób

skondensowany,

co

w

tabeli

jest

przedstawiane.



Należy unikać określeń liczba i ilość.



Nie powinno się w tytule powtarzać treści

zawartych w tytułach wierszy i kolumn, które

stanowią tzw. główkę tabeli.



Tytuły kolumn winny być zwięzłe z podaniem

jednostek, jeżeli przedstawia się większą

liczbę cech.



Można stosować skróty lub znaki umowne, aby

nie stwarzać pustych miejsc w kolumnach, gdyż

tabela traci na przejrzystości.



W

tabeli

podajemy

wyliczone

parametry

statystyczne np. odchylenie standardowe (SD),

błąd standardowy (SE) lub NIR



.



Odchylenia i błędy standardowe podajemy

najczęściej

bezpośrednio

przy

średnich

arytmetycznych, natomiast NIR na dole tabeli.



Można stosować znaki umowne: (-) zdarzenie nie

wystąpiło, nie dotyczy, nie badano; (0) zjawisko

istnieje ale było bardzo małe; (*) różnica lub

parametr istotny; (**) różnica lub parametr

wysoce istotny; (ns) różnica nieistotna.



Błędem jest podawanie liczb ze zbyt dużą

dokładnością, stosujemy zasadę podawania liczb

do 3 miejsc znaczących.



W razie konieczności należy stosować zamianę

jednostek

podstawowych

układu

SI,

wykorzystując przedrostki lub podając mnożnik

w główce lub tytule tabeli.

6

Ogólne zasady sporządzania
wykresów



Wykres lub rysunek musi mieć tytuł, który

umieszcza się u dołu pod rysunkiem.



Pole wykresu powinno być zbliżone do pola

kwadratu.



Tytuły osi umieszczamy przy końcach osi lub

równolegle do nich.



Osie powinny być czytelnie opisane tj. posiadać

słowny opis tego, co przedstawiają wraz z

jednostkami np. wysokość roślin [cm]



Jednostki na osi powinny być umieszczane co

określoną ich liczbę w obrębie całej osi.



Cała przestrzeń ograniczona osiami powinna być

wypełniona treścią rysunku; w tym celu należy

stosować przerwania osi.



Wykres powinien mieć legendę, którą
umieszczamy na wykresie lub ze względu
na większą czytelność przenosimy do
tytułu.



Należy pamiętać, że na wykresie mogą
być

przedstawione

wyliczone

miary

statystyczne.



Odchylenia

i

błędy

standardowe

zaznaczamy pionowymi kreskami od
punktów oznaczających średnie.



NIR

umieszczamy

najczęściej

nad

wartościami

średnimi,

uwzględniając

skalę liczbową osi Y.

8

Podział wykresów

1.Wykresy pojedyncze



liniowe (diagramy) - przedstawiamy na nich czynniki

ilościowe lub cechy ciągłe



słupkowe (histogramy) - przedstawiamy za ich

pomocą czynniki jakościowe i ilościowe lub cechy

skokowe



kołowe - najczęściej przedstawiają udziały %



powierzchniowe

2.Wykresy

złożone

(kombinacje

wykresów

pojedynczych)

3.Wykresy wielokrotne (kilka wykresów opatrzonych

wspólnym tytułem i legendą)

4.Wykresy wielowymiarowe



słupkowe



płaszczyznowe (płaszczyzny reakcji)

9

Histogram, diagram

Histogram jest wykresem słupkowym, w którym
podstawę
słupka stanowi długość przedziału, a wysokość
słupka
stanowi jego liczebność. Histogram może być
wykonany
z szeregu rozdzielczego zmiennej ciągłej i skokowej.

Diagram jest wykresem w postaci linii łamanej,
powstałej
poprzez połączenie prostymi punktów wyznaczonych
na podstawie środka przedziału i jego liczebności.
Diagram
może być wykonany z szeregu rozdzielczego
zmiennej ciągłej.

Odmiana

Lipnik

Strzelce

Średnio

N

60

N

12

0

N

70

N

100

N

1

N

2

ogółe

m

%

Akt

(n) 42,

1

42,

6

42,

4

48,7

40,5

44,

6

45,

4

41,

6

43,5

65

STH

296

(n) 42,

5

40,

1

41,

3

52,8

49,8

51,

2

47,

7

45,

0

46,3

69

Bajka

(op

)

65,

4

62,

1

63,

7

73,0

68,2

70,

6

69,

2

65,

2

67,2

10

0

50,

0

48,

3

49,

1

58,2

52,8

55,

5

54,

1

50,

6

52,3

NIR

0,05

(SNK) dla N

1,37

O

2,26

O(N)

3,20

N(O)

2,54

1,99

3,27

4,62

3,69

 

x

x

x

Tab. 1. Plon ziarna (dt ha

-1

)

odmian nagoziarnistych (n) i

oplewionej (op) owsa

w zależności od zastosowanej dawki nawożenia azotowego

(N kg ha

-1

)

w dwóch miejscowościach

Trait

Cultivar

Differenc

e

1

LSD

0.05

2

Warko

Amilo

Marder

RAH

849

c

e

= 350 [mol m

-2

s

-1

]

A

[mol m

-2

s

-

1

]

20.5 b

3

22.3 ab

23.0 a

22.1 ab

1.2

n.s.

E

[mmol m

-2

s

-1

]

2.79 c

2.98 b

3.29 a

3.02 b

0.27

0.185

g’

s

[mol m

-2

s

-1

]

0.63 c

0.85 b

1.06 a

0.86 b

0.22

0.192

WUE

[mmol mol

-

1

]

7.35 a

7.48 a

6.99 a

7.32 a

0.26

n.s.

c

e

= 1300 [mol m

-2

s

-1

]

A

[mol m

-2

s

-

1

]

32.5 a

33.2 a

35.3 a

32.0 a

0.8

n.s.

E

[mmol m

-2

s

-1

]

2.30 c

2.57 b

3.07 a

2.72 b

0.46

0.239

g’

s

[mol m

-2

s

-1

]

0.45 c

0.63 b

0.86 a

0.69 b

0.24

0.170

WUE

[mmol mol

-

1

]

14.1 a

12.9 ab

11.5 b

11.8 b

1.9

n.s.

Table 2. Gas exchange parameters for control plants of four winter rye cultivars,
averaged over all measuring terms.

1 between average effect of both forms of rye
2 according to Scheffé test for compering group of means
3 means in table followed horizontally by the same letter do not differ significantly at p =0.05
according to Duncan test

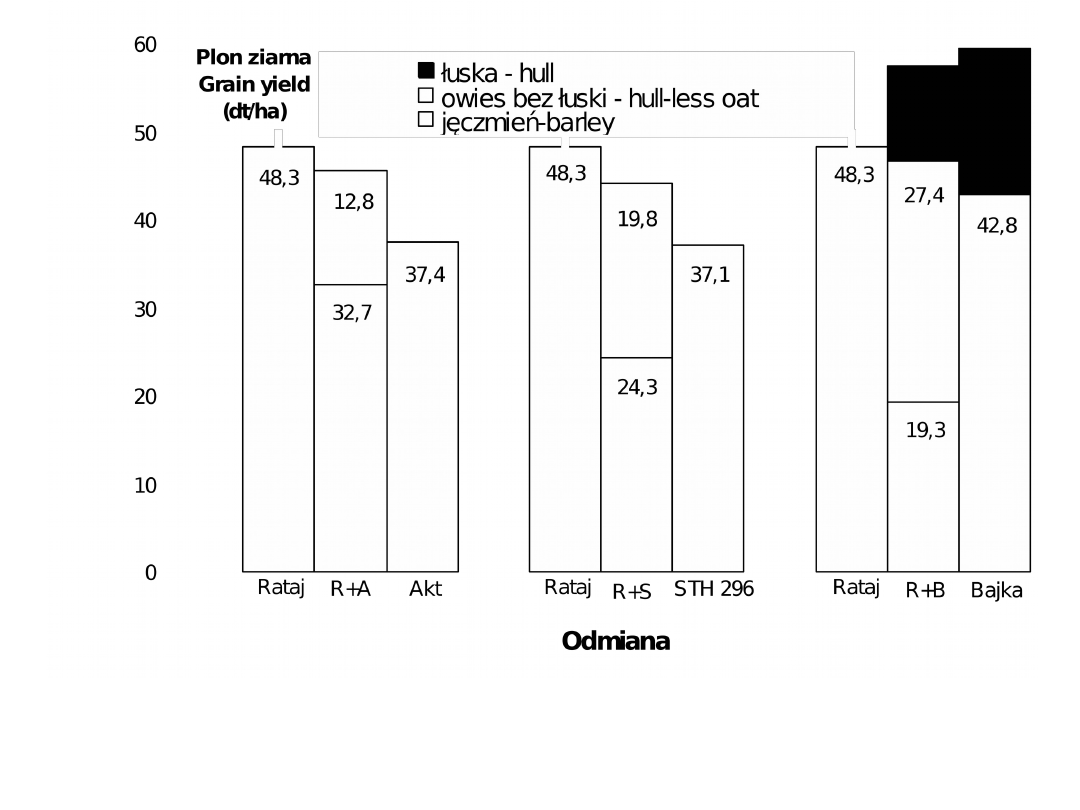
Rys.1. Plon ziarna mieszanek owsa z jęczmieniem (dt
ha

-1

) z

wyszczególnieniem udziału plewki owsa oplewionego
(Lipnik)

30(186)

32(200)

59(228)

71(246)

Fazy rozwojowe wg DC (l. dni od siewu)

0

2

4

6

8

10

12

14

16

18

20

22

24

26

S

u

c

h

a

m

a

s

a

r

o

ś

li

n

y

[

g

]

30(186)

32(200)

59(228)

71(246)

0

2

4

6

8

10

12

14

16

18

20

22

24

26

30(186)

32(200)

59(228)

71(246)

0

2

4

6

8

10

12

14

16

18

20

22

24

26

30(186)

32(200)

59(228)

71(246)

0

2

4

6

8

10

12

14

16

18

20

22

24

26

Nawid
NSIN 490
NS 310P/89
WS 66N/85
Walet

NAD 1495
NSIN 893
WM 1R/89

CHD 894
CSIN 893
Walet

WID 496
WSIN 1595
WS 79P/94
NS 426N/91
Walet

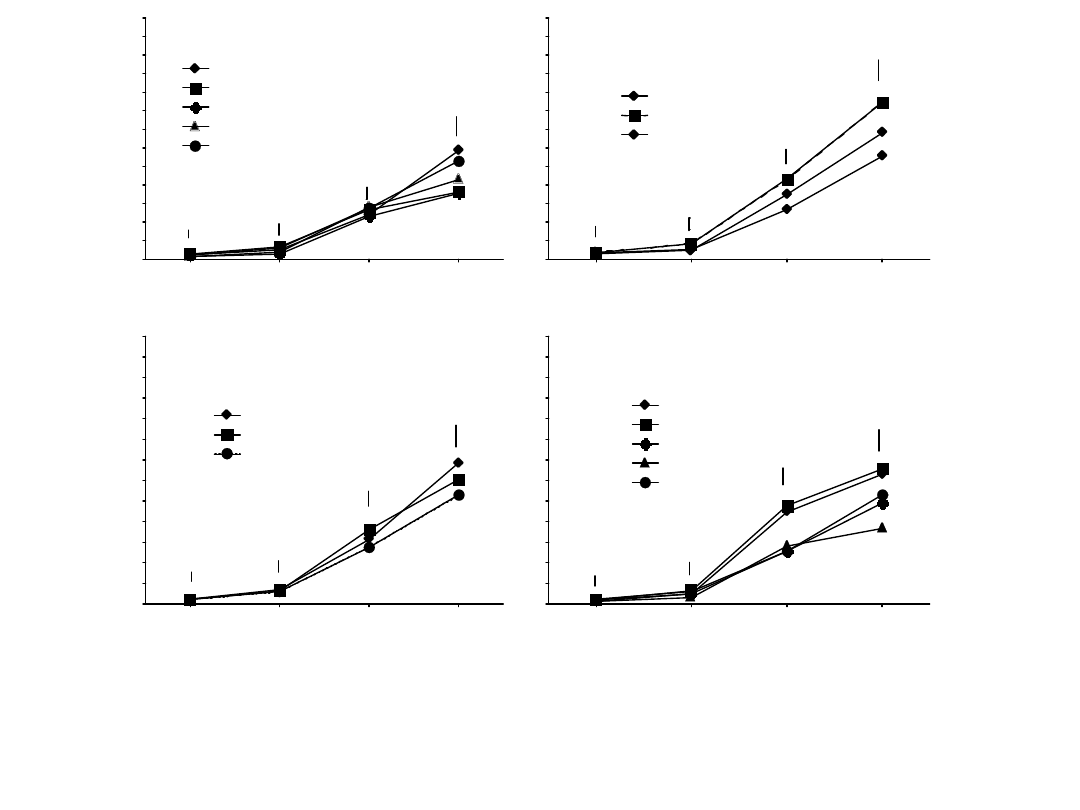
Rys.2. Sucha masa roślin mieszańców i ich komponentów

lo

g

Y

-4

,8

P

l

o

n

z

i

a

r

n

a

(

d

t

/

h

a

)

8,7

8,2

5,8

5,2

9,0

9,0

9,0

8,9

8,8

8,6

7,4

7,0

30

60

90

120

30

60

90

120

30

60

90

120

0,0

0,2

0,4

0,6

0,8

1,0

1,2

1,4

1,6

1,8

0

10

20

30

40

50

60

70

80

90

N (kg/ha)

y=66,

5+0,0

67x R

2

=0,99

6

LR / m

2

LK / R

LZ / K

MTZ

y=4

7,0+

0,43

0x-0

,001

83x

2

R

2

=0,9

99

N

MAX

=11

7

y=5

6,6+

0,25

3x-0

,000

944

x

2

R

2

=0,9

99

N

MAX

=13

4

1997

1998

1997-1998

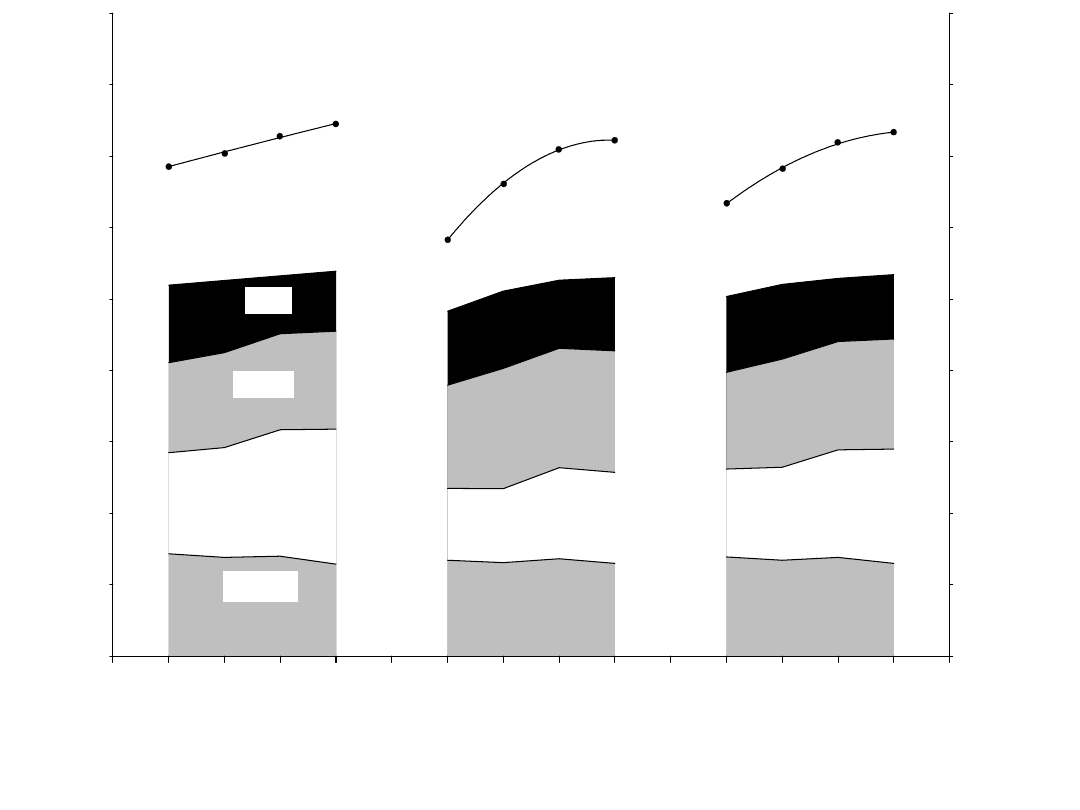
Rys.3. Wpływ dawek azotu na: komponenty plonu ujęte w formie logarytmicznej (Y1),
wyleganie roślin (nad słupkami) i plon ziarna w formie linii regresji (Y2) w
poszczególnych latach badań

U

d

z

ia

ł

(%

)

>2,8
2,5-2,8
2,2-2,5
2,0-2,2
1,8-2,2
<1,8

N

R

M

MO

A

30

60

90

120

C

K

1997

1998

0

10

20

30

40

50

60

70

80

90

100

Frakcje ziarna
(mm)

N-Nawid
R-RAH 394
M-Marder
MO-Motto
A-Amilo

C-Cerone
K-Kontrola

Odmiana Cultivars

Dawki azotu Nitrogen doses

Lata Years

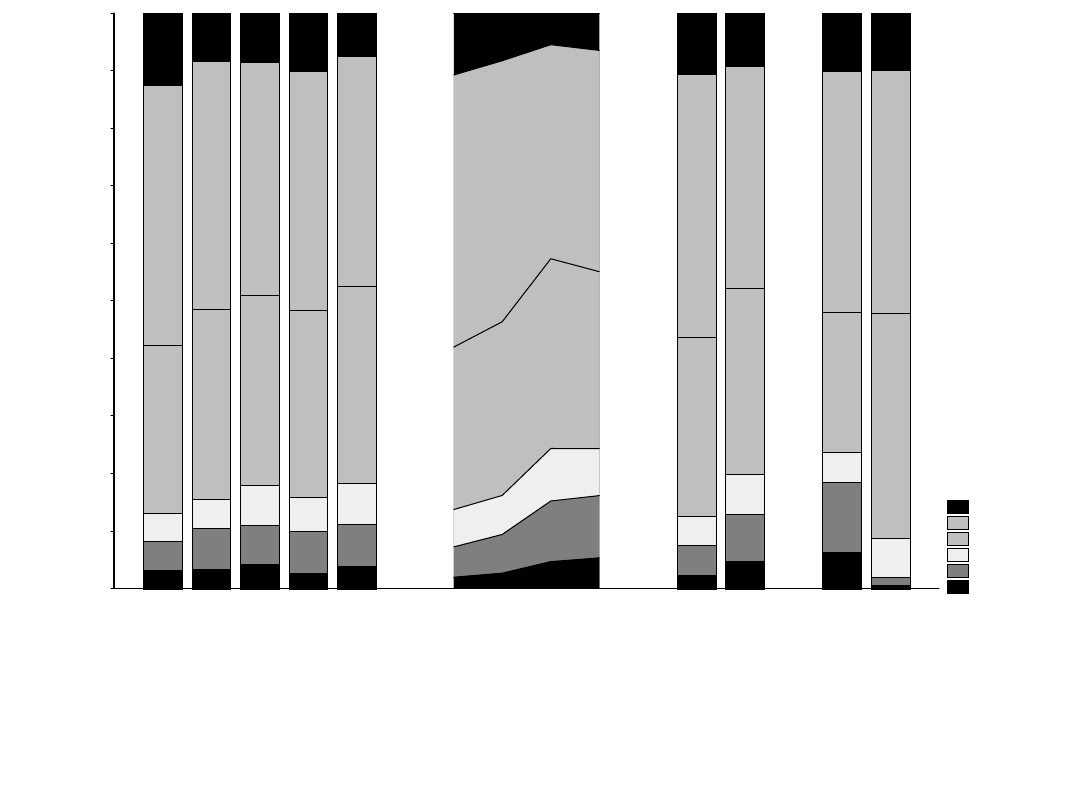
Rys.4. Frakcje ziarna w zależności od odmiany, nawożenia azotem,
regulatora wzrostu i lat badań