Regresja liniowa i paraboliczna (metoda najmniejszych
kwadratów)

Pierwiastki wielomianu kwadratowego

Pochodna funkcji

Informatyka - EXCEL

Remigiusz Nowak

Grzegorz Brus

Wydział Energetyki i Paliw

Katedra Podstawowych Problemów Energetyki

Metoda najmniejszych kwadratów (Regresja
liniowa)

1/8

 Dane: (x

1

, x

2

, x

3

, x

4

, …, x

n

), (y

1

, y

2

, y

3

, y

4

, …, y

n

)

 Szukane: y = mx + b, a dokładnie y = (m±δm)·x +

(b±δb)

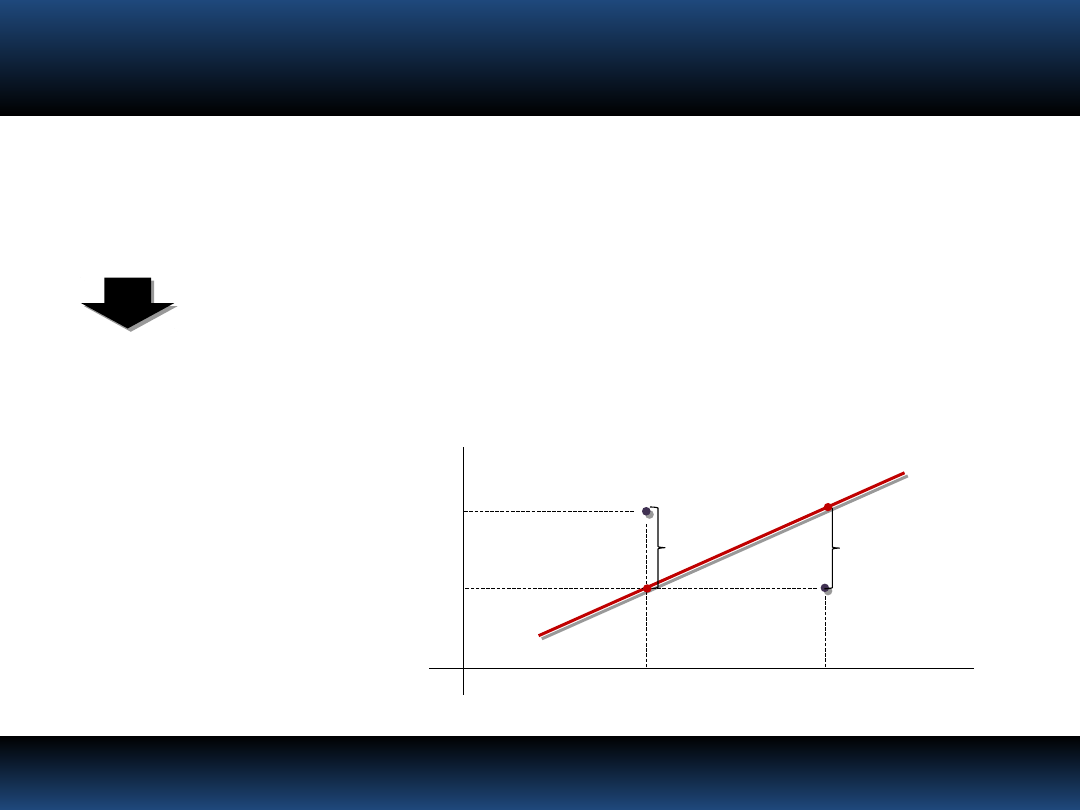
 Różnicę pomiędzy wartością zmierzoną, a przybliżaną

przez dopasowaną linię wyraża zależność:

)

(

)

,

(

)

(

)

,

(

)

(

)

,

(

2

2

2

1

1

1

b

mx

y

b

m

b

mx

y

b

m

b

mx

y

b

m

n

n

n



























x

y

y =

mx

+ b

x

2

y

1

y

2

x

1

ε

1

(m,b)

ε

2

(m,b)

Informatyka - EXCEL

Metoda najmniejszych kwadratów (Regresja
liniowa)

2/8

 Cel: Wyznaczenie takich m i b, dla których:



 







min

)

(

...

)

(

)

(

2

2

2

2

2

1

1





















b

mx

y

b

mx

y

b

mx

y

n

n





min

)

(

1

2











n

i

i

i

b

mx

y

 W celu obliczenia parametrów m i b, dla których minimalizuje się

powyższe równanie musimy policzyć jego pochodną względem
zmiennej m i b, a następnie powstałe równania przyrównać do
zera













0

)

(

2

...

)

(

2

)

(

2

2

2

2

1

1

1























b

mx

y

x

b

mx

y

x

b

mx

y

x

n

n

n

m





b







 







0

)

(

2

...

)

(

2

)

(

2

2

2

1

1























b

mx

y

b

mx

y

b

mx

y

n

n

Informatyka - EXCEL

Metoda najmniejszych kwadratów (Regresja
liniowa)

3/8

 Porządkując powyższe równania otrzymujemy







 



n

n

n

n

y

x

y

x

y

x

b

x

x

x

m

x

x

x























...

...

2

...

2

2

2

1

1

2

1

2

2

2

2

1

m





b













n

n

y

y

y

nb

m

x

x

x

















...

...

2

2

1

2

1

 Co ostatecznie doprowadza nas do układu równań w

postaci

































































n

i

i

n

i

i

n

i

i

i

n

i

i

n

i

i

y

nb

m

x

y

x

b

x

m

x

1

1

1

1

1

2

Układ ten możemy rozwiązać

np. metodą Cramera (wyznaczników)

Informatyka - EXCEL

Zadanie 1

4/8

(a) Korzystając z metody najmniejszych kwadratów dopasuj

linię prostą do

następującego zestawu danych:

x

y

0

27.6

10

31

20

34

30

37

40

40

50

42.6

60

45.5

70

48.3

80

51.1

90

54

100

56.7

Informatyka - EXCEL

Zadanie 1

4/8

(a) Korzystając z metody najmniejszych kwadratów dopasuj

linię prostą do

następującego zestawu danych:

x

y

0

27.6

10

31

20

34

30

37

40

40

50

42.6

60

45.5

70

48.3

80

51.1

90

54

100

56.7

(a) ODP a) y = 0,2880

+28,1227

Informatyka - EXCEL

Niepewność wyznaczenia wartości m i b

5/8

 Odchylenie standardowe (niepewność) współczynników

m i b wyznaczamy z następujących wzorów

W

n

n

y

a

2

2























n

i

i

i

y

mx

b

y

1

2

2



























n

i

n

i

i

i

x

x

b

W

1

2

1

2

,gdzie ,

n

x

n

i

i

a

b







1

2





 Korelacja (informuje nas jak dobrze dana krzywa

dopasowała się do punktów eksperymentalnych)









































































 















2

1

1

2

1

2

1

2

1

1

1

n

i

i

n

i

i

n

i

n

i

i

i

n

i

n

i

n

i

i

i

i

i

y

y

n

x

x

n

y

x

y

x

n

R

1

;

1





R

Informatyka - EXCEL

Zadanie 1

6/8

(a) Korzystając z metody najmniejszych kwadratów dopasuj

linię prostą do

następującego zestawu danych:

x

y

0

27.6

10

31

20

34

30

37

40

40

50

42.6

60

45.5

70

48.3

80

51.1

90

54

100

56.7

ODP a) y = 0,2880
+28,1227

(b) Korzystają z powyższych wzorów wyznacz

odchylenia standardowe wartości m i b oraz
współczynnik korelacji R

Informatyka - EXCEL

Zadanie 1

6/8

(a) Korzystając z metody najmniejszych kwadratów dopasuj

linię prostą do

następującego zestawu danych:

x

y

0

27.6

10

31

20

34

30

37

40

40

50

42.6

60

45.5

70

48.3

80

51.1

90

54

100

56.7

ODP a) y = 0,2880

+28,1227

(b) Korzystają z powyższych wzorów wyznacz

odchylenia standardowe wartości m i b oraz
współczynnik korelacji R

ODP b) y = 0,2880

±0,0023

+

28,1227

±0,1383

R = 0,9997

Informatyka - EXCEL

Zadanie 2

7/8

W oparciu o poniższy układ równań dopasuj

współczynniki paraboli do następującego zestawu
danych eksperymentalnych

c

bx

ax

y







2























































































































































































n

i

i

i

n

i

i

n

i

i

n

i

i

n

i

i

i

n

i

i

n

i

i

n

i

i

n

i

i

n

i

i

n

i

i

y

x

c

x

b

x

a

x

y

x

c

x

b

x

a

x

y

nc

b

x

a

x

1

2

1

2

1

3

1

4

1

1

1

2

1

3

1

1

1

2

x

y

1.2

4.5

1.5

5.1

1.8

5.8

2.6

6.7

3.1

7.0

4.3

7.3

4.9

7.6

5.3

7.4

5.7

5.7

6.4

7.2

7.1

6.9

7.6

6.6

8.6

5.1

Informatyka - EXCEL

Zadanie 3

8/8

Sporządź arkusz kalkulacyjny obliczający

pierwiastki dowolnego wielomianu kwadratowego w
postaci

c

bx

ax

y







2

Zadanie 4

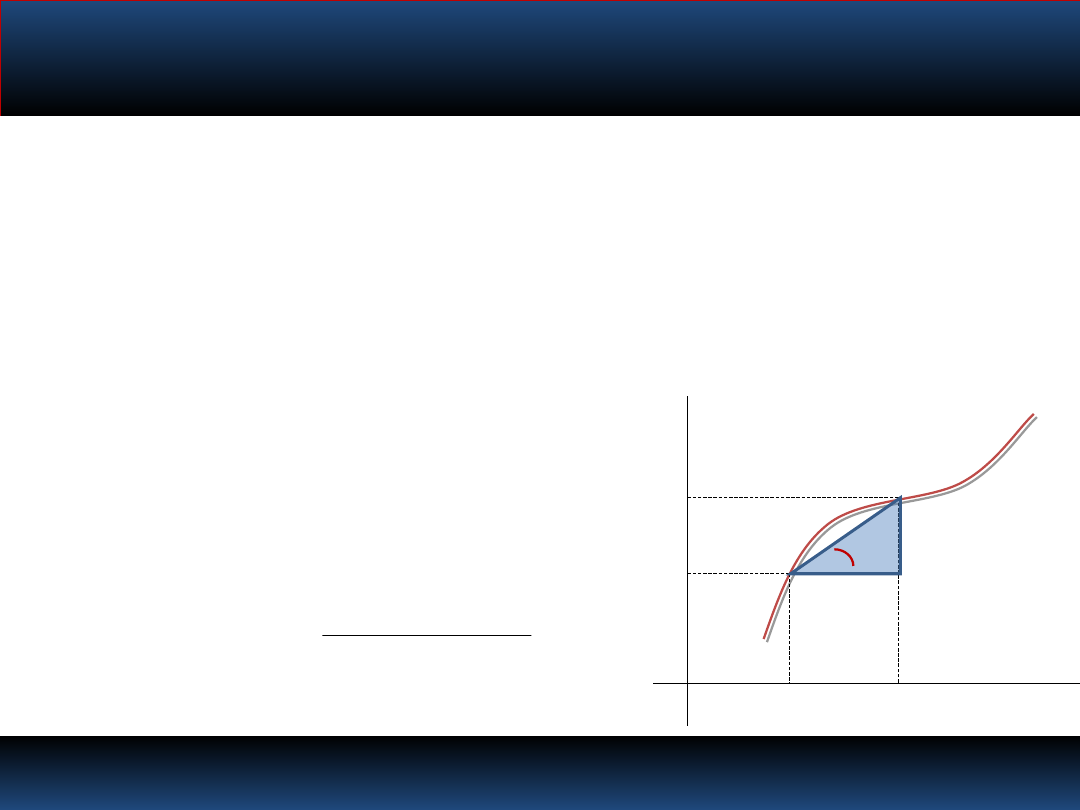
W oparciu o wzór definicyjny pochodnej funkcji,

wyznacz pochodną dowolnej funkcji i narysuj jej
wykres

x

0

X

0

+

h

f(x

0

)

f(x

0

+h)

h

x

f

h

x

f

x

f

h

)

(

)

(

lim

)

(

'

0

0

0











tg

x

f



)

(

'



Informatyka - EXCEL