1

Nazwa modułu kształcenia

(przedmiotu)

Systemy pomiarowe w

mechatronice

Kod modułu kształcenia

E47/EM/6

Rodzaj modułu kształcenia

(obowiązkowy lub wybieralny)

obowiązkowy

Rodzaj studiów

stacjonarne, I-go stopnia

Obszar kształcenia

Nauki techniczne

Kierunek studiów

Elektrotechnika

Specjalność

Elektromechatronika

Profil kształcenia

praktyczny

Rok studiów

trzeci

Semestr

szósty

Rodzaj zajęć i liczba godzin

dydaktycznych

30 w., 30 lab.

Liczba punktów ECTS

5

Tytuł/stopień naukowy, imię,

nazwisko, adres e-mail wykładowcy

(wykładowców)

Dr hab. inż. Andrzej Odon, prof.

nadzw.

[e-mail]

mgr inż. Grzegorz Pilzak

mgr inz. Waldemar Hawrot

2

II. Cel (cele) modułu kształcenia

Zapoznanie się z zagadnieniami statycznych i dynamicznych
właściwości sensorów i przetworników pomiarowych oraz miarami
ich niedokładności, metodami przetwarzania i rejestracji sygnałów
zmiennych w czasie oraz zastosowania zaawansowanych
systemów pomiarowych.
Opanowanie

umiejętności

właściwego

doboru

narzędzi

pomiarowych dla realizacji zadań inżynierskich w zakresie
statycznych i dynamicznych pomiarów wielkości elektrycznych i
nieelektrycznych.

III. Wymagania wstępne w zakresie wiedzy, umiejętności

oraz kompetencji społecznych

Podstawowa wiedza w zakresie matematyki, fizyki, podstaw
elektrotechniki

i

metrologii.

Umiejętność

efektywnego

samokształcenia w dziedzinie związanej z wybranym kierunkiem
studiów.

3

•Treści kształcenia

Symbol treści kształcenia
Opis treści kształcenia

TK_01
Podstawowe pojęcia dotyczące błędów i niepewności pomiarów. Wybrane zagadnienia
przetwarzania niezniekształcającego -  właściwości statyczne i dynamiczne sensorów i
przetworników pomiarowych. Dopasowanie przetworników w torze pomiarowym.

TK_02
Analogowe elementy sprzętowe systemów pomiarowych – sensory, analogowe
przetworniki pomiarowe, układy kondycjonowania sygnałów toru pomiarowego,

TK_03
Cyfrowe przetwarzanie sygnałów ciągłych – próbkowanie, zjawisko aliasingu,
kwantowanie, kodowanie, błędy kwantowania, dokładność pomiaru. Elementy
sprzętowe techniki przetwarzania cyfrowego - komparatory, układy próbkująco-
pamiętające, przetworniki impulsowo-czasowe, przetworniki analogowo-cyfrowe i
cyfrowo-analogowe.

TK_04
Zastosowanie zaawansowanych technik pomiarowych do wizualizacji, rejestracji i
pomiarów sygnałów oraz akwizycji i przetwarzania danych – rejestratory cyfrowe i
oscyloskopy cyfrowe, karty pomiarowe, przegląd interfejsów, oprogramowanie
elementów systemów pomiarowych (LabView, DasyLab)

TK_05
Dot. treści ćw. lab.: badanie właściwości dynamicznych i statycznych sensorów do
pomiaru temperatury, przemieszczeń i parametrów promieniowania i wybranych
elementów układu kondycjonowania sygnału (wzmacniacze pomiarowe, przetworniki
wartości średniej i szczytowej, filtry aktywne)

4

Zalecana literatura

1. M. Gruca, J. Grzelka, M. Pyrc, S. Szwaja, W. Tutak, Miernictwo i

systemy pomiarowe, Częstochowa 2008

2. W. Nawrocki, Komputerowe systemy pomiarowe, WKŁ 2002

3. A. Chwaleba, M Poniński, A. Siedlecki ‑ Metrologia elektryczna,

WNT, Warszawa, 2010.

4. A. Cysewska-Sobusiak ‑ Podstawy Metrologii i inżynierii

pomiarowej, Wyd. Politechniki Poznańskiej, 2010.

5. 6. J. Rydzewski, Pomiary oscyloskopowe, WNT, Warszawa, 2007.

6. S. Tumański – Technika pomiarowa, WNT 2007.

7. A. Zatorski, R. Sroka – Podstawy metrologii elektrycznej, Wyd.

AGH, Kraków, 2011.

8.J. Grzelka, E. Mazur, M. Gruca, W. Tutak ‑ Miernictwo i systemy

pomiarowe - laboratorium, WPC, Częstochowa, 2004

9. J. Zakrzewski , Czujniki i przetworniki pomiarowe. WPŚl. Gliwice

2004.

5

1. Struktura komputerowego

systemu pomiarowego

6

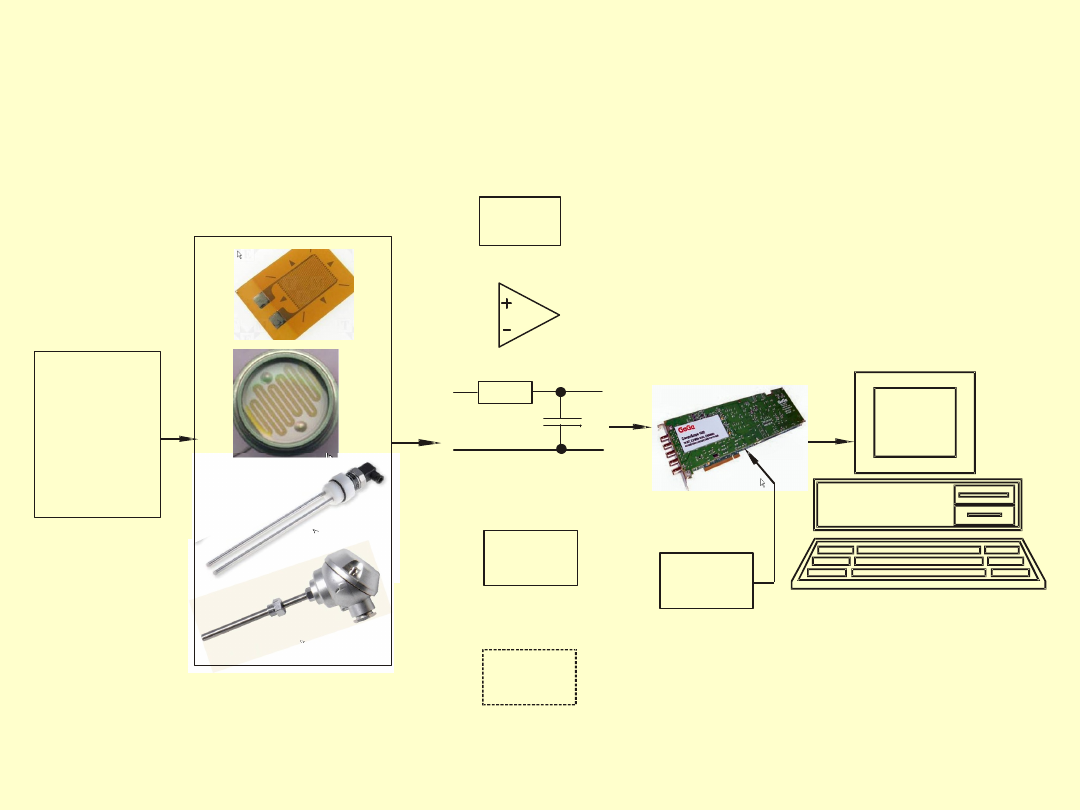
Struktura
komputerowego
systemu pomiarowego

O b je k t

Z ja w is k o

C z u jn ik i

U k ła d

k o n d y c jo n o w a n ia

K a r ta

p o m ia r o w a

z u k ła d e m

p r z e tw o r n ik a

a n a lo g . - c y fr.

w z m a c n ia c z

F i ltr

z a s ila c z

I n n e r o d z a j e

p r z e tw o r n ik ó w

.

P r z e tw o r n ik

n a p ię c i e - p r ą d .

U / I

A / C

7

Tor pomiarowy

– to droga przebiegu sygnału od jego źródła, które

stanowi badane zjawisko fizyczne, poprzez człony przetwarzające,
porównujące i elementy transmisyjne – do urządzeń wyjściowych,
przy pomocy których uzyskuje się zobrazowanie wyników pomiarów
[

Robert Czabanowski

SENSORY I SYSTEMY POMIAROWE, Oficyna Wyd. Poltechmiki Wrocławskiej 2010]

System pomiarowy

– zestaw spełniających określone funkcje i

współpracujących ze sobą przyrządów pomiarowych i urządzeń
dodatkowych - przeznaczonych do zbierania, porównywania,
rejestracji i przetwarzania sygnałów o mierzonych wielkościach
fizycznych – umożliwiających określenie stanu obiektu badanego

[Robert

Czabanowski SENSORY I SYSTEMY POMIAROWE, Oficyna Wyd. Poltechmiki Wrocławskiej 2010].

Analogowy system pomiarowy

– przetwarzanie sygnału nie zmienia

jego ciągłego charakteru, a wynik pomiaru przedstawia się w postaci
odczytywanych lub rejestrowanych – najczęściej w funkcji czasu –
sygnałów analogowych

[Robert Czabanowski SENSORY I SYSTEMY POMIAROWE, Oficyna Wyd.

Poltechmiki Wrocławskiej 2010].

.

Cyfrowy system pomiarowy

– na pewnym etapie przetwarzania

sygnału
pomiarowego występuje dyskretyzacja sygnału analogowego
(przetwarzanie
analogowo-cyfrowe) a wynik przedstawia się w postaci cyfrowej [

Robert

Czabanowski SENSORY I SYSTEMY POMIAROWE, Oficyna Wyd. Poltechmiki Wrocławskiej 2010].

.

8

Czujnik

(inna nazwa sensor) – element systemu pomiarowego, który

dokonuje
przetworzenia wielkości nieelektrycznej na elektryczną.

Układ kondycjonowania (kondycjoner)

ma za zadanie dopasowanie

czujnika do
typowego układu wejścia komputera. Zazwyczaj wyjściowy sygnał
kondycjonera jest sygnałem analogowym. [

S. Tumański, Technika pomiarowa

].

Przykładowe zadania układów kondycjonowania:

- zasilanie sensora prądem stałym lub zmiennym

- zabezpieczanie wejść układu

- przesuwanie poziomu sygnału

- wzmacnianie

- przetwarzanie na sygnał prądowy dla celów transmisji (standard 5-
20 mA)

- linearyzacja

- przełączanie sygnałów analogowych z czujników pomiarowych

- izolacja galwaniczna

- filtracja

9

Nazewnictwo – problemy z jednolitością i jednoznacznością stosowanych
pojęć

- Niektórzy autorzy zamiast stosować nazewnictwo np..

czujnik

termoelektryczny

określają mianem -

przetwornik termoelektryczny

. Jest to w pewnym stopniu

uzasadnione, bo każdy czujnik realizuje operację przetwarzania. Spotyka się
również
inne określenia np. przetwornik pierwotny

-Wiele komercyjnie oferowanych czujników zawiera integralnie wmontowany
przetwornik
i wówczas nazwa „przetwornik rezystancyjny” jest w pełni uzasadniona

- Coraz częściej stosuje się tzw. czujniki inteligentne ( w zasadzie miniaturowy
System pomiarowy) wyposazone w wyjście interfejsu typu Ethernet )

10

2.

Właściwości statyczne i dynamiczne przetworników

pomiarowych

Treści omawiane w tym rozdziale dotyczyć mogą zarówno całego całego toru
pomiarowego (przetwornik + czujnik), jak i indywidualnie każdego z tych
elementów

2.1. Właściwości statyczne

Są opisywane za pomocą charakterystyk statycznych i takich parametrów jak
czułość przetwarzania, błąd przesunięcia zera, błąd nieliniowości

2.2. Właściwości dynamiczne

Są opisywane za pomocą charakterystyk
częstotliwościowych i
czasowych (odpowiedź na wymuszenie skokowe)

11

2.2.1. Charakterystyki częstotliwościowe

a) Badanie charakterystyk częstotliwościowych liniowego przetwornika pomiarowego

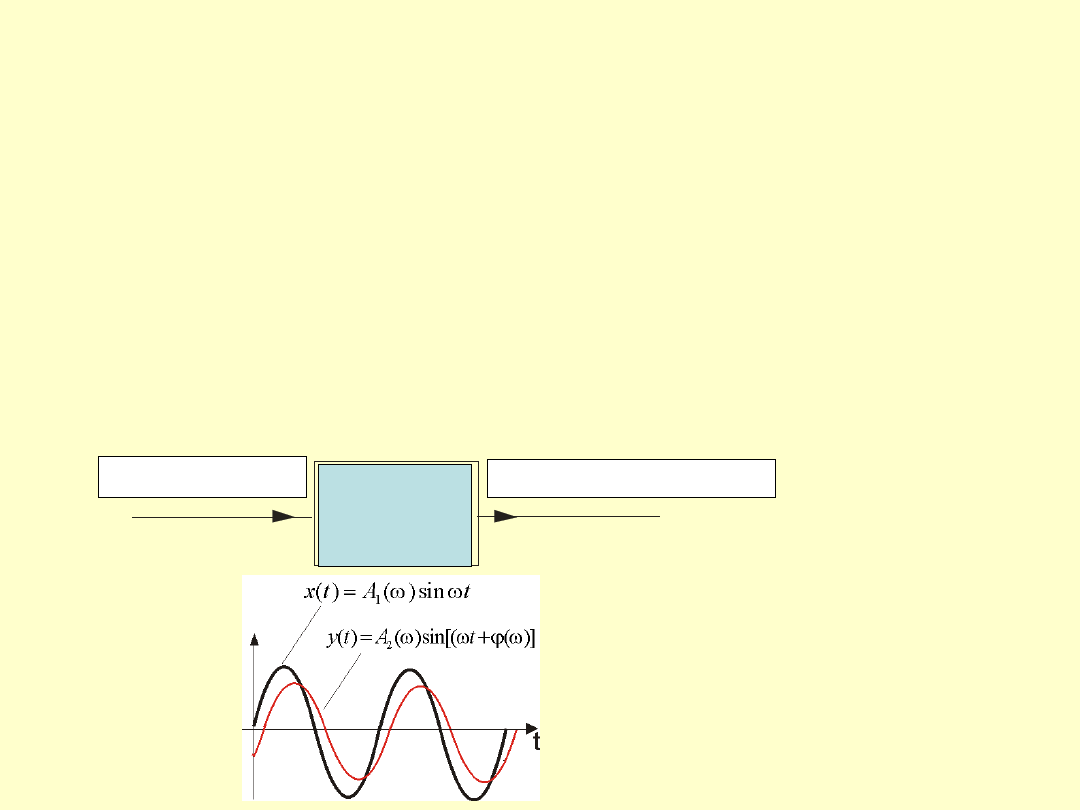
Jeżeli na wejście liniowego przetwornika pomiarowego doprowadzone
zostanie wymuszenie sinusoidalne (sygnał o przebiegu sinusoidalnym)

t

A

t

x





sin

)

(

)

(

1



o amplitudzie A1, pulsacji ω (ω=2Πf) i fazie = 0

0

, to na wyjściu (po zaniku

procesów przejściowych) pojawi się odpowiedź sinusoidalna:

)]

(

sin[(

)

(

)

(

2













t

A

t

y

o tej samej pulsacji, ale w ogólnym przypadku o innej amplitudzie i innej fazie φ.
Charakterystyki częstotliwościowe wyznacza się dla zakresu pulsacji od ω = 0 do ω →

∞

t

A

t

x



 sin

)

(

)

(

1



)]

(

sin[(

)

(

)

(

2













t

A

t

y

Liniowy

element

automatyki

Badanie, którego celem jest
sporządzenie

charakterystyk

częstotliwościowych,

można

przeprowadzić

w

sposób

eksperymentalny

lub

teoretyczny – w tym drugim
przypadku wykorzystując opis
matematyczny wielkości zwanej
transmitancją widmową G(jω)

Przetwornik

12

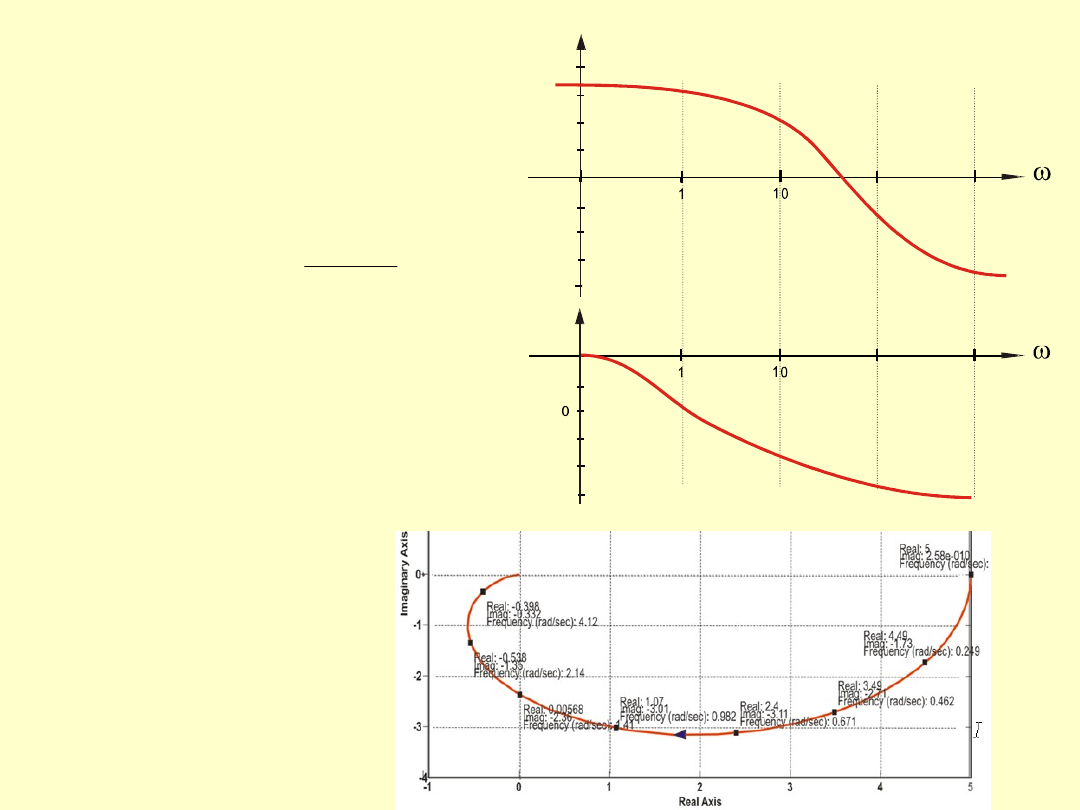
Wynik badania:

• Charakterystyka Bodego

- amplitudowe charakterystyki
częstotliwościowe :

)

(

)

(

log

20

)

(

1

2







A

A

L



- fazowe charakterystyki
częstotliwościowe

)

(

)

(







f



• Charakterystyka Nyquista

- 4 0

- 3 0

-

-

-

2

9

- 1 3 5

- 1 8 0

- 2 2 5

0

-

-

1

4 5

0

0

0

1 0

2 0

3 0

4 0

0

0

,

,

1

1

1 0 0

1 0 0

1 0 0 0

1 0 0 0

)

( 

L

]

) [

(

0





13

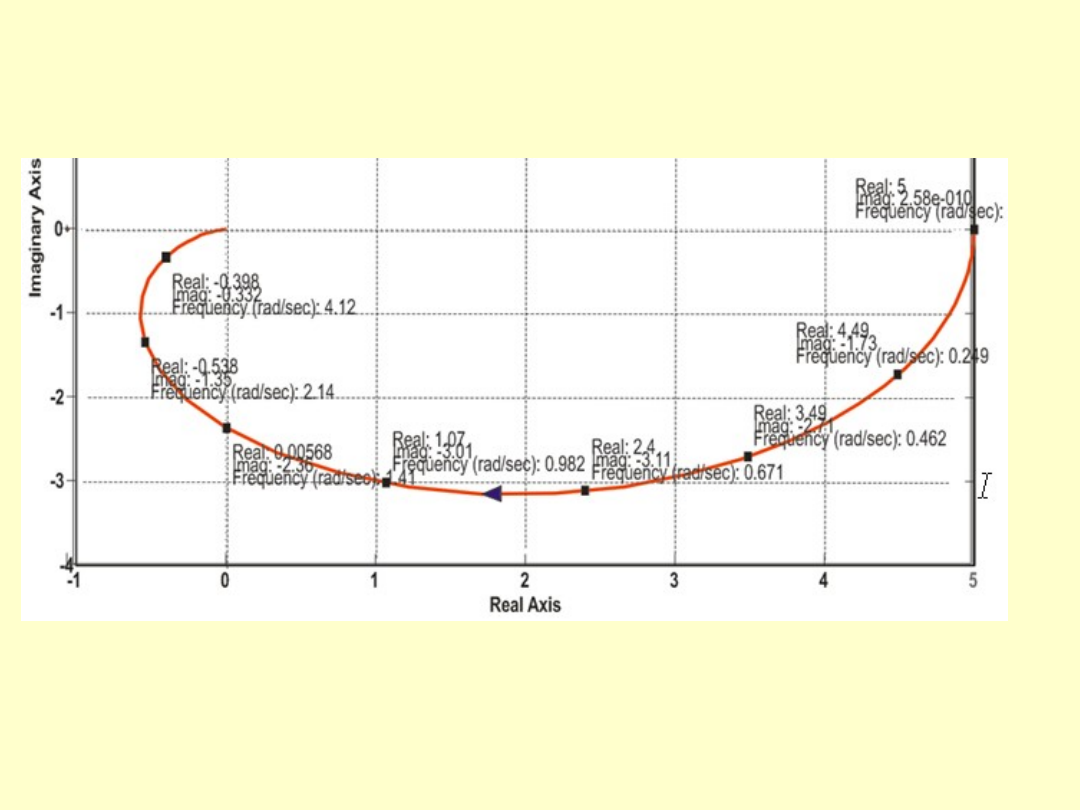
• Charakterystyka Nyquista

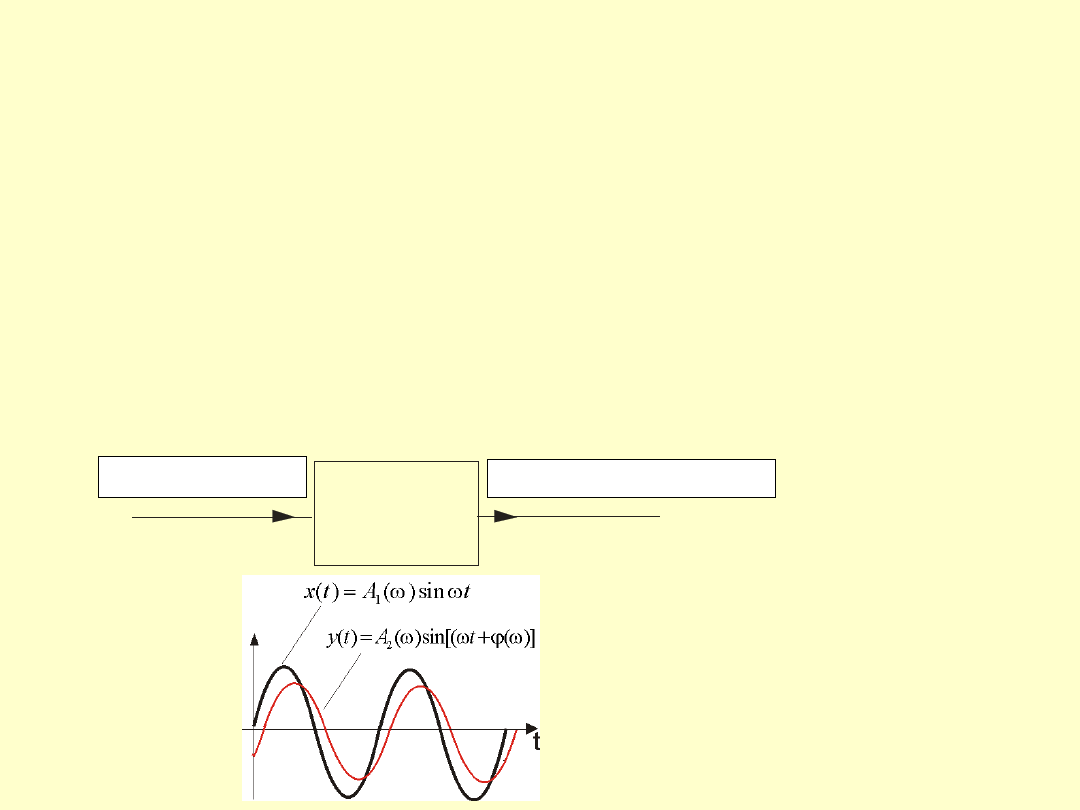
14

9.1. Pojęcia podstawowe, definicje

a) Badanie charakterystyk częstotliwościowych liniowego elementu automatyki

Jeżeli na wejście elementu lub układu liniowego stabilnego wprowadzone
zostanie wymuszenie sinusoidalne

t

A

t

x





sin

)

(

)

(

1



o amplitudzie A1, pulsacji ω (ω=2Πf) i fazie = 0

0

, to na wyjściu (po

zaniknięciu procesów przejściowych) pojawi się odpowiedź sinusoidalna:

)]

(

sin[(

)

(

)

(

2













t

A

t

y

o tej samej pulsacji, ale w ogólnym przypadku o innej amplitudzie i innej fazie φ.
Charakterystyki częstotliwościowe wyznacza się dla zakresu pulsacji od ω = 0 do ω →

∞

t

A

t

x



 sin

)

(

)

(

1



)]

(

sin[(

)

(

)

(

2













t

A

t

y

Liniowy

element

automatyki

Badanie, którego celem jest
sporządzenie

charakterystyk

częstotliwościowych,

można

przeprowadzić

w

sposób

eksperymentalny

lub

teoretyczny – tym drugim
przypadku wykorzystując opis
matematyczny wielkości zwanej
transmitancją widmową G(jω)
elementu

lub

układu

automatyki

15

b) Transmitancja widmowa

Transmitancja widmowa G(jω) jest podstawą charakterystyk
częstotliwościowych i definiujemy ją jako:

Transmitancja widmowa jest funkcją zespoloną i może być
przedstawiona w postaci wykładniczej lub algebraicznej.





j

s

s

G

j

G





)

(

)

(

1

3

)

(





s

s

G

1

3

)

(









j

j

G

W celu określenia wzoru na G(jω) podstawiamy s=jω i
otrzymujemy:

Przykład: transmitancja operatorowa ma postać:

• Postać wykładnicza transmitancji widmowej

)

(

)

(

1

)]

(

[(

2

)

(

)

(

)

(

)

(

)

(

)

(

























j

t

j

t

j

e

M

e

A

e

A

j

X

j

Y

j

G









gdzie: M(ω): moduł transmitancji widmowej:

M(ω) = |G(jω) |=A2(ω)/ A1(ω)

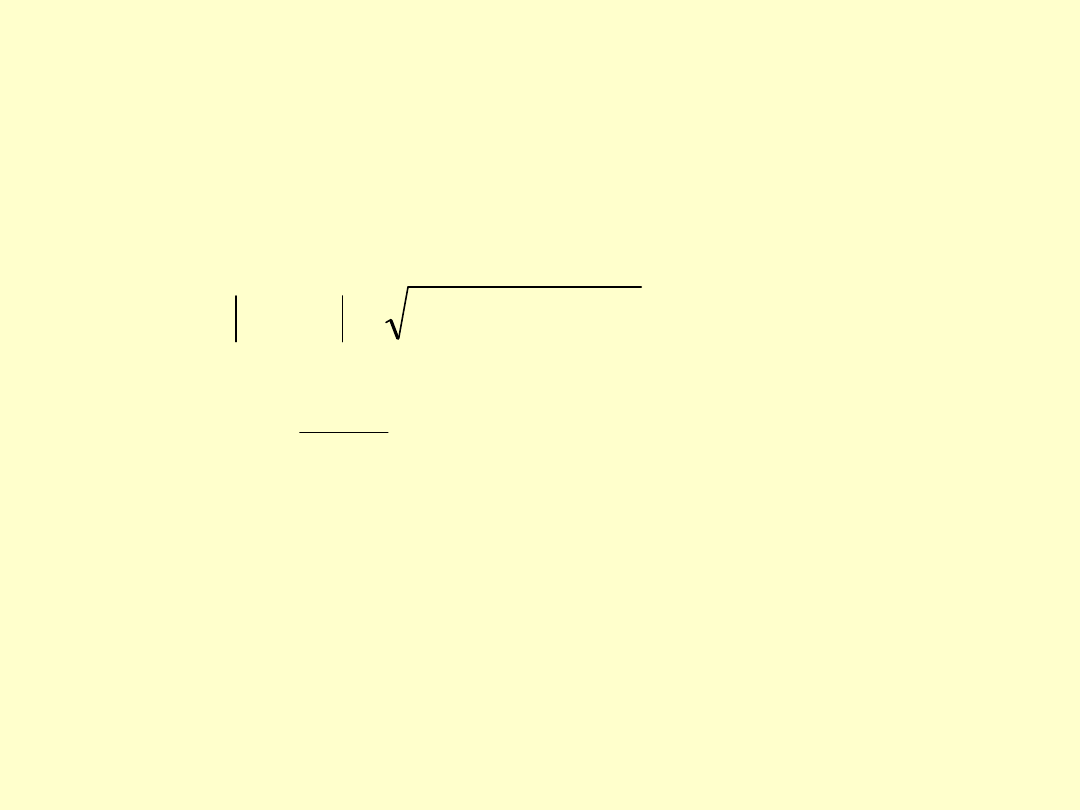
16

•

Postać algebraiczna transmitancji widmowej

)

(

)

(

)

(







jQ

P

j

G





gdzie:
P(ω)=Re[G(jω)
]
Q(ω)=
Im[G(jω)]

)

(

)

(

)

(

)

(

2

2









Q

P

j

G

M







- moduł transmitancji G(jω)

)

(

)

(

)

(









P

Q

arctg



- argument transmitancji G(jω

)

17

9.2. Charakterystyki częstotliwościowe Nyquista i Bodego

a) charakterystyka amplitudowo-fazowa (wykres Nyquista)

Charakterystyka amplitudowo-fazowa (wykres Nyquista) jest to
miejsce geometryczne punktów, które wyznaczają końce wektorów
G(jω) na płaszczyźnie zmiennej zespolonej przy zwiększaniu pulsacji
ω od wartości ω = 0 do ω → ∞

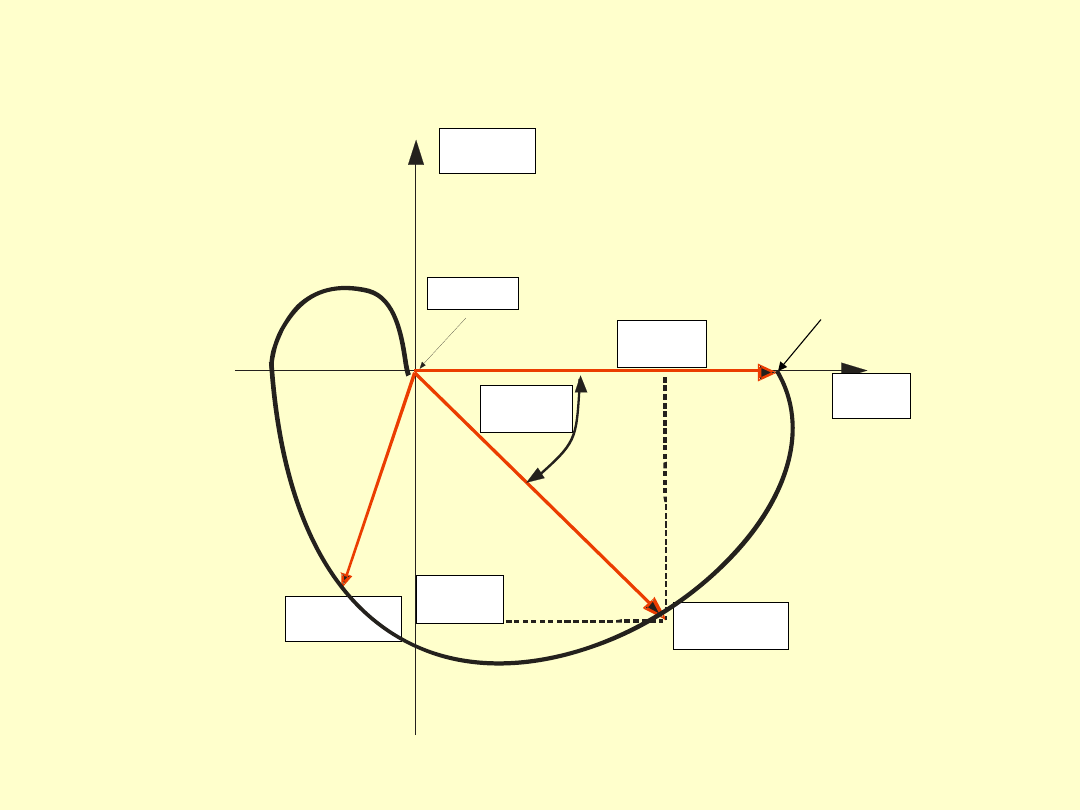
18

)

(

jQ

)

(

P

)

(

0



P

0

0





)

(

1



Q

)

(

1



P

)

(

1

1



j

G

)

(

2

2



j

G

Ą





)

(

1

1





19

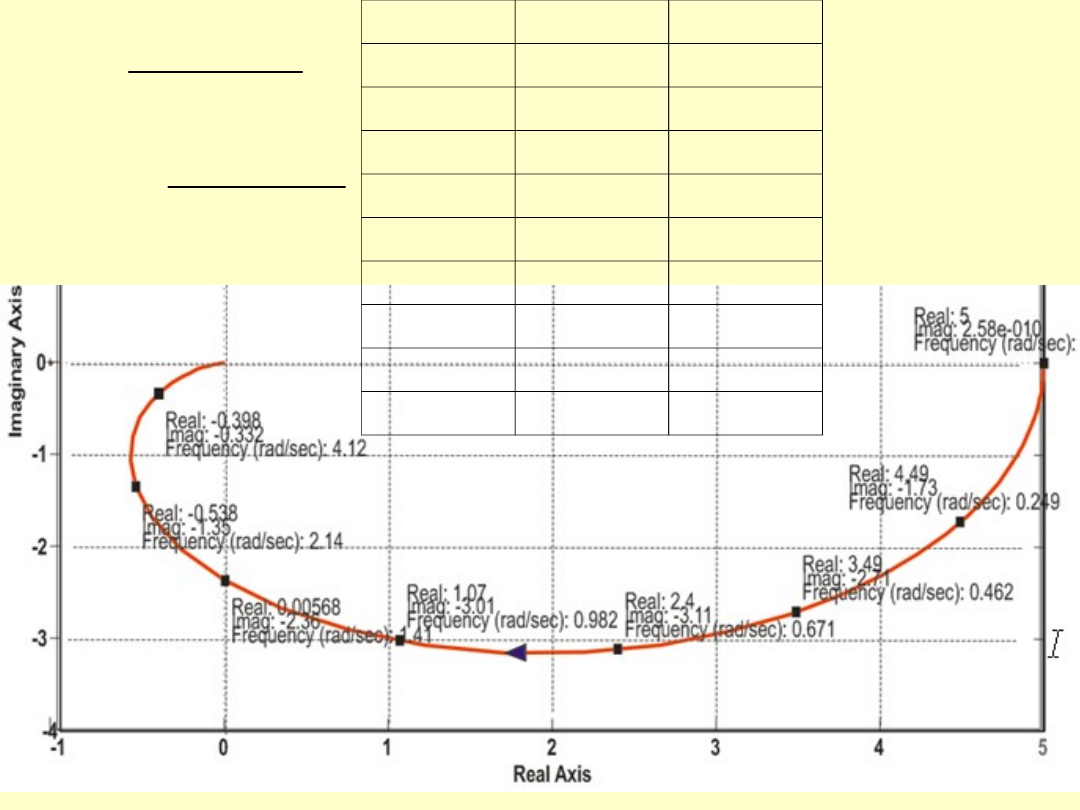
Przykład 1
Wyznaczyć częstotliwościową zespoloną charakterystykę charakterystykę
Nyquista dla elementu, którego transmitancja operatorowa wyrażona jest
wzorem:

)

2

)(

1

(

10

)

(







s

s

s

G

)

2

)(

1

(

10

)

(







s

s

s

G

•

→

)

2

)(

1

(

10

)

(













j

j

j

G

•

Postać algebraiczna transmitancji widmowej G(jω):

4

5

30

4

5

10

20

4

5

30

10

20

9

4

4

30

10

20

)

3

(

)

2

((

30

10

20

]

3

)

2

][(

3

)

2

[(

]

3

)

2

[(

10

2

2

10

)

2

)(

1

(

10

)

(

2

4

2

4

2

2

4

2

2

4

2

2

2

2

2

2

2

2

2

2











































































































































j

j

j

j

j

j

j

j

j

j

j

j

j

G

20

4

5

10

20

)

(

2

4

2

















P

4

5

30

)

(

2

4

















Q

ω[1/s]

P(ω)

Q(ω)

0

5

0

0,249

4,49

-1,73

0,462

3,49

-2,71

0,671

2,4

-3,11

0,982

1,07

-3,01

1,41

-0,056

--2,36

2,14

-0,538

-1,35

4,12

-0,398

-0,332

∞

0

0

21

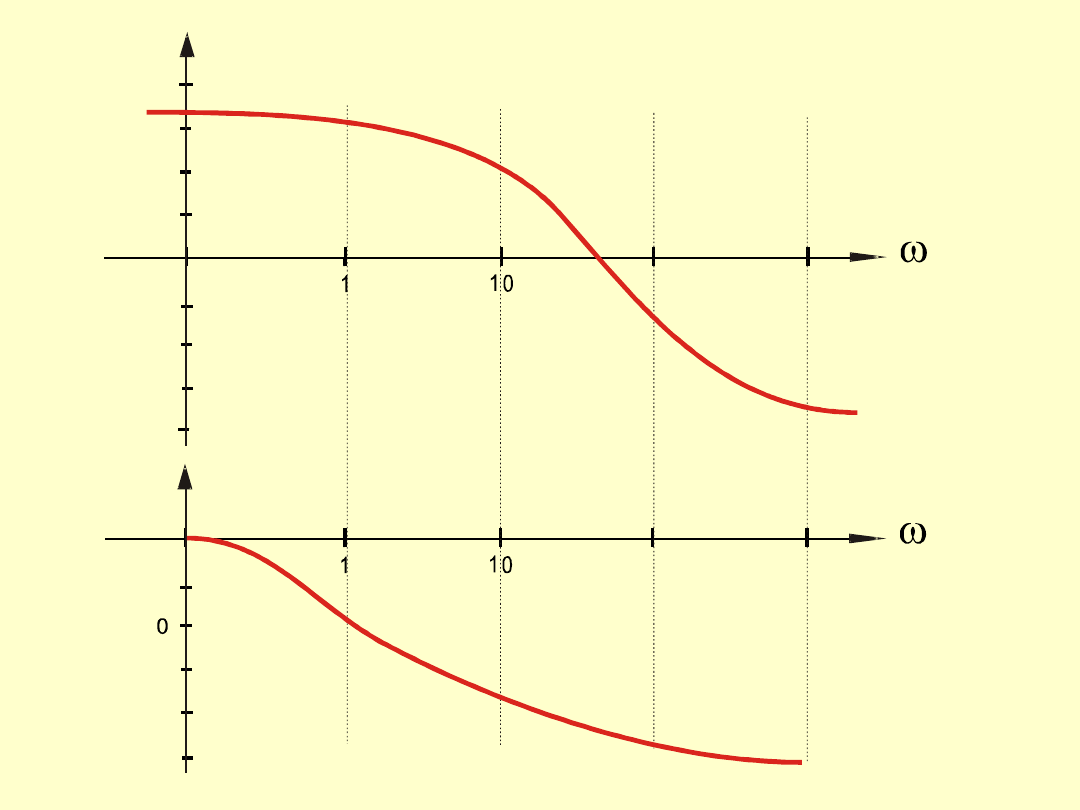
b) Częstotliwościowe charakterystyki logarytmiczne (Charakterystyki Bodego)

Wykonuje się dwa osobne, usytuowane jeden pod drugim, wykresy:



amplitudowej charakterystyki częstotliwościowej L(ω), przy

czym L(ω)obliczamy z zależności L(ω) = 20log M(ω) [dB] (wynik
wyrażony jest w dB) zatem:

2

2

)]

(

[

)]

(

[

log

20

)

(







Q

P

L





• fazowej charakterystyki częstotliwościowej
φ (ω)

Podziałka osi odciętych obydwu wykresów przedstawiona
jest
w skali logarytmicznej.

22

- 4 0

- 3 0

-

-

-

2

9

- 1 3 5

- 1 8 0

- 2 2 5

0

-

-

1

4 5

0

0

0

1 0

2 0

3 0

4 0

0

0

,

,

1

1

1 0 0

1 0 0

1 0 0 0

1 0 0 0

)

( 

L

]

) [

(

0





23

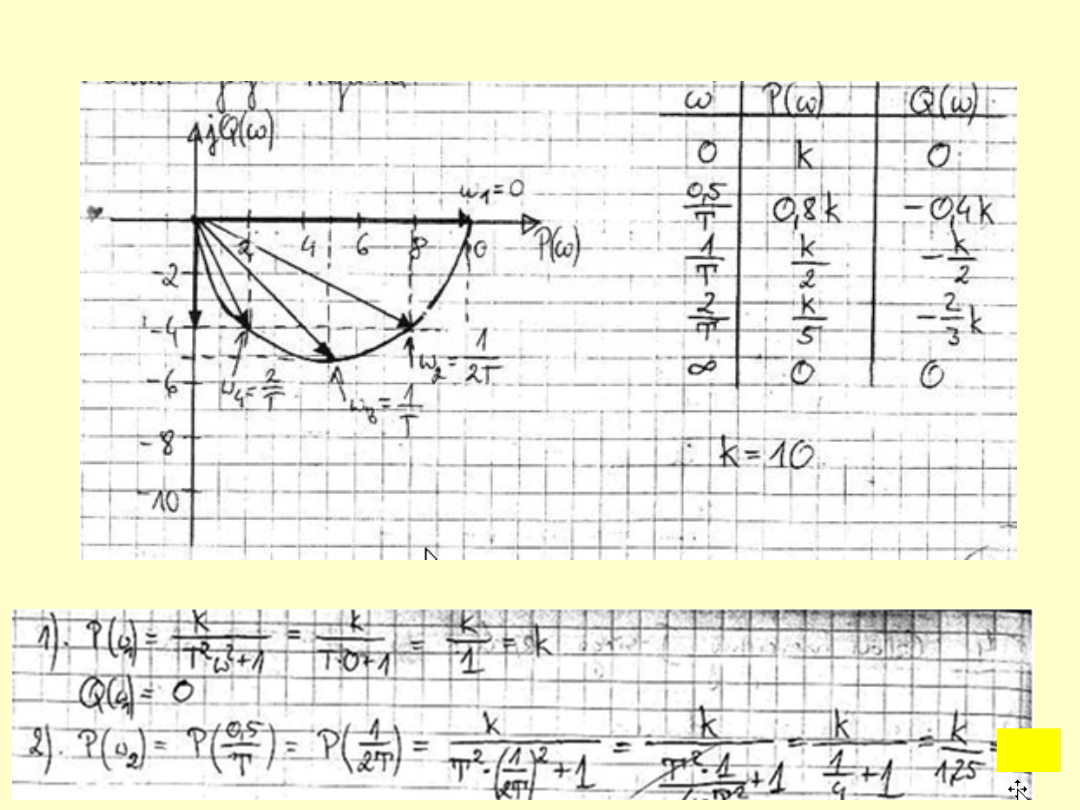
10.4 Człon inercyjny I rzędu

a)

Transmitancja

widmowa

b) P(ω), Q(ω)

24

c) Charakterystyka Nyquista

Przykładowe obliczenia:

0,8

25

Przykładowe obliczenia:

26

d) Charakterystyka Bodego

wstawiam P(ω), Q(ω):

Zatem φ(ω):

27

• Obliczamy L(ω): i φ(ω) dla kolejno zwiększajacych
się wartości pulsacji wyrażonej w jednostkach
względnych jako:

• Wprowadzamy pojęcie tzw. pulsacji

granicznej:

T

g

1





g





Przykładowe obliczenia:

1)

dB

K

L

g

g

20

0

20

1

01

,

0

log

20

10

log

20

1

)

(

log

20

log

20

)

01

,

0

(

2

2

1































2)

dB

L

g

20

)

1

,

0

(

1









3)

dB

L

g

17

)

1

(

1









4)

dB

L

g

0

)

10

(

1









5)

dB

L

g

20

)

100

(

1











28

L (

z lin e a r y z o w a n a

 

n a c h y le n ie :

- 2 0 d B / d e k a d ę

1

10

1

)

(











T

j

T

j

k

j

G







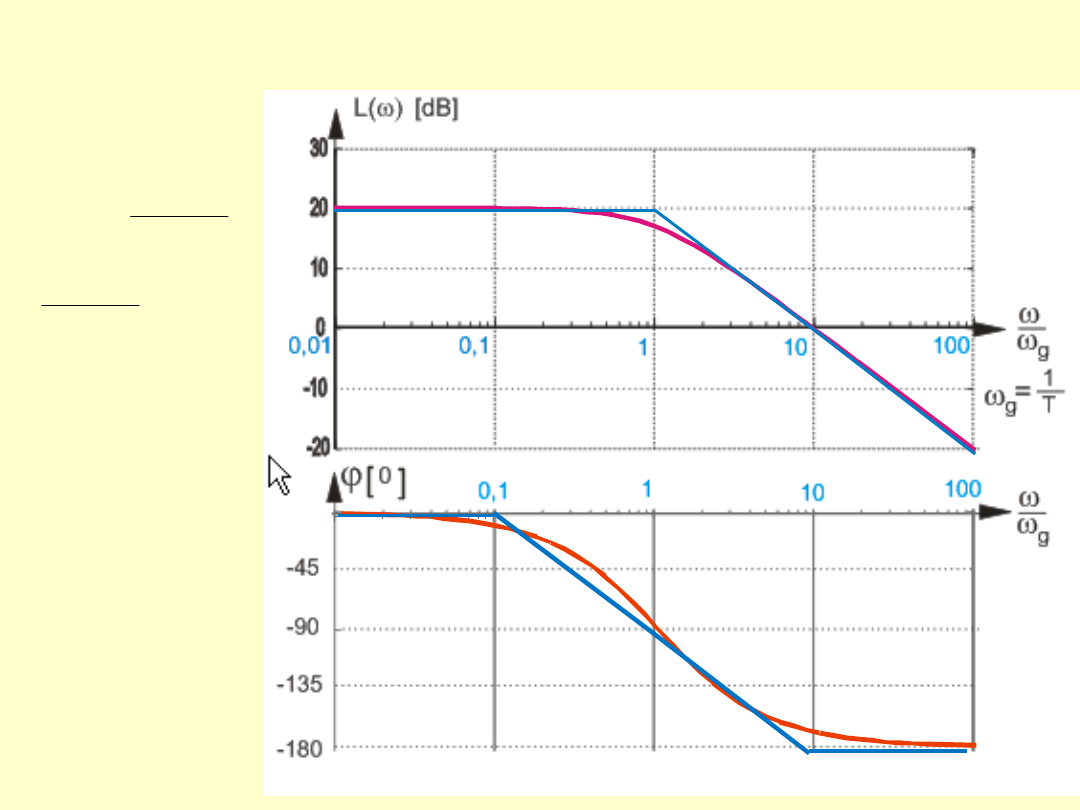
Charakterystyka Bodego członu inercyjnego I rzędu

wykres wykonano dla k=10

29

Charakterystyka zlinearyzowana składa się z dwóch pólprostych.
Pierwsza jest równoległa do osi pulsacji dla pulsacji spełniajacych warunek:

g









0

gdzi

e:

T

g

1





Druga półprosta zaczyna się w punkcie odpowiadającym pulsacji ω

g

,

przy czym nachylenie tej półprostej wynosi 20 db/dekadę

Zależności matematyczne opisujace obydwie półproste:



























g

g

T

k

L













dla

log

20

log

20

0

dla

log

20

)

(