Grafika w programie

MATLAB

dr inż. Henryk Olszewski

2

Grafika

Funkcje graficzne programu MATLAB:

tworzenie wykresów dwuwymiarowych,

tworzenie wykresów trójwymiarowych,

wyświetlanie wykresów ciągłych i dyskretnych,

tworzenie grafiki wektorowej i rastrowej.

3

Wykresy 2D

Funkcja plot umożliwia wykreślania danych przechowywanych we wektorach.
Powyższa funkcja generuje dwuwymiarową krzywą złożoną z punktów:

których współrzędne zostały określone we wektorach x i y. Wektory te muszą być
równej długości.

Sposoby wywoływania funkcji plot:

rysowanie wykresu elementów wektora y względem elementów wektora x;
jeśli jeden z argumentów jest macierzą, a drugi wektorem, ciąg elementów
wektora jest rysowany względem wierszy lub kolumn macierzy:

» plot(x,y)

–

rysowanie wykresu elementów wektora y, przyjmując x=1:length(y):

» plot(y)





i

i

y

,

x

4

Wykresy 2D

Sposoby wywoływania funkcji plot:

rysowanie wykresu y(x) z określeniem wyglądu linii; s - łańcuch znaków zawierający
kody wyglądu linii:

» plot(x,y,s)

–

rysowanie w jednym oknie wielu wykresów: y1(x1), y2(x2) itd.:

» plot(x1,y1,x2,y2,...)

–

rysowanie w jednym oknie wielu wykresów z określeniem wyglądu linii każdego z nich:

» plot(x1,y1,s1,x2,y2,s2,...)

Łańcuchy znaków określające sposób rysowania linii mogą zawierać symbole odnoszące się do:

rodzaju linii,

rodzaju markera,

koloru linii.

5

Wykresy 2D

Symbole określające rodzaj linii:

‘-’

linia ciągła

‘--’

linia kreskowana

‘:’

linia kropkowana

‘-.’

linia kreska-kropka (oś symetrii)

Symbole określające kolor linii:

‘y’

kolor żółty

‘m’

kolor karmazynowy

‘c’

kolor turkusowy

‘r’

kolor czerwony

‘g’

kolor zielony

6

Wykresy 2D

Symbole określające kolor linii:

‘b’

kolor niebieski

‘w’

kolor biały

‘k’

kolor czarny

Symbole określające rodzaj markera punktu wykresu:

‘+’

krzyżyk

‘*’

gwiazdka

‘.’

kropka

‘o’

kółko

‘x’

iks

‘s’

kwadrat

7

Wykresy 2D

Symbole określające rodzaj markera punktu wykresu:

‘d’

romb

‘p’

gwiazdka pięcioramienna

‘h’

gwiazdka sześcioramienna

‘v’

trójkąt skierowany w dół

‘^’

trójkąt skierowany w górę

‘<’

trójkąt skierowany w lewo

‘>’

trójkąt skierowany w prawo

-1

-0.8

-0.6

-0.4

-0.2

0

0.2

0.4

0.6

0.8

1

-1

-0.8

-0.6

-0.4

-0.2

0

0.2

0.4

0.6

0.8

1

8

Funkcja linspace

W generowaniu danych do wykresów pomocna jest funkcja linspace:

» linspace(x1,x2,N)

tworząca wektor wierszowy N liczb rozłożonych równomiernie w
przedziel od x1 do x2.

Polecenie:

» linspace(x1,x2)

generuje domyślnie 100 liczb z przedziału od x1 do x2.

9

Wykresy 2D

Funkcja plot spełnia różne funkcje w zależności od liczby
argumentów. Jeżeli y jest wektorem, to polecenie plot(y)
generuje wykres liniowy elementów wektora y w funkcji indeksu
elementów. Jeżeli określimy dwa wektory argumentów, to
polecenie plot(x,y) wyświetla wektor y w funkcji x.

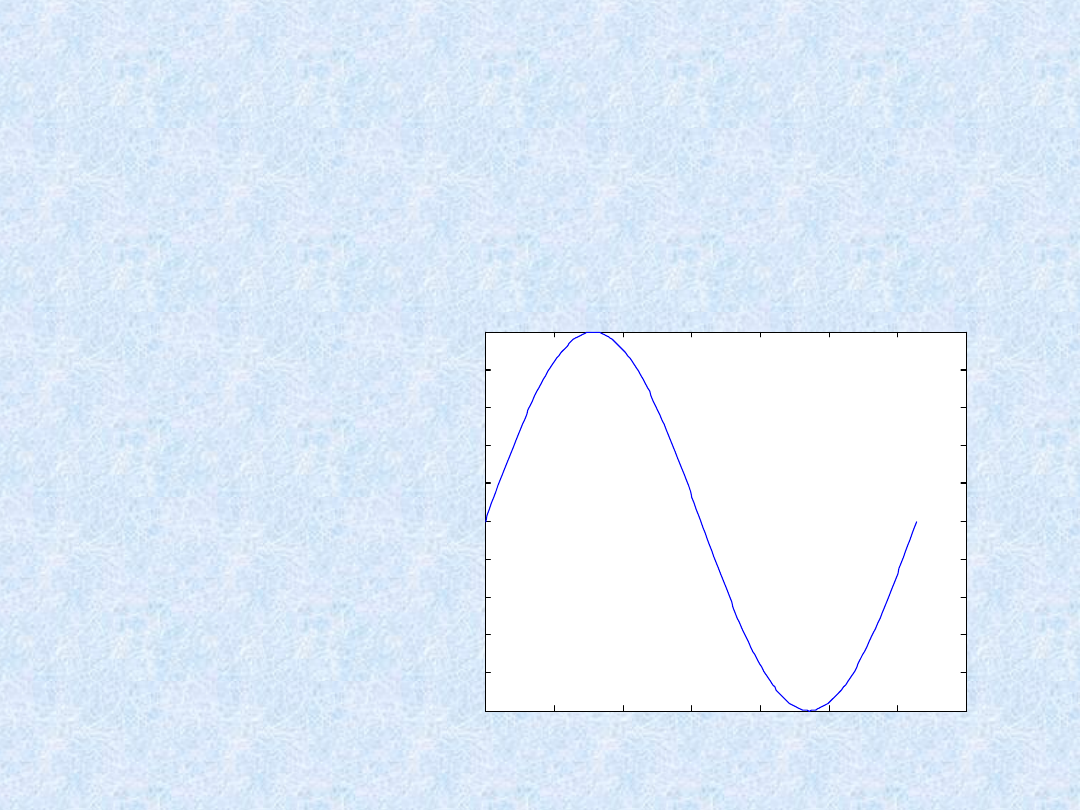
Np. w celu wyświetlenia wykresu funkcji sinus w

przedziale od zera do 2 należy:

» t = 0:pi/100:2*pi;
» y = sin(t);
» plot(t,y)

0

1

2

3

4

5

6

7

-1

-0.8

-0.6

-0.4

-0.2

0

0.2

0.4

0.6

0.8

1

10

Wykresy 2D

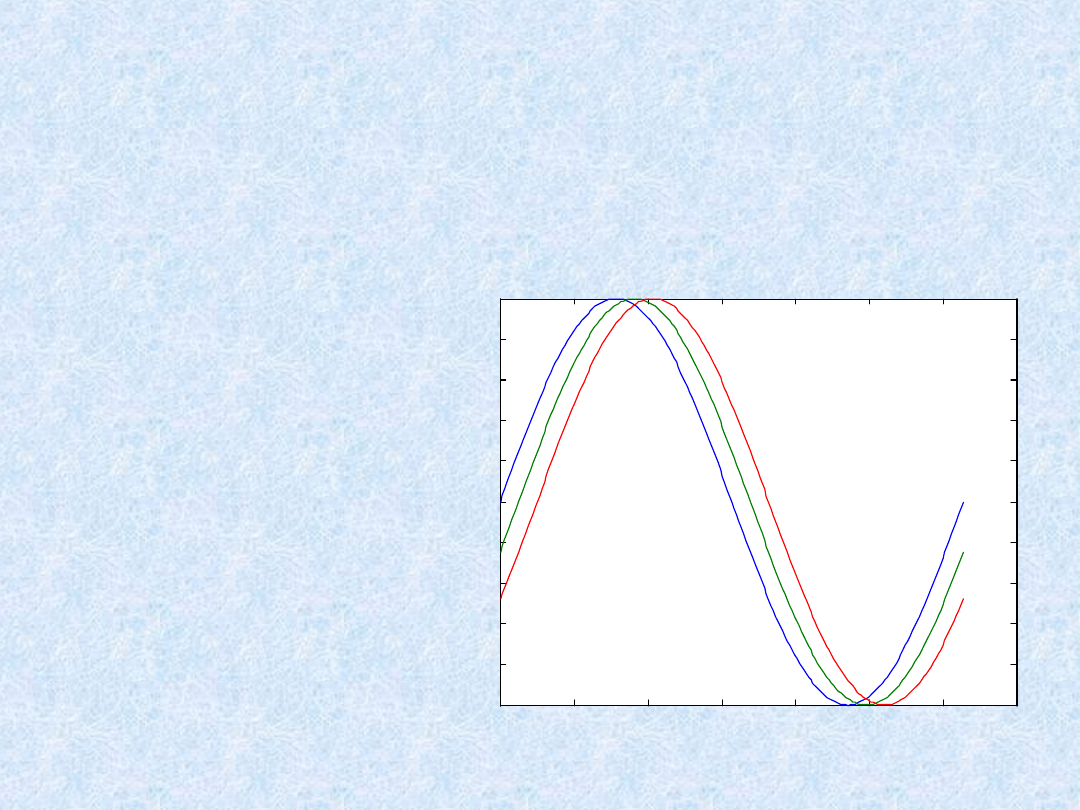
W programie MATLAB istnieje możliwość wyświetlenia na jednym
wykresie kilku przebiegów x-y. MATLAB automatycznie będzie
przyporządkowywał kolejnym przebiegom kolory (z domyślnej listy
kolorów, którą użytkownik może zmieniać), dzięki czemu istnieje
możliwość odróżnienia od siebie poszczególnych zbiorów danych.  
 

»

y2 = sin(t-.25);

»

y3 = sin(t-.5);

»

plot(t,y,t,y2,t,y3)

0

1

2

3

4

5

6

7

-1

-0.8

-0.6

-0.4

-0.2

0

0.2

0.4

0.6

0.8

1

11

Wykresy 2D

Istnieje również możliwość zdefiniowania koloru, rodzaju linii oraz markerów w

poszczególnych punktach definiujących wykres:

 

»

plot(x,y,'color_style_marker')

  color_style_marker jest to 1-, 2- lub 3-znakowy łańcuch (ograniczony apostrofami)

definiujący kolor, rodzaj linii oraz rodzaj markerów:

• Kolory linii są określane znakami: 'c', 'm', 'y', 'r', 'g', 'b', 'w' i 'k', które oznaczają: cyan – jasno

niebieski, magenta – fioletowy, yellow –żółty, red – czerwony, green – zielony, blue –
niebieski, white – biały, black – czarny.

• Rodzaje linii są określone znakami: '-' linia ciągła, '- -' linia kreskowa, ':' linia kropkowa,

'-.' linia osi symetrii i 'none' jeżeli żadna linia nie ma być rysowana.

• Najczęściej używanymi markerami w punktach definiujących wykres są: '+', 'o', '*' i 'x'.

Przykład:

»

plot(x,y,'y:+')

12

Wykresy 2D

W programie MATLAB oprócz wykresów liniowych można wykonywać wykresy
słupkowe, schodkowe, liniowe z naniesionymi zakresami błędów w
poszczególnych punktach pomiarowych, biegunowe.
 
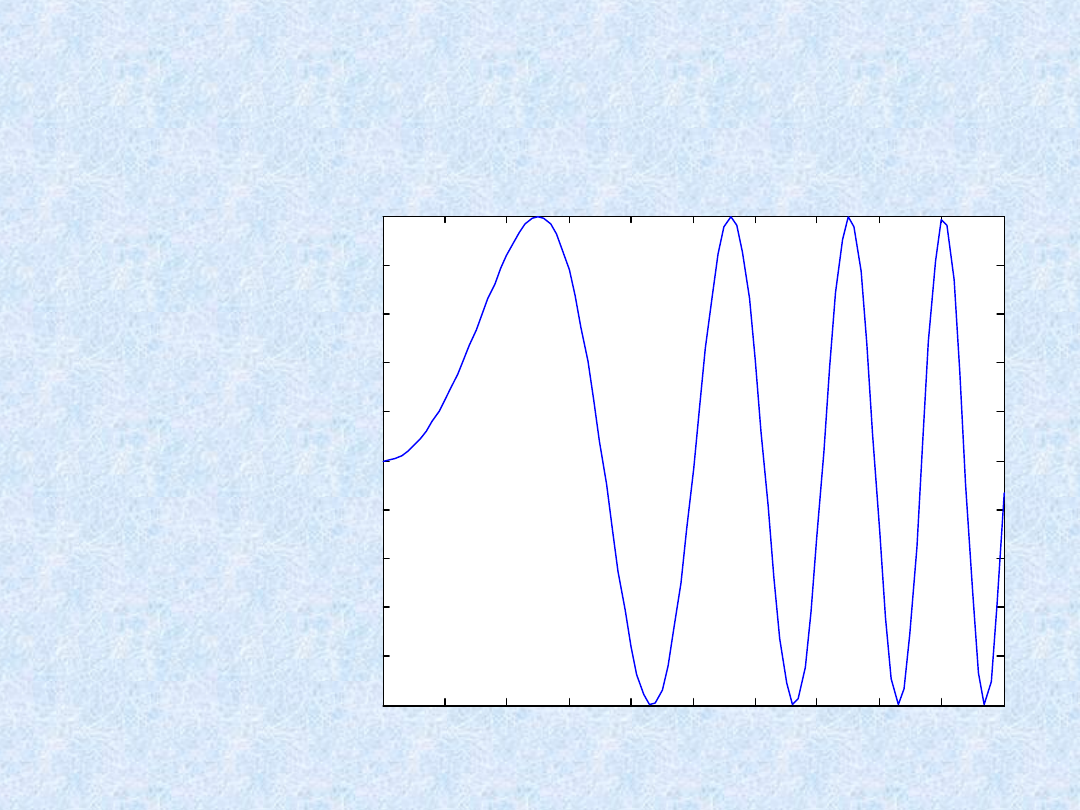
Wykres liniowy:

»

x=0:0.05:5

»

y=sin(x.^2)

»

plot(x,y)

0

0.5

1

1.5

2

2.5

3

3.5

4

4.5

5

-1

-0.8

-0.6

-0.4

-0.2

0

0.2

0.4

0.6

0.8

1

13

Wykresy 2D

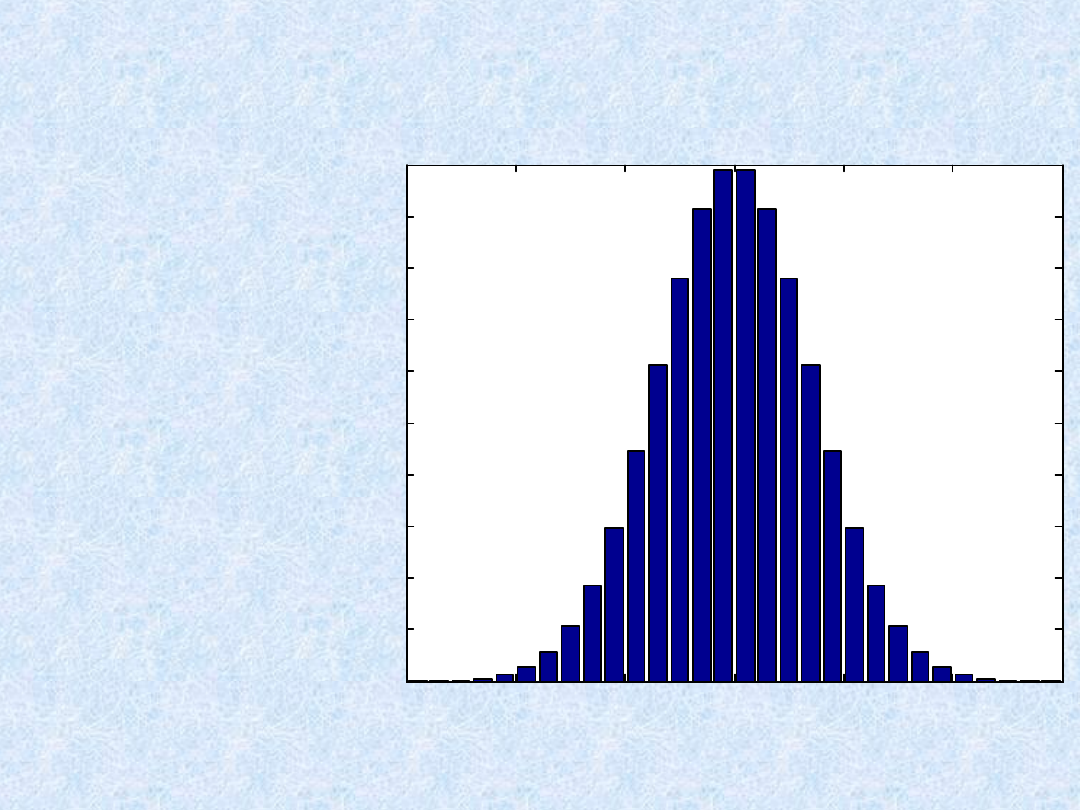
Wykres słupkowy:

»

x = -2.9:0.2:2.9

»

bar(x,exp(-x.*x))

-3

-2

-1

0

1

2

3

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

14

Wykresy 2D

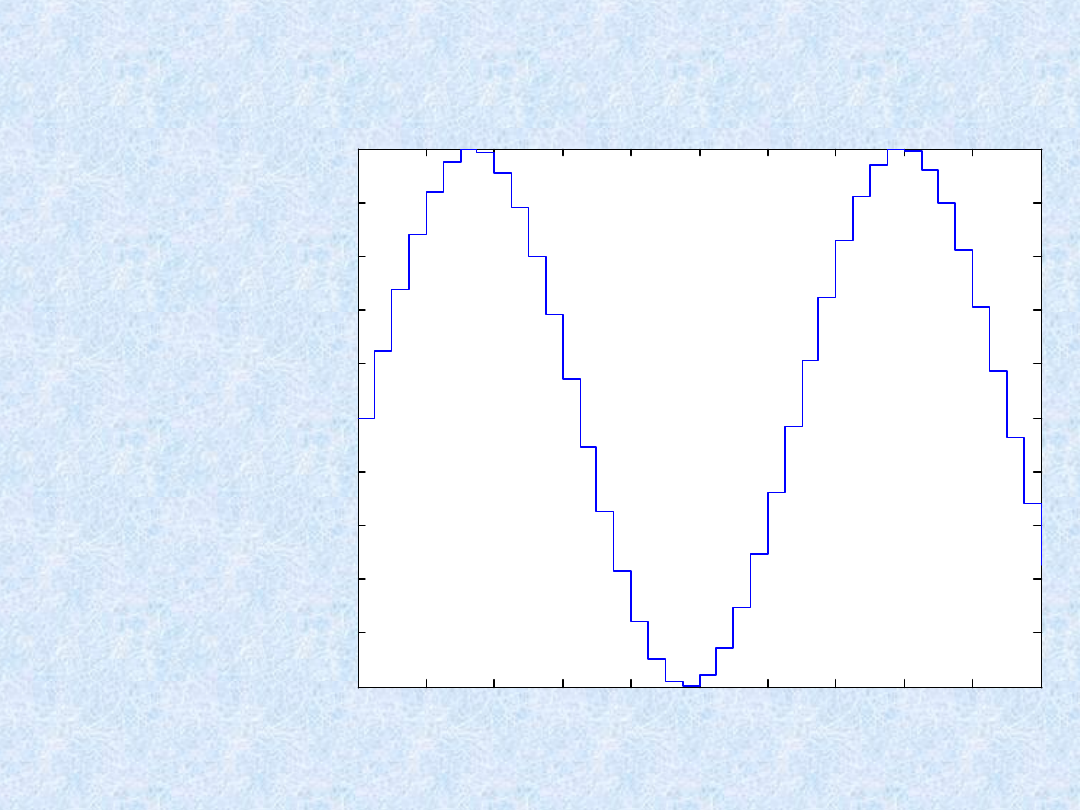
Wykres schodkowy:

»

x=0:0.25:10

»

stairs(x,sin(x))

0

1

2

3

4

5

6

7

8

9

10

-1

-0.8

-0.6

-0.4

-0.2

0

0.2

0.4

0.6

0.8

1

15

Wykresy 2D

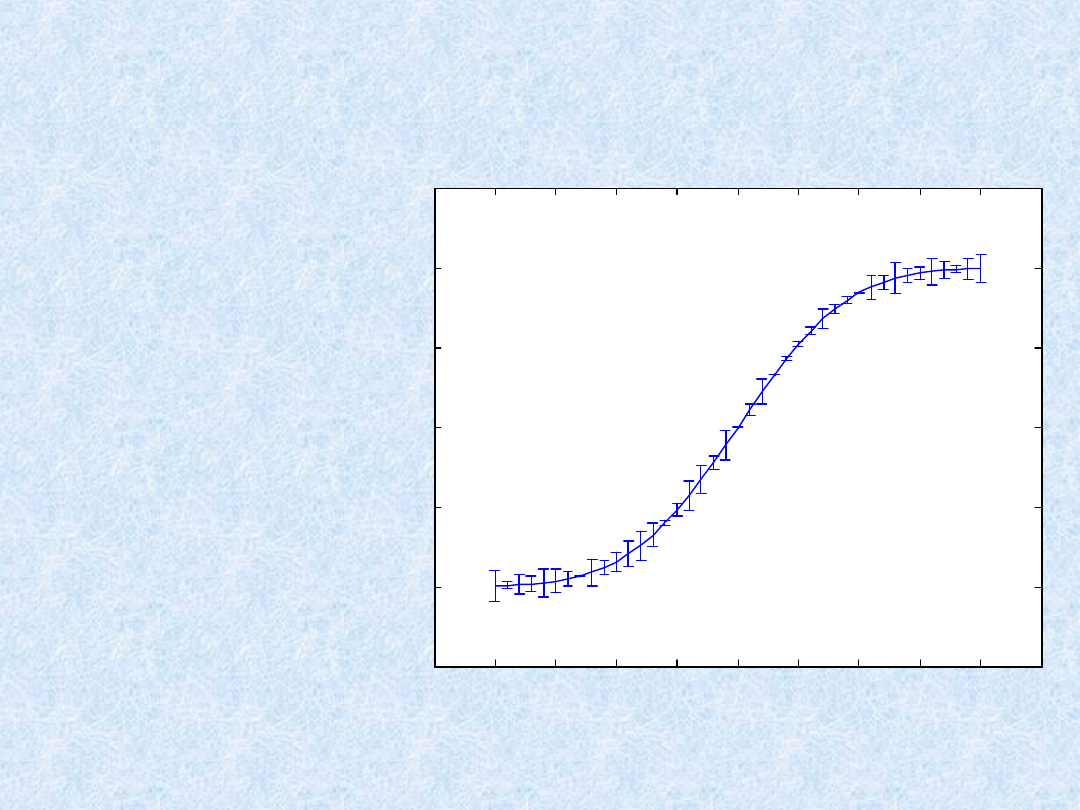
Wykres liniowy z naniesionymi zakresami błędów w punktach
danych:

»

x=-2:0.1:2

»

y=erf(x)

»

e=rand(size(x))/10

»

errorbar(x,y,e)

-2.5

-2

-1.5

-1

-0.5

0

0.5

1

1.5

2

2.5

-1.5

-1

-0.5

0

0.5

1

1.5

16

Wykresy 2D

Wykres biegunowy:
Rysowanie wykresów w biegunowym układzie współrzędnych (Θ, r) służy funkcja:

»

polar(theta,r,s)

gdzie:

theta - wektor katów (w radianach) dla poszczególnych punktów,
r - wektor odległości punktów od początku układu współrzędnych.

Argument s jest argumentem opcjonalnym, określającym wygląd rysowanej linii
(tak, jak w przypadku funkcji plot).

0.1

0.2

0.3

0.4

0.5

30

210

60

240

90

270

120

300

150

330

180

0

17

Wykresy 2D

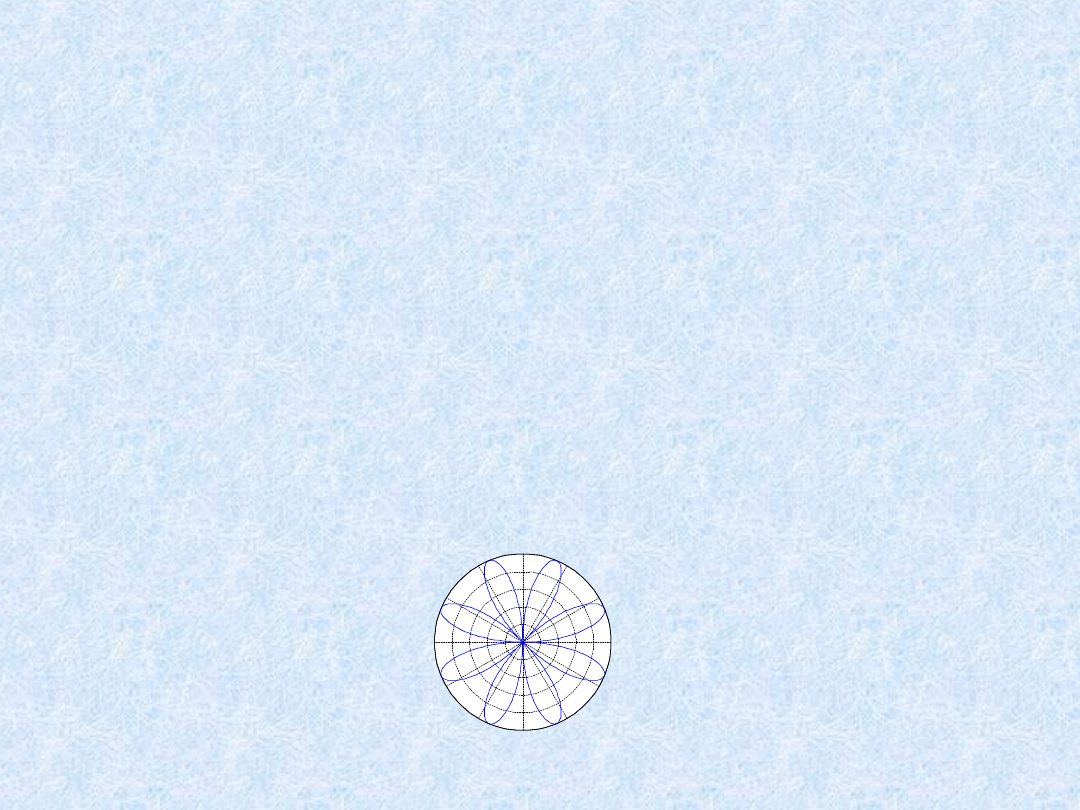
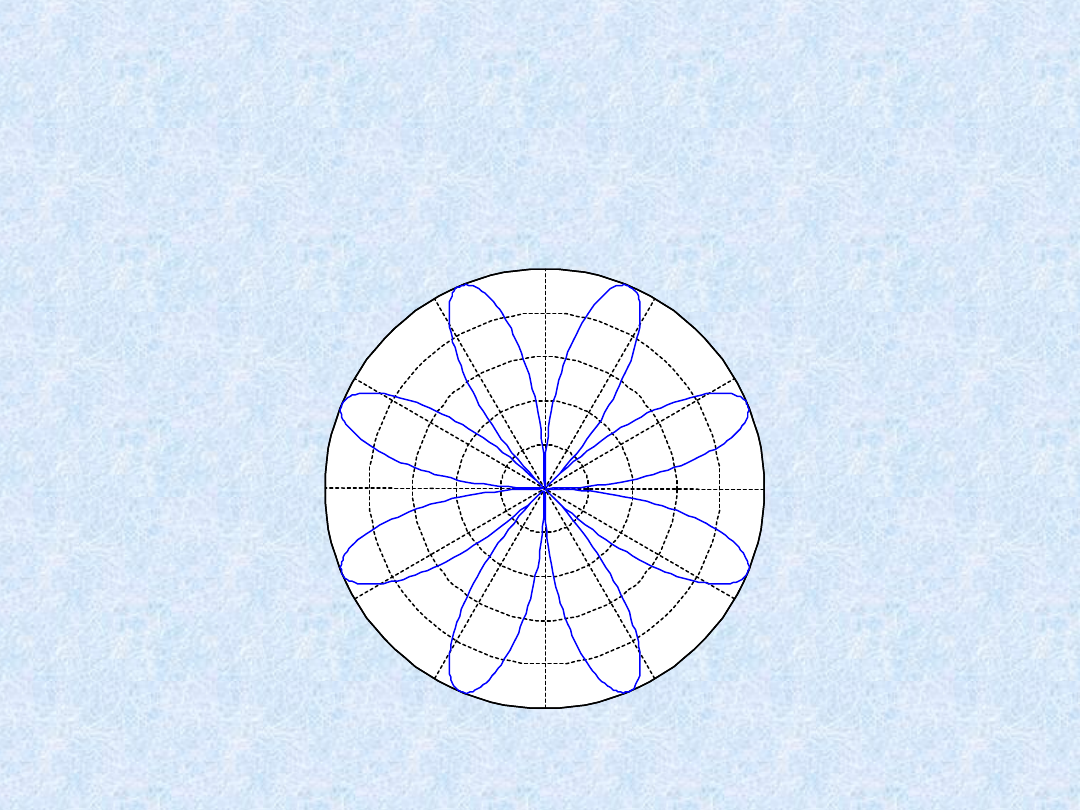
Wykres biegunowy:

»

t=0:.01:2*pi

»

polar(t,abs(sin(2*t).*cos(2*t)))

0.1

0.2

0.3

0.4

0.5

30

210

60

240

90

270

120

300

150

330

180

0

18

Wykresy 2D

Wykres w skali logarytmicznej:
Funkcje rysujące wykresy w skali logarytmicznej:

wyświetlenie wykresu ze skalą logarytmiczną na obu osiach:

»

loglog(x,y,s)

•

wyświetlenie wykresu ze skalą logarytmiczną na osi x:

»

semilogx(x,y,s)

wyświetlenie wykresu ze skalą logarytmiczną na osi y:

»

semilogy(x,y,s)

Funkcja logspace generuje wektor wierszowy N liczb rozmieszczonych logarytmicznie między wartościami 10

x1

a

10

x2

:

»

logspace(x1,x2,N)

Wywołanie funkcji bez argumentu N pozwala na wygenerowanie wektora wierszowego 50 liczb.

19

Funkcja erf

Funkcja erf oblicza funkcję błędu. Polecenie:

»

y = erf(x)

znajduje funkcję błędu dla każdego elementu wektora x. Wektor x musi być
wektorem rzeczywistym. Funkcja błędu zdefiniowana jest jako:
 







x

t

dt

e

x

erf

0

2

2

)

(



20

Wykresy zmiennych zespolonych

Funkcje rysujące wykresy danych zespolonych:

wyświetlenie wykresu Im(z)=f(Re(z)) - jeżeli z jest macierzą o elementach zespolonych,
równoważne poleceniu: plot(real(z),imag(z),s):

»

plot(z,s)

•

wyświetlenie wykresu, na którym elementy macierzy zespolonej z są przedstawione w postaci
strzałek o wspólnym początku i grotach w punktach opisanych przez współrzędne x=real(z),
y=imag(z); x i y są współrzędnymi kartezjańskimi, wykres jest rysowany w biegunowym układzie
współrzędnych:

»

compass(z,s)

lub

»

compass(x,y,s)

•

wyświetlenie wykresu, na którym elementy macierzy zespolonej z są przedstawione w postaci
strzałek o początkach rozmieszczonych równomiernie na osi x; długość strzałek są równe
modułom elementów macierzy z, a kąty nachylenia strzałek - ich argumentom:

»

feather(z,s)

lub

»

feather(x,y,s)

21

Wykresy zmiennych zespolonych

W przypadku, gdy argumenty funkcji plot są zespolone, część urojona jest pomijana z wyjątkiem przypadku,
gdy funkcja plot posiada tylko jeden argument. W tym przypadku polecenie to generuje wykres części
rzeczywistej w funkcji części zespolonej. Stąd polecenie:

»

plot(Z)

gdzie: Z jest zespolonym wektorem lub macierzą jest równoważne poleceniu:

»

plot(real(Z),imag(Z))

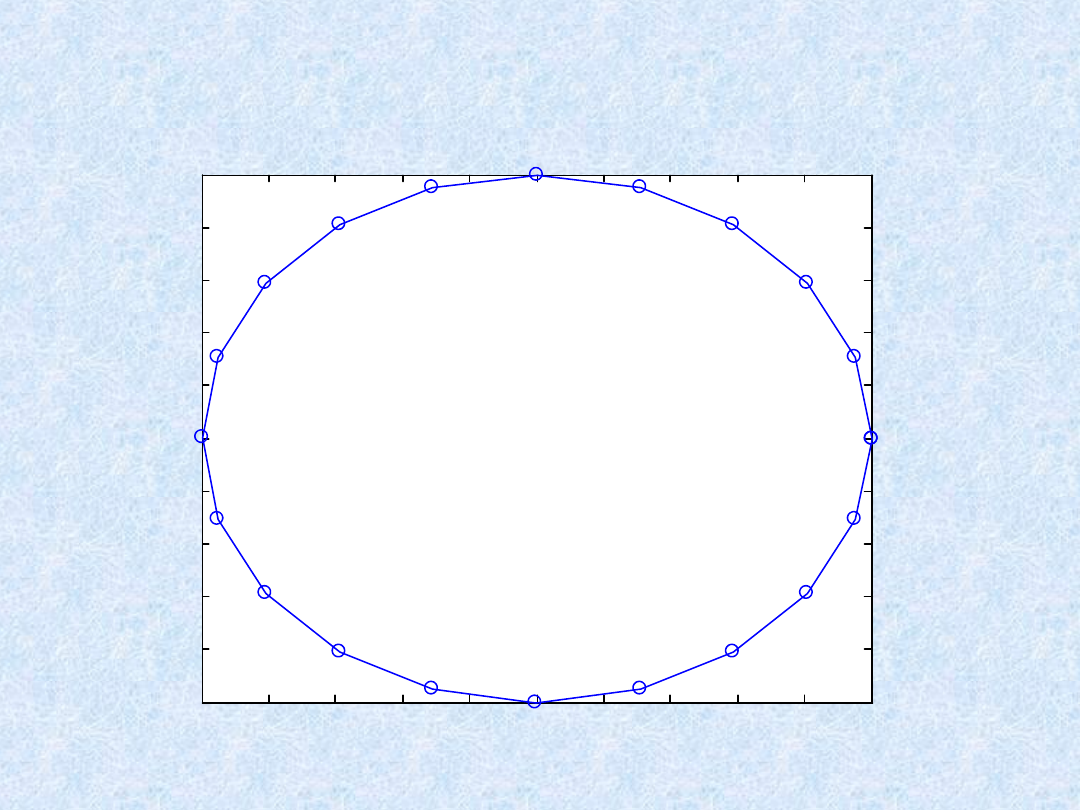
Np. polecenia:

»

t = 0:pi/10:2*pi;

»

plot(exp(i*t),'-o')

22

Wykresy zmiennych zespolonych

wyświetlają 20-węzłowy wielokąt z wierzchołkami oznaczonymi
markerami „o”:

-1

-0.8

-0.6

-0.4

-0.2

0

0.2

0.4

0.6

0.8

1

-1

-0.8

-0.6

-0.4

-0.2

0

0.2

0.4

0.6

0.8

1

23

Skalowanie i nakładanie wykresów

Wyświetlanie wykresu w oknie graficznym powoduje jednoczesne wyczyszczenie okna i usunięcie
poprzedniego rysunku.

Funkcja hold pozwala na dodanie wykresu do znajdującego się w oknie rysunkowym. generalnie do
przeskalowania wykresu i zmiany jego orientacji. Polecenie:

»

hold on/off

wyłącza - on lub włącza - of tryb czyszczenia ekranu. Sprawdzenie stanu przełącznika hold umożliwia
funkcja ishold, która zwraca wartość 1, gdy jest on aktywny (hold on) lub 0 w przeciwnym
przypadku.

Zakres osi program MATLAB wybiera automatycznie na podstawie zakresu danych tak, aby wszystkie
wartości (od najmniejszej do największej) zostały wyświetlone. Zmianę wyglądu osi pozwala funkcja
axis.

24

Skalowanie i nakładanie wykresów

Wywołania funkcji axis:

ustawienie zakresu osi x i y:

» axis([xmin xmax ymin ymax])

•

włączenie trybu automatycznego ustawienia zakresu osi:

» axis auto

•

włączenie trybu automatycznego ustawienia zakresu osi; po włączeniu przełącznika hold wszystkie kolejne
wykresy będą rysowane w tym samym układzie współrzędnych:

» axis manual

•

zmiana układu współrzędnych na macierzowy, z początkiem układu współrzędnych w lewy górnym rogu:

» axis ij

•

zmiana układu współrzędnych na kartezjański (domyślny):

25

Skalowanie i nakładanie wykresów

Wywołania funkcji axis:

zmiana układu współrzędnych na kartezjański (domyślny):

» axis xy

•

zmiana skalowania osi w taki sposób, aby jednostka na podziałce miała ten sam rozmiar na wszystkich osiach:

» axis equal

•

zmiana rozmiaru osi na takie same, jak rozmiary wykresu:

» axis image

•

ustawienie jednakowego rozmiaru wszystkich osi:

» axis square

•

przywrócenie standardowego ustawienia rozmiaru osi:

» axis normal

26

Skalowanie i nakładanie wykresów

Wywołania funkcji axis:

ukrycie osi wraz z ich opisem:

» axis off

•

przywrócenie wyświetlenia osi:

» axis on

•

zwrócenie aktualnego ustawienia układu współrzędnych: s1 - auto lub manual, s2 - on lub
of (osie wyświetlane lub nie), s3 - xy lub ij:

» [s1,s2,s3]=axis(‘state’)

•

zwrócenie wektora wierszowego v=[xmin xmax ymin ymax]:

» v=axis

27

Skalowanie i nakładanie wykresów

Funkcja axis służy generalnie do przeskalowania wykresu i zmiany jego orientacji. Program MATLAB
automatycznie znajduje wartości maksymalne i minimalne wyświetlanych danych i na ich podstawie
przyjmuje okno wyświetlania wykresu oraz etykiety osi. Funkcja axis pozwala na ingerencję użytkownika
w ten proces:
 

»

axis([xmin xmax ymin ymax])

 
W przypadku funkcji axis istnieje również szereg predefiniowanych zmiennych ułatwiających kontrolę nad
osiami wykresu. Np. w wyniku polecenia:

»

axis square

osie x i y mają tę samą długość, zaś polecenie:

»

axis equal

powoduje, że poszczególne przyrosty zmiennych na osiach x i y są tej samej długości.

28

Skalowanie i nakładanie wykresów

Stąd polecenie:

»

plot(exp(i*t))

poprzedzone przez axis square lub axis equal spowoduje wyświetlenie figury zbliżonej do okręgu.

Polecenie:

»

axis auto

umożliwia powrót do automatycznego, domyślnego skalowania.

Polecenie:

»

axis on

przywraca wyświetlanie etykiet i skali osi, zaś polecenie:

»

axis off

wyłącza wyświetlanie etykiet i skali osi.

29

Funkcja fplot

Funkcja plot umożliwia narysowanie dowolnej funkcji po zapisaniu jej argumentu w postaci wektora. Dokładność takiego rozwiązania jest uzależniona od sposobu dyskretyzacji zadanego
przedziału. W celu narysowania możliwie najbardziej precyzyjnego wykresu funkcji należy skorzystać z funkcji fplot :

»

fplot(f,[x0,xk])

gdzie:

f - łańcuch znaków zawierający nazwę funkcji,
x0, xk - początek i koniec przedziału rysowanej funkcji.

Wywołanie funkcji:

»

fplot(f,[x0,xk])

generuje wektor argumentów x i wartości funkcji y. Wykres ten można następnie narysować przy pomocy polecenia:

»

plot(x,y)

 

30

Opisywanie wykresów

Funkcje opisujące wykresy:

wyświetlenie łańcucha znaków tekst jako opisu osi x aktywnego wykresu:

» xlabel(tekst)

•

wyświetlenie łańcucha znaków tekst jako opisu osi y aktywnego wykresu:

» ylabel(tekst)

•

wyświetlenie łańcucha znaków tekst jako tytułu aktywnego wykresu:

» title(tekst)

•

wyświetlenie łańcucha znaków tekst w miejscu określonym przez współrzędne x i y:

» text(x,y,tekst)

•

wyświetlenie legendy; łańcuch znaków s1 jest opisem odnoszącym się do pierwszego
wykresu, s2 - do drugiego itd.:

» legend(s1,s2,...)

31

Opisywanie wykresów

Funkcje opisujące wykresy:

włączenie/wyłączenie wyświetlania pomocniczej siatki
współrzędnych:

» grid on/off

-3

-2

-1

0

1

2

3

-1

-0.8

-0.6

-0.4

-0.2

0

0.2

0.4

0.6

0.8

1

-





t





si

n(

t)

Wykres funkcji sin

przebieg funkcji

przebieg funkcji

32

Opisywanie wykresów

Funkcje xlabel, ylabel i zlabel wyświetlają etykiety osi x, y i z. Funkcja title dodaje nagłówek w
górnej części okna rysunkowego, zaś funkcja text wstawia tekst w dowolnym punkcie wykresu. Do tego
celu służy również polecenie gtext – tekst jest wstawiany w punkcie wskazanym przez użytkownika. Dzięki
notacji edytora T

e

X można wygenerować litery greckiego alfabetu, symbole matematyczne oraz wybrać

inne czcionki. Np. polecenie \leq generuje znak , \pi znak  zaś \it wybiera czcionkę pochyłą:

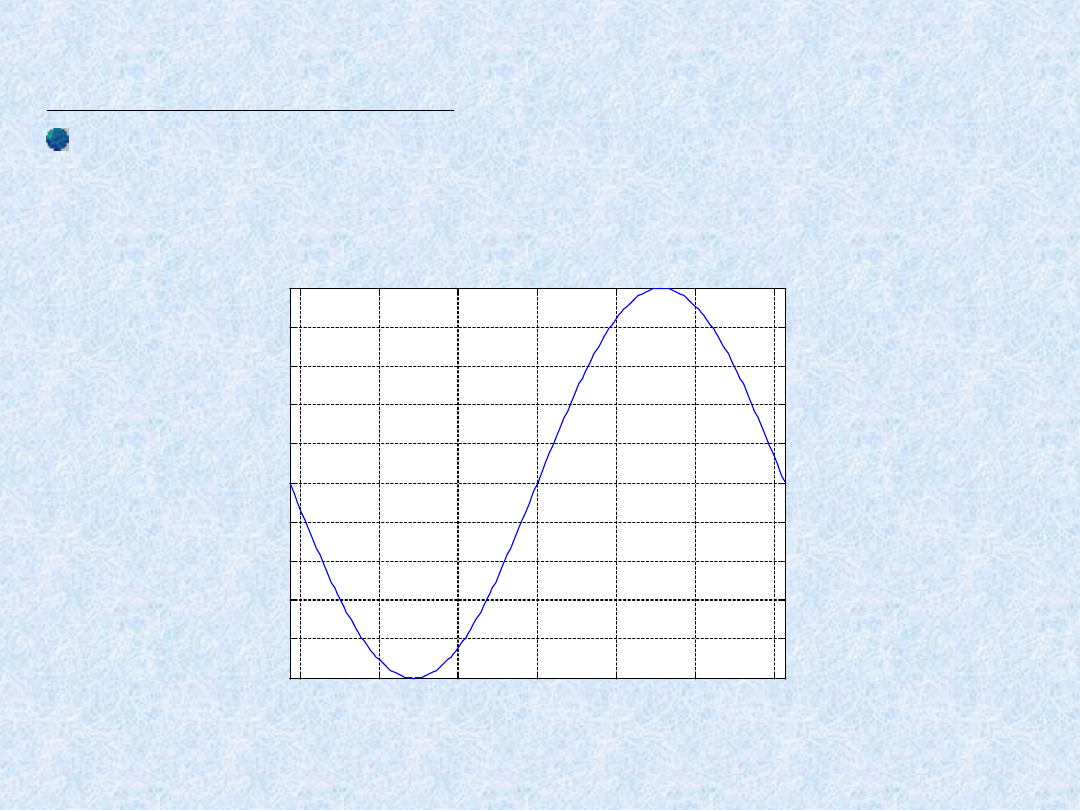
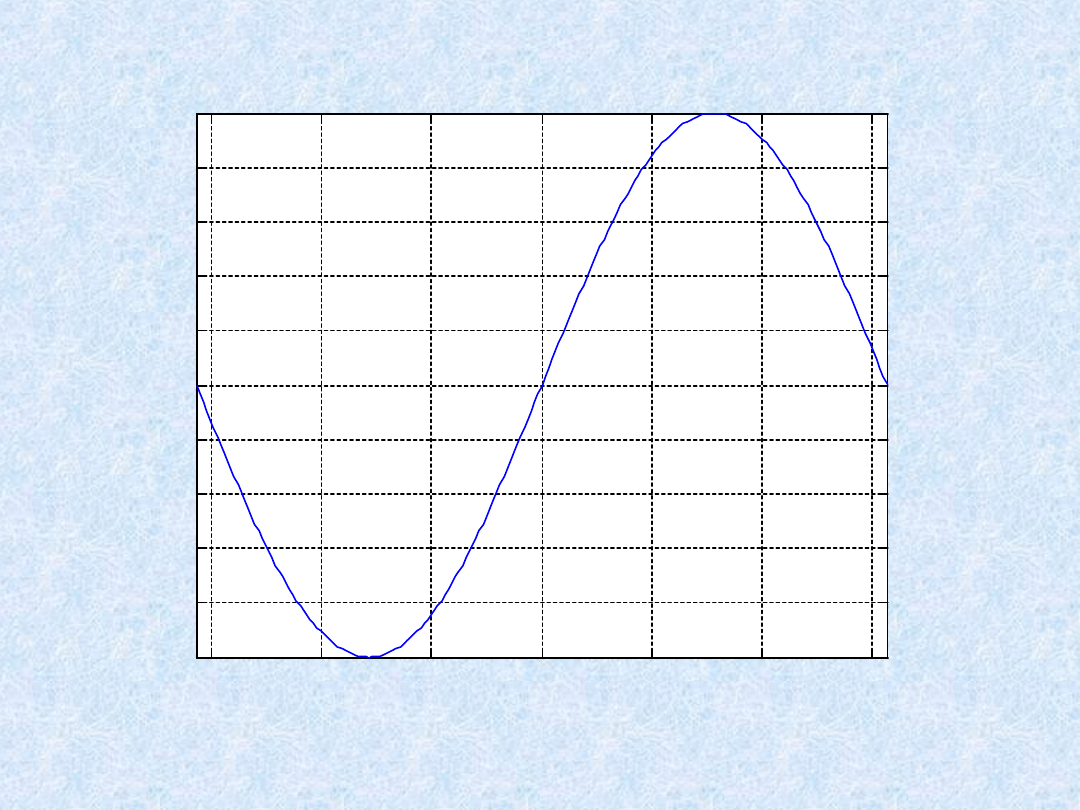
t = -pi:pi/100:pi;
y = sin(t);
plot(t,y)
axis([-pi pi -1 1])
xlabel('-\pi \leq \itt \leq \pi')
ylabel('sin(t)')
title(‘Wykres funkcji sin')
text(1,-1/3,'\it{przebieg funkcji}'); grid on
text(1,-1/3,'\it{przebieg funkcji}')

-3

-2

-1

0

1

2

3

-1

-0.8

-0.6

-0.4

-0.2

0

0.2

0.4

0.6

0.8

1

-





t





si

n(

t)

Wykres funkcji sin

przebieg funkcji

przebieg funkcji

33

Opisywanie wykresów

-3

-2

-1

0

1

2

3

-1

-0.8

-0.6

-0.4

-0.2

0

0.2

0.4

0.6

0.8

1

-





t





si

n(

t)

Wykres funkcji sin

przebieg funkcji

przebieg funkcji

34

Wykresy 3D

Wyświetlenie linii

Funkcja plot3d umożliwia rysowanie wykresów funkcji trzech zmiennych. Polecenie:

» plot3(x,y,z,s)

wyświetla krzywą złożoną z punktów (x, y, z), których współrzędne zostały określone
w wektorach x, y i z. Wektory muszą być tej samej długości. Opcjonalny argument s
jest łańcuchem znaków określającym wygląd rysowanej linii.

Umieszczenie wiele wykresów w jednym oknie rysunkowym umożliwia polecenie:

» plot3(x1,y1,z1,s1,x2,y2,z2,s2,...)

35

Wykresy 3D

Opisywanie wykresów

Wykresy trójwymiarowe są opisywane za pomocą tych samych funkcji co wykresy dwuwymiarowe.
Polecenie

» zlabel(tekst)

wyświetla łańcuch znaków tekst jako opis osi z aktywnego wykresu.

Polecenie

» zlabel(tekst)

wyświetla łańcuch znaków tekst w punkcie (x, y, z) wykresu.

Funkcja axis umożliwia zmianę zakresów trzech osi:

» axis([xmin xmax ymin ymax zmin zmax])

36

Wykresy 3D

Wyświetlenie funkcji dwóch zmiennych

Powierzchnie w programie MATLAB rysowane są jako wykresy funkcji z=f(x,y), współrzędne punktów (x,y)
określone są za pomocą wektorów X i Y.

Wykres trójwymiarowy tworzymy na dwuwymiarowej płaszczyźnie ekranu, na początek należy
wygenerować siatkę na płaszczyźnie XY w tych węzłach, w których wyznaczane są wartości funkcji z. Do
tego celu służy funkcja meshgrid:

» [x,y] = meshgrid(X,Y)

która transformuje obszar opisany przez wektory X i Y (z przestrzeni 3D) na dwie macierze x i y we
współrzędnych ekranowych 2D. Wydanie polecenia:

» [x,y] = meshgrid(X)

jest równoważne poleceniu:

» [x,y] = meshgrid(X,X)

37

Wykresy 3D

Wyświetlenie funkcji dwóch zmiennych
W celu wyświetlenia funkcji dwóch zmiennych z = f (x,y), należy wygenerować dwie macierze X i Y
zawierające współrzędne wierszy i kolumn macierzy dziedziny funkcji. Powyższe macierze służą do
obliczenia i wyświetlenia funkcji. Funkcja meshgrid przekształca dziedzinę określoną poprzez pojedynczy
wektor lub dwa wektory x i y w macierze X i Y wykorzystywane w obliczeniach funkcji dwóch zmiennych.
Wiersze macierzy X są kopiami wektora x, zaś kolumny macierzy Y są kopiami wektora y.

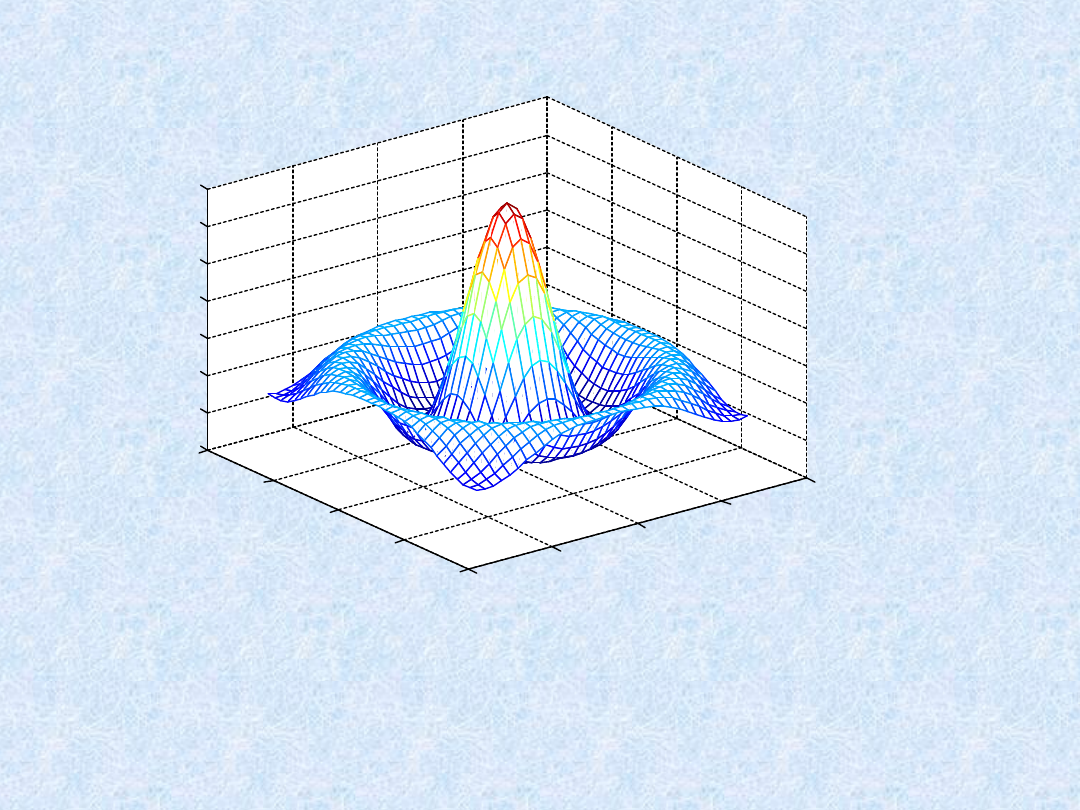
W celu obliczenia dwuwymiarowej funkcji sinc, sin(r)/r, dwóch argumentów x i y należy wydać

następujące polecenia:
 

» [X,Y] = meshgrid(-8:.5:8);
» R = sqrt(X.^2 + Y.^2) + eps;
» Z = sin(R)./R;
» mesh(X,Y,Z)

38

Wykresy 3D

W powyższym przykładzie R jest odległością od początku układu współrzędnych, który
jest środkowym elementem macierzy. Dodanie elementu eps zabezpiecza przed
dzieleniem 0/0 w początku układu współrzędnych.

-10

-5

0

5

10

-10

-5

0

5

10

-0.4

-0.2

0

0.2

0.4

0.6

0.8

1

39

-10

-5

0

5

10

-10

-5

0

5

10

-0.4

-0.2

0

0.2

0.4

0.6

0.8

1

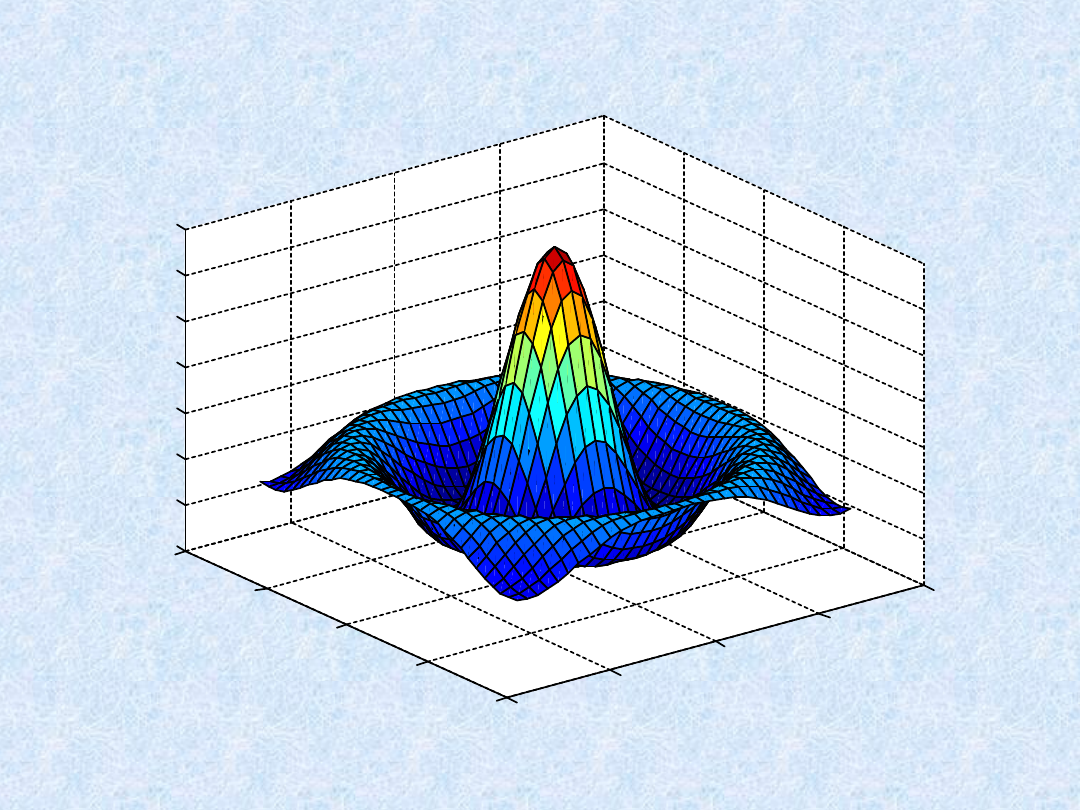
Wykresy 3D - przykłady

» surf(X,Y,Z)

40

-10

-5

0

5

10

-10

-5

0

5

10

-0.4

-0.2

0

0.2

0.4

0.6

0.8

1

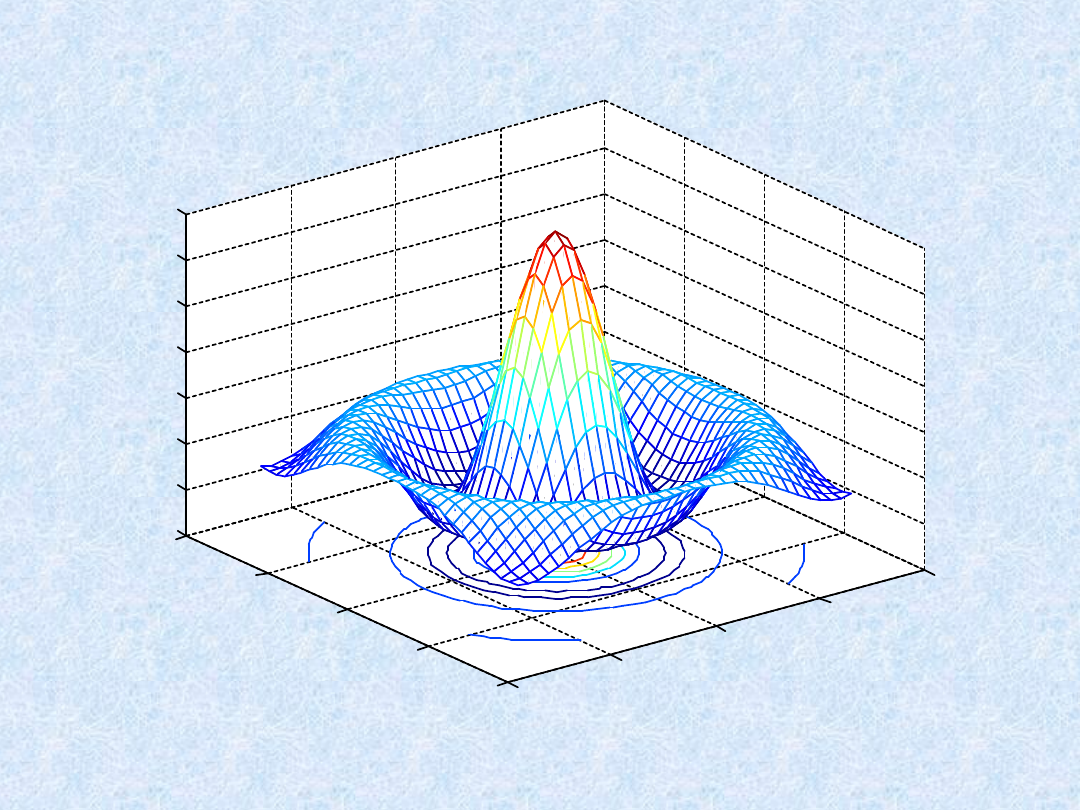
Wykresy 3D - przykłady

» meshc(X,Y,Z)

41

-10

-5

0

5

10

-10

-5

0

5

10

-0.4

-0.2

0

0.2

0.4

0.6

0.8

1

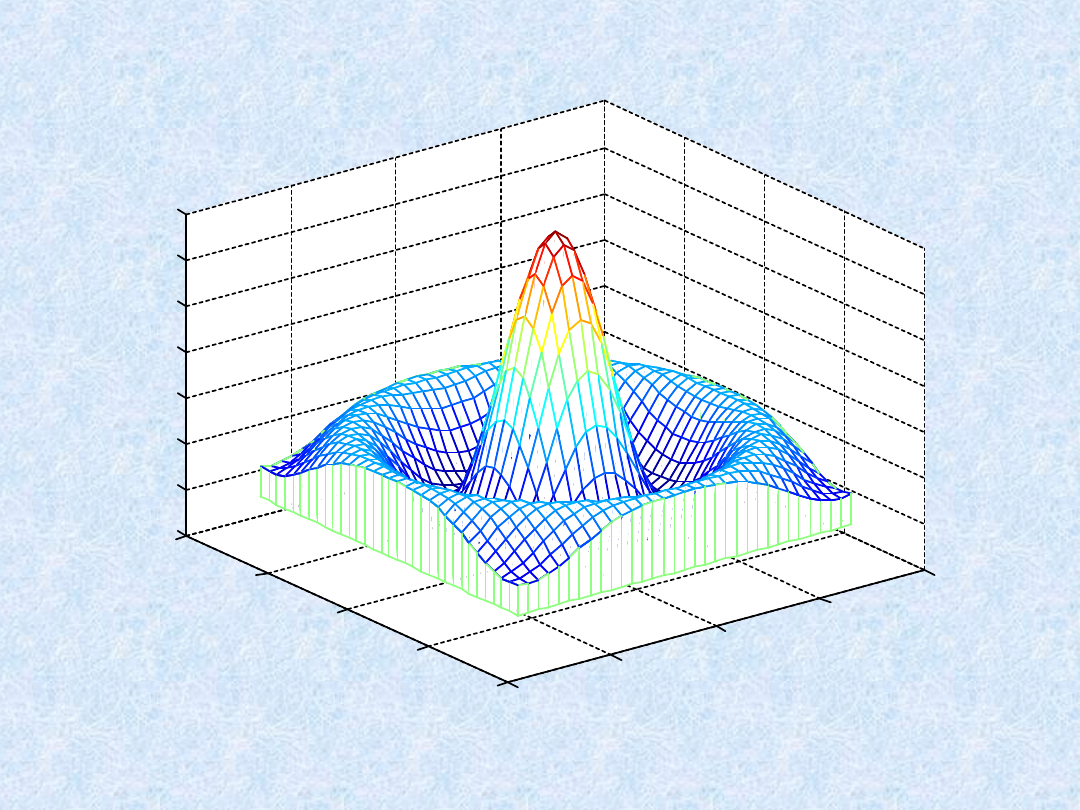
Wykresy 3D - przykłady

» meshz(X,Y,Z)

42

-10

-5

0

5

10

-10

-5

0

5

10

-0.4

-0.2

0

0.2

0.4

0.6

0.8

1

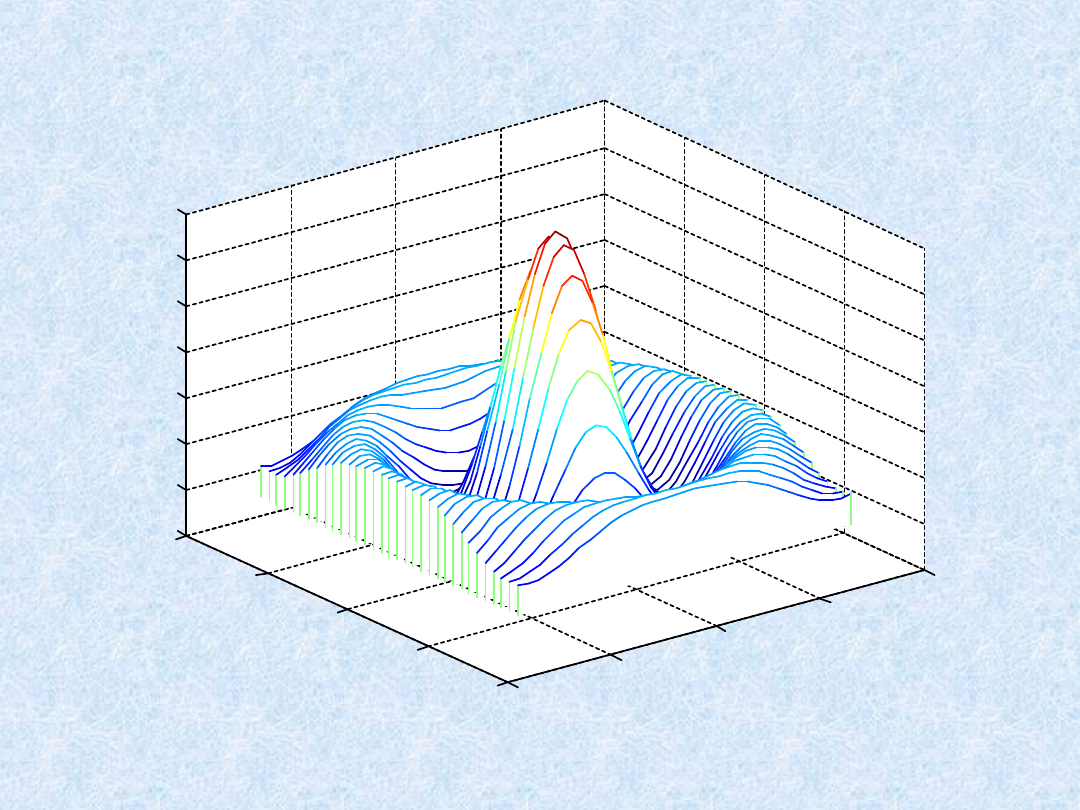
Wykresy 3D - przykłady

» waterfall(X,Y,Z)

43

-8

-6

-4

-2

0

2

4

6

8

-8

-6

-4

-2

0

2

4

6

8

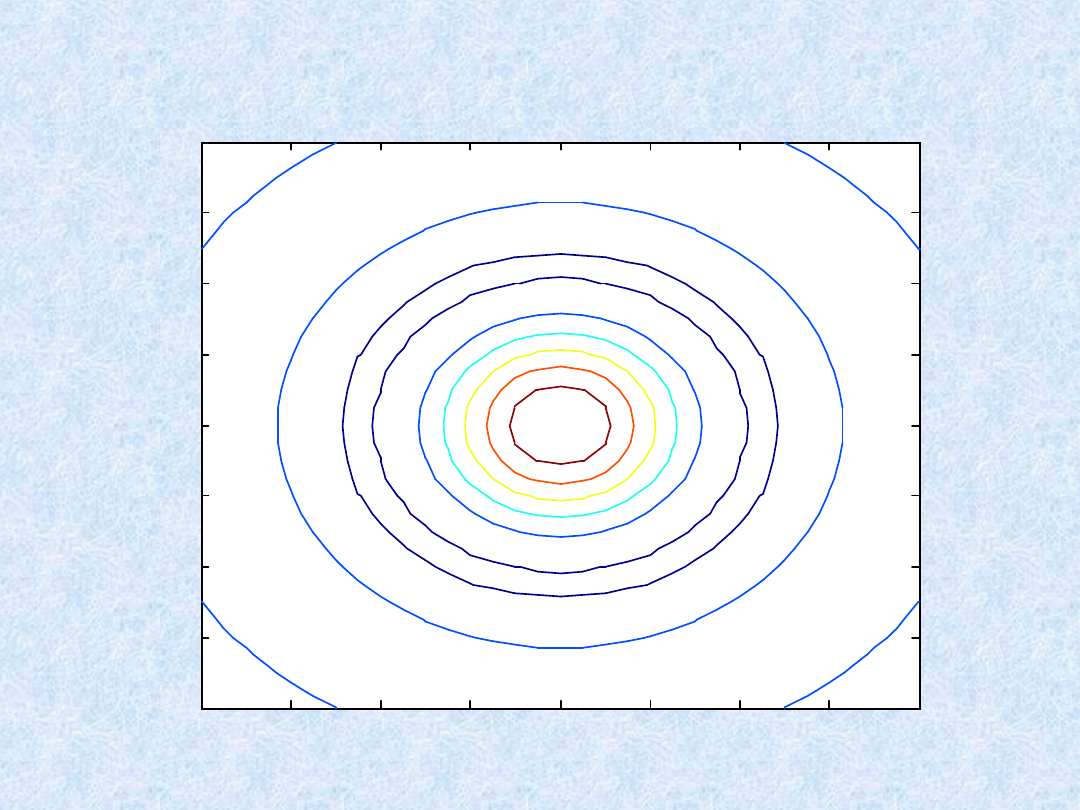
Wykresy 3D - przykłady

» contour(X,Y,Z)

44

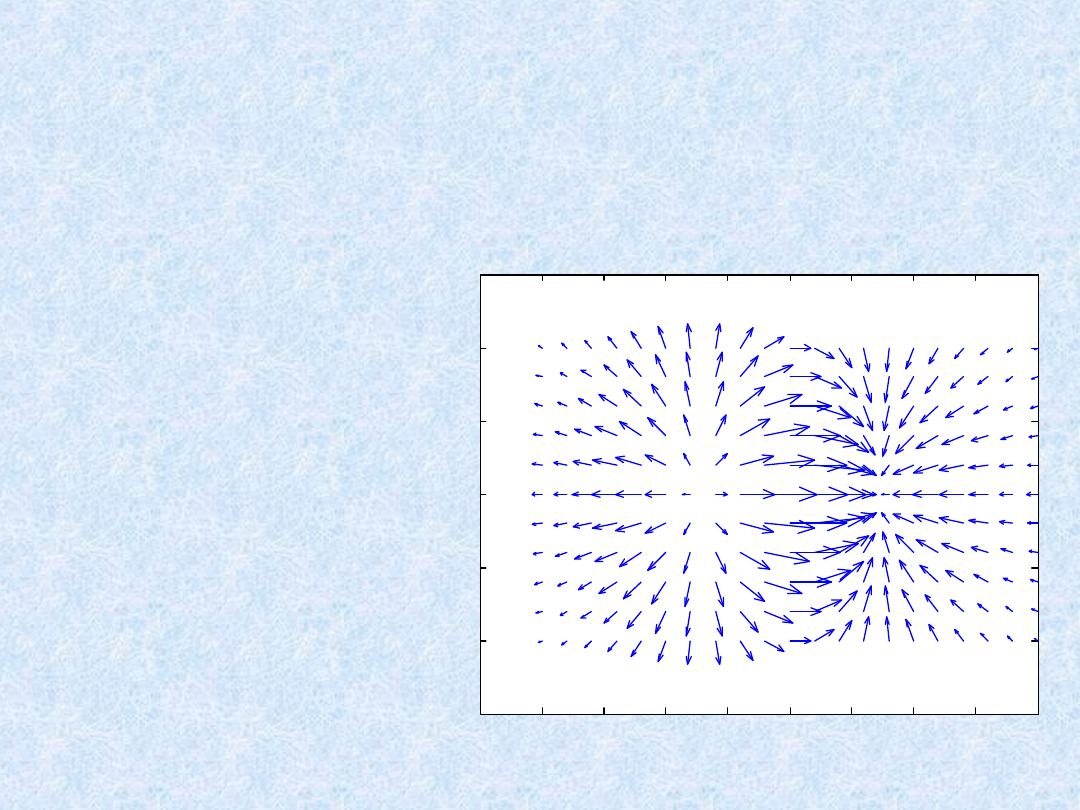
Wykresy 3D - przykłady

» x = -2:.2:2; y = -1:.2:1;
»[xx,yy] = meshgrid(x,y);
» zz = xx.*exp(-xx.^2-yy.^2);
»[px,py] = gradient(zz,.2,.2);
» quiver(x,y,px,py,2);

-2.5

-2

-1.5

-1

-0.5

0

0.5

1

1.5

2

-1.5

-1

-0.5

0

0.5

1

1.5

45

Wykresy 3D

Mapy kolorów

Mapa kolorów jest macierzą trójkolumnową, której elementami są liczby rzeczywiste z zakresu 0.01.0.

Każdy wiersz macierzy jest wektorem RGB (ang. read green blue) definiującym dany kolor za pomocą
intensywności trzech podstawowych kolorów: czerwonego, zielonego i niebieskiego. Funkcja
colormap pozwala na odczytanie i zmianę kolorów mapy kolorów przypisanej aktywnemu rysunkowi.
Polecenie:

» m=colormap

zwraca aktualną mapę kolorów m. Zmiana aktualnej mapy kolorów na mapę m następuje po wywołaniu
polecenia:

» colormap(m)

Standardową mapę kolorów przywraca polecenie:

» colormap(‘default’)

46

Wykresy 3D

Mapy kolorów

mapa odcieni szarości:

» gray

•

mapa kolorów ciepłych - do czarnego, przez odcienie czerwonego, pomarańczowego i żółtego, aż do białego:

» hot

•

mapa kolorów zimnych - od turkusowego do karmazynowego:

» cool

•

mapa kolorów zmieniających się od czerwonego, przez pomarańczowy, do żółtego:

» autumn

•

mapa odcieni kolorów żółtego i zielonego:

» summer

47

Wykresy 3D

Mapy kolorów

standardowa mapa kolorów w systemie HSV; każdy wiersz
macierzy zawiera 3 liczby z przedziału <0,1> opisujące
odcień, nasycenie i jaskrawość; odcień zmienia się od koloru
czerwonego, przez żółty, zielony, turkusowy, niebieski,
karmazynowy, z powrotem do czerwonego; nasycenie
zerowe oznacza, że kolory będą odcieniami szarości:

» hsv

48

Wykresy 3D

Zmiana kierunku obserwacji wykresu

Funkcja view pozwala na zmianę kierunku, z którego oglądany jest aktywny układ współrzędnych. W poleceniu:

» view(az,el)

argumentu az i el oznaczają azymut i elewację (kąt podniesienia) położenia oka obserwatora.

Azymut jest kąt mierzony w płaszczyźnie XY, rosnący w kierunku przeciwnym do kierunku ruchu wskazówek
zegara.

Elewacja jest to kąt pomiędzy płaszczyzną XY a prostą łączącą oko obserwatora ze środkiem wykresu. Kąty
podawane są w stopniach.

Polecenie:

» view(2)

ustawia kierunek obserwacji tak, jak dla wykresów dwuwymiarowych: az=0º, el =90º.

49

Wykresy 3D

Zmiana kierunku obserwacji wykresu

Polecenie:

» view(3)

ustawia standardowy kierunek obserwacji wykresów trójwymiarowych: az=37.5º, el
=30º.

Polecenie:

» [az,el]=view

zwraca aktualne ustawienia azymutu i elewacji.

50

Obrazy statyczne grafiki rastrowej

Program MATLAB umożliwia również wyświetlanie obrazów zapamiętanych w plikach graficznych
rastrowych (formaty, np. JPG, BMP, TIFF, PCX) i definiowanie macierzy opisujących obrazy.
Zaawansowaną obróbkę obrazów umożliwia biblioteka Image Processing Toolbox.

Funkcje obsługujące obrazy:

wyświetlenie w aktywnym układzie współrzędnych obrazu opisanego macierzą c - każdemu
elementowi macierzy c odpowiada jeden punkt; elementy macierzy c są traktowane jako
indeksy kolorów w mapie kolorów; wygląd obrazu zależy od rodzaju użytej mapy kolorów;

» image(c)

skalowanie danych opisanych macierzą c do pełnego zakresu bieżącej mapy kolorów i
wyświetlenie obrazu

» imagesc(c)

51

Obrazy statyczne grafiki rastrowej

Funkcje obsługujące obrazy:

wczytanie do macierzy A obrazu z pliku graficznego o nazwie określonej
łańcuchem znaków plik i we formacie f (np. ‘jpg’); domyślnie program
MATLAB poszukuje pliku plik.f w katalogu bieżącym - jeśli plik znajduje się
w innym katalogu, należy podać w nazwie ścieżkę dostępu:

» A=imread(plik,f)

zapisanie obrazu określonego macierzą A w pliku graficznym o podanej
nazwie we formacie f (tak, jak w przypadku funkcji imread):

» imwrite(A,plik,f)

52

Zarządzanie oknami rysunkowymi

Grafika w programie MATLAB wyświetlana jest w oknach
rysunkowych. Funkcje graficzne wyświetlają wyniki swoich
działań w otwartym oknie rysunkowym lub jeśli żadne okno nie
jest otwarte, automatycznie tworzą nowe.

Jednocześnie może być otwartych wiele okien. Jedno z nich jest
oknem aktywnym i do niego program MATLAB kieruje grafikę.
Domyślnie aktywne jest okno otwarte ostatnio.

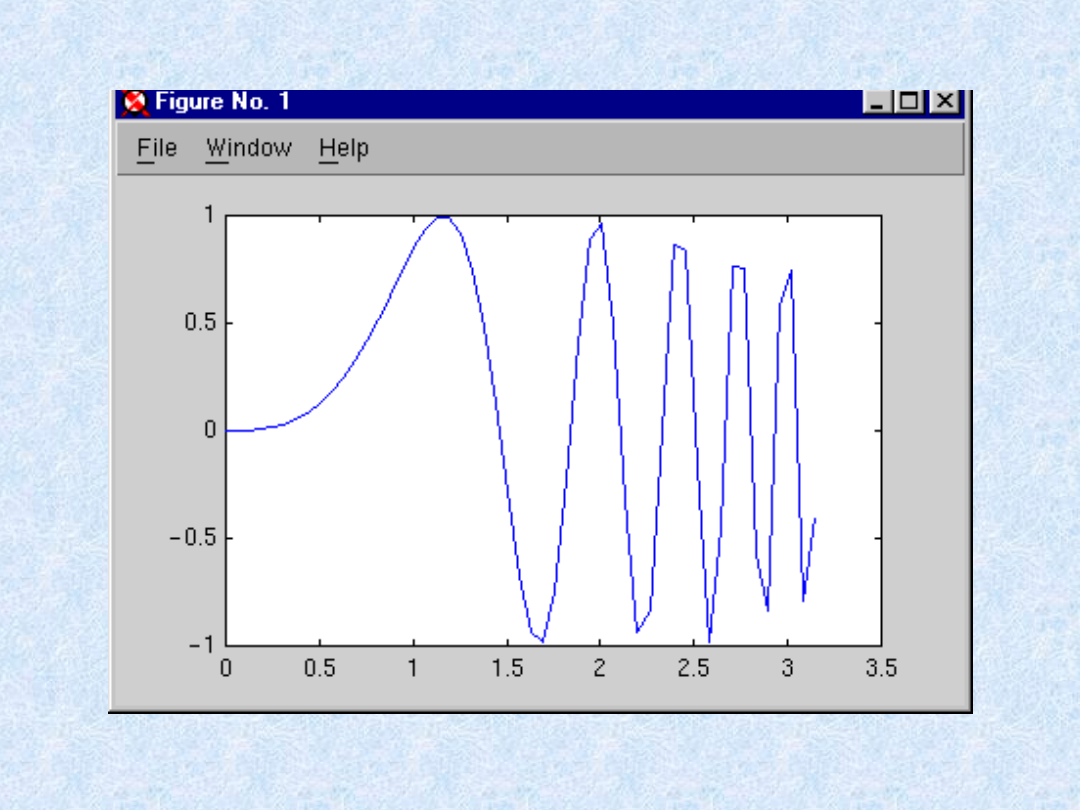
Funkcja figure umożliwia tworzenie nowych okien. Każde nowe
okno otrzymuje kolejny numer, widoczny w jego nagłówku:
„Figure No. 1”, „Figure No. 2”.

53

Zarządzanie oknami rysunkowymi

54

Zarządzanie oknami rysunkowymi

Funkcje wykonujące operacje na oknach rysunkowych:

tworzenie nowego okna rysunkowego i uaktywnianie jego:

» figure

•

uaktywnianie okna rysunkowego o numerze n (jeśli jest
otwarte) lub utworzenie nowego okna i przyporządkowanie
mu numeru n:

» figure(n)

•

zamykanie okna aktywnego:

» close

•

zamykanie okna o numerze n; argument funkcji może być
macierzą zawierającą numery zamykanych okien:

» close(n)

55

Zarządzanie oknami rysunkowymi

Funkcje wykonujące operacje na oknach rysunkowych:

zamykanie wszystkich okien:

» close all

•

usuwanie zawartości aktywnego okna:

» clf

56

Macierze rysunkowe

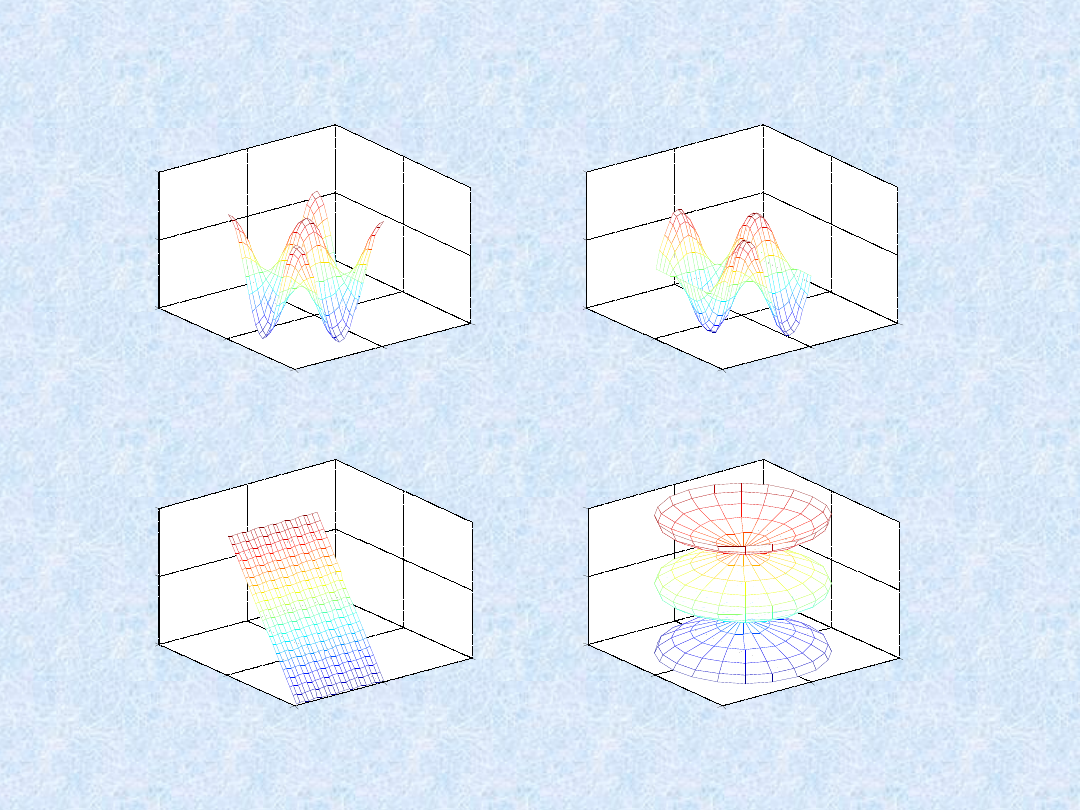
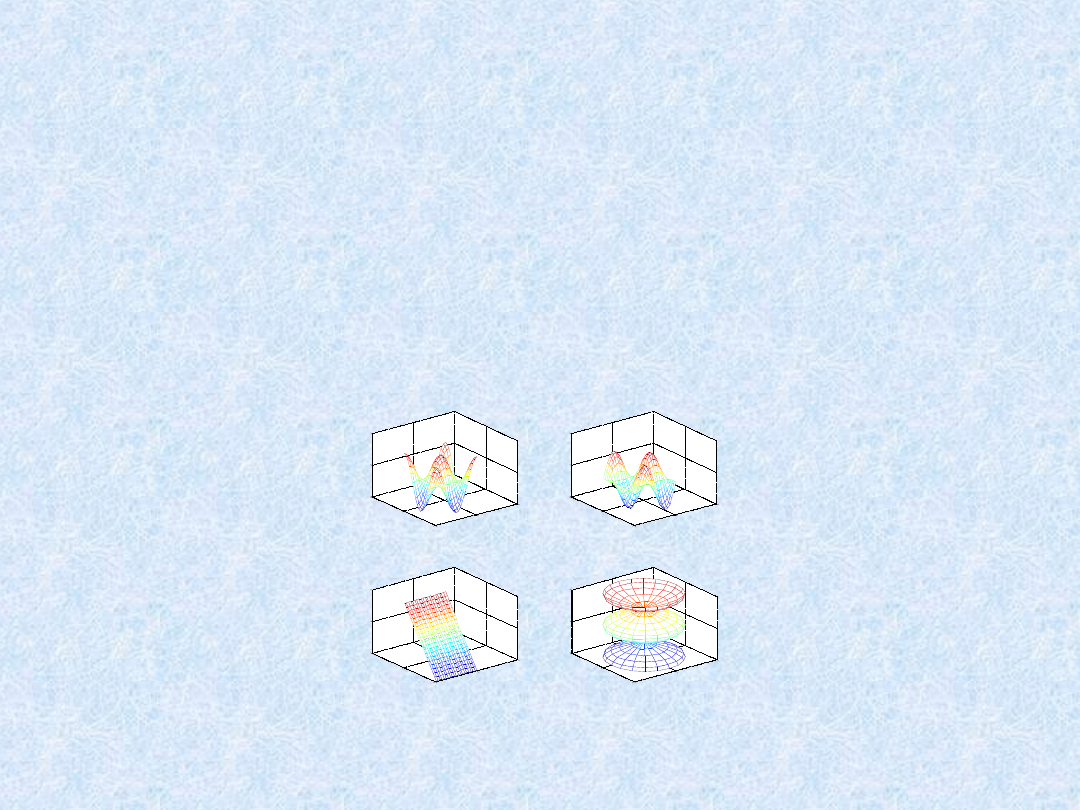
Funkcja subplot umożliwia wyświetlenie kilku wykresów w tym samym
oknie rysunkowym. Polecenie:

subplot(m,n,p)

dzieli okno rysunkowe na macierz o wymiarach m-n, której elementami
są okna poszczególnych wykresów, parametr p wybiera p-te okno
wykresu jako bieżące. Wykresy są numerowane wierszami, począwszy od
pierwszego wiersza znajdującego się u góry okna rysunkowego. W celu
wyświetlenia wykresów w czterech odrębnych oknach wykresów należy:

t = 0:pi/10:2*pi;

[X,Y,Z] = cylinder(4*cos(t));
subplot(2,2,1)
mesh(X)
subplot(2,2,2); mesh(Y)
subplot(2,2,3); mesh(Z)
subplot(2,2,4); mesh(X,Y,Z)

57

Macierze rysunkowe

0

20

40

0

20

40

-5

0

5

0

20

40

0

20

40

-5

0

5

0

20

40

0

20

40

0

0.5

1

-5

0

5

-5

0

5

0

0.5

1

58

Macierze rysunkowe

Inne wywołanie funkcji subplot:

subplot(‘Position’,[lewy dolny szerokość wysokość])

tworzy w obrębie aktywnego okna rysunkowego nowe
prostokątne okno o podanym położeniu i wymiarach. Położenie
jest podawane względem lewego dolnego wierzchołka okna.
Parametry

szerokość=wysokość=1

oznaczają

układ

o

rozmiarach rysunku.

0

20

40

0

20

40

-5

0

5

0

20

40

0

20

40

-5

0

5

0

20

40

0

20

40

0

0.5

1

-5

0

5

-5

0

5

0

0.5

1

Dziękuję za uwagę