Multimedialna

pomoc dydaktyczna.

Wykonała: Karolina

Olech

 

                                   

Obliczanie wytrzymałościowe

belek zginanych.

Zastosowanie wzoru

Żurawskiego.

Przykładowe zadania.

Zadanie 1.

Belka swobodnie podparta na dwóch podporach, A i
B, obciążona jest na końcu wysięgnika siłą
skupioną P (rys.1a) Sprawdzić wytrzymałość belki,
jeśli dopuszczalne naprężenia przy zginaniu k

s

=

1200 kG/cm

2

.

Wymiary przekroju poprzecznego belki podano na
rys.1b

Wpływ sił poprzecznych
pominąć

Dane:

P = 800 kG, a = 20 cm, l = 100 cm.

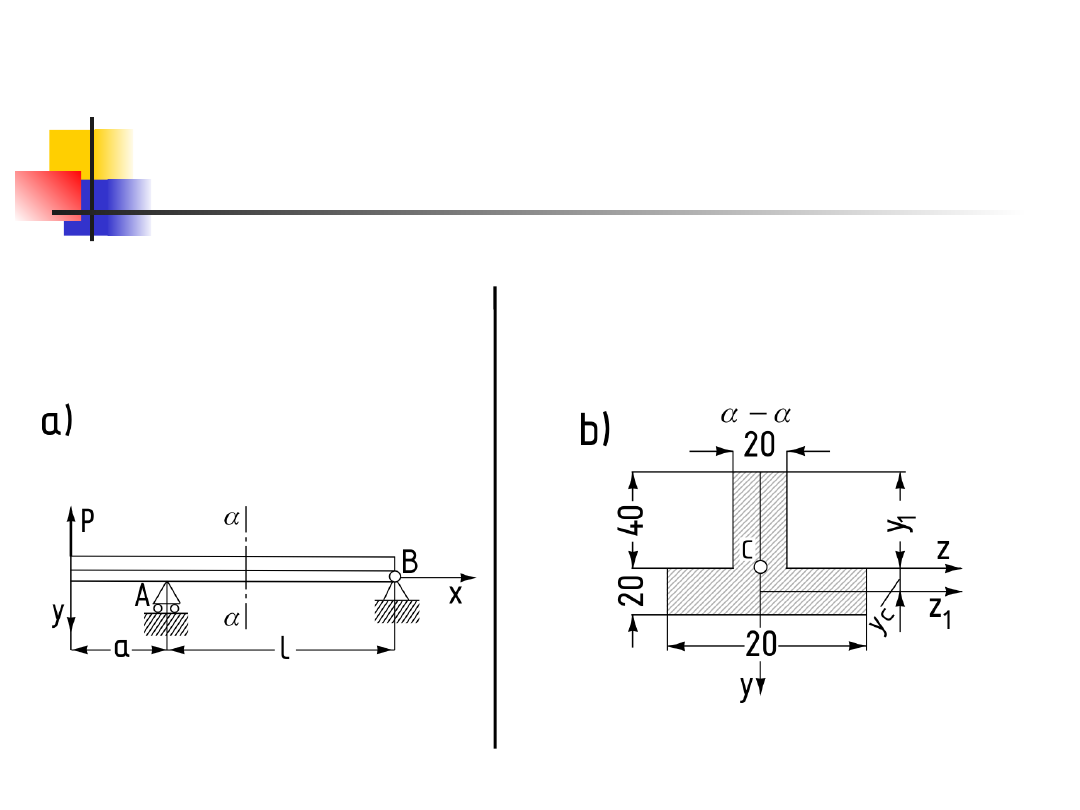
Rysunek

Rys. 1a

Rys. 1b

Rozwiązanie

Z wykresu momentów zginających (rys.2)
wynika, że maksymalna wartość momentu
zginającego

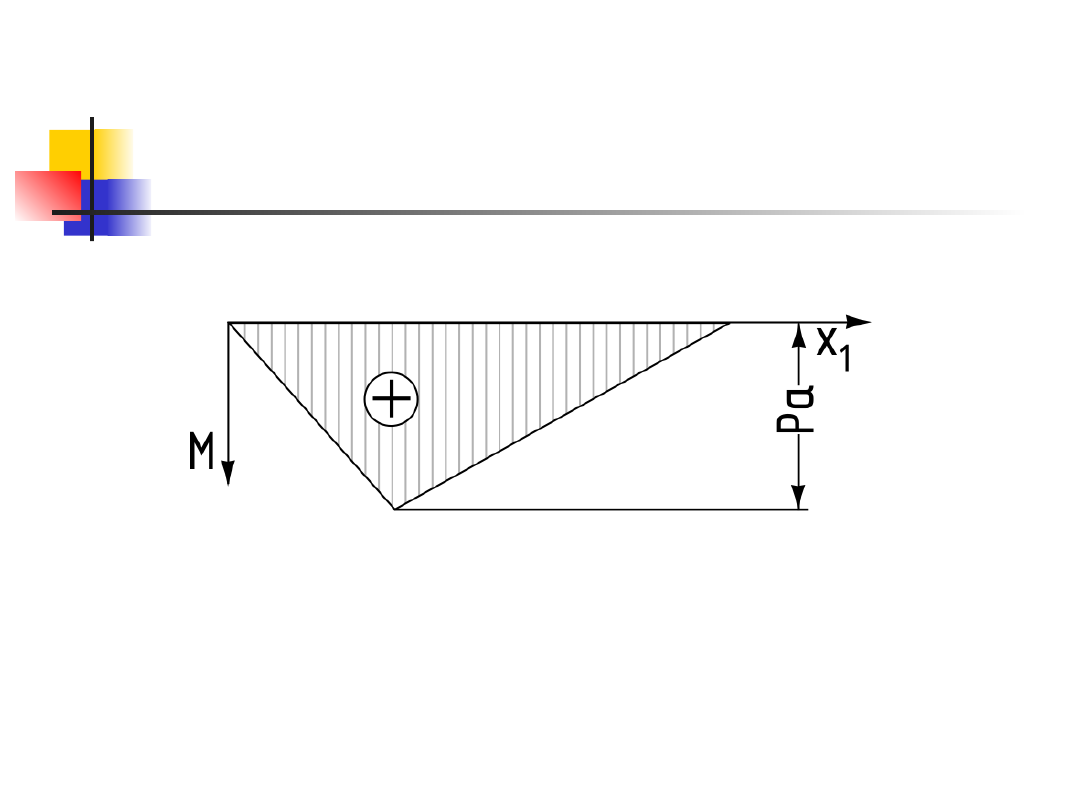
Rys 2

Rozwiązanie cd.

Następnie przechodzimy do wyznaczenia wskażnika
wytrzymałości przekroju na zginanie. Na początku
określamy położenie środka ciężkości pola
przekroju poprzecznego belki.
Moment statyczny pola przekroju względem osi z

1

Pole

przekroju

Rozwiązanie cd.

Współrzędne środka ciężkości

Osią objęta przekroju jest więc oś
centralna z.

Moment bezwładności pola przekroju względem
osi z

Rozwiązanie cd.

Najmniejszy wskażnik wytrzymałości przekroju
na zginanie

Największe naprężenia zginające

Rozwiązanie cd.

Ponieważ po stronie włókien rozciąganych
wartości naprężeń normalnych są mniejsze od
powyższej obliczonych wartości, sprawdzenie
wytrzymałości belki ograniczymy do warunku

.

/

1200

/

1000

2

2

max

cm

kG

k

cm

kG

g









Zadanie 2.

Pręt o przekroju pierścieniowym osadzonym jest
na dwóch podporach: przegubowej w punkcie A i
przegubowo-przesuwanej w punkcie B (rys. 3a).
Określić wymiary przekroju poprzecznego, jeśli
wiadomo, że dopuszczalne naprężenia dla
materiału pręta wynoszą:

2

/

1000

cm

kG

K

g



Dane :

P = 40kG, l =
30cm,

8

,

0

/





D

d



Rys 3a i b

Rozwiązanie

Maksymalna wartość momentu
zginającego (rys.3b) wynosi:

Wskażnik wytrzymałości przekroju
pierścieniowego o Średnicy D i d określa wzór:

Rozwiązanie cd.

Formułujemy warunek wytrzymałościowy:

z którego wyznaczmy średnicę zewnętrzną D:

Przyjmujemy ostatecznie: D = 27 mm, d = 21
mm

Zadnie 3.

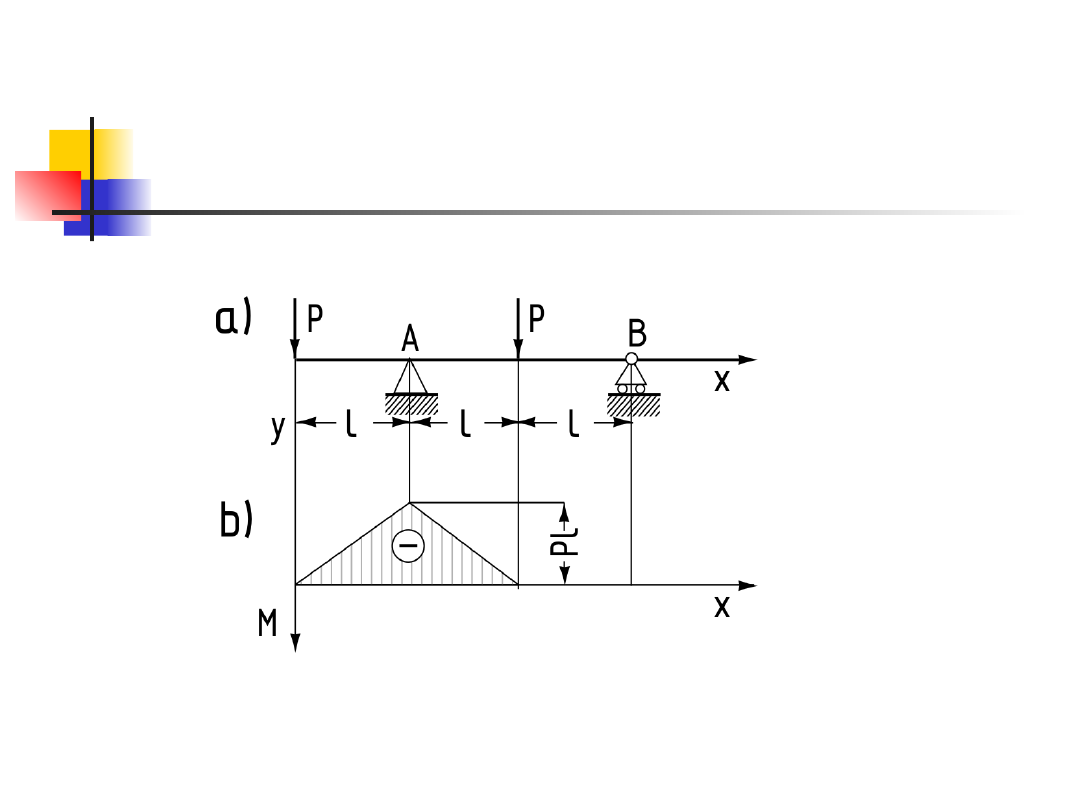
Przy bezpośrednim obciążeniu belki AB (rys. 4a)
siłą skupioną P, w przekroju jej działania zostały
przekroczone naprężenia dopuszczalne o 30%.
Obliczyć rozpiętość dodatkowej belki CD, która
pozwoli na zmniejszenie w rozpatrywanej belce
naprężeń do wartości dopuszczalnej.

Dane:

l = 6 m.

Rys 4a i b

Rozwiązanie

Przy stałym przekroju belki naprężenia
normalne są proporcjonalne do momentu
zginającego. Maksymalny moment zginający
belkę AB, obciążoną bezpośrednio siłą P,
wynosi (wykres EFG na rys 4b)

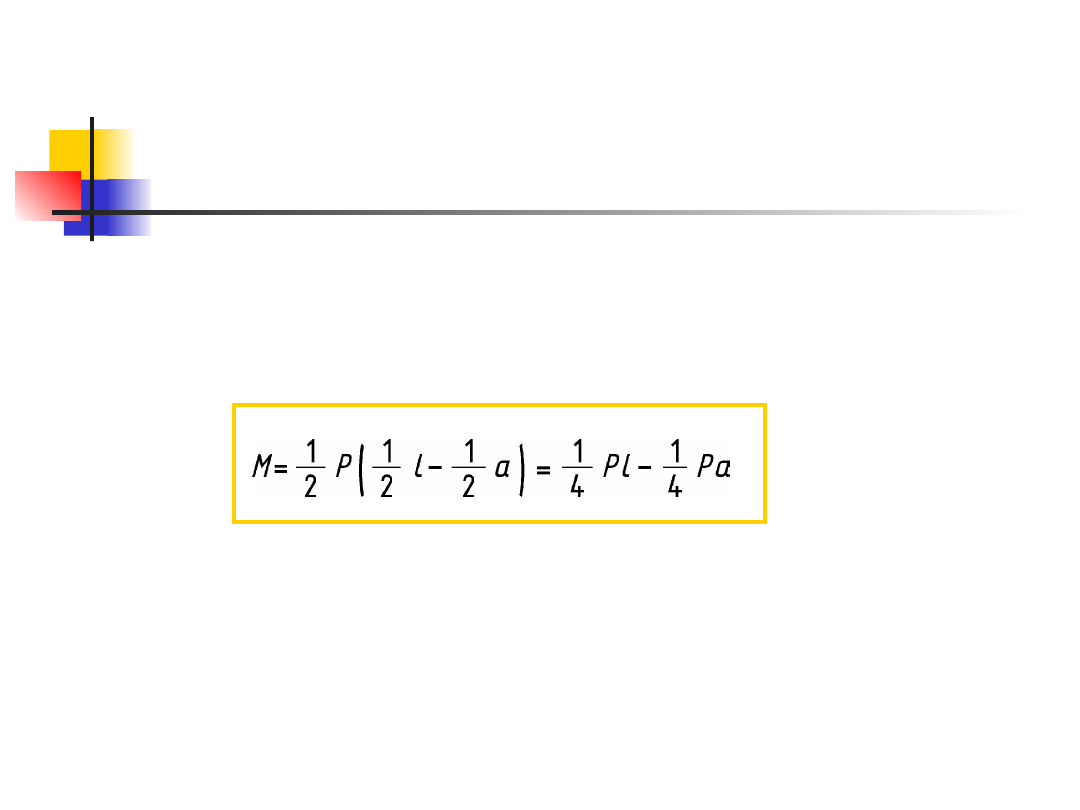
Rozwiązanie cd.

Przy obciążeniu przenoszonym przez belkę
pomocniczą CD maksymalny moment (wykres
ELMG)

(Odcinek KH)

Rozwiązanie cd.

a stąd:

Aby wartości naprężeń zmniejszyły się do
wartości naprężeń dopuszczalnych, moment
wynikający z działania belki pomocniczej (wykres
LFM) musi być równy 30% M

max

czyli:

Zadanie 3.

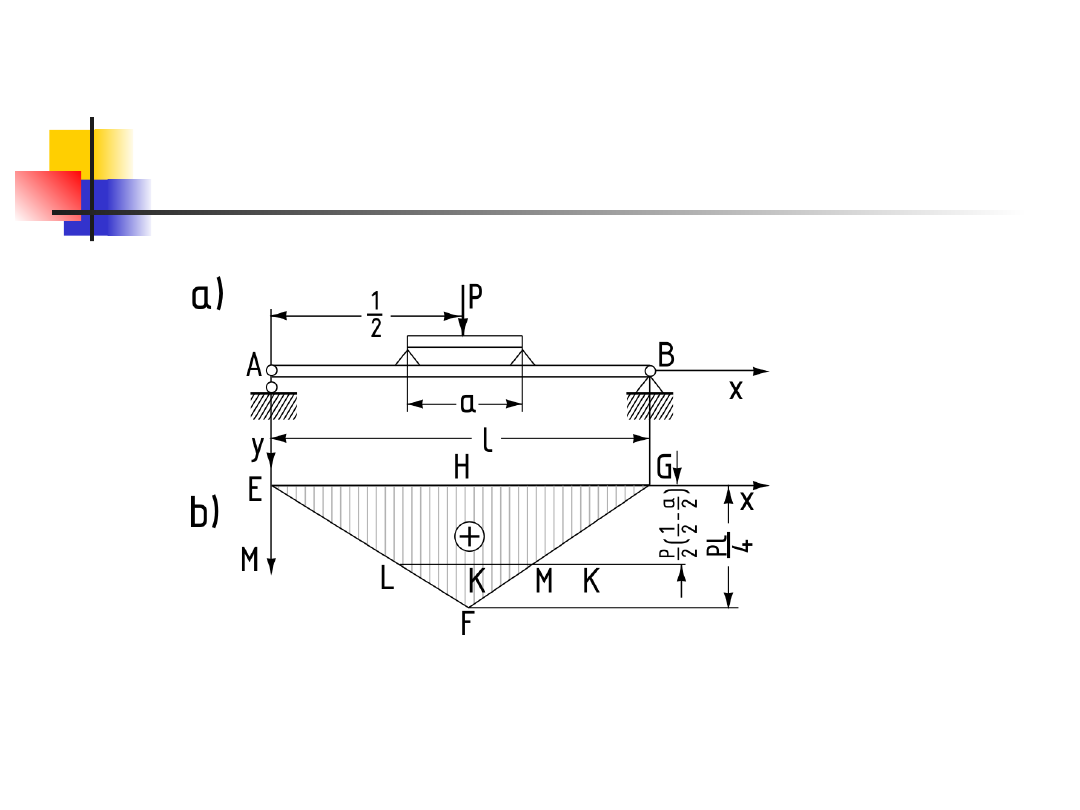
Belka o przekroju ceowym, swobodnie podparta,
obciążona jest momentem skupionym M (rys.5a).
Obliczyć dopuszczalną wartość momentu M dla
dwóch przypadków położenia ceownika (rys.
5b,c). Dopuszczalne naprężenia na zginanie
wynoszą:

Wpływ sił poprzecznych

pominąć.

Dane:

l = 5m, a = 2m.

2

/

1600

cm

kG

k

g



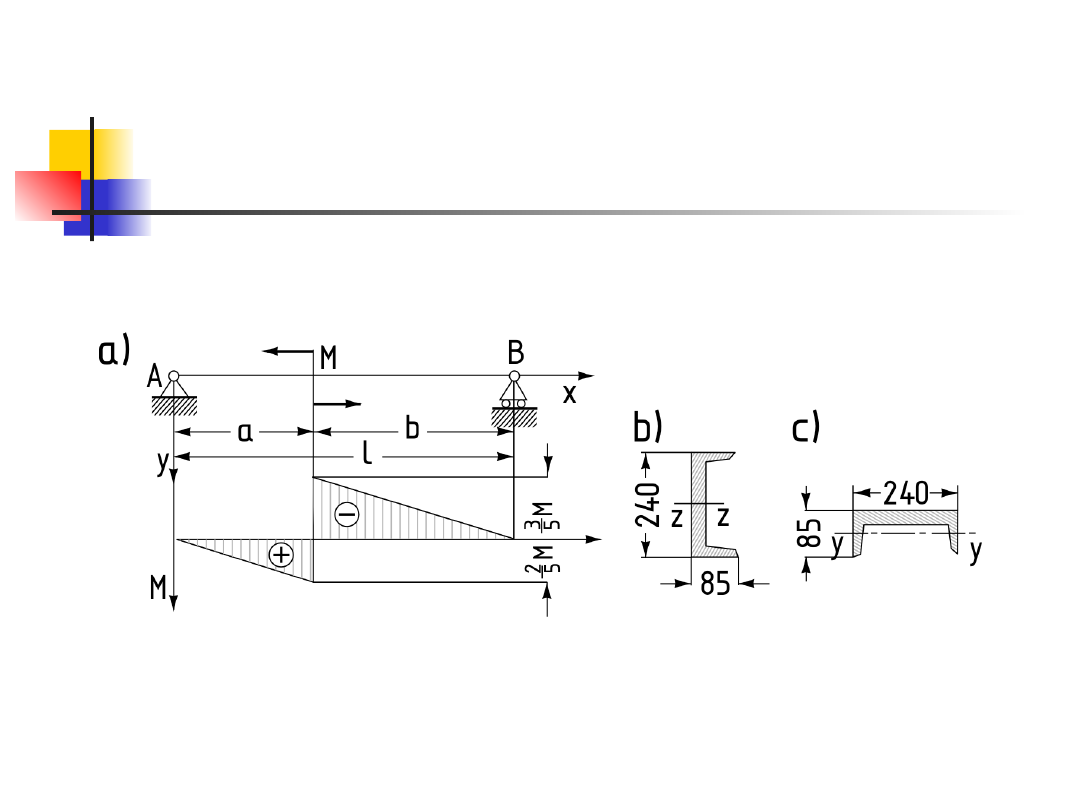
Rysunek 5

.

Rozwiązanie

Przy położeniu ceownika takim jak na rys. 5

znajdujemy z tablic dla danego ceownika

wartość wskaźnika wytrzymałości na zginanie

W

z

= 300cm

3.

Maksymalny moment zginający

Z wykresów zginających wynik,

że

Rozwiązanie cd.

Uwzględniając obliczoną wartość M

max

otrzymujemy

Przy takim położeniu ceownika jak na rys.

5c

Zadanie 4.

Drewniana belka swobodnie podparta (rys 6a),

o przekroju kołowym i długości l = 4, obciążona

jest równomiernie rozłożonym obciążeniem

ciągłym q = 50 kG/m. Wyznaczyć średnicę

przekroju belki, jeśli dopuszczalne naprężenie

wynoszą k

g

= 120 kG/cm

2

. Ile razy zwiększy się

przekrój belki, jeśli obciążenie wzrośnie

dziesięciokrotnie?

Wpływ sił

poprzecznych pominąć.

Rozwiązanie

Dla przekroju kołowego wskaźnik na zginanie

określa wzór:

Maksymalny moment zginający belkę wynosi:

Z warunku wytrzymałościowego:

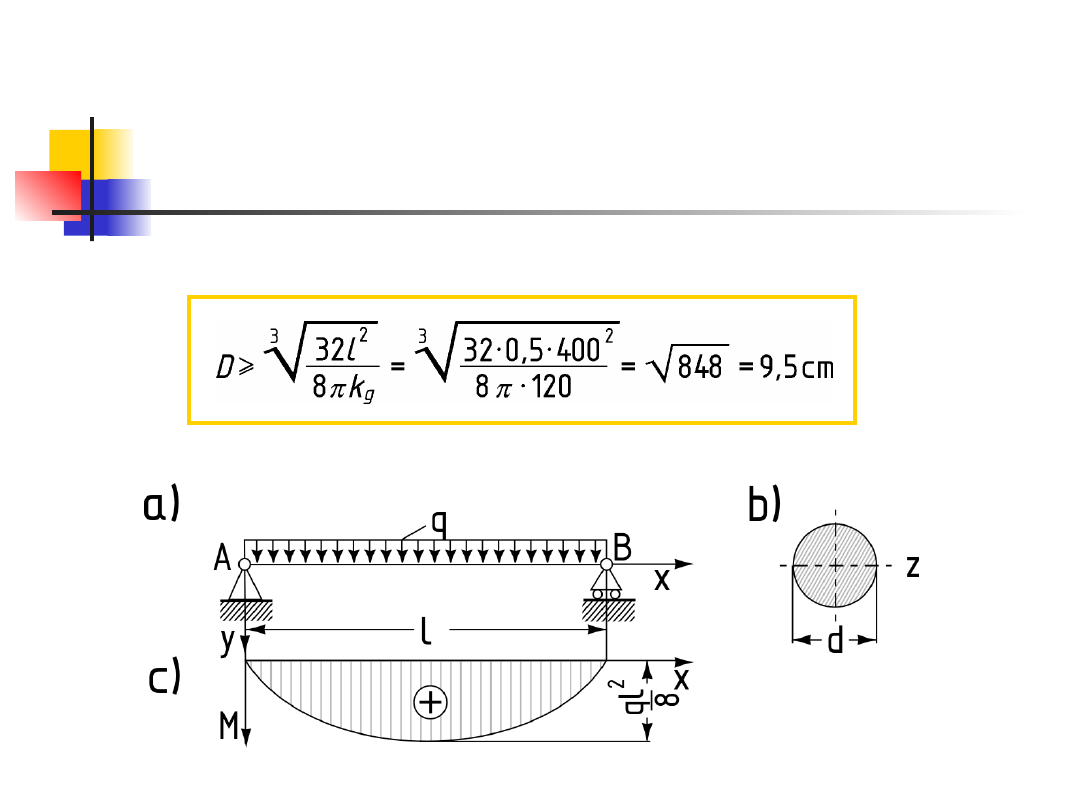
Rozwiązanie cd.

otrzymujemy

Rozwiązanie cd.

Pole przekroju takiej belki

Przy zwiększaniu dziesięciokrotnym obciążenia:

q1 = 10q = 500kG/m, otrzymujemy:

Rozwiązanie cd.

Pole przekroju wynosi wówczas:

Odp.
A zatem przekrój belki zwiększy się 4,6 raza.

Zadanie 5.

Dobrać wymiary przekroju poprzecznego belki

zginanej,

w której maksymalny moment zginający wynosi

M

max

= 360 kGm. Kształt przekroju podano na

rys. 6.

Dane

k

g

= 120 kG/cm

2

b/h = 0,75

d/D = 0,75

Przyjąć, że płaszczyzna obciążenia przechodzi

przez pionową oś symetrii przekroju.

Wpływ sił poprzecznych pominąć.

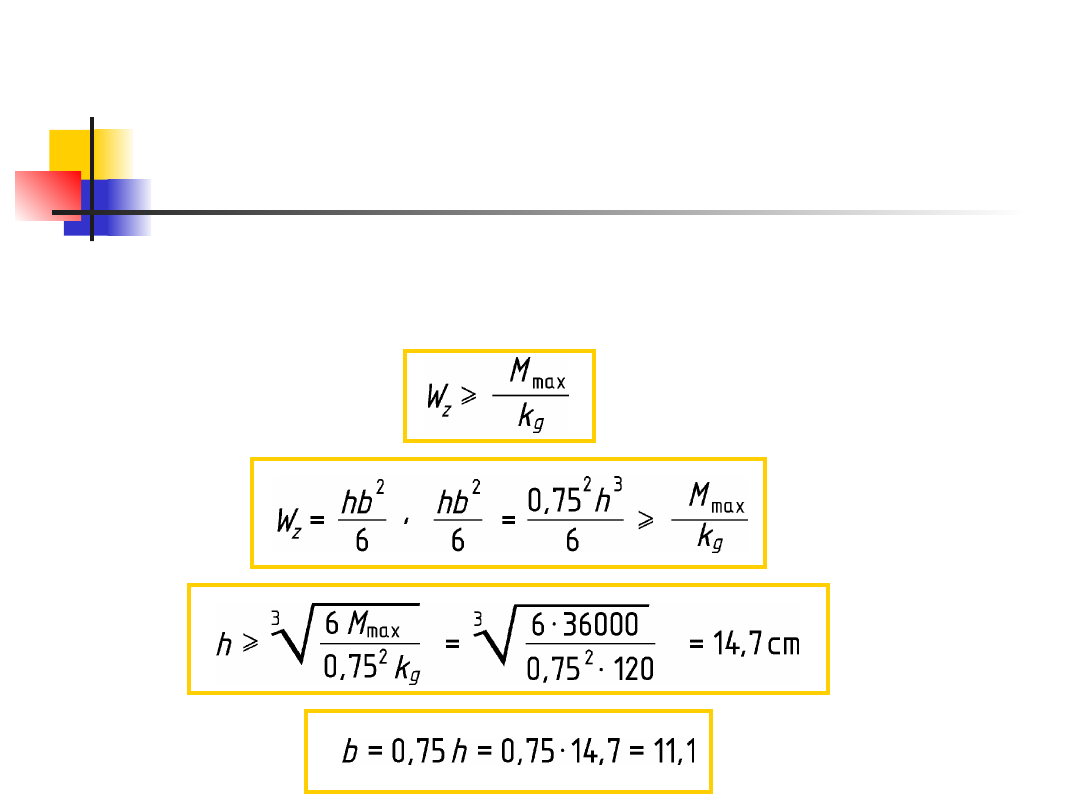
Rozwiązanie .

Przekrój prostokątny (rys. 6a). Wymiary

przekroju określamy z warunku

wytrzymałościowego w postaci:

Rozwiązanie cd.

Przekrój prostokątny (rys. 6b)

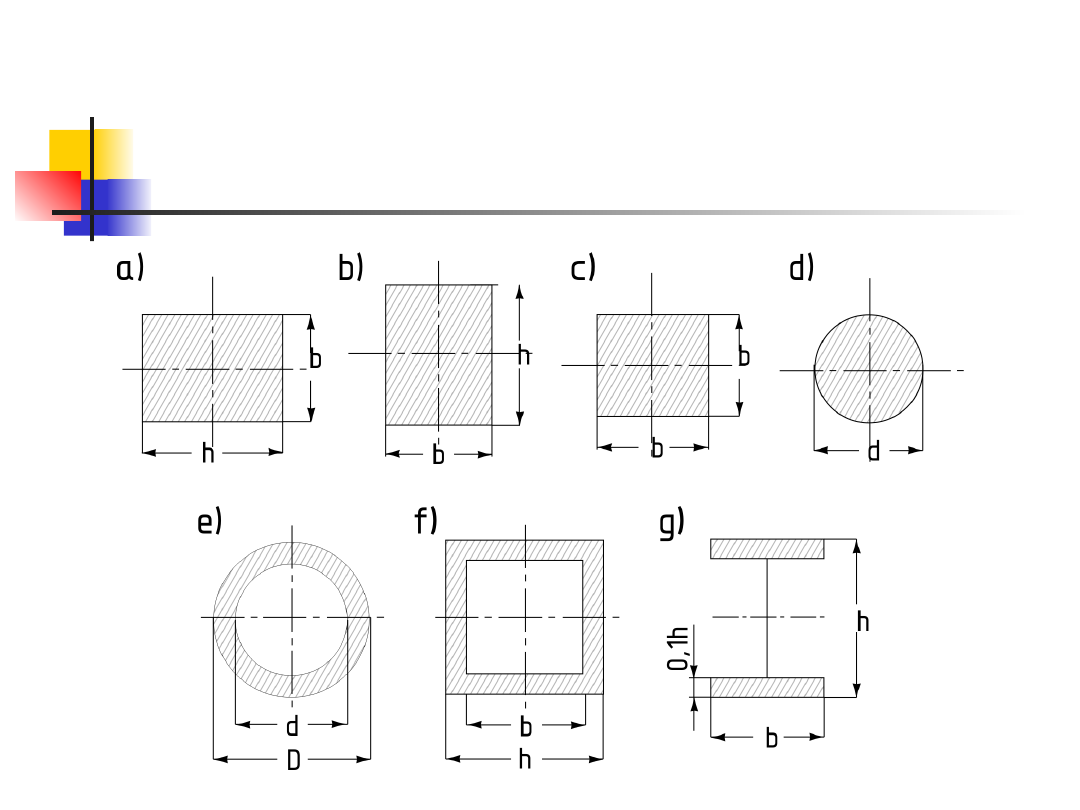
Rysunek 6.

Rozwiązanie cd.

Przekrój kwadratowy (rys. 6c)

Przekrój kołowy (rys. 6d)

Rozwiązanie cd.

Przekrój pierścieniowy (rys. 6e)

Rozwiązanie cd.

Przekrój kwadratowy drążony (rys. 6f)

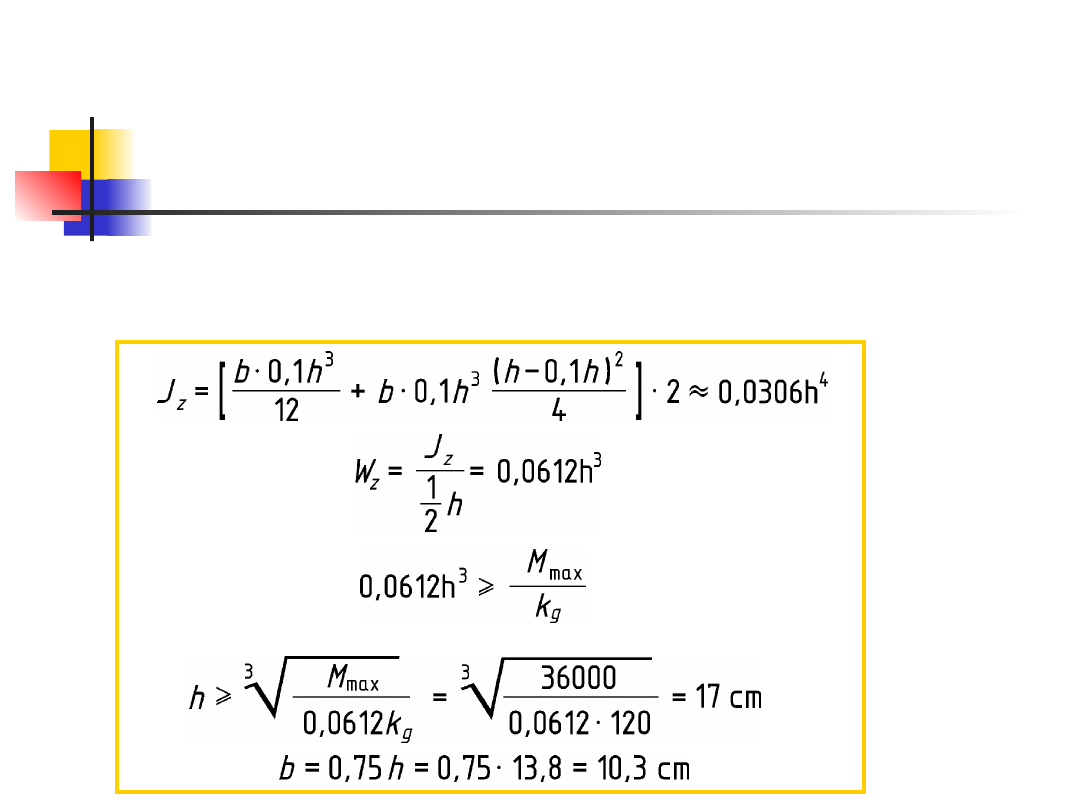
Rozwiązanie cd.

Przekrój dwuteowy (rys. 6g). Moment

bezwładności przekroju względem osi

obojętnej:

Zadanie 6.

Belka o przekroju dwuteowym, którego wymiary

(w mm) podano na rys. 7a, jest zginana siłami

poprzecznymi, wywołującymi w przekroju

niebezpiecznym moment zginający M

max

= 400

000 kGcm. Maksymalna siła poprzeczna wynosi

T= 8000 kG.

Oblicz naprężenia normalne i styczne w

punktach 1, 2, 3 i 4 przekroju niebezpiecznego.

Dane:
M

max

= 400 000 kGcm

T = 8000 kG

Rozwiązanie.

Moment bezwładności przekroju poprzecznego

względem osi obojętnej

Określamy wartości naprężeń normalnych w

punktach przekroju o współrzędnych:
y

1

= 20 cm

y

2

= y

3

= 18,5 cm

y

4

= 0

Rozwiązanie cd.

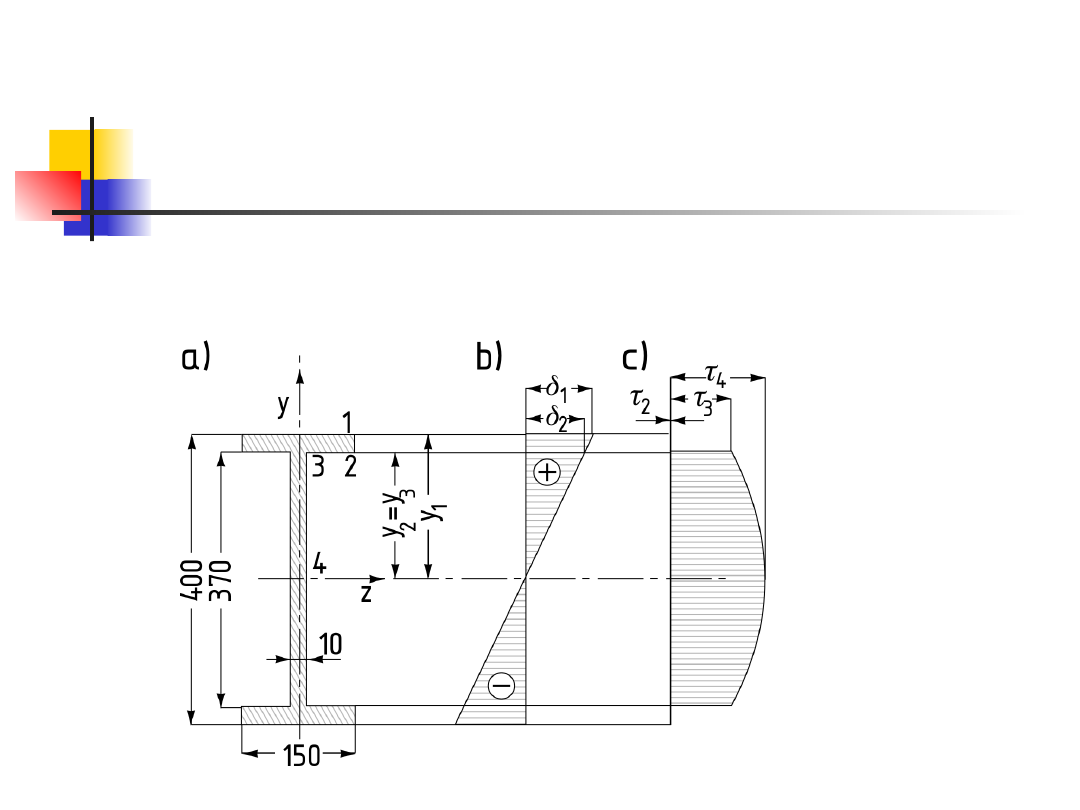
Rysunek 7.

Wykres naprężeń normalnych przedstawiono

na rys. 7b.

Rozwiązanie cd.

Przejdźmy teraz do określenia wartości

naprężeń stałych.

Dla ich obliczenia wykorzystujemy wzór

Żurawskiego

Na początku wyznaczymy momenty statyczne

części przekroju odciętego warstwą odległą o y

1

,

y

2

= y

3

oraz

y

4

= 0, względem osi obojętnej z:

Rozwiązanie cd.

Po podstawieniu tych wartości do wzoru

Żurawskiego otrzymujemy:

Literatura

1. Władysław Siuta „Mechanika Techniczna”
Warszawa 1954 r.
Wydawnictwa Szkolne i Pedagogiczne
2. Jan Misiak Mechanika Techniczna
Statyka i wytrzymałość materiałów tom 1
Wydawnictwa naukowo – techniczne
Warszawa 1996,1997,2003.
3. Józef Kubik,Janusz Mielniczuk, Arnold Wilczyński
„Mechanika techniczna”
Warszawa 1983
Państwowe wydawnictwo naukowe.