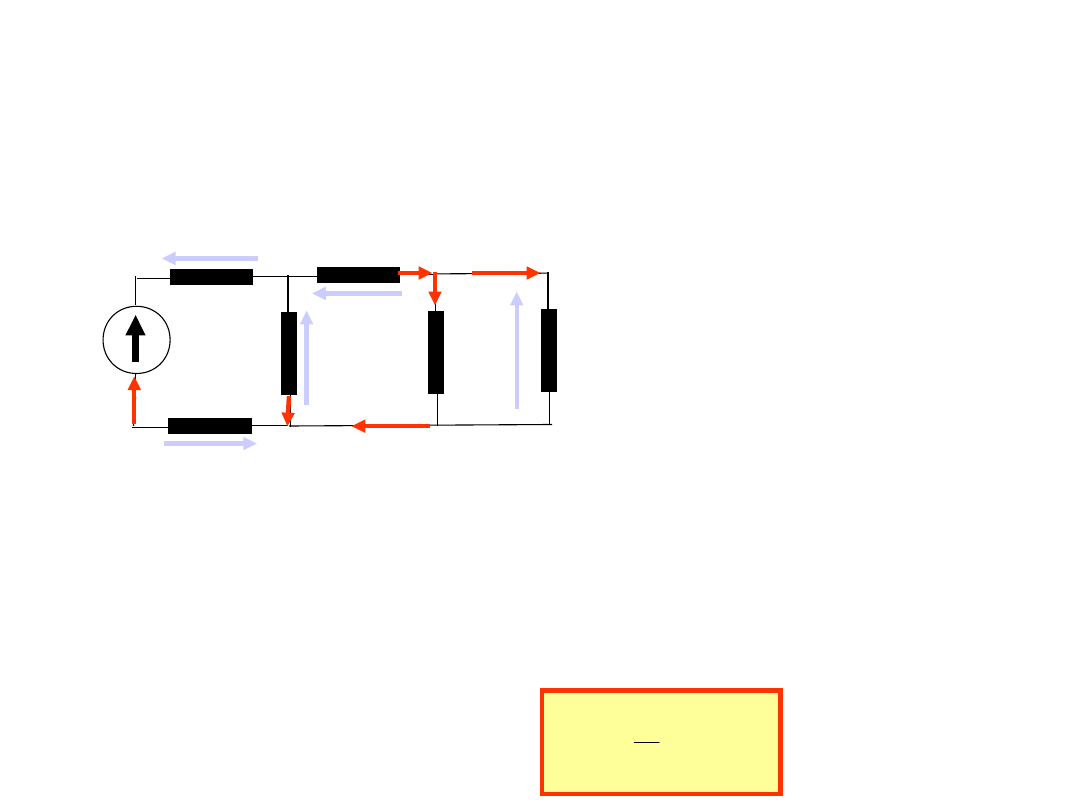
1. Obliczyć spadki napięć na wszystkich rezystorach w obwodzie:

48V

0.7

0.5

17

0.35

7

10

a =7, b =10

R

1

=0.7Ω, R

2

=0.5Ω, R

3

=17Ω, R

4

=0.35Ω, R

5

=7Ω, R

6

=10Ω.

Metoda podobieństwa

0.7A

7V

1A

1.7A

0.85V

7.85V

0.462A

1.7A

2.162A

0.757V

1.513V

E

0.7

=0.757+1.513+7.85=10.1V

Współczynnik podobieństwa

k=4.743

Rzeczywiste spadki napięcia: U

56

=7k=33.2V; U

2

=0.85k=4.03V

U

3

=7.85k=37.23V; U

4

=0.757k=3.59V; U

1

=1.513k=7.176V

2. Podać wzór na wartość średnią okresowego napięcia u(t),
jeżeli okres wynosi T.

 





T

0

sr

dt

t

u

T

1

U

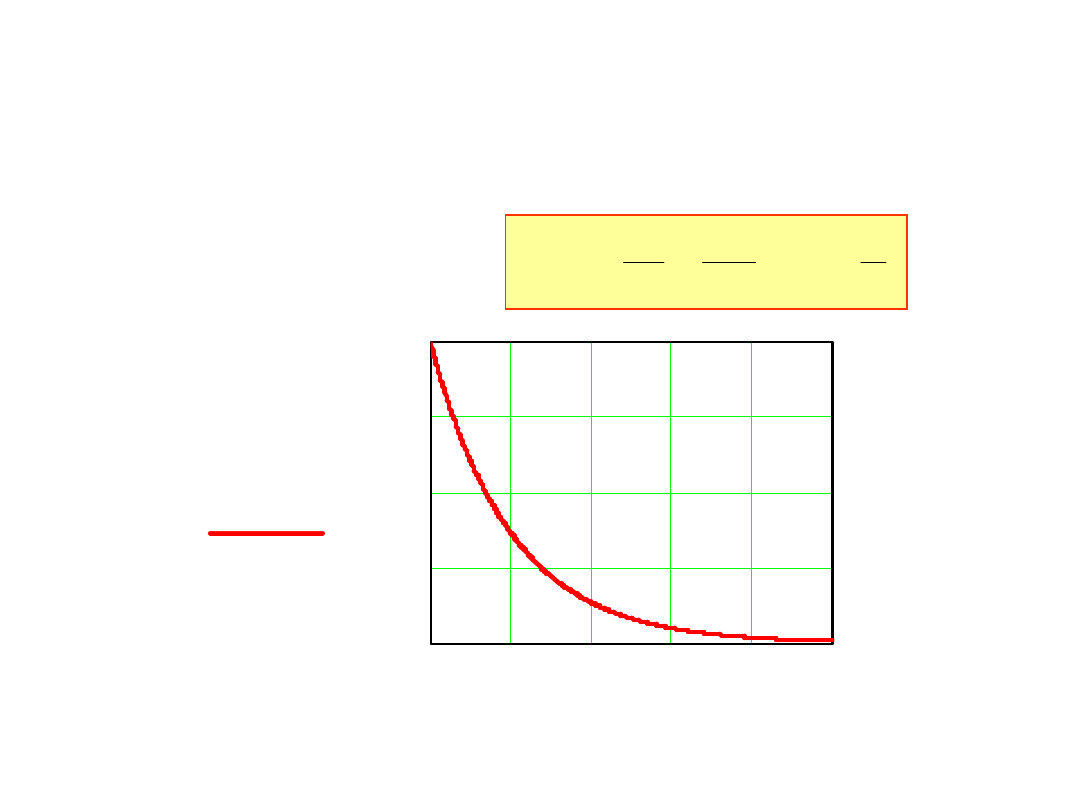
3. Napięcie na kondensatorze jest u(t)=U[1-exp(-t/T)] dla czasów
t≥0 i u(t)=0 dla czasów t<0. Obliczyć i narysować przebieg prądu
i(t) płynącego przez kondensator, jeżeli jego pojemność wynosi C.

Prąd płynący przez kondensator, na którym mamy spadek napięcia
u(t) obliczamy z zależności:

 











 





T

t

exp

T

CU

dt

du

C

t

i

0 1 2 3 4 5

0

0.25

0.5

0.75

1

i t

( )

t

i(τ)/I

m

τ=t/T

I

m

=CU/T

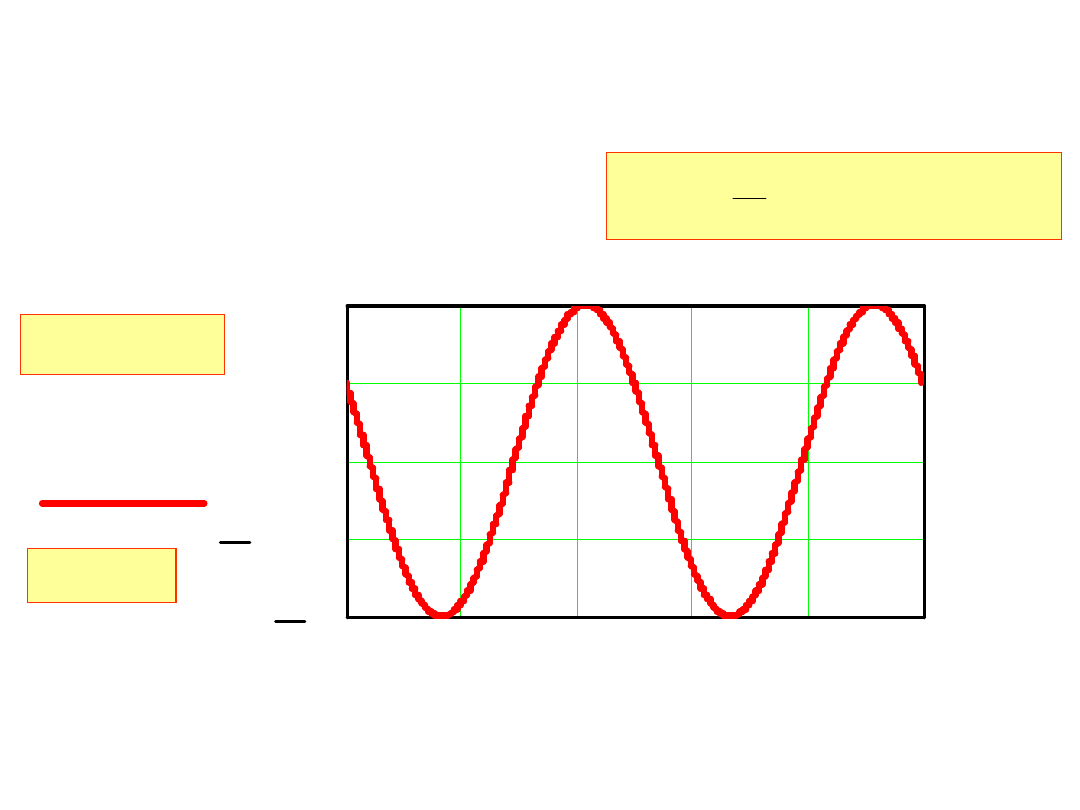
4. Prąd płynący przez indukcyjność L jest i(t)=I

m

sin(ωt+φ).

Obliczyć i narysować przebieg spadku napięcia na indukcyjności
w funkcji czasu.

Spadek napięcia na indukcyjności jest:

 

















t

cos

LI

dt

di

L

t

u

m

0 2.51

5.03

7.54

10.05

12.57

1

0.5

0

0.5

1

u t

( )

t

u(t)/U

m

U

m

=ωLI

m

τ=ωt

φ=60

0

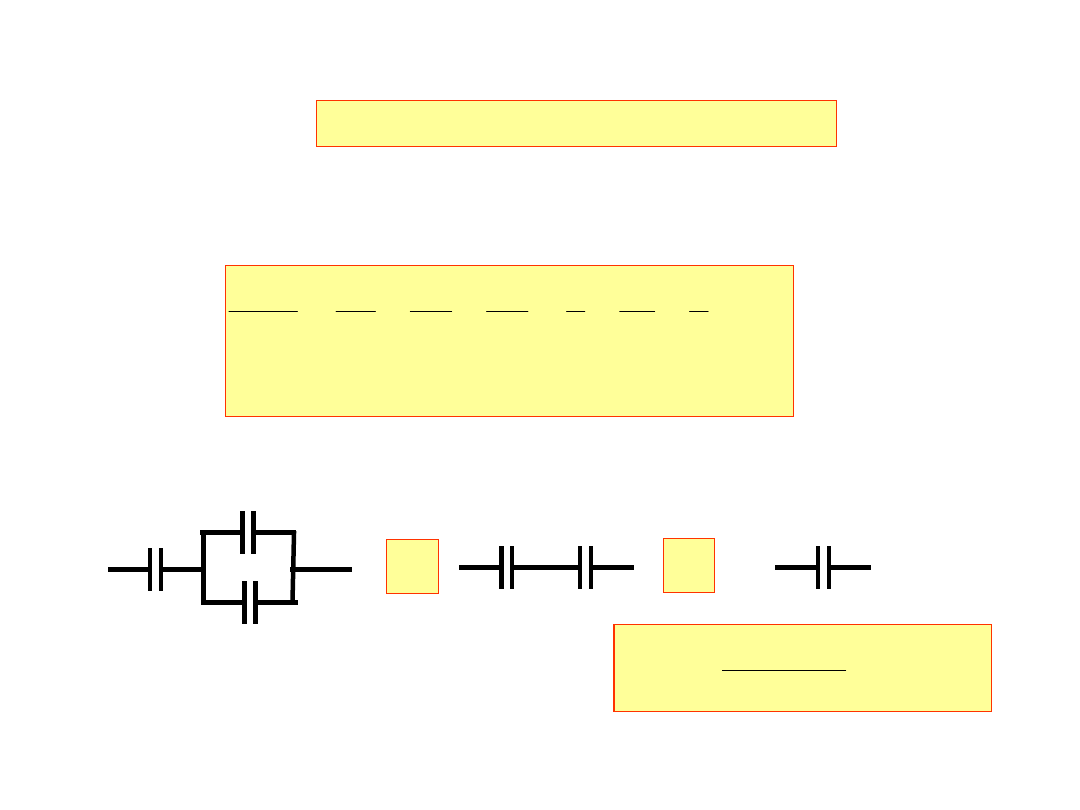
7. Obliczyć pojemność zastępczą układu kondensatorów:

50μF

100μF

150μF

5. Podać postać analityczną sygnału zmodulowanego
częstotliwościowo.

 

 









0

f

0

m

t

t

m

k

f

2

cos

S

t

s











6. Indukcyjności L

1

=5mH, L

2

=10mH i L

3

=2mH połączono

równolegle. Ile wynosi indukcyjność zastępcza?

mH

25

.

1

L

8

.

0

2

1

10

1

5

1

L

1

L

1

L

1

L

1

zast

3

2

1

zast

















→

50μF 250μF

→

C

zast

F

7

.

41

250

50

250

50

C

zast











8. Pojemność kondensatora wynosi 100pF. Kondensator włączono
do obwodu zasilanego ze źródła o częstotliwości 1MHz.
Ile wynosi reaktancja tego kondensatora?





























k

59

.

1

1592

X

10

100

10

2

1

X

fC

2

1

C

1

X

C

12

6

C

C

a=5 b=8

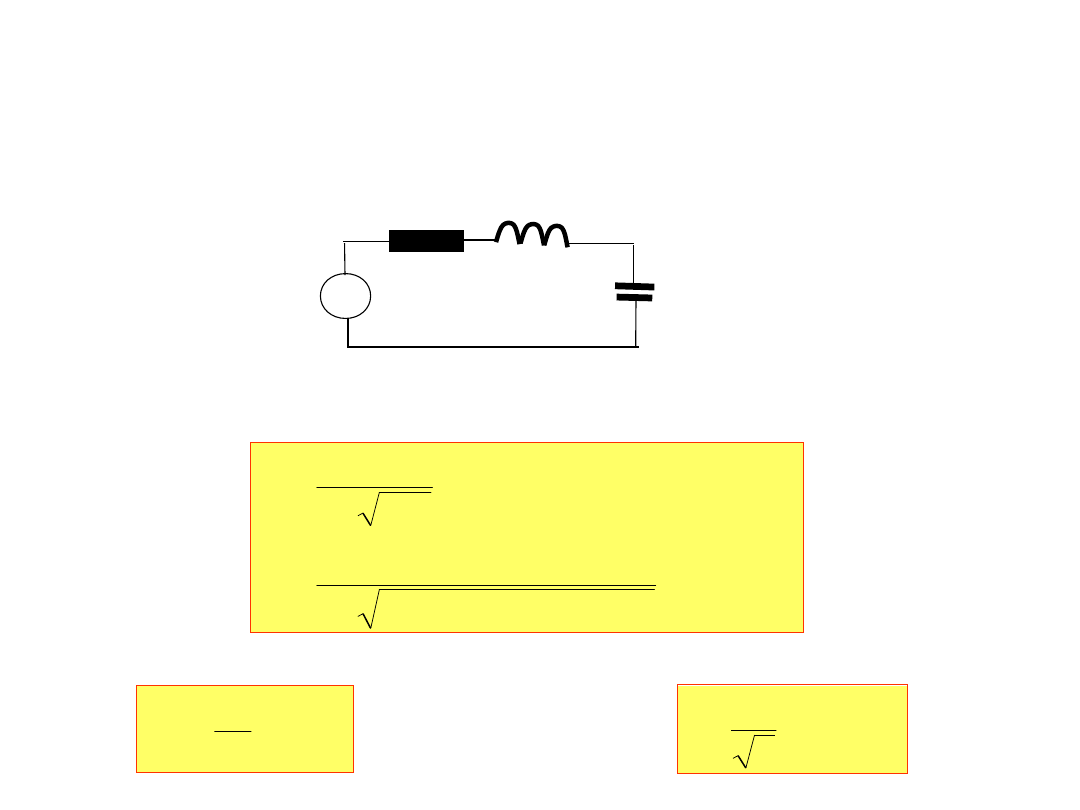
1.Obliczyć częstotliwość, dla której prąd w obwodzie osiąga
największą wartość i podać wartość tego prądu.

~

5Ω 24mH

130μF

50sin(ωt)

Największa wartość prądu wystąpi jeżeli częstotliwość źródła
zasilania będzie równa częstotliwości rezonansu f

r

:

Hz

1

.

90

10

130

10

24

2

1

f

LC

2

1

f

6

3

r

r





















Amplituda prądu przy zasilaniu obwodu SEM o częstotliwości

jest , wartość skuteczna

A

10

5

50

I

m





A

07

.

7

2

10

I





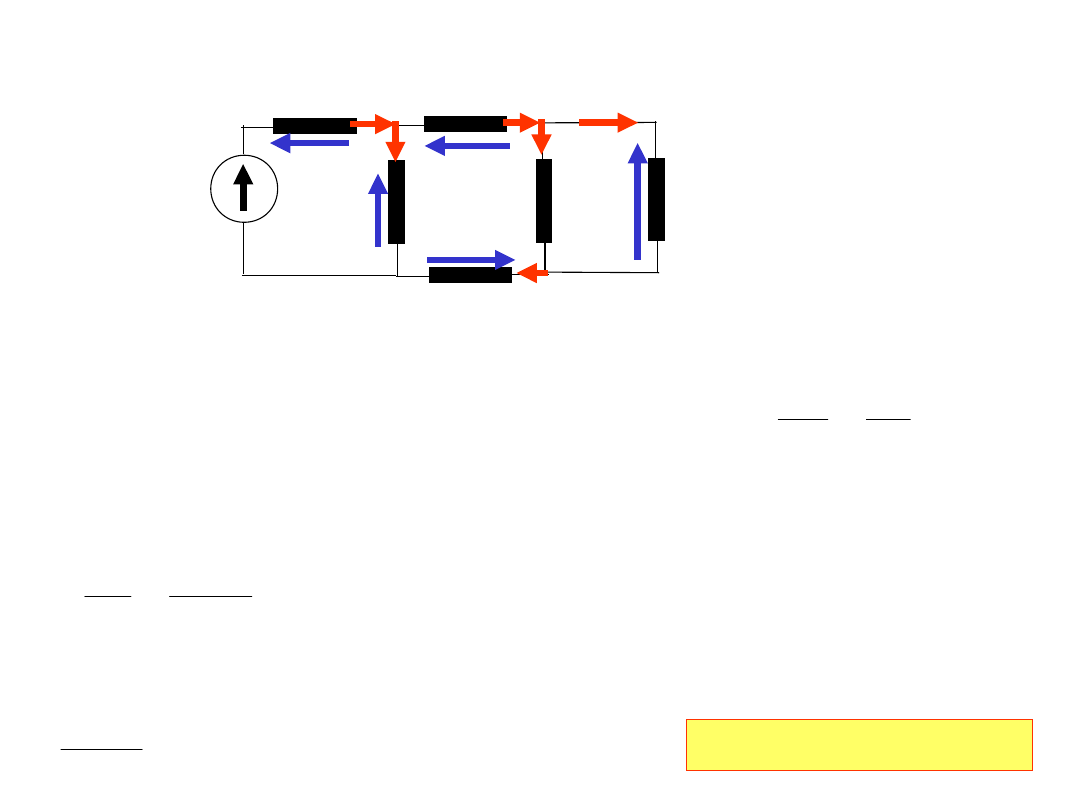
2. Wyznaczyć moc pobieraną przez rezystor R.

24Ω

2.5Ω

2.5Ω

3.9Ω

1.6Ω R=0.5Ω

24V

Najprostszą metodą jest metoda podobieństwa:

I

R

Przyjmujemy: I

R

=3.2A, U

R

=0.5·3.2=1.6V,

U

R

I

5

A

1

6

.

1

6

.

1

6

.

1

U

I

R

5







I

4

I

3

I

3

=I

4

=I

5

+I

R

=3.2+1=4.2A, U

2

=U

4

+U

R

+U

3

=3.9·4.2+2.5·4.2+1.6=28.48V,

I

2

U

3

U

4

U

2

I

1

,

A

4

.

11

5

.

2

48

.

28

5

.

2

U

I

2

2







I

1

=I

2

+I

4

=11.4+4.2=15.6A, U

1

=24·I

1

=374.4V

U

1

E=U

1

+U

2

=28.5+374.4=402.9V, współczynnik podobieństwa:

,

05957

.

0

9

.

402

24

k





prąd I

R

=k·3.2=0.191A,

mW

2

.

18

I

5

.

0

P

2

R

R







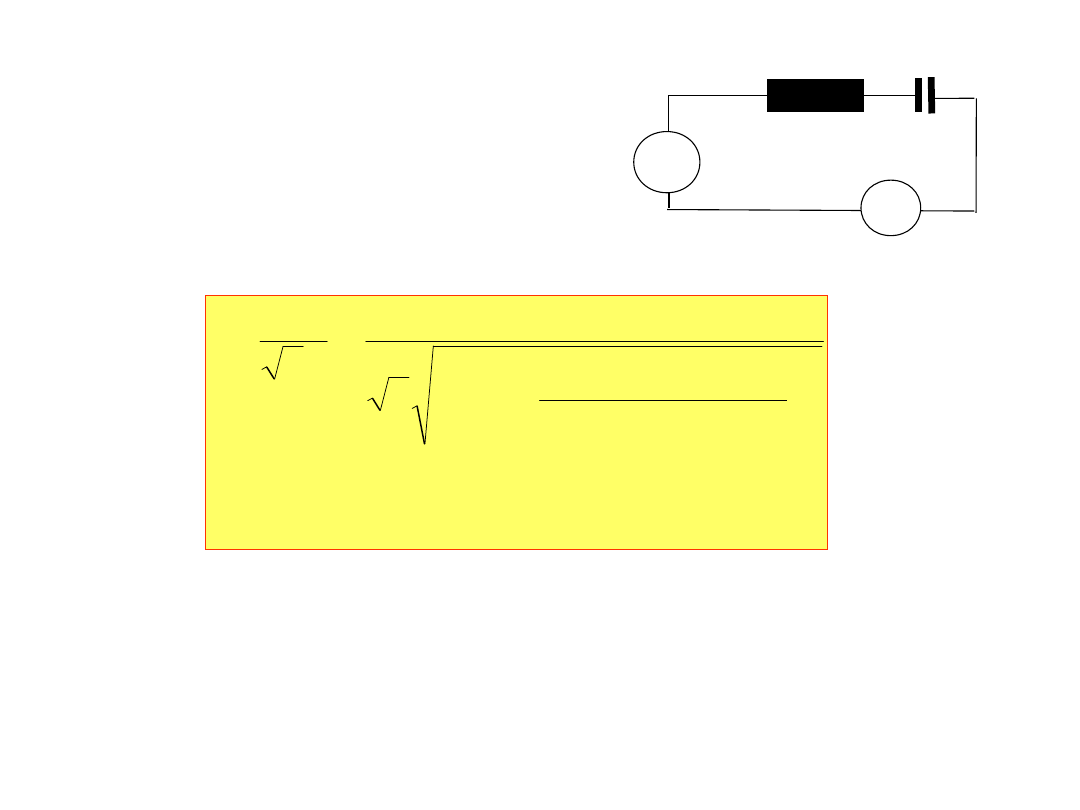
3. Obliczyć wskazania amperomierza.

~

25Ω

80μF

A

E

m

=325V

f=150Hz

Wskazanie amperomierza jest równe:

A

12

.

8

I

10

80

150

2

1

25

2

325

Z

2

E

I

2

6

2

m































4. Napięcie zasilania obwodu jest e(t)=20sin(628t+45

0

). Prąd płynący

ze źródła jest i(t)=4sin(628t+75

0

). Obliczyć moc czynną, bierną

i pozorną wydatkowaną przez źródło.

Przesunięcie fazowe między prądem a napięciem jest 75

0

-45

0

=30

0

Poszczególne moce są:
moc czynna: P=0.5·20·4cos(30

0

)=34.6W

moc bierna: Q=0.5·20·4sin(30

0

)=20VAr

moc pozorna: S=0.5·20·4=40VA

5. Obliczyć ile razy zmieni się reaktancja kondensatora
o pojemności C=100a[μF], jeżeli częstotliwość zasilania
wzrośnie 10-krotnie.

fC

2

1

C

1

X

C









Jeżeli częstotliwość wzrośnie 10-krotnie, to reaktancja jest:

10

X

fC

10

2

1

C

1

X

C

C













Zmiana reaktancji jest:

1

.

0

X

X

k

C

C







6. Podać definicję wartości średniej przebiegu okresowego
napięcia u(t), którego okres wynosi T.

 





T

0

sr

dt

t

u

T

1

U

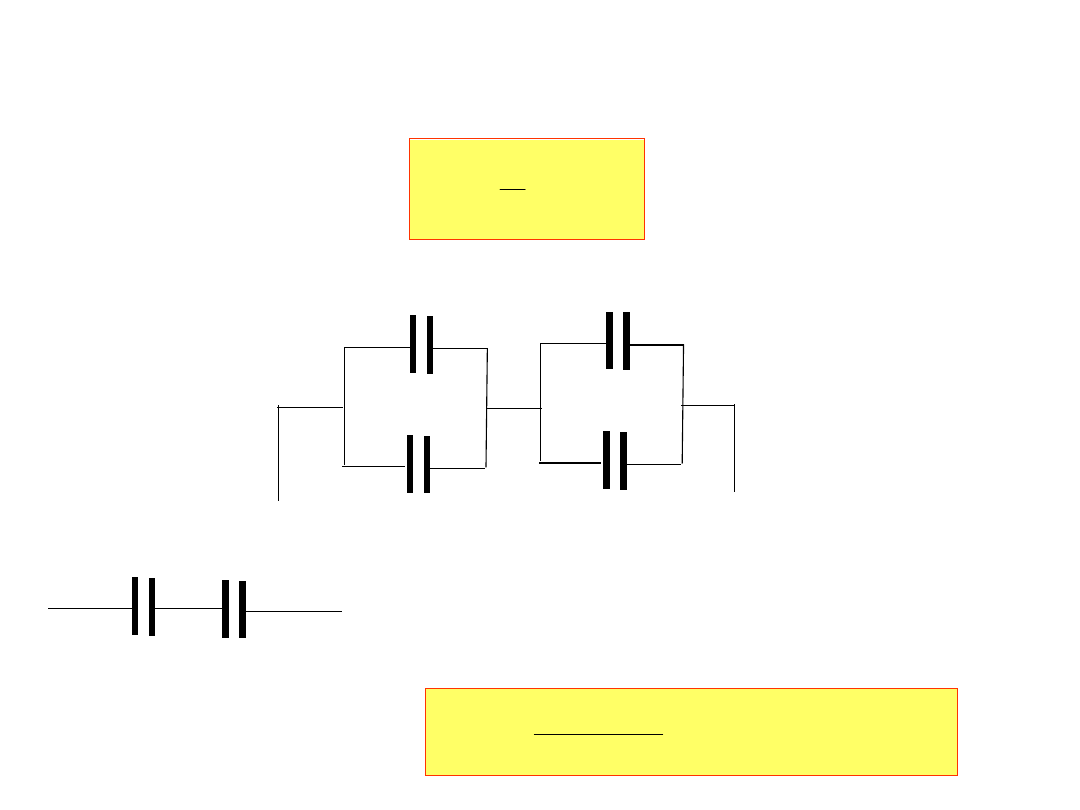
7. Obliczyć pojemność zastępczą układu:

8μF

5μF

250nF

800 nF

8+5=13μF

250+800=1050nF=1.05μF

Pojemność zastępcza:

nF

972

F

972

.

0

05

.

1

13

05

.

1

13

C

zast













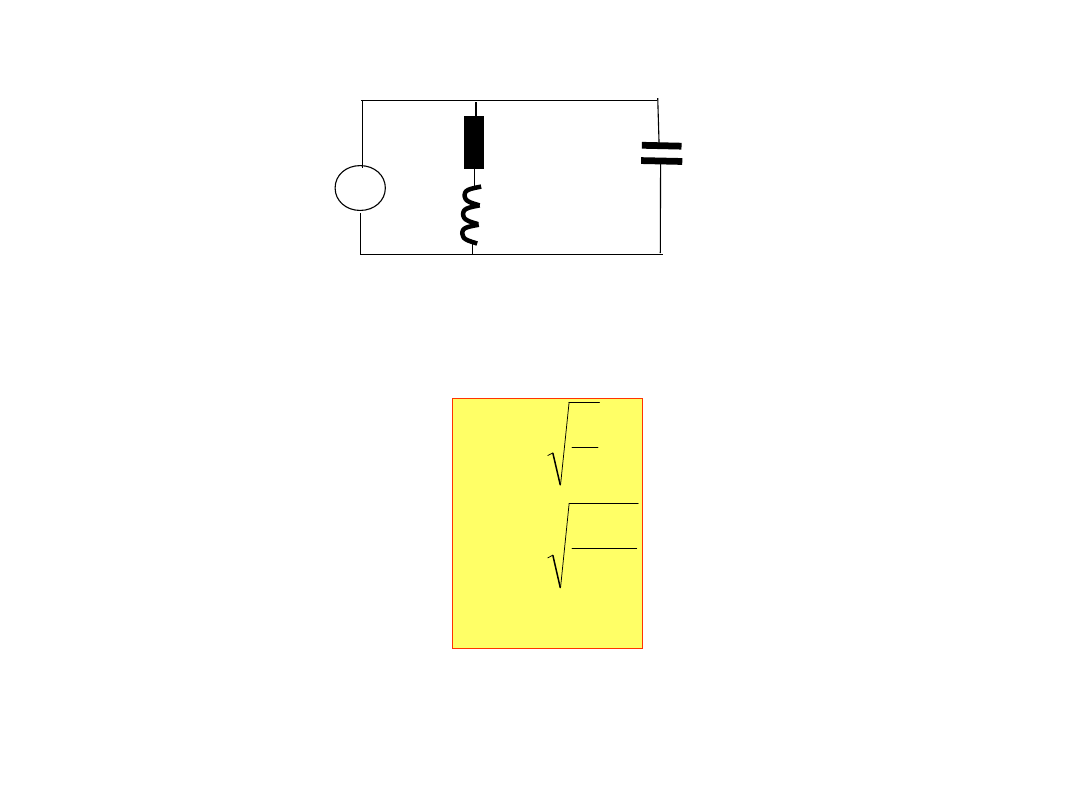
8. Obliczyć rezystancję krytyczną dla obwodu:

~

160mH

1μF

50Ω

20sin(628t)

Rezystancję krytyczną obwodu wyznaczamy z zależności:











400

R

10

16

.

0

R

C

L

R

kr

6

kr

kr

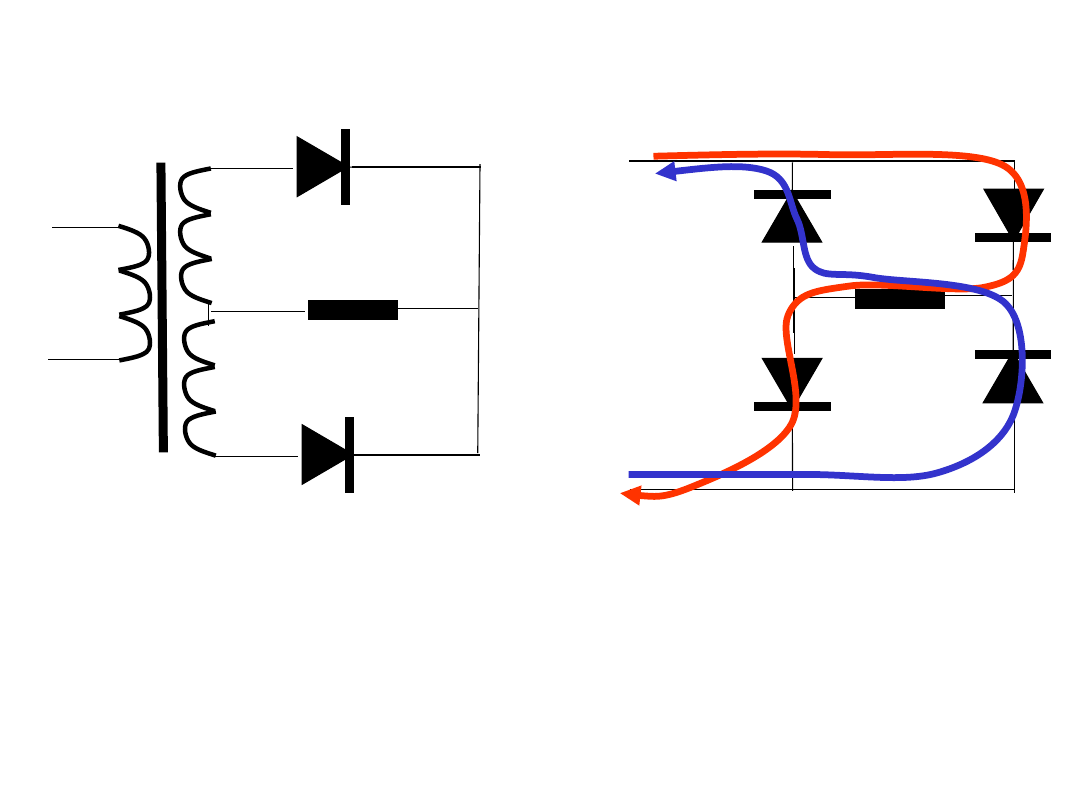
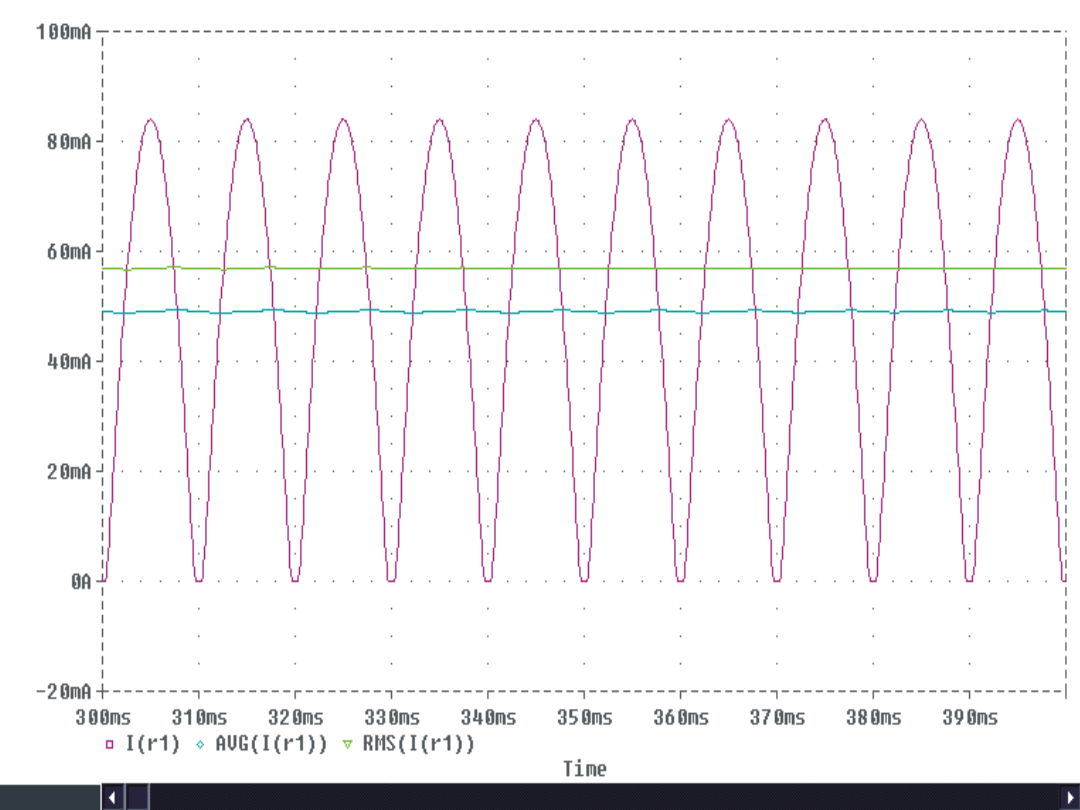
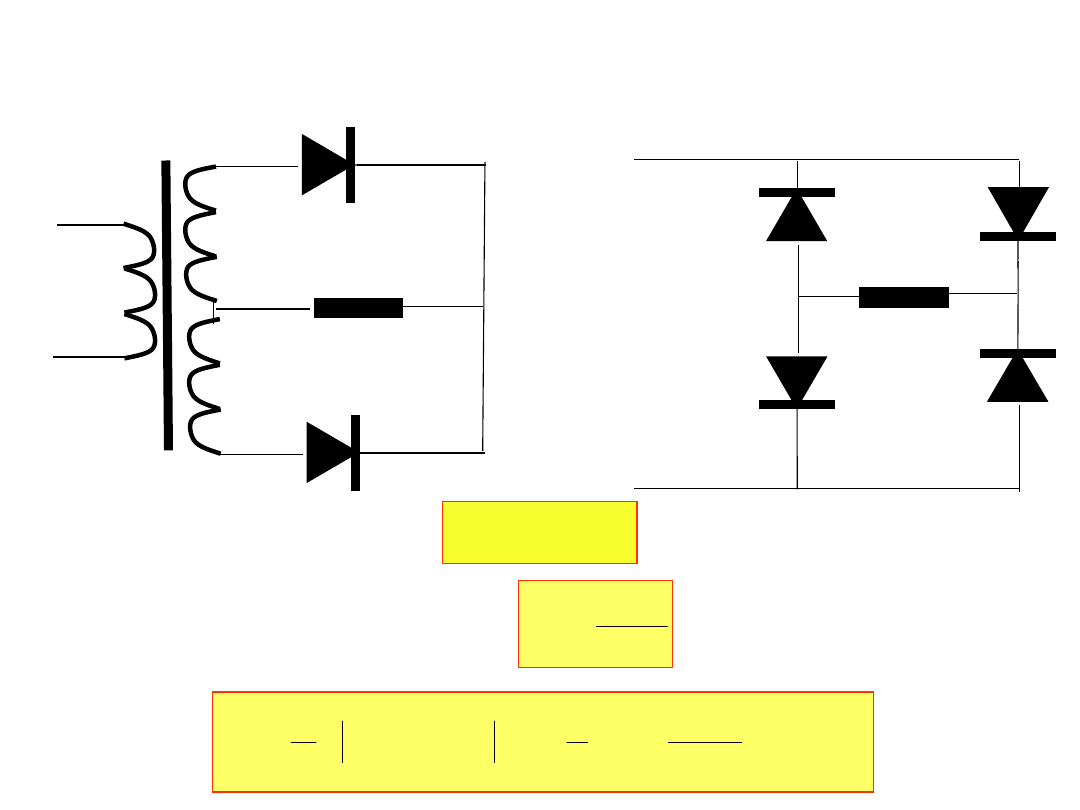
1. Narysować schemat prostownika dwupołówkowego i przebieg
w czasie prądu płynącego w obciążeniu rezystancyjnym.

R

~

lub

R

~

+

-

i(t)

+

-

i(t)

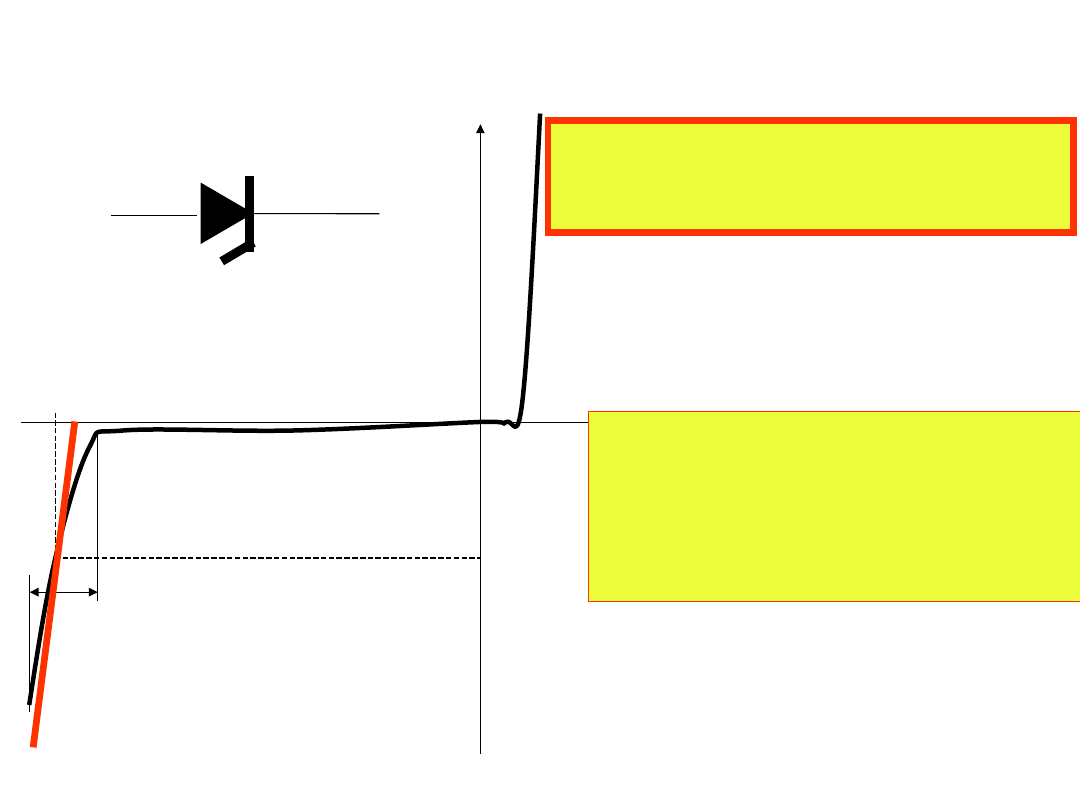
2. Podać charakterystykę diody Zenera i podać zastosowanie.

U

I Są to diody pracujące

w zakresie przebicia

I

z

U

z

U

z

– napięcie Zenera

lub napięcie
stabilizacji.

U

z

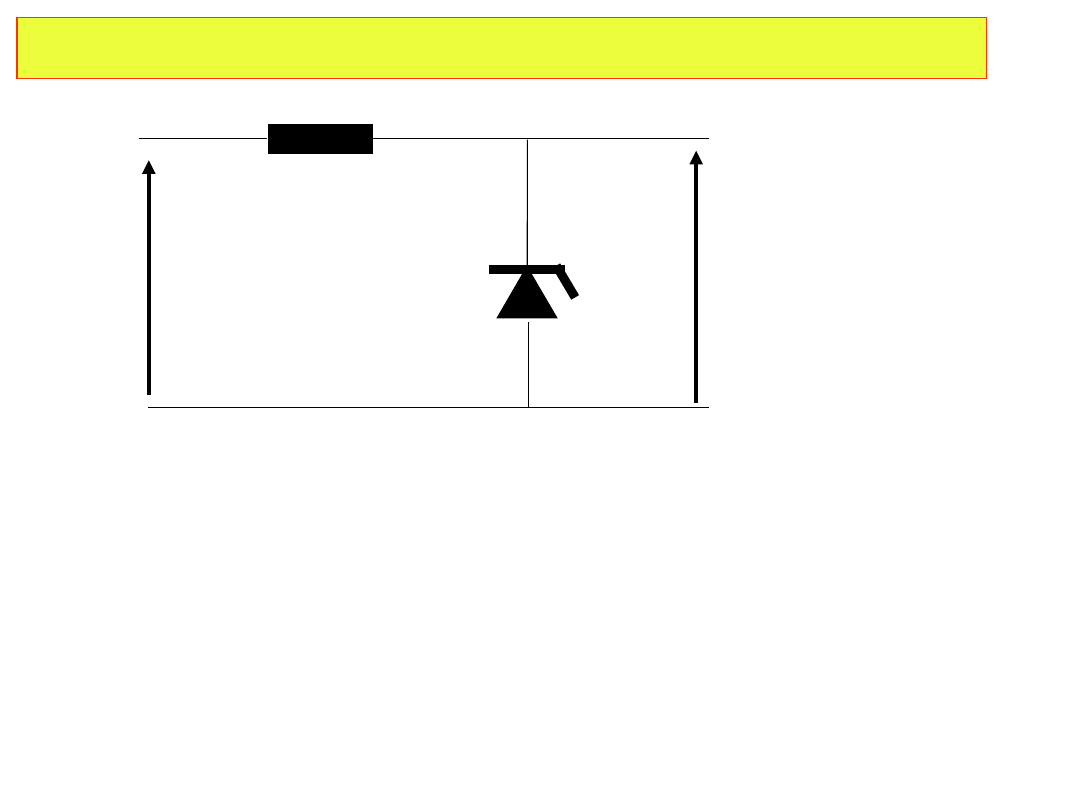
Schemat stabilizatora na diodzie Zenera

R

U

wyj

D

Z

U

wej

3. Podać prosty schemat wzmacniacza zbudowanego na z użyciem
tranzystora bipolarnego.

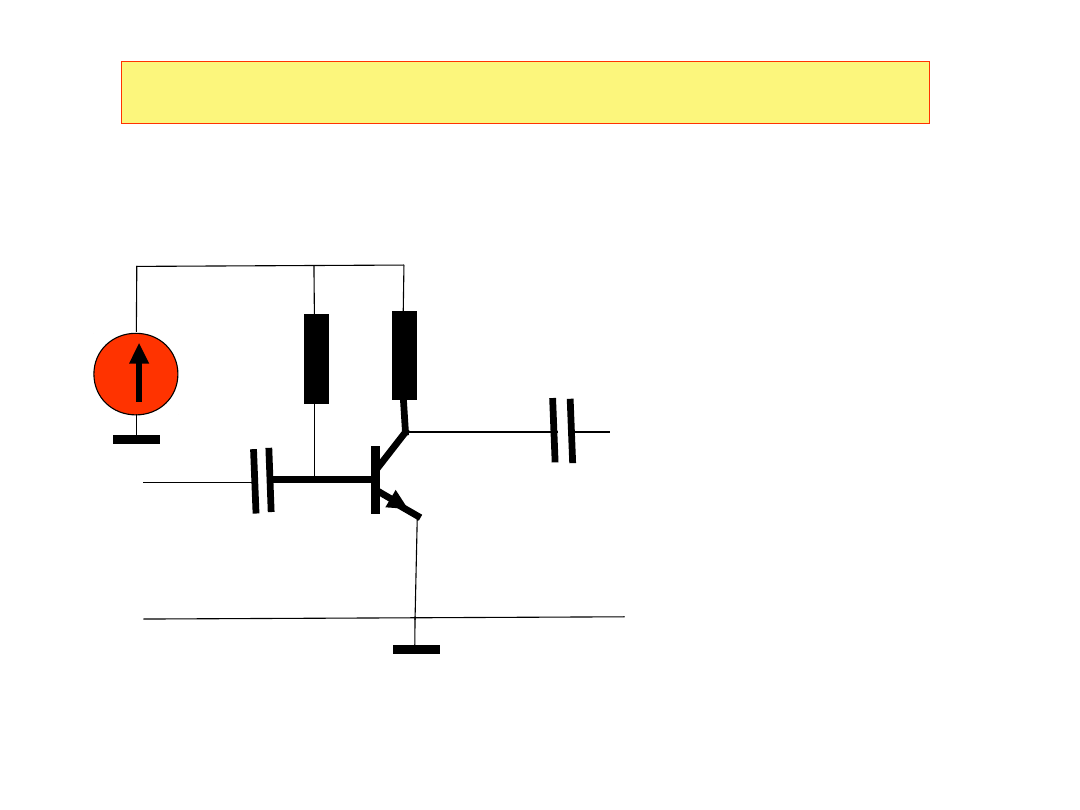
Prosty wzmacniacz tranzystorowy

wejście

wyjście

R

B

E

R

C

C

2

C

1

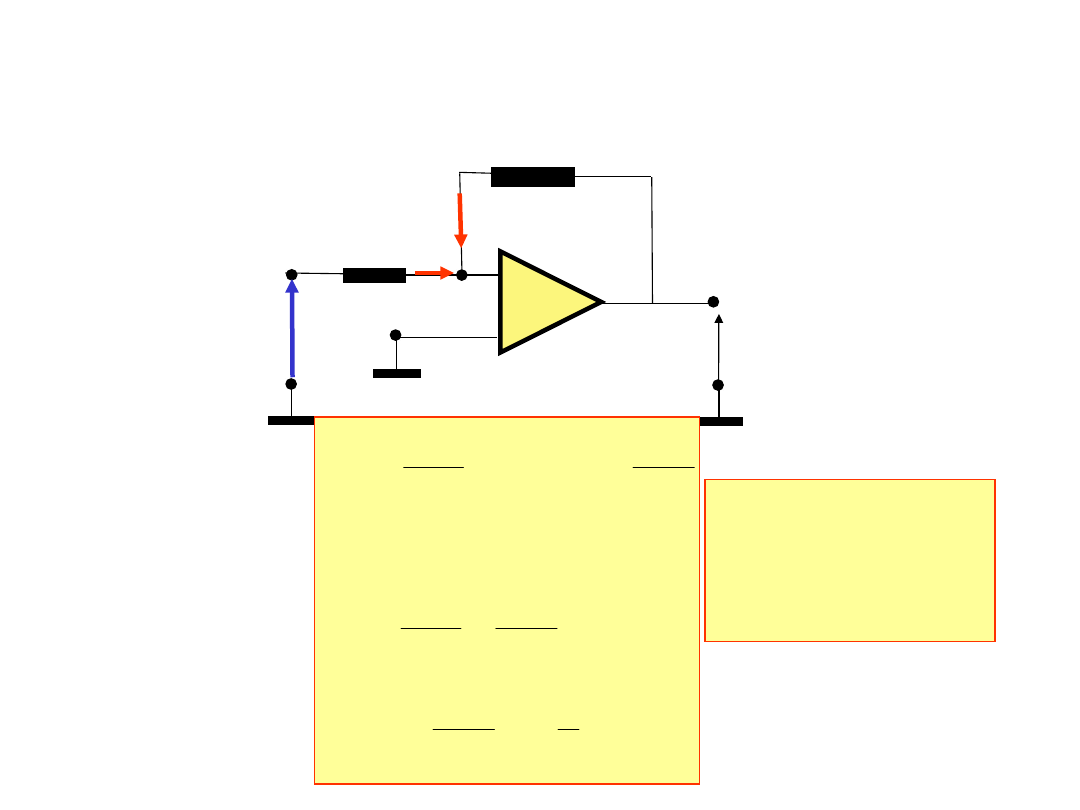
4. Obliczyć współczynnik wzmocnienia wzmacniacza operacyjnego

+

-

u

wej

b[kΩ]

a[kΩ]

u

wyj

i

wej

i

sprz

0

a

b

u

u

0

b

u

a

u

0

i

i

b

u

i

;

a

u

i

wej

wyj

wyj

wej

sprz

wej

wyj

sprz

wej

wej

















współczynnik

wzmocniena

K=b/a

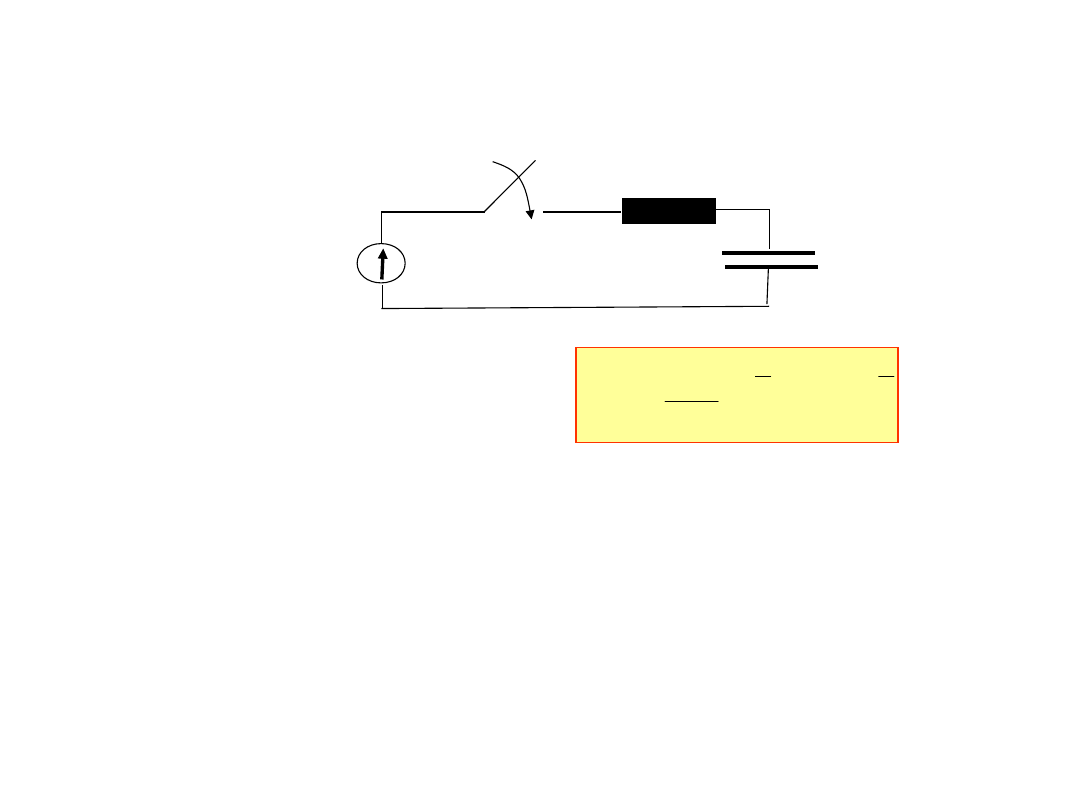
5. Podać i narysować przebieg w czasie prądu ładowania
kondensatora załączonego na źródło napięcia stałego o SEM
wynoszącym 10a[V].

10a[V]

b[μF]

a[Ω]

t=0

Prąd ładowania kondensatora:

 

T

t

T

t

e

10

e

a

a

10

t

i









gdzie T=a·b·10

-6

[s]= a·b[μs]

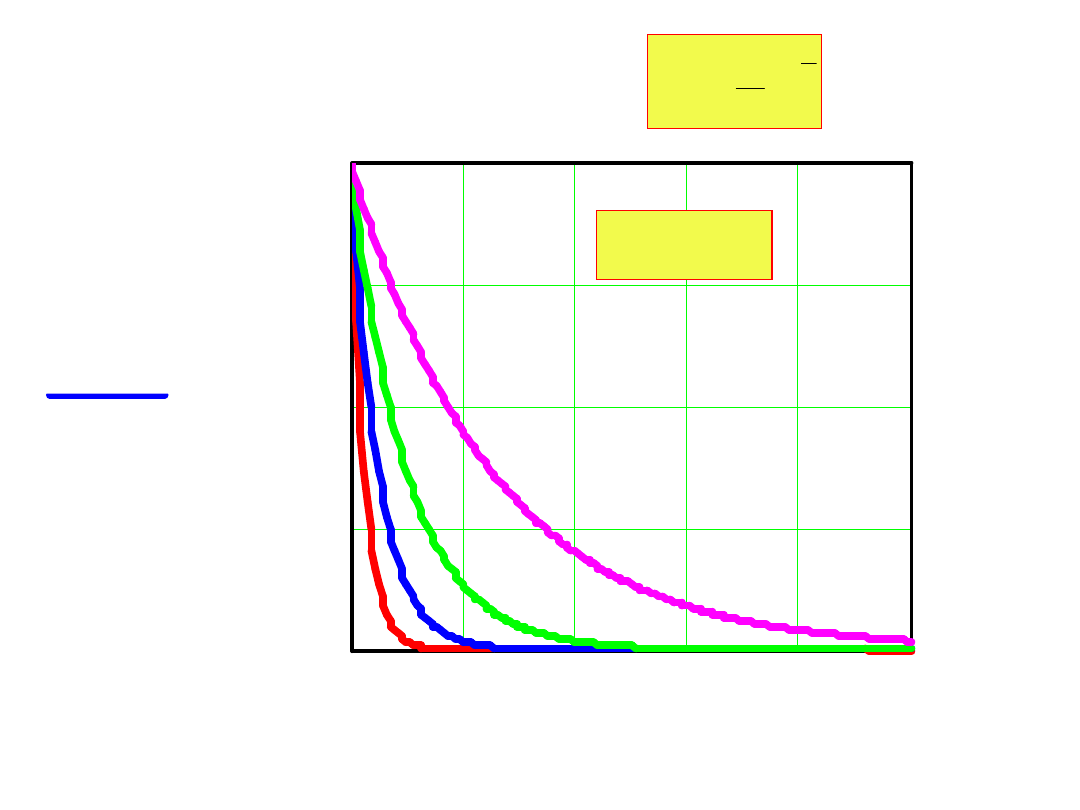
Prąd płynący w obwodzie jest:

 

T

t

e

R

E

t

i





0

0.4 0.8 1.2 1.6

2

0

0.25

0.5

0.75

1

i x

0.05



(

)

i x

0.1



(

)

i x

0.2



(

)

i x

0.5



(

)

x

i(t,T=0.05)/I

0

i(t,T=0.1)/I

0

i(t,T=0.2)/I

0

i(t,T=0.5)/I

0

I

0

=E/R

6. Ile wynosi napięcie U

wyj

?

20a[V]

a·b[kΩ]

b[kΩ]

U

wyj

1

a

a

20

U

b

b

b

a

a

20

U

wyj

wyj













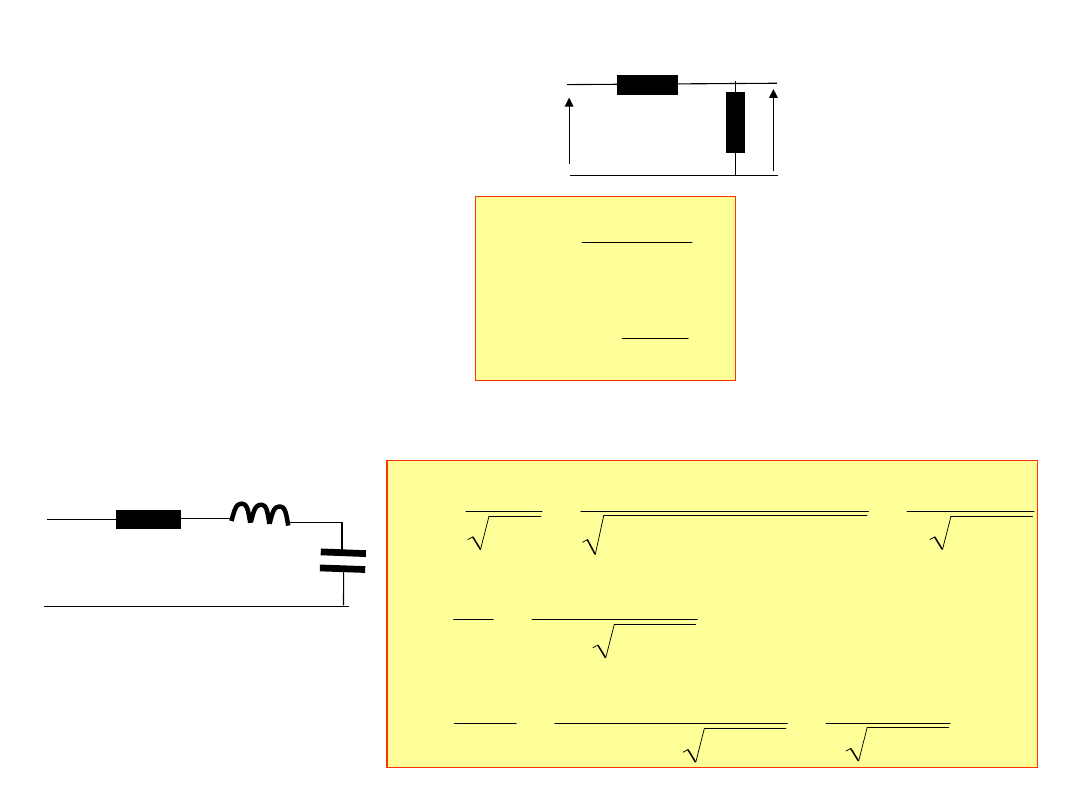
7. Obliczyć częstotliwość rezonansu i dobroć:

a[kΩ]b[mH]

a·b[μF]

a

1

.

0

a

01

.

0

a

1

.

0

b

10

a

10

b

10

R

L

Q

a

1

.

0

b

2

10

2

f

a

1

.

0

b

10

10

b

a

10

b

1

LC

1

3

3

4

r

4

r

r

4

6

3

r

























































8. Napięcie zasilania wynosi e(t)=100asin(628t+50

0

), a prąd

wydatkowany przez źródło jest i(t)=5bsin(628t+80

0

). Wyznaczyć

moc czynną, bierną i pozorną wydatkowaną przez to źródło.

Kąt fazowy φ=80

0

-50

0

=30

0

Moc czynna: P=0.5·5·b·100·a·cos(30

0

)=250·0.866·a·b=217·a·b [W]

moc bierna: Q=0.5·5·b·100·a·sin(30

0

)=250·0.5·a·b=125·a·b [VAr]

moc pozorna: S= 0.5·5·b·100·a= 250·a·b[VA]

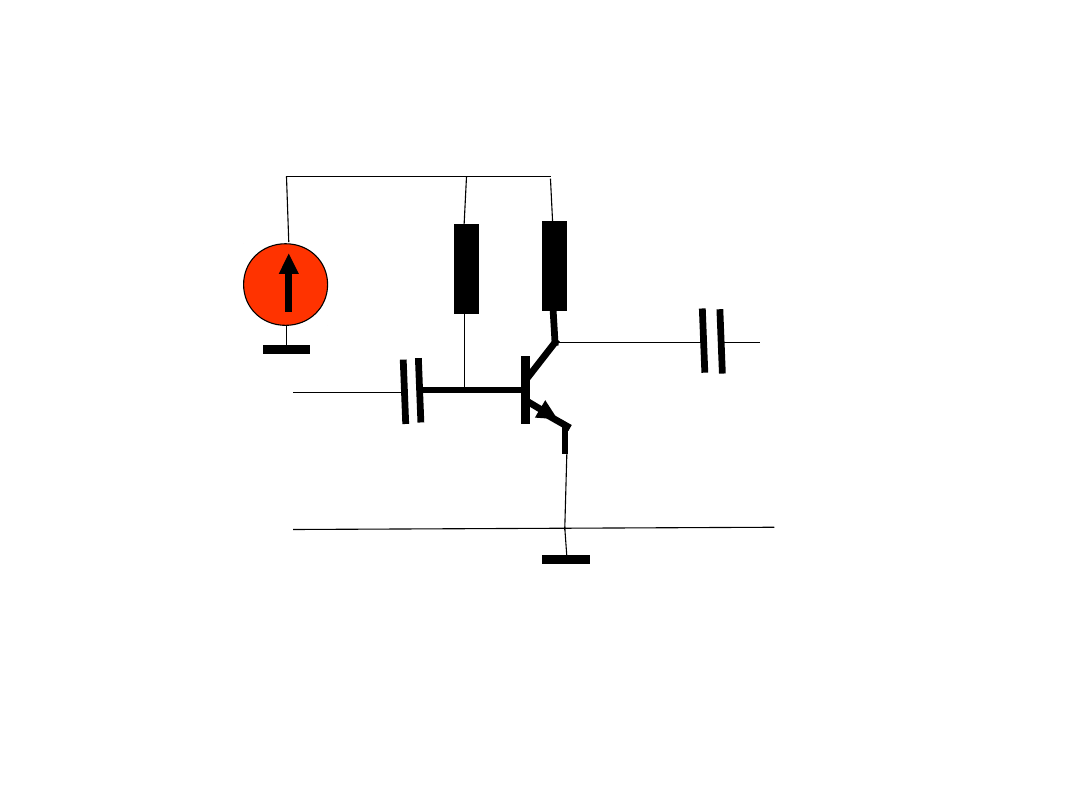
1. Podać prosty schemat wzmacniacza zbudowanego na z użyciem
tranzystora bipolarnego.

wejście

wyjście

R

B

E

R

C

C

2

C

1

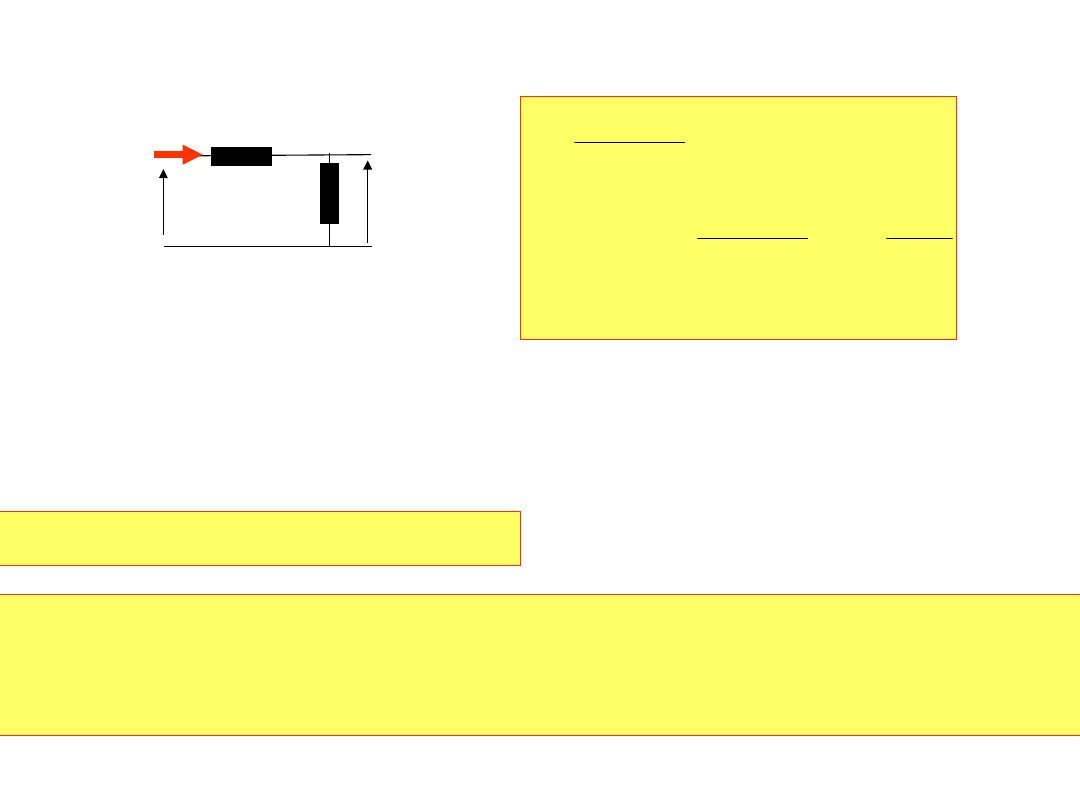
2. Ile wynosi napięcie U

wyj

?

20a[V]

a·b[kΩ]

b[kΩ]

U

wyj

3. Napięcie zasilania wynosi e(t)=100asin(628t+35

0

), a prąd

wydatkowany przez źródło jest i(t)=5bsin(628t+80

0

). Wyznaczyć

moc czynną, bierną i pozorną wydatkowaną przez to źródło.

I

V

5

.

17

U

1

a

a

20

b

b

a

ab

20

bI

U

b

b

a

a

20

I

wyj

wyj





















a=7; b=8

Kąt fazowy φ=80

0

-35

0

=45

0

Moc czynna: P=0.5·100·a·5·b·cos(φ)=9899W=9.9kW
Moc bierna: Q=0.5·100·a·5·b·sin(φ)=9899VAr=9.9kVAr
Moc pozorna: S= 0.5·100·a·5·b=14000VA=14kVA

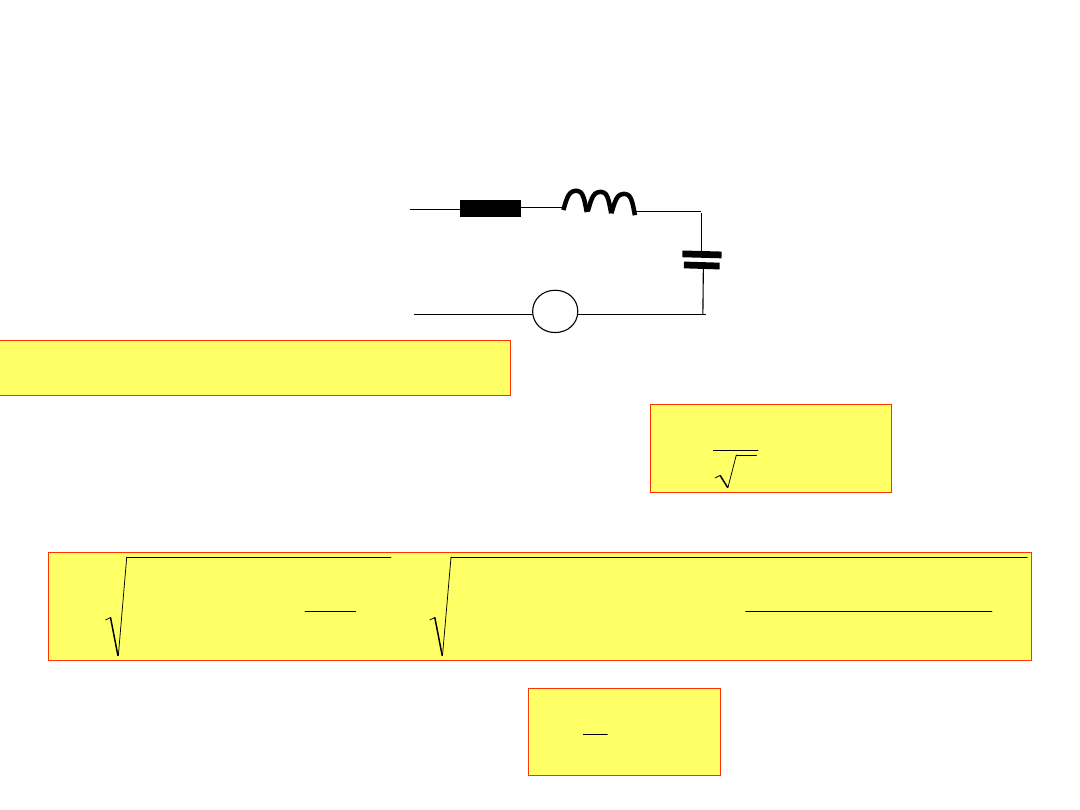
4. Obliczyć wskazanie amperomierza, jeżeli układ jest zasilany
napięciem sinusoidalnie zmiennym o amplitudzie 50V
i częstotliwości 1kHz.

a[Ω] b[mH]

100·b[μF]

A

Pulsacja: ω=2πf=6283s

-1

Wartość skuteczna SEM zasilającej:

V

4

.

35

2

50

E





Moduł impedancji:

2

6

3

2

2

2

10

b

100

6283

1

10

b

6283

a

C

1

L

R

z



















































A

7

.

0

z

E

I





Prąd amperomierza:

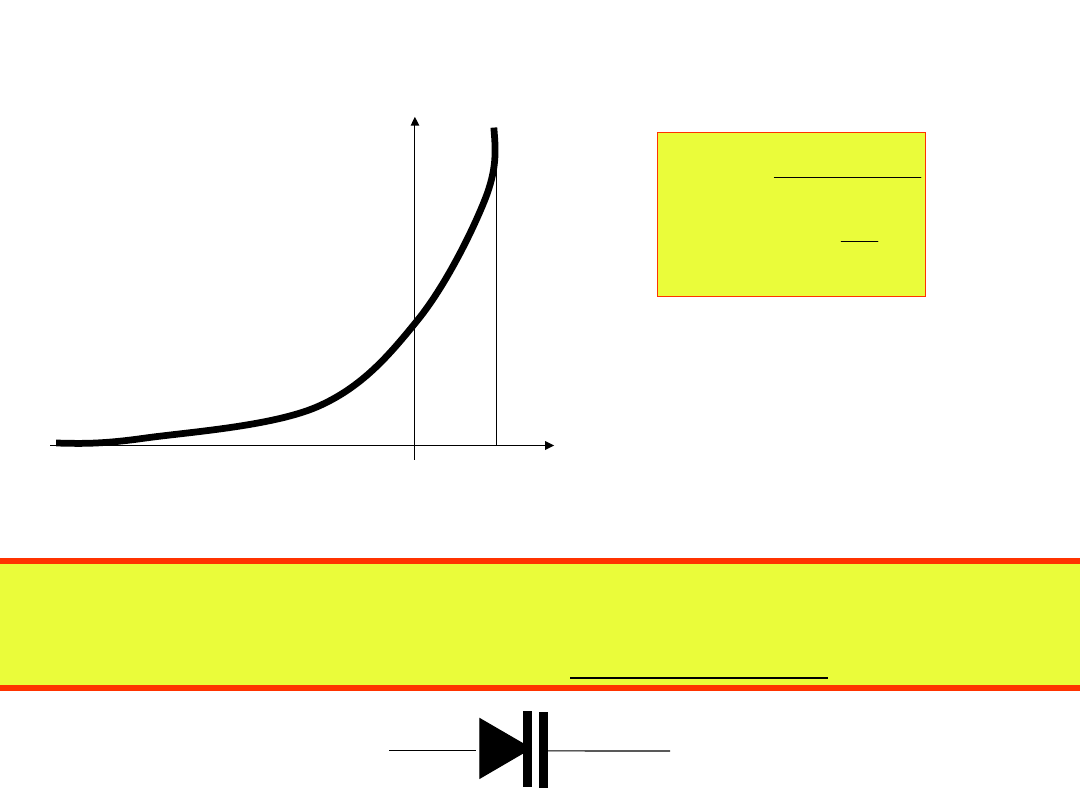
C(U)

U

V

j

C(0)

 

 

m

j

V

U

1

0

C

U

C

















V

j

– bariera potencjału

złącza równa
0.7÷0.9V dla diod
krzemowych.

Dioda, w której wykorzystuje się pojemność złącza

jest nazywana warikapem.

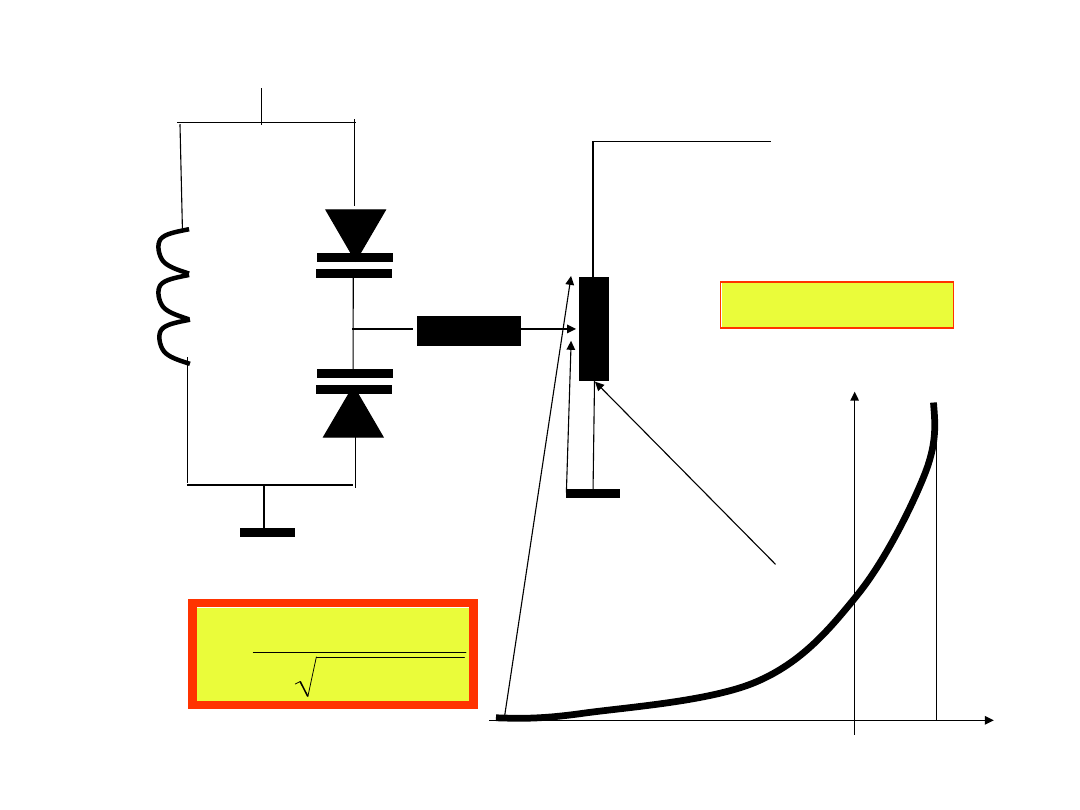
5. Podać przykład zastosowania diody warikapowej.

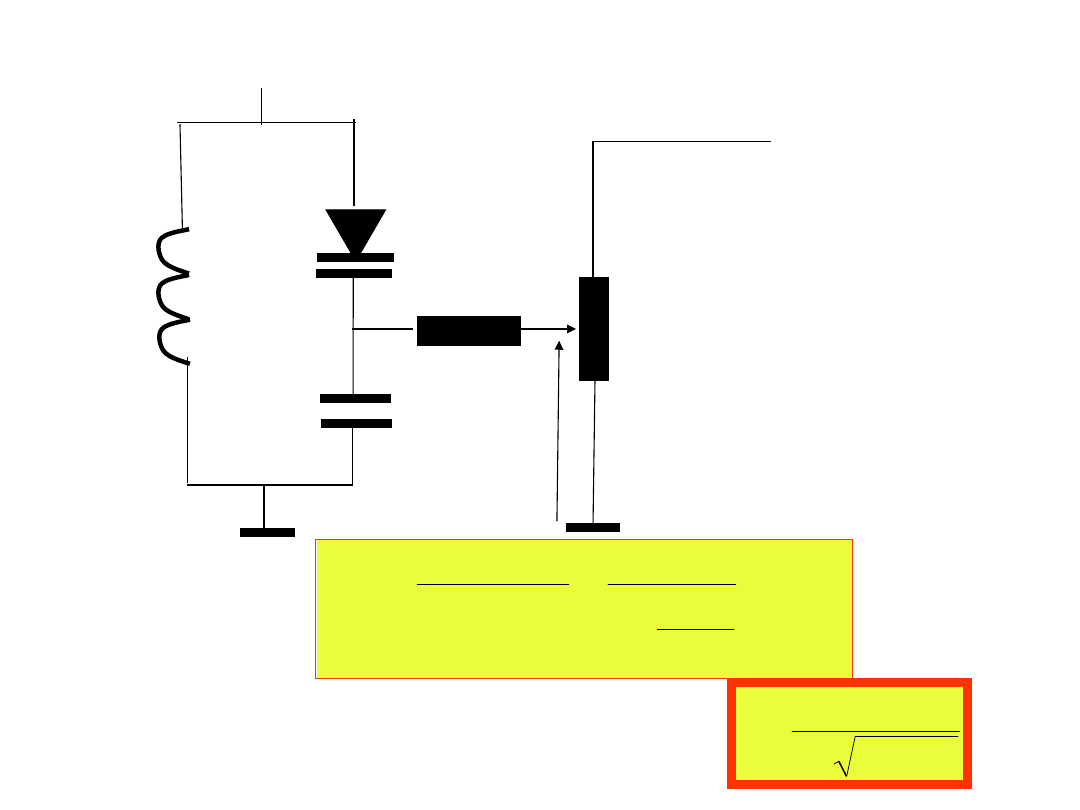
Obwody rezonansowe przestrajane warikapem.

R

+E

P

U

L

C

2

C(U)

Przyjmuje się

C

2

>C(U)

Zastępczą pojemność
określa równość:

 

 

 

 

 

U

C

C

U

C

1

U

C

C

U

C

C

U

C

C

2

2

2

zas











i częstotliwość rezonansowa obwodu:

 

U

LC

2

1

f





R

+E

P

U

L

C(U)

C(U)

Pojemność zastępcza:

 

U

C

5

.

0

C

zast



Częstotliwość rezonansowa

obwodu:

 

U

LC

5

.

0

2

1

f





C(U)

U

V

j

C(0)

-E

R

~

R=b[]

6. Narysować schemat prostownika dwupołówkowego. Jeżeli
SEM zasilania jest e(t)=100asin(300t)[V], a obciążeniem jest rezystor
R=b[Ω], to ile wynosi średni prąd płynący przez rezystor?

R

~

lub

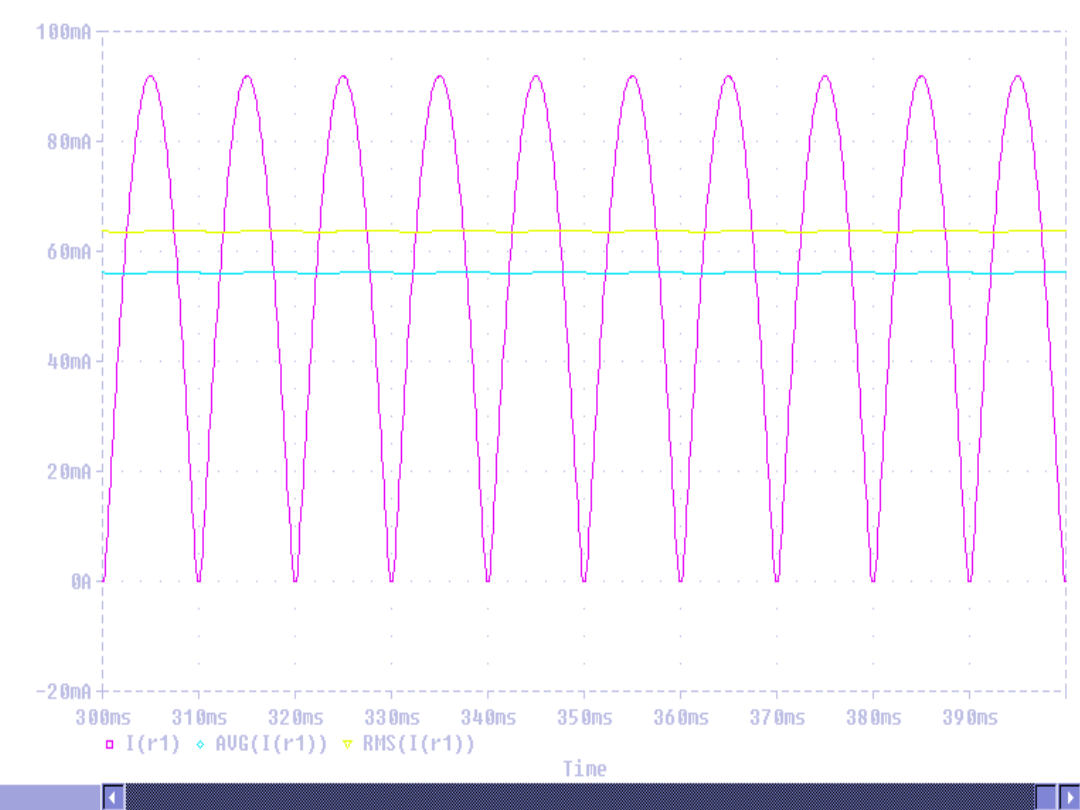
Maksymalna wartość prądu:

b

a

100

I

m



, a prąd średni, to

 

A

7

.

55

b

a

200

I

2

dt

t

sin

I

T

1

I

m

T

0

m

sr

















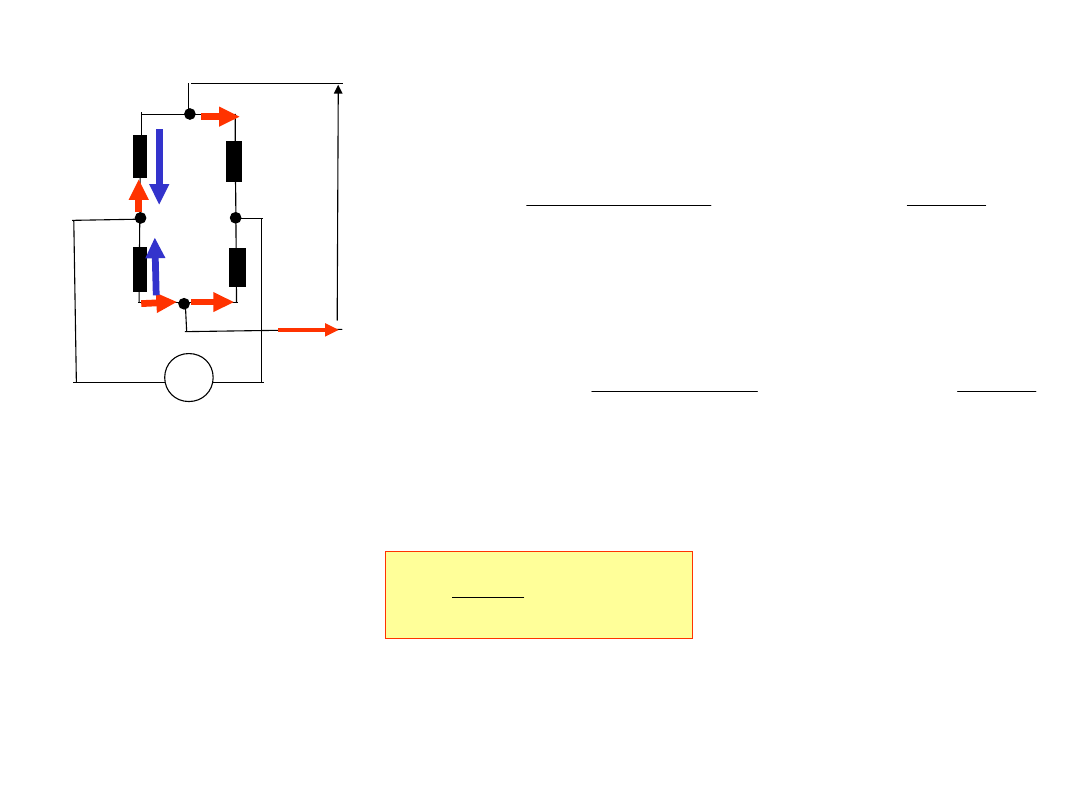
7. Ile powinna wynosić rezystancja R, aby napięcie U

wyj

=0?

=

u

z

u

wyj

a·b[kΩ]

(a+b)[kΩ]

a[kΩ]

R

I=0

I

a

I

R

I

ab

I

a+b

I

ab

=I

a+b

=I

1

i I

a

=I

R

=I

2

bo I=0





R

a

E

I

oraz

b

a

b

a

E

I

2

1













U

ab

U

a

U

ab

-U

a

+u

wyj

=0, ale u

wyj

=0 czyli U

ab

=U

a





R

a

Ea

a

I

U

b

a

ab

Eab

ab

I

U

2

a

1

ab

















stąd ab(a+R)=a[ab+(a+b)] → a

2

b+abR=a

2

b+a(a+b)

stąd









k

875

.

1

b

b

a

R

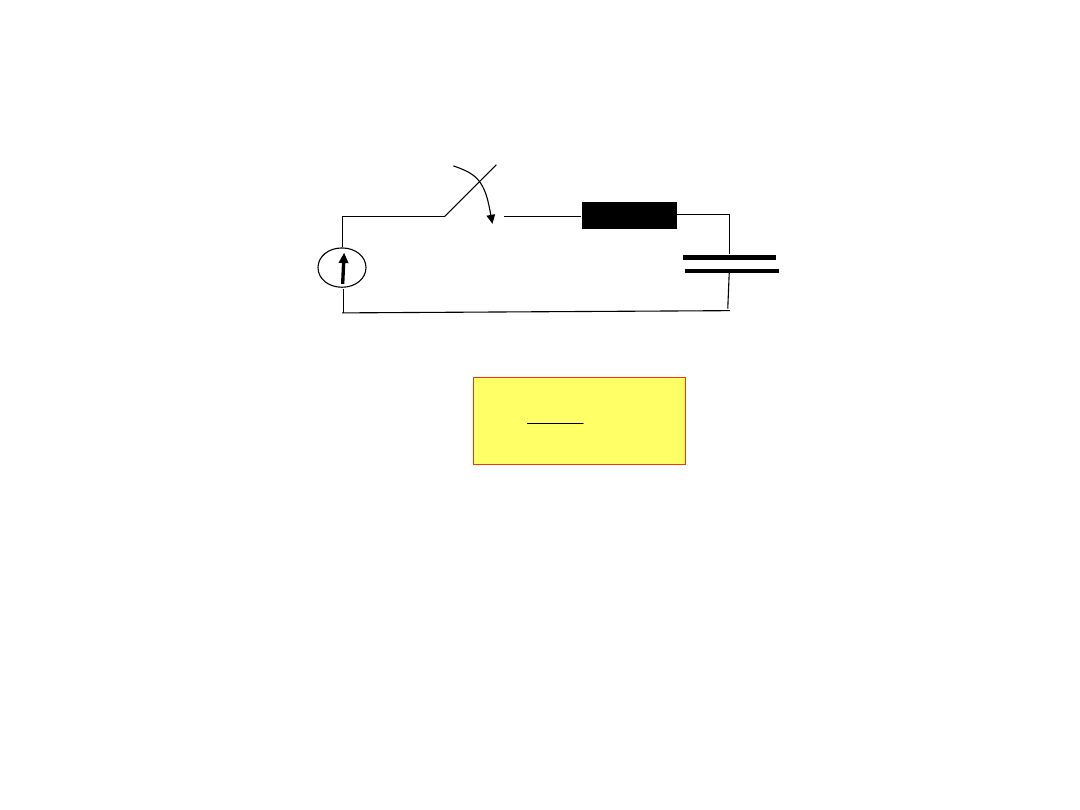
8. Podać i narysować przebieg w czasie prądu ładowania
kondensatora załączonego na źródło napięcia stałego o SEM
wynoszącym 10b[V].

10b[V]

a[μF]

t=0

b[Ω]

Amplituda prądu:

A

10

b

b

10

I





Stała czasowa: T=RC=b·a·10

-6

=5.6·10

-5

s=56μs