Budżetowanie kapitałowe

Budżetowanie nakładów

kapitałowych

• Jest procesem planowania nakładów

na inwestycje w środki trwałe, które

będą generowały przepływy pieniężne

w okresie dłuższym niż rok. Jest to

analiza finansowa projektów

inwestycyjnych pod kątem

podejmowania decyzji odnośnie ich

przyszłej realizacji.

• Poświęcane są na nie corocznie

olbrzymie środki.

Decyzje inwestycyjne

• Zmieniają obecny stan środków

pieniężnych w firmie

• W istotny sposób wpływają na

przyszłość jednostki

• Angażują znaczne środki pieniężne
• Wpływają na płynność w chwili

obecnej i w przyszłości

Ocena decyzji

inwestycyjnych

• Musi obejmować analizę kosztów i

korzyści zarówno w okresie krótkim
jak i długim

• Wpływ na pozycje konkurencyjną

jednostki

• Na łańcuch wartości jednostki
• Na strategię jednostki

Strategia jednostki

• Nie może być daną niezmienną

• Ciągłe formowanie strategii

• Uwzględnianie celów firmy

• Badanie wpływu projektu na wszystkie

podmioty wewnętrzne i procesy
przedsiębiorstwa

Problemy budżetowania

• Wpływ decyzji na wiele kolejnych lat
• Poziom rzeczowego majątku trwałego
• Wybór momentu realizacji projektu
• Angażowanie znacznych nakładów

finansowych

• Indywidualne podchodzenie do oceny

konkretnych projektów
inwestycyjnych

Klasyfikacja projektów

• Zastąpienie aktywów takim samym

środkiem trwałym

• Zastąpienie aktywów z redukcja kosztów
• Ekspansja istniejących produktów oraz

ekspansja na istniejących rynkach

• Ekspansja nowych produktów oraz

ekspansja na nowych rynkach

• Projekty związane ze środowiskiem

naturalnym lub bezpieczeństwem

• inne

Metody oceny opłacalności

inwestycji

• Metody nie uwzględniające zmianę

wartości pieniądza w czasie

• Metody uwzględniające zmianę

wartości pieniądza w czasie

Metody nie uwzględniające

zmiany wartości pieniądza w

czasie

• Księgowa stopa zwrotu

• Okres zwrotu

KSIĘGOWA STOPA ZWROTU

PRZYKŁAD 1

•

jedną z najczęściej stosowanych miar służących do oceny efektywności inwestycji jest
księgowa stopa zwrotu, czyli stosunek zysku do nakładów inwestycyjnych,

•

załóżmy, że wymagana przez przedsiębiorstwo X minimalna księgowa stopa zwrotu
wynosi 9%; przedsiębiorstwo zamierza podjąć projekt, którego charakterystyka jest
następująca:

nakłady inwestycyjne

100000

czas trwania projektu

5 lat

przepływy pieniężne netto (zysk + amortyzacja):

rok 1

20000

rok 2

27000

rok 3

30000

rok 4

35000

rok 5

30000

roczna amortyzacja prosta

20000

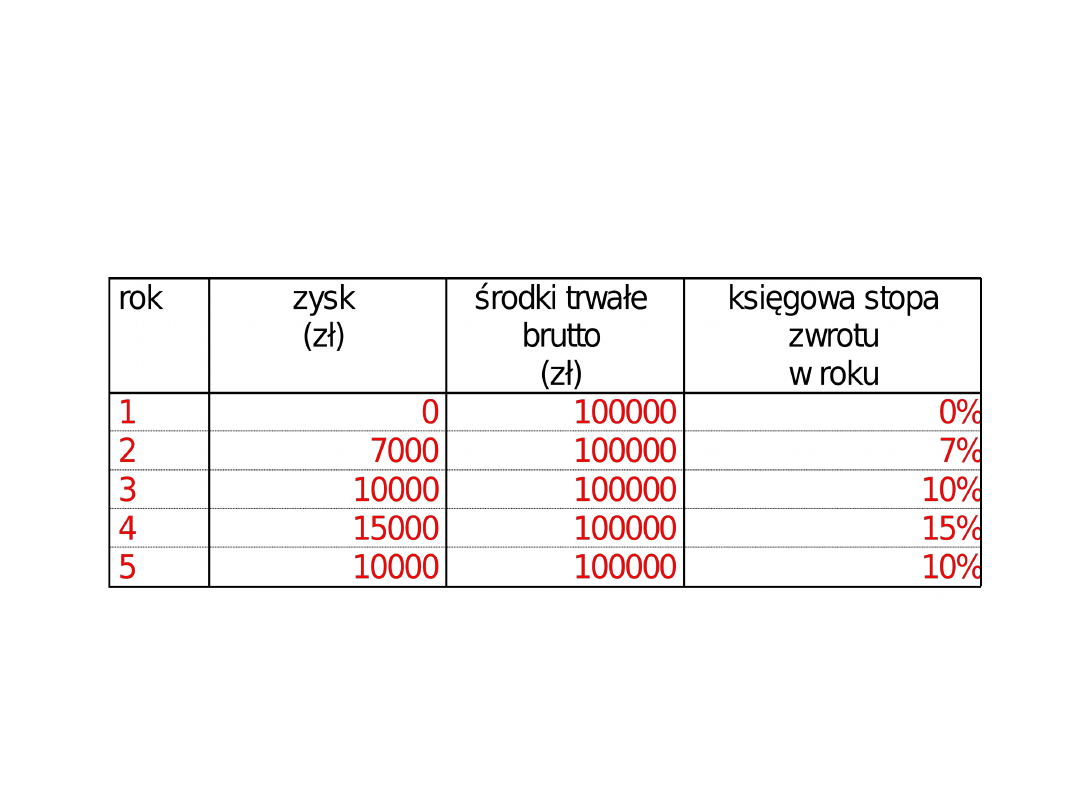
KSIĘGOWA STOPA ZWROTU

PRZYKŁAD 1

KSIĘGOWA STOPA ZWROTU

PRZYKŁAD 1

• konieczne jest więc obliczenie przeciętnej stopy zwrotu z

projektu na przestrzeni pięciu lat; dane pomocnicze do
wyliczeń przedstawione są niżej

KSIĘGOWA STOPA ZWROTU

WADY I ZALETY

• podstawową wadą księgowej stopy zwrotu jako metody

szacowania opłacalności inwestycji (niezależnie od sposobu
obliczania) jest to, że nie uwzględnia ona wartości
pieniądza w czasie – w rezultacie rentowność projektu
jest zwykle zawyżana,

• drugą znaczącą wadą księgowej stopy zwrotu jest to, że

opiera się na koncepcji zysku księgowego a nie
przepływach pieniężnych

OKRES ZWROTU

DEFINICJA

• okres zwrotu definiujemy jako liczbę lat, po których

wpływy wynikające z realizacji danego projektu
zrównają się z nakładami,

• dla zilustrowania tej metody przyjmijmy, że

przedsiębiorstwo ABC zamierza podjąć jeden z dwóch
projektów, w celu obliczenia okresu zwrotu poniesionych
nakładów tworzymy tabelę skumulowanych przepływów
pieniężnych netto projektu w okresie od t = 0 do t = 5

OKRES ZWROTU - PRZYKŁAD 2

OKRES ZWROTU - PRZYKŁAD 2

• ponieważ w końcu trzeciego roku inwestycji do “pokrycia” zostało

jeszcze 500 zł nakładów, a w roku czwartym nastąpił wpływ
środków pieniężnych netto w wysokości 2000 zł to pełne pokrycie
kosztów projektu drugiego będzie miało miejsce w (500 zł/2000 zł
= 1/4) jednej czwartej roku czwartego;

• stąd okres zwrotu tego projektu wynosi 3,25 roku

OKRES ZWROTU WADY I ZALETY

• im krótszy jest okres, po którym następuje zwrot

poniesionych nakładów tym projekt uważany jest za lepszy;
jeżeli firma ma problemy z płynnością lub też pragnie zaangażować
środki w inne przedsięwzięcia wówczas menedżer może wybrać
projekt pierwszy, ponieważ jego okres zwrotu jest krótszy,

• okres zwrotu projektu jest stosunkowo prostą metodą oceny

projektów inwestycyjnych i z tego powodu często bywa
wykorzystywany jako wstępna miara opłacalności inwestycji,

• projekty inwestycyjne nie powinny być jednak oceniane wyłącznie

na podstawie tego kryterium;

• należy zwrócić uwagę na to, że okres zwrotu jako kryterium

decyzyjne ma dwie zasadnicze wady – po pierwsze nie
uwzględnia wartości pieniądza w czasie, a po drugie bierze
pod uwagę tylko przepływy pieniężne do wysokości
nakładów inwestycyjnych

Wartość pieniądza w czasie

• Uwzględnienie dyskontowania
• Uwzględnienie oprocentowania

– Procent zwykły
– Procent składany

PROCENT SKŁADANY I

DYSKONTOWANIE

PROCENT SKŁADANY

• wartość przyszła 1 zł zainwestowanego na n lat na rachunku

oprocentowanym w wysokości r, po n latach wzrośnie do:

gdzie:
FVIF

r,n

- przyszła wartość jednostki kapitału ulokowanego na

procent składany (future value interest factor – FVIF)

• za pomocą powyższego wzoru można obliczyć, że zainwestowanie

1 zł na 4 lata na 8% rachunku da nam po tym okresie:





n

n

r,

r

1

FVIF







 



zl

1,3605

08

,

0

1

r

1

FVIF

4

n

n

r,











PROCENT SKŁADANY I DYSKONTOWANIE

DYSKONTOWANIE

•

fundamentalną dla budżetowania nakładów kapitałowych kwestię obliczania obecnej
wartości przyszłych strumieni pieniężnych (dyskontowanie) można wyrazić
następująco:

gdzie:

PV

- bieżąca wartość przyszłej jednostki kapitału ulokowanego na n okresów na

procent

składany,

r

- stopa procentowa,

n

- liczba okresów

•

zależność ta oznacza, że jeżeli suma zł nią wyrażona zostanie zainwestowana teraz,
to przy danym r za n lat wartość jej wzrośnie do 1 zł





n

r

1

1

PV





PROCENT SKŁADANY I DYSKONTOWANIE

WARTOŚĆ BIEŻĄCA

•

bieżącą wartość przyszłej sumy w przypadku gdy różna jest ona od zera obliczamy
następująco:

gdzie:

PVIF - obecna wartość jednostki kapitału (present value interest factor – PVIF)
PV

- wartość bieżąca,

FV

- wartość przyszła

n

n

n

r,

n

r

1

1

FV

PVIF

FV

PV























PROCENT SKŁADANY I DYSKONTOWANIE

WARTOŚĆ BIEŻĄCA

• wartość bieżąca (PV) może być zdefiniowana jako obecny

ekwiwalent kwoty gotówki, którą firma otrzyma (lub wypłaci) w
pewnym momencie w przyszłości (n) zdyskontowanej określoną
stopą zwrotu (r)

Metody uwzględniające

zmianę wartości pieniądza

w czasie

• Zdyskontowany okres zwrotu
• Wartość bieżąca netto
• Wartość końcowa netto
• Wewnętrzna stopa zwrotu

ZDYSKONTOWANY OKRES ZWROTU

DEFINICJA

• metoda ta jest podobna do klasycznej metody okresu

zwrotu za wyjątkiem tego, że przyszłe strumienie
pieniężne są dyskontowane wymaganą stopą zwrotu
(kosztem kapitału),

• zdyskontowany okres zwrotu będzie zatem definiowany jako

liczba lat, po których zdyskontowany i skumulowany
strumień gotówki netto będzie się równał zeru

ZDYSKONTOWANY OKRES ZWROTU

PRZYKŁAD 3

•

załóżmy, że koszt kapitału wynosi 10%, a przepływy pieniężne netto związane z
realizacją projektu inwestycyjnego są następujące:

projekt 1

rok

przepływy

pieniężne netto

(zł)

czynnik

dyskontujący

(10%)

zdyskontowane

przepływy

pieniężne (zł)

skumulowane

i zdyskontowane

przepływy pien. (zł)

0

(2000)

1

(2000)

(2000)

1

500

0,9091

455

(1545)

2

500

0,8264

413

(1132)

3

1000

0,7513

751

(381)

4

1000

0,6830

683

302

5

1000

0,6209

621

923

rok

projekt 1

projekt 2

0

(2000)

(2000)

1

500

1000

2

500

500

3

1000

400

4

1000

1000

5

1000

1000

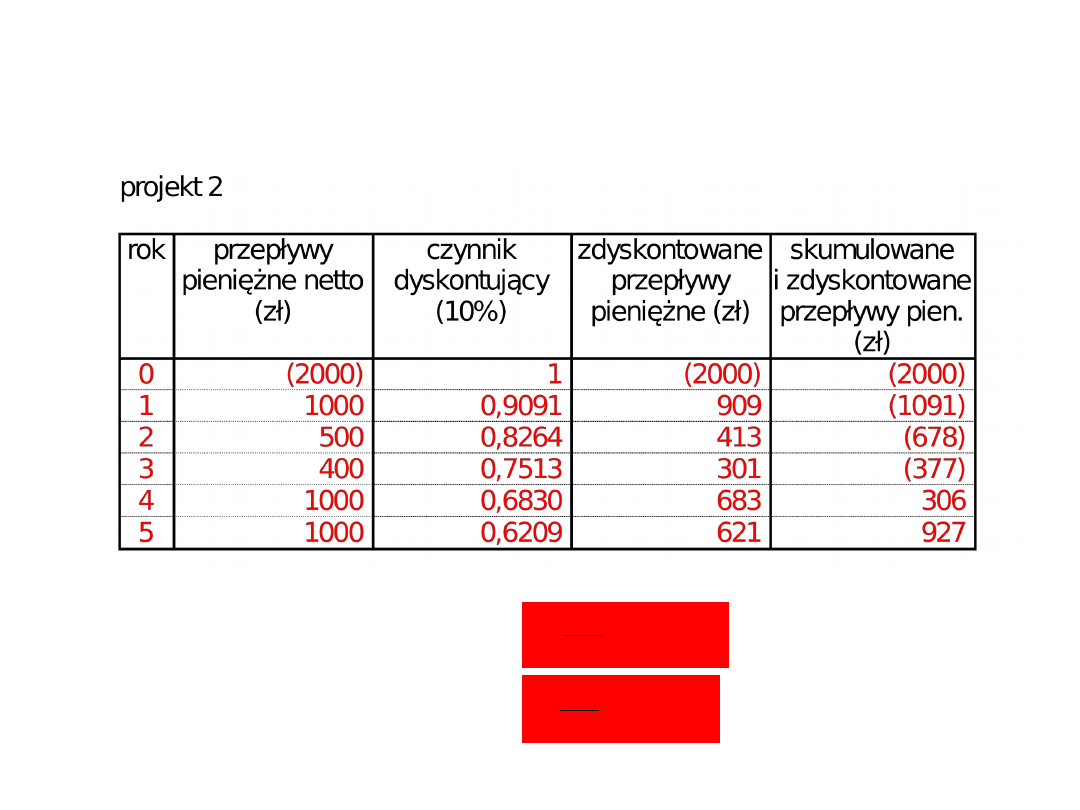
ZDYSKONTOWANY OKRES ZWROTU

PRZYKŁAD 3

•

zwrot poniesionych nakładów nastąpił więc w przypadku zarówno projektu 1 jak i 2 w

czwartym roku realizacji, dokładne wielkości są następujące

zdyskontowany okres zwrotu (1) =

zdyskontowany okres zwrotu (2) =

roku

44

,

3

683

302

4





roku

3,55

683

377

3





ZDYSKONTOWANY OKRES ZWROTU

WADY I ZALETY

• klasyczna metoda okresu zwrotu określa liczbę lat, po których

nakłady i wpływy pieniężne z inwestycji zrównają się w sensie
rachunkowym; metoda ta nie uwzględnia jednak jakże ważnej kwestii
kosztu kapitału,

• zdyskontowany okres zwrotu w przeciwieństwie do klasycznego

uwzględnia koszt kapitału,

• należy podkreślić, że okres zwrotu (zarówno zwykły jak i

zdyskontowany) dostarcza jednej istotnej informacji, a mianowicie
odpowiada na pytanie jak długo dany projekt wiąże określone
środki, im krótszy jest ten okres (przy niezmienności innych
czynników), tym projekt jest lepszy,

• uważa się także, że przepływy pieniężne odległe w czasie są

bardziej ryzykowne – okres zwrotu stosowany jest więc czasami
jako prosta miara płynności i ryzyka inwestycji (okres zwrotu nie jest
natomiast miarą rentowności projektu)

WARTOŚĆ BIEŻĄCA NETTO

DEFINICJA

• każda typowa inwestycja generuje serię przepływów pieniężnych

CF

t

, gdzie t jest rokiem wystąpienia danego przepływu; dla t=1,...n

ciąg przybiera postać CF

1

, CF

2

, CF

3

,.....CF

n

, obecna wartość tego

strumienia jest następująca:

n

n

3

3

2

2

1

r)

(1

CF

.......

r)

(1

CF

r)

(1

CF

r

1

CF

PV



















K

PV

NPV





Wartość bieżąca netto

• Wartość bieżąca wpływów z

inwestycji

• -

• Początkowe nakłady

• =

• Wartość bieżąca netto

Realizacja inwestycji

• NPV>0 realizacja inwestycji
• NPV=0 nie ma znaczenia
• NPV<0 zaniechanie

• jeżeli mamy do czynienia z dwoma

wykluczającymi się projektami, to
akceptujemy ten o wyższej wartości
bieżącej netto

WARTOŚĆ BIEŻĄCA NETTO

PRZYKŁAD 4

• załóżmy, że firma XYZ rozważa zainwestowanie 20000 zł w

urządzenia do pakowania żywności; koszt kapitału wynosi 24%, a
okres eksploatacji aktywów 4 lata, po którym to okresie będzie miała
miejsce sprzedaż – możliwa do uzyskania cena wynosi 4000 zł (cena
ta będzie równa wartości księgowej środka trwałego); należy obliczyć
opłacalność inwestycji wiedząc, że szacowane zyski są następujące:

• rozwiązanie rozpoczniemy od obliczenia rocznej amortyzacji, przy

założeniu amortyzacji liniowej, roczna rata odpisów amortyzacyjnych
wyniesie:

zl

4000

4

zl

4000

zl

20000

latach

w

a

użytkowani

okres

końcowa

wartość

koszt









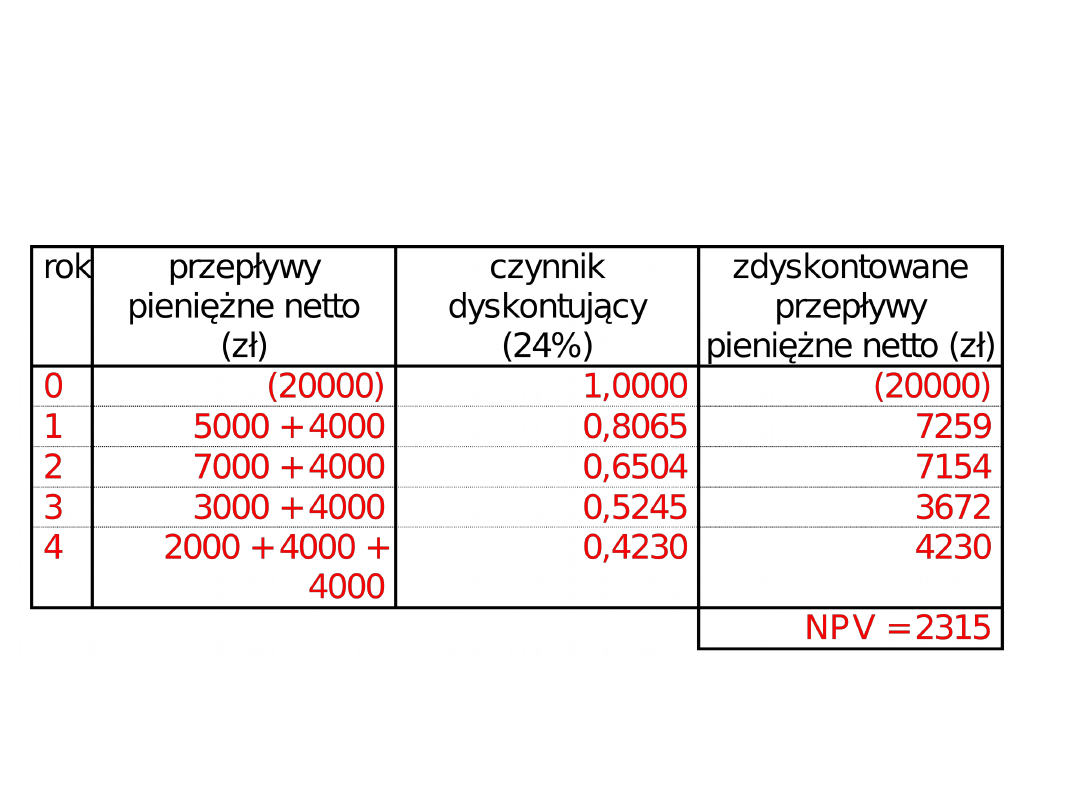
WARTOŚĆ BIEŻĄCA NETTO

PRZYKŁAD 4

Poprawność ustalenia NPV

• Poprawność ustalenia kosztu kapitału
• Prawidłowy szacunek przepływów

pieniężnych w przyszłości

• Wpływ inflacji

INDEKS ZYSKOWNOŚCI

DEFINICJA

• metoda indeksu zyskowności (rentowności) jest zmodyfikowaną

formą metody wartości bieżącej netto,

• NPV obliczaliśmy odejmując od zdyskontowanych wpływów

zdyskontowane wydatki,

• PI (profitability indeks) obliczamy dzieląc zdyskontowane

wpływy przez zdyskontowane wydatki,

• kryterium akceptacji projektu jest następujące:

– PI > 1 akceptacja,
– PI < 1 odrzucenie,
– PI = 1 nie ma znaczenia,

• przy porównywaniu projektów za lepszy uznamy ten którego

indeks rentowności jest większy

INDEKS ZYSKOWNOŚCI

PRZYKŁAD 5

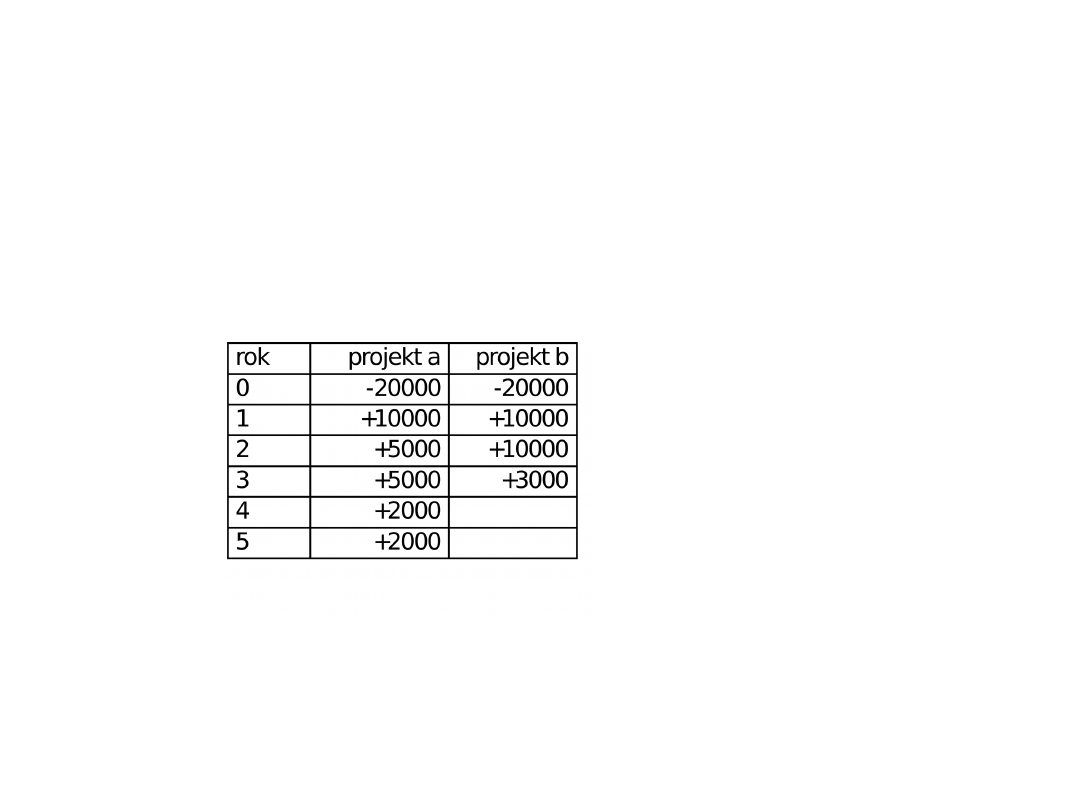
• mamy do wyboru dwa projekty inwestycyjne, których zdyskontowane

przepływy pieniężne podane są poniżej; na podstawie kryterium
indeksu rentowności należy dokonać wyboru projektu najlepszego

• PI a = (10000 zł + 5000 zł + 5000 zł + 2000 zł + 2000 zł)/20000 zł =

1,20

• PI b = (10000 zł + 10000 zł + 3000 zł)/20000 zł = 1,15

INDEKS ZYSKOWNOŚCI

CECHY

• indeks rentowności umożliwia porównywanie stóp zwrotu z

inwestycji różniących się skalą,

• wykorzystywane jest przede wszystkim do rozwiązywania

problemów związanych z racjonowaniem kapitału
(uporządkowanie projektów według malejącej wartości PI oraz
wybór na tej podstawie projektów do realizacji w warunkach
racjonowania kapitału, prowadzi do maksymalizacji NPV
realizowanych projektów),

• kryteria NPV, IRR i PI prowadzą do takich samych decyzji o

przyjęciu czy odrzuceniu pojedynczego projektu,

• w przypadku projektów wzajemnie się wykluczających mogą

jednak dawać nieco inne reguły decyzyjne

Wartość końcowa netto

• Jest ona różnicą pomiędzy przepływami

pieniężnymi po zrealizowaniu projektu

• A sumą,
• Która byłaby dostępna gdyby projekt

nie był realizowany

• Jest to nadwyżka jaka generuje projekt

WARTOŚĆ KOŃCOWA NETTO

DEFINICJA

• w pewnych warunkach, bardziej przejrzystą od NPV miarą efektywności

poniesionych nakładów inwestycyjnych może się okazać NTV - wartość
końcowa netto,

• należy jednak podkreślić, że obie miary dają taką samą odpowiedź na

pytanie o zaakceptowanie bądź odrzucenie projektu,

w metodzie wartości końcowej netto decyzje zapadają według

schematu:

• NTV > 0

akceptacja,

• NTV < 0

odrzucenie,

• NTV = 0

decyzja nie ma znaczenia

WARTOŚĆ KOŃCOWA NETTO

• załóżmy, że przedsiębiorstwo A dysponuje 12000 zł i rozważa

podjęcie następujących projektów:
(1) ulokowanie 10000 zł w aktywach trwałych, które wygenerują
strumienie pieniężne w kolejnych latach: 7700 zł, 9680 zł, 1331 zł,
po trzech latach wartość aktywów będzie się równała zero,
(2) ulokowanie całej kwoty 12000 zł na 10% rachunku bankowym,

• należy zdecydować, który z powyższych projektów jest lepszy

WARTOŚĆ KOŃCOWA NETTO

projekt 1

• po pierwsze firma wpłaci 2000 zł na 10% rachunek

bankowy, za trzy lata uzyska:

• jeżeli przedsięwzięcie zostanie podjęte to

wygeneruje w kolejnych latach odpowiednio: 7700

zł (na dwa lata), 9680 zł (na rok), 1331 zł (na

“zero” lat), które to zostaną ulokowane na 10%

rachunkach; w końcu okresu da to dodatkowo:

• razem projekt 1 po trzech latach wygeneruje

2662

zł + 21296 zł = 23958 zł

zl

2662

1,331

zl

2000





zl

21296

zl

1331

zl

10648

zl

9317

1,000

zl

1331

1,100

zl

9680

1,2100

zl

7700



















WARTOŚĆ KOŃCOWA NETTO

projekt 2
• w przypadku ulokowania całej sumy w banku firma uzyska po

trzech latach:

• zauważmy, że:

• ogólną zależność można wyrazić równaniem:

zl

15972

1,331

zl

12000

0,1)

(1

zl

12000

3











zl

7986

zl

15972

zl

23958

NTV







NTV

0,1)

(1

NPV

3

1







n

r)

NPV(1

NTV





WARTOŚĆ KOŃCOWA NETTO

• NPV jest używana częściej wówczas,

gdy np. zakładamy spłaty kredytów

zaciągniętych na inwestycje i chcemy

wiedzieć jaka jest obecna wartość

przyszłych strumieni pieniężnych,

• NTV natomiast liczymy przy

założeniu reinwestycji przepływów

pieniężnych,

• obie metody tworzą jednak takie

same reguły decyzyjne

WEWNĘTRZNA STOPA ZWROTU

DEFINICJA

• wewnętrzna stopa zwrotu jest definiowana jako taka, przy której obecna

wartość (PV) oczekiwanych przyszłych wpływów gotówkowych zrówna
się z obecną wartością oczekiwanych nakładów:
PV wpływów = PV nakładów
PV wpływów – PV nakładów = 0

• lewa strona równania jest określona wzorem na NPV, w którym niewiadomą jest r,

przyjmijmy, że r = IRR:

• wewnętrzna stopa zwrotu projektu (IRR) jest zwykle porównywana z

kosztem kapitału (k), a decyzja odnośnie inwestowania zapada według
schematu:

• IRR > k

inwestować,

• IRR < k

zaniechać inwestycji,

• IRR = k

decyzja nie ma znaczenia

0

IRR)

(1

CF

.....

IRR)

(1

CF

IRR)

(1

CF

IRR)

(1

CF

n

n

2

2

1

1

0

0



















Wewnętrzna stopa zwrotu

• Stopa zwrotu przy, której NPV danego

projektu jest równa zero

• Jeśli jest ona wyższa niż oczekiwana przez

jednostkę stopa zwrotu to należy
inwestować

• Jeśli zaś jest ona niższa wówczas należy

zaniechać inwestycji

• Jeśli obie stopy są sobie równe decyzja nie

ma znaczenia

WEWNĘTRZNA STOPA ZWROTU

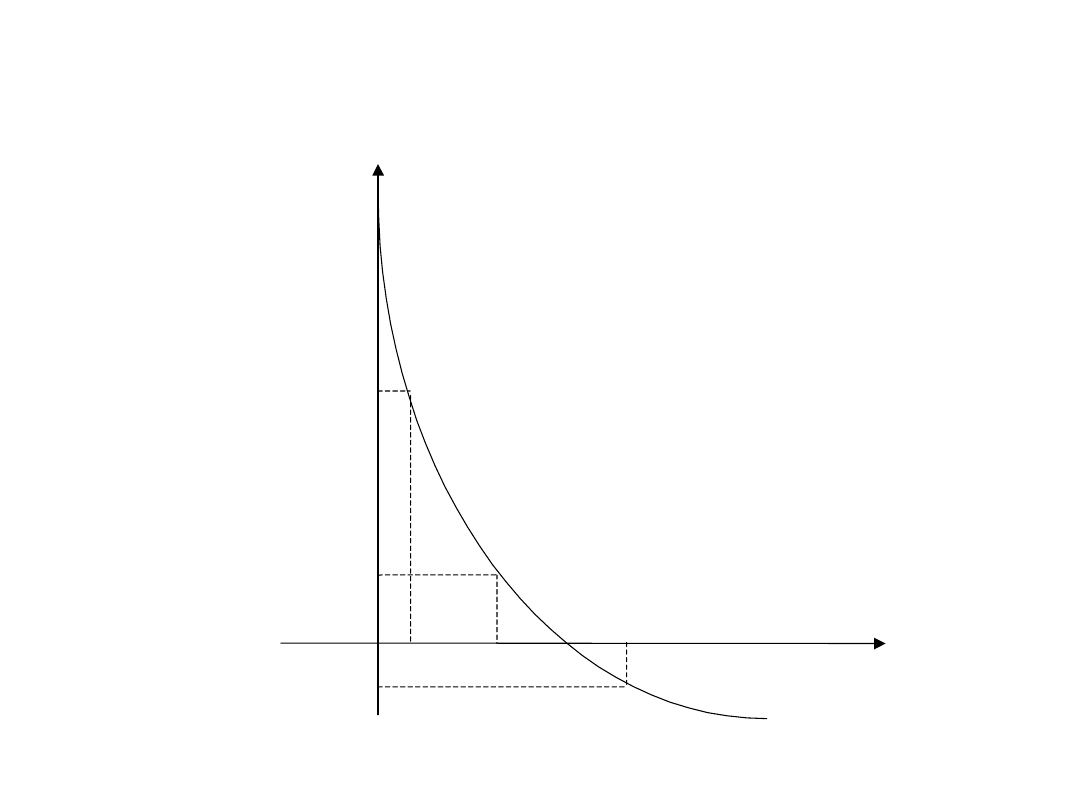
NPV W ZALEŻNOŚCI OD ZMIAN CZYNNIKA

DYSKONTUJĄCEGO

17000 zł

9616 zł

czynnik

dyskontując

y

- 1728 zł

2315 zł

10%

36%

24%

NPV

WEWNĘTRZNA STOPA ZWROTU

PRZYKŁAD 6

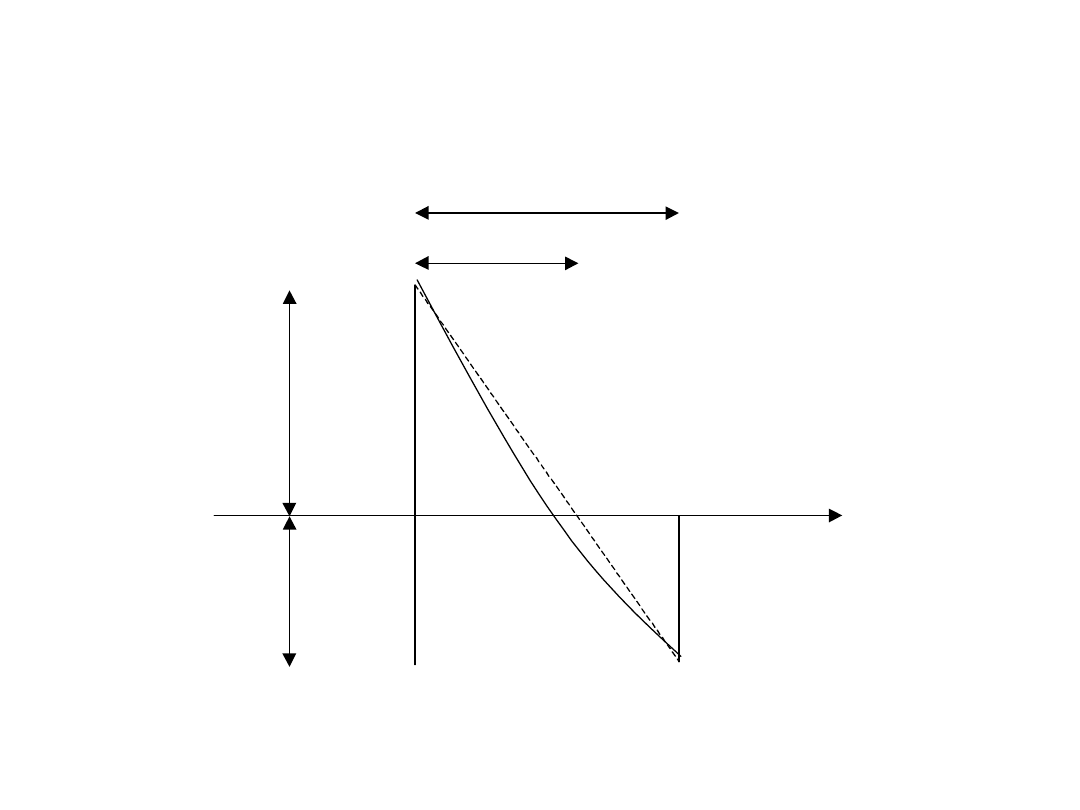
• chcąc uzyskać lepsze oszacowanie wewnętrznej stopy zwrotu,

najpierw poprzez proces prób i błędów staramy się określić dwie
wartości NPV charakteryzujące się tym, że jedna z nich jest
nieznacznie większa, a druga nieznacznie mniejsza od zera,

• następnie stosując interpolację szacujemy wartość IRR (szacujemy

r, przy którym NPV=0). Spróbujmy określić NPV dla r = 30% (NPV
= + 119i r = 32% (NPV = - 531)

WEWNĘTRZNA STOPA ZWROTU

PRZYKŁAD 6

-531

+11

9

Z

Q

I

P

czynnik

dyskontując

y

Y

X

30%

32%

3.8. WEWNĘTRZNA STOPA ZWROTU

PRZYKŁAD 6

Y

X

Q

Z







0,3662%

2%

531

119

119

Q

Y

X

Z













30,3662%

0,3662%

30%

IRR







Kryteria oceny metod

• Metoda musi uwzględniać przepływy

pieniężne w ciągu całego czasu
trwania projektu

• Metoda musi uwzględniać zmianę

wartości pieniądza w czasie

• Przy wykluczających się wzajemnie

projektach musi wybierać ten który
maksymalizuje wartość
przedsiębiorstwa

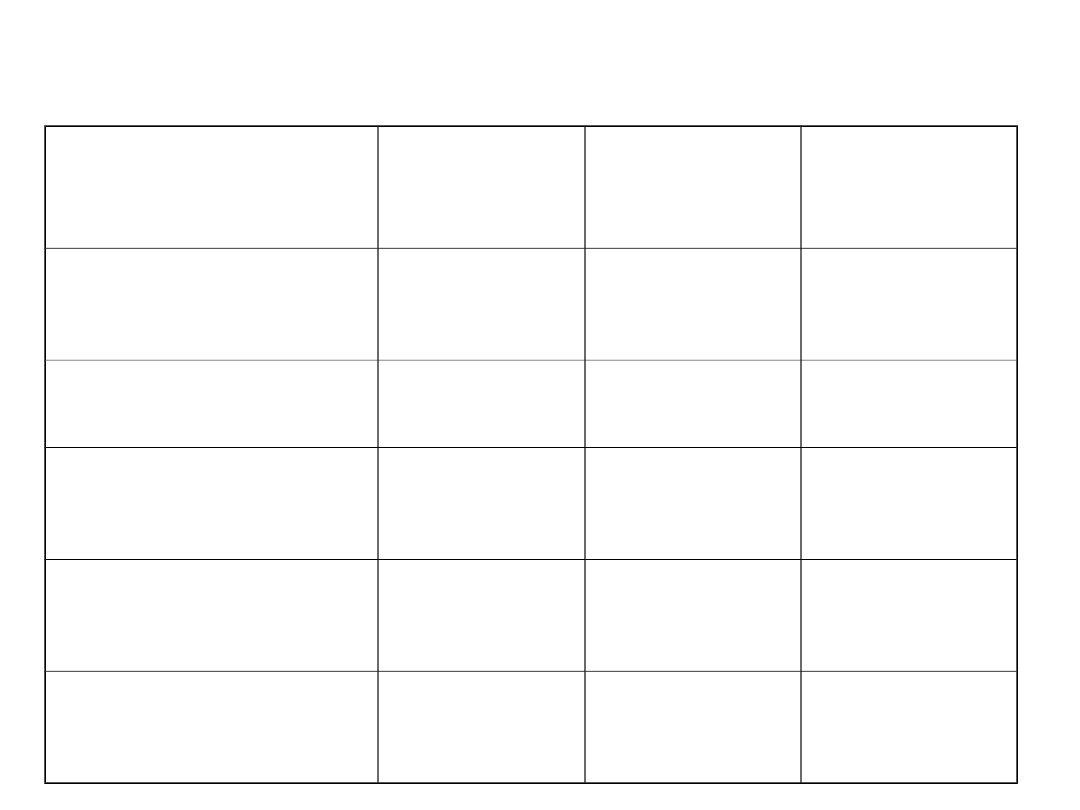
Porównanie metod

Metoda\
Kryterium

Kryteriu

m 1

Kryteriu

m 2

Kryteriu

m 3

Księgowa
stopa zwrotu

+

-

-

Okres zwrotu

-

-

-

Zdyskontowan

y okres zwrotu

-

+

-

Wartość
bieżąca netto

+

+

+

Wewnętrzna

stopa zwrotu

+

+

-