Spektroskopia molekularna

Wykład 7

Spektroskopia

oscylacyjna w

podczerwieni- widma

IR

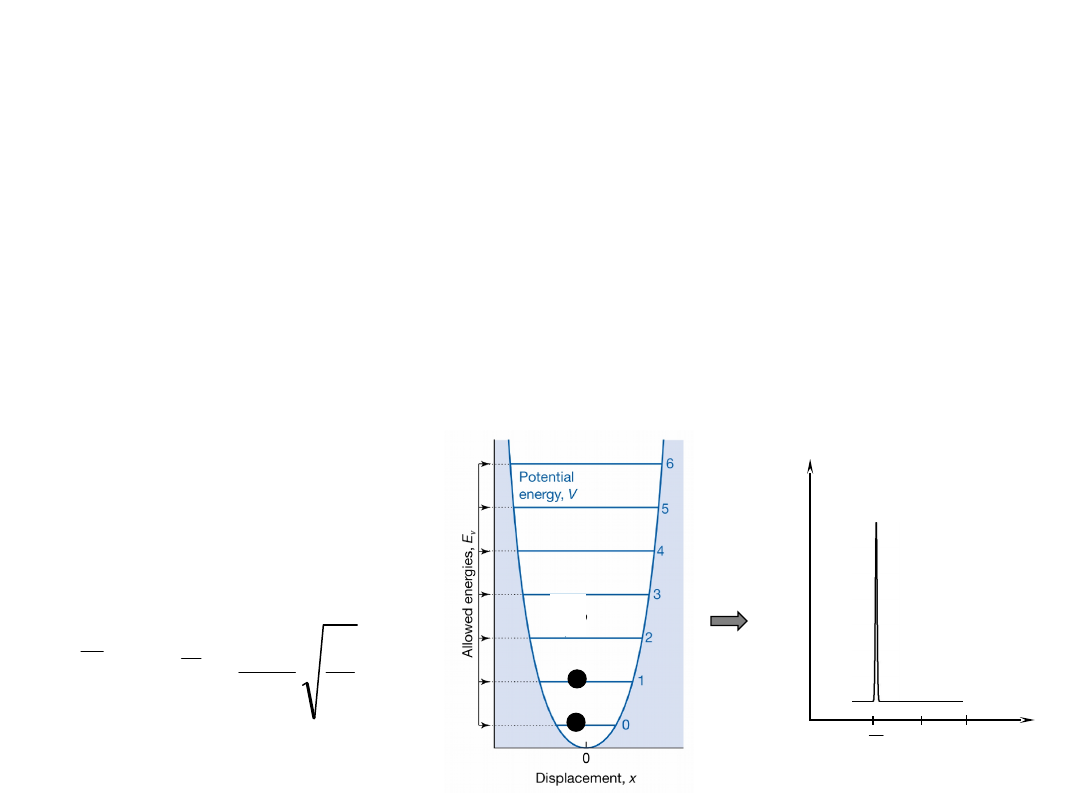
Widmo IR jest
zdominowane
przez przejścia z
podstawowego poziomu
oscylacyjnego na
pierwszy
poziom wzbudzony.

Zgodnie z regułą wyboru dla oscylatora harmonicznego:

1

v 





)

0

1

( 

Zgodnie z rozkładem Boltzmanna w temperaturze pokojowej
(kT=207 cm

-1

) większość cząsteczek przebywa na

podstawowym poziomie oscylacyjnym (v=0).

wavenumber (cm

-1

)

A

b

so

rb

e

d

In

te

n

si

ty









k

c

E

2

1

0

1









Widmo IR oscylatora harmonicznego

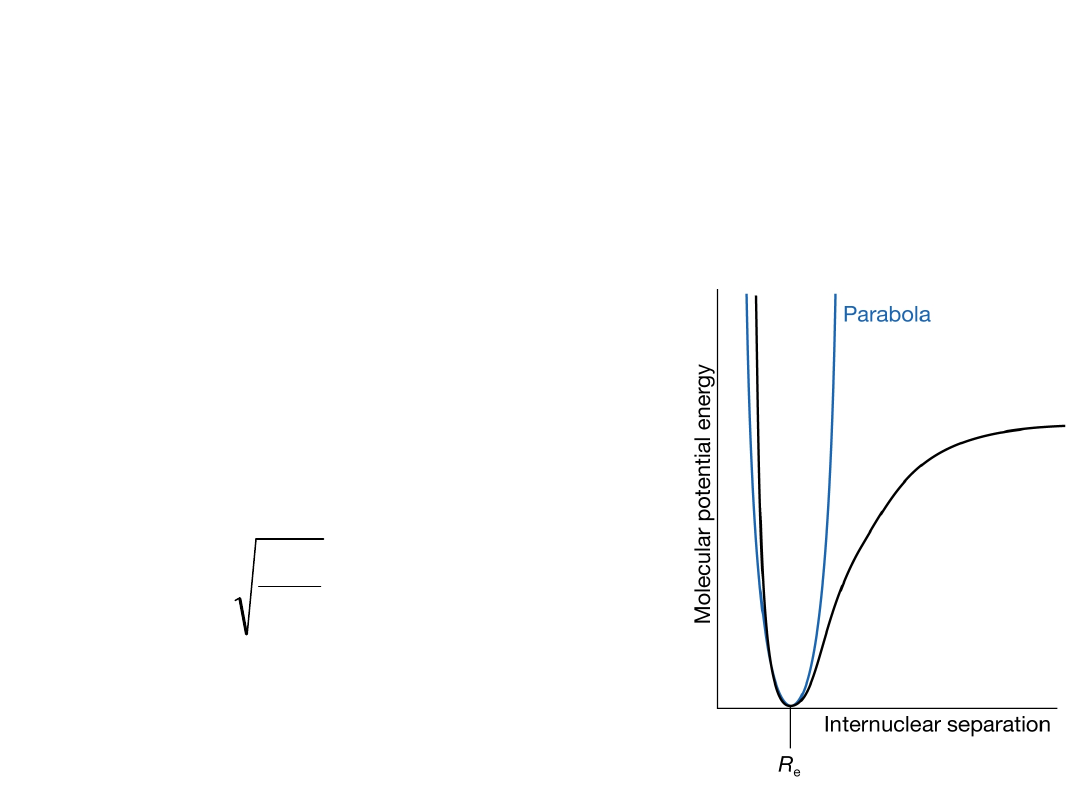
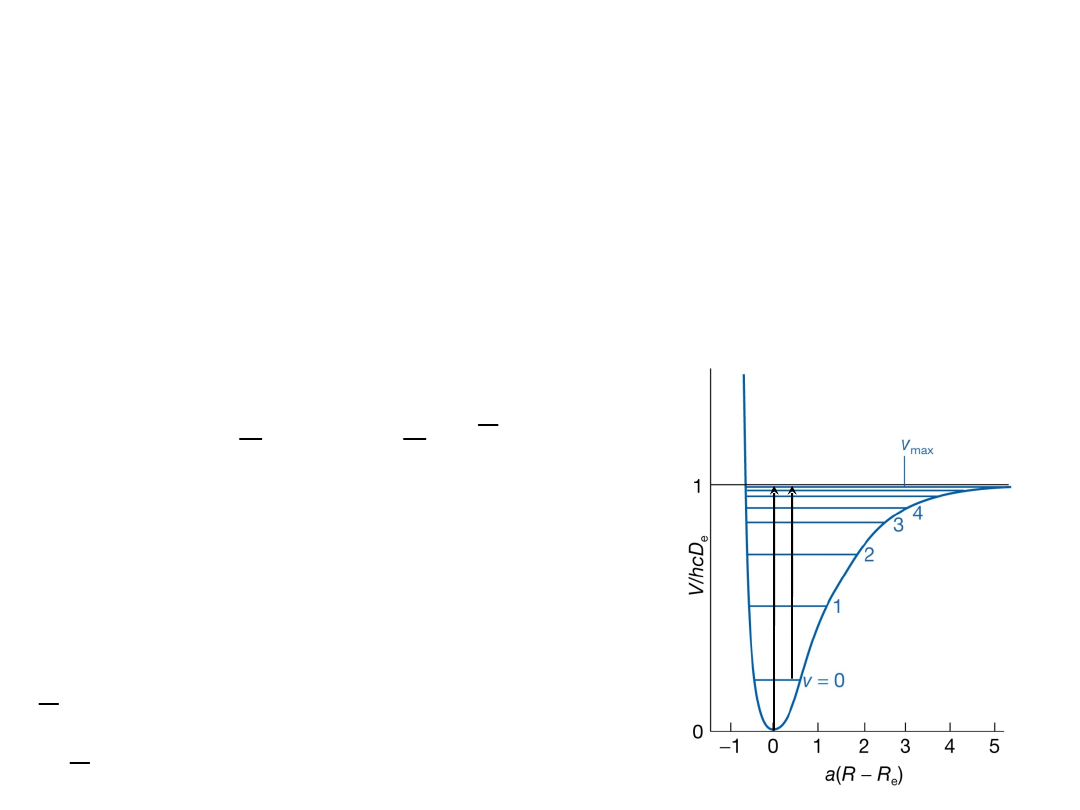
Dla większych wychyleń
międzyatomowy potencjał V jest
lepiej opisany potencjałem
Morse’a (anharmoniczność):

Oscylator

an

harmoniczny

Oscylator harmoniczny jest dobry przybliżeniem
tylko dla małych odchyleń z położenia równowagi
(drgania o małej amplitudzie).





e

e

R

R

a

e

D

a

e

D

R

V

e

2

2

1

)

(

2

)

(

















D

e

– głębokość krzywej

a – szerokość krzywej

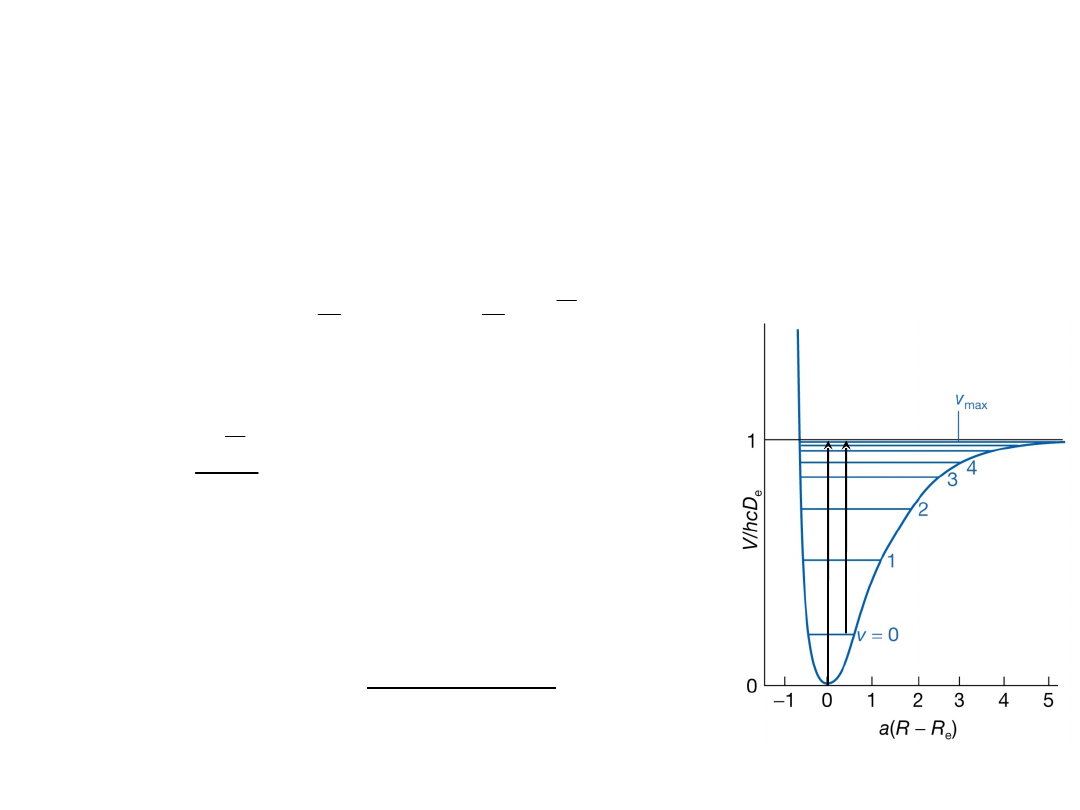
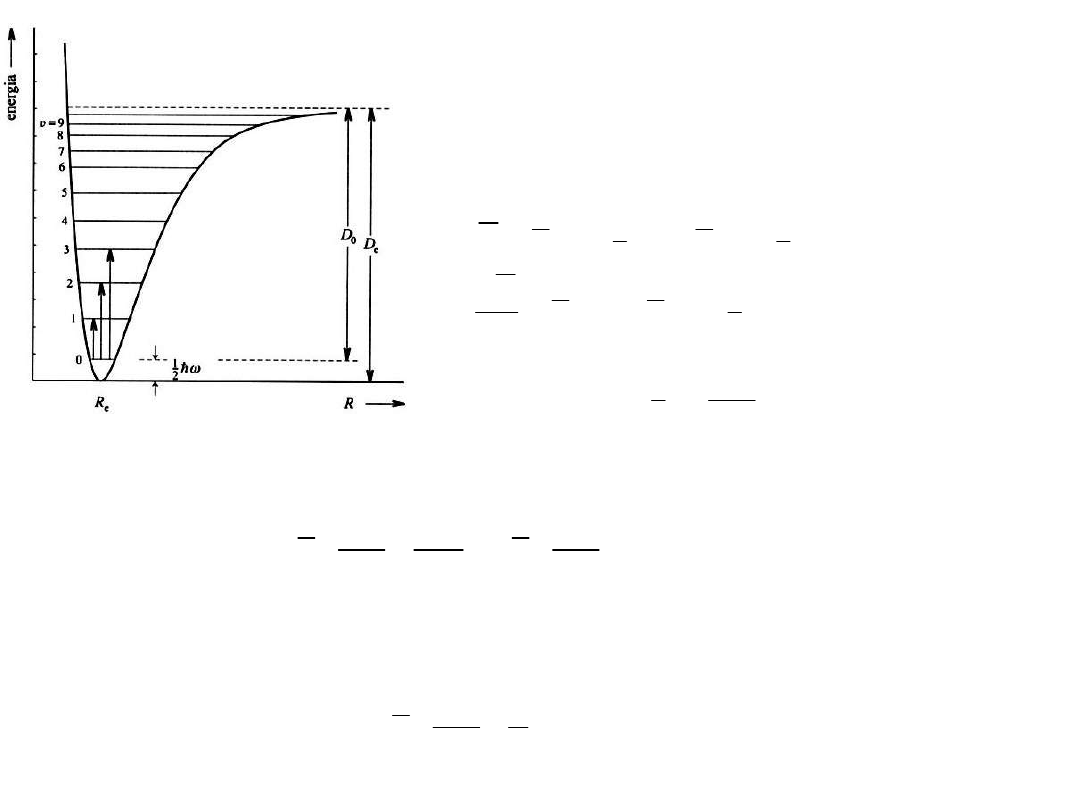
Poziomy energii nie są już równo
odległe. Ponadto liczba poziomów
oscylacyjnych jest skończona: dla
energii większych niż E

v

max

następuje

dysocjacja wiązania.

Oscylator

an

harmoniczny

e

e

e

e

e

D

x

x

hc

E

4

v

,...,

2

,

1

,

0

v

)

2

1

v

(

)

2

1

v

(

max

2

v



























Kiedy potencjał oscylacji jest opisany krzywą Morse’a
dozwolone poziomy energii oscylacyjnej dane są
wzorem:

D

e

D

o

Oscylator

an

harmoniczny

Zadanie:

Cząsteczka

1

H

35

Cl jest opisana potencjałem Morse’a.

Przyjmując, że energia wiązania D

e

nie zmienia się

po deuterowaniu obliczyć energię dysocjacji D

0

dla

1

H

35

Cl i

2

H

35

Cl.

J

10

602177

.

1

eV

1

s

m

10

9979

.

2

s

J

10

62608

.

6

19

1

8

1

34





















c

h

1

1

cm

05

.

52

cm

7

.

2989

eV

33

.

5











e

e

e

e

x

D





D

e

D

o

0

0

2

v

)

2

1

v

(

)

2

1

v

(

E

D

D

x

hc

E

e

e

e























Dane:

Oscylator

an

harmoniczny

Zadanie:
Rozwiązanie

eV

15

.

5

J

10

2452

.

8

J

10

5396

.

8

eV

33

.

5

J

10

9436

.

2

4

1

2

1

01741

.

0

05

.

52

19

0

0

19

20

0































 













E

D

D

D

x

hc

E

x

e

e

e

e

e

e









1

2

1

cm

3

.

2144

2

1

2

2

1

cm

7

.

2989

2

1

1

2

2

1

1

1

1





















HCl

HCl

HCl

HCl

HCl

HCl

HCl

HCl

HCl

k

c

c

k

k

c

























eV

20

.

5

J

10

3284

.

8

J

10

1111

.

2

4

1

2

1

19

0

0

20

0

2

























 







E

D

D

x

hc

E

e

HCl

e



stała anharmoniczności obu
cząsteczek

energia drgań zerowych

1

H

35

Cl

energia wiązania obu cząsteczek

energia dysocjacji

1

H

35

Cl

częstość drgań

1

H

35

Cl

stała siłowa obu cząsteczek

częstość drgań

2

H

35

Cl

energia drgań zerowych

2

H

35

Cl

energia dysocjacji

2

H

35

Cl

Wniosek:

Energia dysocjacji D

0

jest różna

dla cząsteczek zawierających
różne izotopy.
Natomiast przyjmujemy, że
energia wiązania D

e

jest taka

sama dla obu cząsteczek

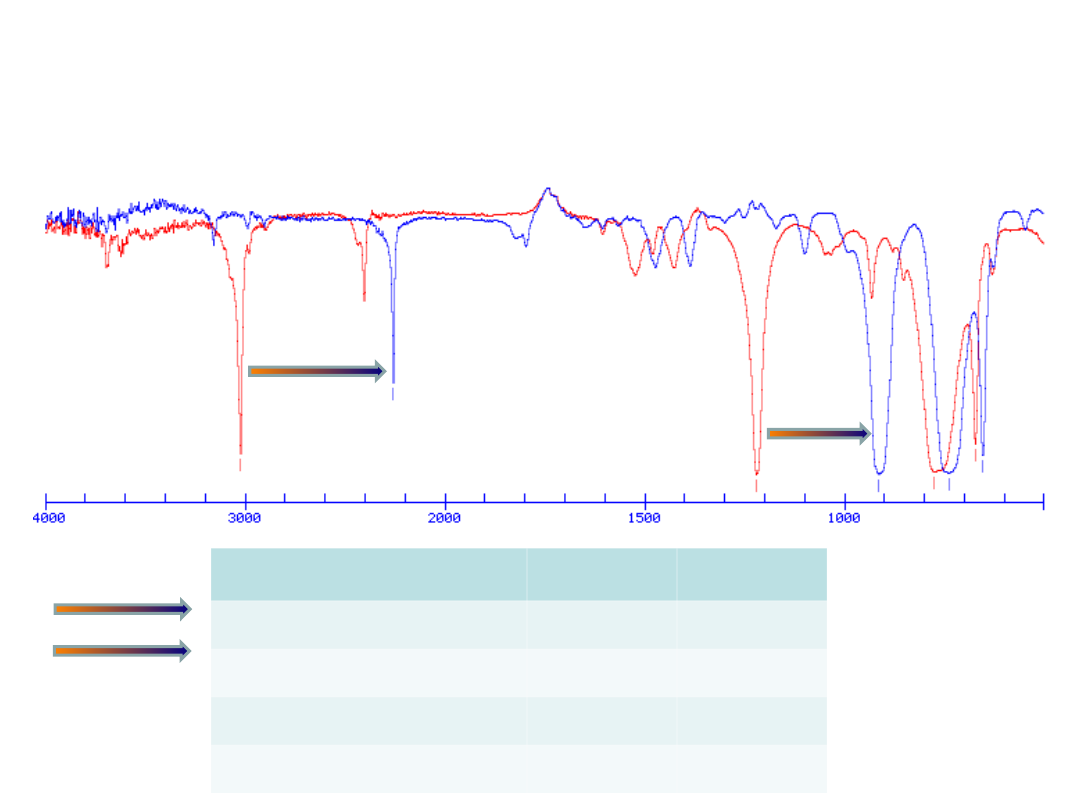
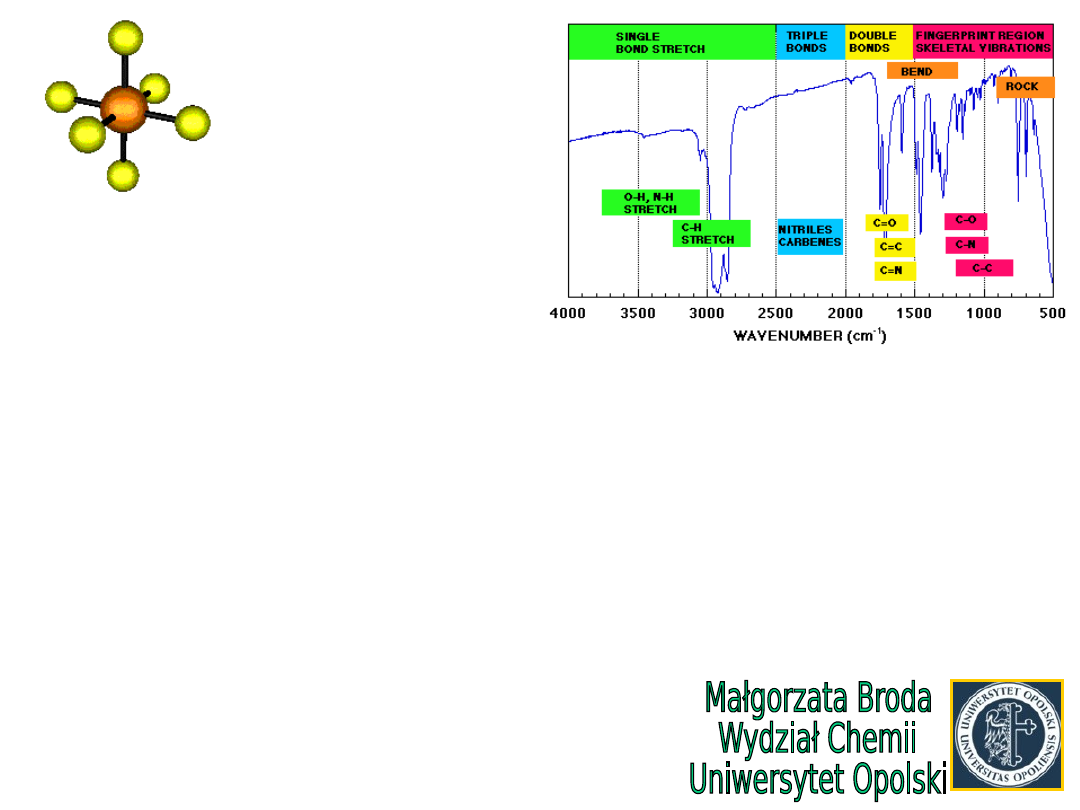
Widma IR

chloroformu

i

deuterochloroformu

Przesunięcie pasma
na
skutek zastąpienia H
atomem D (2x masa)

Rodzaj drgania

CHCl

3

CDCl

3

C-H rozciągające

3020

2256

C-H zginające

1219

912

C-Cl rozciągające

773

737

C-Cl zginające

671

652

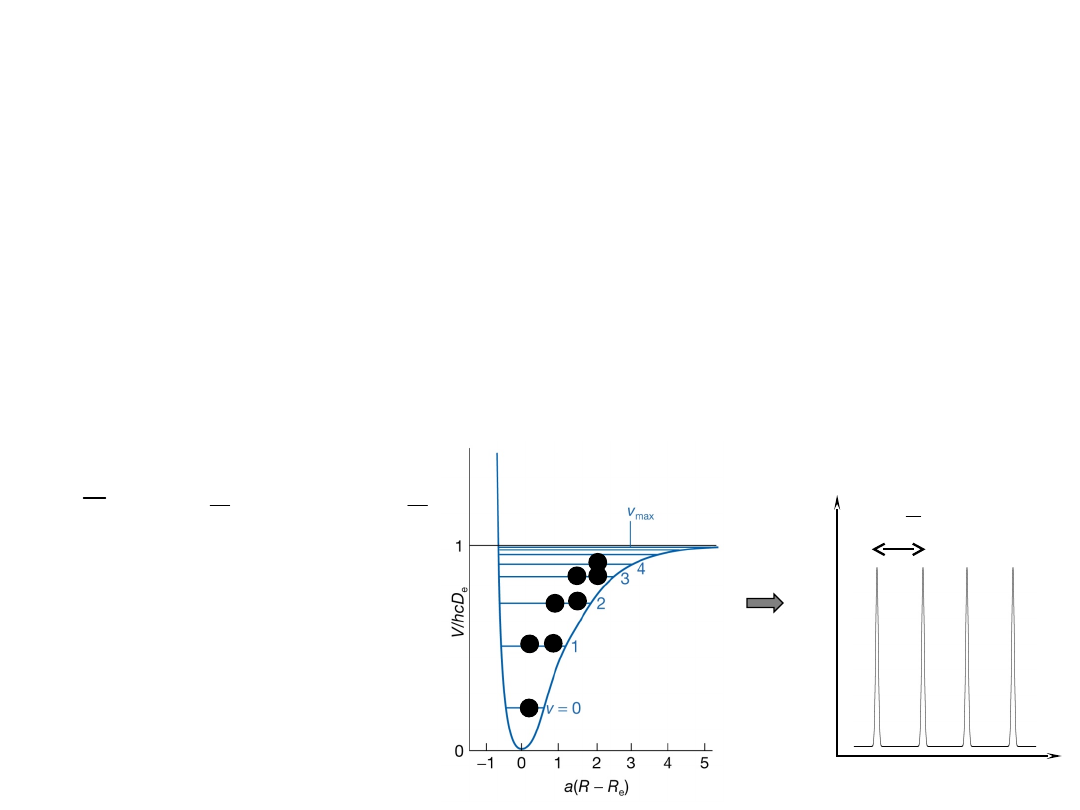
Widmo IR oscylatora

an

harmonicznego

- pasma gorące

Jeżeli cząsteczka znajduje się na wzbudzonych
poziomach oscylacyjnych, mogą być zaobserwowane
sygnały emisyjne pochodzące od przejść innych niż
1←0. W przybliżeniu harmonicznym sygnały powinny
pojawiać się przy tej samej częstości. W
rzeczywistości, obserwujemy je w nieco
innych pozycjach ze względu na anharmoniczność
drgań.

e

e

e

x

E





)

1

v

(

2

v

1

v













wavenumb
er

E

m

it

te

d

I

n

te

n

si

ty

e

e

x



2

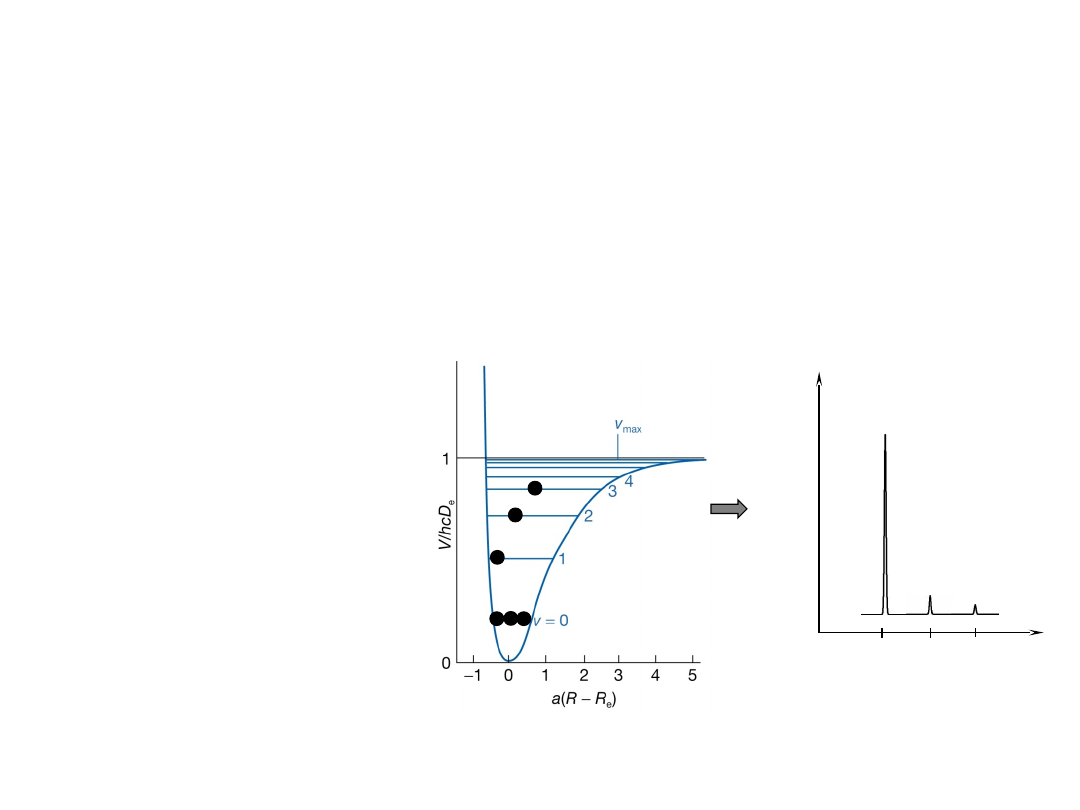
Eksperymentalnym
potwierdzeniem jest
obecność słabych
nadtonów w widmie
absorpcyjnym,
odpowiadającym
przejściom

2←0

,

3←0

, …itd.

Widmo IR oscylatora

an

harmonicznego

- nadtony

Reguła wyboru wynika z przybliżenia
harmonicznego.
Gdy weźmiemy pod uwagę anharmoniczność reguła
wyboru

nie jest ściśle zachowana i wszystkie

wartości  są dozwolone.

1

v 





wavenumber (cm

-1

)

A

b

so

rb

e

d

In

te

n

si

ty



~

1

v 





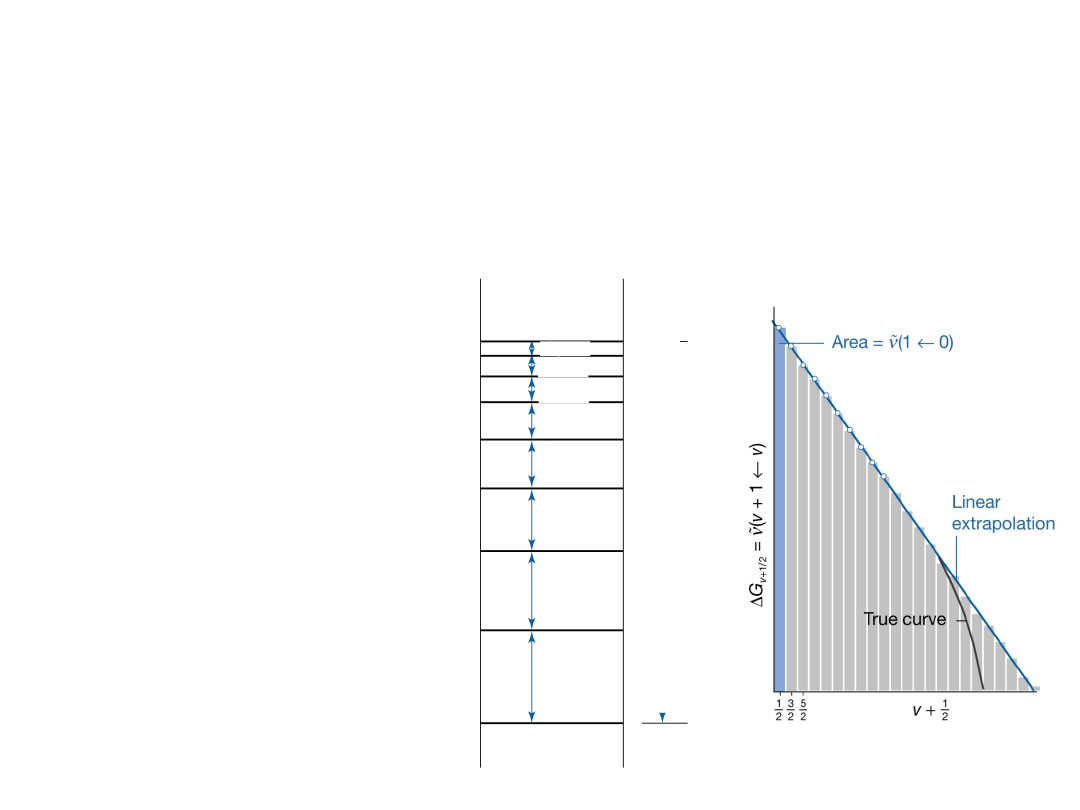
Z widma IR można wyznaczyć

energię dysocjacji D

0

Dlatego, jeżeli kilka
przejść oscylacyjnych
jest znanych energia
dysocjacji może być
oszacowana na
podstawie np. tzw.
diagramów Birge-
Sponera.

Suma energii wszystkich przejść oscylacyjnych
dwuatomowej cząsteczki odpowiada energii dysocjacji
D

0

:

)

v

(

)

1

v

(

...

1/2

v

v

1/2

v

2

/

3

2

/

1

G

G

G

G

G

G

D

o































G

1/2

G

3/2

G

5/2

G

7/2

G

9/2

G

11/2

G

13/2

G

15/2

D

0





G

3

/2



G

3

/2



G

5

/2



G

7

/2



G

9

/2



G

1

1

/2



G

1

3

/2





G

1

5

/2

Z widma IR można wyznaczyć

energię dysocjacji D

0

W miarę wzrostu liczby kwantowej v, różnice
pomiędzy poziomami oscylacyjnymi dążą do
zera.

0

)

v

(

2

v

)

v

(

)

v

(

2

1

2

2

1

2

1

















e

e

e

e

e

e

x

d

E

d

x

E









Stąd:

e

x

2

1

)

v

(

2

1

max





Odpowiadająca liczbie kwantowej v

max

energia to energia wiązania

D

e

:































e

e

e

e

e

e

e

x

x

x

x

D

4

1

4

2

1

2





A energia dysocjacji D

0

wynosi:





















2

1

4

1

0

0

e

e

e

x

E

D

D



Z widma IR można wyznaczyć

energię dysocjacji D

0

x

e



e

[cm

-1

]

k

[N m

-1

]

D

o

[

kJ mol

-1

]

D

o

[kJ mol

-1

]

HI

0,017

2

2308

312

388

295

HBr

0,017

1

2649

409

448

363

HCl

0,017

4

2991

513

497

428

HF

0,021

8

4138

960

543

564

NO

0,007

3

1904

1597

769

630

CO

0,006

1

2170

1905

1052

1072

Obliczone z x

e

i



e

Bardziej dokładne wartości uzyskane z
widm UV

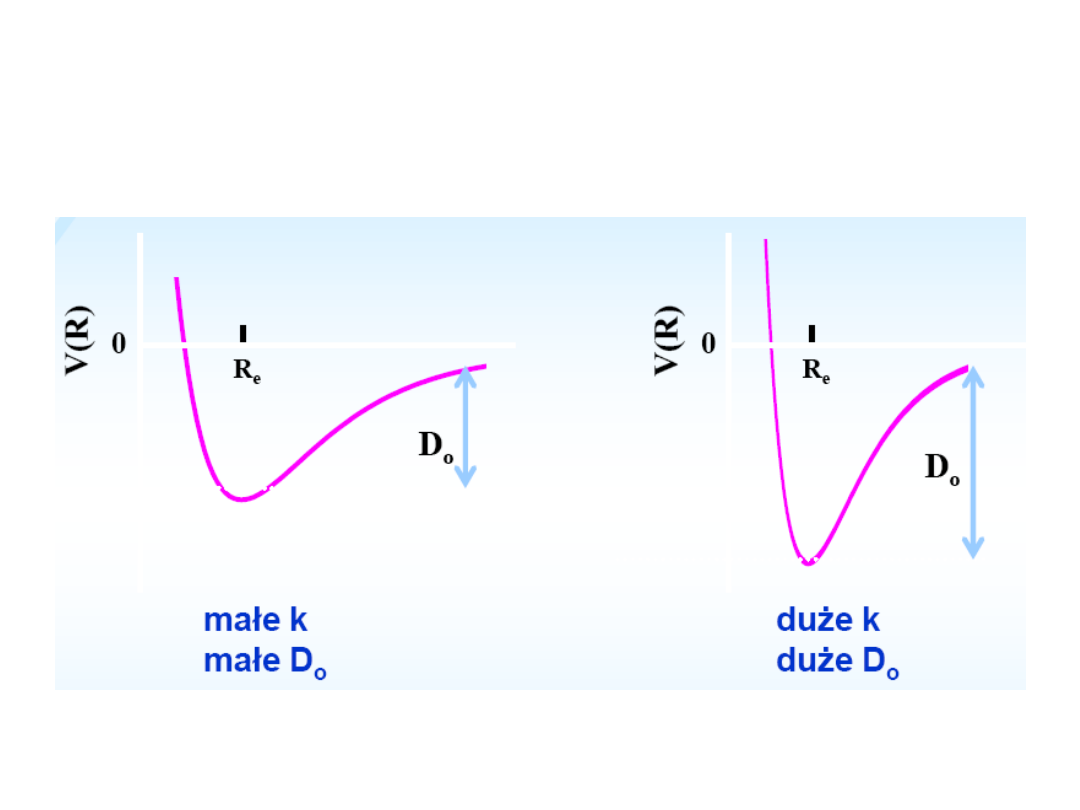
Zależność pomiędzy k i

energią dysocjacji D

0

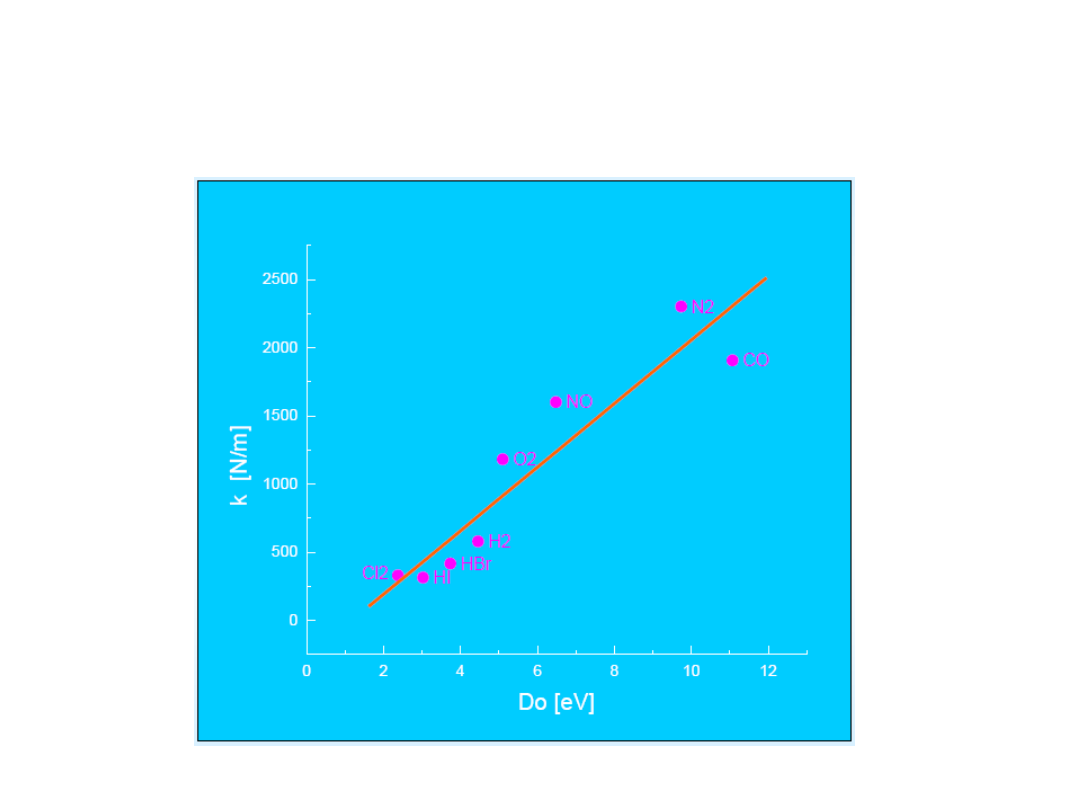
Zależność pomiędzy k i

energią dysocjacji D

0

Zależność pomiędzy stałą siłową (k) i mocą wiązania (Do) jest w
przybliżeniu liniowa

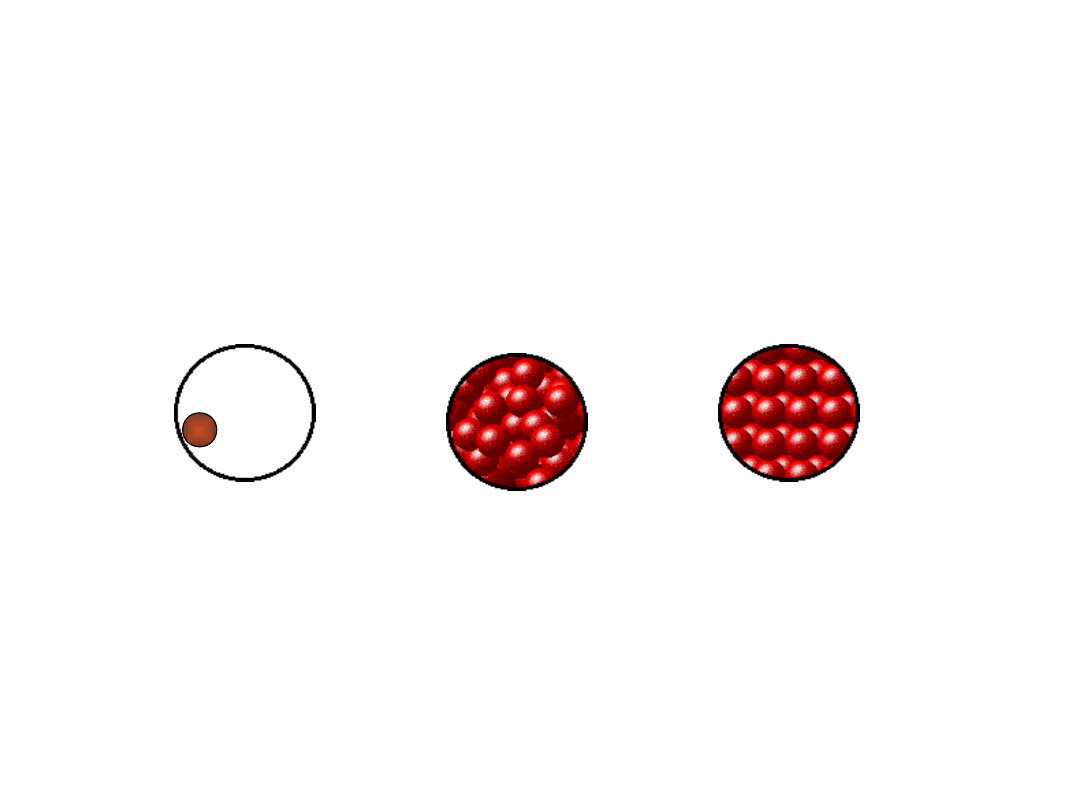
Spektroskopia w fazie

skondensowanej

Cząsteczki w fazie skondensowanej (ciecze/ciała stałe) są w

ciągłym kontakcie ze swoim otoczeniem co oznacza, że nie
mogą swobodnie rotować. Dlatego w wyrażeniu na energię
oscylacyjno-rotacyjną pomijamy składnik rotacyjny

.

Pomimo zahamowanej rotacji w fazach skondensowanych widma

oscylacyjne pokazują strukturę oscylacyjną. Otoczenie może
tylko zakłócać poziomy oscylacyjne ale nie może całkowicie
hamować oscylacji.

gaz

ciało stałe

ciecz

Spektroskopia w fazie

skondensowanej

Zanik struktury rotacyjnej w widmach oscylacyjnych i poszerzenie

pasm

można tłumaczyć na dwa sposoby:



Poszerzenie pasm wynikające z zasady nieoznaczoności –

cząsteczki próbują rotować, ale zderzenia z sąsiadami przerywa
ruch obrotowy a więc czas życia na dowolnym poziomie J’’ jest
bardzo krótki. Zgodnie z zasadą nieoznaczoności Heissenberga
odległości pomiędzy poziomami rozszerzają się

E

 / czas życia



Otoczenie zakłóca poziomy oscylacyjne – cząsteczki danego

rodzaju mają nieco różne lokalne otoczenie więc absorbują przy
nieco innych częstościach – uśrednienie w próbce
makroskopowej powoduje że pasma są poszerzone

Wniosek:

Widma IR faz skondensowanych nie wykazują struktury

rotacyjnej ale poszerzenie pasm wynikające z indywidualnych
przejść oscylacyjnych

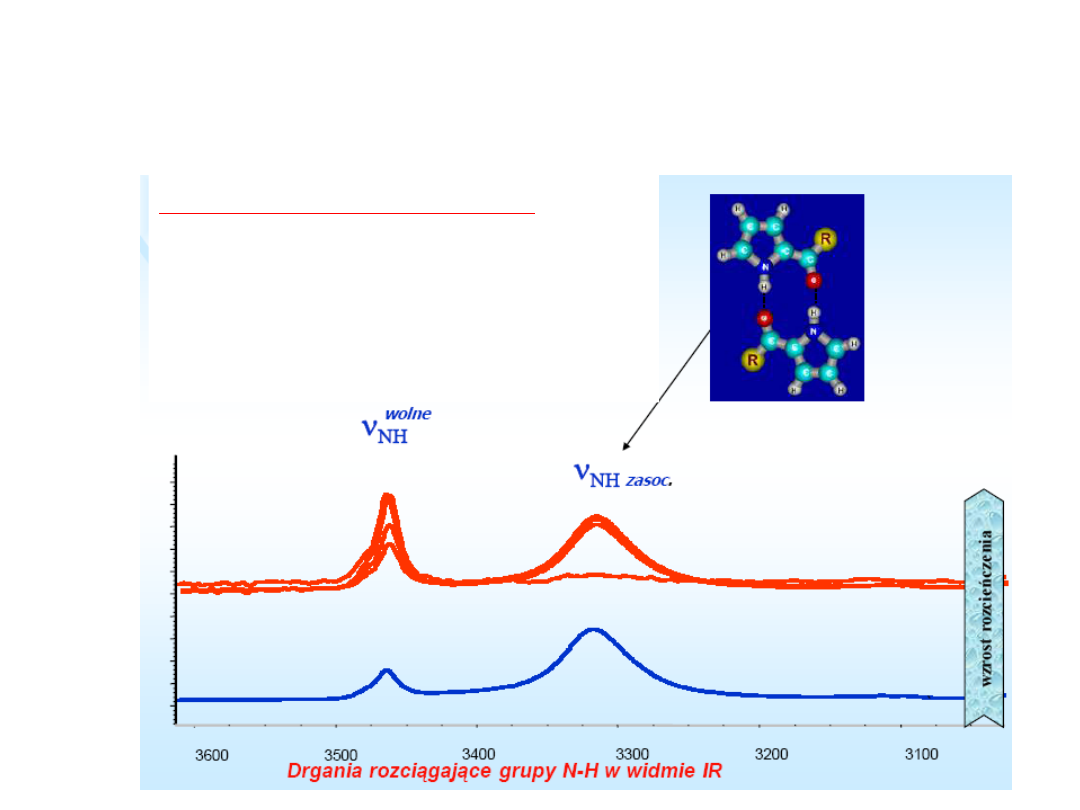
Wiązania wodorowe

międzycząsteczkowe w IR

Zmniejszanie stężenia

powoduje szybsze zmniejszanie
się pasma pochodzącego od
asocjatów (dimerów) niż pasma
pochodzącego od drgań grupy
N-H w monomerze.

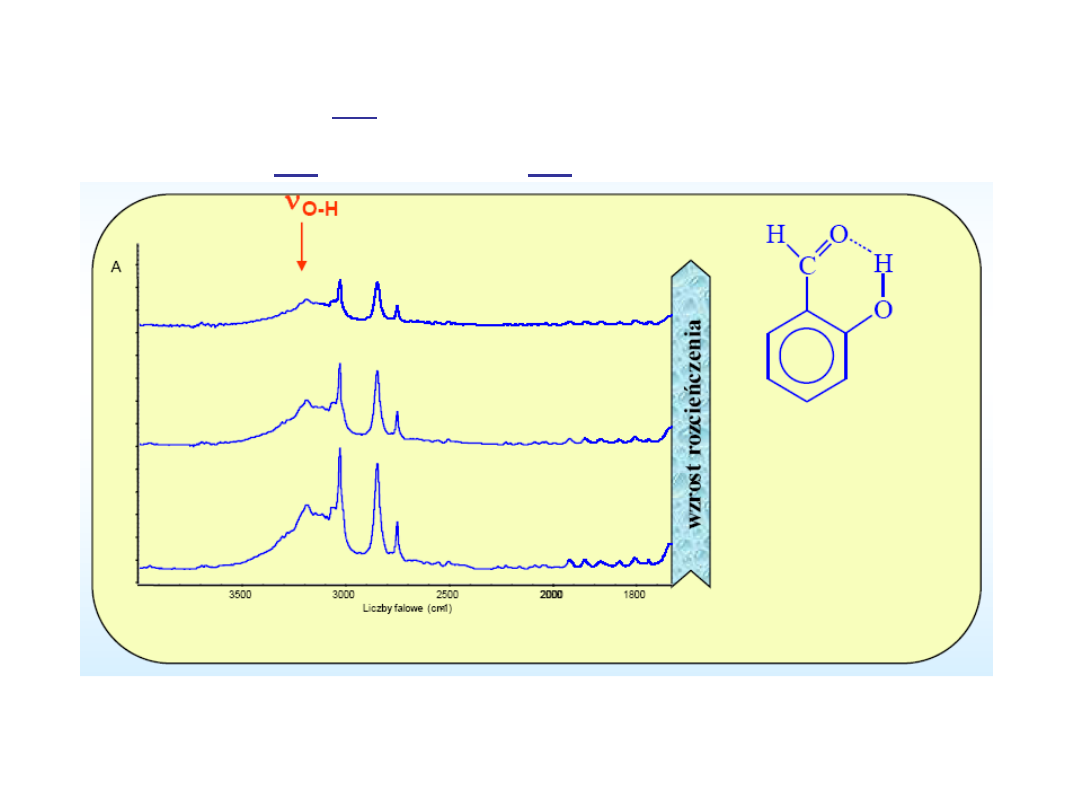
Jeżeli grupa OH tworzy wiązanie wodorowe
wewnątrz cząsteczki to pasmo 

s

(OH) nie zmienia

położenia po rozcieńczeniu

Zmiany w widmie oscylacyjnym

WWW – wewnątrzcząsteczkowe

wiązanie wodorowe

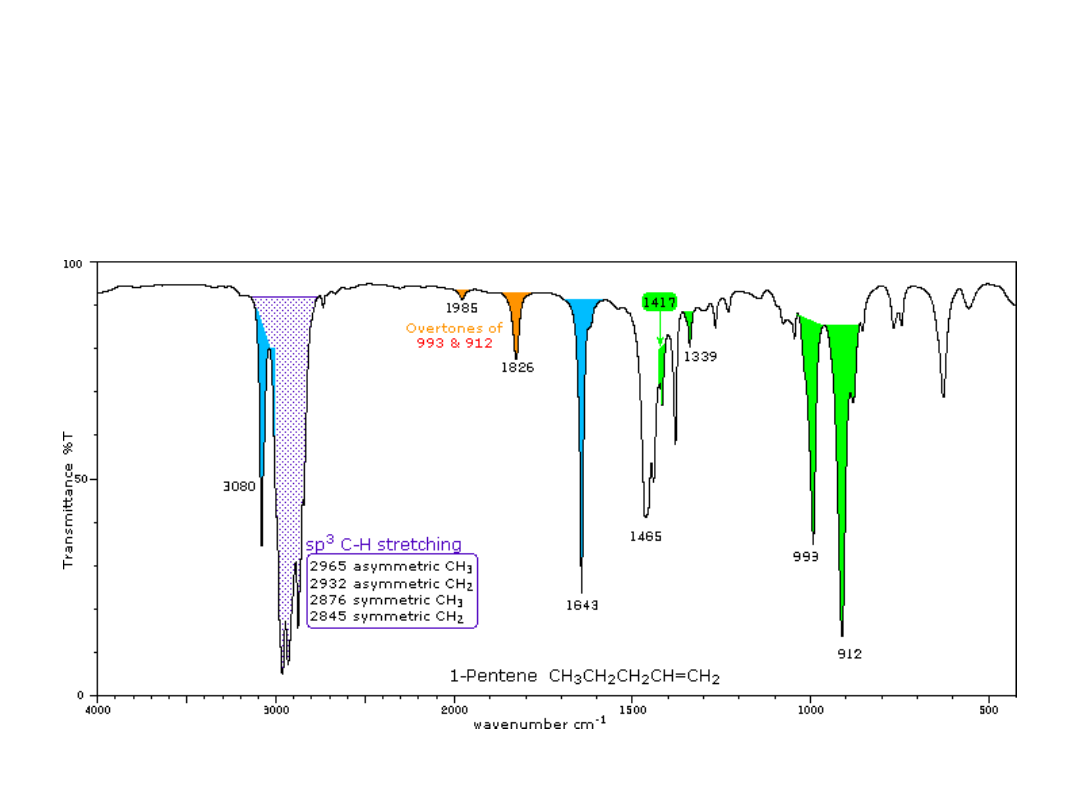
Pasma drgań rozciągających są

niebieskie

,

Pasma drgań zginających są

zielone

.

Nadtony są

pomarańczowe

.

Granica na 3000 cm

-1

pomiędzy drganiami rozciągającymi sp

2

i sp

3

C-H jest widoczna.

Widma alkenów

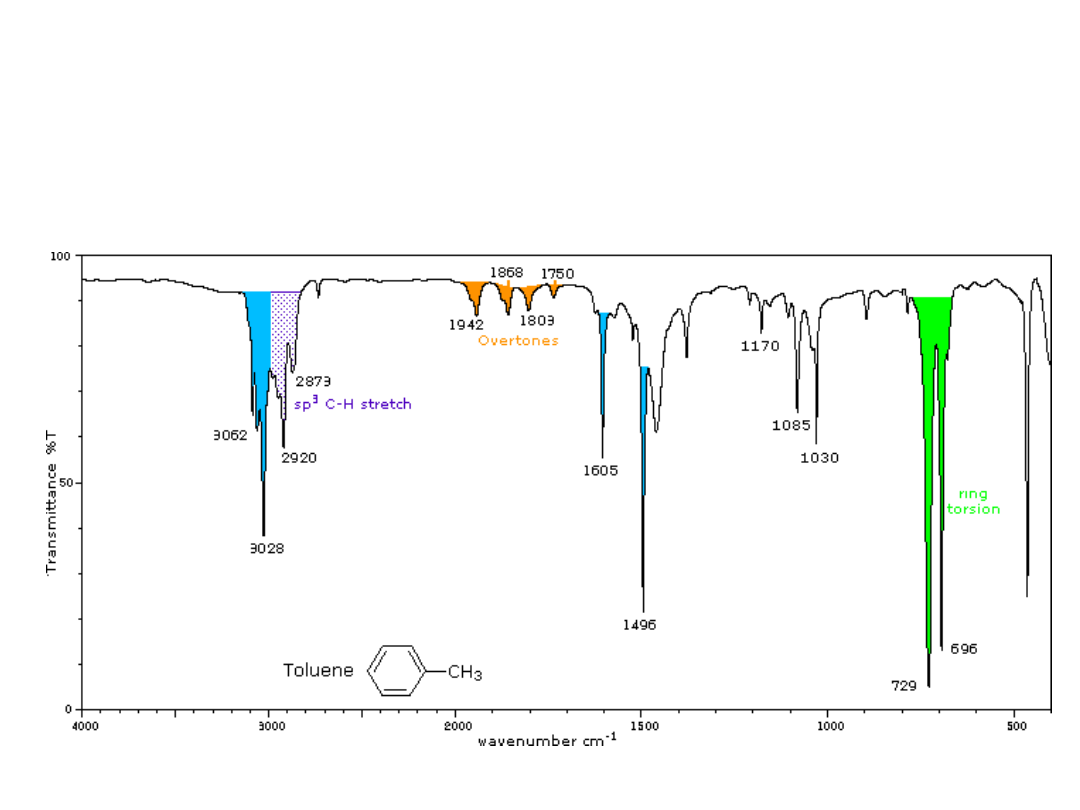
Drgania zginające C-H w płaszczyźnie (950 –1250);
Nadtony i pasma kombinacyjne (1600-2000)
Wąskie, słabe pasma– podstawiony benzen

Widma związków

aromatycznych

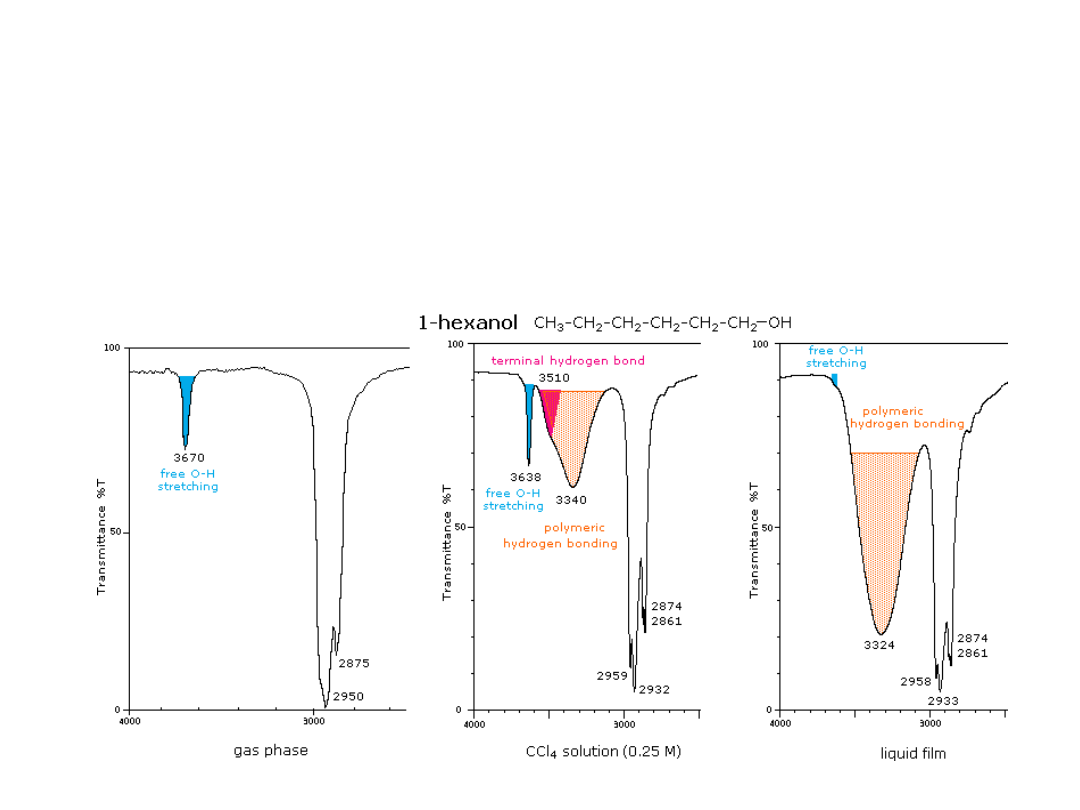
Pasma drgań O-H i N-H w zakresie 3400-3100 cm

-1

silne i szerokie (z

powodu wiązania wodorowego)
Wąskie pasmo wolnej grupy O-H występuje około 3600

cm-1 w:

- bardzo rozcieńczonych roztworach
- w widmach mierzonych w fazie gazowej

Widma alkoholi i fenoli

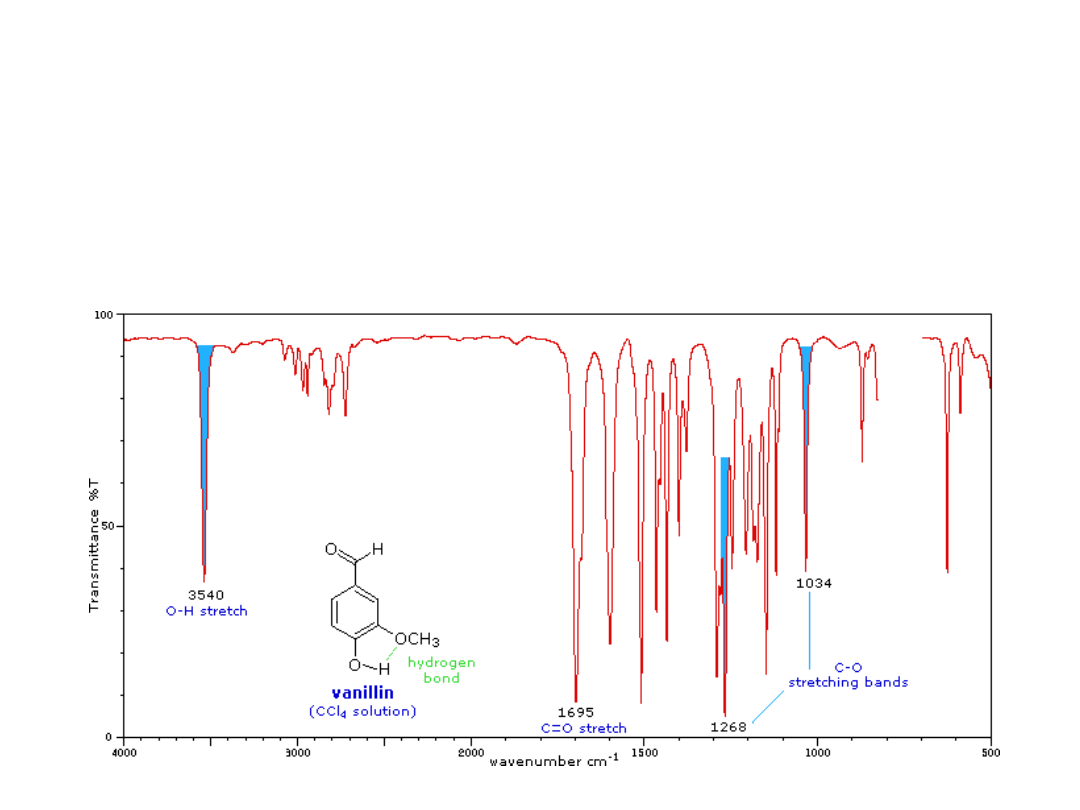
W przypadku wewnątrzcząsteczkowego wiązania
wodorowego

–

występuje pasmo grupy O-H o zwiększonej
intensywności
w zakresie od 3500 do 3600 cm

-1

.

Widma alkoholi i fenoli

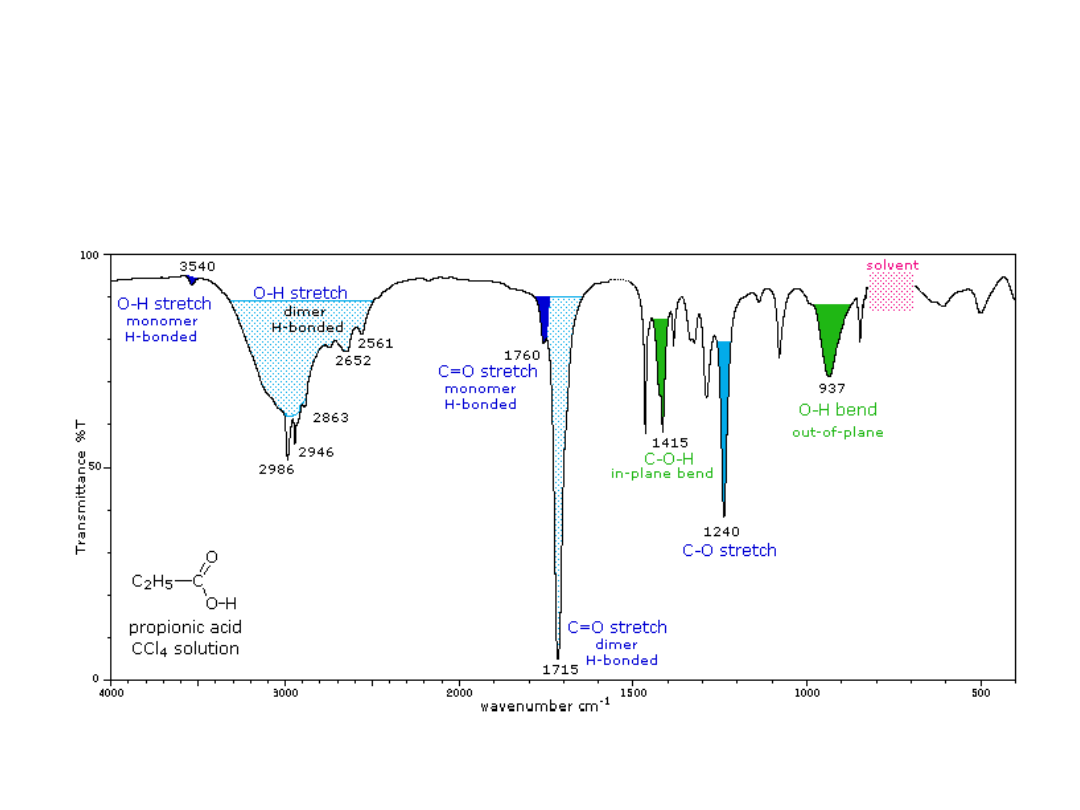
Pasmo drgania rozciągającego grupy C=O jest zwykle bardzo
intensywne z powodu dużej polarności tej grupy.

Widma kwasów karboksylowych

Korelacja pomiędzy częstością A-

H)

a innymi wielkościami opisującymi

wiązanie wodorowe



1937 Budger i Bauer

A-H) vs E

HB



1952 Rundle

A-H) vs r

A…B



1967 Ratajczak

A-H) vs r

A…B



1969 Bellamy i Pace



AH

vs r

AH

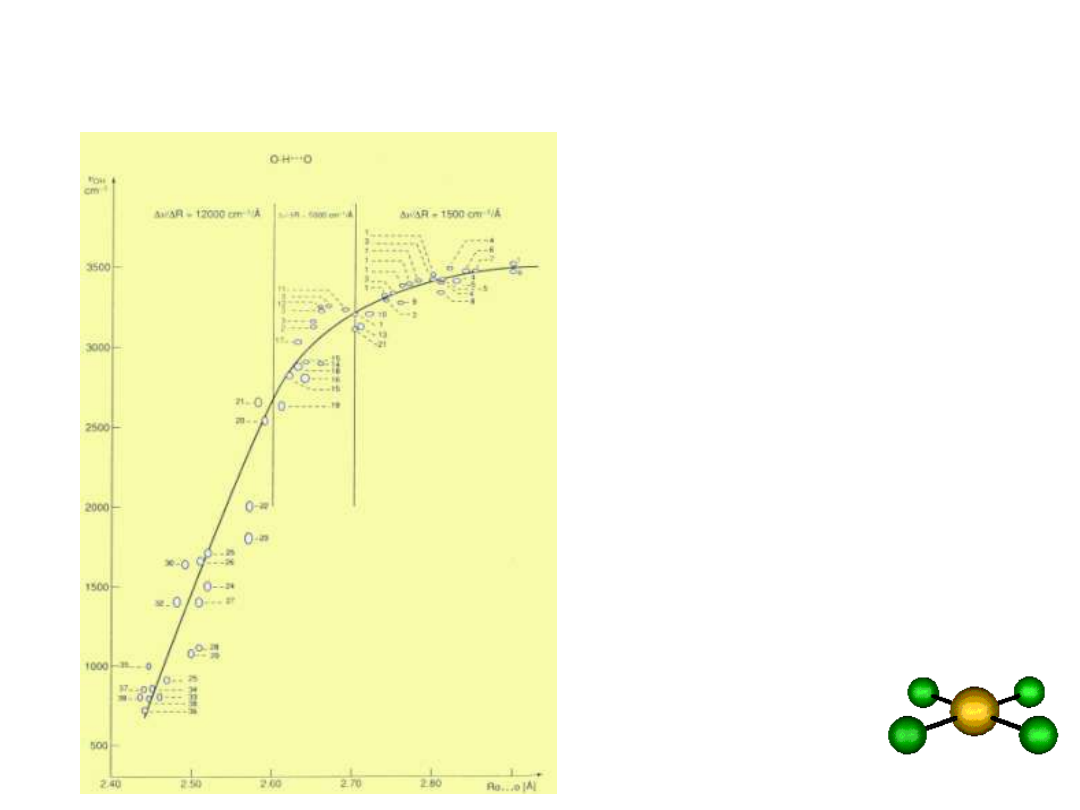
Korelacja OH) vs

R

O…O

wiązanie
wodorowe

silne średnie słabe

Novak; Structure and Bonding 18,
177, 1974

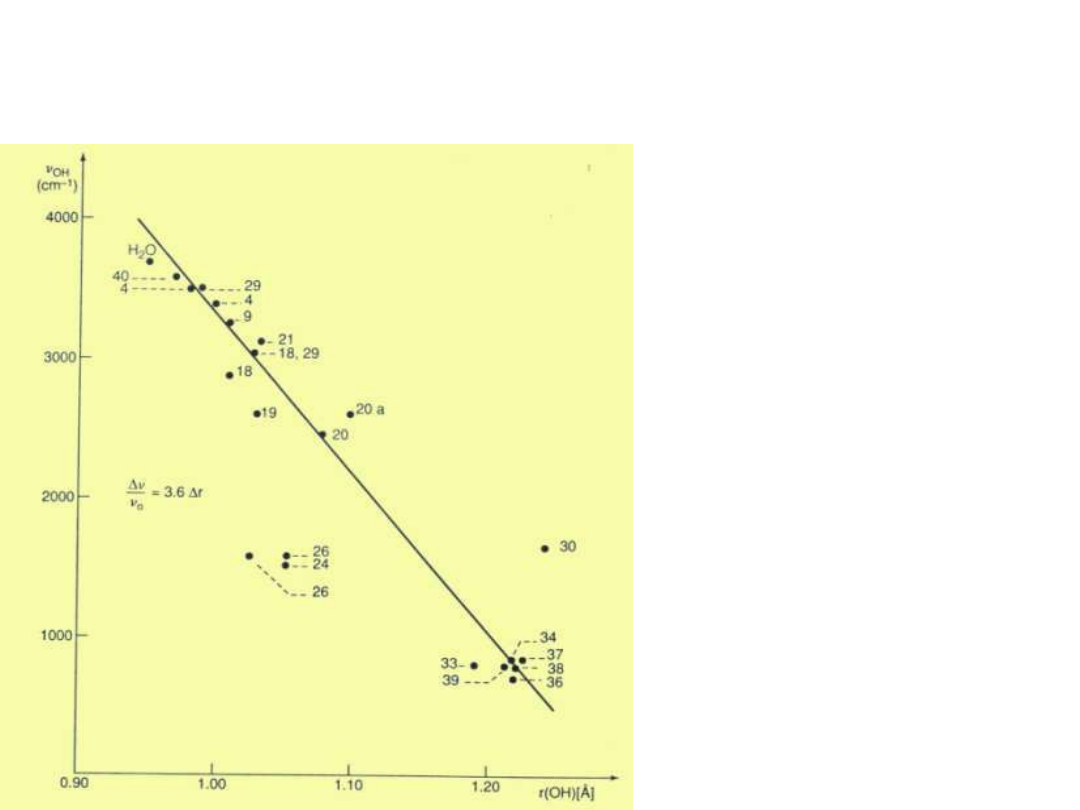
Zależność (O-H) vs r

O-H

Novak; Structure and
Bonding
18, 177, 1974

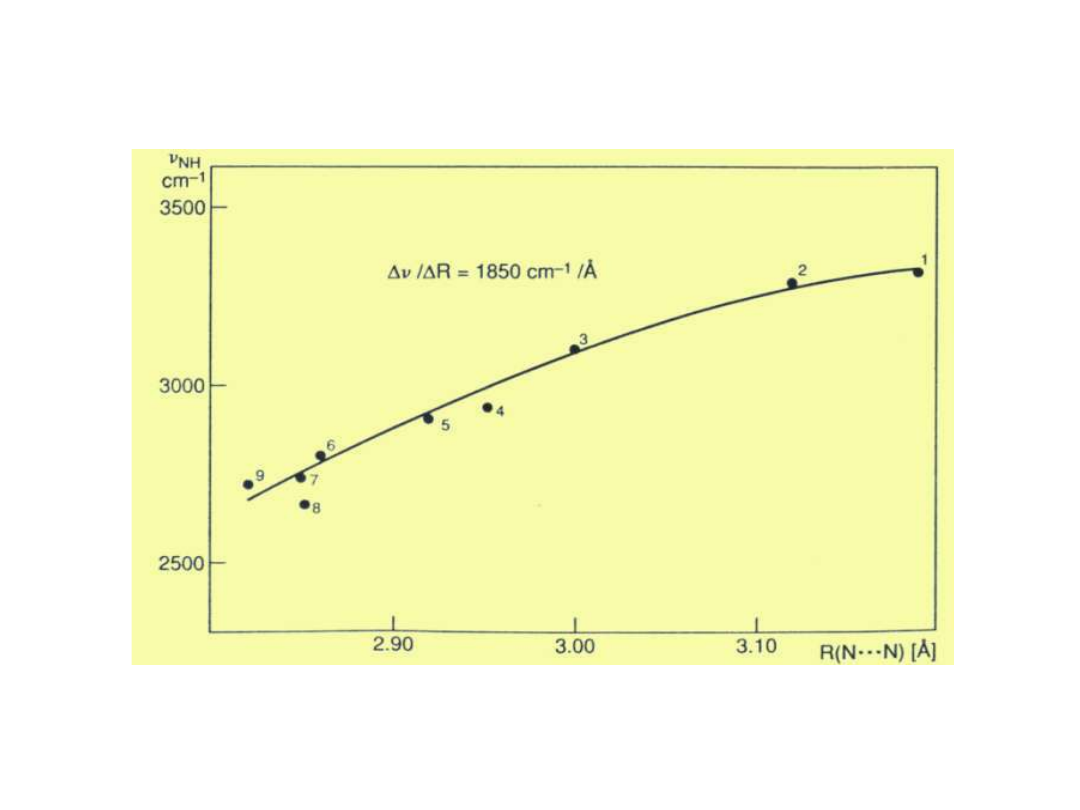
Zależność (N-H) vs R

N-(H)…N

Novak; Structure and Bonding 18,
177, 1974