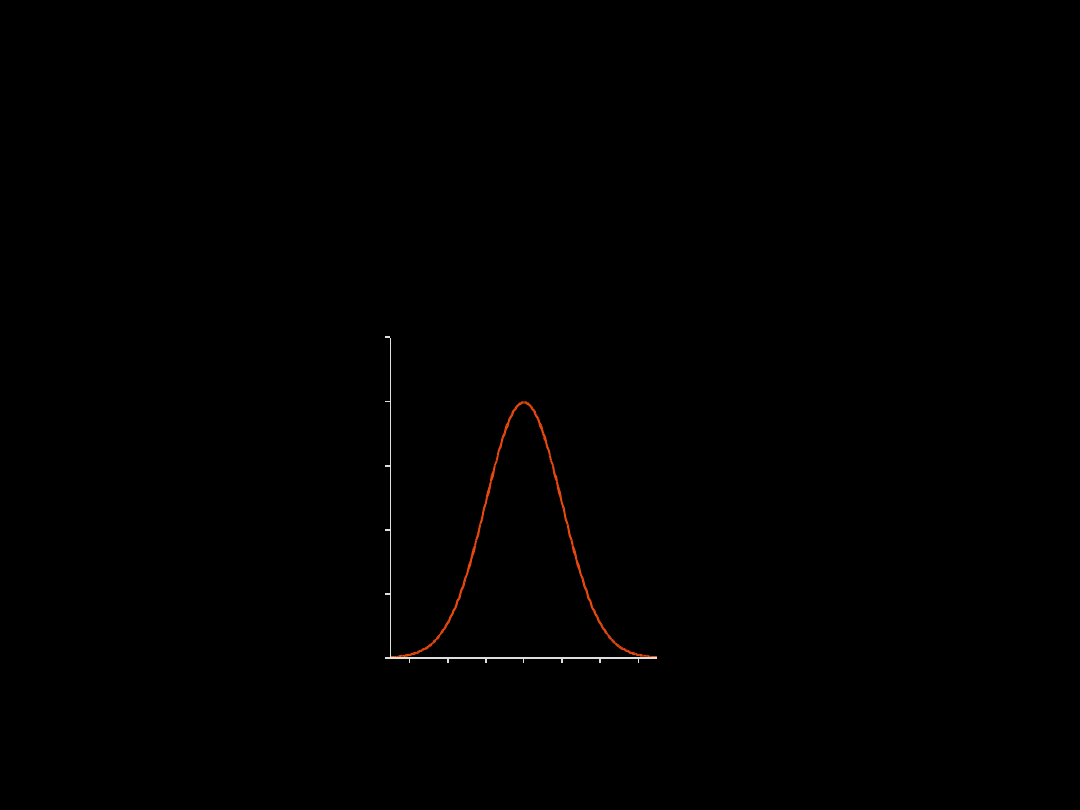
ROZKŁAD NORMALNY

Rozkład normalny o średniej arytmetycznej 0 i odchyleniu standardowym 1

nazywa się

rozkładem normalnym standaryzowanym

Rozkład Gaussa

Większość pomiarów w biologii ma rozkład zbliżony do rozkładu normalnego

-3 -2 -1 0

1

2

3

0,0

0,1

0,2

0,3

0,4

0,5

Oba skrzydła rozkładu normalnego ciągną się w nieskończoność – krzywa

nigdy nie styka się z osią X. Rozkład ten jest symetryczny względem wartości

średniej

p

δ

STANDARYZACJA POMIARÓW

Brodziec piskliwy o długości skrzydła 111 mm

(średnia populacji 113,0 mm; s =

1,6 mm)

Łęczak o długości skrzydła 127 mm

(średnia populacji 128,4 mm; s = 3,2 mm)

Który z tych ptaków jest stosunkowo
większy?

Standaryzacja pomiaru

s

x

x

Z





25

,

1

6

,

1

0

,

113

111









bp

Z

44

,

0

2

,

3

4

,

128

127









Ł

Z

Oba osobniki są mniejsze od przeciętnej wielkości osobników w badanej
populacji. Brodziec piskliwy jest mniejszy o 1,25 odchylenia standardowego, a
łęczak o 0,44 odchylenia standardowego od średniej.

Osobnik brodźca piskliwego jest stosunkowo mniejszym ptakiem niż osobnik
łęczaka.

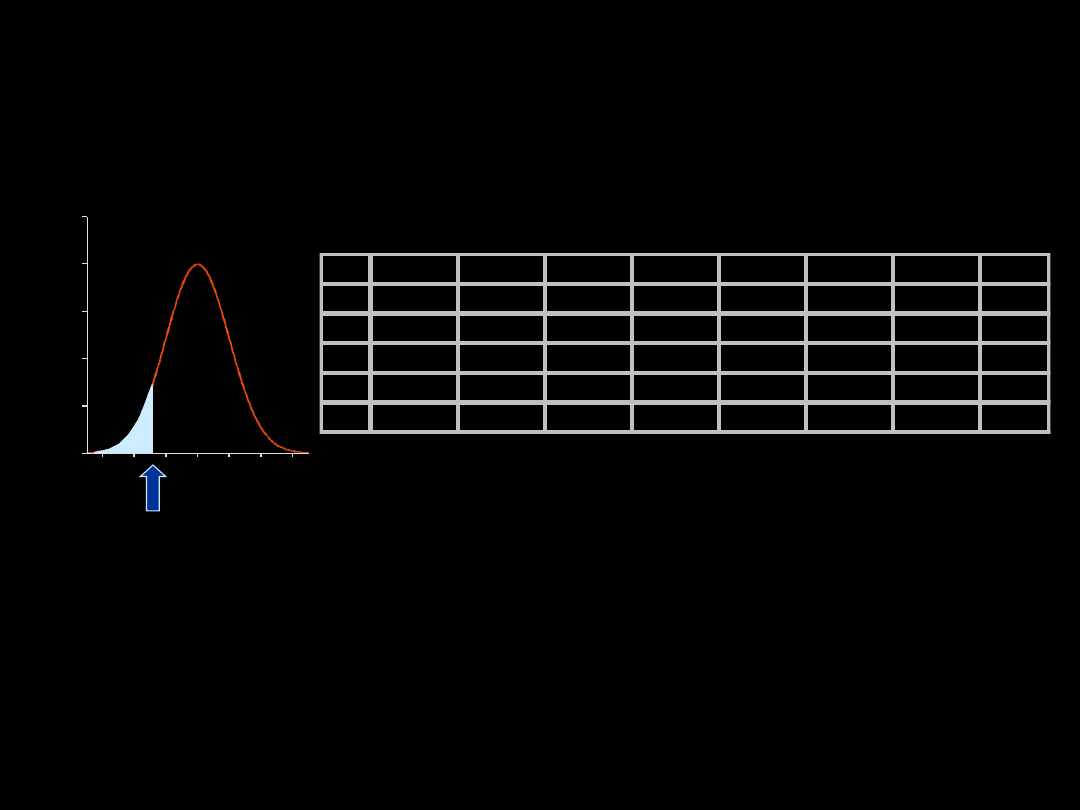
STANDARYZACJA POMIARÓW

Brodziec piskliwy o długości skrzydła 111 mm

25

,

1





bp

Z

Jakie jest prawdopodobieństwo, że wśród schwytanych brodźców piskliwych spotkamy
osobnika o długości skrzydła mniejszej niż 111 mm?

-3 -2 -1

0

1

2

3

0,0

0,1

0,2

0,3

0,4

0,5

-1,25

Prawdopodobieństwo to wynosi 0,1056 czyli 10,56%

Z

0

1

2

3

4

5

6

…

…

…

…

…

…

…

…

…

…

1,1

0,1357 0,1335 0,1314 0,1292 0,1271 0,1251

0,123

…

1,2

0,1151 0,1131 0,1112 0,1093 0,1075

0,1056

0,1038

…

1,3

0,0968 0,0951 0,0934 0,0918 0,0901 0,0885 0,0869

…

…

…

…

…

…

…

…

…

…

Ile brodźców piskliwych o długości skrzydła poniżej 111 mm możemy spodziewać się w
próbie liczącej 500 osobników

?

0,1056 * 500 = 52,8

W takiej próbie możemy spodziewać się 53 osobników o dł. skrzydła mniejszej niż 111 mm

Jaka część tej populacji ma długość skrzydła poniżej 111 mm

?

10,56%

STANDARYZACJA POMIARÓW

Jakie jest prawdopodobieństwo, że schwytany brodziec piskliwy o długości skrzydła 109
mm należy do tej populacji?

Brodziec piskliwy o długości skrzydła 109 mm jest mniejszy od średniej w
badanej populacji o 2,5 odchylenia standardowego

5

,

2

6

,

1

0

,

113

109









bp

Z

Z

0

1

2

3

4

5

6

…

…

…

…

…

…

…

…

…

…

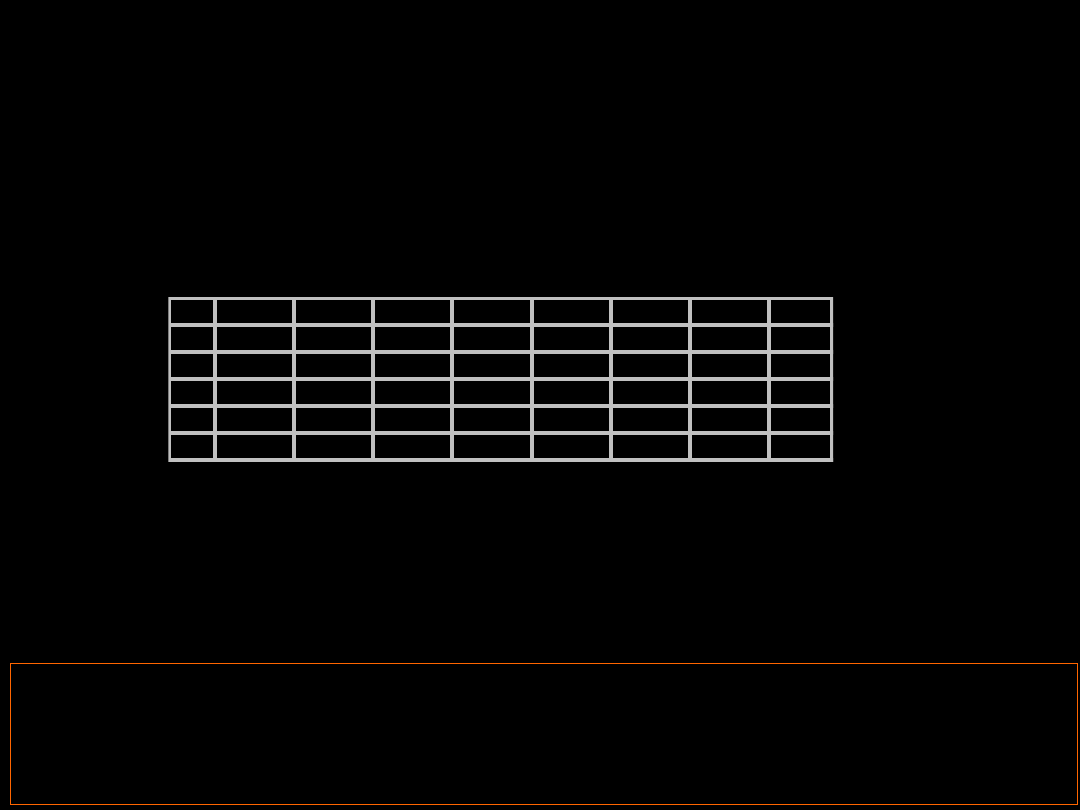
2,4

0,0082 0,0080 0,0078 0,0075 0,0073 0,0071 0,0069

…

2,5

0,0062

0,0060 0,0059 0,0057 0,0055 0,0054 0,0052

…

2,6

0,0047 0,0045 0,0044 0,0043 0,0041 0,0040 0,0039

…

…

…

…

…

…

…

…

…

…

Prawdopodobieństwo to jest bardzo małe i wynosi 0,0062 czyli 0,62%

NA JAKIEJ PODSTAWIE PODJĄĆ DECYZJĘ O TYM CZY

OSOBNIK TEN NALEŻY DO TEJ POPULACJI, CZY TEŻ

NIE?

Brodziec piskliwy

(średnia populacji 113,0 mm; s = 1,6 mm)

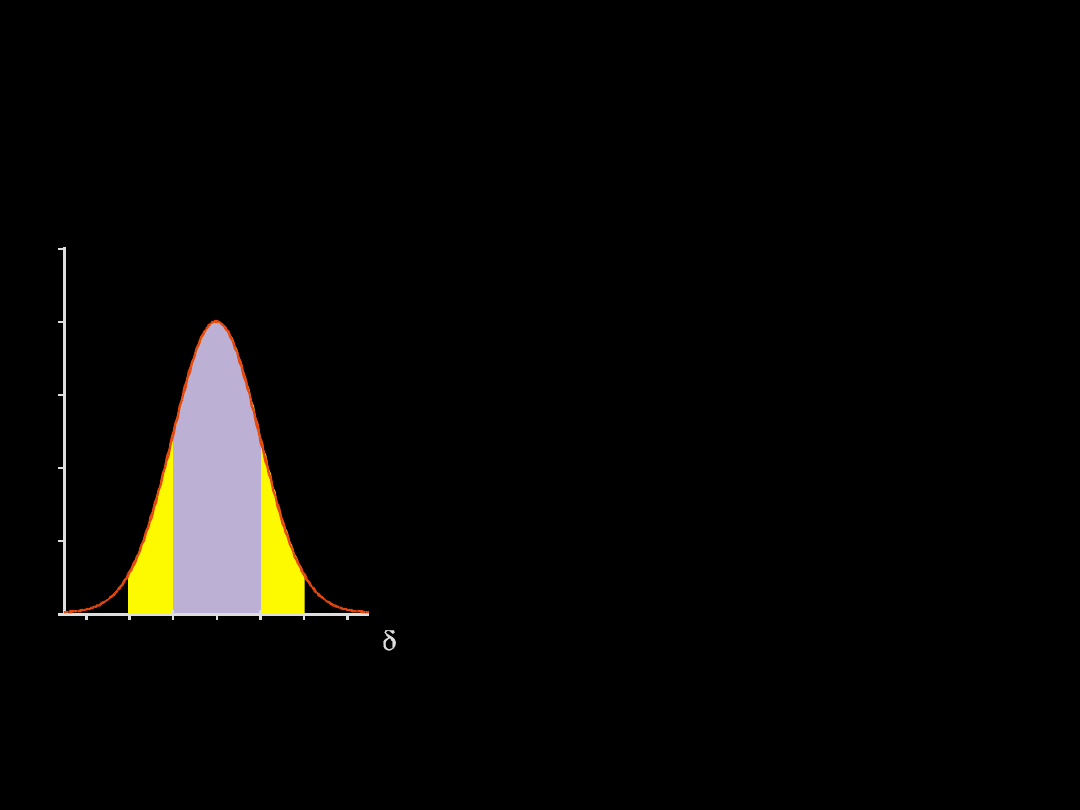
ROZKŁAD NORMALNY

Powierzchnia pod krzywą normalną standaryzowaną wynosi 1

Wiadomo że:

w zasięgu ±1 odchylenia standardowego mieści

się 68,27% wszystkich pomiarów

Powierzchnię pod krzywą normalną standaryzowaną można odczytać ze

specjalnych tablic

w zasięgu ±3 odchyleń standardowych mieści się

99,73% wszystkich pomiarów

-3 -2 -1 0

1

2

3

0,0

0,1

0,2

0,3

0,4

0,5

p

w zasięgu ±2 odchyleń standardowych mieści się

95,44% wszystkich pomiarów

Wystąpienie pomiaru leżącego poza zakresem ±3 odchyleń standardowych
jest mało prawdopodobne. Prawdopodobieństwo jego uzyskania wynosi 1 -
0,9973 = 0,0027

Prawo trzech sigm (3δ)

POZIOM ISTOTNOŚCI

Brodziec piskliwy -

średnia populacji 113,0 mm; s =

1,6 mm

5

,

2

6

,

1

0

,

113

109









bp

Z

NA JAKIEJ PODSTAWIE PODJĄĆ DECYZJĘ O TYM CZY

OSOBNIK TEN NALEŻY DO TEJ POPULACJI, CZY TEZ

NIE?

Prawdopodobieństwo spotkania w badanej populacji osobnika o długości
skrzydła 109 mm jest bardzo małe i wynosi 0,0062 czyli 0,62%

NAJCZĘSCIEJ W NAUKACH BIOLOGICZNYCH

PRZYJMUJE SIĘ WARTOŚĆ TAKIEGO

GRANICZNEGO PRAWDOPODOBIEŃSTWA

0,05

JAKIE JEST GRANICZNE PRAWDOPODOBIEŃSTWO,

PONIŻEJ KTÓREGO PODEJMIEMY DECYZJE O TYM, ŻE

DANY OSOBNIK NIE NALEŻY DO BADANEJ

POPULACJI?

PRAWDOPODOBIEŃSTWO TO NAZYWA SIĘ

POZIOMEM ISTOTNOŚCI

POZIOM ISTOTNOŚCI

Brodziec piskliwy -

średnia populacji 113,0 mm; s = 1,6 mm

5

,

2

6

,

1

0

,

113

109









bp

Z

Prawdopodobieństwo spotkania w badanej populacji osobnika o długości
skrzydła 109 mm jest bardzo małe i wynosi 0,0062 czyli 0,62%

Poziom istotności (prawdopodobieństwo graniczne) wynosi 0,05 czyli 5%

Podejmujemy decyzję, że ten osobnik, o długości skrzydła 109 mm nie
należy do badanej populacji. Ryzyko pomyłki jest mniejsze niż 0,05 i wynosi
0,0062.

WNIOSKOWANIE STATYSTYCZNIE

NIGDY NIE JEST PROWADZONE ZE

100% PEWNOŚCIĄ, LECZ ZAWSZE

Z PEWNYM

PRAWDOPODOBIEŃSTWEM

POPEŁNIENIA BŁEDU

HIPOTEZY STATYSTYCZNE

H

0

– Hipoteza zerowa – zakłada brak różnicy (nieistotność różnicy)

H

A

: długość skrzydła schwytanego brodźca piskliwego różni się

istotnie od średniej z populacji

H

0

: długość skrzydła schwytanego brodźca piskliwego nie różni się

istotnie od średniej z populacji

H

A

– Hipoteza alternatywna jest przeciwieństwem hipotezy zerowej

Każda test statystyczny rozpoczyna się od sformułowania hipotez

Następnie przyjmujemy poziom istotności (prawdopodobieństwo graniczne)

0,05

Wyznaczamy obszar krytyczny, czyli zbiór wyników, których wystąpienie jest
mało prawdopodobne – mniej prawdopodobne niż założone
prawdopodobieństwo graniczne (poziom istotności). Czyli w naukach
biologicznych najczęściej obszar krytyczny zawiera wyniki, których
wystąpienie jest mniej prawdopodobne niż 0,05

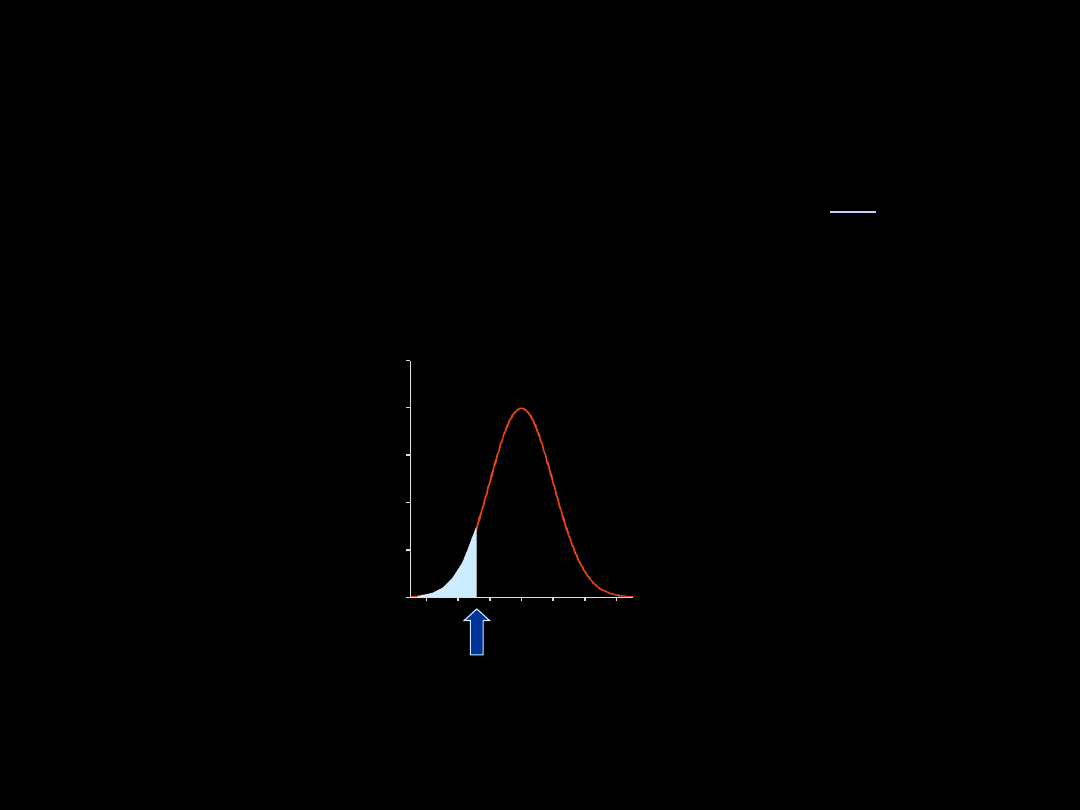
HIPOTEZY STATYSTYCZNE

Obszar krytyczny może być jednostronny (prawostronny lub lewostronny),
gdy hipoteza zerowa i alternatywna badają zależność „większe niż”,
„mniejsze niż”

H

A

: długość skrzydła schwytanego brodźca piskliwego jest istotnie

mniejsza od średniej z populacji

H

0

: długość skrzydła schwytanego brodźca piskliwego nie jest istotnie

mniejsza od średniej z populacji

-3 -2 -1

0

1

2

3

0,0

0,1

0,2

0,3

0,4

0,5

wartość
krytyczna

Jeśli otrzymany wynik pomiaru długości skrzydła znajdzie się w obszarze
krytycznym – hipotezę zerową należy odrzucić i przyjąć hipotezę
alternatywna

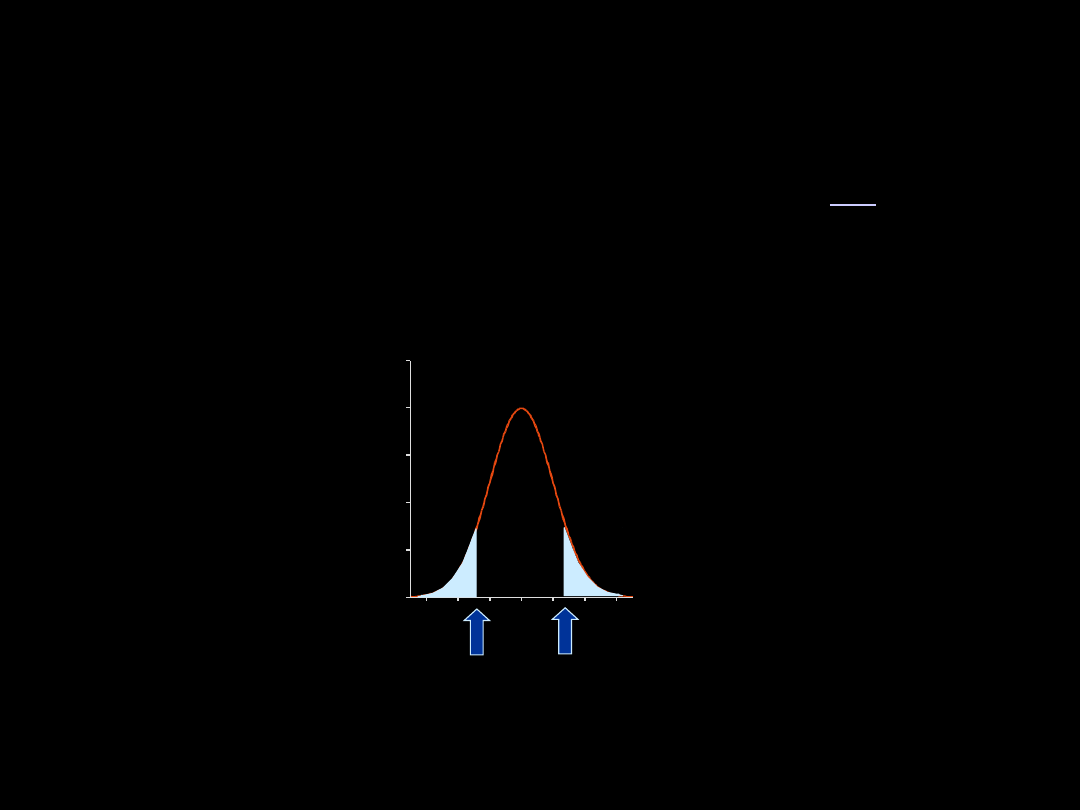
HIPOTEZY STATYSTYCZNE

Obszar krytyczny może być dwustronny, gdy hipoteza zerowa i alternatywna
badają zależność „równy”, „nie równy”

-3 -2 -1

0

1

2

3

0,0

0,1

0,2

0,3

0,4

0,5

Jeśli otrzymany wynik pomiaru długości skrzydła znajdzie się w obszarze
krytycznym – hipotezę zerową należy odrzucić i przyjąć hipotezę
alternatywna

H

A

: długość skrzydła schwytanego brodźca piskliwego różni się

istotnie od średniej z populacji

H

0

: długość skrzydła schwytanego brodźca piskliwego nie różni się

istotnie od średniej z populacji

wartości

krytyczne

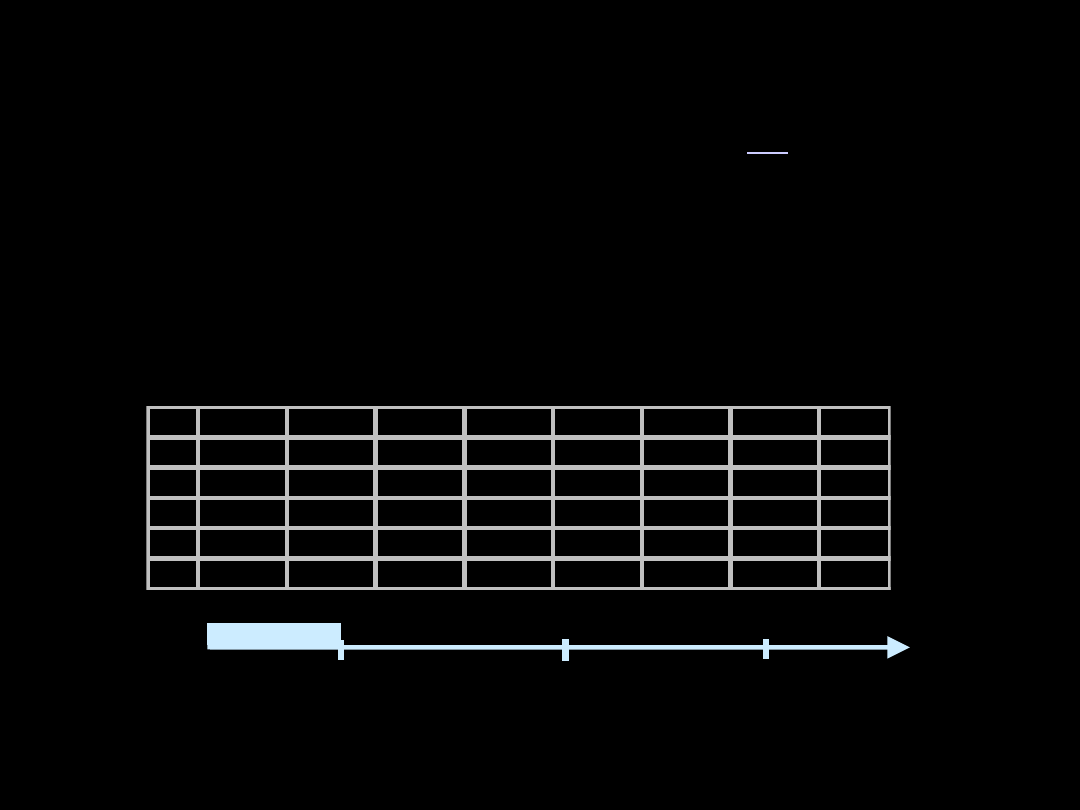
Brodziec piskliwy o długości skrzydła 109 mm (

średnia populacji 113,0 mm; s

= 1,6) mm

0

1,645

-1,645

HIPOTEZY STATYSTYCZNE

H

A

: długość skrzydła schwytanego brodźca piskliwego jest istotnie mniejsza

od średniej z populacji

H

0

: długość skrzydła schwytanego brodźca piskliwego nie jest istotnie

mniejsza od średniej z populacji

 =

0,05

Z

0

1

2

3

4

5

6

…

…

…

…

…

…

…

…

…

…

1,5

0,0668 0,0655 0,0643 0,0630 0,0618 0,0606 0,0594

…

1,6

0,0548 0,0537 0,0526 0,0516

0,0505 0,0495

0,0485

…

1,7

0,0446 0,0436 0,0427 0,0418 0,0409 0,0401 0,0392

…

…

…

…

…

…

…

…

…

…

Wyznaczamy obszar krytyczny jednostronny

X

-2,5

5

,

2

6

,

1

0

,

113

109









bp

Z

Długość skrzydła schwytanego brodźca piskliwego jest istotnie mniejsza od
średniej z populacji

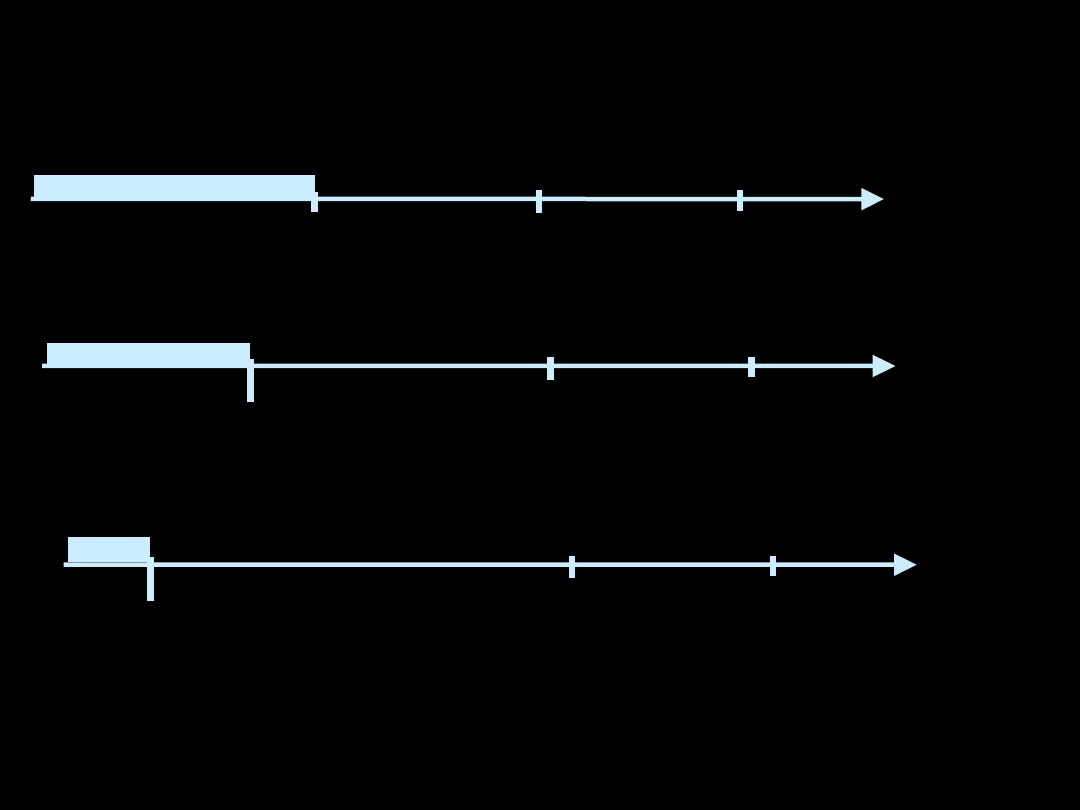
HIPOTEZY STATYSTYCZNE

 =

0,05

 =

0,01

 =

0,001

0

-1,645

X

-2,5

-2,325

X

-2,5

-3,100

X

-2,5

0

0

Czym niższy poziom istotności tym trudniej jest odrzucić hipotezę zerowa.

Czym niższy poziom istotności tym wyższy poziom wiarygodności hipotezy alternatywnej

BŁĄD PIERWSZEGO I DRUGIEGO RODZAJU

Hipoteza zerowa

prawdziwa

Hipoteza zerowa

fałszywa

Hipoteza zerowa
odrzucona

Błąd pierwszego

rodzaju (α)

Decyzja prawidłowa

Hipoteza zerowa nie
odrzucona

Decyzja prawidłowa

Błąd drugiego

rodzaju (β)

Zmniejszenie prawdopodobieństwa popełnienia błędu pierwszego rodzaju
zwiększa prawdopodobieństwo popełnienia błędu drugiego rodzaju

Zmiana poziomu istotności z 0,05 na 0,01 zmniejsza prawdopodobieństwo
odrzucenia hipotezy zerowej (prawdopodobieństwo błędu pierwszego
rodzaju), lecz zwiększa prawdopodobieństwo popełnienia błędu drugiego
rodzaju – czyli nie odrzucenia hipotezy zerowej gdy jest ona fałszywa.

Szansa popełnienia błędu drugiego rodzaju przy danym poziomie
istotności zmniejsza się przy wzroście liczebności próby

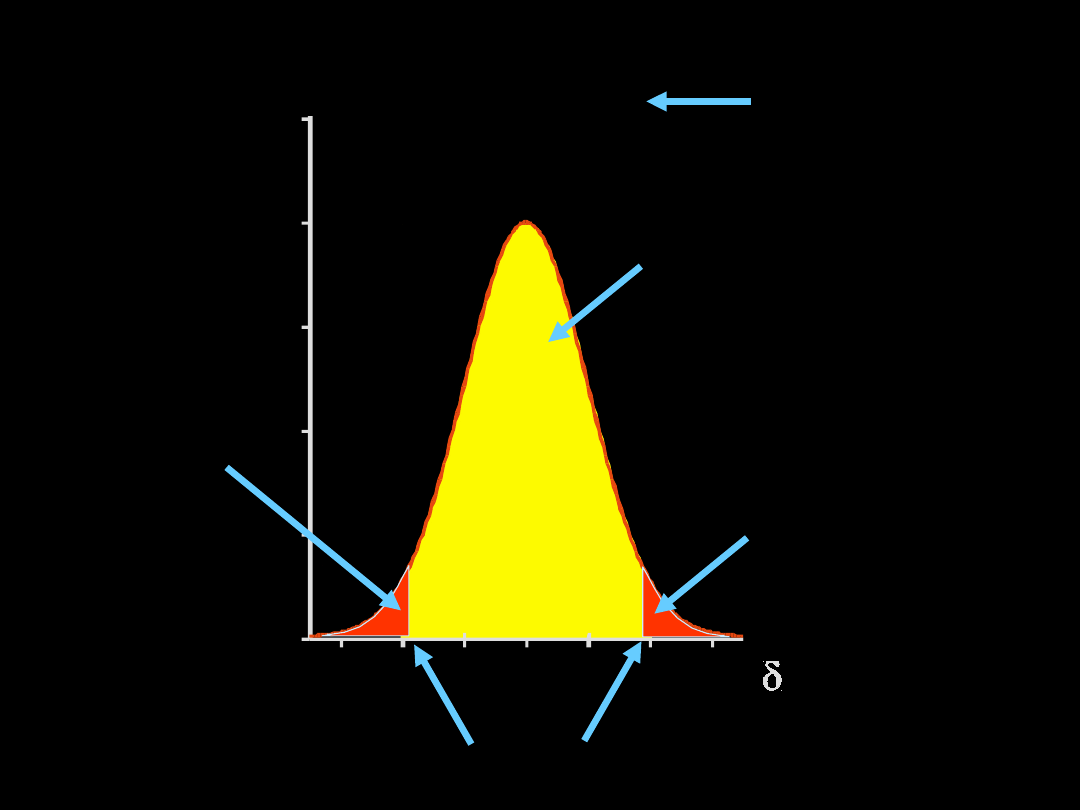
HIPOTEZY STATYSTYCZNE

-3 -2 -1 0

1

2

3

0,0

0,1

0,2

0,3

0,4

0,5

p

przedział

ufności

obszar

krytyczny

 =

0,05

poziom

istotności

wartość

krytyczna

obszar

krytyczny