TESTOWANIE HIPOTEZ

DOTYCZĄCYCH WIELU

PRÓB

Jeśli porównujemy kilka prób ze sobą za pomocą testów
dla dwóch prób - koniecznie należy stosować odpowiednie
poprawki obniżające prawdopodobieństwo popełnienia
błędu I rodzaju.

PORÓWANIA WIELOKROTNE - ZAPLANOWANE

Testując hipotezę, że 2 próby pochodzą z tej samej populacji przy
poziomie istotności 0,05 (5%) uzyskujemy prawdopodobieństwo
poprawnego przyjęcia hipotezy zerowej 0,95 (95%).

Testując hipotezę, że 3 próby pochodzą z tej samej populacji przy
poziomie istotności 0,05 (5%) uzyskujemy prawdopodobieństwo
poprawnego przyjęcia hipotezy zerowej 0,95

3

= 0,86 (86%). Oznacza

to, że przy takim porównaniu poziom istotności wynosi 0,14 (14%)
zamiast zakładanego 0,05 (5%).

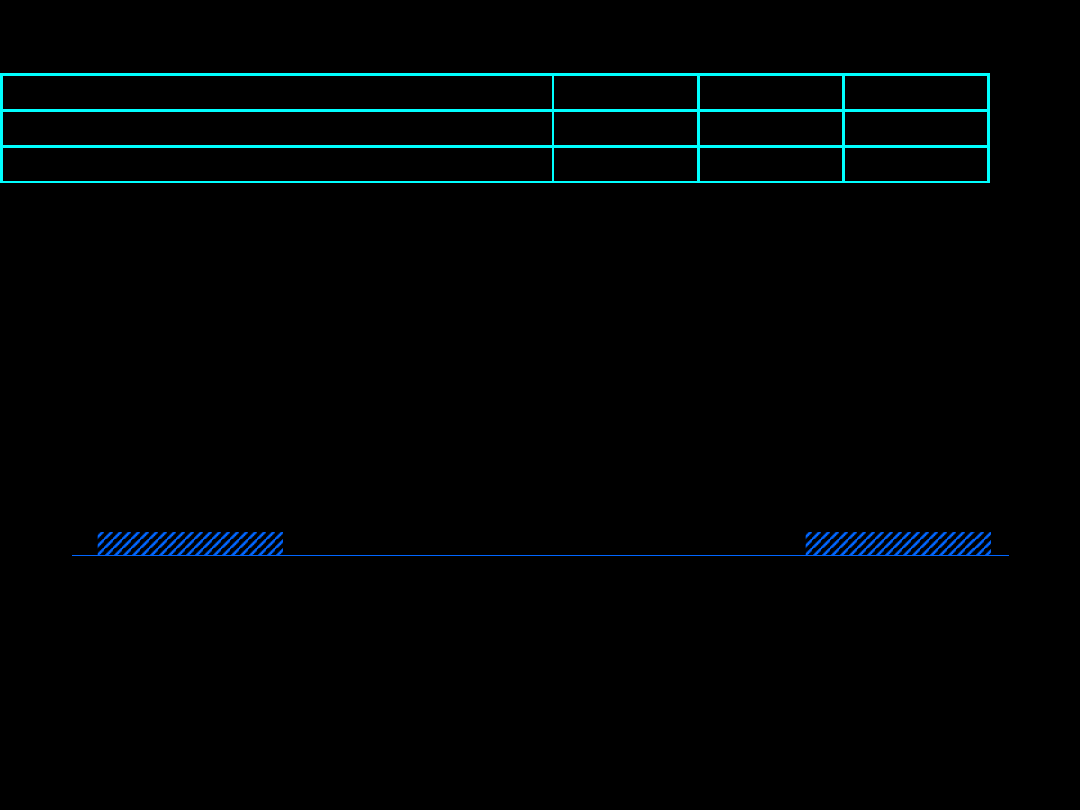
METODA Dunn-Šidáka

k

a

a

1

)

1

(

1

'







α

– zakładany poziom istotności

α’

– nowy poziom istotności

k

– liczba testów porównujących dwie próby

017

,

0

95

,

0

1

)

05

,

0

1

(

1

'

3

1

3

1













a

Przy testowaniu 3 prób testami dla dwóch prób poziom

istotności z 0,05 zmienia się na 0,017

METODA Bonferroniego

k

a

a 

''

Przy testowaniu 3 prób testami dla dwóch prób poziom

istotności z 0,05 zmienia się na 0,017

017

,

0

3

05

,

0

''





a

Nie można stosować porównań niezaplanowanych po
analizie wariancji. Wykonuje się wtedy tzw. testy testy
zaplanowane nazywane też a posteriori lub post-hoc.

ANOVA

1. Oblicza się średnią arytmetyczną dla danej próby
2. Odejmuje się od każdego elementu próby średnią - otrzymując się

w ten sposób odchylenia poszczególnych pomiarów od średniej

3. Podnosi się każdą wartość odchylenia od średniej do kwadratu
4. Dodaje się kwadraty odchyleń od średniej otrzymując sumę

kwadratów odchyleń

5. Dzieląc sumę kwadratów odchyleń przez liczebność próby

otrzymuje się wariancję danej próby

 

2

1

1

2

n

x

x

s

n

i

i











ANALIZA WARIANCJI - WPROWADZENIE

Gdyby wartości wszystkich elementów w próbie były takie same, to

wariancja wynosiłaby zero

Wariancja wskazuje na zmienność danej cechy w próbie

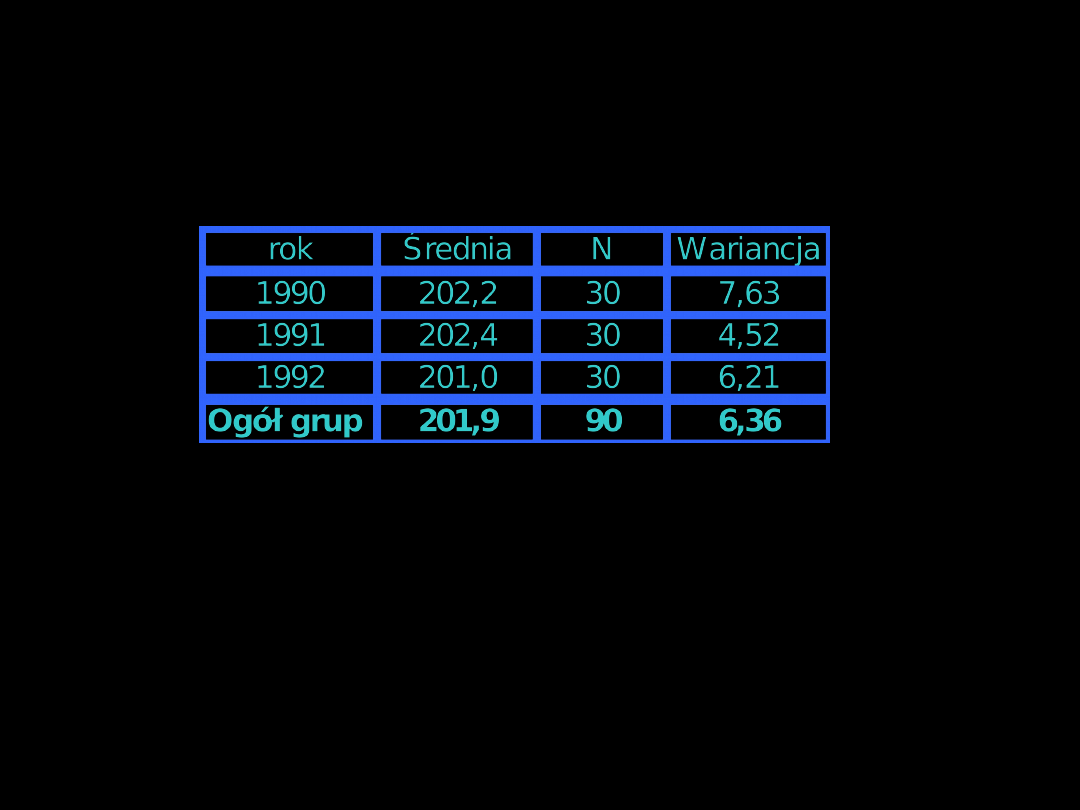
ANALIZA WARIANCJI - WPROWADZENIE

Pomierzono w trzech kolejnych sezonach zimowych w Gdańsku
zmierzono po 30 młodych łysek. Należy sprawdzić czy średnia
długość skrzydła u tego gatunku w kolejnych latach jest taka sama
(czy ptaki te pochodzą z tej samej populacji).

Wariancja ogólna (na podstawie wszystkich 90 pomiarów)

6,36

Wariancja wewnątrzgrupowa (średnia arytmetyczna ważona z 3 wariancji

)

6,12

Wariancja międzygrupowa (wariancja między średnimi) 0,5678 * 30
=

17,03

Wartość wariancji obliczonej ze średnich należy pomnożyć przez liczebność
grup

Gdyby pomiary pochodziły z różnych populacji, to
zmienność (wariancja) między grupami byłaby większa
niż wewnątrz grup.

ANALIZA WARIANCJI - WPROWADZENIE

Do oceny czy wariancja międzygrupowa istotnie różni się od wariancji
wewnątrzgrupowej stosuje się statystykę

F (test F)

Wartość statystyki

F

otrzymuje się dzieląc międzygrupową sumę

kwadratów odchyleń przez wewnątrzgrupową sumę kwadratów
odchyleń

Jeśli wartość

F

jest mniejsza od 1, lub wariancja międzygrupowa jest

mniejsza od 1, to w takim przypadku hipotezę zerową przyjmuje się
od razu
Statystyka

F

ma rozkład F Snedecora. Istotność różnic bada się

porównując otrzymaną wartość

F

z wartością teoretyczną dla danej

liczby stopni swobody

Dla rozpatrywanego przykładu:

F=2,78

;

df

międzygr

.=(k-1) = 3 – 1 =

2

df

wewnątrzgr.

=

(

N-k) = 90 – 3 =

87

Wartość teoretyczna dla poziomu istotności 0,05 i df

1

=2 oraz df

2

=87 wynosi

3,84

-3,84

3,84

0

2,78

x

Otrzymana wartość F leży poza obszarem krytycznym. Nie ma podstaw do
odrzucenia H

0

Łyski zimujące w Gdańsku w badanych sezonach pochodziły z tej samej
populacji.

ANALIZA WARIANCJI - OGRANICZENIA

ANOVA dotyczy danych w skali interwałowej lub ilorazowej

• Próby powinny być niezależne i losowe

• Wariancje w poszczególnych grupach muszą być sobie równe

• Każda z prób musi pochodzić z populacji o rozkładzie
normalnym

• Średnie w grupach nie mogą być skorelowane z wariancjami

(tzw. model addytywny)

W praktyce jednak okazało się, że ANOVA jest
stosunkowo odporna na niewielkie odstępstwa od
wymagań o normalności rozkładów i jednorodności
wariancji w próbach.

Podobnie jak przy innych procedurach parametrycznych istnieją
pewne warunki, które muszą zostać spełnione, aby móc
stosować ANOVA:

ANOVA – NIEZALEŻNOŚĆ I LOSOWOŚĆ PRÓB

Elementy do prób muszą być wybierane losowo i niezależnie.
Wybór danego elementu nie może zmieniać
prawdopodobieństwa wybrania innego.

ANOVA – ZGODNOŚĆ Z ROZKŁADEM NORMALNYM

Założenie o normalności rozkładu dotyczy każdej z badanych
prób

W przypadku rozkładów skrajnie odbiegających od rozkładu
normalnego zaleca się transformację danych lub stosowanie
nieparametrycznego odpowiednika ANOVA – testu Kruskala-
Wallisa

Wraz ze wzrostem próby zwiększa się odporność ANOVA na
odstępstwa od rozkładu normalnego.

ANOVA – JEDNORODNOŚĆ WARIANCJI

Do sprawdzenia założenia o jednorodności wariancji służą testy
porównujące wariancje w próbach.

Test Levena

– w ostatnich latach krytykowany za nieodporność na

odchylenia od normalności rozkładów w próbach.

Test Browna–Forsythe’a

– ostatnio bardziej polecany od testu Levena

ze względu na większą odporność na odchylenia od normalności
rozkładów w próbach.

Test Bartletta

– może dawać mylne wyniki przy odstępstwach od

normalności rozkładów w próbach.

Test Hartleya

i

test Cochrana

– wymagają by liczebności w próbach

były jednakowe.

ANOVA jest dość odporna na odstępstwa od założenia o jednorodności
wariancji, szczególnie przy podobnych liczebnościach w grupach. W
przypadku dużych różnic między wariancjami zaleca się
transformację danych lub stosowanie testu Kruskala-Wallisa

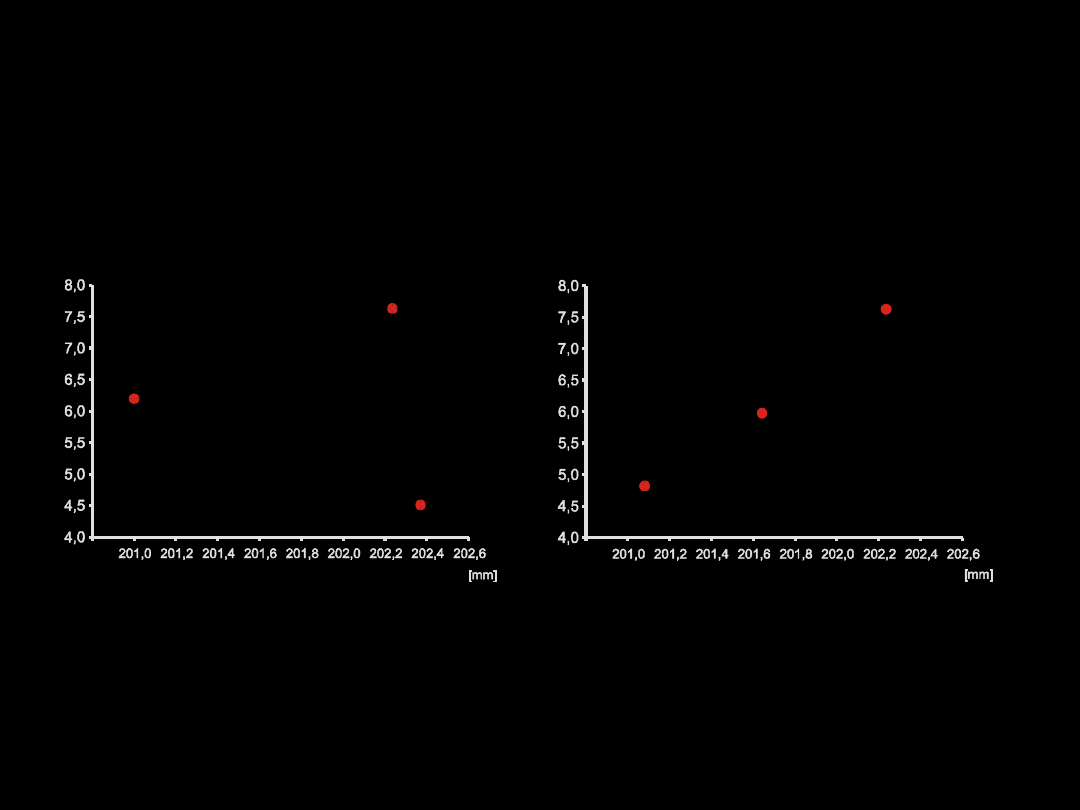
ANOVA – BRAK KORELACJI MIĘDZY ŚREDNIMI I WARIANCJAMI

Do sprawdzenia tego założenia służy wykres punktowy pokazujący
zależność wariancji (lub odchylenia standardowego) od średniej w
grupach.

Punkty na wykresie nie mogą układać się wzdłuż przekątnej.

Takie ułożenie wskazuje na korelację wariancji i średnich (im większa
wartość średniej, tym większa wariancja) – tzw.

multiplikatywność

ś r e d n ia

w

ar

ia

nc

ja

ś r e d n ia

w

ar

ia

nc

ja

multiplikatywność

addytywność

Model multiplikatywny występuje najczęściej w eksperymentach
gdzie bada się zmienność danej cechy w czasie, lub gdy wartość
pomiaru zależy od wartości początkowej – np. względny przyrost
ciężaru, zmiany liczebności.

Model multiplikatywny można sprowadzić do addytywnego
logarytmując dane

Przyczyną korelacji między wariancjami i średnimi często bywają obserwacje
odstające

ANALIZA WARIANCJI

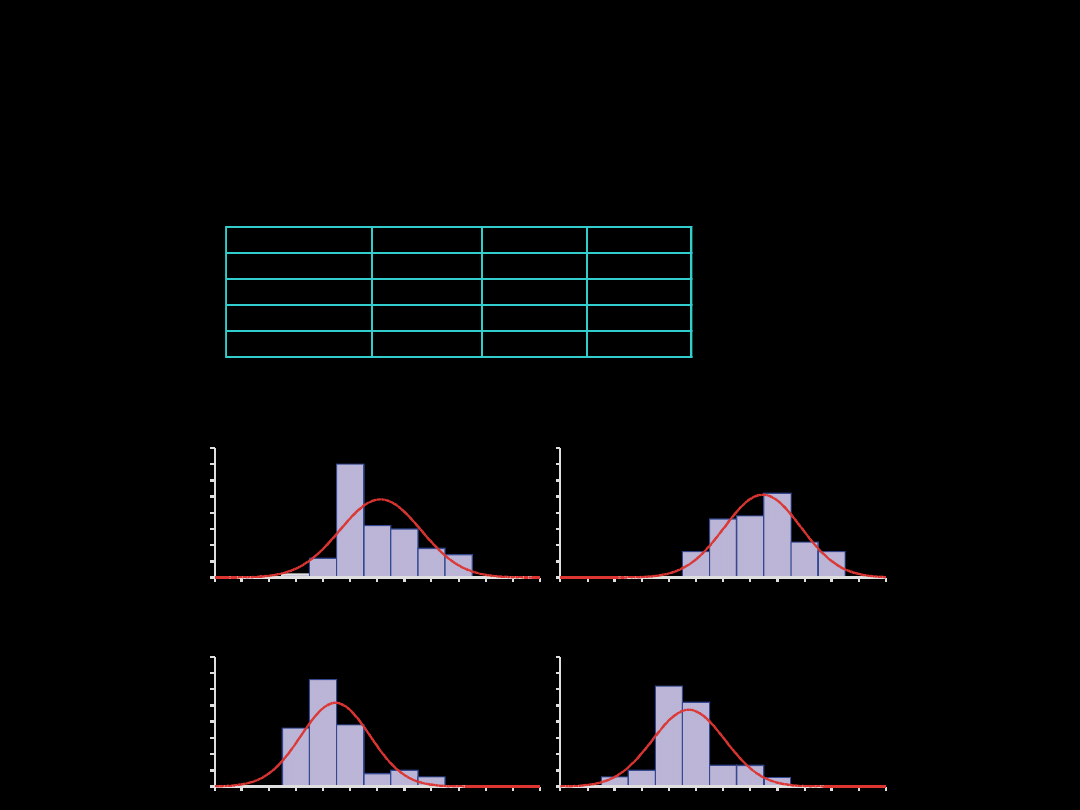
Badano wielkość zniesienia u 4 gatunków sikor. Należy sprawdzić, czy gatunki
te różnią się średnią liczbą składanych jaj

H

0

: Średnia liczba jaj składanych przez 4 gatunki sikor jest taka sama.

H

A

: Średnia liczba jaj składanych przez 4 gatunki sikor

nie

jest taka sama.

Przykład 13

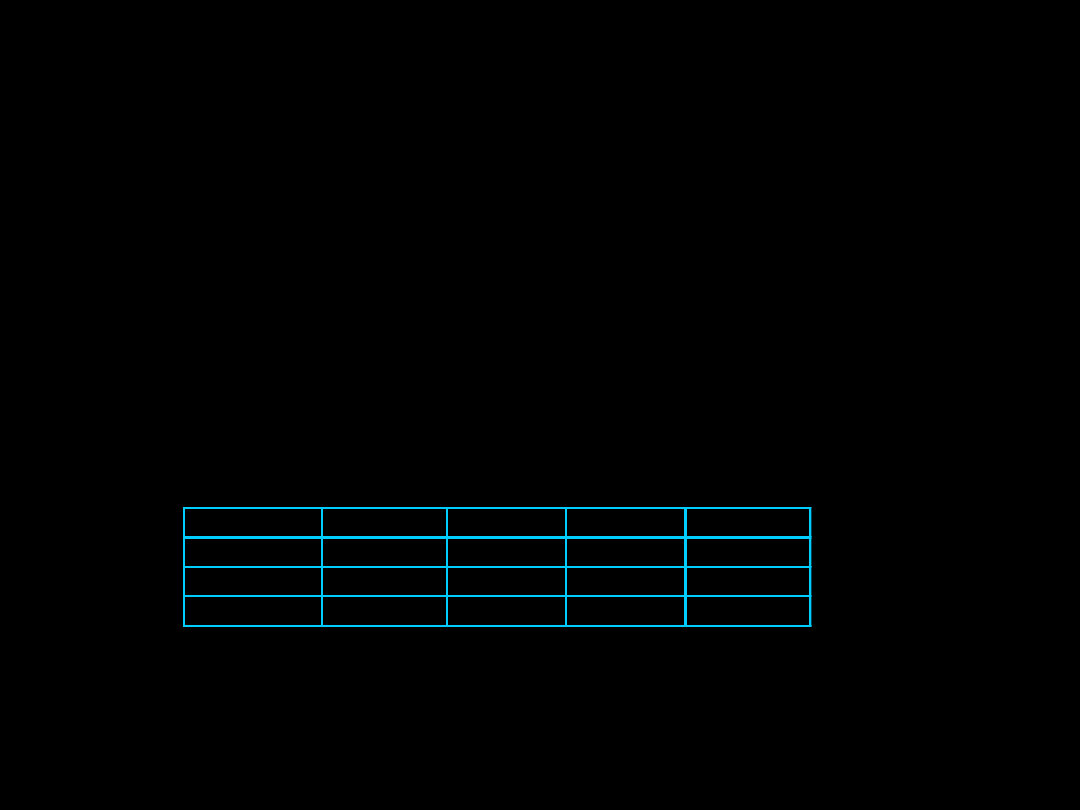
Sprawdzanie założenia o normalności rozkładów

GATUNEK

średnia

N

SD

bogatka

8,1

90

1,49

modraszka

9,4

90

1,41

czarnogłówka

6,4

82

1,27

szarytka

6,7

79

1,23

4

5

6

7

8

9

1 0 1 1 1 2

0

1 0

2 0

3 0

4 0

4

5

6

7

8

9

1 0 1 1 1 2

4

5

6

7

8

9

1 0 1 1 1 2

4

5

6

7

8

9

1 0 1 1 1 2

0

1 0

2 0

3 0

4 0

N

N

c z a r n o g łó w k a

m o d r a s z k a

s z a r y tk a

b o g a tk a

ANALIZA WARIANCJI

Przykład 13 cd.

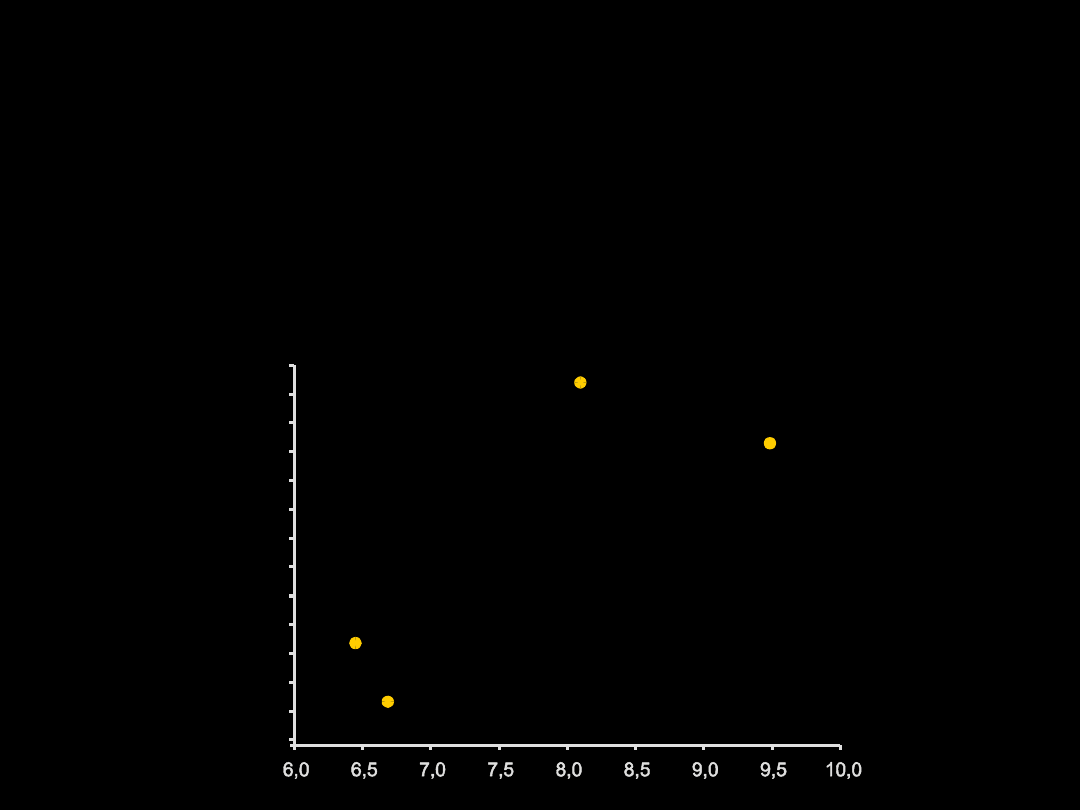
Sprawdzanie założenia o jednorodności wariancji

Test Levena; F

3,337

=2,48;

p=0,061

Test Browna-Forsythe’a; F

3,337

=2,97;

p=0,032

Test Bartletta; 

2=3,15

;

p=0,368

Sprawdzanie założenia o braku korelacji między średnimi i wariancjami

1 , 2 0

1 , 2 2

1 , 2 4

1 , 2 6

1 , 2 8

1 , 3 0

1 , 3 2

1 , 3 4

1 , 3 6

1 , 3 8

1 , 4 0

1 , 4 2

1 , 4 4

1 , 4 6

ś r e d n ia

od

ch

yl

en

ie

st

a

nd

ar

do

w

e

ANALIZA WARIANCJI

Przykład 13 cd.

ANOVA; F

3,337

=90,62;

p<0,0001

Cztery badane gatunki sikor wysoce istotnie różnią się

średnią wielkością zniesienia

Hipotezę zerową odrzucamy z prawdopodobieństwem popełnienia błędu

mniejszym niż 0,0001 (0.01%)

Do sprawdzenia istotności różnic między poszczególnymi
próbami służą testy post-hoc (a-posteriori)

ANOVA nie daje odpowiedzi które próby różnią się między
sobą

W wyniku ANOVA otrzymaliśmy informację, że badane
próby (gatunki) nie pochodzą z jednej populacji (populacji
statystycznej).

ANALIZA WARIANCJI -

testy post-hoc

Testy post-hoc (a-posteriori) wykonuje się wyłącznie po ANOVA, gdy
ANOVA wykazała istotne różnice między próbami

Test Scheffego

– test najbardziej konserwatywny. Prawdopodobieństwo

odrzucenia prawdziwej H

0

jest stałe i najmniejsze spośród testów post-hoc,

niezależnie od liczby porównywanych prób.

Test Tukeya

– test mniej konserwatywny od poprzedniego.

Prawdopodobieństwo odrzucenia prawdziwej H

0

jest stałe, niezależnie od

liczby porównywanych prób.
Test Tukeya

dla grup o nierównej liczebności nazywany jest

testem Spjotvolla

i Stolinea

Test Newmana-Keulsa

– test mniej konserwatywny od poprzednich.

Prawdopodobieństwo odrzucenia prawdziwej H

0

nie

jest stałe i wzrasta wraz z

liczbą porównywanych prób. Nie jest polecany gdy liczba porównywanych
grup jest duża.

Test Duncana

– test najmniej konserwatywny. Prawdopodobieństwo

odrzucenia prawdziwej H

0

nie

jest stałe i wzrasta wraz z liczbą

porównywanych prób. Np. przy k=10 i α=0,05, prawdopodobieństwo
popełnienia błędu I rodzaju wynosi 0,40 (40%). Nie jest polecany gdy liczba
porównywanych grup jest duża.

ANOVA dla dwóch prób (porównująca dwie średnie wartości) jest
tożsama z testem t-Studenta. W tym przypadku wykonywanie testów
post-hoc nie ma sensu.

ANALIZA WARIANCJI -

testy post-hoc

Testy post-hoc można uporządkować w zależności od
prawdopodobieństwa popełnienia błędu I i II rodzaju

test Scheffego

test Tukeya test Newmana-Keulsa

test Duncana

Prawdopodobieństwo popełnienia błędu I rodzaju

(odrzucenie

prawdziwej H

0

)

Prawdopodobieństwo popełnienia błędu II rodzaju

(przyjęcie

fałszywej H

0

)

Decyzja o wyborze testu post-hoc opiera się na znaczeniu błędów I i II
rodzaju w prowadzonych badaniach.

Jeśli w badaniach koncentrujemy się na prostym porównaniu średnich
w próbach, to najbardziej polecany jest test Tukeya.

Może się zdarzyć (zwłaszcz przy małych próbach), że pomimo
odrzucenia Ho
przez ANOVA i stwierdzeniu, że badane próby nie pochodzą z jednej
populacji, test post-hoc nie wykaże istotnych różnic. Wynikać to może
m.in. z faktu, że ANOVA jest silniejszą procedurą niż stosowany test
post-hoc. Można w takim przypadku wybrać mniej konserwatywny
test post-hoc.

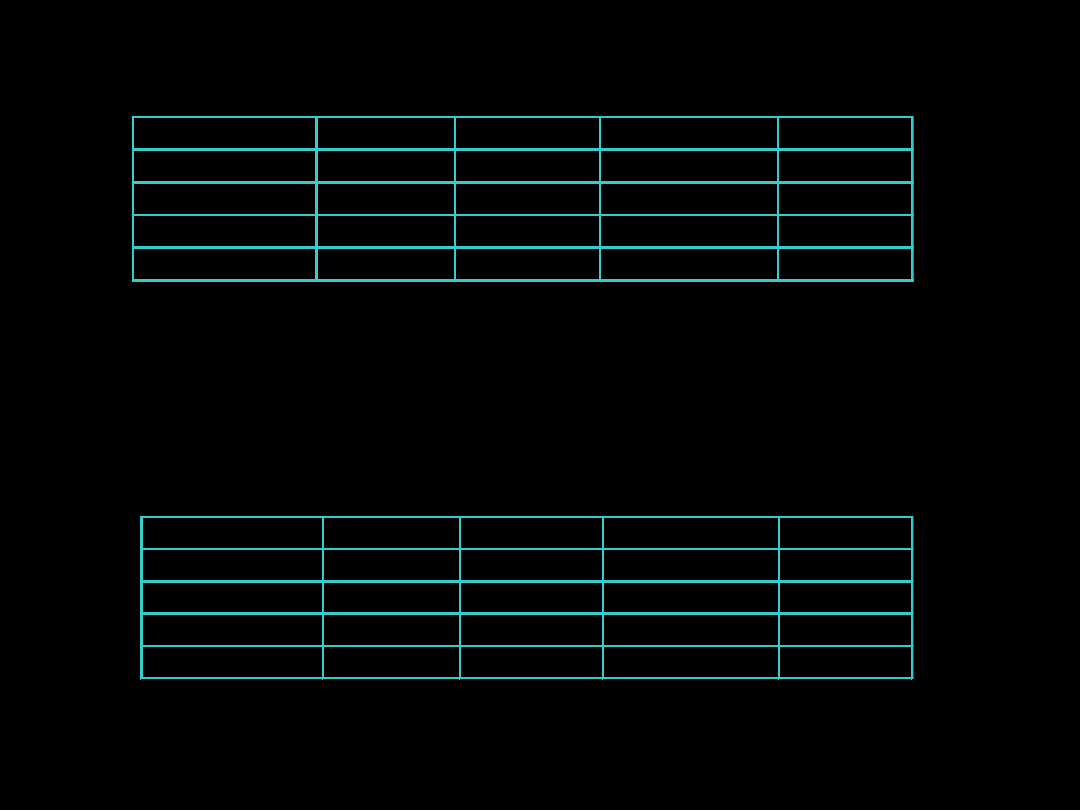
ANALIZA WARIANCJI

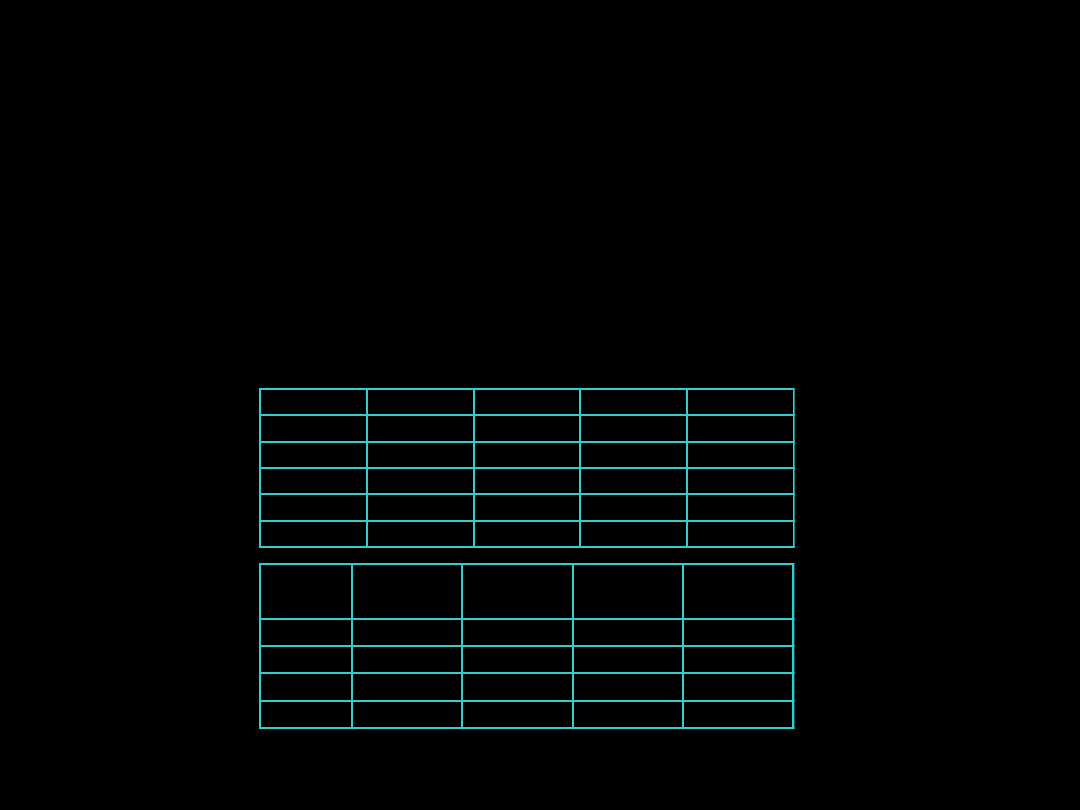
Przykład 13 cd.

bogatka

modraszka czarnogłówka szarytka

bogatka

0,000008

0,000008 0,000008

modraszka

0,000008

0,000008 0,000008

czarnogłówka

0,000008

0,000008

0,700051

szarytka

0,000008

0,000008

0,700051

Wyniki testu Tukeya – tabela z wartościami p

Wyniki testu Tukeya – układ grup jednorodnych

średnia

1

2

3

bogatka

8,1

****

modraszka

9,4

****

czarnogłówka

6,4

****

szarytka

6,7

****

Badane 4 gatunki sikor różnią się istotnie pod względem liczby składanych jaj
(ANOVA; F3,337=90,62; p<0,0001). Bogatka i modraszka składają średnio
więcej jaj niż czarnogłówka i szarytka, a modraszka składa istotnie więcej jaj od
bogatki (test Tukeya; p<0,05).

Badane 4 gatunki sikor różnią się istotnie pod względem liczby składanych jaj
(ANOVA; F3,337=90,62; p<0,0001). Jedynie średnia liczba jaj składanych
przez czarnogłówkę i szarytkę nie różni się istotnie (test Tukeya; p>0,05).

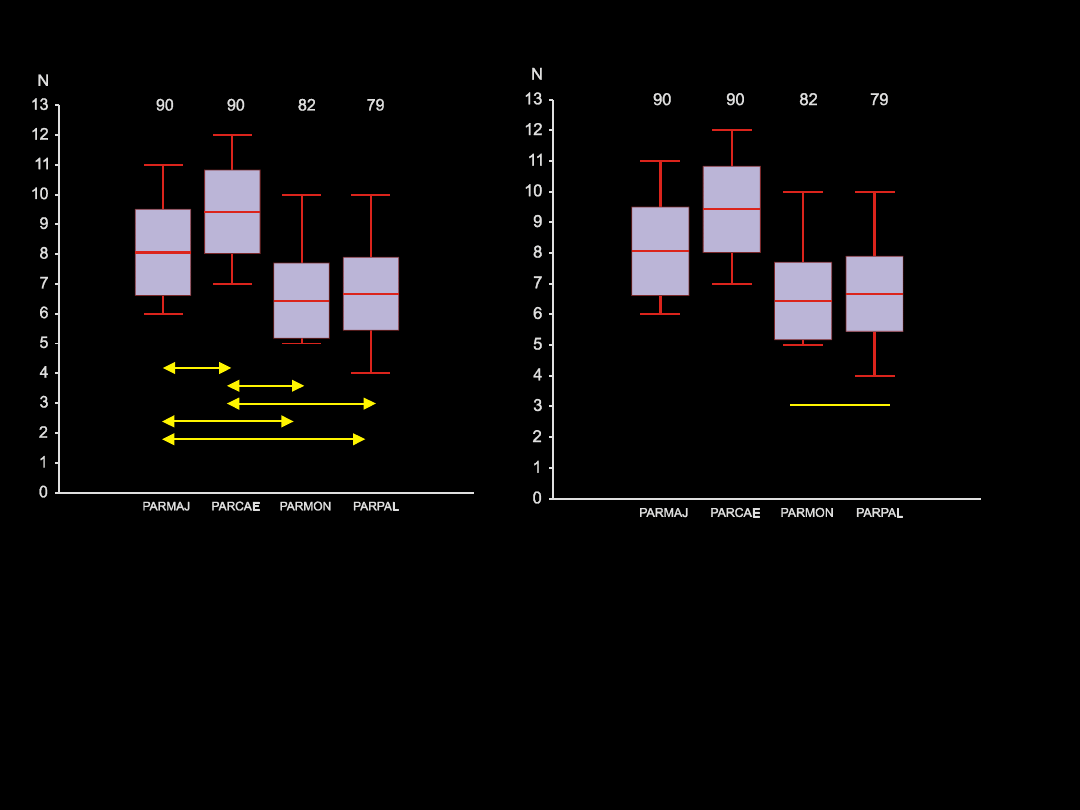
ANALIZA WARIANCJI

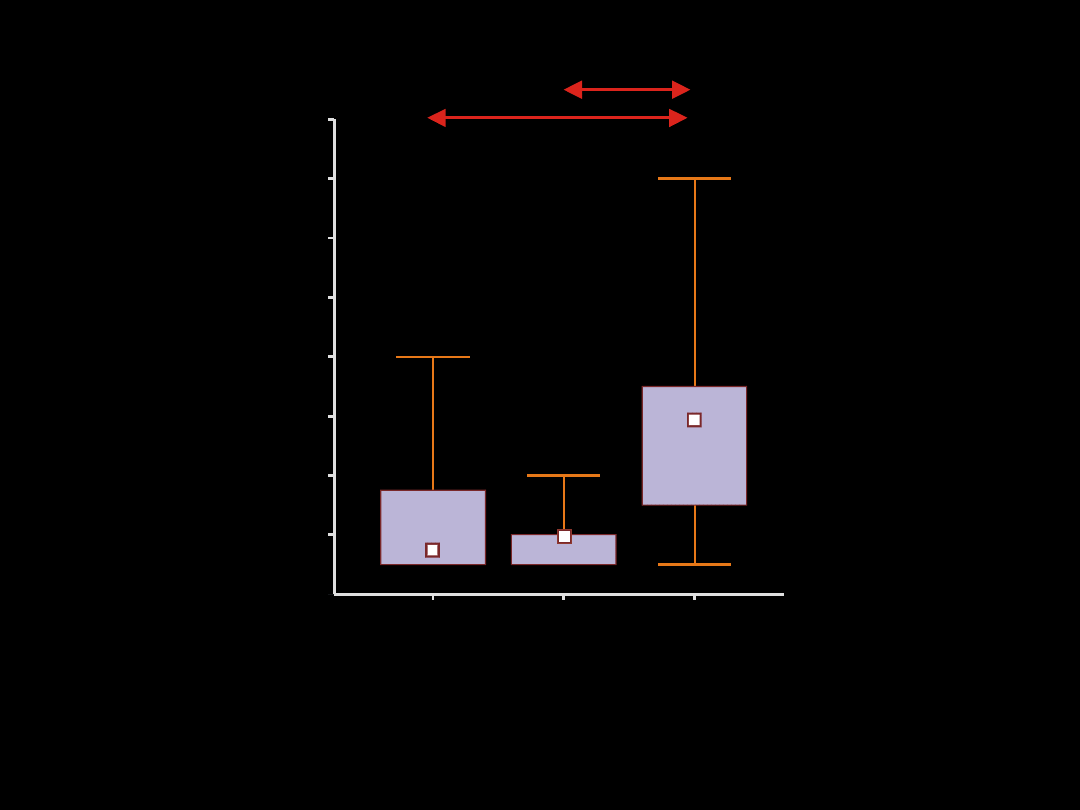
Przykład 13 cd.

Porównanie wielkości zniesienia u
4 gatunków sikor. Linia pozioma –
średnia, prostokąt – odchylenie
standardowe, linia pionowa
zakres. Strzałki oznaczają różnice
istotne statystycznie (test Tukeya;
p<0,05). Nad słupkami podano
liczebności prób.

Porównanie wielkości zniesienia u
4 gatunków sikor. Linia pozioma –
średnia, prostokąt – odchylenie
standardowe, linia pionowa
zakres. zaznaczono grupę
jednorodną (test Tukeya; p>0,05).
Nad słupkami podano liczebności
prób.

ANALIZA WARIANCJI – porównanie z grupą kontrolną

Gdy w eksperymencie jedna z grup jest traktowana jako grupa
kontrolna zalecanym testem post-hoc jest

test Dunetta

ANOVA; F

2,93

=14,77;

p<0,0001

Wylosowano 3 grupy po 32 poletka. W dwóch grupach stosowano
dwa różne nawozy. Trzecią grupę poletek traktowano jako grupę
kontrolną. Należy sprawdzić czy nawozy istotnie zwiększyły plon.

Po odrzuceniu H

0

zastosowano test Dunetta jednostronny, ponieważ w

eksperymencie zakładano zwiększenie plonu, a więc interesujące są tylko te
różnice gdzie średni plon z poletek eksperymentalnych jest większy od
średniego plonu z grupy poletek kontrolnych.

poletka

kontr.

a

0,00006

b

0,88823

p

Jedynie nawóz stosowany w grupie poletek „a” istotnie zwiększa plon

Przykład 14

WIELOCZYNNIKOWA ANALIZA WARIANCJI

ANOVA wieloczynnikowa ocenia wpływ kilku czynników na badaną

zmienną. Pozwala także zbadać istotność interakcji miedzy tymi

czynnikami.

ANOVA wieloczynnikowa wymaga starannego zaplanowania badań,
tak aby liczebność próby była wystarczająca na każdym poziomie
oddziaływania czynników grupujących oraz by w każdej grupie
spełnione były założenia wymagane przy stosowaniu ANOVA.

ANOVA wieloczynnikowa może dotyczyć sytuacji gdy w każdej grupie
występuje 1 pomiar (tzw. ANOVA bez powtórzeń). Np. wpływ
temperatury (10˚C, 20˚C i 30˚C) i czasu naświetlania (4h, 10h i 16h)
na tempo wzrostu fasoli, gdzie dla każdej temperatury i dla każdego
czasu naświetlania eksperyment prowadzono na 1 osobniku fasoli.

czas naświetlania (h)

4 4 4 10 10 10 16 16 16

temperatura (°C)

10 20 30 10 20 30 10 20 30

WIELOCZYNNIKOWA ANALIZA WARIANCJI

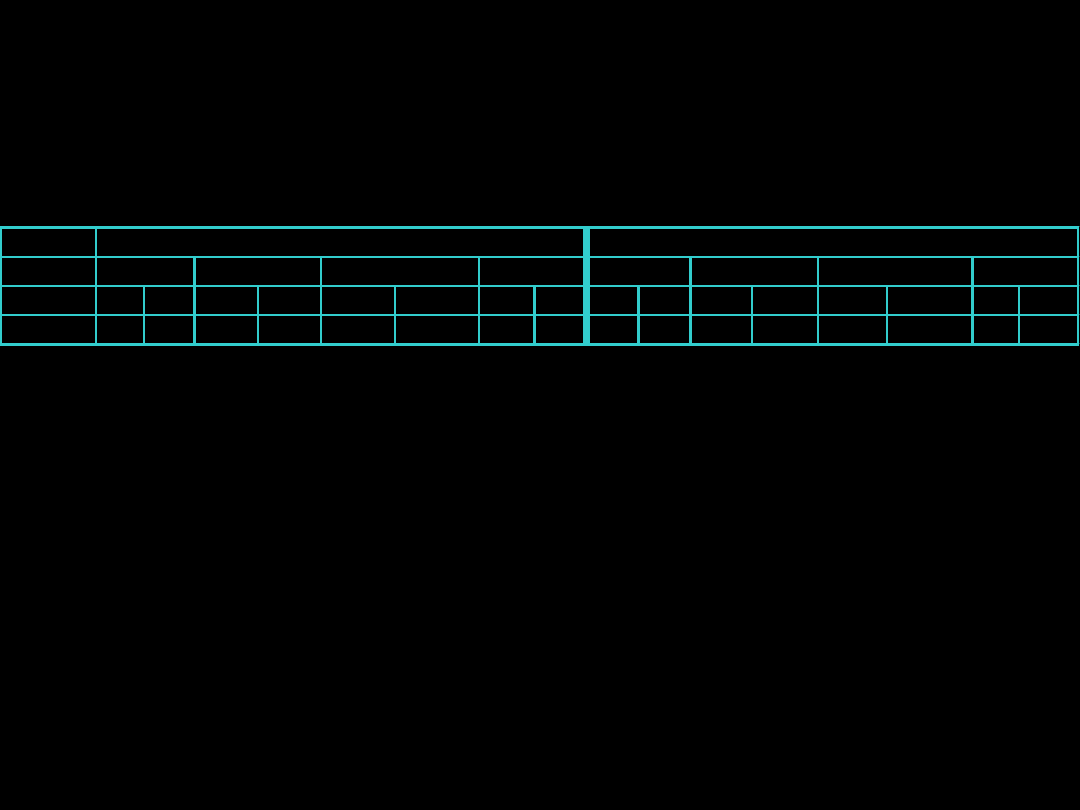
Przykład 15

Badano wielkość zniesienia u 4 gatunków sikor w dwóch typach lasu. Należy
sprawdzić, czy na średnią liczbę składanych jaj wpływa przynależność
gatunkowa i typ lasu.

df

MS

F

p

gatunek

3

165,39

91,30

0,000000

typ lasu

1

3,98

2,20 0,139286

interakcja

3

1,07

0,59 0,621602

Błąd

333

1,81

Wynik ANOVA II

Cztery gatunki sikor różnią się pod względem liczby znoszonych jaj. Liczba
składanych jaj przez te gatunki nie zależy od typu lasu (ANOVA II).

ANOVA II; F

3,333

=91,30;

p<0,0001

ANOVA II; F

1,333

=2,20;

p>0,05

Nie stwierdzono interakcji między czynnikami (między typem lasu i
gatunkiem sikory)

WIELOCZYNNIKOWA ANALIZA WARIANCJI

ANOVA wieloczynnikowa może być przeprowadzona w układzie
hierarchicznym (hierarchiczna ANOVA).

Przykład 16

Za pomocą hierarchicznej ANOVA można ocenić zarówno wpływ typu
lasu na wielkość zniesienia 4 gatunków sikor, jak również wpływ
statusu ochronnego na danym terenie.

gatunek
typ lasu a

b

a

b

a

b

a

b

a

b

a

b

a

b

a

b

N

20 25

26

19

23

18

20 20

25 20

18

27

20

21

20 19

bogatka modraszka czarnogłówka szarytka

bogatka modraszka czarnogłówka szarytka

park narodowy

tereny podmiejskie

ANOVA

Jeśli założenia ANOVA nie są spełnione, to można:

Przeanalizować dane pod kątem występowania pojedynczych
wartości
znacznie odbiegających od pozostałych (tzw. outliers) i sprawdzić, czy
można je wyeliminować.

Dokonać transformacji danych

Usunąć z analizy grupę najbardziej odbiegającą od założeń ANOVA
Zastosować nieparametryczny odpowiednik ANOVA –

test Kruskala-

Wallisa

Log(x),
log(x+1),

x

5

,

0



x

x

x arcsin

'

Rodzaj transformacji dobiera się na podstawie analizy zależności między

średnimi i wariancjami w grupach

Jeśli dane występują w postaci proporcji lub udziałów procentowych
należy je transformować za pomocą funkcji arcussinus

Interpretację wyników analizy danych transformowanych
przeprowadza się tak samo jak analizę danych surowych.

TEST KRUSKALA-WALLISA

Jest to test nieparametryczny, za pomocą którego sprawdzamy H

0

że

badane próby pochodzą z jednej populacji. Test ten bazuje na
rangach pomiarów, a nie na ich wartościach, można więc badać nim
różnice między medianami z poszczególnych prób.

Przy porównywaniu 2 prób jest tożsamy z testem Manna-Whitneya.

Ma zastosowanie do danych w skali porządkowej, interwałowej i
ilorazowej.

Teoretycznie warunkiem do stosowania testu Kruskala-Wallisa jest
równość wariancji w próbach i podobieństwo kształtu ich rozkładów.
Jednak warunek ten pomija się w praktyce, ponieważ nawet duże
odstępstwa od niego nie wpływają znacząco na uzyskiwane wyniki.

Testu Kruskala-Wallisa nie powinno się stosować do danych,
zbieranych w oparciu o skalę pomiarową ze sztucznymi
ograniczeniami, gdzie znaczna część pomiarów wypada na krańcu
skali. W takim przypadku stosuje się

test

mediany dla wielu prób

.

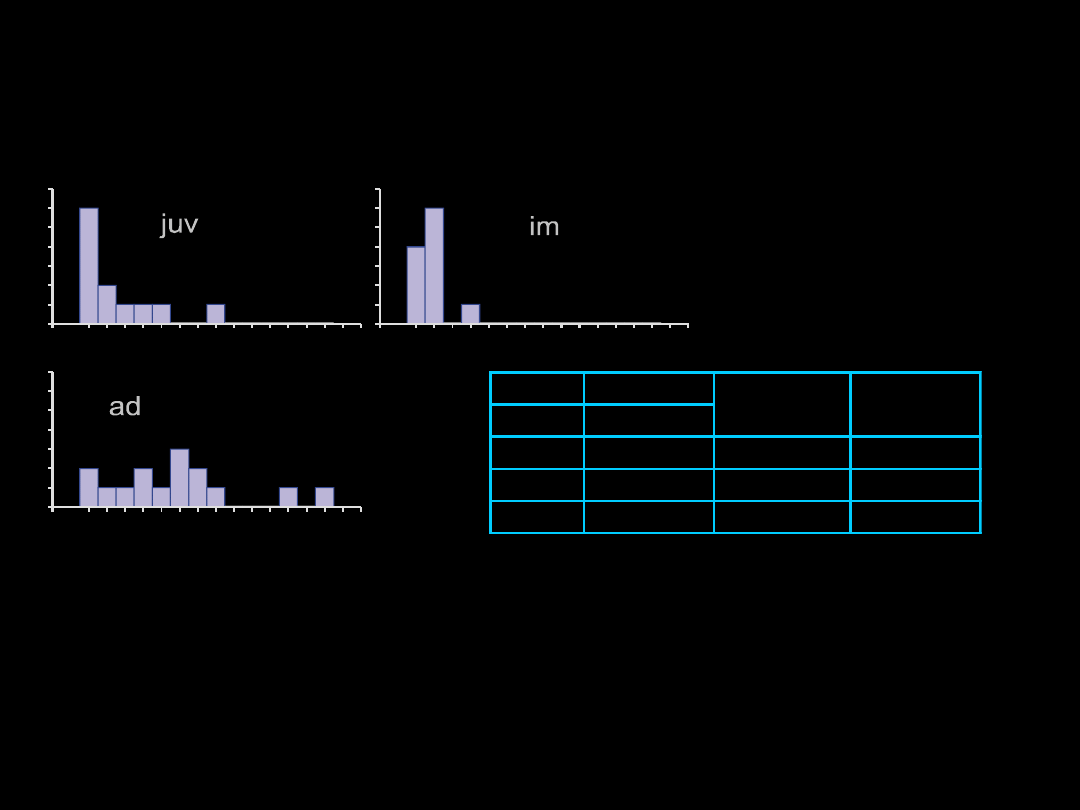
TEST KRUSKALA-WALLISA

Przykład 17

wiek

N

ad

12

185,0

15,4

im

11

153,5

14,0

juv

15

402,5

26,8

Suma rang Średnia

ranga

Badano czas pozostawania ostrygojadów na żerowisku podczas jesiennej migracji na
podstawie ponownych schwytań ptaków zaobrączkowanych. Należy sprawdzić czy ptaki
pierwszoroczne (juv), drugoroczne (im) i dorosłe (ad) różnią się czasem przebywania.

Test Kruskala-Wallisa: H

2,38

=11,42 p

=0,0033

Ptaki pierwszoroczne, drugoroczne i dorosłe istotnie różnią się czasem przybywania na żerowisku.

1

3

5

7

9

1 1

1 3

1

3

5

7

9

1 1

1 3

1

3

5

7

9

1 1

1 3

0

2

4

6

N

0

2

4

6

N

Po odrzuceniu H

0

, podobnie jak w ANOVA trzeba zastosować test

post-hoc, aby dowiedzieć się które grupy różnią się od siebie
istotnie. Testem takim jest

test Dunna.

Test Dunna

x

A

B

S

R

R

Q





Test Dunna wykonujemy po odrzuceniu H

0

przez test Kruskala-Wallisa.

Nie jest on dostępny we wszystkich statystycznych programach
komputerowych

Oblicza się wartość Q według wzoru:
Gdzie R

A

i R

B

oznaczają średnią rangę obliczaną

dla każdej próby (iloraz sumy rang i liczebności
próby)



















B

A

x

n

n

N

N

S

1

1

*

12

)

1

(

*

Mianownik oblicza się według
wzoru:

Gdzie N – suma liczebności wszystkich
prób; n

A

i n

B

– liczebności porównywanych

prób







































B

A

x

n

n

N

t

N

N

S

1

1

*

)

1

(

*

12

12

)

1

(

*

Jeśli obecne są rangi wiązane to wzór ten przybiera
postać:















 



i

i

t

t

t

3

Gdzie:

Gdzie t

i

– liczba elementów w obrębie danej pary wiązanej

Test Dunna

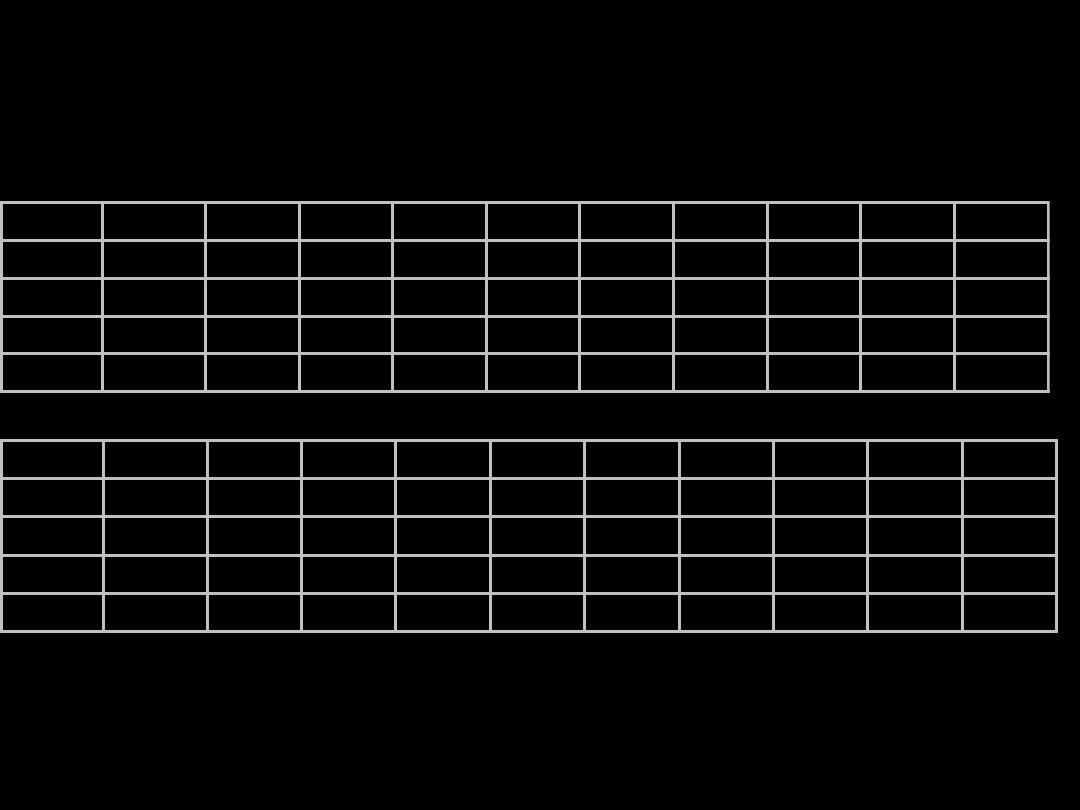
Wartości krytyczne testu Dunna odczytuje się poniższej tablicy dla
określonego poziomu istotności

()

i liczby porównywanych grup

(k)

.

α

k

2

3

4

5

6

7

8

9

10

0,05

1,960 2,394 2,639 2,807 2,936 3,038 3,124 3,197 3,261

0,01

2,576 2,936 3,144 3,291 3,403 3,494 3,570 3,635 3,692

0,005

2,807 3,144 3,342 3,481 3,588 3,675 3,748 3,810 3,865

0,001

3,291 3,588 3,765 3,891 3,988 4,067 4,134 4,191 4,241

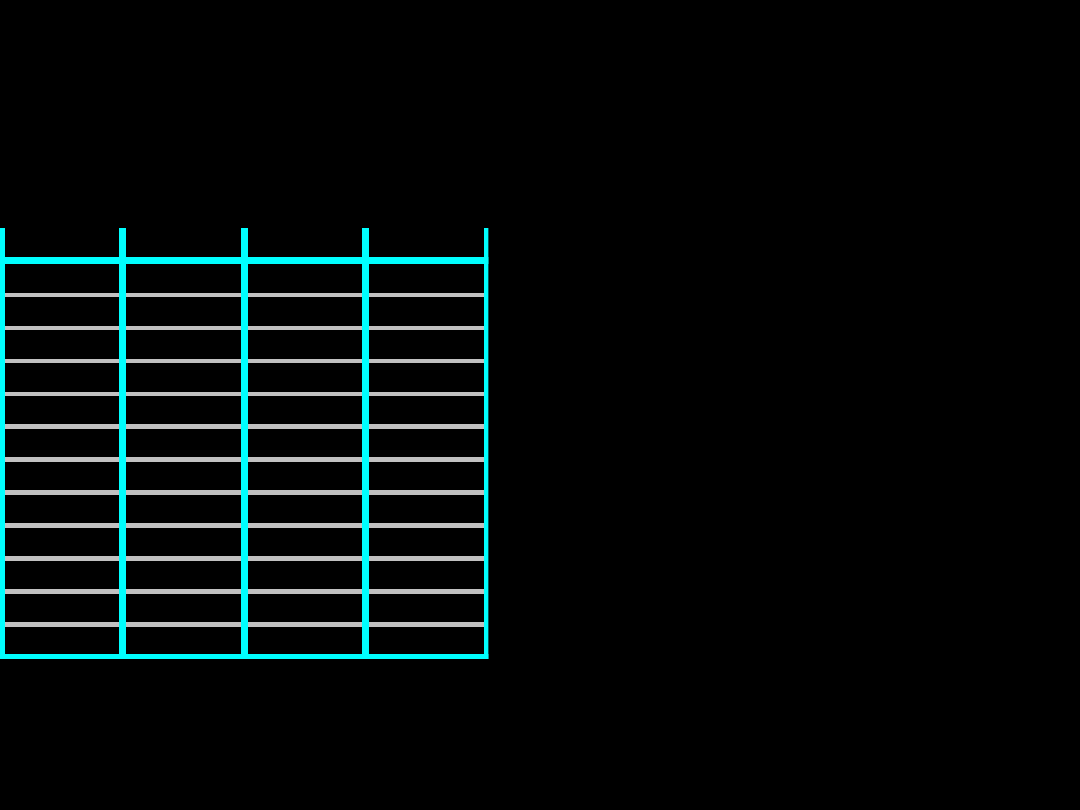
11

12

13

14

15

16

17

18

19

20

0,05

3,317 3,368 3,414 3,456 3,494 3,529 3,562 3,593 3,622 3,649

0,01

3,743 3,789 3,830 3,868 3,902 3,935 3,965 3,993 4,019 4,044

0,005

3,914 3,957 3,997 4,034 4,067 4,098 4,127 4,154 4,179 4,203

0,001

4,286 4,326 4,363 4,397 4,428 4,456 4,483 4,508 4,532 4,554

Np. dla 4 grup i poziomu istotności 0,05 wartość krytyczna wynosi

2,639

Test Dunna

Przykład 18

Badano czas pozostawania ostrygojadów na żerowisku podczas jesiennej migracji na
podstawie ponownych schwytań ptaków zaobrączkowanych. Należy sprawdzić czy ptaki
pierwszoroczne (juv), drugoroczne (im) i dorosłe (ad) różnią się czasem przebywania.

Test Kruskala-Wallisa: H

2,38

=11,42 p

=0,0033

wiek dni wiek dni wiek dni wiek dni

ad

1 ad

2 ad

4

juv

7

ad

1 ad

2

im

4

juv

7

ad

1

im

2

juv

4

ad

1

im

2

juv

4

ad

8

ad

1

im

2

juv

8

ad

1

im

2

ad

5

im

1 im

2

juv

5 juv

12

im

1 im

2

im

1

juv

2 juv

6 juv

14

im

1

juv

6

juv

1

ad

3

juv

6

juv

1 juv

3

Rangi wiązane

Dla 1 dnia – 12 elementów
Dla 2 dni – 9 elementów
Dla 3 dni – 2 elementy
Dla 4 dni – 4 elementy
Dla 5 dni – 2 elementy
Dla 6 dni – 3 elementy
Dla 7 dni – 2 elementy
Dla 8 dni – 2 elementy

)

2

2

(

)

2

2

(

)

3

3

(

)

2

2

(

)

4

4

(

)

2

2

(

)

9

9

(

)

12

12

(

3

3

3

3

3

3

3

3



































t

2544





t

Test Dunna

Przykład 18 cd.

Próby uporzadkowane wg. średniej rangi

juv

ad

im

średnia ranga

26,8

15,4

14,0

n

15

12

11

2544





t

308

,

4

11

1

15

1

*

)

1

38

(

*

12

2544

12

)

1

38

(

*

38

1

1

*

)

1

(

*

12

12

)

1

(

*











































































B

A

x

n

n

N

t

N

N

S

Testowanie rozpoczyna się od prób najbardziej się od siebie
różniących

971

,

2

308

,

4

0

,

14

8

,

26











x

A

B

S

R

R

Q

Q

0,05;3

=2,394

-2,394

2,394

0

2,971

x

Wartość krytyczna

Otrzymana wartość leży w obszarze krytycznym – odrzucamy H

0

.

Ptaki pierwszoroczne i drugoroczne różnią się istotnie pod
względem czasu przebywania na żerowisku.

Test Dunna

Przykład 18 cd.

Próby uporzadkowane wg. średniej rangi

juv

ad

im

średnia ranga

26,8

15,4

14,0

n

15

12

11

Następnie porównujemy kolejną parę, gdzie spodziewamy się istotnej różnicy:
juv-ad.

712

,

2

203

,

4

4

,

15

8

,

26











x

A

B

S

R

R

Q

Q

0,05;3

=2,394

-2,394

2,394

0

2,712

x

Wartość krytyczna

203

,

4

12

1

15

1

*

)

1

38

(

*

12

2544

12

)

1

38

(

*

38





































x

S

Otrzymana wartość leży w obszarze krytycznym – odrzucamy H

0

.

Ptaki pierwszoroczne i dorosłe różnią się istotnie pod względem
czasu przebywania na żerowisku.

Test Dunna

Przykład 18 cd.

Próby uporzadkowane wg. średniej rangi

juv

ad

im

średnia ranga

26,8

15,4

14,0

n

15

12

11

Następnie porównujemy ostatnią parę: im-ad.

481

,

1

945

,

0

0

,

14

4

,

15











x

A

B

S

R

R

Q

Q

0,05;3

=2,394

-2,394

2,394

0

1,481

x

Wartość krytyczna

945

,

0

11

1

12

1

*

)

1

38

(

*

12

2544

12

)

1

38

(

*

38





































x

S

Otrzymana wartość leży poza obszarem krytycznym – nie ma
podstaw do odrzucenia H

0

. Ptaki drugoroczne i dorosłe nie różnią

się istotnie pod względem czasu przebywania na żerowisku.

Test Dunna

Przykład 18 cd.

Ptaki pierwszoroczne, drugoroczne i dorosłe istotnie różnią się
czasem przybywania na żerowisku (test Kruskala-Wallisa; H

2,38

=11,42;

p =0,0033). Ptaki pierwszoroczne pozostają na nim istotnie dłużej niż
drugoroczne i dorosłe (test Dunna; p<0,05).

a d

im

ju v

0

2

4

6

8

1 0

1 2

1 4

1 6

[d n i]

1 5

1 1

1 2

TEST MEDIANY DLA WIELU PRÓB

Testu mediany dla wielu prób testuje H

0

że badanie próby pochodzą z

populacji o takiej samej medianie. Szczególnie zalecany jest, gdy
dane, zbierane są w oparciu o skalę pomiarową ze sztucznymi
ograniczeniami, gdzie znaczna część pomiarów wypada na krańcu
skali.

Podobnie jak w teście mediany dla dwóch prób wyznacza się medianę
łączną dla wszystkich prób, a następnie oblicza ile pomiarów w
poszczególnych próbach leży powyżej, a ile poniżej wspólnej mediany.
Otrzymana w ten sposób tabelę kontyngencji analizuje się za pomocą

testu chi-kwadrat

Przykład 19

Badano czas pozostawania ostrygojadów na żerowisku podczas jesiennej migracji na
podstawie ponownych schwytań ptaków zaobrączkowanych. Należy sprawdzić czy ptaki
pierwszoroczne (juv), drugoroczne (im) i dorosłe (ad) różnią się czasem przebywania.

ad

im

juv

Razem

<=Me

8

10

3

21

>Me

4

1

12

17

Razem

12

11

15

38

TEST MEDIANY;



2

=13,83; p<0,05

Ptaki pierwszoroczne, drugoroczne i dorosłe istotnie różnią się czasem przybywania na żerowisku.

Po odrzuceniu H0, trzeba zastosować test post-hoc, aby dowiedzieć się które grupy
różnią się od siebie istotnie. Testem takim jest

test Levyego.

TEST FRIEDMANA (ANOVA Friedmana)

Test Friedmana jest testem nieparametrycznym, rozwinięciem testu znaków
na więcej niż 2 próby.

Przykład 20

Badano czas reakcji na pojawienie się pokarmu w klatce u 17 młodych samców zięby w
4 kolejnych dniach. Pokarm pojawiał się zawsze w tym samym miejscu klatki, o tej
samej godzinie. Każdy z ptaków trzymany był w oddzielnej klatce. Należy sprawdzić czy
czas reakcji (czas od pojawienia się pokarmu do rozpoczęcia jego pobierania w
sekundach) zmienia się w kolejnych dniach

.

osobn.

dzień 1

dzień 2

dzień 3

dzień 4

1

0,73

1,23

0,83

1,15

2

1,33

1,53

1,48

1,06

3

0,81

0,72

1,34

0,43

…

…

…

…

…

17

1,57

1,39

1,46

0,99

Baza danych
przygotowana do
testu Friedmana

Wyniki testu
Friedmana

Średnia

Suma

ranga

rang

dzień 1

3,2

54,5

1,31

0,25

dzień 2

3,0

51,0

1,30

0,26

dzień 3

2,4

41,5

1,25

0,23

dzień 4

1,4

23,0

1,01

0,25

Średnia

Odch.std

ANOVA Friedmana;



2

17,3

=21,34;

p<0,001

Gdy liczba grup wynosi dwa lepiej jest stosować test Wilcoxona

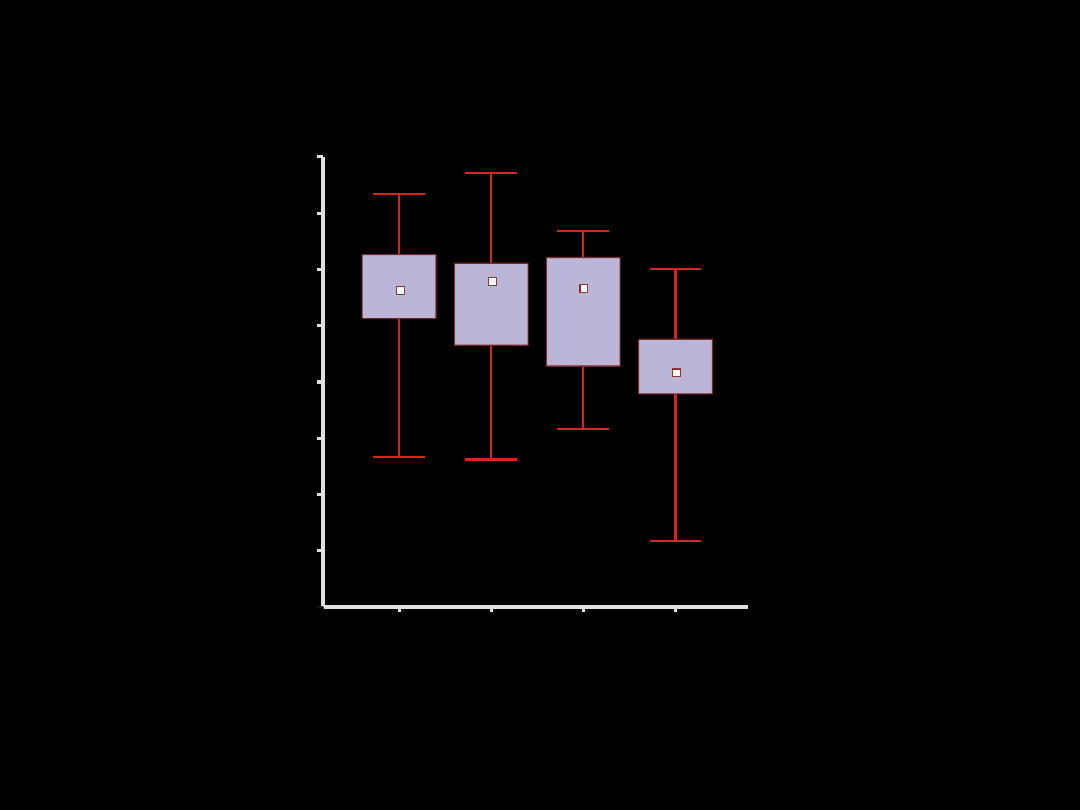
TEST FRIEDMANA (ANOVA Friedmana)

Przykład 20

d z ie ń 1

d z ie ń 2

d z ie ń 3

d z ie ń 4

0 , 2

0 , 4

0 , 6

0 , 8

1 , 0

1 , 2

1 , 4

1 , 6

1 , 8

[s ]

Czas reakcji u badanych ptaków zmienia się istotnie (maleje) w czasie
trwania eksperymentu (ANOVA Friedmana; 

2

17,3

=21,34; p<0,001).