Analiza portfelowa

Literatura: W. Dębski, rozdz.

9

Efektem zarządzania portfelem

inwestycyjnym jest minimalizacja

ryzyka. Przy podejmowaniu

decyzji inwestycyjnych powinno

brać się pod uwagę

oczekiwaną

stopę zysku

(stopa zwrotu) oraz

stopień ryzyka

towarzyszącego

inwestycji (tzn. ile stopa

rzeczywista może się różnić od

oczekiwanej)

Oczekiwana stopa zysku:

• R = p

i

R

i

gdzie:

• R – oczekiwana stopa zysku z danego

papieru wartościowego (w %)

• R

i

– i-ta możliwa wartość stopy zysku

uzyskana z danego papieru wart.

• p

i

- prawdopodobieństwo wystąpienia i-

tej możliwej wartości stopy zysku na
danym papierze wart.

• m - liczba możliwych do osiągnięcia

wartości stopy zysku





m

i 1

W praktyce do obliczenia

oczekiwanej stopy zysku z

akcji korzysta się z danych

przeszłych (np. danych

miesięcznych, kwartalnych,

rocznych)

Korzystając ze wzoru:

• R = R

t

R

t

= (P

t

– P

t-1

+D

t

)/ P

t-

1

– gdzie:

• R

t

– stopa zysku osiągnięta na danym

papierze wart. w okresie t

• n – liczba okresów
• P – cena akcji
• D – wypłacona dywidenda w okresie t





n

t

n

1

1

Przykład 1

Dodatkowym czynnikiem,

który powinien zostać

wzięty pod uwagę przy

podejmowaniu decyzji

inwestycyjnej jest

stopień

ryzyka

. Oblicza się je na

podstawie wariancji

papieru wartościowego

lub odchylenia

standardowego.

Ze względu na

interpretację w praktyce

stosuje się odchylenie

standardowe, czyli

przeciętne odchylenie

możliwych stóp zysku

danego papieru

wartościowego od

oczekiwanej stopy zysku.

Im wyższe odchylenie,

tym większe ryzyko.

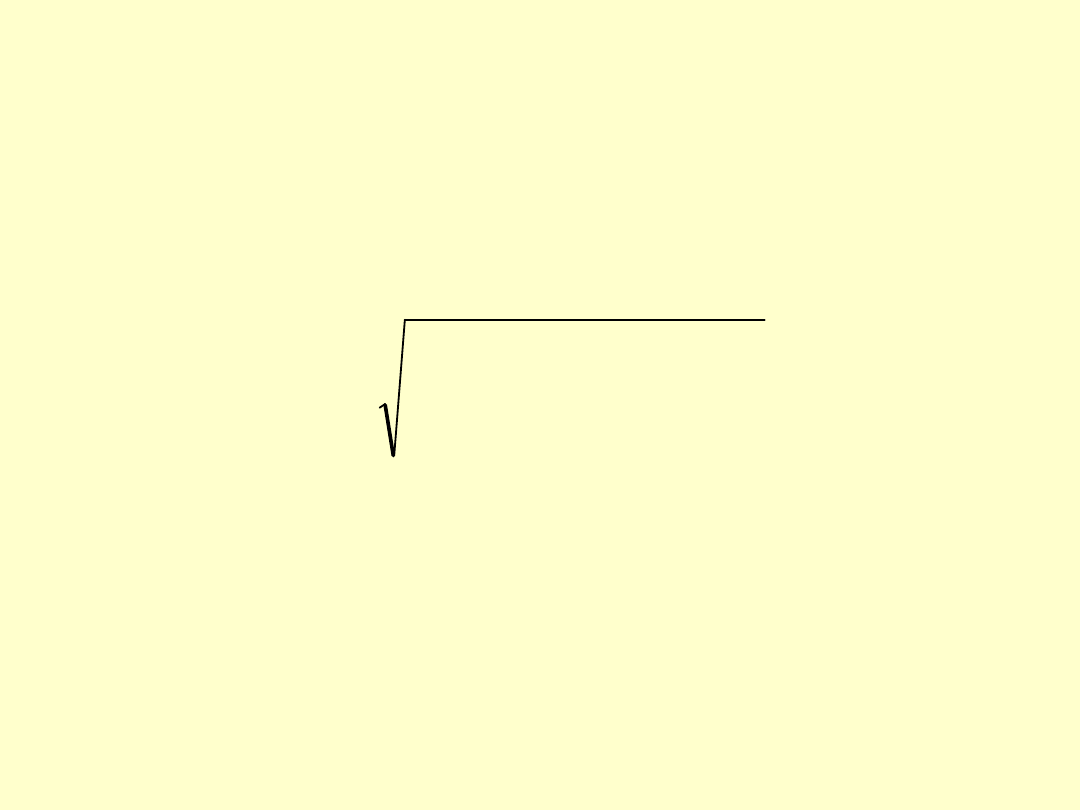
Odchylenie standardowe:

• Ze względu na interpretację w praktyce

stosuje się

czyli przeciętne odchylenie względu na

interpretację w praktyce stosuje się odchylenie
standardowe, czyli przeciętne odchylenie
możliwych stóp zysku danego papieru
wartościowego od oczekiwanej stopy zysku. Im
wyższe odchylenie, tym większe ryzyko. stóp
zysku danego papieru wartościowego od
oczekiwanej stopy zysku. Im wyższe
odchylenie, tym większe ryzyko.











m

i

t

n

R

R

1

2

)

1

/(

]

)

(

[



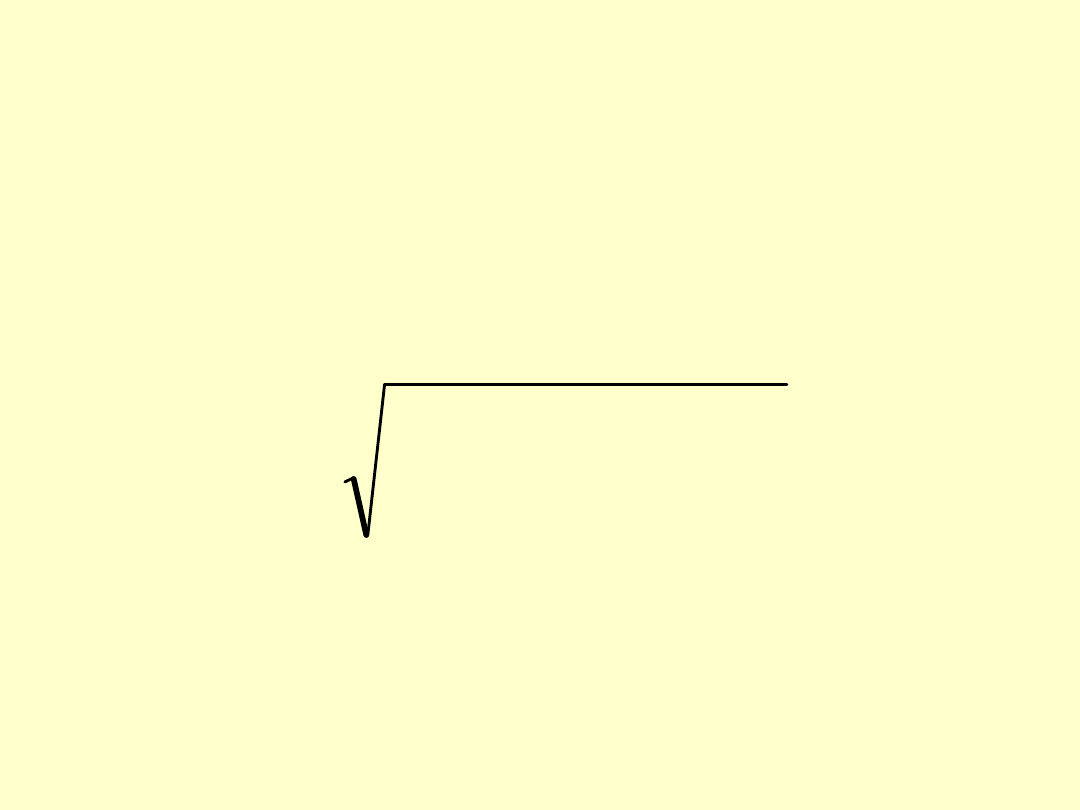
Biorąc pod uwagę jedynie

niekorzystne odchylenia (wartości

ujemne), możemy policzyć

semiodchylenie standardowe,

korzystając ze wzoru:

gdzie: d

i

=R

i

-R dla R

i

<R oraz 0 dla

R

i

>=R









m

t

t

n

d

S

1

2

)

1

/(

)

(



Racjonalnie postępujący

inwestor będzie maksymalizował

stopę zwrotu przy minimalizacji

ryzyka!

Powinno się stosować

zasadę minimalnego ryzyka

względem zysku, co obliczamy

według wzoru:

dla R0

R

V





Przykład 2

W praktyce portfel

inwestycyjny składa się z

różnych papierów

wartościowych

lub z

różnych akcji.

Wtedy oczekiwaną stopę zysku z

portfela liczy się w następujący

sposób:

• R

p

=

dla i=1,2,....n U

i

=P

i

n

i

/

Gdzie:
- R

p

- oczekiwana stopa zysku portfela

- R

i

– oczekiwana stopa zysku z posiadania

i-tej akcji

- n – ilość akcji (aktywów) w portfelu
- n

i

– liczba sztuk i-tej akcji

- U

i

– udział i-tej akcji w portfelu

- P

i

- cena rynkowa i-tej akcji

i

n

i

i

R

U



1

i

n

i

i

n

P



1

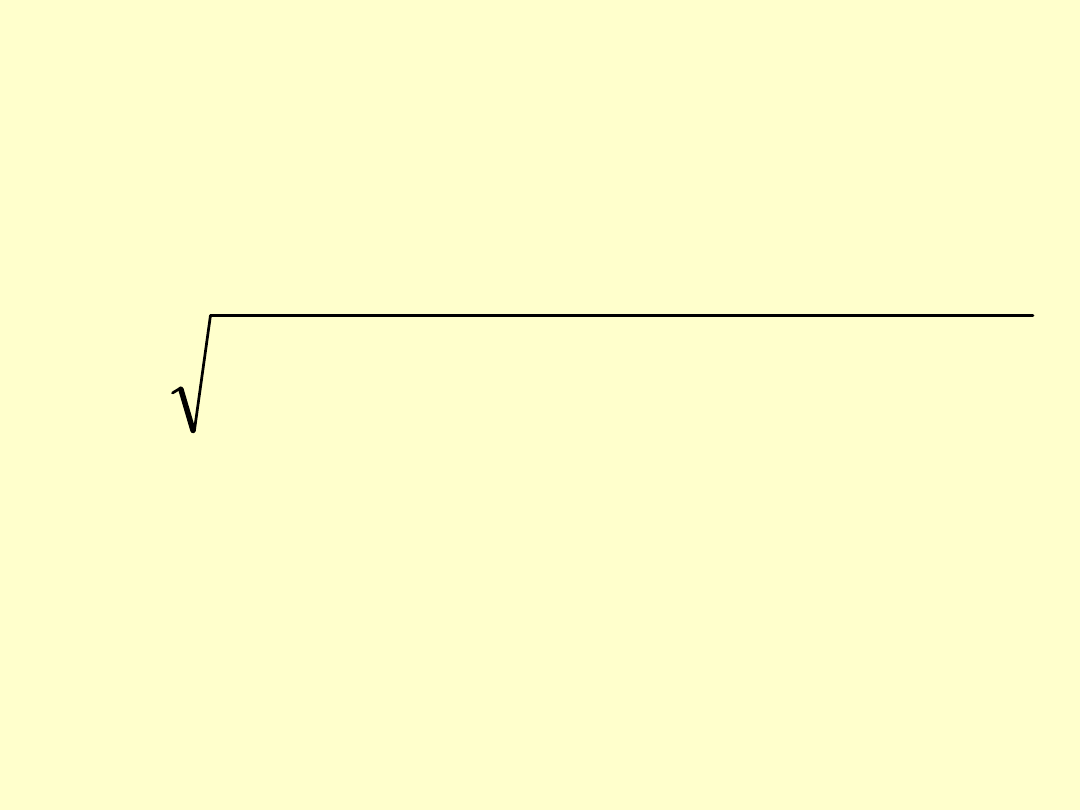
Stopień ryzyka (dla portfela

składającego się z dwóch różnych

papierów wartościowych):

gdzie: - współczynnik

korelacji (mierzy stopień powiązania

stóp zysku dwóch papierów

wartościowych).



12

2

1

2

1

2

2

2

2

2

1

2

1

2













U

U

U

U

p







Współczynnik korelacji:

• przyjmuje wartości [-1,1]
• Im wyższa wartość bezwzględna tym

silniejsze powiązanie stóp zysku

• Wartość dodatnia wskazuje, że

wzrostowi stopy zysku jednego
papieru wartościowego towarzyszy
wzrost stopy zysku drugiego papieru
wartościowego. I odwrotnie.

Redukcję ryzyka portfela

inwestycyjnego można

osiągnąć również gdy w

portfelu będą znajdować

się papiery wartościowe

silnie nieskorelowane

dodatnio.

Analiza portfelowa

c.d.

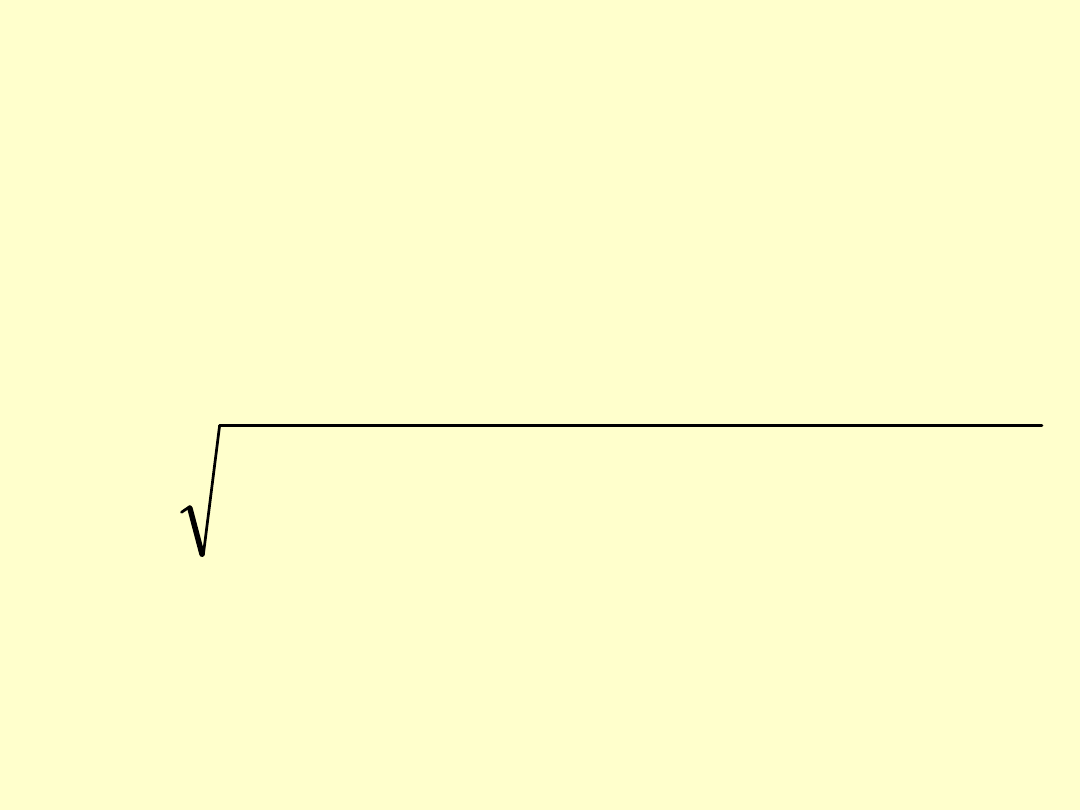
Portfel

dwuskładnikowy:

R

p

= U

1

R

1

+ U

2

R

2

12

2

1

2

1

2

2

2

2

2

1

2

1

2













U

U

U

U

p







Przypadek 1:

doskonała korelacja

dodatnia, współczynnik

korelacji = 1

przykład 1

• Wniosek: zawsze zmniejszenie

ryzyka odbywa się kosztem spadku
stopy zwrotu

Przypadek 2:

doskonała korelacja

ujemna, współczynnik

korelacji = -1

Przykład 2

Przypadek 3:

całkowity brak korelacji,

współczynnik korelacji = 0

Przykład 3

Wnioski:

• Znaczną redukcję ryzyka portfela

dwuskładnikowego można osiągnąć
poprzez zmiany w składzie portfela.

• Zazwyczaj przejście z portfela

jednoskładnikowego do portfela
dwuskładnikowego zmniejsza ryzyko,
jednocześnie w niektórych przypadkach
zwiększając stopę zwrotu. Jest to

dywersyfikacja

portfela.