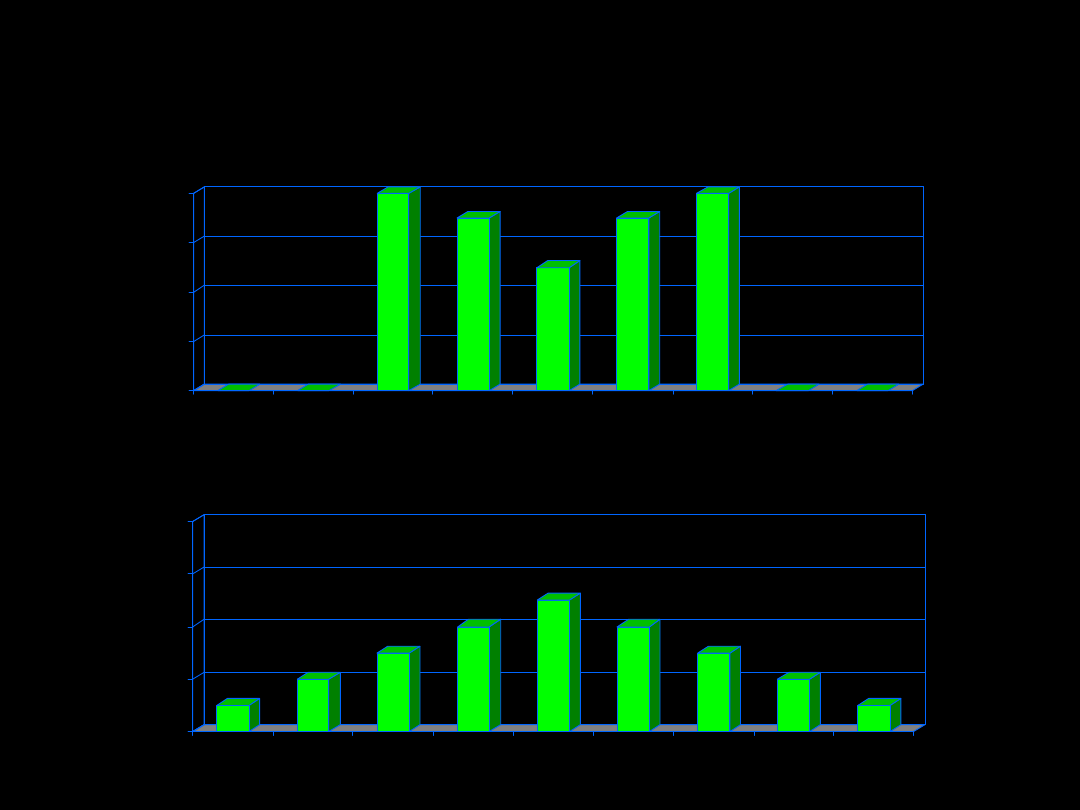
Rozkład liczby jaj w gniazdach dwóch gatunków
ptaków
0
2
4
6
8
1
2
3
3
4
5
6
7
8
0
2
4
6
8
1
2
3
3
4
5
6
7
8
N
N
liczba jaj
liczba jaj
Próbę (populację) charakteryzuje się
za pomocą następujących statystyk
(parametrów):
• Miary położenia
• centralne
- charakteryzują
przeciętny
poziom wartości
zmiennej
•
kwantyle
- wartości zmiennej,
które
dzielą uporządkowany
zbiór danych na
określone części
•
Miary (wskaźniki) rozproszenia
-
oceniają
rozrzut wartości
zmiennej
• klasyczne
• pozycyjne
• Miary zmienności
Modalna
(Moda) (M
0
)- wartość zmiennej, która występuje
najczęściej
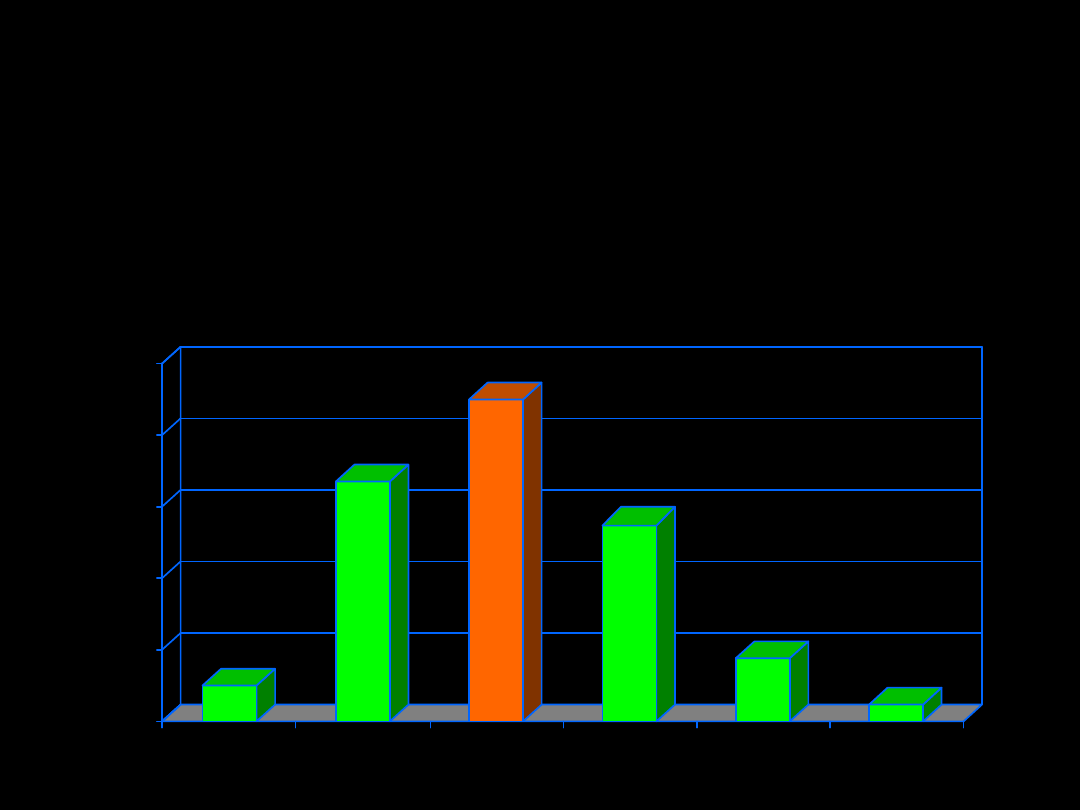
CENTRALNE MIARY
POŁOŻENIA
0
20
40
60
80
100
1
2
3
4
5
6
Liczba plam na pokrywie pewnego gatunku chrząszcza
Rozkład jednomodalny
N
Modalna
0
20
40
60
80
100
1
2
3
4
5
6
3,5
N
• dla małych prób wyznaczenie mody jest często
problematyczne
• w praktyce ma bardzo ograniczone zastosowanie
Modalna
1
-
1
0
1
-
0
0
n
-
n
-
n
*
2
n
-
n
*
h
x
Mo
Dla szeregów rozdzielczych wartość modalną
wyznacza się ze wzoru interpolacyjnego
x
0
- dolna granica przedziału mody (modalnego)
h - szerokość przedziału
n
0
- liczebność w przedziale mody
n
0+1
- liczebność przedziału następnego po modalnym
n
0-1
- liczebność przedziału poprzedzającego
Dla szeregów rozdzielczych (nawet gdy próba jest duża) jej
wartość jest uzależniona od przyjętego podziału na
klasy
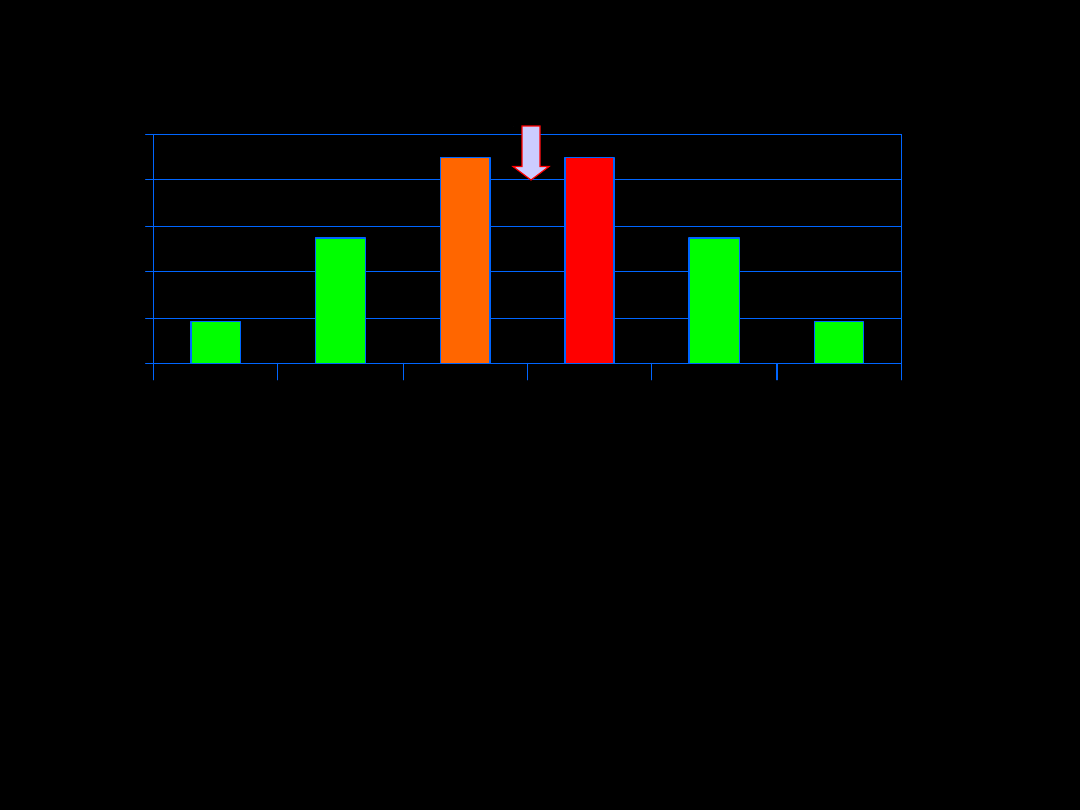
Rozkłady wielomodalne
(świadczą o niejednorodności zbioru danych)
0
20
40
60
80
100
1
2
3
4
5
6
Liczba plam na pokrywie pewnego gatunku chrząszcza
Rozkład dwumodalny
(bimodalny)
0
20
40
60
80
100
1
2
3
4
5
6
Rozkład trójmodalny
(trimodalny)
CENTRALNE MIARY POŁOŻENIA
Średnia arytmetyczna
- suma wszystkich wartości
zmiennej
podzielona przez ich liczebność
•służy do oszacowania średniej populacji; wraz ze
wzrostem liczebności próby jej wartość jest coraz
bliższa średniej populacji
•ma zastosowanie do danych w skali interwałowej i
ilorazowej
•duży wpływ na jej wartość mają wartości skrajne
zmiennej, zwłaszcza przy małej liczebności próby
• obliczanie jej dla rozkładów znacznie odbiegających
od normalnego nie ma sensu
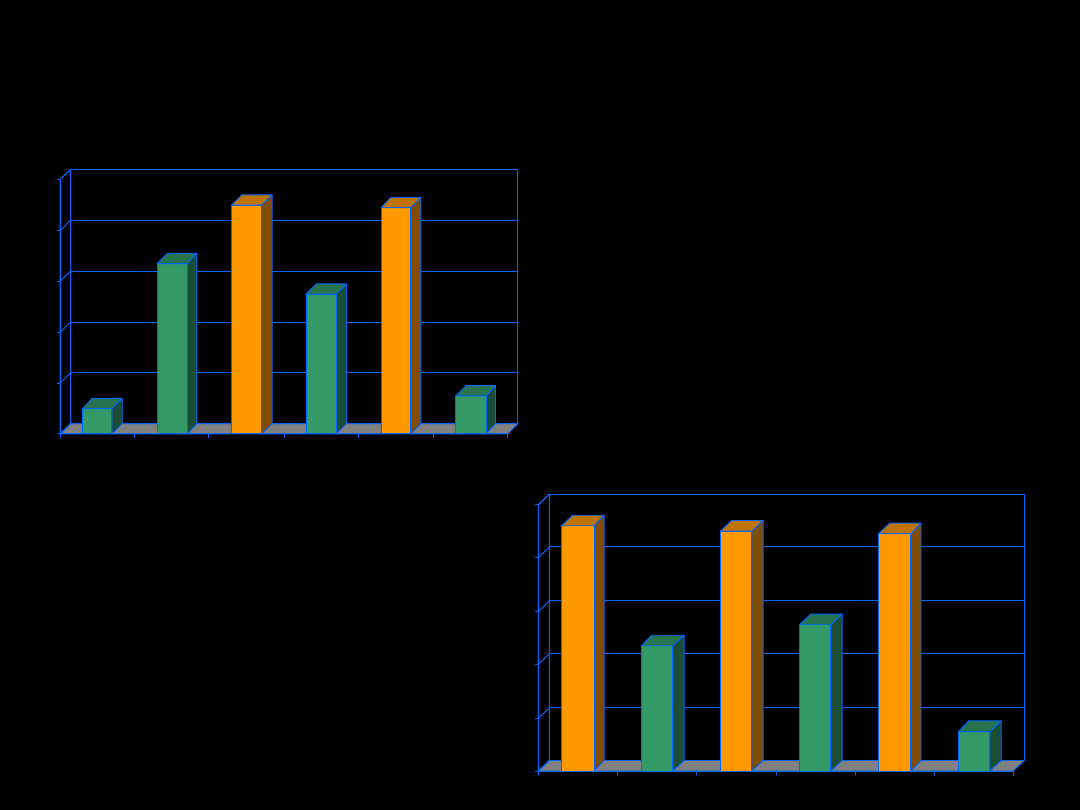
x
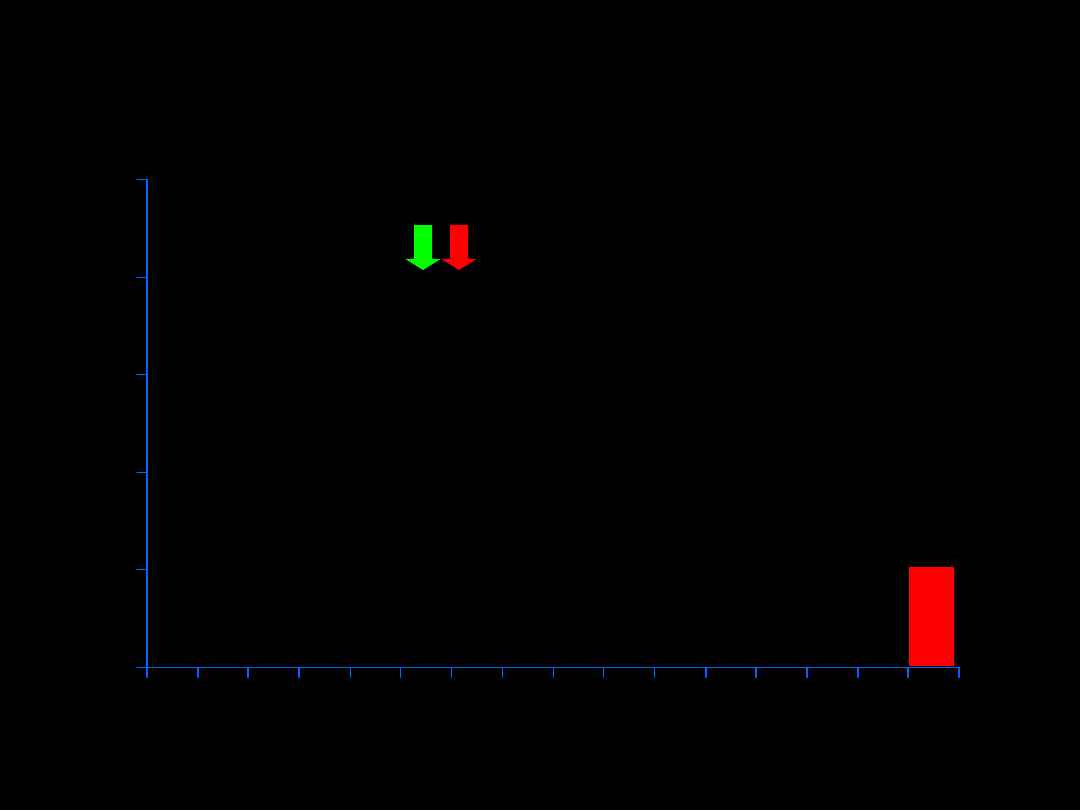
0
1
2
3
4
5
20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35
N
[mm]
Rozkład długości skrzydła pewnego gatunku motyla
2
5
,0
m
m
N=16
2
5
,6
m
m
N=17
0
20
40
60
80
100
120
20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35
N
[mm]
=27,4
x
Rozkład długości skrzydła pewnego gatunku motyla
Średnia arytmetyczna ważona
Stosuje się ją, gdy obliczamy średnią z już obliczonych
średnich i gdy nie są one równocenne, np.: różna
liczebność prób, różna powierzchnia badawcza z której
pobrano próby, różna dokładność pomiarów.
w
i
- tzw. waga. Może to być np.liczebność próby, powierzchnia lasu,
itp. Przy obliczaniu średniej z pomiarów mierzonych z różną
dokładnością wagi są odwrotnością kwadratów błędu.
n
i
1
i
i
n
i
1
i
i
i
w
w
x
*
w
x
Średnia arytmetyczna ważona
Należy obliczyć średnią pierśnicę sosen o określonym wieku,
rosnących w danym kompleksie leśnym
Osoba
mierząc
a
Średnia
[cm]
N
A
75,0
5
B
68,3
20
C
69,2
30
D
60,5
100
7
,
63
)
100
30
20
5
(
)
100
*
5
,
60
(
)
30
*
2
,
69
(
)
20
*
3
,
68
(
)
5
*
0
,
75
(
w
x
*
w
x
n
i
1
i
i
n
i
1
i
i
i
w
=68,
2
x
Wynik obliczenia średniej ze średnich uzyskanych przez
poszczególne osoby
Średnia arytmetyczna ważona
Należy obliczyć średnią pierśnicę sosen o określonym wieku,
rosnących w danym kompleksie leśnym
7
,
75
1
1
1
1
1
1
......
5
1
5
1
5
1
5
1
1
1
*
83
1
1
*
85
1
1
*
79
......
5
1
*
70
5
1
*
65
5
1
*
70
5
1
*
60
w
x
*
w
x
2
2
2
2
2
2
2
2
2
2
2
2
2
2
n
i
1
i
i
n
i
1
i
i
i
w
=72,
0
x
Wynik obliczenia średniej ze wszystkich
wyników
1) 60; 70; 65; 70; 55; 60; 80; 75; 75; 70 – dokładność 5 cm
2) 59; 71; 69; 82; 66; 78; 88; 79; 85; 83 – dokładność 1 cm
Dwie osoby otrzymały następujące wyniki w cm
Przy obliczaniu średniej z pomiarów mierzonych z różną dokładnością wagi są
odwrotnością kwadratów błędu.
średnia geometryczna
- stosuje się ją gdy wyniki
zmieniają się w przybliżeniu w postępie geometrycznym.
Np. obliczając średnią ze współczynników śmiertelności lub
przyrostu w szeregach czasowych.
n
n
3
2
1
G
x
*
...
*
x
*
x
*
x
X
średnia harmoniczna
-służy do obliczania tzw.
efektywnej wielkości populacji (genetyka populacyjna) lub
przy obliczaniu średniej wartości z pomiarów, które różnią
się od siebie o kilka rzędów wielkości.
n
i
1
i
i
H
x
1
n
x
• Można ją stosować do liczb dodatnich
• Pozwala nadać większe znaczenie mniejszym wartościom w zbiorze
danych
Obliczanie średniej geometrycznej ma sens tylko dla liczb
nieujemnych
Jeśli jeden z elementów jest równy 0, to średnia geometryczna też
równa się 0.
KWANTYLE
KWANTYLE
-
wartości, które dzielą zbiór danych na
części o jednakowej liczbie elementów.
Do najczęściej stosowanych należą:
•
Kwartyle
(wartości ćwiartkowe) - podział na 4 części
•
mediana = drugi kwartyl (dzieli zbiór na 2 części)
•
Decyle
- podział na 10 części
•
Percentyle
(centyle) - podział na 100 części
Mają zastosowanie do danych w skali interwałowej,
ilorazowej i porządkowej
Wyznaczanie decyli ma sens gdy liczebność próby jest duża (N100)
Mediana
(Me) – (drugi kwartyl) wartość środkowa, która
dzieli uporządkowany zbiór danych na dwie równe części.
Oznacza to, że tyle samo pomiarów znajduje się powyżej i
poniżej mediany. Gdy liczba pomiarów jest parzysta, to
oblicza się średnią z dwóch sąsiadujących, środkowych
elementów.
MEDIANA
•
na jej wartość nie mają wpływu wartości skrajne
• może być stosowana w przypadku rozkładów różnych od
normalnego
• może być stosowana do skali interwałowej, ilorazowej i
porządkowej
• żeby wyznaczyć medianę nie musimy dysponować wszystkimi
pomiarami - trzeba tylko znać ich pozycję w
uporządkowanym szeregu
np: 0, 1, 2, 5, 6, 7, 9 Me = 5
np: 0, 1, 2, 5, 6, 7, 9, 11 Me = 5,5
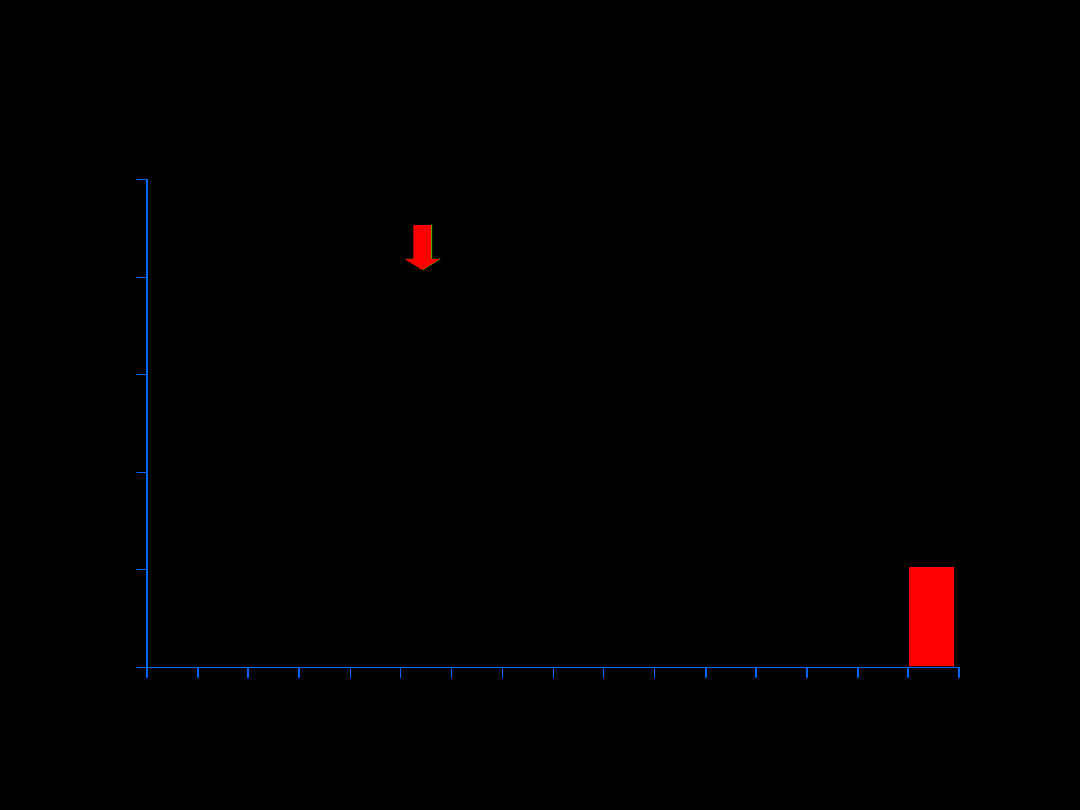
N
[mm]
0
1
2
3
4
5
20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35
Rozkład długości skrzydła pewnego gatunku motyla
2
5
m
m
N=16
N=17
2
5
m
m
0
1
2
3
4
5
20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35
N
[mm]
2
5
,0
m
m
Me=
x
W rozkładach symetrycznych mediana równa się średniej arytmetycznej
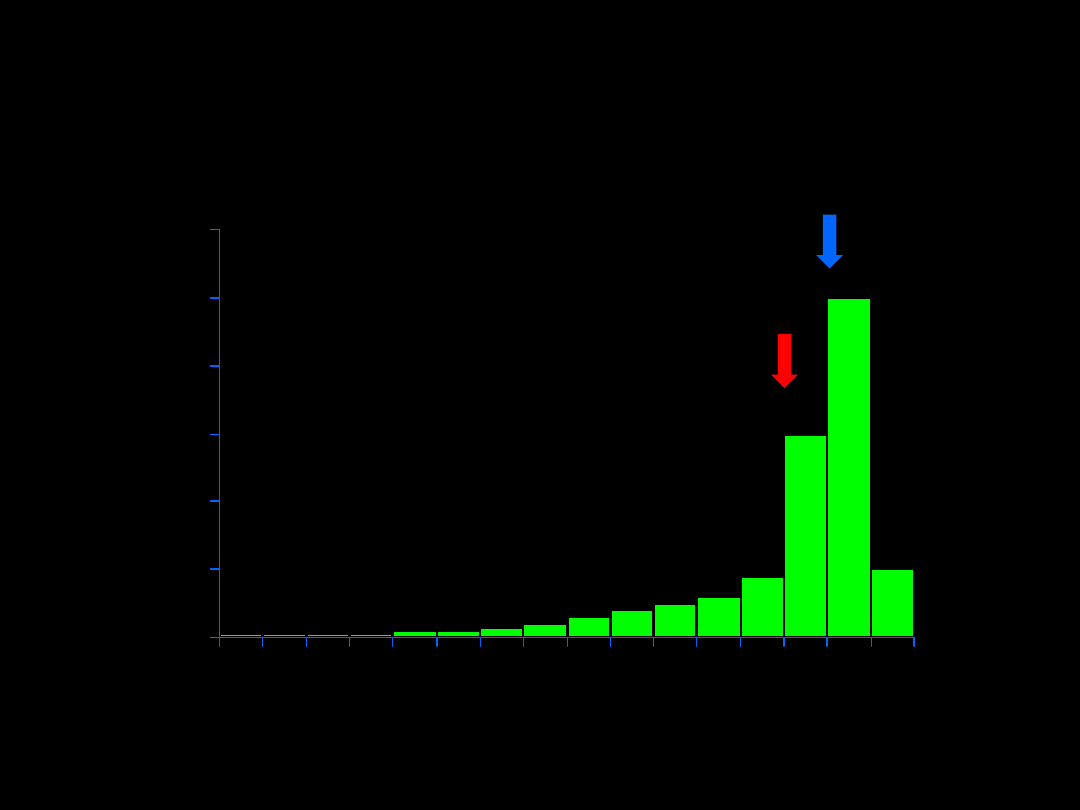
0
20
40
60
80
100
120
20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35
Me=33,5
N
[mm]
=32,5
x
Mediana i średnia arytmetyczna w rozkładach skośnych
o
o
o
F
2
N
*
n
h
x
Me
x
0
- dolna granica przedziału mediany
h - szerokość przedziału
n
0
- liczebność w przedziale mediany
N - liczebność próby
F
0
- liczebność skumulowana przedziału poprzedniego
Jeśli występują rangi wiązane, lub gdy dane
pogrupowane są w szereg przedziałowy, to do
wyznaczenia mediany zaleca się stosować wzór
interpolacyjny
MEDIANA
WYZNACZANIE MEDIANY DLA DANYCH CIĄGŁYCH
• Gdy liczba pomiarów jest nieparzysta, to medianę
stanowi wartość środkowego elementu szeregu.
• Gdy liczba pomiarów jest parzysta, to oblicza się średnią
z dwóch sąsiadujących, środkowych elementów.
• Jeśli dane pogrupowane są w szereg przedziałowy, to
medianę stanowi środek przedziału, w którym ona się
znajduje.
MEDIANA
WYZNACZANIE MEDIANY DLA DANYCH NIECIĄGŁYCH
Liczba
dni
N
1-4
32
5-9
16
10-13
2
14-17
2
Me=2,5
N=52
Dane nieciągłe
Ciężar
nasiona
[g]
N
1-4
32
5-9
16
10-13
2
14-17
2
Me=3,3
N=52
Dane ciągłe
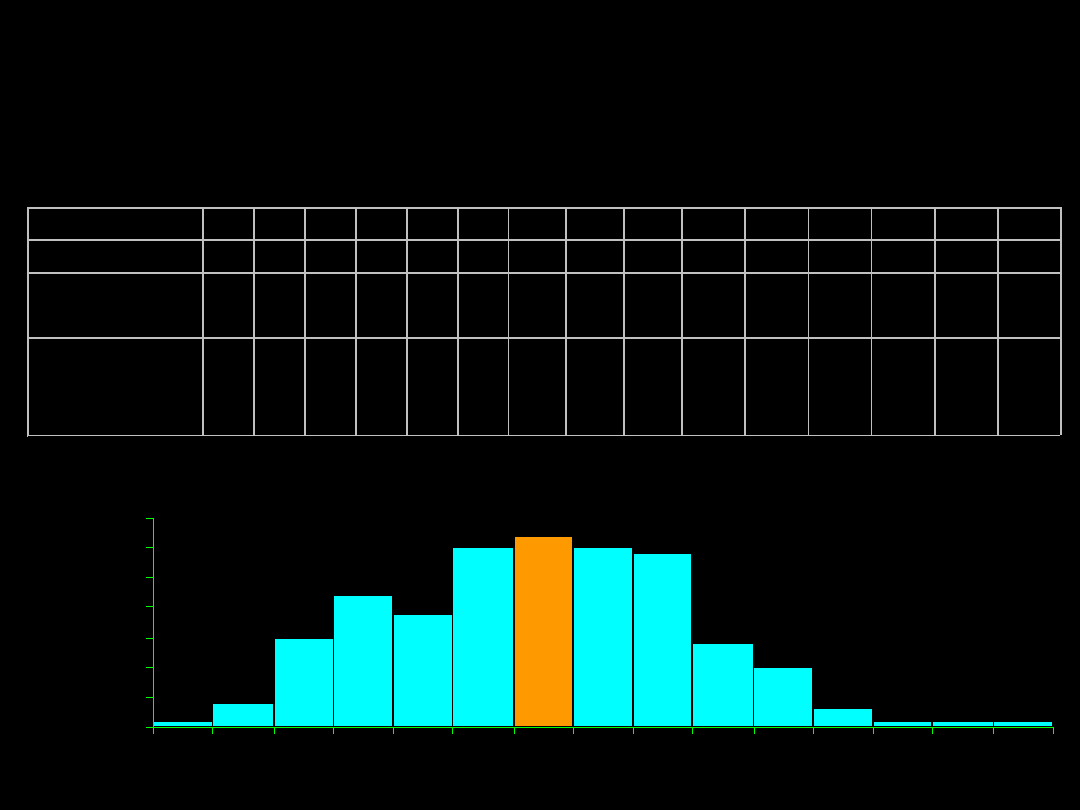
Mediana ma też zastosowanie przy analizie zjawisk
fenologicznych do obliczania środkowej (przeciętnej) daty
np. przelotu, pojawu, kwitnienia itp.
data
1 V 2 V 3 V 4 V 5 V 6 V
7 V
8 V 9 V 10 V 11 V 12 V 13 V 14 V 15 V
liczebność
1
4 15 22 19 30
32
30
29
14
10
3
1
1
1
szereg
skumulowany
1
5 20 42 61 91
123
153 182 196 206 209 210 211 212
szereg
procentowy
skumulowany
0
2
9 20 29 43
58
72
86
92
97
99
99 100 100
Liczba osobników pewnego gatunku rośliny zakwitających w kolejnych dniach
0
5
10
15
20
25
30
35
1 V
2 V
3 V
4 V
5 V
6 V
7 V
8 V
9 V 10 V 11 V 12 V 13 V 14 V 15 V
N
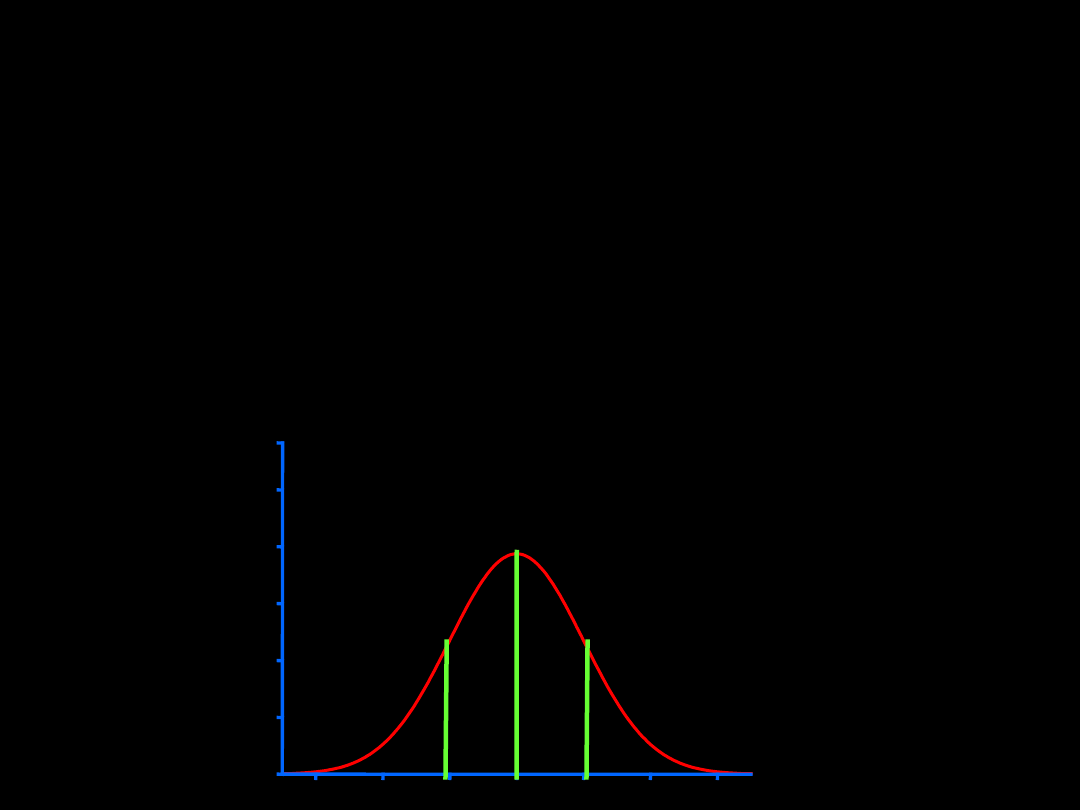
drugi kwartyl (Q
2
) = mediana
Pierwszy kwartyl
(Q
1
) - 25% elementów zbioru ma wartości nie
większe, a 75% nie mniejsze od tego elementu.
Trzeci kwartyl
(Q
3
) - 75% elementów zbioru ma wartości nie
większe, a 25% nie mniejsze od tego elementu.
KWARTYLE
-3
-2
-1
0
1
2
3
0,0
0,1
0,2
0,3
0,4
0,5
0,6
25%
25%
25%
25%
wartości, które dzielą uporządkowany zbiór danych na
cztery równe części
WYZNACZANIE PIERWSZEGO I
TRZECIEGO KWARTYLA
A: 1, 2, 4, 5, 8, 12, 13, 18, 22 (N=9)
B: 1, 2, 4, 5, 8, 12, 13, 18, 22,
25 (N=10)
4
X
Q
)
1
n
(
1
1
)
1
n
(
3
Q
X
Q
wynik zaokrągla się do najbliższej liczby
będącej wielokrotnością 0,5
(13+18)/2=
25,5
X
(8)
=
18
OBLICZANIE KWARTYLI DLA DANYCH NIECIĄGŁYCH
)
5
,
2
(
)
1
9
(
1
4
X
X
Q
(2+4)/2=
3
)
5
,
7
(
)
5
,
2
(
)
1
9
(
1
X
X
X
Q
)
3
(
)
75
,
2
(
)
1
10
(
1
4
X
X
X
Q
(2+4)/2=
3
)
8
(
)
3
(
)
1
10
(
1
X
X
X
Q
Jeśli występują rangi wiązane, lub gdy dane pogrupowane są w
szereg przedziałowy, to do wyznaczenia kwartyli zaleca się stosować
wzór interpolacyjny
o
o
o
1
F
4
N
*
n
h
x
Q
o
o
o
3
F
4
3N
*
n
h
x
Q
x
0
- dolna granica przedziału pierwszego lub trzeciego
kwartyla
h - szerokość przedziału
n
0
- liczebność przedziału pierwszego lub trzeciego
kwartyla
N - liczebność próby
F
0
- liczebność skumulowana przedziału poprzedniego
OBLICZANIE KWARTYLI DLA DANYCH CIĄGŁYCH
WYZNACZANIE PIERWSZEGO I
TRZECIEGO KWARTYLA
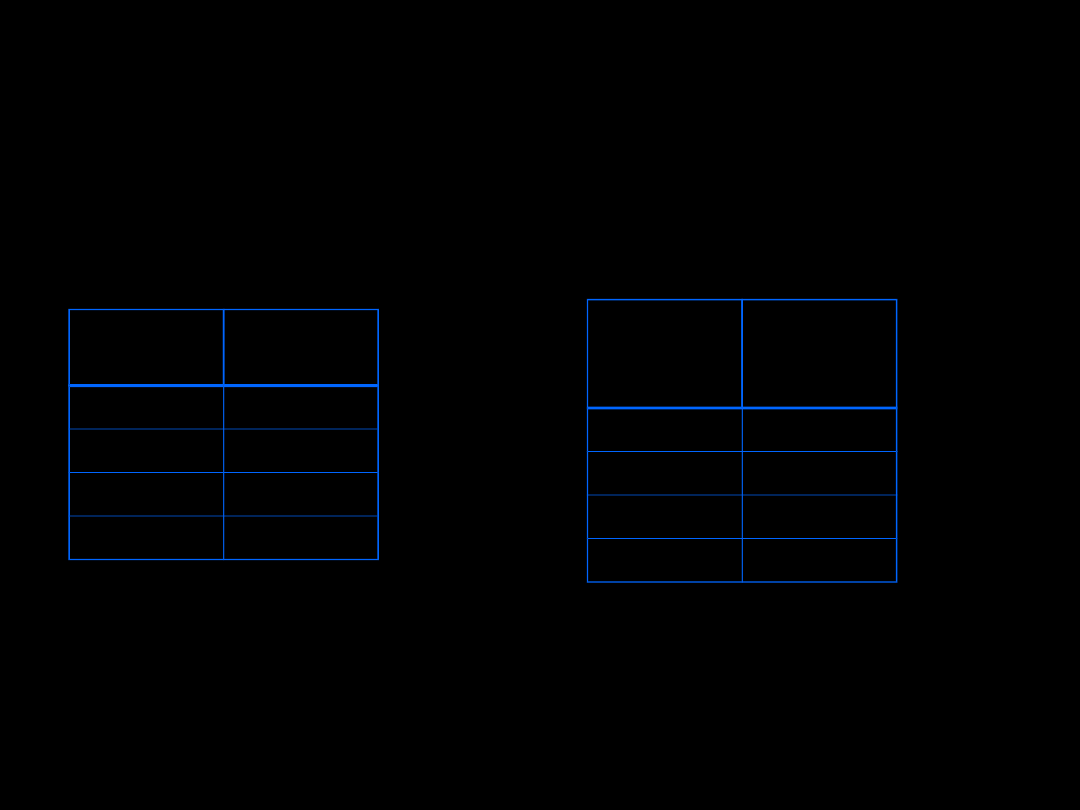
WYZNACZANIE PIERWSZEGO I
TRZECIEGO KWARTYLA
Liczba
dni
N
2
2
3
32
4
16
5
2
Ciężar
nasiona
[g]
N
2
2
3
32
4
16
5
2
Me=3
N=52
Dane nieciągłe
Me=3,3
N=52
Dane ciągłe
Q
1
=3
Q
3
=4
Q
1
=2,8
Q
3
=3,7
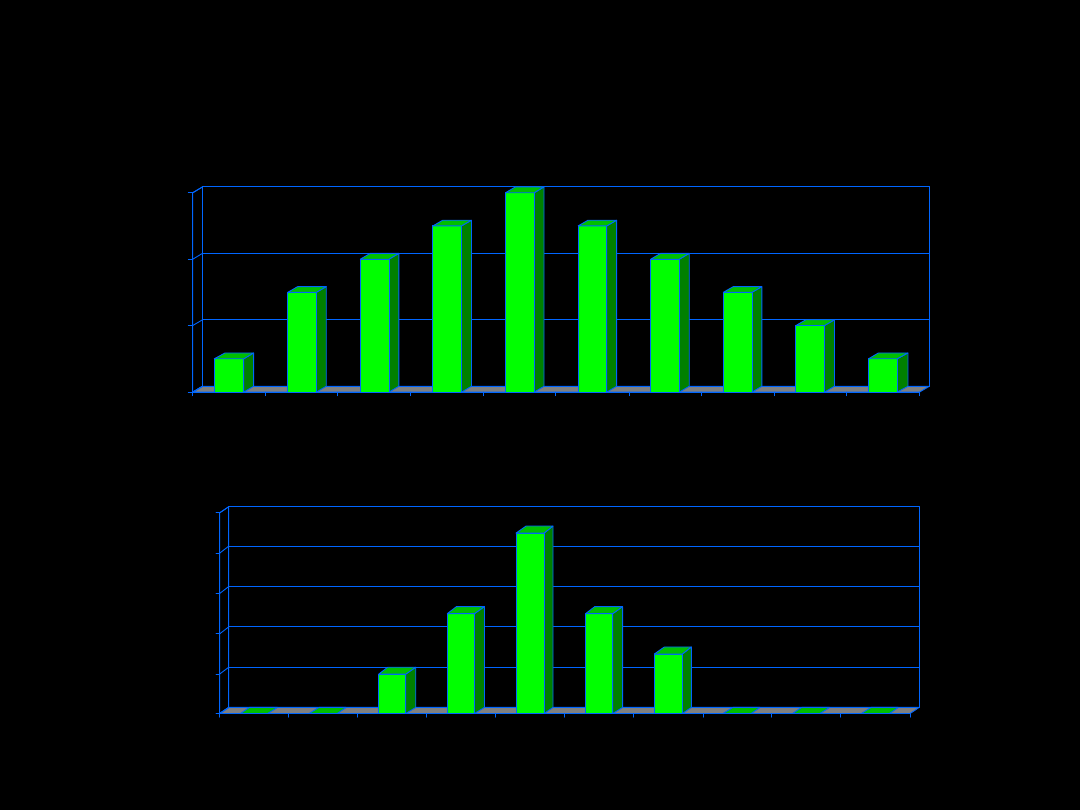
MIARY ROZPROSZENIA
Rozkład liczby nasion w strąkach pewnej rośliny
0
2
4
6
1
2
3
3
4
5
6
7
8
9
N
N
0
2
4
6
8
10
1 2 3 3 4 5 6 7 8 9
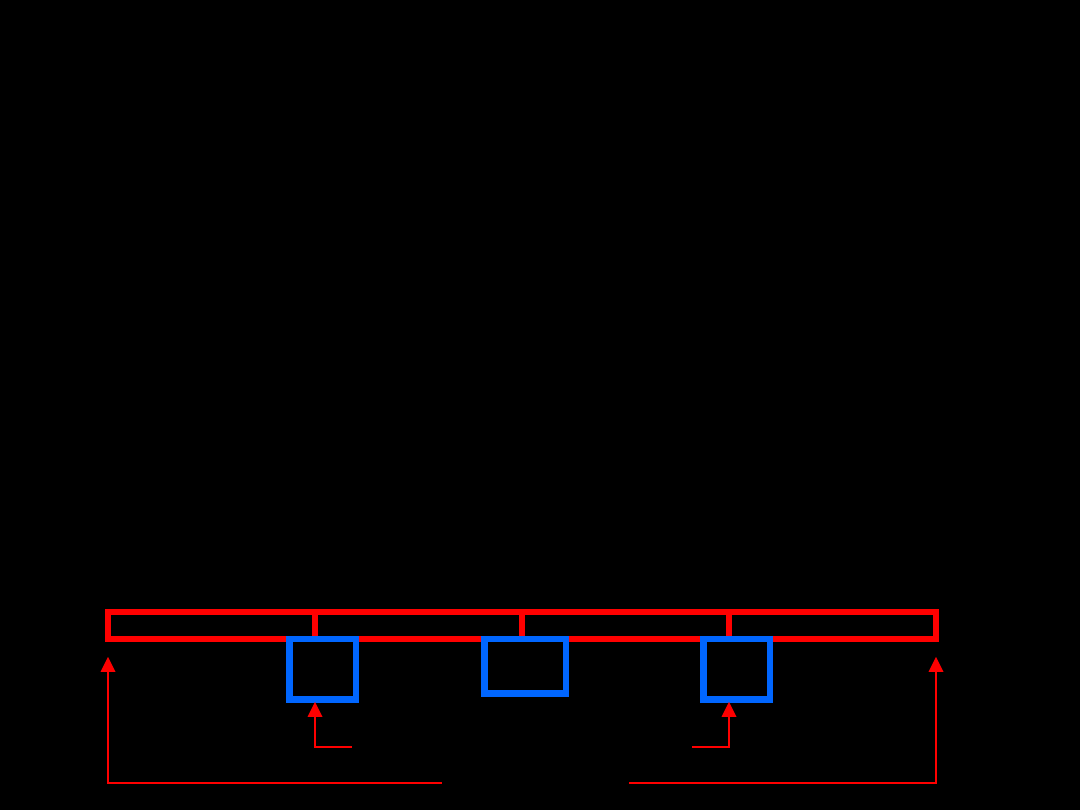
Rozstęp
- różnica między największą i najmniejszą
wartością w zbiorze danych
Określają go tylko dwie skrajne wartości, a pozostałe
pomiary nie mają wpływu na jego wartość
Częściej podaje się zamiast niego zakres od 5% do 95%
wszystkich wartości wokół średniej arytmetycznej (lub
mediany)
Rozstęp międzykwartylarny
(międzykwartylowy)
(kwartylny) (odchylenie ćwiartkowe)
- różnica miedzy
trzecim i pierwszym kwartylem.
Jest to część zbioru danych zawierająca 50% wszystkich
wartości wokół średniej arytmetycznej (lub mediany)
Me
Q
3
Q
1
Rozstęp
Odchylenie ćwiartkowe
Odchylenie standardowe i wariancja
1. Obliczyć średnią arytmetyczną
2. Odjąć od każdego elementu szeregu średnią - otrzymuje się
odchylenia od
średniej
3. Podnosimy każdą wartość odchylenia od średniej do kwadratu i
sumujemy je otrzymując sumę kwadratów odchyleń
4. Obliczamy wariancję
2
1
1
2
n
x
x
s
n
i
i
Odchylenie standardowe wyrażone jest w tych samych jednostkach,
co średnia arytmetyczna
.
Informuje o ile średnio poszczególne pomiary różnią się od średniej,
czyli jaki jest błąd bezwzględny pojedynczego wyniku.
Jest najważniejszą miarą rozrzutu danych wokół średniej
5. Odchylenie standardowe jest pierwiastkiem kwadratowym z wariancji
Współczynnik zmienności
•
Dotyczy tylko skali ilorazowej
•
Wynik często mnoży się przez 100 aby wyrazić go w procentach
•
Umożliwia porównanie zmienności szeregów statystycznych
różniących się
znacznie wartością średniej
x
s
V
W przypadku małych prób stosuje się zmodyfikowany wzór
x
s
*
n
*
4
1
1
V
n
x
s
odchylenie standardowe
średnia arytmetyczna
liczebność próby
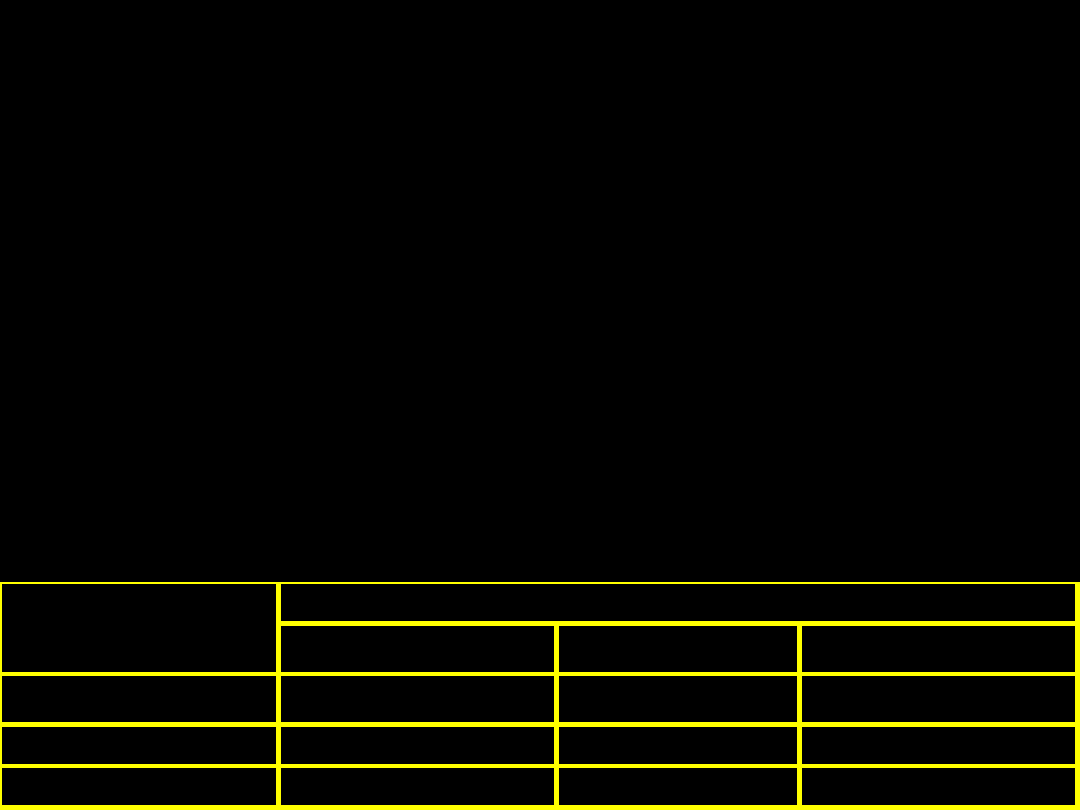
Wskaźnik różnorodności biologicznej
Dla danych w skali nominalnej
WSKAŹNIK RÓŻNORODNOŚCI SHANNON-
WIENERA
(wskaźnik Shanon-Weavera)
log - logarytm o podstawie dziesiętnej ale może być dowolny
logarytm, ponieważ można przeliczać wartości logarytmów o różnej
podstawie:
n
)
f
log(
*
f
)
n
log(
*
n
'
H
k
i
1
i
k - liczba kategorii; f - liczba obserwacji w danej kategorii
Wartości do przeliczania logarytmów o różnej podstawie
Podstawa 2 (log
2
) Podstawa e (ln) Podstawa 10 (log)
Podstawa 2 (log
2
)
1,0000
1,4427
3,3219
Podstawa e (ln)
0,6931
1,0000
2,3026
Podstawa 10 (log)
0,3010
0,4343
1,0000
Przeliczanie z:
Przeliczanie na:
max
'
H
'
H
'
J
Wskaźnik jednorodności
(J’)
odnosi
obserwowaną różnorodność do maksymalnej
możliwej różnorodności:
Teoretyczna, maksymalna
różnorodność
)
k
log(
'
H
max
•
Jeśli na 20 drzew aż 19 to brzozy, mówimy o bardzo niskiej
zmienności
(różnorodności)
• Jeśli na 20 drzew odnotowaliśmy po 5 brzóz, grabów, klonów i
buków,
mówimy o bardzo wysokiej zmienności
(różnorodności)
wartość współczynnika różnorodności zależy od liczby kategorii (gatunków)
PRZYKŁAD:
H’=0,68
(k=5)
H’=0,68
(k=10)
H’max= log 5 = 0,6989 = 0,70
H’max= log
10 = 1,00
J’ = 0,97
J’=0,68
PODSUMOWANIE
•
Rozkład jednomodalny i względnie symetryczny -
średnia arytmetyczna
•
Rozkład jednomodalny i niesymetryczny -
mediana
•
Rozkład wielomodalny -
wartości modalne
Do skali porządkowej nie stosuje się wzorów interpolacyjnych
Skala interwałowa
Skala ilorazowa
Skala porządkowa
Skala nominalna
Modalna
Mediana
(kwantyle)
Średnia arytmetyczna
Modalna
Mediana
(kwantyle)
Średnia arytmetyczna
Modalna
Mediana
(kwantyle)
Miary położenia
PODSUMOWANIE
•
Średnia arytmetyczna ------
Odchylenie standardowe
•
Mediana ------------------------
Odchylenie ćwiartkowe
Skala interwałowa Skala ilorazowa Skala porządkowa Skala nominalna
Rozstępy
Odchylenie
standardowe
Rozstępy
Odchylenie
standardowe
Współczynnik
zmienności
Rozstępy
Wskaźnik
różnorodności
Miary rozproszenia i zmienności
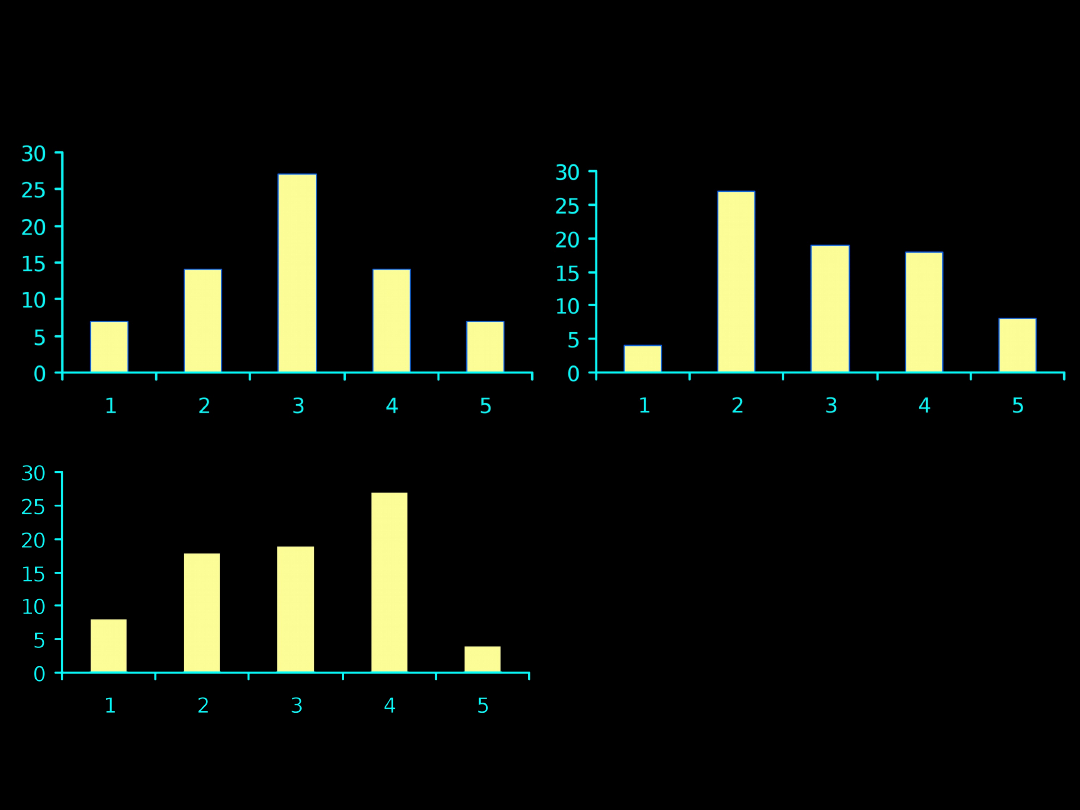
MIARA SKOŚNOŚCI (SYMETRII) ROZKŁADU
średnia arytmetyczna = 3,0
odchylenie standardowe = 1,11
N
N
N
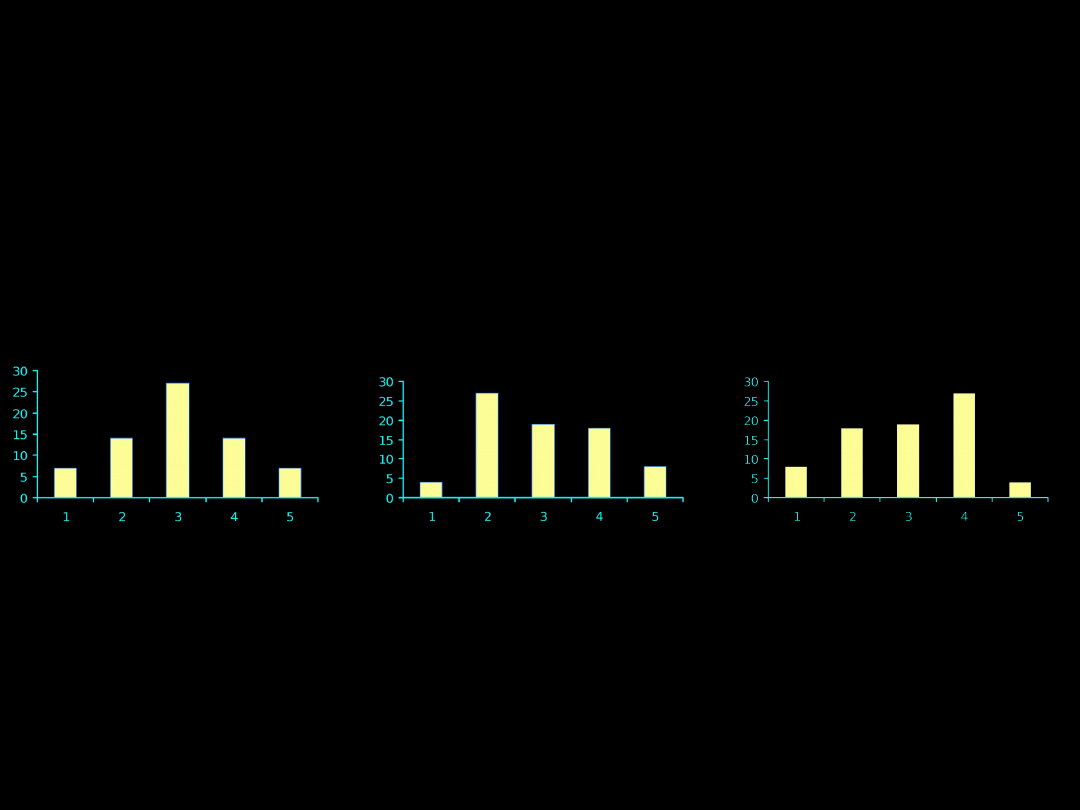
MIARA SKOŚNOŚCI (SYMETRII) ROZKŁADU
Współczynnik skośności (asymetrii) rozkładu
• gdy jest równy 0 – rozkład idealnie symetryczny
(A)
• gdy jest dodatni – rozkład prawoskośny
(B)
• gdy jest ujemny – rozkład lewoskośny
(C)
(A)
(B)
(C)
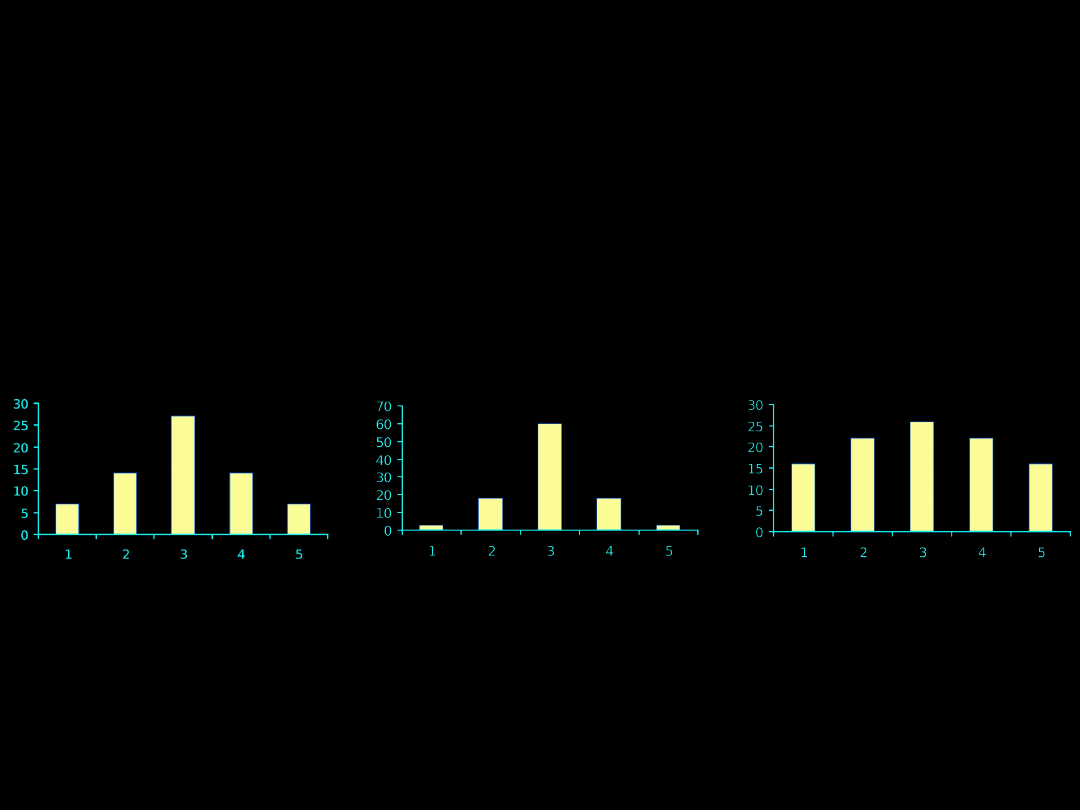
MIARA KONCENTRACJI (SPŁASZCZENIA) ROZKŁADU
Kurtoza
• gdy jest równa 0 – rozkład normalny (mezokurtyczny)
(A)
• gdy jest dodatnia – rozkład wysmukły (leptokurtyczny)
(B)
• gdy jest ujemna – rozkład spłaszczony (platykurtyczny)
(C)
(A
)
(B
)
(C)
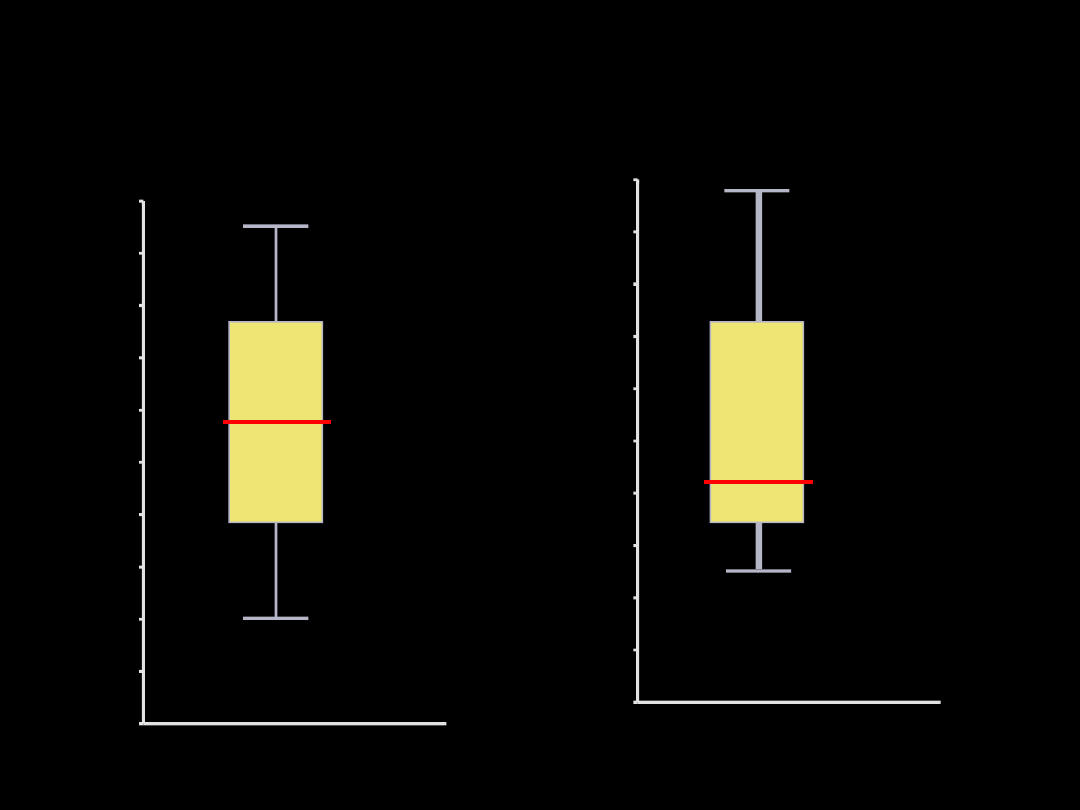
Wykres ramkowy
(wykres „pudełko z wąsami”)
10
20
12
14
16
18
[kg]
10
20
12
14
16
18
[kg]
x
+ s
- s
max
min
max
min
Me
Q3
Q1
Dla średniej arytmetycznej
Dla mediany
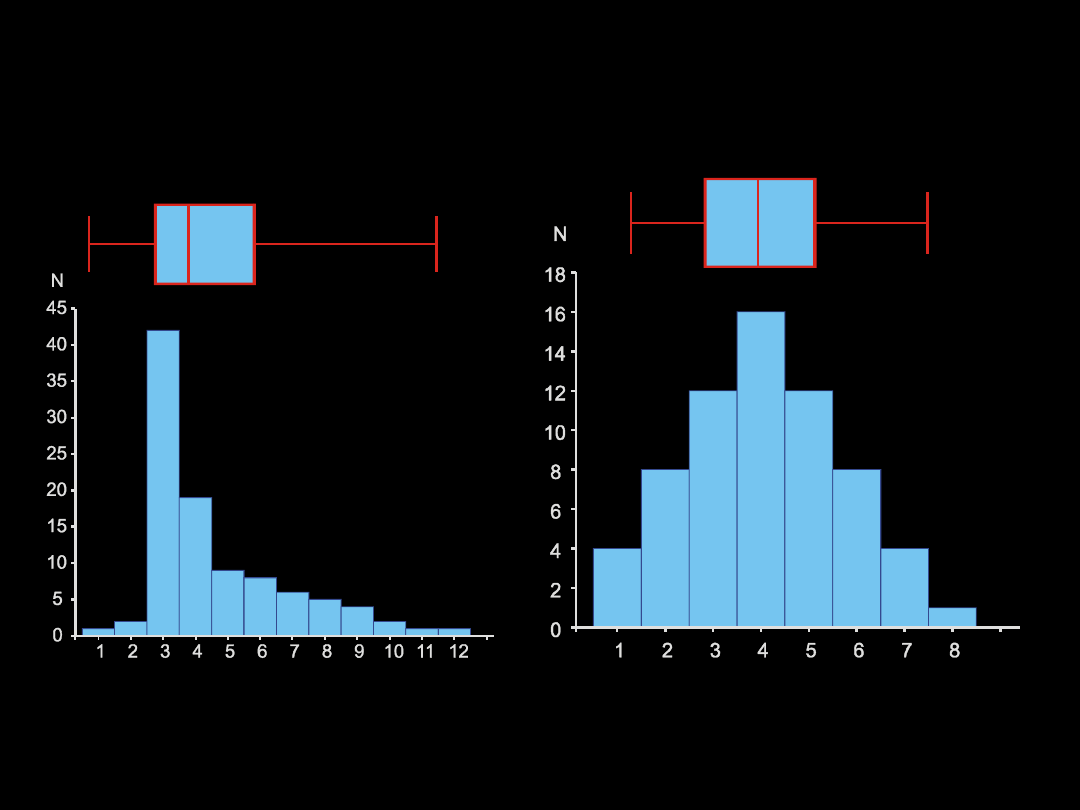
Skośność = 1,30
Rozkład prawoskośny
Rozkład symetryczny
Skośność = 0,11
Wykres ramkowy
